Nearly assumptionless screening for the mutually-exciting multivariate Hawkes process

Abstract

We consider the task of learning the structure of the graph underlying a mutually-exciting multivariate Hawkes process in the high-dimensional setting. We propose a simple and computationally inexpensive edge screening approach. Under a subset of the assumptions required for penalized estimation approaches to recover the graph, this edge screening approach has the sure screening property: with high probability, the screened edge set is a superset of the true edge set. Furthermore, the screened edge set is relatively small. We illustrate the performance of this new edge screening approach in simulation studies.

1. Introduction

1.1. Overview of the multivariate Hawkes process

In a seminal paper, Hawkes (1971) proposed the multivariate Hawkes process, a multivariate point process model in which a past event may trigger the occurrence of future events. The Hawkes process and its variants have been widely applied to model recurrent events, with notable applications in modeling earthquakes (Ogata, 1988), crime rates (Mohler et al., 2011), interactions in social networks (Simma and Jordan, 2012; Perry and Wolfe, 2013; Zhou, Zha and Song, 2013a,b), financial events (Chavez-Demoulin, Davison and McNeil, 2005; Bowsher, 2007; Aït-Sahalia, Cacho-Diaz and Laeven, 2015), and spiking histories of neurons (see e.g., Brillinger, 1988; Okatan, Wilson and Brown, 2005; Paninski, Pillow and Lewi, 2007; Pillow et al., 2008).

In this section, we provide a very brief review of the multivariate Hawkes process. A more comprehensive discussion can be found in Liniger (2009) and Zhu (2013).

Following Brémaud and Massoulié (1996), we define a simple point process N on ℝ⁺ as a family {N(A)}_{A∈ℬ(ℝ⁺)} taking integer values (including positive infinity), where ℬ(ℝ⁺) denotes the Borel σ-algebra of the positive half of the real line. Further let t₁, t₂, … ∈ ℝ⁺ be the event times of N. In this notation, N(A) = Σ_i 𝟙_[ti∈A] for A ∈ ℬ(ℝ⁺). We write N ([t, t + dt)) as dN(t), where dt denotes an arbitrary small increment of t. Let ℋ_t be the history of N up to time t. Then the ℋ_t-predictable intensity process of N is defined as

$$\lambda (t)\mathrm{d}t=\mathbb{P}(\mathrm{d}N(t)=1/{\mathscr{H}}_t).$$ (1)

Now suppose that N is a marked point process, in which each event time t_i is associated with a mark m_i ∈ {1, …, p} (see e.g., Definition 6.4.I. in Daley and Vere-Jones, 2003). We can then view N as a multivariate point process (N_j)_j=1,…,p, of which the jth component process is given by N_j(A) = Σ_i 𝟙[_ti∈A,mi=j] for A ∈ ℬ(ℝ⁺). To simplify the notation, we let t_j,1, t_j,2, … ∈ ℝ⁺ denote the event times of N_j.

The intensity of the jth component process is

$${\lambda }_j(t)\mathrm{d}t=\mathbb{P}(\mathrm{d}{N}_j(t)=1\mid {\mathcal{H}}_t).$$

In the case of the linear Hawkes process, this function takes the form (Brémaud and Massoulié, 1996; Hansen, Reynaud-Bouret and Rivoirard, 2015)

$${\lambda }_j(t)={\mu }_j+\sum _{k=1}^p\left(\sum _{i:t_{k,i}\le t}{\omega }_{j,k}(t-t_{k,i})\right).$$ (2)

We refer to μ_j ∈ ℝ as the background intensity, and ω_j,k(·): ℝ⁺ ↦ ℝ as the transfer function.

For p fixed, Brémaud and Massoulié (1996) established that the linear Hawkes process with intensity function (2) is stationary given the following assumption.

Assumption 1

Let Ω be a p × p matrix whose entries are ${\mathrm{\Omega }}_{j,k}={\int }_0^{\infty }\mid {\omega }_{j,k}(\mathrm{\Delta })\mid \mathrm{d}\mathrm{\Delta }$, for j, k = 1, …, p. We assume that the spectral norm of Ω is strictly less than 1, i.e., Γ_max(Ω) ≤ γ_Ω < 1, where γ_ω is a generic constant.

We now define a directed graph with node set {1, …, p} and edge set

$$\mathcal{E}\equiv \{(j,k):{\omega }_{j,k}\ne 0,1\le j,k\le p\},$$ (3)

for ω_j,k given in (2). Let

$$s\equiv \underset{1\le j\le p}{max}\sum _{k=1}^p{𝟙}_{\{(j,k)\in \mathcal{E}\}}$$ (4)

denote the maximum in-degree of the nodes in the graph. In this paper, we propose a simple screening procedure that can be used to obtain a small superset of the edge set ℰ.

1.2. Estimation and theory for the Hawkes process

We first consider the low-dimensional setting, in which the dimension of the process, p, is fixed, and T, the time period during which the point process is observed, is allowed to grow. In this setting, asymptotic properties such as the central limit theorem have been established; for instance, see Bacry et al. (2013) and Zhu (2013). Consequently, estimating the edge set ℰ is straightforward in low dimensions.

In high dimensions, when p might be large, we can fit the Hawkes process model using a penalized estimator of the form

$$\underset{{\omega }_{j,k}\in \mathcal{F},1\le j,k\le p}{\text{minimize}}\mathcal{L}({\omega }_{j,k};{\{N_j\}}_{j=1}^p)+\lambda \sum _{j,k}\mathcal{P}({\omega }_{j,k};{\{N_j\}}_{j=1}^p),$$ (5)

where $\mathcal{L}(·;{\{N_j\}}_{j=1}^p)$ is a loss function, based on, e.g., the log-likelihood (Bacry, Gaïffas and Muzy, 2015) or least squares (Hansen, Reynaud-Bouret and Rivoirard, 2015); $\mathcal{P}(·;{\{N_j\}}_{j=1}^p)$ is a penalty function, such as the lasso (Hansen, Reynaud-Bouret and Rivoirard, 2015); λ is a nonnegative tuning parameter; and ℱ is a suitable function class. Then, a natural estimator for ℰ is {(j, k): ω̂_j,k ≠ 0}.

Recently, Reynaud-Bouret and Schbath (2010), Bacry, Gaïffas and Muzy (2015), and Hansen, Reynaud-Bouret and Rivoirard (2015) have established that under certain assumptions, penalized estimation approaches of the form (5) are consistent in high dimensions, provided that the edge set ℰ is sparse. For instance, Hansen, Reynaud-Bouret and Rivoirard (2015) establish the oracle inequality of the lasso estimator for the Hawkes process, given that certain conditions hold on the observed event times. However, to show that these conditions hold with high probability for arbitrary samples, these theoretical results require that the point process is mutually-exciting — that is, an event in one component process can increase, but cannot decrease, the probability of an event in another component process. This amounts to assuming that ω_j,k(Δ) ≥ 0 for all Δ ≥ 0, for ω_j,k defined in (1).

When the dimension p is large, penalized estimation procedures of the form (5) (Bacry, Gaïffas and Muzy, 2015; Hansen, Reynaud-Bouret and Rivoirard, 2015) become computationally expensive: they require 𝒪(Tp²) operations per iteration in an iterative algorithm. This is problematic in contemporary applications, in which p can be on the order of tens of thousands (Ahrens et al., 2013). These concerns motivate us to propose a simple and computationally-efficient edge screening procedure for estimating the true edge set ℰ in high dimensions. Under very few assumptions, our proposed screening procedure is guaranteed to select a small superset of the true edge set ℰ.

1.3. Organization of paper

The rest of this paper proceeds as follows. In Section 2, we introduce our screening procedure for estimating the edge set ℰ, and establish its theoretical properties. We present simulation results in support of our proposed procedure in Section 3. Proofs of theoretical results are presented in Section 4, and the Discussion is in Section 5.

2. An edge screening procedure

2.1. Approach

For j = 1, …, p, let Λ_j denote the mean intensity of the jth point process introduced in Section 1. That is,

$${\mathrm{\Lambda }}_j\equiv \mathbb{E}[\mathrm{d}{N}_j(t)]/\mathrm{d}t.$$ (6)

Following Equation 5 of Hawkes (1971), for any Δ ∈ ℝ, the (infinitesimal) cross-covariance of the jth and kth processes is defined as

$$V_{j,k}(\mathrm{\Delta })\equiv \{\begin{array}{ll}\mathbb{E}[\mathrm{d}{N}_j(t)\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}td(t-\mathrm{\Delta })\}-{\mathrm{\Lambda }}_j{\mathrm{\Lambda }}_k\hfill & j\ne k\hfill \\ \mathbb{E}[\mathrm{d}{N}_k(t)\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}t\mathrm{d}(t-\mathrm{\Delta })\}-{\mathrm{\Lambda }}_k^2-{\mathrm{\Lambda }}_k\delta (\mathrm{\Delta })\hfill & j=k\hfill \end{array},$$ (7)

where δ(·) is the Dirac delta function, which satisfies ${\int }_{-\infty }^{\infty }\delta (x)\mathrm{d}x=1$ and δ(x) = 0 for x ≠ 0.

For a given value of Δ, we can estimate the cross-covariance function V_j,k(Δ) using kernel smoothing:

$${\widehat{V}}_{j,k}(\mathrm{\Delta })=\{\begin{array}{ll}\frac{1}{Th}{\iint }_{{[0,T]}^2}K\left(\frac{(t^{\prime }-t)+\mathrm{\Delta }}{h}\right)\mathrm{d}{N}_j(t)\mathrm{d}{N}_k(t^{\prime })-\frac{1}{T^2}{N}_j([0,T])N_k([0,T])\hfill & j\ne k\hfill \\ \frac{1}{Th}{\iint }_{{[0,T]}^2\backslash \{t=t^{\prime }\}}K\left(\frac{(t^{\prime }-t)+\mathrm{\Delta }}{h}\right)\mathrm{d}{N}_k(t)\mathrm{d}{N}_k(t^{\prime })-\frac{1}{T^2}{N}_k^2([0,T])\hfill & j=k\hfill \end{array},$$ (8)

where K(·) is a kernel function with bandwidth h, and ${\int }_0^{T}f(t)\mathrm{d}{N}_j(t)$ is the Stieltjes integral, defined as

$${\int }_0^{T}f(t)\mathrm{d}{N}_j(t)\equiv \sum _{i:t_{j,i}\in [0,T]}f(t_{j,i}).$$

In this paper, we focus on kernel functions that are bounded by 1 and are defined on a bounded support, i.e., 0 ≤ K(x/h) ≤ 1 for x ∈ [−h, h], and K(x/h) = 0 for x ∉ [−h, h] (e.g., the Epanechnikov kernel).

Let B denote a tuning parameter that defines the time range of interest for V_j,k(Δ), i.e. Δ ∈ [−B, B]. For any ζ, we define the set of screened edges as

$$\widehat{\mathcal{E}}(\zeta )\equiv \{(j,k):{\Vert {\widehat{V}}_{j,k}\Vert }_{2,[-B,B]}>\zeta \},$$ (9)

where ${\Vert f\Vert }_{2,[l,u]}\equiv {\{{\int }_l^u{f}^2(t)\mathrm{d}t\}}^{1/2}$ is the ℓ₂-norm of a function f on the interval [l, u].

The screened edge set ℰ̂(ζ) in (9) can be calculated quickly: ||V̂_j,k||_2,[−B,B] can be calculated in 𝒪(T) computations, and so ℰ̂(ζ) can be calculated in 𝒪(Tp²) computations. The procedure can be easily parallellized.

There are three tuning parameters in the procedure: the bandwidth h in (8), the range B in (9), and the screening threshold ζ in (9). The bandwidth h can be chosen by cross-validation. The range B can be selected based on the problem setting. For instance, when using the multivariate Hawkes process to model a spike train data set in neuroscience, we can set B to equal the maximum time gap between a spike and the spike it can possibly evoke. The choice of screening threshold ζ can be determined based on the sparsity level that we expect based on our prior knowledge. Alternatively, we may wish to use a small value of ζ in order to reduce the chance of false negative edges in ℰ̂(ζ), or a larger value due to limited computational resources in our downstream analysis.

2.2. Theoretical results

We consider the asymptotics of triangular arrays (Greenshtein and Ritov, 2004), where the dimension p is allowed to grow with T. When unrestricted, it is possible to cook up extreme networks, where, for instance, the mean intensity Λ_j in (6) diverges to infinity. To avoid such cases, we pose the following regularity assumption.

Assumption 2

There exist positive constants Λ_min, Λ_max, and V_max such that 0 < Λ_min ≤ Λ_j ≤ Λ_max and max_Δ∈ℝ |V_j,k(Δ)| ≤ V_max for all 1 ≤ j, k ≤ p, where Λ_j and V_j,k are defined in (6) and (7), respectively. Furthermore, Λ_min, Λ_max, and V_max are generic constants that do not depend on p.

Next, we make some standard assumptions on the transfer functions ω_j,k in (2).

Assumption 3

The following hold:

1. The transfer functions are non-negative: ω_j,k(Δ) ≥ 0 for all Δ ≥ 0.

2. There exists a positive constant β_min such that

   $$\underset{(j,k):{\omega }_{j,k}\ne 0}{min}\left({\int }_0^{\infty }{\omega }_{j,k}^2(\mathrm{\Delta })\mathrm{d}\mathrm{\Delta }\right)\ge {\beta }_{min}^2.$$

3. There exist positive constants b, θ₀, and C such that, for all 1 ≤ j, k ≤ p, and for any Δ₁, Δ₂ ∈ ℝ, supp(ω_j,k) ⊂ (0, b], max_Δ |ω_j,k(Δ)| ≤ C, and |ω_j,k(Δ₁) − ω_j,k(Δ₂)| ≤ θ₀|Δ₁ − Δ₂|.

Assumption 3(a) guarantees that the multivariate Hawkes process is mutually-exciting: that is, an event may trigger (but cannot inhibit) future events. This assumption is shared by the original proposal of Hawkes (1971). Furthermore, existing theory for penalized estimators for the Hawkes process requires this assumption (Bacry, Gaïffas and Muzy, 2015; Hansen, Reynaud-Bouret and Rivoirard, 2015).

Assumption 3(b) guarantees that the non-zero transfer functions are nonnegligible. Such an assumption is needed in order to establish variable selection consistency (Bühlmann and van de Geer, 2011; Wainwright, 2009) for the penalized estimator (5).

Assumption 3(c) guarantees that the transfer functions are sufficiently smooth; this guarantees that the cross-covariances are smooth (see Section A.2 in Appendix), and hence can be estimated using a kernel smoother (8). Instead of Assumption 3(c), we could assume that ω_j,k is an exponential function (Bacry, Gaïffas and Muzy, 2015) or that it is well-approximated by a set of smooth basis functions (Hansen, Reynaud-Bouret and Rivoirard, 2015).

Recall that s was defined in (4). We now state our main result.

Theorem 1

Suppose that the Hawkes process (2) satisfies Assumptions 1–3. Let h = c₁s^−1/2T^−1/6 in(8) and ζ = 2c₂s^1/2T^−1/6 in (9) for some constants c₁ and c₂. Then, for some positive constants c₃ and c₄, with probability at least 1 − c₃T^7/6s^1/2p² exp(−c₄T^1/6),

1. ℰ ⊂ ℰ̂(ζ);

2. $\mathit{card}\left(\widehat{\mathcal{E}}(\zeta )\right)=\mathcal{O}\left(\mathit{card}(\mathcal{E})s^{-1}{T}^{1/3}{\gamma }_{\mathrm{\Omega }}{(1-{\gamma }_{\mathrm{\Omega }})}^{-2}{\mathrm{\Lambda }}_{max}^2\right)$.

Theorem 1(a) guarantees that, with high probability, the screened edge set ℰ̂(ζ) contains the true edge set ℰ. Therefore, screening does not result in false negatives. This is referred to as the sure screening property in the literature (Fan and Lv, 2008; Fan, Samworth and Wu, 2009; Fan and Song, 2010; Fan, Feng and Song, 2011; Fan, Ma and Dai, 2014; Liu, Li and Wu, 2014; Song et al., 2014; Luo, Song and Witten, 2014). Typically, establishing the sure screening property requires assuming that the marginal association between a pair of nodes in ℰ is sufficiently large; see e.g. Condition 3 in Fan and Lv (2008) and Condition C in Fan, Feng and Song (2011). In contrast, Theorem 1(a) requires only that the conditional association between a pair of nodes in ℰ is sufficiently large; see Assumption 3(b).

Theorem 1(b) guarantees that ℰ̂(ζ) is a relatively small set, on the order of 𝒪(card(ℰ)s⁻¹T^1/3). Suppose that p² ∝ s^−1/2 exp(c₄T^1/6−ε) for some positive constant ε < 1/6; this is the high-dimensional regime, in which the probability statement in Theorem 1 converges to one. Then the size of ℰ̂(ζ), 𝒪(card(ℰ)s⁻¹T^1/3), can be much smaller than p², the total number of node pairs. We note that the rate of T^1/3 is comparable to existing results for non-parametric screening in the literature (see e.g., Fan, Feng and Song 2011; Fan, Ma and Dai 2014).

To summarize, Theorem 1 guarantees that under a small subset of the assumptions required for penalized estimation methods to recover the edge set ℰ, the screened edge set ℰ̂(ζ) (9) is small and contains no false negatives. We note that this is not the case for other types of models. For instance, in the case of the Gaussian graphical model, Luo, Song and Witten (2014) considered estimating the conditional dependence graph by screening the marginal covariances. In order for this procedure to have the sure screening property, one must make an assumption on the minimum marginal covariance associated with an edge in the graph, which is not required for variable selection consistency of penalized estimators (Cai, Liu and Luo, 2011; Luo, Song and Witten, 2014; Ravikumar et al., 2011; Saegusa and Shojaie, 2016).

It is important to note that Theorem 1 considers an oracle procedure, where the tuning parameters depend on unknown parameters. The heuristic selection guidelines suggested at the end of Section 2.1 may not satisfy the requirements of Theorem 1. We leave the discussion of optimal tuning parameter selection criteria for future research. Also, note that the bandwidth h ∝ T^−1/6 is wider than the typical bandwidth for kernel smoothing, which is T^−1/3 (Tsybakov, 2009). This is because we aim to minimize a concentration bound on V̂_j,k − V_j,k (see the proof of Lemma 3 in the Appendix), rather than the usual mean integrated square error as in, e.g., Theorem 1.1 in Tsybakov (2009).

Remark 1

In light of Theorem 1, consider applying a constraint induced by ℰ̂(ζ) to (5):

$$\underset{{\omega }_{j,k}\in \mathcal{F},1\le j,k\le p}{\mathit{minimize}}\mathcal{L}({\omega }_{j,k};{\{N_j\}}_{j=1}^p)+\lambda \sum _{j,k}\mathcal{P}({\omega }_{j,k};{\{N_j\}}_{j=1}^p)\mathit{subject}to{\omega }_{j,k}=0\mathit{for}(j,k)\notin \widehat{\mathcal{E}}(\zeta ).$$ (10)

Theorem 1 can be combined with existing results on consistency of penalized estimators of the Hawkes process (Bacry, Gaïffas and Muzy, 2015; Hansen, Reynaud-Bouret and Rivoirard, 2015) in order to establish that (10) results in consistent estimation of the transfer functions ω_j,k. As a concrete example, Hansen, Reynaud-Bouret and Rivoirard (2015) considered (10) with $\mathcal{L}({\omega }_{j,k};{\{N_j\}}_{j=1}^p)$ taken to be the least-squares loss, and $\mathcal{P}({\omega }_{j,k};{\{N_j\}}_{j=1}^p)$ a lasso-type penalty. Our simulation experiments in Section 3 indicate that in this setting, (10) can actually have better small-sample performance than (5) when p is very large. Furthermore, solving (10) can be much faster than solving (5): the former requires 𝒪(T^4/3s⁻¹card(ℰ)) computations per iteration, compared to 𝒪(Tp²) per iteration for the latter (using e.g. coordinate descent, Friedman, Hastie and Tibshirani, 2010). In the high-dimensional regime when p² ∝ s^−1/2 exp(c₄T^1/6−ε) for some positive constant ε < 1/6, we have that T^4/3s⁻¹card(ℰ) ≪ Tp². We note that in order to solve (10), we must first compute ℰ̂(ζ), which requires an additional one-time computational cost of 𝒪(Tp²).

3. Simulation

3.1. Simulation set-up

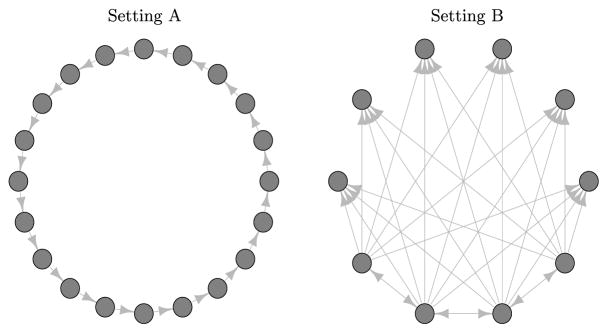
In this section, we investigate the performance of our screening procedure in a simulation study with p = 100 point processes. Intensity functions are given by (2), with μ_j = 0.75 for j = 1, …, p, and ω_j,k(t) = 2t exp(1 − 5t) for (j, k) ∈ ℰ. By definition, ω_j,k = 0 for all (j, k) ∉ ℰ. We consider two settings for the edge set ℰ, Setting A and Setting B. These settings are displayed in Figure 1.

Fig 1.

Left: In Setting A, the edge set ℰ is composed of 5 connected components, each of which is a chain graph containing 20 nodes. Right: In Setting B, ℰ is composed of 10 connected components, each of which contains 10 nodes.

In what follows, it will be useful to think about the (undirected) node pairs as belonging to three types. (i) We let

$$\stackrel{\sim }{\mathcal{E}}\equiv \{(j,k):(j,k)\in \mathcal{E}\text{or}(k,j)\in \mathcal{E}\}.$$ (11)

(ii) With a slight abuse of notation, we will use ℰ̃^c ∩ supp(V) to denote node pairs that are not in ℰ̃ with non-zero population cross-covariance, defined in (7). (iii) Continuing to slightly abuse notation, we will use ℰ̃^c\supp(V) to denote node pairs that are not in ℰ̃ and that have zero population cross-covariance.

Throughout the simulation, we set the bandwidth h in (8) to equal T^−1/6, and the range of interest B in (9) to equal 5. Thus, h satisfies the requirements of Theorem 1, and [−B, B] covers the majority of the mass of the transfer function ω_j,k. However, these simulation results are not sensitive to the particular choices of h or B.

3.2. Investigation of the estimated cross-covariances

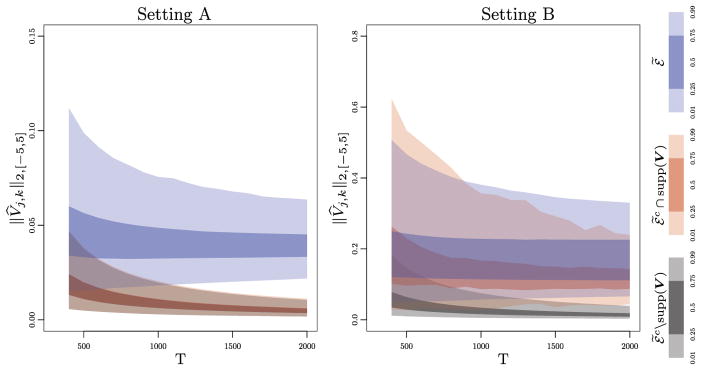
In Setting A, within a single connected component, all of the node pairs that are not in ℰ̃ are in ℰ̃^c ∩ supp(V). However, for the most part, the population cross-covariances corresponding to node pairs in ℰ̃^c ∩ supp(V) are quite small, because they are induced by paths of length two and greater. This can be seen from the left-hand panel of Figure 2. Given the left-hand panel of Figure 2, we expect the proposed screening procedure to work very well in Setting A: for a sufficiently large value of the time period T, there exists a value of ζ such that, with high probability, ℰ̂(ζ) = ℰ̃.

Fig. 2.

The quantiles of ||V̂_jk||_2,[−5,5] are displayed, for node pairs in ℰ̃ (11), ℰ̃^c∩ supp(V), and ℰ̃^c\supp(V), as a function of the time period T. Left: Results for Setting A. The estimated cross-covariances of node pairs in ℰ̃^c\supp(V) and ℰ̃^c ∩ supp(V) overlap. Center: Results for Setting B. The estimated cross-covariances of node pairs in ℰ̃ and ℰ̃^c ∩ supp(V) overlap. Right: The color legend is displayed.

In Setting B, six nodes receive directed edges from the same set of four nodes. Therefore, we expect the pairs among these six nodes to be in the set ℰ̃^c ∩ supp(V), and to have substantial population cross-covariances. This intuition is supported by the center panel of Figure 2, which indicates that the node pairs in ℰ̃^c ∩ supp(V) have relatively large estimated cross-covariances, on the same order as the node pairs in ℰ̃. In light of Figure 2, we anticipate that for a sufficiently large value of the time period T, the screened edge set ℰ̂(ζ) will contain the edges in ℰ̃ as well as many of the edges in ℰ̃^c ∩ supp(V).

3.3. Size of smallest screened edge set

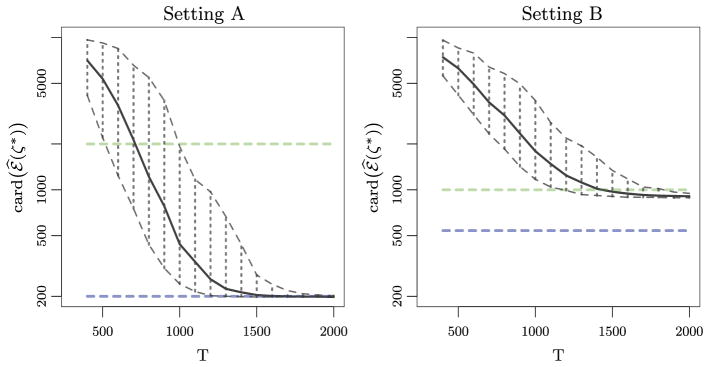
We now define ζ^* ≡ max {ζ : ℰ ⊆ ℰ̂(ζ)}, and calculate card(ℰ̂(ζ^*)). This represents the size of the smallest screened edge set that contains the true edge set.

Results, averaged over 200 simulated data sets, are shown in Figure 3.

Fig. 3.

For each of 200 simulated data sets, we calculated card(ℰ̂(ζ^*)), where ζ^* ≡ max {ζ : ℰ ⊆ ℰ̂(ζ)}, as a function of the time period T. The curves represent the mean of card(ℰ̂(ζ^*)) ( ); the 2.5% and 97.5% quantiles of card(ℰ̂(ζ^*)) ( ); card(ℰ̃) ( ); and card(supp(V)) ( ). Left: Data generated under Setting A. Right: Data generated under Setting B.

We see that in Setting A, for sufficiently large T, card(ℰ̂(ζ^*)) = card(ℰ̃), which implies that ℰ̂(ζ^*) = ℰ̃. In other words, in Setting A, the screening procedure yields perfect recovery of the set ℰ̃ (11). This is in line with our intuition based on the left-hand panel of Figure 2.

In contrast, in Setting B, even when T is very large, card(ℰ̂(ζ^*)) > card(ℰ̃), which implies that ℰ̂(ζ^*) ⊇ ℰ̃. This was expected based on the center panel of Figure 2.

3.4. Performance of constrained penalized estimation

We now consider the performance of the estimator (10), which we obtain by calculating the screened edge set ℰ̂(ζ), and then performing a penalized regression subject to the constraint that ω_jk = 0 for (j, k) ∉ ℰ̂(ζ). Note that rather than assuming a specific functional form for ω_j,k, Hansen, Reynaud-Bouret and Rivoirard (2015) use a basis expansion to estimate ω_j,k. Following their lead, we use a basis of step functions, of the form 𝟙_{((m−1)/2,m/2]}(t) for m = 1, …, 6. Instead of applying a lasso penalty to the basis function coefficients (Hansen, Reynaud-Bouret and Rivoirard, 2015), we employ a group lasso penalty for every 1 ≤ j, k ≤ p (Yuan and Lin, 2006; Simon and Tibshirani, 2012). Thus, (10) consists of a squared error loss function and a group lasso penalty. We let

$${\widehat{\mathcal{E}}}_{\mathcal{P}}\equiv \{(j,k):\exists \mathrm{\Delta }\text{s.t.}{\widehat{\omega }}_{j,k}(\mathrm{\Delta })\ne 0\},$$ (12)

where ω̂_j,k solves (10).

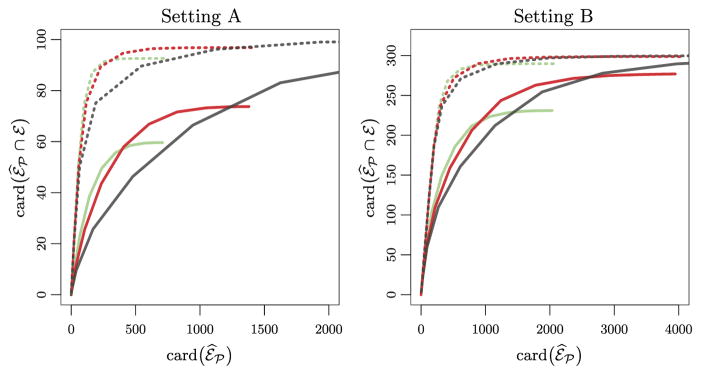
Results are shown in Figure 4. In Setting A, solving the constrained optimization problem (10) leads to substantially better performance than solving the unconstrained problem (5). The improvement is especially noticeable when T is small. In Setting B, solving the constrained optimization problem (10) leads to only a slight improvement in performance relative to solving the unconstrained problem (5), since, as we have learned from Figures 2 and 3, the screened set ℰ̂(ζ) contains many edges in ℰ̃^c ∩ supp(V). In both settings, solving the constrained optimization problem leads to substantial computational improvements.

Fig. 4.

The constrained penalized optimization problem (10) was performed, for a range of values of the tuning parameter λ. The x-axis displays the size of the estimated edge set ℰ̂_℘ (12), and the y-axis displays the number of true positives, averaged over 200 simulated data sets. The curves represent performance when ζ is chosen to yield card(ℰ̂(ζ)) = 4card(ℰ̃) (T = 300 [ ]and T = 600 [ ]), and when ζ is chosen to yield card(ℰ̂(ζ)) = 8card(ℰ̃) (T = 300 [ ] and T = 600 [ ]). We also display performance of the unconstrained penalized optimization problem (5) (T = 300 [ ] and T = 600 [ ]).

4. Proofs of theoretical results

In this section, we prove Theorem 1. In Section 4.1, we review an important property of the Hawkes process, the Wiener-Hopf integral equation. In Section 4.2, we list three technical lemmas used in the proof of Theorem 1. Theorem 1 is proved in Section 4.3. Proofs of the technical lemmas are provided in the Appendix.

4.1. The Wiener-Hopf integral equation

Recall that the transfer functions ω = {ω_j,k}_1≤j,k≤p were defined in (2), the cross-covariances V = {V_j,k}_1≤j,k≤p were defined in (7), and the mean intensities Λ = (Λ₁, …, Λ_p)^T were defined in (6). If the Hawkes process defined in (2) is stationary, then for any Δ ∈ ℝ⁺,

$$\mathit{V}(\mathrm{\Delta })=\mathit{\omega }(\mathrm{\Delta })\text{diag}(\mathbf{\Lambda })+(\mathit{\omega }\ast \mathit{V})(\mathrm{\Delta }),$$ (13)

where

$${[\mathit{\omega }\ast \mathit{V}]}_{j,k}(\mathrm{\Delta })\equiv \sum _{l=1}^p[{\omega }_{j,l}\ast V_{l,k}](\mathrm{\Delta })$$

and

$$[{\omega }_{j,l}\ast V_{l,k}](\mathrm{\Delta })\equiv {\int }_0^{\infty }{\omega }_{j,l}({\mathrm{\Delta }}^{\prime })V_{l,k}(\mathrm{\Delta }-{\mathrm{\Delta }}^{\prime })\mathrm{d}{\mathrm{\Delta }}^{\prime }.$$

Equation (13) belongs to a class of integral equations known as the Wiener-Hopf integral equations.

4.2. Technical lemmas

We state three lemmas used to prove Theorem 1, and provide their proofs in the Appendix. The following lemma is a direct consequence of (13) and our assumptions. Recall that [0, b] is a superset of supp(ω_j,k) introduced in Assumption 3.

Lemma 1

Under Assumptions 1–3, for sufficiently large B such that B ≥ b, we have that ||V_j,k||_2,[−B,B] ≥ β_minΛ_min for (j, k) ∈ ℰ.

The next lemma shows that the cross-covariance is Lipschitz continuous given the smoothness assumption on ω_j,k (Assumption 3(c)). We will use this lemma in the proof of Theorem 1, in order to bound the bias of the kernel smoothing estimator (8). Recall that s, the maximum node in-degree, was defined in (4).

Lemma 2

Under Assumptions 1–3, the cross-covariance function is Lipschitz for 1 ≤ j, k ≤ p. More specifically, there exists some θ₁ > 0 such that |V_j,k(x) − V_j,k(y)| ≤ θ₁s|x − y| for any x, y ∈ ℝ.

Recall that the bandwidth h was defined in (8). The following concentration inequality holds on the estimated cross-covariance.

Lemma 3

Suppose that Assumptions 1–3 hold, and let h = c₁s^−1/2T^−1/6 for some constant c₁. Then

$$\mathbb{P}\left(\underset{1\le j\le k\le p}{\cap }\left[{\Vert {\widehat{V}}_{j,k}-V_{j,k}\Vert }_{2,[-B,B]}\le c_2{s}^{1/2}{T}^{-1/6}\right]\right)\ge 1-c_3{s}^{1/2}{T}^{7/6}{p}^2{e}^{-c_4{T}^{1/6}}.$$

4.3. Proof of Theorem 1

Proof

In what follows, we will consider the event

$$\mathcal{M}\equiv \left\{{\Vert {\widehat{V}}_{j,k}-V_{j,k}\Vert }_{2,[-B,B]}\le c_2{s}^{1/2}{T}^{-1/6}\text{for}\text{all}1\le j,k\le p\right\}.$$

We will first show that part (b) of Theorem 1 holds. From the Wiener-Hopf equation, (13), for each (j, k), we can write

$$V_{j,k}={\omega }_{j,k}{\mathrm{\Lambda }}_k+{\mathit{\omega }}_{j,·}\ast {\mathit{V}}_{·,k}.$$ (14)

We thus have

$$\begin{array}{l}{\Vert V_{j,k}\Vert }_{2,(-\infty ,\infty )}\le {\mathrm{\Lambda }}_k{\Vert {\omega }_{j,k}\Vert }_{2,(-\infty ,\infty )}+{\Vert {\mathit{\omega }}_{j,·}\ast {\mathit{V}}_{·,k}\Vert }_{2,(-\infty ,\infty )}\\ \le {\mathrm{\Lambda }}_k{\Vert {\omega }_{j,k}\Vert }_{2,(-\infty ,\infty )}+\sum _{l=1}^p{\Vert {\omega }_{j,l}\ast V_{l,k}\Vert }_{2,(-\infty ,\infty )}\\ \le {\mathrm{\Lambda }}_k{\Vert {\omega }_{j,k}\Vert }_{2,(-\infty ,\infty )}+\sum _{l=1}^p\left({\int }_{-\infty }^{\infty }\mid {\omega }_{j,l}(\mathrm{\Delta })\mid \mathrm{d}\mathrm{\Delta }\right){\Vert V_{l,k}\Vert }_{2,(-\infty ,\infty )},\end{array}$$ (15)

where the last inequality follows from Young’s inequality (see e.g., Theorem 3.9.4 in Bogachev (2007)), which takes the form

$${\Vert f\ast g\Vert }_{r,(-\infty ,\infty )}\le {\Vert f\Vert }_{p,(-\infty ,\infty )}{\Vert g\Vert }_{q,(-\infty ,\infty )},\frac{1}{p}+\frac{1}{q}=\frac{1}{r}+1,$$ (16)

with ${\Vert f\Vert }_{p,(-\infty ,\infty )}\equiv {[{\int }_{-\infty }^{\infty }{\mid f(x)\mid }^p\mathrm{d}x]}^{1/p}$. Here, we let r = q = 2, p = 1, f = ω_j,l, and g = V_l,k.

From Assumption 3(c), we know that ω_j,k is bounded by C. Therefore, by the Cauchy-Schwartz inequality,

$$\Vert {\omega }_{j,k}{\Vert }_{2,ℝ}={\left\{{\int }_{-\infty }^{\infty }{\omega }_{j,k}^2(\mathrm{\Delta })\mathrm{d}\mathrm{\Delta }\right\}}^{1/2}\le {\left\{{\int }_{-\infty }^{\infty }C\mid {\omega }_{j,k}(\mathrm{\Delta })\mid \mathrm{d}\mathrm{\Delta }\right\}}^{1/2}=C^{1/2}{\mathrm{\Omega }}_{j,k}^{1/2}.$$

Using (15) and letting V̄_j,k ≡ ||V_j,k||_{2,(−∞,∞)}, we get

$${\overline{V}}_{j,k}\le C^{1/2}{\mathrm{\Omega }}_{j,k}^{1/2}{\mathrm{\Lambda }}_k+{\mathbf{\Omega }}_{j,·}·{\overline{\mathit{V}}}_{·,k}.$$ (17)

The ℓ₂-norm of the vector V̄_·,k can then be bounded using the triangle inequality,

$$\mid {\overline{\mathit{V}}}_{·,k}{\Vert }_2\le C^{1/2}{\mathrm{\Lambda }}_k{\left[\sum _{j=1}^p{\mathrm{\Omega }}_{j,k}\right]}^{1/2}+{\Vert \mathbf{\Omega }{\overline{\mathit{V}}}_{·,k}\Vert }_2.$$

Thus, by Assumption 1,

$${\Vert {\overline{\mathit{V}}}_{·,k}\Vert }_2\le C^{1/2}{\mathrm{\Lambda }}_k{\Vert {\mathbf{\Omega }}_{·,k}\Vert }_1^{1/2}+{\gamma }_{\mathrm{\Omega }}{\Vert {\overline{\mathit{V}}}_{·,k}\Vert }_2.$$

Rearranging the terms, and using the fact that γ_Ω < 1, gives

$${\Vert {\overline{\mathit{V}}}_{·,k}\Vert }_2\le C^{1/2}{(1-{\gamma }_{\mathrm{\Omega }})}^{-1}{\mathrm{\Lambda }}_{max}{\Vert {\mathbf{\Omega }}_{·,k}\Vert }_1^{1/2}.$$ (18)

Hence,

$$\sum _{j,k}{\overline{V}}_{j,k}^2=\sum _k{\Vert {\overline{\mathit{V}}}_{·,k}\Vert }_2^2\le C{(1-{\gamma }_{\mathrm{\Omega }})}^{-2}{\mathrm{\Lambda }}_{max}^2\sum _{k=1}^p{\Vert {\mathbf{\Omega }}_{·,k}\Vert }_1.$$ (19)

Now, recall that the number of non-zero elements in Ω is card(ℰ), and Ω_j,k ≤ γ_Ω. Thus, the inequality becomes

$$\sum _{j,k}{\overline{V}}_{j,k}^2\le C{(1-{\gamma }_{\mathrm{\Omega }})}^{-2}{\mathrm{\Lambda }}_{max}^2\text{card}(\mathcal{E}){\gamma }_{\mathrm{\Omega }}.$$ (20)

Hence, no more than $(C/c_2^2)\text{card}(\mathcal{E})s^{-1}{T}^{1/3}{\gamma }_{\mathrm{\Omega }}{(1-{\gamma }_{\mathrm{\Omega }})}^{-2}{\mathrm{\Lambda }}_{max}^2$ elements of V̄_j,k exceed c₂s^1/2T^−1/6. Recalling that V̄_j,k = ||V_j,k||_{2,(−∞,∞)}, this implies that no more than

$$(C/c_2^2)\text{card}(\mathcal{E})s^{-1}{T}^{1/3}{\gamma }_{\mathrm{\Omega }}{(1-{\gamma }_{\mathrm{\Omega }})}^{-2}{\mathrm{\Lambda }}_{max}^2$$

elements of ||V_j,k||_2,(−B,B) exceed c₂s^1/2T^−1/6.

Given the event ℳ, only edges in the set

$$\{(j,k):{\Vert V_{j,k}\Vert }_{2,[-B,B]}\ge c_2{s}^{1/2}{T}^{-1/6},1\le j,k\le p\}$$

can be contained in ℰ̂(ζ) for ζ = 2c₂s^1/2T^−1/6. This implies that the size of ℰ̂(ζ) is on the order of $(C/c_2^2)\text{card}(\mathcal{E})s^{-1}{T}^{1/3}{\gamma }_{\mathrm{\Omega }}{(1-{\gamma }_{\mathrm{\Omega }})}^{-2}{\mathrm{\Lambda }}_{max}^2$.

We now proceed to prove part (a) of Theorem 1. Lemma 1 states that ||V_j,k||_2,[−B,B] ≥ β_minΛ_min for (j, k) ∈ ℰ. If the event ℳ holds, then for T sufficiently large, ||V̂_j,k||_2,[−B,B] > 2c₂s^1/2T^−1/6 = ζ for (j, k) ∈ ℰ. Therefore, ℰ ⊂ ℰ̂(ζ).

Finally, Theorem 1 follows from the fact that, by Lemma 3, the event ℳ holds with probability at least 1 − c₃s^1/2T^7/6p² exp(−c₄T^1/6).

5. Discussion

In this paper, we have proposed a very simple procedure for screening the edge set in a multivariate Hawkes process. Provided that the process is mutually-exciting, we establish that this screening procedure can lead to a very small screened edge set, without incurring any false negatives. In fact, this result holds under a subset of the conditions required to establish model selection consistency of penalized regression estimators for the Hawkes process (Wainwright, 2009; Hansen, Reynaud-Bouret and Rivoirard, 2015). Therefore, this screening should always be performed whenever estimating the graph for a mutually-exciting Hawkes process.

The proposed screening procedure boils down to just screening pairs of nodes by thresholding an estimate of their cross-covariance. In fact, this approach is commonly taken within the neuroscience literature, with a goal of estimating the functional connectivity among a set of p neuronal spike trains (Okatan, Wilson and Brown, 2005; Pillow et al., 2008; Mishchencko, Vogelstein and Paninski, 2011; Berry et al., 2012). Therefore, this paper sheds light on the theoretical foundations for an approach that is often used in practice.

Appendix A: Technical proofs

A.1. Proof of Lemma 1

Proof

First, we observe that, if V_j,k is non-negative for all j and k, then ω_j,l*V_l,k is non-negative for any j, l, k. Under Assumption 1, we know that (13) holds. We can see from (13) that

$$V_{j,k}(\mathrm{\Delta })\ge {\omega }_{j,k}(\mathrm{\Delta }){\mathrm{\Lambda }}_k.$$

Therefore, we have

$${\Vert V_{j,k}(\mathrm{\Delta })\Vert }_{2,[-B,B]}\ge {\Vert {\omega }_{j,k}(\mathrm{\Delta })\Vert }_{2,[-B,B]}{\mathrm{\Lambda }}_{min}={\Vert {\omega }_{j,k}(\mathrm{\Delta })\Vert }_{2,[0,b]}{\mathrm{\Lambda }}_{min},$$ (21)

where the inequality follows from Assumption 2 and the equality holds since

$$\text{supp}({\omega }_{j,k})\subset (0,b]\subset [-B,B].$$

From Assumption 3(b), we have that ||V_j,k(Δ)||_2,[−B,B] ≥ β_minΛ_min for (j, k) ∈ ℰ.

We now show that the elements of V are non-negative, i.e., V_l,k(Δ) ≥ 0 for 1 ≤ l, k ≤ p, and Δ ∈ ℝ. Recall from the definition (7) in the main paper that

$$\begin{array}{l}{V}_{l,k}(\mathrm{\Delta })\equiv \mathbb{E}[\mathrm{d}{N}_l(t)\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}t\mathrm{d}(t-\mathrm{\Delta })\}-{\mathrm{\Lambda }}_l{\mathrm{\Lambda }}_k\\ \equiv \mathbb{E}[{\lambda }_l(t)\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}-{\mathrm{\Lambda }}_l{\mathrm{\Lambda }}_k,\end{array}$$ (22)

where the second equality follows from

$$\mathbb{E}[\mathrm{d}{N}_l(t)\mathrm{d}{N}_k(t-\mathrm{\Delta })]=\mathbb{E}[\mathbb{E}[\mathrm{d}{N}_l(t)\mid {\mathcal{H}}_t]\mathrm{d}{N}_k(t-\mathrm{\Delta })]=\mathbb{E}[{\lambda }_l(t)\mathrm{d}{N}_k(t-\mathrm{\Delta })]\mathrm{d}t.$$ (23)

In this proof, we use the Stieltjes integral to rewrite λ_l(t) in (2) as

$${\lambda }_l(t)={\mu }_l+\sum _{k=1}^p\left(\sum _{i:t_{k,i}\le t}{\omega }_{l,k}(t-t_{k,i})\right)={\mu }_l+\sum _{k=1}^p{\int }_0^{\infty }{\omega }_{l,k}(\mathrm{\Delta })\mathrm{d}{N}_k(t-\mathrm{\Delta }).$$ (24)

Plugging in λ_l(t) from (24) into (22) gives

$$\begin{array}{l}{V}_{l,k}(\mathrm{\Delta })=-{\mathrm{\Lambda }}_l{\mathrm{\Lambda }}_k+\mathbb{E}[{\mu }_l\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}\\ +\mathbb{E}\left[\sum _{m=1}^p{\int }_0^b{\omega }_{l,m}({\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })\right]/\{\mathrm{d}(t-\mathrm{\Delta })\}\\ =\sum _{m=1}^p{\int }_0^b{\omega }_{l,m}({\mathrm{\Delta }}^{\prime })\mathbb{E}[\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}\\ +\mathbb{E}[{\mu }_l\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}-{\mathrm{\Lambda }}_l\mathbb{E}[\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\},\end{array}$$

where we use the definition Λ_k = 𝔼[dN_k(t − Δ)]/{d(t − Δ)}.

Using the fact that (see e.g., Hawkes and Oakes (1974))

$${\mathrm{\Lambda }}_l={\mu }_l+\sum _{m=1}^p{\int }_0^b{\omega }_{l,m}({\mathrm{\Delta }}^{\prime })\mathrm{d}{\mathrm{\Delta }}^{\prime }{\mu }_m,$$

we have

$$\begin{array}{l}{V}_{l,k}(\mathrm{\Delta })=\sum _{m=1}^p{\int }_0^b{\omega }_{l,m}({\mathrm{\Delta }}^{\prime })\mathbb{E}[\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}\\ +\mathbb{E}[{\mu }_l\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}\\ -\left\{{\mu }_l+\sum _{m=1}^p{\int }_0^b{\omega }_{l,m}({\mathrm{\Delta }}^{\prime }){\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }\right\}\mathbb{E}[\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}\\ =\sum _{m=1}^p{\int }_0^b{\omega }_{l,m}({\mathrm{\Delta }}^{\prime })\mathbb{E}[\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}\\ -\sum _{m=1}^p{\int }_0^b{\omega }_{l,m}({\mathrm{\Delta }}^{\prime }){\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }\mathbb{E}[\mathrm{d}{N}_k(t-\mathrm{\Delta })]/\{\mathrm{d}(t-\mathrm{\Delta })\}.\end{array}$$

Rearranging the terms gives

$$V_{l,k}(\mathrm{\Delta })=\sum _{m=1}^p{\int }_0^b\frac{{\omega }_{l,m}({\mathrm{\Delta }}^{\prime })}{\mathrm{d}(t-\mathrm{\Delta })}\left\{\mathbb{E}[\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })]-\mathbb{E}[{\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }\mathrm{d}{N}_k(t-\mathrm{\Delta })]\right\}.$$ (25)

Next, we will rewrite (25) by taking the conditional expectation of dN_k or dN_m as in (23). Note here that, when Δ′ < Δ, we condition dN_m on the history up to t − Δ′, i.e., ℋ_{t − Δ′}. Given ℋ_{t − Δ′}, dN_k(t − Δ) is fixed since t − Δ < t − Δ′. When Δ′ > Δ, we condition dN_k on the history up to t − Δ. These cases are discussed separately in the following.

When Δ′ < Δ, for each integral of the summation, it holds that

$$\mathbb{E}\{\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })\}=\mathbb{E}\{{\lambda }_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{\mathrm{\Delta }}^{\prime }\mathrm{d}{N}_k(t-\mathrm{\Delta })\}.$$

From the definition of λ_m(t) in (2), we know that λ_m(t − Δ′) ≥ μ_m. Hence, in (25), if Δ′ < Δ, it holds that

$$\mathbb{E}\{\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })\}/\{\mathrm{d}(t-\mathrm{\Delta })\}-\mathbb{E}\{{\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }\mathrm{d}{N}_k(t-\mathrm{\Delta })\}/\{\mathrm{d}(t-\mathrm{\Delta })\}\ge 0.$$ (26)

On the other hand, when Δ′ ≥ Δ, we have

$$\begin{array}{l}\mathbb{E}\{\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })\}/\{\mathrm{d}(t-\mathrm{\Delta })\}-\mathbb{E}\{{\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }\mathrm{d}{N}_k(t-\mathrm{\Delta })\}/\{\mathrm{d}(t-\mathrm{\Delta })\}\\ =\mathbb{E}\{\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime }){\lambda }_k(t-\mathrm{\Delta })\}-\mathbb{E}\{{\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }{\lambda }_k(t-\mathrm{\Delta })\}\\ =\mathbb{E}\{\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime }){\lambda }_k(t-\mathrm{\Delta })\}-{\mu }_m{\mathrm{\Lambda }}_k\mathrm{d}{\mathrm{\Delta }}^{\prime }.\end{array}$$

Expanding λ_k and Λ_k yields

$$\begin{array}{l}\mathbb{E}\{\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime }){\lambda }_k(t-\mathrm{\Delta })\}-{\mu }_m{\mathrm{\Lambda }}_k\mathrm{d}{\mathrm{\Delta }}^{\prime }\\ =\mathbb{E}\{\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime }){\mu }_k\}+\sum _{i=1}^p{\int }_0^b{\omega }_{k,i}({\mathrm{\Delta }}^{″})\mathbb{E}[\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_i(t-\mathrm{\Delta }-{\mathrm{\Delta }}^{″})]\\ -{\mu }_m{\mu }_k\mathrm{d}{\mathrm{\Delta }}^{\prime }-\sum _{i=1}^p{\int }_0^b{\omega }_{k,i}({\mathrm{\Delta }}^{″})\mathrm{d}{\mathrm{\Delta }}^{″}{\mu }_i{\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }\\ =({\mathrm{\Lambda }}_m-{\mu }_m){\mu }_k\mathrm{d}{\mathrm{\Delta }}^{\prime }\\ +\sum _{i=1}^p{\int }_0^b{\omega }_{k,i}({\mathrm{\Delta }}^{″})\left\{\mathbb{E}[\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_i(t-\mathrm{\Delta }-{\mathrm{\Delta }}^{″})]-{\mu }_i{\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }\mathrm{d}{\mathrm{\Delta }}^{″}\right\}.\end{array}$$

Now, observe that Λ_m ≥ μ_m and 𝔼{dN_i(t − Δ − Δ″) dN_m(t − Δ′)}/{dΔ′dΔ″} ≥ μ_iμ_m by the nature of the mutually-exciting process. Thus, for Δ′ ≥ Δ,

$$\mathbb{E}\{\mathrm{d}{N}_m(t-{\mathrm{\Delta }}^{\prime })\mathrm{d}{N}_k(t-\mathrm{\Delta })\}/\{\mathrm{d}(t-\mathrm{\Delta })\}-\mathbb{E}\{{\mu }_m\mathrm{d}{\mathrm{\Delta }}^{\prime }\mathrm{d}{N}_k(t-\mathrm{\Delta })\}/\{\mathrm{d}(t-\mathrm{\Delta })\}\ge 0.$$ (27)

Applying both (26) and (27) to (25) shows that V_l,k(Δ) ≥ 0.

A.2. Proof of Lemma 2

Proof

For any Δ ≥ 0, the integral equation (13) gives

$$V_{j,k}(\mathrm{\Delta })={\omega }_{j,k}(\mathrm{\Delta }){\mathrm{\Lambda }}_k+({\mathit{\omega }}_{j,·}\ast {\mathit{V}}_{·,k})(\mathrm{\Delta }).$$ (28)

For any x, y ≥ 0, we can write

$$\begin{array}{l}\mid V_{j,k}(x)-V_{j,k}(y)\mid =\mid \{{\omega }_{j,k}(x)-{\omega }_{j,k}(y)\}{\mathrm{\Lambda }}_k+({\mathit{\omega }}_{j,·}\ast {\mathit{V}}_{·,k})(x)-({\mathit{\omega }}_{j,·}\ast {\mathit{V}}_{·,k})(y)\mid \\ =\left|\{{\omega }_{j,k}(x)-{\omega }_{j,k}(y)\}{\mathrm{\Lambda }}_k+\sum _{l=1}^p\{{\omega }_{j,l}\ast V_{l,k}(x)-{\omega }_{j,l}\ast V_{l,k}(y)\}\right|\\ =\left|\{{\omega }_{j,k}(x)-{\omega }_{j,k}(y)\}{\mathrm{\Lambda }}_k+\sum _{l\in {\mathcal{E}}_j}\{{\omega }_{j,l}\ast V_{l,k}(x)-{\omega }_{j,l}\ast V_{l,k}(y)\}\right|,\end{array}$$ (29)

where the last inequality holds since ω_j,l ≡ 0 for l ∉ ε_j. We then have

$$\mid V_{j,k}(x)-V_{j,k}(y)\mid \le \underset{\mathrm{I}}{\underbrace{|\{{\omega }_{j,k}(x)-{\omega }_{j,k}(y)\}{\mathrm{\Lambda }}_k|}}+\sum _{l\in {\mathcal{E}}_j}\underset{{\text{II}}_l}{\underbrace{|{\omega }_{j,l}\ast V_{l,k}(x)-{\omega }_{j,l}\ast V_{l,k}(y)|}}.$$ (30)

For I, we know from Assumptions 2 and 3(c) that

$$\mathrm{I}\equiv |\{{\omega }_{j,k}(x)-{\omega }_{j,k}(y)\}{\mathrm{\Lambda }}_k|\le {\theta }_0{\mathrm{\Lambda }}_{max}\mid x-y\mid .$$ (31)

For II_l, we can expand the convolution

$$\begin{array}{l}{\text{II}}_l=\left|{\int }_0^b{\omega }_{j,l}(\mathrm{\Delta })V_{l,k}(x-\mathrm{\Delta })\mathrm{d}\mathrm{\Delta }-{\int }_0^b{\omega }_{j,l}(\mathrm{\Delta })V_{l,k}(y-\mathrm{\Delta })\mathrm{d}\mathrm{\Delta }\right|\\ =\left|{\int }_{-x}^{b-x}{\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+x)V_{l,k}(-{\mathrm{\Delta }}^{\prime })\mathrm{d}{\mathrm{\Delta }}^{\prime }-{\int }_{-y}^{b-y}{\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+y)V_{l,k}(-{\mathrm{\Delta }}^{\prime })\mathrm{d}{\mathrm{\Delta }}^{\prime }\right|.\end{array}$$

Without loss of generality, we consider only the case that x ≥ y. We can decompose the integrals into parts on the intervals [−x, − y), [−y, b–x), and [b–x, b–y] as

$$\begin{array}{l}{\text{II}}_l\le \left|{\int }_{-y}^{b-x}\{{\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+x)-{\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+y)\}{V}_{l,k}(-{\mathrm{\Delta }}^{\prime })\mathrm{d}{\mathrm{\Delta }}^{\prime }\right|\\ +\left|{\int }_{-x}^{-y}{\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+x)V_{l,k}(-{\mathrm{\Delta }}^{\prime })\mathrm{d}{\mathrm{\Delta }}^{\prime }\right|+\left|{\int }_{b-x}^{b-y}{\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+y)V_{l,k}(-{\mathrm{\Delta }}^{\prime })\mathrm{d}{\mathrm{\Delta }}^{\prime }\right|\\ \le {\int }_{-y}^{b-x}{\theta }_0\mid {\mathrm{\Delta }}^{\prime }+x-{\mathrm{\Delta }}^{\prime }-y\mid \mid V_{l,k}(-{\mathrm{\Delta }}^{\prime })\mid \mathrm{d}{\mathrm{\Delta }}^{\prime }\\ +{\int }_{-x}^{-y}\mid {\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+x)V_{l,k}(-{\mathrm{\Delta }}^{\prime })\mid \mathrm{d}{\mathrm{\Delta }}^{\prime }+{\int }_{b-x}^{b-y}\mid {\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+y)V_{l,k}(-{\mathrm{\Delta }}^{\prime })\mid \mathrm{d}{\mathrm{\Delta }}^{\prime }\\ \le {\int }_{-y}^{b-x}{\theta }_0\mid x-y\mid V_{max}\mathrm{d}{\mathrm{\Delta }}^{\prime }+{\int }_{-x}^{-y}\mid {\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+x)\mid V_{max}\mathrm{d}{\mathrm{\Delta }}^{\prime }\\ +{\int }_{b-x}^{b-y}\mid {\omega }_{j,l}({\mathrm{\Delta }}^{\prime }+y)\mid V_{max}\mathrm{d}{\mathrm{\Delta }}^{\prime }\\ \le (b-x+y){\theta }_0\mid x-y\mid V_{max}+2C(x-y)V_{max},\end{array}$$

where we use Assumption 3(c) in the second inequality, Assumptions 2 in the third inequality, and the boundedness of ω_j,l from Assumption 3(c) in the last inequality. Recalling that x ≥ y, we have

$${\text{II}}_l\le (b{\theta }_0{V}_{max}+2C{V}_{max})\mid x-y\mid ,$$ (32)

Finally, plugging (31) and (32) into (30) gives

$$\mid V_{j,k}(x)-V_{j,k}(y)\mid \le {\theta }_0{\mathrm{\Lambda }}_{max}\mid x-y\mid +s(b{\theta }_0{V}_{max}+2C{V}_{max})\mid x-y\mid \le s{\theta }_1\mid x-y\mid ,$$ (33)

where we set θ₁ ≡ θ₀Λ_max + bθ₀V_max + 2CV_max. Note that the last inequality holds as long as s ≥ 1. (The result also holds if s = 0: in this case, the second term in (30) is zero for every j and the bound (31) suffices.)

A.3. Proof of Lemma 3

Recall that the estimator of the cross-covariance (8) takes the form

$$\frac{1}{h}\underset{{\mathrm{I}}_{j,k}}{\underbrace{\frac{1}{T}{\iint }_{{[0,T]}^2}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)\mathrm{d}{N}_j(t^{\prime })\mathrm{d}{N}_k(t)}}-\underset{{\text{II}}_j}{\underbrace{\left[\frac{1}{T}{\int }_0^T\mathrm{d}{N}_j(t)\right]}}\underset{{\text{II}}_k}{\underbrace{\left[\frac{1}{T}{\int }_0^T\mathrm{d}{N}_k(t)\right]}}.$$

The proof of Lemma 3 uses the following result. Lemma 4 is based on Proposition 3 of Hansen, Reynaud-Bouret and Rivoirard (2015); for completeness, we provide its proof in Section A.4.

Lemma 4

Suppose that Assumption 1 holds. We have

$$\mathbb{P}\left(\underset{1\le j\le k\le p}{\cap }\left[\mid {\mathrm{I}}_{j,k}-\mathbb{E}{\mathrm{I}}_{j,k}\mid \ge c_6{T}^{-1/3}\right]\right)\le c_5{p}^{2}Texp(-c_4{T}^{1/6}),$$ (34)

$$\mathbb{P}\left(\underset{1\le j\le p}{\cap }\left[\mid {\text{II}}_j-\mathbb{E}{\text{II}}_j\mid \ge c_6{T}^{-1/3+1/18}\right]\right\}\le c_5{p}^{2}Texp(-c_4{T}^{1/6}),$$ (35)

where c₄, c₅, and c₆ are constants.

We are now ready to prove Lemma 3.

Proof

First, note that

$$\begin{array}{l}\mid \mathbb{E}{\mathrm{I}}_{j,k}-h[V_{j,k}(\mathrm{\Delta })+{\mathrm{\Lambda }}_j{\mathrm{\Lambda }}_k]\mid \\ =|\frac{1}{T}{\iint }_{{[0,T]}^2}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)\mathbb{E}[\mathrm{d}{N}_j(t^{\prime })\mathrm{d}{N}_k(t)]\\ -\frac{1}{T}{\iint }_{{[0,T]}^2}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)[V_{j,k}(\mathrm{\Delta })+{\mathrm{\Lambda }}_j{\mathrm{\Lambda }}_k]\mathrm{d}t\mathrm{d}{t}^{\prime }|\\ =|\frac{1}{T}{\iint }_{{[0,T]}^2}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)\{\mathbb{E}[\mathrm{d}{N}_j(t^{\prime })\mathrm{d}{N}_k(t)]-{\mathrm{\Lambda }}_j{\mathrm{\Lambda }}_k\mathrm{d}t\mathrm{d}{t}^{\prime }\}\\ -\frac{1}{T}{\iint }_{{[0,T]}^2}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)V_{j,k}(\mathrm{\Delta })\mathrm{d}t\mathrm{d}{t}^{\prime }|\\ =|\frac{1}{T}{\iint }_{{[0,T]}^2}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)V_{j,k}(t^{\prime }-t)\mathrm{d}t\mathrm{d}{t}^{\prime }\\ -\frac{1}{T}{\iint }_{{[0,T]}^2}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)V_{j,k}(\mathrm{\Delta })\mathrm{d}t\mathrm{d}{t}^{\prime }|\\ =\left|\frac{1}{T}{\iint }_{{[0,T]}^2}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)[V_{j,k}(t^{\prime }-t)-V_{j,k}(\mathrm{\Delta })]\mathrm{d}t\mathrm{d}{t}^{\prime }\right|,\end{array}$$ (36)

where we use the definition of V in the third equality. Using the fact that the kernel K(x/h) is defined on [−h, h], we can write

$$\begin{array}{l}\mid \mathbb{E}{\mathrm{I}}_{j,k}-h[V_{j,k}(\mathrm{\Delta })+{\mathrm{\Lambda }}_j{\mathrm{\Lambda }}_k]\mid \\ =\left|\frac{1}{T}{\int }_0^T{\int }_{max(0,t-\mathrm{\Delta }-h)}^{min(T,t-\mathrm{\Delta }+h)}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right)[V_{j,k}(t^{\prime }-t)-V_{j,k}(\mathrm{\Delta })]\mathrm{d}t\mathrm{d}{t}^{\prime }\right|\\ \le \frac{1}{T}{\int }_0^T{\int }_{max(0,t-\mathrm{\Delta }-h)}^{min(T,t-\mathrm{\Delta }+h)}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right){\theta }_{1}s\mid t^{\prime }-t-\mathrm{\Delta }\mid \mathrm{d}t\mathrm{d}{t}^{\prime }\\ \le \frac{1}{T}{\int }_0^T{\int }_{max(0,t-\mathrm{\Delta }-h)}^{min(T,t-\mathrm{\Delta }+h)}K\left(\frac{t-t^{\prime }+\mathrm{\Delta }}{h}\right){\theta }_{1}hs\mathrm{d}t\mathrm{d}{t}^{\prime }\\ \le \frac{1}{T}{\int }_0^{T}2{\theta }_{1}s{h}^2\mathrm{d}t\\ =2{\theta }_{1}s{h}^2,\end{array}$$ (37)

where the first inequality follows from Lemma 2.

Recall that II_j ≡ T⁻¹N_j(T) and II_k ≡ T⁻¹N_k(T). Applying Lemma 4 and (37), we have, with probability at least 1 − 2c₅p²T exp(−c₄T^1/6),

$$\begin{array}{l}\left|{\widehat{V}}_{j,k}(\mathrm{\Delta })-V_{j,k}(\mathrm{\Delta })\right|\\ \le \frac{1}{h}\mid {\mathrm{I}}_{j,k}-\mathbb{E}{\mathrm{I}}_{j,k}\mid +\frac{1}{h}\mid \mathbb{E}{\mathrm{I}}_{j,k}-\mathbb{E}[\mathrm{d}{N}_j(t-\mathrm{\Delta })\mathrm{d}{N}_k(t)]/(\mathrm{d}t\mathrm{d}\mathrm{\Delta })\mid \\ +\left|\frac{1}{T^2}(N_j(T)-T{\mathrm{\Lambda }}_j)N_k(T)\right|+\left|{\mathrm{\Lambda }}_j\frac{1}{T}{N}_k(T)-{\mathrm{\Lambda }}_j{\mathrm{\Lambda }}_k\right|\\ \le c_6{T}^{-1/3}{h}^{-1}+2{\theta }_{1}hs+\\ (\Vert {\mathrm{\Lambda }}_{max}+c_6{T}^{-1/3+1/18})c_6{T}^{-1/3+1/18}+{\mathrm{\Lambda }}_{max}{c}_6{T}^{-1/3+1/18}.\end{array}$$ (38)

Letting h = c₁s^−1/2T^−1/6, (38) can be written as

$$\left|{\widehat{V}}_{j,k}(\mathrm{\Delta })-V_{j,k}(\mathrm{\Delta })\right|\le c_2^{\prime }{s}^{1/2}{T}^{-1/6}.$$ (39)

Lastly, we need a uniform bound on V̂_j,k − V_j,k on the region [−B,B]. We first see that the above probability statement holds for a grid of ⌈s^1/2T^1/6⌉ points on [−B,B], denoted as ${\{{\mathrm{\Delta }}_i\}}_{i=1}^{\lceil s^{1/2}{T}^{1/6}\rceil }$. The gap between adjacent points on this grid is bounded by 2Bs^−1/2T^−1/6. Furthermore, for any Δ ∈ [−B,B], we can find a point on the grid Δ_i such that |Δ − Δ_i| ≤ 2B/⌈s^1/2T^1/6⌉ ≤ 2Bs^−1/2T^−1/6. From basic calculus we get that, for all Δ ∈ [−B,B],

$$\begin{array}{l}\left|{\widehat{V}}_{j,k}(\mathrm{\Delta })-V_{j,k}(\mathrm{\Delta })\right|\\ =\left|{\widehat{V}}_{j,k}(\mathrm{\Delta })-{\widehat{V}}_{j,k}({\mathrm{\Delta }}_i)+{\widehat{V}}_{j,k}({\mathrm{\Delta }}_i)-V_{j,k}({\mathrm{\Delta }}_i)+V_{j,k}({\mathrm{\Delta }}_i)-V_{j,k}(\mathrm{\Delta })\right|\\ \le 2B{s}^{-1/2}{T}^{-1/6}+C_2^{\prime }{s}^{1/2}{T}^{-1/6}+{\theta }_{1}s{s}^{-1/2}{T}^{-1/6}\\ \le c_2{s}^{1/2}{T}^{-1/6},\end{array}$$ (40)

for some constant c₂.

Therefore, with probability at least 1 − c₃s^1/2p²T^7/6 exp(−c₄T^1/6),

$${\Vert {\widehat{V}}_{j,k}-V_{j,k}\Vert }_{2,[-B,B]}\le c_2{s}^{1/2}{T}^{-1/6}.$$ (41)

A.4. Proof of Lemma 4

Lemma 4 follows directly from the proof of Proposition 3 in Hansen, Reynaud-Bouret and Rivoirard (2015). The only difference is that we want a polynomial bound on the deviation, while Hansen, Reynaud-Bouret and Rivoirard (2015) consider a logarithmic bound. For completeness, we state the proof of Lemma 4 below, but note that the proof is almost identical to the proof of Proposition 3 in Hansen, Reynaud-Bouret and Rivoirard (2015). We refer the interested readers to the original proof in Section 7.4.3 of Hansen, Reynaud-Bouret and Rivoirard (2015) for more details.

Throughout this section, we assume that N ≡ (N₁, …, N_p)^T is defined on the full real line. We first state some notation that is only used in this section.

1. Following Hansen, Reynaud-Bouret and Rivoirard (2015), we use $C_{a_1,a_2,\dots }^{(i)}$ to denote a constant that depends only on a₁, a₂, …; and we use the superscript i to indicate that this is the ith constant appearing in the proof.

2. Without loss of generality, we assume that supp(ω_j,k) ⊂ (0, 1], as in Hansen, Reynaud-Bouret and Rivoirard (2015).

3. As in Hansen, Reynaud-Bouret and Rivoirard (2015), we introduce a function Z(N) such that Z(N) depends only on {dN(t′), t′∈ [−A, 0)}, and there exist two non-negative constants η and d such that

   $$\mid Z(\mathit{N})\mid \le d\left\{1+{\left(\sum _{l=1}^p{N}_l([-A,0)]\right)}^{\eta }\right\}.$$ (42)

4. We also introduce the (time) shift operator S_t so that Z ○ S_t(N) depends only on {dN(t′), t′∈ [−A + t, t)}, in the same way as Z(N) depends on the points of N in [−A, 0).

We are now ready to prove the lemma. When proving the bound (34), we only discuss the case when j ≠ k. The proof for the case when j = k follows from the same argument and is thus omitted.

Proof

In this proof, we will consider a probability bound for [Z ○ S_t(N) − 𝔼(Z)] dt ≥ u, where, for some κ ∈ (0, 1) to be specified later,

$$u=c_6{T}^{(1-\kappa )(1-\eta )+\kappa }.$$ (43)

Note that, by applying the bound to −Z(·), we can obtain a bound for|Z ○ S_t(N) − 𝔼(Z)|. To complete the proof, we will verify the statements (34) and (35) by considering some specific choices of Z(·).

For any positive integer k such that x ≡ T/(2k) > A, we have

$$\begin{array}{l}\mathbb{P}\left({\int }_0^T[Z\circ S_t(\mathit{N})-\mathbb{E}(Z)]\mathrm{d}t\ge u\right)\\ =\mathbb{P}\left(\sum _{q=0}^{k-1}{\int }_{2qx}^{2qx+x}[Z\circ S_t(\mathit{N})-\mathbb{E}(Z)]\mathrm{d}t+{\int }_{2qx+x}^{2qx+2x}[Z\circ S_t(\mathit{N})-\mathbb{E}(Z)]\mathrm{d}t\ge u\right)\\ \le 2\mathbb{P}\left(\sum _{q=0}^{k-1}{\int }_{2qx}^{2qx+x}[Z\circ S_t(\mathit{N})-\mathbb{E}(Z)]\mathrm{d}t\ge \frac{u}{2}\right),\end{array}$$

where the inequality follows from the stationarity of N. As in Reynaud-Bouret and Roy (2006), let ${\{{\stackrel{\sim }{M}}_q^x\}}_{q=1}^{\infty }$ be a sequence of independent Hawkes processes, each of which is stationary with intensities λ(t) ≡ (λ₁(t), …, λ_p(t))^T. See Section 3 of Reynaud-Bouret and Roy (2006) for more details on the construction of ${\{{\stackrel{\sim }{M}}_q^x\}}_{q=1}^{\infty }$. For each q, let $M_q^x$ be the truncated process associated with ${\stackrel{\sim }{M}}_q^x$, where truncation means that we only consider the points in [2qx − A, 2qx + x]. Now, if we set

$$F_q={\int }_{2qx}^{2qx+x}[Z\circ S_t(M_q^x)-\mathbb{E}(Z)]\mathrm{d}t,$$ (44)

then

$$\mathbb{P}\left({\int }_0^T[Z\circ S_t(\mathit{N})-\mathbb{E}(Z)]\mathrm{d}t\ge u\right)\le 2\mathbb{P}\left(\sum _{q=0}^{k-1}{F}_q\ge \frac{u}{2}\right)+2\sum _{q=0}^{k-1}\mathbb{P}\left(T_{e,q}>\frac{T}{2k}-A\right),$$ (45)

where T_e,q is the time to extinction of the process $M_q^x$. The extinction time T_e,q is introduced in Sections 2.2 and 3 in Reynaud-Bouret and Roy (2006). Roughly speaking, it is the last time when there is an event for the Hawkes process with intensity λ(t) of the form (2), with background intensity μ ≡ (μ₁, …, μ_p)^T set to 0 for t ≥ 0. Since T_e,q is identically distributed for all q, we can focus on one T_e,q. Denoting by a_l the ancestral points with marks l and by $H_{a_l}^l$ the length of the corresponding cluster whose origin is a_l, we have:

$$T_{e,q}=\underset{l\in \{1,\dots ,p\}}{max}\underset{a_l}{max}\{a_l+H_{a_l}^l\}.$$ (46)

Then by the exact argument on page 48 of Hansen, Reynaud-Bouret and Rivoirard (2015), we have

$$\mathbb{P}(T_{e,q}\le a)\ge 1-\sum _{l=1}^p{\mu }^{(l)}{\mathrm{c}}_l/{\vartheta }_{l}exp(-{\vartheta }_{l}a).$$ (47)

Thus, there exists a constant $C_A^{(1)}$ depending on A such that if we take $k=\lfloor C_A^{(1)}{T}^{\kappa }\rfloor$, for some κ ∈ (0, 1) to be specified later, then

$$\sum _{q=0}^{k-1}\mathbb{P}\left(T_{e,q}>\frac{T}{2k}-A\right)\le T^{\kappa }pexp(-c_4{T}^{1-\kappa }),$$ (48)

where c₄ is a constant. Note that x = T/2k ≈ T^1−κ is larger than A for T large enough (depending on A).

Now, note that the event 𝒯 ≡ {T_e,q ≤ T/2k − A, for all q = 0, …, k} only depends on the process N. We will first find a probability bound for the first term in (45). In other words, we will show that, given the event 𝒯,

$$\mathbb{P}\left({\int }_0^T\left[Z\circ S_t(\mathit{N})-\mathbb{E}(Z)\right]\mathrm{d}t\ge u\right)\le c_{5}Texp(-c_4{T}^{1-\kappa }).$$ (49)

Let

$$B=\mathbb{P}\left(\sum _{q=0}^{k-1}{F}_q\ge \frac{u}{2}\right).$$

Consider the measurable events

$${\mathrm{\Omega }}_q=\left\{\underset{t}{sup}\{M_q^x{\mid }_{[t-A,t)}\}\le \stackrel{\sim }{\mathcal{N}}\right\},$$

where 𝒩̃ is a constant that will be defined later and $M_q^x{\mid }_{[t-A,t)}$ represents the number of points of $M_q^x$ lying in [t − A, t). Let Ω = ∩_{0≤q≤k–1} Ω_q. Then

$$B\le \mathbb{P}\left(\sum _{q=0}^{k-1}{F}_q\ge u/2\text{and}\mathrm{\Omega }\right)+\mathbb{P}\left({\mathrm{\Omega }}^c\right).$$

We have $\mathbb{P}({\mathrm{\Omega }}^c)\le {\sum }_q\mathbb{P}({\mathrm{\Omega }}_q^c)$, where each $\mathbb{P}({\mathrm{\Omega }}_q^c)$ can be easily controlled. Indeed, it is sufficient to split [2qx–A, 2qx+x] into intervals of size A (there are about $C_A^{(2)}{T}^{1-\kappa }$ of these) and require the number of points in each sub-interval to be smaller than 𝒩̃/2. By stationarity, we then obtain

$$\mathbb{P}\left({\mathrm{\Omega }}_q^c\right)\le C_A^{(2)}{T}^{1-\kappa }\mathbb{P}(N_{[-A,0]}>\stackrel{\sim }{\mathcal{N}}/2).$$

Using Proposition 2 in Hansen, Reynaud-Bouret and Rivoirard (2015) with u = [𝒩̃/2] + 1/2, we obtain:

$$\mathbb{P}\left({\mathrm{\Omega }}_q^c\right)\le C_A^{(2)}{T}^{1-\kappa }exp(-C_A^{(3)},\stackrel{\sim }{\mathcal{N}})$$

and, thus,

$$\mathbb{P}\left({\mathrm{\Omega }}_q^c\right)\le C_A^{(4)}Texp(-C_A^{(3)}\stackrel{\sim }{\mathcal{N}}).$$

Note that this control holds for any positive choice of 𝒩̃. Thus, for any 𝒩̃ > 0,

$$\mathbb{P}\left(\exists t\in [0,T]\text{such}\text{that}{M}_q^x{\mid }_{t-A,t)}>\stackrel{\sim }{\mathcal{N}}\right)\le C_A^{(2)}{T}^{1-\kappa }exp(-C_A^{(3)}\stackrel{\sim }{\mathcal{N}}).$$ (50)

Hence by taking $\stackrel{\sim }{\mathcal{N}}=C_A^{(5)}{T}^{1-\kappa }$, for $C_A^{(5)}$ large enough, the right-hand side of (50) is smaller than $C_A^{(2)}{T}^{1-\kappa }exp(-c_4{T}^{1-\kappa })$.

It remains to obtain the rate of D ≡ ℘(Σ_q F_q ≥ u/2 and Ω). For any positive constant ε that will be chosen later, we have:

$$\begin{array}{lll}D\hfill & \le \hfill & {\mathrm{e}}^{-\epsilon u/2}\mathbb{E}\left({\mathrm{e}}^{\epsilon {\mathrm{\sum }}_q{F}_q}\prod _q{𝟙}_{{\mathrm{\Omega }}_q}\right)\hfill \\ \hfill & \le \hfill & {\mathrm{e}}^{-\epsilon u/2}\prod _q\mathbb{E}\left({\mathrm{e}}^{\epsilon F_q}{𝟙}_{{\mathrm{\Omega }}_q}\right),\hfill \end{array}$$ (51)

since the variables ${\{M_q^x\}}_q$ are independent. But,

$$\mathbb{E}\left({\mathrm{e}}^{\epsilon F_q}{𝟙}_{{\mathrm{\Omega }}_q}\right)=1+\epsilon \mathbb{E}(F_q{𝟙}_{{\mathrm{\Omega }}_q})+\sum _{j\ge 2}\frac{{\epsilon }^j}{j!}\mathbb{E}\left(F_q^j{𝟙}_{{\mathrm{\Omega }}_q}\right)$$

and $\mathbb{E}(F_q{𝟙}_{{\mathrm{\Omega }}_q})=\mathbb{E}(F_q)-\mathbb{E}(F_q{𝟙}_{{\mathrm{\Omega }}_q^c})=-\mathbb{E}(F_q{𝟙}_{{\mathrm{\Omega }}_q^c})$.

Next note that if for any integer l,

$$l\stackrel{\sim }{\mathcal{N}}<\underset{t}{sup}{M}_q^x{\mid }_{[t-A,t)}\le (l+1)\stackrel{\sim }{\mathcal{N}},$$

then

$$\mid F_q\mid \le xd\left[{(l+1)}^{\eta }{\stackrel{\sim }{\mathcal{N}}}^{\eta }+1\right]x\mathbb{E}(Z).$$

Hence, cutting ${\mathrm{\Omega }}_q^c$ into slices of the type { $l\stackrel{\sim }{\mathcal{N}}<{sup}_t{M}_q^x{\mid }_{[t-A,t)}\le (l+1)\stackrel{\sim }{\mathcal{N}}$} and using (50) with $\stackrel{\sim }{\mathcal{N}}=C_A^{(5)}{T}^{1-\kappa }$ for a large enough $C_A^{(5)}$, we obtain

$$\begin{array}{l}|\mathbb{E}(F_q{𝟙}_{{\mathrm{\Omega }}_q})|=|\mathbb{E}(F_q{𝟙}_{{\mathrm{\Omega }}_q^c})|\\ \le \sum _{l=1}^{+\infty }x\left(d\left[{(l+1)}^{\eta }{\stackrel{\sim }{\mathcal{N}}}^{\eta }+1\right]+|\mathbb{E}(Z)|\right)\\ \times \mathbb{P}\left(\exists t\in [0,T]\text{such}\text{that}{M}_q^x{\mid }_{[t-A,t)}>\ell \stackrel{\sim }{\mathcal{N}}\right)\\ \le C_A^{(2)}\sum _{l=1}^{+\infty }x\left(d\left[{(l+1)}^{\eta }{\stackrel{\sim }{\mathcal{N}}}^{\eta }+1\right]+|\mathbb{E}(Z)|\right)T^{1-\kappa }exp(-c_{4}l\stackrel{\sim }{\mathcal{N}})\\ \le C_A^{(6)}\sum _{l=1}^{+\infty }x\left(d{\stackrel{\sim }{\mathcal{N}}}^{\eta }+|\mathbb{E}(Z)|\right)T^{1-\kappa }{2}^{l\eta }exp\{-c_{4}l\stackrel{\sim }{\mathcal{N}}\}\\ \le C_A^{(7)}{T}^{2-2\kappa }d{\stackrel{\sim }{\mathcal{N}}}^{\eta }\frac{exp(-c_4\stackrel{\sim }{\mathcal{N}})}{1-2^{\eta }exp(-c_4\stackrel{\sim }{\mathcal{N}})},\end{array}$$

where in the last inequality, we have used the fact that $\mid \mathbb{E}(Z)\mid \le d\mathbb{E}[{\mathit{N}}_{[-A,0)}^{\eta }]$ by (42). Plugging $\stackrel{\sim }{\mathcal{N}}=C_A^{(5)}{T}^{1-\kappa }$ into the above equation gives

$$\mid \mathbb{E}(F_q{𝟙}_{{\mathrm{\Omega }}_q})\mid \le z_1\equiv C_A^{(8)}d{T}^{2-2\kappa }{T}^{(1-\kappa )\eta }exp(-c_4{T}^{1-\kappa }).$$

In the same way, following Hansen, Reynaud-Bouret and Rivoirard (2015), we can write

$$\mathbb{E}(F_q^j{𝟙}_{{\mathrm{\Omega }}_q})\le \mathbb{E}(F_q^j{𝟙}_{{\mathrm{\Omega }}_q})z_b^{j-2},$$ (52)

where $z_b\equiv xd[{\stackrel{\sim }{\mathcal{N}}}^{\eta }+1]+x\mathbb{E}(Z)=C_{\eta ,A}^{(9)}d{T}^{(1-\kappa )(1+\eta )}$. Then, by stationarity,

$$\begin{array}{lll}\mathbb{E}(F_q^2{𝟙}_{{\mathrm{\Omega }}_q})\hfill & \le \hfill & x\mathbb{E}\left[{\int }_{2qx}^{2qx+x}{\left[Z\circ S_{t^{\prime }}\left(M_q^x\right)-\mathbb{E}(Z)\right]}^2{\cap }_{\tau \in ℝ}{𝟙}_{M_q^x{\mid }_{[\tau -A,\tau )}\le \stackrel{\sim }{\mathcal{N}}\}}\mathrm{d}{t}^{\prime }\right]\hfill \\ \hfill & \le \hfill & x\mathbb{E}\left[{\int }_{2qx}^{2qx+x}{\left[Z\circ S_{t^{\prime }}\left(M_q^x\right)-\mathbb{E}(Z)\right]}^2{𝟙}_{\{M_q^x{\mid }_{[t^{\prime }-A,t^{\prime })}\le \stackrel{\sim }{\mathcal{N}}\}}\mathrm{d}{t}^{\prime }\right]\hfill \\ \hfill & \le \hfill & x^2\mathbb{E}\left({\left[Z(\mathit{N})-\mathbb{E}(Z)\right]}^2{𝟙}_{N_{[-A,0)}\le \stackrel{\sim }{\mathcal{N}}}\right)\hfill \\ \hfill & \le \hfill & z_v\equiv C_{\eta ,A}^{(10)}{T}^{2-2\kappa }{\sigma }^2,\hfill \end{array}$$

where σ² ≡ 𝔼[Z(N) − 𝔼(Z)]. Going back to (51), by (52), we have

$$\begin{array}{lll}D\hfill & \le \hfill & exp\left[-\frac{\epsilon u}{2}+klog\left(1+\epsilon z_1+\sum _{j\ge 2}{z}_v{z}_b^{j-2}\frac{{\epsilon }^j}{j!}\right)\right]\hfill \\ \hfill & \le \hfill & exp\left[-\epsilon \left(\frac{u}{2}-k{z}_1\right)+k\sum _{j\ge 2}{z}_v{z}_b^{j-2}\frac{{\epsilon }^j}{j!}\right],\hfill \end{array}$$

using the fact that log(1 + u) ≤ u. Since

$$k{z}_1=C_{\eta }^{(10)}d{T}^{\kappa }{T}^{(2+\eta )(1-\kappa )}exp(-c_4{T}^{1-\kappa }),$$

one can choose c₆ in the definition (43) of u (not depending on d) such that $u/2-k{z}_1\ge \sqrt{2k{z}_{v}z}+\frac{1}{3}{z}_{b}z$ for some z = c₄T^{κ–2η(1–κ)}. Hence,

$$D\le exp\left[-\epsilon \left(\sqrt{2k{z}_{v}z}+\frac{1}{3}{z}_{b}z\right)+k\sum _{j\ge 2}{z}_v{z}_b^{j-2}\frac{{\epsilon }^j}{j!}\right].$$

One can choose ε (as in the proof of the Bernstein inequality in Massart (2007), page 25) to obtain a bound on the right-hand side in the form of e^−z. We can then choose c₄ large enough, and only depending on η and A, to guarantee that D ≤ e^−z ≤ c₅ exp(−c₄T^1–κ).

In summary, we have shown that, given the event 𝒯,

$$\mathbb{P}\left({\int }_0^T\left[Z\circ S_t(\mathit{N})-\mathbb{E}(Z)\right]\mathrm{d}t\ge u\right)\le c_{5}exp(-c_4{T}^{1-\kappa })+C_A^{(4)}Texp(-c_4{T}^{1-\kappa }).$$

With a slight abuse of notation, letting $c_5=max(c_5,C_A^{(4)})$ gives (49).

To complete the proof, we apply the concentration inequality (49) with some specific choices of Z(·).

For each pair (j, k), let

$$Z\circ S_t(\mathit{N})\equiv {\int }_{t-h}^{t+h}K\left(\frac{t^{\prime }-t+\mathrm{\Delta }}{h}\right)\mathrm{d}{N}_j(t^{\prime })\mathrm{d}{N}_k(t)/\mathrm{d}t.$$

We can check that d = 1 and η = 2 satisfy (42). Then with κ = 5/6 in (49), we get, given the event 𝒯,

$$\mathbb{P}\left(\mid {\mathrm{I}}_{j,k}-\mathbb{E}{\mathrm{I}}_{j,k}\mid \ge c_6{T}^{-1/3}\right)\le c_{5}Texp(-c_4{T}^{1/6}).$$

Applying a union bound for all pairs (j, k), we have, given the event 𝒯,

$$\mathbb{P}\left(\underset{1\le j\le k\le p}{\cap }\left[\mid {\mathrm{I}}_{j,k}-\mathbb{E}{\mathrm{I}}_{j,k}\mid \ge c_6{T}^{-1/3}\right]\right)\le c_{5}T{p}^{2}exp(-c_4{T}^{1/6}).$$ (53)

Recall from the concentration inequality (48) that the event 𝒯 holds with probability at least 1–pT ^1/6 exp(−c₄T^1/6). Thus, given that pT ^1/6 exp(−c₄T^1/6) is dominated by the right-hand side of (53), it holds unconditionally that

$$\mathbb{P}\left(\underset{1\le j\le k\le p}{\cap }\left[\mid {\mathrm{I}}_{j,k}-\mathbb{E}{\mathrm{I}}_{j,k}\mid \ge c_6{T}^{-1/3}\right]\right\}\le c_{5}T{p}^{2}exp(-c_4{T}^{1/6}),$$

which is the statement on I_j,k in (34).

The statement on II_l, l = j, k, in (35) can be shown in a similar manner by taking Z ○ S_t(N) ≡ dN_j(t)/dt, with η = 1, and κ = 13/18.