Equivalence of binormal likelihood-ratio and bi-chi-squared ROC curve models

Abstract

A basic assumption for a meaningful diagnostic decision variable is that there is a monotone relationship between it and its likelihood ratio. This relationship, however, generally does not hold for a decision variable that results in a binormal ROC curve. As a result, receiver operating characteristic (ROC) curve estimation based on the assumption of a binormal ROC-curve model produces improper ROC curves that have “hooks,” are not concave over the entire domain, and cross the chance line. Although in practice this “improperness” is usually not noticeable, sometimes it is evident and problematic. To avoid this problem, Metz and Pan proposed basing ROC-curve estimation on the assumption of a binormal likelihood-ratio (binormal-LR) model, which states that the decision variable is an increasing transformation of the likelihood-ratio function of a random variable having normal conditional diseased and nondiseased distributions. However, their development is not easy to follow. I show that the binormal-LR model is equivalent to a bi-chi-squared model in the sense that the families of corresponding ROC curves are the same. The bi-chi-squared formulation provides an easier-to-follow development of the binormal-LR ROC curve and its properties in terms of well-known distributions.

1. Introduction

Receiver operating characteristic (ROC) curve analysis is a well-established method for evaluating and comparing the performance of diagnostic tests [1, 2, 3]. Throughout I assume that the purpose of a diagnostic test is to classify subjects as diseased or not diseased, based on whether a decision variable (DV) exceeds a threshold value. The performance of a diagnostic test as a function of the threshold value is typically described by an ROC curve, which is a plot of sensitivity versus 1–specificity for all possible threshold values. Sensitivity and 1–specificity are often referred to as true positive fraction (tpf) and false positive fraction (fpf), respectively. A commonly reported ROC-curve summary measure is the area under the ROC curve (AUC).

A parametric estimate of the ROC curve is often based on the assumption of a binormal ROC curve. A binormal ROC curve can be defined either in terms of its functional form or in terms of the distribution of a DV: (1) An ROC curve that plots as a straight line in probit space (i.e., a plot of Φ⁻¹ (tpf) vs. Φ⁻¹ (fpf)) is a binormal ROC curve with binormal parameters a and b, where a is the intercept and b is the slope. (2) Equivalently, a binormal ROC curve corresponds to a DV having a binormal distribution, i.e., the DV is normally distributed for nondiseased subjects as well as for diseased subjects. These two definitions are related by the equations a = (μ₂ – μ₁)/σ₂ and b = σ₁/σ₂, where (μ₂, ${\sigma }_1^2$) and (μ₁, ${\sigma }_2^2$) denote the mean and variance parameter pairs for the nondiseased and diseased distributions for a binormal DV. In this paper I primarily utilize the second definition of the binormal ROC curve. Because an ROC curve is invariate to an increasing transformation of the DV, more generally a binormal ROC curve corresponds to a DV that follows the binormal model, which states that there exists an increasing transformation such that the transformed DV has a binormal distribution. For large samples the assumption of a binormal ROC curve has been shown to perform well for DV distributions that can vary greatly from the binormal distribution [4, 5, 6, 7].

For example, consider a study where a radiologist is asked to assign likelihood-of-disease confidence levels to images using a discrete five-level ordinal integer scale (e.g., 1 = “definitely not diseased”, . . . , 5 = “definitely diseased”); for this situation the investigator might assume that the observed ordinal ratings represent the binning of values of a latent (i.e., unobserved) continuous DV that represents the reader's likelihood-of-disease perception. A binormal ROC curve is appropriate if we assume that the latent DV has a binormal distribution or is an increasing transformation of a binormal DV.

In most situations a meaningful DV should be an increasing transformation of the likelihood ratio (likelihood of being diseased divided by likelihood of not being diseased) [2]. According to Egan [8, pp 19, 37], a DV having this property and its corresponding ROC curve are said to be proper; otherwise, they are said to be improper. A proper ROC curve is concave (down) everywhere and never crosses the chance line [2]. For a given test result, a proper DV provides the optimal criterion for classifying subjects in the sense that the resulting proper ROC curve is uniformly above all other ROC curves based on the test result [2].

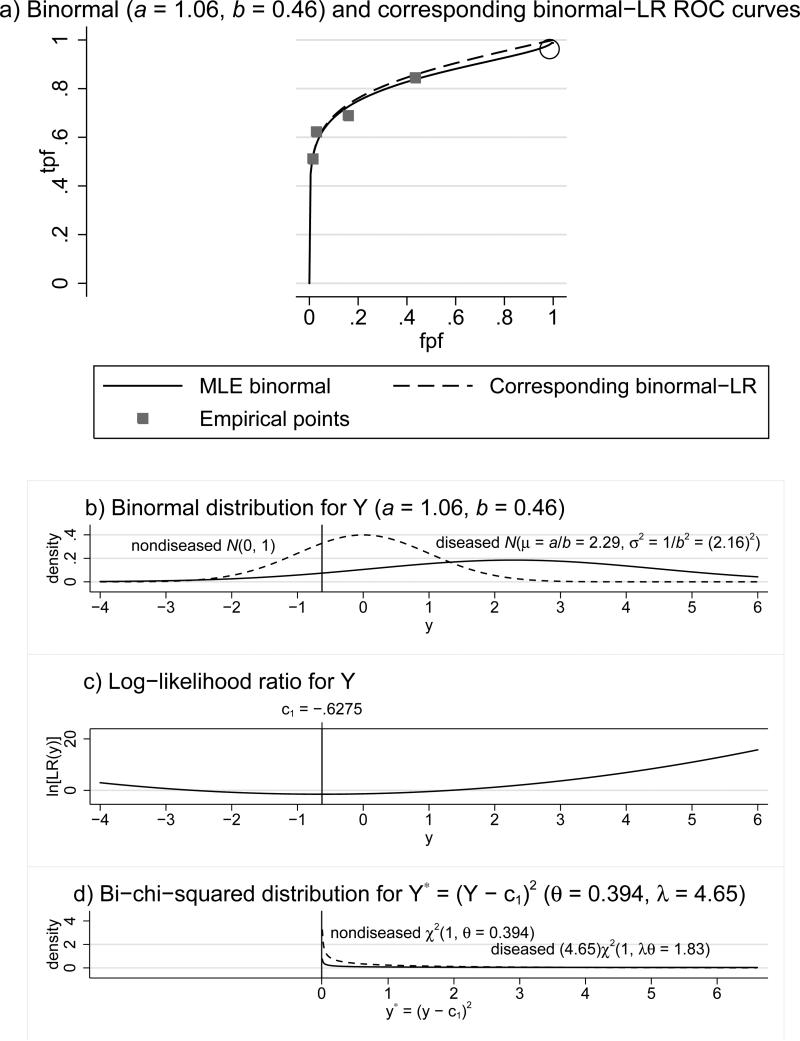
The binormal ROC curve is improper unless the binormal DV conditional diseased and nondiseased distribution variances are equal. When it is improper, there is a single fpf value such that the ROC curve is concave on one side and convex (concave up) on the other side; there also is a single fpf value where the ROC curve crosses the chance line [2], resulting in a “hooked” ROC curve. For example, rating data [9] from a radiologist that result in a hooked estimated binormal ROC curve estimate are presented in Table 1, with the hooked ROC curve displayed in Figure 1a (solid line).

Table 1.

ROC rating data for a radiologist [9].

	Rating
Status	1	2	3	4	5	Total
Nondiseased	39	19	9	1	1	69
Diseased	7	7	3	5	23	45

The estimated binormal ROC curve is displayed in Figure 1a.

Figure 1.

Binormal ROC curve (with b < 1) and related plots. The binormal ROC curve (solid line) in (a) is the maximum likelihood estimate for the data given in Table 1; the circle indicates the hook in it. For the corresponding binormal random variable Y, the binormal conditional densities and the log-likelihood ratio are displayed in (b) and (c), respectively. where c₁ = –ab/(1 – b²) is the threshold where the log-likelihood ratio attains its minimum. The bi-chi-squared conditional densities for Y* = (Y – c₁)² are displayed in (d), and the binormal-LR ROC curve, based on Y*, is the dashed line in (a). Notes: the nondiseased and diseased densities are denoted by the dashed and solid lines, respectively, in (b) and (d); χ² (1, ν) denotes a chi-squared distribution with one degree of freedom and noncentrality parameter ν; LR: likelihood ratio function; λ = 1/b²; θ = a²b²/(1 – b²)².

For the typical situation where the binormal DV diseased-distribution variance is larger, the binormal ROC curve is convex for large fpf values and exhibits a hook in the upper right corner, as in Figure 1a, resulting in a threshold below which the likelihood ratio increases as the DV decreases. In practical terms, the convexity implies that below this threshold, the more “normal” an image appears the more likely it is to be diseased. Although for many situations the region of convexity and the hook and chance-line crossing are not noticeable, for some situations they can be noticeable enough to call into question the validity of conclusions based on the fitted curve. In addition, for some data sets, which Metz [10] refers to as degenerate data sets, the binormal likelihood is maximized when one or more of the parameter estimates is on the border of the parameter space, resulting in binormal ROC curves which have unacceptable zigzag shapes.

To circumvent these problems, Metz and Pan [11, 12] proposed estimating the ROC curve under the assumption that the DV is an increasing transformation of the likelihood-ratio transformation of a binormal random variable. The resulting ROC curve is always proper. Although they refer to their model as the proper binormal model, I find this name misleading since the underlying assumed decision-variable model is not binormal; thus, I will instead use the terminology of Hillis and Berbaum [13] and refer to their model as the binormal likelihood-ratio model (binormal-LR model).

Today this approach is often used for ROC analysis of radiologic imaging data. If the maximum-likelihood binormal ROC curve does not exhibit a noticeable hook, then typically the corresponding maximum-likelihood binormal-LR ROC curve is virtually identical to it. On the other hand, when the binormal hook is noticeable, the binormal-LR ROC curve provides a more acceptable curve because it is concave and hence has no hook. Thus this approach is appealing for researchers familiar with the binormal-model approach, but who want to avoid its problems.

However, the Metz and Pan [12] development is not easy to follow, especially for researchers that do not have extensive statistical training, and contains several important omissions: they do not provide an equation expressing tpf as an analytic function of fpf and vice versa and do not provide proofs for area-under-the-ROC curve (AUC) and partial area-under-the-ROC curve (pAUC) formulas. I show that the binormal-LR model is equivalent to a bi-chi-squared model in the sense that both models result in the same family of ROC curves. The bi-chi-squared model approach allows for specification of tpf and fpf as analytic functions of each other, straightforward derivation of AUC and pAUC formulas and other properties, and an easier-to-follow development of the binormal-LR ROC curve.

An outline of this paper is as follows. I define the binormal-LR ROC curve and corresponding notation in Section 2. I show in Section 3 that, provided b ≠ 1, the family of binormal-LR ROC curves is equivalent to the family based on a proper bi-chi-squared model. Formulas for the binormal-LR ROC curve, AUC, and pAUC are derived in Section 4 using the bi-chi-squared model. I compare the bi-chi-squared and Metz and Pan approaches in Section 5, and discuss estimation using the bi-chi-squared approach in Section 6. Examples are presented in Section 7, followed by concluding remarks.

2. Binormal likelihood-ratio ROC curve definition and notation

Let ROC_LR;a,b denote a binormal-LR ROC curve based on the likelihood ratio transformation of a binormal random variable having binormal parameters a and b, where –∞ < a < ∞, b > 0. For example, let Y be a binormal random variable with conditional distribution (Y|D = 0) ~ N (0, 1), where D is an indicator of disease status, with D = 1 denoting diseased and D = 0 denoting nondiseased. It follows that (Y|D = 1) ~ N(a/b, 1/b²). Let LR_Y (·) denote the likelihood ratio function for Y; i.e.

$${\mathrm{LR}}_Y\left(y\right)=\frac{f_Y(y\mid D=1)}{f_Y(y\mid D=0)}=\frac{b\varphi \left(\frac{y-a∕b}{1∕b}\right)}{\varphi \left(y\right)}=\frac{b\varphi (by-a)}{\varphi \left(y\right)}$$

where f_Y (·|D = d) denotes the density function for Y conditional on disease status d and ϕ(·) is the standard normal density function. Then ROC_LR;a,b is based on the DV LR_Y (Y). As noted in the previous section, ROC_LR;a,b is proper and hence also concave.

Because the ROC curve corresponding to LR_Y (Y) is invariant to increasing transformations of LR_Y (Y), ROC_LR;a,b can also be defined by

$$U=\ln \left[{\mathrm{LR}}_Y\left(Y\right)\right]=\ln \left(b\right)+\frac{1}{2}[(1-b^2)Y^2+2abY-a^2]$$ (1)

More generally, if Ỹ is a binomial random variable with binormal parameters a and b and conditional distributions (Ỹ|D = 0) ~ N(μ₁, ${\sigma }_1^2$) and (Ỹ|D = 1) ~ N(μ₂, ${\sigma }_2^2$), then it is straightforward to show that the log-likelihood function can be written in the form

$$\ln \left[{\mathrm{LR}}_{\tilde{Y}}\left(\tilde{Y}\right)\right]=\ln \left(b\right)+\frac{1}{2}\left[(1-b^2){\left(\frac{\tilde{Y}-{\mu }_1}{{\sigma }_1}\right)}^2+2ab\left(\frac{\tilde{Y}-{\mu }_1}{{\sigma }_1}\right)-a^2\right]$$

which has the same form as (1) but with Y replaced by (Ỹ – μ₁)/σ₁. It is easy to show that ((Ỹ – μ₁)/σ₁|D = 0) ~ N(0, 1) and ((Ỹ – μ₁)/σ₁|D = 1) ~ N(a/b, 1/b²). It follows that ln [LR_Ỹ(Ỹ)] and ln [LR_Y(Y)] have the same conditional distributions, and hence define the same binormal-LR ROC curve. Thus we see that ROC_LR;a,b is uniquely determined by a and b.

When estimating the binormal-LR ROC curve, Metz and Pan assume that the DV has the same distribution as the likelihood-ratio transformation of a binormal random variable (or more generally, as an increasing transformation of the likelihood-ratio transformation of a binormal random variable). Although each binormal-LR ROC curve is defined by a pair of a and b parameters of a corresponding binormal random variable, the role of the corresponding binormal random variable is only to define the distribution of the binormal-LR DV and of itself is generally not useful for practical purposes. A common misunderstanding among researchers is that Metz and Pan estimate binormal a and b parameters under the assumption that the DV has a binormal distribution and then use the corresponding binormal-LR ROC curve (i.e., having the same a and b values) as the estimate – this is not what they do. Instead, they estimate the binormal-LR ROC curve a and b parameters under the assumption that the DV has a binormal-LR distribution. Thus for a given data set, the estimated binormal-LR ROC curve a and b values will in general differ from the estimated binormal ROC curve a and b values.

3. Relationship between binormal-LR and bi-chi-squared ROC curves

In this section I show for b ≠ 1 that ROC_LR;a,b can be defined by a DV having a noncentral bi-chi-squared distribution with 1 degree of freedom, up to a scale factor. For b = 1 I show that ROC_LR;a,b is the same as the binormal ROC curve. Throughout I assume that Y is a binormal random variable with binormal parameters a and b. Because a and b uniquely determine ROC_LR;a,b, I will without loss of generality assume Y has conditional distributions (Y|D = 0) ~ N(0, 1) and (Y|D = 1) ~ N(a/b, 1/b²).

3.1. Results for b ≠ 1

It is straightforward to show that U (1) can be written in the form

$$U=g(a,b)+\frac{(1-b^2)}{2}{(Y-c_1)}^2$$ (2)

where

$$c_1=-\frac{ab}{(1-b^2)}$$ (3)

For b < 1 it follows from (2) that u = ln [LR_Y (y)] is quadratic in y and attains its minimum value at y = c₁. Hence

$$Y^{\ast }\equiv {(Y-c_1)}^2={\left(Y+\frac{ab}{(1-b^2)}\right)}^2$$

is an increasing transformation of U and ROC_LR;a,b can be equivalently defined based on Y ^* as the DV. (Note that here and elsewhere, the term increasing transformation refers to a strictly increasing transformation.)

Figure 1b displays the conditional distributions for Y , where Y has a binormal distribution with parameters a = 1.06, b = 0.464; this is the binormal distribution corresponding to the hooked binormal ROC curve displayed in Figure 1a. The relationship between U and Y is displayed in Figure 1c.

Let ${\chi }_{1;\nu }^2$ denote a noncentral chi-square distribution with 1 degree of freedom and noncentrality parameter ν. It is well known that ${\chi }_{1;\nu }^2$ is the distribution of a squared normal random variable having unit variance and mean $\sqrt{\nu }$. Because $(Y-c_1\mid D=0)\sim N(\frac{ab}{(1-b^2)},1)$ and $(Y-c_1\mid D=1)\sim N(\frac{a}{b(1-b^2)},1∕b^2)=\frac{1}{b}N(\frac{a}{(1-b^2)},1)$, it follows that

$$\begin{array}{cc}\hfill Y^{\ast }\mid (D=0)& \sim {\chi }_{1;\frac{a^2{b}^2}{{(1-b^2)}^2}}^2\hfill \\ \hfill Y^{\ast }\mid (D=1)& \sim \frac{1}{b^2}{\chi }_{1;\frac{a^2}{{(1-b^2)}^2}}^2\hfill \end{array}$$ (4)

A parameterization that I will use for derivations and computational formulas is

$$\begin{array}{cc}\hfill Y^{\ast }\mid (D=0)\sim & {\chi }_{1;\theta }^2\hfill \\ \hfill Y^{\ast }\mid (D=1)\sim & \lambda {\chi }_{1;\lambda \theta }^2\hfill \end{array}$$ (5)

where the unconstrained parameter space is given by

$$\lambda >0,\theta \ge 0$$

From (4-5) it follows that

$$\theta =\frac{a^2{b}^2}{{(1-b^2)}^2},\lambda =\frac{1}{b^2}$$ (6)

Thus the (λ, θ) parameter space corresponding to {(a, b) : 0 < b < 1} is

$$\lambda >1,\theta \ge 0$$

From (3) and (6) it follows that

$$\theta =c_1^2$$

and hence θ can be interpreted, in terms of Y, as the squared difference between the nondiseased mean and the threshold where the likelihood ratio attains its minimum.

The conditional distributions for Y* are displayed in Figure 1d and the binormal-LR ROC curve defined by Y* is displayed as the dashed line in Figure 1a. To create the plot of the ROC curve in Figure 1a, θ and λ were computed with a = 1.06, b = 0.464 using (6), and then tpf was computed as a function of fpf using formula (13), derived in Section 4.1.

Using well-known results for the noncentral chi-square distribution, the conditional means and variances are given by

$$\begin{array}{cc}\hfill E[Y^{\ast }\mid (D=0)]& =1+\theta \hfill \\ \hfill E[Y^{\ast }\mid (D=1)]& =\lambda (1+\lambda \theta )\hfill \\ \hfill \mathrm{var}[Y^{\ast }\mid (D=0)]& =2+4\theta \hfill \\ \hfill \mathrm{var}[Y^{\ast }\mid (D=1)]& ={\lambda }^2(2+4\lambda \theta )\hfill \end{array}$$ (7)

In summary I have shown for b < 1 that ROC_LR;a,b can be defined by Y*, which has conditional noncentral chi-square distributions with 1 degree of freedom (d.f.), up to a scale factor. In addition, Y* is proper because it is an increasing transformation of the likelihood ratio function of Y. Hence Y* has a proper bi-chi-squared distribution.

If b > 1 then it follows from (2) that u = ln [LR_Y (y)] is quadratic in y, attains its maximum value at y = c₁, and –Y* = –(Y – c₁)² is an increasing transformation of U. Thus –Y* is proper and ROC_LR;a,b can be equivalently defined based on –Y* as the DV. The conditional distributions for Y* are again given by (5) with equations (6-7) still applicable, but now with

$$0<\lambda <1,\theta \ge 0$$

Hence –Y* has a proper negative bi-chi-squared distribution.

Figure S1a (available in the online Supporting Materials) displays the ROC curve defined by a binormal random variable Y with parameters a = 8.65, b = 4.40. For this curve the hook occurs in the lower left corner of the graph and is barely discernible. The conditional distributions for Y, the relationship between U and Y, and the conditional distributions of –Y* are displayed in Figures S1b, S1c, and S1d, respectively. The corresponding binormal-LR ROC curve, defined by –Y*, is displayed as the dashed line in Figure S1a.

No constraints were placed on a in deriving the distribution of Y*. From (4) we see that the conditional distributions of Y* are invariant to the sign of a. It follows that the binormal-LR curve is invariant to the sign of a :

$${\mathrm{ROC}}_{\mathrm{LR};a,b}={\mathrm{ROC}}_{\mathrm{LR};-a,b}$$ (8)

Metz and Pan [12, p. 5] state that “Without loss of generality, we assume that a ≥ 0 and b > 0 . . . ” but do not give any particular reason for this assumption; in particular, they do not note that the binormal-LR curve is invariant to the sign of a. It is natural to assume a ≥ 0 for performing binormal ROC curve estimation because a < 0 represents the unlikely situation that a DV performs worse than chance. However, because the binormal-LR ROC curve corresponds to a proper DV, it cannot depict a DV that performs worse than chance, and hence it would at first appear that we should not constrain a ≤ 0 in order to obtain the most inclusive set of binormal-LR curves. However, the invariance result (8) shows that the set of binormal-LR ROC curves remains unchanged by the constraint a ≥ 0.

3.2. Summary

I now formally summarize the results from Section 3.1.

Result 1

The family of binormal-LR ROC curves for –∞ < a < ∞, b ≠ 1, is given by

$$\{{\mathrm{ROC}}_{\mathrm{LR};a,b}:a\ge 0,b>0,b\ne 1\}$$

Result 1 follows from the invariance property (8).

Motivated by the results from Section 3.1, I now formally define the particular one-degree-of-freedom two-parameter bi-chi-squared distribution that is utilized in this paper. Although a bi-chi-squared distribution could more generally have more than one degree of freedom and more or less than two parameters, for simplicity I refer to this particular form as the bi-chi-squared distribution.

Definition 1

A decision variable X has a bi-chi-squared distribution with parameters λ > 0, θ ≥ 0 if its conditional distributions are given by

$$\begin{array}{cc}\hfill X\mid (D=0)\sim & {\chi }_{1;\theta }^2\hfill \\ \hfill X\mid (D=1)\sim & \lambda {\chi }_{1;\lambda \theta }^2\hfill \end{array}$$

Note that the noncentrality parameter θ functions as a shape parameter for the nondiseased-case distribution. For the diseased-case distribution, λ functions in the dual role of both a shape (through its effect on the noncentrality parameter) and scale parameter. As λ increases for a given value of θ, the mean and variance of the diseased distribution increase, with λ = 1 corresponding to equal conditional distributions.

Definition 2

The bi-chi-squared model states that the decision variable is an increasing transformation of a decision variable having either a positive (with λ > 1) or negative (with λ < 1) bi-chi-squared distribution. That is, the decision variable is an increasing function of W, defined by

$$W=\{\begin{array}{cc}{Y}^{\ast },\hfill & \lambda \ge 1\hfill \\ -Y^{\ast },\hfill & \lambda <1\hfill \end{array}\phantom{\}}$$ (9)

where Y* has a bi-chi-squared distribution with parameters θ and λ. The corresponding bi-chi-squared ROC curve is defined by W and will be denoted by ROC_χ²;λ,θ.

Theorem 1 below states that a binormal-LR ROC curve (with b ≠ 1) can be defined by a bi-chi-squared DV, as was shown in Section 3.1.

Theorem 1

Fix a ≥ 0, b > 0 with b ≠ 1. Define θ and λ by (6). Then

$${\mathrm{ROC}}_{LR;a,b}={\mathrm{ROC}}_{{\chi }^2;\lambda ,\theta }$$ (10)

Because (6) defines a one-to-one mapping from {(a, b) : a ≥ 0, b > 0, b ≠ 1} to {(λ, θ) : θ ≥ 0, λ > 0, λ ≠ 1} with

$$a=\sqrt{\frac{\theta {(\lambda -1)}^2}{\lambda }},b=\frac{1}{\sqrt{\lambda }}$$ (11)

it follows that the family of binormal-LR ROC curves with b ≠ 1 is equal to the family of bi-chi-squared ROC curves with λ ≠ 1, as formally stated in the following Corollary. Thus the binormal-LR model and bi-chi-squared model are equivalent in the sense that they result in the same families of ROC curves.

Corollary 1

$$\{{\mathrm{ROC}}_{\mathrm{LR};a,b}:a\ge 0,b>0,b\ne 1\}=\{{\mathrm{ROC}}_{{\chi }^2;\lambda ,\theta }:\theta \ge 0,\lambda >0,\lambda \ne 1\}$$

Table 2 provides a summary of the main results from Sections 3.1-2

Table 2.

Binormal likelihood-ratio ROC curve: original definition and corresponding bi-chi-squared formulation.

a) Original definition of ROCLR;a,b (based on log-likelihood-ratio):

$U=\ln \left[{\mathrm{LR}}_Y\left(Y\right)\right]=g(a,b)+\frac{(1-b^2)}{2}{(Y-c_1)}^2$

ROCLR;a,b = {(Pr (U ≥ c|D = 0), Pr (U ≥ c|D = 1)) : –∞ < c < ∞}

b) Bi-chi-square formulation:

Y* ≡ (Y – c1)2

$Y^{\ast }\mid (D=0)\sim {\chi }_{1;\theta }^2$

$Y^{\ast }\mid (D=1)\sim \lambda {\chi }_{1;\lambda \theta }^2$

${\mathrm{ROC}}_{{\chi }^2;\lambda ,\theta }=\{\begin{array}{cc}\{\mathrm{Pr}(Y^{\ast }\ge c\mid D=0),\mathrm{Pr}(Y^{\ast }\ge c\mid D=1):c\ge 0\},\hfill & \lambda \ge 1\hfill \\ \{\mathrm{Pr}(-Y^{\ast }\ge c\mid D=0),\mathrm{Pr}(-Y^{\ast }\ge c\mid D=1):c\le 0\},\hfill & \lambda <1\hfill \end{array}\phantom{\}}$

or equivalently,

ROCχ2;λ,θ = {(Pr (W > c|D = 0), Pr (W > c|D = 1)) : –∞ < c < ∞}

where

$W=\{\begin{array}{cc}{Y}^{\ast },\hfill & \lambda \ge 1\hfill \\ -Y^{\ast },\hfill & \lambda <1\hfill \end{array}\phantom{\}}$

c) Relationship (b ≠ 1):

ROCLR;a,b = ROCχ2;λ,θ

where

$\theta =\frac{a^2{b}^2}{{(1-b^2)}^2}$

$\lambda =\frac{1}{b^2}$

Notes: Y is binormal with conditional distributions Y | (D = 0) ~ N (0, 1), Y| (D = 1) ~ N (a/b, 1/b²); LR_Y (·) is the likelihood ratio function for Y; c₁ = –ab/ (1 – b²) is the threshold where LR_Y (·) attains its minimum (b < 1) or maximum (b > 1); ROC_LR;a,b is the binormal likelihood-ratio ROC curve with parameters a and b; ROC_χ²;λ,θ is the bi-chi-squared ROC curve with parameters λ > 0 and θ ≥ 0.

3.3. Results for b = 1

3.3.1. Case: a ≠ 0

The condition b = 1 implies that Y has conditional distributions (Y|D = 0) ~ N (0, 1) and (Y|D = 1) ~ N (a, 1). Then from (1), U = ln [LR_Y (Y)] takes the form

$$U=aY-\frac{1}{2}{a}^2$$

Let ROC_Bin;a,b denote a binormal ROC curve with binormal parameters a and b. It follows that if a > 0 then U is an increasing transformation of Y; hence ROC_LR;a,b=1 = ROC_Bin;a,b=1. If a < 0 then U is an increasing transformation of –Y; because –Y is binormal with binormal parameters |a| and b = 1, it follows that ROC_LR;a<0,b=1 = ROC_Bin;|a|,b=1. Thus, as was true for b ≠ 1, the binormal-LR ROC curve is invariant to the sign of a.

3.3.2. Case: a = 0

For a = 0 and b = 1 the conditional distributions of Y are the same and U = ln [LR_Y (Y)] = 0, which defines a discrete ROC curve with only two points, (0, 0) and (1, 1); hence depending on the threshold chosen, all subjects are classified either as diseased or nondiseased. In contrast, the ROC curve based on Y is the chance line tpf = fpf. Noting that the binormal-LR curve converges to the chance line as a approaches 0 for b = 1, I arbitrarily define ROC_LR;a=0,b=1 to be the chance line, i.e.,

$${\mathrm{ROC}}_{\mathrm{LR};a=0,b=1}\equiv {\mathrm{ROC}}_{\mathrm{Bin};a=0,b=1}$$

This situation is not discussed in the Metz and Pan development.

3.3.3. Inclusion of λ = 1 in the bi-chi-squared parameter space

Setting λ = 1 for any value of θ in (5) results in both conditional distributions of Y* (5) having ${\chi }_{1;\theta }^2$ distributions and a chance-line ROC curve. It follows that

$${\mathrm{ROC}}_{{\chi }^2;\lambda =1,\theta }={\mathrm{ROC}}_{\mathrm{LR};a=0,b=1}={\mathrm{ROC}}_{\mathrm{Bin};a=0,b=1}$$

Thus the chance line is the only concave binormal ROC curve (i.e., b = 1) that can be exactly represented by a bi-chi-squared ROC curve.

4. Formulas

In this section I derive basic formulas for the bi-chi-squared curve. Results from this section are presented in Table 3.

Table 3.

Tpf, fpf, AUC, and pAUC for the bi-chi-squared ROC curve.

a) Bi-chi-squared ROC curve:

${\mathrm{ROC}}_{x^2,\lambda ,\theta }=\{\begin{array}{cc}\{1-F_{\theta }\left(c\right),1-F_{\lambda \theta }(c∕\lambda ):c\ge 0\},\hfill & \lambda >1\hfill \\ \{F_{\theta }\left(c\right),F_{\lambda \theta }(c∕\lambda ):c\ge 0\},\hfill & \lambda <1\hfill \end{array}\phantom{\}}$

b) Tpf for fixed fpf, 0 < fpf < 1:

$\mathrm{tpf}\left(\mathrm{fpf}\right)=\{\begin{array}{cc}1-F_{\lambda \theta }\left[\frac{1}{\lambda }{F}_{\theta }^{-1}(1-\mathrm{fpf})\right],\hfill & \lambda >1\hfill \\ F_{\lambda \theta }\left[\frac{1}{\lambda }{F}_{\theta }^{-1}\left(\mathrm{fpf}\right)\right],\hfill & \lambda <1\hfill \end{array}\phantom{\}}$

c) Fpf for fixed tpf, 0 < tpf < 1:

$\mathrm{fpf}\left(\mathrm{tpf}\right)=\{\begin{array}{cc}1-F_{\theta }\left[\lambda F_{\lambda \theta }^{-1}(1-\mathrm{tpf})\right],\hfill & \lambda >1\hfill \\ F_{\theta }\left[\lambda F_{\lambda \theta }^{-1}\left(\mathrm{tpf}\right)\right],\hfill & \lambda <1\hfill \end{array}\phantom{\}}$

d) AUC:

$\mathrm{AUC}=\{\begin{array}{cc}{F}_{\mathrm{BVN}}(u_1,y_2;\rho )+F_{\mathrm{BVN}}(-u_1,-u_2;\rho ),\hfill & \lambda >1\hfill \\ 1-[F_{\mathrm{BVN}}(u_1,u_2;\rho )+F_{\mathrm{BVN}}(-u_1,-u_2;\rho )],\hfill & \lambda <1\hfill \end{array}\phantom{\}}$

where

$u_1=\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},u_2=\sqrt{\theta }\sqrt{\lambda +1},\rho =-\frac{\lambda -1}{\lambda +1}$

e) AUC alternative expression, proposed by Metz & Pan [11, 12]:

$\mathrm{AUC}=\Phi \left(\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}}\right)+2F_{\mathrm{BVN}}\left(-\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},0;-\frac{2\sqrt{\lambda }}{\lambda +1}\right),\lambda \ne 1$

f) Partial AUC:

${\mathrm{pAUC}}_{\mathrm{fpf}}(0,{\mathrm{fpf}}_0)=\{\begin{array}{c}{F}_{\mathrm{BVN}}(u_1,y_1;{\rho }_1)+F_{\mathrm{BVN}}(-u_1,-y_2;{\rho }_1)+F_{\mathrm{BVN}}(-u_2,y_1;{\rho }_1)+F_{\mathrm{BVN}}(u_2,-y_2;{\rho }_1),\lambda >1\hfill \\ {\mathrm{fpf}}_0-F_{\mathrm{BVN}}(u_1,u_2;\rho )-F_{\mathrm{BVN}}(-u_1,-u_2;,\rho )+F_{\mathrm{BVN}}(u_1,y_3;{\rho }_1)+F_{\mathrm{BVN}}(-u_1,-y_4;{\rho }_1)+F_{\mathrm{BVN}}(-u_2,y_3;{\rho }_1)+F_{\mathrm{BVN}}(u_2,-y_4;{\rho }_1),\lambda <1\hfill \end{array}\phantom{\}}$

${\mathrm{pAUC}}_{\mathrm{tpf}}({\mathrm{tpf}}_0,1)=\mathrm{Auc}-{\mathrm{pAUC}}_{\mathrm{tpf}}(0,\mathrm{fpf}\left({\mathrm{tpf}}_0\right))-{\mathrm{tpf}}_0\times [1-\mathrm{fpf}\left({\mathrm{tpf}}_0\right)]$

where ρ, u1 and u2 are defined in (d) and

${\rho }_1=\frac{-1}{\sqrt{\lambda +1}}$

$y_1=\sqrt{\theta }-\sqrt{F_{\theta }^{-1}(1-{\mathrm{fpf}}_0)},y_2=\sqrt{\theta }+\sqrt{F_{\theta }^{-1}(1-{\mathrm{fpf}}_0)}$

$y_3=\sqrt{\theta }-\sqrt{F_{\theta }^{-1}\left({\mathrm{fpf}}_0\right)},y_4=\sqrt{\theta }+\sqrt{F_{\theta }^{-1}\left({\mathrm{fpf}}_0\right)}$

Notes: ROC_x²;λ,θ denotes the bi-chi-squared ROC curve, where λ > 0 and θ ≥ 0; F_v denotes the distribution function for a random variable having a chi-squared distribution with one degree of freedom and noncentrality parameter V; F_BVN (·,·; ρ) denotes the standardized bivariate normal distribution function with correlation ρ; Φ denotes the standard normal distribution function; tpf = true positive fraction; fpf = false positive fraction.

4.1. Tpf for fixed fpf

4.1.1. Derivation and results for λ > 1

Letting F_ν denote the distribution function for a random variable having a chi-squared distribution with one degree of freedom and noncentrality parameter ν, it follows from (9) that

$${\mathrm{ROC}}_{{\chi }^2;\lambda ,\theta }=\{(1-F_{\theta }\left(c\right),1-F_{\lambda \theta }(c∕\lambda )):c\ge 0\}$$ (12)

From (12) we can express c in terms of fpf: $c=F_{\theta }^{-1}(1-\mathrm{fpf})$. Substituting into (12) yields

$${\mathrm{ROC}}_{{\chi }^2;\lambda ,\theta }=\left\{\left(\mathrm{fpf},1-F_{\lambda \theta }\left(\frac{1}{\lambda }{F}_{\theta }^{-1}(1-\mathrm{fpf})\right)\right):0<\mathrm{fpf}<1\right\}$$

Thus

$$\mathrm{tpf}\left(\mathrm{fpf}\right)=1-F_{\lambda \theta }\left(\frac{1}{\lambda }{F}_{\theta }^{-1}(1-\mathrm{fpf})\right),0<\mathrm{fpf}<1$$ (13)

4.1.2. Derivation and results for λ < 1

It follows from (9) that

$${\mathrm{ROC}}_{{\chi }^2;\lambda ,\theta }=\{(F_{\theta }\left(c\right),F_{\lambda \theta }(c∕\lambda )):c\ge 0\}$$ (14)

Expressing c in (14) in terms of fpf results in the equivalent expression

$${\mathrm{ROC}}_{{\chi }^2;\lambda ,\theta }=\left\{\left(\mathrm{fpf},F_{\lambda \theta }\left(\frac{1}{\lambda }{F}_{\theta }^{-1}\left(\mathrm{fpf}\right)\right)\right):0<\mathrm{fpf}<1\right\}$$

Thus

$$\mathrm{tpf}\left(\mathrm{fpf}\right)=F_{\lambda \theta }\left(\frac{1}{\lambda }{F}_{\theta }^{-1}\left(\mathrm{fpf}\right)\right)$$

Formulas expressing fpf as a function of tpf, which are included in Table 3, can be derived from the above results.

4.2. AUC

4.2.1. Derivation and results for λ > 1

Fix λ > 1. Let AUC_χ² denote the area under the bi-chi-squared ROC curve. Let $Y_D^{\ast }$ and $Y_{\stackrel{‒}{D}}^{\ast }$ denote independent random variables with the same distributions as Y*|(D = 0) and Y*|(D = 1), respectively. That is,

$$Y_{\stackrel{‒}{D}}^{\ast }\sim {\chi }_{1;\theta }^2\text{and}{Y}_D^{\ast }\sim \lambda {\chi }_{1;\lambda \theta }^2$$

Bamber [14] shows that the probability of a continuous diseased test result exceeding a continuous nondiseased test result is equal to the AUC. It follows from (9) that

$${\mathrm{AUC}}_{{\chi }^2}=\mathrm{Pr}\left(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast }\right)$$

Let X_D̄ and X_D be independent random variables such that

$$X_{\stackrel{‒}{D}}\sim N\left(\sqrt{\theta },1\right)$$

$$X_D\sim \sqrt{\lambda }N\left(\sqrt{\lambda \theta },1\right)=N\left(\lambda \sqrt{\theta },\lambda \right)$$ (15)

Then

$$X_{\stackrel{‒}{D}}^2\sim {\chi }_{1;\theta }^2\text{and}{X}_D^2\sim \lambda {\chi }_{1;\lambda \theta }^2$$

Thus

$$\begin{array}{cc}\hfill {\mathrm{AUC}}_{{\chi }^2}=& \mathrm{Pr}\left(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast }\right)\hfill \\ \hfill =& \mathrm{Pr}\left(X_D^2>X_{\stackrel{‒}{D}}^2\right)\hfill \\ \hfill =& \mathrm{Pr}(X_D>X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}}>0)+\mathrm{Pr}(X_D<X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}}<0)+\mathrm{Pr}(X_D<-X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}}>0)+\mathrm{Pr}(X_D>-X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}}<0)\hfill \end{array}$$

It follows that

$${\mathrm{AUC}}_{{\chi }^2}=\mathrm{Pr}\left(A_1\right)+\mathrm{Pr}\left(A_2\right)$$

where the mutually exclusive events A₁ and A₂ are defined by

$$\begin{array}{cc}\hfill A_1=& \{X_D>X_{\stackrel{‒}{D}},X_D>-X_{\stackrel{‒}{D}}\}\hfill \\ \hfill A_2=& \mathrm{Pr}\{X_D<X_{\stackrel{‒}{D}},X_D<-X_{\stackrel{‒}{D}}\}\hfill \end{array}$$

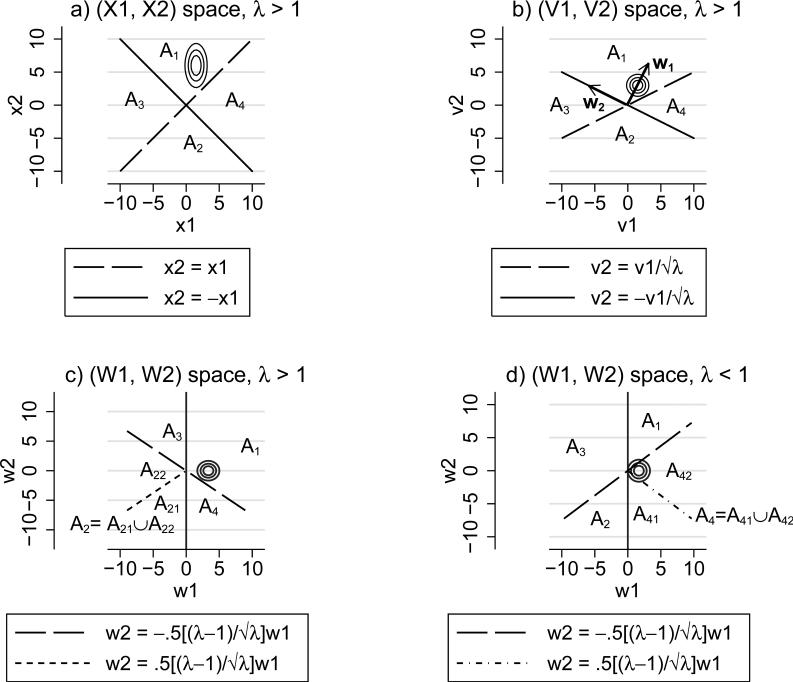
The contour plot of the bivariate (X_D̄, X_D) density function and subspaces corresponding to A₁ and A₂ are graphically displayed in Figure 2a. Note that X_D̄ and X_D are notated as X₁ and X₂, respectively, in the figure. Also displayed are the subspaces corresponding to A₃ and A₄, defined by

$$\begin{array}{cc}\hfill A_3=& \mathrm{Pr}\{X_D>X_{\stackrel{‒}{D}},X_D<-X_{\stackrel{‒}{D}}\}\hfill \\ \hfill A_4=& \mathrm{Pr}(X_D<X_{\stackrel{‒}{D}},X_D>-X_{\stackrel{‒}{D}})\hfill \end{array}$$

Figure 2.

Plots related to AUC proofs. X₁ and X₂ are independent random variables such that $X_1\sim N(\sqrt{\theta },1)$ and $X_2\sim N(\lambda \sqrt{\theta },\lambda )$; thus $X_1^2\sim {\chi }_{1;\theta }^2$ and $X_2^2\sim \lambda {\chi }_{1;\lambda \theta }^2$. For plots (a), (b) and (c), θ = 2.25, λ = 4; for plot (d) θ = 2.25, λ = 0.25. Plot (a) shows the contour plot of the (X₁, X₂) density function and the subspaces corresponding to events A₁, A₂, A₃ and A₄. Plot (b) shows the transformed contour plot and subspaces in the (V₁, V₂) space, where V₁ = X₁ and $V_2=X_2∕\sqrt{\lambda }$. Plot (b) also shows the column vectors of the orthogonal matrix $P=\frac{\sqrt{\lambda }}{\sqrt{1+\lambda }}[{(\frac{1}{\sqrt{\lambda }},1)}^{\prime },{(-1,\frac{1}{\sqrt{\lambda }})}^{\prime }]$, denoted by w₁ and w₂, up to a scaling constant. Plot (c) shows the transformed contour plot and subspaces in the (W₁, W₂) space, where (W₁, W₂)′ = P′ (V₁, V₂)′; i.e. W₁ and W₂ are the components of the projections onto the normalized w₁ and w₂ vectors in (b). Plot (d) is similar to (c), except that λ = 0.25.

Let F_BVN(·, ·, ρ) denote the distribution function for a standardized bivariate normal distribution with correlation ρ, and let MVN (μ₁, μ₂, ${\sigma }_1^2$, ${\sigma }_2^2$, σ₁₂) denote a bivariate normal distribution with means μ₁, μ₂, variances ${\sigma }_1^2$, ${\sigma }_2^2$, and covariance σ₁₂. Writing A₁ and A₂ in the form

$$\begin{array}{cc}\hfill A_1=& \{-(X_D-X_{\stackrel{‒}{D}})<0,-(X_D+X_{\stackrel{‒}{D}})<0\}\hfill \\ \hfill A_2=& \{X_D-X_{\stackrel{‒}{D}}<0,X_D+X_{\stackrel{‒}{D}}<0\}\hfill \end{array}$$

and noting that

$$(X_D-X_{\stackrel{‒}{D}},X_D+X_{\stackrel{‒}{D}})\sim \mathrm{MVN}\left(\sqrt{\theta }(\lambda -1),\sqrt{\theta }(\lambda +1),\lambda +1,\lambda +1,\lambda -1\right)$$

it follows that

$$\begin{array}{cc}\hfill \mathrm{Pr}\left(A_1\right)=& F_{\mathrm{BVN}}\left(\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},\frac{\sqrt{\theta }(\lambda +1)}{\sqrt{\lambda +1}};\frac{\lambda -1}{\lambda +1}\right)\hfill \\ \hfill \mathrm{Pr}\left(A_2\right)=& F_{\mathrm{BVN}}\left(-\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},\frac{\sqrt{\theta }(\lambda +1)}{\sqrt{\lambda +1}};\frac{\lambda -1}{\lambda +1}\right)\hfill \end{array}$$

Hence

$${\mathrm{AUC}}_{{\chi }^2}=F_{\mathrm{BVN}}(u_1,u_2;,\rho )+F_{\mathrm{BVN}}(-u_1,-u_2;,\rho )$$ (16)

where

$$u_1=\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},u_2=\sqrt{\theta }\sqrt{(\lambda +1)},\rho =\frac{\lambda -1}{\lambda +1}$$ (17)

4.2.2. Derivation and results for λ < 1

Fix λ < 1. From (9) and Bamber's result [14] we have

$${\mathrm{AUC}}_{{\chi }^2}=\mathrm{Pr}\left(-Y_D^{\ast }>-Y_{\stackrel{‒}{D}}^{\ast }\right)=\mathrm{Pr}\left(Y_D^{\ast }<Y_{\stackrel{‒}{D}}^{\ast }\right)$$

It follows that

$${\mathrm{AUC}}_{{\chi }^2}=1-\mathrm{Pr}\left(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast }\right)$$ (18)

Since the derivation for Pr($Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast }$) in Section 4.2.1 did not depend on the value of λ, it follows that the formula for Pr($Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast }$) for λ < 1 is the same as for λ > 1. Hence

$${\mathrm{AUC}}_{{\chi }^2}=1-[F_{\mathrm{BVN}}(u_1,u_2;\rho )+F_{\mathrm{BVN}}(-u_1,-u_2;,\rho )]$$ (19)

where u₁, u₂, and ρ are given by (17). Because A₁, A₂, A₃ and A₄ are mutually exclusive with ${\sum }_{i=1}^{4}P\left(A_i\right)=1$, it also follows from (18) that

$${\mathrm{AUC}}_{{\chi }^2}=\mathrm{Pr}\left(A_3\right)+\left(A_4\right)$$ (20)

Although a formula similar to (16) could be derived from this expression, for our purposes (20) will be used for deriving the alternative AUC expression (discussed below) in Appendix A.

4.2.3. Alternative AUC expression

Metz and Pan [11, 12] present an alternative expression for AUC_χ², expressing it as the sum of the AUC of the corresponding binormal ROC curve plus a nonnegative term. However, they do not provide a proof for their results. For completeness I derive their result in Appendix A. I show in Section 5 that their result, in terms of the bi-chi-squared parameterization, is given by

$${\mathrm{AUC}}_{{\chi }^2}=\Phi \left(\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}}\right)+2F_{\mathrm{BVN}}\left(-\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},0;-\frac{2\sqrt{\lambda }}{\lambda +1}\right),\lambda \ne 1$$ (21)

The first term on the right side is the AUC of the corresponding binormal ROC curve.

4.3. Partial AUC

Two different partial areas under the ROC curve have been proposed [15, 16, 17]: the area under the ROC curve over an fpf interval (fpf₁ < fpf₂), which I denote by pAUC_fpf (fpf₁, fpf₂), and the area to the right of the ROC curve over a tpf interval (tpf₁ < tpf₂), which I denote by pAUC_tpf (tpf₁, tpf₂). Both partial areas are often normalized by dividing by the length of the interval, which allows the partial area to be interpreted as the average value of tpf or fpf over their respective intervals. Furthermore, it is easy to geometrically show

$${\mathrm{pAUC}}_{\mathrm{tpf}}({\mathrm{tpf}}_0,1)=\mathrm{AUC}-{\mathrm{pAUC}}_{\mathrm{fpf}}(0,\mathrm{fpf}\left({\mathrm{tpf}}_0\right))-{\mathrm{tpf}}_0\times [1-\mathrm{fpf}\left({\mathrm{tpf}}_0\right)]$$

Because pAUC_fpf (fpf₁, fpf₂) = pAUC_fpf (0, fpf₂) – pAUC_fpf (0, fpf₁) and pAUC_tpf (tpf₁, tpf₂) = pAUC_tpf (tpf₁, 1) – pAUC_tpf (tpf₂, 1), it suffices to derive only the formula for pAUC_fpf (0, fpf₀), which is derived in Appendix B and presented in Table 3.

Pan and Metz [11] provide partial AUC formulas but do not provide proofs. Although their formulas are different from the ones in this paper, I was able to empirically demonstrate equality of their partial AUC formulas with the formulas derived in this paper by comparing partial AUC results from PROPROC with those computed using the formulas in this paper. I do not include analytical proofs showing equivalence because their formulas have no clear conceptual advantage and require the use of numerical methods.

5. Comparison with Metz and Pan approach

5.1. Metz and Pan approach

Metz and Pan [12] derive results for ROC_LR;a,b based on the DV

$$V=\frac{(b+1)Y}{a+\sqrt{a^2+2(1-b^2)Y}}$$ (22)

which is an increasing transformation of LR_Y (Y). They use the (d_a, c) parameterization for V , given by

$$d_a=\frac{\sqrt{2}a}{\sqrt{1+b^2}},0\le d_a<\infty$$ (23)

$$c=\frac{b-1}{b+1},-1<c<1$$ (24)

The positive density support of V is given by

$$\begin{array}{cc}\hfill \frac{d_a}{4c}\sqrt{1+c^2}\le V\le \infty ,& \text{if}c<0\hfill \\ \hfill -\infty \le V\le \infty ,& \text{if}c=0\hfill \\ \hfill -\infty \le V\le \frac{d_a}{4c}\sqrt{1+c^2},& \text{if}c>0\hfill \end{array}$$

Metz and Pan [11, 12] do not write tpf as an analytic function of fpf or vice versa. Instead, for c ≠ 0 they give the following formulas for fpf and tpf corresponding to threshold v_c:

$$\mathrm{fpf}\left(v_c\right)=\Phi \left[-(1-c)v_c-\frac{d_a}{2}\sqrt{1+c^2}\right]+\left\{\Phi \left[-(1-c)v_c+\frac{d_a}{2c}\sqrt{1+c^2}\right]-H\left(c\right)\right\}$$ (25)

$$\mathrm{tpf}\left(v_c\right)=\Phi \left[-(1+c)v_c+\frac{d_a}{2}\sqrt{1+c^2}\right]+\left\{\Phi \left[-(1+c)v_c+\frac{d_a}{2c}\sqrt{1+c^2}\right]-H\left(c\right)\right\}$$ (26)

where H (c) = 0 if c < 0 and H (c) = 1 if c < 0.

Metz and Pan [11, 12] give the following AUC formula without proof:

$$\mathrm{AUC}=\Phi \left(\frac{d_a}{\sqrt{2}}\right)+2F_{\mathrm{BVN}}\left(-\frac{d_a}{\sqrt{2}},0;-\frac{1-c^2}{1+c^2}\right)$$ (27)

Using the relationships between the bi-chi-squared (λ, θ) and Metz and Pan (d_a, c) parameterizations discussed below, in terms of the (λ, θ) parameterization (27) takes the form of equation (21).

5.2. Parameterization relationships

It follows from (23-24) that

$$a=d_a\sqrt{\frac{1+c^2}{{(1-c)}^2}}\text{and}b=\frac{c+1}{1-c}$$ (28)

Using (28) and (11) it is straightforward to derive the relationships between the bi-chi-squared (λ, θ) and Metz and Pan (d_a, c) parameterizations, c ≠ 0 and λ ≠ 1:

$$\lambda =\frac{{(1-c)}^2}{{(c+1)}^2},\theta =\frac{1}{16c^2}{d}_a^2(c^2+1){(c+1)}^2$$

and

$$c=\frac{1-\sqrt{\lambda }}{1+\sqrt{\lambda }},d_a=\frac{\sqrt{2\theta {(\lambda -1)}^2}}{\sqrt{(\lambda +1)}}$$

It follows that c is a strictly decreasing function of λ and d_a is a strictly increasing function of θ for fixed λ.

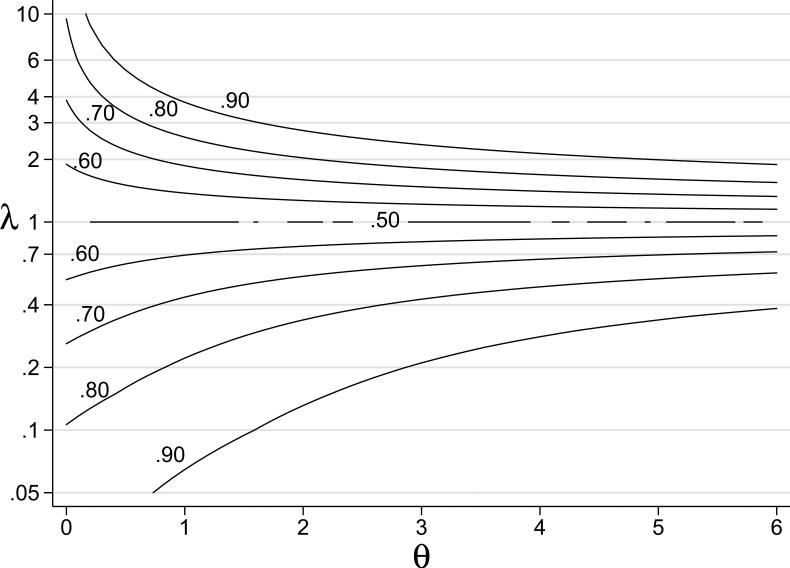
According to Metz and Pan [12, p. 12], an important computational reason they preferred the (d_a, c) parameterization was because for fixed d_a there is a one-to-one relationship between AUC and c in each of the {c < 0} and {c < 0} regions; specifically, AUC is an increasing (decreasing) function of c if c < 0 (c < 0). Similarly, for fixed θ, AUC in an increasing (decreasing) function of λ if λ < 1 (λ < 1); a proof is provided in Appendix C. It can also be shown for fixed λ ≠ 1 that AUC is an increasing function of θ. Figure 3 illustrates how the AUC changes with increasing or decreasing theta or lambda, given the value of the other parameter.

Figure 3.

Contour map of AUC in the bi-chi-squared parameter space. There is a one-to-one relationship between the values of λ and AUC for each value of θ in the region λ > 1 and also in the region λ < 1. Notes: for λ = 1 the ROC curve is the chance line with AUC = 0.5; the λ-axis is scaled logarithmically.

5.3. Advantages of the bi-chi-squared approach

The bi-chi-squared approach has two important advantages over the Metz and Pan approach. First, it is conceptually easier to explain and understand: because the log likelihood-ratio function of a binormal random variable Y is symmetric about c₁, it follows that either Y* = (Y – c₁)² or –Y* is an increasing transformation of LR_Y (Y) and hence can be used as the DV for defining the binormal-LR ROC curve.. In contrast, it is not immediately obvious that V (22) is an increasing transformation of LR_Y (Y). The second advantage is that the conditional distributions of Y* are familiar chi-squared distributions, which allows for easy derivation of statistical properties with no further need to consider the relationship between Y* and Y. In contrast, the conditional distributions of V are not familiar and have support boundaries that are functions of the distribution parameters, making derivations more tedious. The conditional densities of V are not described analytically or graphically by Metz and Pan. For example, Metz and Pan derive results for tpf and fpf by determining the conditional probabilities of regions of Y that map into (V > v_c), rather than working directly with the conditional distributions of V .

6. Estimation

Software for estimating the binormal-LR ROC curve has been extensively developed by Charles Metz and colleagues [11, 12, 18] at the University of Chicago, with much of the work undertaken in collaboration with Kevin Berbaum and colleagues at the University of Iowa. This software was originally called PROPROC, but recently has been renamed PBM; however, the program has remained essentially the same (personal communications with Charles E. Metz, June 3, 2012, and Lorenzo L. Pesce, March 13, 2014). The algorithm is extremely fast and has undergone extensive testing. It can be downloaded in various formats from websites at either university (http://metz-roc.uchicago.edu/ and http://perception.radiology.uiowa.edu/). PROPROC is used with the stand-alone multireader ROC software OR-DBM MRMC 2.5 [19] as well as the program OR/DBM MRMC 3.0 for SAS [20], both freely available at http://perception.radiology.uiowa.edu/.

In this section I show that the bi-chi-squared model makes it is possible to estimate ROC-curve parameters for discrete rating data using standard statistical software to maximize the likelihood function; I refer to such an algorithm as a bi-chi-squared algorithm. Specifically, I describe a bi-chi-squared algorithm that uses the SAS procedure NLMIXED to maximize the likelihood.

I emphasize that the bi-chi-squared algorithm developed in this section is not intended for general use, but rather for empirically validating the bi-chi-squared approach. In Example 1 in Section 7 I show that AUC estimates for a real data set obtained using the bi-chi-squared algorithm are virtually identical to those obtained using the PROPROC algorithm.

6.1. Assumptions

The basic assumption when estimating the binormal-LR ROC curve is that the DV, explicit or implicit, has the same distribution as the likelihood-ratio transformation of a binormal random variable (or more generally, as an increasing transformation of the likelihood-ratio transformation of a binormal random variable); this is the approach taken by Metz and Pan. As discussed in Section 2, it is important to note that they do not assume the DV has a binormal distribution. Similarly, for estimation purposes using the bi-chi-squared approach, I assume the DV follows the bi-chi-squared model, not the binormal model.

6.2. Bi-chi-squared algorithm

6.2.1. Likelihood function

I assume that a reader's ordinal likelihood-of-disease ratings represent the binning of values of a latent bi-chi-squared model DV; i.e., the DV has either a positive (with λ ≥ 1) or negative (with λ < 1) bi-chi-squared distribution. Specifically, letting R denote an observed rating variable having p distinct values r₁ < ... < r_p and letting L denote the latent DV, it is assumed that Pr (R = r_i) = Pr (c_i–1 < c_i), where –∞ = c₀ < c₁ < ... < c_p–1 < c_p = ∞; i.e., (c_i–1, c_i) is the latent bin corresponding to R = r_i.

Furthermore, I assume that the reader assigns likelihood-of-disease ratings independently to n₀ nondiseased and n₁ diseased case images. Let n_0i and n_1i denote the number of nondiseased and diseased cases assigned rating r_i, respectively; thus ${\sum }_{i=1}^p{n}_{0i}=n_0$ and ${\sum }_{i=1}^p{n}_{1i}=n_1$. The log likelihood, after deleting terms that do not depend on model parameters, is given by

$$ll=\sum _{i=1}^p{n}_{0i}\ln \mathrm{Pr}(R=r_i\mid D=0)+\sum _{i=1}^p{n}_{1i}\ln \mathrm{Pr}(R=r_i\mid D=1)$$

Define

$$\begin{array}{cc}\hfill {\mathrm{fpf}}_i& \equiv \mathrm{Pr}(R\ge r_i\mid D=0)=\mathrm{Pr}(L>c_{i-1}\mid D=1)\hfill \\ \hfill {\mathrm{tpf}}_i& \equiv \mathrm{Pr}(R\ge r_i\mid D=0)=\mathrm{Pr}(L>c_{i-1}\mid D=1)\hfill \end{array}$$

i = 1,..., p and

${\mathrm{fpf}}_{p+1}={\mathrm{tpf}}_{p+1}\equiv 0$

Then

$$ll=\sum _{i=1}^p{n}_{0i}\ln ({\mathrm{fpf}}_i-{\mathrm{fpf}}_{i+1})+\sum _{i=1}^p{n}_{1i}\ln ({\mathrm{tpf}}_i-{\mathrm{tpf}}_{i+1})$$ (29)

A bi-chi-squared algorithm maximizes ll with respect to {λ, θ, c₁,..., c_p–1}, or alternatively with respect to another parameterization such as $\{\lambda ,\theta ,{\mathrm{fpf}}_1,\dots ,{\mathrm{fpf}}_p\}$ or $\{\lambda ,\theta ,{\Delta }_1,\dots ,{\Delta }_p\}$ , where Δ_i = fpf_i – fpf_i+1. Here the bi-chi-squared parameter space is λ < 0, θ ≥ 0. Note that I have included λ = 1 in the parameter space, which for any value of θ corresponds to the chance-line ROC curve as discussed in Section 3.3.3.

With this approach, maximum likelihood estimation excludes the subset of proper binormal ROC curves. This approach is justified because any proper binormal ROC curve (thus b = 1) can be approximated by a bi-chi-squared curve with arbitrary precision. I note that PROPROC and PBM take a similar approach (Lorenzo L. Pesce, personal communication, April 18, 2014.)

6.2.2. Maximizing the likelihood using PROC NLMIXED

Using the parameterization {λ, θ, Δ₁,..., Δ_p}, where Δ_i = fpf_i – fpf_i+1 (and thus ${\sum }_{i=1}^p{\Delta }_i=1$), I use the SAS procedure NLMIXED to compute parameter estimates that maximize ll (29) for the data set in Example 1 in Section 7. There are five possible ratings: r_i = i, i = 1,..., 5. For initial 1 in Section set ${\widehat{\Delta }}_{i,\text{initial}}=\max ({\widehat{\Delta }}_i,.001)$, i = 1,2,3,4, where ${\widehat{\Delta }}_i$ is the empirical estimate (i.e., proportion of nondiseased subjects assigned rating i). The algorithm sets ${\widehat{\Delta }}_{5;\text{initial}}=1-{\sum }_{i=1}^4{\widehat{\Delta }}_{i;\text{initial}}$. To avoid ${\widehat{\Delta }}_{5;\text{initial}}$ < .0001, if ${\sum }_i^4{\widehat{\Delta }}_{i;\text{initial}}$ < 0.999 then I modify ${\widehat{\Delta }}_{i;\text{initial}}$ i = 1,2,3,4 by subtracting a small constant from one of them to ensure that ${\sum }_i^4{\widehat{\Delta }}_{i;\text{initial}}\le 0.999$. This process results in initial Δ_i = fpf_i – fpf_i+1 estimates close to the empirical estimates, but with no estimates less than .001 for each of the ten modality-reader combinations. Initial estimates for λ and θ are computed using (6) with a and b replaced by binormal-model estimates. The log-likelihood function is computed using equation (29) with tpf_i replaced by

$${\mathrm{tpf}}_i=\{\begin{array}{cc}1-F_{\lambda \theta }\left[\frac{1}{\lambda }{F}_{\theta }^{-1}(1-{\mathrm{fpf}}_i)\right],\hfill & \lambda \ge 1\hfill \\ F_{\lambda \theta }\left[\frac{1}{\lambda }{F}_{\theta }^{-1}\left({\mathrm{fpf}}_i\right)\right],\hfill & \lambda <1\hfill \end{array}\phantom{\}}$$ (30)

where the fpf_i are computed from the Δ_i. Note that (30) combines the expressions for tpf(fpf) for λ < 1 and b < 1 from Table 3b and also includes λ = 1 for which the expression reduces to tpf_i = fpf_i.

The SAS code used for computing the ROC parameter estimates for Example 1 is provided in Appendices S1 and S2, available in the online Supporting Materials. Two version of the codes are provided: a simple version without macros in Appendix S1 that estimates the bi-chi-squared ROC curve for one reader-treatment combination, and a more extensive version with macros in Appendix S2 that does the complete Example 1 analysis. The code is somewhat similar to that provided by Gönen [21, Chapter 5], who discusses estimating the binormal ROC curve using the SAS NLMIXED procedure. The main difference is that the bi-chi-squared code involves deltas rather than thresholds in the parameterization; this seemed to be a more natural approach because of the need to accommodate both the positive and negative bi-chi-squared distributions. Gönen [21, Appendix] provides a short introduction to PROC NLMIXED, which I recommend for the reader who is not familiar with PROC NLMIXED.

Although the code in Appendix S2 works well for the Example 1 data in the next section, again it should be noted that it is not intended for general use, but rather for validation of the bi-chi-squared approach. In particular, a program for general use would need a more rigorous approach for selecting starting values and need to be more thoroughly tested. For example, Pesce et al. [18] describe a rigorous method for selecting initial estimates for PROPROC.

6.3. Continuous data

For continuous data, Metz et al. [22] propose defining categories of the observed data that correspond to vertical or horizontal jumps in the empirical ROC curve and then applying the approach used for ordinal discrete data to the defined categories. Specifically, they state that “ML estimation of an ROC curve from continuously-distributed data is equivalent to ML estimation from ordinal category data if truth state runs in the rank-ordered data (described next) are interpreted as categorical data.” This method of categorization is referred to as the LABROC4 categorization scheme and is discussed in the context of fitting binormal-LR models by Metz and Pan [12] and by Pesce and Metz [18]. Similarly, the bi-chi-squared algorithm for discrete data can be applied to continuous data.

6.4. Relationship between bi-chi-squared and PROPROC/PBM algorithms

Both the bi-chi-squared and PROPROC/PBM estimation algorithms maximize the same log-likelihood function (29), but with different formulas used for fpf and tpf. Bi-chi-squared uses (30), derived from the bi-chi-squared model, to estimate tpf as a function of fpf, whereas PROPROC/PBM uses (25) and (26), derived from the relationship between V (22) and Y, to compute fpf and tpf as functions of a threshold. Of course, the bi-chi-squared algorithm could also have computed tpf and fpf as functions of a threshold. Thus the log-likelihood functions are the same but parameterized differently.

From a computational perspective neither parameterization appears to have a substantive advantage if similar starting values and likelihood maximization techniques are used. This conjecture is based on the similarities between the parameterizations as discussed in Section 5.2, but further study is needed. Furthermore, it appears that the initial estimates and optimization approach discussed by Pesce and Metz [18] could be adapted for the bi-chi-squared parameterization. From my perspective, the main advantage of the bi-chi-squared approach is not computational, but as previously discussed, easier conceptual understanding and derivation of properties.

7. Examples

7.1. Example 1: Comparison of binormal, bi-chi-squared, PROPROC algorithm results

In this example I estimate the AUC for ten ROC curves using the PROPROC and bi-chi-squared algorithms under the assumption of a binormal-LR/bi-chi-squared model for the DV. The PROPROC algorithm estimates are computed using OR/DBM MRMC 3.0 for SAS [20] and the bi-chi-squared estimates are computed using the bi-chi-squared algorithm discussed in Section 6.2, as implemented by SAS code provided in Appendix S2 in the online Supporting Materials. Binormal estimates of a and b, computed using OR/DBM MRMC 3.0 for SAS [20], are used to compute initial λ and θ estimates for the bi-chi-squared algorithm using relationship (6).

The data are from a study [9] that compares the relative performance of single spin-echo magnetic resonance imaging (MRI) and cine MRI in detecting thoracic aortic dissection. There are 114 patients, 45 with an aortic dissection and 69 without. Five radiologists independently interpret all of the images using a five-point ordinal scale. Data for one of the reader-modality combinations (reader 5, cine MRI) are presented in Table 1.

Table 4 presents the AUC estimates for both algorithms and parameter estimates resulting from the bi-chi-squared algorithm. The AUC values in Table 4 are the same for both algorithms except for reader 3 and modality 1, for which the AUCs are 0.908 (PROPROC) and 0.929 (bi-chi-squared) with the PROPROC solution having the higher likelihood. This discrepancy for reader 3 and modality 1 was resolved by running the bi-chi-squared algorithm again but with several other starting values, which resulted in a value of AUC equal to the PROPROC value; the revised bi-chi-squared values are shown within parentheses.

Table 4.

Maximum likelihood parameter estimates for binormal-LR ROC curves for Van Dyke [9] data for comparing spin-echo and cine MRI in detecting thoracic aortic dissection. For the bi-chi-squared algorithm, initial estimates of λ and θ are functions of binomial parameter estimates and initial delta estimates are empirically estimated.

		AUC		Bi-Chi parameter estimates
Modality	Reader	PROPROC	Bi-Chi	λ	θ
1	1	0.934	0.934	3.418921	1.706011
1	2	0.891	0.891	3.172872	1.324854
1	3	0.908	0.929 (0.908)	2.532216 (46.929408)	3.239197 (0.006334)
1	4	0.977	0.977	786.713272	0.000017
1	5	0.841	0.841	9.366031	0.059426
2	1	0.952	0.952	3.788983	1.697356
2	2	0.926	0.926	73.205625	0.000024
2	3	0.930	0.930	3.940212	1.234458
2	4	1.000	1.000	1.283937	780.544368
2	5	0.943	0.943	12.075745	0.217397

Notes: Modality 1 = spin-echo MRI, 2 = cine MRI; PROPROC and Bi-Chi are the PROPROC and bi-chi-squared algorithms, respectively. The discrepancy between the PROPROC and bi-chi-squared AUC values for reader 3, modality 1 was resolved by rerunning the bi-chi-squared algorithm using several other starting values, which resulted in the values shown in parentheses.

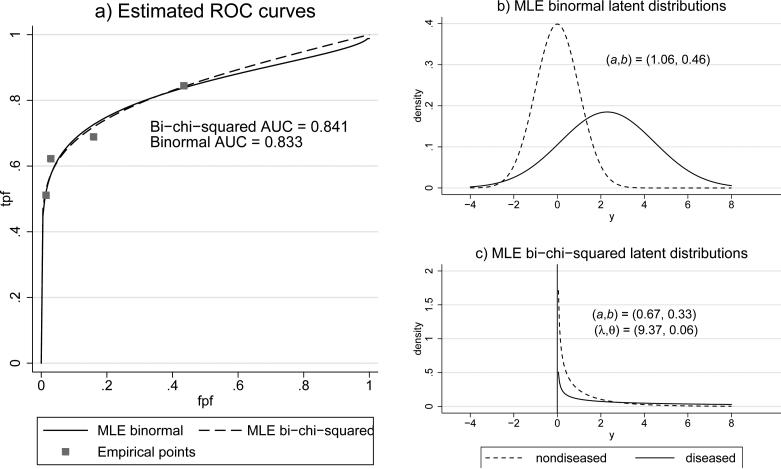
7.2. Example 2: Comparison of estimated binormal and bi-chi-squared ROC curves and latent distributions

Figure 4a shows the binormal and bi-chi-squared maximum-likelihood estimated (MLE) ROC curves for the data in Table 1a. The corresponding binormal and bi-chi-squared latent distributions are displayed in Figures 4b and 4c. (Note that the binormal MLE ROC curve and its latent DV distribution are also shown in Figures 1a and 1b, respectively.)

Figure 4.

Maximum-likelihood estimated binormal and bi-chi-squared ROC curves with corresponding latent decision variable distributions for Table 1a data (reader 5, modality 1). Note: MLE: maximum likelihood estimated.

Figure 4b includes the binormal MLE estimates: a = 1.06 and b = 0.46. Figure 4c includes the bi-chi-squared (λ θ) estimates and the corresponding estimates a = 0.67 and b = 0.33 computed using (11). Thus the a and b estimates for the binormal MLE curve are different than those for the bi-chi-squared MLE curve, as is generally the case. In contrast, in Figure 1a the binormal and bi-chi-squared (or binormal-LR) ROC curves have the same (a = 1.06, b = 0.46) parameter values because only the binormal ROC curve is estimated from the data; the purpose of Figure 1a is to display the binormal-LR ROC curve that is defined by that same a and b values. The distinction between these two graphs is important: although each possible binormal ROC curve defines a corresponding binormal-LR ROC curve having the same a and b values, as illustrated by Figure 1a, if binormal and binormal-LR ROC curves are estimated from the same data then the parameter values will typically differ, as illustrated in Figure 4 and previously discussed in Section 2.

Both ROC curves in Figure 4a are similar for fpf values less than that of the last empirical operating point. However, for greater fpf values the ROC curves are discernibly different: the binormal curve has a hook in the upper right corner in contrast to the binormal-LR curve, which has no hook because it is concave. As a result, the binormal-LR curve has the higher AUC (0.841 vs. 0.833).

7.3. Example 3: Interpretation of bi-chi-squared parameters in terms of similarity with corresponding binormal ROC curve

When presented with bi-chi-squared estimation results such as in Table 4, it is natural to ask if it is possible to know which of the bi-chi-squared ROC curves is approximated by its corresponding binormal curve from an examination of the (λ, θ) values. One way to answer this question is to determine if the corresponding binormal ROC curve has discernible improperness; if it does not, then the bi-chi-squared curve will be closely approximated by it. Along these lines, Metz and Pan [12, pp 15-16] write “For a given pair of curve parameter values, the corresponding proper and conventional binormal ROC curves are indistinguishable if and only if no ‘hook’ is evident in the conventional binormal ROC ... Empirically, this occurs if and only if $d_a\le 6\mid c\mid$.”

The degree of improperness of the corresponding binormal ROC curve can be measured by the binormal mean-to-sigma ratio, defined by

$$r=\frac{a}{1-b}$$ (31)

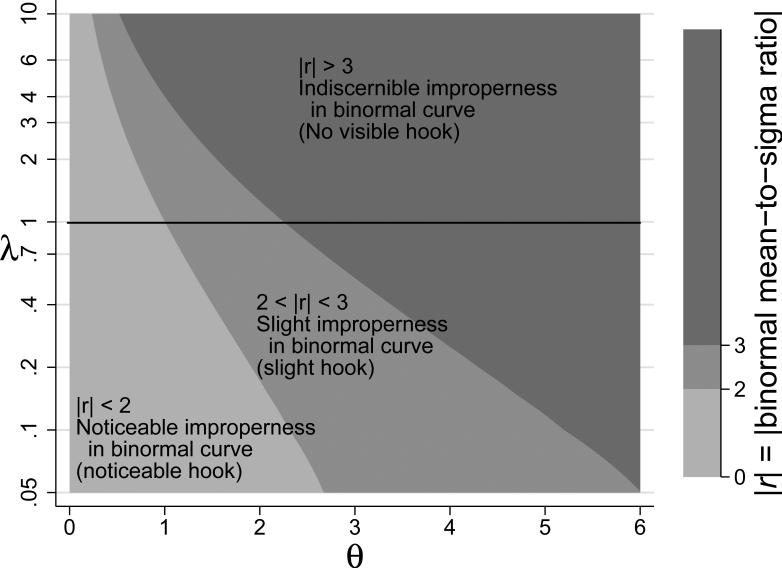
Hillis and Berbaum [13] note that Φ (r) is the unique fpf where the binormal ROC curve crosses the chance line. Based on this result, they classify the improperness of a binormal ROC curve as indiscernible if |r ≥ 3, noticeable if |r| ≤ 2, and slight if 2 < |r| < 3. From (11) and (31) it follows that

$$r=\{\begin{array}{cc}\sqrt{\theta }\left(\sqrt{\lambda }+1\right),\hfill & \lambda >1\hfill \\ -\sqrt{\theta }\left(\sqrt{\lambda }+1\right)\hfill & \lambda <1\hfill \end{array}\phantom{\}}$$

and hence

$$\mid r\mid =\sqrt{\theta }\left(\sqrt{\lambda }+1\right),\lambda \ne 1$$

Figure 5 displays a contour map of |r| in the bi-chi-squared parameter space. This figure shows the region where the bi-chi-squared ROC curves are similar to their corresponding binormal curves. For example, we see that if λ < 1 and θ ≥ 2V25 then the two curves are similar because |r| ≥ 3.

Figure 5.

Improperness of the binormal model corresponding to a bi-chi-squared model. Improperness categories are defined in terms of |r|, where r = a/(1 – b)) is the mean-to-sigma ratio for the corresponding binormal model, as discussed by Hillis and Berbaum [13]. Notes: a and b define the binormal model corresponding to the bi-chi-squared model defined by (θ, λ), i.e., $a=\sqrt{\theta {(\lambda -1)}^2∕\lambda }$ and $b=1∕\sqrt{\lambda }$; the λ-axis is scaled logarithmically; values of r for λ = 1 are not included because r is not defined if λ = 1.

Alternatively, I could have rewritten the Metz and Pan inequality d_a ≤ 6 |c| in terms of the bi-chi-squared parameterization. However, the advantage of the proposed method is that it is based on an interpretable index of improperness for the corresponding binormal ROC curve.

8. Discussion

The binormal-LR model assumption is attractive to researchers because it always results in proper estimated ROC curves, including curves similar to “acceptable” binormal ROC curves, i.e., binormal curves that are not noticeably nonconcave. For this reason binormal-LR ROC curve estimation has become common in radiologic diagnostic studies.

Metz and Pan [11, 12] provide a detailed development of the binormal-LR ROC curve; however, their development is not easy to follow, especially for researchers that do not have extensive statistical training. The main contribution of this paper is the recognition that the binormal-LR model (with equal-variance ROC curves excluded) is equivalent to a bi-chi-squared model. The bi-chi-squared approach is easier to explain and understand, and allows for easier derivation of statistical properties. This paper develops the bi-chi-squared approach and uses it to fill in some of the omissions in the Metz and Pan papers, such as writing tpf and fpf as analytic functions of each other and providing proofs for the AUC and partial AUC formulas; furthermore, it illustrates how the approach makes it possible to fit ROC curves using standard statistical software. It is important to note the bi-chi-squared model discussed in this paper involves only one-degree-of-freedom noncentral bi-chi-squared distributions.

In my opinion the terms proper binormal ROC curve and proper binormal model used by Metz and Pan are misnomers because the only way an ROC curve can be both proper and binormal is for it to be an equal-variance (b = 1) binormal curve. Thus I recommend that these terms not be used, but instead suggest the terms binormal-LR ROC curve and binormal-LR model. Although it might seem reasonable to alternatively use the terms bi-chi-squared ROC curve and bi-chi-squared model, in general I do not recommend these terms because they involve a particular form of the bi-chi-squared distribution and hence are not as specific as binormal-LR ROC curve and binormal-LR model. However, I do recommend these terms when it is important to indicate that the bi-chi-squared distribution was used for conceptualization, estimation or derivation of results.

Because a bi-chi-squared distribution looks much different than a binormal distribution, it might at first seem that the assumption of a bi-chi-squared model is a major change from the assumption of a binormal model in terms of the underlying DV. In this paper I derived results by showing that a binormal-LR curve with parameters (a, b < 1) can be based on the bi-chi-squared random variable Y* = (Y – c₁)² where Y is binormal with parameters (a, b) and c₁ is the point where its likelihood ratio attains its minimum. Alternatively, because Y* is an increasing transformation of |Y – c₁|, I could have derived results based on |Y – c₁| as the DV, which has a bi-folded-normal distribution [23]. When the binormal DV is not visibly improper, the shape of the distribution of |Y – c₁| is similar to that of the corresponding binormal DV, except for the left tail where both distributions end at zero. Thus we can consider the DVs of the bi-chi-squared and binormal models to be similar after an increasing transformation when improperness is not visible in the corresponding binormal model. The reason I chose the bi-chi-squared approach over the bi-folded-normal approach was because the chi-squared distribution is more familiar.

Other two-parameter proper ROC models that have been proposed include the two-parameter bigamma model proposed by Dorfman et al. [24], a contaminated binormal model [25], a weighted power-function ROC curve model [26], and more generally a method for constructing pairs of diseased and nondiseased distributions that have a specified monotonic likelihood ratio [27]. Although these models have been extensively compared with the binormal model, there has been little study devoted to comparing them with each other; this is an area for future research.

Because a central chi-squared distribution is a particular form of a gamma distribution, it might seem that the proposed bi-chi-squared model would be closely related to the bigamma model proposed by Dorfman et al. [24]. For their model the two parameters are the conventional shape and scale parameters. The conditional nondiseased and diseased distributions have gamma distributions with the same shape parameter but different scale parameters. Their model includes bi-chi-squared (now using the term more generally) models where the two conditional distributions have central chi-squared distributions with the same degrees of freedom (which can be any positive integer) but different scale parameters. In contrast, the binormal-LR bi-chi-squared conditional distributions are noncentral chi-squared with one degree of freedom, but do not have the same shape (unless λ = 1 which results in the chance-line ROC curve). The bigamma model assumes that the diseased distribution variance is not less than that of the nondiseased distribution, but the bi-chi-squared model in this paper does not have this limitation. Comparison of these two approaches is an area for future research.

A. Alternative AUC formula derivation

In this section I derive the alternative AUC formula (21), which I restate below:

$${\mathrm{AUC}}_{{\chi }^2}=\Phi \left(\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}}\right)+2F_{\mathrm{BVN}}\left(-\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},0;-\frac{2\sqrt{\lambda }}{\lambda +1}\right),\lambda \ne 1$$

Notation and definitions are the same as in Section 4.2. Recall that X_D̄ and X_D are independent random variables such that X_D̄ ~ N ($\sqrt{\theta }$, 1) and X_D ~ N (λ$\sqrt{\theta }$, λ), and A₁, A₂, A₃ and A₄ are mutually exclusive events defined by

$$\begin{array}{cc}\hfill A_1=& \{X_D>X_{\stackrel{‒}{D}},X_D>-X_{\stackrel{‒}{D}}\},A_2=\{X_D<X_{\stackrel{‒}{D}},X_D<-X_{\stackrel{‒}{D}}\}\hfill \\ \hfill A_3=& \{X_D>X_{\stackrel{‒}{D}},X_D<-X_{\stackrel{‒}{D}}\},A_4=\{X_D<X_{\stackrel{‒}{D}},X_D>-X_{\stackrel{‒}{D}}\}\hfill \end{array}$$ (A1)

with their corresponding (X_D̄, X_D) subspaces graphically displayed in Figure 2a. In Section (4.2.1) I showed that

$${\mathrm{AUC}}_{{\chi }^2}=\{\begin{array}{cc}\mathrm{Pr}\left(A_1\right)+\mathrm{Pr}\left(A_2\right),\hfill & \lambda >1\hfill \\ \mathrm{Pr}\left(A_3\right)+\mathrm{Pr}\left(A_4\right),\hfill & \lambda <1\hfill \end{array}\phantom{\}}$$ (A2)

Define X = X_D̄ if D = 0, X = X_D if D = 1. It is easy to show that X has a binormal distribution with a and b defined by (11), i.e., X is a binormal DV that corresponds to a bi-chi-squared ROC curve with parameters λ and θ. The binormal AUC for X is given by

$$\begin{array}{cc}\hfill {\mathrm{AUC}}_{\mathrm{bin}}=& \mathrm{Pr}(X_D>X_{\stackrel{‒}{D}})\hfill \\ \hfill =& \Phi \left(\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{1+\lambda }}\right)\hfill \\ \hfill =& \mathrm{Pr}\left(A_1\right)+\mathrm{Pr}\left(A_3\right)\hfill \end{array}$$ (A3)

It follows from (A2) and (A3) that

$${\mathrm{AUC}}_{{\chi }^2}=\{\begin{array}{cc}{\mathrm{AUC}}_{\mathrm{bin}}+\mathrm{Pr}\left(A_2\right)-\mathrm{Pr}\left(A_3\right),\hfill & \lambda >1\hfill \\ {\mathrm{AUC}}_{\mathrm{bin}}+\mathrm{Pr}\left(A_4\right)-\mathrm{Pr}\left(A_1\right),\hfill & \lambda <1\hfill \end{array}\phantom{\}}$$

Thus to prove (21) I only need to show

$$2F_{\mathrm{BVN}}\left(-\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},0;-\frac{2\sqrt{\lambda }}{\lambda +1}\right)=\{\begin{array}{cc}\mathrm{Pr}\left(A_2\right)-\mathrm{Pr}\left(A_3\right),\hfill & \lambda >1\hfill \\ \mathrm{Pr}\left(A_4\right)-\mathrm{Pr}\left(A_1\right),\hfill & \lambda <1\hfill \end{array}\phantom{\}}$$ (A4)

To prove (A4) I first define the transformation

$$\left(\begin{array}{c}\hfill W_1\hfill \\ \hfill W_2\hfill \end{array}\right)=P^{\prime }{\Sigma }^{-\frac{1}{2}}\left(\begin{array}{c}\hfill X_{\stackrel{‒}{D}}\hfill \\ \hfill X_D\hfill \end{array}\right)$$ (A5)

where

$$P=\frac{\sqrt{\lambda }}{\sqrt{1+\lambda }}\left(\begin{array}{cc}\hfill \frac{1}{\sqrt{\lambda }}\hfill & \hfill -1\hfill \\ \hfill 1\hfill & \hfill \frac{1}{\sqrt{\lambda }}\hfill \end{array}\right),\Sigma =\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \lambda \hfill \end{array}\right),{\Sigma }^{-\frac{1}{2}}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{\sqrt{\lambda }}\hfill \end{array}\right)$$

Note that Σ is the covariance matrix of (X_D̄, X_D) and ${\Sigma }^{-\frac{1}{2}}{\Sigma }^{-\frac{1}{2}}={\Sigma }^{-1}$.

The transformation defined by (A5) consists of two steps: (1) The product ${\Sigma }^{-\frac{1}{2}}{(X_{\stackrel{‒}{D}},X_D)}^{\prime }$ results in a rescaling of X_D̄ and X_D, resulting in independent standard normal random variables V₁ = X_D̄ and $V_2=X_D∕\sqrt{\lambda }$. This transformation is illustrated in Figure 2b, which shows the contour lines for the (V₁, V₂) density function; the subspaces corresponding to events A₁, A₂, A₃ and A₄; and the orthogonal column vectors of the P matrix (up to a scale constant), denoted by w₁ and w₂. Note that w₂ coincides with the line $V_2=V_1∕\sqrt{\lambda }$, which is the transformed X_D = X_D̄ line from Figure 2a. (2) Multiplying by P′ results in a counterclockwise rotation of the (V₁, V₂) axes such that W₁ and W₂ are the components of the projections onto the w₁ and w₂ vectors (after unit-length normalization), respectively, in Figure 2b; i.e., $W_1=\frac{\sqrt{\lambda }}{\sqrt{1+\lambda }}(V_1∕\sqrt{\lambda }+V_2)$ and $W_2=\frac{\sqrt{\lambda }}{\sqrt{1+\lambda }}(-V_1+V_2∕\sqrt{\lambda })$.

It follows from (A5) that

$$(W_1,W_2)\sim \mathrm{MVN}\left(\sqrt{\theta }\sqrt{\lambda +1},0,1,1,0\right)$$ (A6)

The independence of W₁ and W₂ and E (W₂) = 0 imply that the density of (W₁, W₂), denoted by f(W₁, W₂), is symmetric about the line w₂ = 0; i.e., f_{(W1, W2)} (w₁, w₂) = f_{(W1, W2)} (w₁, –w₂) for all (w₁, w₂).

A.1. Derivation for λ > 1

Figure 2c shows the contour lines for the (W₁, W₂) density function and the subspaces corresponding to the events A₁, A₂, A₃ and A₄ in the (W₁, W₂) space. Comparing Figure 2c to Figure 2a shows that the x₂ = x₁ and x₂ = –x₁ lines in Figure 2a correspond to the w₂ = 0 and $w_2=-.5[(\lambda -1)∕\sqrt{\lambda }]w_1$ lines in Figure 2c. In Figure 2c, A₂ has been partitioned into two mutually exclusive subsets, A₂₁ and A₂₂ with the added line $w_2=.5[(\lambda -1)∕\sqrt{\lambda }]w_1$ separating the two subsets: $A_{21}=A_2\cap \{W_2\le .5[(\lambda -1)∕\sqrt{\lambda }]W_1\}$ and $A_{22}=A_2\cap \{W_2>.5[(\lambda -1)∕\sqrt{\lambda }]W_1\}$ with Pr (A₁) = Pr (A₁₁) + Pr (A₁₂).

It follows from the symmetry of f_{(W1, W2)} about the line w₂ = 0 that

$$\mathrm{Pr}\left(A_{21}\right)=\mathrm{Pr}\left(A_3\right)$$

Thus

$$\begin{array}{cc}\hfill \mathrm{Pr}\left(A_2\right)-\mathrm{Pr}\left(A_3\right)=& \mathrm{Pr}\left(A_2\right)-\mathrm{Pr}\left(A_{21}\right)\hfill \\ \hfill =& \mathrm{Pr}\left(A_{22}\right)\hfill \\ \hfill =& \mathrm{Pr}\left(W_2<-\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1,W_2>\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1\right)\hfill \\ \hfill =& 2\mathrm{Pr}\left(W_2<-\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1,W_2>0\right)\hfill \end{array}$$

and hence we can write

$$\mathrm{Pr}\left(A_2\right)-\mathrm{Pr}\left(A_3\right)=2\mathrm{Pr}\left(W_2+\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1<0,-W_2<0\right)$$ (A7)

From (A6) it follows that

$$\left(-W_2,W_2+\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1\right)\sim \mathrm{MVN}\left(0,\frac{1}{2}\frac{\sqrt{\theta }}{\sqrt{\lambda }}(\lambda -1)\sqrt{\lambda +1},1,\frac{{(1+\lambda )}^2}{4\lambda },-1\right)$$ (A8)

From (A7) and (A8) it follows that

$$\mathrm{Pr}\left(A_2\right)-\mathrm{Pr}\left(A_3\right)=2F_{\mathrm{BVN}}\left(-\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},0;-\frac{2\sqrt{\lambda }}{\lambda +1}\right)$$

A.2. Derivation for λ < 1

Figure 2d is similar to Figure 2c, with the difference being that λ = 4 for Figure 2c and λ = .25 for Figure 2d. For this reason, the line $w_2=-.5[(\lambda -1)∕\sqrt{\lambda }]w_1$ has a positive slope in Figure 2d, whereas it had a negative slope in Figure 2c. In Figure 2d, A₄ has been partitioned into two mutually exclusive subsets, A₄₁ and A₄₂ with the added line $w_2=.5[(\lambda -1)∕\sqrt{\lambda }]w_1$ separating the two subsets: $A_{41}=A_4\cap \{W_2\le .5[(\lambda -1)∕\sqrt{\lambda }]W_1\}$ and $A_{42}=A_4\cap \{W_2>.5[(\lambda -1)∕\sqrt{\lambda }]W_1\}$, with Pr (A₄) = Pr (A₄₁) + Pr (A₄₂).

It follows from the symmetry of f_{(W1, W2)} about the line w₂ = 0 that

$$\mathrm{Pr}\left(A_{41}\right)=\mathrm{Pr}\left(A_1\right)$$

Thus

$$\begin{array}{cc}\hfill \mathrm{Pr}\left(A_4\right)-\mathrm{Pr}\left(A_1\right)=& \mathrm{Pr}\left(A_4\right)-\mathrm{Pr}\left(A_{41}\right)\hfill \\ \hfill =& \mathrm{Pr}\left(A_{42}\right)\hfill \\ \hfill =& \mathrm{Pr}\left(W_2<-\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1,W_2>\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1\right)\hfill \\ \hfill =& 2\mathrm{Pr}\left(W_2<-\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1,W_2>0\right)\hfill \end{array}$$

and hence we can write

$$\mathrm{Pr}\left(A_4\right)-\mathrm{Pr}\left(A_1\right)=2\mathrm{Pr}\left(W_2+\frac{(\lambda -1)}{2\sqrt{\lambda }}{W}_1<0,-W_2<0\right)$$ (A9)

Note that the right side of (A9) is identical in form to the right side of (A7). From (A9) and (A8) it follows that

$$\mathrm{Pr}\left(A_4\right)-\mathrm{Pr}\left(A_1\right)=2F_{\mathrm{BVN}}\left(-\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},0;-\frac{2\sqrt{\lambda }}{\lambda +1}\right)$$

B. Partial AUC derivation

In this section I derive the formula for the partial area under the bi-chi-squared partial ROC curve, pAUC (0, fpf₀), where 0 < fpf₀ < 1. For the derivations I use the following result [2, 28].

Result 2

Let Y denote a decision variable having continuous conditional distributions, and let Y_D̄ and Y_D denote independent random variables having the same distributions as the nondiseased and diseased conditional distributions of Y, respectively. Let ξ_fpf0 denote the threshold corresponding to fpf₀; i.e., Pr (Y_D̄ > ξ_fpf0) = fpf₀. Then

$$\mathrm{pAUC}(0,{\mathrm{fpf}}_0)=\mathrm{Pr}\left[Y_D>Y_{\stackrel{‒}{D}},Y_{\stackrel{‒}{D}}>{\xi }_{{\mathrm{fpf}}_0}\right]$$ (B1)

Let ρ, $Y_D^{\ast }$, $Y_{\stackrel{‒}{D}}^{\ast }$, X_D̄, X_D be defined as in Section 4.2.1, and again let F_ν denote the distribution function for a random variable having a ${\chi }_{1;\nu }^2$ distribution.

B.1. Derivation and results for λ > 1

Define ξ_fpf0 by $\mathrm{Pr}(Y_{\stackrel{‒}{D}}^{\ast }>{\xi }_{{\mathrm{fpf}}_0})={\mathrm{fpf}}_0$, or equivalently

$${\xi }_{{\mathrm{fpf}}_0}=F_{\theta }^{-1}(1-{\mathrm{fpf}}_0)$$

It follows from (15) and (B1) that the bi-chi-squared partial AUC is given by

$$\begin{array}{cc}\hfill {\mathrm{pAUC}}_{\mathrm{fpf}}(0,{\mathrm{fpf}}_0)=& \mathrm{Pr}\left[Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast },Y_{\stackrel{‒}{D}}^{\ast }>{\xi }_{{\mathrm{fpf}}_0}\right]\hfill \\ \hfill =& \mathrm{Pr}\left(X_D^2>X_{\stackrel{‒}{D}}^2,X_{\stackrel{‒}{D}}^2>{\xi }_{{\mathrm{fpf}}_0}\right)\hfill \\ \hfill =& \mathrm{Pr}\left(X_D>X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}}>\sqrt{{\xi }_{{\mathrm{fpf}}_0}}\right)+\mathrm{Pr}\left(X_D<X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}}<-\sqrt{{\xi }_{{\mathrm{fpf}}_0}}\right)+\mathrm{Pr}\left(X_D<-X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}}>\sqrt{{\xi }_{{\mathrm{fpf}}_0}}\right)+\mathrm{Pr}\left(X_D>-X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}}<-\sqrt{{\xi }_{{\mathrm{fpf}}_0}}\right)\hfill \end{array}$$

or equivalently,

$${\mathrm{pAUC}}_{\mathrm{fpf}}(0,{\mathrm{fpf}}_0)=\mathrm{Pr}\left(-(X_D-X_{\stackrel{‒}{D}})<0,-X_{\stackrel{‒}{D}}<-\sqrt{{\xi }_{{\mathrm{fpf}}_0}}\right)+\mathrm{Pr}\left(X_D-X_{\stackrel{‒}{D}}<0,X_{\stackrel{‒}{D}}<-\sqrt{{\xi }_{{\mathrm{fpf}}_0}}\right)+\mathrm{Pr}\left(X_D+X_{\stackrel{‒}{D}}<0,-X_{\stackrel{‒}{D}}<-\sqrt{{\xi }_{{\mathrm{fpf}}_0}}\right)+\mathrm{Pr}\left(-(X_D+X_{\stackrel{‒}{D}})<0,X_{\stackrel{‒}{D}}<-\sqrt{{\xi }_{{\mathrm{fpf}}_0}}\right)$$ (B2)

Noting that

$$\begin{array}{cc}\hfill (X_D+X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}})\sim & \mathrm{MVN}(\sqrt{\theta }(\lambda +1),\sqrt{\theta },\lambda +1,1,1)\hfill \\ \hfill (X_D-X_{\stackrel{‒}{D}},X_{\stackrel{‒}{D}})\sim & \mathrm{MVN}(\sqrt{\theta }(\lambda -1),\sqrt{\theta },\lambda +1,1,-1)\hfill \end{array}$$

and defining

$${\rho }_1=\frac{-1}{\sqrt{\lambda +1}}$$

it follows from (B2) that

$${\mathrm{pAUC}}_{\mathrm{fpf}}(0,{\mathrm{fpf}}_0)=F_{\mathrm{BVN}}\left(\frac{\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},\sqrt{\theta }-\sqrt{{\xi }_{{\mathrm{fpf}}_0}};{\rho }_1\right)+F_{\mathrm{BVN}}\left(\frac{-\sqrt{\theta }(\lambda -1)}{\sqrt{\lambda +1}},-\sqrt{\theta }-\sqrt{{\xi }_{{\mathrm{fpf}}_0}};{\rho }_1\right)+F_{\mathrm{BVN}}\left(\frac{-\sqrt{\theta }(\lambda +1)}{\sqrt{\lambda +1}},\sqrt{\theta }-\sqrt{{\xi }_{{\mathrm{fpf}}_0};{\rho }_1}\right)+F_{\mathrm{BVN}}\left(\frac{\sqrt{\theta }(\lambda +1)}{\sqrt{\lambda +1}},-\sqrt{\theta }-\sqrt{{\xi }_{{\mathrm{fpf}}_0}};{\rho }_1\right)$$ (B3)

Let u₁ and u₂ be defined by (17) and define

$$\begin{array}{cc}\hfill y_1=& \sqrt{\theta }-\sqrt{{\xi }_{{\mathrm{fpf}}_0}}=\sqrt{\theta }-\sqrt{F_{\theta }^{-1}(1-{\mathrm{fpf}}_0)}\hfill \\ \hfill y_2=& \sqrt{\theta }+\sqrt{{\xi }_{{\mathrm{fpf}}_0}}=\sqrt{\theta }+\sqrt{F_{\theta }^{-1}(1-{\mathrm{fpf}}_0)}\hfill \end{array}$$ (B4)

From (B3) and (B4) it follows that

$${\mathrm{pAUC}}_{\mathrm{fpf}}(0,{\mathrm{fpf}}_0)=F_{\mathrm{BVN}}(u_1,y_1;{\rho }_1)+F_{\mathrm{BVN}}(-u_1,-y_2;{\rho }_1)+F_{\mathrm{BVN}}(-u_2,y_1;{\rho }_1)+F_{\mathrm{BVN}}(u_2,-y_2;{\rho }_1)$$ (B5)

B.2. Derivation and results for λ < 1

It follows from (B1) that

$${\mathrm{pAUC}}_{\mathrm{fpf}}(0,{\mathrm{fpf}}_0)=\mathrm{Pr}\left[-Y_D^{\ast }>-Y_{\stackrel{‒}{D}}^{\ast },-Y_{\stackrel{‒}{D}}^{\ast }>{\tilde{\xi }}_{{\mathrm{fpf}}_0}\right]$$

where ${\tilde{\xi }}_{{\mathrm{fpf}}_0}$ is such that $\mathrm{Pr}(-Y_{\stackrel{‒}{D}}^{\ast }>{\tilde{\xi }}_{{\mathrm{fpf}}_0})=\mathrm{fpf}$. It follows that

$$\mathrm{Pr}\left(Y_{\stackrel{‒}{D}}^{\ast }<-{\tilde{\xi }}_{{\mathrm{fpf}}_0}\right)={\mathrm{fpf}}_0$$

and

$$-{\tilde{\xi }}_{{\mathrm{fpf}}_0}={\xi }_{1-{\mathrm{fpf}}_0}$$

We have

$$\begin{array}{cc}\hfill {\mathrm{pAUC}}_{\mathrm{fpf}}(0,{\mathrm{fpf}}_0)=& \mathrm{Pr}\left[-Y_D^{\ast }>-Y_{\stackrel{‒}{D}}^{\ast },-Y_{\stackrel{‒}{D}}^{\ast }>{\tilde{\xi }}_{{\mathrm{fpf}}_0}\right]\hfill \\ \hfill =& \mathrm{Pr}\left[Y_D^{\ast }<Y_{\stackrel{‒}{D}}^{\ast },Y_{\stackrel{‒}{D}}^{\ast }<-{\tilde{\xi }}_{{\mathrm{fpf}}_0}\right]\hfill \\ \hfill =& \mathrm{Pr}\left(Y_{\stackrel{‒}{D}}^{\ast }<-{\tilde{\xi }}_{{\mathrm{fpf}}_0}\right)-\mathrm{Pr}\left(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast },Y_{\stackrel{‒}{D}}^{\ast }<-{\tilde{\xi }}_{{\mathrm{fpf}}_0}\right)\hfill \\ \hfill =& {\mathrm{fpf}}_0-\mathrm{Pr}\left(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast },Y_{\stackrel{‒}{D}}^{\ast }<-{\tilde{\xi }}_{{\mathrm{fpf}}_0}={\xi }_{1-{\mathrm{fpf}}_0}\right)\hfill \\ \hfill =& {\mathrm{fpf}}_0-\left[\mathrm{Pr}(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast })-\mathrm{Pr}\left(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast },Y_{\stackrel{‒}{D}}^{\ast }>{\xi }_{1-{\mathrm{fpf}}_0}\right)\right]\hfill \end{array}$$ (B6)

Because the derivations for $\mathrm{Pr}(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast })$ and $\mathrm{Pr}(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast },Y_{\stackrel{‒}{D}}^{\ast }>{\xi }_{{\mathrm{fpf}}_0})$ for λ > 1 in Sections 4.2.1 and B.1, respectively, do not depend on the value of λ, it follows that $\mathrm{Pr}(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast })$ and $\mathrm{Pr}(Y_D^{\ast }>Y_{\stackrel{‒}{D}}^{\ast },Y_{\stackrel{‒}{D}}^{\ast }>{\xi }_{1-{\mathrm{fpf}}_0})$ in (B6) can be replaced by the right side of equations (16) and (B5), respectively, with fpf₀ replaced by 1 – fpf₀ in the definitions of y₁ and y₂ (B4). It follows that

$${\mathrm{pAUC}}_{\mathrm{fpf}}(0,{\mathrm{fpf}}_0)={\mathrm{fpf}}_0-[F_{\mathrm{BVN}}(u_1,u_2;\rho )+F_{\mathrm{BVN}}(-u_1,-u_2;\rho )]+[F_{\mathrm{BVN}}(u_1,y_3;{\rho }_1)+F_{\mathrm{BVN}}(-u_1,-y_4;{\rho }_1)+F_{\mathrm{BVN}}(-u_2,y_3;{\rho }_1)+F_{\mathrm{BVN}}(u_2,-y_4;{\rho }_1)]$$ (B7)

where u₁ and u₂ are defined by (17) and

$$\begin{array}{cc}\hfill y_3=& \sqrt{\theta }-\sqrt{{\xi }_{1-{\mathrm{fpf}}_0}}=\sqrt{\theta }-\sqrt{F_{\theta }^{-1}\left({\mathrm{fpf}}_0\right)}\hfill \\ \hfill y_4=& \sqrt{\theta }+\sqrt{{\xi }_{1-{\mathrm{fpf}}_0}}=\sqrt{\theta }+\sqrt{F_{\theta }^{-1}\left({\mathrm{fpf}}_0\right)}\hfill \end{array}$$

C. Relationships between λ, θ and AUC for the bi-chi-squared ROC curve

In this section I show for fixed θ that AUC in an increasing (decreasing) function of λ if λ > 1 (λ < 1).

To show this result for λ > 1, fix θ > 0 and let λ₁ and λ₂ be such that 0 < λ₁ < λ₂. Let Y₁ and Y₂ denote bi-chi-squared DVs having parameter pairs (θ, λ₁) and (θ, λ₂), respectively, and let AUC₁ and AUC₂ denote their corresponding AUCs. Let c > 0 denote an arbitrary threshold and let fpf_i (c) and tpf_i (c) denote the corresponding fpf and tpf values: fpf_i (c) = Pr (Y_i > c|D = 0), tpf_i (c) = Pr (Y_i > c|D = 1) for i = 1, 2. Note that fpf₁ (c) = fpf₂ (c) because $(Y_i\mid D=0)\sim {\chi }_{1;\theta }^2,i=1,2$. Thus tpf₂ (c) > tpf₁ (c) for all c < 0 implies AUC₂ > AUC₁, and hence it suffices to show tpf₂ (c) > tpf₁ (c).

Let V_ξ denote a random variable having a ${\chi }_{1;\xi }^2$ distribution. It is straightforward to show

$$\mathrm{Pr}({\lambda }_2{V}_{{\lambda }_2\theta }>c)>\mathrm{Pr}({\lambda }_1{V}_{{\lambda }_2\theta }>c)$$ (C1)

and

$$\mathrm{Pr}(V_{{\lambda }_2\theta }>c∕{\lambda }_1)>\mathrm{Pr}(V_{{\lambda }_1\theta }>c∕{\lambda }_1)$$ (C2)

To show (C2), note that $\mathrm{Pr}(V_{{\lambda }_i\theta }>c∕{\lambda }_1)=1-\mathrm{Pr}(\mid Z+\sqrt{{\lambda }_i\theta }\mid <\sqrt{c∕{\lambda }_1})$, i = 1, 2, where Z is a standard normal random variable. Using (C1) and (C2) we can write tpf₂ (c) = Pr (Y₂ > c|D = 1) = Pr (λ₂V_λ2θ > c) > Pr (λ₁V_λ2θ < c) = Pr (V_λ2θ > c/λ₁) > Pr (V_λ1θ > c/λ₁) = Pr (λ₁V_λ1θ > c) = Pr (Y₁ > c|D = 1) = tpf₁ (c); thus we have shown tpf₂ (c) > tpf₁ (c) for arbitrary c. The proof for λ < 1 is similar.

It can similarly be shown for fixed λ ≠ 1 that AUC is an increasing function of θ.