Rapid evaporation-driven chemical pre-concentration and separation on paper

Abstract

Airflow-enhanced evaporation is investigated as a method for rapid chemical preconcentration on a thin porous substrate. The mechanism is described by combining 1D models of capillary rise, chromatography, and pervaporation concentration. It is shown that the effective length of the column can be shorter than its actual length, allowing concentrate to be held at a stagnation point and then released for separation, and that the Péclet number, which determines the concentration performance, is determined only by the substrate properties. The differential equations are solved dynamically, and it is shown that faster concentration can be achieved during capillary filling. Experiments are carried out using chromatography paper in a ducted airflow, and concentration is quantified by optical imaging of water-soluble food dyes. Good agreement with the model is obtained, and concentration factors of ≈100 are achieved in 10 min using Brilliant Blue FCF. Partial separation of Brilliant Blue from Tartrazine is demonstrated immediately following concentration, on a single unpatterned substrate. The mechanism may provide a method for improving the sensitivity of lab-on-paper devices.

I. INTRODUCTION

Great strides have been made in developing paper as a substrate for water-based lab-on-a-chip devices,^1,2 with the aim of providing low-cost medical diagnosis for the developing world. Flow is driven by capillary action, channels have been defined using wax patterning, ink-jet printing, toner printing, and boundary shaping,^3–6 and devices have been fabricated with hollow and closed channels.^7,8 Detection has been mainly carried out using colorimetric assays for off-site analysis via the ubiquitous smartphone;^9,10 however, electrochemical detection has also been investigated.^11,12 Several reviews are available.^13–15

Several well-known methods of preconcentration have been adapted to increase sensitivity in paper devices, including isotachophoresis,^16,17 isoelectric focusing,¹⁸ and field amplified sample stacking.¹⁹ The most commonly used method is ion concentration polarization (ICP).^20–23 This can provide concentration factors of 100–1000 in 2–10 min after filling but requires nanoporous membranes, electrodes, and relatively high voltages.

In this paper, we explore an alternative mechanism that can operate on a bare substrate, concentrate during filling, and provide a hold-up function that allows subsequent separation operations. The driving force is solvent evaporation, which is well known to concentrate nonvolatile compounds at stagnation points. An everyday example, coffee staining (which involves ambient evaporation of a finite source in a semi-cylindrical geometry), has been extensively studied,^24,25 and the effect has also been exploited in paper devices using ambient evaporation.^26,27 Here, we investigate inherent limits and show that a performance comparable to ICP can be achieved using evaporation-driven capillary pumping.

Pumps based on ambient evaporation were developed some years ago.^28–30 Following the observation of permeation-induced flows in poly(dimethyl siloxane),^31,32 airflow-enhanced PDMS pervaporation pumps were used to induce concentration in microfluidic channels.^33–35 Similar systems have been constructed for concentration of bacteria and viruses,^36,37 and concentration has also been carried out using microstructured media.^38–40 Evaporation pumps with greater capacity were subsequently developed using porous media^41–43 and used for sample injection.^44,45

We show that ducted airflow can provide the enhanced evaporation needed for rapid concentration of water-soluble dyes on paper. The device is extremely simple. A paper strip is filled with a dilute aqueous solution from a reservoir by capillary action. Evaporation then leads to an advective flow that concentrates nonvolatile compounds near or at the tip of the column. The mechanism involves capillary rise, microfluidic concentration, and paper chromatography. All are very well known. However, there are three main differences from earlier work. First, we show theoretically that the effective length of the column can be shorter than its actual length if the rate of evaporation is high enough. Consequently, concentrate may be held at a stagnation point and then released for capillary-pumped separation. Second, we show that the Péclet number, which determines the concentration performance, is defined only by the properties of the substrate. Third, we solve the governing equations dynamically and show that faster concentration can be achieved during capillary filling. Theoretical predictions are confirmed using dyes and un-patterned chromatography paper, with a fan-driven ducted airflow derived from ambient air. Rapid concentration requires relatively high fan drive power (15 W). However, there is scope to reduce power using dry air, optimised duct dimensions, and local heating. A unique advantage is the control of stagnation, which allows concentration to be followed by other capillary-pumped operations.

A model for capillary rise in the presence of evaporation is presented in Sec. II. The solvent velocity profile is combined with a differential equation model of separation in Sec. III, and concentration is simulated for different initial wetting conditions. Experimental materials and methods are described in Sec. IV. The concentration and separation of concentrate are demonstrated in Sec. V. Conclusions are drawn in Sec. VI.

II. CAPILLARY RISE

In this section, we derive the solvent velocity profile obtained during evaporation-dominated capillary rise, using a combination of earlier models.

A. Device geometry

Figure 1 shows an evaporation concentrator, arranged to allow comparison with earlier pervaporation devices.^46,47 Solutes are transferred from a reservoir at the right-hand end towards a tip at the left via a porous substrate of length L, thickness d, and uniform (but unimportant) width. The medium transports a mobile phase by capillary action. This phase is assumed to be volatile, and evaporation is enhanced by airflow on either side. In contrast, solutes are assumed to be soluble but nonvolatile. Consequently, solutes will accumulate at the tip, in a concentration profile derived from a balance between the effects of advection and diffusion.

FIG. 1.

Principle of airflow enhanced paper concentration.

One key difference from earlier work is the replacement of a pervaporation membrane over a channel with a porous substrate that allows increased evaporation and chromatographic effects. At low evaporation rates, solutes will concentrate at the tip; however, increased evaporation can lead to concentration at a closer point H_e from the reservoir, where concentrate may be held up. Very high evaporation can also allow concentration during the wetting phase. A model may be constructed by combining concepts from capillary rise, chromatography, and concentration. For simplicity, we use 1D analysis throughout. To aid comparison with standard models, we use the Y co-ordinate for capillary ascent and the X co-ordinate for concentration.

B. Capillary transport and evaporation

In a vertical capillary tube, rise is modelled using the Lucas-Washburn equation, which balances the effects of surface tension, gravitational force, and viscous drag in Poiseuille flow.^48,49 For media such as paper, the equation must be modified to include permeability and porosity. Early models of wicking assume uniform filling,⁵⁰ while later models consider the observed distribution of fluid.⁵¹ Evaporation is typically ignored, except in the related phenomenon of rising damp.⁵² Here, the substrate is horizontal, so gravitational force can be ignored, but evaporation must now be included. However, for simplicity, we assume full filling.

Assuming a fluid velocity V in the Y direction, a uniform volumetric rate of evaporation u_e per unit area from the two sides together, and a rise H from the reservoir, the continuity equation at time T is

$$Vd=v_e\left(H-Y\right)+d\hspace{0.17em}\frac{dH}{dT}.$$ (1)

Here, v_e = u_e/ε, where ε is the porosity. Equation (1) can be derived from a balance between the input fluid flow (the first term), the loss of fluid by evaporation (the second), and the change of stored fluid due to extension of the column (the third), assuming a constant column width.

In porous media, the volumetric flow rate q per unit cross-sectional area is linked to the gradient in pressure P using Darcy's law⁵³

$$q=\hspace{0.17em}-\left(\frac{\kappa }{\eta }\right)\frac{\partial P}{\partial Y}.$$ (2)

Here, κ is the permeability of the stationary phase and η is the dynamic viscosity of the mobile phase. The relationship between flow and velocity is q = εV. Substitution gives

$$-\left(\frac{\kappa }{\eta \epsilon }\right)\frac{\partial P}{\partial Y}=\left(\frac{v_e}{d}\right)\left(H-Y\right)+\frac{dH}{dT}.$$ (3)

Integrating both sides between Y = 0 and Y = H then gives

$$-\left(\frac{\kappa }{\eta \epsilon }\right)\left[P\left(H\right)-P\left(0\right)\right]=\left(\frac{v_e}{2d}\right)H^2+H\frac{dH}{dT}.$$ (4)

Since P(0) – P(H) = P_C, where P_C is the capillary pressure, we obtain

$$H\frac{dH}{dT}=\frac{P_c\kappa }{\eta \epsilon }-\frac{v_e{H}^2}{2d}.$$ (5)

Noting that H dH/dT = ½ dH²/dT, Eq. (5) can be recast as a first-order differential equation in H², namely,

$$\frac{d{H}^2}{dT}+\frac{v_e{H}^2}{d}=\frac{{2P}_c\kappa }{\eta \epsilon }.$$ (6)

For the initial conditions H = 0 at T = 0, the solution can now be found analytically in terms of a complementary function and a particular integral as

$$H=\hspace{0.17em}{H}_e\hspace{0.17em}\surd \{1-\exp \left(-\frac{T}{{\tau }_e}\right)\}.$$ (7)

Here, H_e = √(2τ_eP_cκ/ηε) is the evaporation-dominated rise and τ_e = d/v_e is a characteristic time constant. Assuming fixed material and geometric parameters, H_e is controlled by the value of v_e and consequently may be smaller than the substrate length L if v_e is high enough.

Evaporation depends on temperature and relative humidity (RH). However, the former is simple to control using air conditioning. At constant temperature, the rate of evaporation is a linear function of relative humidity (RH), falling to zero at 100% RH.⁵⁴ A decrease in RH from (say) 50% to 0% will therefore increase v_e by 2, reduce τ_e by the same factor, and reduce H_e by √2. Evaporation can also be enhanced by airflow, which continually replaces the boundary layer between the substrate and its surround with less saturated air.

To model similar phenomena with the substrate arranged vertically, P_C is simply replaced by P_C − ρgH, where ρ is the fluid density and g is the gravitational constant. Equation (5) must then generally be solved numerically. However, in the absence of evaporation, it is simple to show that this leads to a steady state capillary rise height, H_C = P_C/ρg, allowing P_C to be determined experimentally from a measurement of H_C.

C. Velocity profile

Differentiating Eq. (7) and re-arranging, we may then obtain dH/dT as

$$\frac{dH}{dT}=\frac{(H_e^2-H^2)}{2{\tau }_{e}H}.$$ (8)

Equations (1) and (8) then allow the general expression for the fluid velocity to be found as

$$V\left(Y,\hspace{0.17em}T\right)=\{H-Y+\left(H_e^2-H^2\right)/2H\}/{\tau }_e\hspace{1em}\mathrm{f}\mathrm{o}\mathrm{r}\hspace{0.17em}\hspace{0.17em}Y\le H.$$ (9)

Equation (9) implies that V(0, 0) is infinite, a result that in reality is prevented by additional flow restrictions. Ignoring this aspect, the velocity profile is an offset, truncated linear variation, which tends gradually to the equilibrium profile V_E(Y) = (1/τ_e) (H_e − Y). In the X co-ordinate system of the following section, the velocity is U(X) = −V(H_e − X). Introducing the normalised time t = T/τ_e and position x = X/H_e, the normalised velocity u = Uτ_e/H_e becomes

$$u\left(x,t\right)=-\left\{x-\left(1-h\right)+\left(1-h^2\right)/2h\right\}\hspace{1em}\mathrm{f}\mathrm{o}\mathrm{r}\hspace{0.17em}\hspace{0.17em}x\ge 1-h,$$ (10)

with h = H/H_e = {1 − exp(−t)}^1/2. Figure 2 shows normalised velocity profiles |u| calculated from Eq. (10) for different normalised times t. At short times, the substrate is only partly wetted; however, as t increases, the liquid gradually fills the column from the right hand end. In all cases, the velocity profile is linear in the wetted region and zero elsewhere. In addition, each profile has an offset that gradually tends to zero, and at long times, the profile tends to u = −x.

FIG. 2.

Theoretical variation of normalised velocity |u| with normalised position x during capillary fill, at different normalised times t as indicated.

D. Substrate length

The above results have been derived without considering the finite length L of the substrate. If L > H_e, flow will clearly be held up at an intermediate stagnation point where concentration may occur. The disadvantage of this approach is that unsteady evaporation (for example, due to variations in ambient humidity) may lead to “wandering” of the stagnation point and reduced concentration. However, if concentration is carried out for a fixed time and evaporation is then suppressed, further capillary transport can be used for chromatographic separation. If L < H_e, on the other hand, a two-stage model must be used, the first describing rise to the tip and the second relaxation to equilibrium. Here, we shall ignore the details and simply note that the equilibrium profile must then be V_E′(Y) = (1/τ_e) (L − Y), as is generally assumed directly. The advantage now is that the stagnation point is fixed, simplifying subsequent analysis. However, if L is significantly less than H_e, concentration may be reduced. The most controllable approach is therefore likely to involve evaporation into dry air from a substrate length just less than H_e.

III. CONCENTRATION

In this section, we present a 1D theoretical model of concentration, based on standard differential equation models of chromatographic separation.⁵⁵ Such models consider transport, diffusion, and concentration but ignore transverse velocity profiles arising from shear forces and associated effects such as Taylor's dispersion.

A. Concentration

We model a single solute with diffusion coefficient D and concentration C_L and C_S in the liquid and solid phases, in the X co-ordinate system. Assuming a variable flow velocity U, the continuity equation becomes

$$\epsilon \frac{\partial C_L}{\partial T}+\left(1-\epsilon \right)\frac{\partial C_S}{\partial T}=\epsilon D\frac{{\partial }^2{C}_L}{\partial X^2}-\epsilon \frac{\partial {(UC}_L)}{\partial X}.$$ (11)

As usual, the first two terms describe accumulation and the last two model diffusion and transport. Now, C_S and C_L are related by the adsorption isotherm C_S = f(C_L). Writing ∂C_S/∂T = f′ ∂C_L/∂T and expanding the final term, we obtain

$$\left(1+F{f}^{\prime }\right)\frac{\partial C_L}{\partial T}=D\frac{{\partial }^2{C}_L}{\partial X^2}-(U\frac{\partial C_L}{\partial X}+C_L\frac{\partial U}{\partial X}).$$ (12)

Here, F = (1 − ε)/ε is the ratio of the volumes of the stationary and mobile phases. The function f depends on the adsorption process, which may involve monolayer or multilayer adsorption; common models include the linear, Langmuir, Freundlich, and BET isotherms.⁵⁶ Once C_L is known, C_S can be found from the isotherm, and the average concentration C_AV (which is optically measurable) can be evaluated as C_AV = εC_L + (1 − ε)C_S. Here, for simplicity, we assume the linear isotherm C_S = aC_L, where a is Henry's coefficient. In this case, 1 + Ff′ = 1/R_f, where R_f = 1/(1 + Fa) is the retardation or retention factor, and C_AV is proportional to C_L.

In terms of the normalised time t = T/τ_e and normalised position x = X/H_e, we obtain

$$R_f^{-1}\frac{\partial C_L}{\partial t}={Pe}^{-1}\frac{{\partial }^2{C}_L}{\partial x^2}-(u\frac{\partial C_L}{\partial x}+C_L\frac{\partial u}{\partial x}).$$ (13)

Here, Pe = H_e²/Dτ_e is the Péclet number, which denotes the relative significance of advection and diffusion.⁵⁷ To reduce the absolute time taken to achieve concentration effects, τ_e should be small, so large values of v_e and small values of d are required. R_f also affects timescales directly. It is well known from the studies of pervaporation concentrators that Pe controls the normalised width of the concentration peak.⁴⁷ However, since H_e² = 2τ_eP_cκ/ηε, here Pe = 2P_cκ/ηεD and is therefore a function only of material parameters; variations in v_e will not affect its value. Large values require substrates with high permeability, high capillary pressure, and low porosity, solvents with low viscosity, and solutes with low diffusion coefficients. Different solutes will have different R_f and Pe values. Consequently, each solute in a multi-component solution will concentrate differently.

B. Wetting conditions

There are now two different velocity profiles that may be assumed. For pre-wetted columns, we may assume that steady flow conditions have already been reached before the introduction of any solute, so u = −x. With this assumption, Eq. (13) reduces to

$$R_f^{-1}\frac{\partial C_L}{\partial t}={Pe}^{-1}\frac{{\partial }^2{C}_L}{\partial x^2}+x\frac{\partial C_L}{\partial x}+C_L\hspace{1em}\mathrm{for}\hspace{0.17em}\hspace{0.17em}0\le x\le h.$$ (14)

When R_f = 1, the model therefore corresponds exactly to previous descriptions of pervaporation concentrators.⁴⁷ For a single solute, the evolution of local concentration when the input is connected to a reservoir with a concentration C_L0 at t = 0 can be found by solving Eq. (14) subject to the conditions C_L(x, 0) = 0, C_L(1, t) = C_L0, and ∂C_L/∂x = 0|_x=0. Partial differential equations may easily be solved numerically for fixed conditions; here, we have used the MATLAB^® solver “pdepe.” Conversely, if the column is initially dry, the full velocity profile in Eq. (10) must be used, and the equation is integrated with a moving boundary condition ∂C_L/∂x = 0|_x=h. It is now harder to obtain a solution. Here, we have circumvented the problem by retaining the condition ∂C_L/∂x = 0|_x=0, so the same solver may be used. We then modify Eq. (9) so that there is no flow (u = 0) and no diffusion (Pe⁻¹ = 0) in the “dry” part of the column, namely, 0 ≤ x ≤ h. The price paid for the simplicity of this approach is a reduction in accuracy caused by discontinuity.

C. Numerical results

Figure 3 shows the spatial variation of the concentration factor CF = C_L/C_L0 near x = 0 at different normalised times t as indicated, for low values of R_f (0.25) and Pe (1000). The full and dashed lines show the results for substrates that are initially wet and dry, respectively. Here, both the retardation factor and Péclet number are so small that the column has filled before any significant concentration takes place, and similar variations of CF are obtained in each case. The concentration profile gradually evolves until the column is filled with solute and then stabilises into the so-called “hyperbolic ramp” CF = 1/x for large values of x; however, for small values of x, the profile never stabilises but instead tends to the Gaussian variation CF = R_f(t − t_f) √(2Pe/π) exp(−Pe x²/2), where t_f is a normalised filling time. The width of the peak clearly depends on 1/√Pe, while its maximum increases linearly, at a rate dependent on √Pe.⁴⁷

FIG. 3.

Spatial variation of normalised concentration C_L/C_L0, at different normalised times t as indicated, for R_f = 0.25 and Pe = 1000. Full and dashed lines show prewetted and unwetted cases, respectively.

Figure 4 shows the associated time-variations of the maximum concentration. The results for initially wet and dry substrates (full and dashed lines, respectively) are again almost indistinguishable: in each case, the relative concentration rises slowly until the column is filled with solute and then rises more rapidly until the linear regime is reached.

FIG. 4.

Variation of peak normalised concentration C_L/C_L0 with normalised time t, for R_f = 0.25 and Pe = 1000. Full and dashed lines show prewetted and unwetted cases, respectively.

Figure 5 shows results corresponding to Fig. 3 but for larger values of R_f (1.00) and Pe (16 000). The timescale has been reduced by a factor of four, to compensate for the fourfold increase in R_f. At long times, the Gaussian concentration peak has become sharper and higher, reflecting the fourfold increase in √Pe. In addition, there is now a clear difference between the results for initially wet and dry substrates. In the latter case, both the retardation factor and Péclet number are so large that concentration can take place during filling itself.

FIG. 5.

Spatial variation of normalised concentration C_L/C_L0, at different normalised times t as indicated, for R_f = 1 and Pe = 16 000. Full and dashed lines show prewetted and unwetted cases, respectively.

Figure 6 shows results corresponding to Fig. 4. As expected, the slope of the curve has risen by a factor of four in the linear regime, and once again, there is a difference between initially wet and dry substrates. However, the advantage of immediate concentration clearly becomes less significant at longer times.

FIG. 6.

Variation of peak normalised concentration C_L/C_L0 with normalised time t, for R_f  = 1 and Pe = 16 000. Full and dashed lines show prewetted and unwetted cases, respectively.

IV. MATERIALS AND METHODS

Concentration was investigated using cellulose paper and water-soluble food dye. In this section, we describe materials' characterisation and the equipment used to enhance evaporation. All experiments were performed in ambient laboratory conditions, which were monitored using a temperature and humidity meter (Type 971, Fluke) but not controlled. During 85 experiments performed over 1 year, the mean temperature was 23.5 °C, with a standard deviation of 1.5 °C. The mean relative humidity was 46%, with a standard deviation of 5.5%. The final experiments were performed at 22 °C, 50% RH.

A. Substrate properties

The substrate was 1 Chr paper (3001‐845, Whatman; thickness, 0.18 mm; and pore size, 11 μm). Its properties were investigated using separate measurements of capillary rise, carried out with long strips of paper arranged vertically. The points in Fig. 7 show two sets of data, which were obtained first with a saturated surround to suppress evaporation. In the first case, the potential rise height is greater than the available length of paper (300 mm), while in the second case, evaporation has limited the rise to H_e ≈ 114 mm. The properties of the substrate were extracted from the first set of data by matching to the prediction of Eq. (5) (full line), including the additional gravitational term but suppressing evaporation. Matching was carried out by adjusting the parameters κ/ηε and H_c to obtain best fits at the start and end of the curve, yielding κ/ηε = 7.7 × 10⁻¹⁰ m³ s kg⁻¹ and H_c = 600 mm (corresponding to a capillary pressure of P_c = 5886 N/m²).

FIG. 7.

Comparison between experimental and theoretical variations of capillary rise with time for Whatman Chr1 paper, with and without evaporation.

B. Solute properties and Péclet number

Concentration was carried out using water-soluble dyes, the triphenylmethane dye Brilliant Blue FCF and the synthetic lemon yellow dye Tartrazine. Brilliant Blue (erioglaucine disodium salt or C₃₇H₃₄N₂Na₂O₉S₃, also known as acid blue 9, E133, and CI 42090) is used as a food dye, despite some effects to health,⁵⁸ and as a tracer in soil science. Its diffusion coefficient is known to be D = 5.68 × 10⁻¹⁰ m²/s.⁵⁹ Maximum optical absorption occurs at a wavelength of 630 nm, allowing the relative concentration to be deduced from changes in the red channel of an [R G B] image.^60,61 Dye was obtained at ≥97% purity (80717, Sigma Aldrich) and dissolved in de-ionised (DI) water, and a concentration maximising the experimental dynamic range (6.25 × 10⁻⁶g/ml) was used. Its retardation factor on Whatman paper is quoted as close to unity,²⁵ and we have verified it as R_f ≈ 0.98. From the above data, a Péclet number Pe = 2P_cκ/ηεD approaching 16 000 can be estimated, corresponding to the higher value used for earlier simulations. Tartrazine (C₁₆H₉N₄Na₃O₉S₂, acid yellow 23, E102, C.I. 19140) is also used as a food dye but has been blamed for allergic reactions.⁶² Its diffusion coefficient is D = 4.9 × 10⁻¹⁰ m² s⁻¹, and maximum absorption occurs at a wavelength of 425 nm.⁶³ Dye was obtained at 85% purity (TO388, Sigma Aldrich) and again dissolved in DI water at a low concentration (2.5 × 10⁻⁵g/ml). We have measured its retardation factor as R_f ≈ 0.88.

C. Ambient evaporation velocity and time constant

The high Péclet number of Brilliant Blue suggests that sharp concentration profiles can be obtained in open air without special measures, and we have verified this experimentally. However, the time-scales are relatively long and may be estimated as follows: The ambient evaporation velocity can be extracted from the second set of data in Fig. 7, by matching again to the prediction of Eq. (5) but now also including the evaporation term. The result is v_eAmb ≈ 100 nm/s, yielding a time constant of τ_eAmb = 1800 s or 30 min. From Fig. 6, we would expect a 100-fold relative increase in the concentration to be achievable at a time T ≈ 6τ_eAmb or around 3 h, in agreement with observations. Reducing this time to (say) 3 min would require a 60-fold increase in v_e. If this could be achieved, the evaporation-dominated rise would also reduce to H_e ≈ 114/√(60) ≈ 15 mm, allowing concentration to be achieved rapidly in a compact column.

D. Apparatus for enhanced evaporation

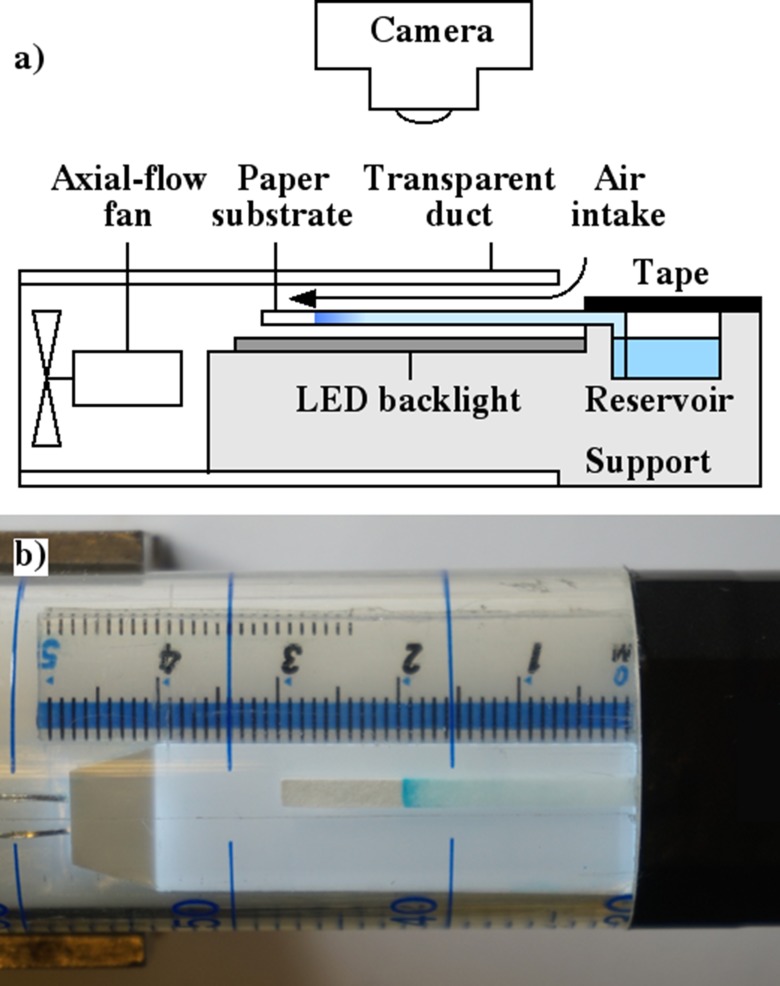
The necessary increase in v_e was obtained using a rapid air stream. Figure 8(a) shows a schematic and Fig. 8(b) a photograph of the experimental apparatus. The substrate consisted of a 2 mm wide paper strip, attached to a plastic support using PVC tape. The longer left-hand (LH) section was arranged as a horizontal cantilever, while the RH section was bent through a right angle to allow immersion in a small, machined reservoir used to contain the source. This arrangement allowed an evaporation section up to 40 mm long, fed by a shorter (5 mm) capillary transport section. The cantilever was surrounded by a transparent laminar flow duct, which had an air intake at the RH end and was driven by an axial-flow fan at the LH end. Airflow was induced using a 22 CFM axial fan (D481T-012KA-3, Micronel) driven by a DC supply. We were unable to measure the air velocity induced by the fan directly. However, we have measured its rotational speed using a light source and a photodetector and found a linear variation with drive voltage. Consequently, we expect a similar variation in the air velocity. At low airflow, long wetted cantilevers tended to collapse. Such experiments were therefore performed with the apparatus rotated by 90°. However, as the airflow rose, cantilevers experienced aerodynamic lift.

FIG. 8.

(a) Schematic and (b) realisation of the apparatus for rapid concentration, showing Brilliant Blue concentrated at an intermediate point along a strip of chromatography paper.

E. Airflow-enhanced evaporation

In separate experiments, the evaporation rate was quantified by the measurement of mass loss using a microbalance (BasBal 240, Mettler). The inset in Fig. 9 shows the apparatus used, which had a larger fluid reservoir, a vertical column with a larger duct, and a wider (20 mm) paper column. Figure 9 shows the results. The rate of mass loss varies linearly with fan drive voltage, being enhanced approximately ten-fold compared with the background rate using a 10 V drive. Greater enhancement was achieved using larger voltages and the smaller duct of the final rig.

FIG. 9.

Variation of the rate of mass loss with fan drive voltage, compared with the background rate. Inset: experimental apparatus for the mass flow measurement.

Evaporation velocity was estimated by measuring the capillary rise at different fan drive voltages and carrying out a best fit to the theoretical variation. To do so, proportionality was assumed between v_e and V as described above, and the column length was corrected to include the capillary transport section. Figure 10 shows the comparison between the experiment and theory. There is clearly reasonable qualitative agreement, and the results show that an evaporation velocity ≈50 times the ambient value can indeed be achieved if the effective column length can be reduced below ≈2 cm. The main feature preventing a further increase in v_e is that the tape seal attaching the cantilever tended to lift in very rapid airflow, opening parallel capillary transport channels along the sides of the paper strip.

FIG. 10.

Comparison of experimental and theoretical variations of evaporation-dominated capillary rise height H_e with evaporation velocity v_e.

V. CONCENTRATION AND SEPARATION

In this section, we describe the characterisation of experimental concentration by image processing and present results for concentration and separation.

A. Image processing

Concentration was quantified optically. A 40 mm long white InGaN light-emitting diode (LED) array (KWB-R3912W-1W, LuckyLight) behind the substrate was used for illumination and a camera for photography, allowing relative dye concentrations to be extracted via MATLAB-based image processing.⁶⁰ Figure 11 shows an example panel display, for a concentration experiment involving Brilliant Blue in isolation. A baseline image [Fig. 11(a)] is compared with a later image [Fig. 11(b)]. Guidelines are used to select areas for analysis and correct registration. Variations of R, G, and B pixel brightness are extracted along the strip [Figs. 11(c) and 11(d)]. Here, the R channel is significantly reduced, while the G and B channels are largely unaffected. The transmission variation is found from the ratio of R channel brightness in the two images [Fig. 11(e)]. The relative concentration (referenced to the value at x = 1) is extracted using the Beer-Lambert law [Fig. 11(f)] and compared to the 1/x variation of the hyperbolic ramp (dashed line).

FIG. 11.

Image processing used to extract the dye concentration: (a) and (c) initial image and initial spatial variations of the R, G, and B channels; (b) and (d) corresponding results for a later image; and (e) and (f) spatial variation in relative transmission and concentration.

In practice, the extracted value is sensitive to experimental factors: small variations strip position caused by airflow (which may be corrected by monitoring brightness in dry regions) and by the change in transmission caused by wetting (which reduces scattering at short wavelengths). For example, the B and G channel values are higher in the wetted region between the dashed lines in Fig. 11(c) than in Fig. 11(d). This effect can be corrected by calibration. Similar processing was carried out to extract the concentration of Tartrazine in isolation, using the B channel. Quantitative extraction of the concentration was less effective for mixtures because of the residual overlap of absorption spectra.

B. Concentration

Experiments were carried out with substrate mounted both vertically and horizontally and using both prewetted and unwetted substrates. Here, we present results only for dry, horizontal substrates, which gave the fastest concentration and simply required injection of dye through the tape covering the reservoir. At low airflows, when the filling time was a fraction of the concentration time, the results obtained from wetted and unwetted substrates became indistinguishable, and too slow for practical use. Concentration factors were deliberately limited to avoid saturating the substrate. Figure 12 shows typical images of a 30 mm long strip (rotated through 90° for presentation purposes) recorded at 1.5 min intervals during an experiment carried out using Brilliant Blue at a fan voltage of 20 V (which required a drive power of 15 W). There is little colour change during the filling stage. However, after around 6 min, the dye has reached the evaporation-dominated limit (here, H_e ≈ 20 mm). At this point, the flow is held up, and a blue band of increasing strength provides evidence of concentration. After 12 min, the airflow is switched off, and capillary action drives the concentrate to the tip of the strip (L ≈ 30 mm), dispersing as it propagates.

FIG. 12.

Spatial distribution of Brilliant Blue FCF at different absolute times T (in minutes) as indicated.

Figures 13 shows the variation of concentration factor C_L/C_L0 with normalised position x, at different absolute times T. The concentration profiles are clearly similar to the dashed-line variations in Fig. 5. At short times, the point of maximum concentration advances as the solvent front propagates; at longer times, it becomes stabilised at x = 0 and a maximum concentration factor of ≈120 is obtained at T = 12 min. However, several departures from the theoretical predictions may be seen. First, the concentration does not apparently fall to zero in unwetted regions of the substrate (A) because the transmission through dry paper is slightly higher than that of wet paper. Second, there is a shallow hump in the hyperbolic ramp (B). Possible explanations for this effect include variations in the ducted airflow, paper thickness, or water content with the position. Third, there is a small rise in the concentration at x = 1 (C), almost certainly due to parasitic capillary flow around the edges of the substrate. Despite this, the concentration profiles are largely as expected during both the filling and the concentration phases.

FIG. 13.

Measured spatial variations of the concentration factor of Brilliant Blue FCF at different absolute times T (in minutes) during the experiment shown in Fig. 11.

The circles in Fig. 14 show the time variation of the peak concentration factor. The concentration rate is initially low but rises on completion of filling, in qualitative agreement with the dashed line theoretical prediction of Fig. 6. The crosses show the results obtained at lower fan voltages (10 and 5 V, which required drive powers of 2.5 W and 0.5 W, respectively). Similar characteristics are obtained, confirming that the concentration rate can be controlled by evaporation velocity v_e.

FIG. 14.

Variation of the relative concentration of Brilliant Blue FCF with absolute time T at different fan drive voltages.

At 20 V, the time taken to achieve a 100-fold concentration (10 min) is comparable to that required using ion concentration polarization, for which the filling time is conventionally ignored. Unfortunately, this time is approximately three times larger than the previous theoretical estimate (≈3 min). The obvious explanation is the 5 mm long capillary pumping section between the evaporation region and the reservoir, which acts as a flow restrictor. Faster concentration would therefore be achieved if the length of this section could be reduced, for example, by patterning a reservoir directly on the paper substrate. The use of dry air, a more volatile solvent, or a thinner substrate would have a similar effect.

Other departures from ideal behaviour have been noted. Variations in airflow cause the stagnation point to wander. Depletion of the reservoir level results in an increase in the length of the capillary pumping section and a steady reduction in H_e. Finally, high concentrations of the adsorbate saturate the substrate. All three effects cause a reduction in the apparent concentration. The first two should be controllable by careful design. However, the third is inherent, especially for mixtures containing solutes with very different retardation factors. The solute with the largest R_f will concentrate first and preferentially occupy adsorption sites. Saturation effects may then lead to a “banded” concentration profile.

Concentration data are subject to several errors. The concentration factor is affected by inaccuracy in the optical measurement of relative transmission, due primarily to the curvature of the flow front and motion of the paper cantilever. From variations in the saturation concentration measured in a small number of experiments, we estimate this error as ±15%. The time taken to achieve a given concentration is affected by any variation in ambient conditions. From the variation in relative humidity in our experiments, we estimate this as ±100 × 5.5/46 = 12%.

C. Separation

Separation experiments were carried out using a light green mixture of Brilliant Blue and Tartrazine. Figure 15 shows images of a 40 mm long strip (again, rotated through 90° for presentation) recorded at different times T in minutes. Brilliant Blue reaches the hold-up point (here, at H_e ≈ 17 mm) slightly faster than Tartrazine and concentrates more sharply. After 10 min, the airflow is switched off, reducing the evaporation rate almost to zero. Capillary action then drives the concentrate away from the original stagnation point towards the tip of the strip (L = 40 mm), separating the blue and yellow dyes as it propagates due to the difference in retardation factors noted in Sec. IV (R_f ≈ 1 and R_f ≈ 0.88 for Brilliant Blue and Tartrazine, respectively). Of course, the solvent here is itself a dilute dye mixture, so complete separation will never be possible. In addition, ambient evaporation allows further concentration.

FIG. 15.

Spatial distribution of Brilliant Blue FCF and Tartrazine at different times T (in minutes) as indicated.

Despite this, extracted concentrations of the individual dye allow clear identification of the two components. For example, Fig. 16 shows concentration profiles at T = 15 min. Here, the original stagnation point is at x = 0, and capillary flow has driven the concentrate towards the substrate tip at around x = (17–40)/17 = −1.35. These results show that at least partial separation is possible and confirm the ability of controlled evaporation to allow complex operations on the same unpatterned substrate. However, further work is required to control separation and quantify the two dye concentrations more accurately.

FIG. 16.

Measured spatial variations of the concentration factor of Brilliant Blue FCF and Tartrazine at T = 15 min during the experiment shown in Fig. 15.

VI. CONCLUSIONS

We have demonstrated rapid concentration of water-soluble, nonvolatile solutes on paper using airflow-enhanced evaporation. The results show good agreement with the 1D theory for a two-phase system with a linear adsorption isotherm. In contrast to pervaporation-based microfluidic concentration, the introduction of a stationary phase renders concentration solute-dependent. However, the elimination of the membrane increases the rate of evaporation, which in turn increases the speed of concentration. We have shown that the maximum theoretical value of Pe depends only on material parameters and that chromatography paper offers excellent performance. Thin-layer substrates would also be suitable, especially if these may be nanostructured to allow large capillary rise heights. Potential applications include concentration of biofluids, when detection might be carried out using colorimetric indicators located near the tip or by paper spray mass spectrometry. However, in contrast to ion concentration polarization, the concentrate may also be held up at an intermediate stagnation point if the evaporation rate is high enough and then released to allow capillary pumped operations such as analysis or separation.

Incorporation of preconcentration into a lab-on-paper device such as a lateral flow assay (LFA) would require several modifications. The sample pad must be enlarged to store a larger fluid volume and sealed to prevent direct evaporation. A short open zone must be provided before the conjugate pad to allow evaporative concentration, with the LFA substrate mounted as a cantilever in a ducted airflow. Operation would then take place much as shown in Fig. 12, with the sample being first concentrated and then released for analysis. However, careful control and calibration would be required for consistent performance.

Further work is required to investigate nonlinear effects, especially saturation (which limits concentration of single analytes) and competitive adsorption (which might prevent concentration of weak components of a multi-analyte system). This work is in progress.