Abstract
Pooling plays an important role in generating a discriminative video representation. In this paper, we propose a new semantic pooling approach for challenging event analysis tasks (e.g. event detection, recognition, and recounting) in long untrimmed Internet videos, especially when only a few shots/segments are relevant to the event of interest while many other shots are irrelevant or even misleading. The commonly adopted pooling strategies aggregate the shots indifferently in one way or another, resulting in a great loss of information. Instead, in this work we first define a novel notion of semantic saliency that assesses the relevance of each shot with the event of interest. We then prioritize the shots according to their saliency scores since shots that are semantically more salient are expected to contribute more to the final event analysis. Next, we propose a new isotonic regularizer that is able to exploit the constructed semantic ordering information. The resulting nearly-isotonic support vector machine classifier exhibits higher discriminative power in event analysis tasks. Computationally, we develop an efficient implementation using the proximal gradient algorithm, and we prove new and closed-form proximal steps. We conduct extensive experiments on three real-world video datasets and achieve promising improvements.
Index Terms: Complex Event Detection, Event Recognition, Event Recounting, Semantic Saliency, Nearly-Isotonic SVM
1 Introduction
Modern consumer electronics (e.g. smart phones) have made video acquisition convenient for the general public. Consequently, the number of videos freely available on Internet has been exploding, thanks also to the appearance of large video hosting websites (e.g. YouTube). How to store, index, classify, recognize, and eventually make sense of the vast information contained in these videos has become an important challenge for the computer vision and multimedia communities [1]–[4], and a lot of recent work has been devoted to this exciting field which we generally refer as event analysis on untrimmed videos. In this work we will consider three specific event analysis tasks: event detection, event recognition, and event recounting.
In event detection, a large number of unseen videos is presented and a learning algorithm must rank them according to their likelihood of containing an event of interest, such as birthday party or dog show, while in event recognition, we aim to classify the unseen videos into multiple pre-defined event categories. If a video is declared to contain some event, we might be interested in knowing why, and ask the algorithm to return “evidences,” which is the goal of event recounting. The key to many event analysis tasks, including the aforementioned three, is a compact and discriminative representation of the video contents. Deep learning approaches, e.g. convolutional neural networks (CNNs), have become increasingly popular in this regard. The standard way [5], [6] is to extract local descriptors using CNNs on each frame of a video clip and then aggregate video-wise, through either average-pooling or max-pooling or even more complicated pooling strategies, e.g. [7], [8]. While effective in reducing size, pooling may result in the loss of structural or temporal information. On the other hand, retaining all frame features may not be desirable either, for computational or statistical reasons, especially in light of the limited number of training examples.
Instead, in this work we consider an intermediate strategy. We first split each video into multiple shots, and for each shot we randomly sample one key frame whose extracted features will be used to represent the entire shot. Instead of conducting pooling on the shot-level, we prioritize the shots according to their “relevance” to the event of interest. Next, to overcome the small sample size issue due to limited training data, we propose to train an “informed” classifier that puts larger weights on more relevant shots. As we verify in our experimental studies, leveraging this ordering bias can significantly enhance the discriminative power of the statistical classifier.
More precisely, in §3 we propose a new prioritizing procedure based on the notion of semantic saliency. Prioritizing objects according to saliency [9] is ubiquitous in visual tasks such as segmentation [10] and video summarization [11]. However, instead of borrowing an existing saliency algorithm, we prefer a more “supervised” notion that is closely related to our event analysis tasks. To this end, we first train 1,534 concept detectors using datasets available online (e.g., TRECVID SIN dataset, Google sports [12], UCF101 dataset [13] and YFCC dataset [14]), resulting in a probability vector for each shot that indicates the relative presence of individual concepts. Then, using the skip-gram model [15] in natural language processing, we pre-learn a relevance vector that measures the a priori relevance of each concept name with the textual description (provided in most video event datasets) of the event of interest. Lastly, by taking a weighted combination of the probability vector (likelihood) and the relevance vector (prior), we obtain the proposed semantic saliency of each shot. Rearranging the shots according to their saliency scores yields the desired prioritization.
The prioritized shot-level representations of each video can then be used to perform event analysis tasks. For event detection, we feed the prioritized representations into a linear large margin classifier such as support vector machines (SVM). Intuitively, shots with higher semantic saliency scores are expected to be more relevant to the event of interest, hence providing more discriminative information. To incorporate this carefully constructed order information, we propose, in §4, a new isotonic regularizer that encourages the classifier to put more weights on more salient shots. Our isotonic regularizer is not convex, but as we show in §5, the popular proximal gradient algorithm can still be applied, hence enjoying the strong convergence guarantees recently established in [16]. The key component, namely the proximal map of the isotonic regularizer, despite being nonconvex, is solved globally and exactly in linear time through a sequence of reductions. The final algorithm, which we call nearly-isotonic SVM (NI-SVM), is very efficient and runs quickly on large real video datasets. For comparison, we also propose an alternative convex variant, although its performance is found to be inferior.
In §6 we extend NI-SVM to the event recognition task by combining the multiclass support vector machines with our isotonic regularizer. After properly smoothing the multiclass hinge loss we can again apply the proximal gradient algorithm, whose per-step complexity scales only linearly with the problem size. In §7 we show how the weights of the proposed NI-SVM can be combined straightforwardly to define a recounting score, which can then be used to rank the shots and perform event recounting.
In §8 we validate the proposed approach through extensive experiments conducted on three real-world unconstrained video datasets (CCV, MED13, MED14), and achieve promising improvements measured by the mean average precision. Finally, in §9 we conclude the paper with some future directions. A preliminary version of this work appeared previously in [17].
2 Complex Event Analysis
In this section, we briefly review related works on the three event analysis tasks that we will study: event detection, event recognition, and event recounting.
2.1 Event detection
Event detection refers to the task in which a learning algorithm must rank a large number of unseen videos according to their likelihood of containing an event of interest [18]. Events are complex, and may be composed of several scenes, objects, actions, and the rich interactions between them. On the application side, event detection is the first important step in video analysis towards automatic categorization, recognition, search, and retrieval (just to name a few) hence it has attracted much attention in the computer vision and multimedia communities.
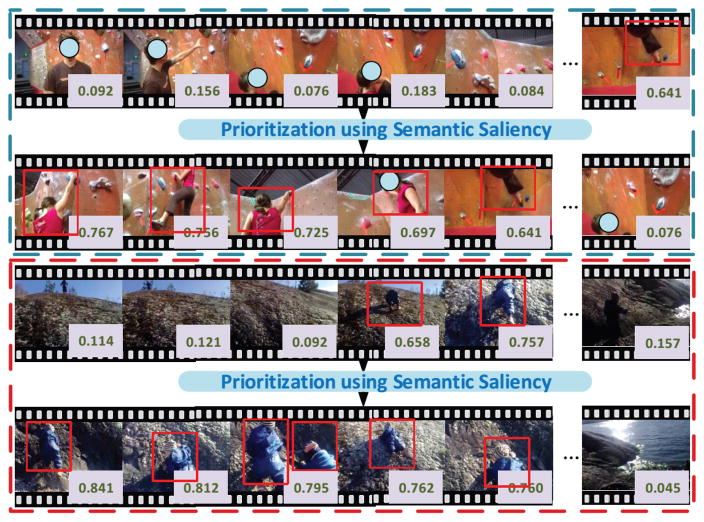
Complex event detection on unconstrained Internet videos is very challenging for the following reasons: 1) Unlike professional video recordings (e.g. films), the quality of Internet videos varies considerably, making them difficult to model statistically; 2) Events are complex and can be ambiguous: the “wedding shower” event consists of multiple defining concepts such as hugging (action), laughing (action) and veil (object), and can take place indoors (e.g. in a house) or outdoors (e.g. in a park), resulting in dramatic intra-class variations [19]; 3) Positive training examples are very limited. In the 10Ex competition organized by NIST, only 10 positive training examples and 5000 negative examples are provided, creating a highly imbalanced ranking problem; 4) A video clip can last from a few minutes to several hours, with the evidence possibly scattering anywhere, see Figure 1 for an example.
Fig. 1.
Two Internet video examples, where the same event “Rock Climbing” happened in very different time frames. The number in each frame indicates its saliency score, which describes how this keyframe is relevant to the specified event. We use this saliency information to prioritize the video shot representations.
A decent video event detection system usually consists of a good feature extraction module and a sophisticated statistical classification module. Various low-level features, e.g. SIFT [20], Space-Time Interest Points [21] and improved dense trajectories [22] have been used. Recently, CNN features have shown great promise in video classification [12], [23], with a number of subsequent improvements. To name a few, [24] argued that 3D CNNs with small 3 × 3 × 3 kernels are more suitable for spatiotemporal features such as in human action recognition; [25] achieved very impressive performance improvements on event detection by incorporating a set of latent concept descriptors, appropriately encoded using the vector of locally aggregated descriptors (VLAD) method; [26] carried out a thorough investigation of the influence of various components on event detection, such as different ways of performing spatial and temporal pooling and feature normalization, and different choices of CNN layers and classifiers; [27] proposed a hybrid deep learning framework that is able to model static spatial information, short-term motion, as well as long-term temporal clues in videos. Similar to those works, our event detection system also relies on CNN features, however, our focus in this work is on how to semantically pool the CNN features in a flexible way to improve the end classifier.
It has been observed, see e.g. [26], that large improvements on detection accuracy can be achieved by pooling the feature representations carefully and/or using statistically more powerful classifiers. In the first regard, [28] introduced student-t mixtures to improve the Fisher vector encoding in [29] (that is based on Gaussian mixtures); [7] divided each video (probabilistically) into the composition of several scenes and performed average pooling over the separate classifiers for different scene components; [8] performed average pooling over dynamically selected shots where (combinatorial) selection is achieved through latent structural SVM; [30] also proposed to select important shots using latent structural SVM but also considered evidence localization to simultaneously perform event detection and recounting; lastly, [31] proposed a simple matching approach to rank hence select most discriminative fragments. The above-mentioned works are similar to ours in the sense of prioritizing the shot representations in one way or another. However, we use additional data that is freely available online to perform the prioritization hence reducing the burden of acquiring many labeled training data, and we introduce a new classifier NI-SVM to account for the inevitable inaccuracy in prioritization. On the second regard, which is orthogonal to our work here, a number of previous works [2], [32], [33] have considered aggregating complementary features at the video level while others considered combining multiple statistical classifiers [34]– [36], including those trying to model the temporal information explicitly [37], [38].
There has also been resurgent interest in incorporating visual attention to visual tasks, see e.g. [39] on image caption generation and [40] on action recognition. These works share a conceptual similarity to our semantic saliency consideration below but a thorough investigation is beyond the scope of this work.
2.2 Event recognition
The goal of event recognition is to classify each test data into multiple pre-defined event categories. Due to the apparent similarity, event recognition research has been largely driven by adapting and extending the advances in the image recognition field to unconstrained video data.
Indeed, event recognition has been attempted on single static photos [41], [42], photo collections [43], and unconstrained videos [29], [44], [45]. For instance, [41] proposed a generative model to integrate cues such as scene, object categories and people to segment and recover the event category in a single image, while [42] further exploited user context, location, and user-provided tags and comments on a photo sharing website. [43] treated a photo collection as time series data and extended the discriminative hidden Markov models to the multiclass event recognition setting. Similar to our work, [44] also considered decomposing a complex video event into several low-level events (which we call concepts). [44] further modeled the relation between concepts and events through probabilistic graphical models and learned a discriminative model by using latent support vector machines. In contrast, we learn the relation between concepts and events through the skip-gram language model and exploit this information to prioritize the video shot representations.
2.3 Event recounting
In event recounting, we are interested in knowing why a certain detection/recognition decision, e.g. this video contains the “horse riding competition” event, is made. Usually, a recounting algorithm is expected to return some evidences (e.g. sample frames) to support the decision. Event recounting is very useful since it helps locate the video segment that contains the event of interest. In order to recount a multimedia event semantically and comprehensibly, it is useful to characterize an event as a juxtaposition of various semantic concepts, such as actions, scenes and objects, which are more descriptive and meaningful. Thus, unlike event detection or recognition, mid-level concept representations of the video contents, thanks to their interpretability, are usually preferred to low-level features.
Most existing event recounting approaches focus on the temporal domain. In [46], [47], the authors apply object and action detectors or low-level visual features to localize temporal key evidences, and a video-level classifier is trained to rank the key frames or shots. These approaches built on the assumption that classifiers that can distinguish positive and negative exemplars can also be used to distinguish the informative shots. However, they treat the shots or key frames equally, which may be dominated by the ubiquitous but non-informative ones. To overcome this limitation, [37] formulated the recounting problem as multiple instance learning, which aims to learn a instance-level event detection and recounting model by selecting the informative shots or key frames during the training process. [48] proposed a rule-based recounting approach to collect the evidence, involving human knowledge heavily. In [49], a generative And-OR graph model is used to represent the causal relationship between action concepts only. None of these works explicitly exploited saliency information. Finally, we mention that the very recent works [50] also considered a joint framework for event detection and event recounting simultaneously.
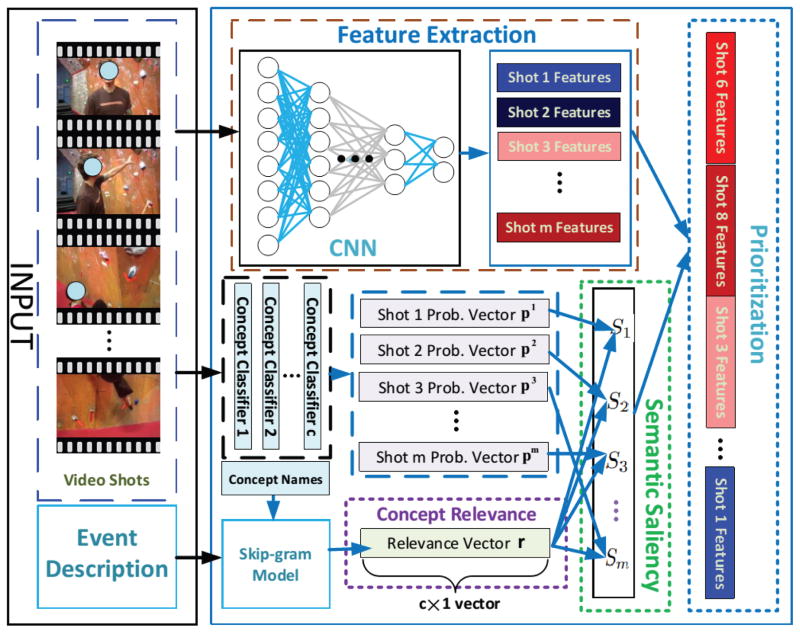
3 Prioritization using Semantic Saliency
As we mentioned before, a good feature extraction module is vital for event analysis. Thus we first describe our feature extraction method. Since not all video shots are equally relevant to the event of interest, we develop in this section a new prioritization procedure to reorder them. Then in §4 and §6 we propose the nearly-isotonic SVM classifier to exploit this ordering information. The overall system is illustrated in Figure 2 and we discuss it block by block in the sequel.
Fig. 2.
Each input video is divided into multiple shots, and each event has a short textual description. CNN is used to extract features (§3.1). ImageNet concept names and skip-gram model are used to derive a probability vector (§3.2) and a relevance vector (§3.3), which are combined to yield the new semantic saliency and used for prioritizing shots in the classifier training (§3.4).
3.1 Feature extraction
To extract representative features from videos, we first segment each video into m shots [v1, …, vm] using the color histogram difference as the indication of the shot boundary. Other segmentation or change-point detection algorithms, such as [51], may also be used. For simplicity, we randomly sample one key frame (or, as suggested by an anonymous reviewer, choose the center frame) from each shot and extract the frame level CNN descriptors using the architecture of [52]. The key insight in [52] is that by using smaller convolution filters (3 × 3) and very deep architecture (16–19 layers), significant improvement on the ImageNet Challenge 2014 can be achieved. Due to its excellent performance on images, we therefore choose to apply the same architecture to our video datasets after sampling key frames. With some abuse of notation, the extracted CNN features (from fc6, the first fully-connected layer) of all m shots are still written collectively as [v1, …, vm] ∈ ℝd×m. In our experiments, we set m as the average number of keyframes for all videos. For example, in the TRECVID MED14 dataset, the average number of keyframes is 51. When the video has more than m shots, we rank these shots according to their semantic saliency scores and keep the top m ranked shots. In this way, 9.3% shots in the MEDTest14 dataset are removed. When the video has less than m shots, we uniformly sample m keyframes from this video. We do not explicitly model temporal information in this work, although conceivably it could further aid our system.
3.2 Concept detectors
We collect a concept vocabulary of c = 1, 534 concepts from online available datasets (e.g., TRECVID SIN dataset, Google sports [12], UCF101 dataset [13] and YFCC dataset [14]), each accompanied with an entity description (e.g., rope climbing, skiing, fencing, diving, playing piano, horse race). These concepts can be used to aid event analysis. For example, we would expect concepts such as horse race and horse riding to be relevant to the event “horse competition.” Thus we train a detector/classifier for each concept in the vocabulary. All c concept classifiers/detectors will be applied to each video shot vj, resulting in a c-dimensional probability vector , with the entry pk standing for the (relative) probability of having the k-th concept appear in the shot vj. Finally, we will combine the probability vector p and the concept relevance (defined next) to yield the semantic saliency scores.
3.3 Concept relevance
Events come with short textual descriptions. For example, the event dog show in the TRECVID MED14 is defined as “a competitive exhibition of dogs.” We exploit this textual information by learning a semantic relevance score between the event description and the individual concept names (note that stop words are removed using NLTK [53]). More precisely, a skip-gram model [15] can be trained using the English Wikipedia dump (http://dumps.wikimedia.org/enwiki/). The skip-gram model learns a D-dimensional vector space representation of words by fitting the joint probability of the co-occurrence of surrounding contexts on large unstructured text data, and places semantically similar words near each other in the embedding vector space. Thus, it is able to capture a large number of precise syntactic and semantic word relationships. To learn the vector representation of short phrases consisting of multiple words, we aggregate the word embeddings using Fisher vectors [54] and follow mostly [55] except our embedding vectors are from the skip-gram model. In the Fisher vector, each phrase (i.e., a set of words) is described as the gradient of the log-likelihood of these observations on an underlying probabilistic model, and we use vlfeat [56] to generate the Fisher vector for each phrase. After normalizing the length of the respective vector representations, we compute the cosine distance between the event description and each concept name, resulting in a relevance vector r ∈ ℝc, where rk measures the a priori relevance of the k-th concept to the event of interest. Note that the concept relevance vector r is event dependent, and we repeat the procedure for each event in our training data.
3.4 Semantic saliency
Lastly, we define the semantic saliency score of each video shot as a weighted combination of the concept probability vector p (the likelihood, different for each video shot, see §3.2) and the concept relevance vector r (the prior, same for all shots, see §3.3):
| (1) |
Repeating this for each shot vj, j = 1, …, m, of a video generates its saliency vector s = [s1, …, sm]. Note that this saliency vector s is event dependent, and we derive it separately for each event in our training data. Intuitively, the saliency score sj evaluates the importance of the j-th shot to the event of interest. The most salient shots are those most likely to contain the specified event, hence they should carry more weight in the final classifier boundary. Thus we prioritize the shots by reordering them such that
| (2) |
i.e., the shots are ranked in a descending order of saliency. Importantly, note that different videos are likely reordered differently. After prioritization, it is desirable to train an event classifier that takes this valuable ordering information into account, which motivates the isotonic regularizer that we propose in the next section. Note that all our results can be extended to a partial ordering, i.e., allowing some shots to be incomparable (when their scores are very close, for instance).
The definition of our semantic saliency essentially follows the zero-shot learning framework of [57]. It is convenient because it is fully automatic. We note that the recent work [58] proposed a different approach for event detection when the number of labeled training examples is limited. A potentially superior approach is to extract relevant keyframes from the positive training exemplars and use these to define saliency. However, the downside of this alternative is that it requires some human intervention/labeling.
4 Nearly-Isotonic Support Vector Machines for event detection
As described above, we represent each video Vi, i = 1, …, n, as a matrix [ ], where are the extracted CNN features from the j-th shot. In this section we consider event detection, that is, decide whether or not a test video belongs to an event of interest. As the usual practice, we model the event detection as a binary classification problem, and we reorder the shot-level CNN features according to their semantic saliency scores as defined in §3.4. The resulting feature representation is denoted as , to distinguish the original representation Vi.
To perform event detection, we then employ the large margin binary support vector machines (SVM):
| (3) |
where λ ≥ 0 is the regularization constant, and the loss function ℓ: ℝ × ℝ → ℝ measures the discrepancy between the true label yi ∈ {1, −1} and the prediction . For instance, we can use
the least squares loss: ;
the hinge loss: ℓ(y, t) = (1 − yt)+, where as usual (t)+: = max{t, 0} is the positive part;
the squared hinge loss: ;
the logistic loss: ℓ(y, t) = log(1 + exp(−yt)).
Note that the hinge loss is not differentiable, however, both the squared hinge loss and the logistic loss can be used instead as its smooth approximation. In practice, which loss works best is largely problem and feature dependent. For our experiments, the squared hinge loss seems to work comparably well. To detect a test video V, we use the usual sign rule:
| (4) |
The regularizer Ω in (3) is introduced to induce some desirable structures on the classifier weight matrix W, and will play a major role in the sequel. In vanilla SVM, (the squared Frobenius norm), which penalizes large weight matrices to avoid overfitting. Another useful regularizer is Ω(w) = ||W||1 (the ℓ1-norm, sum of absolute values), which encourages sparsity hence is effective for feature selection. However, neither of the abovementioned regularizers is able to exploit the order information that we carefully constructed in §3. In fact, both of them are invariant to column reorderings. Instead, we propose below a new isotonic regularizer that respects the prioritization we performed on the shots using their saliency scores.
4.1 The isotonic regularizer
Let us assume momentarily that d = 1, i.e., there is only a single feature. This assumption, although unrealistic, simplifies our presentation and will be removed later. As mentioned, we want to learn a weight vector that respects the saliency order in our shot-level features, since more relevant shots are expected to contribute more to the final detection boundary. This motivates us to consider the following isotonic regularizer:
| (5) |
To see the rationale behind, let us use the absolute value |wj| of the weight vector to indicate the contribution of the j-th shot to the final decision rule sign(Σj vjwj). Since the shots are arranged in decreasing order of relevance, we would expect roughly |w1| ≥ |w2| ≥ ⋯ ≥ |wm|, i.e., the weights (in magnitude) align well with the saliency order we constructed in §3.4. If this is the case, the regularizer ||w||ι would be 0, i.e. incurring no penalty. On the other hand, we pay a linear cost for violating any of the saliency orders, i.e., if instead |wj| > |wj−1| for some j, we suffer a cost equal to the difference |wj| − |wj−1|. Clearly, the more we deviate from a pair of saliency order, the more we are penalized. Equipping Ω(w) = ||w||ι in (3) we obtain a new classification method which we call the nearly-isotonic SVM (NI-SVM):
| (6) |
Exploiting order information in statistical estimation has a long history, see the wonderful book [59] for early applications. Similar regularizers to (5) have also appeared recently. For instance, [60] dropped the absolute values in (5) and considered:
| (7) |
while [61] replaced the positive part in (5) with the absolute value:
| (8) |
The well-known total variation (semi)norm [62]:
| (9) |
is also widely used in image denoising problems. These alternative regularizers bear a clear similarity to ours, however, we believe our formulation (5) is more appropriate for our setting (see §8.2.4 below for empirical verification): The weight vector w has signed entries, and the order we aim to force is one-directional. Indeed, the alternative regularizer (8) will always incur a cost except when |wj| = |wj−1|, a condition that is too stringent to be useful in our setting. Similarly, for two negative entries 0 > wj > wj−1, the alternative regularizer (7) would incur an unnecessary penalty wj − wj−1 > 0. The same problem also occurs for the total variation norm (9). Note that all four regularizers (5), (7), (8), and (9) are nondifferentiable while (5) and (8) are also nonconvex. Nevertheless, we can still design an efficient algorithm for solving NI-SVM (with regularizer (5)). Before that, however, let us mention how to extend to multiple features (d > 1).
4.2 Extending to multiple features
When d > 1, each video representation Vi is a matrix in ℝd×m, hence accordingly the linear classifier we learn is indexed by the weight matrix W ∈ ℝd×m. Inspecting the NI-SVM formulation (6), we note first that the loss term extends immediately: the standard inner product 〈Ṽi, W〉 in ℝd×m extends straightforwardly for any d. For the isotonic regularizer, we need to summarize all d importance measures (each contributed by a feature). There are multiple ways to achieve this, and we consider two particularly convenient ones here:
| (10) |
| (11) |
where Wi,: (resp. W:,j) is the i-th row (resp. j-th column) of the matrix W. The first regularizer (10) simply sums the vector isotonic regularizer along each feature dimension, while the second regularizer (11) first aggregates the shot-level importance by computing the Euclidean norm of the d weights and then applies the vector isotonic regularizer on top. When d = 1, both (10) and (11) reduce to the vector isotonic regularizer (5), but we expect them to behave differently when d > 1. The corresponding NISVM formulation (6) with the matrix regularizers (10) and (11) will be called respectively NI-SVM1 and NI-SVM2.
4.3 A convex alternative
The matrix isotonic regularizers (10) and (11) are not convex, making the corresponding NI-SVM1 and NI-SVM2 formulations also nonconvex. In this section we propose a simple convex alternative, mainly as a comparison baseline against the above nonconvex formulations.
To this end, we add a nonnegative constraint on the classifier weight matrix W:
| (12) |
where ||W||ι can be either ||W||ι,1 (NI-SVM1+) or ||W||ι,2 (NISVM2+). Note that the convexity in (12) is gained by placing a restriction on the classifier, which in turn may jeopardize its prediction performance (verified in our experiments). On the other hand, the nonnegative constraint encourages a sparse weight matrix W, in a spirit similar to nonnegative matrix factorization [63], since our video representation Ṽi is nonnegative as well. This may in turn be beneficial in interpretation tasks.
4.4 Kernelization
The proposed NI-SVM cannot be directly kernelized due to the isotonic regularizers (10) or (11), which are not functions of the ℓ2 norm [64]. We mention two indirect ways for kernelization: (1). We can apply the isotonic regularizers on the dual SVM formulation; (2). For translation-invariant kernels (e.g. Gaussian), we can approximately derive from the kernel an explicit, finite dimensional, and nonlinear feature transformation ϕ(·) [65]. Applying ϕ(·) first to the video representations we can proceed to develop NI-SVM as before. These ideas will be pursued in our future work.
5 Solving NI-SVM by the proximal gradient
The matrix isotonic regularizers (10) and (11) are both nonsmooth and nonconvex, making the optimization of the NI-SVM formulation (6) a very challenging task. Fortunately, the proximal gradient algorithm (see e.g. [66]) has been recently extended in [16] to handle “definable” functions that need not be convex or smooth. In this section we first briefly recall the proximal gradient algorithm, and then we show how to efficiently implement its key component (e.g. the proximal map) for our NI-SVM formulation.
5.1 The proximal gradient
The proximal gradient (PG) algorithm is particularly suitable for solving the general composite minimization problem:
| (13) |
For our NI-SVM formulation (6), the loss term corresponds to the function f and the matrix isotonic regularizer corresponds to the function g. PG performs the following two steps repeatedly until converging to a critical point [16]:
| (14) |
| (15) |
where η > 0 a suitably chosen step size. In essence, (14) is a usual gradient step w.r.t. f, while (15) is a proximal step w.r.t. g, known as the proximal map . The proximal map is a natural generalization of the Euclidean projection operator onto a closed set, and it is well-defined if the function g does not decrease faster than a quadratic function. For instance, when g is the 1-norm, then is the well-known soft-shrinkage operator.
Since evaluating the gradient ∇f is straightforward (for the nondifferentiable hinge loss, we will see how to approximate it using the logistic loss in §6), the efficiency of PG (14)–(15) hinges on our capability of computing the proximal map (15) quickly, which itself is a minimization problem. This is a great advantage of the PG algorithm: it encapsulates the nonconvexity and nonsmoothness of the function g entirely into the proximal map (15). If the function g is “simple” enough so that its proximal map can be solved in closed-form, then we bypass the nonconvex and nonsmooth issue completely. This is indeed the case for our matrix isotonic regularizers (10) and (11), as we demonstrate next.
5.2 Proximal map for the isotonic regularizer
In this subsection we show that the proximal map for both matrix isotonic regularizers (10) and (11) can be computed exactly in linear time. This is achieved through a sequence of reductions.
5.2.1 Reducing to the vector case
We first reduce the proximal maps for the matrix isotonic regularizers (10) and (11):
| (16) |
| (17) |
to their vector cousin:
| (18) |
where w, z ∈ ℝm and ||·||ι is defined in (5).
For (16) this reduction is obvious as ||W||ι.,1 is separable in rows of the matrix W, so we need only apply (18) to each row of W independently. For (17) its objective function expands as follows:
| (19) |
Now consider the decomposition Z = ΘΛ, where each column of Θ has unit Euclidean norm and Λ is diagonal with zi in the i-th diagonal. Clearly, the regularizer ||Z||ι,2 only depends on Λ, and for fixed Λ, the first term in (19) is minimized precisely when for all j. Plugging it back we can solve the diagonal matrix Λ = diag(z) by:
| (20) |
which clearly is in the form of the vector problem (18).
Therefore, we need only focus on the vector proximal map (18). Note that the isotonic regularizer ||w||ι is not convex, thus its proximal map in (18) is not a convex problem. Nevertheless, we will show how to solve it exactly and globally in linear time.
5.2.2 Reducing to the convex case
Crucially, we observe that the vector isotonic regularizer ||z||ι is invariant to the sign changes of any component zi, but the quadratic term is minimized when the signs of w and z match. Thus, at any minimizer of (18) we must have sign(wi) = sign(zi) for all i, further reducing the vector problem (18) to:
| (21) |
| (22) |
where |w| is the component-wise absolute value of w, and
| (23) |
If we can solve (21), now a convex problem thanks to the nonnegative constraint, then we can immediately recover
| (24) |
(The multiplication on the right-hand side is component-wise.)
5.2.3 Reducing to the total variation norm
Two elementary observations turn out to be key in solving (21) efficiently: (a). Under the nonnegative constraint z ≥ 0, we have
| (25) |
which follows from applying the identity 2(t)+ = t + |t| to each term (|zj| − |zj−1|)+. (b). The function κ in (23), i.e., the nonnegative constraint, is invariant to permutations of the coordinates.
Denote h(z) = zm − z1, and recall from (21) that we need to solve the proximal map of the function
| (26) |
Then, we have the following decomposition rule, whose proof, based on [67], can be found in the supplement:
Theorem 1
Denote ei the i-th canonical basis in ℝm. For any η, γ ≥ 0 and for all w ∈ ℝm,
| (27) |
| (28) |
| (29) |
| (30) |
Note that we have also allowed including an additional squared 2-norm or 1-norm in the above decomposition. Such flexibility can be very useful in some applications where it is desirable to avoid overfitting or to induce sparsity. The key insight in Theorem 1 is that the computation of the seemingly complicated proximal maps (c.f. left-hand sides of (27) and (28)) can be accomplished by executing, sequentially, some very elementary proximal maps (c.f. right-hand sides of (27) and (28)). We have not specified the proximal map of the total variation norm , however, it has a well-known linear time exact algorithm, see e.g. [68].
Algorithm 1.
Proximal Gradient for NI-SVM
5.2.4 Putting things together
We summarize the above reductions and steps in Algorithm 1. Despite the nonconvexity and nonsmoothness, Algorithm 1 computes the proximal maps of the matrix isotonic regularizers (10) and (11) globally and exactly in linear time. It is clear that each iteration of the proximal gradient costs O(dmn) in time complexity while it costs O(dm) in space complexity.
Conveniently, the proximal gradient Algorithm 1 we developed above for NI-SVM can be easily recycled for the convex alternative in §4.3, with only a single slight change: We do not backup or restore the sign (e.g. omitting lines 14 and 19 in Algorithm 1).
6 Multiclass NI-SVM event recognition
In this section we consider the event recognition problem, that is, to decide which of the k events does a test video V = [v1, …, vm] belong to. Like previous work we model event recognition as a multiclass classification problem, i.e. the label y ∈ {1, …, k}. In the following we extend our NI-SVM formulation (6) to this multiclass setting by following the work of [69].
For each event e and video Vi, following §3 we compute its saliency score vector si,e, which then induces a permutation matrix Pi,e ∈ ℝd×m such that Vi,e = ViPi,e, i.e. we reorder the video representation Vi so that its saliency vector is ordered decreasingly. For each event e we train a classifier represented as We ∈ ℝd×m, and we define the multiclass loss as
| (31) |
| (32) |
where is the indicator function. Clearly the multiclass loss ℓi couples the k classifiers due to the max operator in (32): it is zero if the true prediction 〈Vi,yi,Wyi〉 is larger than any other prediction 〈Vi,e, We〉, e ≠ yi by at least a margin of size 1, otherwise we pay a linear cost w.r.t. the most confusing wrong label.
Now we are ready to present the multiclass NI-SVM:
| (33) |
Depending on whether p = 1 or p = 2, we will denote (33) as or . By adding the nonnegative constraint We ≥ 0, we again have a convex alternative, which will be denoted respectively as and . To recognize a test video V, we resort to the max-prediction rule:
| (34) |
where ties are broken arbitrarily. Of course for k = 2, the multiclass formulation (33) reduces to the binary formulation (6) (with the hinge loss).
We can again optimize the multiclass formulation (33) using the proximal gradient, except one small problem: the multiclass hinge loss (32) is not differentiable. Nevertheless, there is a well-known smoothing technique to get around this issue, using the following inequality:
| (35) |
| (36) |
Therefore, as long as the smoothing parameter μ is small, we can adequately approximate the max function using the log-sum-exp function, which is clearly differentiable (with Lipschitz continuous gradient). Applying this technique to the multiclass loss (32) we get rid of the nonsmoothness of the loss, and make the proximal gradient applicable again. Of course, the binary hinge loss can be dealt with analogously, although it is often easier to use simply the squared binary hinge loss.
As to the proximal map of the regularizer g in (33), we need only apply the steps in Section 5.2 independently to each of the k classifier weights We, thanks to separability. The entire procedure is very similar to Algorithm 1 hence we do not reproduce the pseudo-code here. It suffices to note that each iteration costs O(dmnk) in time and O(dmk) in space.
7 Event Recounting using NI-SVM
As mentioned in §2.3, event recounting aims at providing comprehensible evidences to justify a detection/recognition decision. Here we present a simple scoring approach on top of NI-SVM to perform event recounting. The idea is that the NI-SVM classifier is designed to assign larger weights to more semantically salient shots, thus it is natural to use these weights to compute a recounting score for each shot. More specifically, for each test video Ṽ = [ṽ1, …, ṽm] that is declared to contain the event of interest, we compute the recounting score for its j-th shot as follows:
| (37) |
where recall that W = [w1, …, wm] is the classifier weight returned by (the binary) NI-SVM. Then, we rank the shots using the scores ℛ𝒮j above and return the top ones as evidence. Note that our decision rule for event detection is
| (38) |
hence a shot with a large recounting score ℛ𝒮j is likely to contribute a lot to or even determine the decision.
A similar scoring approach can be used to recount event recognition results. Interestingly, in this multiclass scenario, if a test video is declared to belong to event e, then shots with large negative scores 〈vj, 〉 for all e′ ≠ e can also be considered as evidences to support event e.
8 Experiments
In this section we carry out extensive experiments to validate the proposed approach, on three event analysis tasks: event detection, event recounting, and event recognition. Our main goal is to verify that carefully exploiting the order information given by our semantic saliency, such as in our proposed nearly-isotonic SVM, can indeed improve the performance relatively.
8.1 Experimental setup
Let us first describe our experimental setup.
8.1.1 Datasets
We test on the following three real video datasets.
MED141: The TRECVID MEDTest 2014 dataset contains approximately 100 positive training exemplars per event, and all events share ~5000 negative training exemplars. The test set has about 23,000 videos. There are in total 20 events, with descriptions. To our best knowledge, this is the largest (35,914 videos in total) public dataset for event analysis.
MED132: Similar as MED14. Note that 10 of its 20 events overlap with those of MED14.
CCVsub: The official Columbia Consumer Video dataset [70] contains 9,317 videos in total with 20 semantic categories, including scenes like “beach,” objects like “cat,” and events like “baseball” and “parade.” For our purpose we only use the 15 event categories. For each event we use its own training data as positive and all other training data as negative, totaling 4,659 training videos and 4,658 testing videos.
8.1.2 Concept classifier vocabulary
We pre-train 1,534 concept classifiers using TRECVID SIN dataset (346 classes), Google sports (478 classes) [12], UCF101 dataset (101 classes) [13] and YFCC dataset (609 classes) [14].We first extract improved dense trajectory (IDT) features with the code provided in [22] and encode with the Fisher vector representation [71]. Then, on top of the extracted low-level features, the cascade SVM [72] was trained for each semantic concept. Similarly, we extract the improved dense trajectory features on all shots of each video in the three video datasets mentioned in §8.1.1 and apply the concept detectors to derive their semantic representations.
8.1.3 Parameter tuning
As mentioned in §3.1 we use the CNN architecture in [52] to extract 4096 features on one keyframe per video shot. The regularization constants of our method λ and γ (c.f. Algorithm 1) are selected using cross-validation from the range {10−4, 10−3, …, 103, 104}. We will also study the influence of some of the choices we made in our system, such as initialization, shot segmentation, concept detectors, frame sampling, etc.
8.2 Event detection
In this section, we evaluate the performance of the proposed NI-SVM for complex event detection. According to the NIST standard, we detect each event separately. For the two MED datasets, we consider both 100Ex (100 positive training examples) and 10Ex (10 positive training examples), which are split by NIST. The CCVsub dataset does not provide such splits.
8.2.1 Evaluation metric
According to the NIST standard, we evaluate the event detection performance by the mean Average Precision (mAP). Average precision is a single-valued metric approximating the area under the precision-recall curve, and is widely used in information retrieval tasks. Denote R as the number of true relevant videos in a test dataset. At any index j, let Rj be the number of relevant videos in the top j list. Then, AP is defined as
| (39) |
where Ij = 1 if the j-th video is relevant (positive) and 0 otherwise. When all relevant videos are ranked on top of the irrelevant ones, AP achieves its largest value 1.0. Thus, a larger AP usually indicates a better performance.
8.2.2 Comparison under a single type of feature
We first present experimental results on comparing different configurations in our algorithm. For our NI-SVM formulations we consider both the least squares loss and the squared3 hinge loss . We use the subscript 1 and 2 respectively to distinguish the matrix isotonic regularizers (10) and (11). A further subscript + is used to signal the convex alternative in §4.3. More precisely, we compare the following variations:
LSA: least squares loss with average-pooling on the video shots. Note that pooling is performed on the selected m keyframes, for fairness and efficiency.
LSM: least squares loss with max-pooling.
LST: least squares loss without pooling, but the shots are prioritized according to their saliency scores.
NI-LS1: least squares loss with isotonic regularizer (10).
NI-LS2: least squares loss with isotonic regularizer (11).
NI-LS1+: nonnegative convex version of NI-LS1.
NI-LS2+: nonnegative convex version of NI-LS2.
Similarly, for the squared hinge loss, we replace “LS” throughout with “SVM”. As suggested in §5.2.3, additional and ℓ1 regularizers can be incorporated. The performance in terms of mAP is reported in Table 1 and Table 2, with further details deferred to Tables 10 to 15 in the supplement. We remark that our proposed approach requires additional data (although can be very different from the training videos) to derive semantic saliency, while most alternatives we compare to are based on low-level features only hence do not require additional data.
TABLE 6.
Comparison against ranking SVM (RSVM) [74]. Time is shown in seconds (smaller is better) and mAP is in percentage.
| MED14 (100Ex)
|
MED13 (100Ex)
|
CCVsub
|
||||
|---|---|---|---|---|---|---|
| RSVM | NI-SVM2 | RSVM | NI-SVM2 | RSVM | NI-SVM2 | |
| Training Time | 52.8 | 12.4 | 49.6 | 10.7 | 32.3 | 8.8 |
| Test Time | 1.8 | 1.3 | 1.6 | 1.0 | 1.2 | 0.7 |
| mAP | 28.8 | 34.4 | 34.7 | 39.2 | 71.9 | 78.3 |
TABLE 7.
Video statistics and recounting accuracy.
| MED13 | MED14 | |
|---|---|---|
| Average Video Length | 164.3 seconds | 188.4 seconds |
| Average Shot Length | 6.1 seconds | 8.3 seconds |
| Average Accuracy | 91.4% | 85.7% |
From the experimental results, we observe:
Generally, the nearly isotonic variants (with prefix NI) perform well, verifying that properly exploiting the order information can significantly improve the performance. Moreover, the matrix isotonic regularizer (11) (subscript 2) generally performs better than the matrix isotonic regularizer (10) (subscript 1).
The squared hinge loss on average performs better than the least squares loss, unanimously across all methods.
Additional -norm regularization (left panel) generally outperforms additional ℓ1-norm regularization (right panel). We hypothesize that it is because the CNN features we use are very discriminative hence sparsity does not help here.
The convex variants (with subscript +) have poorer performance than the nonconvex counterparts (but still competitive against average-pooling), possibly because the nonnegative constraint is too restrictive. Empirically we also found that the nonconvex variants are quite robust against initializations (random or using the convex variant), likely because we are able to solve the proximal maps exactly.
In Figure 3 we present an example from event “horse riding competition” to demonstrate our prioritization and semantic saliency. Another example can be found in Figure 6 of the supplement.
Fig. 3.
Qualitative analysis of the prioritization effect. A positive test video from event “Horse Riding Competition” is used as an example. The first row shows the original video shots; the second row depicts prioritized video shots, having its weight (in norm) on the bottom left and semantic saliency on the bottom right; and the third row presents the most salient concepts detected in these shots.
We further compare to a few recent state-of-the-art alternatives that use a single4 type of feature. The results are shown in Table 3. Note that whenever possible we have quoted the numbers directly from the references, while if not available we used code from the respective authors to obtain the results ourselves. It is clear that the proposed framework with its best variant NI-SVM2 compares favorably against the other methods. The improvement is more significant under the more challenging 10Ex setting, possibly because the saliency information constructed using additional data is more pronounced when labeled training examples are limited. With more labeled training examples (e.g. 100Ex), the improvement due to NI-SVM starts to diminish, and the impact of feature or architectural design starts to dominate.
TABLE 1.
Performance (mAP) w.r.t. different configurations on the TRECVID MEDTest2014 (100Ex), MEDTest2013 (100Ex) and CCVsub datasets. Squared hinge loss is used. (Larger mAP is better.)
|
regularized
|
ℓ1 regularized
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVMA | SVMM | SVMT | NI-SVM1 | NI-SVM1+ | NI-SVM2 | NI-SVM2+ | SVMA | SVMM | SVMT | NI-SVM1 | NI-SVM1+ | NI-SVM2 | NI-SVM2+ | |
| MED14 | 27.2 | 24.5 | 30.1 | 32.2 | 30.4 | 34.4 | 31.0 | 26.5 | 24.9 | 27.6 | 29.1 | 27.8 | 28.2 | 26.1 |
| MED13 | 31.1 | 29.2 | 36.0 | 38.1 | 36.4 | 39.2 | 37.4 | 31.8 | 30.9 | 34.2 | 35.4 | 38.2 | 34.4 | 32.0 |
| CCVsub | 73.8 | 71.6 | 75.3 | 77.9 | 75.0 | 78.3 | 76.8 | 73.1 | 71.6 | 74.5 | 75.1 | 74.5 | 72.9 | 75.5 |
8.2.3 Comparison against state-of-the-art systems
We also compare to some state-of-the-art systems that usually fuse multiple types of features. For fair comparison, we have fused the CNN feature and the additional IDT feature for our method (only in this section). The results are shown in Table 4, from which we observe that the proposed system again performs competitively, especially in the 10Ex setting, for reasons mentioned before. Note that CNN-Exp [26] achieved the best performance on MEDTest 2014 (100Ex), at the expense of employing a more costly kernel SVM classifier while all other methods used linear SVM.
TABLE 2.
Performance (mAP) w.r.t. different configurations on the TRECVID MEDTest2014 (100Ex), MEDTest2013 (100Ex) and CCVsub datasets. Least square loss is used. (Larger mAP is better.)
|
regularized
|
ℓ1 regularized
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LSA | LSM | LST | NI-LS1 | NI-LS1+ | NI-LS2 | NI-LS2+ | LSA | LSM | LST | NI-LS1 | NI-LS1+ | NI-LS2 | NI-LS2+ | |
| MED14 | 25.9 | 23.2 | 27.3 | 30.9 | 28.9 | 32.9 | 29.4 | 25.1 | 23.6 | 25.4 | 27.8 | 26.2 | 26.7 | 24.6 |
| MED13 | 29.8 | 28.1 | 35.6 | 36.8 | 35.1 | 38.3 | 36.0 | 30.6 | 29.5 | 33.7 | 34.2 | 34.1 | 33.2 | 30.8 |
| CCVsub | 72.7 | 70.5 | 74.1 | 76.7 | 73.9 | 77.3 | 75.7 | 71.8 | 70.3 | 73.5 | 73.8 | 73.3 | 71.6 | 74.3 |
8.2.4 Results w.r.t. different isotonic regularizers
In this section, we compare different isotonic regularizers that have appeared in the literature:
All of the above isotonic regularizers are extended to the matrix setting as illustrated in §4.2. Table 5 gives the performance in terms of mAP on MED14, MED13 and CCVsub in terms of 100Ex setting, where we use the least squares loss, an additional regularizer, and the matrix extension (11). Full details can be found in Figures 7 to 9 in the supplement. As expected, our isotonic regularizer ||·||ι achieves the best overall performance, likely because it aligns in the most appropriate way with the semantic saliency.
TABLE 3.
mAP comparison against state-of-the-art alternatives that use a single type of feature on the TRECVID MEDTest 2014, MEDTest 2013 and CCVsub datasets.
| MED14
|
MED13
|
CCVsub | |||
|---|---|---|---|---|---|
| 100Ex | 10Ex | 100Ex | 10Ex | ||
| LTS [38] | 27.5 | 16.8 | 34.6 | 18.2 | 73.4 |
| SED [37] | 29.6 | 18.4 | 36.2 | 20.1 | 74.7 |
| DP [8] | 28.8 | 17.6 | 35.3 | 19.5 | 74.1 |
| STN [12] | 30.4 | 19.8 | 37.1 | 20.4 | 75.8 |
| C3D [24] | 31.4 | 20.5 | 36.9 | 22.2 | 77.2 |
| MIFS [73] | 29.0 | 14.9 | 36.3 | 19.3 | – |
| CNN-Exp [26] | 29.7 | – | – | – | – |
| CNN + VLAD [25] | 35.7 | 23.2 | 40.3 | 25.6 | – |
| NI-SVM2 | 34.4 | 26.1 | 39.2 | 26.8 | 78.3 |
8.2.5 Comparison against ranking SVM
We also compared NI-SVM against ranking SVM [74] in terms of both accuracy and efficiency. The results are reported in Table 6, from which we observe that the proposed algorithm significantly outperforms ranking SVM (with average pooling and regularization) in both running time and accuracy (mAP). Note that ranking SVM is a more direct way to optimize mAP, however, unlike our method, it cannot exploit the semantic saliency information. Computationally, our proximal gradient algorithm also appears to be much more efficient, thanks to the closed-form proximal steps (c.f. Theorem 1).
TABLE 4.
mAP comparison against state-of-the-art systems that fuse multiple types of features on the TRECVID MEDTest 2014 and MEDTest 2013 datasets.
8.2.6 Sensitivity analysis
Sensitivity w.r.t. tuning parameters λ and γ
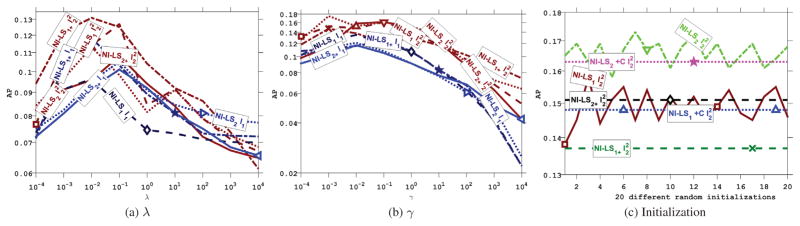
We conduct experiments to assess the sensitivity of NI-SVM w.r.t. the regularization parameters λ and γ. We report the results on MEDTest2014 in Figure 4a and Figure 4b, and defer the results on MEDTest 2013 and CCVsub to Figures 10 and 11 in the supplement. To be more specific, we first fix γ = 1, which is the median of its allowed range of values, and we record the AP by varying λ in Figure 4a, from which we observe that the performance is relatively robust against the parameter λ. Generally speaking, the best performance is obtained when λ is in the range of {10−3, 10−2, 10−1}. Then, we fix λ at the median value 1 and test the sensitivity against the parameter γ. The AP with varying γ is shown in Figure 4b, from which we see that the performance degrades when γ is overly large. The best performance is obtained when γ is in the range of {10−2, 10−1, 100}.
Fig. 4.
Performance sensitivity w.r.t. λ, γ and initialization on the TRECVID MEDTest 2014 dataset.
Sensitivity w.r.t. random initializations
The formulation of NI-SVM is nonconvex, hence in theory it could have multiple local optima. In practice we observed that the proximal gradient in Algorithm 1 always converged to a reasonable solution. To test this point, we repeatedly run Algorithm 1 20 times, each with a different initialization. We also tried to initialize Algorithm 1 with the (globally) optimal solution of the convex variant in §4.3. The results in terms of AP on MEDTest 2014 are depicted in Figure 4c (and Figures 12 to 15 in the supplement). It is clear that the convex variants (with subscript +) have stable performance w.r.t. different initializations, thanks to convexity. The nonconvex variants exhibit small variations, and if we initialize it by the solution of the convex variant, we get slightly worse but stable performance. Overall, Algorithm 1 converged to a reasonable solution rather quickly.
More sensitivity analysis can be found in the supplement.
8.3 Event recounting
We conduct experiments on event recounting in this section, using the scoring method detailed in §7. We only consider the event detection setting for succinctness.
8.3.1 Evaluation metric
Evaluating the performance of event recounting algorithms is challenging for the following reasons: (1) there is no ground truth information provided; (2) there are relatively few previous works that can be compared against. Instead, we compare to a natural baseline as follows. We first train a video-level event classifier, and then apply it to the shots to rank them accordingly. Lastly, the top ranked shots are returned as evidence. Following the NIST pipeline, we use Amazon Mechanical Turk to invite 10 volunteers for the evaluation purpose. Before evaluation, the volunteers are asked to read the event description in text, and watch five positive videos in the training set. Then, our evaluation system randomly chooses 10 positive videos from the test set, and presents the top evidence shots generated by the baseline and our proposed method. The judges are asked to decide if these evidence shots are relevant (true/false), and which method gives more informative evidence shots (better/similar/worse). To make fair comparison, the judges are not aware which shot is generated by which method during evaluation. Based on the judges’ responses, we consider two metrics: 1) average accuracy, which is the percentage of relevant evidence shots; 2) relative performance, which counts judges’ preferences of the baseline or the proposed approach.
8.3.2 Results
We summarize the average length of the test videos, the average length of evidence shots returned by our proposed approach, and the average accuracy derived from the judge’s responses in Table 7. The results are quite promising: the proposed approach achieves 91.4% and 85.7% average accuracy by returning only 3.8% and 4.5% evidence shots in the original videos, respectively. This clearly demonstrates that the classifier weights of NI-SVM are reasonable in capturing the relative importance of the individual shots, in a way that is comprehensible to humans. The results also seem to indicate that MED14 is more challenging than MED13.
TABLE 5.
mAP comparison of different isotonic regularizers on TRECVID MEDTest 2014, MEDTest 2013 and CCVsub.
| MED14 (100Ex) | MED13 (100Ex) | CCVsub | |
|---|---|---|---|
| ||w||ι | 34.4 | 39.2 | 78.3 |
| ||w||+ | 29.4 | 35.0 | 73.8 |
| ||w||a | 30.3 | 36.2 | 75.1 |
| ||w||tv | 31.1 | 36.9 | 76.7 |
The judges’ preferences between the proposed method and the baseline are averaged and recorded in Table 8. It is clear that the proposed method is subjectively better for most events on both datasets.
TABLE 8.
Event recounting results on MED13 and MED14. For each event, we randomly pick 10 positive test videos and ask 10 judges to rate better, similar, or worse between the proposed method and the baseline. The results among judges are averaged.
| MED14
|
MED13
|
||||||
|---|---|---|---|---|---|---|---|
| ID | Better | Worse | Similar | ID | Better | Worse | Similar |
| E006 | 7 | 1 | 2 | E021 | 7 | 3 | 0 |
| E007 | 9 | 0 | 1 | E022 | 3 | 4 | 3 |
| E008 | 6 | 1 | 3 | E023 | 6 | 2 | 2 |
| E009 | 7 | 2 | 1 | E024 | 6 | 1 | 3 |
| E010 | 8 | 2 | 0 | E025 | 5 | 3 | 2 |
| E011 | 6 | 3 | 1 | E026 | 7 | 1 | 2 |
| E012 | 7 | 1 | 2 | E027 | 6 | 3 | 1 |
| E013 | 4 | 6 | 0 | E028 | 7 | 1 | 2 |
| E014 | 6 | 2 | 2 | E029 | 5 | 2 | 3 |
| E015 | 4 | 1 | 5 | E030 | 4 | 1 | 5 |
| E021 | 7 | 2 | 1 | E031 | 8 | 0 | 2 |
| E022 | 3 | 4 | 3 | E032 | 7 | 1 | 2 |
| E023 | 5 | 3 | 2 | E033 | 8 | 1 | 1 |
| E024 | 6 | 1 | 3 | E034 | 5 | 0 | 5 |
| E025 | 6 | 3 | 1 | E035 | 4 | 1 | 5 |
| E026 | 7 | 2 | 1 | E036 | 6 | 1 | 3 |
| E027 | 4 | 4 | 2 | E037 | 5 | 3 | 2 |
| E028 | 6 | 1 | 3 | E038 | 4 | 5 | 1 |
| E029 | 5 | 3 | 2 | E039 | 4 | 0 | 6 |
| E030 | 4 | 2 | 4 | E040 | 7 | 1 | 2 |
|
| |||||||
| Total | 117 | 44 | 39 | Total | 114 | 33 | 52 |
8.4 Event recognition
In this section we evaluate the multiclass NI-SVMm proposed in §6 for event recognition.
8.4.1 Evaluation metric
A widely adopted evaluation metric in the multiclass setting is the F1 score, which is simply the harmonic mean of the recall (r) and precision (p): , where recall (r) is the fraction of relevant videos retrieved by the system and precision (p) is the fraction of retrieved videos that are relevant. The F1 scores for different events are averaged.
8.4.2 Competitors
We compare the following multiclass algorithms:
: the multiclass SVM [69] with average-pooling on the video shots.
: the multiclass SVM [69] with max-pooling.
: the multiclass SVM [69] without pooling, but the shots are prioritized according to their saliency scores.
: the proposed method with isotonic regularizer (10).
: the proposed method with isotonic regularizer (11).
: nonnegative convex version of .
: nonnegative convex version of .
We can again add additional ℓ1 or regularizer, without any computational cost.
Note that in the multiclass setting, we only use training videos belonging to some event while recall that in event detection, for each event we use a lot more training videos as negatives, especially those that do not belong to any event. Thus, the results here cannot be directly compared to the ones in §8.2.
8.4.3 Results
The experimental results are tabulated in Table 9, from which we make the following observations: (1) Similar as in event detection, average-pooling consistently performs better than max-pooling on all three datasets; (2) further outperforms average-pooling, verifying that pooling can also be detrimental for event recognition, if naively done; (3) The proposed multiclass NI-SVMm variants achieve the best performance on all three datasets, confirming again the benefits of exploiting the semantic ordering information. (4) Additional -norm regularization generally outperforms additional ℓ1-norm regularization, although we found the latter usually leads to much sparser solution (hence may result in significantly reduced test time).
TABLE 9.
Mean F1 score (mF1) on MED14, MED13, and CCVsub datasets. A larger mF1 indicates better performance.
|
regularized
|
ℓ1 regularized
|
||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
| MED14 | 38.4 | 34.6 | 39.7 | 41.3 | 40.3 | 44.7 | 42.2 | 37.1 | 35.8 | 37.9 | 39.5 | 38.7 | 39.8 | 36.3 | |||||||||||||
| MED13 | 48.5 | 45.2 | 49.4 | 52.6 | 50.3 | 53.5 | 52.1 | 46.8 | 45.7 | 47.3 | 50.1 | 51.6 | 48.2 | 45.8 | |||||||||||||
| CCVsub | 81.6 | 78.7 | 82.4 | 84.8 | 82.6 | 86.1 | 85.0 | 79.8 | 78.4 | 81.6 | 82.3 | 82.1 | 81.4 | 82.6 | |||||||||||||
9 Conclusion
Based on the observation that not all video shots are equally relevant to an event of interest, in this work we propose to prioritize the video shots using a novel notion of semantic saliency. Through a suitable isotonic regularizer we design the “informed” nearly-isotonic SVM classifier (NI-SVM) that is able to exploit the carefully constructed ordering information. An efficient proximal gradient implementation, with new and closed-form proximal steps, is developed. We further extend NI-SVM to the multiclass setting to perform event recognition. Extensive experiments on three real video datasets are conducted to validate the proposed algorithms on video analysis tasks such as event detection, recognition, and recounting. In the future, we plan to incorporate temporal and spatial information to define a more refined notion of saliency. We also plan to explore NI-SVM in other applications, such as sparse coding with time series data. Interestingly, the recent work [75], based on a completely different technique, demonstrated that the ordering structure (temporal or spatial) can largely improve sparse coding. It would be very interesting to see how our isotonic regularizers perform in their setting.
Supplementary Material
Acknowledgments
We thank the reviewers and the associate editor for numerous critical comments that largely improved our manuscript. We thank Mark Schmidt for sharing prettyPlot. This work was supported by NIH R01GM087694 and P30DA035778, the Data to Decisions Cooperative Research Centre www.d2dcrc.com.au, and NSFC (U1509206).
Biographies

Xiaojun Chang received the PhD degree in computer science from Centre for Quantum Computation and Intelligent Systems (QCIS), University of Technology Sydney, Australia in 2016. He is currently a postdoc in the language technology institute of Carnegie Mellon University. His main research interests include machine learning, data mining and computer vision.

Yao-Liang Yu received his PhD in computing science from Univerisity of Alberta in 2013, after which he spent two and a half years in the machine learning department of Carnegie Mellon University. He is currently an assistant professor with the David R. Cheriton School of Computer Science at University of Waterloo. His main research interests include robust methods, representation learning, kernel methods, convex and nonconvex optimization, distributed system, and applications in computer vision.

Yi Yang received the Ph.D. degree in computer science from Zhejiang University, Hangzhou, China, in 2010. He is currently an associate professor with University of Technology Sydney, Australia. He was a Post-Doctoral Research with the School of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA. His current research interest includes machine learning and its applications to multimedia content analysis and computer vision.

Eric P. Xing received the PhD in molecular biology from Rutgers University, and another PhD in computer science from UC Berkeley. He is a professor of machine learning in the School of Computer Science, Carnegie Mellon University. His principal research interests lie in the development of machine learning and statistical methodology; especially for solving problems involving automated learning, reasoning, and decision-making in high-dimensional, multimodal, and dynamic possible worlds in social and biological systems. He is an associate editor of the Annals of Applied Statistics (AOAS), the Journal of American Statistical Association (JASA), the IEEE Transactions of Pattern Analysis and Machine Intelligence (PAMI), the PLoS Journal of Computational Biology, and an action editor of the Machine Learning Journal (MLJ), the Journal of Machine Learning Research (JMLR). He is a member of the US Defense Advanced Research Projects Agency (DARPA) Information Science and Technology (ISAT) Advisory Group, and a Program chair of ICML 2014.
Footnotes
The convergence guarantee for PG requires the loss to be smooth, hence excludes the usual hinge loss.
Technically speaking, our method used two types of features: IDT for deriving the saliency scores and CNN for training the classifier.
Contributor Information
Xiaojun Chang, Centre for Quantum Computation and Intelligent Systems, University of Technology Sydney, Sydney, NSW 2007, Australia.
Yao-Liang Yu, Machine Learning Department, Carnegie Mellon University, Pittsburgh, PA, 15213, USA.
Yi Yang, Centre for Quantum Computation and Intelligent Systems, University of Technology Sydney, Sydney, NSW 2007, Australia.
Eric P. Xing, Machine Learning Department, Carnegie Mellon University, Pittsburgh, PA, 15213, USA
References
- 1.Ma Z, Yang Y, Sebe N, Zheng K, Hauptmann AG. Multimedia event detection using a classifier-specific intermediate representation. IEEE Transactions on Multimedia. 2013;15(7):1628–1637. [Google Scholar]
- 2.Tamrakar A, Ali S, Yu Q, Liu J, Javed O, Divakaran A, Cheng H, Sawhney H. Evaluation of low-level features and their combinations for complex event detection in open source videos. CVPR; 2012. [Google Scholar]
- 3.Ma Z, Yang Y, Sebe N, Hauptmann AG. Knowledge adaptation with partially shared features for event detection using few exemplars. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2014;36(9):1789–1802. doi: 10.1109/TPAMI.2014.2306419. [DOI] [PubMed] [Google Scholar]
- 4.Yang Y, Nie F, Xu D, Luo J, Zhuang Y, Pan Y. A multimedia retrieval framework based on semi-supervised ranking and relevance feedback. IEEE Trans Pattern Anal Mach Intell. 2012;34(4):723–742. doi: 10.1109/TPAMI.2011.170. [DOI] [PubMed] [Google Scholar]
- 5.Aly R, Arandjelovic R, Chatfield K, Douze M, Fernando B, Harchaoui Z, KM, et al. The axes submissions at Trecvid 2013. 2013. [Google Scholar]
- 6.Yu S-I, Jiang L, Xu Z, Lan Z, Xu S, Chang X, et al. Informedia@TRECVID 2014 MED and MER. 2014. [Google Scholar]
- 7.Cao L, Mu Y, Natsev A, Chang S-F, Hua G, Smith JR. Scene aligned pooling for complex video recognition. ECCV; 2012. [Google Scholar]
- 8.Li W, Yu Q, Divakaran A, Vasconcelos N. Dynamic pooling for complex event recognition. ICCV; 2013. [Google Scholar]
- 9.Koch C, Ullman S. Shifts in selective visual attention: Towards the underlying neural circuitry. Human Neurobiology. 1985;4:219–227. [PubMed] [Google Scholar]
- 10.Rahtu E, Kannala J, Salo M, Heikkilä J. Segmenting salient objects from images and videos. ECCV; 2010. [Google Scholar]
- 11.Lee YJ, Ghosh J, Grauman K. Discovering important people and objects for egocentric video summarization. CVPR; 2012. pp. 1346–1353. [Google Scholar]
- 12.Karpathy A, Toderici G, Shetty S, Leung T, Sukthankar R, Li F-F. Large-scale video classification with convolutional neural networks. CVPR; 2014. [Google Scholar]
- 13.Soomro K, Zamir AR, Shah M. UCF101: A dataset of 101 human actions classes from videos in the wild. 2012. [Google Scholar]
- 14.Thomee B, Shamma DA, Friedland G, Elizalde B, Ni K, Poland D, Borth D, Li L. The new data and new challenges in multimedia research. CoRR. 2015;abs/1503.01817 [Google Scholar]
- 15.Mikolov T, Sutskever I, Chen K, Corrado GS, Dean J. Distributed representations of words and phrases and their compositionality. NIPS; 2013. [Google Scholar]
- 16.Bolte J, Sabach S, Teboulle M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Mathematical Programming, Series A. 2014;146:459–494. [Google Scholar]
- 17.Chang X, Yang Y, Xing EP, Yu Y. Complex event detection using semantic saliency and nearly-isotonic SVM. ICML; 2015. [Google Scholar]
- 18.Duan L, Xu D, Tsang IW, Luo J. Visual event recognition in videos by learning from web data. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2012;34(9):1667–1680. doi: 10.1109/TPAMI.2011.265. [DOI] [PubMed] [Google Scholar]
- 19.Wu F, Liu Y, Zhuang Y. Tensor-based transductive learning for multimodality video semantic concept detection. IEEE Transactions on Multimedia. 2009;11(5):868–878. [Google Scholar]
- 20.Lowe DG. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision. 2004;60(2):91–110. [Google Scholar]
- 21.Laptev I, Caputo B, Schüldt C, Lindeberg T. Local velocity-adapted motion events for spatio-temporal recognition. Computer Vision and Image Understanding. 2007;108(3):207–229. [Google Scholar]
- 22.Wang H, Schmid C. Action recognition with improved trajectories. ICCV; 2013. [Google Scholar]
- 23.Simonyan K, Zisserman A. Two-stream convolutional networks for action recognition in videos. NIPS; 2013. [Google Scholar]
- 24.Tran D, Bourdev LD, Fergus R, Torresani L, Paluri M. Learning spatiotemporal features with 3d convolutional networks. ICCV; 2015. [Google Scholar]
- 25.Xu Z, Yang Y, Hauptmann AG. A discriminative CNN video representation for event detection. CVPR; 2015. [Google Scholar]
- 26.Zha S, Luisier F, Andrews W, Srivastava N, Salakhutdinov R. Exploiting image-trained CNN architectures for unconstrained video classification. BMVC; 2015. [Google Scholar]
- 27.Wu Z, Wang X, Jiang Y, Ye H, Xue X. Modeling spatial-temporal clues in a hybrid deep learning framework for video classification. ACM Conference on Multimedia Conference, MM; 2015. [Google Scholar]
- 28.Nagel M, Mensink T, Snoek CG. Event Fisher vectors: Robust encoding visual diversity of visual streams. BMVC; 2015. [Google Scholar]
- 29.Oneaţă D, Verbeek J, Schmid C. Action and event recognition with Fisher vectors on a compact feature set. ICCV; 2013. [Google Scholar]
- 30.Sun C, Nevatia R. DISCOVER: Discovering important segments for classification of video events and recounting. CVPR; 2014. [Google Scholar]
- 31.Mettes P, van Gemert JC, Cappallo S, Mensink T, Snoek CGM. Bag-of-fragments: Selecting and encoding video fragments for event detection and recounting. ICMR; 2015. [Google Scholar]
- 32.Natarajan P, Wu S, Vitaladevuni S, Zhuang X, Tsakalidis S, Park U, Prasad R, Natarajan P. Multimodal feature fusion for robust event detection in web videos. CVPR; 2012. pp. 1298–1305. [Google Scholar]
- 33.Tang K, Yao B, Li F-F, Koller D. Combining the right features for complex event recognition. ICCV; 2013. [Google Scholar]
- 34.Liu J, McCloskey S, Liu Y. Local expert forest of score fusion for video event classification. European Conference on Computer Vision (ECCV); 2012. [Google Scholar]
- 35.Liu D, Lai K-T, Ye G, Chen M-S, Chang S-F. Sample-specific late fusion for visual category recognition. CVPR; 2013. [Google Scholar]
- 36.Vahdat A, Cannons K, Mori G, Oh S, Kim I. Compositional models for video event detection: A multiple kernel learning latent variable approach. ICCV; 2013. [Google Scholar]
- 37.Lai K-T, Liu D, Chen M-S, Chang S-F. Recognizing complex events in videos by learning key static-dynamic evidences. ECCV; 2014. [Google Scholar]
- 38.Tang K, Li F-F, Koller D. Learning latent temporal structure for complex event detection. CVPR; 2012. [Google Scholar]
- 39.Xu K, Ba JL, Kiros R, Cho K, Courville A, Salakhutdinov R, Zemel RS, Bengio Y. Show, attend and tell: Neural image caption generation with visual attention. ICML; 2015. [Google Scholar]
- 40.Sharma S, Kiros R, Salakhutdinov R. Action recognition using visual attention. 2016. arXiv:1511.04119. [Google Scholar]
- 41.Li L, Li F. What, where and who? Classifying events by scene and object recognition. ICCV; 2007. [Google Scholar]
- 42.McAuley JJ, Leskovec J. Image labeling on a network: Using social-network metadata for image classification. ECCV; 2012. [Google Scholar]
- 43.Bossard L, Guillaumin M, Gool LV. Event recognition in photo collections with a stopwatch HMM. ICCV; 2013. [Google Scholar]
- 44.Izadinia H, Shah M. Recognizing complex events using large margin joint low-level event model. ECCV; 2012. [Google Scholar]
- 45.Zhang X, Yang Y, Zhang Y, Luan H, Li J, Zhang H, Chua TS. Enhancing video event recognition using automatically constructed semantic-visual knowledge base. IEEE Transactions on Multimedia. 2015;17(9):1562–1575. [Google Scholar]
- 46.Liu J, Yu Q, Javed O, Ali S, Tamrakar A, Divakaran A, Cheng H, Sawhney HS. Video event recognition using concept attributes. WACV; 2013. [Google Scholar]
- 47.Sun C, Burns B, Nevatia R, Snoek C, Bolles B, Myers GK, Wang W, Yeh E. ISOMER: informative segment observations for multimedia event recounting. ICMR; 2014. [Google Scholar]
- 48.Tan CC, Jiang Y, Ngo C. Towards textually describing complex video contents with audio-visual concept classifiers. ACM MM; 2011. pp. 655–658. [Google Scholar]
- 49.Gupta A, Srinivasan P, Shi J, Davis LS. Understanding videos, constructing plots learning a visually grounded storyline model from annotated videos. CVPR; 2009. [Google Scholar]
- 50.Chang X, Yu Y-L, Yang Y, Hauptmann AG. Searching persuasively: Joint event detection and evidence recounting with limited supervision. ACM MM; 2015. [Google Scholar]
- 51.Yuan J, Wang H, Xiao L, Zheng W, Li J, Lin F, Zhang B. A formal study of shot boundary detection. IEEE Transactions on Circuits and Systems for Video Technology. 2007;17(2):168–186. [Google Scholar]
- 52.Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. ICLR; 2015. [Google Scholar]
- 53.Bird S. Nltk: the natural language toolkit. Proceedings of the COLING/ACL on Interactive presentation sessions; 2006. [Google Scholar]
- 54.Sánchez J, Perronnin F, Mensink T, Verbeek JJ. Image classification with the Fisher vector: Theory and practice. International Journal of Computer Vision. 2013;105(3):222–245. [Google Scholar]
- 55.Clinchant S, Perronnin F. Textual similarity with a bag-of-embedded-words model. ICTIR; 2013. [Google Scholar]
- 56.Vedaldi A, Fulkerson B. Vlfeat: an open and portable library of computer vision algorithms. ACM MM; 2010. [Google Scholar]
- 57.Lampert CH, Nickisch H, Harmeling S. Learning to detect unseen object classes by between-class attribute transfer. CVPR; 2009. [Google Scholar]
- 58.Habibian A, Mensink T, Snoek CG. Videostory embeddings recognize events when examples are scarce. 2015. arXiv:1511.02492. [DOI] [PubMed] [Google Scholar]
- 59.Barlow RE, Bartholomew DJ, Bremner JM, Brunk HD. Statistical inference under order restrictions: The theory and application of isotonic regression. John Wiley & Sons; 1972. [Google Scholar]
- 60.Tibshirani RJ, Hoefling H, Tibshirani R. Nearly-isotonic regression. Technometrics. 2011;53(1):54–61. [Google Scholar]
- 61.Yang S, Yuan L, Lai Y-C, Shen X, Wonka P, Ye J. Feature grouping and selection over an undirected graph. KDD; 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D. 1992;60:259–268. [Google Scholar]
- 63.Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401:788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- 64.Yu Y, Cheng H, Schuurmans D, Szepesvári C. Characterizing the representer theorem. ICML; 2013. [Google Scholar]
- 65.Rahimi A, Recht B. Weighted sums of random kitchen sinks: Replacing minimization with randomization in learning. NIPS; 2006. [Google Scholar]
- 66.Fukushima M, Mine H. A generalized proximal point algorithm for certain non-convex minimization problems. International Journal of Systems Science. 1981;12(8):989–1000. [Google Scholar]
- 67.Yu Y. On decomposing the proximal map. NIPS; 2013. [Google Scholar]
- 68.Davies PL, Kovac A. Local extremes, runs, strings and multiresolution. The Annals of Statistics. 2001;29(1):1–65. [Google Scholar]
- 69.Crammer K, Singer Y. On the algorithmic implementation of multiclass kernel-based vector machines. Journal of Machine Learning Research. 2001;2:265–292. [Google Scholar]
- 70.Jiang Y, Ye G, Chang S, Ellis DPW, Loui AC. Consumer video understanding: A benchmark database and an evaluation of human and machine performance. ICMR; 2011. [Google Scholar]
- 71.Perronnin F, Sánchez J, Mensink T. Improving the Fisher kernel for large-scale image classification. ECCV; 2010. [Google Scholar]
- 72.Graf HP, Cosatto E, Bottou L, Durdanovic I, Vapnik V. Parallel support vector machines: The cascade SVM. NIPS; 2004. [Google Scholar]
- 73.Lan Z, Lin M, Li X, Hauptmann AG, Raj B. Beyond gaussian pyramid: Multi-skip feature stacking for action recognition. CVPR; 2015. [Google Scholar]
- 74.Joachims T. Training linear svms in linear time. ACM SIGKDD; 2006. [Google Scholar]
- 75.Ni B, Moulin P, Yan S. Order preserving sparse coding. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2015;37(8):1615–1628. doi: 10.1109/TPAMI.2014.2362935. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.