Water Dynamics in the Hydration Shells of Biomolecules

Abstract

The structure and function of biomolecules are strongly influenced by their hydration shells. Structural fluctuations and molecular excitations of hydrating water molecules cover a broad range in space and time, from individual water molecules to larger pools and from femtosecond to microsecond time scales. Recent progress in theory and molecular dynamics simulations as well as in ultrafast vibrational spectroscopy has led to new and detailed insight into fluctuations of water structure, elementary water motions, electric fields at hydrated biointerfaces, and processes of vibrational relaxation and energy dissipation. Here, we review recent advances in both theory and experiment, focusing on hydrated DNA, proteins, and phospholipids, and compare dynamics in the hydration shells to bulk water.

1. Introduction

Water is a major prerequisite for life, and most biological processes occur in an aqueous environment.¹ The water environment can be an active partner in this context; it can strongly influence the structure and function of biomolecules within it.^2,3 The most relevant interactions are hydrogen bonds (H bonds),⁴ a mainly local type of weak bonding among water molecules and between water and the polar or ionic groups of the biomolecule, long-range Coulomb forces, and hydrophobic forces,⁵ with the latter being less well understood but nonetheless relevant for the aggregation of hydrophobic moieties and/or protein folding. At ambient temperature, biomolecules and their aqueous environment execute assorted thermal motions which result in structure fluctuations on a multitude of time scales.

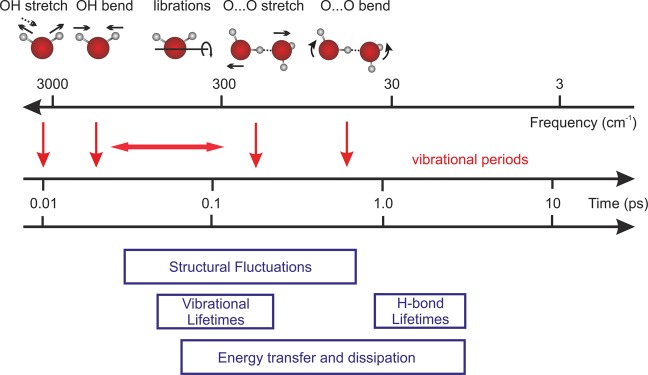
In recent years, the structural and vibrational dynamics of bulk water have been studied in detail by theory, simulation, and experiment.^6,7 The liquid consists of a network of water molecules in which each H₂O forms on average slightly less than four H bonds with its neighbors, two via the hydrogen-donating OH groups and two via the hydrogen-accepting oxygen atom. The molecular arrangement is dynamic; it fluctuates due to thermal excitation of low-frequency modes, and H bonds are broken and reformed on a picosecond time scale. Different regimes in time for the more rapid structural dynamics can be distinguished, as illustrated schematically in Figure 1. The shortest times shown are the vibrational periods of the intramolecular OH stretching and bending vibrations, which are approximately 10 (0.01 ps) and 20 fs. On a time scale between several tens and several hundreds of femtoseconds, librational (hindered rotational) motions of water molecules occur; at short times these are localized on a single or a few molecules and are more delocalized over groups of molecules at hundreds of femtoseconds, representing truly intermolecular modes. H-bond stretching vibrations, i.e., motions of the two outer oxygen atoms changing the H-bond length, have a period of 200 fs, while H-bond bending has periods of 600–800 fs.

Figure 1.

Time scales and processes in bulk H₂O. Red arrows above the logarithmic time axis mark the periods of vibrational and librational degrees of freedom schematically illustrated at the top of the figure. Horizontal boxes below the time axis illustrate the time range covered by particular processes of bulk water dynamics.

The fluctuations arising from thermal excitation of the intermolecular modes result in a fast loss of intermolecular structural correlation, with the fastest decay components in the sub-100 fs regime.⁸⁻¹² Vibrational lifetimes of OH stretch and bend excitations are each approximately 200 fs, while high-frequency librations decay within less than 100 fs.¹³⁻¹⁶ The OH stretch vibrations relax via the v = 2 and 1 states of the OH bend vibration, while the OH bend vibration relaxes via a libration of the bend-excited molecule.^17,18 In the latter process, coupling of the bend vibration to a librational overtone level of the bend-excited molecule defines the predominant relaxation pathway. Subsequent energy redistribution among librations and other water intermolecular modes results in the formation of a vibrationally hot water ground state within roughly 1 ps. The resonant transfer of OH stretch excitations between different water molecules occurs on a 100 fs time scale, contributing to the fast 100 fs anisotropy decay of the vibrational excitation,¹⁹ while molecular reorientation occurs on a slower ∼2.5 ps time scale.

A particularly important process in water is the exchange of hydrogen-bond partners via breaking and reformation of stable H bonds, which in neat water occurs in a time range between 1 and 5 ps. At the molecular level, this behavior has been explained by the jump mechanism which invokes a reorientation of water molecules mainly through sudden, large-amplitude angular jumps when a water hydroxyl (OH) group trades H-bond acceptors, a process induced, e.g., by the activated formation of transient five-coordinated water defects.^20,21 The angular jump defines the duration of the net passage through this transition state, which is on the order of 200 fs, which is short compared to the picosecond time scale of the period for which a particular H bond exists. In this review, our primary focus will be on the femtosecond and picosecond dynamics shown in Figure 1 and how they are affected by a biomolecule, while the much longer time scales arising, for example, from slow biomolecular conformational motions (see, e.g., ref (22)) will not be discussed.

In order to describe the peculiar properties of water next to biomolecules and biomolecular ensembles such as membranes, the concept of a hydration shell has been employed,^23,24 suggested by the concept which existed long before for simple solutes. In a qualitative picture, the hydration shell consists of the first water layer—or sometimes the first few water layers—surrounding the biomolecule and interacting with it or at least noticeably influenced by it. A more quantitative definition depends on the particular property considered and represents a nontrivial issue. On the other hand, the aqueous environment “sufficiently” far from the biomolecular surface should display properties of bulk-like water. From the viewpoint of both structure and dynamics, the distinction of the hydration shell from bulk water poses major challenges and requires the combination of structure-sensitive and time-resolved spectroscopic and computational methods to gain quantitative insight.

In comparison to the detailed knowledge acquired on bulk water’s structure and dynamics, there is much less understanding of the behavior of water in hydration shells. Indeed, there are different conflicting concepts about the spatial range over which water structure around a biomolecule deviates from bulk water and about the character of water dynamics in the neighborhood of a biomolecule. We identify the main issues in the following.

• (i)The generally nonplanar and corrugated surface of a biomolecule defines steric boundary conditions for the adjacent hydration shell. As a result, the spatial arrangement of water molecules in the first hydration layer is different from bulk water, and their vibrational and rotational degrees of freedom are modified.²⁵⁻²⁸ Moving from the first water layer to larger distances from the biomolecular surface, the hydration shell gradually assumes the bulk water structure. The length scale on which this structural adaptation occurs is quite controversial, with the numbers of water layers considered to be involved ranging between 2 and more than 10.
• (ii)Polar and/or charged groups at the biomolecular surface interact with the first water layer through electric forces and local H bonds, thus adding to the structural heterogeneity of the hydration layers. Such groups and water molecules are both sources of electric fields, but currently the strength and spatial range of these fields are barely characterized. Another issue concerns the occurrence and strength of H bonds between hydrating water and the biomolecule. There is a large variety of geometries ranging from the comparably strong H bonds between phosphate groups and up to 6 water molecules to the clathrate water structures around hydrophobic cholines that do not form H bonds with the solute.^29,30 The variety of interactions and structures leads to a temporal variety in hydration shell dynamics and a behavior different from bulk water to a degree remaining to be quantified.
• (iii)Dynamics of water in a hydration shell have remained highly controversial, and different perspectives have been inferred based on different methods. In a first picture, a more rigid water structure with a pronounced slowing down of structure fluctuations and rotational motion and a concomitant increase of H-bond lifetimes has been claimed, i.e., so-called “biological water”.^31,32 In contrast, both recent simulations at the molecular level and experimental work have challenged this concept and reported a moderate slowing down of water dynamics by the rather modest factors of 2–3 compared to the bulk.³³⁻³⁵
• (iv)Finally, the close attention given to hydration shell dynamics is often justified by the role that they have been suggested to play in the conformational dynamics of biomolecules. Water is commonly seen as a lubricant of biomolecular motions^2,3 or even their cause. For example, in the so-called “slaving” picture,³⁶⁻³⁸ fluctuations of the surrounding water molecules control large-scale protein motions, but this picture is still debated, and recent studies have led to contradictory views.³⁹⁻⁴¹ In addition to their effect on the biomolecular flexibility, hydration shell dynamics have been suggested to be essential to the biomolecular function and, e.g., to govern the antifreeze activity of some proteins⁴² and the catalytic activity of enzymes.⁴³ To be functional, proteins are often considered to require a minimum hydration level of approximately 0.3 g of water per gram of protein, i.e., close to a monolayer of water.⁴⁴ However, while protein flexibility and enzymatic activity clearly increase with increasing hydration level, a series of experimental results has established that enzyme proteins can remain flexible and functional, respectively, at extremely low humidity (below 0.03 g of water per gram of protein)⁴⁵ and when water is replaced by an organic solvent⁴⁶ or by a polymer corona.⁴⁷ All these results raise questions about the strict requirement of a dynamical hydration shell for biomolecular function.

In this review, we discuss recent progress in understanding water dynamics in hydration shells around biomolecules. We present an overview of theoretical, computational, and experimental results, with a particular emphasis on the femto- to picosecond dynamics of hydration shells and the interactions between water and biomolecules (cf. time range shown in Figure 1). The review’s scope includes results for phospholipids, DNA, and hydrated proteins. We point out that there are a number of—partly complementary—reviews in which other aspects of water dynamics and the hydration of ions and biomolecules have been discussed.^{2,23,24,31,32,48−56}

The remainder of this review is organized as follows. Section 2 addresses the definition of the hydration shell and presents an overview of methods which have provided insight into hydration structures and dynamics. We discuss in section 3 equilibrium fluctuations and H-bond dynamics together with the underlying molecular interactions. Section 4 focuses on energy exchange of biomolecules with their hydration shell and the role of water for the dissipation of excess energy. Electric fields at hydrated biointerfaces are discussed in section 5. In each section, we provide an overview of the theoretical concepts and methods as well as complementary experimental results. Our conclusions are presented in section 6.

2. How the Hydration Shell Can Be Defined and Probed

The intuitive idea of a hydration layer surrounding a biomolecule is clear: a sheath of water molecules covering the biomolecule, whose properties differ from those in the bulk due to the biomolecule’s proximity (Figure 2). However, providing a rigorous and specific definition of this labile layer is challenging, since difficult central issues quickly arise: How thick is it? Is the thickness uniform over the molecule? Does it depend on the property being probed? In fact, what criteria should be used to address these questions? The hydration shell is usually defined in a perturbative perspective: it includes all those water molecules whose properties (e.g., their dynamics) are noticeably affected by the biomolecule’s presence. Such a definition immediately gives the alert that the water molecules defined to be in the hydration layer can well depend on the experimental technique. Accordingly, we now give a brief review of the key numerical and experimental techniques employed to measure the perturbation’s intensity and discuss which water molecules and which dynamical properties they probe.

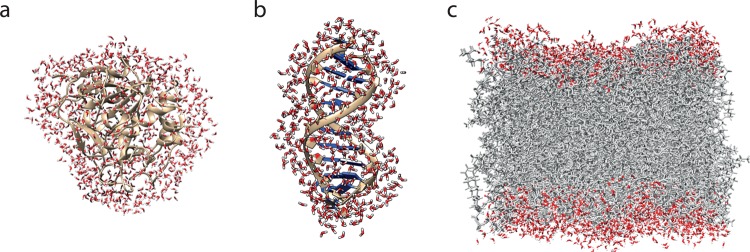
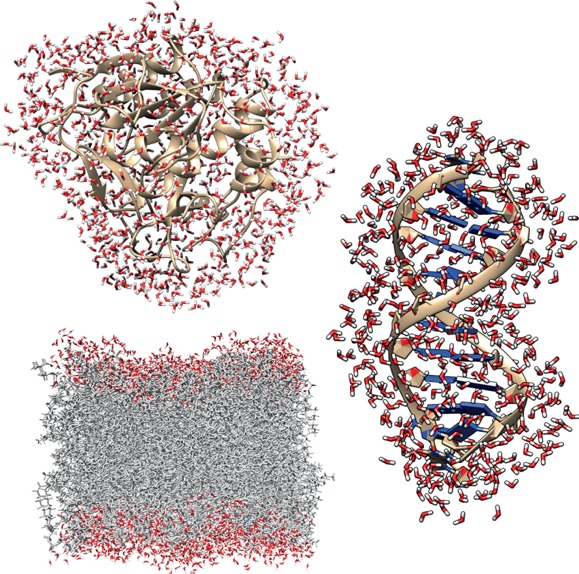
Figure 2.

Typical hydration shells of (a) a protein, (b) a DNA double strand, and (c) a phospholipid bilayer (snapshots from simulations described in refs (57−59)).

2.1. Numerical Simulations

On the molecular simulation side, there is at least the asset of precision in the hydration shell definition. Molecular dynamics simulations typically employ geometric criteria. As an example, all those water molecules whose oxygen lies within a given maximum distance from the closest biomolecule atom could be selected to define the layer. An intuitively appealing aspect of this is that this maximum distance is usually taken to include the first layer of water molecules (typically 3.5 Å). However, refinements paying attention to the nature of the biomolecular site, e.g., hydrophobic or hydrophilic (especially polar), introduce a variation of this choice. The former type sites tend to repel water molecules, while the latter tend to attract them. In any case, the hydration shell thickness around a given site can then be determined as the distance to the first minimum in the radial distribution function (see, e.g., refs (57, 58, 60, and 61)). Even more sophisticated definitions are possible, e.g., involving a Voronoi tessellation of space, assigning to each heavy atom a polyhedron including all points in space closer to it than to any other site; all water polyhedra in contact with a biomolecule polyhedron are taken to be in the first shell.⁶²⁻⁶⁴

A broad range of dynamical properties can be calculated for the water molecules present in the hydration shell, including the rotational, translational, and hydrogen-bond dynamics, the residence time, i.e., the time spent by a water molecule in the hydration shell before leaving into the bulk, and various experimentally accessible dynamical quantities. Numerical simulations have been extensively applied to protein,^{34,57,58,61,63,65−92} DNA,^{33,58,93−104} and phospholipid^30,105−115 hydration dynamics. Such simulations have shown that the effect of the biomolecule on these dynamical properties is essentially limited to the first hydration layer.^58,116 We note that determining the dynamical properties of the first shell by exclusively considering water molecules that continuously reside within the first shell is likely to lead to artifacts. Since most hydration shell molecules exhibit frequent exchanges with the second water layer, this procedure artificially focuses on a small fraction of very slow molecules, as shown in the case of ionic hydration shells.¹¹⁷

2.2. Experiments

Experimentally, no such precise geometric selection of the water molecules in contact with the biomolecule is possible. As will be discussed below, different strategies have therefore been designed to gain information about the hydration shell dynamics, involving, for example, measurements at different concentrations, different hydration levels, and the use of a local spectroscopic probe. Although there now exists a broad range of techniques which can provide valuable information about the water dynamics in the vicinity of biomolecules, it is important to observe that none of them can currently provide an unambiguous determination of the number of water molecules affected by the biomolecule’s presence.

Historically, the first techniques employed to investigate water dynamics around proteins and DNA were dielectric relaxation and nuclear magnetic resonance (NMR) measurements, and the subsequent advent of ultrafast laser pulses opened the way to the first time-resolved studies by time-dependent Stokes shift (TDSS) measurements. In our brief description below, we will not follow this historical perspective but rather discuss these methods according to the type of strategy that is chosen—whether water dynamics are directly measured or whether a local probe is employed—and to the type of dynamics that is measured—the motions of individual water molecules or some more collective dynamics.

2.2.1. Direct Probes of Hydration Shell Structure

Time-averaged equilibrium structures of water and hydration shells have been studied by X-ray and neutron diffraction from both crystallized and disordered molecular ensembles. X-ray diffraction maps electron densities and thus is mostly sensitive to heavier atoms such as carbon, nitrogen, and oxygen, while neutron scattering gives insight into the pattern of hydrogens.^118−120 In crystalline samples, positions and—to a limited extent—orientations of individual water molecules have been derived from diffraction patterns, while the disordered character of liquid samples allows extracting radial distribution functions of atom pairs only. Such extensive work is beyond the scope of the present review, and we just briefly refer to results which are relevant in our hydration dynamics context.

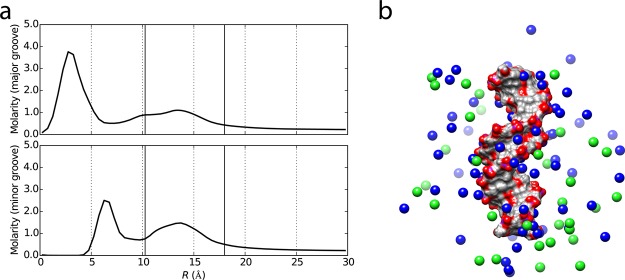
Diffraction studies of crystallized samples have shown that the surface structures of phospholipid membranes and reverse micelles, of DNA, and of proteins define specific boundary conditions for the arrangement of water molecules in the first few hydration layers. Moreover, the heterogeneity of a biomolecular surface with its different nonpolar, polar, and/or ionic groups results in markedly different local hydration geometries, i.e., the hydration shell displays structural variety even for a particular biomolecule. Examples are the different water geometries around phosphate and choline groups in phospholipids, the different hydration structures in the major and minor grooves of DNA—with the latter containing a rigid “spine of water”—and the highly heterogeneous hydration patterns of proteins.^{25,26,121−123}

Small-angle X-ray and neutron scattering (SAXS and SANS) map structural features on a nanometer scale distinctly longer than chemical bonds.^121,124 Scattering data from hydrated proteins and complementary molecular dynamics simulations have suggested a mass density of the first hydration layer which is some 15% higher than the density of bulk water.^124,125 An open and partly controversial issue is the spatial extent of the hydration shell, i.e., the distance scale on which the surrounding water shell assumes bulk-like properties (see ref (2) and references therein). Small-angle X-ray scattering has also been applied to determine radial distributions of counterions around DNA, a topic we will consider in section 5.2.

2.2.2. Dynamics of Individual Water Molecules

The first group of discussed techniques—nuclear magnetic resonance (NMR), neutron scattering, and ultrafast infrared spectroscopies—directly probe the dynamics of individual water molecules or atoms, but the collected signal is averaged over all these molecules within the sample. In dilute solutions, the signal is thus usually dominated by bulk water, obscuring the contribution of the small fraction of water molecules nestled against the biomolecule whose properties differ from those of the bulk. In concentrated solutions, the fraction of water molecules being affected by a biomolecule is larger, but interactions of water molecules with multiple biomolecules lead to complex nonlinear effects.

NMR can access the water molecular reorientation time by measuring the longitudinal spin relaxation rates of water hydrogen or oxygen isotopes, to which it is proportional.¹²⁶ Typical resonance frequencies accessible in magnetic relaxation dispersion (MRD) experiments can resolve the dynamics of water molecules which move on a nanosecond time scale or slower (Figure 3). This can therefore be used to study the extremely slow dynamics of protein internal water molecules²² and of some specific water molecules bound to the DNA minor groove at low temperature.^127,128 For all water molecules whose dynamics are much faster, MRD provides the mean rotational correlation time, which is thus averaged over the bulk and diverse hydration shell environments. The consequence of this averaging is that the mean rotational time is unable to discriminate between quite different situations, for example, one with a small hydration shell with strongly retarded dynamics and another with a moderate slowdown affecting many water molecules. This ambiguity is resolved by estimating separately the number of water molecules affected by the biomolecule via, e.g., molecular dynamics (MD) simulations or solvent-accessible surface area¹²⁹ calculations. These determinations usually assume that the solute-induced perturbation is short ranged and is usually considered to extend only to the first layer of water molecules next to the biomolecular interface, i.e., typically within 3.5–4 Å. For the motions usually probed, e.g., the reorientation of a water molecular vector (or tensor for the isotopic variant ¹⁷OH₂), this assumption has been independently supported by several MD simulations.^58,116 A valuable asset of MRD is its great sensitivity; this allows its effective operation in dilute aqueous solutions and the determination of the effect of a single biomolecule on the dynamics of the surrounding water molecules.

Figure 3.

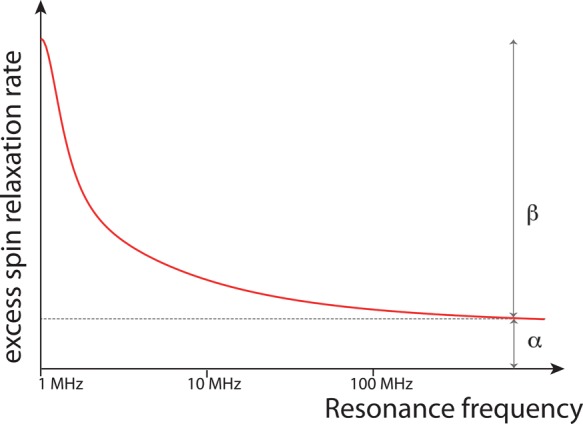
Magnetic relaxation dispersion probes, as a function of the resonance frequency, the water excess spin relaxation rate in the aqueous biomolecule solution relative to the bulk. The rate is the sum of two contributions: a constant α due to the N_α hydration shell water molecules which move on a time scale faster than 1 ns and cannot be resolved, with α ∝ N_α (⟨τ_hyd⟩/τ_bulk – 1), where ⟨τ_hyd⟩ and τ_bulk are the average hydration shell and bulk reorientation times, and a sum of two Lorentzians whose total amplitude is β and is proportional to the number N_β of slower water molecules.⁴⁸

Other types of NMR measurements have also been used to study biomolecular hydration dynamics, including nuclear Overhauser effect (NOE) spectroscopy. As will be discussed in the following section, early NOE results^28,130 suggested that dynamics in the hydration shell are much slower than in the bulk, but it was subsequently shown that the NOE signal is mostly sensitive to long-range dipole–dipole couplings with bulk water,¹³¹ so that these conclusions should be revised. More recently, NOE spectroscopy has been used to map the hydration dynamics of a protein encapsulated in a reverse micelle.^132,133 Further details about the different NMR techniques and their application to the study of biomolecular hydration dynamics can be found in ref (48).

Incoherent elastic and quasi-elastic neutron scattering (EINS and QENS)^134−139 measure the displacement of individual water hydrogen atoms. In order to specifically probe the water hydrogen atoms and not those belonging to the biomolecule, the latter are replaced by deuterium atoms, whose scattering cross section is much lower. By varying the scattering wavenumber, QENS spectra probe the hydrogen motions over different length scales. Those motions are then commonly modeled as resulting from a combination of center-of-mass translations and molecular rotations to obtain information about water translational and rotational dynamics. However, the inferred rotational relaxation times can be ambiguous because they are very sensitive to the model chosen for the analysis.^140,141 Neutron scattering experiments are typically performed on high biomolecular concentration aqueous solutions^135,142 and hydrated powders.¹³⁸ This has the advantage that all water molecules then belong to a hydration shell. However, it has also the disadvantage that complicating nonlinear effects are induced at very high concentrations when a water molecule becomes simultaneously affected by several solute biomolecules; the dynamics of hydration shell water molecules are not equivalent at low and high concentrations (see section 3.4).

Recently, femtosecond pump–probe infrared spectroscopy has been used to measure the reorientation dynamics of water molecules in aqueous protein solutions.¹⁴³ Following an initial vibrational excitation by a polarized pulse, the anisotropy decay is measured with a femtosecond time resolution. Since this decay is the sum of the rotational relaxations of all water molecules within the sample, one could hope to determine simultaneously the number of perturbed water molecules and their respective reorientation times. There are, however, complicating issues here. Due to the short, approximately picosecond, lifetime of the water stretch vibration, this technique is mostly sensitive to the reorientation of fast, bulk-like water molecules and cannot resolve the hydration shell dynamics which occur at longer pump–probe delays. Concentrated biomolecule solutions are typically employed to have a measurable contribution from these slower water molecules, which appears as a residual anisotropy value at long delays. However, since the latter increases both with the number of slow water molecules and with their reorientation time, these measurements do not provide an unambiguous determination of the hydration shell size and dynamics.

2.2.3. Collective Water Dynamics

A second group of techniques includes dielectric relaxation (DR), depolarized light scattering (DLS), optical Kerr-effect (OKE), and terahertz (THz) spectroscopies, which probe different “collective’ dynamics of water molecules and possibly of the biomolecule itself. We pause to note that here we use the term collective to characterize an observable that is defined by summing over very many molecules without any intrinsic length constraint, e.g., the total dipole moment probed by DR or the total polarizability tensor probed by OKE and DLS. An example of a contrasting noncollective variable, the torque on a single water molecule, while formally involving a sum over many other molecules with which the specified water interacts, is in effect restricted to a much smaller number of molecules by the spatial dependence of the torque.

An illustration of how different the single-molecule and collective relaxation time scales can be is provided by different measures of water reorientation. At room temperature, the collective Debye relaxation time¹⁴⁴ for the total dipole is approximately twice as long as the (first-order Legendre polynomial) reorientation time of an individual molecule’s dipole.¹⁴⁵ A precise determination of the typical length scales and number of water molecules involved in collective rearrangements remains difficult. An exception is the case of the low-frequency band probed at 80 cm^–1 by THz spectroscopy, where simulations¹⁴⁶ have suggested that the band arises from an umbrella-like motion of two hydrogen-bonded tetrahedra along the connecting hydrogen-bond axis.

Finally, we stress the important distinction that needs to be made between the collective character of an observable and the degree of cooperativity of a relaxation process, for example, the number of water molecules that have to “reorganize”. For example, the relaxation of single-molecule observables implies the cooperative rearrangement of more than one molecule, as shown, for example, in the jump reorientation mechanism which explicitly involves the motions of the reorienting molecule’s initial and final partners.^20,21 On a related point, we remark that the broad distribution of water dynamics found in biomolecular hydration shells has sometimes been considered to be an indication of the glassy character of the hydration shell,⁸⁵ thereby implying an enhanced cooperativity with respect to the bulk. While the dynamics of glasses are indeed heterogeneous, we will see in section 3.2 that this heterogeneity is simply due to the very different local environments found at the biomolecule’s interface: it does not imply that water dynamics are more cooperative than in the bulk.

DR measures the relaxation of the total electric dipole which arises from intermolecular modes and the collective reorientation of the water molecules. DLS and OKE are sensitive to the total polarizability tensor relaxation; because the water molecular polarizability tensor is almost isotropic, these techniques essentially probe collective translational rearrangements. THz spectroscopy measures the absorbance in the far-infrared frequency range corresponding to collective hydrogen-bond network distortions. All of these techniques provide spectra in the frequency domain. Any average slowdown in the water dynamics between the bulk and an aqueous solution containing the biomolecule can, for example, be inferred from the detection of an additional band at a lower frequency. However, a precise determination of how many water molecules are perturbed remains challenging, since deconvoluting spectra usually requires assumptions about the underlying relaxation time distribution.

THz absorption spectra measured over a range of biomolecule concentrations in water have been interpreted in terms of a “dynamical hydration shell” extending to radial distances of some 20 Å from the protein surface.^42,147−149 These conclusions about the shell’s extent originated from an analysis of the THz spectra concentration dependence with a three-component model (protein, shell, and bulk) which requires severe approximations,¹⁵⁰ including the assumptions that the shell is dynamically homogeneous and that proteins are uniformly distributed in the solution. In addition, such claims are difficult to reconcile with THz absorption and ultrafast infrared studies of water nanopools confined in reverse micelle structures with ionic headgroups. For example, one can consider water’s collective librational motions whose L2 band displays two components in ∼20 Å water pools with peak frequencies around 18 and 24 THz; the latter frequency is very close to the L2 peak of bulk water and clearly points to a bulk-like water core in the center of the nanopool.¹⁵¹ Moreover, the existence of a bulk-like water core on this length scale is strongly suggested by femtosecond nonlinear infrared spectroscopy in combination with MD simulations, which map the ultrafast structure fluctuations and vibrational dynamics of water.^152−154

2.2.4. Spectroscopic Probes of Water Dynamics

In the third group of discussed techniques, there is a shift of perspective: instead of directly probing water properties, one employs a local spectroscopic probe whose properties are affected by the solvent dynamics. This requires spectroscopic probes with properties sensitive to the particular type of environment and to its interactions with the biomolecule. These can be either a chemical group that is naturally present in the biomolecule or a synthetic probe that can be selectively placed in different locations to probe the local dynamics. Attractive features of these techniques are that they require neither high solute concentrations nor any assumption on the number of water molecules affected. However, it is not obvious that they always specifically report on water molecules located exclusively in the immediate probe vicinity nor is it obvious that motions of either water molecules farther from the biomolecule or of parts of the biomolecule itself do not make an important contribution.

Among this group of techniques, a first approach has been the measurement of time-dependent Stokes shifts (TDSS) (Figure 4).³¹ In its pump–probe version, a first subpicosecond optical pulse electronically excites a chromophore within the biomolecule; this can be either an extrinsic synthetic dye or an already present intrinsic group, such as the tryptophan aromatic side chain in proteins (an analogous approach was pioneered in earlier photon-echo spectroscopy experiments¹⁵⁵). Electronic excitation induces a change in the chromophore’s charge distribution, and by the Franck–Condon principle, the “frozen” (nuclear aspects of the) surrounding hydration structure that was equilibrated to the electronic ground state charge distribution now finds itself in an unstable, nonequilibrium state. In response, the water solvent thus starts dynamically relaxing toward a new equilibrium structure appropriate to the newly produced excited electronic state. As the solvent relaxes, lowering its free energy, the fluorescence emission frequency drops; this is conventionally described via the time-dependent Stokes shift—the difference between the absorption and the fluorescence energies—which increases from zero to its equilibrium value. A second ultrafast pulse can be used to measure the evolving fluorescence emission frequency through a stimulated emission process; scanning the time delay between the pump and the probe pulses provides the full time-resolved solvent relaxation (which is why these are often called “solvation dynamics” experiments). TDSS at short times is likely to be sensitive to relatively few water molecules. However, at long times it can potentially become sensitive to collective motions involving several, possibly numerous, water molecules and possibly involving motions of the biomolecule itself, since these also influence the chromophore’s fluorescence energy. Whether the short time or long time motions are of relevance depends on the question posed. If, for example, the issue is the rate of an internal configurational isomerization involving a charge redistribution, which of either of these types of water dynamics could be most relevant depends on the reaction’s barrier frequency. Finally, a major drawback of fluorescence probes consists in their invasive character with respect to structure. Their attachment to or incorporation into a biomolecule changes the equilibrium arrangement of water molecules and in some cases the biomolecular structure as well.^33,100

Figure 4.

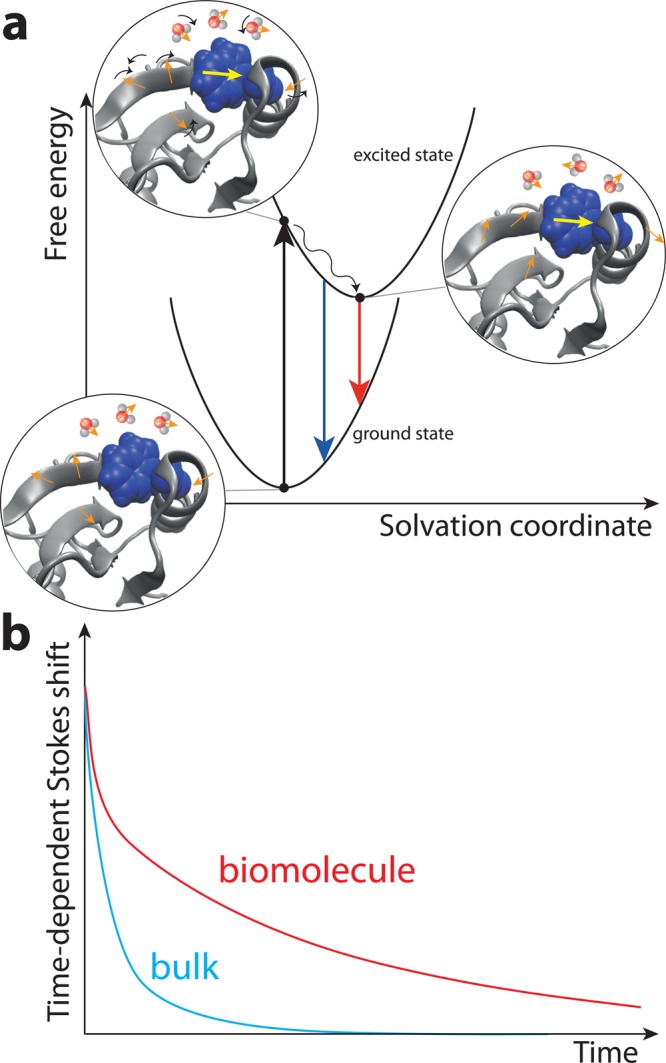
Schematic description of the pump–probe time-dependent Stokes shift measurement of solvation dynamics.³¹ (a) Electronic ground and excited state free energy surfaces of the chromophore attached to the biomolecule along the solvation coordinate that describes the electrostatic environment produced by the solvent and the polar and charged sites on the biomolecule. (b) Typical time-dependent Stokes shift decay in time for the chromophore in bulk water and attached to the biomolecule.

Another type of probe that can be fruitfully used to measure the local hydration dynamics is provided by the vibrations of a biomolecule’s functional groups which are located at the interface with its hydration shell. They represent local probes which leave the equilibrium geometries untouched and—on the other hand—map local interactions with, and fluctuating forces from, the water environment. This concept has first been applied in steady-state infrared spectroscopy of DNA’s phosphate vibrations, where spectral shifts have been used to characterize the hydration level.¹⁵⁶ Recently, ultrafast two-dimensional infrared (2D-IR) spectroscopy of interfacial modes in phospholipid membranes and reverse micelles and in DNA has given highly specific insight into the dynamics of interfacial water and the local electric fields at the interface.^157,158 Synthetic metal–carbonyl vibrational probes have also been employed to investigate the local hydration dynamics in different protein-exposed sites^159−161 using the long vibrational lifetime of the metal–carbonyl probe to access the hydration shell hydrogen-bond dynamics occurring on a time scale of several picoseconds.

The response of vibrational probes to a fluctuating water shell and the exchange of vibrational energy between biomolecules and hydrating water have been studied by methods of femtosecond nonlinear infrared spectroscopy.^6,7,162 Time-resolved pump–probe methods and 2D-IR spectroscopy map the third-order nonlinear response of the ensemble of vibrators. In the sequential regime of pump–probe spectroscopy, a first pump pulse excites the vibration resonantly on its v = 0 → 1 transition and a delayed probe pulse measures changes of vibrational absorption (Figure 5a). Spectral dispersion of the probe pulse after interaction with the sample allows the measurement of transient spectra at a fixed delay time. On the v = 0 → 1 transition, excitation results in a decrease of absorption due to the depopulation of the v = 0 ground state and stimulated emission from the v = 1 excited state back to the v = 0 state, while an enhanced, anharmonically red-shifted absorption occurs on the v = 1 → 2 transition. The decay kinetics of the latter transition directly reflect the depopulation of the v = 1 state by vibrational relaxation and thus the vibrational lifetime. In general, both transient spectra and vibrational kinetics of an interfacial vibrational probe are influenced by the surrounding hydration shell. At negative time delays when the probe pulse interacts with the sample before the pump, one observes the so-called perturbed free induction decay (PFID); this is a signal that originates from the pump’s destruction of a coherent vibrational polarization the probe pulse has induced on the v = 0 → 1 transition. The rise time of the PFID toward zero delay is determined by the vibrational dephasing time. Details of the pump–probe method and applications to hydrogen-bonded systems including water have been discussed in ref (7).

Figure 5.

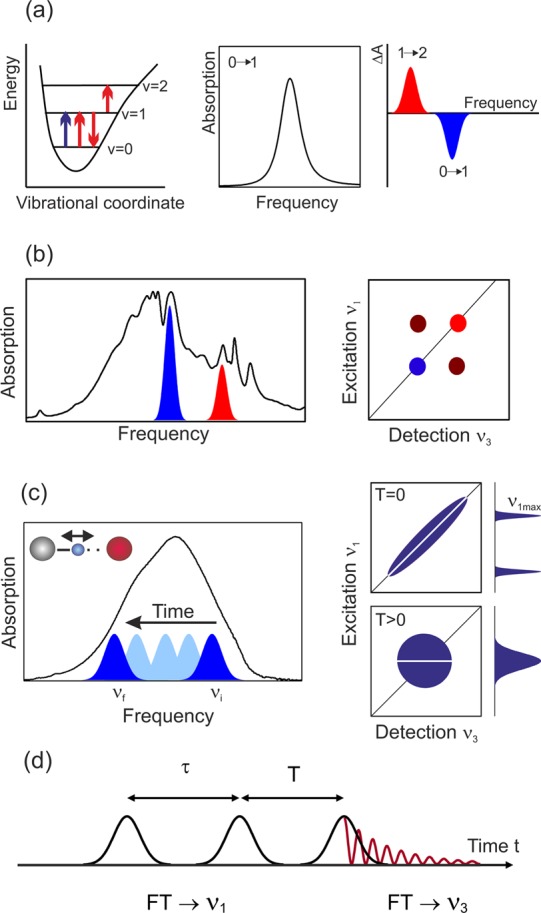
(a) Pump–probe spectroscopy. Excitation by an ultrashort pump pulse (blue arrow, left) results in a transient change of the linear absorption spectrum (middle), which is measured by the probe pulse (red arrows, left). An absorption decrease ΔA < 0 occurs on the v = 0 → 1 transition, while the v = 1 → 2 absorption is enhanced (right panel). (b) (Left) Linear infrared absorption with contributions from different vibrational transitions. (Right) Nonlinear 2D infrared spectrum consisting of peaks on the diagonal ν₁ = ν₃ (colored) and off-diagonal (cross) peaks (black). The strength of cross peaks reflects the vibrational coupling strength. (c) (Left) Spectral diffusion from an initial frequency ν_i to a frequency ν_f within an inhomogeneously broadened vibrational band. In the 2D spectrum, this process leads to a change from an elliptic to a round line shape with increasing waiting time T. This loss of frequency correlation can be quantified with the help of so-called center lines (CLs, white) which connect the maximum signals at different detection frequencies ν₃. The decrease of the CL slope as a function of T is a measure for the correlation decay. (d) Pulse sequence in 3-pulse photon echo experiments with the coherence time τ, the waiting time T, and the real time t.

Couplings between vibrations and frequency fluctuations induced by the hydration shell and the biomolecule are made visible by 2D-IR spectroscopy (Figure 5b and 5c).¹⁶² In this method, one generates a vibrational excitation that in general is coupled to other vibrations of the system and thus generates a nonlinear signal on other vibrational transitions, so-called cross peaks. Moreover, the excitation is subject to fluctuating forces from the hydration shell and the biomolecule, resulting in a modulation of its transition frequency, a process called spectral diffusion. Spectral diffusion shows up in the line shapes of 2D signals, in particular, of peaks on the frequency diagonal ν₁ = ν₃. These line shapes allow a separation of spectral diffusion from static broadening, e.g., by an inhomogeneous distribution of transition frequencies. The frequency fluctuation correlation function ⟨δν(t)δν(0)⟩ (FFCF), which represents an ensemble-averaged quantity characterizing the different time scales of fluctuations, enters directly into the measured 2D line shapes. Here, δν(t) = ν(t) – ν₀ represents the deviation of the transition frequency ν(t) at time t from its time average ν₀. In the reverse direction, a comparison of experimental and calculated 2D spectra allows for identifying the main terms in the FFCF.

Nonlinear 2D spectroscopy works in the time domain and—for third-order signals—requires interactions with a sequence of 3 infrared pulses (Figure 5d). Here, both 3-pulse pump–probe and photon-echo methods are applied. The first two interactions are separated by the coherence time τ, while the third interaction occurs at the population or waiting time T after the interaction with the second pulse. Spectrally resolved detection, which in photon-echo-based schemes involves heterodyning with a fourth local oscillator pulse, allows the generation of a detection frequency axis ν₃. The excitation frequency axis is generated by Fourier-transforming signals measured for different coherence times τ from the time into the frequency domain. Measurements of 2D spectra as a function of waiting time T give insight into the time evolution of couplings and line shapes. Results of ultrafast infrared spectroscopy will be discussed in sections 3–5.

Instead of working with dilute solutions, studies have been made with samples at a limited and well-defined level of hydration, in particular for DNA. This approach relies on the preparation of solid thin DNA films or fibers which are placed in an atmosphere of well-defined humidity, e.g., in a closed sample cell.^163−165 The DNA concentration in the film can be varied in a wide range. After exchanging the initially present Na⁺ counterions against lipid surfactants such as cetyltrimethylamine (CTMA), the surfactant aliphatic tail serves as a spacer between DNA molecules.¹⁶⁶ The level of humidity is determined by gravimetric measurements and/or via vibrational bands undergoing characteristic spectral shifts upon a change of hydration, such as those of the phosphate stretch vibrations.^156,167 Starting from an essentially dehydrated film sample, this technique allows the building of the hydration shell layer by layer.

Finally, another technique using NMR to probe the water dynamics around a synthetic local probe was recently introduced. Overhauser dynamic nuclear polarization (ODNP)-enhanced NMR relaxometry¹⁶⁸ employs a nitroxide spin label which can efficiently transfer its spin polarization to the surrounding water protons and enhance their NMR signal. By attaching the spin label to different protein residues,¹⁶⁹ DNA phosphate backbone groups,¹⁷⁰ and phospholipid bilayer sites,¹⁷¹ these experiments provide an estimate of the translational dynamics of water molecules within approximately 10 Å from the spin probe in these different environments. With this feature, this novel approach could provide an interesting complement to existing techniques. However, in addition to the issue of the perturbation induced by the spin probe itself on the water dynamics (which applies to all techniques employing a synthetic probe), the discrepancy between some of the ODNP results and those obtained by other experimental techniques and by simulations remains to be explained (see, e.g., the contrast between ODNP and simulation in ref (169)), and the impact of the assumptions in the model used to interpret the data remains to be assessed.¹⁶⁸

3. Structural Dynamics of the Hydration Shell—Equilibrium Fluctuations and H-Bond Dynamics

After our discussion in section 2 of the spatial range over which a biomolecule affects the dynamics of surrounding water molecules, there still remain related and essential questions to be discussed. These concern the extent to which the water dynamics are affected by the biomolecule. Does a biomolecular interface accelerate or retard the dynamics of water molecules in the hydration shell compared to those of the bulk water? What is the magnitude of this effect? The answer to these key questions is not immediately obvious; as we shall see, while most studies have concluded that biomolecules induce a degree of slowdown of water dynamics, the suggested dynamical retardation factors relative to the bulk vary considerably by several orders of magnitude.

Since an important part of the experimental insight into hydration shell dynamics that has been gained originates from spectroscopic studies and, in particular, ultrafast spectroscopies, it should be stressed that spectroscopy probes the time-averaged or transient response function and—in the case of nonlinear ultrafast methods—the higher order response of the system to a sequence of ultrashort pulses. Thus, spectroscopic measurements do not directly probe structure and/or structural dynamics. Information on transient molecular arrangements and hydration geometries can be inferred only with the help of theoretical models or simulations.

3.1. Shell Structural Dynamics

As illustrated in Figure 1, water dynamics cover a broad range of motions with a hierarchy of time scales, which can be affected differently by a biomolecule. Accordingly, we now address each type of motion separately.

3.1.1. Ultrafast Structural Dynamics

Fluctuations of the equilibrium hydration structure around phospholipid membranes and reverse micelles, DNA, and proteins have mainly been studied by femtosecond infrared spectroscopy, in particular, by recording 2D-IR spectra and measuring pump–probe anisotropies. The fastest fluctuations are connected with thermally excited intra- and intermolecular vibrational and librational motions of water molecules and low-frequency motions of the biomolecule itself. Such excitations cause a modulation of transition frequencies of vibrational probes, i.e., spectral diffusion, which is manifested in their 2D line shapes and quantified with the help of the frequency fluctuation correlation function (FFCF, cf. section 2.2.4). In general, the population decay of the vibrational probe impacts the 2D line shape as well, in the simplest case resulting in an additional lifetime broadening; processes of population relaxation will be discussed in section 4.1.

A first group of molecular dynamics (MD) simulations and 2D experiments has focused on OH stretch excitations of the water shell.^{33,35,111,154,172} We recall that OH stretch probes are not spatially selective, so that the 2D line shapes are averaged over water molecules close to and far away from the biomolecule. Both water around DNA and water pools in phospholipid reverse micelles have been studied over a range of hydration levels. For low water concentrations, the 2D spectra display predominantly inhomogeneous line shapes, which reflect a distribution of interaction geometries between water molecules and the biomolecule which is quasi-static on the time scale of the experiments. A propos that time scale, it should be noted that 2D methods are “blind” to dynamics that are much slower than the femto- to picosecond population decay of the excited OH stretch vibrations. For approximately 2 complete water layers around DNA, one observes a gradual subpicosecond decay of the FFCF—which is significantly slower than the sub-100 fs initial decay observed for bulk water—to a residual value which again is a measure for inhomogeneous broadening. For larger water pools in phospholipid reverse micelles, a pronounced sub-500 fs decay and a residual inhomogeneous broadening are observed.¹⁵⁴ This behavior is in qualitative agreement with the FFCFs derived from MD simulations.¹¹¹ The slowed-down FFCF decay of water around DNA has been assigned to a slowing down of orientational water dynamics and a reduced rate of OH stretch resonant energy transfer between water molecules. Large water pools in reverse micelles consist of a bulk-like core with a fast FFCF decay and interfacial water with a distribution of site geometries and a slower decay. The experiment averages over the two species.

The 2D-IR spectra of interfacial probe vibrations such as the phosphate vibrations of phospholipids and DNA and other backbone vibrations of DNA give more specific information on fluctuations in the hydration shell since they predominantly probe the first few water layers. For both fully hydrated phospholipid head groups in reverse micelles and fully hydrated DNA (cf. Figure 14), an initial 300 fs decay of the FFCF is followed by a long-lived contribution for the decay time for which a lower limit of 10 ps has been derived.^157,158,173 A similar FFCF is found for DNA with only two complete hydration layers; this suggests that the fluctuating forces on the interfacial vibrations (which govern the FFCF) originate mainly from the first two water layers; this behavior will be discussed in more detail in section 5. MD simulations of spectral diffusion of the asymmetric phosphate stretch vibration in hydrated DNA give a similar behavior of the FFCF.¹⁷²

Figure 14.

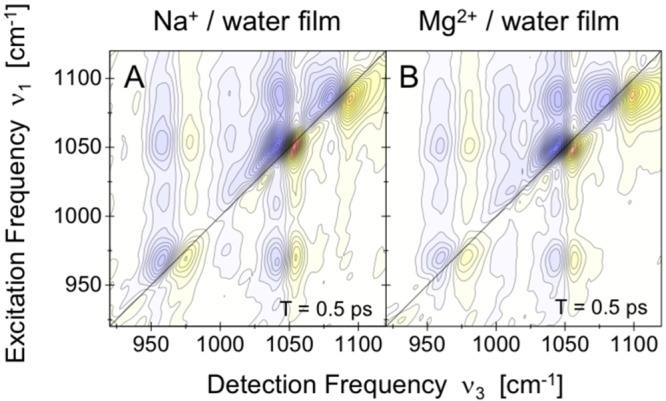
2D infrared spectra of fully hydrated salmon testes DNA with (A) Na⁺ and (B) Mg²⁺ counterions (Reprinted with permission from ref (173). Copyright 2016 American Chemical Society.). Exchange of counterions has a negligible influence on spectral positions and line shapes of the different contributions to the 2D spectra.

The slowing-down of interfacial water has been rationalized by invoking the impact of the steric restrictions imposed by the corrugated biomolecular surface on librational and other intermolecular motions. We will see in section 3.1.2 that the interface topography and the resulting steric constraints on the dynamics of water are a key factor affecting the picosecond rearrangements of the hydrogen-bond network. In the case of phospholipids, the orientation of water molecules is largely determined by the strong local electric field created by the oppositely charged choline and phosphate groups, and the hydration shell dynamics may include a low-frequency component due to the slow phospholipid headgroup rearrangements. When OH stretch vibrations are probed at reduced hydration levels, another mechanism of spectral diffusion—the resonant energy transfer between OH stretch oscillators on different water molecules—is slowed down because of the reduced concentration.^8,19 Such qualitative pictures need further analysis by in-depth theory and simulations, a challenging issue in view of the structural complexity of the hydrated interface.

3.1.2. Picosecond to Nanosecond Hydrogen-Bond Network Rearrangements

We now address the dynamics of hydration shell water molecules occurring on a slower time scale, from a few picoseconds up to a nanosecond. On this time scale, water molecules may exchange their hydrogen-bond partners, reorient, and leave the hydration shell. Two important reference times here are, first, for the dynamics in the bulk ∼2 ps for the reorientation time of a water molecule and, second, for the biomolecule’s own dynamics with a typical tumbling time in the nanosecond range.

We now review some important measurements of the hydration layer dynamics, starting with the historical experiments—that were erroneously interpreted as indicating the presence of an extremely slow, almost ice-like, layer around proteins and DNA—and ending with more recent experiments which clearly suggest the hydration layer to instead be more moderately retarded, although consensus on the slowdown’s magnitude has yet to be achieved. An introduction to the different techniques whose results are described now can be found in section 2.

The older studies suggested that a rigid water layer existed around proteins. This conclusion followed from the estimation of a typical protein size from the protein’s NMR-determined tumbling time τ_reor. This size was estimated through the Debye–Stokes–Einstein (DSE) equation τ_reor = 4πηa³/(3k_BT) involving the radius a of the protein approximated by a sphere as well as the solvent shear viscosity η and the temperature T. The protein sizes so obtained via DSE—which assumes overdamped, rotational diffusion of the solute and a continuum hydrodynamic solvent—were systematically larger than those found from crystal structures, which was explained by a frozen water layer moving together with the protein; this is the so-called “solvent-berg”, which thus increases the protein’s hydrodynamic radius.^23,174 However, it was subsequently shown that in fact the simple continuum hydrodynamic picture is not valid for the protein hydration layer.^48,52,77,175 The DSE therefore does not apply, and the picture of an ice-like layer is not supported.

The presence of very slow water molecules around proteins had been also suggested by a second technique: dielectric relaxation (DR) spectroscopy experiments. The relaxation of the aqueous protein solution’s total dipole moment is probed by this technique, and the frequency domain spectrum reveals the characteristic time scales of the different motions involved in this total dipole’s relaxation. A nanosecond time scale observed in the DR spectrum was traditionally explained by the very strong retardation of typically half the hydration shell water molecules, again providing a suggestion of very slow intrinsic water motion.¹⁷⁶ However, more recent work¹⁷⁷ suggests that this time scale has a different origin; instead, it is due to slow hydration layer rearrangements which are induced by slow protein conformational motions. Alternately stated, the intrinsic water dynamics are not “frozen”; they are instead rapid, but they rapidly respond to the extrinsic, slow protein dynamics to which they are coupled and thus follow those slow protein motions.

Finally, there was a further older suggestion of slow hydration shell dynamics around proteins and DNA. Nuclear Overhauser effect NMR experiments exploiting magnetization transfer between water and protein protons were at first interpreted^28,130 as showing that hydration shell water dynamics occur on the 300 ps to 1 ns time scale. However, this conclusion was compromised by subsequent work¹³¹ which showed that these studies had not properly accounted for labile protein hydrogens and for long-range protein proton–bulk water couplings, with the conclusion that NOE measurements are actually more sensitive to bulk dynamics than to hydration shell dynamics.

It will be evident from our account above that an accurate perception of the water dynamics in biomolecular hydration layers has proved quite challenging in the past. However, fortunately, more recent studies have helped to clarify these dynamics, as we now recount.

Magnetic relaxation dispersion has provided a much improved characterization of biomolecular hydration dynamics.⁴⁸ In this variant of NMR that we described in section 2, the longitudinal spin relaxation rate is measured at different resonance frequencies, which provides some information on the average water rotational relaxation times within the shell. In MRD studies of a series of globular proteins^178−180—including ribonuclease A, lysozyme, myoglobin, trypsin, serum albumin, ubiquitin, bovine pancreatic trypsin inhibitor, bovine β-lactoglobulin, and a hyperactive insect antifreeze protein—the hydration layer’s room-temperature rotational dynamics was shown to be on average only moderately retarded compared to bulk water, by a factor ≈ 2–6. Regarding the translational dynamics of protein hydration shell water molecules, separate NMR studies on lysozyme and bovine serum albumin determined a retardation factor of merely 3.^181,182 Similarly, for DNA, MRD studies also indicated that there are no long-lived water molecules tumbling together with the DNA;^127,183 except for a few extremely slow water molecules—forming the spine of hydration confined within the DNA minor groove and reorienting on a time scale of a few hundreds of picoseconds—the average rotational relaxation time within the hydration layer is only 5–6 times slower than in the bulk at room temperature.^127,128,184

These uniform experimental conclusions of only modest water slowdown were in stark contrast with the prior suggestions of an ice-like hydration layer that we described above. Further, these newer conclusions were subsequently supported by extensive MD simulations on a series of proteins^57,61,63,73 and DNA^58,100 in dilute aqueous solutions. These calculations determined the molecular reorientation time averaged over all water molecules present in the first hydration shell and—consistent with the observable probed in MRD (see section 2)—found slowdown factors of 2–6 relative to the bulk, in excellent agreement with the NMR result (we need to note here that as will be discussed in section 3.2, the biomolecular hydration layer is very heterogeneous in character, and this average slowdown factor actually conceals a broad distribution of dynamics).

The first time-resolved experimental investigations of protein^185−187 and DNA^188−192 hydration dynamics were provided by TDSS experiments. These studies probed the solvation dynamics of the natural tryptophan chromophore in Subtilisin Carlsberg and Staphylococcus nuclease proteins and of a synthetic DNA base or a groove-bound chromophore in a DNA dodecamer duplex. When the solvation dynamics decays were compared for the same chromophore when at the biomolecular interface and when isolated in aqueous solution, the dynamics were found to be slower within the hydration layer. There is another, important qualitative distinction between these cases: the TDSS decay exhibits a single, subpicosecond component in bulk water, but it is biphasic in the biomolecular case, with a first picosecond component and a second slower time scale. This slow component was measured in different TDSS relaxation experiments, with a very large span of time scales determined in different experiments, ranging from 20 ps^185,188,189 (i.e., 15 times slower than in bulk water) to hundreds of picoseconds or even tens of nanoseconds in certain experiments on DNA.¹⁹⁰ The faster decay was assigned to bulk-like labile water molecules, while the slower decay was interpreted as due to ordered water molecules strongly interacting with the biomolecular interface.³¹

However, the origins of these two decays have in fact been much debated for both proteins and DNA.^{32,34,88,100,193} TDSS has the advantage of being time resolved on the time scale of hydration shell rearrangements and of using a local probe that can be placed in different locations at the biomolecular interface. However, the interpretation of TDSS experiments faces several difficulties. First, regarding the probe’s nature, large synthetic chromophores can by their presence induce an additional perturbation of the water dynamics. Second, for the commonly employed tryptophan probe which occurs naturally in proteins, the complex electronic excited state dynamics involving a conical intersection between two states close in energy¹⁹⁴ increase the difficulty of the TDSS analysis. In addition, since the TDSS fluorescence energy depends on the electric field or potential experienced by the probe due to all sources in the system, the TDSS solvation dynamics are sensitive not only to the rearrangements within the probe’s first hydration shell but also to longer range collective dynamics, including the slow motions of the biomolecule and of the water molecules that it displaces. Subsequent simulations concluded this slow TDSS time scale to instead arise from slow biomolecular conformational motions,^{33,34,100,101,193} sometimes induced by the chromophore itself as in the case of the DNA synthetic base.¹⁰¹ While recent simulations have shown that some hydration shell water molecules can exhibit extremely slow dynamics (see section 3.2), these represent a very small fraction of the shell population. In addition, subsequent femtosecond infrared studies¹⁶⁰ using a metal–carbonyl probe—which are probably sensitive to dynamics more local than is TDSS—found a very limited retardation factor of 1.8 for the water dynamics within the lysozyme protein hydration layer, thus providing further support to the idea of a moderate average slowdown in biomolecular hydration shells.

The characterization of water dynamics within biomolecular hydration shells has been further complemented by a number of other techniques, including, for example, optical Kerr-effect (OKE) spectroscopy measurements on proteins^195,196 and on DNA¹⁹⁷ together with depolarized light scattering^54,198,199 studies of protein hydration dynamics. These techniques probe collective water translational dynamics, e.g., the relaxation of the total system’s electric polarizability tensor. The frequency spectra are typically described as consisting of a sum of distinct bands, whose frequency can be used to infer the dynamical effect induced by the biomolecule on the hydration shell. Typical slowdown factors of 6–7 were determined for proteins,^196,198 and a retardation factor of 20 was recently suggested for a fraction of the DNA hydration shell.¹⁹⁷ These retardation factors do not represent a weighted average over the entire hydration layer; instead, they correspond to a subpopulation within the hydration shell whose dynamics appear as a distinct peak in the frequency spectrum. They are therefore not inconsistent with the results coming from NMR and molecular dynamics simulations described in this section. Although the latter find a more moderate average slowdown, they do suggest that the broad distribution of slowdown factors does extend to such larger values than the average.

It seems fair to say that the original idea discussed at the beginning of this subsection of a “biological water” scenario—an intrinsically slow ice-like hydration shell moving rigidly with a protein—has now been completely discounted. On the other hand, it is clear that the exact magnitude of the water dynamics slowdown in protein and DNA biomolecular hydration shells remains a topic of lively discussion. Progress toward ultimate clarification will be much aided if it is appreciated that different techniques appear to give different results, signaling that careful attention to just which dynamics are being probed is essential.

3.1.3. Micro- to Millisecond Internal Water Dynamics

We have so far largely focused on water molecules outside of the biomolecule, but in proteins, for example, some water molecules can be found buried inside cavities in the protein interior. These internal water molecules are an integral part of the protein structure and can only exchange with the bulk with the aid of rare protein structural fluctuations. These are very slow dynamics occurring on a time scale ranging from micro- to milliseconds. They can be studied with NMR and owing to recent advances in computer simulations also with millisecond molecular dynamics simulations. While these extremely slow dynamics are beyond the scope of the present review, we mention in passing a recent effort combining NMR and simulations which has provided an improved understanding of the mechanism allowing the formation of transient water chains connecting these internal water molecules to the bulk.^22,200

3.2. Heterogeneous Dynamics within the Shell

As we have just detailed, the biomolecular interface’s presence clearly perturbs the dynamics of water there compared with the bulk, even though the magnitude of this effect continues to be debated. However, is this perturbation identical everywhere within the hydration layer or is the impact of some sites more significant than others? A priori, the second option seems more likely: a biomolecule’s exposed surface is certainly a very chemically and topologically heterogeneous interface. The different chemical groups present there include charged, polar, and apolar groups and–of special interest here—H-bond acceptors and donors, and in addition, the exposed surface’s shape is usually rough on the molecular level, with an array of pockets, protrusions, and grooves.

MD simulations indicate that the biomolecular interfacial water dynamics are indeed sensitive to the interface’s inhomogeneous character. In particular, probes of the water molecule’s rotational dynamics and of its residence time within the first shell support this view. Standard residence times measure the time spent by each water molecule within the first hydration layer before departing for the bulk. Although exact values of such times may vary with chosen hydration shell thickness and with the details of the calculation procedure,²⁰¹ MD simulations have shown that the residence time distribution follows a broad power law.^82,83 An additional indication that the dynamics of the different water molecules within the biomolecular hydration layer are affected to different degrees is provided by the distribution of reorientation times. These times characterize the typical rotational dynamics and are quantitatively defined as the time integral of a time-correlation function (tcf) of the molecule’s orientation. This tcf compares this orientation at an initial time and after a given delay, and tracks how quickly the water molecule “forgets” its initial orientation. The strong suggestion of a distribution of different sites with different water dynamics is provided by the pronounced nonexponential decay observed when the tcf is computed for all water molecules initially present in a protein’s or DNA strand’s hydration layer.^58,63,73

Identifying which sites produce greater and smaller perturbations requires a site-resolved mapping of the dynamics, and this is extremely challenging for all experimental techniques. For example, the often-employed and very valuable dynamical perturbation factor determined by NMR is intrinsically averaged over the entire hydration shell and so is not associated with any specific site. MRD can be used to determine the parameters of an assumed distribution of relaxation times¹⁷⁹ but cannot identify the locations on the biomolecular surface responsible for the distribution’s different components. Recent NOE-NMR work^132,133 has obtained a spatial mapping of water dynamics around ubiquitin but at the cost of, e.g., encapsulation of the protein in a reverse micelle. The confinement was necessary to retard all water molecules so that their dynamics can be resolved with the nanosecond resolution of the experiment. However, it was shown⁵⁷ via simulations for the subtilisin protein that confinement has a strong but nonuniform effect on the hydration layer dynamics; the dynamics in a free aqueous solution are not simply proportional to those measured in confinement.

The first site-resolved mapping of a fluorescent chromophore solvation dynamics within a biomolecular hydration shell was generated via TDSS experiments^39,202 on a series of different protein mutants, with the chromophore’s location systematically scanned over the protein’s exposed surface. The decay time scales—and thus the hydration dynamics—were found to tend to be shorter next to hydrophobic and/or flexible groups. More recently, a 2D-IR study^159−161 has investigated the water H-bond dynamics within a protein hydration layer with both a femtosecond time resolution and a spatial resolution of approximately a few Angstroms. This study measured the water OH stretch vibrational frequency dynamics next to a metal carbonyl probe, which can in principle be attached at different protein surface locations. The results for two probe locations on lysozyme showed that the water H-bond dynamics are almost bulk-like next to exposed, flexible groups and are more retarded in more constraining hydrophobic environments.

MD simulation is a tool well suited for site-specific investigations of water dynamics: for each protein or DNA site, the reorientation time of water molecules initially neighboring it can be determined. The resulting hydration layer relaxation time distributions have been determined for a series of globular proteins^57,61,73—including lysozyme, ubiquitin, subtilisin Carlsberg, acetylcholinesterase, and a hyperactive antifreeze protein—and for a DNA dodecamer duplex.⁵⁸Figure 6 shows the resulting mapping on the exposed surfaces of a DNA strand and of a series of different globular proteins in their native state. Despite their chemically heterogeneous and topologically rough character, the exposed surfaces’ hydration layer water dynamics are fairly similar for most of the exposed surface and are only moderately slower than in the bulk. The sites where water is more retarded are instead mainly associated with specific and buried locations, e.g., clefts and pockets, enzymatic active sites, and DNA minor grooves. The corresponding distributions of retardation factors reveal that for a major fraction (∼75%) of the hydration shell the slowdown is moderate and lies between 1 and 3; for the remaining ∼25% fraction, the distributions exhibit a long tail at larger slowdown values which can be very approximately fit by a power law (Figure 6). While the series of globular proteins in Figure 6 have very different sizes, secondary structures, and biological functions, including enzymes, the ubiquitin tag protein, and an antifreeze protein that depresses the water freezing point, the distributions of retardation factors are strikingly similar; the molecular explanation of this similarity will be discussed in the next section. The distribution obtained for DNA exhibits the same shape, except for a shoulder at intermediate slowdown values which was shown to arise from the phosphate backbone sites.⁵⁸ While the commonly used stretched-exponential function may offer a numerically satisfactory fit of the reorientation tcf averaged over the shell, the associated distribution of reorientation times bears no resemblance to the distributions directly determined from simulations. This discrepancy was thus suggested^57,73 to call into question the validity of mode-coupling theory arguments assigning the nonexponential tcf decay to a collective glassy behavior within the hydration shell.^85,116

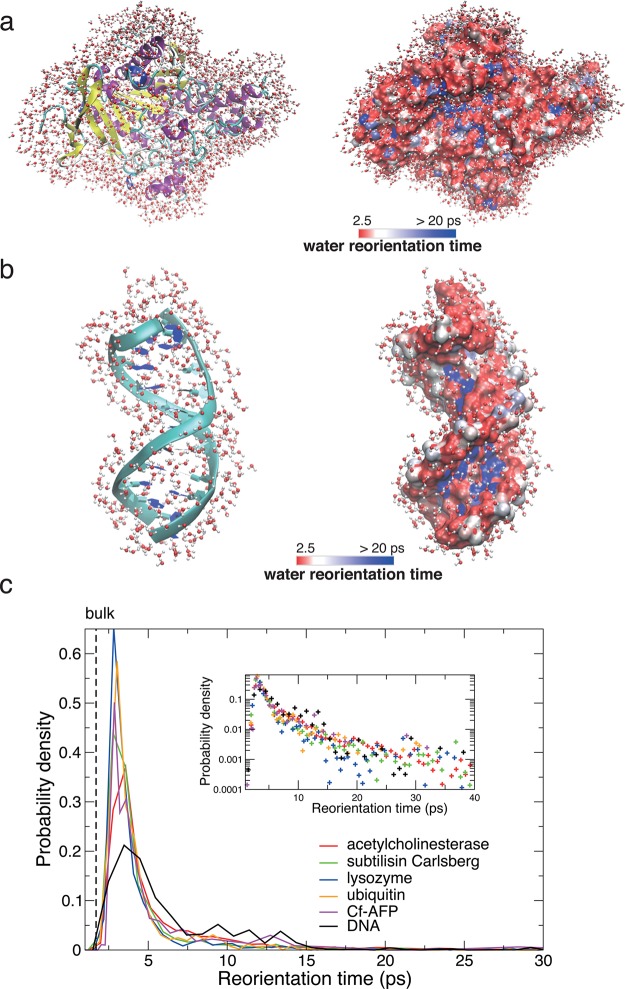
Figure 6.

(a) Acetylcholinesterase enzyme with its hydration shell water molecules (left), and map of water reorientation dynamics in the shell⁵⁷ (right). (b) Idem around a DNA dodecamer.⁵⁸ (c) Probability density of water reorientation times next to a series of globular proteins^57,61 and next to DNA⁵⁸ on a linear scale and on a semilog scale in the inset.

Our discussion has shown that simulations have revealed how much the dynamics of water can vary from one biomolecular surface to another. As will be discussed in the next section, an additional source of heterogeneity in the hydration layer dynamics arises from the conformational fluctuations of the biomolecule.⁵⁸

3.3. Jump Model

Clear progress is being made in the detailed characterization of hydration dynamics within biomolecular hydration shells and their site-resolved mapping. Nonetheless, central challenges remain: to identify the biomolecular features and the character of the water dynamics that are actually responsible for the different time scales of the hydration dynamics, as well as to elucidate, for example, the respective importance of the biomolecule’s exposed surface topography, of confinement, and of the variety of chemical groups at the water interface.

In order to understand how a biomolecule affects the water hydrogen-bond and reorientation dynamics, it is fruitful to first return to the reference situation in the bulk. While the reorientation of water molecules in neat water was long considered to follow the Debye rotational diffusion picture and to take place via a series of very small angular steps, recent theoretical^{20,21,203−205} and experimental^206,207 work argue for a quite different picture: the water molecule reorients predominantly via a mechanism involving sudden, large-amplitude jumps when a water hydroxyl (OH) group trades H-bond acceptors (Figure 7a). An additional, but usually minor, contribution arises from the slower tumbling of the frame of the intact H-bonded complex. The extended jump model (EJM) was developed to relate these jump features to the water molecular reorientation time. The interested reader may consult ref (21) for further model details and applications to various simple solutes.

Figure 7.

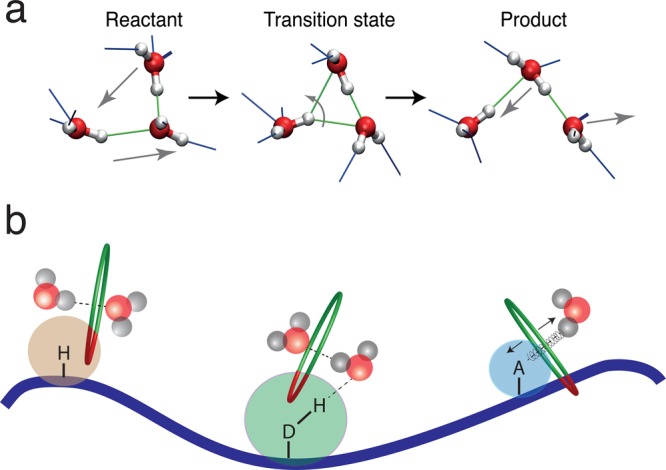
(a) Molecular jump mechanism for water reorientation.²⁰ (b) Schematic figure with a protein interface and the three types of sites, respectively hydrophobic, H-bond donor, and H-bond acceptor, together with a pictorial representation of the types of perturbation they induce on water dynamics (excluded volume and H-bond strength factors).

An important feature of this novel picture is that this concerted trading of H-bond acceptors can be regarded as a chemical reaction—complete with transition state—whose kinetics are determined by a free energy barrier due both to the approach of the new acceptor and to the elongation of the initial H bond.^203,204 The effect of a solute interface on the water H-bond dynamics can then be determined via the solute’s impact on these two coordinates. The water jump rate constant depends on two key local solute features; these reflect the solute’s topographical and chemical aspects and are now described.

The first feature is related to the solute’s interface topography. It occurs for any type of solute and interface and is a consequence of the partial hindrance of the approach of a new water H-bond partner compared to the bulk situation. This produces a jump rate slowdown, quantified by the transition-state-excluded volume factor ρ_V.¹⁴⁰ A water molecule next to a locally convex solute site experiences a slowdown of typically less than 2,¹⁴⁰ while for a water molecule in a concave pocket this steric slowdown factor usually exceeds 2.^140,208

The second feature is determined by the initial H-bond strength in the water’s H-bond complex.²⁰⁹ Compared to the bulk situation, it accelerates (decelerates) the jump rate if the initial bond is weaker (stronger) than a water–water H bond; this is quantified by the transition state H-bond strength factor ρ_HB. This effect can have both an enthalpic origin, e.g., for a negatively charged initial H-bond acceptor like a protein carboxylate group or a DNA phosphate group with a large interaction energy with the water molecule,²⁰⁹ and an entropic origin when the initial H-bonded pair is held together by the shape of the local interface (as occurs, e.g., in nonbiological cavities²¹⁰).

Each feature provides a quantitative, multiplicative factor—associated with the transition, or activated, state of the reaction—affecting the jump rate.²¹ The reaction rate’s overall perturbation factor relative to the bulk is then the product ρ = ρ_Vρ_HB. Figure 7b schematically summarizes the key effects expected for the three main types of sites found at a biomolecular interface: hydrophobic groups, H-bond donors, and H-bond acceptors. Hydrophobic groups only affect H-bond jump dynamics by hindering a new water H-bond acceptor’s approach through an excluded volume effect. H-bond donors and acceptors act differently: the donors can form bonds of different strengths, but these bonds essentially act only on the water oxygen around which the angular jump occurs. The resulting torque’s influence on the OH reorientation thus is negligible, and H-bond donors, like hydrophobic groups, perturb water dynamics mainly via their excluded-volume effect. On the other hand, H-bond acceptor groups can impact water H-bond dynamics via both their excluded volume effect and the strength of the H-bond formed with water.

The jump model has been applied to a broad gamut of situations, ranging from small solutes²¹ to interfaces^211,212 and nanopores.^210,213 We focus here on its application to biomolecules, including protein,^57,61,72,73 DNA,⁵⁸ and phospholipid bilayers’¹⁰⁸ hydration layers. Large angular jumps were shown to remain the main reorientation mechanism for water in the vicinity of biomolecules,^57,58,73 and the model-predicted water reorientation time distribution is in good agreement with that directly computed,⁷³ which gives confidence in the model’s use to analyze the hydration shell’s dynamics. The jump picture provides a simple analysis of the distribution of perturbation factors within the hydration shell, and it clearly separates the respective contributions from the local topography (ρ_V) and from the strength of the water–biomolecular site interaction (ρ_HB). While this approach is not expected to yield highly accurate quantitative predictions, it often performs quite well. An important aspect of the jump model is that it depends only very weakly on the force field adopted; this is due to its reliance on the identification of the hydration shell dynamical perturbations’ physical mechanisms.

For the very large fraction of water molecules within globular protein or DNA hydration shells that are moderately retarded with respect to the bulk (slowdown factor < 2–3) (Figure 6), the jump model suggests that this slowdown is due to the local topography of the biomolecule’s interface which hinders the H-bond rearrangements.^57,58,61,73 The slowdown factor scales inversely with the solvent exposure of the site, and the width of the peak in the slowdown factor distribution arises from the corrugated biomolecular interface, with its succession of protrusions, pockets, grooves, and clefts. This latter aspect probably explains, for example, why a series of globular proteins exhibits similar distributions of slowdown factors.⁵⁷ The entropic nature of this steric slowdown is further supported by the weak temperature dependence of the average slowdown measured for the entire hydration shell for proteins by MRD¹⁷⁹ and reproduced in MD simulations.⁶¹ (In supercooled conditions, a stronger temperature dependence is observed,¹⁷⁹ but it was shown²¹⁴ to arise from the constraints imposed by the biomolecular interface on the local water structure.)

For DNA, the smaller peak at intermediate slowdown factor values (4 < ρ < 10) was shown to arise from water molecules next to the phosphate backbone.^58,61 While these sites are well solvent exposed, the strong H bond with the phosphate sites causes the observed slowdown. Although one might have expected to find the slowest water dynamics in the most energetically stable hydration sites, the fact that these phosphate groups are not always the slowest sites (see the following paragraph) illustrates the unusual feature that there is no necessary systematic correlation between dynamics and thermodynamics. The DNA phosphate oxygens are the first ones to be hydrated at low humidity, but they induce a much more limited slowdown than other groove sites.

The tail of the slowdown factor distribution was shown to arise from water molecules which are buried in protein pockets or more especially in the DNA minor groove while donating a strong H bond to a biomolecular site (particularly in the “spine of hydration”).^57,58,61,73 Both the excluded-volume and H-bond strength factors contribute to yield strongly retarded dynamics.

The jump analysis indicates that an essential part of the effect induced by a biomolecule on its hydration shell arises from its local topography. However, a biomolecule is not a rigid object, and its conformation fluctuates. This can therefore induce fluctuations of the local hydration dynamics, i.e., in one given site the water jump rate can change with the biomolecular conformation. Two limits can be considered.⁵⁸ In the first, water dynamics are much faster than the relevant dynamics of the biomolecule, which can be considered to be static vis-a-vis the jump. Here there is an inhomogeneous distribution of systems with different water dynamics. In the other, second extreme, the biomolecule samples are in different local conformations before the hydration shell rearranges and the resulting water dynamics are equilibrated to and averaged over these conformations, and they display no temporal heterogeneity. (These two limits have the spectral analogies of inhomogeneous and homogeneous, motionally narrowed broadening.²¹⁵) It was shown⁵⁸ that the susceptibility of hydration dynamics vis-a-vis conformational fluctuations is enhanced in confined sites, e.g., in the DNA minor groove where a small widening of the groove can significantly accelerate the water dynamics. In these sites, the water and DNA groove dynamics occur on a similar time scale, thus showing that the biomolecule can neither be considered to be static nor be in equilibrium with the hydration layer dynamics (or in an extreme limit, be slaved to those dynamics). Similar considerations should apply to protein pockets.

With respect to globular proteins, unfolded and intrinsically disordered proteins exhibit a much lower fraction of pockets and confined sites. Because of their different local topography, the retardation factor distribution is expected to be narrower and the average slowdown to be more limited, in agreement with MRD measurements²¹⁶ and MD simulations.^74,92

The same excluded-volume and H-bond strength considerations that have been discussed here have now been shown to describe water jump dynamics next to small solutes and next to large biomolecules. Jumps are not expected to be dramatically more cooperative at protein and DNA interfaces than in the case of smaller solutes. However, protein and DNA hydration dynamics cannot be simply extrapolated from the water dynamics next to their amino acid or nucleobase building blocks in dilute aqueous solution. The most obvious cooperative effect arises from the topographical factor, since confining geometries found, e.g., in pockets and grooves require the presence of several residues or bases.

3.4. From Dilute Biomolecule Aqueous Solutions to Living Cells

Thus far, our discussion has focused on the case of a dilute biomolecule in aqueous solution, where the different water dynamics in the hydration shell and in the bulk are caused by a single biomolecule. This simple situation is obviously an indispensable step toward a molecular understanding of how biomolecules affect water dynamics, but it remains far from the typical conditions encountered, for example, in cells. In living cells, between 5% and 40% of the volume is occupied by proteins, ions, and other biomolecules,²¹⁷ which clearly indicates a very crowded environment (Figure 8). Crowded conditions are expected to increase the viscosity and slow down the dynamics of water. Simulations²¹⁸ of proteins in highly crowded environments have supported this idea and suggested that water diffusion and dielectric relaxation is retarded and that the protein hydration structure is affected. Further, 2D-IR experiments¹⁵⁹ have shown that the slowdown is not simply proportional to the solvent composition but instead occurs rather abruptly. The crowding effects on the hydration dynamics were also found to sensitively depend on the type of crowding agent and especially on the size of the molecules.¹⁵⁹ In a complementary simulation study,¹⁵⁹ the dynamics of water molecules, between two proteins and between four proteins arranged in a tetrahedron, were studied as a function of the distance between proteins (Figure 9). For decreasing protein separations, the water dynamics slow down abruptly, but interestingly, this transition toward much slower dynamics was found to take place at much shorter distances for the protein pair than for the protein tetrahedron. This shows that the apparent hydration shell thickness increases with concentration and that biomolecular hydration shell dynamics strongly slow down as the concentration increases, as found and explained for smaller solutes.^60,140,209 Models neglecting this important feature, such as those currently used, e.g., to interpret THz spectra and to infer the hydration shell thickness from the change in THz absorbance at high concentration,^42,147−149 are thus likely to lead to strong overestimates of the low concentration hydration shell extent.¹⁵⁰

Figure 8.

Schematic representation of part of an E. coli cell, including cell wall (green), cytoplasm area (blue and purple), and nucleoid region (yellow and orange). Water molecules are not shown (Illustration by David S. Goodsell, the Scripps Research Institute²¹⁹).

Figure 9.

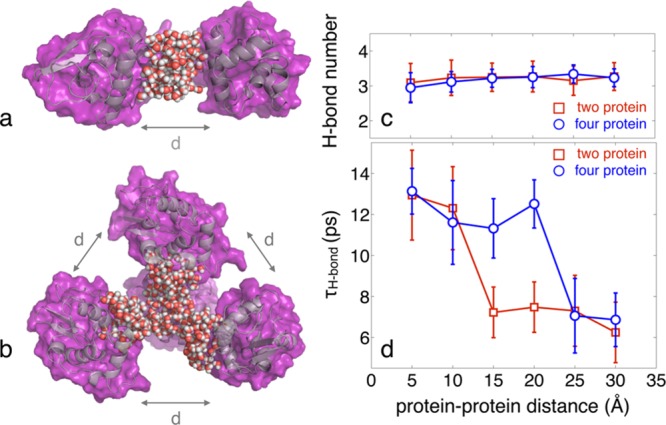
Effect of crowding on water structure and dynamics. For water molecules between two proteins (a) and four proteins (b), the number of H bonds is practically unchanged with the degree of confinement (c), while the H-bond dynamics exhibit a sharp transition at a distance which changes markedly with the confining geometry (d) (Reprinted with permission from ref (159). Copyright 2014 American Chemical Society.). There are alternate definitions for the HB lifetime than the one employed here, see, e.g., ref (58).

We note that these results further suggest that in such conditions a ligand approaching different protein or DNA sites will experience hydration dynamics fairly different than represented on the single-biomolecule maps shown in Figure 6, since now the water dynamics will be simultaneously affected by the biomolecule and by the ligand.

The dynamics of water in living cells were measured by NMR^220,221 and QENS.^{137,222−225} In E. coli, QENS reported water translational dynamics similar to those in the bulk,²²³ and NMR²²⁰ concluded that more than 80% of the cell water has bulk-like rotational dynamics, while the dynamics of water molecules in direct contact with biomolecules are similar to those measured in the hydration layer of large proteins in dilute solution. This remarkable and somewhat surprising result suggests that despite the crowded environment a very large fraction of intracellular water is not perturbed by the various biomolecules. NMR²²⁰ found similar rotational dynamics in cells from the H. marismortui halophile, despite the much higher ion concentration. In contrast, QENS measurements²²² on the same halophilic cells suggested that the translational dynamics are 250 times slower than in the bulk. The decoupling that these two results would suggest between the rotational and the translational water dynamics is surprising given that both motions are governed by the same hydrogen-bond exchanges.²⁰ However, it has been suggested²²⁶ that this discrepancy may arise from the model used for the interpretation of the QENS spectra in which a decoupling between rotation and translation is assumed and where the dynamic heterogeneity is not explicitly considered.

4. Vibrational Excitations and Energy Dissipation

Energy exchange between a biomolecule and its hydration shell plays a central role in both the relaxation of nonequilibrium excitations and the energetics of biochemical reactions. One primary function of the hydration shell in the first aspect of this exchange consists in accepting vibrational energy and effecting its equilibration in space and time; this serves to avoid structural damage from large amounts of excess energy localized in the biomolecule or—even worse—localized on particular subunits of it. This “heat bath” role is highly relevant in the relaxation of vibrational and electronic excitations, e.g., in nucleobases, which display excited state lifetimes in the subpico- to picosecond regime and decay predominantly by internal conversion. The substantial transfer of the initial electronic energy—typically on the order of several 10 000 cm^–1—into the vibrational manifold initiates a cascade of redistribution processes in both the biomolecule and the water shell. Eventually this combined system evolves into a vibrationally hot ground state. Equilibration of thermal energy is the process which establishes an equilibrium population distribution of vibrational modes within the combined system which then is characterized by an elevated vibrational temperature. The final cooling step consists in spatial energy transport, i.e., heat conduction, within the water environment, typically occurring on micro- to millisecond time scales.

While this general scenario is expected to be similar to that of smaller solute molecules in a liquid environment, for most biomolecules the time scales and relaxation pathways are not well understood. Compared to smaller systems, a source of the additional complexity are the energy redistribution and transport processes within the biomolecule which can extend over lengths of several tens of Angstroms. The major issues here include the following.

• (1)Radiationless and vibrational relaxation within a biomolecule: What are the time scales and pathways of radiationless and vibrational relaxation and energy redistribution within the extended biomolecules? Does relaxation establish local equilibrium states of particular functional units or is there equilibration within the entire vibrational manifold of the biomolecule? How do the kinetics of processes within the biomolecule compare with the rates of energy exchange with the hydration shell? Can energy transport to the solvent “shortcut”, i.e., dominate over, energy transfer within the biomolecule and provide the major route to overall energy equilibration?
• (2)Energy exchange with and within the water shell: Do the heterogeneous hydration geometries present at the biomolecular surface result in a variety of local energy transfer rates from the biomolecule to the hydration shell? What are the molecular couplings underlying this energy transfer, i.e., what are the roles of resonant vibrational energy transfer via, e.g., dipole couplings and direct anharmonic couplings of (delocalized) low-frequency modes of the biomolecule and the water shell? To what extent do the hydrogen bonds between water and the biomolecule affect the energy transfer rates and pathways? How fast is the energy transfer from the first and second hydration layers into the bulk water environment, and what are the properties of a vibrationally hot ground state of biomolecule and water shell?

Radiationless and vibrational relaxation, the first group of processes, define the intramolecular distribution of vibrational populations which is relevant for interactions with the water shell. In contrast to a widespread belief, the existence of an intramolecular quasi-equilibrium distribution, i.e., a Bose–Einstein distribution with a well-defined vibrational temperature, has remained unproven in most cases. Moreover, its formation can extend well into the picosecond time domain and thus occur in parallel to energy transfer to the hydration shell, making a separation of time scales of intra- and intermolecular processes impossible. In the following, we first address such issues in section 4.1, followed by discussion of energy exchange with and within the water shell in section 4.2.

4.1. Radiationless Processes, Vibrational Relaxation, and Energy Transport in Hydrated Biomolecules

The ultrafast dynamics of electronically excited states in biomolecules have been studied in the context of photochemical reactions, excitonic transport phenomena, and radiationless relaxation and much has been learned. Decay processes of the first excited state of nucleobases alone and in DNA and RNA structures have been addressed by femtosecond time-resolved fluorescence and photoelectron spectroscopy, pump–probe measurements of transient absorption, and theoretical calculations.^227,228 After excitation of ¹ππ* states of individual nucleobases or nucleobase pairs in the gas phase and in solution, subpico- to picosecond decay times of the excited states have been measured.^229−231 The short lifetimes have been rationalized with a potential energy surface picture invoking internal conversion through conical intersections acting as photochemical “funnels” for transitions between the excited and the ground electronic states. There remain controversies about a number of aspects here, e.g., the number of conical intersections involved, the role of optically dark ¹nπ* and of triplet states, and a potential contribution to the overall decay pathway of proton transfer steps in base pairs. In contrast, much longer excited state lifetimes of tens to hundreds of picoseconds have been found in DNA oligomers and helices. This behavior has been attributed to a delocalized excitonic character of the initially excited states which first decay into optically dark exciplex states; these states then decay back to the ground state on a longer time scale. This final decay step has been regarded as an internal conversion process.²²⁸

In all cases, the major fraction of the initial (electronic) excitation energy is transferred into the vibrational manifold of the biomolecule. The creation of a vibrationally hot ground state after internal conversion has been inferred from transient changes of the initial S₀–S₁ absorption spectrum.²³² The transient spectra display a strongly enhanced tail of absorption below the purely electronic 00 transition, pointing to excess populations of Franck–Condon active modes after repopulation of the ground state.²³³ In most cases, the extent to which the generated vibrational population distribution represents an equilibrium distribution characterized by a vibrational temperature is unknown. In this connection, it should be noted that the transient energy content of the vibrational manifold depends on the internal conversion rate relative to the cooling rate, i.e., the rate of energy transfer to the environment. For fast subpicosecond internal conversion, large amounts of vibrational excess energy are transiently stored in the manifold, while for a slow picosecond decay of excited states the deviation from thermal equilibrium is much smaller. Energy transfer to the water shell processes will be discussed in section 4.2.

In the electronic ground state, the vibrational lifetimes of biomolecules are similar to those in heterocyclic aromatic molecules. As an illustration, they cover a broad range from approximately 300 fs for phosphate stretch vibrations up to several picoseconds for particular fingerprint modes. There are a few examples where the pathway of intramolecular vibrational relaxation is known, at least in part. NH stretch excitations of nucleobases in DNA oligomers decay predominantly through NH bend overtone and combination tone levels. Subpicosecond anti-Stokes Raman experiments have shown that the NH stretch decay induces pronounced excess populations of the v = 1 states of several modes between 1330 and 1660 cm^–1, predominantly those containing a pronounced NH bend contribution.²³⁴ The vibrational populations remain nonthermal for several picoseconds, in contrast to the frequently invoked picture of subpicosecond intramolecular equilibration. The different example of the asymmetric PO₂^– stretch vibration exhibits a lifetime of about 300 fs for phosphate ions in water, as well as for phosphate groups in DNA and phospholipids.^235−237 In the latter, this lifetime is rather insensitive to the level of hydration. This feature points to a relaxation pathway involving other modes of the phosphate group itself, for instance, the symmetric PO₂^– stretch vibration and/or combination tones involving PO₂ twisting and bending modes.

Vibrational excitations and couplings of peptides and secondary peptide structures have been studied extensively by 2D-IR spectroscopy of the structure-sensitive amide I and II bands.^238,239 This work has aimed at characterizing equilibrium structures of peptides and unraveling structural transformations such as peptide folding and unfolding using the related frequency shifts of amide vibrations as structural probes. Vibrational relaxation and energy redistribution were addressed only indirectly. We refer to the review by M. Zanni et al. providing a detailed overview on such studies.²⁴⁰

The spatial transport of vibrational energy within a biomolecule represents an important aspect of vibrational dynamics in view of the large spatial extension and/or oligomeric character of many biomolecules. Such processes have been recently studied in ultrafast pump–probe experiments where the pump pulse induces a spatially localized heating of the molecule and the propagation of excess energy through the molecular structure is mapped by probing localized vibrations of particular functional groups.^241−244 In the related approach of relaxation-assisted 2D infrared spectroscopy, the nonlinear vibrational response following an initial vibrational excitation is recorded via 2D infrared spectra at different frequencies and waiting times.²⁴⁵

Experiments on self-assembled monolayers of nanometer-long hydrocarbon chains have given a heat propagation speed on the order of 1 nm/ps (1000 m/s), which corresponds to a propagation length of approximately 6 C–C bonds per picosecond.²⁴¹ This value is less than one-half of the acoustic velocity in systems like polyethylene, a behavior that has been attributed to the predominance of some intramolecular vibrational excitations in the heat propagation. For peptide helices, a series of experiments has shown that internal conversion in an electronically excited azobenzene chromophore attached to the helix provides the initial vibrational excess energy.^242−244 About 30% of this energy is fed into the helix for further propagation, while 70% is transferred to the surrounding solvent. Apart from the initial energy injection into the peptide helix, heat transport is found to be diffusive in character, with values around 0.02 nm²/ps of the heat diffusivity D, the ratio of thermal conductivity to the volumetric heat capacity.²⁴² Theoretical simulations give noticeably higher values around 0.1 nm²/ps for this system and between 0.07 and 0.2 nm²/ps for other systems.^242,246 Later experiments on the same system, which have covered a temperature range from 220 to 300 K, suggest that there is inefficient ballistic heat transport through phonon-like low-frequency modes at low temperature and more efficient diffusive transport at temperatures above 270 K.²⁴⁴ In considering these results, it is important to note that both experiments and heat diffusion models average over a multitude of low-frequency excitations, i.e., the contributions of modes with different degrees of delocalization within the biomolecule, and that the intermode couplings relevant for energy transfer are not known. Moreover, it is difficult to make a clear separation of intrabiomolecular energy transport from parallel transport through the adjacent solvent shell. On the other hand, these results clearly establish a picosecond time scale of heat transport which limits the speed of vibrational equilibration between biomolecular sites at nanometer distances from each other and thus the formation of a globally equilibrated ground state.

4.2. Energy Exchange with the Water Shell

The energy content of a vibrationally excited biomolecule and the transfer of excess vibrational energy to the water shell or solvent have been studied with different types of spectroscopic probes. One signature of the large amounts of excess energy redistributed in internal conversion of electronically excited states is that this leads to a reshaping of the electronic S₀–S₁ absorption band, in particular an enhancement of its low-frequency tail by transient excess populations of Franck–Condon active modes. In following a concept introduced for smaller molecules in solution,²⁴⁷ energy transfer to the solvent has been mapped by a time-resolved measurement of the decay of enhanced absorption toward its initial equilibrium value (Figure 10a). A reliable extraction of the energy transfer, i.e., the cooling time, requires data recorded over a large frequency range within the absorption band, since the signal decay times depend on the individual spectral position within the band. This spectral position dependence is due to the fact that a certain change in internal energy content leads to changes of vibrational populations depending on the individual vibrational frequency, even for an equilibrium distribution characterized by a vibrational temperature. Another complication of this technique consists in its sensitivity to vibrational population of Franck–Condon active modes only, which typically provide just a small subset of the entire vibrational manifold.

Figure 10.

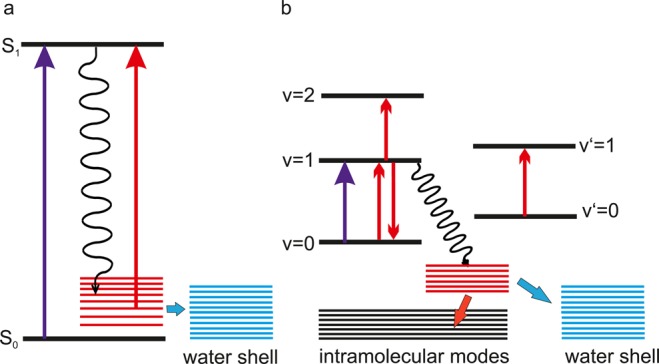
Schematic illustration of energy relaxation pathways as mapped in pump–probe experiments. (a) Optical excitation to an electronically excited state S₁ (blue arrow) initiates an internal conversion process (wavy arrow) which results in excess populations of higher levels of intramolecular modes (levels shown in red). These populations lead to an enhancement of the low-energy tail of the S₀–S₁ absorption spectrum (red arrow), which is measured by a delayed probe pulse. With increasing delay between excitation and probe pulse, the absorption enhancement decays by energy transfer to the water shell. (b) Relaxation pathways after resonant excitation of a vibration (blue arrow, oscillator levels v = 0, 1, and 2). Decay of the v = 1 state generates nonequilibrium populations of intramolecular low-frequency modes which are anharmonically coupled to the initially excited vibration (red levels). As a result, the vibrational transition frequency between the v′ = 0 and the v′ = 1 states is different from that of the initial v = 0 to 1 transition. Subsequent vibrational relaxation leads to a decay of the excess populations of the red levels and the related frequency shift, populating other modes in the vibrational manifold of the molecule (short red arrow) and/or modes of the water shell (short blue arrow, blue levels). Vertical red arrows: Transitions contributing to the absorption changes measured in a pump–probe experiment.

The method just described has been applied to individual nucleobases in solution, which all display subpicosecond internal conversion rates from the excited ¹ππ* states, resulting in a strong transient heating of their vibrational manifold.²³² With the assumption of a heated equilibrium distribution of vibrational populations, vibrational temperatures on the order of 1000 K have been estimated. Numerical fits of time-resolved absorption transients have been interpreted in terms of cooling times between 0.4 and 2 ps for adenosine in water; these times are substantially shorter than the 4–13 ps decays measured with methyladenine in methanol and acetonitrile²⁴⁸ and are also faster than the tens of picoseconds cooling times of other heteroaromatic molecules in nonpolar solvents. These facts have led to speculations that intermolecular hydrogen bonding to water molecules accelerates the energy transfer from the nucleoside into water.²²⁸ For the case of nucleobases in oligomers, the excited state lifetimes are typically longer than their vibrational cooling times, thereby limiting the accumulation of excess energy in the biomolecule and, thus, hampering the application of this method to them.

The situation is evidently different for proteins. Recently, the structural stability of proteins under conditions of a fast heating by several hundreds of Kelvins has been studied with a novel approach.²⁴⁹ An ensemble of 36-residue villin protein headpiece molecules was attached to the surface of a gold nanoparticle, and the prepared nanoparticles were dissolved in D₂O. Then in a pump–probe approach the gold nanoparticles were heated by femtosecond laser excitation to a transient phonon temperature of approximately 1300 K. The response of the protein molecules to this temperature induces a blue shift of the proteins’ amide-I vibrational absorption, which was mapped with mid-infrared probe pulses. The protein layer reached a maximum temperature of around 600 K after 75 ps and subsequently cooled down on a time scale extending to several nanoseconds. The cooling cycle was found to be fully reversible, without inducing either unfolding processes or other major structure changes of the proteins. This finding led to the conclusion that thermally triggered changes of protein structure require substantially longer deposition times of excess energy than observed here, pointing to slow dynamics of the required structure-changing processes.

In the electronic ground state, energy transfer processes have been studied after excitation of infrared active modes from the fingerprint range around 1200 cm^–1 up to the OH or NH stretching regions between 3200 and 3400 cm^–1 (Figure 10b). Intramolecular vibrational relaxation transfers excess energy to low-frequency modes, some of which couple anharmonically to the initially excited or other high-frequency spectator modes in their v = 0 ground state. Because of the anharmonic coupling and the excess population of the low-frequency modes, the high-frequency modes display a spectral reshaping; in particular, there are spectral shifts whose sign depends on the sign of the anharmonic coupling terms.²⁵⁰ Subsequent energy transfer from the low-frequency modes into the aqueous environment reduces these modes’ excess populations, resulting in a decay of the spectral shifts. A time-resolved measurement—either of differential absorption, i.e., the difference between the transient and the equilibrium spectrum, or of 2D infrared spectra as a function of waiting time—allows following of the time evolution of the spectral changes and thus the flow of excess energy out of the transiently heated manifold.

Vibrational energy transfer into the aqueous environment of phospholipids in reverse micelles and DNA oligomers in thin films has been studied in pump–probe experiments mapping the time evolution of the asymmetric phosphate stretch vibration at different hydration levels.^236,237 The fact that phosphate groups are primary hydration sites at which up to 6 water molecules are accommodated via hydrogen bonds to the free PO₂ oxygens makes phosphate vibrations specific reporter modes. We have mentioned in this review several times that the spectral position of the asymmetric PO₂ stretch band depends on the level of hydration; to be specific, it moves from 1250 to 1230 cm^–1 when going from dehydrated to fully hydrated samples. Moreover, the short 300 fs lifetime of the v = 1 state of the asymmetric PO₂ stretch vibration results in a rapid deposition of excess energy in the vibrational manifold.

At low hydration levels of less than two water molecules per phosphate group, the pump–probe spectra observed after the PO₂ population decay display a red shift of the phosphate stretch vibration in both phospholipids (Figure 11a and 11b) and DNA. This shift to lower frequency is caused by the excess population of low-frequency modes of the phospholipids and of DNA which anharmonically couple to the PO₂ stretching mode. The red shift decays with time constants of 1.5 ps and approximately 20 ps in phospholipids and DNA, respectively. Such kinetics mainly reflect the redistribution of excess energy into intramolecular modes coupling only weakly to the phosphate vibrations. In view of the extended molecular structure of both phospholipids and DNA, intramolecular energy migration away from the phosphate groups may contribute as well.

Figure 11.

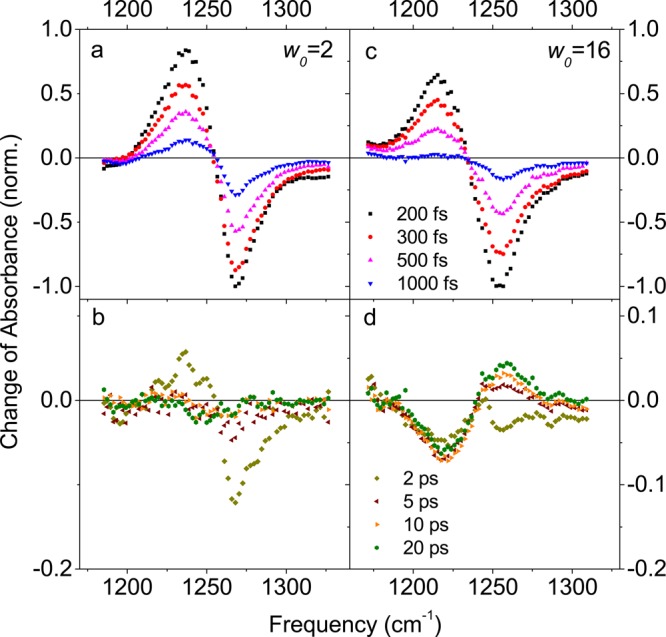
Pump–probe spectra of DOPC reverse micelles with (a and b) w₀ = 2 and (c and d) w₀ = 16 water molecules per phosphate head (Reprinted with permission from ref (237). Copyright 2011 American Chemical Society.). In the experiments, the asymmetric PO₂ stretch vibration is resonantly excited by a 150 fs pulse, and the resulting change of absorption ΔA = −log (T/T₀) at a fixed delay time is measured as a function of probe frequency (with T and T₀ being the sample transmissions with and without excitation). Spectra at early delays reflect population relaxation of the excited mode (cf. Figure 5a), whereas absorption changes at late delay times (lower panels) are a signature of a hot vibrational ground state. At low hydration (w₀ = 2), the PO₂ stretch band undergoes a transient red shift at late delay times, whereas a transient blue shift is observed at high hydration levels (w₀ = 16).

Upon addition of a hydration shell, the behavior of the phosphate vibrations changes drastically. In phospholipids (Figure 11c and 11d), the asymmetric PO₂ stretching band displays a transient blue shift instead of a red shift and a faster decay with a time constant of 1 ps. In DNA surrounded by two complete layers of water molecules, the pump–probe transients display only the initial 300 fs population decay of the phosphate stretch vibration; slower kinetics that were observed in the absence of the shell are absent. This points to a very efficient energy transfer from DNA into the water shell which occurs on a subpicosecond time scale similar to the population decay.

To clarify the origin of the blue shift of the PO₂ stretch band, the water environment was transiently heated by exciting OH stretch vibrations. The femtosecond decay of the OH stretch excitations results in the formation of a hot water ground state on a time scale of approximately 1 ps. Probing the (unexcited) asymmetric phosphate stretch vibration of the phospholipids and/or DNA one again observes a blue shift of the asymmetric PO₂ stretch vibration, in this case induced by the heated water environment. Thus, the blue shift of the phosphate vibration (cf. Figure 11d) is a hallmark of a hot ground state of the aqueous environment and the biomolecules which—after PO₂ stretch excitation—is formed by energy transfer from the biomolecules to the water shell or—after direct OH stretch excitation—via energy redistribution within the water pool which couples to the PO₂ stretch spectator mode. The blue shift points to a modified phosphate–water interaction. The phosphate–water interaction includes two major mechanisms affecting the vibrational frequency, local phosphate–water hydrogen bonds and electrostatic interactions by which the PO₂ moiety is polarized electronically, a mechanism also changing the vibrational potential.²³⁵

Experiments at different hydration levels allow estimation of the minimum size of a water pool required for its function as a heat sink. This issue has been studied by 2D-IR spectroscopy of water pools in phospholipid reverse micelles.¹⁵⁴ The formation of a hot ground state after OH stretch relaxation, which is a central reflection feature of a heat sink function, is manifested in a blue-shifted OH stretch absorption by water molecules in an environment with weakened or even broken hydrogen bonds (Figure 12). In the OH stretch 2D spectra, this effect gives rise to a homogeneously broadened blue-shifted component around 3550 cm^–1. Such hot ground state formation is observed at a minimum hydration level of 3 water molecules per phosphate headgroup, which constitute a local water shell. The formation of the hot ground state occurs on a 500–1000 fs time scale, consistent with the 400 fs population decay of the OH stretch mode at this water level. The fastest structural fluctuations of the water arrangement are in the same time range, as suggested by the disappearance of inhomogeneous broadening in the 2D spectral envelopes. For larger water pools, hot ground state formation becomes faster and approaches the kinetics observed in bulk water.

Figure 12.

Absorptive 2D-IR spectra of the OH stretching vibration of water inside DOPC reverse micelles for the waiting times indicated and 3 different hydrations w₀ = 1 (first row), w₀ = 3 (second row), and w₀ = 16 (third row) (Reprinted with permission from ref (154). Copyright 2012 American Chemical Society.). Spectra are taken with parallel linear polarization of the pulses. Contour lines indicate 10% steps in the measured 2D signals. Spectra at low water content (w₀ = 1) show a persistent predominantly inhomogeneously broadened line due to a heterogeneous distribution of H-bond geometries of single water molecules bound to the phosphate groups. With increasing water content, the spectral diffusion rates increase as a result of vibrational energy dissipation into local water pools. Blue-shifted absorption around 3550 cm^–1 is due to the hot water ground state.

This set of experiments demonstrates the water shell’s function as a heat sink for vibrational excess energy and reveals the few picosecond time scale of the underlying energy redistribution and transfer processes. The formation of a hot ground state includes energy transfer processes from the first few water layers around a biomolecule into the bulk of the liquid, which occur on the same picosecond time scale and are kinetically inseparable from the biomolecule-to-water energy transfer.^17,154 This picture is in line with recent theoretical work that has addressed the energy transfer mechanisms to and within a water environment with the help of a power/work formulation,^18,251−253 which allows for separate computation of the different energy fluxes. The main part of excess energy is typically transferred to the first hydration layer, with hindered rotational (librational) degrees of freedom being the main acceptors and strongly dominating over translations. Coupling between librations delocalizes excess energy on a femtosecond time scale and thus dominates the spatial spreading of excess energy within the water shell and beyond.

5. Electric Fields at Hydrated Biointerfaces

Electric interactions play a fundamental role for the properties of hydrated biointerfaces. From the viewpoint of electrodynamics, such interfaces represent a fluctuating many-body ensemble of ionic and polar molecular entities, and within these interfaces, the biomolecule’s polar and ionic groups and the dipolar water molecules interact via electric fields on the order of megavolts/cm (MV/cm). The role of water molecules in this scenario is 2-fold: they are both sources of electric fields and constituents of a polarizable dielectric, affecting the local electric fields. Fluctuations of these fields occur on a multitude of time scales, due to thermal equilibrium ensemble structural fluctuations. These fluctuations naturally have a strong impact on the frequency spectrum of electric force with important contributions over a wide range of frequencies up to librations around 20 THz.

An understanding of such electric interactions at the molecular level calls for answers to a number of key questions. Among these are what is the field strength at the interface and to what extent do these electric fields impact biomolecular functions and/or impose boundary conditions on functional processes? What is the effective spatial reach of the electric fields and how do they vary with distance from the interface? What is the frequency spectrum of fluctuating electric forces and how are vibrations, rotations, and other elementary excitations affected by them? Is the concept of a spatially inhomogeneous and frequency-dependent dielectric function appropriate to account for the role of water?

There has been extensive theoretical, simulation, and—to lesser extent—experimental work on such issues. However, it seems fair to say that a consistent and/or quantitative understanding for a large class of biointerfaces has yet to be reached. Here, we will restrict our focus to interfacial electric fields and related dynamics on femto- to picosecond time scales from the viewpoint of theory, simulation, and experiment. We refer the reader elsewhere for extensive studies of biointerfaces and membranes subject to static and/or slowly pulsed electric fields.^254,255

5.1. Theory and Simulations

Thus far, we have not had occasion to discuss any impact of ions in the environment of the biomolecule. Proteins typically have a low surface charge density, but DNA with its negatively charged phosphate groups in its backbone can interact with counterions and other ions in its neighborhood, so that electric fields become of interest here. In this section, we adopt the following definitions, illustrated for DNA. The term “counterions” refers to the oppositely charged ions that counterbalance the charge on the biomolecule, e.g., for DNA in water having a negatively charged helix with N phosphate groups, there are N counterions (one cation per phosphate, for example, Na⁺). As for the term “ions”, we will mean all other ions in solution that are not counterions but are simply ions of positive or negative charge, for example, a collection of Na⁺ and Cl^– ions, with an in-principle arbitrary concentration satisfying electroneutrality for these ions. (Such ions are often not present in, e.g., MD simulations due to the computational difficulties of their inclusion.)

Our entry to this DNA topic is via polyelectrolyte theories, which were first introduced by Manning^256,257 for describing the electrostatic properties of DNA and/or other rod-like molecules.^258,259 Polyelectrolyte theory has introduced the concept of counterions electrostatically bound to a polyion, a polymer consisting of repeating ionized units. A counterion is considered bound if its spatial position is fixed relative to the position of the ionized units of the polyion. (Thus, not all of the counterions are necessarily bound.) The most elementary approaches mimic the DNA double helix either as a cylinder with a uniform negative charge density at its surface or as an infinitely long polyion chain with a constant linear charge density ρ_lin = −2e/d_charge, where d_charge is the distance between neighboring ionic groups on the polyion and −2e represents the charge of two phosphate ions. A striking feature of the latter description which has attracted much attention is that for a counterion interacting with the polyion chain, the statistical configuration integral diverges if ρ_lin exceeds a critical value and the system becomes (mechanically) unstable (for a detailed discussion, see ref (257)). This instability is avoided by a mechanism called “counterion condensation”: the concentration of positively charged counterions is enhanced in a volume close to the surface for charge compensation, thus reducing the linear charge density. For singly charged counterions and DNA with two singly charged phosphate groups per base pair, the condition for this condensation’s occurrence is Γ = (λ_B/d_charge) > 2, where Γ is the Manning parameter and λ_B = e²/(4πϵ₀ϵkT) is the Bjerrum length at which the Coulomb and thermal kinetic energies are the same.²⁵⁷ For a solution dielectric constant ϵ₀ = 80, a temperature T = 300 K, and d_charge = 0.17 nm for a B-DNA helix, Γ has a value of 4.22. The fraction of polyion-bound counterions is given by η = (1 – 1/Γ) and the net charge of a phosphate group, which is reduced in the presence of counterion condensation, is 1/(NΓ), where N is the counterion valency. This gives the large bound fraction value η = 0.76 and a net phosphate charge of −0.24 for B-DNA with monovalent counterions.

More sophisticated models treat the electrostatic interactions at the atomic level by considering the hydrated double-helix structure of DNA plus the counterions plus additional ions in the aqueous environment. The ionic species and phosphate groups are described either as point charges or as charged spheres of a finite radius R,²⁶⁰ while the embedding water molecules are treated either as a dielectric continuum or as point dipoles. Two of the major directions in theory are (i) the solution of the Poisson–Boltzmann (PB) equation in a static geometry and (ii) MD simulations combining classical trajectories of the different constituents with an electrostatic interaction potential, now discussed in turn.

(i) In the PB picture, the biomolecular system with an electronic charge density ρ(r) is surrounded by a medium described as having a spatially dependent bulk relative dielectric constant ϵ(r).²⁶¹ The system’s counterions and ions—in particular, the former—are embedded in the medium with a charge z_ie (e = elementary charge) of ions of type i and a concentration c_0i(r) in the absence and c_i(r) = c_0i(r) exp(−E_p(r)/kT) in the presence of interactions. Here E_p(r) is the potential energy surface determining the potential of mean force for the counterions and ions. We note that this approach allows for a net excess charge of the total system, i.e., the total charge of the biomolecule ∫dVρ(r) can be different from ∑_i c_0iz_ie, the sum of counterion and ion charges in the environment (note that condensed counterions are included in the environment in this definition). The PB picture’s basic concept consists in equating E_p(r) with the mean electrostatic potential V(r), leading to the well-known nonlinear PB equation (SI units)

1

which is usually applied in its linearized form

2

Early applications of PB theory to biomolecular systems treated simplified spherical or cylindrical charge distributions ρ(r), while more recent work has taken the molecular structure into account. The DNA’s charge distribution has been modeled by placing point-like (partial) charges at atomic positions of the time-averaged equilibrium structure and solving the PB equation by finite difference methods on a geometric lattice.²⁶² A most critical issue is the choice of the dielectric function ϵ(r), which is expected to be different within the biomolecule and in the surrounding medium.²⁶³ A frequently applied approximation assumes a small value of ϵ < 4 within the biomolecule and a large value ϵ ≈ 80 in the environment, the latter being close to water’s static dielectric constant. At the DNA–water interface, such models are connected with a step-like discontinuity of ϵ which occurs on a length scale much shorter than typical values of the Debye screening length 1/l_Debye² = κ² = (∑_ic_0iz_ie²)/(ϵ₀ϵkT). A more gradual change of ϵ(r) follows from the theory of ionic saturation.²⁶⁴ Such PB calculations have been performed for DNA embedded in a water shell with different salt concentrations and give a radial dependence of electrostatic potentials that is strongly influenced by the counterion distribution concentrated on a length scale of 10–20 Å from the DNA helical axis.²⁶²

The dielectric continuum picture for hydrating water has been combined with MD simulations which consider the phosphate groups of DNA and the counterions at the atomic level.²⁶⁵ Different approaches for the dielectric function inserted into the denominator of the pairwise additive electrostatic interaction potential between the charges have been compared, and both the energetics and the spatial distribution of counterions have been calculated. The results indicate that there is a counterion distribution in the neighborhood of the DNA–water interface with—depending on the interaction potential—up to 80% of counterions located within a 20 Å distance from the DNA axis. The interfacial electric fields involved are on the order of 1 MV/cm.

However, there are major shortcomings of the PB picture; these include the neglect of the molecular structure and electronic polarizability of water and ionic groups, the lack of local interfacial interactions such as H bonds, the assumption of a static dielectric function, and the neglect of explicit ion–ion correlations. In the relevant multigiga- to terahertz frequency range of structural—and thus electric—fluctuations, the real part of water’s dielectric function has values much smaller than the static value ϵ(ω = 0) ≈ 80. We consider a more molecular approach next.

(ii) The more microscopic approach of MD simulations has been employed with the inclusion of all constituents of a hydrated biomolecule and surrounding water molecules and ions, with one counterion per phosphate.^{33,53,94,98,266−270} (We recall that some simulations include counterions but no further ions in solution.) Coulomb interactions are treated on the basis of force fields at different levels of sophistication,²⁷¹ different water models ranging from rigid nonpolarizable approaches (TIP3P, TIP4P) to flexible polarizable water molecules (SPC) have been applied, and ions have been treated as charged spheres with the CHARMM force field. Full molecular dynamics simulations including explicit molecular-level water require a large numerical effort, allow only a limited size of the simulation box, and currently permit trajectories up to a maximum time interval of a microsecond. To enhance the computational efficiency, effective ion–DNA potentials have been derived from a full simulation in order to reproduce the radial solute–solvent distributions.²⁷²

An overview of early simulation results on DNA has been presented in ref (267), and references to more recent works can be found in the review in ref (273). Molecular dynamics simulations of hydrated B-DNA^{94,268,274−277} have provided detailed insight into the time-averaged location of counterions around DNA and their spatial distribution functions. A recent and particularly noteworthy simulation²⁷⁸ was extended into the microsecond regime and explicitly included a physiological 150 mM K⁺Cl^– ion concentration around the double-stranded DNA oligomers consisting of 18 base pairs, 36 phosphate groups, and their Na⁺ counterions (Figure 13). In a fashion similar to but less pronounced than the predictions of dielectric continuum models discussed above, there is an enhanced distribution of positive ions in the general neighborhood of the DNA–water interface with ∼75% of these ions residing at radial distances from the helical axis of less than 20 Å. Two layers of ions are formed, with maxima in the radial distribution function at r ≈ 5–7 and 12 Å. There are preferred sites for the cations: the two oxygen atoms of the PO₂^– moieties of the backbone, with a preference for the O1 oxygen atom oriented toward the DNA minor groove. To a limited extent, sodium and potassium counterions reside in the minor groove, modifiying the chain of tightly bound water molecules (ion occupancy changes with the DNA sequence;²⁷⁸ for the sequence studied in ref (58), the minor groove ion occupancy is below 10% and ions were shown to only affect the few molecules in their hydration shell and to have a small effect on the overall DNA first hydration shell dynamics). It is important to note that the K⁺ ion atmosphere extends to a radial distance of some 25 Å (Figure 2 of ref (278)). Finally, counterion residence times around phosphates are on the order of 100 ps and range from 100 ps to more than 10 ns^275,276 in the grooves, with limited diffusive motion along the grooves.

Figure 13.

(a) Radial distribution of K⁺ ions along the distance to the DNA helical axis, averaged over a series of microsecond simulations of different tetranucleotides at physiological ion concentration, in the major (upper panel) and minor (lower panel) grooves (Reproduced with permission from ref (278). Copyright 2015.). (b) Distribution of K⁺ (blue) and Cl⁻ (green) ions around DNA, where the oxygen and phosphorus atoms are highlighted in red and purple, from a snapshot of the simulation described in ref (278) (Image courtesy of R. Lavery).

Molecular dynamics simulations have also been used to analyze electronic charge densities, electric potentials, and polarizations of phospholipid membranes and bilayers.^{105,106,279−281} Neutral phospholipids with a negatively charged phosphate and a positively charged choline unit in their headgroup display a headgroup dipole on the order of 20 D; this is an impressive size and is typically 10 times larger than the dipole moment of a water molecule. In the time-averaged structure of phospholipid layers, the headgroup dipoles make an angle of some 70° with the surface normal and govern the structure of the aqueous solvation shell. Phosphate groups form strong intermolecular H bonds with their first water shell, while a clathrate water structure exists around the non-hydrogen-bonding choline groups. A substantial fraction of water molecules bridge neighboring phospholipid headgroups. The high electron density of the phospholipid headgroups—together with the gradient in water concentration between the outer and inner part of the (bi)layer—causes a strong change of the electric potential, producing electric fields on the order of 10 MV/cm (10⁹ V/m) at the phospholipid surface, i.e., on the same order of magnitude as electric fields in polar liquids.^282,283 Orientational dynamics and structural fluctuations of interfacial water are slowed down somewhat compared to the bulk, with water–phosphate H-bond lifetimes typically exceeding 10 ps.

5.2. Experimental Studies

Experimental information on local electric fields and interactions, counterion distributions, and other structural aspects of charged biomolecular systems has remained very limited. While indirect structural information is available from electron spin resonance methods,²⁸⁴ small-angle X-ray scattering (SAXS) represents a direct probe of time-averaged counterion distributions around DNA,^285−287 and we focus on this method first. SAXS experiments have been performed both under nonresonant conditions and with X-ray photon energies in the range of ionic X-ray absorption edges. The latter method enhances the ion scattering signal and thus the contrast to signals originating from other constituents of the sample.^286,287 Indeed, SAXS has given quantitative radial distributions of counterions of different valency around short DNA oligomers containing some 25 base pairs. While the radial counterion density follows the predictions discussed in section 5.1 of Poisson–Boltzmann theory and early molecular dynamics simulations in a qualitative way, there are substantial quantitative discrepancies. The experiments suggest that the counterions—in particular, those with a high electron density—are more closely localized to the DNA surface than is predicted by theory and simulation. As a result, the counterion atmosphere is concentrated in a smaller volume around DNA; this behavior should be highly relevant for the salt-dependent collective behavior of DNA ensembles.

An experimental probe of local electric fields themselves is provided by the vibrational Stark effect.^282,288 This method is based on applying a static external field E of up to several MV/cm to the sample and measuring the field-induced shift Δν_E of vibrational bands. From such data, a Stark tuning rate a = Δν_E/E is derived, representing the spectral shift per unit field. The extraction of the field from this data is now discussed.

Reference measurements with nitrile, carbonyl, azide, and phosphate stretching oscillators in nonpolar and/or weakly polar solvents have provided experimental Stark tuning rates in the range from a = 0.5 to a = 2 cm^–1/(MV/cm). An empirical correction factor on the order of f ≈ 2 is introduced to account for the fact that the local electric field acting on the oscillator is different from the externally applied field, resulting in a smaller local-field tuning rate of a/f. Stark tuning rates in the local field calculated from high-level theory are on the order of 0.5 cm^–1/(MV/cm) in most cases.^{282,289−291}

The local electric fields acting on an oscillator in a biomolecular environment are estimated by comparing the spectral position of its vibrational band with the reference measurement. Assuming that this frequency shift Δν is exclusively due to the action of the local field then allows the field to be calculated with the help of the Stark tuning rate. Local electric fields between several tens of MV/cm and 140 MV/cm have been derived in this fashion for a variety of biomolecular systems. It should be noted that this method provides time-averaged local fields and neglects any high-frequency fluctuations of electric interactions. Moreover, it is based on the two key assumptions that (i) the origin of vibrational frequency shifts in a biomolecular environment is mainly electrostatic and (ii) the linear relation between vibrational frequency shifts and the low electric fields in the reference measurements can be extrapolated to the much higher local fields in the biomolecule.

The ever-present fluctuating electric fields in a biomolecular environment influence both vibrational transition energies and line shapes. In contrast to steady-state Stark spectroscopy, ultrafast 2D-IR spectroscopy reveals the influence of electric fields on the intrinsic time scales of fluctuations that have been discussed in section 3 of this review. Applying this technique to hydrated biointerfaces requires specific vibrational probes that are located at or close to the biomolecular system’s surface. In phospholipids and DNA, the stretching vibrations of the phosphate group are appropriately sensitive probes of interfacial electric fields, and in DNA these are complemented by other vibrations of the phosphodiester backbone.^{156,157,172,292}

Recent work has combined 2D-IR spectroscopy of DNA backbone modes at different hydration levels with theoretical calculations and has provided quantitative insight into interfacial fields and their fluctation.^{158,173,291,293} As a prototype native DNA system, salmon testes DNA has been studied under fully hydrated conditions, with more than 150 water molecules per base pair and Na⁺ or Mg²⁺ counterions. Thin films of this DNA were prepared by exchanging the Na⁺ cations with lipid cetyltrimethylammonium (CTMA⁺) counterions, resulting in DNA–lipid complexes forming a smooth, approximately 10 μm thick layer on an optical substrate. These films were held at a hydration level of 20–30 water molecules per base pair—which roughly corresponds to two water layers around the double helix—and at a hydration level of less than 2 waters/base pair. Figure 14 displays 2D spectra of the fully hydrated samples with Na⁺ and Mg²⁺ counterions, in which the diagonal peaks in the spectra originate from the 6 backbone normal modes between 950 and 1150 cm^–1. The peaks’ elliptic shape and orientation along the diagonal reflects inhomogeneous broadening due to structural disorder, while the spectral widths along the antidiagonal direction are determined by spectral diffusion due to the fluctuating electric fields and—to lesser extent—by lifetime broadening. The spectral positions and line shapes of the diagonal peaks remain unchanged when the counterions are exchanged, as does the rich pattern of the off-diagonal peaks which reflect vibrational intermode couplings and energy transfer. The 2D spectra measured with 2 water layers around DNA (20–30 waters/base pair) and CTMA⁺ counterions display nearly unchanged line shapes of the diagonal peaks and, in particular, display very similar spectral profiles along the antidiagonal direction. Upon dehydration, the line shapes undergo moderate changes, as discussed in ref (173).

These experimental 2D spectra have been analyzed by a 3-fold combination of perturbation theory for calculating the third-order vibrational response functions, the Kubo line shape theory with a frequency-fluctuation correlation function (FFCF) consisting of two exponential terms, and a rate equation model to account for vibrational energy transfer between backbone modes.^158,173 The FFCF comprises a first component with an amplitude (Δν₁)² and a correlation decay time τ₁ = 300 fs and a second component with an amplitude (Δν₂)² and a decay time τ₂ > 10 ps. The first component describes spectral diffusion caused by the fluctuating electric fields; the second results in an inhomogeneous broadening of the 2D line shapes, reflecting a distribution of local hydration site geometries, i.e., structural disorder. The experimental spectra at all hydration levels and for different counterions are quantitatively reproduced by keeping the correlation decay times fixed and varying the amplitudes Δν_1,2. These Δν₁ amplitudes enter into the antidiagonal line widths and have absolute values between 7 and 11 cm^–1 for the different backbone vibrations. Such values are very similar for the fully hydrated DNA and the DNA surrounded by only two water layers.

The fact that the 2D spectra are unaffected by the particular choice of counterion and by addition of water molecules beyond the first two layers indicates two important features: (i) the interfacial electric fields originate mainly from the water molecules in the first two layers and not the counterions and (ii) the range of the electric fields is limited to a length corresponding roughly to the thickness of only two water layers. The correlation decay time of 300 fs is a measure for the time scale of the local electric field fluctuations. Their amplitude ΔE = Δν₁/a can be estimated from the FFCF amplitudes Δν₁ ≈ 10 cm^–1 and the theoretical electric field tuning rates a = 0.4–0.75 cm^–1/(MV/cm) reported for phosphate vibrations in refs (172, 290, and 291); this gives values of ΔE = 13–25 MV/cm.

Very recently, the short-range character of interfacial electric fields, their dependence on the radial distance from the interface, and their absolute value have been analyzed by theoretical calculations for the dimethylphosphate anion in bulk water, which is a model system for the DNA backbone.²⁹¹ This work gives contributions to the time-averaged electric field of some 60 MV/cm of the first water layer and 18 MV/cm of the second water layer; it also gives the fluctuation amplitudes on the order of 25 MV/cm, which are in good agreement with the numbers estimated above from the 2D line shapes. Such results demonstrate the potential of 2D-IR spectroscopy in combination with in-depth theory to unravel the electric fields at hydrated biointerfaces on the fields’ intrinsic length and time scales.

6. Concluding Remarks

In this review, we discussed water dynamics in the hydration shells of biomolecules, focusing on the underlying basic mechanisms and interactions. The intrinsic time scales of elementary molecular processes here are ultrafast. They cover a time range from sub-100 fs for the fastest structural fluctuations in the water shell up to tens of picoseconds for the escape of some water molecules from the shell into the bulk and for energy transport within biomolecules and from them into the hydration shell. Slower dynamics extending into the microsecond regime are mainly governed by the dynamics of the biomolecule, inducing structure changes in and energy exchange with the water shell. While there is a large variety of biomolecular systems with their own special structures and properties, the water dynamics around these systems are governed by molecular mechanisms that are similar to those in bulk water but which are modified by the steric, electric, and other boundary conditions set by the biomolecule. Indeed, the fundamental molecular mechanisms that explain the dynamics of water in the vicinity of biomolecules are the same as for water next to, e.g., polymers, ions or small solutes. In this sense, biomolecular hydration water is not a distinct species and the concept of “biological water” is highly misleading.⁵⁶

The main features of water structure and dynamics around biomolecules are the following.

• (1)The arrangement and local interactions of water molecules in the first layer around the biomolecule are strongly influenced by the heterogeneous geometric and chemical character of the biomolecular surface. The spatial corrugation and the apolar, polar, and/or ionic character of hydrophobic and hydrophilic groups set specific local boundary conditions for interactions with the layer’s water molecules. As a result, water interactions and dynamics at phospholipid, DNA, and protein surfaces are highly heterogeneous: they exhibit a strong spatial heterogeneity in the first layer and throughout the hydration shell, and they cover a broad range of strengths and time scales.
• (2)Starting from the interfacial water layer, the hydration shell assumes the structure of bulk-like water within a few layers, typically less than five layers. Claims of a significant long-range modification of the structure and dynamics of water around biomolecules lack theoretical and experimental evidence, and they are not supported by experiments mapping time-averaged or transient water structure and dynamics.
• (3)The fastest fluctuations of water structure in the first few water layers occur on a time scale of a few hundred femtoseconds and are mainly related to water’s librational (hindered rotational) degrees of freedom. Water reorientation takes place on a time scale ranging from the ∼2 ps bulk value to several tens of picoseconds and occurs primarily by rapid jumps rather than by reorientational diffusion. The slowing down of water’s structure fluctuations is limited, i.e., on average less than a factor of 5 compared to bulk water, except for those special water molecules with marked spatial constraints such as water located in the minor groove of DNA and/or in clefts of protein surfaces.
• (4)The biomolecular shell hydrogen-bond network rearranges via the large-amplitude jumps executed by water molecules when they exchange hydrogen-bond acceptors. These jumps are retarded by the biomolecular interface, mostly by an entropic, steric factor due to the hindering of the approach of a new acceptor by the interface, and also by an enthalpic factor arising from the strength of the water–biomolecule hydrogen bond to be broken. The jumps occur on time scales ranging from bulk-like values of a few picoseconds for water molecules in well-solvent-exposed sites to several tens of picoseconds in confined and strongly hydrogen-bonded sites.
• (5)The water shell around biomolecules serves as a heat sink for excess energy released in the radiationless decay of electronically excited states and/or vibrational relaxation. Energy transfer from the biomolecule to the hydration shell occurs on subpico- to picosecond time scales, depending on the particular type of excitation, local hydration geometries, and coupling strengths between the low-frequency modes involved. Fully hydrated phosphate groups are particularly efficient “transmitters” of excess energy. In general, energy transfer to the hydration shell competes with the redistribution and spatial transport of energy within a biomolecule which extends well into the picosecond regime with consideration of the molecular energy levels involved in the energy transfer pathways always being required.
• (6)Electric fields at the interface between a biomolecule and its water shell reach values up to 100 MV/cm. Water molecules in the first two hydration layers are a major source of such fields, whose range is limited to a sub-10 Å length scale. The structural fluctuations of the water shell (and of the biomolecule and ion and counterion atmosphere) result in amplitude fluctuations of local electric fields of up to several tens of MV/cm, covering a very broad frequency spectrum up to terahertz frequencies.

Owing to the rich combination of experimental, numerical, and theoretical approaches described in this review, the key features of the dynamics of water around biomolecules are now fairly well understood and found to rely on a small set of general physical principles. This state of affairs represents a major step forward, and this molecular understanding will be instrumental in addressing two challenging arenas in which exciting new developments can be expected.

The first challenge is to gain a comparable understanding of water dynamics in actual biochemical systems. This arena includes, for example, the more physiologically relevant crowded situations found within living cells²²⁰ and water molecules within membrane channels.²⁹⁴ To investigate these very complex systems, experimental techniques with enhanced sensitivity and selectivity will be required. These studies will thus benefit from new experimental techniques combining a sub-Angstrom spatial resolution with femto- to picosecond time resolution in order to map the spatiotemporal dynamics of hydrated biomolecules in a preferably noninvasive way. Time-resolved structure-sensitive methods including femtosecond X-ray diffraction, scattering, and absorption together with electron diffraction can be anticipated to bring major progress in this arena. Such methods will directly provide snapshots of transient hydration structures and insight into transient distributions of electron density, overcoming the feature that the structural interpretation of current optical spectroscopy methods can sometimes be ambiguous. Novel theoretical developments will also be required in several directions. These include, for example, the ability to describe the crowded situations where a water molecule is simultaneously affected by several biomolecules and ions to describe any collective dynamics that are relevant, e.g., dielectric, TDSS, THz, and OKE experiments, and finally to improve our understanding of the interplay between the water H-bond fluctuations and the biomolecular electrostatic interactions.

The second, and arguably most important, challenge related to water dynamics in a biochemical context is to understand the consequences of the perturbed hydration dynamics on the properties and on the function of biomolecules, including their elementary biochemical reactions. While the presence of water is largely considered to be indispensable to life, it is still an open question as to whether water’s dynamics set the time scale of some important biochemical processes. Historically, protein hydration dynamics had been thought to be extremely slow, but the current picture suggests the opposite: that—with the exception of confined protein pocket and narrow DNA grooves—most biomolecular hydration shell rearrangements occur on a time scale that is faster than that of biomolecular motions. Hydration dynamics are thus less likely to be limiting even though they have been recently suggested to be essential, for example, for the lubrication of conformational motions, for protein folding, and for the catalytic activity of enzymes. Such interesting suggestions require careful scrutiny. In this connection, new experimental and theoretical developments will be required to carefully quantify the importance of equilibrium effects, where water lowers the energetic barriers for the processes, but the dynamical hydration shell rearrangements are in fact not limiting. For elementary biochemical reaction steps, any truly dynamical effects need to be discovered and explained. One possibility could arise when the perturbed water dynamics change the translational and rotational friction experienced by a ligand approaching a binding site, thus significantly impacting the rate and possibly the productivity of the biomolecular encounter. Another possibility is that the water dynamics change the local dielectric properties and thus relevant biomolecular electrostatic interactions; this might influence whether important charges can or cannot enter regions required for biomolecular reaction.

We have just addressed only two arenas for the future of water dynamics investigation; no doubt others will be found as the field advances. In any event, we can confidently assert that research in these areas will greatly enhance our understanding of biochemical processes at the molecular level.

Glossary

Abbreviations

2D-IR

two-dimensional infrared

DR

dielectric relaxation

DSE

Debye–Stokes–Einstein

EINS

elastic incoherent neutron scattering

EJM

extended jump model

FFCF

frequency fluctuation correlation function

fs

femtosecond

H bond

hydrogen bond

MD

molecular dynamics

MRD

magnetic relaxation dispersion

NMR

nuclear magnetic resonance

NOE

nuclear Overhauser effect

OKE

optical Kerr effet

PB

Poisson–Boltzmann

PFID

perturbed free-induction decay

ps

picosecond

QENS

quasi-elastic neutron scattering

SANS

small-angle neutron scattering

SAXS

small-angle X-ray scattering

tcf

time-correlation function

TDSS

time-dependent Stokes shift

THz

terahertz

Biographies

Damien Laage’s research interests focus on chemical reactivity and spectroscopy in solutions and biochemical environments. He received his Ph.D. degree in 2001 from Ecole Normale Supérieure (ENS) and University of Paris (UPMC) with James T. Hynes and Monique Martin. He was a postdoctoral fellow at ETH Zürich with Michele Parrinello and in 2002 joined ENS. He is currently CNRS Director of Research and holds a joint appointment as Professor of theoretical chemistry at ENS.

Thomas Elsaesser is a director at the Max-Born-Institute for Nonlinear Optics and Short-Pulse Spectroscopy, Berlin, Germany, and holds a joint appointment as a professor for experimental physics with Humboldt University, Berlin. Ultrafast processes in condensed matter represent his main area of research. He received his Dr. rer. nat. degree from the Technical University of Munich in 1986 and worked there as a research associate until 1993. In 1990, he spent a postdoctoral period at AT&T Bell Laboratories, Holmdel, NJ. He finished his habilitation at the TU Munich in 1991 and joined the newly established Max-Born-Institute in 1993.

James T. Hynes received his A.B. degree from Catholic University in 1965 and his Ph.D. degree from Princeton University with J. M. Deutch in 1969. After an NIH postdoctoral fellowship at MIT with Irwin Oppenheim, he joined the University of Colorado, Boulder faculty in 1971. He is currently Stanley J. Cristol Distinguished Professor of Chemistry and Biochemistry. Since 1999 he has also been CNRS Director of Research at ENS. His research focuses on reaction and allied dynamics in solution and biomolecules and at interfaces.

The authors declare no competing financial interest.