Validation of Aura Microwave Limb Sounder stratospheric water vapor measurements by the NOAA frost point hygrometer

Abstract

Differences between stratospheric water vapor measurements by NOAA frost point hygrometers (FPHs) and the Aura Microwave Limb Sounder (MLS) are evaluated for the period August 2004 through December 2012 at Boulder, Colorado, Hilo, Hawaii, and Lauder, New Zealand. Two groups of MLS profiles coincident with the FPH soundings at each site are identified using unique sets of spatiotemporal criteria. Before evaluating the differences between coincident FPH and MLS profiles, each FPH profile is convolved with the MLS averaging kernels for eight pressure levels from 100 to 26 hPa (~16 to 25 km) to reduce its vertical resolution to that of the MLS water vapor retrievals. The mean FPH – MLS differences at every pressure level (100 to 26 hPa) are well within the combined measurement uncertainties of the two instruments. However, the mean differences at 100 and 83 hPa are statistically significant and negative, ranging from −0.46 ± 0.22 ppmv (−10.3 ± 4.8%) to −0.10 ± 0.05 ppmv (−2.2 ± 1.2%). Mean differences at the six pressure levels from 68 to 26 hPa are on average 0.8% (0.04 ppmv), and only a few are statistically significant. The FPH – MLS differences at each site are examined for temporal trends using weighted linear regression analyses. The vast majority of trends determined here are not statistically significant, and most are smaller than the minimum trends detectable in this analysis. Except at 100 and 83 hPa, the average agreement between MLS retrievals and FPH measurements of stratospheric water vapor is better than 1%.

1. Introduction

Water vapor in the upper troposphere and lower stratosphere (UTLS) plays an influential role in determining the Earth’s climate. Even small variations in the abundance of UTLS water vapor can significantly modulate the flux of outgoing long-wave radiation, prompting responsive changes in global surface temperatures. Solomon et al. [2010] demonstrated that the rapid 10% drop in UTLS water vapor near the end of 2000 [Randel et al., 2006] reduced the global surface warming from long-lived greenhouse gases and aerosols by 25% during 2000–2009. This sensitive connection with climate dictates that UTLS water vapor be closely monitored for changes, especially those that may result from our warming planet.

Historic and contemporary discrepancies between stratospheric water vapor measurements by a number of balloon-, aircraft-, and satellite-based instruments impede our ability to accurately quantify the radiative effects of variations in UTLS water vapor. Weinstock et al. [2009] reported longstanding 1–1.5 ppmv differences between aircraft-based measurements by the Harvard University Lyman-alpha photo-fragment fluorescence hygrometer and those by the Aura Microwave Limb Sounder (MLS), the NOAA frost point hygrometer (FPH), and the cryogenic frost point hygrometer (CFH). A recent comparison of in situ water vapor measurements by aircraft- and balloon-borne instruments during the 2011 Mid-latitude Airborne Cirrus Properties Experiment reveals smaller but statistically significant in situ measurement differences of 0.4–0.8 ppmv (10–20%) [Rollins et al., 2013]. Vömel et al. [2007a] demonstrated good agreement between CFH and NOAA FPH stratospheric water vapor measurements, a result corroborated by Rollins et al. [2013].

MLS water vapor retrievals have been previously compared with measurements by ground- and balloon-based instruments, but earlier versions of MLS retrievals (v1.5 and v2.2) were used (current version is v3.3). Vömel et al. [2007b] compared 1 to 11 CFH profiles obtained at each of 10 different sites during 2005–2007 with coincident MLS soundings. They found (for v2.2) that MLS retrievals and CFH measurements agreed to within 2.7 ± 8.7% over the pressure range 68 to 22 hPa, while at 83 and 100 hPa the mean MLS – CFH discrepancies were 3.6 ± 12.7% and −1.0 ± 9.7%, respectively. Vömel et al. [2007b] also reported large negative mean MLS – CFH differences over the pressure range 316 to 147 hPa and a statistically significant mean difference of −24 ± 16% at 178 hPa, supporting the conclusion of Barnes et al. [2008] of a dry (low) bias in MLS retrievals in the upper troposphere.

2. Instruments

The Global Monitoring Division of NOAA’s Earth System Research Laboratory has monitored UTLS water vapor over Boulder, Colorado (40°N, 105.2°W), since 1980 using balloon-borne FPHs. This 33 year record of >380 high-quality soundings, the longest continuous UTLS water vapor measurement record in existence, depicts a net increase in stratospheric water vapor of ~1 ppmv (27%) over Boulder since 1980 [Oltmans et al., 2000; Scherer et al., 2008; Hurst et al., 2011]. The climate impacts of this long-term increase are uncertain because it is based on only one measurement location in the world.

Since August 2004, the Aura Microwave Limb Sounder (MLS) has been monitoring UTLS water vapor around the globe, making ~3500 profile measurements each day. The FPH and MLS measurement systems are complementary because of the fundamental differences in their capabilities. Frost point hygrometers measure water vapor from the surface to the middle stratosphere at high vertical resolution (5–10 m), but the soundings are infrequent (1–2 per month) and performed at only a few locations around the globe. Satellite-borne remote sensors, specifically limb sounders, can make water vapor measurements at thousands of locations each day but at a vertical resolution of 2–3 km in the lower stratosphere [Lambert et al., 2007]. The combination of infrequent and geographically sparse FPH measurements at high vertical resolution with temporally and spatially dense near-global satellite measurements at coarse vertical resolution provides independent corroboration of observed variations in UTLS water vapor. Given the importance of accurate long-term measurement records of UTLS water vapor to radiative transfer and climate models, it is essential to routinely perform comparisons of satellite- and sonde-based water vapor measurements to check for drifts in their calibrations.

2.1. NOAA Frost Point Hygrometer (FPH)

The NOAA FPH is a compact, lightweight, balloon-borne instrument capable of measuring atmospheric water vapor from the very moist planetary boundary layer to the extremely dry middle stratosphere. Frost point hygrometry relies on the growth and subsequent control of a thin layer of ice on a temperature-controlled mirror. Frost coverage on the mirror, monitored by an infrared LED beam coupled with a photodiode detector, is controlled using Proportional-Integral-Derivative logic. The frost point temperature is attained when the frost layer on the mirror is stable, signaling equilibrium between the ice surface and water vapor in the overlying air. Frost point temperatures measured by a thermistor embedded in the mirror are converted to water vapor partial pressures using the Goff-Gratch formulation of the Clausius-Clapeyron equation [Goff, 1957]. Partial pressures are transformed into water vapor mixing ratios using the ambient pressure measured by an accompanying radiosonde.

Though the original design of the NOAA FPH has been improved upon throughout the years, the fundamental measurement principle and calibration procedure have remained the same [Mastenbrook and Oltmans, 1983; Oltmans and Hofmann, 1995; Oltmans et al., 2000; Vömel et al., 1995]. Frost point hygrometry provides a valuable advantage to the long-term monitoring of water vapor; the only calibration required is that of the thermistor in each mirror. No water vapor calibration standards or scale are required, as these are difficult to accurately produce and maintain for decades. Each batch of thermistors is carefully calibrated against an NIST-certified temperature probe and a small archive of previously calibrated thermistors. The well-established measurement principle and calibration procedure are conducive to maintaining stable measurement accuracy over the long term.

Frost point measurements are made at a vertical resolution of 5–10 m (every 1–2 s) from the surface to a typical altitude of 27 km (~18 hPa). The accuracy and precision of stratospheric water vapor measurements by the NOAA FPH (Table 1) are estimated as 10% and 4%, respectively [Vömel et al., 1995; Hurst et al., 2011]. An additional source of measurement uncertainty exists during balloon ascent, especially above the tropopause. Surfaces of flight train components (i.e., balloon skin, parachute) may accumulate moisture during transit through the troposphere and later shed it into the ascent path of the FPH, intermittently contaminating the measurements as the instrument swings in and out of the balloon’s wake. For this reason, a pressure-activated valve system has been deployed on many FPH balloons that allows helium to escape before the balloon bursts [Mastenbrook, 1966]. After the valve opens, the ascending balloon slows, reaches neutral buoyancy, and then descends at a controlled rate similar to that of the ascending balloon (5 m s⁻¹). FPH measurements made during controlled descent through the stratosphere are of much higher quality and vertical resolution than those made during instrument free fall after a balloon bursts. Since the FPH is the lead component in the flight train during controlled descent, the measurements are free from contamination and are highly beneficial in revealing any contamination in the ascent profiles. Since August 2004, 63 to 75% of the FPH balloons launched at the three sites have turned around instead of bursting. Some balloons did not have valves and others burst prior to reaching the valve activation pressure.

Table 1.

Precision and Accuracy of Aura Microwave Limb Sounder (MLS) Retrievals and NOAA Frost Point Hygrometer (FPH) Measurements^a

Pressure (hPa)	MLS				FPH		MLS and FPH
	Precisionb		Accuracy		Precisionc	Accuracyd	Precisione		Accuracyf
	%	ppmv	%	ppmv	ppmv	ppmv	%	ppmv	%	ppmv
18	6	0.31	8.3	0.42	0.20	0.51	7.2	0.37	13.0	0.66
22	6	0.30	7	0.35	0.20	0.50	7.2	0.36	12.2	0.61
26	6	0.30	6.3	0.31	0.20	0.50	7.2	0.36	11.8	0.58
32	6	0.29	5.5	0.26	0.19	0.48	7.2	0.34	11.4	0.55
38	6	0.28	4.8	0.22	0.19	0.46	7.2	0.33	11.1	0.51
46	6	0.27	4	0.18	0.18	0.45	7.2	0.32	10.8	0.48
56	7	0.31	5	0.22	0.18	0.44	8.1	0.35	11.2	0.49
68	8	0.34	6	0.25	0.17	0.42	8.9	0.38	11.7	0.49
83	10	0.40	7	0.28	0.16	0.40	10.8	0.43	12.2	0.49
100	15	0.61	8	0.32	0.16	0.40	15.5	0.63	12.8	0.52

^aAll precision and accuracy estimates in mixing ratio units (ppmv) are the products of relative (%) precision and accuracy estimates and the mean stratospheric water vapor mixing ratios measured by MLS at each retrieval pressure level during 2004–2012.

^bMLS single profile precision and accuracy values in % units from Livesey et al. [2013].

^cFPH stratospheric measurement precision estimate of 4% from Hurst et al. [2011].

^dFPH stratospheric measurement accuracy estimate of 10% from Vömel et al. [1995].

^eMLS and FPH precision values combined in quadrature.

^fMLS and FPH accuracy values combined in quadrature.

During the comparison period evaluated here (August 2004 through December 2012), there were 135 FPH flights from Boulder (Table 2). Monthly FPH flights were initiated at Lauder, New Zealand (45.0°S, 169.7°E), in August 2004, and that record includes 97 high-quality soundings during the comparison period. Hilo, Hawaii (19.7°N, 155.1°W), was established as a NOAA FPH sounding site in December 2010, and a total of 24 flights are available for this comparison.

Table 2.

MLS Overpass Coincidences with FPH Flights

FPH Site	FPH Flights Na	Criteria Set #1		Criteria Set #2		Common Flights Nd
		Flights Nb	Profiles Nc	Flights Nb	Profiles Nc
Boulder	135	115	634	130	1294	111
Hilo	24	23	105	23	193	23
Lauder	97	96	352	95	929	94

^aNumber of FPH flights at each site, August 2004 – December 2012.

^bNumber of FPH flights where at least one MLS profile meets the specified set of coincidence criteria.

^cNumber of MLS profiles meeting the specified set of coincidence criteria.

^dNumber of FPH flights where at least one MLS profile meets both sets of coincidence criteria.

2.2. Aura Microwave Limb Sounder

The Microwave Limb Sounder (MLS) on the Earth Observing System Aura satellite has provided quasi-global (82°S–82°N) UTLS water vapor measurements since August 2004. MLS views thermal microwave emission from the atmosphere at 183.31 GHz as it scans the Earth’s limb from near the surface to 90 km, making ~3500 profile measurements each day at latitude intervals of ~1.5° [Lambert et al., 2007; Read et al., 2007]. Water vapor is retrieved from the measured radiances at 55 different pressure levels, from 316 hPa to well above 0.1 hPa. From 100 to 18 hPa, there are 10 retrieval levels (Table 1) at evenly spaced pressure levels in log(P) space. Retrievals from 18 to 46 hPa carry a single profile precision value of 6% that grows with pressure to 15% at 100 hPa. The optimal measurement accuracy of 4% at 46 hPa degrades above and below, to 8% at both 18 and 100 hPa (Table 1).

This paper utilizes the MLS version 3.3 station overpass data files for Boulder, Hilo, and Lauder that are downloadable from the Aura validation data center (AVDC) at http://avdc.gsfc.nasa.gov/index.php?site=709508733&id=41&go=list&path=/H2O. The data in these files are quality assured by the AVDC team using status flags, quality flags, and precision and convergence values. The files include only overpasses within ±5° latitude and ±8° longitude of each of the ~80 sites for which they are written. For each of the three NOAA FPH sites, these spatial criteria identify a “cluster” of 1–7 (mean = 6) coincident MLS profiles for each FPH flight. The mode and mean of time intervals between coincident MLS overpasses of a NOAA FPH site are 12 and 16 h, respectively.

3. Data Selection and Reduction Methods

FPH profiles are compared to MLS water vapor retrievals at eight pressure levels from 100 to 26 hPa. At altitudes below 100 hPa, roughly the pressure at the summertime tropopause over Boulder, comparisons of only measurement disparities become difficult because UT water vapor is variable on time and length scales similar to or less than the spatiotemporal differences between coincident MLS and FPH profiles (see below for coincidence criteria). In other words, there is little assurance that FPH and MLS measurements made several hours and hundreds of kilometers apart actually sampled the same UT air mass.

Water vapor measurements by the FPH and MLS differ substantially in their spatiotemporal densities and vertical resolution, requiring that their data be horizontally and temporally matched and the balloon measurements vertically averaged before conducting a comparison. First, the MLS overpass data must be filtered to include only those profiles close in space and time to the FPH flights. Second, the vertical resolution of the FPH profiles must be reduced to that of the MLS profiles in a way that simulates the MLS retrieval method.

3.1. Criteria for MLS Coincidences With FPH Flights

For this study, two unique sets of temporal and spatial criteria are applied to the MLS overpass data to identify two clusters of profiles that are coincident with each FPH flight. Both sets of criteria employ a more stringent latitude difference requirement than the ±5° used to construct the AVDC station overpass data files. This assures smaller meridional separations between coincident MLS and FPH profiles while typically maintaining 4–10 MLS profiles in each coincidence cluster.

Criteria set #1 requires that an MLS profile was obtained within 16 h of the FPH launch time and was located within ±2° of latitude (±223 km) and ±8° of longitude of the FPH launch site. The longitude criterion translates to zonal distance requirements of ±680 km from Boulder, ±840 km from Hilo, and ±630 km from Lauder. The temporal requirement of <16 h was implemented to purposefully include data from two to three coincident MLS overpasses of each site for most FPH flights (see end of section 2.2). In comparing CFH and MLS profiles, Vömel et al. [2007b] required temporal and spatial differences <6 h and <300 km but found no changes to the results when these constraints were relaxed to <12 h and <900 km. Criteria set #1 identifies at least one coincident MLS profile for 115 of the 135 FPH flights launched at Boulder from August 2004 through December 2012 (Table 2). At least one coincident MLS profile is identified for 23 of 24 FPH flights at Hilo and for 96 of 97 flights at Lauder. Overpass clusters generated by criteria set #1 are comprised of an average of 5.5, 4.6, and 3.7 MLS profiles coincident with each FPH flight at Boulder, Hilo, and Lauder, respectively.

Criteria set #2 requires time differences <16 h, meridional and zonal distance differences <500 and <1000 km, respectively, and a <5° difference between the average equivalent latitudes of the MLS and FPH profiles between 70 and 30 hPa. The equivalent latitude criterion ensures that the stratospheric air masses measured by the MLS and FPH have similar dynamical histories [e.g., Manney et al., 2007]. The less rigorous meridional and zonal distance requirements of this criteria set identify 80–170% more coincident MLS profiles per overpass cluster than criteria set #1 (Table 2).

Instead of comparing each FPH profile to all of the MLS profiles in the coincident cluster, each cluster is condensed into a single profile composed of the median value of the cluster mixing ratios at each of 10 MLS retrieval pressures (100–18 hPa). Here it is beneficial to employ median instead of mean values because the former are far less sensitive to anomalous retrievals than the latter. Each FPH profile is now compared to a single MLS median profile from each coincidence group. The typical variability (standard deviation) of MLS retrievals at each pressure level within a coincidence cluster is depicted by error bars on the example MLS median profiles (Figure 1).

Figure 1.

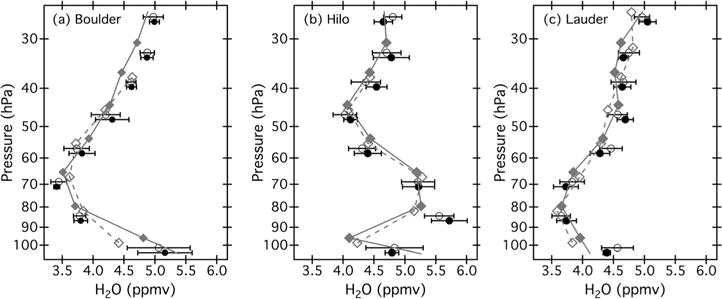
Examples of Aura Microwave Limb Sounder (MLS) median and convolved NOAA frost point hygrometer (FPH) water vapor profiles at eight MLS retrieval pressures from 100 to 26 hPa (logarithmic pressure scale) over (a) Boulder, (b) Hilo, and (c) Lauder. MLS median profiles from coincidence groups #1 and #2, depicted as filled black circles and open black circles, respectively, have horizontal error bars spanning ±1 standard deviation. FPH-AK profiles A and B (filled gray diamonds and open gray diamonds) are connected with solid and dashed gray lines, respectively. Markers bunched at each of the MLS retrieval pressures are slightly offset in the vertical to improve their visibility. See Table 1 for a list of MLS retrieval pressures.

Before comparing MLS and FPH profile data, the two groups of MLS median profiles created by the two sets of coincidence criteria are compared to one another to check for biases that might arise from the criteria differences. For Boulder, Hilo, and Lauder, there are 111, 23, and 94 FPH flights common to both groups (#1 and #2) of MLS median profiles, accounting for 85–100% of all FPH flights with at least one coincident MLS profile (Table 2). MLS median profiles common to the groups #2 and #1 are subtracted (denoted MLS – MLS), and the mean differences are computed at each retrieval pressure (Table 3 and Figure 2). Differences outside the 99.7% confidence interval (mean ± 3σ) for each pressure level are removed as extreme outliers, excluding 21 (1.9%), 0, and 8 (0.9%) of the MLS median profile values for Boulder, Hilo, and Lauder. Mean differences for each pressure level are recalculated using the slightly smaller data populations.

Table 3.

Mean Differences Between MLS Median Profile Groups and Convolved FPH Profile Groups^a

Pressure(hPa)	Boulder		Hilo		Lauder
	MLS – MLS ΔH2O (ppmv)b	FPH – FPH ΔH2O (ppmv)c	MLS – MLS ΔH2O (ppmv)	FPH – FPH ΔH2O (ppmv)	MLS – MLS ΔH2O (ppmv)	FPH – FPH ΔH2O (ppmv)
18	−0.01 ± 0.02		−0.03 ± 0.04		0.01 ± 0.02
22	−0.02 ± 0.02		0.00 ± 0.05		0.02 ± 0.03
26	−0.01 ± 0.02	−0.07 ± 0.10	0.04 ± 0.04		0.02 ± 0.03	−0.07 ± 0.23
32	0.00 ± 0.02	−0.01 ± 0.03	0.04 ± 0.05	0.03 ± 0.09	0.03 ± 0.02	−0.01 ± 0.05
38	−0.03 ± 0.02	0.05 ± 0.03	−0.01 ± 0.04	−0.02 ± 0.06	0.02 ± 0.02	0.04 ± 0.04
46	−0.02 ± 0.03	0.01 ± 0.03	0.00 ± 0.04	−0.05 ± 0.04	0.01 ± 0.03	0.03 ± 0.04
56	−0.01 ± 0.02	−0.07 ± 0.03	0.01 ± 0.04	−0.04 ± 0.06	0.01 ± 0.03	−0.03 ± 0.04
68	−0.01 ± 0.02	0.04 ± 0.03	0.01 ± 0.09	0.02 ± 0.06	0.00 ± 0.03	−0.01 ± 0.03
83	−0.03 ± 0.04	0.07 ± 0.02	−0.02 ± 0.06	0.03 ± 0.09	0.00 ± 0.03	0.06 ± 0.03
100	0.01 ± 0.04	−0.10 ± 0.04	−0.02 ± 0.08	−0.07 ± 0.11	0.02 ± 0.04	0.02 ± 0.04

^aMean differences presented in bold face type are statistically significant at the 95% level of confidence.

^bMean values ± 95% confidence intervals of differences between the MLS median profiles in coincidence groups #2 and #1.

^cMean values ± 95% confidence intervals of differences between the convolved FPH profiles in groups B and A.

Figure 2.

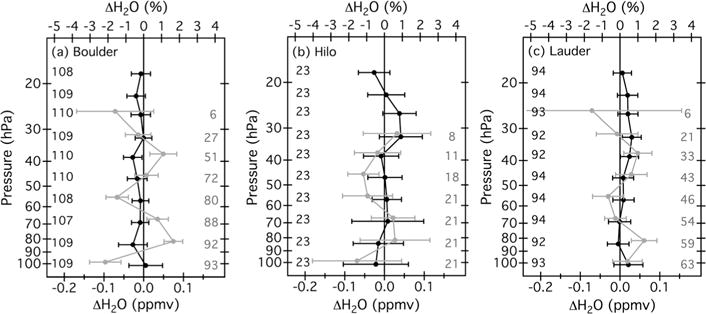
Mean differences between MLS median profile groups #2 and #1 (black) and between the convolved FPH profile groups B and A (gray) at 10 pressure levels from 100 to 18 hPa (logarithmic pressure scale) over (a) Boulder, (b) Hilo, and (c) Lauder. Error bars span the 95% confidence intervals of the mean differences. The numbers of MLS – MLS (black) and FPH – FPH (gray) differences that determine the mean values at each pressure level are listed.

In this paper the statistical significance of mean differences and regression slopes is judged against their 95% confidence intervals. A bias or trend is deemed statistically significant if its absolute value is larger than its 95% confidence interval. Unless otherwise noted, the uncertainty of a bias or trend is expressed as the 95% confidence interval, calculated as the product of the standard error (σ/√N) of the mean difference or trend slope and the Student’s T value (T_0.95,N−1) for a two-tailed normal distribution with 95% probability for N observations. In most cases here, the Student’s T value is ~2. Averages of mean differences or trends across multiple pressure levels, sites, or profile groups are calculated as weighted averages using the 95% confidence intervals as statistical weights. Difference and trend values expressed as percentages are relative to the mean water vapor mixing ratios measured at each retrieval pressure by MLS during 2004–2012. These range from 4.0 ppmv at 100 hPa to 5.1 ppmv at 18 hPa.

For the two groups of median profiles, only the mean MLS – MLS differences at 38 hPa over Boulder and 32 hPa over Lauder are statistically significant (Table 3 and Figure 2), implying that all other mean differences are not significant biases. Averages of mean MLS – MLS differences for the 10 retrieval pressures from 100 to 18 hPa are −0.01± 0.01 ppmv (−0.3 ±0.2%) for Boulder, 0.00± 0.02 ppmv (0.1± 0.3%) for Hilo, and 0.01 ±0.01 ppmv (0.3 ±0.2%) for Lauder. Over this same pressure range, the average magnitudes (absolute values) of mean differences are 0.01 ±0.01 ppmv (0.3± 0.2%) for Boulder, 0.02± 0.02 ppmv (0.4 ±0.3%) for Hilo, and 0.01± 0.01 ppmv (0.3 ±0.2%) for Lauder. Even though there are essentially no statistically significant biases between them, both groups of MLS median profiles will be used to evaluate differences between the FPH and MLS profiles at the three sites.

3.2. FPH Profiles Convolved With MLS Averaging Kernels

Water vapor measurements by the FPH are recorded at a vertical resolution of 5–10 m but are reported in 250 m altitude bins to reduce measurement noise for statistical analyses. For comparison with MLS data, the FPH vertical resolution is degraded to that of the MLS retrievals (~3 km in the lower stratosphere) and placed on the MLS pressure grid using the averaging kernels and forward model smoothing function described by Read et al. [2007]. The MLS averaging kernel for each retrieval pressure level in the lower stratosphere incorporates data from roughly two pressure levels below to two levels above [Lambert et al., 2007]. All profile convolutions performed in this work utilize the MLS averaging kernels for equatorial latitudes rather than the alternative 70°N kernels specifically developed for high northern latitudes. Each convolution is based on a 250 m resolution FPH profile and an a priori estimate of the water vapor profile on the low-resolution MLS grid.

Two different types of a priori and FPH profiles are ingested by the forward model to check for systematic biases between the two groups of convolved FPH profiles, hereinafter designated FPH-AK (averaging kernel) groups “A” and “B.” The a priori profiles for convolution group “A” are the median MLS profiles in coincidence group #1 and for group “B” are the actual a priori profiles used to retrieve the MLS profiles coincident with FPH flights.

The FPH profile data convolved into FPH-AK group “A” are preferentially based on measurements made during balloon descent to minimize the potential influences of intermittent measurement contamination during ascent, as described in section 2.1. No profile interpolations or extrapolations are performed to fill gaps. If there are substantial data gaps in the descent profiles, they are replaced by ascent profiles. The FPH profiles convolved into FPH-AK group “B” combine ascent and descent measurements. Small data gaps in the input profiles are filled by interpolation, but no extrapolations are performed. At each MLS retrieval pressure, the “B” convolutions require that FPH data span 95% of the full pressure range of the averaging kernel; otherwise, no mixing ratio is output for that pressure level in the FPH-AK “B” profile. This provides a safeguard against a potential bias in the convolved profiles due to poor vertical coverage of the input data. Since FPH profiles do not always reach above 26 hPa (~25 km), this substantially reduces the data populations of FPH-AK “B” profiles at the highest altitudes (Figure 2). More than 95% of the group “A” FPH-AK profiles are populated at 26 hPa since they were convolved without this data coverage requirement.

Differences between the two groups of convolved FPH profiles (denoted FPH – FPH) are evaluated for statistical biases that could result from the dissimilar a priori and FPH profiles ingested by the forward model. The 99.7% (3σ) confidence interval test described above is used to exclude 9 (1.7%), 0 and 4 (1.2%) extreme outlier values from the FPH-AK profiles for Boulder, Hilo, and Lauder. Mean differences for each pressure level are then recalculated (Table 3 and Figure 2). Note that the paucity of data in the FPH-AK “B” profiles at 26 hPa over Boulder and Lauder and at 32 hPa over Hilo (Figure 2) diminishes the statistical meaning of comparison results for these levels.

Averages of the FPH – FPH mean differences for the eight pressure levels (100 to 26 hPa) are 0.01 ± 0.01 ppmv (0.2 ± 0.2%) for Boulder and 0.02 ± 0.01 ppmv (0.3 ± 0.3%) for Lauder. For 100 to 32 hPa above Hilo, the mean differences average −0.02 ± 0.02 ppmv (−0.5 ± 0.5%). The magnitudes of mean differences average 0.05 ± 0.01 ppmv (1.1 ± 0.2%) for Boulder, 0.04 ± 0.02 ppmv (0.9 ± 0.5%) for Hilo, and 0.03 ± 0.01 ppmv (0.7 ± 0.3%) for Lauder. These are 2–4 times the average magnitudes of MLS – MLS differences. Eight of the FPH – FPH mean differences are statistically significant (Table 3 and Figure 2) compared to only two for the MLS – MLS differences. Disparities between the convolved profiles in groups “A” and “B” are predominantly caused by mixing ratio differences as great as 0.03 ppmv (0.7%) between the two groups of input FPH profiles.

4. FPH – MLS Bias Evaluations

Differences between the convolved FPH and MLS median profiles (denoted FPH – MLS) are evaluated for statistical biases at each of eight pressure levels from 100 to 26 hPa. Four unique combinations of FPH-AK profile groups A and B with MLS median profile groups 1 and 2 are analyzed to ascertain whether significant biases between FPH and MLS measurements (if any) stem from the choice of MLS coincidence criteria or FPH profile convolution methods. The pairing of FPH-AK profile group B with MLS median profile group 1 creates group “B1” of FPH – MLS differences by uniting the more stringent spatial requirements for coincidence with the stricter >95% FPH data coverage safeguard for the convolved FPH profiles. This produces the smallest group of FPH – MLS differences meeting the combined criteria, especially at the highest altitudes. Merging the less rigorously defined MLS median profile group 2 with FPH-AK group A (without the data coverage safeguard) creates group A2 of FPH – MLS differences. The other difference groups (A1 and B2) are also analyzed in an attempt to reveal which procedure, the identification of coincident MLS profiles or the convolution of FPH profiles, plays a greater role in determining the FPH – MLS differences.

For each FPH flight, the MLS median profile is subtracted from the convolved FPH profile. The mean difference over all flights is then calculated at each of the eight MLS retrieval pressures from 100 to 26 hPa (Figure 3 and Table 4). At each pressure level, extreme outliers in the four groups of FPH – MLS differences, identified by the 99.7% (3σ) confidence interval test, are removed to exclude at most 1.4% of the FPH – MLS differences at each site from further evaluation.

Figure 3.

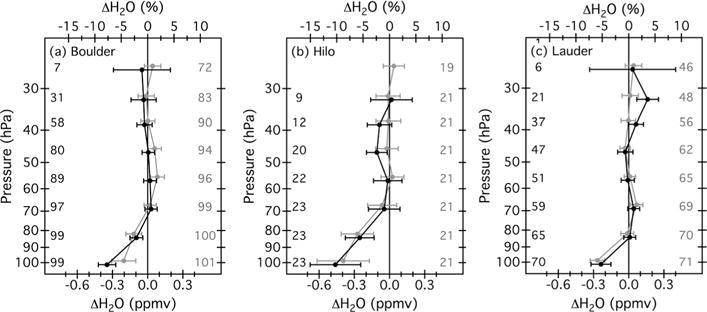
Mean FPH – MLS differences for profile groups B1 (black) and A2 (gray) at eight pressures from 100 to 26 hPa over (a) Boulder, (b) Hilo, and (c) Lauder. Error bars span the 95% confidence intervals of the mean differences. The numbers of FPH – MLS differences in profile groups B1 (black) and A2 (gray) that determine the mean values at each pressure level are listed.

Table 4.

Mean Differences Between Convolved FPH Profiles and MLS Median Profiles^a

Pressure(hPa)	Boulder		Hilo		Lauder
	B1 ΔH2O (ppmv)b	A2 ΔH2O (ppmv)c	B1 ΔH2O (ppmv)	A2 ΔH2O (ppmv)	B1 ΔH2O (ppmv)	A2 ΔH2O (ppmv)
26	−0.05 ± 0.24	0.04 ± 0.07		0.04 ± 0.09	0.03 ± 0.37	0.04 ± 0.07
32	−0.03 ± 0.11	−0.01 ± 0.07	0.02 ± 0.18	−0.01 ± 0.10	0.16 ± 0.09	0.01 ± 0.07
38	−0.03 ± 0.07	0.00 ± 0.06	−0.09 ± 0.11	−0.01 ± 0.11	0.06 ± 0.06	0.00 ± 0.06
46	0.01 ± 0.05	0.06 ± 0.06	−0.11 ± 0.09	−0.02 ± 0.10	−0.03 ± 0.07	−0.03 ± 0.05
56	0.02 ± 0.06	0.08 ± 0.06	0.03 ± 0.12	0.03 ± 0.10	−0.01 ± 0.06	0.01 ± 0.05
68	0.03 ± 0.05	0.02 ± 0.05	−0.05 ± 0.13	−0.06 ± 0.12	0.04 ± 0.05	0.07 ± 0.05
83	−0.10 ± 0.05	−0.12 ± 0.07	−0.25 ± 0.12	−0.27 ± 0.14	0.01 ± 0.05	−0.01 ± 0.06
100	−0.35 ± 0.07	−0.21 ± 0.10	−0.46 ± 0.22	−0.40 ± 0.22	−0.24 ± 0.28	−0.27 ± 0.06

^aMean differences presented in bold face type are statistically significant at the 95% level of confidence.

^bMean values ± 95% confidence intervals of the FPH – MLS differences in profile group B1.

^cMean values ± 95% confidence intervals of the FPH – MLS differences in profile group A2.

Each of the B1 and A2 mean differences at 100 and 83 hPa represents statistically significant biases except those at 83 hPa over Lauder (Figure 3 and Table 4). Mean B1 and A2 differences at 100 hPa over all three sites average −0.29 ± 0.04 ppmv (−6.3 ± 0.8%) and at 83 hPa over Boulder and Hilo average −0.13 ± 0.04 ppmv (−2.9 ± 0.8%). The mean differences at 100 and 83 hPa are systematically negative, larger than most of the mean differences at other pressure levels, and consistent between the B1 and A2 groups, indicating a wet (high) bias in the MLS retrievals.

From 68 to 26 hPa, there are four statistically significant mean differences for the B1 and A2 profile groups, but these are scattered among various pressure levels over different sites, and their statistical significance is inconsistent between the B1 and A2 groups (Table 4). Averages of the mean differences at six pressure levels from 68 to 26 hPa range from −0.07 ± 0.05 ppmv (−1.5 ± 1.2%) for the B1 group at Hilo to 0.03 ± 0.03 ppmv (0.8 ± 0.6%) for the B1 group at Lauder. Across the B1 and A2 groups at all three sites, the mean FPH – MLS differences (68 to 26 hPa) average 0.02 ± 0.01 ppmv (0.4 ± 0.3%) with a mean magnitude of 0.03 ± 0.01 ppmv (0.8 ± 0.3%). The 95% confidence intervals of the B1 mean differences are considerably larger at 32 and 26 hPa because of the low data populations of the FPH-AK group B profiles at these highest altitudes.

The general lack of statistically significant biases between the FPH and MLS over the 68 to 26 hPa pressure range implies that the measurement errors of both instruments are random or systematically smaller than the variability of FPH – MLS differences. The mean FPH – MLS differences determined here demonstrate considerably better agreement than the 2.7% reported for the CFH and MLS at these pressures by Vömel et al. [2007b]. However, note that these previously reported comparisons relied on only 1–11 CFH profiles at each of 10 different sites and were based on the previous version (2.2) of MLS retrievals.

At all pressure levels, the mean differences for the A1 and B2 profile groups (not shown) are very similar to those of the A2 and B1 groups, respectively. Mean differences for groups A1 and B2 at 100 hPa over all three sites average −0.28 ± 0.04 ppmv (−6.1 ± 0.8%) and at 83 hPa over Boulder and Hilo average −0.15 ± 0.04 ppmv (−3.2 ± 0.8%), in excellent agreement with the mean differences for groups B1 and A2. All statistically significant mean differences for groups A2 and B1 are also statistically significant for groups A1 and B2, respectively. In fact, with the exception of 32 hPa over Boulder, the site-specific A2 and A1 mean differences and the B1 and B2 mean differences at each pressure level are statistically indistinguishable (within their uncertainties). This evaluation of all four groups of mean differences implies that disparities between the convolved FPH profile groups A and B, not between the MLS coincident profile groups 1 and 2, are the predominant influences in determining the FPH – MLS differences. This conclusion is supported by the average magnitudes of FPH – FPH differences being 2–4 times the average magnitudes of MLS – MLS differences (Table 3).

The significant negative FPH – MLS differences at 83 hPa over Boulder and Hilo and at 100 hPa over the three sites signify that the MLS mixing ratios retrieved at these pressure levels are generally greater than those measured by the FPH (Figures 1b–1c). Vömel et al. [2007b] reported mean MLS – CFH differences of 3.6% and −1.0% at 83 and 100 hPa, respectively, that were not statistically significant, but again their comparison was based on version 2.2 of MLS retrievals and far fewer profiles. The mean FPH – MLS differences as large as 0.46 ppmv (10%) found here for pressure levels near the tropopause have important implications for radiation transfer and climate models. Solomon et al. [2010] concluded that the rapid 10% decrease in stratospheric water vapor after the year 2000 reduced by 25% (0.1 W m⁻²) the radiative forcing expected from other long-lived greenhouse gases. The FPH – MLS measurement biases revealed here are suggestive of a 10% inaccuracy in near-tropopause water vapor abundance that would lead to significant uncertainties when estimating the attenuation of outgoing long-wave radiation by UTLS water vapor.

Ignoring the B1 mean differences at 26 hPa, the variability of FPH – MLS differences at 100 and 83 hPa is generally greater than at higher altitudes (Table 4). This may be in part due to degradation of the MLS measurement precision with increasing pressure, from 6–8% at 68–18 hPa to 10% at 83 hPa to 15% at 100 hPa (Table 1). It is also likely that spatiotemporal mismatches between “coincident” MLS and FPH profiles contribute to the increased variability of differences, especially at 83 and 100 hPa where the greatest potential exists for upper tropospheric air masses to influence water vapor mixing ratios.

Tropopause pressures above Hilo averaged (±1σ) 118 ± 32 hPa during the FPH flights studied here while those above Boulder and Lauder averaged 182 ± 49 and 230 ± 34 hPa, respectively. Therefore, the water vapor mixing ratios at 100 and 83 hPa over Hilo are the most likely to be influenced by upper tropospheric air masses, followed by Boulder. With the lowest altitude tropopause, Lauder is least likely to be affected. These hypotheses are supported by the sizes of the uncertainties of mean FPH – MLS differences at the three sites (Table 4). Intuitively, the more variable mixing ratios of UT air masses will widen the variability of FPH – MLS differences at the highest pressure levels (Figure 3), but this should not cause the large biases at these pressures. Water vapor gradients in the UT are often steep; mixing ratios can increase by an order of magnitude from the tropopause to 1–2 km below. Though the MLS retrievals and convolved FPH profiles at 100 and 83 hPa should analogously incorporate data at higher and lower pressures, even small differences in the UT region of steep water vapor gradients could lead to sizeable disparities. It is also possible that the use of equatorial MLS averaging kernels to convolve the Boulder and Lauder FPH profiles (alternative kernels are for northern polar latitudes) could produce some discrepancies, but this conjecture is unsupported by similarity of FPH – MLS differences at 100 hPa over Boulder (40°N), Hilo (20°N), and Lauder (45°S).

All but three B1 and A2 mean differences for the eight pressure levels from 100 to 26 hPa (Table 4) are within the estimated accuracy limits of the MLS retrievals (Table 1) that range from 0.18 to 0.42 ppmv (4.0 to 8.3%). The exceptions are for 100 hPa over Boulder and Hilo where statistically significant mean FPH – MLS differences are large and negative. Without exception, the mean differences in Table 4 are within the combined FPH and MLS accuracy estimates that range from 0.48 to 0.66 ppmv (10.8 to 13.0%). On average, the 95% confidence intervals in Table 4 are ~30% of the estimated MLS precision values and ~25% of the combined FPH and MLS precision estimates. Only one 95% confidence interval (for B1 at 32 hPa over Lauder) exceeds the MLS precision estimate (Table 1), but the large standard error at that level is an artifact of the small number of data points (N = 6) that comprise the mean FPH – MLS difference.

It may be possible to reduce the variability of FPH – MLS differences at 83 and 100 hPa by tightening the spatiotemporal coincidence criteria, but this would increase the standard errors of mean FPH – MLS differences as the number of MLS profiles decreases, making it more difficult to expose statistically significant biases. The computation and use of median MLS mixing ratio profiles in this study serve to minimize the chances that an anomalous MLS profile can skew the FPH – MLS differences. Although it would be informative to differentiate between the contributions of measurement imprecision and less than perfect FPH and MLS coincidences to the variability of FPH – MLS differences, such an analysis is beyond the scope of this paper.

5. FPH – MLS Trend Evaluations

To determine accurate trends in UTLS water vapor, it is imperative that any drift in sensor calibration is either small relative to real atmospheric changes or quantitatively well understood and therefore accurately removable from the observations. The calibration of MLS depends on regular assessments of instrumental diagnostics and ground-truth validation, some of which can be provided by FPH profiles. Statistically significant biases between the MLS retrievals and FPH measurements at 100 and 83 hPa are revealed above. Here we analyze FPH – MLS differences at the three sites for temporal trends that might indicate a time-dependent calibration drift in one or both of these sensors.

Trend analyses are performed independently at each MLS retrieval pressure level over each site using weighted linear regression analyses of time series of FPH – MLS differences. All four groups of FPH – MLS differences are analyzed for trends to check the consistency of results. Reciprocals of the squares of the total uncertainties of FPH – MLS differences for individual flights are employed as statistical weights for the regression fits. Total uncertainties are the combination (in quadrature) of the standard errors of MLS median mixing ratios within each overpass cluster and the FPH measurement accuracy estimate for each pressure level (Table 1). The total uncertainties for B1 differences at 46 hPa over each site are depicted by error bars in Figure 4. Initial fits of each time series expose a small number of extreme outliers with residuals outside the 99.7% (3σ) confidence interval. These are removed and the time series refit to generate the regression slopes and their uncertainties in Tables 5 and 6 and Figure 5.

Figure 4.

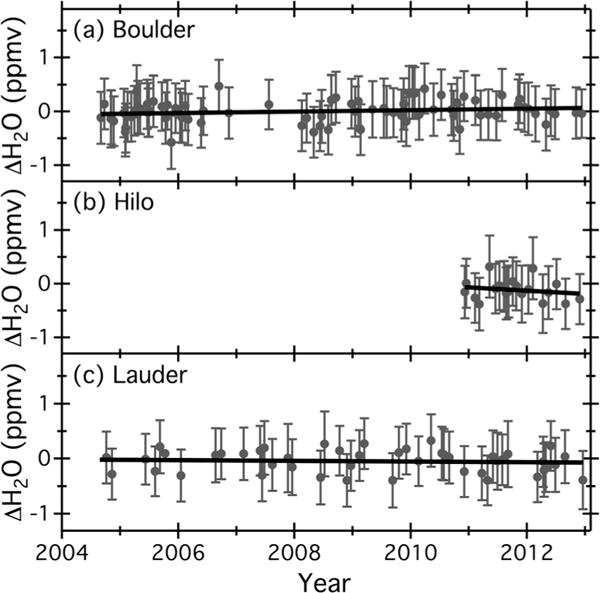
Linear trends in the FPH – MLS differences of profile group B1 at 46 hPa, as determined by weighted regression fits. Error bars depict the uncertainties of the FPH – MLS differences that provide statistical weights for the fits. Regression slopes and their uncertainties are presented graphically in Figure 5 and numerically in Tables 5 and 6.

Table 5.

Temporal Trends of FPH –MLS Differences in Profile Group B1^a

Pressure(hPa)	Boulder		Hilo		Lauder
	Trendb (ppmv yr−1)	Uncertaintyc (ppmv yr−1)	Trend (ppmv yr−1)	Uncertainty (ppmv yr−1)	Trend (ppmv yr−1)	Uncertainty (ppmv yr−1)
26	0.11	0.26			0.09	0.23
32	0.07	0.08	−0.01	0.79	0.02	0.10
38	0.03	0.05	0.18	0.72	0.01	0.08
46	0.01	0.04	−0.06	0.41	−0.01	0.06
56	0.02	0.04	−0.04	0.39	−0.01	0.06
68	0.00	0.04	−0.12	0.38	0.00	0.05
83	0.01	0.04	−0.06	0.39	−0.01	0.05
100	0.04	0.04	−0.01	0.40	−0.03	0.05

^aNone of the trends are statistically significant at the 95% level of confidence.

^bTrends are slopes of weighted linear regression fits to FPH – MLS differences in profile group B1.

^cTrend uncertainties are the 95% confidence limits of regression slopes.

Table 6.

Temporal Trends of FPH – MLS Differences in Profile Group A2^a

Pressure(hPa)	Boulder		Hilo		Lauder
	Trendb (ppmv yr−1)	Uncertaintyc (ppmv yr−1)	Trend (ppmv yr−1)	Uncertainty (ppmv yr−1)	Trend (ppmv yr−1)	Uncertainty (ppmv yr−1)
26	0.04	0.04	0.06	0.44	0.03	0.06
32	0.04	0.04	0.09	0.41	0.02	0.05
38	0.05	0.04	0.08	0.40	0.01	0.05
46	0.04	0.04	0.13	0.39	0.02	0.05
56	0.01	0.04	0.02	0.39	0.01	0.05
68	0.01	0.04	−0.16	0.39	−0.02	0.05
83	0.03	0.04	−0.05	0.41	−0.02	0.05
100	0.04	0.04	0.11	0.41	−0.01	0.05

^aTrends presented in bold face type are statistically significant at the 95% level of confidence.

^bTrends are the slopes of weighted linear regression fits to FPH – MLS differences in profile group A2.

^cTrend uncertainties are the 95% confidence intervals of regression slopes.

Figure 5.

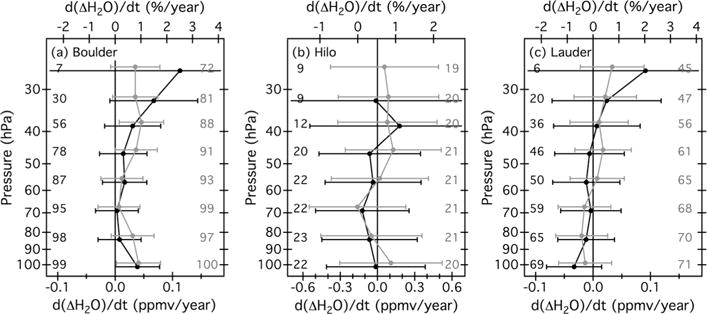
Slopes of the regression fits to the B1 (black) and A2 (gray) groups of FPH – MLS differences at eight MLS retrieval pressures from 100 to 26 hPa over (a) Boulder, (b) Hilo, and (c) Lauder. Note that the x axis range for Hilo is much larger than for Boulder and Lauder. Error bars span the 95% confidence intervals of the regression slopes. The numbers of FPH – MLS differences in groups B1 (black) and A2 (gray) employed in the regression fits at each pressure level are listed.

Except for the A2 differences at 100 and 38 hPa over Boulder, none of the regression slopes in Tables 5 and 6 and Figure 5 depict statistically significant temporal trends in FPH – MLS differences. For each site, the slopes for the B1 and A2 groups are statistically indistinguishable (within the uncertainties) at every pressure level, demonstrating a high level of consistency in the results. Average slopes for B1 and A2 differences at the eight pressure levels from 100 to 26 hPa are 0.03 ± 0.01 ppmv yr⁻¹ (0.6 ± 0.2% yr⁻¹) over Boulder, 0.0 ± 0.11 ppmv yr⁻¹ (0.0 ± 2.4% yr⁻¹) over Hilo, and 0.0 ± 0.01 ppmv yr⁻¹ (0.0 ± 0.3% yr⁻¹) over Lauder (Figure 5). Slopes for the A1 and B2 differences (not shown) are statistically indistinguishable from the A2 and B1 slopes, respectively. Compared to Boulder and Lauder, the confidence intervals of the slopes for Hilo are on average 8–11 times larger because of the shorter measurement record there.

The results show a near-complete absence of detectable drifts in the MLS and FPH calibrations or implicate similar drifts in both data sets. Though plausible, the notion of similar drifts in the calibrations of both instruments is highly unlikely because the data evaluated in this work are for three locations with dissimilar distributions of UTLS water vapor and other environmental parameters such as temperature. This analysis concludes that the calibrations of stratospheric water vapor measurements by the MLS and FPH have been stable, at least to the levels of uncertainty in the regression slopes, from August 2004 through December 2012.

The minimum magnitudes of trends detectable in this analysis are calculated from the variance and autocorrelation of residuals of the linear regression fits according to equation (3) in Weatherhead et al. [1998]. The detection limits for trends in FPH – MLS differences generally decrease with altitude as both the autocorrelation and variance of residuals diminish. With 8.4 years of data at Boulder and Lauder, the minimum detectable trends for 100–26 hPa average (±1σ) 0.038 ± 0.011 ppmv yr⁻¹ (0.84 ± 0.24% yr⁻¹) and 0.031 ± 0.009 ppmv yr⁻¹ (0.69 ± 0.20% yr⁻¹), respectively. With only 2.1 years of data at Hilo, the average minimum detectable trend is 0.27 ± 0.11 ppmv yr⁻¹ (5.9 ± 2.5% yr⁻¹), 7–9 times those for Boulder and Lauder.

The average magnitudes of trends in FPH – MLS differences for 100 to 26 hPa are 0.03 ± 0.01 ppmv yr⁻¹ (0.6 ± 0.2% yr⁻¹) over Boulder, 0.08 ± 0.11 ppmv yr⁻¹ (1.7 ± 2.4% yr⁻¹) over Hilo, and 0.02 ± 0.01 ppmv yr⁻¹ (0.3 ± 0.3% yr⁻¹) over Lauder. These are all smaller than the average minimum detectable trends presented above. In fact, the vast majority of trends for the FPH – MLS difference groups B1 and A2 are smaller in magnitude than the calculated minimum detectable trends at each pressure level.

Though the vast majority of the FPH – MLS difference trends deduced here are not statistically significant, there may be small but important calibration drifts in one or both data sets that are currently undetectable. Given the demonstrated sensitivity of climate to even small changes in stratospheric water vapor abundance [Solomon et al., 2010], these could have important ramifications for radiative transfer and climate models. With only 8.4 years of FPH – MLS differences at Boulder and Lauder, the undetectable calibration drifts could be as large as 0.8% yr⁻¹ (0.04 ppmv yr⁻¹). For perspective, this value is comparable to the average annual increase of 0.9 ± 0.2% yr⁻¹ (0.04 ± 0.01 ppmv yr⁻¹) in stratospheric water vapor over Boulder since 1980 [Oltmans et al., 2000; Scherer et al., 2008; Hurst et al., 2011]. If the residuals of fits to the Boulder measurement record had the same variances and autocorrelations as those of the fits to FPH – MLS differences, the trend over Boulder would be detectable after 7–10 years. Lowering the minimum detectable trends in FPH – MLS differences to 0.5% yr⁻¹ and 0.1% yr⁻¹ at the three FPH sites will require measurement record lengths of 10–12 years and 30–34 years, respectively. It is therefore imperative that UTLS water vapor measurements by both satellite- and balloon-based instruments continue far into the future if small but radiatively important trends are to be detected.

6. Summary

Stratospheric water vapor retrievals from MLS are compared to NOAA FPH profiles at three sites to evaluate statistical biases between their measurements. Two different sets of spatiotemporal criteria (#1 and #2) for coincidence between FPH flights and MLS overpass profiles identify two clusters of coincident MLS profiles for each FPH flight. Each cluster is distilled into a single MLS median profile for comparison with the FPH profile. At least one coincident cluster of MLS profiles is identified for 115 (Boulder), 23 (Hilo), and 95 (Lauder) FPH flights conducted from August 2004 (December 2010 for Hilo) through December 2012. FPH profiles were convolved with the MLS averaging kernels using two different types of FPH and a priori profiles as input, generating groups “A” and “B” of convolved profiles. Pairing the two groups of coincident MLS profiles with the two groups of convolved FPH profiles creates four unique groups of FPH – MLS differences (A1, A2, B1, and B2).

The FPH – MLS differences for each of the four profile groups are evaluated for biases and temporal trends at eight different MLS retrieval pressures (from 100 to 26 hPa) over each site. Results for the A1 and A2 profile groups are similar, as are results for the B1 and B2 groups, implying that disparities between groups A and B of convolved FPH profiles, not between the MLS coincident profile groups 1 and 2, are the predominant influences in determining the FPH – MLS differences.

Mean FPH – MLS differences for the six MLS retrieval pressures from 68 to 26 hPa average 0.02 ± 0.01 ppmv (0.4 ± 0.3%) across the three sites, with an average magnitude of 0.03 ± 0.01 ppmv (0.8 ± 0.3%). Four of the mean differences for the B1 and A2 profile groups are statistically significant, but these biases are scattered among various pressure levels over different sites, and their statistical significance is inconsistent between the B1 and A2 groups. Over the 68–26 hPa pressure range, the average agreement between MLS retrievals and FPH measurements of stratospheric water vapor is better than 1%.

Statistically significant negative mean FPH – MLS differences as large as 0.46 ppmv (−10%) are revealed at 100 hPa over all three sites and at 83 hPa over Boulder and Hilo. This result is independent of the choice of coincident MLS and convolved FPH profile groups. The biases for 100 hPa over Boulder and Hilo are larger in magnitude than the estimated accuracy of MLS retrievals at this pressure, but none of the mean FPH – MLS differences exceed the combined accuracy estimates of FPH measurements and MLS retrievals (Table 1). It is likely that larger variations in FPH – MLS differences at 100 and 83 hPa are driven by the influences of UT air masses with greater water vapor variability, especially at Hilo and Boulder where mean tropopause pressures during FPH flights were 118 ± 32 and 182 ± 49 hPa, respectively. However, it is not readily apparent how the influences of UT air masses would lead to large biases between the FPH and MLS mixing ratios at these altitudes. These biases generate considerable uncertainties in the abundance of water vapor near the tropopause and thus have important implications for radiative transfer and climate models.

The multiple-year records of FPH – MLS differences at each site are analyzed for temporal trends using weighted linear regression fits. Only two regression slopes for the A2 profile group are statistically significant at the 95% level of confidence. No statistical trends are found for the B1 profile group. The vast majority of regression slopes are smaller in magnitude than the minimum trends detectable in the time series of FPH – MLS differences. Minimum detectable trends in the 8.4 year records at Boulder and Lauder average (±1σ) 0.038 ± 0.011 ppmv yr⁻¹ (0.84 ± 0.24% yr⁻¹) and 0.031 ± 0.009 ppmv yr⁻¹ (0.69 ± 0.20% yr⁻¹), respectively. The average minimum detectable trend over 2.1 years at Hilo, 0.27 ± 0.11 ppmv yr⁻¹ (5.9 ± 2.5% yr⁻¹), is 7–9 times larger because of the much shorter record.

The lack of significant and consistent trends in FPH – MLS differences indicates that the calibrations of MLS and FPH stratospheric water vapor measurements from August 2004 through December 2012 have been stable, at least to the levels of uncertainty in this analysis. The detection of trends with magnitudes as low as 0.5% yr⁻¹ and 0.1% yr⁻¹ will require 10–12 years and 30–34 years of comparison data at each site, respectively. It is therefore imperative that measurements of UTLS water vapor abundance continue well into the future if small but radiatively important trends are to be detected.

In addition to the capability of the FPH and MLS measurement systems to provide complementary information about water vapor changes in the UTLS, the uncertain future of satellite-based water vapor sensors and their ability to produce records with the accuracy and stability of MLS argues strongly for the perpetuation and enhancement of balloon-borne FPH observations. This comparison paper provides assurance that research quality balloon-borne observations of UTLS water vapor compatible with the MLS record can be maintained if a gap should occur in the space-based monitoring capability, albeit with limited geographic coverage. These measurements would be invaluable in tying together the measurement records of MLS and its successor(s) if the temporal overlap between them is short or nonexistent.

Key Points.

• No statistical biases between FPH and MLS H₂O measurements: 68 to 26 hPa

• Significant biases between FPH and MLS H₂O measurements at 83 and 100 hPa

• No significant temporal changes in FPH-MLS measurement differences 2004–2012