Effects of reflex delays on postural control during unstable seated balance

Abstract

Patients with low-back pain (LBP) exhibit longer trunk muscle reflex latencies and poorer postural control than healthy individuals. We hypothesized that balance during a simulated postural control task would become impaired when the delays exhibited by LBP patients were incorporated into neuromuscular control. The task chosen for this investigation was seated balancing, which emphasizes trunk muscles’ contribution in postural control. This task was modeled in Simulink^™ as a fourth order linearized dynamic system with feedback delays. Optimization (minimizing error between experimental and model data) of state variables was used to determine neuromuscular control parameters. Experimental data were obtained from 7 subjects during 5 perturbation trials while balancing on the seat with eyes closed. Model accuracy, reflecting the ability of the model to capture the dynamics of seated balance, was correlated with seated balance performance (r = 0.91, p<0.001). To minimize the risk of erroneous findings from inaccurate modeling, only the best five balancers’ data were used for hypothesis testing. In these five subjects, feedback delays in modeled neuromuscular control were increased to determine their effect on task stability, trunk displacement and trunk moment. Simulations showed that longer delays found in LBP, in general, did not produce unstable balancing, but did result in increased trunk displacement (p<0.001) and trunk moment (p = 0.001). This impairment in neuromuscular control in chronic LBP patients could possibly exacerbate their condition by increasing tissue strain (more spinal displacement) and stress (more spinal loading).

1. Introduction

The human spine is a complex mechanical structure which is inherently unstable. In vitro experimentation on the lumbar spine has demonstrated that an osteoligamentous spine (spine devoid of muscles) buckles under a 90N (~20 lbs) load (Crisco et al., 1992). Clearly, without trunk muscles and the resistance they provide, the spine is incapable of supporting any significant load, or for that matter, simply the mass of the upper body (McGill, 2002).

Most modeling approaches investigating spinal stability have been limited to static models in which the potential energy of the system is evaluated during an infinitesimally small deflection to determine if the system is at a relative minimum of the potential energy (Bergmark, 1989; Crisco and Panjabi, 1991; Gardner-Morse et al., 1995; Cholewicki and McGill, 1996; Granata and Marras, 2000). These models have been useful particularly for illustrating the need to have highly orchestrated trunk muscle recruitment to maintain stability in a multi-segment, multi-degrees-of-freedom spine (Bergmark, 1989). However, these models do not account for timing of muscle activation and its effect on stability. Timing, and in particular delays in controlling a system, can have a profound effect on its performance, and if the delays are significant, will lead to instability.

There is growing evidence that people with low-back pain (LBP) have longer reflex delays than healthy individuals (Magnusson et al., 1996; Wilder et al., 1996; Radebold et al., 2000; Reeves et al., 2005). And more recently, it has been shown that athletes with longer reflex delays are more likely to suffer a low-back injury (Cholewicki et al., 2005). Although statistically significant, it is unclear if longer delays found in these studies, are clinically relevant. For instance, could these slightly longer delays (ranging upwards of 20ms) explain differences in postural control between LBP patients and healthy individuals (Luoto et al., 1998; Radebold et al., 2001)? In the Radebold study using seated balance, the LBP group had 32% more postural sway than the healthy controls.

Consequently, the goal of this paper was to evaluate the effects of delays on postural control. The task chosen for this investigation was unstable seated balancing, which isolates trunk muscle control in postural stability. Because of the inherently unstable dynamics, this system requires feedback control to maintain stable behavior, and as such provides a useful model for evaluating delays in feedback control loops. Performance indicators for this task were balance stability, and trunk displacement and trunk moment required to stabilize the system. In this experiment, seated balancing was stable when rotational seat displacements were bounded by ±20°, which reflects the rotation limits before the seat’s sides touched down onto the support surface. The current study addressed three questions: do longer feedback delays result in significantly (1) more unstable balance trials, (2) larger trunk displacements, and (3) higher trunk moments?

2. Methods

2.1. Unstable seated balance experiment

2.1.1. Subjects

Seven subjects volunteered for this study and signed the consent form approved by Yale University Human Investigation Committee. Anthropometric data are provided in Table 1.

Table 1.

Subject anthropometric data.

Subject	Sex	Age	Height	Weight	m1	m2	l1	l12	l2	I1	I2
1	M	38	1.78	82.7	43.3	51.8	0.28	0.08	0.25	0.94	1.92
2	F	25	1.70	63.6	34.0	43.0	0.30	0.08	0.17	0.56	1.82
3	F	39	1.68	67	35.9	44.5	0.19	0.12	0.11	0.41	1.78
4	M	36	1.75	78.5	42.1	49.8	0.19	0.125	0.09	0.54	1.82
5	F	35	1.64	54.0	28.9	38.4	0.18	0.12	0.12	0.27	1.68
6	M	49	1.68	83.9	45.9	52.3	0.19	0.08	0.15	0.71	1.85
7	M	28	1.75	77.1	44.3	51.8	0.24	0.02	0.21	0.66	1.85

Symbols correspond to those found in Fig. 2. Note that m₂ and I₂ include the seat. Weight and mass is measured in kg, height and length in meters (m), and inertia is measured in kgm².

2.1.2. Task

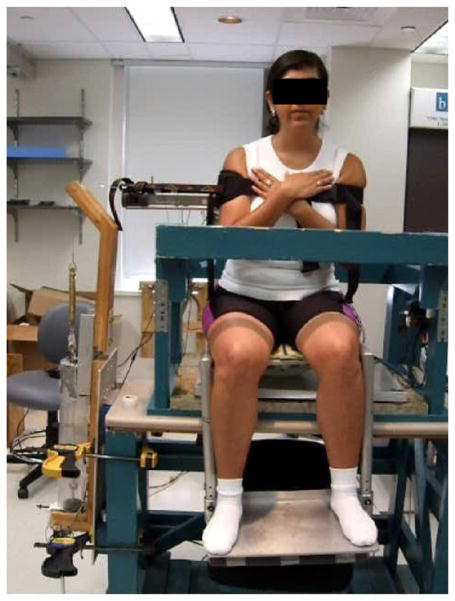
Subjects were placed on a seat equipped with leg and foot supports to prevent any lower body movement (Fig. 1) (Cholewicki et al., 2000). A 40 cm diameter polyester resin half-cylinder was attached to the bottom of the seat that was placed at the edge of a table. The half-cylinder constrained movement to the coronal plane. Each subject was instructed to maintain her/his balance while sitting on the seat with arms crossed. A safety railing around the seat provided security in case of loss of balance.

Fig. 1.

Subject positioned in the unstable seat.

To obtain insight into trunk neuromuscular control, a perturbation was applied to the system and the response to this perturbation was recorded. In this study, we used a perturbation of initial conditions. To apply this perturbation, subjects were instructed to pull against a cable attached to a harness around their trunk at approximately the T7 level. The cable was held by an electromagnet allowing for the generation of resistive force while the magnet was activated. For all trials, the resistive force came from the right side of the subject (Fig. 1). This force was balanced by a displacement of the upper and lower body away from the equilibrium position that generated an equal but opposite pull. Subjects were instructed to maintain a steady tension of 20N on the cable. Verbal feedback was provided to help subjects reach this tension. After some random time interval, the electromagnet was deactivated and the cable released resulting in a system that was no longer in equilibrium. The subject’s response, bringing the system back to the equilibrium position, was recorded.

The Phoenix motion capture system (Visualeyez^™, Phoenix Technology Inc., Burnaby, BC, Canada) tracked the motion of the following segments 1 s before and 7 s after release: the upper body, L4L5 lumbar position, and lower body that included the seat. L4L5 was chosen given the large percentage of lumbar injuries occurring at this level (Smith et al., 1944) and to facilitate anthropometric modeling. Light emitting diodes (LEDs) were placed on the upper trunk approximately at T9, between L4L5 spinous processes, and two LEDs were placed along the back edge of the seat to track movement of the lower body. To capture the release time, one LED was placed on the cable held by the electromagnet. Motion capture data were sampled at 100Hz and were filtered with a 4th order Butterworth filter at 8 Hz. As will be discussed in more detail shortly, the motion of these segments following release was used to set the feedback gains, passive stiffness and damping, and delays for the seated balance model.

Subjects were given 1 min of balance practice with their eyes open and then closed. Next, the harness was placed around the subject, and 5 release trials were performed with their eyes closed. Only successful trials in which the subject was able to maintain balance without having the seat touch down onto the support surface were retained.

To obtain anthropometric data, the position of the subject’s body segments in the seated posture was recorded with the Visualeyez^™ system. Anatomical landmarks were based on Winter (1979). This information was later used to calculate segmental inertial parameters (SIPs) for the upper body mass (mass above L4L5) and lower body mass (mass below L4L5 including the seat). SIPs for all segments except the thorax, abdomen, and thigh were obtained from a proportional anthropometric model (Winter, 1979). SIPs for the thorax, abdomen and thigh were obtained using a geometric model (Yeadon, 1990; Kingma et al., 1996). Segment density data were obtained from Dempster (1967). Moment of inertia of the seat was measured using a pendulum technique (Chandler et al., 1975).

2.2. Unstable seated balance model

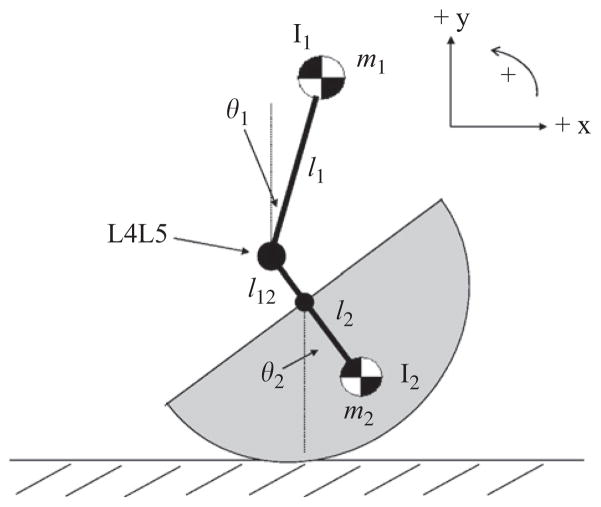
The unstable seated balance system was described by two second order differential equations representing the equations of motion for the upper body mass (m₁) and the lower body mass (m₂) (see Fig. 2). For complex systems, the Euler–Lagrange method is useful for obtaining the equations of motion. Expressions for the kinetic and potential energy for both masses were obtained

Fig. 2.

Simple model of the seated balance system.

2.2.1. Kinetic energy

$$\begin{array}{ll}\hfill {\stackrel{.}{x}}_{m_1}& =l_1{\stackrel{.}{\theta }}_{1}cos{\theta }_1+l_{12}{\stackrel{.}{\theta }}_{2}cos{\theta }_2+r{\stackrel{.}{\theta }}_2\hfill \\ \hfill {\stackrel{.}{y}}_{m_1}& =-l_1{\stackrel{.}{\theta }}_{1}sin{\theta }_1-l_{12}{\stackrel{.}{\theta }}_{2}sin{\theta }_2\hfill \\ \hfill {\stackrel{.}{x}}_{m_2}& =r{\stackrel{.}{\theta }}_2-l_2{\stackrel{.}{\theta }}_{2}cos{\theta }_2\hfill \\ \hfill {\stackrel{.}{y}}_{m_2}& =l_2{\stackrel{.}{\theta }}_{2}sin{\theta }_2\hfill \\ \hfill {\stackrel{.}{p}}_1^2& ={\stackrel{.}{x}}_{m_1}^2+{\stackrel{.}{y}}_{m_1}^2\hfill \\ \hfill {\stackrel{.}{p}}_2^2& ={\stackrel{.}{x}}_{m_2}^2+{\stackrel{.}{y}}_{m_2}^2\hfill \\ \hfill T_1& =\frac{1}{2}{m}_1{\stackrel{.}{p}}_1^2+\frac{1}{2}{I}_1{\stackrel{.}{\theta }}_1^2\hfill \\ \hfill T_2& =\frac{1}{2}{m}_1{\stackrel{.}{p}}_1^2+\frac{1}{2}{I}_1{\stackrel{.}{\theta }}_2^2\hfill \\ \hfill T& =T_1+T_2\hfill \end{array}$$ (1)

where ẋ_m1 and ẏ_m1 are the horizontal and vertical components of the linear velocity of m₁ and ẋ_m2 and ẏ_m2 are the horizontal and vertical components of the linear velocity of m₂. ṗ₁ and ṗ₂ are the linear velocities of m₁ and m₂, respectively. r reflects the radius of the half-cylinder.

2.2.2. Potential energy

$$\begin{array}{ll}\hfill V_1& =m_{1}g(r+l_{1}cos{\theta }_1+l_{12}cos{\theta }_2)+\frac{1}{2}k{({\theta }_2-{\theta }_1)}^2\hfill \\ \hfill V_2& =m_{2}g(r-l_{2}cos{\theta }_2)\hfill \\ \hfill V& =V_1+V_2\hfill \end{array}$$ (2)

where g represents gravity and k represents the passive intervertebral stiffness and intrinsic muscle stiffness at L4L5 prior to force release.

Next, kinetic and potential energy equations were included in the Lagrangian equation.

$$L=T-V$$ (3)

The equations of motion were then derived from the Lagrangian

$$\begin{array}{ll}\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{d}L}{\mathrm{d}{\stackrel{.}{\theta }}_1}-\frac{\mathrm{d}L}{\mathrm{d}{\theta }_1}\hfill & =-\tau \hfill \\ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{d}L}{\mathrm{d}{\stackrel{.}{\theta }}_2}-\frac{\mathrm{d}L}{\mathrm{d}{\theta }_2}\hfill & =\tau \hfill \end{array}$$ (4)

where τ represents the torque input from trunk neuromuscular control about L4L5. As will be discussed shortly, τ is comprised of feedback gains for the four state variables passing through feedback delays, reflecting non-intrinsic contributions to neuromuscular control. The four state variables used to stabilize the system were upper body displacement and velocity, and lower body displacement and velocity.

Linearizing the non-linear equations around the equilibrium state, the equations of motion can be expressed as

$$\begin{array}{l}\left[\begin{array}{cc}{m}_1{l}_1^2+I_1& m_1{l}_{1}r+m_1{l}_1{l}_{12}\\ m_1{l}_{1}r+m_1{l}_1{l}_{12}& (m_1+m_2)r^2+2(m_1-m_2)l_{12}r+m_1{l}_{12}^2+m_2{l}_2^2+I_2\end{array}\right]\left[\begin{array}{c}{\ddot{\theta }}_1\\ {\ddot{\vartheta }}_2\end{array}\right]\\ +\left[\begin{array}{cc}k-m_1{l}_{1}g& -k\\ -k& k-m_1{l}_{2}g+m_2{l}_{2}g\end{array}\right]\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right]=\left[\begin{array}{c}\tau \\ -\tau \end{array}\right]\end{array}$$ (5)

which then were expressed in state equation notation

$$\left[\begin{array}{c}{\stackrel{.}{x}}_1\\ {\stackrel{.}{x}}_2\\ {\stackrel{.}{x}}_3\\ {\stackrel{.}{x}}_4\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ f_{11}& g_{11}& f_{12}& g_{12}\\ 0& 0& 0& 1\\ f_{21}& g_{21}& f_{22}& g_{22}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]+\left[\begin{array}{c}0\\ h_{12}-h_{11}\\ 0\\ h_{22}-h_{21}\end{array}\right]\tau$$ (6)

where x₁ represents θ₁, x₂ represents θ̇₁, x₃ represents θ₂, and x₄ represents θ̇₂, f_ij represents elements of matrix F (Eq. (7)), and h_ij represents elements of matrix H (Eq. (9)). Passive damping (b) properties of the system were included after the equations of motion were derived from the Lagrangian and are captured by the g_ij elements of matrix G (Eq. (8)).

$$\begin{array}{l}F=\left[\begin{array}{cc}{f}_{11}& f_{12}\\ f_{21}& f_{22}\end{array}\right]\\ F={\left[\begin{array}{cc}{m}_1{l}_1^2+I_1& m_1{l}_{1}r+m_1{l}_1{l}_{12}\\ m_1{l}_{1}r+m_1{l}_1{l}_{12}& (m_1+m_2)r^2+2(m_1-m_2)l_{12}r+m_1{l}_{12}^2+m_2{l}_2^2+I_2\end{array}\right]}^{-1}\times \left[\begin{array}{cc}k-m_1{l}_{1}g& -k\\ -k& k-m_1{l}_{2}g+m_2{l}_{2}g\end{array}\right]\end{array}$$ (7)

$$\begin{array}{l}G=\left[\begin{array}{cc}{g}_{11}& g_{12}\\ g_{21}& g_{22}\end{array}\right]\\ G={\left[\begin{array}{cc}{m}_1{l}_1^2+I_1& m_1{l}_{1}r+m_1{l}_1{l}_{12}\\ m_1{l}_{1}r+m_1{l}_1{l}_{12}& (m_1+m_2)r^2+2(m_1-m_2)l_{12}r+m_1{l}_{12}^2+m_2{l}_2^2+I_2\end{array}\right]}^{-1}\times \left[\begin{array}{cc}b& -b\\ -b& b\end{array}\right]\end{array}$$ (8)

$$\begin{array}{l}H=\left[\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{22}\end{array}\right]\\ H={\left[\begin{array}{cc}{m}_1{l}_1^2+I_1& m_1{l}_{1}r+m_1{l}_1{l}_{12}\\ m_1{l}_{1}r+m_1{l}_1{l}_{12}& (m_1+m_2)r^2+2(m_1-m_2)l_{12}r+m_1{l}_{12}^2+m_2{l}_2^2+I_2\end{array}\right]}^{-1}\end{array}$$ (9)

State equations along with state feedback were then modeled in Simulink^™ (The Mathworks Inc., Natick, MA, USA), which allows for the inclusion of feedback delays. The “fminsearch” optimization program in Matlab^™ (The Mathworks Inc., Natick, MA, USA) was used to determine the appropriate state feedback gains, feedback delays, and passive stiffness and damping to minimize the error between experimental and model data (upper and lower body displacement and velocity) for each subject on each trial. No weighting was used in the cost function. An optimization constraint was included so that feedback delays and passive stiffness and damping could not be negative. In addition, feedback delays were limited between 10 and 120ms to represent solely reflexive contributions (Zedka et al., 1999; Matthews, 1991). Electromechanical lag, which was incorporated in the Simulink model, was based on Prochazka et al. (1997).

To assess the effect of delays on postural control, the delays obtained with optimization for each trial were incrementally increased by 5ms until the system became unstable (seat rotational displacement exceeding ±20°). For each delay interval, the following performance indicators were assessed: (1) the number of balance trials that were unstable, (2) the largest range of trunk displacement (θ₂−θ₁), and (3) the largest trunk moment. When the task was unstable, trunk displacement and trunk moment data were not recorded. Both values could be extremely large when the system is unstable and unbounded during the 7 s simulation. For data analysis, only complete sets of data for delay ranging from 0 to 20ms were used to determine if delays increase trunk displacement and trunk moment. By removing the extreme values during the unstable trials and only including complete data sets, our estimates of the effects of delays are conservative.

Two regression equations were used to determine if longer delays, ranging from 0ms (representing no adjustment to delays estimated with optimization) to 20ms of additional delays, significantly increased trunk displacements and trunk moments. The difference between no additional delay (0 ms) and additional delay was used for regression analysis. To determine if model accuracy was related to balance performance, θ̇₂ error (error between experimental and model data for lower body angular velocity) and the average lower body angular velocity (deg/s) during the trial (quantitative performance) were correlated.

A critical p-value of 0.05 was used to test significance.

3. Results

All 7 subjects completed 5 trials. However, the ability to balance, qualitatively speaking, on an unstable seat varied between subjects. There were three subjects (Subject 3, 6, and 7) that had no difficulty regulating tension in the cable prior to release while maintaining balance, and who were able to recover quickly with minimal oscillations after release. This group will be referred to as the Good Balancers. Two subjects had minor difficulty regulating tension in the cable and maintaining balance before the release. After the release, they were able to regain their balance without much difficulty and could maintain steady equilibrium. This group will be referred to as the Average Balancers (Subject 1 and 2). The final group, termed the Bad Balancers (Subject 4 and 5), had difficulty both developing the required tension and maintaining steady equilibrium before and after the release. They tended to have more seat touch downs following release (unstable trials), than the other subjects. This qualitative terminology was consistent with quantitative performance, expressed as the average seat velocity during the 7 s trial (Table 2).

Table 2.

Average (std) feedback delay and critical delay for each subject, and average error between experimental and model data for upper and lower body angle (deg) and velocity (deg/s).

Subject	Delay (ms)	Critical delay (ms)	θ1 error (deg)	θ2 error (deg)	θ̇1 error (deg/s)	θ̇2 error (deg/s)	Quantitative performance (deg/s)	Qualitative performance
1	22(9)	45(6)	1.2(0.4)	0.7(0.3)	3.5(0.9)	2.6(1.0)	5.4 (1.0)	Average
2	13(4)	62(19)	1.3(0.2)	0.9(0.2)	4.3(0.9)	2.7(0.5)	6.5 (0.3)	Average
3	17(5)	83(29)	0.6(0.4)	0.5(0.3)	1.5(0.5)	1.5(0.3)	3.6 (0.4)	Good
4	25(13)	36(18)	1.9(0.4)	2.2(0.3)	8.1(0.9)	6.0(0.7)	7.2 (1.1)	Bad
5	32(7)	82(33)	1.8(0.7)	4.4(1.1)	5.7(1.2)	8.1(1.9)	11.2 (2.0)	Bad
6	27(7)	90(18)	1.3(0.4)	0.9(0.2)	2.7(0.6)	2.7(0.6)	5.0 (0.3)	Good
7	22(7)	53(4)	0.5(0.3)	0.9(0.3)	1.7(0.3)	2.8(0.4)	4.4 (0.4)	Good

Error represents the average error per sampling point during the 7 s trial. Quantitative performance represents the average lower body angular velocity (deg/s) during the trial from experimental data. Table values represent the average across five trials with standard deviations in parentheses.

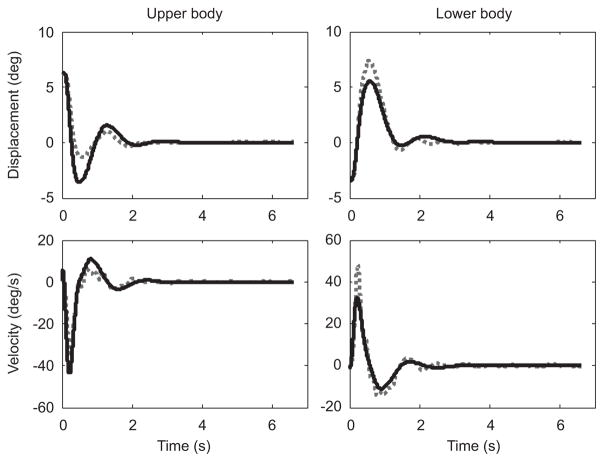
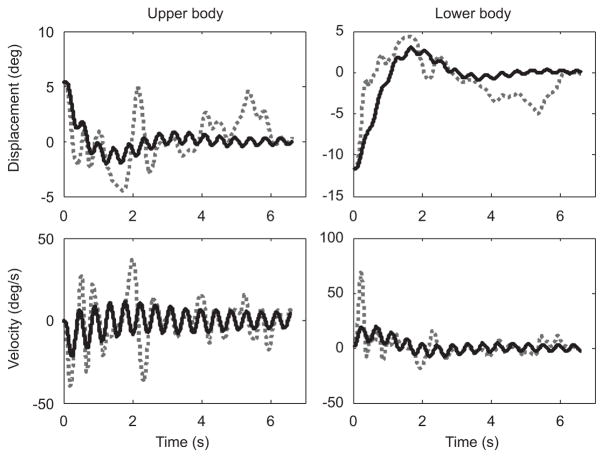
The ability of the linear model to capture the dynamics of the task varied between groups. The average error between experimental and model data were the smallest for the Good Balancers followed by the Average Balancers, with the Bad Balancers error being considerably greater than the other two groups (Table 2). Fig. 3 shows how well the linear model fitted the experimental data for one of the Good Balancers (Subject 3). Fig. 4 shows how the linear model had difficulty capturing the motion of a Bad Balancer (Subject 4). Model accuracy was significantly related to balance performance (r = 0.91, p<0.001), suggesting that the model was more accurate at capturing the dynamics of better balancers.

Fig. 3.

Experimental (broken line) and model (solid line) data for a single trial of a Good Balancer (Subject 3). The close fit illustrates that the linear approximation of task dynamics captured the motion of the system quite accurately.

Fig. 4.

Experimental (broken line) and model (solid line) data for a single trial of a Bad Balancer (Subject 4). Linear model was not able to fit the data very well.

The critical delay, the point at which the system became unstable, varied between subjects (Table 2). Furthermore, there was no consistent pattern between groups. The Good Balancers did not have longer critical delays or for that matter a larger margin between predicted delays with optimization and critical delays. In general, delays found in subjects were not close to the critical delay.

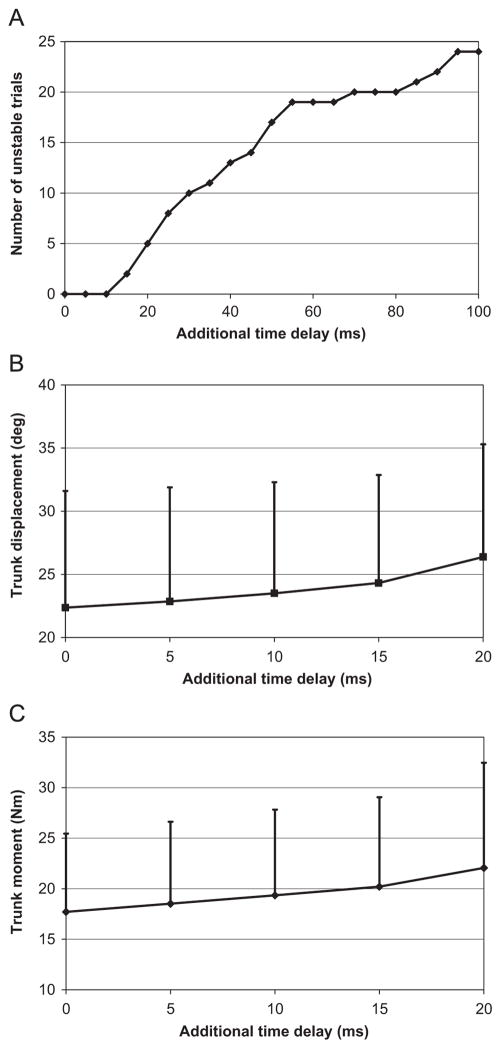
Given that the linear model had difficulty capturing the dynamics of the Bad Balancers, only the Good and Average Balancers were used to assess the effects of delays on balance stability, trunk displacement and trunk moment. Increasing model feedback delays by 20ms caused 5 out of 25 trials to become unstable (Fig. 5A). Trunk displacement increased significantly (p = 0.001) with delays (Fig. 5B). Trunk moment data revealed a similar trend with moments increasing significantly (p<0.001) with longer delays (Fig. 5C). The average delay predicted by optimization for the Good and Average groups combined was 20.1ms (SD = 1.9) and the average critical delay for this same group was 66.5ms (SD = 9.3) suggesting there was an ample margin for stability.

Fig. 5.

Unstable seated balance simulations with additional time delays. (A) The number of unstable trials (seat displacement greater than ±20°). Note that the total number of trials was 25 (5 subjects × 5 trials). (B) The largest range of trunk displacement (θ₂−θ₁) following release averaged across all trials. (C) The largest trunk moment following release averaged across all trials. Error bars represent standard deviations.

4. Discussion

For the most part, the linear model was able to approximate the dynamics of unstable seated balancing. Only the Bad Balancers resulted in a poor fit between experimental and model data. For this reason, Subject 4 and 5 model simulations were not used to address the specific question of whether an increase in delays impairs neuromuscular performance. With the other two groups, optimization had better success fitting their data. As was shown in Fig. 3, a 4th order, linear time-invariant model appears to be able to reproduce the dynamics of seated balancing quite accurately. By removing Bad Balancers, there is a possibility that the findings from the study could be biased based on the quality of neuromuscular control. Ideally, it would be preferable to investigate the effects of delays on people both with good and bad neuromuscular control. We believe that this may be possible by increasing the radius of the half-cylinder to make seated balancing less difficult. We suspect that the uncontrolled oscillations after the cable release will be diminished making fitting of the data possible. It is also possible that we may need to increase the order of the system, include non-linear terms, or use time varying parameters in the modeling of system. All of which would significantly increase the complexity of modeling. Even with the omission of the two Bad Balancers, the current study has merit. By investigating individuals with good neuromuscular control, we can isolate the effects of delays on postural control. Obviously, other factors can impair performance (i.e., neuromuscular noise, inappropriate feedback gains, etc…), but the goal of this paper was to determine if longer delays, by themselves, can contribute to degraded postural control.

Clearly, longer feedback delays produce more balance instability (Fig. 5A), trunk displacement (Fig. 5B) and trunk moment (Fig. 5C). But, are longer feedback delays found in people with LBP clinically significant? As the results show, only 5 out of 25 trials became unstable with the addition of 20 ms, reflecting the longer latencies found in LBP patients (Radebold et al., 2001). We suspect that other factors like inappropriate feedback control (having the wrong feedback gains) or possibly too much neuromuscular noise may play more of a role in determining who will be successful at balancing. For instance, when first exposed to unstable seated balance, people appear to stiffen their trunk and tend to over-react to small disturbances. We often see growing oscillations, which are indicative of unstable feedback control, before the subject touches down. With practice, subjects learn to tune their neuromuscular system to produce appropriate feedback control to complete the task, and with more practice, refine this control to improve performance.

In terms of postural performance, our results suggest that the additional delays found in LBP patients can increase trunk displacement and trunk moment. In terms of trunk displacement, the additional 20ms delay increased displacement by approximately 15%. So it appears that delays alone cannot account for differences in postural control found between those with and without LBP, given that the differences observed in the Radebold et al. (2001) study were 32% between groups. Once again, other factors such as inappropriate feedback control or more neuromuscular noise may result in additional impairment found in the LBP group.

It should be noted that the effects of delays are more pronounced when the system is closer to the point of instability (closer to the critical delay). We plan to investigate whether people with LBP are closer to the point of instability in a future study by comparing feedback control in people with and without LBP. More specifically, we plan to determine where the dominant poles in the complex plane cluster between these two groups. We suspect that the LBP group may be closer to the imaginary axis, which is the boundary for stability. If this is true, it may be possible to modify some elements of feedback control, such as feedback gains or possibly delays, to make neuromuscular control for the LBP population more robust. The goal of future rehabilitation efforts may well lie in tuning the neuromuscular system of LBP patients to minimize any impairments, thus reducing harmful spine displacement and loading.

One methodological issue that needs to be addressed is model validity. Mathematically, it is very complicated to model a system with delays. There exist tools in linear system theory that make it possible to approximate such systems. However, linear approximations can produce erroneous results if the simplified model does not capture the dynamics very well. Therefore, before testing the effects of delays on postural control, we evaluated the ability of a linear model to fit experimental data. Based on quality of fit, only Good and Average Balancers data were used for analysis. Additionally, with optimization, there is always the possibility that convergence on a solution may not represent the true solution (i.e., feedback gains in the model do not represent true neuromuscular feedback gains). To check if the model feedback gains were realistic, we predicted trunk muscle effort from simulation results and compared it to effort levels from a previous experimental study (Reeves et al., 2006). During seated balance with eyes closed, trunk muscle effort recorded with EMG was 4.8% of maximum voluntary effort (MVE). As shown in Fig. 5C, simulated trunk moment at 0ms additional delay was 17.7 Nm. In an unpublished study, we found that the maximum trunk moment effort in the lateral direction was 76 Nm, which suggests that the simulated effort level was approximately 23% MVE. Given that our simulated trunk moment reflects the maximum moment after the release, the feedback gains appear to be realistic. Furthermore, it should be pointed out that feedback delays predicted with optimization (20.1 ms) were consistent with the short reflex loop delays found in paraspinal muscles (19.3 ms) (Zedka et al., 1999), which also supports the validity of the model.