Item Response Theory to Quantify Longitudinal Placebo and Paliperidone Effects on PANSS Scores in Schizophrenia

Abstract

As biomarkers are lacking, multi‐item questionnaire‐based tools like the Positive and Negative Syndrome Scale (PANSS) are used to quantify disease severity in schizophrenia. Analyzing composite PANSS scores as continuous data discards information and violates the numerical nature of the scale. Here a longitudinal analysis based on Item Response Theory is presented using PANSS data from phase III clinical trials. Latent disease severity variables were derived from item‐level data on the positive, negative, and general PANSS subscales each. On all subscales, the time course of placebo responses were best described with Weibull models, and dose‐independent functions with exponential models to describe the onset of the full effect were used to describe paliperidone's effect. Placebo and drug effect were most pronounced on the positive subscale. The final model successfully describes the time course of treatment effects on the individual PANSS item‐levels, on all PANSS subscale levels, and on the total score level.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Composite (sub)scores of the Positive and Negative Syndrome Scale (PANSS), used to quantify disease severity in schizophrenia, are generally analyzed as continuous data, which discards information and is not true to the nature of the data.

WHAT QUESTION DID THE STUDY ADDRESS?

☑ Can Item Response Theory (IRT) be used to describe longitudinal PANSS data upon placebo and drug treatment on item‐level, subscale level, and total score level with a single model?

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ IRT can be successfully applied to the analysis of PANSS data. This technique is versatile enough to not only allow description of item‐level data and total score data, but also of various subscales consisting of subsets of items.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ The improved statistical power that likely results from a longitudinal IRT analysis may improve success rates in clinical trials in schizophrenia, bringing effective treatment faster and more reliably to patients.

Schizophrenia is a brain disorder that is characterized by distortions in thinking, perception, emotions, language, sense of self, and behavior.1 Twenty‐one million people are affected by schizophrenia worldwide1 and due to its early onset and chronic nature, costs for society are high. The disease mechanism is not fully understood and physiological biomarkers to diagnose or quantify the disease severity are lacking; diagnosis and quantifications are therefore based on assessments by psychiatrists using questionnaire‐based tools.

The Positive and Negative Syndrome Scale (PANSS) is one of many clinical assessment scales used for longitudinal disease severity measurements in schizophrenia trials.2 PANSS is a composite psychological and functional scale of 30 items each ranked by a psychiatrist from 1 (absence of symptoms) to 7 (extreme symptoms). The scale is divided into three subscales. The positive subscale consists of 7 items and assesses aspects related to excess or distortion of normal function (e.g., hallucinations). The negative subscale also consists of 7 items and assesses reduction or loss of normal function (e.g., emotional withdrawal). Finally, the general subscale consists of 16 items assessing psychopathology (e.g., anxiety).2

As PANSS scores range from 30 to 210, they are generally analyzed as continuous data, but this does not respect the numerical nature and underlying distribution of these data. Moreover, information may get lost in merging item‐level scores into composite scores, decreasing the power of the data analysis, contributing to the high failure rates for clinical trials in schizophrenia, and preventing potentially efficacious drugs to reach the market. Recently, it was shown that the application of Item Response Theory (IRT) in the analysis of ADAS‐cog scores in studies on Alzheimer's disease increases the precision of the cognitive dysfunction measure,3 leading to increased sensitivity to temporal changes.4, 5 Contrary to analyzing single composite scores, IRT analyses are based on the unobserved (latent) variable that a questionnaire aims to quantify (e.g., disease severity). The latent variable value at each timepoint is derived from simultaneously evaluating all item‐level data of multi‐item scales.

The current project consisted of a pharmacometric analysis based on IRT and was performed on longitudinal PANSS data from phase III trials in schizophrenia, quantifying the time course and magnitude of the placebo response as well as of the response to paliperidone (also known as 9‐hydroxyrisperidone) treatment. Compliant with the nature of the PANSS scale, separate latent variables were estimated for each of the three subscales, after which correlations were included to connect the individual subscales.

METHODS

Data

A total of 102,481 records of item‐level PANSS scores were available from three randomized, double‐blind, phase III studies (SCH‐303,6 SCH‐304,7 and SCH‐3058), including 1,650 diagnosed schizophrenic patients experiencing an acute episode. Details on patients included in this analysis are provided in Table 1. Patients were randomized double‐blind to treatment arms and the protocol did not allow for dose adjustments. The duration of all studies was 6 weeks with scheduled visits on days 0, 4, 8, 15, 22, 29, 36, and 42. Per protocol, individuals were hospitalized for the first 2 weeks, after which they could be discharged at the discretion of the investigator. Combined dropout at the end of these three studies was 41.5%.

Table 1.

Characteristics of patients included in the current analysis

Patient characteristic		n (%)	Median (range)
Treatment	Placebo	344 (21)
	Oral paliperidone 3 mg QD	124 (7.5)
	Oral paliperidone 6 mg QD	230 (14)
	Oral paliperidone 9 mg QD	242 (15)
	Oral paliperidone 12 mg QD	241 (15)
	Oral paliperidone 15 mg QD	111 (6.7)
	Oral olanzapine 10 mg QD	358 (21)
Sex	M	1043 (63)
	F	607 (37)
Age (yr)			38 (18–76)
Disease duration (yrs)			9.0 (0–49)
PANSS score at baseline			93 (65–147)
Patients included in the US		579 (35)
Patients discharged during study		1015 (62)
Patients dropped out during study		685 (42)

Protocols were approved by independent Ethics Committees and informed consent was obtained from patients before inclusion.

Nonlinear mixed effects model

The nonlinear mixed effects analysis was performed using NONMEM 7.3 (ICON, Ellicot City, MD) facilitated by Pirana, Perl‐speaks‐NONMEM (PsN), and Xpose.9

Item characteristics curves

The IRT model describes the probability (P) for each score of each item as a function of the disease severity of a patient, with the latter being an unobserved latent variable. For each item, these probabilities were derived from an ordered categorical model, using item characteristics curves (ICCs) based on difficulty parameters specific for each of the scores (BGE#, see also Supplemental Model Codes) and a joint discrimination parameter (SLP).

$$P(Y\ge \#)=\frac{1}{1+e^{-SLP\left(DS-BGE\#\right)}}$$ (1)

To establish the ICCs, all observations were used as independent observations under the model (i.e., after taking into account the latent variable for disease severity). ICC parameters were estimated as fixed effects, and disease severities as random effects. The disease severity distribution at baseline was fixed to a standard normal distribution, thereby defining the scale for the disease distribution. The disease severity distribution for later observations was assumed to be normally distributed with an estimated mean and variance. For items without an observation of a score of 7 at baseline, probabilities for scores of 1, 2, 3, 4, 5, and ≥6 were estimated. Data for each subscale were analyzed separately for establishment of the ICC parameters.

Potential deviation from the normality assumption of the latent variable was investigated by testing a semiparametric Box‐Cox distribution (η_Box‐Cox):

$${\eta }_{Box-Cox}=\frac{({(e^{{\eta }_{normal}})}^{SHP}-1)}{SHP}$$ (2)

in which η_normal represents a random variable from a standard normal distribution, and the shape parameter (SHP) is estimated.10

The model in Eq. 1 assumes the probability of a score of 1 (absence of symptoms) for each item to asymptote to 1 as the disease severity approaches –∞ (i.e., completely “healthy”). This assumption was investigated by testing the estimation of a value lower than 1 for this asymptote. Similarly, at infinitely high disease severities, the model assumes the probability of the highest score to asymptote to 1. As observed frequencies of the highest scores were low for all items (∼0.09%), the appropriateness of this assumption was not investigated further.

Establishment of the ICCs defined the scale for the disease states. The obtained parameters for the ICCs were therefore fixed for the subsequent modeling of correlations and changes in disease states over time, including:

1. Estimation of correlations between the disease severities on the three subscales at baseline;

2. Estimation of the time course of placebo response on the disease severities on all subscales, and subsequent estimation of the correlations between disease severities at baseline and placebo response within each subscale, and correlations between placebo responses on the different subscales;

3. Estimation of the time course of paliperidone response on the disease severities, and subsequent estimation of the correlations between disease severity at baseline and drug response within each subscale, and correlations between drug responses on the different subscales.

For the longitudinal analyses in Steps 2 and 3, changes in disease severities were modeled over time. Per definition, disease severity on each subscale is expressed relative to the disease severity distribution on that subscale at baseline. At any time, a disease severity of −1 indicates, for instance, the disease severity of an individual is one standard deviation “healthier” than the typical individual in the current dataset at baseline.

Baseline model

Baseline data from individuals allocated to all treatment arms were used to estimate individual disease severities for each subscale at baseline and the correlations between disease severities on these subscales. As the variances were fixed to 1 and the $OMEGA BLOCK functionality in NONMEM does not allow fixing variances while estimating covariances, the correlations were estimated using Cholesky decomposition. As can be seen in the Supplementary Model Code, the magnitude of variances and correlations are estimated as fixed effects and can therefore be estimated or fixed as desired. Due to long run times and model instability, parameter estimates from this step were fixed in subsequent steps.

Placebo model

The following models were tested to describe temporal changes in the disease severity of the patients on placebo treatment: linear model, bilinear model, power model, exponential model, and Weibull model. Inclusion of interindividual variability (IIV) was tested for model parameters.

Placebo models were first developed for each of the subscales separately, after which the three submodels were combined. Correlations were estimated between the disease severity at baseline and IIV parameters of the placebo model within each subscale, and between IIV parameters of the placebo model of the three subscales. To improve run times and model stability, only statistically significant correlations that were higher than 0.1 or lower than −0.1, were retained. Estimated parameters were fixed in subsequent steps.

Drug response model

Individual pharmacokinetic data were not available and therefore dose–response relationships were investigated for paliperidone. The following drug response models were tested: step‐function (i.e., no dose‐dependencies), linear model, log‐linear model, exponential model, and E_max model with and without Hill factor. A linear and an exponential function were tested to describe the time delay to reach the full drug response. The time course of disease severity in individual patients on active treatment was described as the sum of the baseline disease severity, the placebo response, and the drug response. Inclusion of IIV was tested for different model parameters.

After optimizing the drug response models for each of the subscales, the three submodels were combined. Regarding the drug response, correlations were estimated between the disease severity at baseline and the drug response within subscales as well as between the IIV parameters describing the magnitude of the drug response between the three subscales. Again, only significant correlations higher than 0.1 or lower than −0.1 were retained.

Dropout model

To describe dropout patterns, a previously developed model by Friberg et al.11 was fitted to the current dataset. The published logistic regression model included the following covariates: time after start of treatment in a second‐order polynomial function with estimated peak, last PANSS score, difference between the last and second‐to‐last PANSS score, difference between last PANSS and baseline PANSS score, location of study within or outside the US, and first week as an outpatient. Contrary to the previous published analysis, time of hospital discharge was unknown in the current study; it was, however, reported whether patients were hospitalized throughout the study or not. As per protocol, patients were hospitalized for the first 2 weeks of the studies; all patients who were not hospitalized throughout the entire study were assumed to become outpatients on day 15 of the study and, contrary to the previous analysis, the outpatient effect was described to last till the end of the study. Additionally, paliperidone dose was tested as a covariate in this model.

Model evaluation

Throughout the analysis, model selection was based on the objective function values (OFV) of the fits. A difference in OFV corresponding to a significance level of 0.05 was considered statistically significant, assuming a χ²‐distribution.

Model predictions using the obtained ICCs and correlations at baseline were assessed by plotting the frequency distribution of each score of each item at baseline in the observed dataset and in 100 simulated datasets in a bar plot. The predictions of the total PANSS score obtained by summation of all 30 item scores from the baseline measurement within an individual were evaluated in a plot depicting the observed percentage of each total score to the median and 95% prediction interval of these percentages in the same 100 model simulations.

For the longitudinal data, predictions of total PANSS scores over time were evaluated in VPC plots stratified by treatment arm using PsN and Xpose.9 Due to long run‐times and limitations in data processing capacities in R, the VPCs were based on 20 simulated datasets taking dropout patterns into account. Predictions of scores on the three subscales, as well as individual item scores were also evaluated in VPCs of these simulated datasets.

RESULTS

Item characteristics curves

Histograms of the individual post‐hoc disease severities at baseline did not suggest major skewness for any of the subscores and when Box‐Cox distributions were fitted, the estimated shape parameters suggested the distributions to approach normality. The normal distributions of disease severities at baseline were therefore retained. For all items, the probability for a score of 1 was estimated to approach 1 when the disease severity was approaching –∞. The model in Eq. 1 was therefore retained for all items.

The model code for the estimation of the ICCs is provided as supplementary material and obtained parameter estimates are provided in Supplemental Table 1.

Figure 1 shows examples of the obtained ICCs for two items, an overview of the ICCs for all items is provided in Supplemental Figure 1. On all three subscales, the mean of the distribution of disease severity after baseline was negative, suggesting a trend of improvement in disease severity upon treatment on all subscales. The variance in disease severities at these timepoints increased to values greater than baseline values.

Figure 1.

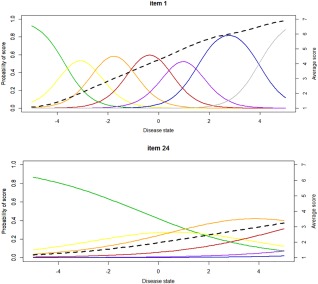
Examples of item characteristics curves for item 1 (delusions) and item 24 (disorientation). Indicated as a function of the disease state are the probabilities of obtaining a score of 1 (green), a score of 2 (yellow), a score of 3 (orange), a score of 4 (red), a score of 5 (purple), a score of 6 (blue), and a score of 7 (gray). The dotted black line indicates the average score for a particular item as a function of the disease state. The slope parameter (SLP) for item 1 is higher compared to item 24, resulting in improved discrimination of the disease state with the score of item 1. Moreover, the score of item 24 increases at higher disease state values compared to item 1, indicating that high scores of this item only occur in very sick patients.

Baseline model

The correlation between the positive and general subscales at baseline was 0.525, and between the negative and general subscale this correlation was 0.384, suggesting that a relatively high disease severity on the general scale is associated with higher disease severities on the positive and negative subscale. The estimated correlation between the positive and negative subscales at baseline was low (–0.108), indicating that these subscales measure different aspects of the disease.

The bar plot depicted in Supplemental Figure 2 shows close agreement in the percentages of observed scores for each item at baseline and the predicted percentage of these scores in 100 simulations using the baseline model, confirming that individual item scores can be accurately predicted. Figure 2 shows that the frequency distribution of the total PANSS score at baseline is also predicted accurately with this model.

Figure 2.

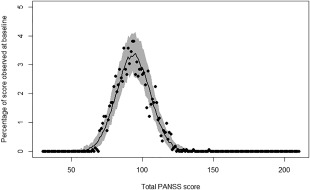
Percentage of times a total PANSS score is observed in the dataset at baseline (symbols), and median value (line), and 95% prediction interval (shaded area) of percentages of times these scores were obtained in 100 simulated datasets using the baseline model.

Placebo model

On all three subscales, the temporal changes in disease severities in patients on placebo treatment were best described by a Weibull model:

$$D{S}_{ij}=D{S}_{i,base}-A_{\max }\cdot {(1-e^{-\frac{\text{ln}\left(2\right)}{HL\cdot t_j}})}^{POW}$$ (3)

in which DS_ij is the disease severity of individual i at time j, DS_i,base is the disease severity at baseline for individual i, A_max is the disease severity asymptote or maximum placebo response, HL is the half‐life to obtain the maximum response, and POW is the Weibull exponent.

The placebo response was largest on the positive subscale, with A_max being −0.413, indicating the typical disease severity to improve to 0.413 standard deviations “healthier” than the typical individual in the current dataset at baseline. For the negative and general subscales, A_max was −0.173 and −0.144, respectively. The time course of the placebo response was similar on all subscales with half‐lives around 10 days. Figure 3 illustrates the temporal changes in disease state for a typical individual on placebo treatment for each of the three subscales.

Figure 3.

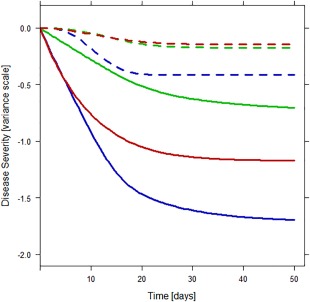
Longitudinal changes in disease state for typical individuals on placebo treatment (dotted lines) and paliperidone treatment (solid lines) for the positive (blue), negative (green), and general (red) subscale, according to our model.

IIV was included on the disease severity asymptotes in a normal distribution and on half‐life parameters in a log‐normal distribution. On the positive subscale the correlation between DS_ij and the HL was 0.106, indicating that a higher disease severity at baseline will slightly increase the time to reach the maximum placebo response. The correlation between A_max on the positive and general subscale was approaching unity and was therefore fixed to 1. The correlation between A_max on the positive/general subscale and the negative subscales was also high, with a value of 0.895. The correlations between the HL on the different subscales ranged between 0.563 and 0.882.

In Figure 4 , the VPCs of the total PANSS score and PANSS subscores over time in the placebo‐treated patients are depicted. Supplemental Figure 3 shows the VPC of each individual item in the placebo model. These VPCs illustrate how the temporal changes in disease states translate into changes on the PANSS (sub)scores in this population. It can be seen that the placebo model can accurately describe the observed scores over time on all these levels.

Figure 4.

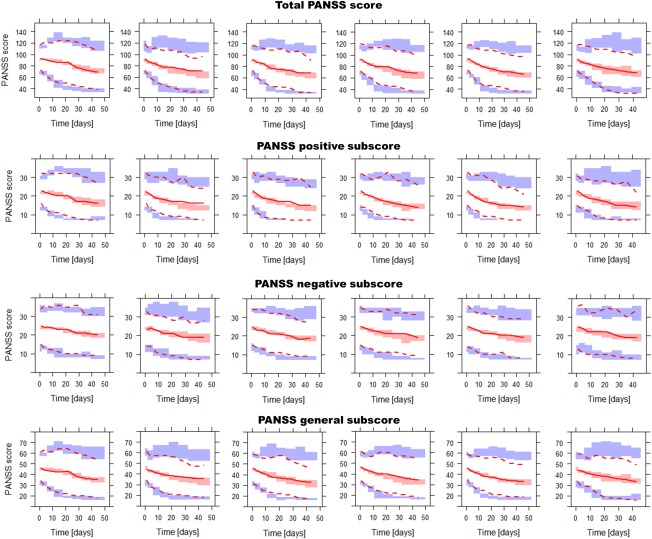
Visual predictive check in all treatment arms of the total PANSS score and the PANSS score on the three subscales. The lines represent 2.5^th, 50^th, and 97.5^th percentiles of the observed data, the shaded areas represent the 95% confidence intervals of these percentiles based on 20 simulated datasets. From left to right, the columns show the results for the following daily paliperidone doses: 0 mg (placebo), 3 mg, 6 mg, 9 mg, 12 mg, and 15 mg.

Drug response model

Paliperidone drug response was modeled as additive to the placebo response on the latent variable scale. In the range from 3 to 15 mg once daily, dose‐dependencies could not be observed in the clinical response on any of the three subscales, and therefore the same effects for all doses were used to describe the drug response on the PANSS subscales.

With a value of −1.30, the drug response was highest on the positive subscale, indicating that upon paliperidone treatment, the disease severity in the typical individual improves with an additional 1.30 points on the scale of standard deviation in disease severities at baseline compared to the placebo response (–0.413). Typical values for the drug responses on the negative and general scale were −0.572 and −1.03, respectively. Correlations between disease severity at baseline and the drug response within the same subscale were −0.468 on the positive subscale and −0.495 on the negative subscale; for the general scale this correlation was not statistically significant. Correlations between the drug responses on the different subscales could only be identified between the positive and general subscale, with the value being −0.721.

The delay in onset of the full drug response was best described by an exponential function on all subscales. IIV parameters were not included in this function, as they could not be estimated independently from the IIV in the time course of the placebo response. The half‐life of reaching full drug response was around 9 days on all subscales. Figure 3 illustrates the temporal changes in disease state for a typical individual on paliperidone treatment for each of the three subscales.

Figure 4 shows the VPCs for this model of the total PANSS score and of the PANSS subscores over time in patients on different doses of paliperidone. Supplemental Figure 4 shows the VPC of all individual PANSS items for all patients on paliperidone treatment combined. The scores of the individual items can be predicted reasonably well, although a number of items show an overprediction of the score 1 and underprediction of the score 3, but this does not negatively affect the model's ability to predict the time course of the composite PANSS scores.

Dropout model

Combined dropout in the dataset was 41.5%. A previously developed dropout model11 was fitted to the current dataset. The parameters were estimated with a relative standard error below 30% and they were within 25% of the previously published estimates, with the exception of the parameter related to the difference between the last two observed PANSS scores, which was more than twice as high. Moreover, in the current dataset an increased dropout was observed in patients on 15 mg q.d. paliperidone.

An overview of all model parameters in the longitudinal and dropout models is provided in Table 2. Estimation and simulation codes for the final are provided as a supplementary file.

Table 2.

Parameter estimates of the final base model, placebo model, and drug effect model as provided in the Supplementary simulation model code

THETA in NM simulation code	Parameter description (unit)	Estimated value	Estimate of variance of IIV on parameter (THETA number)
Baseline model
9	Correlation between disease severity at baseline on positive and negative scale (–)	−0.108	—
10	Correlation between disease severity at baseline on positive and general scale (–)	0.525	—
19	Correlation between disease severity at baseline on negative and general scale (–)	0.384	—
Placebo model
65	Weibull asymptote positive scale (–)	−0.413	4.22 (TH(1))
68	Weibull asymptote negative scale (–)	−0.173	2.21 (TH(2))
71	Weibull asymptote general scale (–)	−0.144	5.78 (TH(1)*TH(64))
66	Half‐life positive scale (days)	8.47	0.328 (TH(3))
69	Half‐life negative scale (days)	11.3	0.498 (TH(4))
72	Half‐life general scale (days)	10.2	0.325 (TH(5))
67	Weibull exponent positive scale (–)	2.86	—
70	Weibull exponent negative scale (–)	2.46	—
73	Weibull exponent positive scale (–)	1.96	—
21	Correlation disease severity at baseline and Weibull asymptote negative scale (–)	−0.182	—
13	Correlation disease severity at baseline and half‐life positive scale (–)	0.106	—
‐	Correlation Weibull asymptote on positive and general scale (–)	1 FIX	—
36	Correlation Weibull asymptote on positive/general scale and negative scale (–)	0.895	—
49	Correlation half‐life on positive and negative scale (–)	0.563	—
50	Correlation half‐life on positive and general scale (–)	0.882	—
54	Correlation half‐life on negative and general scale (–)	0.673	—
Drug effect model
74	Drug effect positive scale (–)	−1.30	0.193 (TH(6))
75	Drug effect negative scale (–)	−0.572	0.0214 (TH(7))
76	Drug effect general scale (–)	−1.03	0.00719 (TH(8))
Derived from 77	Half‐life to reach full drug effect positive scale (days)	8.21	—
Derived from 78	Half‐life to reach full drug effect negative scale (days)	13.1	—
Derived from 79	Half‐life to reach full drug effect general scale (days)	5.98	—
16	Correlation disease severity at baseline and drug effect positive scale (–)	−0.468	—
26	Correlation disease severity at baseline and drug effect negative scale (–)	−0.495	—
62	Correlation drug effect on positive and general scale (–)	−0.721	—
Dropout model
80	Intercept	−5.29	—
81	Time slope parameter (day−1)	−0.0027	—
82	Time peak (day)	29.6	—
83	Parameter related to previous observed PANSS score	0.0175	—
84	Parameter related to difference between the last two observed PANSS scores	0.0454	—
85	Parameter related to difference between the previous observed PANSS score and baseline score	0.0285	—
86	Parameter included for patients of studies in US	0.768	—
87	Parameter included in first after two weeks, when patients were discharged during the study	−0.374	—
88	Parameter included for patients receiving 15 mg paliperidon	−0.397	—

DISCUSSION

We developed the first IRT‐based longitudinal model, describing placebo effects and paliperidone's effects on a PANSS item‐level, subscale level, and total score level in phase III schizophrenia trials.

Good psychometric properties of the PANSS have already been confirmed using an IRT approach12 and the ICCs of that study correspond well with our ICCs, presented in the supplementary file. Both our analysis and the previous analysis show the positive and negative items to be most discriminative of disease severity, suggesting that these subscales are more sensitive to change than the general subscale.

Our application of IRT on longitudinal PANSS data has multiple benefits, of which an increase in statistical power may be the most important, as many late‐phase clinical trials in schizophrenia fail to show statistically significant drug effects. Model‐based approaches in analyzing multiple repeated measurements are known to generally increase the statistical power of detecting drug effects in clinical trials,13, 14, 15 and, similar to Alzheimer's disease,3, 4, 5 IRT may further increase the statistical power of observing drug effects in schizophrenia, by using all item‐level information to derive a latent variable, instead of only analyzing a composite score. Moreover, IRT allows for pooling of data from multiple studies, even when different clinical scales to quantify disease severity are used.

Analyzing PANSS item‐level data does come at a cost. Compared to analyzing total PANSS scores, the size of a dataset increases about 30‐fold, requiring increased computational and data storage capacities besides increasing computational run times. As a result, the VPCs in the current analysis are only based on a limited number of 20 simulations. The fluctuations in the width of the shaded confidence intervals from one bin to another would likely be smoother with more simulations, but we believe that they are stable enough to provide an evaluation of the model agreement with the data. Although the VPCs generally show an adequate description of the observed PANSS data, some deviations between observed data and 95% prediction intervals can be observed that potentially indicate misspecification.

Currently, another restrictive factor for IRT analyses is the limited availability of diagnostics for the longitudinal data. Simulation‐based diagnostics by means of VPCs are currently the most suitable option; however, due to the large dropout and total PANSS score being a covariate for dropout, model development for all subscales was primarily guided by NONMEM's objective function value and only after finalizing all three submodels could VPCs be constructed for evaluation. As a result, it cannot be excluded that misspecification in one part of the model is nullified by misspecification in another part, to yield acceptable VPCs on the subscales and total score. Slight overprediction of a score of 1 and underprediction of a score of 3, seen in some individual items, may for instance have yielded the observed unbiased predictions on the composite scales.

The possibility to model PANSS scores on different levels allowed us to investigate parameter correlations within as well as between the PANSS subscales. Despite that different classifications of the PANSS items have been proposed, consensus on any of these is not strong16 and we therefore adhered to traditional classifications in positive, negative, and general subscales. In future analyses, IRT methodologies would be suited to aid in the optimization of PANSS subclassifications. The increase in the number of estimated parameters upon inclusion of the correlations negatively influenced the ability to obtain standard errors from NONMEM, decreased model stability, and increased the number of local minima in the search space. As a result, model parameters had to be fixed during model development and a condition number or relative standard errors cannot be reported for the final model. This also prevented us from pursuing a covariate analysis. To avoid local minima, many intermediate models were fitted multiple times with different initial estimates.

In addition to schizophrenia and Alzheimer's disease, IRT is likely to be useful in a wide range of diseases for which no biomarker is easily available to directly establish disease severity, and for which multi‐item scales are used to indirectly score disease severity, which is the case for most neurodegenerative and psychological drugs. Undoubtedly, with the promise the application of IRT concepts holds for pharmacometric analyses of longitudinal clinical data, future research efforts will yield methodologies to handle some of the complicating factors encountered in the current analysis. The newly developed Sampling Importance Resampling (SIR) method could, for instance, prove beneficial in obtaining confidence intervals for parameter estimates.17 Despite the concerns outlined above, the IRT approach did allow us to accurately describe longitudinal phase III PANSS data on all levels with a single model. Our confidence in the obtained model is strengthened by the similarities between our results and previously reported results based on more traditional analyses.

Like previous reports, our analysis shows highly variable responses upon both placebo and paliperidone treatment, but with a clear improvement of the disease state in typical patients and with the response in drug treatment groups being higher than the response in placebo‐treated groups. The Weibull model has been reported before to describe the placebo response on the total PANSS score18 and on the three PANSS subscales19 in schizophrenia studies well, albeit with slightly higher half‐life parameters, and the time course for the onset of the paliperidone response also correlates well with previous reports.19, 20 Moreover, traditional data analysis techniques could also not identify dose‐dependencies in the response to paliperidone treatment in the range from 3 to 15 mg once daily.21

Analogously to a previous study analyzing the composite PANSS subscores, our analysis shows the highest response to both placebo and paliperidone treatment for the positive subscale.19, 22 For the placebo treatment, the differences between the response on the negative and general subscale were small but lowest for the general subscale, while this difference was larger in the patients on active treatment with the lowest response on the negative subscale. This is also in line with previous reports.19 As far as we know, correlations between IIV parameters as defined in the current analysis have not been investigated previously. In our analysis, the correlations between the disease states on the three subscales at baseline was moderate to low, while the correlation between effect magnitude and time course of the effects are positive and moderate to high for the placebo effect and the only correlation that could be identified on the magnitude of drug effect was relatively high but negative. Although antipsychotic drug effects are generally believed to favor positive rather than negative symptoms,19 it cannot be concluded whether such observations reflect an absence of correlation between the effects on these scales or only a reduced magnitude of the effect on the negative scale, making a comparison with our findings difficult.

In conclusion, IRT has been successfully applied to yield a single model that can predict the time course of PANSS scores at different levels upon placebo and paliperidone treatment. The increase in statistical power in this disease area has yet to be proven, but is likely given results in other disease areas.3, 4, 5 This increased statistical power may improve the characterization of treatment‐related longitudinal changes in schizophrenia disease states, yielding increased sensitivity to detect drug effects in phase III clinical trials.

Supporting information

Supplemental Figure 1. Item characteristics curves for all PANSS items. Indicated as a function of the disease state are the probabilities of obtaining a score of 1 (green), a score of 2 (yellow), a score of 3 (orange), a score of 4 (red), a score of 5 (purple), a score of 6 (blue), and a score of 7 (grey). The dotted black line indicates the average score for a particular item as a function of the disease state.

Supplemental Figure 2. Frequency distribution of each score as observed for each item at baseline (left bar of each item) and as simulated in 100 datasets for each item (right bar of each item) based on the baseline model. Green indicates a score of 1, yellow a score of 2, orange a score of 3, red a score of 4, purple a score of 5, blue a score of 6, and black a score of 7.

Supplemental figure 3. Visual predictive check of individual PANSS item scores in the placebo treated group. The symbols and lines represent the observed frequency of each score, and the shaded areas indicate the 95% confidence intervals of the frequencies of each score in 20 simulated datasets.

Supplemental figure 4. Visual predictive check of individual PANSS item scores in the groups on paliperidone treatment. The symbols and lines represent the observed frequency of each score and the shaded areas indicate the 95% confidence intervals of the frequencies of each score in 20 simulated datasets.

Supplemental Table 1. Parameter estimates of the item characteristics curves.

IIC model code. NONMEM model code for the estimation of the ICCs for the positive PANSS items.

Final estimation code. NONMEM model code for the final model.

Final simulation code. NONMEM simulation code for the final model.

Dataset. Example dataset for 3 individuals, containing mock data in the DV column.