Development of Physiologically Based Organ Models to Evaluate the Pharmacokinetics of Drugs in the Testes and the Thyroid Gland

Abstract

We extended a generic whole‐body physiologically based pharmacokinetic (PBPK) model for rats and humans for organs of the reproductive and endocrine systems (i.e., the testes and the thyroid gland). An extensive literature search was performed, first, to determine the most generic organ model structures for testes and thyroid across species, and, second, to identify the corresponding anatomic and physiological parameters in rats and humans. The testes and thyroid organ models were implemented in the PBPK modeling software PK‐Sim and MoBi. The capability of the PBPK approach to simulate the testes and thyroid tissue concentration data was demonstrated using a series of test compounds. The presented organ model structures and parameterization yielded a close agreement between observed and simulated tissue concentrations over time. The organ models are ready to be used to predict the pharmacokinetics of passively entering drugs in the testes and thyroid tissue in a generic PBPK modeling framework.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ The majority of PBPK models represent only a set of organs and tissues known to have a substantial impact on absorption, distribution, metabolism, and elimination of a certain compound (e.g., eliminating organs, such as the kidneys and liver), the organs of the gastrointestinal tract as site of drug absorption, and large organs acting as a potential storage depot, such as adipose tissue, muscle, and skin. Further organs are not routinely incorporated in generic PBPK models.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ We developed a generic PBPK model, including the testes and the thyroid gland, which are relevant for the assessment of toxicity and related side effects of a drug.

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ We provide the generic organ model structures and the respective set of anatomic and physiological data required to predict the tissue concentration of drugs in the testes and thyroid tissue.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ This will allow broadening the field of PBPK modeling applications, for example, in human risk assessment.

Physiologically based pharmacokinetic (PBPK) modeling is widely used to predict the concentration of drugs in plasma and at the site of drug action. Further applications include the extrapolation from animal species to humans (e.g., to predict the first dose in man), and scaling from adults to pediatrics or diseased populations. Most of the PBPK models available in literature or implemented in software platforms represent only a set of organs and tissues chosen because they are known to have a substantial impact on absorption, distribution, metabolism, and elimination (ADME) of a compound (e.g., eliminating organs, such as the kidneys and liver, the organs of the gastrointestinal tract as site of drug absorption, and large organs acting as potential storage depot such as adipose tissue, muscle, and skin). Additional organs (including e.g., bone marrow and organs of the reproductive system) are covered to a different extent by PBPK platforms.

A further field of PBPK modeling includes human risk assessment. Here, the focus lies on predicting the drug concentration in organs that are relevant for the assessment of toxicity and related side effects. Among them are organs of the reproductive and endocrine system, such as the testes and ovaries, the thyroid gland, and the adrenal glands. Typically, these organs are small in size and even though significant tissue concentrations can be reached, no significant impact on the overall pharmacokinetics of a drug in the body is observable. Consequently, there is no consolidated summary of anatomic and physiological data needed to parameterize the respective PBPK models. Furthermore, there are few PBPK models available in literature that incorporates organs of the reproductive system or the thyroid gland. These models are tailored to a specific question and cannot be easily implemented in a generic PBPK framework. One reason is the inconsistent use of the organ model structures across publications (e.g., blood‐flow limited and permeability limited distribution, active transport processes). Second, these models do not make use of established in silico methods to predict the tissue‐to‐plasma partition coefficients.1, 2, 3, 4 As a result, currently, little attention has been shown to the precise handling of organs relevant for toxicity assessment in a generic PBPK model.

In the present study, we focused on the development of organ models for the testes and the thyroid gland. The testes are responsible for spermatogenesis and the synthesis of androgens, primarily testosterone.5, 6 Substances targeting the testes may cause dysregulation of the homeostasis of sexual hormones or even lead to infertility. The thyroid gland is the site of production of thyroid hormones, primarily T3 and T4, as well as calcitonin. Thyroid hormones are responsible for the regulation of metabolism, and play an essential role in the development and differentiation of all cells of the body, whereas calcitonin is essential in the control of bone resorption and calcium homeostasis.7, 8

Based on an extensive literature search, we identified the most generic organ model structure for the testes and thyroid across species to be used in a generic whole‐body PBPK model. The literature survey included the collection of the corresponding set of anatomic and physiological parameters in rats and humans in addition to the parameters that are required to determine the tissue‐to‐plasma partition coefficients by the most prominent in silico methods. We completed our analyses with the development of the organ models using observed tissue concentration data for a series of test compounds. Finally, the newly identified organ model structures and parameters were implemented in the commercial modeling platform PK‐Sim and MoBi (http://www.systems-biology.com/products/pk-sim/).

METHODS

Literature search

In the first step, a systematic literature search was performed to identify the anatomic compartments of the testes and the thyroid gland that are most relevant for drug distribution into these organs in rats and humans. Once the organ model structure was set, available literature data for the respective anatomic and physiological parameters (i.e., volume of the organs, blood flow rate through the organs, volume fractions of vascular, interstitial, intracellular and luminal (in case of thyroid) space, and interstitial‐to‐cellular surface area) was included. Last, the physiological parameters required to calculate the tissue‐to‐plasma partition coefficients by the PK‐Sim standard method1, 2 and the method by Rodgers et al.3 and Rogers and Rowland4 were identified from the literature sources. The literature search was performed using PubMed and/or Google Scholar.

The acceptance rules for a particular parameter value were: (1) clear assignment of species, and (2) clear description of the method of analysis or source of the value. If more than one value was available in the literature for a specific parameter, the most reasonable one was chosen based on the following criteria: (1) for consistency, parameter values from identical references were preferred over parameters from different references; (2) if a particular parameter value was supported by more than one reference, this value was chosen over potential values from further references; (3) we preferentially chose parameter values that were determined using the most advanced measurement methods and experimental setup (e.g., blood flow rates should have been determined in unconscious animals); and (4) if there was no obvious preference for a particular reference, the mean of all literature values was used.

In case no information on a particular parameter value could be found in the literature, the respective value was determined based on cross‐species (i.e., the rat value was used for the human or vice versa) or cross‐organ scaling (i.e., the value of other organs was used for the testes or thyroid).

Selection of compounds for organ model development

Test compounds were chosen based on the following criteria: (1) availability of intense sampling data in rat plasma and tissue, as well as human plasma; (2) compound is given as an intravenous application in rats and humans; (3) passive diffusion is the main route of tissue penetration; and (4) diverse set of compounds with respect to electrostatic charges (to develop the organ models using partition coefficients calculated by the method of Rodgers et al.3 and Rodgers & Rowland4; for the testes only).

For testes, fentanyl, alfentanil, and thiopental, and for thyroid gland, omadacycline, amiodarone and its metabolite desethylamiodarone, and propylthiouracil were selected to be suitable as test compounds.

Workflow and organ model development approach

The development of the whole‐body PBPK model, including the testes and thyroid organ models, was done in a stepwise approach. An overview of the workflow is depicted in Figure 1.1, 2 Please note that, for the thyroid, the extrapolation from rat to human was not performed because there was no biological information on how to extrapolate the parameters of the binding kinetics of amiodarone/desethylamiodarone and propylthiouracil to the constituents of the thyroid gland.

Figure 1.

Workflow of the organ model development approach for testes and thyroid gland in rats and humans. A detailed description of the generic physiologically based pharmacokinetic (PBPK) model implemented in PK‐Sim can be found e.g., in ref. 1 and 2. K^t:p, tissue‐to‐plasma partition coefficient; PK, pharmacokinetic.

PBPK model development for the test compounds

Table 1, 1, 2, 3, 4,9, 10, 11, 12, 13, 14, 15 summarizes all processes and input parameters relevant for the PBPK models of the six test compounds. A more detailed description of the test compounds and the respective PBPK models can be found in the Supplementary Section SI.

Table 1.

Summary of the input parameters of the PBPK models of the six compounds used for the validation of the testes and thyroid organ models

	Fentanyl	Alfentanil	Thiopental
Protein binding	Linear over the therapeutic concentration range
Fraction unbound, rat, %	16.69	16.49	21.710
Fraction unbound, human, %	15.69	7.99	13.611,12
Distribution
Partition coefficient model	Rodgers & Rowland3,4	Rodgers & Rowland3,4	PK‐Sim standard3,4
pKa	9.0, base3	6.5, weak base4
Lipophilicity	2.59	1.79	1.97
Cellular permeability model	PK‐Sim standard3,4	PK‐Sim standard3,4	PK‐Sim standard3,4
Metabolism	Hepatic via CYP3A4	Hepatic via CYP3A4	Hepatic
Clearance, rat, mL/min/kg	154.38	28.67	Saturable mechanism Vmax: 2.98 µmol/L/min KM: 0.39 µM
Clearance, human, mL/min/kg	10.20	4.64	3.87
	Omadacycline	AMD	Propylthiouracil
Protein binding	Linear over the therapeutic concentration range
Fraction unbound, %	74.113	0.085 AMD14 0.085 DEAa	43.015
Distribution
Partition coefficient model	PK‐Sim standard3,4	PK‐Sim standard3,4	PK‐Sim standard3,4
Lipophilicity	2.42	5.29 AMD 6.33 DEA	0.70
Binding to constituents of the thyroidal colloid		Interaction with ID‐1 KD = 14.3 nM AMD KD = 4.2 nM DEA	Inhibition of TPO‐mediated iodination kon = 0.0041 L/min/µmol kel = 0.0018 min−1
Cellular permeability model	PK‐Sim standard3,4	PK‐Sim standard3,4	PK‐Sim standard3,4
Metabolism		Hepatic	Hepatic
Intrinsic clearance, L/min		12.92 AMD 146.85 DEA	Saturable mechanism Vmax: 0.33 µmol/L/min KM: 3.4 µM
Excretion
GFR fractionb	1
Biliary clearance, mL/min/kg	6.45

If no reference is given, the particular parameter value was determined by fitting the PBPK model to the observed data.

AMD, amiodarone; CYP, cytochrome P450; DEA, desethylamiodarone; GFR, glomerular filtration rate; ID‐1, type 1 iodothyronine deiodinase; K_D, dissociation constant; K_M, Michaelis‐Menten constant (substrate concentration at half‐maximum reaction rate); PBPK, physiologically based pharmacokinetic; TPO, thyroid peroxidase; V_max, maximum reaction rate.

^aAssumed to be identical to the value observed for AMD.

^bFraction of GFR used for passive renal elimination.

Software

The PBPK model was implemented using the software PK‐Sim and MoBi version 6.3.2. Parameter identifications were performed using the built‐in module (method: Monte‐Carlo with predefined settings).

RESULTS

Anatomic Compartments

The main constituent of the testes are the seminiferous tubules where spermatogenesis occurs.5, 6 The seminiferous tubules are located in the lobules of the testis and are surrounded by interstitial fluid and blood vessels. The interstitial fluid contains Leydig cells, which are responsible for the production of testosterone to regulate spermatogenesis. The blood vessels are surrounded by a layer of unfenestrated endothelial cells, which form a tight junction barrier as part of the blood‐testis barrier.5, 6 Figure 2 a shows a schematic representation of a cross section of three seminiferous tubules. In rodents, the outer membrane consists of a single layer of peritubular myeloid cells, whereas in primates, several layers surround the tubule.5, 6 The peritubular cells were shown to restrict the penetration of particular substances into the tubule of rodent testes and are thought to contribute to the blood‐testis barrier. The seminiferous epithelium is built of Sertoli cells. Specialized junctions between adjacent Sertoli cells form the main part of the blood‐testis barrier (also known as Sertoli cell barrier), which divides the epithelium into the basal and the adluminal compartment. Transport proteins involved in the blood‐testis barrier include transferrin, P‐glycoprotein (P‐gp), and multidrug resistance protein (MDR).5, 6

Figure 2.

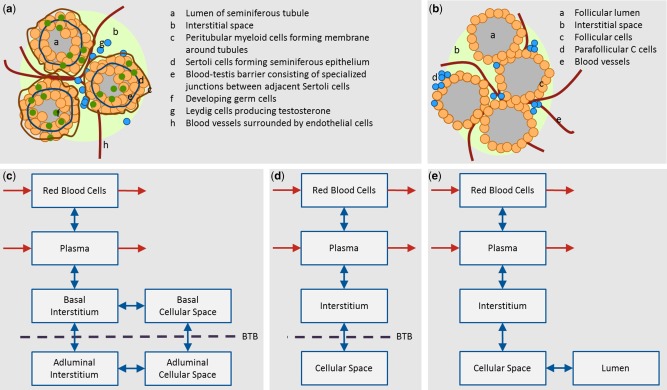
(a) Cross section of three seminiferous tubules of the testes. (b) Cross section of four follicles of the thyroid gland. (c, d, e) Proposed organ model structures in a generic whole body physiologically based pharmacokinetic model for testes and thyroid. Red arrows indicate the distribution of a drug into and out of the organ via the blood flow. Blue arrows indicate passive diffusion between the compartments of the organ. (c) Structure most closely representing the physiology of the testes by dividing the interstitial and cellular space into the basal and adluminal compartments. (d) Final lumped model structure assuming that the blood‐testis barrier (BTB) is located between the interstitial and cellular space – see text for details. (e) Structure representing the physiology of the thyroid gland.

The thyroid gland consists of two lobes that are connected by an isthmus. The lobes are composed of spherical follicles, which are the secretory units of the organ.7 Figure 2 b shows a schematic representation of a cross section of four follicles. Each follicle is surrounded by a single layer of follicular cells. The follicular lumen is filled with colloid, which contains thyroglobulin and other proteins that are required for the synthesis of thyroid hormones. It is noteworthy, that the luminal space can make up to 45% of the thyroid volume depending on the iodide supply and sex. The spaces between follicles are filled with interstitial fluid. Clusters of parafollicular C cells, which are responsible for the secretion of calcitonin, can be found there.7, 8

Generic organ model structure

From a PBPK modeling point of view, the testes divide into the following compartments relevant for drug distribution: vascular space (i.e., red blood cells and plasma), interstitial space, and cellular space. The blood‐testis barrier further divides the interstitial and cellular spaces into the basal and adluminal sides. Please note that this is only relevant for drugs that are prevented from entering or are actively transported out of the adluminal compartment. Figure 2 c shows a schematic representation of the six‐compartment organ structure of the testes. To our knowledge, there are no data available to specify the size of the basal or adluminal compartments on the one hand. On the other hand, when measuring drug concentration in the testes, one will not be able to distinguish the basal and adluminal compartments. Thus, we reduced the six‐compartment structure to four compartments in the following way: if we assume that (1) the cellular space is densely packed (i.e., drugs directly pass from the basal cellular space into the adluminal cellular space without re‐entering the interstitial space); and (2) the adluminal compartment is much larger in volume compared to the basal compartment (i.e., all cells belong to the adluminal compartment), we can lump together the basal and adluminal interstitial space to form the interstitial compartment as well as the basal and adluminal cellular space to form the cellular compartment. The blood‐testis barrier would now act between the interstitial and cellular spaces. The final four‐compartment organ structure of the testes is shown in Figure 2 d.

The thyroid gland divides into five compartments relevant for drug distribution: vascular space (i.e., red blood cells and plasma), interstitial space, cellular space, and luminal space (compare Figure 2 e). The follicular lumen is considered as a separate compartment as it takes up a considerable size of the thyroid gland and it is the major site of action of drugs interfering with thyroid activity.8

Parameterization

A summary of the anatomic and physiological parameters as well as parameters required for the calculation of tissue‐to‐plasma partition coefficients based on the PK‐Sim standard method1, 2 and the method by Rodgers et al.3 and Rodgers and Rowland4 are listed in Table 2.16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40

Table 2.

Anatomic and physiological parameters of the testes and thyroid gland in the standard rat and human and parameters required for the calculation of tissue‐to‐plasma partition coefficients for small molecule drugs

	Male rat (0.23 g)				Male human (73 kg)
	Testes		Thyroid		Testes		Thyroid
Volume, L	0.002a	18–24	1.14e‐5	23,24	0.035	25	0.02	25
Specific blood flow rate, mL/min/100 g organ weight	18.91	16,26	833.33	27	9.29	25	487.50	25
Volume fraction of vascular space, %	3.0	19	5.6	28	6.1l	25	15.9l	25
Volume fraction of interstitial space, %	6.2	29	10.0i		6.2m		8.9o
Volume fraction of cellular space, %	90.8b		60.0	30	87.7b		53.5o
Volume fraction of luminal space, %	–		24.4	30	–		21.7o
Surface area between interstitial and cellular space, cm2	1,970c	Fit	20.65j	Fit	16,854c		36,193j
Partition coefficients based on PK‐Sim standard
Total water, % of tissue volume	86.0	31, 32	74.4	33	81.0	25	78.4	25
Total lipid, % of tissue volume	3.32	31	4.4d		1.60	34	4.4	25
Protein % of tissue volume	12.0d		6.7	35	12.0	25	14.0	25
Partition coefficients based on Rodgers & Rowland3,4
Total water, % of tissue volume	86.0	31,32	74.4	33	81.0	25	78.4	25
Intracellular water, % of tissue volume	82.88e		56.4e		78.06n		59.4n
Extracellular water, % of tissue volume	3.12	36	18.0	36	2.94n		19.0n
Total phospholipid, % of tissue volume	1.42	31,32,34	0.34d		0.90	34	0.34	37
Neutral phospholipid, % of tissue volume	1.16	31	0.302k	35	0.78	38	0.28	37
Tissue concentration of acidic phospholipids, mg/g	2.6	31	0.38k	35	1.2	38	0.60	37
Neutral lipid, % of tissue volume	1.90f		4.06f		0.70f		3.86f
Tissue‐to‐plasma albumin ratio	0.031g, h	42	0.050g, h	42	0.019g, h	42	0.027g, h	42
Tissue‐to‐plasma lipoprotein ratio	0.031g, h	41	0.050g, h	41	0.031g, h	41	0.045g, h	41

It is assumed that reported literature values refer to wet organ weights if not stated otherwise. Conversions from weight to volume and vice versa were based on a tissue density of 1 g/mL.

^aMean of literature values.

^bCalculated as 100% minus the volume fractions of vascular and interstitial space.

^cDetermined based on the formula²: ${\text{surface} \text{area} \left[{\text{cm}}^2\right] = p_1·\left(\raisebox{1ex}{$\mathrm{V}[\text{mL}]$}\!\left/ \!\raisebox{-1ex}{$p_2$}\right.\right)}^{0.75}$, where p₁ and p₂ are scaling parameters. p₂ was set to 2.5 as reported in ref. 2; and p₁ was estimated using the rat tissue data, see Supplementary Section SII for details.

^dHuman value.

^eCalculated as the difference between total and extracellular water.

^fCalculated as the difference between total lipid and total phospholipid.

^gMost frequent value of reported organs/value of carcass.

^hConversion from interstitial‐to‐plasma (I2P) into tissue‐to‐plasma ratio by I2P times fractional volume of interstitial space

ⁱCalculated as the difference between volume fraction of stroma (interstitial space, connective tissue, and blood vessels)³⁰ and volume fraction of follicular capillaries.²⁸

^jDetermined based on the formula: $\text{surface} \text{area} \left[\mathrm{c}\mathrm{m}2\right] = {\mathrm{S}\mathrm{A}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}·{\mathrm{N}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}\mathrm{s}}·\mathrm{O}\mathrm{W}$, where SA_cell is the surface area of a single thyroidal cell, N_cells is the number of cells per g thyroid tissue, and OW is the thyroid organ weight. Malendowicz & Bednarek³⁰ reported the number of cells to be 508.9 106 cells/g thyroid in male rats and the rat tissue data was used to estimate SA_cell, see Supplementary Section SII for details.

^kScaled so that neutral and acidic phospholipids sum up to 100% (in ref. 37 neutral and acidic phospholipids sum up to 97.7%, remaining part declared as “others”).

^lConversion from % of total blood volume to % of organ weight based on total blood volume of 5.3 L.25

^mRat value.

ⁿTotal water divided according to ratio of intracellular to extracellular water in rats.

^oFractions scaled to sum up to 100% minus the volume fraction of vascular space according to the ratios of volume fractions of interstitial to cellular to luminal space observed in rats.

A total of 70 parameters were collected from the literature in order to parameterize both organ models in rats and human. Twenty‐five of 34 and 27 of 36 parameters could be clearly identified based on literature information for testes and thyroid, respectively. The remaining parameters were determined based on cross‐species and cross‐organ scaling, and two parameters were determined by fitting the testes and thyroid organ model with experimental data.

Parameter values for volume and blood flow rate in rats and humans were readily available in the literature with an average coefficient of variation of about 25–30%. For testes, no parameter value could be found for the volume fraction of interstitial space in humans. Here, the rat value was used. Similarly, the rat value was used for the ratio of extracellular to intracellular water in humans, and the human value was used for the volume fraction of proteins in rats. For the thyroid, the ratios of volume fractions of interstitial, cellular, and luminal spaces, as well as the ratio of extracellular to intracellular water were taken from the rat, whereas the human values were used for the volume fractions of total lipids and total phospholipids in rats.

The albumin and lipoprotein tissue‐to‐plasma ratios have not been determined in the testes and thyroid glands. Here, we used the most frequent value reported for other organs,41, 42 which also corresponds to the value of their carcass compartment.

The interstitial‐to‐cellular surface area was estimated to be 1,970 cm² (95% confidence interval ranging from 761–3,130 cm²) in rat testes and 20.65 cm² (95% confidence interval ranging from 4.24–37.13 cm²) in rat thyroid by simultaneously fitting the PBPK models of the test compounds to the observed tissue concentration data. Extrapolation to humans yielded a surface area of 16,854 cm² in the testes and 36,193 cm² in the thyroid (see Supplementary Section SII for details). For the thyroid, we assumed that the cellular‐to‐lumen surface area is identical to the interstitial‐to‐cellular surface area due to the even arrangement in a single layer of densely packed cuboidal cells in the follicle.7

Due to the lack of a generally accepted a priori method to determine the distribution of a drug into the constituents of the colloid in the follicular lumen of the thyroid gland, we assumed that the lumen‐to‐plasma partition coefficient is identical to the intracellular‐to‐plasma partition coefficient.

In the whole‐body PBPK model implemented in PK‐Sim,2 all organ masses sum up to the body weight. The mass gain due to the introduction of an additional organ was corrected by evenly subtracting mass from the two largest organs with respect to volume (i.e., adipose tissue and muscle). In PK‐Sim, the cardiac output is defined as the blood flow rate of the lungs, which is the sum of the organ blood flows entering the lungs. Organ blood flow rates are implemented as specific blood flow rates per organ weight. When reducing the size of adipose and muscle tissue, this in turn leads to a decrease, whereas the introduction of the testes and thyroid compartment leads to an increase of blood flow entering the lungs. Overall, the cardiac output is only marginally changed (0.05% for rats and 1.60% for humans) due to the introduction of the testes and thyroid glands.

Development of the testes organ model in rats

Figure 3 ^39, 43 (left) shows the simulated and observed plasma concentration of fentanyl, alfentanil, and thiopental in the rat. For all three drugs, the PBPK model describes very well the experimental data. Figure 3 ^39, 43 (right) shows the modeling results for testes tissue. For fentanyl and alfentanil, the model describes very well the observed data demonstrating that the anatomic and physiological parameterization of the testes, in combination with the parameters required for the calculation of the tissue‐to‐plasma partition coefficient, is reasonable. For thiopental, the model tends to overestimate the observed tissue concentration in an acceptable range by a factor of no more than two.

Figure 3.

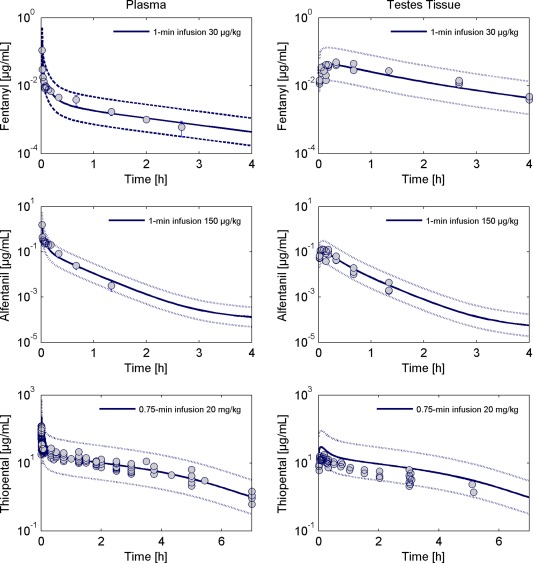
Observed and simulated total concentration of fentanyl (top), alfentanil (middle), and thiopental (bottom) in plasma (left) and testes tissue (right) in rats. The simulated tissue concentration corresponds to the volume‐weighted sum of the interstitial and intracellular concentrations. Circles represent individual or mean ± SD of observed data extracted from literature.39, 43 The solid lines are the model simulations and the dotted lines margin the 95% predictive check interval resulting from the measurement error.

The ratio between drug exposure in testes tissue and plasma is the highest for fentanyl, which is also reflected by the higher value of the intracellular‐to‐plasma partition coefficient for fentanyl (K^ic:p = 6.81) compared to alfentanil (K^ic:p = 0.39) and thiopental (K^ic:p = 0.93).

Extrapolation to humans

Extrapolation from rats to humans was done by substituting the respective anatomic and physiological data of rats with the human values while the organ model structure was kept. Figure 4 ^11, 12, 39, 40 (left) shows that the extrapolated model describes very well the plasma pharmacokinetics of fentanyl, alfentanil, and thiopental in humans. The predicted tissue concentration in testes is shown in Figure 4 ^11, 12, 39, 40 (right). In accordance with the observation in rats, fentanyl shows a higher ratio of drug exposure in testes tissue and plasma compared to alfentanil and thiopental. For all three compounds, the intracellular‐to‐plasma partition coefficients in humans are predicted to be a factor of two to three lower than the values in rats (fentanyl K^ic:p = 2.74, alfentanil K^ic:p = 0.13, and thiopental K^ic:p = 0.35) suggesting that, overall, the drug exposure in testes tissue is less pronounced in humans compared with rats. Looking at the physiological parameters relevant for the calculation of the intracellular‐to‐plasma partition coefficients, the fractional volume of total lipid content is about a factor two lower in humans compared with rats. Thus, the volume fractions of neutral and acidic phospholipids and neutral lipids are lower as well, whereas all other parameters (e.g., water and protein content) are in a comparable range between rats and humans. Thus, the differences in lipid composition result in the differently predicted values for the intracellular‐to‐plasma partition coefficients in rats and humans.

Figure 4.

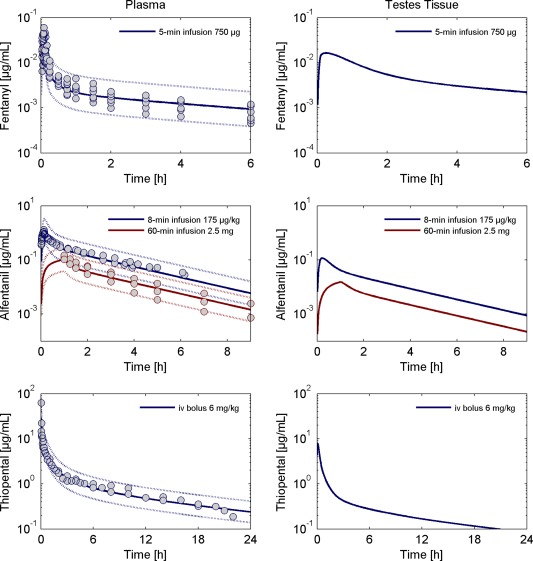
Left: Observed and simulated total concentration of fentanyl (top), alfentanil (middle), and thiopental (bottom) in plasma in humans. Circles represent individual or mean ± SD of observed data extracted from literature.11, 12, 39, 40 The solid lines are the model simulations and the dotted lines margin the 95% predictive check interval resulting from the measurement error. Right: Predictions of the testes tissue concentration for the standard human. The predicted tissue concentration corresponds to the volume‐weighted sum of the interstitial and intracellular concentrations.

Development of the thyroid organ model

Figure 5 ^13, 44, 45 (left) shows the simulated and observed concentrations of omadacycline, amiodarone and its metabolite, and propylthiouracil in plasma of rats. For all test compounds, the plasma pharmacokinetics is well described by the PBPK model.

Figure 5.

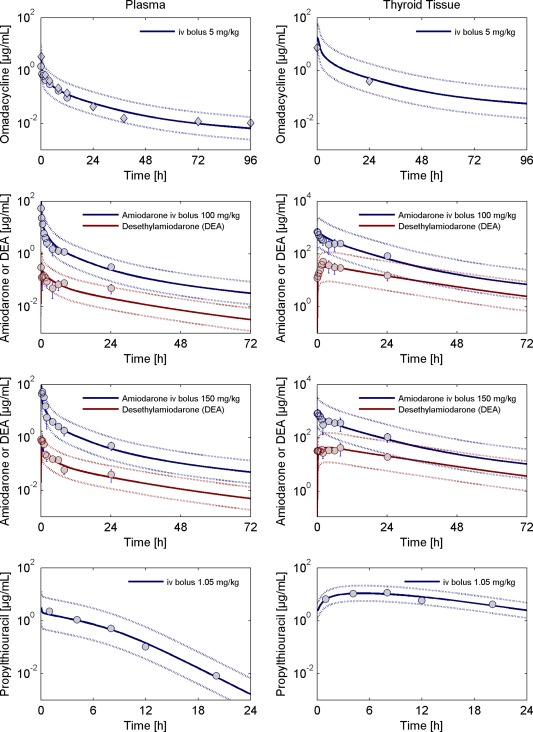
Left: Observed and simulated total concentration of omadacycline (top), amiodarone and desethylamiodarone (middle), and propylthiouracil (bottom) in plasma in rats. Right: Observed and simulated concentration time profiles in thyroid tissue of rats. The simulated tissue concentration corresponds to the volume‐weighted sum of the interstitial, intracellular, and luminal concentrations. Circles represent individual or mean ± SD of observed data extracted from literature.13, 44, 45 For omadacycline, diamonds represent the concentration of total radioactivity (as omadacycline does not undergo metabolism, the total radioactivity is assumed to reflect the concentration of the parent drug). The solid lines are the model simulations and the dotted lines margin the 95% predictive check interval resulting from the measurement error.

After establishing the PBPK models describing the plasma concentration of all test compounds, model development for the thyroid gland was done in a stepwise approach. First, the PBPK model for omadacycline was developed because, to our knowledge, there are no active processes involved in the distribution of omadacycline into the compartments of the thyroid gland. In ref. 13, measurements of omadacycline in the thyroid gland are based on total radioactivity. As omadacycline does not undergo metabolism, the total radioactivity is assumed to reflect the concentration of the parent drug. This is supported by the similar levels of plasma measurements based on concentration data and total radioactivity (compare Figure 5).13, 44, 45

Second, the PBPK model for amiodarone and its metabolite desethylamiodarone (DEA) was developed. Using the passive diffusion model of drug influx into and the efflux out of the thyroid compartments demonstrated that the initial distribution phase is driven by passive diffusion, whereas the terminal phase is influenced by some kind of trapping mechanism. Amiodarone and DEA are known to interfere with the action of thyroid hormones by several mechanisms, including the inhibition of type 1 iodothyronine deiodinase in the follicular lumen of the thyroid gland.46 Thus, we incorporated a hypothetical reversible binding of amiodarone and DEA to the iodothyronine deiodinase.

In a simultaneous model fit, we determined the parameters of amiodarone and DEA binding, as well as together with the omadacycline data, the interstitial‐to‐cellular/cellular‐to‐lumen surface area. The surface area was estimated to be 20.63 cm² (95% confidence interval ranging from 4.24–37.13 cm²). Figure 5 ^13, 44, 45 shows that our model simulations correspond well with the experimental thyroid tissue concentration data for omadacycline, amiodarone, and DEA.

In the last step, we developed the model for propylthiouracil (PTU), which is known to significantly accumulate in the thyroid gland. PTU inhibits the synthesis of thyroid hormones by irreversibly inhibiting the thyroid peroxidase‐mediated iodination of tyrosine residues in thyroglobulin in the follicular lumen. This process leads to the formation of an inactive form of PTU.8 In our model, we included the irreversible formation of inactive PTU in addition to a slow elimination of the inactive form. As shown in Figure 5,13, 44, 45 this results in a very good description of the observed thyroid tissue concentration data.

DISCUSSION

The presented PBPK modeling approach based on a sound review of the literature provides generic organ model structures and parameterizations of the testes and the thyroid gland in rats and humans. In addition, parameters required for the calculation of partition coefficients, based on the PK‐Sim standard method1, 2 and the method by Rodgers et al.3 and Rodgers and Rowland,4 were collected in order to provide a generic PBPK modeling framework. The presented models can be applied to the prediction of tissue pharmacokinetics of further compounds of interest.

The testes and thyroid organ models were developed using a series of test compounds that preferentially enter the testes or thyroid tissue by passive diffusion. The limiting factor in the selection of test compounds, however, was the availability of densely sampled tissue concentration data in literature. For testes, we identified a total of three compounds, alfentanil, fentanyl, and thiopental that fulfilled our criteria to be accepted as candidates for model development.

For the thyroid, typically, tissue concentration data was only available for compounds with the site of a desired (like propylthiouracil) or undesired (like amiodarone) action in the thyroid gland; therefore, these compounds accumulate in the thyroid tissue by drug‐specific processes. As the only compound with available tissue concentration data, omadacycline enters the thyroid gland by passive diffusion only. Therefore, we used omadacycline to demonstrate that the generic organ model structure and parameterization of the thyroid gland yielded a good description of the thyroid tissue concentration.

To describe the thyroidal drug accumulation in our PBPK model, we incorporated an irreversible binding of propylthiouracil and a reversible binding of amiodarone to the constituents of the follicular colloid according to their respective mechanism of action. However, these processes are unique to the drugs under consideration and cannot be applied 1:1 with other drugs. When applying the thyroid organ model to other compounds, it is critical to evaluate if interactions with thyroid‐specific tissue constituents are to be expected. This is particularly relevant when looking at compounds that are known to interfere with the activity of the thyroid gland (e.g., by inhibiting the synthesis of thyroid hormones or the maintenance of calcium homeostasis). It is noteworthy that the presented thyroid organ model can be applied to identify the existence of such processes if it is not known for a particular drug.

For humans, there was no reference reporting tissue concentration data for testes or thyroid so that it was not possible to compare our model predictions to observed data. Extrapolation of the modeling approach from rats to humans, therefore, relies on the well‐reviewed literature database of the anatomic and physiological parameters. Importantly, the simulations of tissue concentration in rats are in very close agreement with the experimental data. Therefore, one can argue that the predications of tissue levels in the testes and thyroid gland in humans are expected to be within a reasonable range of the real data.

About three‐fourths of all parameters required to parameterize the testes and thyroid organ models could be clearly identified from literature references. Among them there were typically more than two references for organ volumes and blood flow rates with an average coefficient of variation of about 25–30%. The most variable parameter was the blood flow rate through the testes and thyroid in humans. For parameters not available in literature, we provided reasonable assumptions to replace the missing value (e.g., by cross‐species scaling; i.e., the rat value was used for the human one and vice versa). As the only organ‐specific parameter, the interstitial‐to‐cellular/cellular‐to‐lumen surface areas were estimated using our compound database. To identify the impact of variability/uncertainty in the model parameters, we performed a sensitivity analysis exemplary for the prediction of the testes tissue concentration. We found that the tissue‐to‐plasma partition coefficient is the parameter with the highest uncertainty and the strongest impact on the tissue pharmacokinetics. As expected, changes in the blood flow rate as well as the interstitial‐to‐cellular surface area (SA) yielded a proportional change in maximum tissue concentration (tC_max), whereas the impact on tissue area under the curve (tAUC) was negligible for the drugs under consideration (see Supplementary Section SIII). The impact of changes in SA on tC_max and tAUC will become more pronounced for drugs with a lower permeability.

For the thyroid gland, the organ volume as well as the size of the luminal space is varied between sexes and dependent on the iodine supply. Female rats are reported to have a larger organ volume relative to the body weight, and the volume fraction of the luminal space in female rats is about twice the size of the lumen in male animals. This is a result of the different supply by sex hormones and starts to develop during puberty.30 In humans, it is shown that iodine insufficiency leads to a significant increase in the volume of the thyroid gland together with a reduction in the size of the follicular lumen.7, 25 These changes need to be considered when applying the thyroid organ model to PBPK models of female subjects or populations with suspected iodine insufficiency.

Due to the lack of a generally accepted a priori method to determine the distribution of a drug into the constituents of the colloid in the follicular lumen of the thyroid gland, we assumed that the lumen‐to‐plasma partition coefficient is identical to the intracellular‐to‐plasma partition coefficient. This can also be regarded as lumping together the cellular and luminal spaces of the thyroid gland to form a single compartment for drug distribution. As demonstrated for omadacycline, this is a reasonable assumption for compounds that do not show a particularly high affinity for any of the constituents of the follicular colloid. In other cases, additional active processes need to be considered in the model.

Overall, the presented organ model structures and parameterizations for testes and thyroid adequately described the tissue pharmacokinetics of a series of test compounds. The sound database of anatomic and physiological data renders it possible to use the organ models in a generic framework to predict the levels of tissue concentration in rats and humans for passively diffusing drugs.

Supporting information

Supporting Information

Supporting Information