Abstract
Cell migration is essential in many aspects of biology. Many basic migration processes, including adhesion, membrane protrusion and tension, cytoskeletal polymerization, and contraction, have to act in concert to regulate cell migration. At the same time, substrate topography modulates these processes. In this work, we study how substrate curvature at micrometer scale regulates cell motility. We have developed a 3D mechanical model of single cell migration and simulated migration on curved substrates with different curvatures. The simulation results show that cell migration is more persistent on concave surfaces than on convex surfaces. We have further calculated analytically the cell shape and protrusion force for cells on curved substrates. We have shown that while cells spread out more on convex surfaces than on concave ones, the protrusion force magnitude in the direction of migration is larger on concave surfaces than on convex ones. These results offer a novel biomechanical explanation to substrate curvature regulation of cell migration: geometric constrains bias the direction of the protrusion force and facilitates persistent migration on concave surfaces.
Keywords: Substrate curvature, 3D cell model, cell migration, cell motility, cell morphology
1 Introduction
Cell migration plays an essential role in a number of physiological and pathological processes, including morphogenesis[1–3], inflammation[4–6], wound healing[7], and tumor metastasis[8]. It is well accepted that 3D cell migration is in many ways different from 2D and that physical properties of the extracellular matrix (ECM), such as stiffness, crosslinking and pore size, affect 3D migration [9–13]. However, it is surprising and puzzling that cells can detect the mechanical properties of the matrix and switch their migration mode accordingly[14]. Furthermore, as cells move along, around, and through the network of ECM fibers, they remodel the structure of the fiber network. This remodeling also changes the mechanical properties of the ECM, which in turn modulates the cell migration patterns. However, how 3D ECM architecture regulates cell migration is still not well understood.
The features of ECM architecture can range from nanometers to micrometers. For example, collagen fibers, with diameters ranging from 20–200 nm, can form hierarchically structured micrometer-scale collagen bundles [15]. The nano- and micrometer-scale architecture of these fibers influence cell polarity and promote migration along collagen fibrils by providing contact guidance cues [16, 17]. Basement membrane complexes are another class of ECM superstructures that can provide both concave and convex surfaces for cell migration in 3D. Furthermore, advanced multi-photon microscopy studies using combined third harmonic generation and second harmonic generation techniques have revealed tissue tracks and curved spaces available for tumor cell invasion in vivo [18]. In particular, micrometer-scale tracks [19] in the interstitial matrix [20] have been considered as a critical factor in providing both physical guidance and a path of least resistance for invading tumor cells [21].
Studies of cell migration in 3D in vitro and in vivo have revealed several differences when compared with cell migration in 2D, including their mechanics, signaling, and morphology[3]. However, we have little understanding how cells sense substrate curvature. Most of our understanding of cell migration comes from assays of cell migration on 2D flat substrate because of its compatibility with microscopy imaging. Thanks to recent advances in the fabrication of ECM models that mimic subsets of selected properties of the complex natural ECM [22], especially those in tissue engineering and regenerative medicine [23], we have begun to appreciate the effects of substrate curvature and topography on cell response. E.g., the BAR domain proteins can sense curvature on the nanometer scale [24], nanotopography can steer the dynamics of cell’s scaffolding by biasing actin polymerization waves [25], and asymmetric nanotopography may bias cytoskeletal dynamics and promote unidirectional cell migration [26]. Numerous experiments have shown cell alignment on topographically patterned surfaces with sizes comparable to the dimensions of the cell [27, 28]. We have yet to discover the molecular or mechanical mechanisms that enable cells to sense micrometer-scale curvatures.
It is believed that cell migration is a cyclic multi-step process comprising of (1) actin polymerization-dependent pseudopod protrusion; (2) integrin-mediated adhesion to ECM; (3) contact-dependent ECM cleavage by proteases; (4) actomyosin-mediated contraction; and (5) retraction and translocation of the cell body [29]. Contact-dependent ECM cleavage by proteases is only constitutively active in mesenchymal cells, including fibroblasts and some solid tumor cells that display prominent protrusions adhering to the ECM, resulting in a spindle-shaped morphology. In contrast, leukocyte movement is characterized by rapidly deforming ellipsoidal morphology with small protrusions, weak adhesion, and lack of proteolysis [30], which is known as amoeboid cell migration. In this work, we focus on the biomechanical aspect of cell-ECM interaction, without considering the degradation or production of matrix materials.
Based on experimental observations, mathematical models of cell migration have attempted to explain certain features of the biomechanics of cell migration using force balance. Examples include constitutive mechanical description of cells [31], continuous force-balance calculations coupled to reaction-diffusion kinetics to describe single cell migration [32], specific mechanical treatment of focal adhesion as springs [33], and cytoskeletal flow in 2D keratocyte migration [34, 35]. A recent review provided a summary of such efforts [36]. However, how substrate curvature affects cell migration has not been studied in detail. A mechanical model of cell migration on a 3D cylindrical substrate based on cytoskeletal stress, in particular, due to myosin contractile machinery, mimicked cell migration on thick collagen bundles [37].
In this paper, we aim to decipher, based on simple geometric and mechanical considerations, how curvature might regulate cell migration. We focused on single cell migration on a curved, rigid substrate, which does not degrade nor deform. We combined a computation model and analytical approach. To study how substrate curvature regulates cell migration behavior, we develop a computational 3D cell migration model to simulate cell migration on both convex and concave substrates. For cell shape adaption to substrate curvature, we construct a simplified geometrical model to analyze cell shape using the cell shape index. To understand how curvature regulates cell motility mechanically, we analyzed force balance at the focal adhesion sites under geometric constraints. The results show significant differences between concave and convex surfaces, some of which are consistent with experimental observations of single cell migrations, while others await further experiments to validation.
2. Model
We introduce a 3D computational cell model for simulating single cell migration on a curved substrate. We also present in this paper a geometric model of a cell on a curved substrate to determine the cell morphology and a mechanical model for protrusion force. Our computational and analytical methods together provide a mechanical picture of the curvature regulation of 3D cell migration.
2.1 3D single cell migration model
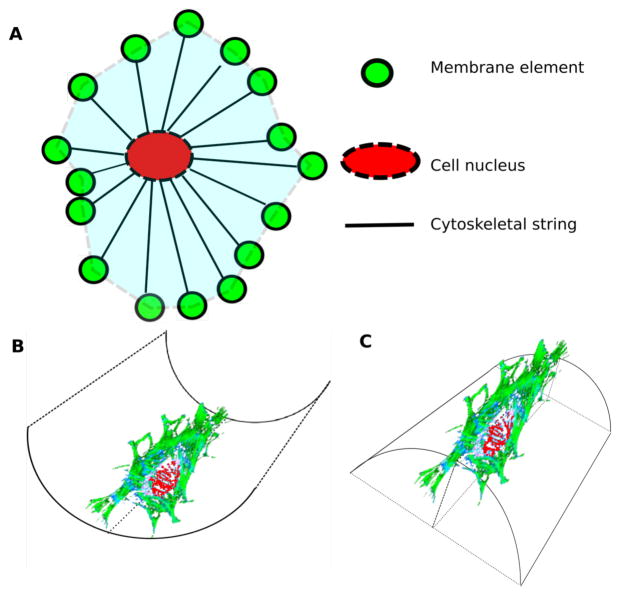
We developed a 3D cell migration model that takes into account cell-substrate adhesion, cytoskeletal polymerization, contraction, and protrusion dynamics. As illustrated in figure 1(A), the 3D model consists of a cell surface, a nucleus, and a cytoskeletal structure. The cell surface is a collection of membrane elements. This element-based representation is adapted from the subcellular elements model [38]. We used the Morse potential [39],
Figure 1.
Scheme of 3D cell model (A) and single cell migration on substrate with negative (B) and positive(C) curvature.
to describe the interaction between membrane elements. In this equation, r is the distance between the membrane elements, u0 is the minimum potential, req is the equilibrium distance, and ρ is a scaling factor. The parameter values are listed in Table 1. The Morse potential is a better approximation than the elastic potential because it explicitly includes the effect of bond breaking when the inter-elements distance is beyond the interaction range Rmax. This feature allows for large-scale local cell membrane deformation, which is necessary for simulating membrane protrusion during migration. We modeled the cell nucleus as a solid sphere, whose deformation is negligible because we focus on a cell on a surface where the cell nucleus is not confined. The membrane elements are connected to the cell nucleus through cytoskeletal strings. As the first order approximation, we treated the cytoskeletal strings as Hookean springs. We simulated this cell membrane element model and compare it with the original subcellular element model [38]. The effective Hookean spring constant of cytoskeletal string k is derived as the effective cell elastic rigidity divided by the number of strings.
Table 1.
Parameters of the 3D single cell migration model. (D: Derived, F: Fitted, M: model parameters)
| Cell parameters | ||
|---|---|---|
| Cell radius | 10 μm | M |
| Number of membrane elements per cell | 128 | M |
| Cytoskeletal string constant k | 7.81E-2 nN/μm | D |
| req | 3.52 μm | M |
| u0 | 0.75 | M |
| ρ | 2.03 | M |
| Maximum interaction range Rmax | 6.68 μm | M |
| Nucleus radius rn | 3 μm | M |
| Number of integrin per element | 250 | F |
| Integrin binding rate | 100/s | F |
| Focal adhesion parameters | ||
| LA | 20 – 25 nm | [42, 43] |
| LN | 5 nm | [43] |
| dA | 55 nm | [44] |
| dN | 5nm | [44] |
| Flow | 10 pN | [45, 46] |
| FHigh | 20–60 pN | [47–49] |
| T | 30 seconds | [50] |
Focal adhesion (FA) comprises of physical linkages between the trans-membrane integrin receptors, surrounding extracellular matrix, and intracellular structures that connect to the cytoskeleton [40]. The strength of FA is adjusted through the local balance of cytoskeletal dynamics, cellular tension, and mechanical properties of substrate, actin polymerization, actin-bundle organization, and myosin motors sliding on actin filaments. Integrin binding to extracellular ligands is highly dynamic and regulated by factors including the availability of integrin, local distribution of ligands, state of integrin, distance between integrin and ligand, as well as the binding state of neighboring integrin. We model the integrin-substrate adhesion as follows: Integrin binds to ligand to form nascent binding when the integrin-ligand distance is less than LA if integrin is activated, and LN if integrin is non-activated. The nascent integrin-ligand binding can be reinforced to form stable binding if the neighboring integrin-ligand pair is less than dA apart for activated integrin and less than dN apart for non-activated integrin. FA force Fa is a function of the number of bindings on the membrane element with low binding force Flow for nascent bindings and high binding force FHigh for stable bindings. Integrin binding has a maximum life-time T. Parameter values for focal adhesion are in Table 1.
We used the membrane displacement and protrusion dynamics data of HT1080 cells in chick chorioallantoic membrane (CAM) [41] to fit for two model parameters: number of integrin per element and integrin binding rate. We ran simulations of single cell migration on a flat substrate and quantified cell membrane displacement using the coordinates of membrane elements. Through trial and error, we adjusted the number of integrin per element and integrin binding rate such that the number of protrusions per cell is between 4 and 12, and the length of the protrusion is between 4 and 7 microns, as was found in [41].
At the focal adhesion site, the adhesion force, Fa, the contraction force, Fc, and the protrusion force, Fp, are balanced. The force calculation provides the unknown magnitude of the protrusion force. The equation of motion for membrane element i is:
The first term describes the interaction between neighboring membrane elements, where Ni is the elements within interaction range of the Morse potential. This term mimics membrane tension. The second term is the elastic force from the cytoskeletal string, with elastic rigidity k and deformation δXi = Xieq − Xi, which connects to the membrane element. The third term is the focal adhesion force resulting from integrin binding. The fourth term corresponds to the protrusion force. The fifth term corresponds to a weak stochastic component that mimics underlying noise.
Movement of membrane elements results in elongation or shrinkage of the cytoskeletal strings, which in turn moves the nucleus. The morphological dynamics and cell migration behavior are natural consequences of the movement of all membrane elements, cell nucleus, and cytoskeletal strings.
2.2 Geometrical analysis of cell shape
We assume that substrate curvature regulates cell migration through contact. Cells adapt their shape to the contacting substrate during migration, in response to the local geometric constraint. To quantify 3D cell shape in response to substrate curvature, we choose to use the cell shape index, or CSI, to quantify cell deformation. In 2D, , where A is cell area, P is perimeter [51]. It describes the departure of cell shape from a circular projection. In 3D,
| (1) |
where SA is cell surface area, α is a geometric constant. We set α = 60.75, such that a hemispherical “cell” on a flat surface would have CSI=1 [52]. In both 2D and 3D, the CSI measures how much a cell spreads.
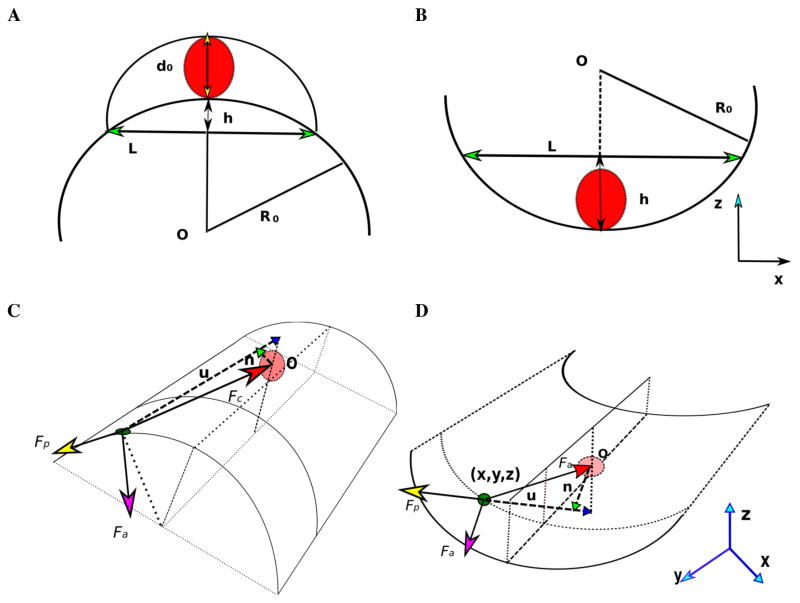
We consider the curved surface of substrate: concave (negative curvature) as the inner surface (figure 1(B)) and convex (positive curvature) as the outer surface (figure 1(C)). We vary the substrate curvature by changing the radius of curvature, R0, (figure 2(A), (B)). We set up the Cartesian coordinate system such that the cells migrate along the y-axis (figure 2). We use simple geometrical approximation (figure 2(A), (B)) to analytically calculate the cell surface area for cell on these surfaces and derive the CSI as a function of R0.
Figure 2. Geometrical representation of cell.
Substrate is the arc with center O and radius R0. Red solid circle with dashed outline represents cell nucleus. (A) Cross-section of the cell on the substrate with convex curvature. Chord (with green arrow marker) with length L is width of cell. Arc segment with height h is bottom arc of cell. d0 is cell nucleus diameter with yellow arrow pointing to the bottom and top arc of cross-section of cell. (B) Cross-section of cell on substrate with concave curvature. Chord (with green arrow) with length L is top arc of cross-section of cell. (C) Force balance at cell-substrate interface for substrate with convex(C) and concave(D) curvature.
We assume that the cell nucleus is a sphere (red solid circle in figure 2) with a diameter of 6 μm. Because we vary R0 from two times to ten times the cell radius (20–100 μm), the cell nucleus is never compressed, we can safely assume that the cell nucleus is not deformed, and the cell volume V0 (figure 2(C)) remains constant as cell spreads out on the surface. We also assume that substrate is always stiff enough such that the substrate does not deform due to cell-interface interaction.
We approximate the shape of the cell on a convex cylindrical substrate as two arcs that are sharing the same chord length L. The inner arc is the interface between cell and substrate. The maximum distance between the bottom and the top of the cell is d0 which is larger than the diameter of cell nucleus. The surface area of the approximated cell contains the upper surface, bottom surface. Assume that cell cross-section area is same within the cell length L0 and the front and back ends are the same. Cell volume is cell length times cell cross-section area. The chord length L is a function of substrate radius R0 and height of lower arc, . Su and Sl are approximated upper and lower arc length of the cross-section [53].
With substitution for L2,
Similarly, the length of the lower arc
The side surface area is:
| (2) |
Cell surface area is a summation of the upper and lower surfaces and two sides:
| (3) |
Hence the surface area for a cell on a convex substrate is:
| (4) |
Cell shape on concave substrate can be approximated using simpler geometry (figure 2(D)). The upper surface can remain flat and the lower surface attaches to the substrate so the cross-section is a line segment and an arc with radius R0. The surface area is a function of R0 and d0.
| (5) |
Using the derived cell surface area as function of curvature and d0, we apply equation (4) and (5) to solve h = 2rn. We vary R0 to compare how CSI changes with R0 for concave and convex surfaces.
2.3 Protrusion force at focal adhesion site
At the focal adhesion site, we consider three major forces on the membrane element: (1) focal adhesion force Fa, the magnitude of which is determined by the number of integrin binding, and the direction is to be determined; (2) cell contraction force Fc, which is a summation of cell membrane tension and actomyosin contractile forces, modeled as a force with fixed magnitude pointing from the element to the center of the nucleus; and (3) the protrusion force Fp, originated from actin filaments polymerize and sterically protrude against the cell membrane, is modeled as a force in the direction of the center of the nuclear to the membrane element and tangent to the surface (figure 2(C) and (D)). We assume that the substrate is non-deformable. By balancing these three forces, we solve for two unknowns: the direction of focal adhesion force and the magnitude of protrusion force.
We set the center of cell nucleus at (0,0,rn − rc), where rn = 3μm is the radius of cell nucleus, rc = 10μm is radius of cell. We set up a coordinate system at focal adhesion site (x,y,z) using orthogonal vectors u⃗, n⃗ and v⃗. We let u⃗ be the direction of protrusion force:
| (6) |
We let n⃗ be on the plane:
| (7) |
and we choose
| (8) |
As these vectors are orthogonal, we have
| (9) |
| (10) |
from which we have
| (11) |
and
| (12) |
Similarly, for concave substrate, we have the three vectors:
| (13) |
| (14) |
We solve for the two unknowns, zu and α using the equations (9) and (10).
| (15) |
| (16) |
We project the adhesion and the protrusion forces on to the u⃗v⃗ plane and solve for the direction of the adhesion force, and the magnitude of the protrusion force.
| (17) |
Note that equation (17) applies to both convex and concave conditions.
At a focal adhesion site, x = R0cos(θ). Since y is the axis of symmetry to the substrate (figure 2 (C) and (D)), we only need to compute Fp for , the minimum of θ is set by the assumption that cell nucleus is not deformed, which is h ≥ 2rn. For , the greater θ is, the closer the focal adhesion force is aligned with direction of migration(y–axis).
3. Results
3.1 Cell on convex substrate has larger cell shape index
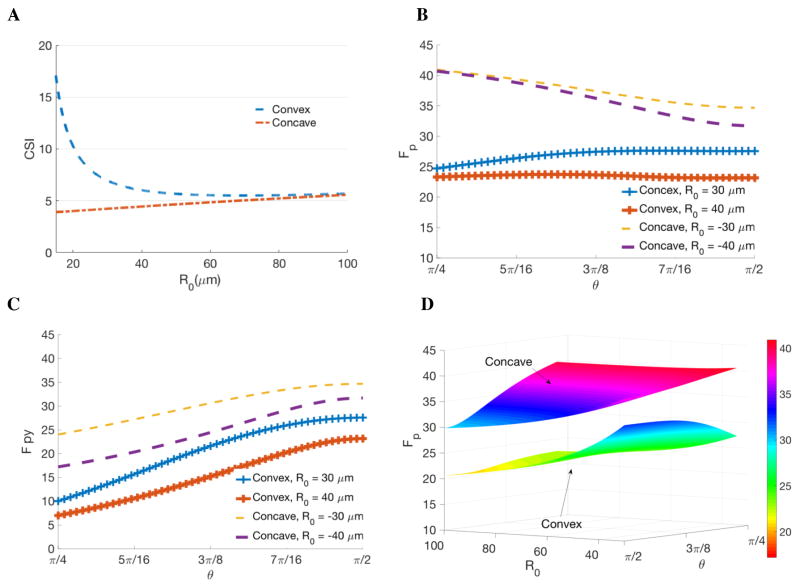
For cells on both convex and concave substrates, the CSI is a monotonic function of R0. The CSI measures the extent a cell spreads: the CSI equals to 1 for a hemispherical shape; the larger CSI value the more stretched a cell is. Figure 3 (A) indicates that the CSI is much larger for cells on a convex substrate than on a concave substrate. When the radius of curvature R0 is large, e.g. R0 >100 μm, 10 times of the cell size, the substrate is effectively flat to the cell. As the radius of curvature R0 decreases (the curvature increases), the CSI for cells on a convex substrate increases, indicating that cells stretch more on a convex substrate. On the other hand, as the curvature increases, the CSI for cells on a concave substrate decreases, corresponding to indicating decreasing cell spread. We see that cells stretch more on a convex substrate, especially when R0 is close to the radius of cell. Conversely, cells on concave substrates spread less than on a flat surface.
Figure 3. Analytical calculation of the cell shape index (CSI) and protrusion force for cells on curved substrates.
(A) The CSI is larger for cells on convex surfaces (blue) than those on concave surfaces (red), indicating cells spread out more on convex surfaces. As the radius of curvature increases (surface tending flat), the CSI decreases for cells on a convex surface, but increases for those on a concave surface, and the CSI values converge as the surface becomes flat. (B) Protrusion force is a function of location of the focal adhesion (in the unit of radians) with R0 equals ± 30μm, ±40 μm, respectively. (C) Projection of the protrusion force on the y-axis: larger for cells on concave surface (dash yellow and purple lines) than on convex surface (blue and orange with + marker). (D) 3D surface plot of the protrusion force as a function of contacting position determined by θ and the radius of curvature, R0, of the substrate.
When the radius of curvature R0 increases from 20μm to 100μm, the CSI on convex substrate decreases faster than the rate of the CSI increases on concave substrate. This suggests that the CSI is more sensitive to convex surfaces in comparison to concave surfaces. When R0 is close to the radius of cell, the CSI shows over 4-fold difference between convex and concave substrates. Analytical result of CSI shows a surprisingly drastic difference even though it is intuitively straightforward that cells spread on a cylinder and are confined inside a tunnel.
3.2 Cells on concave substrate have larger protrusion force
Protrusion force Fp at focal adhesion point (x,y,z) on the substrate is computed using equation (6)–(17). Both Fa and Fc are regulated by many factors independent of substrate curvature, so we fixed the value of Fa and Fc to study how R0 regulates protrusion force (figure 3(B), (C) and (D)).
The magnitude of Fp as a function of R0 (ranging from 20–100μm) shows that the concave substrate facilitates protrusion at the focal adhesion sites. For cells on concave substrates, Fp decreases R0 increases (figure 3(B)), indicating that the more curved the substrate, the larger the prot rauss itohne vfoarlucee oasf facilitated by the curved surface. In this sense, the confinement is promoting the cell protrusion. For single cell migration on a convex substrate, Fp shows the same trend: it increases as the value of R0 decreases, indicating that positive curvature also encourages protrusion.
Protrusion force Fp is also a function of θ. The concave and convex substrates show the opposite trends: for cells on the convex surface, the larger the θ (i.e. the further away from the direction of migration along the y-axis), the smaller the magnitude of Fp (figure 3(C)); for the concave surface, the smaller the θ, the larger the protrusion force Fp. To further study the effect of curvature on migration, we projected the protrusion force to the direction of migration Fpy (figure 3 (C)) and found that the projection of Fp for cell on a substrate with concave curvature is greater than on a convex substrate. They both increase as θ gets closer to , the direction of migration. Furthermore, Fpy increases when we reduce the value of R0; this trend is independent of the direction of curvature. Taken together at the focal adhesion site, protrusion force is larger for cells on concave substrates than convex substrates because the concave substrate promotes protrusion forces.
3.3 Cell migration simulation confirm analytical results
A single cell is initialized with center of mass at the origin O with a small distance δ = 0.1μm to the substrate. We ran 10 independent simulations, each for 3 simulated hours of single cell migration on curved substrate with varied R0. We measured the cell surface area and the cell trajectories.
3.3.1 Cell on convex substrate shows larger CSI
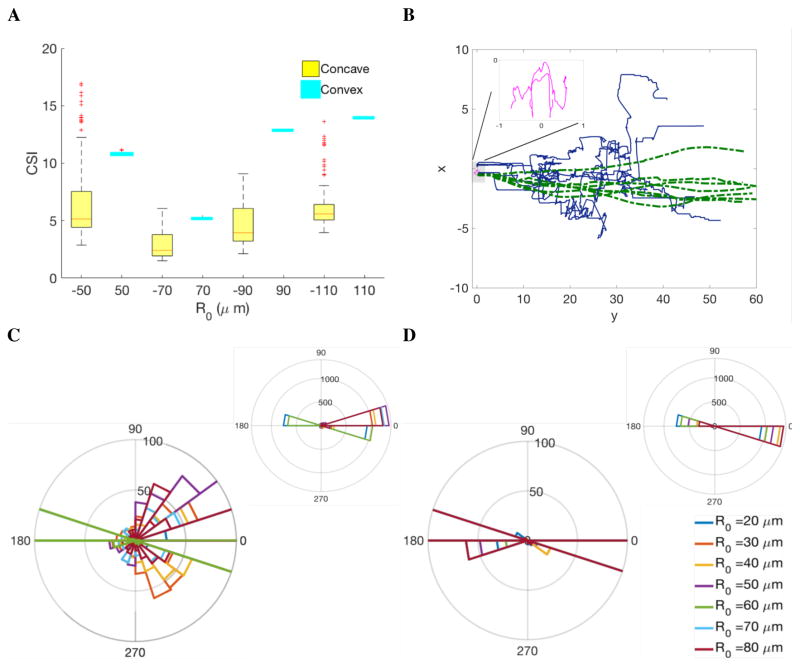
For each simulated cell, we output the position of each membrane element and use Delaunay triangulation (DT) to generate a triangular mesh of the cell surface. The areas of these triangles sum up to approximate the total surface area, which leads to the 3D CSI. The CSI of a single cell migrating on a convex substrate is statistically greater than cells on concave substrate (figure 4(A)).
Figure 4. Simulated cell shape index(A) and cell tracking.
(A) Box plot of cell shape index from simulations of single cell migration with varied substrate curvature. Radius of substrate R0 equals ± 50, ±70, ±90, ±110 μm with yellow for concave and cyan for convex. (B) Simulated cell tracks from 3 hours’ cell migration on curved substrate, projected on the xy plane: blue line for convex substrate, dashed green for concave substrate, magenta for flat substrate. Insert shows zoomed in cell tracks on a flat surface. (C) Angular distribution of instantaneous cell velocity on convex substrate with low frequency details (left) and the whole distribution (upper right). (D) Angular distribution of instantaneous cell velocity on concave substrate with low frequency details (left) and the whole distribution (upper right).
Comparing the simulated CSI with analytical results, we see the cell shape adapting to the cell-substrate interface and the protrusion driven cell deformation are two competing factors that regulate cellular morphological features. Analytical calculations show that, for a cell migrating on a convex substrate, with the increasing R0, the CSI decreases (figure 3(A) blue dash line), while the cell protrusion force at the focal adhesion sites increases (figure 3(B). As a result, the simulated CSI shows a biphasic behavior: contact adaption dominates for small R0; and the protrusion force dominates for large R0. Further, more detailed investigation is required to quantitatively understand the CSI dependence.
3.3.2 Cell tracks show higher persistence on concave substrate
We projected 3D cell migration tracks onto the xy plane (figure 4(B)). Cell migration on the concave substrate (green) shows higher directionality and efficiency, in comparison with cells on the convex substrate (blue). Cells on a flat substrate show random walk trajectories because of the protrusion force generated at the focal adhesion site is not sufficient to drive cell polarization and ensure directional migration. The cell trajectories on concave substrates show more persistency in the y-direction, while the trajectories on convex surfaces show more variation in the transverse direction. This observation is consistent with a recent experiment where T lymphocytes migrated on sinusoidal wavy surfaces [54]. The T-lymphocytes were found to prefer the concave surfaces, as more cells were found in the troughs than on the ridges. In addition, the cells in the troughs migrated in straighter lines, and cells on the ridges showed random trajectories. The motility analysis from the T-lymphocyte experiment also suggested that concave substrate promotes cell migration, and that the effect is more prominent when the radius of curvature is small, similar to the cell size [54]. These results agree with our protrusion force calculations and confirm that concave substrate provides geometric constraints that facilitate protrusion force along the long axis of a cylindrically curved substrate, and promotes more persistent migration.
To further quantify the migration tracks, we computed the velocity of the center of mass of the cells. The polar distribution plot of the direction for cells on convex substrates (figure 4(C)) shows a much wider low-frequency variation (figure 4(C) lower left), compared to a much narrower distribution for cells on concave substrates (figure 4(D)). This distribution further indicates the persistent migration on concave substrates. In conclusion, substrate curvature regulates cell motility through modulating cell protrusion force at the focal adhesion site.
4. Discussion
Cell migration through a 3D ECM is one of the most fundamental processes of living systems. Many cells, including those in development, wound healing, and cancer invasion, can change their behavior and switch their migration pattern depending on the local ECM geometry. The critical question: “what are the key ECM and cell characteristics that determine the migration pattern?” is still unanswered.
To address this question, we chose to start on a simple system that is also physiologically relevant: cells on curved substrates without proteolysis. We have developed a 3D cell migration model and geometry based analysis to investigate cell shape and cell migration on curved substrates. We varied the radius of the curved substrate, effectively providing a wide range of curvature, both negative and positive. The results offer qualitative understanding on how curvature regulates cell shape, and quantitatively investigates the effect of substrate curvature on cell motility. We show that cells spread out more on convex surface than on concave ones, which is rather intuitive, as concave surfaces confine cells. Our results also suggest that, when we consider only biomechanics of integrin-mediated adhesion, cell contraction, and protrusion, curved surfaces provide geometric constraint and modulate the direction of protrusion force. On concave substrates, the negative curvature promotes protrusion force along the length of the cylindrical surface, effectively promoting persistent migration in the long axis. Cells on convex surfaces, without the protrusion force advantage, migrate in diverse directions. The qualitative agreement with cell migration patterns on sinusoidal wavy substrate [54] is remarkable.
The substrate providing geometric confinement has also recently generated many interesting observations and novel mechanisms of cell migration that are integrin-independent, e.g., the osmotic pressure drives cell migration through a narrow channel like a fluid-jet [55]. We focused on integrin-dependent biomechanical cell motility and limited our study to architectures of a few times the cell dimension, without severe confinement.
These results suggest that cells hugging on micrometer-size convex substrates, e.g., collagen bundles, would move rather inefficiently. However, if the collagen bundles are aligned, cell migration pattern could switch to more persistent migration, as cells between aligned bundles would essentially move on concave substrates. This explanation might be relevant to tumor associated collagen signatures [56].
More detailed understanding of how substrate geometry regulates cell migration would require integrated experimental, analytical, and computational study of cellular as well as subcellular dynamics. High-resolution imaging from migration assays of cells on flat and curved surfaces will offer intracellular and cellular level dynamics. For example, we could develop a reaction-diffusion-convection model of integrin-mediated actin polymerization and actomyosin contraction dynamics, based on the detailed spatiotemporal dynamics of actin and myosin from cell image analysis. This model will become the intracellular module of our cell model that dictates the elongation and contraction of the cytoskeletal springs. Many mathematical models of cell migration have treated actin polymerization near the plasma membrane as a Brownian ratchet process, whereby cytoskeletal organization drives the protrusion of the cell membrane [57, 58], and requires that protrusion force is normal to the membrane contacting the growing tips of actin filaments. Our model relaxes this requirement. Instead, we allow the spatiotemporal dynamics of cytoskeletal proteins to determine the interaction between actin fibers and cell membrane, and the force balance between protrusion, adhesion and contraction to determine the protrusion force direction. This feature also allows our model to treat not only the long, thin filopodia, where aligned, crosslinked actin bundles pushes the membrane forward, but also the broad, sheet-like lamellipodia where a branched network of short actin filaments is behind the protruding membrane. Further extension of our cell model, including more detailed modeling of the ECM structure and mechanics, will make it possible to study cell migration under many other, more complex, conditions. Such a model with a more realistic microenvironment may eventually allow us to study cell-ECM interactions in physiologically relevant situations.
Our study provides a new, yet simple mechanical mechanism that substrate curvature can regulate cell migration through geometric semi-confinement and modulate the cell shape as well as membrane protrusions. We have generated server testable predictions and eagerly await experimental efforts to test them.
Acknowledgments
This work was partially supported by NIH 1U01CA143069. XH is supported by the MBD Fellowship at Georgia State University.
References
- 1.Friedl P, Gilmour D. Collective cell migration in morphogenesis, regeneration and cancer. Nat Rev Mol Cell Biol. 2009;10(7):445–57. doi: 10.1038/nrm2720. [DOI] [PubMed] [Google Scholar]
- 2.Ahtiainen L, et al. Directional cell migration, but not proliferation, drives hair placode morphogenesis. Developmental cell. 2014;28(5):588–602. doi: 10.1016/j.devcel.2014.02.003. [DOI] [PubMed] [Google Scholar]
- 3.Friedl P, et al. New dimensions in cell migration. Nature reviews Molecular cell biology. 2012;13(11):743–747. doi: 10.1038/nrm3459. [DOI] [PubMed] [Google Scholar]
- 4.Madden J, et al. Macrophages increase the expression of RhoC in inflammatory breast cancer leading to increased migration. Cancer Research. 2016;76(14 Supplement):3236–3236. [Google Scholar]
- 5.Masopust D, Schenkel JM. The integration of T cell migration, differentiation and function. Nature reviews Immunology. 2013;13(5):309–320. doi: 10.1038/nri3442. [DOI] [PubMed] [Google Scholar]
- 6.Pesic M, Greten FR. Inflammation and cancer: tissue regeneration gone awry. Current Opinion in Cell Biology. 2016;43:55–61. doi: 10.1016/j.ceb.2016.07.010. [DOI] [PubMed] [Google Scholar]
- 7.Shaw TJ, Martin P. Wound repair: a showcase for cell plasticity and migration. Current opinion in cell biology. 2016;42:29–37. doi: 10.1016/j.ceb.2016.04.001. [DOI] [PubMed] [Google Scholar]
- 8.Bravo-Cordero JJ, Hodgson L, Condeelis J. Directed cell invasion and migration during metastasis. Current opinion in cell biology. 2012;24(2):277–283. doi: 10.1016/j.ceb.2011.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nelson CM, Bissell MJ. Of extracellular matrix, scaffolds, and signaling: tissue architecture regulates development, homeostasis, and cancer. Annual review of cell and developmental biology. 2006;22:287. doi: 10.1146/annurev.cellbio.22.010305.104315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yamada KM, Cukierman E. Modeling tissue morphogenesis and cancer in 3D. Cell. 2007;130(4):601–610. doi: 10.1016/j.cell.2007.08.006. [DOI] [PubMed] [Google Scholar]
- 11.Grinnell F, Petroll WM. Cell motility and mechanics in three-dimensional collagen matrices. Annu Rev Cell Dev Biol. 2010;26:335–61. doi: 10.1146/annurev.cellbio.042308.113318. [DOI] [PubMed] [Google Scholar]
- 12.DuFort CC, Paszek MJ, Weaver VM. Balancing forces: architectural control of mechanotransduction. Nature reviews Molecular cell biology. 2011;12(5):308–319. doi: 10.1038/nrm3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Baker BM, Chen CS. Deconstructing the third dimension–how 3D culture microenvironments alter cellular cues. J Cell Sci. 2012;125(13):3015–3024. doi: 10.1242/jcs.079509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Petrie RJ, et al. Nonpolarized signaling reveals two distinct modes of 3D cell migration. The Journal of cell biology. 2012;197(3):439–455. doi: 10.1083/jcb.201201124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Canty EG, et al. Coalignment of plasma membrane channels and protrusions (fibripositors) specifies the parallelism of tendon. The Journal of cell biology. 2004;165(4):553–563. doi: 10.1083/jcb.200312071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Provenzano PP, et al. Collagen density promotes mammary tumor initiation and progression. BMC Med. 2008;6:11. doi: 10.1186/1741-7015-6-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Perentes JY, et al. In vivo imaging of extracellular matrix remodeling by tumor-associated fibroblasts. Nature methods. 2009;6(2):143. doi: 10.1038/nmeth.1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Weigelin B, Bakker GJ, Friedl P. Intravital third harmonic generation microscopy of collective melanoma cell invasion: principles of interface guidance and microvesicle dynamics. Intravital. 2012;1(1):32–43. doi: 10.4161/intv.21223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Alexander S, et al. Preclinical intravital microscopy of the tumour-stroma interface: invasion, metastasis, and therapy response. Curr Opin Cell Biol. 2013;25(5):659–71. doi: 10.1016/j.ceb.2013.07.001. [DOI] [PubMed] [Google Scholar]
- 20.Gritsenko GP, Ilina O, Friedl P. Interstitial guidance of cancer invasion. The Journal of pathology. 2012;226(2):185–199. doi: 10.1002/path.3031. [DOI] [PubMed] [Google Scholar]
- 21.Alexander S, et al. Preclinical intravital microscopy of the tumour-stroma interface: invasion, metastasis, and therapy response. Current opinion in cell biology. 2013;25(5):659–671. doi: 10.1016/j.ceb.2013.07.001. [DOI] [PubMed] [Google Scholar]
- 22.Vogel V, Sheetz M. Local force and geometry sensing regulate cell functions. Nature reviews Molecular cell biology. 2006;7(4):265–275. doi: 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
- 23.Stevens MM. Exploring and Engineering the Cell-Surface Interface. Biophysical Journal. 2011;100(3):189a. [Google Scholar]
- 24.Zimmerberg J, Kozlov MM. How proteins produce cellular membrane curvature. Nat Rev Mol Cell Biol. 2006;7(1):9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 25.Driscoll MK, et al. Cellular contact guidance through dynamic sensing of nanotopography. ACS nano. 2014;8(4):3546–3555. doi: 10.1021/nn406637c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sun X, et al. Asymmetric nanotopography biases cytoskeletal dynamics and promotes unidirectional cell guidance. Proceedings of the National Academy of Sciences. 2015;112(41):12557–12562. doi: 10.1073/pnas.1502970112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Uttayarat P, et al. Topographic guidance of endothelial cells on silicone surfaces with micro-to nanogrooves: Orientation of actin filaments and focal adhesions. Journal of Biomedical Materials Research Part A. 2005;75(3):668–680. doi: 10.1002/jbm.a.30478. [DOI] [PubMed] [Google Scholar]
- 28.Huang NF, et al. Myotube assembly on nanofibrous and micropatterned polymers. Nano letters. 2006;6(3):537–542. doi: 10.1021/nl060060o. [DOI] [PubMed] [Google Scholar]
- 29.Friedl P, Alexander S. Cancer invasion and the microenvironment: plasticity and reciprocity. Cell. 2011;147(5):992–1009. doi: 10.1016/j.cell.2011.11.016. [DOI] [PubMed] [Google Scholar]
- 30.Sabeh F, Shimizu-Hirota R, Weiss SJ. Protease-dependent versus-independent cancer cell invasion programs: three-dimensional amoeboid movement revisited. J Cell Biol. 2009;185(1):11–9. doi: 10.1083/jcb.200807195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lim C, Zhou E, Quek S. Mechanical models for living cells—a review. Journal of biomechanics. 2006;39(2):195–216. doi: 10.1016/j.jbiomech.2004.12.008. [DOI] [PubMed] [Google Scholar]
- 32.Gracheva ME, Othmer HG. A continuum model of motility in ameboid cells. Bulletin of mathematical biology. 2004;66(1):167–193. doi: 10.1016/j.bulm.2003.08.007. [DOI] [PubMed] [Google Scholar]
- 33.Schwarz US, Erdmann T, Bischofs IB. Focal adhesions as mechanosensors: the two-spring model. Biosystems. 2006;83(2):225–232. doi: 10.1016/j.biosystems.2005.05.019. [DOI] [PubMed] [Google Scholar]
- 34.Barnhart EL, et al. An adhesion-dependent switch between mechanisms that determine motile cell shape. PLoS Biol. 2011;9(5):e1001059. doi: 10.1371/journal.pbio.1001059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shao D, Levine H, Rappel WJ. Coupling actin flow, adhesion, and morphology in a computational cell motility model. Proc Natl Acad Sci U S A. 2012;109(18):6851–6. doi: 10.1073/pnas.1203252109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Danuser G, Allard J, Mogilner A. Mathematical modeling of eukaryotic cell migration: insights beyond experiments. Annual review of cell and developmental biology. 2013;29:501. doi: 10.1146/annurev-cellbio-101512-122308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sanz-Herrera JA, et al. On the effect of substrate curvature on cell mechanics. Biomaterials. 2009;30(34):6674–6686. doi: 10.1016/j.biomaterials.2009.08.053. [DOI] [PubMed] [Google Scholar]
- 38.Newman TJ. Single-Cell-Based Models in Biology and Medicine. Springer; 2007. Modeling multicellular structures using the subcellular element model; pp. 221–239. [Google Scholar]
- 39.Sandersius SA, Newman TJ. Modeling cell rheology with the subcellular element model. Physical biology. 2008;5(1):015002. doi: 10.1088/1478-3975/5/1/015002. [DOI] [PubMed] [Google Scholar]
- 40.Kuo JC. Mechanotransduction at focal adhesions: integrating cytoskeletal mechanics in migrating cells. Journal of Cellular and Molecular Medicine. 2013;17(6):704–712. doi: 10.1111/jcmm.12054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sung BH, et al. Directional cell movement through tissues is controlled by exosome secretion. Nature communications. 2015;6 doi: 10.1038/ncomms8164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kong F, et al. Demonstration of catch bonds between an integrin and its ligand. The Journal of cell biology. 2009;185(7):1275–1284. doi: 10.1083/jcb.200810002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Alon R, Dustin ML. Force as a facilitator of integrin conformational changes during leukocyte arrest on blood vessels and antigen-presenting cells. Immunity. 2007;26(1):17–27. doi: 10.1016/j.immuni.2007.01.002. [DOI] [PubMed] [Google Scholar]
- 44.Selhuber-Unkel C, et al. Cooperativity in adhesion cluster formation during initial cell adhesion. Biophysical journal. 2008;95(11):5424–5431. doi: 10.1529/biophysj.108.139584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Liu Y, et al. Nanoparticle tension probes patterned at the nanoscale: impact of integrin clustering on force transmission. Nano letters. 2014;14(10):5539–5546. doi: 10.1021/nl501912g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sun Z, Guo SS, Fässler R. Integrin-mediated mechanotransduction. J Cell Biol. 2016;215(4):445–456. doi: 10.1083/jcb.201609037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Li F, et al. Force measurements of the α5β1 integrin–fibronectin interaction. Biophysical Journal. 2003;84(2):1252–1262. doi: 10.1016/S0006-3495(03)74940-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Litvinov RI, et al. Binding strength and activation state of single fibrinogen-integrin pairs on living cells. Proceedings of the National Academy of Sciences. 2002;99(11):7426–7431. doi: 10.1073/pnas.112194999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sun Z, et al. Mechanical properties of the interaction between fibronectin and α5β1-integrin on vascular smooth muscle cells studied using atomic force microscopy. American Journal of Physiology-Heart and Circulatory Physiology. 2005;289(6):H2526–H2535. doi: 10.1152/ajpheart.00658.2004. [DOI] [PubMed] [Google Scholar]
- 50.Kong F, et al. Cyclic mechanical reinforcement of integrin–ligand interactions. Molecular cell. 2013;49(6):1060–1068. doi: 10.1016/j.molcel.2013.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Matsutani S, Yamamoto N. Neuronal regulation of astrocyte morphology in vitro is mediated by GABAergic signaling. Glia. 1997;20(1):1–9. doi: 10.1002/(sici)1098-1136(199705)20:1<1::aid-glia1>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 52.Tiryaki VM, et al. Texture-based segmentation and a new cell shape index for quantitative analysis of cell spreading in AFM images. Cytometry Part A. 2015;87(12):1090–1100. doi: 10.1002/cyto.a.22739. [DOI] [PubMed] [Google Scholar]
- 53.Harris JW, Stöcker H. Handbook of mathematics and computational science. Springer Science & Business Media; 1998. [Google Scholar]
- 54.Song KH, et al. Sinusoidal wavy surfaces for curvature-guided migration of T lymphocytes. Biomaterials. 2015;51:151–160. doi: 10.1016/j.biomaterials.2015.01.071. [DOI] [PubMed] [Google Scholar]
- 55.Stroka KM, et al. Water permeation drives tumor cell migration in confined microenvironments. Cell. 2014;157(3):611–623. doi: 10.1016/j.cell.2014.02.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Provenzano PP, et al. Collagen reorganization at the tumor-stromal interface facilitates local invasion. BMC Med. 2006;4(1):38. doi: 10.1186/1741-7015-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Peskin CS, Odell GM, Oster GF. Cellular motions and thermal fluctuations: the Brownian ratchet. Biophysical journal. 1993;65(1):316–324. doi: 10.1016/S0006-3495(93)81035-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mogilner A, Oster G. Force generation by actin polymerization II: the elastic ratchet and tethered filaments. Biophysical journal. 2003;84(3):1591–1605. doi: 10.1016/S0006-3495(03)74969-8. [DOI] [PMC free article] [PubMed] [Google Scholar]