Quantification of Neuronal Density across Cortical Depth Using Automated 3D Analysis of Confocal Image Stacks

Abstract

A new framework for measuring densities of immunolabeled neurons across cortical layers was implemented that combines a confocal microscopy sampling strategy with automated analysis of 3D image stacks. Its utility was demonstrated by quantifying neuronal density in macaque cortical areas V1 and V2. Series of overlapping confocal image stacks were acquired, each spanning from the pial surface to the white matter. DAPI channel images were automatically thresholded, and contiguous regions that included multiple clumped nuclear profiles were split using k-means clustering of image pixels for a set of candidate k values determined based on the clump’s area; the most likely candidate segmentation was selected based on criteria that capture expected nuclear profile shape and size. The centroids of putative nuclear profiles estimated from 2D images were then grouped across z planes in an image stack to identify the positions of nuclei in x-y-z. 3D centroids falling outside user-specified exclusion boundaries were deleted, nuclei were classified by the presence or absence of signal in a channel corresponding to an immunolabeled antigen (e.g. the pan-neuronal marker NeuN) at the nuclear centroid location, and the set of classified cells was combined across image stacks to estimate density across cortical depth. The method was validated by comparison with conventional stereological methods. The average neuronal density across cortical layers was 230 × 10³ neurons per mm³ in V1 and 130 × 10³ neurons per mm³ in V2. The method is accurate, flexible, and general enough to measure densities of neurons of various molecularly identified types.

Introduction

Understanding the relationship between the function of the brain and its structure at multiple scales necessitates quantitative investigations of structure at each relevant level. The advent of connectomics has highlighted the need for automated quantification methods to analyze structure down to the level of synapses across large regions of tissue, as the size and scale of the datasets necessary to investigate the statistical structural composition of brain structures exceeds the practical limits of existing manual methods (Helmstaedter and Mitra 2012; Plaza et al. 2014; Lichtman et al. 2014). Even at the level of microstructure—for example, measuring the densities and distributions of different types of neurons in a brain region—the amount of detail that can be captured without implementing automated strategies is limited by the scale of measurements that can be made using even the most efficient manual methods. Many applications across neuroscience, including comparisons of structural changes associated with experimental manipulations, disease states, and age, as well as the building of biologically realistic models of circuits, necessitate accurate quantification of the number of neurons in general and of specific subtypes. To this end, investigators continue to rely on manual quantification by expert observers to obtain sufficiently accurate measurements (West 1999; Schmitz and Hof 2005; Schmitz et al. 2014).

Quantifying particle number and particle density (in our case, cell density) from 2D microscope images is complicated by natural variations in properties such as size, orientation, and shape. Incorrect assumptions about those naturally varying properties can introduce bias into estimates of particle number (West 1999; Schmitz and Hof 2005; Schmitz et al. 2014). Early attempts to respond to these inherent complications focused on identifying potential sources of bias, predicting the effect of individual sources, and then applying correction factors to estimate the true particle number or density. For example, the Abercrombie correction estimates particle number by measuring the number of profiles in a section and multiplying by the ratio between section thickness and the sum of the section thickness plus the mean diameter of objects in the dimension perpendicular to the plane of section (Abercrombie 1946; Guillery 2002).

In subsequent years, investigators identified alternative strategies for measuring cell number that focused on careful methodological design to avoid introducing systematic sources of known or unknown bias. It has become standard to use geometric model-based, theoretically unbiased sampling strategies, generally referred to as stereological methods (Sterio 1984; Gundersen et al. 1988; Weibel 1989; West 1999; Schmitz and Hof 2005). This includes the adoption of counting probes designed to provide unbiased estimates of quantities, such as the optical disector probe or the counting brick probe for measuring particle/object number (Sterio 1984; Howard et al. 1985; Williams and Rakic 1988), as well as the use of efficient systematic random sampling to provide accurate measurements with minimal samples (Weibel 1989; Gundersen et al. 1998). Both the optical disector and counting brick probes eliminate sources of bias from variations in cell size, shape, and orientation through the implementation of exclusion edges or planes in each spatial dimension; that is, objects that intersect any of three boundaries are eliminated from the sample (Gundersen 1977; Sterio 1984; Howard et al. 1985; Williams and Rakic 1988). The optical fractionator is a method that incorporates all of these features to estimate total particle number by counting neurons with uniformly spaced optical disector/counting brick probes that comprise a known fraction of the total volume of the tissue being sampled (Gundersen 1986; West et al. 1991).

Two other cell number measurement strategies that avoid bias by design are the isotropic fractionator (Herculano-Houzel and Lent 2005) and flow fractionator (Collins et al. 2010b; Young et al. 2012) methods. Both approaches involve homogenizing large blocks of tissue, distributing the homogenate evenly in either a Neubauer chamber (isotropic fractionator) or a liquid suspension (flow fractionator), and counting cells in this redistributed preparation. This avoids any systematic bias related to the positioning of cells in tissue, including cell orientation and local variations in density. These methods also avoid size bias because they don’t involve bisecting cells by sectioning or imaging, which would create the potential for oversampling large cells. Each of these methods, however, loses information about the arrangement of neurons within a brain region of interest. Recently, Miller et al. (2014) showed that both the isotropic fractionator and the flow fractionator methods produce estimates of cell and neuron number concordant with those from the optical fractionator method. Therefore, all three methods are likely to produce accurate estimates of neuron number, while only the optical fractionator method retains information about local position of neurons.

While stereological methods are designed to yield an unbiased estimate of numerical density with maximal efficiency, they are nevertheless labor intensive and time consuming. Automatically counting cells takes advantage of computation to expand what an observer can accomplish, enabling sampling over larger regions that can directly capture patterns of local variation. Automatic cell counting, however, is a non-trivial problem. Stained cells can be separated from background by intensity thresholding and identified as contiguous regions of foreground staining, but the dense packing of cells often causes groups of multiple cells to be recognized as single objects. Common strategies for subsequently segmenting these clumps into their constitutive cells include feature detection, including edge-based and blob detection methods; region-growing, including watershed algorithms; model based methods, including level sets; and combinations thereof (Bengtsson et al. 2004; Meijering 2012). Watershed-based methods are very popular but are notorious for over-segmentation, necessitating corrective strategies such as using pre-specified smaller regions as “seeds” for segmentation and/or implementing model-based merging operations following initial segmentation (Malpica et al. 1997; Adiga and Chaudhuri 2000; Bengtsson et al. 2004; Meijering 2012). A review of three representative methods compatible with 3D stereological counting—intensity thresholding only, a watershed plus merging method, and a multiple level sets method—found that none was sufficiently accurate to replace manual counting (Schmitz et al. 2014).

Strategies for segmenting one type of image may not generalize to others that vary in the uniformity of staining, the shapes of objects of interest, and the number and packing density of objects that need to be segmented. These features can vary substantially between different types of labels as well as between different species, types of tissue, or brain areas. It is unsurprising, therefore, that there are so many published methods for cell segmentation, even for seemingly very similar applications, and that while each is described as accurate when evaluated using the type of tissue and stain they were designed to measure, it is rarely the case that an automatic cell counting method, without modification, will perform with the same accuracy when applied to a different preparation.

When considering specifically the measurement of neuronal number and density, the most obvious choice of cell stains is the pan-neuronal marker NeuN (“neuronal nuclei”). NeuN is a neuron-specific nuclear protein that is expressed in neurons of nearly all types in vertebrates, although a handful of specific neuronal populations outside the neocortex have been observed to be devoid of the NeuN protein (Mullen et al. 1992; Wolf et al. 1996). Oberlaender et al. (2009) have described a method that directly segments NeuN images to count neuronal somata, which involves a variety of image pre-processing steps, an implementation of the watershed segmentation algorithm, and a neuron size-based splitting of neuron clusters that were not split by the watershed algorithm. They are also able to compare the locations of identified neurons against other channels labeled with different antibodies, such as GAD67; these strategies are implemented to complement extensive manual neuron counting in Meyer et al. (2010).

The idea that a complete population of cells segmented in one wavelength channel can then be compared against other channels containing specifically labeled subsets of the larger population has also been used to simplify the problem of neuron counting. Rather than segmenting the NeuN channel directly, it is possible to segment cell nuclei labeled with DAPI, a fluorescent stain that visualizes nuclei of all cell types by binding to DNA. This takes advantage of the relatively uniform shape of neuronal nuclei compared to entire neurons, as well as the larger distance between nearby nuclei compared to the somata that include them, thereby simplifying the task of image segmentation. The positions of cells identified in the DAPI channel can then be compared against a channel showing NeuN in order to distinguish neurons from other cell types. This sort of dual-labeling strategy has been used previously (Tsai et al., 2009; LaTorre et al., 2013a, 2013b), although with different algorithms and implementations. Tsai et al. identified the positions of cells in thresholded DAPI images by ultimate morphological erosion plus merging of close objects, and then identified neurons as cells that had more NeuN signal within the region containing the cell’s nucleus than in a shell outside the nucleus. LaTorre et al. (2013a) segmented binarized DAPI images using a strategy based on concavity detection. They then used the NeuN channel to remove DAPI signal that did not overlap with NeuN, effectively eliminating non-neuronal nuclei prior to grouping objects from the two-dimensional DAPI images across multiple planes. Finally, they matched objects across z planes by connecting object profiles that overlapped in x-y, and then corrected for under-segmentation by splitting objects whose centroids shifted by a large amount across z planes (LaTorre et al., 2013b).

Here, we used a related strategy to eliminate some of the most substantial challenges for cell segmentation and enable accurate neuron counting without sacrificing direct measurement of continuous variations in neuron density across layers of cortex. Tissue samples were immunofluorescence labeled and counterstained with DAPI. Confocal image stacks were acquired with each label in a distinct wavelength-separated channel. Images from the DAPI channel were thresholded, and possible multi-object clumps were identified and separated in each image plane, guided by information from nearby image planes. The two-dimensional centroid locations of (DAPI-labeled) nuclear profiles belonging to the same object were then grouped across z planes, yielding a centroid position in x-y-z for each object.

After identifying the positions of all nuclei in an image stack, the image channels visualizing immunolabeled antigens could be examined at each 3D centroid location to classify each cell. Because the DAPI channel was used only for determining marker positions for the approximate center of each cell, this approach reduced the need for precision in parceling all pixels into their native nuclei. As will be described in the Discussion, this strategy also facilitates comparisons of co-expression of antigens other than NeuN, even when those antigens differ in subcellular localization. The use of DAPI rather than NeuN for segmentation also leaves the possibility of avoiding NeuN processing when not required for a given application, and frees a wavelength channel to measure expression of an additional neuron type-specific marker.

To demonstrate the utility of this method, we applied it to the example problem of quantifying the numerical density of neurons in primary visual cortex (V1) and in the second visual cortical area (V2). Because of the increased ease of analyzing large counting volumes and the strategy of sampling continuously across cortical depth, we were able to sample about 32,000 cells (22,000 neurons and 10,000 non-neuronal cells) in V1 and 18,000 cells (12,000 neurons and 7,000 non-neuronal cells) in V2 and measure continuous changes in neuronal density as a function of cortical depth. Although the total number of cells counted in manual stereological studies is not often reported, it is typically much lower. For example, Kim et al. (1997) counted between 630 and 1,547 neurons.

Materials and methods

Tissue preparation

Tissue samples were from six young adult male macaque monkeys (five Macaca fascicularis, M1–M3, M5–M6; one Macaca mulatta, M4) that were used for previous anesthetized electrophysiological experiments (Cavanaugh et al. 2002; Goris et al. 2015). After 5–6 days of acute electrophysiological recording, experiments were terminated by intravenous injection of a lethal dose of pentobarbital (60 mg/kg), and brain death was determined by a flat electroencephalogram. Each animal was perfused transcardially with heparinized 0.01 M phosphate-buffered saline (PBS, pH 7.3), followed by 4 L of 4% paraformaldehyde (PFA) plus 0.125% glutaraldehyde in 0.1 M phosphate buffer (PB, pH 7.4). Extracted brain tissue was blocked and postfixed overnight in 4% PFA at 4°C. Blocks containing V1 and dorsal V2 were cut into serial 50 μm parasagittal sections using a vibratome. Sections were rinsed with 1% sodium borohydride in 0.1 M PB to reduce the antigen masking effects of glutaraldehyde. All sections were immersed in graded sucrose solutions to prepare them for freezing and then stored in cryoprotectant solution at −20°C until the time of immunohistochemical processing.

Free-floating sections were stained for the pan-neuronal marker NeuN using an immunofluorescence protocol adapted from the iDISCO method (Renier et al. 2014), excluding the final brain clearing steps. This protocol was combined with an antigen retrieval procedure, which counteracts the antigen masking effects associated with aldehyde fixation (Shi et al. 1991) and was carried out as previously described in our lab (García-Marín et al. 2013).

Sections were incubated in a sodium citrate buffer solution (3.8% citric acid, 2.4% sodium citrate; pH 8.0) for 15 min in an 80°C water bath, followed by 20 min at room temperature. Sections were next dehydrated in 0%, 50%, 80% and twice in 100% methanol/0.01 M PBS for 30 min each, chilled over ice, and bleached in 5% hydrogen peroxide in 20% DMSO/methanol at 4°C overnight. They were then rinsed twice in 100% methanol for 30 min each, incubated in 20% DMSO/methanol for one hr, and rehydrated in 80%, 50%, and 0% methanol/PBS. They were then incubated twice in 0.3% Triton-X/0.01 M PBS for 30 min at room temperature, and then incubated for 2 hrs at 37°C in 0.3% Triton-X/20% DMSO/0.3M glycine/0.01 M PBS. Sections were blocked for 2 hrs at 37°C in 0.3% Triton-X/10% DMSO/6% NGS/0.01 M PBS, rinsed twice in 0.2% Tween-20/0.01 M PBS with 10 μg/mL heparin (PTwH) for 30 min each, and incubated overnight at 4°C with guinea pig anti-NeuN (1:1000; ABN90P, Millipore, Billerica, MA, USA). Sections were rinsed three times in PTwH and then incubated overnight at 4°C with biotinylated goat anti-guinea pig IgG (1:500; BA-7000, Vector, Burlingame, CA, USA), and finally rinsed and incubated overnight in Alexa Fluor ® 647 streptavidin conjugate antibody (1:2000; S-32357, Invitrogen, Carlsbad, CA, USA). After a final three rinses in PBS, Autofluorescence Eliminator Reagent (2160, Millipore) was used according to the manufacturer’s protocol to minimize lipofuscin-like autofluorescence. Finally, sections were counterstained with 10 μg/mL DAPI (D9542-5MG, Sigma-Aldrich, St. Louis, MO, USA) and mounted in ProLong Gold Antifade Reagent (P-36930, Invitrogen). Some sections were also labeled with additional antibodies in other wavelength-separated channels, but those details are irrelevant to the current study.

Image acquisition

Fluorescence sections were imaged using a Leica TCS SP5 confocal system (Leica Microsystems, Wetzlar, Germany). A 633 nm HeNe laser was used to excite the anti-NeuN-conjugated fluorophore and a 405 nm UV diode laser was used to excite DAPI. Gain and offset levels were set for each channel such that bright labeled regions in preview scan images were at saturation and there was minimal background noise. Image stacks were acquired by specifying an upper and lower z position and acquiring images of each channel sequentially, using a 63× oil-immersion objective lens (NA 1.4, refraction index 1.45), and a pinhole size of 1 airy unit. The z step size was 0.5 or 1 μm, and the (x-y) image resolution per frame was 1024 × 1024 pixels (246.03 μm × 246.03 μm). The scanning speed was 200 Hz for image stacks used for validation and measurement of density in V1 and 400 Hz for stacks used to measure density in V2.

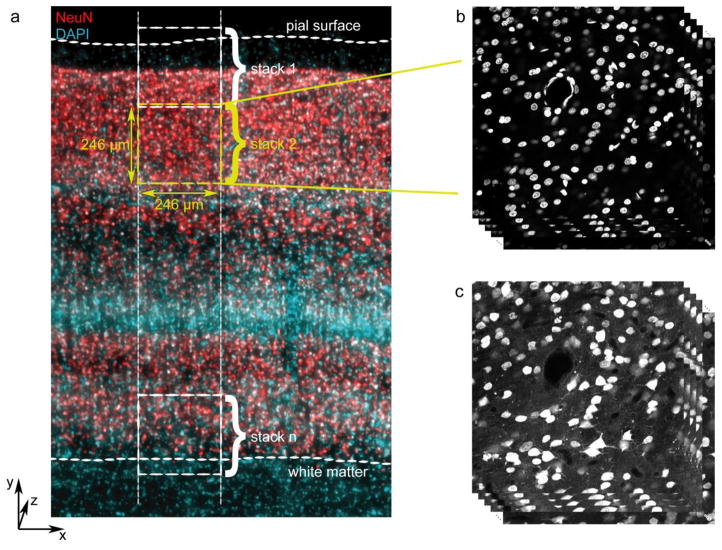
Images were acquired either from the opercular surface of area V1 – confirmed visually by the presence of the stria of Gennari and by the presence of multiple subdivisions of layer 4 (layers 4A, 4B, and 4C) that visibly differed in densities of DAPI-stained nuclei – or from dorsal V2, sampled along the posterior bank of the lunate sulcus. A strip of tissue was selected spanning from the pial surface to the white matter and oriented orthogonal to the pial surface, as shown in Figure 1a. A series of 5–9 z stacks was acquired, beginning with a sample that included the pial surface (Fig. 1a, stack 1) and subsequently moving in the direction of the white matter such that each sequential volume overlapped slightly in the y (pial surface-white matter) dimension and as completely as possible in the x dimension. The final z stack contained the boundary between layer 6 and white matter (Fig. 1a, stack n).

Fig. 1.

Image acquisition. a Schematic of image sampling strategy, overlaid on a micrograph showing NeuN (red) and DAPI (cyan). Sampling regions spanned from slightly above the pial surface to slightly below the layer 6-white matter boundary and were comprised of smaller (246 μm × 246 μm in x-y) image stacks that overlapped slightly in the “y” dimension. b Example image stack showing the DAPI channel. c Example image stack from the same location as (b), but showing the NeuN channel for the same z planes

For the quantification of neuronal density in V1, eleven series of confocal image stacks were acquired, with three to five series from each animal such that the total thickness (z distance) sampled from each animal was greater than 55 μm (corrected for tissue shrinkage) after eliminating guard regions near the surface and regions near the middle of the tissue that were beyond the limit of antibody penetration. One series from monkey M3 was acquired with 0.5 μm z steps, and the other 10 series were acquired with 1 μm z steps. Neuronal density in V2 was measured from seven series of confocal image stacks, with two to three series from each animal such that the total shrinkage-corrected thickness sampled from each animal was greater than 70 μm after eliminating guard regions and regions beyond the limit of antibody penetration. All series from V2 were acquired with 0.5 μm z steps.

Image preprocessing

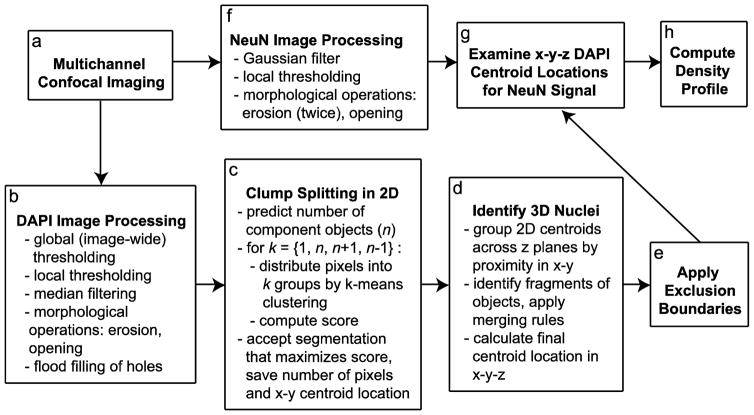
An overview of the automated image analysis procedure is shown in Figure 2. Raw images were exported and saved as grayscale TIFF image stacks. All subsequent image processing and centroid identification was implemented in MATLAB. Because DAPI staining within individual nuclei is often non-uniform in intensity, a median filter (neighborhood size 3 pixels) was applied to eliminate punctate bright regions while preserving the edges of nuclei.

Fig. 2.

Overview of automated counting method. a Images from the DAPI and NeuN channels were processed separately. b–e After preprocessing DAPI images (b), nuclear profiles were identified by thresholding, and probable clumps of multiple nuclear profiles were separated into component profiles in 2D (c). These 2D profiles were matched across z planes and grouped into 3D nuclei (d), and nuclei centered outside specified exclusion boundaries were deleted (e). g The 3D (x-y-z) centroid locations of included nuclei were then evaluated in the NeuN channel, which had been preprocessed separately (f). h Finally, the y positions from the full set of identified cells, each categorized as either NeuN-positive or NeuN-negative, were used to compute density as a function of relative cortical depth

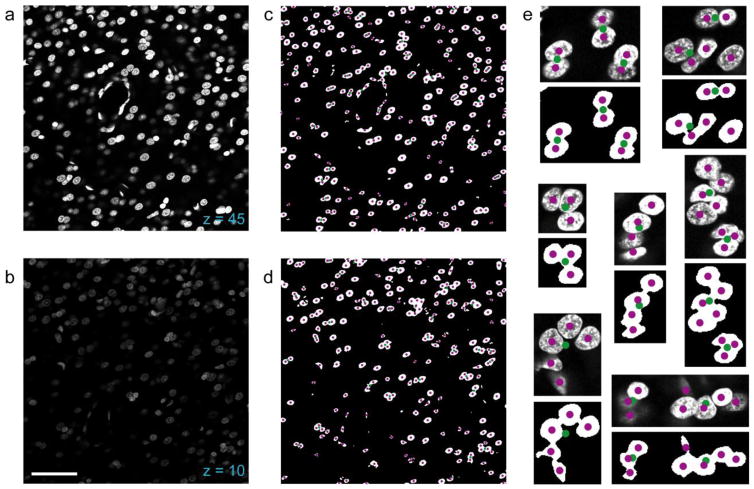
A combination of local and global thresholding on each image (z) plane facilitated the separation of foreground (nuclei) from background despite local variations in background brightness due to tissue autofluorescence and fluorescence from nuclei in other planes. First, all pixels with intensity less than the half the threshold level from Otsu’s (1979) method were set to zero. Second, because focus planes beyond the cut edges of the tissue sometimes included low intensity signal from nuclei in other focus planes that might be misclassified as foreground in the absence of actual foreground signal, a stack-wide minimum threshold level was calculated as half the threshold level from Otsu’s method in a user-specified image plane near the bottom of the section; for each section, any pixels with intensity below this threshold were also set to zero. Local thresholding was then applied using the algorithm of Bradley and Roth (2007), as implemented by Motl (2013). This yielded a series of binary images on which all subsequent operations were performed. A morphological erosion followed by an opening operation were applied, using a disk-shaped structuring element of radius 2 pixels for both operations; this helped to smooth the edges of nuclei, which was useful when detecting concavities in a later step. Finally, regions fully enclosed by foreground pixels were filled by flooding, yielding binary images as shown in Figure 3c–d.

Fig. 3.

DAPI thresholding and clump splitting in 2D. a Example confocal micrograph of the DAPI channel from a z plane near the upper surface of the tissue (closer to the objective lens). b Example confocal micrograph from a z plane closer to the bottom surface of the tissue (closer to the slide). Compared to the image from (a), which was taken from the same image stack, the image in (b) shows considerable attenuation in intensity of the signal. c Binary image obtained by processing the image in (a), with overlaid markers showing the set of centroids of putative nuclei identified as connected component objects (green) and the set of 2D nuclear centroids after segmentation (magenta). d Same as (c), but corresponds to the z plane in (b). The quality of image processing and segmentation is unaffected by the attenuation in signal intensity of the original image. e Higher magnification examples of identified nuclei and their centroid locations before (green) and after (magenta) the clump splitting procedure. Each example is shown as a pair, with the original micrograph above the processed image. Scale bar in (b): 50 μm (a–d), 15 μm (e)

Separation of overlapping nuclei and 2D centroid identification

Putative nuclei were first identified as connected component regions of foreground pixels, each with an associated area and centroid location in x-y; the list of regions included both single nuclear profiles and clumps of multiple profiles that abutted each other (Fig. 3c–e). The median area of contiguous regions exceeding 100 pixels was used as an estimate of the area of a single nuclear profile, and regions with an area exceeding the median value were identified as possible groups of multiple nuclei.

Each region suspected to contain multiple profiles was subjected to the following segmentation procedure. First, the number of distinct nuclei (n) in the clump was predicted by dividing the area of the region by the median area of all regions in the image and rounding to the nearest integer value. Because nuclei vary in size, we also considered that the region could correspond to n+1 or n-1 nuclei. The pixels in the original region were then separated into appropriate subsets by k-means clustering using the squared Euclidean distance metric; this was done for up to four candidate possibilities, with k=1, k=n, k=n+1, and k=n-1. This yielded the sets of pixels corresponding to the proposed subregions as well as the x-y positions of their centroids.

These candidate segmentations were evaluated for their consistency with built-in expectations about nuclear shape. Because cell clusters varied in the number and arrangement of component nuclei, there were multiple features useful for separating them, and different features were often more informative for separating different groups of nuclei. For this reason, it proved useful to consider multiple features when selecting the candidate segmentation most likely to represent the actual nuclei present. Candidates were assigned scores for each of four criteria. The first score was the ratio of the region’s area relative to the area inside the region’s convex hull, with a maximum value of 1 representing a perfectly convex object. The second score measured how well the filled and unfilled pixels in the unsegmented region could be predicted by overlapping area-matched circles centered at the centroids generated by clustering. More specifically, each pixel inside the unsegmented region that fell outside the sets of pixels enclosed by the matched circles and each pixel inside the circles that was not part of the actual object region was considered an error and weighted linearly by distance to the nearest circle center or the edge of the nearest circle, respectively. The criterion score was the sum of squares of these errors. The third score was the absolute value of the difference of one and the original region area divided by k times the median object area. The fourth score compared the candidate segmentation centroids to the centroids of objects in nearby z planes. For each newly assigned centroid it identified the centroids in the z planes 2 μm above and below the current plane that were nearest in x-y. It then took the matching centroid with the minimum x-y distance for each segmented centroid, and computed the mean distance across all segmented candidate centroids as the criterion score.

The second, third, and fourth criterion scores were each normalized by dividing by the maximum candidate score for that criterion and converted to their reciprocal values. A fifth, binary criterion score was computed, which demanded that any segmented centroids have a sufficiently large concavity present between them. All five criterion scores were combined multiplicatively into a summary score for each candidate, with the second criterion score given double (exponential) weight. The selections of criteria and weights were made empirically by iteratively adding criteria and adjusting their relative weighting to correct observed patterns of segmentation errors in the test set of manually annotated image stacks. For example, the demand that centroids have a concavity between them was introduced primarily in response to the observation that some atypically large neuronal nuclei were segmented seemingly arbitrarily into multiple nuclear profiles on the basis of size despite being approximately spherical.

The candidate segmentation that maximized this summary score was selected, and the list of nuclear profiles in the image plane was updated to reflect the newly separated nuclei. At this stage, any profile with pixels intersecting either the rightmost or bottommost edge of the image was tagged for later application of optical disector exclusion boundaries.

Calculation of 3D centroids from 2D centroids

The set of 2D (x-y) centroids from all z planes in a stack were then grouped into 3D objects. For each 2D centroid, the algorithm identified the 2D centroid in the previous z plane that was closest in x-y. If the nearest centroid was within a specified x-y radius (for our images, this was set to 0.5 μm), those centroids were grouped as parts of a single object. If the adjacent plane did not contain a sufficiently close centroid, the algorithm considered the z plane previous to the adjacent plane. This provided some tolerance for missing 2D centroids due to occasional errors in 2D segmentation.

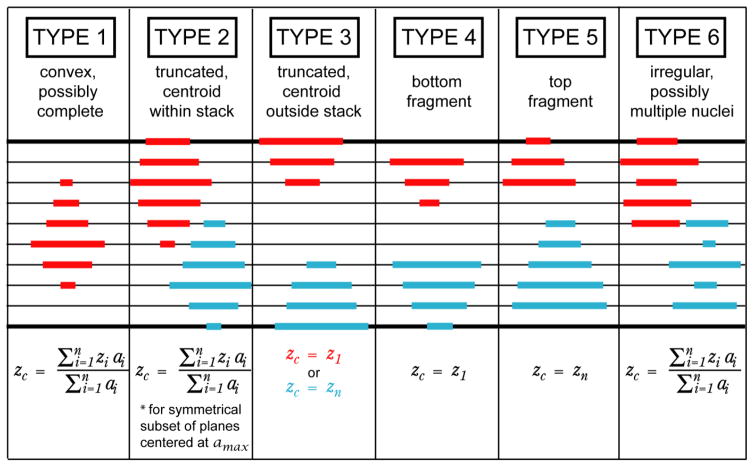
After this first grouping step, 3D objects were classified as one of six types (Fig. 4) based on whether they appeared to be complete convex nuclei. The vector of areas of grouped nuclear profiles, ordered by z plane, was first smoothed with a five-point moving average filter. Type 1: If none of the 2D centroids was in either the highest or lowest plane of the stack, and if the profile areas increased monotonically to a maximum value and then decreased, the object was classified as type one (possibly a complete, convex nucleus). Type 2: If any of the 2D centroids were in either the highest or lowest plane of the stack and the profile areas increased monotonically to a maximum value and then decreased, but the area of the 2D profile in that plane was not the maximal profile area in the object, the object was classified as type two (3D object centroid likely falls within the stack, but object is erroneously truncated). Type 3: If any of the 2D centroids were in either the highest or lowest plane of the stack, and the area of the 2D profile in that plane was also the maximal profile area in the object, the object was classified as type three (actual 3D object centroid likely falls at or beyond the stack boundary). Type 4, 5: If the maximal profile area was at either the highest or lowest z plane of the grouped object, the object was classified as either type four (probable incomplete “bottom” cap) or type five (probable incomplete “top” cap). Type 6: If the smoothed vector of profile areas had multiple local maxima, the object was classified as type six (irregular; possibly multiple nuclei).

Fig. 4.

Object categories used to evaluate merging possibilities and compute z positions of 3D centroids. Top row Object category numbers and descriptions. Middle row Examples of objects that would be categorized as a given object type. Bold black horizontal lines represent the z planes at the boundaries of the image stack, while thinner intermediate horizontal lines represent intervening z planes. Individual nuclear profiles grouped as one object are shown as red or cyan lines, as though viewed from the side (collapsing over either x or y). Bottom row Formula for computing the z position of the 3D centroid, with symbols as follows: z_i, z position of a 2D centroid; z₁, z position of grouped 2D centroid closest to the upper stack boundary; z_n, z position of grouped 2D centroid deepest into the stack; z_c, assigned z position of 3D centroid; a_i, area of the 2D profile corresponding to a 2D centroid; a_max, area of the largest 2D profile in the grouped object

A centroid position in x-y-z was calculated for each 3D object. The x and y positions of the centroid were the medians of the x and y positions of the 2D centroids grouped to form that object. The z position was calculated differently based on the object type, as summarized in the lowest portion of Figure 4. For object types one and six, the centroid z position was equal to the weighted mean of the z positions of the set of 2D centroids in the group, with weight equal to the area of the profile at a given z plane. For type two, a weighted mean was computed as for types one and six, but it was computed for a symmetrical subset of the 2D profiles that included all z planes between the stack boundary and the profile with the largest area, plus an equal number of adjacent z planes on the other side of the largest profile; this was done because it was assumed that part of the nucleus was truncated by the stack boundary, and so a weighted mean across all profiles in the group would have shifted the z position of the centroid toward the middle of the image stack. For types three, four, and five, the 3D centroid z position was set to be the z position of the maximal profile area. After the initial grouping, any groups consisting of only a single 2D centroid were dropped.

Next, we identified separately grouped 3D objects that were likely to be fragments of the same nuclei. First, objects of type four and five were considered, as they were most likely to be fragments of incomplete objects. For each type four/five object, two regions were searched for nearby objects (of any type): first, a spherical search region with radius equal to five-sixths of the median profile diameter, and second, a cylindrical search region with radius in x-y equal to one third the median profile diameter and extent in z equal to the median profile diameter. After considering the type four and five objects, objects of all types were evaluated using a spherical search region with radius equal to two-thirds of the median profile diameter. In all cases, identified nearby objects were only grouped if that grouping would either improve or maintain the similarity of the resulting object to a complete or truncated convex shape; the full set of these merging criteria are shown in Table 1. Finally, any 3D objects within a cylindrical search region with x-y radius two-thirds of the median profile diameter and z length equal to half the z step size were combined, regardless of the effect of their combination on object type.

Table 1.

Merging rules. A pair of objects with a set of types shown in the right column was allowed to be merged if the resulting object was any of the object types in the left column

If Result is Type	Merge if Original Types
1, 2, or 3	any
4 or 5	{4,4}, {4,5}, {5,5}
6	{6,6}

When merging objects, the x, y, and z positions of the new 3D centroids were computed as before. When merging a pair of objects that overlapped in z, the area in a given z plane was the sum of the number of pixels in that plane from both objects being combined, and the 2D (x-y) centroid position in each plane was the mean of 2D centroids in that plane. As a final step, objects were eliminated if they were likely to be false positives based on either of two criteria: they were comprised of fewer than three 2D centroids, or they spanned less than one fourth the median profile diameter in the z dimension.

Application of exclusion boundaries

To avoid sampling biases, the full set of identified nuclear centroids within an image stack was then restricted to a specialized 3D counting volume adapted from the counting box/counting brick (Howard et al. 1985; Williams and Rakic 1988). Any object containing a profile that intersected either the farthest right or the lowest edge of an image was deleted from the set. In the z dimension, the user specified upper and lower z planes as boundaries. Objects with centroids above the upper plane were excluded, while objects with centroids at or below the lower plane were excluded.

For the z stacks used for method validation, the upper z boundaries were determined by identifying the approximate position of the tissue surface and subtracting two z planes, leaving a 1 μm thick guard region between the exclusion boundary and the limit of the tissue. The lower z boundaries were three or four planes (1.5–2 μm) from the lower limit of the image stack.

For the image stacks used to quantify neuron density, the upper and lower tissue surfaces were identified for each stack, as were the limits of antibody penetration in the NeuN channel. A minimum of 3 μm was left as a guard region from each surface. If the NeuN antibody did not penetrate the full depth of the tissue, then the volume was subdivided into two sub-volumes, each starting 3 μm from one tissue surface and extending inward into the tissue to the depth of the NeuN penetration. The depth of each sub-volume was decreased until its volume matched the minimum usable volume from the corresponding surface (upper or lower) across image stacks in the series, such that the same volume was sampled from both surfaces in every image stack from a given series. The number of nuclei from both sub-volumes in an image stack were combined before collapsing across the x and z dimensions to calculate the density profile across cortical depth. In these image stacks, cells were also eliminated if the y positions of their centroids fell within the region of overlap with the image stack immediately below the one being evaluated.

Validation of DAPI segmentation method

A set of seven image stacks were acquired from various layers of area V1, each spanning approximately 10 μm in the z dimension, with 0.5 μm z steps. These image stacks were selected to be representative of the natural variability in cell density and uniformity that occurs across cortical depth. The nuclei in these image stacks were counted manually by placing a marker at the estimated x-y-z centroid of each object using the Cell Counter plugin for ImageJ (NIH, http://imagej.nih.gov/ij/, Rasband 1997–2012). Three stacks were used for determining the appropriate parameters for grouping objects, while the remaining four were held out for validation.

For each image stack, the automatically determined centroids were compared to the manually marked centroids. For the specified range of z planes, we compared the absolute number counted manually with the number counted automatically. We also used an approach similar to that described by Schmitz et al. (2014) to more directly compare the two sets of centroids. For each manually marked centroid, we searched for an automatically marked centroid within a cylindrical region centered at the manually marked centroid (i.e. within a radius of 3 μm in x-y and within 3 μm in z). If there were one or more automatically identified centroids in this search region, the closest was labeled as a match for the manually marked centroid. Automatically identified centroids that were matched to manually marked centroids were used to calculate a true positive rate (number of matched centroids divided by total number of manually marked centroids). Automatically identified centroids that were not matched were considered false positives. The false positive rate was calculated as the number of false positives divided by the number of automatically identified centroids. Manually marked centroids that were not matched with automatically marked centroids were designated false negatives.

Classification of neurons by NeuN staining

The DAPI-labeled nuclei were classified as either neurons or non-neuronal cells (e.g. glia, endothelial cells) by determining whether there was immunolabeling for NeuN at the location of the 3D DAPI centroid. A threshold-based mask was generated for each image plane in the NeuN channel. The NeuN images were blurred with a Gaussian filter with sigma equal to 2 pixels, then converted to a binary mask by first applying the local thresholding algorithm of Bradley and Roth (2005) followed two morphological erosion operations and one opening operation, each with a disk-shaped structuring element of size 2 pixels. In the nearest z plane to a given DAPI centroid, the number of NeuN-positive pixels were counted within a circular region with a radius equal to two thirds the radius of the corresponding DAPI profile. If at least 90% of pixels in this region were NeuN-positive, the object was classified as a neuron.

Calculation of numerical density

After categorizing all cells within the exclusion boundaries, the position of each cell within a counting volume was converted to the distance of that cell from the pial surface in image pixel units. This was done by adding the y-position of the cell within its counting frame to the total number of pixels in the y dimension in counting volumes taken from closer to the pial surface (i.e. 1024 pixels per counting volume) and subtracting the y position of the pial surface in the uppermost counting volume and the cumulative number of overlapping pixels in the y dimension between successive z stacks. The position of the layer 6-white matter boundary was measured, converted by the same calculation to a measure of total cortical depth, and used as a divisor to convert cell positions to units of relative cortical depth (relative cortical depth = cell depth/white matter depth). The normalized cell depths were sorted into 40 equally sized bins (2.5% of total cortical depth each), and the number of cells per bin was quantified. This yielded the distribution of neurons across cortical depth.

The neuronal counts were converted to densities by dividing the number of counted neurons by the sampled volume in each bin, corrected to account for tissue shrinkage. The degree of tissue shrinkage in the z dimension was quantified by identifying the upper and lower surfaces of the mounted tissue section in the confocal images from the DAPI channel and comparing the distance between them (mean measured distance for V1: 35.4 μm ± 1.4 μm SEM, N = 11; mean measured distance for V2: 28.6 μm ± 1.3 μm SEM, N = 7) with the 50 μm thickness of each section at the time of sectioning. The degree of shrinkage in x and y was estimated for each series in the approximate region sampled by identifying the same blood vessels in the immunolabeled section from which counts were made and in an adjacent unprocessed section, imaged using an Olympus VS120-FL virtual slide scanning system (Olympus America, Center Valley, PA, USA). The unprocessed sections were removed from storage, thawed, rinsed three times in 0.01 M PBS or 0.1 M PB, and then mounted on slides and imaged while wet, in the absence of any mounting medium. The extent from the pial surface to the white matter (y length) at the locations of blood vessel landmarks and the horizontal (x) lengths between landmarks at the level of the stria of Gennari were measured from the images acquired of each pair of sections. The means of x and y length measurements in local regions surrounding the sampled sites were used to estimate the degree of shrinkage due to processing. Across sections used for V1, the mean shrinkage in x was 19 percent, while the mean shrinkage in y was 11 percent; that is, the original size in the x dimension was 1.24 times the size after processing, while the original size in the y dimension was 1.12 times the size after processing. Across sections used for V2, the mean shrinkage in x was 20 percent, while the mean shrinkage in y was 15 percent; that is, the original size in the x dimension was 1.26 times the size after processing, while the original size in the y dimension was 1.17 times the size after processing.

Because within-animal samples differed greatly in volume, primarily due to differences in the total depth in the z dimension that was limited by antibody penetration, it was inappropriate to estimate densities for each animal by taking the mean of samples from that animal. Instead, counts within each cortical depth (y) bin were summed, as were bin volumes across samples. The combined bin counts were divided by the combined bin volume to produce an average density profile for each animal. Between animals, total sampled z depth was better matched, so an average density profile was generated by taking the mean of the three animals’ density profiles.

Results

Qualitative evaluation of segmentation performance

Examples of 2D thresholding and clump splitting performance are shown in Figure 3. Thresholding was effective at separating foreground from background both in z planes near the upper surface of the tissue (closer to the objective lens), where the signal was minimally attenuated and many DAPI-labeled pixels were at saturation (Fig. 3a,c), and at planes near the lower surface of the tissue (closer to the slide), where signal was dimmer (Fig. 3b,d).

The strategy for clump splitting – which predicted the number (n) of profiles present in the clump, split them into candidate sets with n, n+1, n-1, and one component profile(s) by k-means clustering, and selected the most likely candidate based on assumptions about the shape of neuronal nuclei – was largely effective at parceling clumps with varying numbers and arrangements of constitutive nuclei. Examples of initially identified connected-component “objects” (green markers) and the resulting constitutive profiles after 2D clump splitting (magenta markers) are shown in Fig. 3c–d, and for selected clumps at higher magnification in Fig. 3e.

Quantitative evaluation of segmentation and 3D grouping performance

The accuracy of the automatically generated 3D centroid locations for nuclear objects in confocal image stacks from DAPI-stained tissue was tested by comparison with manually annotated centroid locations. Test stacks were selected from different cortical layers to represent the natural variability in features such as cell density and nucleus size. Comparing the absolute number of nuclei counted automatically versus manually in a specified volume showed that the automated method accurately estimated the number of nuclei. The ratio of automatically to manually identified nuclei from the test image stacks that had been held out for validation ranged from 0.94 to 1.00, with a mean value of 0.98 (N=4 stacks).

To evaluate whether the numerical accuracy reflected accurate identification of nuclei, we used the approach of Schmitz et al. (2014) to match manually marked centroids with their automatically identified counterparts. More specifically, for each manually annotated centroid, the nearest automatically generated centroid in x-y-z was identified; if this centroid was within a 3 μm radius in x-y and within a 3 μm span in z, the centroid was considered a match for the manually annotated centroid and added to a list of “true positives.” After considering all manually marked centroids, all unpaired manually identified centroids were designated “false negatives” and all unpaired automatically identified centroids were designated “false positives.” For the four test image stacks, the mean true positive rate (number of true positives divided by number of manually counted cells, i.e. recall) was 0.93 (range 0.91 – 0.95). The mean false positive rate (number of false positives divided by number of automatically counted cells, i.e. one minus precision) was 0.05 (range 0.05 – 0.06).

The centroids falling into both error categories were then compared against the NeuN channel to determine the degree to which segmentation errors would influence estimates of the number of neurons. Of 915 identified true positives, 699 (76%) were neurons. In contrast, 30 out of 76 false negatives (39%) and 25 out of 52 false positives (48%) were neurons. True positive and false positive rates were recomputed for each category (neurons and non-neuronal cells). While the mean true positive rate for the four test stacks was 0.93 across both cell categories, the mean true positive rate was 0.96 for neurons and 0.83 for non-neurons, such that the true positive rate for neurons was significantly higher than that for non-neuronal cells (p=0.01, Wilcoxon rank-sum test, one-tailed) and for the full population (p=0.03, Wilcoxon rank-sum test, one-tailed). The mean false positive rate was 0.053 across both cell categories, compared to 0.035 for neurons and 0.11 for non-neurons; the false positive rate for neurons was significantly lower than that for non-neuronal cells (p=0.01, Wilcoxon rank-sum test, one-tailed), but not for the full population (p=0.06, Wilcoxon rank-sum test, one-tailed). Finally, a total error rate, computed as one minus the true positive rate plus the false positive rate, was 0.13 across both cell categories, compared to 0.075 for neurons and 0.28 for non-neurons; the total error rate was significantly lower for neurons compared to both the total population (p=0.01, Wilcoxon rank-sum test, one-tailed) and to non-neuronal cells (p=0.01, Wilcoxon rank-sum test, one-tailed). In this test set, the number of neurons identified automatically (true positives plus false positives: 724) was 99% of the number of neurons identified manually (true positives plus false negatives: 729) within the same counting volume. The number of non-neuronal cells identified automatically (243) was 93% of the number of non-neuronal identified manually (243). While the method was quite accurate overall, it performed even better for segmenting neuronal nuclei. This was unsurprising given that the assumptions about nuclear shape were intended to match the more spherical shape of neuronal nuclei and not the non-spherical shapes characteristic of nuclei of other cell types, such as epithelial cells and astrocytes (Luse 1956; Cammermeyer 1960; Peters et al. 1991). We therefore concluded that the method could accurately measure neuronal density.

Effect of z step size on performance

Image z stacks used to evaluate the accuracy of cell counting and localization had a z step size of 0.5 μm. Therefore, neuronal nuclei with diameters of approximately 6–8 μm would be expected to appear in 12–16 image planes. While some steps in the algorithm were designed to be tolerant of 2D segmentation errors, it would be expected that for image stacks with fewer planes per nucleus, 2D segmentation errors would have a greater impact on counting performance. Therefore, we tested two image stacks that were sampled at 0.5 μm steps through the entire depth of a 50 μm section. In each image stack, we deleted every second z plane, creating a new image stack containing all the same objects but with an effective z step size of 1 μm, such that a single nucleus would be expected to appear in 6–8 image planes. Using the same strategy, we also generated matched image stacks with a step size of 2 μm, such that a single nucleus would be expected to appear in 3–4 image planes. As expected, we initially obtained lower cell counts for the 1 and 2 μm step size image stacks than for the original stacks with a step size of 0.5 μm. Counts were 9% and 12% lower for the two stacks with 1 μm z steps, and 46% and 55% lower for stacks with 2 μm z steps compared to the original stacks. We identified two steps in the 3D grouping algorithm (Fig. 2d) that would be more vulnerable to 2D segmentation errors with larger step sizes. First, after the initial grouping of 2D centroids and before the additional merging steps, we deleted any 3D “groups” that contained only a single 2D centroid – that is, any 2D centroids that were not matched to 2D centroids in the planes immediately above or below them. Second, after all merging steps were completed, we deleted objects that were comprised of fewer than three 2D centroids, or that spanned less than one fourth the median profile diameter in the z dimension. When both of these steps were omitted, the numbers of cells counted in the 1 μm stacks were 100% and 103% of the numbers counted in the original stacks, while 96% and 94% of the original cell counts were obtained from the 2 μm stacks. We concluded that with this modification, the method could be applied to stacks with a z step size of 1 μm, but a 2 μm step size was too large.

Density variation in the z dimension

Although images were sampled from the entire 50 μm depth of each tissue section, analysis was restricted to smaller regions for two reasons. First, as is common practice in stereology, guard regions were implemented at each sectioned surface of the tissue. This practice avoids measuring from regions of the tissue with non-representative cell densities arising from lost caps and other irregularities that arise from sectioning (Coggeshall & Chung, 1984; Hedreen, 1998; von Bartheld, 2012). Second, if the anti-NeuN did not penetrate the full volume of the tissue, regions toward the middle of the section that were beyond the range of antibody penetration were excluded. Because only restricted regions of tissue were analyzed, it was necessary to evaluate whether measurements made from the analyzed regions were representative of the density present in the tissue overall, which would not be the case if tissue shrinkage was non-uniform across the z dimension (Carlo & Stevens, 2011; von Bartheld, 2012; Miller et al., 2014).

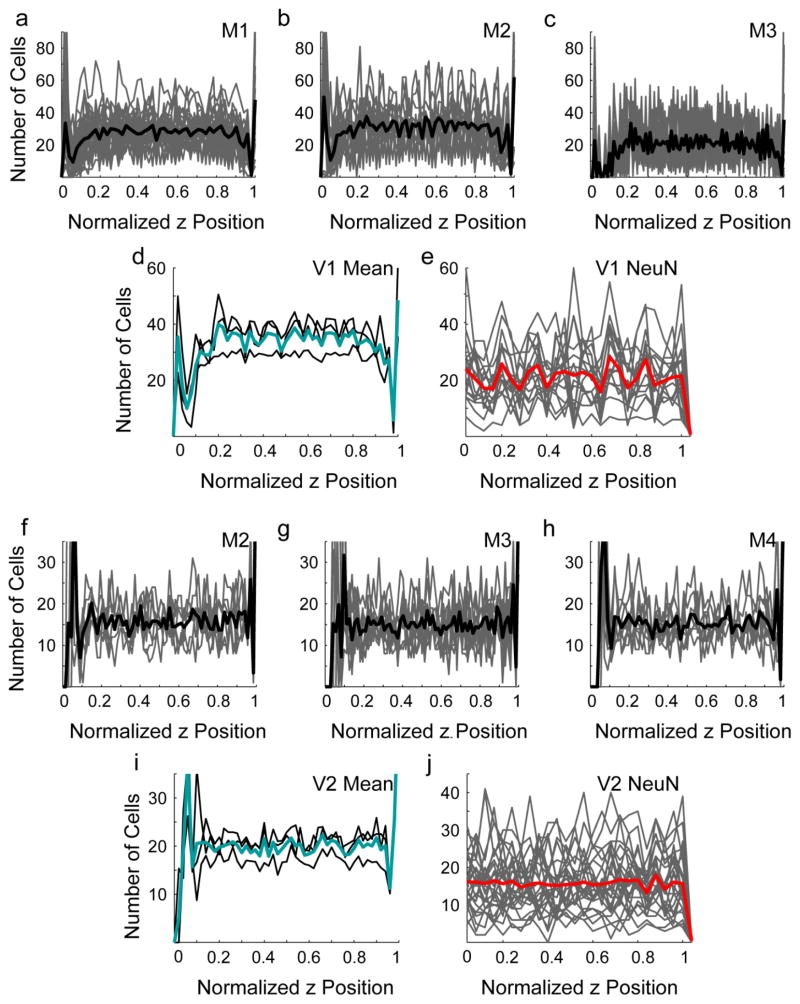
For each sampled image stack, z positions were adjusted by first subtracting the minimum z value in the stack and then dividing by the maximum z value. This was done so that multiple z stacks could be considered together. DAPI-labeled centroid positions were then collapsed across the x and y dimensions, and cell density was measured as a function of z position, using 50 bins for each stack. No systematic variation in density across z position was detected for individual stacks (Fig 5a–c, f–h, gray lines), for their within-animal means (Fig 5a–d, f–i, black lines), or for the means across animals (Fig 5d, i, cyan lines) in either V1 (Fig. 5a–d) or V2 (Fig. 5f–i), with the exception of either abrupt decreases at each tissue surface, in regions that were eliminated by the implemented guard zones, or increases at these locations, due to anomalous edge effects in the automated counting. This suggests that the cell densities measured in restricted zones closer to the cut surfaces of the tissue were generally representative of cell density throughout the tissue section, and that the use of guard regions was appropriate and necessary.

Fig. 5.

Cell density variation in the z dimension. To evaluate whether tissue shrinkage was uniform in the z dimension, the z positions of all 3D centroids from each image stack were adjusted to range from 0 to 1, and were grouped into 50 bins. a–c, f–h Number of cells in each z depth bin from individual animals sampled for V1 (a–c) and V2 (f–h). Gray lines Individual image stacks. Black lines Within-animal means. d, i Reproduction of mean counts per z position from each animal (black), and mean of these values (cyan) for V1 (d) and V2 (i). e, j Number of cells classified as neurons at each z position from individual image stacks (gray lines) and means across all image stacks (red) for which NeuN penetration was thought to be complete in V1 (e) and V2 (j) samples

In three sampled series in V1 and five series in V2, it was determined that anti-NeuN penetrated through the entirety of the tissue section. This was evaluated by measuring neuronal density as a function of z position in the image stacks from these series. No systematic variation in neuronal density across z position was observed in either V1 (Fig. 5e) or V2 (Fig. 5j). Therefore, neither cell nor neuron density measurements are likely to have been artificially distorted by non-uniform tissue shrinkage along the z dimension.

Numerical density of neurons in macaque V1

The automated counting method was used to quantify neuronal density in opercular V1 (eccentricity 2–5 degrees), using eleven series of image stacks spanning from the pial surface to the white matter in tissue from three cynomolgous monkeys. Correcting for tissue shrinkage in the x, y, and z dimensions, this corresponded to a total volume of 0.10 mm³ (mean 0.033 mm³ per animal). The mean density of neurons across all layers in V1 was 230 × 10³ (± 20 × 10³ SEM, N=3) neurons per mm³, ranging from 190 × 10³ to 280 × 10³. The mean density of DAPI labeled cells was 330 × 10³ (± 20 × 10³ SEM, N=3) cells per mm³, ranging from 280 × 10³ to 360 × 10³. The average proportion of cells identified as neurons across animals was 0.70, ranging from 0.69 to 0.72. This corresponds to a non-neuronal to neuronal cell ratio of 0.43, which is quite similar to the glia to neuron ratio by Giannaris and Rosene (2012: ratio = 0.44) but slightly lower than the ratios measured by O’Kusky and Colonnier (1982) (ratio = 0.49) and Collins et al. (2010a) (ratio = 0.51–0.54). It should be noted that the isotropic fractionator method used by Collins et al. (2010a) measures cell densities from homogenized blocks of tissue that should be assumed to include an unknown portion of the white matter, which has a high ratio of glia to neurons. In addition, the use of NeuN to identify neurons in the Giannaris and Rosene (2012) study provides a less ambiguous means of discriminating neurons from glia than the visual inspection of size and chromatin staining patterns of Nissl-stained nuclei used by O’Kusky and Colonnier (1982).

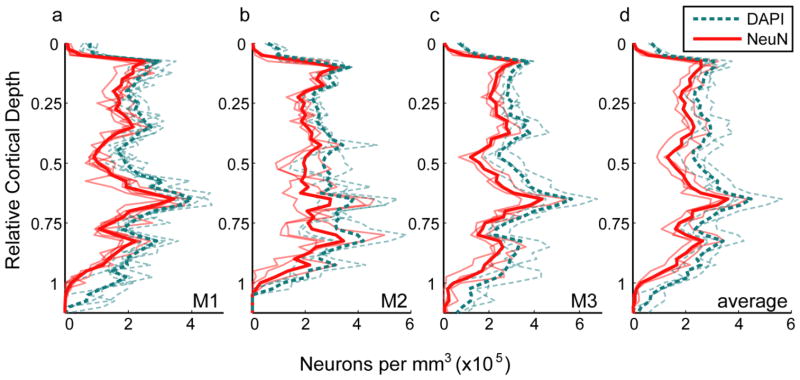
The strength and importance of the method is particularly demonstrated by the ease of generating profiles of neuronal density across cortical depth (Fig. 6). Profiles are shown for individual image series from each animal (Fig. 6a–c, faint lines); for the average across all sampled series from each animal (Fig. 6a–c, bold lines; reproduced in Fig. 6d, faint lines); and for the mean across the three animals in V1 (Fig. 6d, bold lines). Qualitatively, density profiles are highly similar both within and between animals. A common pattern is present across each profile, largely reflecting differences in density between cortical layers. The similarity between profiles was also demonstrable quantitatively; the mean density profile for each animal positively correlated with the density profile averaged across each of the three animals (Pearson’s correlation: 0.95, 0.86, and 0.95 for monkey M1, M2, and M3, respectively). Although there is variation in the precise depth of laminar boundaries from one sample to the next – see, for example, the deeper position of layer 4C (identified by the peak in the density profile) in one series from monkey M2 (Fig. 6b) – there is, nevertheless, a stereotyped sequence of peaks and troughs across depth. For example, there is a peak in density corresponding to the upper part of layer 6, as well as a more prominent peak corresponding to layer 4Cβ. It is also possible to directly observe features such as the gradual increase in density across layer 4C, which would not have been apparent by comparing only the mean densities within pre-specified laminar boundaries.

Fig. 6.

Cell and neuron density in V1. Each panel shows density per mm³ as a function of relative cortical depth (distance below the pial surface divided by the distance from the pial surface to the white matter). Cell depths (y positions) were converted to relative cortical depth and binned with a bin size equal to 2.5% of total cortical depth. The number of cells in each bin was divided by the tissue volume per bin, yielding the distribution of neuronal density across cortical depth. Densities of DAPI-labeled cells (neuronal and non-neuronal) are shown as dashed cyan lines, while densities of NeuN-positive cells (neurons) are shown as solid red lines. a–c Faded lines are density profiles from a single series of image stacks, while bold lines show the average density profile for a single animal, computed as the sum of all within-animal counts in a given depth bin divided by the sum of within-animal bin volumes. a Monkey M1. b Monkey M2. c Monkey M3. d Faded lines are density profiles for individual animals (replicating the bold lines from (a–c)), and the bold lines show the mean of the density profiles from the three animals

Numerical density of neurons in macaque V2

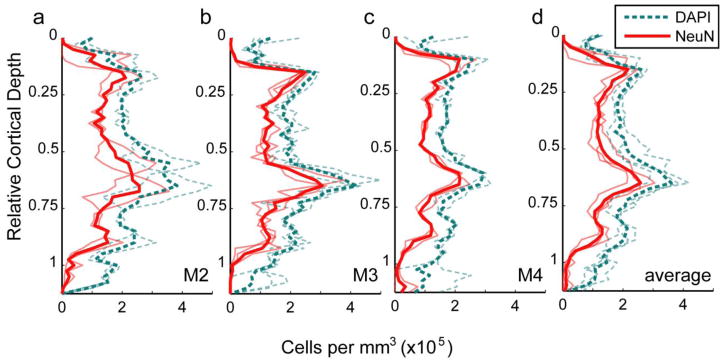
Neuronal density was measured by the same method in parasagittal sections of dorsal V2, using seven series of image stacks spanning from the pial surface to the white matter in tissue from three monkeys (two cynomolgous and one rhesus monkey). Two of these animals were also used to measure neuronal density in V1. Correcting for tissue shrinkage in the x, y, and z dimensions, this corresponded to a total volume of 0.091 mm³ (mean 0.030 mm³ per animal). The mean density of neurons across all layers in dorsal V2 was 130 × 10³ (± 8 × 10³ SEM, N=3) neurons per mm³, ranging from 110 × 10³ to 140 × 10³. The mean density of DAPI labeled cells was 210 × 10³ (± 10 × 10³ SEM, N=3) cells per mm³, ranging from 180 × 10³ to 220 × 10³. The proportion of cells identified as neurons was 0.63 for all three animals, which corresponds to a non-neuronal to neuronal cell ratio of 0.58. The overall density of neurons in V2 was only 57% of the density of neurons measured in V1, and the total cell density was just 63% of the total cell density measured in V1. As in V1, stereotyped changes in density were present across cortical depth, partially reflecting differences between cortical layers (Fig. 7). Neuronal and overall cell densities rise to two major peaks, one corresponding to layer 2 and one to layer 4.

Fig. 7.

Cell and neuron density in V2. Each panel shows density per mm³ as a function of relative cortical depth. Cell depths (y positions) were converted to relative cortical depth and binned with a bin size equal to 2.5% of total cortical depth. The number of cells in each bin was divided by the tissue volume per bin, yielding the distribution of neuronal density across cortical depth. Densities of DAPI-labeled cells (neuronal and non-neuronal) are shown as dashed cyan lines, while densities of NeuN-positive cells (neurons) are shown as solid red lines. a–c Faded lines are density profiles from a single series of image stacks, while bold lines show the average density profile for a single animal, computed as the sum of all within-animal counts in a given depth bin divided by the sum of within-animal bin volumes. a Monkey M2. b Monkey M3. c Monkey M4. d Faded lines are density profiles for individual animals (replicating the bold lines from (a–c)), and the bold lines show the mean of the density profiles from the three animals

Discussion

Automatic cell counting

The method presented here combines automatic neuron counting with the sampling of large regions extending orthogonal to the cortical laminae, which is the major source of structured natural variation in neuron density within a cortical area. The use of automated segmentation and quantification facilitates sampling over large regions, which in turn enables fine-level description of the organization of neurons within a brain region. Numerous strategies to achieve automated quantification have been proposed. Schmitz et al. (2014) evaluated three such algorithms and found that none achieved satisfactory accuracy and precision to serve as a replacement for manual stereologic counting. While it is difficult to compare methods evaluated with different tissue preparations and performance metrics, seemingly better results have been reported using methods that were customized for particular preparations and/or incorporated uniquely tailored object models (Lin et al. 2003; Lin et al. 2007; Oberlaender et al. 2009; LaTorre et al. 2013a, 2013b). The automated counting strategy used here achieved accurate neuron counting by first segmenting DAPI-stained nuclei and then examining the NeuN channel at the location of each nucleus’s centroid in order to identify neurons. This strategy simplified the problem of automatic cell segmentation because neuronal nuclei, unlike entire neurons, have approximately spheroid or ovoid shape. By comparing results generated by the automated method with manual annotations of cell position, we have shown that the method makes large-scale quantification tractable without sacrificing accuracy.

Importantly, the method for automatically counting neurons is sufficiently accurate to be used as an alternative to manual stereological quantification. In four test image stacks that were manually annotated and analyzed by the automatic method, the mean ratio of automatically to manually generated nuclei was 0.98. The method not only counted accurate numbers of nuclei in sample confocal image stacks, but it also correctly identified actual nuclei and their x-y-z positions with true positive rates consistently above 90% and false positive rates consistently below 10% compared with manually annotated nuclei. Furthermore, the errors in automatic cell localization were especially rare for neuronal nuclei, which indicated that they would minimally impact quantification of neurons. The sample regions used for validation were taken from different cortical layers to capture naturally occurring variations that could challenge the robustness of an automated method, but the procedure performed well across samples, indicating its reliability as a tool for quantifying neurons throughout the neocortex. Providing a means for large-scale sampling by reducing the demands on investigator time and labor will be invaluable for future neuroanatomical studies. Schmitz et al. (2014) have shown that there is currently no available software package that can replace manual stereology. However, we have shown that it is possible to selectively combine straightforward algorithms to produce custom software that can accurately measure the number of neurons in a specified tissue volume. Not only do we show that the algorithms that we have implemented work but we also provide a general framework for the implementation that has the flexibility for modification at a number of stages in the process. Therefore the generality of the approach plus specific implementation will be key in adopting this method across a variety of tissue from different brain areas and in different species.

Although our method was accurate in counting cells across types – i.e. for neurons and non-neuronal supporting cells, including macroglia, microglia, and cell types associated with vasculature (Peters et al. 1991)—it performed best for neurons and made more errors on other cell types. This is unsurprising given that the object model was intended to capture the convex, ovoid shape characteristic of neuronal nuclei, whereas other cells, such as endothelial cells, pericytes, and some types of glial cells, have non-ovoid nuclei (Luse 1956; Cammermeyer 1960; Peters et al. 1991). Therefore, the method in its current form should not be used for studies of non-neuronal cell types without modification and/or specific validation with the non-neuronal cell types of interest. It would be possible to extend the strategy we have described to include multiple object models, which has previously been shown to improve the success of other cell segmentation methods (Lin et al. 2007). For the purpose of counting neurons, it might also be useful to incorporate the strategy described by LaTorre et al. (2013a) for removing the brightest objects, which also often correspond to non-neuronal nuclei, during the initial separation of foreground and background. Adopting this strategy would require adjusting the gain settings used for imaging such that most foreground pixels were not at saturation.

Measuring neuronal density

The average numerical density of neurons in area V1, determined using the automated method, was 230 × 10³ neurons per mm³. Previous investigators have measured neuronal density in macaque V1, but reported values differ substantially between studies. Pooling observations from two macaque monkey species, Macaca mulatta and M. fascicularis, O’Kusky and Colonnier (1982) and Beaulieu et al. (1992) counted nuclei in thin tissue sections, differentiated neurons from glia based on their patterns of Nissl staining, and computed numerical density using a theoretical formula for ellipsoids. Both corrected for a linear shrinkage factor of approximately 15% and estimated similar neuronal densities: 120 × 10³ and 110 × 10³ neurons per mm³, respectively. These density values from O’Kusky and Colonnier and Beaulieu et al. have been the standard in the field for the last 20–30 years but are approximately 50% of the density found in the current study.

More recently, three groups have used design-based stereological methods with 3D counting probes in thicker tissue sections to estimate neuronal density in macaque V1. Christensen et al. (2007) used the optical fractionator method and the Cavalieri principle to measure density in several cortical regions from M. mulatta, including occipital cortex, which appears to have included V1 in addition to some cortical areas immediately anterior to V1; therefore, their measured density should be expected to be lower than the neuronal density in V1 alone. They reported 320 × 10³ neurons per mm³ in occipital cortex. If we correct for the 54% tissue shrinkage they measured in cortex as a whole, this value is reduced to 150 × 10³ neurons per mm³. Lewitus et al. (2012) measured densities of 420 × 10³ neurons per mm³ and 330 × 10³ neurons per mm³ in layers 2–6 of V1 in M. mulatta and M. fascicularis, respectively. They also measured glia-to-neuron ratios of 0.27 in M. mulatta and 0.14 in M. fascicularis, which are much lower than the ratios between 0.4 and 0.6 measured by other groups (O’Kusky and Colonnier 1982; Christensen et al. 2007; Collins et al. 2010a; Giannaris and Rosene 2012) and the ratio of 0.4 we measured. Therefore, we suspect that some glia may have been misclassified as neurons in the Lewitus et al. (2012) study. Giannaris and Rosene (2012) differentiated neurons from glia using immunohistochemistry for NeuN and measured a neuronal density of 280 × 10³ neurons per mm³ in layers 2–6 of M. mulatta area V1, with a glia-to-neuron ratio of 0.44. If we assume that this is a more accurate measurement of glia-to-neuron ratio and apply it to the total cell densities measured by Lewitus et al. (2012), their neuronal densities would instead be 370 × 10³ neurons per mm³ in M. mulatta and 270 × 10³ neurons per mm³ in M. fascicularis. The densities Lewitus et al. (2012) and Giannaris and Rosene (2012) measured in layers 2–6 in M. fascicularis and M. mulatta, respectively, were only slightly higher than the density we measured in the same layers, 250 × 10³ neurons per mm³. Because the optical fractionator method has been shown to produce estimates concordant with those from the isotropic fractionator and flow fractionator methods (Miller et al. 2014), and because of their use of NeuN immunohistochemistry to less ambiguously identify neurons, it is likely that the Giannaris and Rosene estimate of total neuron number is accurate, although their estimate of volume and therefore neuronal density might be affected by tissue shrinkage. Overall, we conclude that our estimate of neuronal density in layers 1–6 of macaque V1, 230 × 10³ neurons per mm³, is an accurate measurement, and the automatic counting method we have presented can be used to measure neuronal density in future studies.

Differences in neuronal density in V1 and V2

It has previously been described that overall neuronal density in primate V1 is higher than in other cortical areas (Rockel et al. 1980; Collins et al. 2010a; Srinivasan et al. 2015). In the current study, neuronal density across layers 1 through 6 was 1.8 times higher in V1 than in V2. The difference in measured densities cannot be attributed to eccentricity, which should be approximately matched between areas because dorsal V2 was sampled from parasagittal sections initially processed for the purpose of measuring density in the neighboring V1 tissue. The difference in density between areas also cannot be explained by differences in the proportion of all cells that were neurons in V1 (0.70) and V2 (0.63). Overall cell density was also higher in V1 than in V2, by a factor of 1.6. The difference also cannot be explained by the unique organization of layer 4 in V1. Although layer 4 occupied a larger fraction of the total cortical depth in V1 than in V2, the difference in overall neuronal density between areas does not reflect simply an overrepresentation of this neuron-dense region, since in general, layers in V1 were consistently higher than their homologues in V2. That is, neuronal density in layer 1 of V1 was higher than in layer 1 of V2, and the same was true of relative densities in other matched layers.

The magnitude of tissue shrinkage measured was greater in V2 than in V1, particularly in the z dimension (43% vs. 29%), but this difference was not large enough to entirely account for the difference in cell or neuronal densities between areas. When volumes were uncorrected for tissue shrinkage, the neuronal density in V1 (450 × 10³ neurons per mm³) was still 1.3 times the density in V2 (330 × 10³ neurons per mm³). Note that the shrinkage-corrected density values (V1: 230 × 10³ neurons per mm³, V2: 130 × 10³ neurons per mm³), and the corresponding ratio between V1 and V2 densities (1.8), are more likely accurate. The source of the difference in tissue shrinkage is unknown to us. It may be the case that regions of tissue with different cell packing density and/or average cell size might be differentially susceptible to various sources of shrinkage, which would make it especially critical to properly correct for such effects when comparing cell density between regions.

Compatibility with related applications

The presented method adopts a sampling probe – the “counting brick” (Howard et al. 1985) or “counting box” (Williams and Rakic 1988) – from stereology, although the counting volume used was larger than those commonly used in manual studies. However, rather than overlay a sampling grid and measure within a small counting frame at each grid intersection within the region of interest, we instead sampled a strip of tissue that spanned the full cortical depth. For this demonstration, the locations of these sampled strips were selected unsystematically, but it would be possible to adopt a more thorough strategy of systematic random sampling, using evenly spaced tissue sections from across the entirety of the cortical area and spacing the strips at pre-specified intervals across each tissue sections. It is, therefore, not necessary to abandon unbiased sampling principles in order to use the method we have described. It would also be possible to use the automated image analysis method to analyze disectors sampled according to a more traditional optical fractionator sampling scheme. This would entail sectioning throughout the entirety of a brain region of interest, selecting tissue sections at a consistent interval throughout the set, and placing counting brick sampling probes at evenly spaced grid locations within each of these selected sections. Such a sampling strategy would be appropriate, for example, for estimating the total number of neurons with a brain area, when combined with a stereological method for estimating volume, such as the Cavalieri estimator.

Because the analysis method operates first on individual image stacks and only combines them at the final step, it would require no modification to be used in an optical fractionator study. In the current study of area V1, the 11 image series together were comprised of 76 individual image stacks, with a total volume of 0.10 mm³ (corrected for tissue shrinkage). An adequate investigation of a large area such as primate V1 by the optical fractionator method would likely require the use of more counting frames; however, these could be smaller than the 246 μm × 246 μm images used in the current study, so long as the frames were large enough to consistently include a few examples of individual, unclustered cell profiles so that median profile area reflected the size of a single cell. In general, the time required for the automated segmentation scales with image volume. For demonstration, each image stack from one series was cropped into four equal quadrants, yielding a set of twenty test stacks of 123 μm × 123 μm image frames. The mean segmentation time per image frame for the time-intensive 2D step was 11.2 ± 0.6 (SEM, n=20 stacks) sec in these cropped test stacks, which was just under one fourth of the mean segmentation time per frame for their parent images, 47.1 ± 4.7 (SEM, n=5 stacks) sec. Thus, the same total image volume used in the current study could be divided amongst a larger number of counting frames (distributed systematically within a structure of interest) without increasing processing time.

For a typical series of 5–7 image stacks, determining the exclusion boundaries for each stack and dictating the parameters to use for batch automated processing can take at most 30 min; the image processing itself occupies no user time and can be set to run overnight or while acquiring more images. The acquisition of images creates the major bottleneck in time required to complete a study. For each image series, up to 30 min may be used in selecting a sampling region and carefully checking imaging parameters (a total of 5.5 hr for 11 series, as in our V1 study), with an additional 2–3 min of engaged user time spent adjusting the imaging location between stacks within the series (about 2–3 hr total for our V1 example). An investigator may also choose to pre-specify a grid of overlapping regions to scan automatically, which avoids this adjustment time between stacks. With the Leica SP5 confocal system and imaging parameters used in the current study, the scanning time per 50 μm-thick stack with a 400 Hz scan speed and 0.5 μm z step size was about 15–20 min. During this time, the investigator is largely free to work on other tasks while monitoring scan progress.

An investigator with unrestricted access to a confocal microscope could reasonably obtain a neuronal density estimate within a week, having invested a total of about 15 hours of engaged user time and 20 hours of microscope monitoring time. In contrast, stereologic cell counting by hand for a single study can take multiple weeks or even months to complete (Schmitz et al. 2014). Furthermore, the added richness of the data set, which includes the position of every cell in 3D, leaves open the possibility of unplanned post-hoc analyses – such as measuring the distribution of cells across z position or relative to cytochrome oxidase histological boundaries – or minor adjustments, for example to the assigned location of a laminar boundary. Preserving position information also makes it straightforward to combine neuron counting with a separate analysis of other types of structures within the same tissue region, such as blood vessel reconstruction as described by Tsai et al. (2009).

Therefore the method would be particularly suitable and valuable for studies of neurons in human postmortem brain tissue during development and aging and from individuals with different classes of disorders. We have had preliminary success applying the same method in human brain tissue sections, suggesting that it will generalize across species and is robust to differences in tissue fixation, so long as these differences do not disrupt tissue microstructure or impair immunofluorescence labeling; these tissue quality issues would also affect estimation by manual counting. The analysis procedure was designed to be used specifically with immunofluorescence labeled tissue imaged with a confocal microscope. Because its success depends critically on the relatively uniform shape of neuronal nuclei as identified by DAPI, it is unlikely to perform well at segmenting cells from Nissl stains, in which label is present throughout the cytoplasm. The method is also unlikely to be successful for use with standard microscopes that lack the axial resolution afforded by confocal imaging.

Although NeuN-immunolabeled tissue was used in this study to quantify neuronal density, the strategy presented is not specific to NeuN labeling. Because the object segmentation is performed on nuclei, which are subsequently compared to a threshold-based mask in immunolabeled channels, the method can be applied generally to any type of label for which a proper mask can be generated. This is reasonably trivial for labeling that fills cell bodies, such as NeuN (Fig. 8a–b) and parvalbumin (Fig. 8c–d). Variations in staining intensity within the cell body, including differences in expression between nucleus and cytoplasm, should not pose a problem so long as it is possible to separate stained cells from unstained neuropil by thresholding. For antigens that are present primarily outside the nucleus, i.e. in the cytoplasm or cell membrane, it may often be possible to generate suitable mask images simply by thresholding and then flood filling holes to label the regions containing cell centroids as foreground. We have had some promising success in generating mask images for cells labeled with a marker that is largely restricted to the cell membrane, even in the presence of neuropil staining, such as the potassium channel subunit Kv3.1b (Fig. 8e–f). We anticipate that some antigens will present a particular challenge, such as those with a sufficiently polarized pattern of expression within the cell such that positive cell labeling is not visible in the plane of the nuclear centroid. There may be creative solutions to this type of problem – for example, using the maximum pixel values within a given x-y radius across a specified range of z planes – but such issues will have to be carefully considered when designing experiments.

Fig. 8.

Examples of mask images for immunolabeled tissue. a Tissue labeled with anti-NeuN and used in the current study. b Mask image generated for the micrograph in (a). c Tissue labeled with anti-PV. d Mask image generated for the micrograph in (c). e Tissue labeled with antibody against the potassium channel subunit type Kv3.1b. f Mask image generated for the micrograph in (e). Scale bar in (f) (applies to all panels): 50 μm

The flexibility to apply the method to various types of molecular markers highlights an additional advantage of the method: the ability to identify coexpression of multiple antigens even when those antigens are differently distributed within a cell. For this purpose, the strategy of identifying cells based on their DAPI-stained nuclei and then evaluating expression of antigens is preferable to identifying the “tops” or “bottoms” of cells based on other molecular markers, since those locations may differ for antigens present in different parts of the cell. When studying, for example, coexpression of one antigen expressed only in the cell membrane and another expressed only in the nucleus, the bottom of the cell as defined by the location of the cell membrane will not be visible in cells expressing only the nuclear-specific antigen, whereas the bottom of the cell as defined by the bottom of the nucleus will not be visible in cells expressing only the membrane-specific antigen. The automated method avoids this issue by determining cell position based on a separate channel visualizing DAPI staining. The method identifies a single point within each cell and – unlike manual annotation methods – can localize this point within image planes, which is ideal when applying exclusion boundaries. Because the assignment of this centroid z position is computed as the average of sectional profile z positions weighted by profile area, it should be largely unaffected by failures to detect the small profiles near the upper- or lowermost surfaces of the cell. Furthermore, with some possible exceptions as described above, defining cell position as the approximate equator of the nucleus is useful for evaluating expression of multiple antigens because many will be best detected in this plane, regardless of whether they are primarily expressed in the nucleus, cell membrane, or cytoplasm.

In summary, we have identified a method for automatically quantifying numerical density of immunolabeled, DAPI-counterstained neurons in confocal image stacks. This represents a major advance because, given appropriate sampling design, it matches traditional stereological methods in accuracy but can be used to obtain detailed estimates of the profile of neuronal density across large tissue regions. The sampling strategy we describe here allowed detailed measurement of neuronal density as it varies across cortical depth. This will be of major importance when applied using markers for specific types of neurons, such as parvalbumin and somatostatin, which distinguish distinct classes of inhibitory interneurons with distinct roles in circuit computation (Rudy et al. 2011; Pfeffer et al. 2013; Kepecs and Fishell 2014). For subtypes of neurons that are more sparsely distributed or are concentrated in specific compartments within a cortical area, the method described should enable both accurate counting and description of their arrangement within a region of interest.