People learn other people’s preferences through inverse decision-making

Abstract

People are capable of learning other people’s preferences by observing the choices they make. We propose that this learning relies on inverse decision-making—inverting a decision-making model to infer the preferences that led to an observed choice. In Experiment 1, participants observed 47 choices made by others and ranked them by how strongly each choice suggested that the decision maker had a preference for a specific item. An inverse decision-making model generated predictions that were in accordance with participants’ inferences. Experiment 2 replicated and extended a previous study by Newtson (1974) in which participants observed pairs of choices and made judgments about which choice provided stronger evidence for a preference. Inverse decision-making again predicted the results, including a result that previous accounts could not explain. Experiment 3 used the same method as Experiment 2 and found that participants did not expect decision makers to be perfect utility-maximizers.

Introduction

One way to learn what other people like is by observing the choices they make. For example, suppose that Alice orders a boxed lunch that includes an eggplant sandwich and you want to know how much Alice likes eggplant sandwiches. If Alice ordered the only box with an eggplant sandwich, you might infer that Alice has a strong preference for eggplant sandwiches. If the eggplant sandwich is part of the only box that contains a cookie, you might instead infer that Alice has no particular preference for eggplant sandwiches and she really wanted the cookie. Although people commonly make these sorts of inferences, this example illustrates that someone’s choice could have many different explanations, and deciding which of these explanations is best can be a challenging inductive problem.

Inferences like these have been studied in the literature on interpersonal attribution (Gilbert, 1998; Hamilton, 1998), and have been the target of developmental work with children (Repacholi & Gopnik, 1997; Kushnir, Xu, & Wellman, 2010; Ma & Xu, 2011; Lucas et al., 2014; Diesendruck, Salzer, Kushnir, & Xu, 2015; Hu, Lucas, Griffiths, & Xu, 2015; Luo, Hennefield, Mou, vanMarle, & Markson, in press). Most of this literature, however, does not emphasize computational approaches (for some exceptions, see Lucas et al., 2014; Medcof, 1990; Kunda, 1998). Research in economics and marketing has produced multiple computational methods for inferring consumers’ preferences from their choices (Green & Srinivasan, 1990; Varian, 2006), but these methods have not been explored as psychological models. By contrast, there are multiple psychological models of how people make choices (Busemeyer & Johnson, 2008; Train, 2009; Schneider, Oppenheimer, & Detre, 2007; Shenoy & Yu, 2013), but few attempts to apply models like these to the problem of inferring people’s preferences from observations of their choices. In this paper, we explore a computational approach to preference learning based on inverting a decision-making model and test it as a psychological account. We call this approach inverse decision-making.

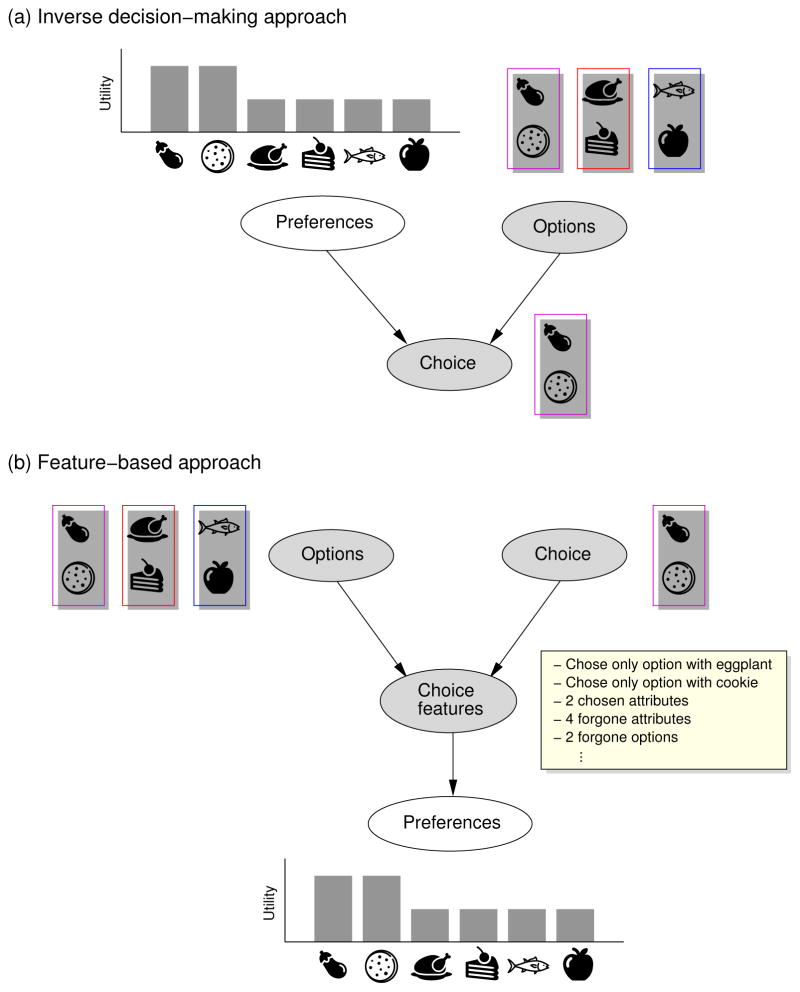
The inverse decision-making approach is illustrated in Figure 1a. The figure shows an example in which Alice chooses between three boxed lunch options: (1) eggplant sandwich and a cookie, (2) turkey sandwich and a slice of cake, and (3) tuna sandwich and an apple. The utility function in Figure 1a (depicted by a bar chart) shows that Alice prefers the eggplant sandwich over the other sandwiches and the cookie over the other desserts. A decision-making model specifies a decision function that maps preferences to choices. Given Alice’s preferences, any standard model of decision-making will predict that Alice will choose the option with an eggplant sandwich and a cookie. The shading on the nodes of the graph in Figure 1a indicates what information about Alice’s choice is visible to an observer. In this case, that includes the three boxed lunch options and Alice’s choice. The unshaded node indicates that Alice’s preferences are not visible to an observer. Even so, the observer can invert a decision-making model to make inferences about the unobserved preferences that led to the observed choice.

Figure 1.

Two approaches to preference learning applied to Alice’s choice of boxed lunch. In both panels, the shaded nodes represent observed information and the unshaded nodes represent inferred information. (a) The inverse decision-making approach specifies a decision function that maps Alice’s preferences and choice options to her choice and then inverts this function to infer the preferences that led to her choice. (b) The feature-based approach maps a set of features directly to the preferences that led to Alice’s choice.

Figure 1b shows an alternative feature-based approach that does not rely on a decision-making model. Instead, this approach characterizes Alice’s choice using a set of features. For example, the features in Figure 1b indicate that Alice chose the only option with an eggplant sandwich and the only option with a cookie, that her choice had two attributes (eggplant sandwich and cookie), that she passed up four attributes (turkey, tuna, cake, apple), and that she passed up two options (the two boxes that she did not choose). These features carry information about Alice’s preferences, and the feature-based approach relies on an inference function that maps choice features to preferences. For example, the larger the number of chosen attributes, the less likely it is that she was specifically interested in the eggplant sandwich, and the larger the number of forgone options, the more likely it is that Alice has a strong preference for eggplant.

The inverse decision-making approach has received little attention in the social psychology literature, but the feature-based approach has served as the basis for several influential accounts of interpersonal attribution (e.g., Jones & Davis, 1965; Kelley, 1973; Newtson, 1974). One example of the feature-based approach is Jones’s and Davis’s (1965) correspondent inference theory (CIT). One choice feature identified by CIT is whether a chosen attribute is common to other options; if not, then the choice is especially informative about the decision maker’s preferences. For example, if Alice chose the only option that included an eggplant sandwich, then her choice provides strong evidence that she was interested in the eggplant sandwich. In CIT, this idea is called the principle of non-common attributes.

The choice features and inference principles identified by CIT and other feature-based approaches are intuitive. In addition, as Figure 1 suggests, there are cases in which inverse decision-making and feature-based approaches make the same inferences about Alice’s preferences. However, feature-based approaches have two fundamental limitations. First, they assert that the inference function respects a set of principles, but they do not provide a complete set of principles or suggest a way to enumerate these principles. Second, CIT makes no clear predictions about how conflicts between different principles should be resolved (Newtson, 1974). Both limitations arise because it is difficult to characterize the inference function directly. The inverse decision-making approach overcomes these limitations by characterizing the inference function indirectly, letting it emerge from some simple assumptions about decision making.

The inverse decision-making approach is an instance of a class of modeling approaches that rely on what Jara-Ettinger, Gweon, Schulz, and Tenenbaum (2016) have called the naïve utility calculus. Naïve utility calculus refers to the expectation people have that others will generally make choices that produce greater utility. Combining naïve utility calculus with inverse reasoning has led to a number of useful accounts of social inference in recent years (Baker, Saxe, & Tenenbaum, 2009; Ullman et al., 2009; Tauber & Steyvers, 2011; Baker & Tenenbaum, 2014; Wu, Baker, Tenenbaum, & Schulz, 2014; Jern & Kemp, 2015; Baker, Jara-Ettinger, Saxe, & Tenenbaum, 2017). However, few studies in this literature have explored the basic question of how people infer what other people like and dislike by observing their choices. Studies that have explored this question have focused on how children learn simple preferences (Lucas et al., 2014), how adults predict other people’s choices (Bergen, Evans, & Tenenbaum, 2010), and how adults take into account deviations from optimal choice behavior when reasoning about other people’s choices (Evans, Stuhlmueller, & Goodman, 2016). However, previous tests of inverse decision-making as a psychological account of how people learn other people’s preferences have been limited. For example, using a model essentially identical to the one we present below, Lucas et al. (2014) tested predictions on children’s inferences for 11 different observed choices. In this paper, we test the inverse decision-making approach in much greater detail, comparing its predictions to adults’ inferences about many more choices: 47 different choices in Experiment 1, 6 different choices in Experiment 2, and 8 different choices in Experiment 3. Testing the model on a greater number of choices allows us to test the robustness of the inverse decision-making approach and more thoroughly compare it to the feature-based approach.

All of our experiments used a preference learning task in which a hypothetical person makes a choice between multiple discrete options, each with multiple attributes. Figure 2 shows a set of such choices. Each choice in the figure has between one and four options, represented as columns. Each option has between one and five attributes, represented by letters, with identical attributes identified by the same letter. The attributes may be desirable, like different candies, or undesirable, like different electric shocks. In all cases, the decision maker chose the leftmost option, which includes attribute X. Suppose that the different attributes are different kinds of candy. Some of the choices in Figure 2 provide strong evidence of a preference for candy X. For instance, consider Choice 47, in which the decision maker chose a single piece of candy X over one piece each of candies A, B, C, and D. Intuitively, this choice provides strong evidence that the decision maker has a preference for candy X. Other choices provide weak evidence of a preference for candy X. In Choice 14, for example, the decision maker chose candy X plus three other pieces of candy over only a single piece of candy. Intuitively, this choice provides little evidence of a preference for candy X because the decision maker may have wanted a piece of candy other than X, or may simply have wanted more candy.

Figure 2.

The set of 47 choices used in Experiment 1. In each case, a decision maker chose one of between 1–5 options. The columns represent different options; different letters represent different attributes. The chosen option is shaded. The choices are ordered by participants’ mean rankings from weakest evidence to strongest evidence of a preference for attribute X.

In the next section, we describe a formal model that can capture these intuitions. We then discuss the results of three experiments that test the model by comparing its predictions to people’s inferences about choices like the ones in Figure 2. Finally, we present an analysis of whether our results could be explained just as well by a feature-based model.

The inverse decision-making model

We will characterize the inference problem as follows. Suppose you observe someone make a choice from a set of n options {o₁, …, o_n}. Each option o_j includes binary attributes from the set {a₁, a₂, …, a_m}. Option o_j can be described by a binary vector a_j of length m denoting whether each attribute is present or absent.

Inverse decision-making is a general approach that can be instantiated in many ways. To create a specific inverse decision-making model, one must first specify the decision function that maps preferences to choices. In this section, we specify one decision function that is based on some simple assumptions that are shared by many decision-making models. Later, in Experiment 1, we consider several common alternative decision functions.

First, we assume that the utilities for attributes are additive. That is, let U_j be the utility for option o_j, where U_j is equal to the sum of the utilities assigned to its attributes a_j. Utilities may be positive if the attributes are desirable, like different candies, or they may be negative if the attributes are undesirable, like different electric shocks. Second, to account for possible hidden factors contributing to a decision maker’s choice, we assume that choices are made probabilistically, favoring options with greater utility (Luce, 1959). One common way of instantiating this assumption leads to the logit model (McFadden, 1974; Train, 2009):

$$p(c=o_j\mid \mathbf{u},\mathbf{A})=\frac{exp(U_j)}{{\sum }_{k=1}^{n}exp(U_k)},$$ (1)

where c is the chosen option, u is a vector of utilities assigned to each attribute, and A = {a₁, …, a_n} specifies the available options and their corresponding attributes.

Inverting the decision function involves reasoning backward from an observed choice to the preferences that motivated it. For example, according to Equation 1, someone with a strong preference for candy X (i.e., someone who assigns a high utility to X) would be more likely to make Choice 47 in Figure 2 (choosing {X} over {A,B,C,D}) than someone with a weak preference for Candy X. Inverting Equation 1 therefore means that observing someone make Choice 47 provides evidence for a strong preference for Candy X. Formally, we invert the decision function using Bayes’s rule:

$$p(\mathbf{u}\mid c,\mathbf{A})=\frac{p(c\mid \mathbf{u},\mathbf{A})p(\mathbf{u})}{p(c\mid \mathbf{A})}.$$ (2)

In simple terms, Equation 2 states that inferences about utilities are made by starting with prior beliefs p(u) about the utilities a decision maker assigns to the attributes and then updating the prior beliefs to posterior beliefs p(u|c,A) after observing the decision maker’s choice.

The denominator on the right of Equation 2—the marginal likelihood p(c|A)—captures the probability of making choice c, averaged over all possible utility assignments. This term takes into account how probable a choice would be, regardless of a decision maker’s preferences. For example, consider Choice 14 in Figure 2, in which the decision maker chose {X,A,B,C} over {D}. A decision maker would be likely to make this choice no matter what her preferences were because the choice provides four candies over one. As a result, the likelihood p(c|u,A) and the marginal likelihood p(c|A) are virtually the same for any value of u, and an inverse decision-making model would predict that Choice 14 provides little information about the decision maker’s preferences. By contrast, Choice 47 would be unlikely unless the decision maker had a strong preference for Candy X. In this case, the likelihood is high and the marginal likelihood is low.

In real-world applications, the prior distribution, p(u), can capture the fact that some attributes (e.g., cookies) tend to be liked more than others (e.g., eggplant), but in our experiments, we kept the task as simple as possible by providing no information about the relative utilities of different attributes. Therefore, when generating predictions for our experiments, we used the same prior distribution for the utilities of each attribute.

Comparing inferences

We tested our inverse decision-making model by asking participants to observe choices made by multiple people and judge which people had stronger preferences. Equation 2 provides a way to infer a decision maker’s utilities but does not provide a way to compare inferences about two people’s utilities for the purpose of judging which person likes something more. Therefore, to generate predictions for our experiments, one must also specify a criterion for ordering choices. We considered four criteria, which we call absolute utility, relative utility, likelihood, and marginal likelihood. First we will define the four models. Then we will discuss several example cases that illustrate differences between the models.

Absolute utility

The absolute utility model orders choices by the mean posterior utility for attribute X. This is computed as follows. For each observed choice, use Equation 2 to compute the posterior probability distribution over utilities. Then compute the mean (expected value) of the posterior distribution over the utility u_x for attribute X:

$$E(u_x\mid c,\mathbf{A}),$$ (3)

and order the choices based on these means.

Relative utility

The absolute utility model requires an inference about the utility of X in isolation, but research suggests that people sometimes think about the utility of an attribute only in relation to other salient possibilities (Ariely, Loewenstein, & Prelec, 2006). The relative utility model captures this idea. The relative utility model orders choices by how strongly each choice suggests that the decision maker assigns the greatest utility to attribute X¹:

$$p(u_x\text{is}\text{greatest}\mid c,\mathbf{A})=\frac{p(c\mid u_x\text{is}\text{greatest},\mathbf{A})p(u_x\text{is}\text{greatest})}{p(c\mid \mathbf{A})},$$ (4)

where p(c|u_x is greatest,A) = ∫ p(c|u,A)p(u|u_x is greatest)du.

Likelihood

The absolute and relative utility models are two versions of the inverse decision-making model that make different assumptions about how observers will compare choices made by others. As discussed previously, the inverse decision-making model incorporates three qualitatively different components: the likelihood p(c|u,A), the prior p(u), and the reciprocal of the marginal likelihood 1/p(c|A). For our experiments, we assumed that the prior was the same for all choices. The two other components, however, vary across choices. The inverse decision-making model predicts that both components should influence preference inferences. To test this prediction, we considered two more ordering criteria that rely on only one of these components: either the likelihood or the marginal likelihood.

The first criterion is based on the likelihood term from the relative utility model in Equation 4. Specifically, the likelihood model orders choices by how likely the observed choice would be if the utility for X were higher than the utility for all other attributes:

$$p(c\mid u_x\text{is}\text{greatest},\mathbf{A}).$$ (5)

The likelihood model is related to a social inference heuristic called pseudo-diagnostic inference. A pseudo-diagnostic inference about someone’s disposition considers how probable the person’s behavior is given a certain disposition, but not how probable the behavior is given other dispositions (Trope & Liberman, 1993; Trope, 1998).

Marginal likelihood

The final ordering criterion is based on the reciprocal of the marginal likelihood of the inverse decision-making model in Equation 2. The marginal likelihood model orders choices by how improbable the observed choice would be, averaged over all possible utility assignments:

$$1/p(c\mid \mathbf{A}).$$ (6)

The marginal likelihood model is related to the idea that unexpected choices that seem to violate random sampling assumptions may provide a clue about underlying preferences (Kushnir et al., 2010; Ma & Xu, 2011; Diesendruck et al., 2015). For example, surprising choices may be best explained in terms of a strong preference for X, but unsurprising choices provide little information about a preference for X in particular.

Examples

To illustrate the differences between the four ordering criteria, we will apply them to selected choices from Figure 2 in a set of worked examples.

Positive utilities

We will use Choice 38 from Figure 2 as an example. In this choice, the decision maker had three options—{A}, {B}, and {X}—and chose {X}. To simplify the calculations for illustrative purposes, we will assume that all utilities are positive and from the set {1, 2}. We will also assume a prior distribution on utilities that places 0.6 probability on utility 1 and 0.4 probability on utility 2.

Absolute utility

To compute predictions for the absolute utility model, we first compute the posterior probability distribution over the utilities assigned to each attribute. Because there are three attributes that can each take on two utility values, there are 2³ = 8 possible utility assignments. Consider one case: u = (u_a = 1, u_b = 1, u_x = 1). Each option in Choice 38 contains only one attribute, so the utility of each option is 1. We compute the posterior probability of this utility assignment using Equation 2:

$$\begin{array}{l}p(\mathbf{u}\mid c=\{\mathrm{X}\},\mathbf{A})\propto p(c\mid \mathbf{u},\mathbf{A})p(\mathbf{u})\\ =\frac{exp(1)}{exp(1)+exp(1)+exp(1)}{(0.6)}^3\end{array}$$

In this computation, we have used the logit model in Equation 1 as the decision function. To compute the full posterior probability distribution over utilities, this calculation must be carried out for all 8 possible utility assignments. The resulting probabilities must then be normalized (i.e., adjusted so that they sum to 1) by dividing each value by the sum of all 8 values. The results of these calculations are shown in Table 1. These results make intuitive sense: After seeing the decision maker choose {X}, possible utility assignments in Table 1 that assign utility of 2 to X have higher probability than possibilities that assign utility of 1.

Table 1.

Posterior probabilities for utility assignments after observing Choice 38.

ua	ub	ux	p(u|c,A)
1	1	1	0.2160
1	1	2	0.2489
1	2	1	0.0916
1	2	2	0.1216
2	1	1	0.0916
2	1	2	0.1216
2	2	1	0.0447
2	2	2	0.0640

The absolute utility model orders choices on the basis of the mean posterior utility assigned to attribute X. To compute this, we first compute the posterior probability over the utility for X. For example:

$$\begin{array}{l}p(u_x=1\mid c=\{\mathrm{X}\},\mathbf{A})=\sum _{u_a,u_b}p(u_a,u_b,u_x=1\mid c=\{\mathrm{X}\},\mathbf{A})\\ =0.2160+0.0916+0.0916+0.0447=\mathrm{0.4439.}\end{array}$$

In this calculation, we have summed all the probabilities in Table 1 for cases in which u_x = 1. We would repeat this calculation for all remaining possible utility assignments for X. In this example, there is only one other possibility: u_x = 2. Because these probabilities must sum to 1, we can conclude that p(u_x = 2|c = {X},A) = 1 − 0.4439 = 0.5561. Finally, we compute the mean posterior utility assigned to X as follows:

$$\begin{array}{l}E(u_x\mid c,\mathbf{A})=\sum _{u_x}{u}_x·p(u_x\mid c=\{\mathrm{X}\},\mathbf{A})\\ =(1)(0.4439)+(2)(0.5561)=\mathrm{1.5561.}\end{array}$$

For comparison, the first column of Table 2 shows E(u_x|c,A) for Choice 38, as well as for Choices 11, 16, and 34. These choices all include the attributes A, B, and X. Note that the prediction for Choice 11 follows directly from the prior probabilities: (1)(0.6)+(2)(0.4). This is because, in Choice 11, X appears in both options, so the choice provides no information about the decision maker’s preference for X. Unlike Choice 38, some of these choices include options that contain two attributes. Recall that we assume that the total utility for an option is the sum of the utilities assigned to each attribute in the option.

Table 2.

Model predictions for four choices, assuming utilities are positive.

		Absolute utility	Relative utility	Likelihood	Marginal likelihood
Choice		E(ux|c,A)	p(ux is greatest|c,A)	p(c|ux is greatest,A)	1/p(c|A)
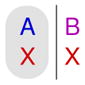
11		1.40	0.62	0.50	2.00
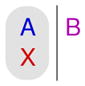
16		1.45	0.65	0.82	1.30
34		1.51	0.73	0.59	2.00
38		1.56	0.77	0.42	3.00

Because the mean posterior utility for X is greater for Choice 38 than for the other choices, the absolute utility model concludes that Choice 38 provides evidence of a stronger preference for attribute X.

Relative utility

The relative utility model computes the posterior probability that the decision maker assigns highest utility to attribute X using Equation 4. To compute this, we must first compute p(u_x is greatest), the prior probability that X has the highest utility. This can be done by summing the prior probabilities assigned to all utility assignments where u_x ≥ u_j for all j. In our example with Choice 38, p(u_x is greatest) = 0.616.

Next, we must compute p(c|u_x is greatest,A), the probability of making a choice given that u_x has the highest utility. In our example, this is computed by summing over utility assignments:

$$p(c\mid u_x\text{is}\text{greatest},\mathbf{A})=\sum _{\mathbf{u}}p(c\mid \mathbf{u},\mathbf{A})p(\mathbf{u}\mid u_x\text{is}\text{greatest}).$$

The first term on the right is the decision function and can be computed using Equation 1, just as we did for the absolute utility model. The second term on the right can be computed by starting with the prior probabilities computed for the absolute utility model, assigning a prior probability of 0 to all utility assignments where u_x is less than the utility for any other attributes, and re-normalizing the probabilities so they sum to 1. For example, for the case in which u = (u_a = 1, u_b = 1, u_x = 1), the prior probability p(u) was computed as (0.6)³ = 0.216 for the absolute utility model. For the relative utility model, p(u|u_x is greatest) = 0.3506. The prior probability is larger for the relative utility model because we have eliminated all utility assignments in which u_x is not highest (3 of the rows in Table 1).

Finally, we compute p(c|A), the marginal likelihood. This is computed as follows:

$$p(c\mid \mathbf{A})=\sum _{\mathbf{u}}p(c\mid \mathbf{u},\mathbf{A})p(\mathbf{u}).$$

The terms in this sum are computed exactly as they were for the absolute utility model.

The second column of Table 2 shows the results of these calculations for four choices. Note that the prediction for Choice 11 once again is determined by the prior probability—this time, the prior probability of u_x having the greatest utility. Because the posterior probability of u_x having greatest utility given Choice 38 is higher than for the other choices, the relative utility model, like the absolute utility model, concludes that Choice 38 provides evidence of a stronger preference for attribute X than the other choices. In fact, Table 2 shows that the order of the relative utility model’s predictions for these choices is identical to the absolute utility model’s predictions. In general, these models produce very similar predictions when utilities are positive. As we will show shortly, however, they sometimes produce different predictions when utilities are negative.

Likelihood

The likelihood model is based on the likelihood term of the relative utility model: p(c|u_x is greatest,A). This term is computed exactly as described above for the relative utility model. The third column of Table 2 shows the result of this computation for the four choices. Once again, Choice 11 is instructive. The model assigns a probability of 0.5 to Choice 11, which is the same as if the decision maker were choosing at random between the two options. This makes sense because attribute X appears in both options. As a result, the decision maker’s choice is unaffected by whether or not X has the highest utility—only the utilities for the other attributes affect the choice.

It is also instructive to compare the model’s predictions for Choices 34 and 38. In Choice 34, the decision maker chose {X} over {A}. In Choice 38, the decision maker chose {X} over {A} and {B}. Therefore, these two choices only differ in the number of available options. According to the model, assuming that X has highest utility, there is a higher probability for choosing {X} when there is one alternative (Choice 34) instead of two (Choice 38). Based on these probabilities, the model would therefore conclude that Choice 34 provides evidence of a stronger preference for X than Choice 38, which does not align with common sense. This prediction is a consequence of the fact that the likelihood model does not take into account how probable a choice is overall—the marginal likelihood.

Marginal likelihood

The marginal likelihood is computed exactly as described above for the relative utility model. The fourth column of Table 2 shows the result of this computation for the four choices. Because the reciprocal of the marginal likelihood is higher for Choice 38 than for the other choices, the marginal likelihood model concludes that Choice 38 provides evidence of a stronger preference for attribute X than the other choices. In this case, the prediction is largely a consequence of the fact that Choice 38 has the largest number of options, so choosing any option in that choice would be more “surprising” than for the other choices. Contrary to the inverse decision-making models, the marginal likelihood model does not rank Choice 11 lowest even though that choice should provide no information about a preference for X. This is because the marginal likelihood model is based on the probability of selecting the option that was actually chosen, not the probability of selecting any option that includes attribute X.

Negative utilities

To illustrate how the absolute and relative utility models can sometimes produce different predictions, we now consider an example in which utilities are negative. This time, we will only compare Choices 16 and 38. Conceptually, the absolute utility model infers a higher tolerance (i.e., greater preference) for X after observing Choice 16 because the decision maker chose to receive two shocks instead of just one. This is a highly improbable choice unless the decision maker considers shocks A and X to both be quite tolerable. By contrast, the relative utility model infers a higher tolerance for X given Choice 38 because that choice is most probable if the decision maker tolerates X the most. For example, even if the decision maker found all of the shocks highly painful, Choice 38 would be probable as long as the decision maker found X to be slightly less painful than the others. On the other hand, Choice 16 provides no way to determine the decision maker’s relative tolerance for shocks A and X.

To make these predictions concrete, we will assume that all utilities are from the set {−2,−1} and we will assume a prior distribution on utilities that places 0.6 probability on utility −1 and 0.4 probability on utility −2. Aside from the different assumptions about utilities, model predictions for both the absolute and relative utility models are generated exactly as described previously for positive utilities. Table 3 shows the resulting numerical predictions. The table confirms that the two models make opposite predictions for these two choices. In this example, the magnitude of the differences between each model’s predictions for the two choices is small but real (i.e., not due to sampling error). As a result of these predictions, the absolute utility model concludes that Choice 16 provides evidence of a higher tolerance for X because it has a higher (less negative) mean posterior utility. The relative utility model concludes that Choice 38 provides evidence of a higher tolerance for X because there is a higher posterior probability that X has highest utility after observing that choice.

Table 3.

Model predictions for two choices, assuming utilities are negative.

		Absolute utility	Relative utility
Choice		E(ux|c,A)	p(ux is greatest|c,A)
16		−1.24	0.79
38		−1.25	0.81

Summary

Although these examples used a simpler setting than our experiments², they illustrate why all components of the inverse decision-making model are important. Accordingly, in the experiments that follow, we predicted that the absolute and relative utility models would predict participants’ inferences better than the likelihood and marginal likelihood models. We conducted three experiments. Experiment 1 compared all of the models’ predictions to people’s judgments for all of the choices in Figure 2. Experiment 2 tested whether the inverse decision-making model can account for an experimental result that previous accounts could not explain. Experiment 3 tested an assumption of our decision function that choices are made probabilistically.

Experiment 1: Ordering choices by strength of evidence for a preference

Method

Participants

85 Carnegie Mellon University undergraduates participated for course credit.

Materials

The set of choices that we used (Figure 2) included every possible unique choice with up to five different attributes, subject to the following constraints: (1) attribute X always appears in the chosen option, (2) there are no duplicate options, (3) each attribute appears in an option at most once, (4) only attributes in the chosen option are repeated in other options, and (5) when attributes appear in multiple options, the number of attributes is held constant across options. The first constraint was necessary for the task described below, the second two constraints created a finite space of choices, and the last two constraints limited attention to what we deemed the most effective cases for testing the inverse decision-making model. For example, the fourth constraint rules out cases like a choice between {X}, {A}, and {A}, which is not meaningfully different from a choice between {X} and {A}. However, we do consider cases like these in Experiment 3. The fifth constraint rules out cases like a choice between {X,A} and {A}, in which the first option clearly dominates the second option when all attributes are desirable. This choice therefore provides no information about the decision maker’s preference for either attribute.

Procedure

There were two between-subjects conditions. In the positive-attributes condition, the attributes were pieces of candy, suggesting that all attributes had positive utility. In the negative-attributes condition, the attributes were electric shocks at different body locations, suggesting that all attributes had negative utility. We randomly assigned participants to conditions, with 43 participants in the positive-attributes condition and 42 participants in the negative-attributes condition.

We gave each participant a set of cards, with one choice printed on each card. The choices were represented visually as in Figure 2 but with differently-colored rectangles instead of letters to indicate the different attributes. In the positive-attributes condition, we told participants that each option was a different bag of candy and that a decision maker in each choice had chosen one of the bags. Participants then ordered the choices by how strongly each choice suggested that the decision maker had a preference for X. In the negative-attributes condition, we told participants that the decision maker in each choice had been part of an experiment involving electric shocks, and the decision maker was given a choice between different sets of electric shocks that he or she would receive. Participants then ordered the choices by how strongly each choice suggested that the decision maker had a tolerance for X. In both conditions, we instructed participants to order the choices as completely as possible, but that they could assign the same ranking to a set of choices if they believed those choices provided equal evidence.

Model implementation

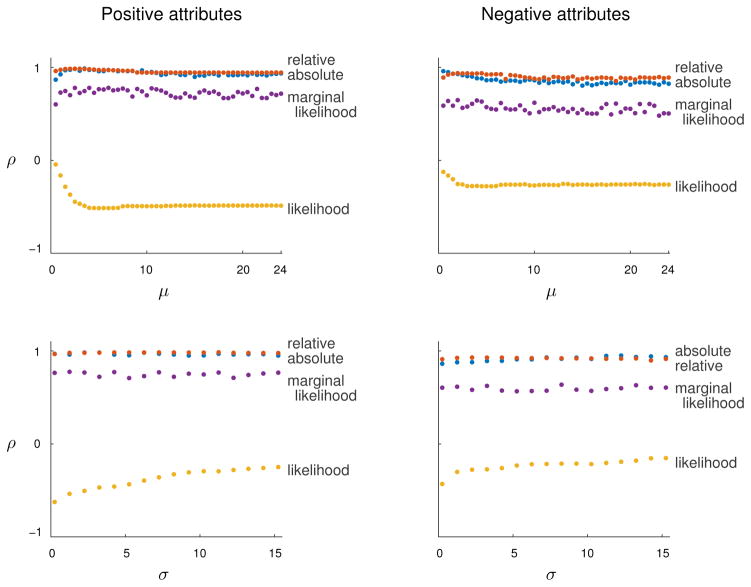
As described in Appendix A, we computed model predictions by generating 20 million samples using a Monte Carlo simulation. We made a standard assumption that utilities are independent and normally distributed (Allenby & Lenk, 1994; Albert & Chib, 1993; McCulloch & Rossi, 1994). The model predictions were generated using the prior distribution u_i ~ 𝒩(μ = 4, σ = 2) for the positive-attributes condition and u_i ~ 𝒩(μ = −4, σ = 2) for the negative-attributes condition. Appendix B describes an analysis in which we varied these parameters. The analysis revealed that the inverse decision-making model’s performance is largely insensitive to specific choices about the prior distribution of utilities.

Results

Two participants from the positive-attributes condition and three participants from the negative-attributes condition were excluded as outliers because their rankings for at least five choices were at least three standard deviations from the mean.

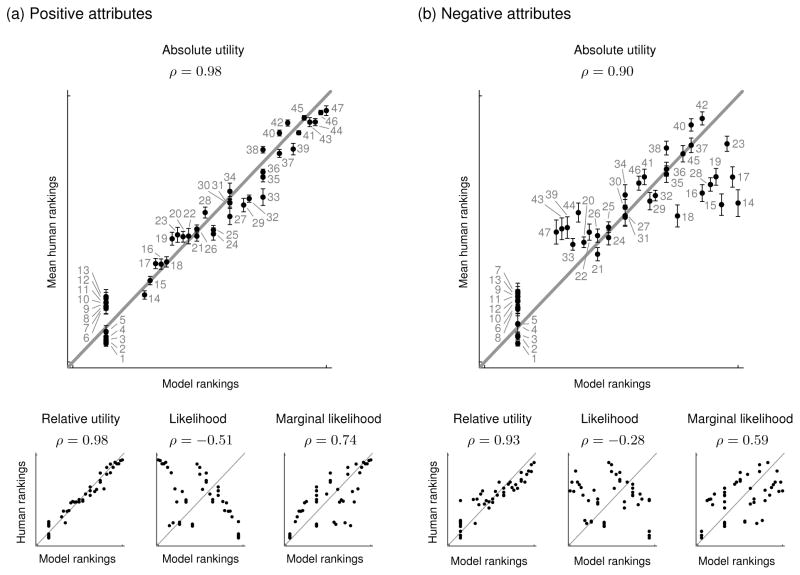
Figure 3 shows the mean human rankings for the remaining participants for each condition compared with the predictions of the four models. (See Appendix A for a complete table of these results.) All rankings are fractional rankings³. The human rankings shown in the figure were generated by first converting each participant’s responses to fractional rankings, and then computing the mean fractional ranking participants assigned to each choice. The diagonal lines in the plots indicate a perfect correspondence between model and human rankings. Thus, the largest deviations from these lines represent the largest deviations in the data from each model’s predictions.

Figure 3.

Experiment 1 results. The plots show mean human and model rankings of the choices in Figure 2 from weakest evidence to strongest evidence of a preference for X for (a) positive attributes and (b) negative attributes. Error bars indicate standard errors and the number labels refer to the choices in Figure 2. The diagonal lines indicate perfect correspondence between model rankings and mean human rankings. The ρs are Spearman rank correlation coefficients.

Results for the positive-attributes condition are shown in Figure 3a. The absolute utility model provides a close overall fit to the human rankings (rank correlation ρ = 0.98 [0.97, 0.99]⁴) and correctly predicts the highest ranked choice and the set of lowest ranked choices. The only clear discrepancy between the model’s predictions and the data is the cluster of points at the lower left representing Choices 6–13. These are all choices in which X appears in all options. Therefore these choices provide no information about a decision maker’s preference for X. Consequently, the model assigns the same ranking to this group as to the group of choices for which there is only a single option (Choices 1–5). However, participants assigned lower rankings to Choices 1–5. One explanation for participants’ rankings is that these choices are the only ones for which there was a single option, making it obvious that no choice had been made. Participants may have focused on this salient detail when making their rankings by grouping Choices 1–5 together instead of grouping them with Choices 6–13.

The overall predictions of the relative utility model (ρ = 0.98 [0.97, 0.99]) are virtually identical to those of the absolute utility model. One exception is the set of predictions for Choices 1–13. Some of these choices provide evidence about attributes other than X, altering the probability that X has the highest utility. For instance, the relative utility model predicts a higher rank for Choice 12 than either participants or the absolute utility model.

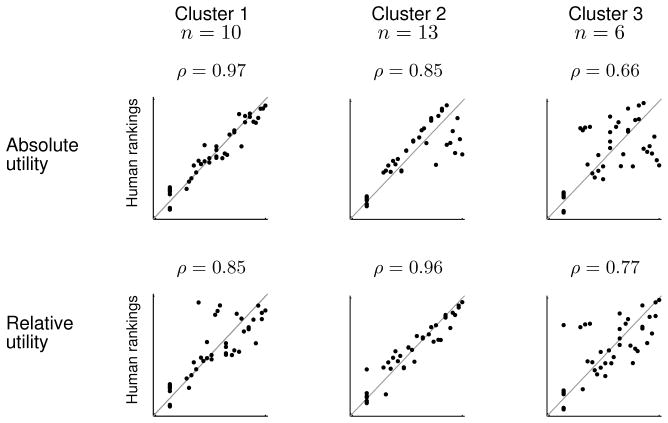
Results for the negative-attributes condition are shown in Figure 3b. Participants in this condition assigned substantially different rankings to many of the choices than participants in the positive-attributes condition. Both inverse decision-making models provide good predictions of participants’ rankings (ρ = 0.90 [0.82, 0.94] for absolute utility; ρ = 0.93 [0.88, 0.96] for relative utility) but neither version achieves the same level of accuracy for the mean human rankings as for positive attributes. Participants in the negative-attributes condition provided less consistent rankings than participants in the positive-attributes condition: the mean rank correlation between individual participants’ rankings and the mean ranking was 0.90 in the positive-attributes condition and 0.76 in the negative-attributes condition. Appendix C describes an analysis suggesting that groups of participants in the negative-attributes condition used different ordering criteria but that the inverse decision-making model does provide accurate predictions for a majority of participants.

The likelihood and marginal likelihood models do not perform well in either condition (ρs = −0.51 [−0.70,−0.26] and 0.74 [0.57, 0.85], respectively, for positive attributes; ρs = −0.28 [−0.52, 0.01] and 0.59 [0.36, 0.75] for negative attributes). Although the marginal likelihood model captures some of the general trends in the data, it makes several major errors. For example, Choice 7 provides no information about a preference for X because it appears in every option. The choice is “surprising” however, because a decision maker choosing at random from these options would make the observed choice only 1/4 of the time. The likelihood model performs even worse, primarily because it does not take into account alternative explanations for why an option was chosen, such as the fact that no other options were available (e.g., Choice 1). The poor performance of these two models suggests that both the likelihood p(c|u,A) and marginal likelihood p(c|A) are important components of the inverse decision-making model.

Alternative decision functions

The inverse decision-making model predictions considered so far have been based on the logit choice model of Equation 1. To test whether the model predictions depend critically on the choice of decision function, we generated inverse decision-making model predictions using two common alternative decision functions.

Probit model

The logit model is limited in some circumstances (Shafto & Bonawitz, 2015). For example, it does not allow for the assumption that utilities for certain attributes are correlated. A common alternative that addresses this limitation is the probit model. The logit and probit models differ in the assumptions they make about unobserved factors that contribute to utility. The logit model assumes that unobserved utilities are distributed according to a Gumbel distribution and the probit model assumes that unobserved utilities are distributed according to a normal distribution (Train, 2009). Unlike the logit model, the probit model decision function does not have a closed-form solution, but can be approximated using Monte Carlo simulation. We generated probit model predictions using the procedure described in Train (2009, Ch. 5).

Linear probability model

An alternative to both the logit and probit models is to simply assume that choice probabilities increase as a linear function of utility. One simple way to capture this assumption is as follows:

$$p(c=o_j\mid \mathbf{u},\mathbf{A})=\frac{U_j}{{\sum }_{k=1}^n{U}_k}.$$ (7)

Note that this model is identical to the logit model in Equation 1, without the exponential function applied to utilities. One limitation of the model above is that it produces nonsensical predictions when utilities are negative. For example, consider a choice with two options and suppose that the utility for Option 1 is −1 and the utility for Option 2 is −2. Applying Equation 7 to these utilities would predict a higher choice probability for Option 2, even though this violates the commonsense expectation that a decision maker would be more likely to choose the option with higher (less negative) utility. Therefore, we modified the model when dealing with negative attributes as follows:

$$p(c=o_j\mid \mathbf{u},\mathbf{A})=\{\begin{array}{ll}1\hfill & \text{if}\text{there}\text{is}\text{only}\text{one}\text{option}\hfill \\ 1-\frac{\mid U_j\mid }{{\sum }_{k=1}^n\mid U_k\mid }\hfill & \text{otherwise}\hfill \end{array}.$$ (8)

The first condition prevents setting the choice probability to 0 when there is only one option.

Model performance

We generated model predictions for Experiment 1 using the probit model and the linear probability model, with the absolute utility criterion. The predictions were based on 20 million samples for the linear probability model and 200,000 samples for the probit model⁵.

Table 4 compares the performance of the probit and linear probability models to the absolute utility logit model discussed earlier. The table shows that all models, except for the linear probability model in the negative-attributes condition, predicted people’s judgments well. The fact that the model predictions do not appear to depend critically on either the sorting criterion (absolute versus relative utility) or the form of the decision function strongly suggests that the strength of the inverse decision-making model is in the basic inverse decision-making assumption, rather than specific assumptions needed to specify an implementation of the model. Therefore, for brevity, for the remainder of this paper, we will only show and discuss results for the inverse decision-making model using the logit decision function and the absolute utility sorting criterion.

Table 4.

Spearman rank correlation coefficients between model predictions and data from Experiment 1.

Model	Positive-attributes	Negative-attributes
Logit	0.98	0.90
Probit	0.97	0.90
Linear	0.96	0.71

An alternative feature-based model

In the Introduction, we contrasted the inverse decision-making approach with a feature-based approach. Recall that the feature-based approach specifies an inference function that maps choice features to preferences (see Figure 1). In this section, we consider whether a feature-based model could account for our results in Experiment 1.

We began by generating a set of 10 features relevant for inferring someone’s preferences. Two features were previously identified by Newtson (1974). We generated the remaining features by attempting to include all other possible features that seemed both simple and relevant. The full set of features is shown in Table 5. The table includes a description of each feature and its type (integer or binary). The last two columns of the table indicate the direction of the feature that would indicate a stronger preference for X, depending on whether attributes are positive or negative. For example, the first feature is the number of chosen attributes. When the attributes are all positive, like pieces of candy, the more attributes there are in the decision maker’s chosen option, the less evidence there is that she was interested specifically in X. When the attributes are all negative, like electric shocks, choosing more attributes suggests that the chosen attributes are especially tolerable.

Table 5.

Features used by our weighted feature model. The last two columns indicate the direction of the feature that would indicate a stronger preference for X when attributes are positive or negative. The two features that include the phrase “max/min” were treated differently for positive and negative attributes. For positive attributes, these features refer to maximums; for negative attributes, these features refer to minimums.

Feature	Type	Positive attributes	Negative attributes
Number of chosen attributes	Integer	−	+
Number of forgone attributes	Integer	+	+
Number of forgone options	Integer	+	+
Number of forgone options containing X	Integer	−	−
Max/min number of attributes in a forgone option	Integer	+	−
X in every option?	Binary	−	−
Chose only option containing X?	Binary	+	+
X the only difference between options?	Binary	+	+
All options have same number of attributes?	Binary	+	+
Chose option with max/min number of attributes?	Binary	−	−

Can a feature-based model perform as well as the inverse decision-making model?

We used this set of features to generate predictions using a standard linear regression model, which we will refer to as the weighted feature model. Specifically, we fit weights on the features in Table 5 to best predict participants’ mean rankings. Our goal was to directly compare the performance of the weighted feature model to the inverse decision-making model. To do this, we trained the weighted feature model using every subset of features in Table 5 to determine the minimum number of features needed by the model to achieve the same level of predictive accuracy as the inverse decision-making model, as measured by Spearman rank correlation. For the positive-attributes condition, the weighted feature model could not outperform the inverse decision-making model even when all ten features were included. For the negative-attributes condition, the weighted feature model needed only two features to outperform the inverse decision-making model.

The weighted feature model has many fitted parameters. By contrast, the inverse decision-making model has no fitted parameters. Therefore, the weighted feature model has a considerable accuracy advantage over the inverse decision-making model. To account for the possibility of over-fitting with the weighted feature model, we conducted a second analysis in which we randomly partitioned the data into training (n = 37), validation (n = 5), and test (n = 5) sets. We used the training set to train the weighted feature model using every subset of features. We then chose the features and corresponding fitted weights that produced the best performance, as measured by Spearman rank correlation, on the validation set. Finally, we used these features and weights to generate predictions for the test set. We repeated this analysis 500 times, each time with different randomly selected partition. For the positive-attributes condition, the mean Spearman rank correlation on the test set was 0.77 (SD = 0.26). For the negative-attributes condition, the mean rank correlation was 0.69 (SD = 0.34). For comparison, we computed Spearman rank correlations using the predictions of the inverse decision-making model on the same test set. The corresponding mean rank correlations were 0.98 (SD = 0.02) and 0.90 (SD = 0.11). These analyses suggest that the weighted feature model can perform well, but is susceptible to over-fitting⁶. By contrast, the inverse decision-making model predicts people’s judgments well and is not fitted at all.

Are deviations from the inverse decision-making approach explained by a feature-based model?

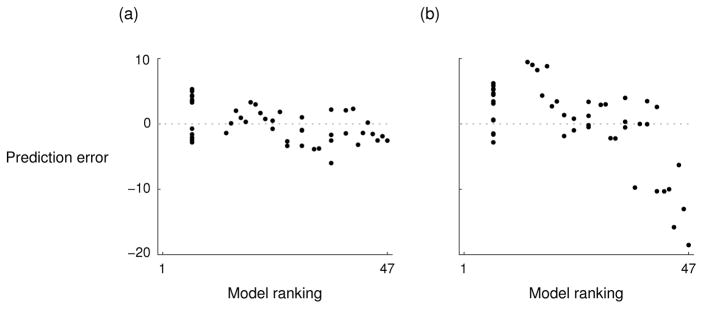
A separate question is whether there is any variance in people’s judgments that is not accounted for by the inverse decision-making model but that could be accounted for by features in Table 5. For example, Figure 4 shows residual plots depicting the prediction error for the inverse decision-making model predictions. Particularly in the negative-attributes condition (Figure 4b), the negative correlation in the plot suggests there are other sources of variance that the model does not account for.

Figure 4.

Residual plots for the inverse decision-making model predictions for (a) the positive-attributes and (b) negative-attributes conditions of Experiment 1.

To test for this possibility, we performed a linear regression on the prediction errors in Figure 4 using the features in Table 5 as predictors. Features that were statistically significant predictors after applying the Bonferroni correction are shown in Table 6. The fact that some features account for variance in the prediction errors of the inverse decision-making model suggests that some participants may have used feature-based strategies that are not entirely consistent with the model. To explore this possibility further, we now analyze the judgments of individual participants.

Table 6.

Statistically significant predictors in a linear regression on the prediction errors in Figure 4.

Condition	Feature	β	p
Positive-attributes	X in every option?	3.9	0.004
Negative-attributes	Number of chosen attributes	−2.4	0.001
	Number of forgone attributes	4.0	0.004
	Number of forgone options	−4.5	0.002
	X in every option?	7.0	< 0.001

Individual differences

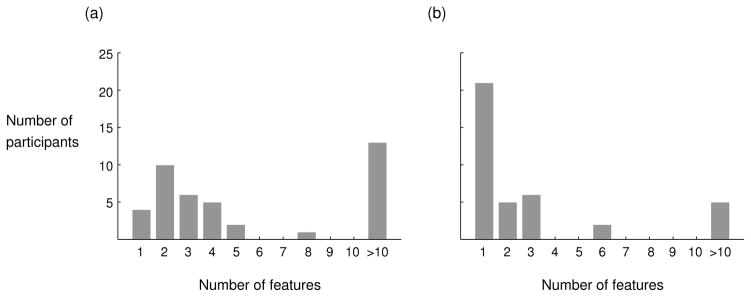
To explore individual differences, we repeated the first weighted feature analysis, described earlier, for individual participant rankings. That is, we fit the weighted feature model to each participant’s rankings individually, using the same procedure described above. The results of this analysis are shown in Figure 5. Figure 5a shows the results for the positive-attributes condition. For a majority of the participants in that condition, at least four features were needed to match the performance of the inverse decision-making model. For 13 of 41 participants in that condition, the weighted feature model could not outperform the inverse decision-making model even when all ten features were included. Figure 5b shows the results for the negative-attributes condition. The weighted feature model performed better in this condition, where 21 of 39 participants were better fit using only one feature. For 7 participants, at least four features were needed to match the performance of the inverse decision-making model, including 5 participants for which the weighted feature model could not outperform the inverse decision-making model even when all ten features were included.

Figure 5.

The minimum number of features from Table 5 needed by the weighted feature model to match the predictive accuracy of the inverse decision-making model for (a) the positive-attributes and (b) the negative-attributes conditions of Experiment 1.

Summary

These analyses do not discredit the feature-based approach, but they do highlight three limitations of the approach. First, as we noted earlier, the approach provides no principled way to enumerate the set of relevant features; we generated the features in Table 5 though brainstorming and discussion. Second, our analyses suggest that a large number of features is often needed to provide a close fit to people’s judgments, especially for judgments about attributes with positive utilities. Third, the feature-based approach provides no principled way to identify which features are most important. For example, even though 21 participants in the negative-attributes condition were better fit using only a single feature, the best-fitting single feature varied from participant to participant. In total, each of five different features was the best-fitting single feature for at least one of the 21 participants. In contrast to these limitations of the feature-based approach, the inverse decision-making approach provides a parsimonious and principled account of our data.

Experiment 2: Accounting for previous results

Although Experiment 1 is more comprehensive than previous studies of preference learning, it used a novel preference learning paradigm unlike those used in previous studies. We conducted a second experiment to show that our approach can account for previous psychological data and can resolve an issue not addressed by previous theories of preference learning.

As noted earlier, previous researchers have highlighted the importance of non-common attributes. Newtson (1974) proposed two versions of this principle. First, the fewer non-common attributes there are in a chosen option, the more certain an observer can be that the decision maker wanted a specific attribute. For example, an observer can be more certain that a decision maker wanted candy X if she chose a bag containing just candy X than if she chose a bag containing candy X and another piece of candy. Second, the more non-common attributes there are in the forgone (i.e., non-chosen) options, the more certain an observer can be that the decision maker wanted a specific attribute in the chosen option. For example, an observer can be more certain that a decision maker wanted candy X if she forwent many bags with different candies than if she forwent just one bag.

Both of these principles follow from the inverse decision-making model. When there are fewer attributes in a chosen option, the observed choice would only be probable if the decision maker assigned high utility to the chosen attributes. Similarly, when there are more attributes in the forgone options, the observed choice would only be probable if the decision maker assigned high utility to the chosen attributes.

Newtson (1974) conducted the first experimental test of these principles. He presented participants with choices made by two people who both chose between three options for what to do on a Friday night: babysit for a professor, go to the beach with some fraternity brothers, or fill in for a friend working in the library. The “attributes” of these options were varied across conditions. The conditions are shown in Figure 6. In each row of the figure, one person made the choice on the left and the other person made the choice on the right. For clarity, we will refer to the person on the left as Lee and the person on the right as Rachel⁷. For example, Figure 6a shows a condition in which Lee had two possible reasons for babysitting: to ingratiate himself with the professor (attribute X) and to get some extra studying done (attribute A). In contrast, Rachel had only one possible reason for babysitting: to ingratiate herself with the professor. Participants were asked to make inferences about which person is more ingratiating.

Figure 6.

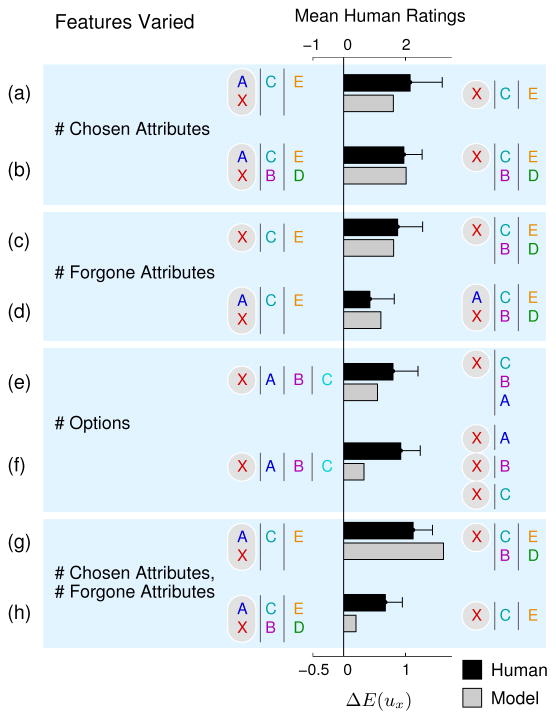
Experiment 2 results. The bars show mean human ratings and inverse decision-making model predictions for the pairs of observed choices in each row. The bars point toward the choice that provides stronger evidence of a preference for X. Error bars indicate 95% confidence intervals. The first six pairs of choices differ with respect to one feature, identified by the labels in the “Features Varied” column. The last two pairs differ with respect to two features.

The comparisons used by Newtson (1974) included all conditions in Figure 6 except 6e and 6f. The six conditions Newtson used were generated by systematically exploring the two versions of the principle of non-common attributes. Conditions 6a through 6d are cases in which only one version of the principle is relevant. For example, in 6a, the number of attributes forgone is the same for Lee and Rachel, and their choices differ only with respect to the number of chosen attributes. As a result, the principle of non-common attributes makes clear predictions in these four conditions. In condition 6g, both versions of the principle are relevant, and they both predict that Rachel values attribute X more than Lee. Therefore the principle of non-common attributes again makes a clear prediction.

Condition 6h is especially interesting because it pits the two versions of the principle against each other. In this condition, Lee chose more attributes than Rachel, but also forwent more attributes. As a result, one principle (more non-common attributes in the forgone options) suggests that Lee values attribute X more, and one principle (fewer non-common attributes in the chosen option) suggests that Rachel values attribute X more. Because Newtson’s principles were not defined in formal terms, he could not predict which principle should carry more weight in this case. As we explain later, however, the inverse decision-making model predicts that Rachel’s preference for X is probably stronger than Lee’s. In Experiment 2, we replicated and extended Newtson’s experiment to show that the inverse decision-making model can account for his results and more.

Method

Participants

160 participants completed the experiment online on Amazon Mechanical Turk. They were paid for their participation.

Materials and Procedure

There were eight between-subjects conditions. Each condition is represented by one row in Figure 6. Each row shows a pair of choices that vary with respect to one or two of four features. In addition to the six conditions used by Newtson (1974), we included two conditions that varied the number of options presented to each person. One of these new conditions (6f) is a case in which a person chose an option on three successive occasions. As in the positive-attributes condition of Experiment 1, the attributes for all conditions were pieces of candy.

We randomly assigned 20 participants to each condition. Each participant saw a pair of choices made by two different people. The positions of the two choices on the screen (left or right) were randomized across participants. For the condition in which the decision maker made three choices, participants read that the person chose the bag containing candy X on three separate occasions.

Participants answered the following question: “Based only on the above information, which person do you think likes candy X more?” They provided their responses on a numerical scale from 1 (Lee likes candy X more) to 8 (Rachel likes candy X more). The names of the decision makers were different in each condition and the polarity of the scale was reversed for half of the participants.

Model implementation

We generated model predictions in the same way as for Experiment 1. For the condition in which multiple choices are observed, we assumed that choices are independent, such that p(c|u,A) = Π_i p(c_i|u,A).

Results

Figure 6 shows, for each condition, the mean human ratings compared with the inverse decision-making model predictions. In the figure, the human ratings are rescaled so that the midpoint of the scale is 0. The model predictions were produced by computing the difference between E(u_x) for each choice. Consistent with the predictions of the inverse decision-making model, participants judged in every case that the choice on the right provides better evidence of a preference for X. We performed one-tailed t-tests to test whether the means in each condition were significantly greater than 0. The results were statistically significant in every condition (p = .025 for the condition in Figure 6d; p = 0.010 for condition 6h; p < .001 for all other conditions). The direction of participants’ judgments from all conditions in Newtson’s (1974) experiment match his results.

Our results replicate the finding that Newtson (1974) could not explain, shown in Figure 6h. To illustrate how the inverse decision-making model explains this result, consider again a simpler setting in which all utilities are drawn from the set {1, 2}. Suppose again that Lee made the choice on the left and Rachel made the choice on the right. We will consider the relative probability that Rachel assigns a probability of 2 to X ( $u_x^R=2$) compared to Lee ( $u_x^L=2$). This can be quantified by the following odds ratio:

$$\frac{P(u_x^R=2\mid \text{Rachel}\text{chose}\{X\})}{P(u_x^L=2\mid \text{Lee}\text{chose}\{X,A\})}=\frac{P(\text{Rachel}\text{chose}\{X\}\mid u_x^R=2)}{P(\text{Lee}\text{chose}\{X,A\}\mid u_x^R=2)},$$

where the ratio on the right-hand side follows from an application of Bayes’s rule. Consider the ratio on the right. If Rachel assigns a utility of 2, the highest possible utility to X, there is a reasonably high probability that she will choose {X} over {C} or {E} because the other two options cannot have higher utility than {X}. However, even if Lee assigns the highest possible utility to X, the probability that he will choose {X,A} over {B,C} and {D,E} is lower than it is for Rachel because it is possible for one of the other options to have higher total utility—for example, if Lee assigns a utility of 1 to A, and a utility of 2 to both B and C. It follows that the ratio on the right exceeds one and therefore the ratio on the left exceeds one, resulting in a slightly stronger preference inference for Rachel.

Newtson was not primarily concerned with comparing the results in individual conditions and his data do not support robust conclusions about the magnitudes of effects for different conditions. Our results are similarly uninformative regarding differences between conditions. We performed two-sample t-tests for all pairs of conditions (28 total comparisons). After applying the Bonferroni correction for multiple comparisons, no comparisons were statistically significant at α = 0.0018. Figure 4 shows that the inverse decision-making model does make predictions about these magnitudes, but experimental designs more sensitive than ours and Newtson’s would be needed to test these predictions.

Experiment 3: Utility-matching vs. utility-maximizing

The inverse decision-making model assumes that choices are made probabilistically to account for possible hidden factors or attributes that contribute to a decision maker’s choice. An alternative model might assume that there are no hidden factors, and that decision makers always maximize utility with respect to the observed attributes alone. We refer to this alternative as the maximizing model. For Experiments 1 and 2, the maximizing model generates predictions that closely match the predictions shown in Figure 3. We therefore designed a third experiment to explore whether people’s inferences are more consistent with the maximizing model or a model that assumes a probabilistic choice function.

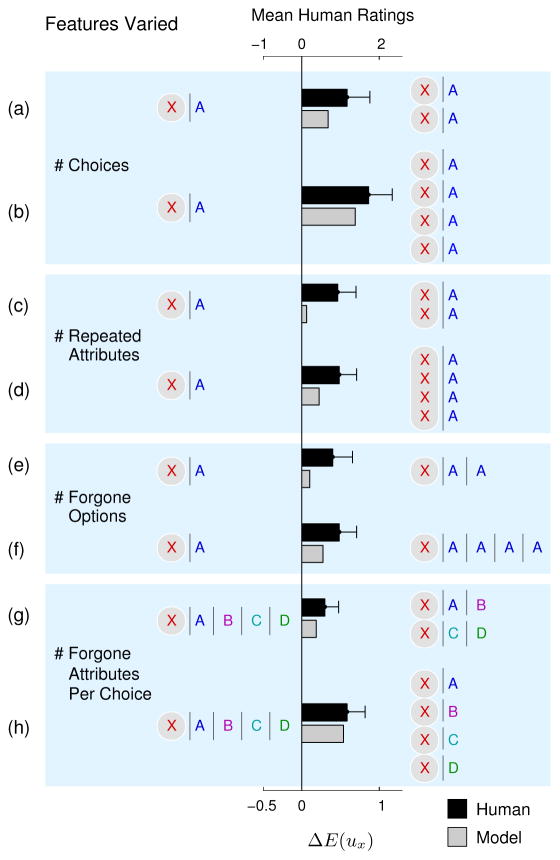
As in Experiment 2, we presented participants with eight pairs of choices and asked them to judge which choice provides better evidence of a preference for X. Figure 7 shows the pairs of choices we used. For each pair of choices, the inverse decision-making model predicts that the choice on the right provides stronger evidence of a preference for X, but the maximizing model predicts that the two choices provide equal evidence. For example, 7a and 7b differ only in the number of times an identical choice is made. If Rachel always makes choices to maximize her utility, then observing Rachel make the same choice more than once cannot provide any new information about her preferences. Thus, if participants judge that the choices on the right provide stronger evidence of a preference for X, they probably are not assuming that Rachel always makes choices this way.

Figure 7.

Experiment 3 results. The bars show mean human ratings and inverse decision-making model predictions for the pairs of observed choices in each row. The bars point toward the choice that provides stronger evidence of a preference for X. Error bars indicate 95% confidence intervals. Predictions for the maximizing model (not shown) are 0 for every comparison.

Method

Participants

30 participants completed the experiment online on Amazon Mechanical Turk. They were paid for their participation.

Materials and Procedure

The design and procedure was nearly identical to Experiment 2, except that the experiment was run within-subjects rather than between-subjects. That is, all 30 participants made a judgment for every pair of choices in Figure 7. The choices were presented in a random order. Unlike in Experiment 2, participants made their judgments on a 1 to 7 scale to allow them to express a belief that the choices provided equal evidence of a preference.

Maximizing model

The maximizing model is identical to the inverse decision-making model except that, instead of using Equation 1, the maximizing model assumes that choices are made to maximize utility:

$$p(c=o_j\mid \mathbf{u},\mathbf{A})=\{\begin{array}{ll}1,\hfill & \text{if}\text{for}\text{all}k,U_j>U_k\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$

Results

Figure 7 shows, for each condition, the mean human ratings compared with the inverse decision-making model predictions. In the figure, the human ratings are rescaled so that the midpoint of the scale is 0. Consistent with the predictions of the inverse decision-making model, but not the maximizing model, participants judged in every case that the choice on the right provides better evidence of a preference for X. We performed one-tailed t-tests to test whether the means were significantly greater than 0. The results were statistically significant in every condition (p = .033 for the condition in Figure 6g; p < .001 for all other conditions). These judgments are consistent with the assumptions of the inverse decision-making model but not the maximizing model.

Discussion

Across three experiments, we found that people’s inferences about other people’s choices were consistent with the inverse decision-making approach. Our results are consistent with previous studies that have tested predictions of the inverse decision-making approach (Bergen et al., 2010; Lucas et al., 2014). However, our results go further than past studies by offering the most comprehensive test to date of an inverse decision-making model as a psychological account of preference learning. In addition to accounting for our own data, the model accounts for previous data and also provides an explanation for a previously unexplained result (Newtson, 1974).

Unlike previous feature-based accounts, inverse decision-making does not directly specify inference principles that map choices to preferences. Instead, it inverts a decision function that maps preferences to choices. Compared to the feature-based approach, our work suggests that the inverse decision-making approach provides a more parsimonious account of how people infer preferences. Specifically, inference principles proposed by earlier accounts, like the principle of non-common effects (Jones & Davis, 1965; Newtson, 1974), emerge naturally under the inverse decision-making approach. Moreover, we found that for many individuals, a feature-based model would need to include many features to match the performance of the inverse decision-making model.

Utility priors

In our tasks, we provided no information about the relative utilities of different attributes. Accordingly, in the inverse decision-making model, we assumed that the prior probability distribution for utilities of different attributes were the same. As we acknowledged earlier, however, in some real-world situations, some attributes tend to be more liked than others. The inverse decision-making model predicts that differences in expectations about the utilities of different attributes should affect inferences about an individual’s preferences. Thus, one question for future work is whether this prediction is true of people’s inferences.

A second question is where people’s prior beliefs about utilities for different attributes come from. One hypothesis is that people base these beliefs on their own preferences (Ames, 2004; Epley, Keysar, Boven, & Gilovich, 2004; Ross, Greene, & House, 1977). Orhun and Urminsky (2013) studied whether this egocentrism hypothesis could account for people’s inferences about other people’s political attitudes from their choices. The researchers found that people’s attitudes toward political candidates influenced their judgments of others’ attitudes toward the same candidates, even when other people voted differently than they did. Orhun and Urminsky (2013) focused only on political attitudes, but future work can explore whether egocentrism can explain people’s inferences about other types of preferences.

Utility functions

Our results provide support for the inverse decision-making approach in general, but future work is needed to clarify the specific assumptions people make about how others make choices. We implemented an inverse decision-making model that treats positive and negative utilities the same way and assumes that utilities are additive. However, neither of these assumptions is fundamental to the inverse decision-making approach and there are reasons to question both assumptions.

First, data from the negative-attributes condition of Experiment 1 suggest that people may reason differently about choices involving positive versus negative utilities. In particular, even though the inverse decision-making model predicted most individual participants’ judgments well in the positive-attributes condition, the model did not perform as well as a simple feature-based model at predicting many participants’ judgments in the negative-attributes condition. Although our experiment focused on reasoning about other people’s choices, this result is consistent with research showing that people treat gains and losses differently when making choices (Kahneman & Tversky, 1979) and predicting future feelings (Kermer, Driver-Linn, Wilson, & Gilbert, 2006). It would be possible to combine the inverse decision-making approach with a more psychologically accurate account of subjective utility. Doing so might better account for people’s inferences about choices involving negative utilities.

Second, we made several assumptions that were reasonable for our tasks but that are clearly violated in other situations. For one, the logit model makes the independence of irrelevant alternatives (IIA) assumption—that the relative choice probabilities between options should be unaffected by the introduction of additional options. In some situations, this assumption is incorrect. For example, consider the classic red bus/blue bus problem (McFadden, 1974). A commuter has a choice between driving a car or taking a red bus. Then a third option, a blue bus, is introduced. Because the blue bus and red bus are identical from the commuter’s standpoint, whatever choice probability the commuter initially assigned to the blue bus will be split evenly between the blue and red buses once the red bus option is introduced. In other words, the addition of the third option changes the relative choice probabilities of the first two options—a violation of the IIA assumption. After observing that the commuter chose to drive, our model would incorrectly infer a stronger preference for driving if there were two bus alternatives than if there were just one. Other decision functions, like the probit model, overcome this limitation by allowing for attributes to be correlated or substituted. As we showed earlier, it is straightforward to incorporate alternative decision functions into the inverse decision-making approach.

Another assumption we made was that utilities are additive. In some real-world domains, this assumption is also clearly violated. For example, a Blu-ray disc and a Blu-ray player are complements: each item has little value without the other. As a result, the utility of both the disc and the player together will exceed the sum of utilities of each item separately. In some domains, interactions between attributes are complex. For example, sometimes combining two ingredients (e.g., chips and salsa) tastes better than either ingredient alone; other times, combining two ingredients (e.g., ice cream and tomatoes) tastes worse than either ingredient alone. Knowledge of complementary attributes and interactions between attributes could affect people’s preference inferences. For example, suppose you observe a decision maker choose an option containing attributes X, A, and B. If attributes A and B are complements, this choice should provide less evidence that the decision maker likes attribute X than if attributes A and B are not complements.

Researchers have developed utility functions to account for cases like these (Tversky & Sattath, 1979; Gershman, Malmaud, & Tenenbaum, 2017). Once again, such functions can be straightforwardly incorporated into the inverse decision-making approach. Empirical work will be needed, however, to study whether people’s inferences about other people’s preferences match the predictions of the inverse decision-making approach in these more complex domains. One study by Bergen et al. (2010) found evidence that people do take some non-additive utility assumptions into account when inferring other people’s preferences and predicting their future choices, but more work will be needed to thoroughly test this hypothesis.

Probabilistic decision functions

Our results from Experiment 3 suggest that people do not necessarily expect others to maximize utility. This conclusion is consistent with many decision functions, like the logit choice model in our inverse decision-making model, which assumes that choices are made probabilistically. A probabilistic decision function accounts for hidden factors that might affect someone’s choice. For example, when choosing between candies, factors like calorie counts, a preference for variety, or a desire not to be wasteful might all contribute to someone’s choice. In other contexts, however, there is little reason to assume that hidden factors are present. For example, decision makers would likely not choose between $10 and $20 probabilistically in proportion to the options’ utilities. Moreover, unlike in our experiments, people would likely not expect others to choose probabilistically between these two options. Future work can explore how expectations about probabilistic versus deterministic choice vary across contexts.

Conclusion

Our work is related to a growing body of research using probabilistic inference and inverse decision-making to explain social inferences (Zaki, 2013). This literature includes recent probabilistic accounts of emotion inference (Ong, Zaki, & Goodman, 2015) and attitude attribution (Walker, Smith, & Vul, 2015), and inverse decision-making accounts of belief and goal inference (Baker et al., 2009; Ullman et al., 2009; Tauber & Steyvers, 2011; Baker & Tenenbaum, 2014; Wu et al., 2014; Jern & Kemp, 2015; Jara-Ettinger et al., 2016; Baker et al., 2017). Although these accounts rely on different formal assumptions, they are all based on the idea that people interpret social behavior by inverting a model of the process that produced the behavior. Our work therefore adds to a growing body of research suggesting that inverse decision-making is a powerful psychological mechanism for social inference.

Highlights.

• We propose that people learn others’ preferences by inverting a decision-making model

• In three experiments, participants inferred people’s preferences from their choices

• Inverse decision-making provided a strong account of participants’ inferences

• Inverse decision-making is more parsimonious and principled than other accounts

Appendix A. Computing model predictions

In the main text, we used a simpler setting to illustrate how to generate model predictions for the four models (absolute utility, relative utility, likelihood, and marginal likelihood). In this Appendix, we explain how to generalize the modeling procedure used in the examples to generate the actual model predictions in the main text. We also provide a table of complete model predictions and results from Experiment 1.

Monte Carlo simulation methods

The model predictions for all experiments assumed a continuous normal prior probability distribution over utilities, unlike the simple discrete prior probability distributions used in the illustrative examples. We generated the model predictions in the main text using Monte Carlo simulation.

We drew n = 20 million utility samples from the prior probability distribution over utilities. For each sample u_i and each choice, we computed p(c|u_i,A). Averaging these computations over samples produces an approximation of p(c|A). Averaging these computations only for samples in which u_x has the greatest utility produces an approximation of p(c|u_ix is greatest,A), where u_ix denotes u_x in sample u_i. We used the first approximation to generate predictions for the marginal likelihood model. We used the second approximation to generate predictions for the likelihood model. We used both approximations to generate predictions for the absolute and relative utility models. Specifically, absolute utility predictions were approximated as follows:

$$E(u_x\mid c,\mathbf{A})\approx \frac{{\sum }_{i=1}^n{u}_{i_x}·p(c\mid {\mathbf{u}}_{\mathbf{i}},\mathbf{A})}{{\sum }_{i=1}^{n}p(c\mid {\mathbf{u}}_{\mathbf{i}},\mathbf{A})}$$

Relative utility model predictions were approximated as follows:

$$p(u_x\text{is}\text{greatest}\mid c,\mathbf{A})\approx \frac{{\sum }_{u_{i_x}\text{is}\text{greatest}}p(c\mid {\mathbf{u}}_{\mathbf{i}},\mathbf{A})}{{\sum }_{i=1}^{n}p(c\mid {\mathbf{u}}_{\mathbf{i}},\mathbf{A})}$$

Complete Experiment 1 results

Table A1.

Mean human fractional rankings and the output of the model computations for the positive-attributes condition of Experiment 1.

	Human	Absolute utility	Relative utility	Likelihood	Marginal likelihood
Choice	Mean (SD)	E(ux|c,A)	p(ux is greatest|c,A)	p(c|ux is greatest,A)	1/p(c|A)
1	4.2 (2.9)	4.00	0.20	1.00	1.00
2	4.5 (2.6)	4.00	0.20	1.00	1.00
3	4.9 (2.6)	4.00	0.20	1.00	1.00
4	5.4 (3.3)	4.00	0.20	1.00	1.00
5	6.3 (6.7)	4.00	0.20	1.00	1.00
6	10.3 (5.7)	4.00	0.20	0.50	2.00
7	10.5 (7.9)	4.00	0.20	0.25	4.00
8	10.7 (4.5)	4.00	0.20	0.50	2.00
9	11.2 (6.4)	4.00	0.20	0.33	3.00
10	11.2 (4.8)	4.00	0.20	0.50	2.00
11	11.3 (5.6)	4.00	0.20	0.50	2.00
12	12.0 (6.6)	4.00	0.21	0.29	3.53
13	12.3 (7.7)	4.00	0.20	0.33	3.00
14	12.6 (4.6)	4.00	0.20	1.00	1.00
15	15.1 (4.6)	4.01	0.20	1.00	1.01
16	17.9 (5.8)	4.12	0.22	0.99	1.10
17	18.0 (5.7)	4.03	0.20	1.00	1.02
18	18.3 (5.7)	4.14	0.22	0.97	1.16
19	22.3 (7.2)	4.19	0.23	0.97	1.18
20	22.7 (5.9)	4.37	0.28	0.44	3.17
21	22.7 (5.4)	4.48	0.31	0.77	2.00
22	22.8 (8.5)	4.47	0.30	0.30	4.94
23	23.0 (8.3)	4.25	0.24	0.96	1.25
24	23.1 (6.8)	4.52	0.31	0.44	3.53
25	23.8 (4.9)	4.52	0.31	0.44	3.53
26	24.0 (4.5)	4.48	0.31	0.77	2.00
27	26.1 (8.9)	4.61	0.33	0.83	2.00
28	26.8 (6.0)	4.51	0.32	0.77	2.06
29	28.1 (7.4)	4.76	0.39	0.39	4.94
30	28.5 (4.6)	4.61	0.33	0.83	2.00
31	28.6 (6.6)	4.61	0.33	0.83	2.00
32	29.2 (4.0)	4.84	0.42	0.66	3.17
33	29.5 (9.1)	4.88	0.43	0.29	7.40
34	30.5 (9.1)	4.61	0.33	0.83	2.00
35	33.0 (5.4)	4.88	0.43	0.71	3.00
36	33.8 (3.2)	4.88	0.43	0.71	3.00
37	37.0 (4.4)	5.05	0.50	0.62	4.00
38	37.7 (4.6)	4.88	0.43	0.71	3.00
39	37.8 (6.4)	5.16	0.55	0.26	10.74
40	40.6 (3.2)	5.05	0.50	0.62	4.00
41	40.6 (2.2)	5.30	0.61	0.24	12.99
42	42.3 (3.4)	5.16	0.55	0.55	5.00
43	42.5 (5.0)	5.52	0.73	0.03	109.14
44	42.5 (3.9)	5.57	0.77	0.11	36.20
45	43.2 (2.6)	5.38	0.66	0.22	15.03
46	44.1 (2.5)	5.59	0.77	0.03	119.41
47	44.4 (5.3)	5.73	0.90	0.00	1555.72

Table A2.

Mean human fractional rankings and the output of the model computations for the negative-attributes condition of Experiment 1.

	Human	Absolute utility	Relative utility	Likelihood	Marginal likelihood
Choice	Mean (SD)	E(ux|c,A)	p(ux is greatest|c,A)	p(c|ux is greatest,A)	1/p(c|A)
1	4.2 (2.6)	−4.00	0.20	1.00	1.00
2	5.4 (3.4)	−4.00	0.20	1.00	1.00
3	5.5 (4.3)	−4.00	0.20	1.00	1.00
4	7.6 (8.9)	−4.00	0.20	1.00	1.00
5	7.6 (11.3)	−4.00	0.20	1.00	1.00
6	10.4 (6.8)	−4.00	0.20	0.50	2.00
7	13.2 (8.8)	−4.00	0.20	0.25	4.00
8	10.1 (4.7)	−4.00	0.20	0.50	2.00
9	12.4 (7.0)	−4.00	0.20	0.33	3.00
10	11.4 (6.6)	−4.00	0.20	0.50	2.00
11	12.2 (8.1)	−4.00	0.20	0.50	2.00
12	11.7 (6.0)	−4.00	0.21	0.29	3.53
13	12.9 (7.3)	−4.00	0.20	0.33	3.00
14	28.5 (14.4)	−2.27	0.25	0.00	1550.36
15	28.2 (11.6)	−2.48	0.32	0.01	109.30
16	30.2 (9.1)	−2.84	0.38	0.18	10.74
17	33.0 (11.0)	−2.29	0.33	0.00	333.71
18	26.2 (11.9)	−3.12	0.32	0.22	7.40
19	33.0 (8.9)	−2.57	0.43	0.09	24.65
20	21.7 (5.7)	−3.63	0.28	0.44	3.17
21	19.6 (7.2)	−3.52	0.31	0.77	2.00
22	23.4 (8.7)	−3.53	0.30	0.30	4.94
23	38.7 (8.2)	−2.45	0.46	0.06	40.31
24	22.5 (8.0)	−3.48	0.31	0.44	3.53
25	24.3 (5.8)	−3.48	0.31	0.44	3.53
26	22.8 (7.1)	−3.52	0.31	0.77	2.00
27	26.3 (11.4)	−3.39	0.33	0.83	2.00
28	31.7 (7.2)	−2.79	0.41	0.17	12.07
29	28.8 (9.4)	−3.24	0.39	0.39	4.94
30	27.7 (8.5)	−3.39	0.33	0.83	2.00
31	26.0 (8.7)	−3.39	0.33	0.83	2.00
32	29.8 (5.6)	−3.16	0.42	0.66	3.17
33	21.3 (6.3)	−3.86	0.23	0.99	1.15
34	29.9 (11.1)	−3.39	0.33	0.83	2.00
35	33.5 (8.9)	−3.12	0.43	0.71	3.00
36	34.3 (7.6)	−3.12	0.43	0.71	3.00
37	38.4 (7.8)	−2.95	0.50	0.62	4.00
38	38.0 (7.4)	−3.12	0.43	0.71	3.00
39	24.2 (11.7)	−3.88	0.22	1.00	1.10
40	42.0 (6.6)	−2.95	0.50	0.62	4.00
41	33.0 (8.3)	−3.36	0.34	0.83	2.08
42	43.1 (7.0)	−2.84	0.55	0.55	5.00
43	24.0 (11.7)	−3.99	0.20	1.00	1.01
44	26.8 (10.3)	−3.79	0.24	0.99	1.20
45	37.0 (8.9)	−3.10	0.44	0.71	3.08
46	31.9 (7.6)	−3.39	0.33	0.83	2.01
47	23.5 (13.0)	−4.00	0.20	1.00	1.00

Appendix B. Experiment 1 model parameter sensitivity analysis

The model predictions were generated assuming a 𝒩(μ = 4, σ = 2) prior probability distribution on each utility for positive attributes and a 𝒩 (μ = −4, σ = 2) prior probability distribution on each utility for negative attributes. To test how strongly our results depended on the parameters of these distributions, we generated model predictions using a variety of different parameter values. First, we generated a series of predictions in which we held σ = 2 constant and varied μ from σ/4 to 12σ (−σ/4 to −12σ for negative attributes) in increments of 0.25. Second, we generated a series of predictions in which we held μ = 4 constant (μ = −4 for negative attributes) and varied σ from |μ|/16 to 4|μ| in increments of 0.25. In all cases, we generated predictions for the absolute utility model, the relative utility model, the likelihood model, and the marginal likelihood model. The predictions were based on 500,000 samples each.

The results of these analyses are shown in Figure B1. As the figure shows, the predictions of the four models were largely insensitive to the settings of the prior probability distribution parameters. Therefore, we used 𝒩(μ = 4, σ = 2) and 𝒩(μ = −4, σ = 2) to generate all the model predictions in the main text.

Figure B1.

Model parameter sensitivity analysis. The plots show a comparison between model predictions and data from Experiment 1 for various settings of the prior probability parameters. ρ is the Spearman rank correlation coefficients between the model predictions and data.

Appendix C. Experiment 1 individual differences

To better understand the poorer performance of the inverse decision-making models in the negative-attributes condition of Experiment 1, we performed a hierarchical clustering analysis of the participants in both conditions. We used rank correlation as a distance metric and average link clustering to build the clusters. We cut the resulting dendrograms at 0.8. We chose this threshold because it produced the most informative clustering for the negative-attributes condition. Specifically, a higher threshold produced many more, smaller clusters, and a lower threshold resulted in fewer, larger clusters that appeared to obscure real differences in the data. Participants’ rankings in the positive-attributes condition were highly correlated: cutting the dendrogram at 0.8 resulted in one cluster that included 32 participants, one cluster that included 7 participants, and 2 singleton clusters.

Participants’ rankings in the negative-attributes condition were more varied: 29 participants in this condition could be grouped into one of three clusters, with the remaining participants in clusters of one or two. We analyzed the three largest clusters independently, excluding the remaining 10 participants who could not be naturally grouped. We compared the mean rankings of each cluster to the predictions of the absolute and relative utility models. Figure C1 shows that the mean rankings of participants in Cluster 1 (n = 10) were better fit by the absolute utility model (absolute utility model ρ = 0.97 [0.94, 0.98]; relative utility model ρ = 0.85 [0.74, 0.91]), the mean rankings of participants in Cluster 2 (n = 13) were better fit by the relative utility model (absolute utility model ρ = 0.85 [0.74, 0.91]; relative utility model ρ = 0.96 [0.92, 0.98]), and the mean rankings of participants in Cluster 3 (n = 6) were not well fit by either the absolute utility model (ρ = 0.66 [0.46, 0.80]) or the relative utility model (ρ = 0.77 [0.61, 0.86]). In sum, about half of participants’ rankings (n = 23) were well predicted by either the absolute or relative utility versions of the inverse decision-making model.

Figure C1.

Comparison of absolute and relative utility model predictions for four clusters of participants in the negative-attributes condition of Experiment 1.