Ligand Field Strength Mediates Electron Delocalization in Octahedral [(^HL)₂Fe₆(L′)_m]ⁿ⁺ Clusters

Abstract

To assess the impact of terminal ligand binding on a variety of cluster properties (redox delocalization, ground-state stabilization, and breadth of redox state accessibility), we prepared three electron-transfer series based on the hexanuclear iron cluster [(^HL)₂Fe₆(L′)_m]ⁿ⁺ in which the terminal ligand field strength was modulated from weak to strong (L′ = DMF, MeCN, CN). The extent of intracore M–M interactions is gauged by M–M distances, spin ground state persistence, and preference for mixed-valence states as determined by electrochemical comproportionation constants. Coordination of DMF to the [(^HL)₂Fe₆] core leads to weaker Fe–Fe interactions, as manifested by the observation of ground states populated only at lower temperatures (<100 K) and by the greater evidence of valence trapping within the mixed-valence states. Comproportionation constants determined electrochemically (K_c = 10⁴–10⁸) indicate that the redox series exhibits electronic delocalization (class II–III), yet no intervalence charge transfer (IVCT) bands are observable in the near-IR spectra. Ligation of the stronger σ donor acetonitrile results in stabilization of spin ground states to higher temperatures (~300 K) and a high degree of valence delocalization (K_c = 10²– 10⁸) with observable IVCT bands. Finally, the anionic cyanide-bound series reveals the highest degree of valence delocalization with the most intense IVCT bands (K_c = 10¹²–10²⁰) and spin ground state population beyond room temperature. Across the series, at a given formal oxidation level, the capping ligand on the hexairon cluster dictates the overall properties of the aggregate, modulating the redox delocalization and the persistence of the intracore coupling of the metal sites.

Graphical abstract

1. INTRODUCTION

Mixed-valence clusters exist in an electronic coupling domain exhibiting redox phenomena intermediate between non-communicative redox centers and bulklike regimes.¹ Coupling of multiple redox reservoirs maximizes the accessible molecular redox breadth while permitting redox load delocalization. Both of these phenomena can be critical for a variety of catalytic functions. Indeed, in nature superspin proteins have been found in a variety of enzymes (e.g., the $S=\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ Fe₈S₈ P cluster in nitrogenase), where they catalyze multielectron transfer reactions.² Beyond simple electron transfer reactivity, new functionality is being discovered wherein novel mixed-valence architectures benefit materials properties, such as orchestrating coupled spin electronic structures for magnetic applications³ and facilitating small-molecule activation catalysis.⁴ Thus, deepening our understanding of how to manipulate mixed-valence architectures within the context of cluster design is of significant importance.

In simple mixed-valence complexes, electron delocalization is dictated by orbital overlap between the two redox sites, typically mediated by a bridging organic ligand.⁵ In the classic Creutz–Taube (CT) ion {[(H₃N)₅Ru]₂(pyz)}⁵⁺ (pyz = pyrazine),⁶ the two Ru centers are at nominally different oxidation states (Ru^II and Ru^III) yet appear to present a fractional oxidation state (Ru^2.5) by most spectroscopic measures and X-ray crystallography (Robin–Day class III delocalized state for mixed valence).⁷ The oxidation state averaging results from a conjugated orbital pathway between the two Ru sites though the π-electron system of the pyrazine bridge.^7k,8 Utilizing different bridging ligands lacking orbital overlap to link the two sites results in valence trapping, where discrete Ru^II and Ru^III sites are distinguishable (class I mixed-valent).⁹ Furthermore, extending the distance between the Ru centers by using large, π-conjugated bridging ligands affords access to intermediate redox delocalization, typical of class II mixed-valent systems.¹⁰

In cluster complexes featuring three or more transition metals, the complexity of potential electronic coupling mechanisms increases. We¹¹ and others¹² have identified that direct M–M orbital interactions (i.e., the direct exchange pathway) can be significant and in some instances can overcome superexchange coupling mechanisms that favor antiferromagnetic coupling. In our own work, we found that targeting cluster assemblies favoring maintenance of the M–M interactions can yield cluster stabilization across broad redox spans, yield large, thermally well-isolated ground states (e.g., S = 6), and facilitate multielectron redox reactivity.^11,13 All of these features arise from the extensive M–M intracore interactions.

In traditional mixed-valent systems (e.g., the CT ion), the electronic properties are largely governed by the charge transfer pathway separating the two redox centers. Manipulation of this pathway (e.g., by employing larger bridging ligands) can dramatically impact the degree to which the redox centers couple electronically.⁹ The hexanuclear iron clusters [(^HL)₂Fe₆(L′)_m]ⁿ⁺ synthesized in our laboratory,^11a where ^HLH₆ = MeC(CH₂NHPh-o-NH₂)₃ and L′ is a terminal ligand, provide a unique opportunity to investigate mixed-valent clusters where the primary charge transfer pathway (the M–M bond) is maintained while secondary influences (i.e., ligand binding to the cluster) can be examined for effects on the overall electronic structure of the aggregate. Towards this goal, we present herein our findings examining the post-redox manipulation of the [Fe₆] clusters, which enables us to probe the extent to which the electronic structure properties of the clusters can be affected by secondary ligand influences. Our interests in this study include the following questions: (1) Can the electron delocalization and M–M bonding within a cluster be modulated by cluster ancillary ligation? For example, can mixed-valent clusters be tuned into different Robin–Day classifications as a function of the ancillary ligand employed, yielding valence-trapped or valence-delocalized cluster cores (Figure 1)? (2) Can the cluster aggregate ground state electronic structure be manipulated by varying the ancillary ligand field strength consistently across an electron-transfer series? Herein we present our findings using the [(^HL)₂Fe₆] core where solvent termination of the cluster produces a dramatic effect on the electronic coupling within the core.

Figure 1.

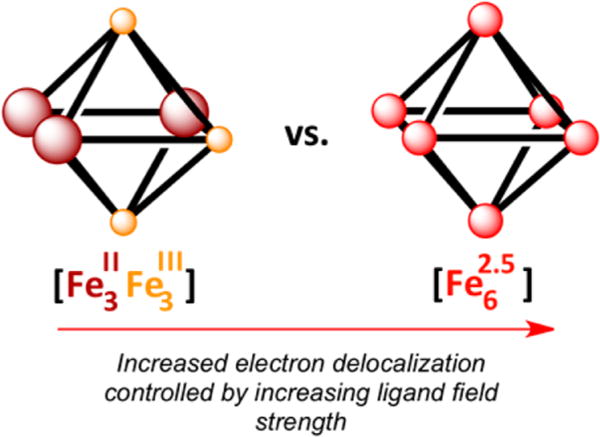
Illustration displaying the removal of three electrons from an all-ferrous octahedral cluster to give a (left) localized or (right) delocalized state.

2. EXPERIMENTAL SECTION

General Considerations

All manipulations involving metal complexes were carried out using standard Schlenk or glovebox techniques under a dinitrogen atmosphere, unless otherwise noted. All glassware was oven-dried for a minimum of 10 h and cooled in an evacuated chamber prior to use in the drybox. Acetonitrile, diethyl ether, and tetrahydrofuran (THF) were dried and deoxygenated on a Glass Contour System (SG Water USA, Nashua, NH) and stored over 4 Å molecular sieves (Strem) prior to use. Acetonitrile-d₃ and dimethylformamide-d₇ (DMF-d₇) were purchased from Cambridge Isotope Laboratories and stored over 4 Å molecular sieves prior to use. DMF (Sure/Seal), propylene carbonate (PC, Sure/Seal), N-methyl-pyrrolidinone (NMP) (Sure/Seal), and dimethylacetamide (DMA, Sure/Seal) were purchased from Sigma-Aldrich and stored over 4 Å sieves prior to use. Nonhalogenated solvents were frequently tested using a solution of sodium benzophenone ketyl in THF for effective water and dioxygen removal. Tetrabutylammonium cyanide, ferrocenium hexafluorophosphate (FcPF₆), and tris(4-bromophenyl)-ammonium hexachloroantimonate ([(4-BrC₆H₄)₃N][SbCl₆]) were purchased from Sigma-Aldrich and used without further purification. Nitrosonium hexafluorophosphate (NOPF₆) and silver tetrafluoroborate were purchased from Strem Chemicals and used without further purification. Fe₂(Mes)₄ (Mes = 2,4,6-Me₃C₆H₂) was prepared by a modified version of a previously reported method (see the Supporting Information).¹⁴ (^HL)₂Fe₆ and its oxidized acetonitrile adducts [(^HL)₂Fe₆(NCMe)_m][PF₆]_n (m = 4, n = 2 (1); m = 6, n = 3 (2); m = 6, n = 4 (3)) were prepared according to the methodology previously reported by our laboratory.^11a All other reagents were purchased from commercial vendors and used without further purification.

[(^HL)₂Fe₆(DMF)₄][PF₆]₂ (n = 2) (4)

Solid [Cp₂Fe][PF₆] (0.240 g, 0.725 mmol) was dissolved in 10 mL of DMF. The oxidant was added to a stirring suspension of (^HL)₂Fe₆ (0.400 g, 0.362 mmol) in 10 mL of DMF. After the suspension was stirred for 12 h or overnight, diethyl ether (~150 mL) was added until no more precipitate formation was observed. The black solid was collected on a medium-porosity fritted glass funnel. The latter was washed with 4 × 5 mL of diethyl ether and 4 × 10 mL of 1:1 THF/Et₂O. The residue was dried under vacuum. The resulting black powder was separated into four portions, and each portion was dissolved in 7 mL of DMF. These four vials were then placed in a bigger container with 60 mL of diethyl ether to grow crystals by vapor diffusion. After ~5 days, 330 mg (54% yield) of black block-shaped crystals suitable for X-ray diffraction were collected. Zero-field ⁵⁷Fe Mössbauer (90 K) δ, |ΔE_Q| (mm/s): component 1, 0.34, 2.54 (γ = 0.24 mm/s) (34%); component 2, 0.52, 2.36 (γ = 0.26 mm/s) (66%). Anal. Calcd for 4 (C₅₈H₇₆F₁₂Fe₆N₁₆O₄P₂): C, 41.31; H, 4.54; N, 13.29%. Found: C, 41.24; H, 4.54; N, 13.22%.

[(^HL)₂Fe₆(DMF)₆][PF₆]₃ (n = 3) (5)

Solid [Cp₂Fe][PF₆] (0.540 g, 1.63 mmol) was dissolved in 15 mL of DMF. The oxidant was added to a stirring suspension of (^HL)₂Fe₆ (0.600 g, 0.543 mmol) in 15 mL of DMF. After the suspension was stirred for 12 h or overnight, diethyl ether (~150 mL) was added until no more precipitate formation was observed. The black solid was collected on a medium-porosity fritted glass funnel. The latter was washed with 4 × 5 mL of diethyl ether and 4 × 10 mL of 1:1 THF/Et₂O. The residue was dried under vacuum. The resulting black powder was separated into four portions, and each portion was dissolved in ~7 mL of DMF. These four vials were then placed in a bigger container with 60 mL of diethyl ether to grow crystals by vapor diffusion. After ~5 days, 550 mg (52% yield) of black block-shaped crystals suitable for X-ray diffraction were collected. Zero-field ⁵⁷Fe Mössbauer (90 K) δ, |ΔE_Q| (mm/s): 0.49, 2.76 (γ = 0.28 mm/s). Anal. Calcd for 5 (C₆₄H₉₀F₁₈Fe₆N₁₈O₆P₃): C, 38.87; H, 4.59; N, 12.75%. Found: C, 38.97; H, 4.63; N, 12.79%.

[(^HL)₂Fe₆(DMF)₆][BF₄]₄ (n = 4) (6)

To a stirring suspension of (^HL)₂Fe₆ (0.053 g, 0.042 mmol) in 2 mL of DMF was added AgBF₄ (0.041 g, 0.209 mmol) as a solid. The resulting mixture was stirred for 3 h and subsequently filtered directly into a vapor diffusion cell containing Et₂O as the diffusing solvent. After ~5 days, 72 mg (89% yield) of black block-shaped crystals suitable for X-ray diffraction were collected. The crystals were a mixture of 5 and 6 as 6 decays in the solid state (see Figure S11). Zero-field ⁵⁷Fe Mössbauer (90 K) δ, |ΔE_Q| (mm/s): 0.44, 2.85 (γ = 0.30 mm/s). Anal. Calcd for 6 (C₆₄H₉₀B₄F₁₆Fe₆N₁₈O₆): C, 40.68; H, 4.80; N, 13.34%. Found: C, 40.85; H, 5.03; N, 13.43%.

[Bu₄N]₃[(^HL)₂Fe₆(CN)₆] (n = 3) (7)

Tetrabutylammonium cyanide (0.191 g, 0.711 mmol) was dissolved in 2 mL of DMF or MeCN. In a second vial, 0.118 mmol of 1 or 4 was dissolved in 5 mL of the same solvent used for the [Bu₄N]CN solution. Before the latter solutions were combined, they were stored at −35 °C for 15 min. The reaction mixture was stirred for 12 h or overnight. Two workup procedures were used successfully: (1) Regardless of the solvent used, the crude solution was placed in a vapor diffusion cell using diethyl ether as the diffusing solvent. After ~5 days, 191 mg (81% yield) of black block-shaped crystals suitable for X-ray diffraction were collected. (2) When MeCN was used, the reaction mixture was dried under vacuum. The resulting powder was washed with 5 × 4 mL of 1:1 THF/Et₂O. This was dried under vacuum to afford 136 mg (99% yield). Crystalline material was obtained by diffusing Et₂O into a concentrated MeCN solution over a week (125 mg, 91% yield). High-quality single-crystal X-ray diffraction data for 7 could not be obtained; instead, the structure of the [Et₄N]⁺ salt was determined. Apart from the [R₄N]⁺ resonances, these two salts share the same ¹H NMR spectrum (Figure S12). FTIR (KBr): 2086 cm⁻¹ (ν_C–N). Zero-field ⁵⁷Fe Mössbauer (90 K) δ, |ΔE_Q| (mm/s): 0.34, 1.38 (γ = 0.30 mm/s). Anal. Calcd for 7 (C₁₀₀H₁₅₆Fe₆N₂₁): C, 60.43; H, 7.91; N, 14.80%. Found: C, 60.37; H, 7.98; N, 14.73%.

[Bu₄N]₂[(^HL)₂Fe₆(CN)₆] (n = 4) (8)

Tetrabutylammonium cyanide (0.167 g, 0.622 mmol) was dissolved in 2 mL of MeCN. In a second vial, 3 (0.200 g, 0.103 mmol) was dissolved in 5 mL of MeCN. These solutions were combined, and the mixture was stirred for 12 h or overnight. Subsequently the solution was vacuum-dried, washed with 5 × 4 mL of THF, and brought back into a concentrated acetonitrile solution, which was placed in a vial for slow Et₂O diffusion. Single crystals suitable for X-ray diffraction were collected this way after ~5 days (0.167 g, 92% yield). FTIR (KBr): 2107 cm⁻¹ (ν_C–N). Zero-field ⁵⁷Fe Mössbauer (90 K) δ, |ΔE_Q| (mm/s): 0.27, 1.55 (γ = 0.32 mm/s). Anal. Calcd for 8 (C₈₄H₁₂₀Fe₆N₂₀): C, 57.81; H, 6.93; N, 16.05%. Found: C, 57.75; H, 6.91; N, 15.97%.

[Bu₄N][(^HL)₂Fe₆(CN)₆] (n = 5) (9)

A solution of NOPF₆ (0.015 g, 0.056 mmol) in 2 mL of acetonitrile was added to a stirring solution of 8 (0.098 g, 0.056 mmol) in 10 mL of MeCN. The resulting mixture was stirred for 2 h, and precipitation occurred. The suspension was poured into 10 mL of Et₂O. The precipitate was filtered with a medium-porosity fritted glass funnel and washed with 2 × 5 mL of THF. The black powder was vacuum-dried to give 65.5 mg (77% yield). FTIR (KBr): 2119 cm⁻¹ (ν_C–N). Zero-field ⁵⁷Fe Mössbauer (90 K) δ, |ΔE_Q| (mm/s): 0.22, 1.61 (γ = 0.26 mm/s). Anal. Calcd for 9 (C₆₈H₈₄Fe₆N₁₉): C, 54.35; H, 5.63; N, 17.71%. Found: C, 54.39; H, 5.54; N, 17.65%.

(^HL)₂Fe₆(CN)₆ (n = 6) (10)

A solution of 8 (0.2174 g, 0.124 mmol) in 10 mL of MeCN was prepared and then added to a stirring solution of [(4-BrC₆H₄)₃N][SbCl₆] (0.2034 g, 0.249 mmol) in 2 mL of MeCN. The reaction mixture was stirred overnight. The fine suspension was filtered through a medium-porosity frit and washed with 5 × 4 mL of MeCN and 5 × 4 mL of THF. The black solid was dried under vacuum (0.139 g, 88% yield). FTIR (KBr): 2130 cm⁻¹ (ν_C–N). Zero-field ⁵⁷Fe Mössbauer (90 K) δ, |ΔE_Q| (mm/s): 0.19, 1.56 (γ = 0.30 mm/s). Anal. Calcd for 10 (C₅₂H₄₈Fe₆N₁₈): C, 49.56; H, 3.84; N, 20.01%. Found: C, 49.51; H, 3.96; N, 19.95%. Oxidation with 2 equiv of NOPF₆ matched the elemental analysis as well. Found: C, 49.44; H, 3.92; N, 19.87%.

X-ray Structure Determinations

Single crystals suitable for X-ray structure analysis were coated with deoxygenated Paratone N oil and mounted in MiTeGen Kapton (polyimide) loops. Data for compounds 4–9 were collected at 100 K on an APEX II CCD or APEX II DUO single-crystal diffractometer. None of the crystals showed significant decay during data collection. The raw data were integrated and corrected for Lorentz and polarization effects using Bruker APEX2 version 2009.1.¹⁵ Absorption corrections were applied using SADABS.¹⁶ Space group assignments were determined by examination of systematic absences, E statistics, and successive refinement of the structures. The program PLATON¹⁷ was employed to confirm the absence of higher symmetry for any of the crystals. The positions of the heavy atoms were determined by direct methods using the program SHELXTL.¹⁸ Successive cycles of least-squares refinement followed by difference Fourier syntheses revealed the positions of the remaining non-hydrogen atoms. Non-hydrogen atoms were refined with anisotropic displacement parameters, and hydrogen atoms were added in idealized positions. Crystallographic data for 4–9 are given in Table S1 in the Supporting Information.

Magnetic Susceptibility Measurements

Magnetic data for 1, 2, 4, 5, 7, and 10 were collected using a Quantum Design MPMS-XL Evercool SQUID magnetometer. A general procedure for sample preparation is as follows: bulk crystals were collected and washed thoroughly with Et₂O. Once only black block-shaped crystals were observed, these were crushed in the presence of Et₂O, and the resulting fine suspension was then dried under high vacuum. The sample powder was then immobilized within a size no. 4 gelatin capsule by adding melted eicosane at 50–60 °C. The gelatin capsule was inserted into a plastic straw. Samples were prepared under a dinitrogen atmosphere. Magnetization data at 100 K from 0 to 7 T were used as a purity test (Figures S26–S31 in the Supporting Information). Variable-temperature direct current (dc) magnetic susceptibility measurements were collected upon heating over the temperature range 1.8–300 K under applied fields of 0.1, 0.5, and 1 T. Variable-temperature variable-field (VTVH) magnetization data were acquired upon heating from 1.8 to 10 K at increasing fields of 1, 2, 3, 4, 5, 6, and 7 T. Data to simulate the Brillouin function were collected at 1.8 K from 0 to 1 T in 50 mT increments and from 1.5 to 7 T in 500 mT increments. The magnetic susceptibility data were corrected for diamagnetism of the sample (estimated using Pascal’s constants) in addition to contributions from the sample holder and eicosane.

Electrochemical Measurements

Cyclic voltammetry and differential pulse voltammetry measurements were performed with a CHI660d potentiostat using a three-electrode cell with a glassy carbon working electrode, a platinum wire as the counter electrode, and a Ag/AgNO₃ reference electrode. All of the potentials are referenced to the Fc/Fc⁺ couple. Saturated AgNO₃ solutions were prepared before each experiment. All of the measurements were done under a dinitrogen atmosphere.

Other Physical Measurements

Elemental analyses were performed by Complete Analysis Laboratories, Inc. (Parsippany, NJ). Zero-field ⁵⁷Fe Mössbauer spectra were collected at 90 K for solid samples (~20 mg) restrained with Paratone N oil. The data were measured with a constant-acceleration spectrometer (SEE Co., Minneapolis, MN). Isomer shifts are given relative to α-Fe metal at 298 K. The data were analyzed using an in-house package written by E. R. King in Igor Pro (Wavemetrics). γ refers to the full-width-at-half-maximum. ¹H NMR spectra were collected on a Varian Mercury 500 or 400 MHz NMR spectrometer with chemical shifts referenced to residual DMF or CH₃CN. Perpendicular-mode continuous-wave (CW) X-band electron paragmagnetic resonance (EPR) spectra were collected at several temperatures for solution and powder samples on a Bruker ElexSys E500 EPR spectrometer. EPR data were simulated by EasySpin¹⁹ in MATLAB. Infrared spectra were acquired on a Varian 1000 FT-IR spectrometer by either (1) pressing the sample into a KBr pellet (~5 mg of sample and 95 mg of KBr) or (2) dissolving ~5 mg of sample and compressing the solution between KBr discs. UV–vis–NIR spectra were collected in 1 mm path length cuvettes on a PerkinElmer Lambda 750 spectrophotometer. All of the solutions were prepared in the glovebox, and the cuvettes were sealed with Teflon tape and a Teflon cap. Absorbance values were kept under 1 for all concentrations measured.

3. RESULTS

3.1. Synthesis and Characterization

The electron-transfer series analyzed in this report are best represented as shown in Scheme 1. The all-ferrous cluster (^HL)₂Fe₆ was prepared in gram quantities as previously described.^11a The solvent adducts were prepared by oxidation of (^HL)₂Fe₆ with n equiv of the oxidant (FcPF₆ or AgBF₄) in the solvent of choice. The general procedure consisted of suspending (^HL)₂Fe₆ in MeCN or DMF, into which the oxidant was added as a solution. The combined solution was left to stir overnight, after which the volatiles were removed in vacuo. Alternatively, a solid could be precipitated from the reaction solution by the addition of diethyl ether to the solution mixture. Washing the collected solids with Et₂O and THF afforded a black material, typical of the oxidized clusters. X-ray-quality crystals of the solvated clusters were grown by diffusing diethyl ether into a concentrated solution of [(^HL)₂Fe₆(L′)_m]ⁿ⁺ in the appropriate solvent (L′ = MeCN, DMF; Scheme 1). Chemical oxidation of (^HL)₂Fe₆ with n equiv of FcPF₆ afforded the acetonitrile-bound series (n = 2) [(^HL)₂Fe₆(NCMe)₄][PF₆]₂ (1), (n = 3) [(^HL)₂ Fe₆ (NCMe)₆][PF₆]₃ (2), and (n = 4) [(^HL)₂Fe₆(NCMe)₆][PF₆]₄ (3).^11a Analogously, chemical oxidation of (^HL)₂Fe₆ with n equiv of FcPF₆ afforded (n = 2) [(^HL)₂Fe₆(DMF)₄][PF₆]₂ (4) and (n = 3) [(^HL)₂Fe₆(DMF)₆][PF₆]₃ (5), whereas 5 equiv of AgBF₄ was used to prepare (n = 4) [(^HL)₂Fe₆(DMF)₆][BF₄]₄ (6).

Scheme 1.

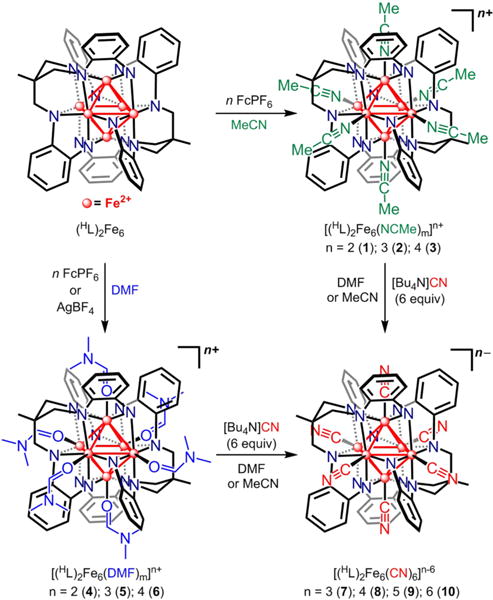
The cyanide-terminated clusters were prepared by adding 6 equiv of [Bu₄N]CN to the solvated cluster at the appropriate oxidation level, [(^HL)₂Fe₆(L′)_m]ⁿ⁺, at −35 °C or room temperature in either DMF or MeCN.²⁰ The reaction solutions were allowed to stir overnight, after which the volatiles were removed in vacuo or precipitation was induced by the addition of diethyl ether. The collected solids were subsequently dried and washed with THF. Crystallization of the collected solids could be achieved by slow diffusion of diethyl ether into DMF or MeCN solutions to afford (n = 3) [Bu₄N]₃[(^HL)₂Fe₆(CN)₆] (7), and (n = 4) [Bu₄N]₂[(^HL)₂Fe₆(CN)₆] (8). X-ray-quality crystals were obtained for clusters 7 and 8 in this manner, whereas X-ray-quality crystals of (n = 5) [Bu₄N][(^HL)₂Fe₆(CN)₆] (9) were obtained by a layering technique in air. The neutral cluster (n = 6) (^HL)₂Fe₆(CN)₆ (10) lacked appreciable solubility, preventing crystallization. Crystalline yields for the cyanide adducts were in excess of 90%.

The nomenclature [(^HL)₂Fe₆(L′)_m]ⁿ⁺ (L′ = MeCN, DMF) for the solvent adducts and [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶ for the cyanide species will be used throughout the rest of this report to maintain consistency when comparing clusters at the same oxidation level. In all cases, n represents the total number of electrons removed from the all-ferrous core. In addition, when necessary the total number of valence electrons of the metallic cluster core will be used.

3.2. Electron-Transfer Series Structures

The local Fe coordination environment in the all-ferrous species can be described best as a square plane comprising four anilido ligands originating from the two ^HL⁶⁻ ligand units. Upon oxidation, solvation or anation at the Fe sites changes the local geometry to square-pyramidal. The overall cluster geometry comprises an anilide edge-bridged octahedral Fe₆ core. The idealized [Fe₆N₁₂] cluster core has O_h symmetry. The metal-to-metal distance (d_Fe–Fe = 2.597(2)–2.765(1) Å) in all instances is within the range where Fe–Fe bonding is invoked.^12b–d,21

Crystals suitable for single-crystal X-ray structure determination were obtained as described above. Representative solid-state molecular structures of 4, 5, and 9 are depicted in Figure 2a–c, respectively. Crystallographic data for compounds 4–9 are presented in Table S1. Comparison of the structures of the MeCN (1–3) and DMF (4–6) solvent adduct clusters reveals the same solvent binding pattern with respect to oxidation level (Figures S2–S4). In this sense, 1 and 4 present two trans-disposed four-coordinate iron sites residing in a local square-planar coordination environment, whereas the other four iron sites are square-pyramidal upon binding L′ in the apical site (Fe–N_MeCN = 2.007(4) Å and Fe–O_DMF = 2.042(6) Å). Similar to the acetonitrile series, where solvent binding is strengthened upon oxidation (Fe–N_MeCN = 2.065(7) Å in 2 and 1.981(3) Å in 3), the Fe–O_DMF distance contracts upon oxidation of 5 (2.09(2) Å) to 6 (2.022(4) Å) (Figure S1).

Figure 2.

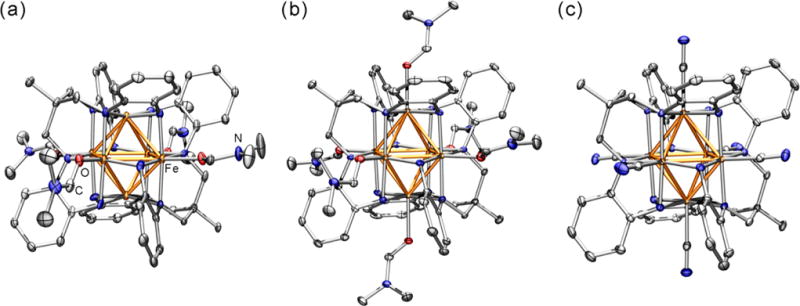
Solid-state molecular crystal structures obtained at 100 K for (a, b) the cations [(^HL)₂Fe₆(DMF)₄]²⁺ in 4 and [(^HL)₂Fe₆(DMF)₆]³⁺ in 5, respectively, and (c) the anion [(^HL)₂Fe₆(CN)₆]⁻ in 9. The Fe, C, N, and O atoms are colored orange, gray, blue, and red, respectively. Thermal ellipsoids are set at 50% probability. Hydrogen atoms have been omitted for clarity.

In addition to the trends observed in the apical ligand coordination versus chemical oxidation of the [Fe₆] core, each consecutive oxidation results in a change in the average Fe–Fe distance (Table 1). As described previously, the average Fe–Fe distance for the members of the acetonitrile electron-transfer series expands in going from (^HL)₂Fe₆ (2.5972(17) Å) to 2 (2.7040(13) Å); 1 and 3 have [Fe₆] cores of approximately the same size, with average Fe–Fe distances of 2.6877(11) and 2.6907(8) Å, respectively. Similarly, in the DMF adducts the average Fe–Fe distance peaks at n = 3 (2.757(3) Å in 5), but in this case 4 (2.690(18) Å) and 6 (2.740(6) Å) differ considerably in size. Among the cyanide adducts, the volume of the [Fe₆] core only decreases with increasing [Fe₆] oxidation level, as the average metal–metal distance goes from 2.752(5) Å in 7 to 2.698(6) Å in 8 and ultimately 2.676(12) Å in 9 (Table 1). Overall, the size changes of the hexanuclear Fe core based on the average metal-to-metal distance suggest that the reorganization energy incurred across different oxidation levels must be minimal if not negligible.

Table 1.

Selected Interatomic Distances (Å) for Compounds 1–9

	4	5	6	7	8	9
Fel – Fe2	2.771(1) (2.780(1)a)	2.7477(8)	2.743(1)	2.730(1)	2.687(1)	2.7105(8)
Fel – Fe3	2.661(1) (2.666(1)a)	2.7654(9)	2.759(1)	2.755(1)	2.715(2)	2.7006(7)
Fel – Fe2′	2.775(1) (2.775(1)a)	2.7646(9)	2.734(1)	2.756(1)	2.712(1)	2.7004(7)
Fel – Fe3′	2.624(1) (2.624(1)a)	2.7634(6)	2.722(1)	2.746(1)	2.678(1)	2.6578(8)
Fe2 – Fe3	2.657(1) (2.655(1)a)	2.7558(8)	2.758(1)	2.769(1)	2.707(1)	2.6453(6)
Fe2 – Fe3′	2.653(1) (2.646(1)a)	2.7489(8)	2.728(1)	2.756(1)	2.691(1)	2.6431(6)
Fe – Fe (avg)	2.690(18)	2.757(3)	2.740(6)	2.752(5)	2.698(6)	2.676(12)
Fe1 – Fe1′	3.913(1)	3.9148(9)	3.869(1)	3.862(2)	3.814(2)	3.7975(8)
Fe2 – Fe2′	3.937(1)	3.8807(9)	3.877(1)	3.897(1)	3.822(1)	3.7803(7)
Fe3 – Fe3′	3.556(1)	3.9040(6)	3.882(1)	3.918(1)	3.812(2)	3.7772(7)
Fe – Fetrans (avg)	3.80(12)	3.89(1)	3.876(3)	3.892(16)	3.816(3)	3.785(13)
Fe1-L1	2.028(4) (2.061 (4)b)	2.133(3)	2.022(5)	1.942(7)	1.935(7)	1.945(4)
Fe2 – L2	2.038(4) (2.041 (4)b)	2.100(3)	2.014(5)	1.954(6)	1.943(6)	1.947(3)
Fe3 – L3		2.058(2)	2.031(5)	1.958(6)	1.941(6)	1.936(3)
Fe – L’ (avg)	2.042(6)	2.09(2)	2.022(4)	1.951(4)	1.939(2)	1.942(3)
Fe – N (avg)	2.002(7)	2.003(6)	2.001(5)	2.006(8)	1.989(8)	1.992(9)
Fe – NH (avg)	1.958(9)	1.964(9)	1.954(8)	1.963(10)	1.940(10)	1.944(11)
Fe – N – Fe (avg)	84(1)	86.80(3)	86.0(1)	86.2(8)	84.9(1)	83.3(2)
Fe – NH – Fe (avg)	87(1)	89.30(7)	89.4(4)	89.3(2)	88.6(3)	88.1(1)
	1	2	3
Fe – Fe (avg)	2.6877(11)	2.7040(13)	2.6907(8)
Fe – Fetrans (avg)	3.79(11)	3.82(1)	3.805(7)
Fe – N (avg)	2.003(11)	1.990(9)	1.978(12)
Fe – NH (avg)	1.960(10)	1.948(11)	1.942(12)
Fe – N – Fe (avg)	84(1)	85.1(2)	85.03(5)
Fe – NH – Fe (avg)	87(1)	88.4(1)	88.3(1)

^aThe absence of a center of inversion in this cluster makes all of the Fe–Fe distances unique. Thus, this distance corresponds to the symmetry-related Fe–Fe contact assuming higher symmetry.

^bThis corresponds to the symmetry-related Fe–O_DMF distance assuming higher symmetry.

Overall, the cluster morphology and local coordination environments show remarkable consistency across the core oxidation levels (n = 0→6) and ancillary ligands examined (Table 1). The intracore Fe–Fe bond distances are most affected by the core oxidation level changes (vide supra), whereas the overall cluster bond metrics show insignificant changes when traversing the redox series. Comparison of the bond angles created by the bridging anilido ligands to the iron sites reveals remarkably little dependence on the core oxidation level, where the Fe–N–Fe angle ranges from 84(1) to 86.80(3)° and the Fe–NH–Fe angle ranges from 87(1) to 89.4(4)°.

3.3. Mössbauer Spectroscopy

The core redox levels across complexes 1–9 were probed by zero-field 57Fe Mössbauer spectroscopy. Each member of the redox series examined displayed a single symmetric quadrupole doublet for isostructural sites, as shown in Figure 3, the data for which are compiled with other relevant spectroscopic data in Table 3.

Figure 3.

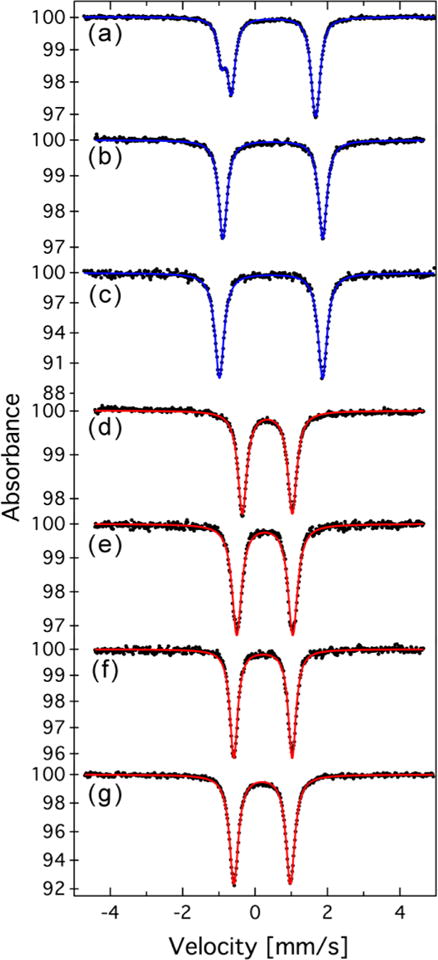
Zero-field ⁵⁷Fe Mössbauer spectra for compounds (a) 4, (b) 5, (c) 6, (d) 7, (e) 8, (f) 9, and (g) 10. Blue (DMF adducts) and red (CN adducts) solid lines represent fits to the data (black dots). The fit parameters are described in the text.

Table 3.

Zero-Field ⁵⁷Fe Mössbauer Spectroscopy (δ, |δE_q|) and NIR Spectroscopy (ν_max, ε_max and δν_1/2) Parameters Along with Electronic Couplings (H_ab1 and H_ab2) and Γ Values Calculated As Described in the Text

ligand (species)	n	δ (mm/s)	|δEq| (mm/s)	solvent	νmax (cm−1)	εmax (M−1 Cm−1)	δν1/2 (cm−1)	Hab1 (cm−1)	Hab2 (cm−1)c	Γ
cyanide (7–10)	3	0.34	1.38	MeCN	7654	1861	1789	1193	–	0.573
				DMF	7623	1883	1728	1177	–	0.587
				DMA	7601	1996	1824	1243	–	0.563
				PC	7642	1931	1820	1225	–	0.566
	4	0.27	1.55	NMP	8140	3357	1266	1410	6318 (6939)	0.707
				MeCN	8198	3238	1278	1396	6123 (6623)	0.705
				DMF	8157	3257	1278	1397	6309 (6919)	0.705
				DMA	8143	3301	1270	1400	6306 (6919)	0.706
				PC	8173	3296	1273	1404	6125 (6644)	0.707
	5	0.22	1.61	–	–	–	–	–	–	–
	6	0.19	1.56	–	–	–	–	–	–	–
MeCN (1–3)	2	0.35 (33%)	2.68	MeCN	–	–	–	–	–	–
		0.46 (67%)	2.18
	3	0.42	2.52		8497	1911	3672	1859	3024 (3201)	0.169
	4	0.40	2.5		8685	2576	3400	2111	–	0.239
DMF (4–6)	2	0.34 (34%)	2.54	DMF	–	–	–	–	–	–
		0.52 (66%)	2.36
	3	0.49	2.76		–	–	–	–	–	–
	4	0.44	2.85		–	–	–	–	–	–
Creutz-Taube iond {[(H3N)5Ru]2(pyz)}5+				MeCN	6173	–	–	–	3292 (3296)
				PC	6250	–	–	–	3307 (3311)
				DMF	6309	–	–	–	3229 (3231)
				DMSO	6309	–	–	–	3272 (3274)
				D2O	6369	5000	1500	658a (2249b)	3165 (3165)

^aCalculated by considering the Ru–Ru distance obtained from the crystal structure.⁷

^bCalculated by considering the Ru–N_pyz distance obtained from the crystal structure.^7k

^cValues without or with parentheses were calculated assuming a partially delocalized system (eq S.3) or a fully delocalized system (eq S.4), respectively.

^dData for the Creutz–Taube ion were taken from refs 7c and 32.

The spectra for 1 and 4 display two overlapping quadrupole doublets (Figure 3a) because of the lowering of the cluster symmetry from ideal octahedral symmetry (O_h) to D_4h resulting from asymmetric solvent coordination to only four iron sites. In the MeCN (1–3), DMF (4–6), and CN (7–10) series, a linear monotonic decrease of the isomer shift as the oxidation level increases is observed. The two quadrupole doublets observed in the n = 2 clusters 1 and 4 have two different isomer shifts. For 1, the values of δ and |ΔE_Q| are 0.35 and 2.68 mm/s, respectively, for component 1 (33%) and 0.46 and 2.18 mm/s, respectively, for component 2 (67%), while for 4 the values are 0.34 and 2.54 mm/s, respectively, for component 1 (34%) and 0.52 and 2.36 mm/s, respectively, for component 2 (66%). The smaller δ was assigned to the four-coordinate iron site and the larger δ to the solvated site. The change in isomer shift among these clusters for the square-planar site is small (|Δδ| = 0.02 mm/s); in contrast, at the solvated sites this difference increases by 5-fold (0.10 mm/s). In both comparisons, δ is more positive for the DMF adduct than for the MeCN adduct.

The spectra for compounds [(^HL)₂Fe₆(DMF)₆][PF₆]₃ (5) and [(^HL)₂Fe₆L(DMF)₆][BF₄]₄ (6) display a single quadrupole doublet (δ, |ΔE_Q| (mm/s) = 0.49, 2.76 (Figure 3b) and 0.44, 2.85 (Figure 3c), respectively). It is interesting to note that for the acetonitrile adduct analogues 2 and 3, the quadrupole splittings are nearly identical (|ΔE_Q| = 2.52 and 2.50 mm/s, respectively). As the coordination environment around each of the six Fe sites remains unchanged and the [Fe₆] cluster structure metrics change subtly upon oxidation of 2 to 3 and 5 to 6, it is not surprising that the electric field gradient around each Fe site, reflected in |ΔE_Q|, remains relatively constant over these consecutive oxidation levels. A line of best fit to δ for the solvated sites across the oxidation levels examined presents a modestly larger slope for the DMF series than for the MeCN series (−0.042(4) vs −0.034(3) mm/s per electron, respectively) as the oxidation level increases (Figure S25).

The spectra for the octahedrally symmetric cyanide clusters display a single symmetric quadrupole doublet (δ, |ΔE_Q| (mm/s) = 0.34, 1.38 for [Bu₄N]₃[(^HL)₂Fe₆(CN)₆] (7); 0.27, 1.55 for [Bu₄N]₂[(^HL)₂Fe₆(CN)₆] (8); 0.22, 1.61 for [Bu₄N][(^HL)₂Fe₆(CN)₆] (9); and 0.19, 1.59 for (^HL)₂Fe₆(CN)₆ (10); Figure 3d–g). A monotonic decrease in the isomer shift is again observed (−0.049(6) mm/s per electron) as the oxidation level increases. Qualitatively, the anionic nature and ligand field strength of cyanide are responsible for the marked difference in δ for the cyanide clusters compared with the solvent adducts with the same total number of valence electrons.

3.4. EPR Spectroscopy

Clusters in which the total number of valence electrons is odd were investigated by perpendicular-mode CW X-band EPR spectroscopy between 3.6 and 100 K. The three n = 3 complexes [(^HL)₂Fe₆(NCMe)₆][PF₆]₃ (2), [(^HL)₂Fe₆(DMF)₆][PF₆]₃ (5), and [Bu₄N]₃[(^HL)₂Fe₆(CN)₆] (7) were investigated in addition to the one available n = 5 cluster, [Bu₄N][(^HL)₂Fe₆(CN)₆] (9). Complex 9 has an isotropic spectrum at 77 K (Figure 4a). Its spectrum was simulated as that of an $S=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ species. The value of g_iso extracted from the simulation is 2.04. The solvated cationic clusters 2 and 5 display similar spectra. The spectrum of the MeCN adduct 2 at 3.6 K (Figure 4b) exhibits an axial environment. It was simulated as the spectrum of an $S=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ species with the axial parameters g_|| = 1.95 and g_⊥ = 2.02, thus giving an average g value of 1.99(2). The spectrum of the related DMF adduct 5 at 3.6 K (Figure 4c) has broader line widths but the same overall axial features. It was simulated as the spectrum of an $S=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ species with g_|| = 1.87 and g_⊥ = 2.01, giving an average g value of 1.96(4).

Figure 4.

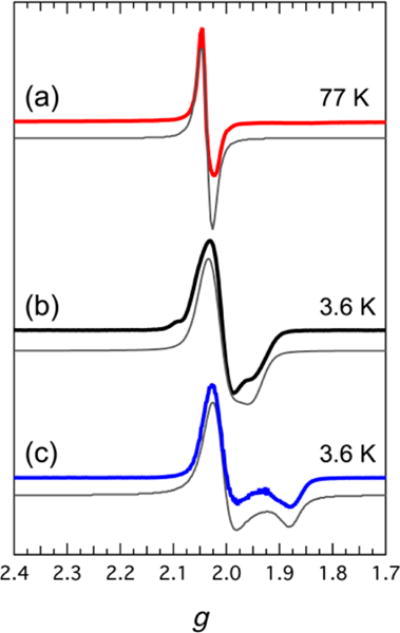
Perpendicular-mode CW X-band EPR spectra of compounds (a) 9, (b) 2, and (c) 5. The simulated spectra are depicted as solid gray lines, and the resulting parameters are described in the text.

In contrast to the simple spectra obtained for 2, 5, and 9, the spectrum of [Bu₄N]₃[(^HL)₂Fe₆(CN)₆] (7) is more complex and displays temperature-dependent behavior (Figure 5). At 3.6 K several absorptions were observed. From low to high field, absorptions were observed at g ≈ 11 and 4.5, and several more appeared in the g range from 2.1 to 1.4. The spectral behavior of 7 was then studied over the temperature range 3.6–100 K. As the temperature was raised to 30 K, the broad absorption at g ≈ 1.4 and the weak one at g = 4.3 disappeared, while the rest persisted to 100 K. The absorption at g ≈ 11 suggests population of a high-spin state $(S>\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)$.^2a,22 The theoretically predicted effective g values for each Kramers doublet of high-multiplicity noninteger spin states under the assumption that the system’s real g values are 2.00 have been described and plotted against the rhombicity parameter |E/D|.²³ On the basis of the g value of ~11, two potential spin states to consider are $S=\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and $S=\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. In the $S=\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ case, this g value could arise from population of the $m_S=\pm \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ doublet at near-axial |E/D| (<0.02) or from the $m_S=\pm \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ doublet at intermediate rhombicities (|E/D| ≈ 0.19). It should be noted that in all cases the highest g value has been predicted to have an absorption-type shape in the derivative spectrum,²⁴ in disagreement with the observed experimental data. Considering the case of population of the $\pm \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ doublet, apart from the high g value two others should be observed at ~8 and slightly less than 2. If the $\pm \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ doublet is populated, then the observation of two other effective g values at ~5 and ~3 would also be predicted. None of these were observed experimentally.

Figure 5.

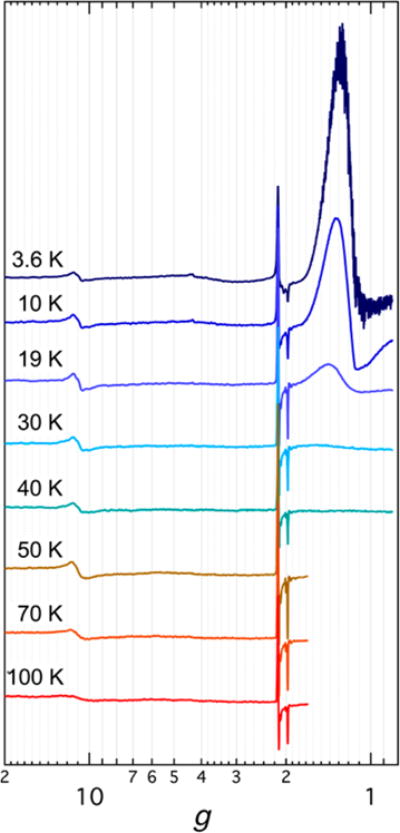
Variable-temperature perpendicular-mode CW X-band EPR spectra of [Bu₄N]₃[(^HL)₂Fe₆(CN)₆] (7). The spectra were recorded in MeCN at 0.6325 mW with a modulation amplitude of 0.5 mT.

The other potential scenario is having a spin ground state of $S=\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. Following the analysis as in the $S=\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ case, the data only fit with population of the $\pm \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ doublet at a rhombicity of ~0.06. The other two expected effective g values would be at ~4.5 and ~1.5. It has been reported that higher doublets for $S\ge \raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ are not seen even at low temperatures because of their very anisotropic g tensors²² and low transition probabilities.^2a The broad low-field (g ≈ 4.5) and high-field (g ≈ 1.5) absorptions seem to follow the same temperature dependence, where they become unobservable at and above 30 K. In contrast, the low-field feature at g ≈ 11 does not follow this temperature behavior and persists until 100 K. Additionally, the rhombic g tensor at g = 2 appears to be independent of the already-discussed transitions. It is known that iron–sulfur clusters of the type [Fe₄S₄(SR)₄]³⁻ can display EPR spectra representative of a single spin entity, physical mixtures, or spin admixtures.²⁵ The EPR spectra for 7 appear to be complex, and we will limit ourselves to use this in correlation with its magnetic susceptibility data.

3.5. Infrared Spectroscopy

The cyanide stretching frequency (ν_C–N) for compounds 7–10 increases linearly with increasing [Fe₆] oxidation level (Figure 6a,b). Trends of the ν_C–N stretching frequency versus coordination number, oxidation state, and hapticity for transition-metal complexes are well-documented.²⁶ The change in the cyanide C–N stretching frequency upon ligation to a metal can be explained by the removal of electron density from the highest occupied molecular orbital of cyanide, which is weakly antibonding with respect to the C–N bond, thus increasing ν_C–N. As the metal becomes more electropositive in higher oxidation states, the M–C σ bond is enhanced, further decreasing the antibonding character in the cyanide linkage. Unsurprisingly, the cyanide stretching frequencies for 7–10 follow a similar trend, where ν_C–N increases with increasing cluster oxidation level, accompanied by shortening of the C–N bond as observed from X-ray crystallography (Figure 6b). For comparison, while ferricyanide ([Fe ^III(CN)₆]³⁻) has ν_C–N = 2135 cm⁻¹, which is very close to that for the all-ferric species 10, ferrocyanide ([Fe^II(CN)₆]²⁻) has ν_C–N = 2098 cm⁻¹, which correlates to a [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶ cluster oxidation level of n = 3 or 4. Interestingly, the stretching frequency of the 33-valence-electron cluster 7 has ν_C–N = 2086 cm⁻¹, which is close to that of free cyanide (2080 cm⁻¹).

Figure 6.

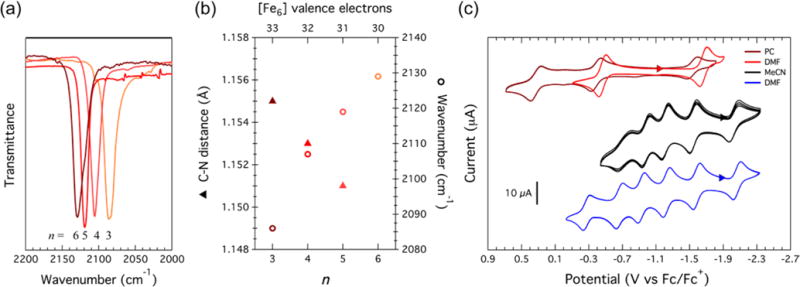
(a) FTIR spectra of the cyanide species and (b) crystallographic CN distance and cyanide stretching frequency versus the cluster oxidation level for n = 3 (7), 4 (8), 5 (9), and 6 (10). (c) Cyclic voltammograms of [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶ taken in DMF (red) and PC (maroon), [(^HL)₂Fe₆(MeCN)₆]ⁿ⁺ in MeCN (black), and [(^HL)₂Fe₆(DMF)₆]ⁿ⁺ in DMF (blue). All were taken in 0.1 M [Bu₄N][PF₆] at room temperature.

3.6. Electrochemistry

The rich redox chemistry displayed by these hexanuclear clusters was evidenced by cyclic voltammetry (Figure 6c). While the solvent adducts present multiple one-electron redox events (five couples observed for MeCN;^11a six couples observed for DMF) in a potential window of ~2 V, the cyanide adducts display only three redox events over a similar potential range. The oxidation levels across the solvent and cyanide adducts will be described according to the notation [Fe₆]ⁿ⁺ and [Fe₆]ⁿ⁻⁶, referring to [(^HL)₂Fe₆(L′)_m]^{n +} (L′ = MeCN, DMF) and [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶, respectively (to avoid ambiguity, the all-ferric cyanide adduct is denoted as ${[{\text{Fe}}_6]}_{\text{CN}}^0$). In the MeCN series, the most reduced species, having 37 valence electrons ([Fe₆]¹⁻), was electrochemically observed and chemically prepared.^11a Electrochemical oxidation of the monoanionic cluster to the all-ferrous cluster occurs at E_1/2 = −2.04 V vs Fc^0/+, followed by successive one-electron oxidations at −1.55, −1.22, −0.99, and −0.72 V vs Fc^0/+ (Table 2). For the DMF adducts, the same oxidation levels were observed as in the MeCN electron-transfer series with the addition of one more oxidation level observed at the anodic end. Traversing consecutive one-electron oxidation steps at E_1/2 = −2.06, −1.58, −1.23, −0.93, −0.67 and −0.27 V vs Fc^0/+ leads to the anodic end point, [Fe₆]⁵⁺.

Table 2.

Half-Wave Potentials (E_1/2), Peak-to-Peak Potentials (ΔE_p), and Comproportionation Constants (K_c) for the DMF, MeCN, and Cyanide Adducts Extracted from Their Cyclic Voltammograms and Diffusion Coefficients (D₀) Obtained by Applying the Randles–Sevcik Equation

redox couple nred/nox	E1/2 (V vs Fc0/+)			ΔEp (mV)			D0 (10−5 cm2/s)		n	Kc
	MeCN	DMF	CNa	MeCN	DMF	CNa	DMFb	CNb		MeCN	DMF	CNa
5/6	–	–	(0.33)	–	–	(127)	–	–	5	–	–	(1.7 × 1012)
4/5	–	−0.27	−0.45 (−0.39)	–	82	83 (113)	2.3 (2.4)	2.8 (2.6)	4	–	4.8 × 106	2.5 × 1020 (0.3 × 1019)
3/4	−0.72	−0.67	−1.66 (−1.53)	134	78	87 (125)	2.8 (2.2)	2.6 (2.8)	3	3.2 × 104	3.0 × 104	–
2/3	−0.99	−0.93	–	66	79	–	2.6 (2.6)	–	2	7.0 × 102	1.3 × 105	–
1/2	−1.22	−1.23	–	61	79	–	2.6 (2.8)	–	1	4.5 × 105	1.3 × 106	–
0/1	−1.55	−1.58	–	60	81	–	2.7 (2.9)	–	0	1.8 × 108	1.5 × 108	–
−1/0	−2.04	−2.06	–	92	88	–	2.6 (2.6)	–	−1	–	3.0 × 1015	–

^aValues without and with parentheses are for the cyclic voltammograms recorded in DMF and PC, respectively.

^bValues without and with parentheses are for the cathodic and anodic scans, respectively.

In contrast to the solvated series, the cyanide adduct electron-transfer series presents a smaller number of redox events spanning from the [Fe₆]³⁻ oxidation level in 7 to the all-ferric level in 10. When the cyclic voltammogram of 7 was recorded in DMF, only two redox waves were observed at −1.66 and −0.45 V vs Fc^0/+, corresponding to the half-wave potentials of the [Fe₆]³⁻/[Fe₆]²⁻ and [Fe₆]²⁻/[Fe₆]¹⁻ couples, respectively. When the higher-dielectric medium propylene carbonate was employed (Figure 6c, maroon trace), then a third redox event became resolved at 0.33 V vs Fc^0/+. This is assigned to the oxidation to give the all-ferric species, ${[{\text{Fe}}_6]}^{1-}/{[{\text{Fe}}_6]}_{\text{CN}}^0$.

The difference between the E_1/2 values (ΔE_1/2) for the couples ${[{\text{Fe}}_6]}^{1-}/{[{\text{Fe}}_6]}_{\text{CN}}^0$ and [Fe₆]²⁻/[Fe₆]¹⁻ in the cyanide series in propylene carbonate is 0.72 V; similarly, the ΔE_1/2 values for [Fe₆]²⁻/[Fe₆]¹⁻ and [Fe₆]³⁻/[Fe₆]²⁻ are 1.14 and 1.21 V in PC and DMF, respectively (Table 2). These large potential differences suggest a large thermodynamic driving force to the intermediate or mixed-valence state. To rule out any major influence of ion-pairing effects²⁷ on the observed ΔE_1/2 values, cyclic voltammetry data were collected on these clusters in solvents of varying dielectric constant (κ). Thus, NMP (κ = 32.5), acetonitrile (κ = 36.6), DMA (κ = 38.8), and PC (κ = 66.1) were used as solvents. Although variations in E_1/2 were observed, ΔE_1/2 remained almost constant (Table S2).

The cyclic voltammograms in Figure 6c have narrow peak-to-peak potentials (ΔE_p). For the DMF series these range from 78 to 88 mV, while those for the MeCN adducts range from 61 to 92 mV, with one exception at 134 mV for the most anodic couple; ΔE_p ranges from 83 to 87 mV in DMF and 113 to 127 mV in PC for the cyanide electron-transfer series (Table 2). Although the difference in ΔE_p is narrow in most of the couples, ΔE_p is insufficient for assessing the reversibility of the redox events observed. Nonetheless, the electrochemical data collected at the lowest scan rate used (10 mV/s) indicate almost ideal behavior for ΔE_p, approaching the theoretical Nernstian value of 59 mV for a one-electron wave.²⁸

To investigate the redox reversibility of the cyanide and DMF electron-transfer series, the scan rate was varied from 100 to 400 mV/s and from 10 to 500 mV/s, respectively. The raw data are presented in Figure 7a,b, only adjusted to reference to the Fc^0/+ couple. For a reversible one-electron transfer, a straight line is expected when the peak current (i) or the normalized current density (j_p) is plotted versus the square root of the scan rate.²⁸ This linear behavior can be fit by using the Randles–Sevcik equation:

$$j_{\mathrm{p}}=269000{n_{\mathrm{e}}}^{3/2}{D_0}^{1/2}{C}_0{\nu }^{1/2}$$

where j_p is the current density in A/cm², n_e is the number of electron equivalents transferred in the redox process, D₀ is the diffusion coefficient in cm²/s, C₀ is the bulk concentration of the species in solution in mol/cm³, and ν is the voltage scan rate in V/s. Thus, by plotting the raw cathodic and anodic j_p values versus ν^1/2, one can determine whether the redox couple is reversible. The peak current density follows a linear relationship as the square root of the scan rate increases. This indicates a reversible electron transfer reaction that is limited by mass transfer diffusion to the electrode. The linear fits to the data are displayed in Figure 7c,d for the cyanide and DMF electron-transfer series, respectively. From the linear fit the diffusion coefficients D₀ (provided in Table 2) were extracted by setting n_e = 1. In general, D₀ is on the order of (2.3–2.9) × 10⁻⁵ cm²/s, independent of the oxidation level or ligand (L′) bound to the cluster. The diffusion coefficients are in line with values for small molecules in solution.²⁹ While larger molecules do tend to give smaller diffusion coefficients, the large diffusion coefficients observed could result from the semispherical nature of the clusters.

Figure 7.

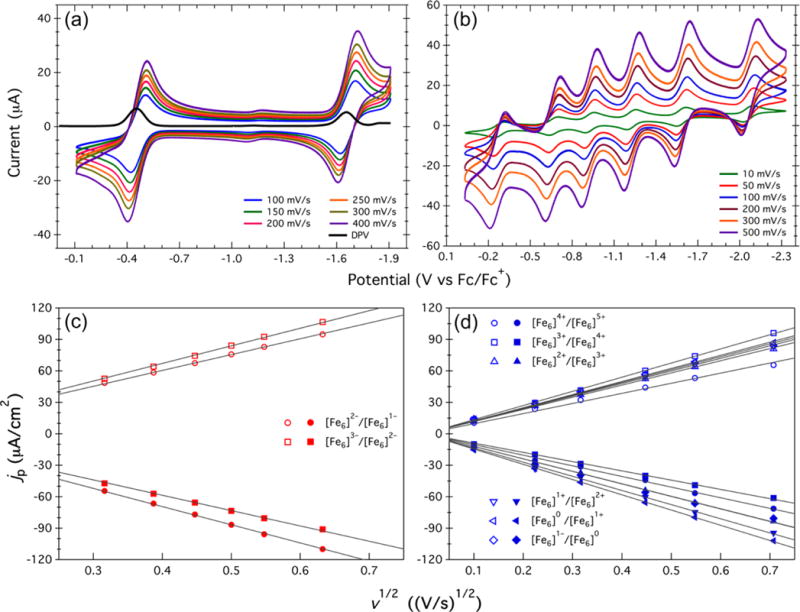
Electrochemical data to test the reversibility of the observed redox couples for the cyanide and DMF electron-transfer series. (a) Cyclic and differential pulse voltammetry (DPV) data for [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶ taken at scan rates ranging from 100 to 400 mV/s in DMF. (b) Cyclic voltammetry of [(^HL)₂Fe₆(DMF)₆]ⁿ⁺ taken at scan rates ranging from 10 to 500 mV/s in DMF. (c, d) Plots of current density (j_p) vs the square root of the scan rate (ν^1/2) extracted from the data in (a) and (b), respectively. All of the data were collected in solutions containing 0.1 M [Bu₄N][PF₆] as the supporting electrolyte.

Comproportionation equilibrium constants (K_c) were calculated from the electrochemical data when possible, and the values are provided in Table 2. Previously, K_c has been used as a parameter to determine the extent of metal–metal interaction in mixed-valence species.⁹ However, the solvent and electrolyte employed may influence their magnitude significantly.³⁰ K_c can be measured spectroscopically³¹ or electrochemically from

$$\mathrm{\Delta }{G}_{\mathrm{c}}^{°}=-\mathit{RT}\ln K_{\mathrm{c}}=-n_{\mathrm{e}}F(\mathrm{\Delta }{E}_{1/2})$$

where $\mathrm{\Delta }{G}_{\mathrm{c}}^{°}$ is the free energy of the comproportionation reaction to form the mixed-valence product, R, T, n_e, and F have their usual meanings, and ΔE_1/2 is the potential difference between the E_1/2 values of adjacent redox couples (vide supra). The calculated comproportionation constants for the MeCN and DMF adducts are in the ranges 10³– 10⁸ and 10⁴– 10⁸, respectively (Figure 8 and Table 2). Although these K_c values indicate significant metal–metal interaction (K_c ≥ 10⁶ is typical of significant delocalization), they are orders of magnitude smaller than those obtained for the cyanide series. Equilibrium constants on the order 10¹²–10¹³ were observed for the comproportionation reactions of the cyanide species in NMP and PC (Table 2 and Table S2):

$${[{\text{Fe}}^6]}_{\text{CN}}^0+{[{\text{Fe}}_6]}^{2-}\rightleftarrows {[{\text{Fe}}_6]}^{1-}$$

Furthermore, the mixed-valence species 8, [Fe₆]²⁻, displayed the largest K_c values observed for any member of the three electron-transfer series studied in this work. These remained constant around 10¹⁹ to 10²⁰ in solvents with dielectric constants ranging from 32.5 (NMP) to 66.1 (PC) (Table S2). Overall, the extracted comproportionation constants for the cyanide series surpass any threshold conventionally defined for fully delocalized systems, e.g., the CT ion (K_c ~ 10⁷).³²

Figure 8.

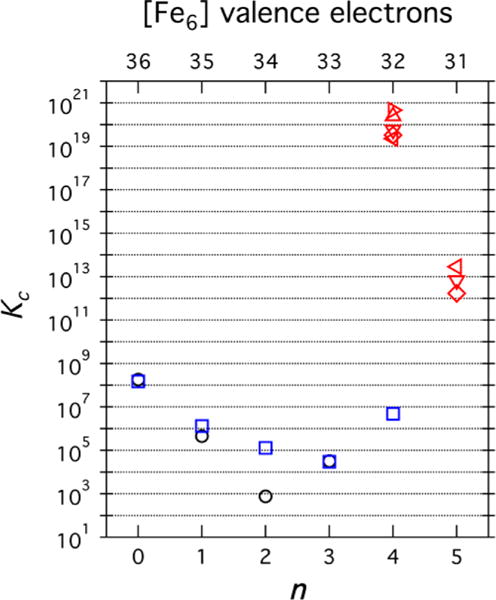
Comproportionation constants versus n (bottom axis) and versus the total number of [Fe₆] valence electrons (top axis). Black circles correspond to the MeCN adduct series, blue squares to the DMF series, and red symbols to the cyanide series in five different solvents.

3.7. Near-Infrared Spectroscopy

Qualitative evidence for the appearance of metal-to-metal charge transfer bands, later termed intervalence charge transfer (IVCT) bands, was realized in the late 1960s when Allen and Hush published a series of examples where mixed-valence species had optical and magnetic properties markedly different from the one-electron-reduced or -oxidized congeners.³³ Shortly thereafter, Robin and Day expanded upon the Allen and Hush report with a compilation of over 800 articles describing this phenomenon.³⁴ As an attempt to classify these, they proposed class designations to describe the extent of electron transfer from localized (or valence-trapped, class I) to partially delocalized (class II), to fully delocalized (class III). This led to the proposal of the first theoretical model to describe the optical properties of mixed-valence compounds.³⁵ This theory considered a two-state model in which the redox sites are linked together by a ligand bridge. Soon after, this classical two-state model was expanded to include vibronic coupling (also called the PKS model)³⁶ and magnetic interactions such as double exchange.³⁷

According to the classical model developed by Hush,³⁵ the IVCT bands yield information regarding the extent of electron delocalization. Thus, from the band peak maximum (ν_max), the molar absorptivity (ε_max), the full-width at half-maximum (Δν_1/2), and the shape, one can determine the electronic coupling (H_ab) between the reactant and product adiabatic energy surfaces. Hush theory has been applied extensively to dinuclear bridged systems, where control of the metal-to-metal distance can be achieved by systematic variation of the bridging ligand.³⁸ The classical example of electron delocalization is that of the CT ion {[(H₃N)₅Ru]₂(pyz)}⁵⁺.⁶

Extensive discussions regarding the magnetic, spectroscopic, and electrochemical data have debated the designation of the CT ion as either partially localized^7a–h or fully delocalized.^7i–p,32 Nevertheless, application of the PKS model to the CT ion reproduces its IVCT band and calculates a ground-state energy surface with a single minimum.³⁹ A qualitative classification of a mixed-valence species can be done by determining the band intensity, shape, and bandwidth at half-maximum. For a class III species, the transitions typically present ε_max ≥ 5000 M⁻¹ cm⁻¹, Δν_1/2 ≤ 2000 cm⁻¹, and asymmetry on the low-energy side and are solvent-independent.³⁵

To investigate the presence of IVCT bands for the clusters examined in this work, near-infrared (NIR) spectra were collected on the soluble species 1–5, 7, and 8. Electronic absorption data were collected at 350–2000 nm (28570–5000 cm⁻¹). In the near-UV–vis range, the DMF adducts display broad absorption bands, which become better resolved upon moving to the MeCN and cyanide adducts (Figures S14–S17). In the NIR region, species with DMF bound display no IVCT bands. This is in contrast to those having MeCN or CN⁻ bound, where absorption bands are observed. Those for the cyanide species are significantly more intense than the ones for the corresponding solvent adducts. The data for each of these are plotted in Figure 9 as reduced absorption (ε/ν) versus ν, as recommended by D’Alessandro and Keene for charge transfer bands.⁴⁰

Figure 9.

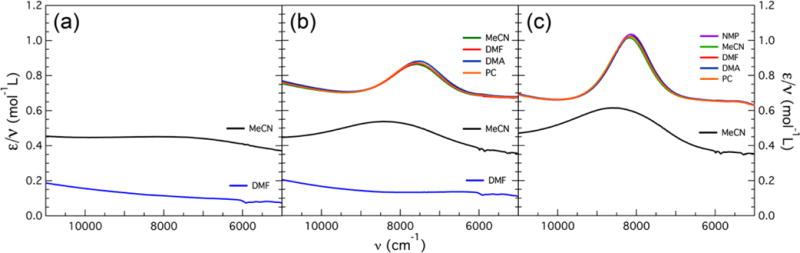
NIR spectra of [(^HL)₂Fe₆(L′)_m]ⁿ⁺ (L′ = MeCN, DMF) and [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶: (a) n = 2, m = 4 species 1 (black) and 4 (blue); (b) n = 3, m = 6 species 2 (black), 5 (blue), and 7 (multicolor); (c) n = 4, m = 6 species 3 (black) and 8 (multicolor). The spectra for the acetonitrile and cyanide adducts are offset on the y axis.

For species 1–3, the reduced absorption increases while the width of the transition band decreases, thus tracking with the overall molecular oxidation level n. The same trend is observed for 7 and 8. On the basis of the nearly ideal Gaussian shapes of the observed bands for 2, 3, 7, and 8, these were fit in this manner to extract ν_max, ε_max, and Δν_1/2. Although 1 displays an IVCT band, it is too broad and thus was not modeled. Because of the propensity of the clusters to undergo solvent exchange, the spectra for clusters 1–5 could be obtained in only one solvent. As the [(^HL)₂Fe₆(CN)₆]^n–6 clusters do not undergo ligand exchange, the spectra of 7 and 8 were obtained in five different solvents: NMP, MeCN, DMF, DMA, and PC. Table 3 lists all of the parameters extracted from fitting of these IVCT bands.

It has been derived theoretically that for a fully delocalized system (single minimum, barrierless electron transfer) the absorption band position becomes solvent-independent.³⁵ This dielectric-medium independence is observed for 7 and 8. The extent of electron delocalization can be quantified by calculating the electronic coupling (H_ab) between the donor and acceptor ground-state energy surfaces. Three methods were employed.

First, the Hush formula (eq S.1 in the Supporting Information) was directly applied. The electronic coupling H_ab1 (Table 3) was extracted by considering the donor–acceptor distance (r_ab) to be the average Fe–Fe contact. It is important to remark that this treatment works well for weakly coupled systems and that it can severely underestimate the magnitude of H_ab.⁴⁰ The second treatment employed was that described by Brunschweig and Sutin⁴¹ relating $\mathrm{\Delta }{G}_c^{°}$ and H_ab (eqs S.3 and S.4). The electronic coupling extracted via this method is listed as H_ab2 in Table 3. The final treatment used introduced the parameter Γ (eq S.5), which classifies the mixed-valence state as weakly coupled class II (0 < Γ < 0.1), moderately coupled class II (0.1 < Γ < 0.5), borderline class II–III (Γ ≈ 0.5), and class III (Γ > 0.5).⁴² This takes into account the observed and predicted IVCT bandwidths. Since a vast amount of data has been reported for the CT ion, this was used as a reference for comparison with the results obtained for the [Fe₆] clusters. The interpretation and comparison of results will be treated in the Discussion.

3.8. Magnetometry

Magnetic Susceptibility

Variable-temperature dc magnetic susceptibility (χ_M) data were collected for the different redox transfer isomers to examine their magnetic behavior. In addition, variable-temperature variable-field magnetization data were collected to determine the cluster spin ground states. The compound [(^HL)₂Fe₆(NCMe)₆][PF₆]₄ (3) with an oxidation level of n = 4 is known to be diamagnetic.^11a The complexes [(^HL)₂Fe₆(DMF)₆][BF₄]₄ (6) and [Bu₄N]₂[(^HL)₂Fe₆(CN)₆] (8) (nominally at the same cluster oxidation level of n = 4) are also diamagnetic and display well-resolved ¹H NMR spectra (Figures S10 and S13). The compiled molar magnetic susceptibility (χ_MT) versus T data for the CN-bound (7, 10), MeCN-bound (1, 2), and DMF-bound species (4, 5) are shown in Figure 10a–c, respectively.

Figure 10.

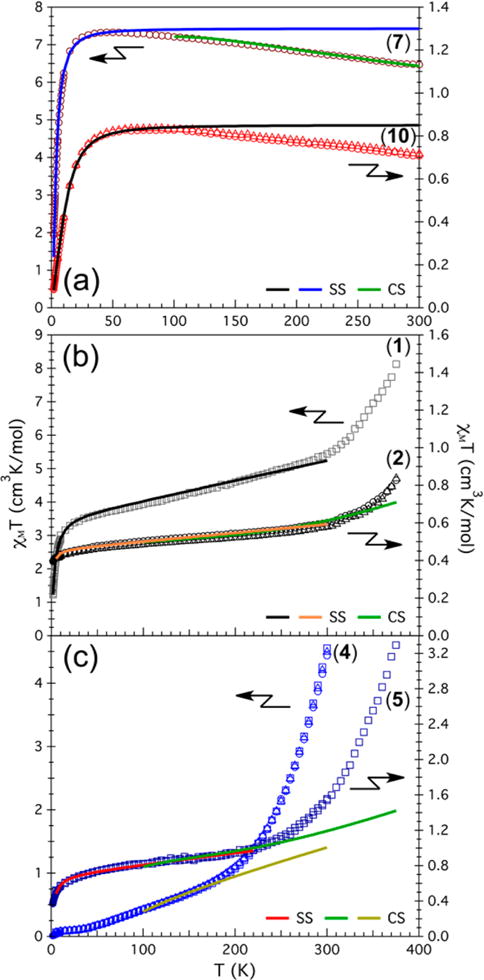
Variable-temperature dc magnetic susceptibility data, χ_MT for (a) cyanide species 7 (maroon) and 10 (red), (b) acetonitrile adducts 1 (gray) and 2 (black), and (c) DMF adducts 4 (blue) and 5 (navy blue). Experimental data are shown as open symbols for 0.1 T (squares), 0.5 T (triangles), and 1 T (circles). Solid lines correspond to fits (or simulations) to the models described in the main text.

At a glance, the measured cyanide species 7 and 10 display similar profiles of their respective χ_MT data as a function of temperature, although at significantly different magnitudes. At 300 K, the χ_MT values for 7 and 10 are 6.51 and 0.72 cm³ K/mol, respectively. As the temperature is lowered, these values increase to maxima of 7.34 cm³ K/mol at 50 K and 0.84 cm³ K/mol at 70–90 K, respectively. Finally, upon further cooling to 1.8 K, rather abrupt decreases in χ_MT to 1.94 and 0.086 cm³ K/mol for 7 and 10, respectively, are observed (Figure 10a).

The magnetic behavior for the MeCN adducts 1 and 2 presents a new phenomenon not observed in 7 and 10: the plateau in χ_MT that persists from ~25 K for both compounds is lost at temperatures above 300 K, and the measured moments increase abruptly (Figure 10b). At 375 K, χ_MT is 8.26 cm³ K/mol for 1 and 0.83 cm³ K/mol for 2; lowering the temperature to 300 K decreases χ_MT significantly to 5.54 and 0.60 cm³ K/mol, respectively. This behavior is followed by a linear decrease in χ_MT for both compounds. Ultimately χ_MT for 1 reaches 3.40 cm³ K/mol at 25 K, and further cooling to 1.8 K causes χ_MT to plummet to 1.23 cm³ K/mol, likely as a result of zero-field splitting. In contrast, 2 exhibits no abrupt downturn but rather a monotonic decrease to 0.39 cm³ K/mol at 1.8 K.

The DMF-bound electron-transfer series displays marked differences compared with the CN- and MeCN-bound series (Figure 10c). The least-oxidized DMF species (4, n = 2), has χ_MT = 4.53 cm³ K/mol at 300 K. This decreases sharply to 1.06 cm³ K/mol at 200 K. Upon further cooling, χ_MT continues decreasing gradually until it reaches 0.013 cm³ K/mol at 1.8 K. For the n = 3 cluster, [(^HL)₂Fe₆(DMF)₆][PF₆]₃ (5), the magnetic susceptibility behaves similarly to its redox isomer with MeCN bound. The moment for 5 at 375 K is 3.30 cm³ K/mol, sharply decreases until 250 K, and settles at 1.10 cm³ K/mol. A plateau in χ_MT follows from 250 to ~10 K, below which a less-pronounced downturn takes the moment to 0.371 cm³ K/mol at 1.8 K.

Reduced Magnetization

The electronic ground state of each of the clusters was investigated further by collecting variable-temperature (1.8–10 K) variable-field (1–7 T) magnetization data. The ground state was then determined for 1, 2, 4, 5, 7, and 10. As mentioned before, 3, 6, and 8 are diamagnetic species; thus, their ground state is S = 0. For the remaining compounds, the data obtained were analyzed by applying the spin Hamiltonian

$$\widehat{H}=D{\widehat{S}}_z^2+E({\widehat{S}}_x^2-{\widehat{S}}_y^2)+g{\mu }_{\mathrm{B}}\mathbf{S}\cdot \mathbf{H}$$

in the program PHI.⁴³ The reduced magnetization data for 7 and 10 are shown in Figures S36 and S37, respectively. On the basis of the VT EPR spectra obtained for 7, a ground state of $S=\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ or $\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ is required in order to record the transitions observed at g ≈ 11. Thus, although no satisfactory fit was obtained for 7 when considering the reduced magnetization data, a ground-state assignment of $S=\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ would account for the EPR transitions and the magnetic susceptibility observed (χ_MT = 7.34 cm³ K/mol for 7 at 50 K). The magnetization saturation of cluster 10 achieved 0.59μ_B at 1.8 K and 7 T. Although the magnitude is low, this can be attributed to zero-field splitting. Thus, it was fitted as an S = 1 state and freely refined to yield g = 1.84, D = −122.4 cm⁻¹, and |E/D| = 0.046.

The MeCN- and DMF-bound clusters were examined in a similar way. As in the case of 10, the reduced magnetization of [(^HL)₂Fe₆(NCMe)₄][PF₆]₂ (1) displays non-superimposable isofield curves, indicating a zero-field-split ground state (Figure S32).⁴⁴ Saturation occurs at 2.41μ_B at 1.8 K and 7 T. These data were fit considering an S = 2 to give the following fitting parameters: g = 2.16, D = −21.6 cm⁻¹, and |E/D| = 0.27. For its oxidized redox isomer 2, the low-temperature magnetization data present superimposable isofield lines that saturate at 0.95μ_B (Figure S33). This observation led us to collect magnetization data at 1.8 K, where the field was varied from 0 to 7 T in small increments. The data were reproduced by simulation with the Brillouin function using $S=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and g = 1.95 (Figure S38). Although a diamagnetic spin ground state was anticipated for [(^HL)₂Fe₆(DMF)₄][PF₆]₂ (4) on the basis of the χ_MT data in Figure 10c, its reduced magnetization displays nonzero saturation (Figure S34). This indicates that the S = 0 ground state is not fully populated even at 1.8 K. The related redox isomer 5 presents reduced magnetization data similar to those of 2. Superimposable isofield curves that saturate at 1.04μ_B at 1.8 K and 7 T are observed (Figure S35). Additional data were obtained at 1.8 K, permitting a simulation of the experimental data using the Brillouin function with the parameters $S=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and g = 2.05 (Figure S39).

Simulation of Magnetic Data

To best describe the magnetic data presented in the previous section, two models were employed: (1) a single spin (SS) model that considers the six-metal-atom cluster to behave as a single-spin entity, as has been done previously,^11a,45 and (2) a coupled spins (CS) model that assumes the spins of metal sites within the cluster to be coupled. In the latter model, the iron sites are coupled through exchange interactions between adjacent (J_cis) and trans-located (J_trans) metal sites. A similar treatment was employed previously for an octahedral hexamanagnese(III) cluster.⁴⁶ The CS method can be described by the spin Hamiltonian

$$\widehat{H}=-2J_{\text{cis}}({\widehat{\mathbf{S}}}_1\cdot {\widehat{\mathbf{S}}}_2+{\widehat{\mathbf{S}}}_1\cdot {\widehat{\mathbf{S}}}_3+{\widehat{\mathbf{S}}}_1\cdot {\widehat{\mathbf{S}}}_4+{\widehat{\mathbf{S}}}_1\cdot {\widehat{\mathbf{S}}}_6+{\widehat{\mathbf{S}}}_2\cdot {\widehat{\mathbf{S}}}_3+{\widehat{\mathbf{S}}}_2\cdot {\widehat{\mathbf{S}}}_5+{\widehat{\mathbf{S}}}_2\cdot {\widehat{\mathbf{S}}}_6+{\widehat{\mathbf{S}}}_3\cdot {\widehat{\mathbf{S}}}_4+{\widehat{\mathbf{S}}}_3\cdot {\widehat{\mathbf{S}}}_5+{\widehat{\mathbf{S}}}_4\cdot {\widehat{\mathbf{S}}}_5+{\widehat{\mathbf{S}}}_4\cdot {\widehat{\mathbf{S}}}_6+{\widehat{\mathbf{S}}}_5\cdot {\widehat{\mathbf{S}}}_6)-2J_{\text{trans}}({\widehat{\mathbf{S}}}_1\cdot {\widehat{\mathbf{S}}}_5+{\widehat{\mathbf{S}}}_2\cdot {\widehat{\mathbf{S}}}_4+{\widehat{\mathbf{S}}}_3\cdot {\widehat{\mathbf{S}}}_6)$$

using the Kambe vector coupling solution,⁴⁷ where all of the J_cis and J_trans exchange interactions are assumed to be equivalent. Both methods were attempted for each data set but not all gave satisfactory results. For the SS model, the low-temperature data were considered down to 1.8 K, but for the CS model the lowest temperature considered was 100 K to avoid any zero-field-splitting effect. The individual spins considered at each Fe site are based on the bound ligand L′ (DMF, MeCN, or CN) and the formal oxidation state, as described in the Supporting Information and shown in Scheme S1. These spins were grouped to give the spins S_a, S_b, S_c, and S as described in the Supporting Information, and the corresponding quantum numbers are used in the following analysis and discussion with the notation [S_a, S_b, S_c]. The magnetic susceptibility data collected and presented in Figure 10a–c were then fit using these two models.

Beginning with the cyanide series, the data for both 7 and 10 were fit considering only the 1.8 to 100 K data via the SS model; the rest were extrapolated using the fit parameters obtained. For 7 the SS model provided the fit parameters D = +4.4 cm⁻¹ and g = 1.94 (blue lines in Figure 10a and Figure S41). The SS model could not account for the downturn at temperatures above 100 K. However, when the CS model was employed with [S_a, S_b, S_c] = [1.5, 1.5, 1.5], the simulation reproduced the data with g = 2, J_cis = 64 cm⁻¹, and J_trans = −90 cm⁻¹ (green line in Figure 10a). For compound 10 no successful CS simulation was obtained. The SS fit parameters that reproduced the data well are D = +28.3 cm⁻¹, |E/D| = 0.28, and g = 1.84 (black lines in Figure 10a and Figure S41). To account for the diamagnetism of 8 at room temperature, it was assumed that strong antiferromagnetic coupling is operative. Simulations via the CS model were carried out to get an approximate magnitude of this coupling. As depicted in Figure S46, the minimum J_cis value needed for [S_a, S_b, S_c] = [1.5, 1.5, 1] to achieve S = 0 at 300 K is less than or equal to −600 cm ⁻¹. Although the magnitude of J_cis is clear, it is less well-defined for J_trans.

The solvent adducts were treated in a similar way using these two models. For [(^HL)₂Fe₆(NCMe)₄][PF₆]₂ (1), no successful CS simulation could be found. The spin ground state determined from its reduced magnetization (S = 2) was used in the SS fit. The parameters that gave a successful fit are D = +9 cm⁻¹, |E/D| = 0.19, g = 2.14, and a large temperature-independent paramagnetism (TIP) of 6.024 × 10⁻³ cm³/mol (black lines in Figure 10b and Figure S40). The behavior of the χ_MT data above 300 K was not fit by either of the two models considered and will be addressed later in the Discussion. As determined by the reduced magnetization data, complex 2 has a spin ground state of $S=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. The doublet ground state was employed in the SS fit in addition to an intermolecular interaction J_inter with the nearest neighbors, z. Thus, the fit parameters that reproduced the susceptibility data up to 300 K are g = 2.21, zJ_inter = −0.28 cm⁻¹, and TIP = 4.55 × 10⁻⁴ cm³/mol (orange line in Figure 10b). The simulation of the χ_MT data for 2 using the CS model with [S_a, S_b, S_c] = [2.5, 2.5, 2.5] gave best simulation parameters as g = 2.22, TIP = 3.6 × 10⁻⁴ cm³/mol, J_cis = −315 cm⁻¹, and J_trans = −390 cm⁻¹ (green line in Figure 10b). Various simulations changing J_cis and Jtrans were computed to give a better idea of other approximate values that would represent the experimental data (Figure S42). As in the case of 1, the high-temperature data (>300 K) will be discussed later. In a similar way as for 8, CS simulations for diamagnetic 3 with [S_a, S_b, S_c] = [2.5, 2.5, 3] yielded estimated values for J_cis below −600 cm⁻¹ (Figure S45).

The formal oxidation levels of the clusters of the DMF electron-transfer series are analogous to those of the acetonitrile-bound species, and thus, they were treated similarly. No SS fit reproduced the χ_MT data for [(^HL)₂Fe₆(DMF)₄]-[PF₆]₂ (4). Attempts to reproduce the data via the CS model for [S_a, S_b, S_c] = [2.5, 2, 2.5] provided crude approximations of the behavior in the low-temperature regime. The best simulation (dark-yellow line in Figure 10c) employed the simulation parameters g = 2.05, J_cis = −95 cm⁻¹, and J_trans = −60 cm⁻¹. Deviations from J_cis = −95 cm⁻¹ significantly impacted the quality of the fit, whereas J_trans was varied from 0 to −120 cm⁻¹ with −60 cm⁻¹ best representing the data (Figure S43). Treatment of the χ_MT data for 5 was carried out in a similar way as for 2. On the basis of the spin ground state of $S=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, the SS fit parameters were g = 2.73, TIP = 1.27 × 10⁻³ cm³ mol⁻¹, and zJ_inter = −0.86 cm⁻¹ (red line in Figure 10c) for the data from 1.8 to 220 K. Using the CS model for [S_a, S_b, S_c] = [2.5, 2.5, 2.5] resulted in the simulation parameters g = 1.96, J_cis = −20 cm⁻¹, and J_trans = −240 cm⁻¹ (green line in Figure 10c). Multiple simulations varying J_cis and J_trans were computed. J_cis was fixed at −20 cm⁻¹ since departure from this value gave qualitatively worse fits to the data. The effect of J_trans is plotted in Figure S44. Last, for diamagnetic 6, which is at nominally the same oxidation level as 3 and 8 (n = 4), CS simulations for [S_a, S_b, S_c] = [2.5, 2.5, 3] yielded estimated values of J_cis below −600 cm⁻¹ (Figure S45).

4. DISCUSSION

When we first reported the (^HL)₂Fe₆ electron-transfer series that featured the neutral all-ferrous complex and the oxidation sequence featuring acetonitrile solvation (e.g., [(^HL)₂Fe₆(NCMe)_m]ⁿ⁺), we used a delocalized molecular orbital description to rationalize the redox-dependent properties, including solvent ligation, [Fe₆] volume, and ground-state electronic structure changes.^11a The delocalized molecular orbital description suggested that direct intracore Fe–Fe interactions dictate the primary interactions between the metal sites. Despite the rudimentary nature of this model, it could adequately account for many of the redox-dependent properties of the electron-transfer series. Following this report, we were interested in probing the nature of the M–M bonding interaction further, especially with regard to how the oxidation load is distributed throughout the octahedral core and how it is affected by the chemical environment. Specifically, we wanted to address the following questions: (1) What is the extent of redox delocalization within the [Fe₆] core? (2) In terms of the influence of the chemical environment, is there a ligand field dependence of the redox delocalization? More specifically, can ancillary ligand binding to the [Fe₆] core alter the nature of direct M–M bonding interactions? (3) Finally, what is the most appropriate descriptor of the electronic structure within clusters featuring close M–M interactions? Are the clusters best viewed as single redox entities with maximal redox delocalization, or are the metal sites redox- and spin-isolated, with the M–M contacts providing an additional pathway for exchange coupling?

To address these questions, we investigated the three cluster redox series [(^HL)₂Fe₆(NCMe)_m]ⁿ⁺ with n = 2–4 (1–3), [(^HL)₂ Fe₆(DMF)_m]ⁿ⁺ with n = 2–4 (4–6), and [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶ with n = 3–6 (7–10), in which acetonitrile, dimethylformamide, and cyanide, respectively, are bound to the cluster. The cluster series were examined by X-ray crystallography, zero-field ⁵⁷Fe Mössbauer spectroscopy, EPR spectroscopy, cyclic voltammetry, NIR and IR spectroscopy, and magnetometry. The spectroscopic probes allowed us to examine the degree of redox delocalization over 10 orders of magnitude in the time domain (EPR, 10⁻⁵–10⁻⁹ s; Mössbauer, 10⁻⁷ s; IR, 10⁻¹¹ s; NIR, 10⁻¹⁴ s).

4.1. Determination of Redox Delocalization

4.1.1. Structural Considerations

The redox-dependent ligation pattern observed within the MeCN series (1–3) is maintained within the DMF series (4–6). As the CN series (7–10) was isolable only for clusters at the n = 3 redox level and higher, the ligation patterns are also preserved within this series. Within these three series, there are no obvious structural changes when different ancillary ligands are used. The n = 2 redox isomorphs 1 and 4 feature nearly identical metrical parameters (Table 1 and Figure 11). As the redox level of the [Fe₆] core is increased (n ≥ 3, decreasing number of [Fe₆] valence electrons), the cluster intracore Fe–Fe distances incrementally decrease. The structural changes that accompany redox changes appear to be more sensitive to the overall cluster valence electron count than the ancillary ligand or cluster spin state. Within the n = 3 cluster series of 2, 5, and 7, clusters 2 and 5 have the same ground state (vide infra), yet 5 and 7 feature markedly longer Fe–Fe contacts than 2. Similarly, within the n = 4 cluster series 3, 6, and 8, where all of the clusters share the same diamagnetic ground state, 3 and 8 are nearly isostructural while the DMF-bound 6 features the longest Fe–Fe contacts within the series. Most importantly, unlike previous examples where redox isolation is prevalent and obvious by structural changes at the trapped-valence metal sites,⁴⁸ none of the clusters examined herein reveal characteristic alterations reflective of redox localization. The Fe–N bond metrics and corresponding amide bond angles are very consistent throughout the whole series (Table 1).

Figure 11.

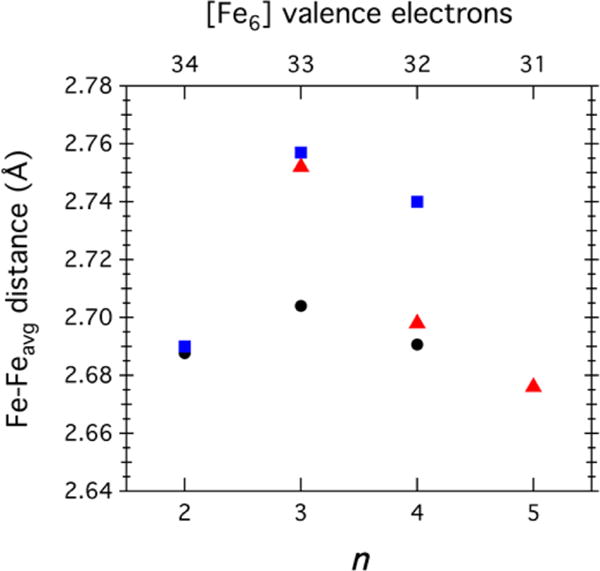
Average intracore Fe–Fe bond lengths as functions of core oxidation level for [(^HL)₂Fe₆(L′)_m]ⁿ⁺ with L′ = NCMe (black ●), DMF (blue ■), or CN (red ▲).

4.1.2. Spectroscopic Considerations

⁵⁷Fe Mössbauer Spectroscopy

Each member of the redox series examined displayed a single symmetric quadrupole doublet for isostructural sites (Figure 3). The appearance of a single quadrupole doublet in any of these clusters, independent of the apical ligand L′, suggests that redox delocalization over the [Fe₆] core occurs faster than the nuclear transition at ⁵⁷Fe (10⁻⁷ s).^12d,49

Cyclic Voltammetry

Comproportionation constants (K_c) obtained from cyclic voltammetry (CV) provide a way to compare mixed-valence complexes and benchmark each species according to the appropriate Robin–Day classification. Valence-trapped, redox-localized mixed-valence complexes exhibit K_c values consistent with electrostatic charging (10–10²), and weakly coupled systems typical of class II delocalization exhibit higher K_c values (10²–10⁴), whereas fully delocalized systems typical of class III exhibit K_c values in excess of 10⁵.⁴⁰ The CV data for [(^HL)₂Fe₆(NCMe)₆]³⁺ (2) reveal five reversible redox events (Figure 6c) and thus six observable redox levels (n = −1 to +4) with K_c values spanning from 7 × 10² to 1.2 × 10⁸ (Figure 8, Table 2). Three of the K_c values determined are in excess of 10⁴, suggestive of a delocalized redox system (the CT ion has K_c ~ 10⁷ as a benchmark for fully delocalized class III behavior).³² The CV data for [(^HL)₂Fe₆(DMF)₆]³⁺ (5) reveal six reversible redox events (Figures 6c and 7b) and thus seven observable electrochemical redox levels (n = −1 to +5) with K_c values spanning from 3 × 10⁴ to 3 × 10¹⁵ (Figure 8, Table 2). As in MeCN-bound 3, DMF ligation to the cluster yields comproportionation constants consistent with a moderately to strongly delocalized system. As previously mentioned, the lability of the MeCN and DMF in 2 and 5, respectively, make determination of the solvent dependence of K_c impossible, thereby limiting the analysis. Finally, the CV data for [(^HL)₂Fe₆(CN)₆]³⁻ (7) reveal three reversible redox events (Figures 6c and 7a) and thus only four observable electrochemical redox levels (n = 3–6) with K_c values spanning from 2 × 10¹² to 3 × 10²⁰ (Figure 8, Table 2). These values are independent of solvent donor number (DN), as gleaned from the CV data recorded in NMP, MeCN, DMF, DMA, and PC (Table S2). On the basis of theoretical grounds, the properties of a class III complex should be solvent-independent.⁵⁰ In this regard, the electron-transfer series [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶ displays a negligible dependence of E_1/2 versus DN of approximately −8.7 mV/DN on average, which is 3 times smaller than that observed for the CT ion (approximately −26.3 mV/DN)³² (Figure 12).

Figure 12.

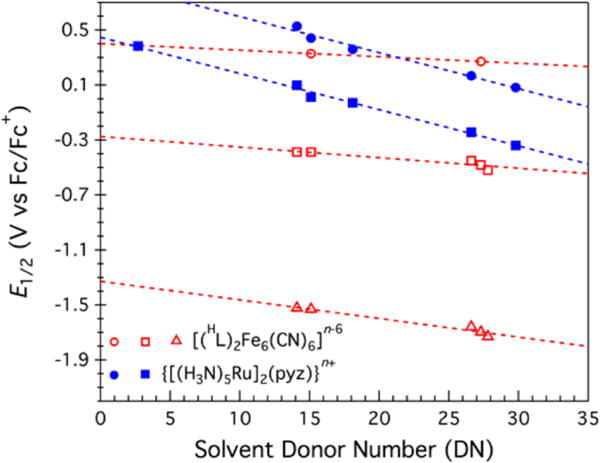
Reduction potentials (E_1/2) as functions of solvent donor number. Redox couples: [(^HL)₂Fe₆(CN)₆]ⁿ⁻⁶ with n = 3/4 (red △, −13.5 mV/DN), 4/5 (red □, −7.7 mV/DN), and 5/6 (red ○, −4.8 mV/DN); {[(NH₃)₅Ru]₂(pyz)}ⁿ⁺ with n = 4/5 (blue ■, −26.4 mV/DN) and 5/6 (blue ●, −26.3 mV/DN).

Examination of the Intervalence Charge Transfer Bands in the NIR Spectrum

Even with K_c values consistent with moderately to strongly delocalized systems, the DMF-bound series 4–6 exhibits no IVCT bands within the NIR region (Figure 9). Broad (Δν_1/2 ≥ 2000 cm⁻¹) and solvent-dependent IVCT bands are characteristic of mixed-valence systems in class II. The MeCN-bound series does exhibit broad (Δν_1/2 = 3400–3672 cm⁻¹) Gaussian-shaped IVCT bands for 2 and 3, whereas the spectrum for 1 is too broad to assign (Figure 9). Spectral analysis by the three methods described (H_ab1, H_ab2, and Γ; Table 3) suggests that the MeCN-bound clusters are moderately coupled class II systems. In contrast, spectral analysis of the two soluble CN-bound redox isomers, 7 and 8, reveals intense (ε_max = 1900–3400 M⁻¹ cm⁻¹), narrower (Δν_1/2 = 1266–1824 cm⁻¹) IVCT bands that yield electronic coupling markers (H_ab1, H_ab2, and Γ) highly suggestive of a fully delocalized class III system. Just as the electrochemical behavior of the CN-bound cluster was solvent-independent, the IVCT frequency maximum was also solvent-independent. According to Hush^51a and Marcus,^51b the total reorganization energy upon electron transfer can be divided into inner-sphere (λ_i) and outer-sphere (λ_o) contributions. In mixed-valence species, the energy of the IVCT band (ν_max) is given by λ_i + λ_o.⁵² Applying a dielectric continuum model predicts a linear dependence of ν_max on solvent dielectric function (1/D_op – 1/D_s; where D_op and D_s are the solvent optical and static dielectric constants, respectively) for weakly coupled systems, where the intercept corresponds to the inner-sphere reorganization energy and the slope is related to the distance between the interacting sites.⁵³ In contrast, when the dependence on the dielectric medium is minimal or absent (λ_o → 0), the mixed-valence species is regarded as strongly delocalized.³⁵ The near solvent independence for the CN series, as indicated by the near zero slope in the ν_max versus (1/D_op – 1/D_s) plot, provides further evidence of the fully delocalized state (Figure 13). In contrast, the CT ion appears to scatter for (1/D_op – 1/D_s) > 0.49.

Figure 13.

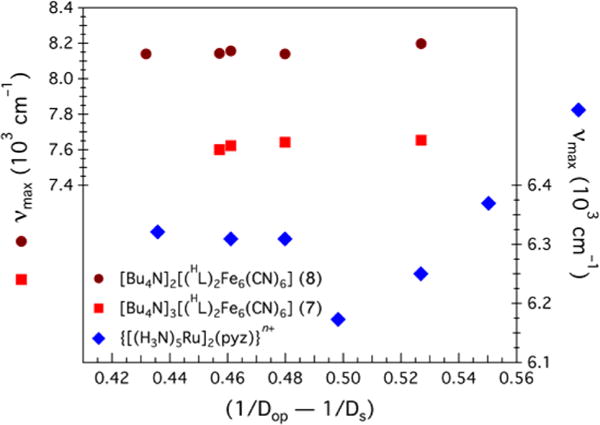
Plots of ν_max vs solvent dielectric function (1/D_op – 1/D_s) for 7, 8, and the CT ion.

Infrared Spectroscopy

The fully delocalized electronic state for the CN redox isomers is also corroborated by the stretching frequency of the CN ligands for the series 7–10. A single narrow stretching frequency (ν_C–N) is observed for each of the redox isomers (Figure 6a) with a nearly linear increase in the vibrational frequency with increasing oxidation level of the cluster (Figure 6b). The cyanide stretching frequency is highly sensitive to the oxidation state of the metal ion to which it is bound, as reflected by the observation of well-separated vibrations for ferricyanide (ν_C–N = 2135 cm⁻¹) and ferrocyanide (ν_C–N = 2098 cm⁻¹). Thus, the single cyanide stretching band suggests that the rate of intramolecular electron transfer is higher than the vibrational frequency of the C–N bond.⁵⁴

4.2. Ground-State Electronic Structure Assignments

From the preceding sections it is clear that the cluster solvation or anation greatly affects the degree to which intracore redox delocalization occurs. Unsurprisingly, the ancillary ligand bound to the cluster also significantly impacts the observed ground-state electronic configurations and furthermore the temperature to which the ground state persists. On the basis of EPR and magnetometry (magnetic susceptibility and reduced magnetization) data, we compile the ground-state electronic assignments in Table 4. The qualitative trend is that upon oxidation and ancillary ligand binding, each of the clusters undergoes a reduction in the number of unpaired electrons from the unsaturated all-ferrous precursor (^HL)₂Fe₆ (S = 6). As previously mentioned, the overall oxidation level of the cluster does not impact the observed ground state (vide supra); rather, the ancillary ligand field strength impacts how thermally isolated the ground state becomes. For the strong-field CN clusters, the ground state is well-isolated for species 7 and 10, where no thermally induced spin-state transition is observed over the temperature range surveyed. For the MeCN clusters 1 and 2, the ground state is observed and uniquely populated until temperatures of about 300 K, at which point thermally induced population of an excited state becomes possible. For the weakest-field ligand surveyed, DMF, the onset of thermal population of excited states occurs at much lower temperatures (200 K for 4 and 5). Qualitatively the ancillary ligand field strength dictates the strength of the ground-state coupling, as is equally reflected by the electrochemical and spectroscopic trends for the three series.

Table 4.

Ground-State (S) Assignments for 1–10.

	[(HL)2Fe6(L′)m]n+ or [(HL)2Fe6(CN)6]n−6
N	MeCN	S	DMF	S	CN	S
2	1	2	4	0
3	2	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$	5	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$	7	$\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$
4	3	0	6	0	8	0
5					9	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$
6					10	1

In attempts to model the magnetic susceptibility versus temperature data, two models were entertained: (1) a single-spin model, in which a delocalized electronic structure dictates that the [Fe₆] core can be adequately represented as a single d-orbital manifold populated with the cluster valence electrons (akin to our previous treatment of the MeCN series^11a), and (2) a coupled-spin model, wherein each iron site within the cluster is coupled to its nearest neighbors by exchange interactions. While the SS model can be interpreted as the strong-coupling limit of the CS model, we still will treat each interpretation separately. As illustrated in Figure 10, both modeling schemes can adequately reproduce certain temperature regimes. However, the CS scheme does not accurately reproduce the susceptibility at lower temperatures (<100 K), where zero-field splitting becomes relevant, or where the susceptibility departs from the spin ground state (i.e., where χ_MT undergoes a sudden upturn with increasing temperatures).

We favor the SS model over the CS model for three reasons: (1) The cluster redox series are nearly isostructural among the three series investigated, and there is no strong correlation between the observed spin ground state and the cluster geometry. The clearest demonstration of this is a comparison of the nearly isostructural n = 3 DMF cluster 5 and CN cluster 7, which feature dramatically different magnetic behaviors and spin ground states yet bear no significant structural differences (Fe–Fe distances or N–Fe–N or Fe–N–Fe angles) that account for the significantly different behaviors. Another geometry-matched pair, 1 and 4, presents the same quandary. (2) In consecutive redox states, dramatic changes observed in the aggregate spin state [e.g., $\mathbf{7}(S=\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)\to \mathbf{8}(S=0)$] would require significant coupling regime changes (e.g., from strongly ferromagnetic to strongly antiferromagnetic). These changes can be rationalized using the SS approach, as has been previously demonstrated, yet it is unclear how the CS model could account for this. (3) The strong temperature dependence of the magnetic susceptibility can be modeled using the SS approach as a thermal equilibrium between two or multiple spin states.⁵⁵ However, without being able to observe the high-temperature plateaus for the magnetic susceptibility in Figure 10, we cannot prove this unambiguously. Modeling of the magnetic behavior of the CN-bound series using the SS method is consistent with the electrochemical and spectroscopic metrics, which clearly designate this redox series to exhibit a fully delocalized electronic state. For the MeCN and DMF series, where the designation of the redox series is best described as between class II and class III, the use of the SS or CS model is less clear.

5. CONCLUSIONS

We have expanded upon our original report of the electron-transfer series afforded by oxidation of (^HL)₂Fe₆ in acetonitrile. The presence of significant intracore Fe–Fe orbital overlap allows for high-spin ground states to be achieved within this cluster geometry. Furthermore, the oxidation level of the cluster dictates a number of physical and spectroscopic changes. We have demonstrated herein that the ancillary ligand field strength affords attendant changes within the respective electron-transfer series. Employing weak-field DMF solvation to the cluster core generates an electron-transfer series that lacks spectroscopically observable IVCT bands yet affords comproportionation constants suggestive of redox delocalization (K_c = 10⁴– 10⁸). Magnetometry studies have revealed a dramatic temperature dependence of the observed ground-state electronic structure. Further examination of the original MeCN redox series has revealed broad, symmetric IVCT bands indicative of a weakly coupled class II system. However, magnetometry has revealed thermally well-isolated ground states observable to room temperature and comproportionation constants suggestive of strong redox delocalization (K_c = 10²– 10⁸). Finally, employing the strong-field CN anion yields a redox transfer series that meets all of the criteria reminiscent of a class III, fully delocalized electronic structure: well-isolated ground states (>300 K), K_c = 10¹²–10²⁰, and prominent, narrow IVCT bands. Quite remarkably, the strongest-field ligand examined, CN, gives rise to the highest observed spin ground states. On the basis of the designation of these redox series as moderately to strongly delocalized, the intracore M–M bonding can be best described by a single-spin model. The unique regime in which these clusters reside, where M–M bonding interactions are significant without effecting maximal valence electron pairing, give rises to highly interesting electronic state configurations. High-spin architectures become achievable and can be further manipulated by external ligation to the core. These types of chemical alteration of weak-field clusters could in turn lead to novel chemical analyte sensing or redox-directed spin amplification. Efforts to demonstrate these processes are currently underway in our laboratory.