Relationship Induced Multi-Template Learning for Diagnosis of Alzheimer’s Disease and Mild Cognitive Impairment

Abstract

As shown in the literature, methods based on multiple templates usually achieve better performance, compared with those using only a single template for processing medical images. However, most existing multi-template based methods simply average or concatenate multiple sets of features extracted from different templates, which potentially ignores important structural information contained in the multi-template data. Accordingly, in this paper, we propose a novel relationship induced multi-template learning method for automatic diagnosis of Alzheimer’s disease (AD) and its prodromal stage, i.e., mild cognitive impairment (MCI), by explicitly modeling structural information in the multi-template data. Specifically, we first nonlinearly register each brain’s magnetic resonance (MR) image separately onto multiple pre-selected templates, and then extract multiple sets of features for this MR image. Next, we develop a novel feature selection algorithm by introducing two regularization terms to model the relationships among templates and among individual subjects. Using these selected features corresponding to multiple templates, we then construct multiple support vector machine (SVM) classifiers. Finally, an ensemble classification is used to combine outputs of all SVM classifiers, for achieving the final result. We evaluate our proposed method on 459 subjects from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database, including 97 AD patients, 128 normal controls (NC), 117 progressive MCI (pMCI) patients, and 117 stable MCI (sMCI) patients. The experimental results demonstrate promising classification performance, compared with several state-of-the-art methods for multi-template based AD/MCI classification.

I. Introduction

BRAIN morphometric pattern analysis using magnetic resonance imaging (MRI) has been widely investigated for automatic diagnosis of Alzheimer’s disease (AD) and its prodromal stage, i.e., mild cognitive impairment (MCI) [1]–[6]. Using MRI data, brain morphometry can not only identify anatomical differences between populations of AD patients and normal controls (NCs) for diagnostics assistance, but also evaluate the progression of MCI [1]–[3]. Recently, many machine learning techniques have been proposed for identification of AD-related neurodegeneration patterns, based on brain morphometry with MRI data [5], [7]–[13]. Existing MRI-based diagnosis methods can be roughly divided into two categories, based on the number of templates used: 1) single-template based methods, where the morphometric representation of brain structures is generated from a specific template [4], [14], [15]; and 2) multi-template based methods, where multiple morphometric representations of each subject are generated from multiple templates [13], [15], [16].

In single-template based methods, one specific template is used as a benchmark space to provide a representation basis, through which one can compare the anatomical structures of different groups of disease-affected patients and NCs [17]–[19]. Specifically, all brain images are often spatially normalized onto a pre-defined template via a certain nonlinear registration method, where the morphometric representation of each brain image can be obtained. It is worth noting that such pre-defined template can be an individual subject’s brain image, or an average brain image generated from the particular image data under study [20]. In the literature, researchers have developed various single-template based morphometry pattern analysis methods, and demonstrated promising results in automatic AD/MCI diagnosis using different classification methods [19], [21]. Among them, voxel-based morphometry (VBM) [2], [22], deformation-based morphometry (DBM) [3], [23], [24], and tensor-based morphometry (TBM) [21], [25], [26] are the most widely used methods. In these methods, after nonlinearly transforming each brain image onto a pre-defined common template space, VBM measures local tissue density of the original brain image directly, while DBM and TBM measure local deformation and Jacobian of the local deformation, respectively. Such measurements can then be regarded as feature representations, which can serve as inputs to multivariate analysis methods (e.g., support vector machines, SVM) to conclude the diagnosis. However, feature representations generated from a single template may not be sufficient enough to reveal the underlying complex differences between groups of patients and normal controls, due to potential bias associated with the use of a single template. Specifically, subjects are acquired from a wide range of patients and normal controls with different ages, ethnicities, races and etc., and therefore a single template could not effectively represent all the subjects.

To address the issue mentioned above, researchers have proposed several methods that can take advantage of multiple diverse templates to compare group differences more efficiently. Although these methods require higher computational costs (compared to single-template based methods), multi-template based methods are very effective in reducing negative impact of registration errors and providing richer representations for morphometric analysis of brain MRI [27]. Recently, several studies [17], [18], [28]–[30] have shown that multi-template based methods can often achieve more accurate diagnosis than single-template based methods. For example, Leporé et al. [19] proposed a multi-template based method by first registering all brain images onto 9 templates that have been nonlinearly aligned to a common space. Then, they computed average deformation tensors from all these templates for each brain image, for enhancing TBM-based monozygotic/dizygotic twin classification. In addition, Koikkalainen et al. [18] developed a multi-template based method to investigate the effects of utilizing mean deformation fields, mean volumetric features, and mean predicted responses of the regression-based classifiers from multiple templates, and showed better AD classification results than single-template based methods. In another work, Min et al. [17] proposed to obtain multiple sets of features from multiple templates for each subject and then to concatenate these features for subsequent classification tasks.

As inferred from literature, most of existing multi-template based methods simply average or concatenate multiple sets of features generated from multiple templates. They do not effectively exploit the underlying structural information of multi-template data. In fact, some very important structural information exists in multi-template data, e.g., the inherent relationships among templates and among subjects. Intuitively, modeling such relationships can bring more prior information into the learning process, thus further boosting the learning performance. To the best of our knowledge, no previous multi-template based methods utilized such relationship information for AD/MCI classification.

Accordingly, in this paper, we propose a novel relationship induced multi-template learning (RIML) method, to explicitly model the structural information of multi-template data for AD/MCI classification. Unlike most previous multi-template based methods (e.g., [18], [19] that averaged the representations from multiple templates, or [17] that simply concatenated features generated from different templates), we retain each template in its original (linearly-aligned) space and focus on feature representations from each template individually. Our proposed method is composed of two main parts: a relationship induced sparse (RIS) feature selection method and an ensemble classification strategy. More specifically, we first spatially normalize each brain image onto multiple pre-selected templates via nonlinear registration, for extracting multiple sets of regional features from multiple templates. Afterwards, our relationship induced multi-task sparse feature selection method is used to select discriminative features in each template space, by considering both the relationship among multiple templates and the relationship among different subjects in the same template space. Then, for each template, we build a support vector machine (SVM) classifier [31] using its respectively selected features. Finally, we combine the outputs of all SVM classifiers from multiple templates to make a final decision through an ensemble classification technique. To evaluate the efficacy of our method, we perform four groups of experiments: 1) AD vs. NC classification, 2) progressive MCI (pMCI) vs. stable MCI (sMCI) classification, 3) pMCI vs. NC classification, and 4) sMCI vs. NC classification. By using a 10-fold cross-validation strategy on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database [9], we achieve a significant performance improvement for each of these four classification tasks, compared with several state-of-the-art methods for AD/MCI diagnosis.

It is worth noting that this work is different from our earlier work in [28]. First, in [28], one template is regarded as the main source, while the other templates are used as supplementary sources to provide guidance information. In this work, we focus on exploring the inherent relationship information in multi-template data, which is different from [28]. Second, the feature selection methods used in this work and our earlier work [28] are also different. The feature selection process in [28] is performed in each individual template space by ignoring the inherent relationships among different templates. In this work, we propose to explicitly model the relationships among templates and among subjects, and then utilize such relationships to guide the multi-task sparse feature selection. Such inherent relationships are important prior information, as they are valuable for the subsequent learning model, conformed by our experiments on the ADNI database.

The rest of this paper is organized as follows. We first describe the proposed method in the ‘Method’ section. Then, we illustrate experiments and results in the ‘Results’ section. In the ‘Discussion’ section, we investigate the influences of parameters and the performance of our method using the proposed ensemble classification strategy, and then discuss the pros/cons of our method. Finally, we draw conclusions and elaborate future research directions in the ‘Conclusion’ section.

II. Method

An overview of our proposed relationship induced multi-template learning (RIML) method for AD/MCI classification is provided in Fig. 1. As can be seen from Fig. 1, there are three main steps in RIML: 1) multi-template feature extraction, 2) relationship induced sparse feature selection, and 3) ensemble classification. In the following, we will introduce each step in detail.

Fig. 1.

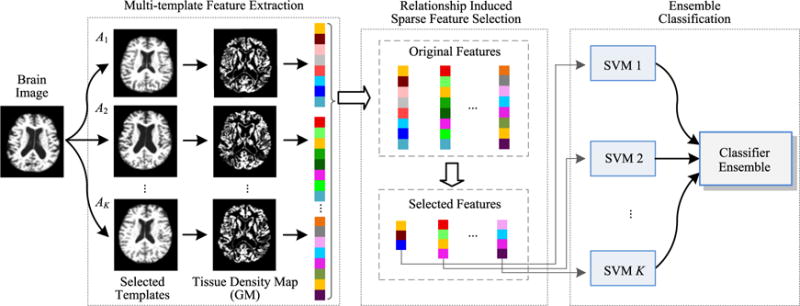
The framework of our relationship induced multi-template learning (RIML) method, which consists of three main steps: 1) multi-template feature extraction, 2) relationship induced sparse feature selection, and 3) ensemble classification.

A. Multi-Template Feature Extraction

In this study, a standard image pre-processing procedure is applied to the T1-weighted MR brain images for each studied subject. Specifically, we first perform a non-parametric non-uniform bias correction (N3) [11] on each MR image to correct intensity inhomogeneity. Next, we perform skull stripping [7], followed by manual correction to ensure that both skull and dura have been cleanly removed. Then, we remove the cerebellum by warping a labeled template to each skull-stripped image. Afterwards, we adopt the FAST method [32] to segment each brain image into three tissues, i.e., gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). Finally, all brain images are affine-aligned using the FLIRT method proposed in [33].

One of the most crucial challenges in multi-template based methods is selecting an appropriate set of templates. Selecting a diverse template set with sufficiently large generalization capability can lead to less registration errors and more efficient/accurate representations. In the literature, different strategies are studied. For instance, Jenkinson et al. [33] randomly selected 30 templates from different categories of subjects. However, there may be different distributions of brain structure in the neuroimaging data within a specific class [34]. As a result, randomly selected templates from these data may not necessarily capture the true distribution of the entire population, which could introduce redundant or insignificant information to the feature respresentations. Generally, those selected templates shall not only be representative enough to cover the entire population, in order to reduce the overall registration errors, but also capture discriminative information of brain abnormality related to diseases. To address this problem, we first cluster all subjects using the Affinity Propagation (AP) algorithm [35], to partition the entire population (i.e., AD and NC brain images) into K non-overlapping clusters. In each cluster, one specific brain image is automatically selected as an exemplar. Then, we treat the exemplar image of each cluster as a template, and construct a template pool by combing all these templates. For the clustering purpose, we use normalized mutual information [35] as the similarity measure, and adopt a bi-section method [36] to find the appropriate preference value for the AP algorithm. Similar to previous multi-template based methods [18], [19], [33], we select 10 templates using the AP algorithm, as shown in Fig. 2. In Fig. 2, the first six templates (i.e., A₁–A₆) are NC subjects, while the last four templates (i.e., A₇–A₁₀) are AD subjects. Although it is possible to add more templates to the template pool, those additional templates can bring more computational costs. Here, we only select templates from AD and NC subjects, as these subjects can cover the entire distribution space using simple normalized mutual information as similarity measure.

Fig. 2.

Ten templates determined by the Affinity Propagation (AP) clustering algorithm.

To obtain multiple sets of features from multiple templates, we perform the following three steps: 1) a registration step to spatially normalize each individual brain image onto multiple templates, 2) a quantification step to obtain morphometric measurement of each brain image, and 3) a segmentation step to obtain a set of regions of interest (ROI) for computing regional features. Similar to the work [37], we utilize a mass-preserving shape transformation framework to capture morphometric patterns of each individual brain image in each of multiple templates.

To this end, for each tissue-segmented brain image (segmented into GM, WM and CSF tissues), we first nonlinearly register them onto K templates (K =10 in this study) separately, by using HAMMER [38], a high-dimensional elastic warping tool. Then, based on these K estimated deformation fields, for each brain tissue, we quantify its voxel-wise tissue density map [39] in each of the K template spaces to reflect the unique deformation behavior of a given brain image, with respect to each template. In this study, we only use gray matter (GM) density map for feature extraction and classification, since AD directly affects GM tissue densities and GM density maps are also widely used in literature [3], [13].

Typically, anatomical structures of multiple templates are often different from each other. Therefore, different templates can provide complementary information [17]–[19]. To efficiently extract the inherent structural information for each template, after registration and quantification steps, we group voxel-wise morphometric features into regional features using watershed segmentation algorithm [37]. This would lead to partitioning each of the templates into its own set of regions of interest (ROIs). To improve both discriminative power and robustness of volumetric features computed from each ROI, we refine each ROI by choosing its most discriminant voxels. Specifically, we first select the most relevant voxel according to the Pearson correlation between this voxel’s tissue density values and class labels across all the training subjects. Then, we iteratively include neighboring voxels until no increase for Pearson correlation, when adding new voxels. Such voxel selection process will lead to a voxel subset for a specific region. Then, the average tissue density value of those selected voxels is computed as feature representation for this ROI. Such voxel selection process helps eliminate irrelevant and noisy features, as confirmed by several previous studies [40], [41]. Finally, the top M (M = 1500 in this study) most discriminative ROI features are selected in each template space. We align each subject, regardless of its class label (e.g., AD or NC), onto the aforementioned K templates for feature extraction. As a result, each subject is represented by K sets of M-dimensional feature vectors. Based on this multi-template feature representation, we perform feature selection and classification, with details given below.

B. Feature Selection

Although we select the most representative regional features for each template space in the feature extraction step above, these features can still be redundant or irrelevant for subsequent classification tasks, since each subject is represented by multiple sets of features. To address this problem, we develop a novel relationship induced sparse (RIS) feature selection method under a multi-task learning framework [14], [42], by treating the classification in each template space as a specific task. We first briefly introduce general formulation for the conventional multi-task feature learning, and then derive our RIS feature selection model.

1) Multi-Task Feature Learning

In our study, we have K learning tasks corresponding to K templates. Denote ${\mathbf{X}}^k={[{\mathbf{x}}_1^k,\dots ,{\mathbf{x}}_n^k,\dots ,{\mathbf{x}}_N^k]}^T\in {ℝ}^{N\times d}$ as training data for the k-th learning task (corresponding to the k-th template) containing totally N subjects, where ${\mathbf{x}}_n^k\in {ℝ}^d$ represents a feature vector of the n-th subject in the k-th template space. Similarly, denote Y = [y₁, …, y_n, …, y_N]^T ∈ ℝ^N as the response vector for training data X^k, where y_n ∈ {−1, 1} is the class label (i.e., normal control or patient) for the n-th subject. Denote W = [w¹, …, w^k, …, w^K] ∈ ℝ^d×k as the weight matrix, where w^k ∈ ℝ^d parameterizes a linear discriminant function for the k-th task. Let w_i represent the i-th row of W. Then, the multi-task feature learning model is formulated as follows [14], [43], [44]:

$$\underset{\mathbf{W}}{min}{\displaystyle \sum _{k=1}^K\Vert \mathbf{Y}-{\mathbf{X}}^k{\mathbf{w}}^k{\Vert }_2^2+\lambda \Vert \mathbf{W}{\Vert }_{2,1}}.$$ (1)

The first term in (1) is the empirical loss on the training data. The second one is a group-sparsity regularizer to encourage the weight matrix W with many zero rows, where ${\Vert \mathbf{W}\Vert }_{2,1}={\displaystyle {\sum }_{i=1}^d{\Vert {\mathbf{w}}_i\Vert }_2}$ is the sum of the l₂-norm of the rows in matrix W. For feature selection purpose, only features corresponding to those rows with non-zero coefficients in W are selected, after solving (1). That is, the l_2,1-norm regularization term ensures only a small number of common features to be jointly selected across different tasks [45]. The parameter λ is a regularization parameter used to balance relative contributions of the two terms in (1). Particularly, a large λ leads to the selection of less number of features, while a small λ urges the algorithm to select more features.

2) Relationship Induced Sparse Feature Selection

It is worth noting that, due to anatomical differences across templates, different sets of features for each brain image generally come from different ROIs. Thus, the l_2,1-norm regularization in (1) is not appropriate for our case, since it jointly selects features across different tasks (i.e., templates). To encourage sparsity of the weight matrix W as well as selection of informative features corresponding to each template space, we propose the following multi-task sparse feature learning model:

$$\underset{\mathbf{W}}{min}{\displaystyle \sum _{k=1}^K\Vert \mathbf{Y}-{\mathbf{X}}^k{\mathbf{w}}^k{\Vert }_2^2}+\lambda \Vert \mathbf{W}{\Vert }_{1,1}$$ (2)

where ${\Vert \mathbf{W}\Vert }_{1,1}={\displaystyle {\sum }_{i=1}^d{\Vert \mathbf{w}\Vert }_1}$ is the sum of l₁-norm of the rows in matrix W. Different from the l_2,1-norm that encourages some rows of W to be zeros, the l_1,1-norm encourages some elements of W to be zeros, which helps select features specific to different tasks [46], [47].

In (1) and (2), a linear mapping function (i.e., f(x) = x^Tw) is learned to transform data in the original high-dimensional feature space to a one-dimensional label space. In all these models, the supervision is limited to only preserve the relationship between the samples and their corresponding class labels, while some other important structural information exists in the multi-template data. We find that preserving the following relationships between the subjects and the templates in the label space could enhance performance of the learned models: 1) the relationship among multiple templates (template-relationship), and 2) the relationship among different subjects (subject-relationship).

1. As illustrated in Fig. 3(a), a subject x_n is represented as ${\mathbf{x}}_n^{k_1}$ and ${\mathbf{x}}_n^{k_2}$ in the k₁-th and the k₂-th template spaces, respectively. After being mapped to the label space, they should also be close to each other (i.e., $f({\mathbf{x}}_n^{k_1})$ should be similar to $f({\mathbf{x}}_n^{k_2})$), since they represent the same subject.

2. Similarly, as shown in Fig. 3(b), if two subjects ${\mathbf{x}}_{n_1}^k$ and ${\mathbf{x}}_{n_2}^k$ in the same k-th template space are very similar, the distance between $f({\mathbf{x}}_{n_1}^k)$ and $f({\mathbf{x}}_{n_2}^k)$ should be also small, implying that the estimated labels of these two subjects are similar.

Fig. 3.

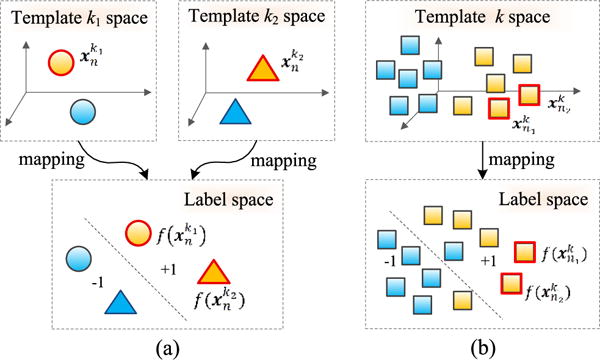
Illustration of structural information, conveyed by (a) relationship between features of two templates (i.e., features of the n-th subject in the k₁-th and the k₂-th template spaces, respectively), and (b) relationship between features of two subjects in the same template (i.e., features of the n₁-th subject and the n₂-th subject in the k-th template space). Here, yellow denotes positive training subjects, while blue denotes negative training subjects. Different shapes (circle, triangle, and square) denote samples in three different template spaces (i.e., the k₁-th template, the k₂-th template, and the k-th template).

Accordingly, in the following, we first introduce a novel template-relationship induced regularization term:

$${\displaystyle \sum _{n=1}^N{\displaystyle \sum _{k_1=1}^K{\displaystyle \sum _{k_2=1}^K{\left(f({\mathbf{x}}_n^{k_1})-f({\mathbf{x}}_n^{k_2})\right)}^2}}}={\displaystyle \sum _{n=1}^{N}tr({({\mathbf{B}}_n\mathbf{W})}^T{\mathbf{L}}_n({\mathbf{B}}_n\mathbf{W}))}$$ (3)

where tr(·) denotes the trace of a square matrix, ${\mathbf{B}}_n={[{\mathbf{x}}_n^1,\dots ,{\mathbf{x}}_n^k,\dots {\mathbf{x}}_n^K]}^T\in {ℝ}^{K\times d}$ represents multiple sets of features derived from K templates for the n-th subject, and L_n ∈ ℝ^K×K is a matrix with diagonal elements being K − 1 and all other elements being −1. By using (3), we can model the relationships among multiple templates explicitly.

Similarly, we propose the following subject-relationship induced regularization term:

$${\displaystyle \sum _{k=1}^K{\displaystyle \sum _{n_1=1}^N{\displaystyle \sum _{n_2=2}^N{S}_{n_1,n_2}^k{\left(f({\mathbf{x}}_{n_1}^k)-f({\mathbf{x}}_{n_2}^k)\right)}^2}}}={\displaystyle \sum _{k=1}^K{\left({\mathbf{X}}^k{\mathbf{w}}^k\right)}^T{\mathbf{L}}^k({\mathbf{X}}^k{\mathbf{w}}^k)}$$ (4)

where X^k is the data matrix in the k-th learning task (i.e., k-th template) as mentioned above, and ${\mathbf{S}}^k={\left\{S_{n_1,n_2}^k\right\}}_{n_1,n_2}^N=1\in {ℝ}^{N\times N}$ denotes a similarity matrix with elements defining the similarity among N training subjects in the k-th template space. Here, L^k = D^k − S^k represents the Laplacian matrix for task k, where D^k is a diagonal matrix with diagonal element $D_{n_1,n_1}^k={\displaystyle {\sum }_{n_2=1}^N{S}_{n_1,n_2}^k}$, and $S_{n_1,n_2}^k$ is defined as

$$S_{n_1,n_2}^k=\{\begin{array}{l}{e}^{-(\Vert {\mathbf{x}}_{n_1}^k-{\mathbf{x}}_{n_2}^k{\Vert }^2)/\sigma ,}\hfill \\ 0,\hfill \end{array}\text{if }{\mathbf{x}}_{n_1}^k\text{and }{\mathbf{x}}_{n_2}^k\text{are }q\text{neighbors otherwise}$$ (5)

where σ is a constant, and q = 3 in this study. It is evident that (4) aims to preserve the local neighboring structures of the original data during mapping, through which we can capture the relationships among subjects explicitly.

By incorporating two relationship induced regularization terms defined in (3) and (4) into (2), the objective function of our proposed relationship induced sparse (RIS) feature selection model can be written as follows:

$$\underset{\mathbf{W}}{min}{\displaystyle \sum _{k=1}^K\Vert \mathbf{Y}-{\mathbf{X}}^k{\mathbf{w}}^k{\Vert }_2^2+{\lambda }_1\Vert \mathbf{W}{\Vert }_{1,1}}+{\lambda }_2{\displaystyle \sum _{n=1}^{N}tr({({\mathbf{B}}_n\mathbf{W})}^T{\mathbf{L}}_n({\mathbf{B}}_n\mathbf{W}))}+{\lambda }_3{\displaystyle \sum _{k=1}^K{\left({\mathbf{X}}^k{\mathbf{w}}^k\right)}^T{\mathbf{L}}^k({\mathbf{X}}^k{\mathbf{w}}^k)}$$ (6)

where λ₁, λ₂, and λ₃ are positive constants used to balance the relative contribution of four terms in the proposed RIS model, and their values can be determined via inner cross-validation on the training data. In (6), the l_1,1-norm regularization term (the 2nd term) ensures only a small number of features to be selected, for each task. The template-relationship induced regularization term (the 3rd term) is used to capture the relationship among different templates, while the subject-relationship regularization term (the 4th term) is employed to preserve local neighboring structures of data in each template space. Note that, if we replace the square loss function with the logistic/hinge loss function in (6), the RIS model could be used directly as a classifier.

The objective function in (6) is convex but non-smooth, because of using the l_1,1-norm regularization term (i.e., ‖W‖_1,1) that is not smooth. This may decrease the optimization efficiency. Fortunately, the objective function, with such non-smooth terms, can be solved by a smooth approximation technique [14], [43], [48]. Specifically, we first adopt a smooth approximation technique to approximate (6) by a smoothed objective function, and then employ the Accelerated Proximal Gradient (APG) algorithm [49] to solve the smoothed objective function.

C. Ensemble Classification

To better take advantage of multiple sets of features generated from multiple templates, we further propose an ensemble classification approach. Particularly, after feature selection using our relationship induced sparse feature selection algorithm, we obtain K feature subsets corresponding to the K templates. Based on these selected features, we can then construct K classifiers separately, with each classifier corresponding to a specific template space. Here, we adopt a linear SVM to perform classification, since linear SVM has good generalization capability across different training data [12], [28], [50], [51]. Next, we adopt the majority voting strategy, a simple and effective classifier fusion method, to combine the outputs of K different SVM classifiers to make a final decision. In this way, majority voting from outputs of K classifiers determine the class label of a new testing subject.

D. Subjects and Experimental Setting

1) Subjects

To evaluate the efficacy of our proposed method, we perform experiments on T1-weighted MRI data in the ADNI database (http://adni.loni.usc.edu/). For diagnostic classification at baseline, we use a total of 459 subjects, randomly selected from those scanned with a 1.5T scanner. These subjects include (i) 97 AD subjects, if diagnosis was AD at baseline; (ii) 128 NC subjects, if diagnosis was normal at baseline; (iii) 117 stable MCI (sMCI) subjects, if diagnosis was MCI at all available time points (0–96 months); (iv) 117 progressive MCI (pMCI) subjects, if diagnosis was MCI at baseline but these subjects converted to AD after baseline within 24 months. The roster IDs of these subjects are listed in Tables S4–S7 in the supplementary material available in the supplementary files/multimedia tab. In Table I, the demographic information of these 459 subjects is provided.

TABLE I.

Demographic Information of 459 Studied Subjects From the ADNI Database

Diagnosis	# Subject	Age	Gender (M/F)	MMSE
AD	97	75.90±6.84	48/49	23.37±1.84
NC	128	76.11±5.10	63/65	29.13±0.96
pMCI	117	75.18±6.97	67/50	26.45±1.66
sMCI	117	75.09±7.65	79/38	27.42±1.78

Note: Values are denoted as mean ± deviation; MMSE means mini-mental state examination; M and F represent male and female, respectively.

2) Experimental Setting

The evaluation of our method is conducted on four different tasks, including 1) AD vs. NC classification, 2) pMCI vs. NC classification, 3) pMCI vs. sMCI classification, and 4) sMCI vs. NC classification. The last two problems are considered to be more difficult than the first two problems, but have received relatively less attention in previous studies. However, it is important to distinguish progressive MCI from stable MCI, and stable MCI from NCs, in order to achieve an early diagnosis and then possibly slow down the progression of MCI to AD via timely therapeutic interventions.

In this study, we adopt a 10-fold cross-validation strategy [28], [52], [53] to evaluate the performances of different methods. Specifically, all samples are partitioned into 10 subsets (with each subset having a roughly equal size), and each time samples in one subset are selected as the test data, while samples in all other nine subsets are used as the training data for performing feature selection and classifier construction. Such process is repeated ten times independently to avoid any bias introduced by the random partitioning of the original data in the cross-validation process. Finally, we measure the average values of corresponding classification results.

To better make use of multiple sets of features generated from multiple templates, we adopt the following two strategies: 1) the feature concatenation method, and 2) our proposed ensemble-based method. Specifically, in the feature concatenation method, features from multiple templates are simply concatenated into a long vector, and the corresponding SVM classifier is constructed using this feature vector. In the ensemble-based method, we treat each feature set individually, and construct multiple SVM classifiers based on these feature sets separately, followed by an ensemble strategy to combine the outputs of all SVMs for making a final decision.

In addition, we compare our RIS algorithm with four feature selection methods, i.e., Pearson correlation (Pearson), COMPARE method proposed in [37] that combines Pearson and SVM-RFE [44], statistical t-test method [54], and Lasso [55] that is widely used for sparse feature selection in neuroimaging analysis. Here, we use Pearson〈con〉, COMPARE〈con〉, t-test〈con〉, and Lasso〈con〉 to denote methods using four different feature selection algorithms (i.e., Pearson, COMPARE, t-test, and Lasso) and the feature concatenation strategy (i.e., 〈con〉), respectively. Similarly, we use Pearson〈ens〉, COMPARE〈ens〉, t-test〈ens〉, and Lasso〈ens〉 to denote methods using four different feature selection algorithms in each of the multiple template spaces during feature selection and then the proposed ensemble method (i.e., 〈ens〉) in the final classification step. For fair comparison, features selected by a specific feature selection algorithm are fed into an SVM classifier.

In our proposed RIS feature selection model, the regularization parameters (i.e., λ₁, λ₁ and λ₃) are, respectively, chosen from the range {10⁻¹⁰, 10⁻⁹,…,10⁰} through an inner cross-validation on the training data. That is, in each fold of 10-fold cross validation, we find the optimal parameters, via cross-validation on the training subset. Note that, no testing data is used in such cross-validation process. Similarly, the parameter for the l₁-norm regularizer in Lasso is selected from {10⁻¹⁰, 10⁻⁹,…,10⁰} through another inner cross-validation on the training data. The parameters σ and q in (5) are set empirically as the mean distance of samples in the training set and 3, respectively. For the t-test method, the p-value is chosen from {0.05, 0.08, 0.10, 0.12, 0.15} via inner cross-validation on the training data. For fair comparison, a linear SVM [31] with default parameter (i.e., C = 1) is used to perform classification. We evaluate performances of different methods via four criteria, i.e., classification accuracy (ACC), sensitivity (SEN), specificity (SPE), and the area under the receiver operating characteristic (ROC) curve (AUC). More specifically, accuracy measures the proportion of subjects that are correctly predicted, sensitivity denotes the proportion of patients that are correctly predicted, and specificity represents the proportion of NCs that are correctly predicted.

III. Results

A. Classification Results Using Single-Template Data

To demonstrate the variability of classification results, achieved by using different single templates even for the same classification task, we perform classification based on single-template data in the first group of experiments. Since our proposed method models the template-relationship that cannot be obtained in the single-template case, we only perform experiments using four feature selection algorithms, including Pearson, COMPARE, t-test and Lasso. In Fig. 4, we show the distribution of results achieved by the different methods using 10 single templates (shown in Fig. 2) in AD vs. NC classification and pMCI vs. sMCI classification, while results of pMCI vs. NC classification and sMCI vs. NC classification are given in Fig. S1 in the supplementary material available in the supplementary files/multimedia tab.

Fig. 4.

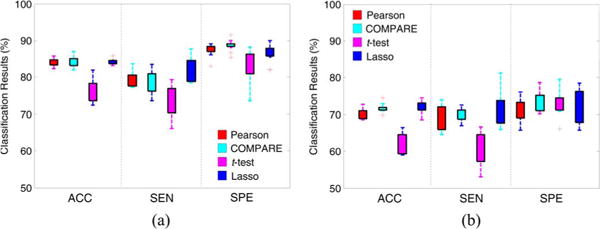
Distributions of classification accuracy (ACC), sensitivity (SEN) and specificity (SPE) achieved by four different single-template based methods in (a) AD vs. NC classification, and (b) pMCI vs. sMCI classification.

From Fig. 4, one can observe that the classification results using different single templates are very different, regardless of different feature selection methods. For example, in AD vs. NC classification, the sensitivities achieved by four methods vary significantly among 10 single templates. There are several reasons leading to different performances when using different templates. First, a certain template may have more representative anatomical structures for the entire population under study, compared with the other templates. In this way, there would be less noise in respective feature representations generated from this template. Second, the disease-related patterns generated from one template may be more discriminative than those derived from other templates.

B. Classification Results Using Multi-Template Data

In the second group of experiments, we perform AD/MCI classification by using multiple templates. Specifically, we compare our method with two categories of methods, i.e., 1) feature concatenation methods (i.e., Pearson〈con〉, COMPARE〈con〉, t-test〈con〉, and Lasso〈con〉), and 2) ensemble methods (i.e., Pearson〈ens〉, COMPARE〈ens〉, t-test〈ens〉, and Lasso〈ens〉). Following the work in [17], for Pearson〈con〉 and COMPARE〈con〉 methods, we first concatenate the regional features extracted from K (K in this study) templates as a 15000-dimensional feature vector. Then, the top m (m = {1,2,…,1500}) features are sequentially selected according to the Pearson correlation (with respect to class labels) for Pearson〈con〉 and according to Pearson + SVM-RFE for COMPARE〈con〉, and then the best classification results are reported. For t-test〈con〉 and Lasso〈con〉, we first concatenate K sets of features, and then use t-test and Lasso to perform feature selection, respectively. In ensemble-based methods, we first perform feature selection using respective algorithms in each of K template spaces, and then learn multiple SVM classifiers based on selected feature subsets in the respective K templates, followed by ensemble classification with majority voting strategy.

For comparison, we also report the averaged classification results of single-template based methods (including Pearson, COMPARE, t-test, and Lasso). The classification results of AD vs. NC and pMCI vs. sMCI are given in Table II, while those of pMCI vs. NC and sMCI vs. NC are shown in Tables S1 and S2 in the supplementary material available in the supplementary files/multimedia tab. We also perform a paired t-test on classification accuracies achieved by our method and by any comparison method, with the corresponding p-values reported in Table II, S1 and S2. In addition, we perform the paired McNemar’s test [56] on the classification accuracies of our proposed method and each compared method, as well as the paired Delong’s test [57] on the AUCs of our method and each compared method, to test whether our method performs statistically better than the compared methods. In the supplementary material available in the supplementary files/multimedia tab, we show the p-values of the McNemar’s test and the Delong’s test in Table S8 and Table S9, respectively. Furthermore, we plot the ROC curves achieved by ensemble-based methods in Fig. 5 and Fig. S2.

TABLE II.

Performance of AD vs. NC and pMCI vs. sMCI Classification With Multiple Templates

Method		AD vs. NC classification					pMCI vs. sMCI classification
		ACC (%)	SEN (%)	SPE (%)	AUC	p-value	ACC (%)	SEN (%)	SPE (%)	AUC	p-value
Single-template based method	Pearson	84.00	79.53	87.45	0.7692	–	68.49	67.80	69.10	0.6285	–
	COMPARE	84.18	75.33	89.17	0.7870	–	70.06	68.08	72.02	0.6356	–
	t-test	76.27	68.50	83.01	0.7496	–	61.99	60.43	73.11	0.6516	–
	Lasso	84.32	81.66	86.36	0.8402	–	72.06	72.04	72.02	0.7203	–
Multi-template based method	Pearson<con>	84.01	81.56	89.23	0.8191	<0.0001	72.78	74.62	70.91	0.7245	0.0014
	COMPARE<con>	84.93	80.11	87.03	0.7907	<0.0001	73.35	75.76	70.83	0.7405	0.0009
	t-test<con>	81.87	70.77	90.71	0.8178	<0.0001	62.16	61.59	75.07	0.6333	0.0003
	Lasso<con>	86.62	84.78	89.80	0.8729	<0.0001	71.49	76.06	66.67	0.7136	0.0008
	Pearson<ens>	85.59	82.44	89.93	0.9151	<0.0001	73.92	73.38	72.32	0.7629	0.0006
	COMPARE<ens>	86.61	85.44	89.23	0.9085	<0.0001	75.56	75.75	73.48	0.7658	0.0007
	t-test<ens>	84.31	74.56	89.70	0.8878	<0.0001	63.36	60.60	71.74	0.7161	0.0013
	Lasso<ens>	87.27	84.78	89.23	0.9279	0.0009	75.32	81.36	69.17	0.7602	0.0011
	Proposed	93.06	94.85	90.49	0.9579	–	79.25	87.92	75.54	0.8344	–

Fig. 5.

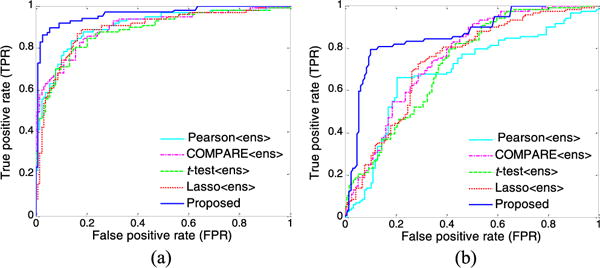
ROC curves achieved by five ensemble-based methods using multiple templates in (a) AD vs. NC classification, and (b) pMCI vs. sMCI classification.

From the results of AD vs. NC classification in Table II and Fig. 5(a), we can observe three main points. First, multi-template based methods generally achieve significantly better performance, compared to single-template based methods (i.e., Pearson, COMPARE, t-test, and Lasso). For example, the highest accuracy achieved by single-template based methods is only 84.32% (achieved by Lasso), which is noticeably lower than those of multi-template based methods. This demonstrates that, compared with the single-template case, the multi-template based methods can achieve better classification performance by taking advantage of richer feature representations for each subject. Second, by using multiple templates, methods that adopt our proposed ensemble classification strategy (i.e., Pearson〈ens〉, COMPARE〈ens〉, t-test〈ens〉, and Lasso〈ens〉) usually outperform their counterparts that simply employ the feature concatenation strategy (i.e., Pearson〈con〉, COMPARE〈con〉, t-test〈con〉, and Lasso〈con〉), in terms of all evaluation criteria. This implies that the feature concatenation strategy may not be a good choice to make use of multiple sets of features generated from multiple templates. Finally, our proposed method using RIS feature selection algorithm achieves consistently better results than that of other methods in terms of classification accuracy, sensitivity, and AUC. Specifically, our method achieves a classification accuracy of 93.06%, a sensitivity of 94.85%, and an AUC of 0.9579, while the second best accuracy is 87.27%, the second best sensitivity is 85.44%, and the second best AUC is 0.9279. Also, results in Table II show that our proposed method is significantly better than that of the compared methods, as demonstrated by very small p-values.

From the results of pMCI vs. sMCI classification shown in Table II and Fig. 5(b), we can observe again that the multi-template based methods usually outperform the single-template based methods. In addition, our method consistently achieves better performance than that of other multi-template based methods. In particular, our method achieves an AUC of 0.8344, while the best AUC achieved by the second best method (i.e., COMPARE〈ens〉) is only 0.7658.

C. Comparison With the State-of-the-Art Methods

We also compare the results achieved by our method with several recent state-of-the-art results reported in the literature using MRI data of ADNI subjects for AD/MCI classification, including five single-template based methods [13]–[16], [50] and five multi-template based methods [17], [18], [28]–[30]. Since very few works report sMCI vs. NC classification results, we only report the results of AD vs. NC and pMCI vs. sMCI in Tables III–IV, while those of pMCI vs. NC are given in Table S3 in the supplementary material available in the supplementary files/multimedia tab.

TABLE III.

Comparison With Existing Studies Using MRI Data of ADNI for AD vs. NC Classification

Method	Feature	Classifier	Subjects	Template	ACC (%)	SEN (%)	SPE (%)
Cuingnet et al. [15]	Voxel-direct-D GM	SVM	137 AD + 162 NC	Single	88.58	81.00	95.00
Zhang et al. [16]	93 ROI GM	SVM	51 AD + 52 NC	Single	86.20	86.00	86.30
Zhang et al. [14]	93 ROI GM	SVM	91 MCI + 50 NC	Single	84.80	–	–
Liu et al. [50]	Voxel-wise GM	SRC ensemble	198 AD + 229 NC	Single	90.80	86.32	94.76
Liu et al. [13]	Voxel-wise GM	SVM ensemble	198 AD + 229 NC	Single	92.00	91.00	93.00
Eskildsen et al. [58]	ROI-wise cortical thickness	LDA	194AD + 226NC	Single	84.50	79.40	88.90
Cho et al. [59]	Cortical thickness	PCA-LDA	128 AD + 160 NC	Single	–	82.00	93.00
Coupé et al. [60]	Hippocampus and entorhinal cortex volume and grading	QDA	60 AD + 60 NC	Single	90.00	88.00	92.00
Duchesne et al. [10]	Tensor-based morphometry	SVM	75 AD + 75 NC	Single	92.00	–	–
Koikkalainen et al. [18]	Tensor-based morphometry	Linear regression	88AD + 115NC	Multiple	86.00	81.00	91.00
Wolz et al. [30]	Four MR features	LDA	198 AD + 231 NC	Multiple	89.00	93.00	85.00
Min et al. [17]	Data-driven ROI GM	SVM	97AD + 128 NC	Multiple	91.64	88.56	93.85
Min et al. [29]	Data-driven ROI GM	SVM	97AD + 128NC	Multiple	90.69	87.56	93.01
Liu et al. [28]	Data-driven ROI GM	SVM ensemble	97AD + 128NC	Multiple	92.51	92.89	88.33
Proposed	Data-driven ROI GM	SVM ensemble	97AD + 128NC	Multiple	93.06	94.85	90.49

Note: SVM means Support Vector Machine; SRC denotes Sparse Regression Classifier; LDA represents Linear Discriminant Analysis; PCA-LDA denotes Principal Component Analysis-Linear Discriminant Analysis; QDA denotes Quadratic Discriminant Analysis.

TABLE IV.

Comparison With Existing Studies Using MRI Data of ADNI for pMCI vs. sMCI Classification.

Method	Feature	Classifier	Subjects	Template	ACC (%)	SEN (%)	SPE (%)
Cuingnet et al. [15]	Voxel-Stand-D GM	SVM	76 pMCI + 134 sMCI	Single	70.40	57.00	78.00
Zhang et al. [14]	ROI GM	SVM	43 pMCI + 48 sMCI	Single	62.00	56.60	60.20
Eskildsen et al. [58]	ROI-wise cortical thickness	LDA	61 pMCI + 134 sMCI	Single	66.70	59.00	70.20
Moradi et al. [61]	Voxel-wise GM	LDS	164 pMCI + 100 sMCI	Single	76.61	88.85	51.59
Cho et al. [59]	Cortical thickness	PCA-LDA	72 pMCI + 131 sMCI	Single	–	63.00	76.00
Gaser et al. [62]	Voxel-wise GM	RVR	133 pMCI + 62 sMCI	Single	75.00	–	–
Koikkalainen et al. [18]	Tensor-based morphometry	Linear regression	54 pMCI + 115 sMCI	Multiple	72.10	77.00	71.00
Wolz et al. [30]	Four MR features	LDA	167 pMCI + 238 sMCI	Multiple	68.00	67.00	69.00
Min et al. [17]	Data-driven ROI GM	SVM	117 pMCI + 117 sMCI	Multiple	72.41	72.12	72.58
Min et al. [29]	Data-driven ROI GM	SVM	117 pMCI + 117 sMCI	Multiple	73.69	76.44	70.76
Liu et al. [28]	Data-driven ROI GM	SVM ensemble	117 pMCI + 117 sMCI	Multiple	78.88	85.45	76.06
Proposed	Data-driven ROI GM	SVM ensemble	117 pMCI + 117 sMCI	Multiple	79.25	87.92	75.54

Note: SVM means Support Vector Machine; LDA represent Linear Discriminant Analysis; LDS means Low Density Separation; PCA-LDA denotes Principal Component Analysis-Linear Discriminant Analysis; RVR represents Relevance Vector Regression.

From Table III, we can have the following observations. First, in AD vs. NC classification, our proposed method is superior to the comparison methods in terms of both classification accuracy and sensitivity. Although researchers in [15] reported the highest specificity, their accuracy and sensitivity are relatively lower than those produced by our method. Second, among six multi-template based methods in AD vs. NC classification, our method achieves consistently better accuracy and sensitivity than methods in [18], [30] that use the averaged feature representation from multi-templates, slightly better in accuracy but much higher in sensitivity than methods used in [17], [29] that concatenate multiple sets of features from multiple templates, and comparable accuracy but higher sensitivity and specificity than the method in [28] that focuses on features from one template with side information provided by the other templates. It is worth noting that high sensitivity may be advantageous for confident AD diagnosis, which is potentially useful in clinical practice. Similar trend can be found in pMCI vs. sMCI classification from Table IV (i.e., our method usually outperforms the competing methods). It is worth noting that the classification accuracies in Table IV are not fully comparable, since the definition in those compared methods may be slightly different due to the use of different cut-off value (i.e., how many months MCI will covert to AD). For instance, the cut-off value for the pMCI definition in both this work and [58] is 24 months, while it is 18 months in [15].

D. Discussion

Several recent studies have demonstrated that multi-template based features contain complementary information for boosting performance of AD/MCI classification [14], [15], [17], [18], [29], [30]. However, the main disadvantage of these existing methods is that the structural information in multi-template data is seldom considered, which may lead to sub-optimal learning performance. For example, the relationships among multiple templates and among different subjects are important prior information, which can be used to further promote performance of AD/MCI classification. Accordingly, we proposed a novel feature selection method, aiming to preserve structural information of multi-template data conveyed by the relationships among templates and among subjects. As can be seen from Table II, the comparison methods that ignore such structural information often do not achieve as good results as our method. We also developed an ensemble classification method, where multiple classifiers, with respect to different template spaces, are combined, via majority voting. Experimental results show that methods using our proposed ensemble classification strategy usually outperform their counterparts with feature concatenation strategy. We now evaluate the influence of parameters and analyze the diversity of multiple classifiers in the proposed ensemble classification method.

1) Effects of Parameters

In our RIS feature selection model, there are three parameters to be tuned, i.e., λ₁, λ₂ and λ₃. In this sub-section, we evaluate the influence of parameters on the performance of our method. Specifically, we independently vary the values of λ₁, λ₂ and λ₃ in the range {10⁻¹⁰, 10⁻¹⁰,…, 10⁰}, and record the corresponding classification results achieved by our method, using different parameters in AD vs. NC classification. In Fig. 6, we show the classification accuracy as a function of two of these three parameters (i.e., λ₁, λ₂ and λ₃). Note that, to facilitate the observation, in Fig. 6, one parameter is fixed as 0.1, when varying two other parameters. From Fig. 6(a)–(c), we can clearly see that the performance of our method slightly fluctuates within a very small range with the increase of parameter values of λ₁, λ₂ and λ₃. In most cases, classification results are generally stable with respect to three parameters, demonstrating that our proposed RIS method is not particularly sensitive to the parameter values.

Fig. 6.

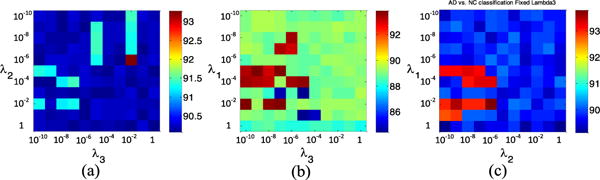
Accuracies of AD vs. NC classification with respect to different parameter values in the proposed RIS model. Note that, in (a)-(c), when two parameters vary, another parameter is fixed as 0.1, for convenience of display. (a) λ₁ = 0.1. (b) λ₂ = 0.1. (c) λ₃ = 0.1.

2) Diversity Analysis

As discussed earlier, in order to make use of multiple sets of features generated from multiple templates, we proposed an ensemble classification strategy. Here, we quantitatively measure the diversity and the mean classification error between any two different SVM classifiers, where each SVM is corresponding to a specific template space. Here, we use Kappa index to measure the diversity [63] of two classifiers. It is worth noting that small Kappa values indicate better diversity, and small mean classification errors imply better accuracies, achieved by a pair of classifiers. In Fig. 7, we plot averaged results among all pairs of classifiers, achieved by five ensemble-based methods (i.e., Pearson〈ens〉, COMPARE〈ens〉, t-test〈ens〉, Lasso〈ens〉, and the proposed method) in the four classification tasks (i.e., AD vs. NC, pMCI vs. NC, pMCI vs. sMCI, and sMCI vs. NC).

Fig. 7.

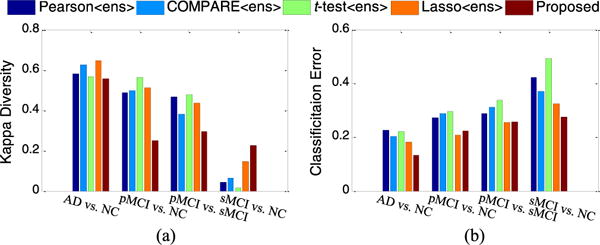
The diversities and mean classification errors achieved by five ensemble-based methods in four classification tasks.

From Fig. 7(a), one can see that our method achieves better diversity than the comparison methods in AD vs. NC, pMCI vs. NC, and pMCI vs. sMCI classification tasks. From Fig. 7(b), we can observe that our method usually obtains lower classification error, compared to other methods. It is worth noting that, although our method obtains slightly less diversity than other methods in sMCI vs. NC classification, it apparently achieves the lowest classification error. Recalling the results in Table II, our method was shown to outperform other ensemble-based methods (i.e., Pearson〈ens〉, COMPARE〈ens〉, t-test〈ens〉 and Lasso〈ens〉), which implies that our method achieves better trade-off between accuracy and diversity.

3) Limitations

There are several limitations that should be considered, in the current study. First, our method has high computational costs, because of the multiple templates used for image registration with HAMMER [38]. One possible solution is to parallelize the registration process by using multiple CPUs. Another solution is to replace the registration method (i.e., HAMMER) with another less computationally expensive technique (e.g., diffeomorphic demos [64]), which may speed up the registration process. Second, the proposed method requires feature representations, generated from different templates, to have the same dimensionality, as we use a feature selection method within the multi-task learning framework. Since there are anatomical differences among multiple templates, features generated from different templates may be of different dimensionality, which is not considered in our current method. Third, we lack consideration of spatial/anatomical correlation relationship among templates [17] in our current method. Actually, the anatomical correlation among templates can also be explored as prior information to further promote performance of the proposed RIS feature selection model, which is one of our future directions. Fourth, the proposed RIS model in (6) is simply used as a feature selection model. If the square loss function is replaced by the logistic (or hinge) loss function, RIS model can be also directly employed as a classification model. In addition, we only evaluate our method on the ADNI dataset. It is interesting to investigate the efficacy of the proposed method on other data sets, such as the Computer-Aided Diagnosis of Dementia (CADDementia) data set [65]. As one of our future work, we will perform such experiments to ensure thorough comparisons between our method and those competing approaches.

IV. Conclusion

In this paper, we proposed a relationship induced multi-template learning method for AD/MCI classification, which can make use of the underlying structure information of multi-template data. To this end, we first extracted multiple sets of feature representations from multiple selected templates, and then proposed a relationship induced sparse feature selection algorithm to reduce the dimensionality of the feature vectors in each template space, followed by an SVM classifier corresponding to each template. Then, we developed an ensemble classification strategy to combine the outputs of multiple SVMs to make a final classification decision. Experimental results on the ADNI database demonstrated that our method achieved significant performance improvement in multi-template based AD/MCI classification, compared with several state-of-the-art methods.