LRTV: MR Image Super-Resolution with Low-Rank and Total Variation Regularizations

Abstract

Image super-resolution (SR) aims to recover high-resolution images from their low-resolution counterparts for improving image analysis and visualization. Interpolation methods, widely used for this purpose, often result in images with blurred edges and blocking effects. More advanced methods such as total variation (TV) retain edge sharpness during image recovery. However, these methods only utilize information from local neighborhoods, neglecting useful information from remote voxels. In this paper, we propose a novel image SR method that integrates both local and global information for effective image recovery. This is achieved by, in addition to TV, low-rank regularization that enables utilization of information throughout the image. The optimization problem can be solved effectively via alternating direction method of multipliers (ADMM). Experiments on MR images of both adult and pediatric subjects demonstrate that the proposed method enhances the details in the recovered high-resolution images, and outperforms methods such as the nearest-neighbor interpolation, cubic interpolation, iterative back projection (IBP), non-local means (NLM), and TV-based up-sampling.

I. Introduction

High-resolution (HR) medical images provide rich structural details that are critical for accurate image post-processing and pathological assessment of bodily organs [1–10]. However, image resolution is limited by factors such as imaging hardware, signal to noise ratio (SNR), and time constraints. Image SNR is proportional to voxel size and the square root of the number of averages in the voxel. Reducing the voxel size from 2×2×2 mm³ to 1×1×1 mm³ will require 64 averages for similar SNR [11]. This requires significantly longer scanning time, which may not be practical clinically.

A possible alternative approach to this problem is image post-processing. For this, interpolation methods (nearest neighbor, linear, and spine) are generally employed due to their simplicity. However, as pointed out in [1], interpolation methods generally blur the sharp edges, introduce blocking artifacts in lines, and are unable to recover fine details. In view of this, we take a super-resolution (SR) approach for resolution enhancement of LR images [3]. Interpolation methods are not considered as SR methods since they do not consider the image degradation process (e.g., blurring, and down-sampling). Multi-frame SR algorithms reconstruct a HR image from multiple LR images [12, 13]. These LR images are typically acquired repeatedly with slightly shifted field of view (FOV). In this paper, we propose a single-frame SR algorithm that requires the acquisition of only one LR image. A number of methods have been proposed for single-image SR [3]. For example, iterative back-projection (IBP) was proposed to estimate the HR image by back projecting the difference between the LR image simulated based on the estimated HR image via imaging blur and the input LR image [14]. This process is repeated to minimize the energy of the difference. Non-local means (NLM) is a method proposed to take advantage of image self-similarity [15]. Specifically, the input LR image is first denoised and the similar patches are used to reconstruct to a HR image. A correction step is then applied to ensure that the down-sampled HR image is close to the denoised LR image. The reconstruction and correction steps are iterated in a multi-scale manner. In another work, NLM was employed to enhance the resolution of a single LR T2 image with the guidance from an HR T1 image [16].

Matrix completion algorithms have recently been shown to be effective in estimating missing values in a matrix from a small sample of known entries [17–19]. For instance, it has been applied to the famous Netflix problem where one needs to infer user preference for unrated movies based on only a small number of rated movies [20]. Matrix completion methods assume that the recovered matrix has low rank and then uses this property as a constraint or regularization to minimize the difference between the given incomplete matrix and the estimated matrix. Candes et al. proved that, low-rank matrices can be perfectly recovered from a small number of given entries under some conditions [18]. In image processing, one advantage of matrix completion is that the remote information from the whole image can be utilized in image recovery. Besides, matrix completion has been widely applied to image/video in-painting and decoding problems. However, low-rank regularization is limited when the matrix to be recovered contain rows or columns that are entirely missing. As shown in Fig. 1, although voxels occluded by the words “Low Rank” can be recovered very well, the voxels masked by white horizontal and vertical lines cannot be recovered. In this case, each missing row or column will be simply filled by an arbitrary combination of other known rows or columns to meet the low rank requirement. This precludes the application of low-rank regularization to SR problem where missing values for many rows and columns need to be recovered in the process of recovering a HR image from a LR image.

Fig. 1.

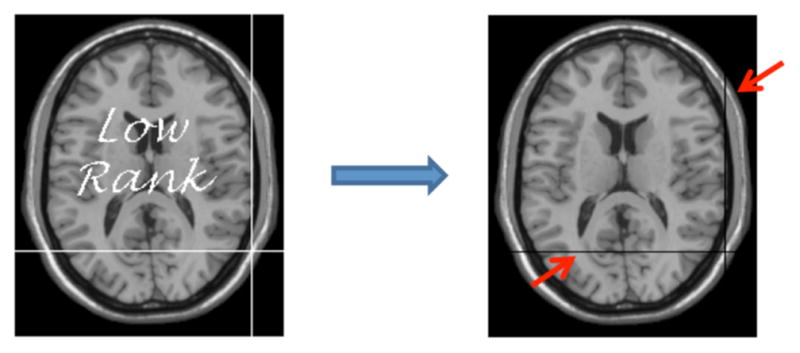
Recovering the missing values using low-rank matrix completion [14]. The red arrows mark the horizontal and vertical lines that the algorithm fails to recover.

The limitation of low-rank regularization in SR problem could be remedied by imposing the additional local spatial consistency. Although local information may not be useful in applications such as the Netflix problem, where different rows (e.g., users) can be considered independently, it is valuable in recovering images. One possible choice is total variation (TV) [21], defined as the integral of the absolute gradients of the image. Recently, TV has been applied to avoid the ringing and smearing caused by interpolation [22].

In this paper, we propose a novel low-rank total variation method, referred to as LRTV, for recovering a HR image from a LR image. Our method 1) explicitly models the blurring effects when an image is down-sampled, 2) combines both low-rank and TV regularizations for more effective image recovery, and 3) works for 3D or 4D images by a tensor formulation [19]. A preliminary version of this work was presented at a conference [23]. The work is significantly extended in this article with more methodological details, validations, and discussions. Experiments on MR images of both adults and pediatric subjects are conducted, and the proposed method is compared to various interpolation methods, as well as the NLM and TV-based up-sampling methods.

II. Method

We first describe how image degradation processes such as blurring and down-sampling effects are modeled. We then describe the solution for the inverse problem of recovering the HR image from the LR image, using low-rank and TV regularization.

A. Super-Resolution Image Reconstruction Framework

As illustrated in Fig. 2, the acquired image is affected by factors such as motion blur, field inhomogeneity, acquisition time, and noise.

Fig. 2.

Observation model in MR image acquisition process.

The observation model could be mathematically formulated as:

$$T=\mathit{DSX}+n$$ (1)

where T denotes the observed LR image, D is a down-sampling operator, S is a blurring operator, X is the HR image that we want to recover, and n represents the observation noise. In the case of single-image SR, the HR image can be estimated using this observation model by minimizing the following cost function:

$$\widehat{X}=\mathit{arg}{\mathit{min}}_X{\Vert \mathit{DSX}-T\Vert }^2$$ (2)

This is a data fidelity term for penalizing the difference between the degraded HR image X and the observed LR image T. Since this is an ill-posed inverse problem, regularization terms are added to stabilize the solution. The cost function is thus rewritten as:

$$\widehat{X}=\mathit{arg}{\text{min}}_X{\Vert \mathit{DSX}-T\Vert }^2+\lambda \Re (X)$$ (3)

where ℜ(X) is the regularization term often defined based on prior knowledge. The parameter λ is used to balance the contributions of the fidelity term and the regularization term.

B. Low-Rank Total-Variation (LRTV) Method

The proposed LRTV method is formulated as follows:

$$\widehat{X}=\mathit{arg}{\text{min}}_X{\Vert \mathit{DSX}-T\Vert }^2+{\lambda }_{\mathit{rank}}\mathit{Rank}(X)+{\lambda }_{tv}TV(X)$$ (4)

where the regularization can be separated into low-rank and total variation terms. λ_rank and λ_tv are the respective tuning parameters for those two terms.

1) Low-Rank Regularization

The rank of a matrix is a measure of nondegenerateness of the matrix, calculated by the maximum number of linearly independent rows or columns in the matrix. The low-rank property implies that some rows or columns in the matrix can be linearly represented by other rows or columns, indicating redundant information in the matrix. Low-rank prior can be used in matrix completion when only a subset of elements is known [18]. Since the rank of a matrix X is a nonconvex function of X, a common approach is to approximate it using the trace norm ||X||_tr, which leads to a convex optimization problem. Recently, Liu et al. extended the low-rank regularization to higher dimensional images and further referred to as tensor completion [19]. Basically, a N-dimensional image X can be seen as a high-order tensor. Since it is an NP-hard problem to compute the rank of a high-order tensor¹, the rank is then approximated as the combination of trace norms of all matrices unfolded along each dimension:

$$\mathit{Rank}(X)={\mathrm{\sum }}_{i=1}^N{\alpha }_i{\Vert X_{(i)}\Vert }_{tr}$$ (5)

where N is the number of image dimensionality. In this study, we use 3D MR images and thus N = 3. ${\{{\alpha }_i\}}_{i=1}^N$ are parameters satisfying α_i ≥ 0 and ${\mathrm{\sum }}_{i=1}^N{\alpha }_i=1$. X_(i) is the unfolded X along the i-th dimension: unfold_i(X) = X_(i). For example, a 3D image with size of U×V×W can be unfolded into three 2D matrices, with sizes of U×(V×W), V×(W×U), and W×(U×V), respectively. ||X_(i)||_tr is the trace norm of the matric X_(i).

2) Total-Variation Regularization

Total variation was proposed as a regularization approach to remove noise and handle proper edges in images [21]. It is defined as the integral of the absolute gradients of an image: TV(X) = ∫|∇X|dxdydz. Minimizing TV will enforce local spatial consistency in image recovery, remove noise, and preserve edges.

C. LRTV Optimization

We use the alternating direction method of multipliers (ADMM) algorithm to solve the cost function in Eq. (4). ADMM is proven to be efficient for solving optimization problems with multiple non-smooth terms in the cost function [24]. First, we introduce N redundant variables ${\{M_i\}}_{i=1}^N$ to simulate X in each dimension i, by requiring that the unfolded X along the i-th dimension X_(i) should be equal to the unfolded M_i along this dimension M_i(i) The new cost function is as follows:

$${\mathit{min}}_{X,{\{M_i\}}_{i=1}^N}{\Vert \mathit{DSX}-T\Vert }^2+{\lambda }_{\mathit{rank}}{\mathrm{\sum }}_{i=1}^N{\alpha }_i{\Vert M_{i(i)}\Vert }_{tr}+{\lambda }_{tv}TV(X),\text{subject}\text{to}{X}_{(i)}=M_{i(i)},i=1,\dots ,N$$ (6)

Algorithm 1.

Low-Rank Total Variation (LRTV) for MR Image Super-Resolution

Input: Low-resolution image T;

Output: Reconstructed high-resolution image X;

Initialize: X = upsample (T)a, Mi = 0, Yi = 0, i = 1,2,3

Repeat

1. Update X based on Eq. (9);

2. Update M based on Eq. (11);

3. Update Y based on Eq. (12);

4. Until difference in the cost function (Eq. (8)) is less than ε;

End

^aThe upsample(·) operator is implemented by nearest-neighbor interpolation.

Based on ADMM in [24], the augmented Lagrangian of the above cost function is written in below, where ${\{U_i\}}_{i=1}^N$ are Lagrangian parameters:

$${\mathit{min}}_{X,{\{M_i\}}_{i=1}^N,{\{Y_i\}}_{i=1}^N}{\Vert \mathit{DSX}-T\Vert }^2+{\lambda }_{\mathit{rank}}{\mathrm{\sum }}_{i=1}^N{\alpha }_i{\Vert M_{i(i)}\Vert }_{tr}+{\lambda }_{tv}TV(X)+{\mathrm{\sum }}_{i=1}^N{U}_i(X_{(i)}-M_{i(i)})+{\mathrm{\sum }}_{i=1}^N\frac{\rho }{2}{\Vert X-M_i\Vert }^2$$ (7)

We further Set Y_i = (1/ρ)U_i, and combine the two linear and quadratic terms for simplicity:

$${\mathit{min}}_{X,{\{M_i\}}_{i=1}^N,{\{Y_i\}}_{i=1}^N}{\Vert \mathit{DSX}-T\Vert }^2+{\lambda }_{\mathit{rank}}{\mathrm{\sum }}_{i=1}^N{\alpha }_i{\Vert M_{i(i)}\Vert }_{tr}+{\lambda }_{tv}TV(X)+{\mathrm{\sum }}_{i=1}^N\frac{\rho }{2}({\Vert X-M_i+Y_i\Vert }^2-{\Vert Y_i\Vert }^2)$$ (8)

According to ADMM [24], we break Eq. (8) into three subproblems below that could be solved by iteratively updating the variables. In the below, k denotes the current iteration step.

Subproblem 1

Update X^(k+1) by minimizing:

$$\mathit{arg}{\mathit{min}}_X{\Vert \mathit{DSX}-T\Vert }^2+{\lambda }_{tv}TV(X)+{\mathrm{\sum }}_{i=1}^N\frac{\rho }{2}{\Vert X-M_i^{(k)}+Y_i^{(k)}\Vert }^2$$ (9)

This subproblem can be solved by gradient descent, where the gradient of TV term is obtained from the associated Euler-Lagrange equation [22].

Subproblem 2

Update ${\left\{M_i^{(k+1)}\right\}}_{i=1}^N$ by minimizing:

$$\underset{{\{M_i\}}_{i=1}^N}{\mathit{min}}{\lambda }_{\mathit{rank}}{\sum }_{i=1}^N{\alpha }_i{\Vert M_{i(i)}\Vert }_{tr}+{\sum }_{i=1}^N\frac{\rho }{2}{\Vert X^{(k+1)}-M_i+Y_i^{(k)}\Vert }^2$$ (10)

which can be solved using a close-form solution according to [17]:

$$M_i={\mathit{fold}}_i\left[{\mathit{SVT}}_{{\lambda }_{\mathit{rank}}{\alpha }_i/\rho }\left(X_{(i)}^{(k+1)}+Y_{i(i)}^{(k)}\right)\right]$$ (11)

where fold_i (·)is the inverse operator of unfold_i (·) i.e., fold_i (M_i(i)) = M_i SVT(·) is the Singular Value Thresholding operator [17] using λ_rankα_i/ρ as the shrinkage parameter.

Subproblem 3

Update ${\left\{{\mathrm{Y}}_{\mathrm{i}}^{(\mathrm{k}+1)}\right\}}_{\mathrm{i}=1}^{\mathrm{N}}$ by:

$$Y_i^{(k+1)}=Y_i^{(k)}+\left(X^{(k+1)}-M_i^{(k+1)}\right)$$ (12)

III. Experimental Results

A. Low-Rank Approximation for Brain Images

We first evaluated whether brain images can be sufficiently characterized using their low-rank approximation. We selected a representative 2D axial slice from the T1 MR phantom in Brainweb², which has a size of 181×181 with in-plane resolution of 1 mm (Fig. 3). We then performed singular value decomposition (SVD) on this image and obtain 174 non-zero singular values. As shown in Fig. 3, singular values decrease dramatically, with most values being close to zero. Next, we remove the small singular values and use the top 30, 60, 90, and 120 singular values to reconstruct the image. Note that the number of used singular values equals to the rank of the recovered image, implying that the recovered image is a low-rank approximation of the original image. The reconstructed images are shown in Fig. 3 for visual inspection and the difference maps between original and reconstructed images are also provided. Signal-to-noise ratio (SNR) in decibels (dB) is used to evaluate the quality of reconstruction: SNR = 20 * log10(||f||/||f − g||), where f is the original HR image and g is the recovered HR image.

Fig. 3.

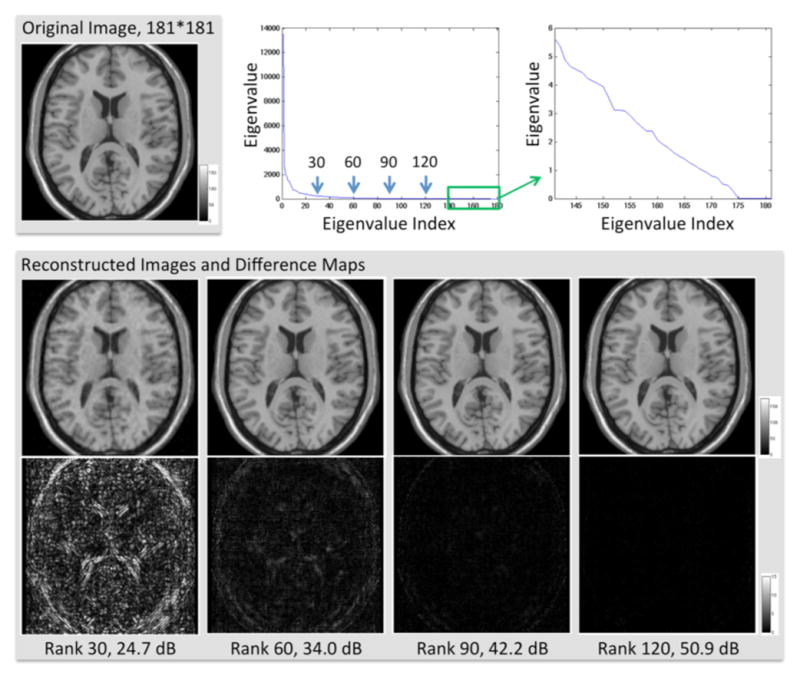
Low-rank approximations of brain images. Top row shows the original image, singular-value plot, and zoomed singular-value plot of indices from 141 to 181. Bottom row shows the four reconstructed images and their differences with the original image by using top 30, 60, 90, and 120 singular values, respectively.

The results show that, by using the top 60 singular values, the reconstructed image has high SNR (34.0db), although small edge information in the brain boundary is lost. When using the top 90 or 120 singular values (out of 174), the resulting image does not show visual differences with respect to the original image. For the 3D Brainweb image with size 181×217×181, it has three ranks for its three unfolded matrices that are less than its longest image size 217. These ranks are relatively low in comparison to the total number of elements, suggesting brain images could be represented using their low-rank approximations with a relatively high SNR.

B. Experimental Settings

We applied our method to a set of down-sampled and blurred 3D brain images and evaluated whether our method can successfully recover the original high-resolution images. To do that, we use HR images as ground truth, and simulate LR images as shown in Fig. 4. Blurring was implemented using a Gaussian kernel with a standard deviation of 1 voxel. The blurred image was then down-sampled by averaging every 8 voxels (to simulate the partial volume effect), resulting in half of the original resolution. The quality of reconstruction of all methods from the input LR images was evaluated by comparing with their corresponding original HR images.

Fig. 4.

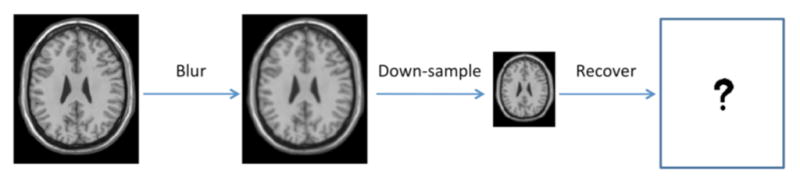
Simulation of low-resolution image from high-resolution image.

A number of comparison methods were also employed, including nearest-neighbor interpolation (NN), spline interpolation (Spline), IBP based up-sampling [14], NLM based up-sampling [15], and TV based up-sampling [22]. The estimated HR images from all methods were compared with the original HR image for accuracy of image recovery by using SNR. Note that, for NLM, we used the implementation made available by the authors³. TV-based up-sampling is realized by setting λ_rank = 0 and ρ = 0 in the proposed method and solving only the subproblem 1. Other methods were implemented by in-house tools.

Parameters were optimized based on a small dataset, consisting of 5 adult and 5 pediatric images as described in the Real Data Evaluation section. In particular, ${\{{\alpha }_{\mathrm{i}}\}}_{\mathrm{i}=1}^3$ are weights to combine unfolded matrices along each spatial dimension in rank computation. All dimensions are assumed to be equally important, i.e., α₁ = α₂ = α₃ = 1/3. The difference between iterations was measured by ||X^k − X^k−1||/||T||, and the program was stopped when this difference is less than ε = 1e – 5 Since TV is a major component of the proposed method, we first optimized TV by setting λ_TV from a group of candidate values (Fig. 5). We thus chose λ_TV = 0.01. Then, we optimized the proposed method by employing the same λ_TV while setting λ_rank from a wide range of candidate values (Fig. 5). We chose the rank regularization as λ_rank = 0.01. As for the input arguments, the blurring kernel (such as Gaussian distribution with 1 voxel standard deviation) was used in IBP, TV, and the proposed method. On the other hand, the default parameters in NLM implementation were used [15]. Both NN and Spline do not have any free parameters that require tuning.

Fig. 5.

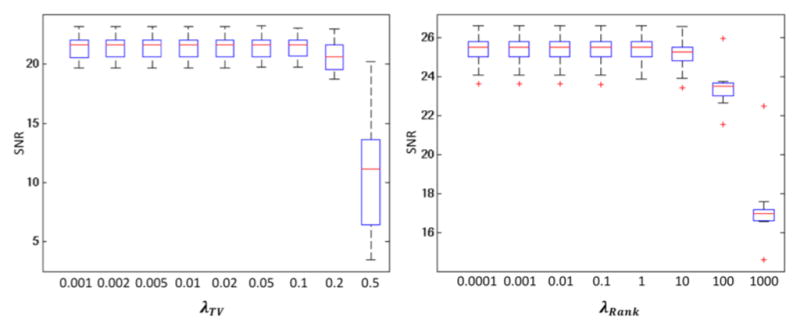
Parameter optimization based on ten images. SNR was used to evaluate the reconstruction performance.

We evaluate the performance of the proposed and comparison methods by comparing the recovered HR images with the original HR image. Besides SNR, we also employ another image quality measurement named Structural Similarity Index (SSIM), which is considered to be correlated with the quality perception of the human visual system (HVS) [25]. SSIM has been used in many image SR studies [15, 26–28]. SSIM is defined as:

$$\mathit{SSIM}(f,g)=(2{\mu }_f{\mu }_g+c_1)(2{\sigma }_{fg}+c_2)/\left(({\mu }_f^2+{\mu }_g^2+c_1)({\sigma }_f^2+{\sigma }_g^2+c_1)\right),$$

where μ_f and μ_g are the mean values respectively in the original HR image g and recovered image g, ${\sigma }_f^2$ and ${\sigma }_g^2$ are the variances, σ_fg is the covariance of two images, c₁ = (k₁L)² and c₂ = (k₂L)² with k₁ = 0.01 and k₂ = 0.03, and L is the dynamic range of voxel values [25]. SSIM ranges from 0 to 1, and 1 means perfect recovery.

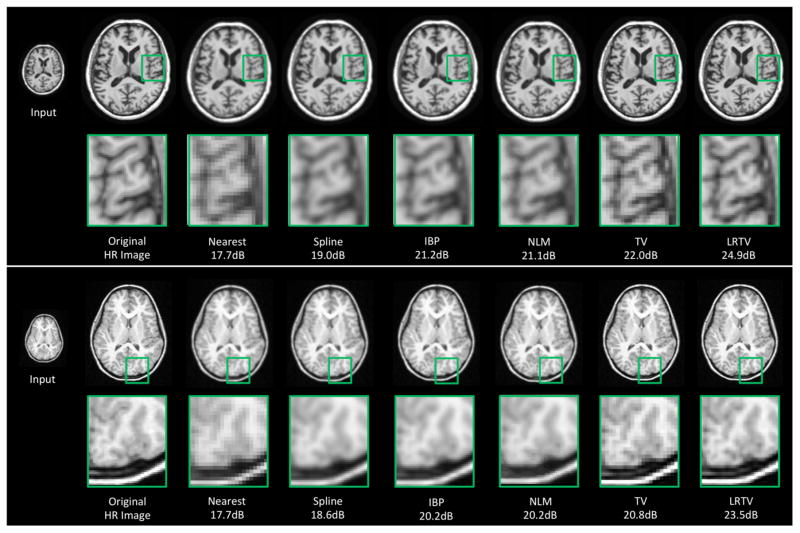
C. Phantom Data Evaluation

We employed the T1 MR phantom from Brainweb to evaluate the recovery performance of the proposed and comparison methods in cases of no noise and with noise. The phantom has image size of 181×217×181 and spatial resolution of 1×1×1 mm³. We downloaded images both without noise and with noise at different levels of 1%, 3%, 5%, 7%, and 9% of the maximum intensity. The noise in the phantom images has Rayleigh statistics in the background and Rician statistics in the signal regions. For our experiment, we generated images with 2×2×2 mm³ resolution using the above-mentioned LR image simulation pipeline (Fig. 4), and upsample it again to 1 mm isotropic resolution using the proposed and comparison methods, respectively.

Fig. 6 demonstrates the results when using noisy data at level of 3% as input image. A typical slice is shown for each of coronal, sagittal, and axial views, and the frontal region in sagittal view is zoomed up for better visual inspection. Compared to the original HR image, results of NN, Spline, IBP, and NLM appear blurry. TV provides better image reconstruction while the proposed method shows more fine details. Fig. 7 shows the SNR and SSIM measurements for all methods while changing the noise level from no noise to 9% noise level. The proposed method outperforms all other comparison methods in all noise levels for both SNR and SSIM. Another observation is that, the SNR improvement of the proposed method over other methods generally reduces when noise level increases, while the SSIM improvement maintains a similar level when the noise level increases.

Fig. 6.

Illustration of upsampling results for simulated data. LR data with 2×2×2 mm³ resolution was upsampled to 1×1×1 mm³. A typical slice for each of coronal, sagittal, and axial views is shown, and a zoom-up of frontal region in sagittal view is also provided.

Fig. 7.

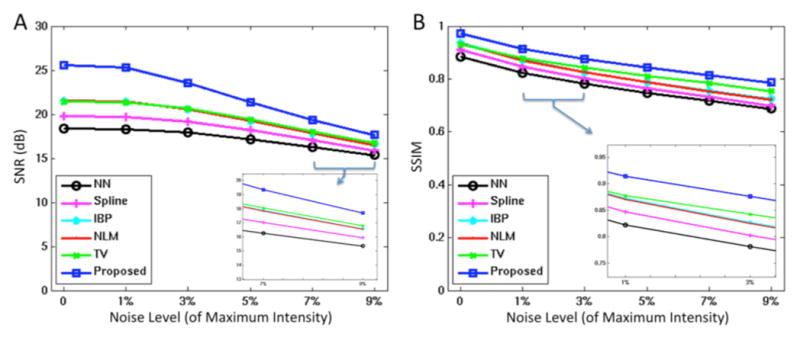
Results of upsampling on simulate data with different noise levels. (A) shows the SNR result, and (B) shows the SSIM result.

D. Real Data Evaluation

We further evaluated the proposed method on two publicly available datasets. First, we randomly selected 45 adult subjects from ADNI⁴, with 15 from Alzheimer’s disease (AD), 15 from mild cognitive impairment (MCI), and 15 from normal controls (NC). Their ages were 75±8 years old at MRI scan. T1 MR images were acquired with 166 sagittal slices at the resolution of 0.95×0.95×1.2 mm³. Second, we also randomly selected 45 pediatric subjects from NDAR (http://ndar.nih.gov/), with age of 11±3 years old at MRI scan. T1 MR images were acquired with 124 sagittal slices at the resolution of 0.94×0.94×1.3 mm³.

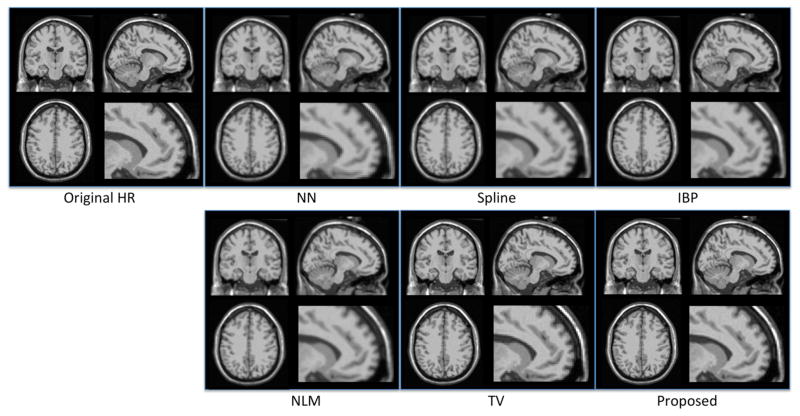
Fig. 8 shows the representative image SR results of an adult scan (upper panel) and a pediatric scan (lower panel). From left to right, the first row of each panel shows the input image, original HR image, the results of NN, Spline, IBP, NLM, TV, and the proposed LRTV method. The close-up views of selected regions are also shown for better visualization. It can be observed that the results of NN and Spline interpolation methods show severe blurring artifacts. The contrast is enhanced in the results of IBP, NLM, and TV up-sampling methods, while the proposed LRTV method best preserves edges and achieves the highest SNR values.

Fig. 8.

Results for upsampling an adult image (upper panel) and a pediatric image (lower panel) with different methods. In each panel, the first row shows the input image and the results by various methods, while the second row shows the close-up views of selected regions in the first row.

Quantitative results on the images of 45 adults and 45 pediatric subjects are shown in Fig. 9. Note that the original images were used as ground truth and the input was LR image simulated following the pipeline of Fig. 4. The proposed method significantly outperforms all comparison methods (p<0.01 using two-sample t-tests). Results on adult subjects demonstrate less variance and higher accuracy than those on pediatric subjects, which may be because the image quality is higher in the matured brain and also clearer gyri/sulci patterns appear in the adult images. No significant difference was found between the adult subjects of AD, MCI, and NC, as shown in Fig. 10.

Fig. 9.

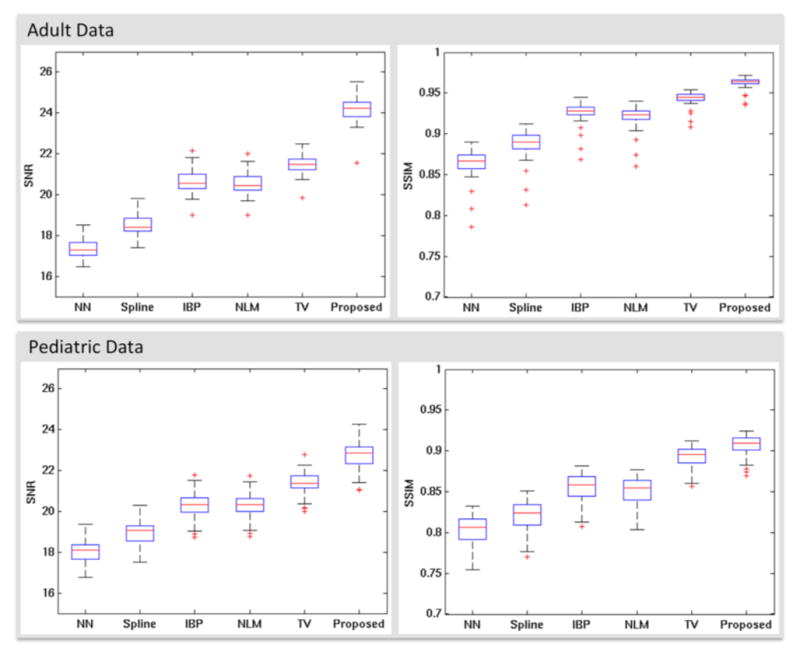
Boxplot of SNR and SSIM results for recovering adult data and pediatric data using different methods. The proposed LRTV method significantly outperforms all other comparison methods (p<0.01 using two-sample t-tests).

Fig. 10.

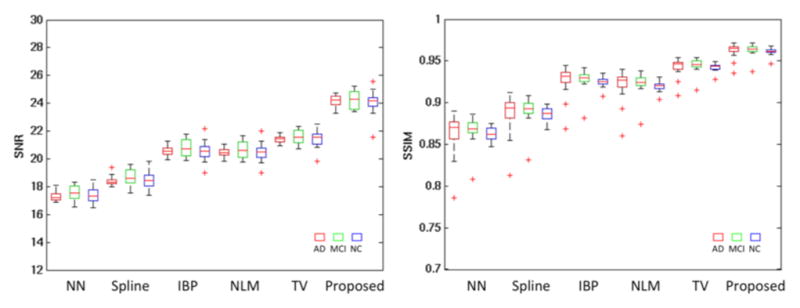
Boxplot of SNR and SSIM results for recovering adult data in groups of AD, MCI, and NC.

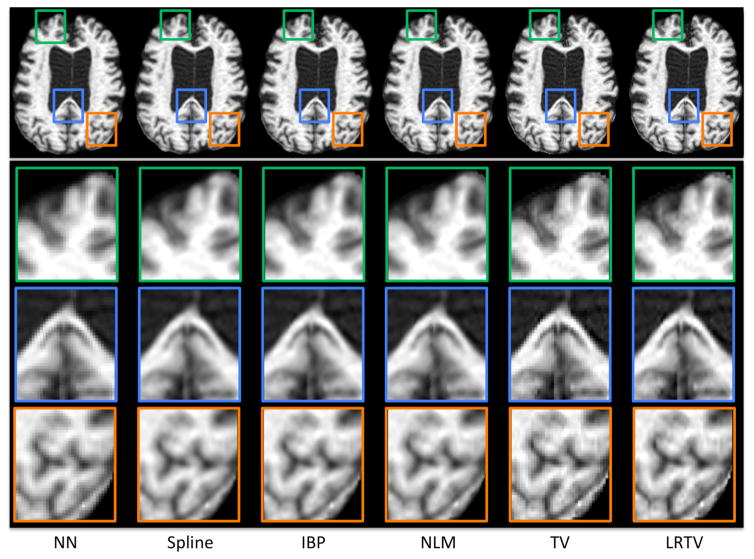
In addition, we applied our method directly to images with typical imaging resolution. Fig. 11 shows the results of a typical AD subject for visual inspection, along with the close-up views of selected representative regions. As it can be observed, the proposed method recovers fine details and also preserves image edges.

Fig. 11.

Upsampling of an image from a typical AD subject. The resolution was thus increased from 0.95×0.95×1.2 mm³ to 0.475×0.475×0.6 mm³. The first row shows the reconstructed results and other rows show the close-up views of the regions selected from the first row.

E. Computational Time

All programs were run in Linux environment on a standard PC using a single thread of an Inter® Xeon® CPU (E5630 1.6 GHz). Interpolation methods are computationally efficient as it takes around 2 seconds for NN and 10 seconds for Spline for one 3D image. For the up-sampling methods, IBP takes 1 min, NLM takes 16 mins, TV takes 5 mins, and the proposed method takes about 30 mins.

IV. Discussion

We have presented a novel super-resolution method for recovering high-resolution image from a single low-resolution image. For the first time, we show that combining low-rank and total-variation regularizations is a viable solution to the SR problem. This combination brings together global and local information for effective recovery of the high-dimensional image. Experimental results indicate that the proposed method is able to remedy the partial volume effect and recover the fine brain structure details from both adult and pediatric images. Quantitative comparisons show that the proposed method outperforms other popular methods such as the interpolation methods based on NN and Spline, and the up-sampling methods based on IBP, NLM, and TV.

The proposed method is computationally expensive compared with other methods. The major reason is that the program spends most of the time solving TV, which is implemented using gradient decent [22] in MATLAB. In future work, we will implement a faster TV solver, such as [29], and also accelerate the program using C++. On the other hand, we’d like to clarify that our main purpose is to show that the TV-based MR image reconstruction can be improved by combining low-rank regularization. When a better TV solver is available, the performance of the proposed method could also be improved.

The proposed method is mainly developed for single-image SR. In the future, we will extend the proposed method to use multiple LR images [12, 13], training datasets [30], and also for more applications such as 4D image recovery in functional MRI or diffusion MRI. The code for the proposed method will be released at our website⁵.