State-Space Analysis of Granger-Geweke Causality Measures with Application to fMRI

Abstract

The recent interest in the dynamics of networks and the advent, across a range of applications, of measuring modalities that operate on different temporal scales have put the spotlight on some significant gaps in the theory of multivariate time series. Fundamental to the description of network dynamics is the direction of interaction between nodes, accompanied by a measure of the strength of such interactions. Granger causality and its associated frequency domain strength measures (GEMs) (due to Geweke) provide a framework for the formulation and analysis of these issues. In pursuing this setup, three significant unresolved issues emerge. First, computing GEMs involves computing submodels of vector time series models, for which reliable methods do not exist. Second, the impact of filtering on GEMs has never been definitively established. Third, the impact of downsampling on GEMs has never been established. In this work, using state-space methods, we resolve all these issues and illustrate the results with some simulations. Our analysis is motivated by some problems in (fMRI) brain imaging, to which we apply it, but it is of general applicability.

1 Introduction

Following the operational development of the notion of (temporal) causality by Granger (1969) and Sims (1972), Granger causality (GC) analysis has become an important part of time series and econometric testing and inference (Hamilton, 1994). It has also been applied in the biosciences (Kaminski & Blinowska, 1991; Bernasconi & Konig, 1999; Ding, Bressler, Yang, & Liang, 2000), climatology (global warming; Suna & Wang, 1996; Kaufmann & Stern, 1997; Triacca, 2005), and, most recently, functional magnetic resonance imaging (fMRI). This last application has stimulated this letter.

Since its introduction into fMRI (Goebel, 2003; Valdes-Sosa, 2004; Roebroeck, Formisano, & Goebel, 2005; Yamashita, Sadato, Okada, & Ozaki, 2005) GC has become the subject of an intense debate: (see Valdes-Sosa, Roebroeck, Daunizeau, & Friston, 2011; Roebroeck, Formisano, & Goebel, 2011) and associated commentary. There are two main issues in that debate that occur more widely in dynamic networks. First is the impact of downsampling on GC. In the fMRI neuroimaging application, causal processes may operate on a timescale on the order of tens of milliseconds, whereas the recorded signals are typically available only on a 1 second timescale, although sampling up to a 100 ms rate is now becoming possible (Feinberg & Yacoub, 2012). So it is natural to wonder if GC analysis on a slower timescale can reveal GC structure (GCS) on a faster timescale. Second is the impact of filtering on GC due to the hemodynamic response function, which relates neural activity to the recorded fMRI signal. Since intuitively GC will be sensitive to time delay, the variability of the hemodynamic response function (HRF), particularly spatially varying delay (called time to onset in the fMRI literature) and time to peak (confusingly sometimes called delay in the fMRI literature) has been suggested as a potential source of problems (Deshpande, Sathian, & Hu, 2010; Handwerker, Gonzalez-Castillo, D’Esposito, & Bandettini, 2012). A referee has, however, pointed out that following David et al. (2008), deconvolution (Glover, 1999) has gained favor (Havlicek, Friston, Jan, Brazdil, & Calhoun, 2011) as a potential means of dealing with this.

An important advance in GC theory and tools was made by Geweke (1982), who provided measures of the strength of causality or influence of one time series on another (henceforth called GEM, for Geweke causality measure), including frequency domain decompositions of them. Subsequently it was pointed out that the GEMs are measures of directional mutual information (Rissannen & Wax, 1987). The GEMs were extended to conditional causality in Geweke (1984). However, GEMs have not found as wide an application as they should have, partly because of some technical difficulties in calculating them, which are discussed further below. But GEMs (and their frequency domain versions) are precisely the tool needed to pursue both GC downsampling and filtering questions.

In the econometric literature, it was appreciated early that downsampling, especially in the presence of aggregation, could cause problems. This was implicit in the work of Sims (1971) and mentioned also in the work of Christiano and Eichenbaum (1987), who gave an example of contradictory causal analysis based on monthly versus quarterly data, and also discussed in Marcet (1991). But precise general conditions under which problems do and do not arise have never been given. We do so in this letter.

Some of the econometric discussion has been framed in terms of sampling of continuous time models (Sims, 1971; Marcet, 1991; Christiano & Eichenbaum, 1987). And authors such as Sims (1971) have suggested that models are best formulated initially in continuous time. While this is a view that I have long shared (and related to the modeling approach advocated by Middleton and Goodwin (1990), we deal with only discrete time models here. To cast our development in terms of continuous time models would require a considerable development of its own without changing our basic message.

The issue at stake, in its simplest form, is the following. Suppose that a pair of (possibly vector) processes exhibit a unidirectional GC relation (a influences b, but b does not influence a), but suppose measurement time series are available only at a slower timescale or as filtered time series or both. Then two questions arise. The first, which we call the forward question, is this: When is the unidirectional GC relation preserved? The second, which we call the reverse question, is harder. Suppose the measurement time series exhibit a unidirectional GC relation. Does that mean the underlying unfiltered faster timescale processes do? The latter question is the more important and so far has received no theoretical attention. The more general form of this issue is to what extent the GC structure (GCS) between two time series is distorted by downsampling and or filtering or both.

In order to resolve these issues, we need to develop some theory and some computational and modeling tools. First, to compute GEMs, one needs to be able to find submodels from a larger model (i.e., one having more time series). Thus, to compute the GEMs between time series x_t, y_t, Geweke (1982, 1984) attempted to avoid this by fitting submodels separately to x_t to y_t and then also fitting a joint model to x_t, y_t. Unfortunately this can generate negative values for some of the frequency domain GEMs (Chen, Bressler, & Ding, 2006). Properly computing submodels will resolve this problem, and previous work has not accomplished this (we discuss the attempts in Dufour & Taamouti, 2010, and Chen et al., 2006, below).

Second, one needs to be able to compute how models transform when they are downsampled. This has been done only in special cases (Pandit & Wu, 1983) or by methods that are not computationally realistic. We provide computationally reliable, state-space-based methods for doing this here.

Third, we need to study the effect of downsampling and filtering on GEMs. We will show how to use the newly developed tools to do this.

To sum up, we can say that previous discussions, including those above, as well as Geweke (1978), Telser (1967), Sims (1971), and Marcet (1991), fail to provide general algorithms for finding submodels or models induced by downsampling. Indeed both these problems have remained open problems in multivariate time series in their own right for several decades, and we resolve them here. Further, there does not seem to have been any theoretical discussion of the effect of filtering on GEMs, and we resolve that here also. To do that, it turns out that state-space models provide the proper framework.

Throughout this work, we deal with the dynamic interaction between two vector time series. It is well known in econometrics that if there is a third vector time series involved in the dynamics but not accounted for, then spurious causality can occur for reasons that have nothing to do with downsampling, a situation discussed by Hsiao (1982) and Geweke (1984). Other causes of spurious causality such as observation noise are also not discussed. Of course, the impact of downsampling in the presence of a third (vector) variable is also of interest but will be pursued elsewhere.

Finally, our whole discussion is carried out in the framework of linear time series models. It is of great interest to pursue nonlinear versions of these issues, but that would be a major separate task.

The remainder of the letter, is organized as follows. In section 2, we review and modify some state-space results important for system identification or model fitting and needed in the following sections. In section 3, we develop state-space methods for computing submodels of innovations state-space models. In section 4, we develop methods for transforming state-space models under downsampling. In section 5, we review GC and GEMs and extend them to a state space-setting. In section 6, we study the effect of filtering on GC via frequency domain GEMs. In section 7, we offer a theory to explain when GC is preserved under downsampling. In section 8, we discuss the reverse GC problem showing how spurious causality can be induced by downsampling. In section 9, we set up the framework for the application of these results to fMRI. This includes discussion of the phase properties of HRFs as well as the impact of deconvolution on the assessment of GC. Conclusions are in section 10. There are three appendixes.

1.1 Acronyms and Notation

GC is Granger causality or Granger causes; GCS is Granger causal structure; dn-gc does not Granger cause; GEM is Geweke causality measure. HRF is hemodynamic response function; SS is state space or state-space model; ISS is innovations state-space model; UC is unit circle; VAR is vector autoregression; VARMA is vector autoregressive moving average process; wp1 is with probability 1. LHS denotes left-hand side. The lag or backshift operator is denoted L or z⁻¹; thus, if x_t is a signal, then Lx_t = z⁻¹ x_t = x_t−1. L or z⁻¹ are causal operators since they operate on the past. L⁻¹ or z are noncausal operators since they operate on the future (so L⁻¹x_t = zx_t = x_t+1). The causal filter $h\left(L\right)={\displaystyle {\sum }_0^{\infty }{h}_r{L}^r}$ is sometimes denoted h, and its noncausal reflection is h^∗ = h^∗(L)= h(L⁻¹).

$X_a^b$ denotes the values x_a, x_a+1, …, x_b, so $X_a^a\equiv x_a$. For stationary processes, we have a = −∞. If M, N are positive semidefinite matrices, then M ≥ N means M−N is positive semidefinite. A stable square matrix is one whose eigenvalues all have modulus < 1.

2 State Space

The computational methods we develop rely on state-space techniques and spectral factorization, the latter being intimately related to the steady-state Kalman filter. In this section, we review and modify some basic results in state-space theory, Kalman filtering, and spectral factorization. Our discussion deals with two vector time series, collected as, $z_t={\left(x_t^T,y_t^T\right)}^T$.

2.1 State-Space Models

We consider a general constant parameter SS model,

$${\xi }_{t+1}=A{\xi }_t+w_t,z_t=C{\xi }_t+v_t,$$ (2.1)

with positive semidefinite noise covariance, $\mathrm{var}\left(\begin{array}{c}{w}_t\\ v_t\end{array}\right)=\left(\begin{array}{cc}Q& S\\ S^T& R\end{array}\right)$. We refer to this as an SS model with parameters (A, C, [Q, R, S]).

It is common with SS models to take S = 0, but for equivalence between the class of VARMA models and the class of state-space models, it is necessary to allow S ≠ 0.

Now by matrix partitioning, $\left|\left(\begin{array}{cc}Q& S\\ S^T& R\end{array}\right)\right|=\left|R\right||Q_s|,Q_s=Q-S{R}^{-1}{S}^T$. So we introduce

• N: Noise Condition. R is positive definite.

N implies that Q_s is positive semidefinite.

2.2 Steady-State Kalman Filter, Innovations State-Space Models, and the Discrete Algebraic Ricatti Equation

We now recall the Kalman filter for mean square estimation of the unobserved state sequence ξ_t from the observed time series z_t. It is given by Kailath, Sayeed, and Hassibi (2000, theorem 9.2.1),

$${\widehat{\xi }}_{t+1}=A{\widehat{\xi }}_t+K_t{e}_t,e_t=z_t-C{\widehat{\xi }}_t,\text{or}{z}_t=C{\widehat{\xi }}_t+e_t,$$

where e_t is the innovations sequence of variance V_t = R + CP_tC^T, $K_t=\left(A{P}_t{C}^T+S\right)V_t^{-1}$ is the Kalman gain sequence, and P_t is the state error variance matrix generated from the Ricatti equation, $P_{t+1}=A{P}_t{A}^T+Q-K_t{V}_t{K}_t^T$.

The Kalman filter is a time-varying filter, but we are interested in its steady state. If there is a steady state (i.e., P_t → P as t → ∞) then the limiting state error variance matrix P will, obey the so-called discrete algebraic Ricatti equation (DARE),

$$P=AP{A}^T+Q-KV{K}^T,$$ (2.2)

where V = R + CPC^T and K = (APC^T + S)V⁻¹ is the corresponding steady-state Kalman gain. With some clever algebra, (Kailath et al., 2000), the DARE can be rewritten (the Ricatti equation can be similarly rewritten) as

$$P=A_{s}P{A}_s^T+Q_s-K_{s}V{K}_s^T,$$

where A_s = A − SR⁻¹C and K_s = A_sPC^TV⁻¹.

We now introduce two assumptions.

• St: Stabilizability condition: A_s, $Q_s^{\frac{1}{2}}$ is stabilizable (see appendix A)

• De: Detectability condition: A_s, C is detectable.

In appendix A, it is shown De is equivalent to A, C being detectable. Also it holds automatically if A is stable.

The resulting steady-state Kalman filter can be written as

$${\widehat{\xi }}_{t+1}=A{\widehat{\xi }}_t+K{\epsilon }_t,z_t=C{\widehat{\xi }}_t+{\epsilon }_t,$$ (2.3)

where ε_t is the steady-state innovation process and has variance matrix V and Kalman gain K. This steady-state filter provides a new state-space representation of the data sequence. We refer to it as an innovations state-space (ISS) model with parameters (A, C, K, V). We summarize this:

Result 1

Given the SS model, equation 2.1, with parameters (A, C, [Q, R, S]), then provided N, St, De hold:

1. The corresponding ISS model, equation 2.3, with parameters (A, C, K, V), can be found by solving the DARE, equation 2.2, which has a unique positive-definite solution P.

2. V is positive definite, (A, C) is detectable, and A−KC is stable so that (A, K) is controllable.

Proof

See appendix A.

Remarks

1. Henceforth an ISS model with parameters (A, C, K, V) will be required to have V positive definite, (A, C) detectable, and (A, K) controllable so that A–KC is stable.

2. It is well known that any VARMA model can be represented as an ISS model and vice versa (Solo, 1986; Hannan & Deistler, 1988).

3. Note that the ISS model with parameters (A, C, K, V) can also be written as the SS model with parameters (A, C, [KVK^T, V, KV]).

4. The DARE is a quadratic matrix equation, but it can be computed using the (numerically reliable) DARE command in Matlab as follows. Compute: [P, L₀, G] = DARE(A^T, C^T, Q, R, S, I) and then, V = R + CPC^T, K = G^T.

5. Note that stationarity is not required for this result.

2.3 Stationarity and Spectral Factorization

Given an ISS model with parameters (A, C, B, Σ_ε), we now introduce

• Assumption EV: Eigenvalue stability condition: A has all eigenvalues with modulus < 1, that is, A is a stability matrix.

With this assumption we can obtain an infinite vector moving average (VMA) representation, an infinite vector autoregressive (VAR) representation, and a spectral factorization.

Before stating these results, we need a definition;

• Definition. Minimum phase transfer function. A matrix H(L) of causal transfer functions is said to be minimum phase (MP) if its inverse exists and is causal and stable. If H(L) is not minimum phase, it is called nonminimum phase (NMP).

Examples

1. Causal and stable. H(L) = 1 − aL, |a| < 1 has inverse $H\_\left(L\right)=\frac{1}{1-aL}={\displaystyle {\sum }_0^{\infty }{a}^r{L}^r}$, which follows from summing the geometric series. Then H_{_}(L) is clearly causal and is stable since its pole $z_p=L_p^{-1}=a$ has modulus < 1 (i.e., it lies inside the unit circle). Another way to state this is to say that H(L) is MP because its zero z_o = a has modulus < 1 (i.e., it lies inside the unit circle, UC).

2. Causal but not stable. $H\left(L\right)=1-\frac{1}{\theta }L,0<\theta <1$ is not minimum phase since $H\_\left(L\right)=\frac{1}{1-\frac{1}{\theta }L}$ is not stable since its pole $z_p=L_p^{-1}=\frac{1}{\theta }$ has modulus > 1. If we rewrite $H\left(L\right)=-\frac{1}{\theta }L\left(1-\theta L^{-1}\right)$, then $H\_\left(L\right)=-\frac{\theta L^{-1}}{1-\theta L^{-1}}=-\theta L^{-1}{\displaystyle {\sum }_0^{\infty }{\theta }^r{L}^{-r}}$. This is stable but not causal since the expansion is in terms of the future. Again we can rephrase this example to say H(L) is NMP because its zero $z_o=\frac{1}{\theta }$ is outside the unit circle.

3. Not causal but stable. H(L) = L(1 − aL), |a| < 1 is nonminimum phase since $H\_\left(L\right)=\frac{L^{-1}}{1-aL}$ is not causal. Note that H_(L) is stable. We can rephrase this as follows. H(L) has two zeros: one is inside the unit circle, and the other is at ∞ (i.e., z = L⁻¹ = ∞ makes H (L) vanish and so is outside the unit circle).

For further discussion of minimum phase filters, see Green (1988) and Solo (1986).

The following result is based on Kailath et al. (2000, theorem 8.3.2) and the surrounding discussion.

Result 2

For the ISS model (A, C, B, Σ_ε) obeying condition Ev we have,

1. Infinite VMA or Wold decomposition:

   $$z_t=H(L){\epsilon }_t=(C{(L^{-1}I-A)}^{-1}B+I){\epsilon }_t=(C{(I-AL)}^{-1}BL+I){\epsilon }_t.$$ (2.4)
2. Infinite VAR representation:

   $${\epsilon }_t=G(L)z_t=\left[I+C{(L^{-1}I-A+KC)}^{-1}K\right]z_t.$$ (2.5)
3. Spectral factorization. Put L = exp(− jλ); then z_t has positive-definite spectrum with spectral factorization as follows:

   $$\begin{array}{ll}{f}_Z(\mathrm{\lambda })& =\left[C{(L^{-1}I-A)}^{-1},I\right]\left[\begin{array}{cc}Q& S\\ S^T& R\end{array}\right]\left[\begin{array}{c}{(LI-A^T)}^{-1}{C}^T\\ I\end{array}\right]\\ & =H(L){\displaystyle {\sum }_{\epsilon }{H}^T(L^{-1})}.\end{array}$$ (2.6)

4. H(L) is minimum phase.

Proof

1. Write equation 2.3, in operator form. The series is convergent wp1 and in mean square since A is stable.

2. Rewrite equation as ${\widehat{\xi }}_{t+1}=\left(A-KC\right){\widehat{\xi }}_t+K{z}_t,{\epsilon }_t=z_t-C{\widehat{\xi }}_t$. Then write this in operator form. The series is convergent wp1 and in mean square since A−KC is stable and z_t is stationary.

3. This follows from standard formulas for spectra of filtered stationary time series applied to (a).

4. From (a),(b) G(L) = H⁻¹ (L) and by (b) G(L) is causal and stable, and the result follows.

Remarks

1. Result 2 is a special case of a general result that given a full-rank multivariate spectrum f_Z(λ), there exists a unique causal stable minimum phase spectral factor H(L) with H(0) = I and positive-definite innovations variance matrix Σ_ε such that equation 2.6 holds (Hannan & Deistler, 1988; Green, 1988). In general detH(L) may have some roots on the unit circle (Hannan & Poskitt, 1988; Green, 1988), but the assumptions in result 2 rule this case out. Such roots mean that some linear combinations of z_t can be perfectly predicted from the past (Hannan & Poskitt, 1988; Green, 1988), something that is not realistic in the fMRI application.

2. Result 2 is also crucial from a system identification or model-fitting point of view. From that point of view, all we can know (from second-order statistics) is the spectrum, and so if, naturally, we want a unique model, the only model we can obtain is the causal stable minimum phase model: the ISS model. The standard approach to SS model fitting is the so-called state-space subspace method (Deistler, Peternell, & Scherer, 1995; Bauer, 2005), and indeed it delivers an ISS model. The alternative approach of fitting a VARMA model (Hannan & Deistler, 1988; Lutkepohl, 1993) is equivalent to getting an ISS model.

3. We need result 1, however, since when we form submodels, we do not immediately get an ISS model; rather, we must compute it.

3 Submodels

Our computation of causality measures requires that we compute induced submodels. In this section, we show how to obtain an ISS submodel from the ISS joint model.

We partition z_t = (x_t, y_t)^T into subvector signals of interest and partition the state-space model correspondingly: $C=\left(\begin{array}{c}{C}_X\\ C_Y\end{array}\right)$ and B = (B_X, B_Y). We first read out an SS submodel for x_t from the ISS model for z_t. We have simply ξ_t+1 = Aξ_t + w_t, x_t = C_Xξ_t + ε_X,t where, $w_t=B\left(\begin{array}{c}{\epsilon }_{X,t}\\ {\epsilon }_{Y,t}\end{array}\right)=B_X{\epsilon }_{X,t}+B_Y{\epsilon }_{Y,t}$. We need to calculate the covariance matrix: $\mathrm{var}(\begin{array}{c}{w}_t\\ {\epsilon }_{X,t}\end{array})=(\begin{array}{cc}Q& \overline{S}\\ {\overline{S}}^T& \overline{R}\end{array})$. We find $\overline{R}={\displaystyle {\sum }_{X,\epsilon }}$, Q = var(w_t) = BΣ_εB^T and $\overline{S}=E(w_t{\epsilon }_{X,t}^T)=B(\begin{array}{c}{\sum }_{X,\epsilon }\\ {\sum }_{YX,\epsilon }\end{array})=B_o$. This leads to:

Theorem 1

Given the joint ISS model, equation 2.3 or 2.4, for z_t, then under condition Ev, the corresponding ISS submodel for x_t, (A, C_X, K_(X), Ω_X) (the bracket notation K_(X) is used to avoid confusion with e.g. C_X, Σ_X,ε which are submatrices), can be found by solving the DARE, equation 2.2, with $\left[Q,\overline{R},\overline{S}\right]=\left[B{\mathit{\sum }}_{\epsilon }{B}^T,{\mathit{\sum }}_{X,\epsilon },B_o\right]$.

Proof

First, we note by partitioning |Σ_ε| = |Σ_X,ε||Σ_(Y|X),ε| where ${\sum }_{(Y|X),\epsilon }={\sum }_{YX,\epsilon }{\sum }_{X,\epsilon }^{-1}{\sum }_{XY;\epsilon }$so that Σ_X,ε and Σ_(Y|X),ε are both positive definite. Now we need only check conditions N, St, De of result 1. We need to show that $\overline{R}={\sum }_{X,\epsilon }$ is positive definite, (A, C_X) is detectable, and ${(A-{\overline{SR}}^{-1}{C}_X,(B{\sum }_{\epsilon }{B}^T-{\overline{SR}}^{-1}{\overline{R}}^T)}^{\frac{1}{2}}$ is stabilizable; in fact, we show it is controllable.

The first is already established. The second follows trivially since A is stable. We use the PBH test (see appendix A) to check the third.

Suppose controllability fails. Then by the PBH test, there exists q ≠ 0 with $\mathrm{\lambda }{q}^T=q^T(A-{\overline{SR}}^{-1}{C}_X)$ and

$$\begin{array}{l}0=q^T{\left(B{\sum }_{\epsilon }{B}^T-{\overline{SR}}^{-1}{\overline{S}}^T\right)}^{\frac{1}{2}}\\ \Rightarrow 0=q^T\left(B{\sum }_{\epsilon }{B}^T-{\overline{SR}}^{-1}{\overline{S}}^T\right)\\ =q^T\left(B{\sum }_{\epsilon }{B}^T-B\left(\begin{array}{c}{\sum }_{X,\epsilon }\\ {\sum }_{YX,\epsilon }\end{array}\right){\sum }_{X,\epsilon }^{-1}\left[{\sum }_{X,\epsilon },{\sum }_{XY,\epsilon }\right]B^T\right)\\ =q^T\left(B_X,B_Y\right)\left(\begin{array}{cc}0& 0\\ 0& {\sum }_{\left(Y|X\right),\epsilon }\end{array}\right)\left(\begin{array}{c}{B}_X^T\\ B_Y^T\end{array}\right)\\ =q^T{B}_Y{\sum }_{\left(Y|X\right),\epsilon }{B}_Y^T\\ \Rightarrow 0=q^T{B}_Y{\sum }_{\left(Y|X\right),\epsilon }{B}_Y^{T}q\\ \Rightarrow 0=\Vert B_Y^{T}q\Vert \Rightarrow q^T{B}_Y=0\end{array}$$

since Σ_(Y|X)ε, is positive definite. But then,

$$\begin{array}{l}\mathrm{\lambda }{q}^T=q^T\left(A-\left(B_X,B_Y\right)\left(\begin{array}{c}{\sum }_{X,\epsilon }\\ {\sum }_{YX,\epsilon }\end{array}\right){\displaystyle {\sum }_{X,\epsilon }^{-1}{C}_X}\right)\\ =q^T(A-\left(B_X{C}_X+B_Y{\sum }_{YX,\epsilon }{\displaystyle {\sum }_{X,\epsilon }^{-1}{C}_X}\right)\\ =q^T\left(A-B_X{C}_X\right).\end{array}$$

Thus, (A − B_XC_X, B_Y) is not controllable. But this is a contradiction since we can find a matrix, namely C_Y, so that A − B_XC_X − B_YC_Y = A − BC is stable.

Remarks

1. For implementation in Matlab, positive definiteness in constructing Q can be an issue. A simple resolution is to use a Cholesky factorization of ${\sum }_{\epsilon }=L_{\epsilon }{L}_{\epsilon }^T$ and form B_ε = BL_ε and then form $Q=B_{\epsilon }{B}_{\epsilon }^T$.

2. The P_(X) matrix from DARE, $\left[P_{\left(X\right)},L_0,G\right]=\mathit{DARE}\left(A^T,C_X^T,B{\sum }_{\epsilon }{B}^T,{\sum }_{X,\epsilon },B_o,I\right)$ obeys $P_{\left(X\right)}=A{P}_{\left(X\right)}{A}^T+B{\sum }_{\epsilon }{B}^T-K_{\left(X\right)}{\mathrm{\Omega }}_X{K}_{\left(X\right)}^T$ and then $K_{\left(X\right)}=\left(A{P}_{\left(X\right)}{C}_X^T+B_o\right){\mathrm{\Omega }}_X^{-1},{\mathrm{\Omega }}_X={\sum }_{X,\epsilon }+C_X{P}_{\left(X\right)}{C}_X^T$.

3. Dufour and Taamouti (2010) discuss a method for obtaining sub-models, but it is flawed. First, it requires computing the inverse of the VAR operator. While this might be feasible (analytically) on a toy example, there is no known numerically reliable way to do this in general (computation of determinants is notoriously ill conditioned). Second, it requires the solution of simultaneous quadratic autocovariance equations to determine VMA parameters for which no algorithm is given. In fact, these are precisely the equations required for a spectral factorization of a VMA process. There are reliable algorithms for doing this, but given the flaw already revealed, we need not discuss this approach any further.

Next we state an important corollary:

Corollary 1

Any submodel is in general a VARMA model, not a VAR. To put it another way, the class of VARMA models is closed under the forming of submodels, whereas the class of VAR models is not.

This means that VAR models are not generic and is a strong argument against their use. Any vector time series can be regarded as a submodel of a larger-dimensional time series and thus must in general obey a VARMA model. This result (which is well known in time series folklore) is significant for econometrics where VAR models are in widespread use.

For the next section we need:

Theorem 2

For the joint ISS model, equation 2.3 or 2.4, for z_t with conditions St, De holding and with induced submodel for x_t given in theorem 1, we have,

$$\begin{array}{l}{f}_X\left(\mathrm{\lambda }\right)=h_X\left(exp\left(-j\mathrm{\lambda }\right)\right){\mathrm{\Omega }}_X{h}_X^T\left(exp\left(j\mathrm{\lambda }\right)\right),\\ h_X\left(L\right)=I+C_X{\left(L^{-1}I-A\right)}^{-1}{K}_{\left(X\right)}=I+L{C}_X{\left(I-AL\right)}^{-1}{K}_{\left(X\right)},\\ ln\left|{\Omega }_X\right|={\displaystyle {\int }_{-\pi }^{\pi }ln\left|f_X\left(\mathrm{\lambda }\right)\right|\frac{d\mathrm{\lambda }}{2\pi }}.\end{array}$$ (3.1)

4 Downsampling

There are two approaches to the problem of finding the model obeyed by a downsampled process: frequency domain and time domain. While the general formula for the spectrum of a downsampled process has long been known, it is not straightforward to use and has not yielded any general computational approach to finding submodels of parameterized spectra.

The spectral formula, however, has made it very clear that downsampling leads to aliasing, so that higher-frequency information is lost. This strongly suggests that GCS will be affected by downsampling.

The most complete (time domain) work on downsampling seems to be that of Pandit and Wu (1983), although they treat only the first- and second-order scalar cases. There is work in the engineering literature for systems with observed inputs, but that is also limited and in any case not helpful here. We follow an SS route.

We begin with the ISS model, equation 2.3. Suppose we downsample the observed signal z_t with sampling multiple m. Let t denote the fine timescale and k the coarse timescale so t = mk. The downsampled signal is ${\overline{z}}_k=z_{\mathit{mt}}$. To develop the SS model for ${\overline{z}}_k$, we iterate the SS model above to obtain

$${\xi }_{t+l}=A^l{\xi }_t+{\displaystyle {\sum }_1^l{A}^{l-i}B{\epsilon }_{t+i-1}}.$$

Now set t = mk, l = m and denote sampled signals, ${\overline{\xi }}_k={\xi }_{mk},{\overline{z}}_k=z_{mk},{\overline{\epsilon }}_k={\epsilon }_{mk}$. Then we find

$${\overline{\xi }}_{k+1}=A^m{\overline{\xi }}_k+w_k,{\overline{z}}_k=C{\overline{\xi }}_k+{\overline{\epsilon }}_k,$$

where $w_k={\displaystyle {\sum }_1^m{A}^{m-i}B{\epsilon }_{km+i-1}}$. We now use result 1 to find the ISS model corresponding to this SS model.

We first have to calculate the model covariances:

$$\begin{array}{l}E({\overline{\epsilon }}_k{\overline{\epsilon }}_k^T)={\sum }_{\epsilon }=R,\\ E(w_k{\overline{\epsilon }}_k^T)=A^{m-1}B{\sum }_{\epsilon }=S_m,\end{array}$$ (4.1)

$$\begin{array}{l}E(w_k{w}_k^T)=Q_m,\\ Q_m={\displaystyle {\sum }_1^m{A}^{m-i}B{\displaystyle {\sum }_{\epsilon }{B}^T{(A^T)}^{m-i}={\displaystyle {\sum }_0^{m-1}{A}^{r}B{\displaystyle {\sum }_{\epsilon }{B}^T{(A^T)}^r,}}}}\\ \Rightarrow Q_m=A{Q}_{m-1}{A}^T+B{\displaystyle {\sum }_{\epsilon }{B}^T},m\ge 2,Q_1=B{\displaystyle {\sum }_{\epsilon }{B}^T},\end{array}$$ (4.2)

We now obtain:

Theorem 3

Given the ISS model, equation 2.3, then under condition Ev, for m > 1, the ISS model for the downsampled process ${\overline{z}}_k=z_{\mathit{mt}}$ is $\left(A^m,C,K_m^{\ast },V_m^{\ast }\right)$, obtained by solving the DARE with SS model (A^m, C, [Q_m, R, S_m]) where Q_m is given in equation 4.2 and S_m is given in equation 4.1.

Proof

Using result 1, we need to show the following. R is positive definite, (A^m,C) is detectable, and (A^m − S_mR⁻¹C), ${\left(Q_m-S_m{R}^{-1}{S}_m^T\right)}^{\frac{1}{2}})$ is stabilizable. In fact, we show controllability. The first holds trivially; the second does as well since A is stable and thus so is A^m. For the third, we use the PBH test.

Suppose controllability fails. Then there is a left eigenvector q (possibly complex) with λq^T = q^T(A^m − S_mR⁻¹C) = q^TA^m−1(A − BC) and $q^T(Q_m-S_m{R}^{-1}{S}_m^T)=0=q^T{\displaystyle {\sum }_0^{m-2}{A}^{r}B{\displaystyle {\sum }_{\epsilon }{B}^T}{(A^T)}^r\Rightarrow {\displaystyle {\sum }_0^{m-2}{q}^H{\displaystyle {\sum }_0^{m-1}{A}^{r}B{\displaystyle {\sum }_{\epsilon }{B}^T{(A^T)}^{r}q=0}}}}$ Since Σ_ε is positive definite, this delivers ${{\displaystyle {\sum }_0^{m-2}\Vert B^T{(A^T)}^{r}q\Vert }}^2=0\Rightarrow B^T{(A^T)}^{r}q=0$ for r = 0, …, m − 2.

Using this, we now find λ−q^T = q^TA^m−1(A − BC) = q^TA^m−2(A − BC)² +q^TA^m−2BC(A − BC) = q^TA^m−2(A − BC)². Iterating this yields λq^T − q^T(A − BC)^m. Thus, if λ_m is an mth root of λ, then λ_mq^T = q^T(A − BC). Since q^T B = 0, we thus conclude that (A − BC, B) is not controllable. But this is a contradiction since (A − BC) + BC = A is stable.

Remark

1. In Matlab, we would compute, $\left[P_m^{\ast },L_0,G_m\right]=\text{DARE}({(A^m)}^T{C}_T,Q_m,{\sum }_{\epsilon },S_m,I)$, yielding $V_m^{\ast }={\sum }_{\epsilon }+C{P}_m^{\ast }{C}^T$ and $K_m^{\ast }=G_m^T$.

2. More specifically $P_m^{\ast }\left(m>1\right)$ obeys $P_m^{\ast }={\overline{A}}_m{P}_m^{\ast }{\overline{A}}_m^T+{\overline{Q}}_m-{\overline{K}}_m{V}_m^{\ast }{\overline{K}}_m^T$, where ${\overline{A}}_m=A^m-S_m{\displaystyle {\sum }_{\epsilon }^{-1}C=A^{m-1}\left(A-BC\right)}$; ${\overline{Q}}_m=Q_m-S_m{\displaystyle {\sum }_{\epsilon }^{-1}{S}_m^T=Q_{m-1}}$; $V_m^{\ast }={\sum }_{\epsilon }+C{P}_m^{\ast }{C}^T$; $K_m^{\ast }={\overline{A}}_m{P}_m^{\ast }{C}^T{\left(V_m^{\ast }\right)}^{-1}$.

5 Granger Causality

In this section, we review and extend some basic results in Granger causality. In particular, we extend GEMs to the state-space setting and show how to compute them reliably.

Since the development of Granger causality, it has become clear (Dufour & Renault, 1998; Dufour & Taamouti, 2010) that in general, one cannot address the causality issue with only one-step-ahead measures as commonly used. One needs to look at causality over all forecast horizons. However one-step measures are sufficient when one is considering only two vector time series as we are (Dufour & Renault, 1998, proposition 2.3).

5.1 Granger Causality Definitions

Our definitions of one-step Granger causality naturally draw on Granger (1963, 1969), Sims (1972), and Solo (1986) but are also influenced by Caines (1976), who, drawing on the work of Pierce and Haugh (1977), distinguished between weak and strong GC, or what Caines calls weak and strong feedback free processes. We introduce:

• Condition WSS: The vector time series x_t, y_t are jointly second-order stationary.

• Definition: Weak Granger causality. Under WSS, we say y_t does not weakly Granger-cause (dn-wgc) x_t if, for all t,

  $$\mathrm{var}\left(X_{t+1}|X_{-\infty }^t,Y_{-\infty }^t\right)=\mathrm{var}\left(X_{t+1}|X_{-\infty }^t\right).$$

  Otherwise, we say y_t weakly Granger causes (wgc) x_t. Because of the elementary identity,

  $$\begin{array}{l}\mathrm{var}(X|Z)=E\left[\mathrm{var}(X|Z,W)\right]+\mathrm{var}\left[E(X|Z,W)\right]\\ =E\left[\mathrm{var}(X|Z,W)\right]+E[(E(X|Z,W)\\ -E(X|Z)){(E(X|Z,W)-E(X|Z))}^T|Z],\end{array}$$

  the equality of variance matrices in the definition also ensures the equality of predictions: $E\left(X_{t+1}|X_{-\infty }^t,Y_{-\infty }^t\right)=E\left(X_{t+1}|X_{-\infty }^t\right)$. This definition agrees with Granger (1969); Caines and Chan (1975), who do not use the designator weak; and Caines (1976) and Solo (1986) who do.
• Definition: Strong Granger causality. Under WSS, we say y_t does not strongly Granger cause (dn-sgc) x_t if, for all t,

  $$\mathrm{var}(X_{t+1}|X_{-\infty }^t,Y_{-\infty }^t,Y_{t+1})=\mathrm{var}(X_{t+1}|X_{-\infty }^t).$$

  Otherwise we say y_t strongly Granger-causes (sgc) x_t. Again, equality of the variance matrices ensures equality of predictions, $E(X_{t+1}|X_{-\infty }^t,Y_{-\infty }^t,Y_{t+1})=E(X_{t+1}|X_{\infty }^t)$. This definition agrees with Caines (1976) and Solo (1986).

• Definition: FBI (feedback interconnected). If x_t Granger-causes y_t and y_t Granger-causes x_t, then we say x_t, y_t are feedback interconnected.

• Definition: UGC (unidirectionally Granger causes). If x_t Granger-causes y_t but y_t dn-gc x_t we say x_t unidirectionally Granger-causes y_t.

5.2 Granger Causality for Stationary State-Space Models

Now we partition z_t = (x_t, y_t)^T into subvector signals of interest and partition the vector MA or state-space model, equation 2.4, correspondingly:

$$\left[\begin{array}{c}{x}_t\\ y_t\end{array}\right]=[I+\left[\begin{array}{c}{C}_X\\ C_Y\end{array}\right]{(L^{-1}I-A)}^{-1}(B_X{B}_Y)\left[\begin{array}{c}{\epsilon }_{X,t}\\ {\epsilon }_{Y,t}\end{array}\right]$$ (5.1)

$$\begin{array}{c}=\left[\begin{array}{c}{H}_{\mathit{XX}}(L)H_{\mathit{XY}}(L)\\ H_{\mathit{YX}}(L)H_{\mathit{YY}}(L)\end{array}\right]\left[\begin{array}{c}{\epsilon }_{X,t}\\ {\epsilon }_{Y,t}\end{array}\right]\\ {\sum }_{\epsilon }=\mathrm{var}\left[\begin{array}{c}{\epsilon }_{X,t}\\ {\epsilon }_{Y,t}\end{array}\right]=\left[\begin{array}{cc}{\sum }_{X,\epsilon }& {\sum }_{XY,\epsilon }\\ {\sum }_{YX,\epsilon }& {\sum }_{Y,\epsilon }\end{array}\right]\\ \left[\begin{array}{c}{H}_{\mathit{XX}}(L)H_{\mathit{XY}}(L)\\ H_{\mathit{YX}}(L)H_{\mathit{YY}}(L)\end{array}\right]=\left[\begin{array}{c}{C}_X{(L^{-1}I-A)}^{-1}{B}_X+I{C}_X{(L^{-1}I-A)}^{-1}{B}_Y\\ C_Y{(L^{-1}I-A)}^{-1}{B}_X{C}_Y{(L^{-1}I-A)}^{-1}{B}_Y+I\end{array}\right].\end{array}$$ (5.2)

Now we recall results of Caines (1976):

Result 3

If $z_t=\left(\begin{array}{c}{x}_t\\ y_t\end{array}\right)$ obeys a Wold model of the form z_t=H_Z (L)ε_t where H_Z(L) is a one-sided square summable moving average polynomial with H_Z(0)= I, which is partitioned as in equation 5.2, then:

1. y_t dn-wgc x_t iff H_XY(L) = 0.

2. y_t dn-sgc x_t iff H_XY(L) = 0 and Σ_XY,_ε = 0.

We can now state a new SS version of this result:

Theorem 4

For the stationary ISS model, equations 5.1 and 5.2:

1. y_t dn-wgc x_t iff C_XA^r B_Y = 0, r ≥ 0.

2. y_t dn-sgc x_t iff C_XA^r B_Y = 0, r ≥ 0 and Σ_XY,ε = 0.

Proof

The proof follows immediately from result 3 since $H_{\mathit{XY}}(L)={\displaystyle {\sum }_0^{\infty }{C}_X{A}^r{B}_Y{L}^{r+1}}$.

Remarks

1. By the Cayley-Hamilton theorem, we can replace part a of theorem 4 with C_XA^rB_Y = 0, 0 ≤ r ≤ n − 1, n = dim (ξ_t).

2. Collecting these equations together gives C_X (B_Y, AB_Y,…, Aⁿ⁻¹B_Y) = 0, which says that the pair (A, B_Y) is not controllable. Also, we have $B_Y^T(C_X^T,A^T{C}_X^T,\dots ,{(A^T)}^{n-1}{C}_X^T)=0$, which says that the pair (C_X, A) is not observable. Thus, the representation of H_XY(L) is not minimal.

From a data analysis point of view, we need to embed this result in a well-behaved hypothesis test. The results of Geweke (1982), suitably modified, allow us to do this.

5.3 Geweke Causality Measures for SS Models

Although much of the discussion in Geweke (1982) is in terms of VARs, we can show it applies more generally. We begin as Geweke (1982) did with the following definitions. First, $F_{Y\to X}=\mathit{ln}\frac{\left|{\mathrm{\Omega }}_X\right|}{\left|{\sum }_{X,\epsilon }\right|}$ is a measure of the gain in using the past of y to predict x beyond using just the past of x; similarly introduce $F_{Y\to X}=\mathit{ln}\frac{|{\mathrm{\Omega }}_Y|}{|{\sum }_{Y,\epsilon }|}$. Thus, for example, F_Y→X is a directional measure of the influence of yt on x_t. Next, define the instantaneous influence measure: $F_{Y.X}=\mathit{ln}\frac{|{\sum }_{X,\epsilon }||{\sum }_{Y,\epsilon }|}{|{\sum }_{\epsilon }|}$. These are then joined in the fundamental decomposition (Geweke, 1982),

$$F_{XoY}=F_{Y\to X}+F_{X\to Y}+F_{Y.X}$$ (5.3)

where, $F_{XoY}=\mathit{ln}\frac{\left|{\mathrm{\Omega }}_X\right|\left|{\mathrm{\Omega }}_Y\right|}{\left|{\sum }_{\epsilon }\right|}$. Geweke (1982) then proceeds to decompose these measures in the frequency domain. Thus, the frequency domain GEM for the dynamic influence of y_t on x_t is given by Geweke (1982),

$$F_{Y\to X}={\displaystyle {\int }_{-\pi }^{\pi }{f}_{Y\to X}(\mathrm{\lambda })\frac{d\mathrm{\lambda }}{2\pi }\text{where}{f}_{Y\to X}(\mathrm{\lambda })=\mathit{ln}\frac{|f_X(\mathrm{\lambda })|}{|f_e(\mathrm{\lambda })|}},$$ (5.4)

and f_e(λ) is assembled (following Geweke, 1982) as follows.

Introduce $W={\sum }_{YX,\epsilon }{\sum }_{X,\epsilon }^{-1}$, and note that ${\epsilon }_{Y,t}-W{\epsilon }_{X,t}$ is uncorrelated with ε_X,t and has variance ${\displaystyle {\sum }_{(Y|X),\epsilon }=}{\displaystyle {\sum }_{Y,\epsilon }-{\displaystyle {\sum }_{YX,\epsilon }{\displaystyle {\sum }_{X,\epsilon }^{-1}{\displaystyle {\sum }_{XY,\epsilon }}}}}$. Then rewrite equation 5.2 as

$$\begin{array}{l}\left[\begin{array}{c}{x}_t\\ y_t\end{array}\right]=\left[\begin{array}{c}{H}_{\mathit{XX}}(L)H_{\mathit{XY}}(L)\\ H_{\mathit{YX}}(L)H_{\mathit{YY}}(L)\end{array}\right]\left[\begin{array}{cc}I& 0\\ W& I\end{array}\right]\left[\begin{array}{cc}I& 0\\ -W& I\end{array}\right]\left[\begin{array}{c}{\epsilon }_{X,t}\\ {\epsilon }_{Y,t}\end{array}\right]\\ =\left[\begin{array}{c}{H}_{\mathit{XX}}(L)+H_{\mathit{XY}}(L)W,H_{\mathit{XY}}(L)\\ H_{\mathit{YX}}(L)+H_{\mathit{YY}}(L)W,H_{\mathit{YY}}(L)\end{array}\right]\left[\begin{array}{c}{\epsilon }_{X,t}\\ {\epsilon }_{Y,t}-W{\epsilon }_{X,t}\end{array}\right].\end{array}$$

This corresponds to equation 3.3 in Geweke (1982) and yields the following expressions corresponding to those in Geweke (1982):

$$f_X(L)=f_e(L)+H_{\mathit{XY}}(L){\displaystyle {\sum }_{(Y|X),\epsilon }{H}_{\mathit{XY}}^T}(L^{-1}),$$ (5.5)

$$\begin{array}{l}{f}_e(L)=H_{eX}(L){\displaystyle {\sum }_{X,\epsilon }{H}_{eX}^T(L^{-1})},\\ H_{eX}(L)=H_{\mathit{XX}}(L)+H_{\mathit{XY}}(L)W.\end{array}$$ (5.6)

Using the SS expressions above, we rewrite H_eX(L) in a form more suited to computation as

$$\begin{array}{l}{H}_{eX}(L)=[C_X{(L^{-1}I-A)}^{-1}{B}_o+I]\\ B_o=B_X+B_Y{\displaystyle {\sum }_{XY,\epsilon }^T{\displaystyle {\sum }_{X,\epsilon }^{-1}=B\left(\begin{array}{c}{\displaystyle {\sum }_{X,\epsilon }}\\ {\displaystyle {\sum }_{YX,\epsilon }}\end{array}\right)}}{\displaystyle {\sum }_{X,\epsilon }^{-1}}.\end{array}$$ (5.7)

Note that then, using theorem 2,

$$\begin{array}{l}{F}_{Y\to X}={\displaystyle {\int }_{-\pi }^{\pi }\mathit{ln}|f_X(\mathrm{\lambda })|\frac{d\mathrm{\lambda }}{2\pi }-}{\displaystyle {\int }_{-\pi }^{\pi }\mathit{ln}|f_e(\mathrm{\lambda })|\frac{d\mathrm{\lambda }}{2\pi }}\\ =\mathit{ln}|{\mathrm{\Omega }}_X|-\mathit{ln}|{\displaystyle {\sum }_{X,\epsilon }}|=\mathit{ln}\frac{|{\mathrm{\Omega }}_X|}{|{\displaystyle {\sum }_{X,\epsilon }}|}.\end{array}$$ (5.8)

Clearly, with L = exp(−jλ), f_X(L) ≥ f_e(L) ⇒ F_Y→X≥0.

Also the instantaneous causality measure is

$$\begin{array}{l}{F}_{Y.X}=\mathit{ln}\frac{|{\displaystyle {\sum }_{X,\epsilon }}||{\displaystyle {\sum }_{Y,\epsilon }}|}{|{\displaystyle {\sum }_{\epsilon }}|}=\mathit{ln}\frac{|{\displaystyle {\sum }_{X,\epsilon }}||{\displaystyle {\sum }_{Y,\epsilon }}|}{|{\displaystyle {\sum }_{(X|Y),\epsilon }}||{\displaystyle {\sum }_{Y,\epsilon }}|}=\mathit{ln}\frac{|{\displaystyle {\sum }_{X,\epsilon }}|}{{\displaystyle {\sum }_{(X|Y),\epsilon }}}\\ {\displaystyle {\sum }_{(X|Y),\epsilon }}={\displaystyle {\sum }_{X,\epsilon }}-{\displaystyle {\sum }_{XY,\epsilon }}{\displaystyle {\sum }_{Y,\epsilon }^{-1}{\displaystyle {\sum }_{YX,\epsilon }}}.\end{array}$$ (5.9)

Clearly Σ_X,ε ≥ Σ_(X|Y),ε so that F_Y.X ≥ 0.

Introduce the normalized cross-covariance-based matrix, ${\mathrm{\Gamma }}_{x,y}={\displaystyle {\sum }_{Y,\epsilon }^{-\frac{1}{2}}}{\displaystyle {\sum }_{YX,\epsilon }}{\displaystyle {\sum }_{X,\epsilon }^{-1}{\displaystyle {\sum }_{YX,\epsilon }}}{\displaystyle {\sum }_{Y,\epsilon }^{-\frac{1}{2}}}$. Then, using a well-known partitioned matrix determinant formula (Magnus & Neudecker, 1999), we find F_Y.X = ln|I − Γ_x,y|. This means that the instantaneous causality measure depends only on the canonical correlations (which are the eigenvalues of Γ_x,y) between ε_X,t, ε_Y,t (Seber, 1984; Kshirsagar, 1972).

To implement these formulas, we need expressions for Ω_X, Ω_Y, f_X(λ). To get them, Geweke (1982) fits separate models to each of x_t and y_t. But this causes positivity problems with f_Y→X(λ) (Chen et al., 2006). Instead we obtain the required quantities from the correct submodel obtained in the previous section. We have:

Theorem 5a

The GEMs can be obtained from the joint ISS model, equation 5.1, and the submodel in theorem 2, as follows:

1. $F_{Y\to X}=\mathit{ln}\frac{\left|{\Omega }_X\right|}{\left|{\sum }_{X,\epsilon }\right|}$ where Ω_X is got from the submodel in theorem 3.

2. The frequency domain GEM f_Y→X(λ), equation 5.4, can be computed from equations 5.6, 3.1, and 5.7.

Ω_Y, F_X→Y, f_X→Y(λ) can be obtained similarly.

Now pulling all this together with the help of result 3, we have an extension of the results of Geweke (1982) to the state-space/VARMA case.

Theorem 5b

For the joint ISS model, equation 5.1:

1. F_Y→X ≥ 0, F_Y.X ≥ 0 and $F_{Y\to X}+F_{Y.X}=\mathit{ln}\frac{\left|{\Omega }_X\right|}{\left|{\mathit{\sum }}_{(X|Y),\epsilon }\right|}$.

2. y_t dn-wgc x_t iff, f_X(L) = f_e(L) which holds iff F_Y→X=0, that is, iff Ω_X = Σ_X,ε.

3. y_t dn-sgc x_t iff f_X(L) = f_e(L) and Σ_(X|Y),ε = Σ_X,ε that is, iff F_Y→X = 0 and F_Y.X=0, that is, iff F_Y→X + F_Y.X = 0 i.e. iff Ω_X = Σ_(X|Y),_ε.

Remarks

1. A very nice nested hypothesis testing explanation of the decomposition 5.3 is given by Parzen in the discussion to Geweke (1982).

2. It is straightforward to see that the GEMs are unaffected by scaling of the variables. This is a problem for other GC measures (Edin, 2010).

3. For completeness, we state extensions of the inferential results in Geweke (1982) without proof. Suppose we fit an SS model to data z_t, t = 1, …, T using, for example, so-called state-space subspace methods (Deistler et al., 1995; Bauer, 2005) or VARMA methods in, for example, Lutkepohl (1993). Let ${\widehat{F}}_{Y\to X}$, ${\widehat{F}}_{X\to Y}$, ${\widehat{F}}_{Y.X}$, ${\widehat{F}}_{XoY}$ be the corresponding GEM estimators. If we denote true values with a superscript 0, we find under some regularity conditions:

   $$\begin{array}{l}{H}_0:F_{Y\to X}^0=0\Rightarrow T{\widehat{F}}_{Y\to X}\Rightarrow {\chi }_{2n{p}_x{p}_Y}^2,\text{as}T\to \infty \\ \text{and}{H}_0:F_{Y.X}^0=0\Rightarrow T{\widehat{F}}_{Y.X}\Rightarrow {\chi }_{p_x{p}_Y}^2.\end{array}$$

   So to test for strong GC, we put these together:

   $$H_0:F_{Y\to X}^0=0,F_{Y.X}^0=0\Rightarrow T({\widehat{F}}_{Y\to X}+{\widehat{F}}_{Y.X})\Rightarrow {\chi }_{(2n+1)p_x{p}_Y}^2.$$

   Together with similar asymptotics for ${\widehat{F}}_{X\to Y}$, ${\widehat{F}}_{XoY}$, we see that the fundamental decomposition, equation 5.3, has a sample version involving a decomposition of a chi-squared into sums of smaller chi-squared statistics.

4. Chen et al. (2006) also attempt to derive F_Y→X without fitting separate models to x_t, y_t. However the proposed procedure to compute f_X(λ) involves a two-sided filter and is thus in error. The only way to get f_X(λ) is by spectral factorization (which produces one-sided or causal filters), as we have done.

5. Other kinds of causality measures have emerged in the literature (Kaminski & Blinowska, 1991; Baccala & Sameshima, 2001; Takahashi, Baccala, & Sameshima, 2008; Pascual-Marqui et al., 2014), but it is not known whether they obey the properties in theorems 5a and 5b. However these properties are crucial to our subsequent analysis.

6 Effect of Filtering on Granger Causality Measures

Now the import of the frequency domain GEM becomes apparent since it allows us to determine the effect of one-sided (or causal) filtering on GC.

We need to be clear on the situation envisaged here. The unfiltered time series are the underlying series of interest, but we have access only to the filtered time series, so we can only find the GEMs from the spectrum of the filtered time series. What we need to know is when those filtered GEMs are the same as the underlying GEMs. We have:

Theorem 6

Suppose we filter z_t with a stable, full-rank, one-sided filter $\Phi \left(L\right)=\left(\begin{array}{cc}{\Phi }_{\mathit{XX}}(L)& 0\\ 0& {\Phi }_{\mathit{YY}}(L)\end{array}\right)$. Then:

1. If Φ(L) is minimum phase, the GEMs (and so GC) are unaffected by filtering.

2. If Φ(L) has the form $\Phi (L)=\psi (L)\overline{\Phi }(L)$ where ψ(L) is a scalar all-pass filter and $\overline{\Phi }(L)$ is stable, minimum phase, then the GEMs (and so GC) are unaffected by filtering.

3. If Φ(L) is nonminimum phase and case b does not hold, then the GEMs (and so GC) are changed by filtering.

Proof

Denote ${\overline{z}}_t=\mathrm{\Phi }(L)z_t=\mathrm{\Phi }(L)H(L){\epsilon }_t$ by result 2a. Then for the frequency domain GEM, we need to find $f_{\overline{Y}\to \overline{X}}\left(\mathrm{\lambda }\right)=\mathit{ln}\frac{|f_{\overline{X}}\left(\mathrm{\lambda }\right)|}{|H_{e\overline{X}}(L){\displaystyle {\sum }_{X,\epsilon }{H}_{e\overline{X}}^T\left(L^{-1}\right)}|}$, where L = exp(−jλ). We find trivially that $|f_{\overline{X}}\left(\mathrm{\lambda }\right)|=|{\mathrm{\Phi }}_X(L)f_X(\mathrm{\lambda }){\mathrm{\Phi }}_X(L^{-1})|=|{\mathrm{\Phi }}_X(L)||f_X(\mathrm{\lambda })||{\mathrm{\Phi }}_X(L^{-1})|$. Finding $H_{e\overline{X}}(L)$ is much more complicated; we need the minimum phase vector moving average or state-space model corresponding to equation 5.2. Taking Φ(L) to be nonminimum phase, we carry out a spectral factorization, $f_{\overline{z}}\left(\mathrm{\lambda }\right)=\overline{H}(L)\overline{\sum }{\overline{H}}^T(L^{-1})$, where $\overline{H}(L)$ is causal, stable, minimum phase with $\overline{H}\left(0\right)=I$ and then, from appendix C, $\overline{H}(L)$, can be written $\overline{H}(L)=\Phi (L)H(L)D(L^{-1})$, $D\left(L^{-1}\right)=J{E}^T\left(L^{-1}\right){\overline{J}}^{-1}$, where E(L) is all pass and J, $\overline{J}$ are constant matrices (Cholesky factors). Writing this in partitioned form,

$$\overline{H}\left(L\right)=\left[\begin{array}{cc}{\mathrm{\Phi }}_X(L)& 0\\ 0& {\mathrm{\Phi }}_Y(L)\end{array}\right]\left[\begin{array}{cc}{H}_{\mathit{XX}}(L)& H_{\mathit{XY}}(L)\\ H_{\mathit{YX}}(L)& H_{\mathit{YY}}(L)\end{array}\right]\left[\begin{array}{cc}{D}_{\mathit{XX}}(L^{-1})& D_{\mathit{XY}}(L^{-1})\\ D_{\mathit{YX}}(L^{-1})& D_{\mathit{YY}}\left(L^{-1}\right)\end{array}\right]$$

yields $H_{e\overline{X}}(L)={\mathrm{\Phi }}_X(L)K_{e\overline{X}}(L)$, where

$$\begin{array}{l}{K}_{e\overline{X}}(L)=H_{\mathit{XX}}(L)(D_{\mathit{XX}}(L^{-1})+D_{\mathit{XY}}(L^{-1}){\sum }_{YX,\epsilon }{\sum }_{X,\epsilon }^{-1}\\ +H_{\mathit{XY}}(L)(D_{\mathit{YY}}(L^{-1}){\sum }_{YX,\epsilon }{\sum }_{X,\epsilon }^{-1}+D_{\mathit{YX}}(L^{-1})).\end{array}$$

Thus, in $f_{\overline{Y}\to \overline{X}}\left(\mathrm{\lambda }\right)$, the |Φ_X(L)| factors cancel giving, $f_{\overline{Y}\to \overline{X}}\left(\mathrm{\lambda }\right)=\mathit{ln}\frac{|f_X(\mathrm{\lambda })|}{\left|K_{e\overline{X}}\left(L\right){\sum }_{X,\epsilon }{K}_{e\overline{X}}^T\left(L^{-1}\right)\right|}$. This will reduce to f_Y→X(λ) iff $K_{e\overline{X}}(L)=H_{eX}(L)K(L^{-1})$ where K(L⁻¹) is all pass, which occurs iff D_XY(L⁻¹) = 0, D_YX(L⁻¹)= 0, D_XX (L⁻¹) = ψ(L⁻¹)I, D_YY (L⁻¹) = ψ(L⁻¹)I where ψ(L⁻¹) is a scalar all-pass filter. Results a, b, and c now follow.

Remark

Result a has also been obtained in the independent work of Seth, Chorley, and Barnett (2013) by different methods.¹

We give three examples:

Example 6A

Differential delay. Suppose $\left(\begin{array}{c}{x}_t\\ y_t\end{array}\right)=\left(\begin{array}{cc}1& 0\\ \rho & 1\end{array}\right)\left(\begin{array}{c}{\epsilon }_t\\ {\nu }_t\end{array}\right)$ where ε_t, ν_t are independent zero mean white noises with variances 1, σ², respectively, while $\Phi \left(L\right)=\left(\begin{array}{cc}1& 0\\ 0& L\end{array}\right)$. So the two series are white noises that exhibit an instantaneous GC. The filtering delays one series relative to the other. Then we have ${\overline{z}}_t=\left(\begin{array}{cc}1& 0\\ 0& L\end{array}\right)\left(\begin{array}{cc}1& 0\\ \rho & 1\end{array}\right)\left(\begin{array}{c}{a}_t\\ b_t\end{array}\right)=\left(\begin{array}{cc}1& 0\\ L_{\rho }& 1\end{array}\right)\left(\begin{array}{c}{a}_t\\ b_t\end{array}\right)=\overline{H}(L)\left(\begin{array}{c}{a}_t\\ b_t\end{array}\right)$, and we see that $\overline{H}\left(0\right)=I$ while $\overline{H}\left(L\right)$ is stable, causal, and invertible; indeed, ${\overline{H}}^{-1}(L)=\left(\begin{array}{cc}1& 0\\ -L\rho & 1\end{array}\right)$. Thus, we see that the differential delay has introduced a spurious dynamic GC relation and the original purely instantaneous GC is lost.

Example 6B

Noncausal filter. We use the same setup as in example 6 A except that now $\mathrm{\Phi }(L)=\left(\begin{array}{cc}1-{\theta }_x{L}^{-1}& 0\\ 0& 1-{\theta }_y{L}^{-1}\end{array}\right)$ where |θ_x| < 1, |θ_y| < 1 and θ_x ≠ θ_y. We rewrite this as −L⁻¹Ψ(L) where $\mathrm{\Psi }(L)=\left(\begin{array}{cc}{\theta }_x(1-\frac{1}{{\theta }_x}L)& 0\\ 0& {\theta }_y(1-\frac{1}{{\theta }_y}L)\end{array}\right)$. Although L⁻¹ is noncausal and so NMP, it is the same for both filters and so by theorem 6b will not affect the GEMS. So we can replace Φ(L) with Ψ(L). Both entries in Ψ(L) are causal but unstable, and so NMP and the GCS will be altered. In fact, we now show this explicitly.

Note, first, how the noncausal filter operates. We have

$${\overline{z}}_t=\mathrm{\Psi }(L)z_t=\left(\begin{array}{cc}{\theta }_x-L& 0\\ 0& {\theta }_y-L\end{array}\right)\left(\begin{array}{c}{x}_t\\ y_t\end{array}\right)=\left(\begin{array}{c}{\theta }_x{x}_t-x_{t+1}\\ {\theta }_y{y}_t-y_{t+1}\end{array}\right).$$

Future values are needed to compute the filtered signal at the current time.

The process ${\overline{z}}_t=\mathrm{\Psi }(L)z_t$ has spectrum $\left(\begin{array}{cc}AA\ast & \rho A\ast B\\ \rho B\ast A& ({\rho }^2+{\sigma }^2)BB\ast \end{array}\right)$ where $A=A(L)={\theta }_x\left(1-\frac{1}{{\theta }_x}L\right)$, $A\ast =A(L^{-1})$ and similarly for B. It is straightforward to check that this has spectral factorization,

$$\left(\begin{array}{cc}a& \frac{\rho }{R^2}a\\ 0& b\end{array}\right)\left(\begin{array}{cc}\frac{{\alpha }^2}{R^2}& 0\\ 0& R^2\end{array}\right)\left(\begin{array}{cc}a\ast & 0\\ \frac{\rho }{R^2}a\ast & b\ast \end{array}\right)=\left(\begin{array}{cc}aa\ast & \rho b\ast a\\ \rho ba\ast & R^{2}bb\ast \end{array}\right),$$

where $R=\sqrt{{\rho }^2+{\sigma }^2}$ and a = 1 − θ_xL, b = 1 − θ_yL. Note that AA^∗ = aa^∗ and A^∗B = ab^∗. This factorization corresponds to the model $\left(\begin{array}{c}{\overline{x}}_t\\ {\overline{y}}_t\end{array}\right)=\left(\begin{array}{cc}a& \frac{\rho }{R^2}a\\ 0& b\end{array}\right)\left(\begin{array}{c}{\epsilon }_{a,t}\\ {\nu }_{b,t}\end{array}\right)$ where ε_a,t, ν_b,t are independent white noises of variances $\frac{{\rho }^2}{R^2}$, R², respectively. We see that the NMP filtering has introduced spurious dynamics and reversed the GCS.

Example 6C

Wiener deconvolution. When filtered versions of x_t, y_t are observed in noise, one can estimate them by using the Wiener fitler (Kailath et al., 2000). The optimal filter uses the joint spectrum, but fMRI practice (Glover, 1999) is to filter each signal separately. This is suboptimal but will still reduce the effect of the noise. Suppose we observe w_x,t = h_x(L)x_t + ε_t where h(L) is a stable filter and ε_t is a white noise of variance σ² independent of x_t. The Wiener filter estimate of x_t is ${\widehat{x}}_t=W_x(L)w_{x,t}$ where (Kailath et al., 2000) $W_x(L)=\frac{h_x^{\ast }}{h_x{h}_x^{\ast }+{\sigma }^2/{\gamma }_x}$ where γ_x = γ_x(L) is the autocovariance generating function of x_t. In fMRI practice (Glover, 1999), γ_x(L) is set to 1. This is sub-optimal and may lead to performance worse than no filtering. But continuing, we carry out a spectral factorization giving $h_x{h}_x^{\ast }+{\sigma }^2={\sigma }_e^2{k}_x{k}_x^{\ast }$ where k_x = k_x(L) is a causal minimum phase filter with k_x(0) = 1. The filter thus becomes $W_x(L)=\frac{h_x^{\ast }}{{\sigma }_e^2{k}_x{k}_x^{\ast }}$. Since k_x is minimum phase and causal, then $k_x^{-1}$ is stable and causal and will not affect the GEMS. We are left with the noncausal filter ${\beta }_x^{\ast }=\frac{h_x^{\ast }}{k_x^{\ast }}$— for example, in the simple case, h_x= 1 − θ_xL, |θ_x| < 1, the spectral factorization reduces to solving a quadratic equation and one obtains k_x = 1 − α_x L, |α_x| < 1 Thus, ${\beta }_x^{\ast }=\frac{1-{\theta }_x{L}^{-1}}{1-{\alpha }_x{L}^{-1}}=1+{\displaystyle {\sum }_1^{\infty }\left({\alpha }_x-{\theta }_x\right){\alpha }_x^{r-1}{L}^{-r}}$. With a similar deconvolution (where β_x ≠ β_y) applied to a noisy filtered version of y_t, we conclude that deconvolution will distort the GCS since the β_x, β_y filters are noncausal.

7 Downsampling and Forwards Granger Causality

We now consider to what extent GC is preserved under downsampling.

Using the sampled notation of our discussion above and defining ${\overline{z}}_x=\left(\begin{array}{c}{\overline{x}}_k\\ {\overline{y}}_k\end{array}\right)$, we have the following result:

Theorem 7

Forwards causality:

1. If y_t dn-sgc x_t, then ${\overline{y}}_k$ dn-sgc ${\overline{x}}_k$.

2. If y_t dn-wgc x_t, then in general ${\overline{y}}_k$ wgc ${\overline{x}}_k$.

Remarks

1. Part a is new, although technically a special case of a result of the author’s established in a non-SS framework.

2. We might consider taking part b as a formalization of longstanding folklore in econometrics (Christiano & Eichenbaum, 1987; Marcet, 1991) that downsampling can destroy unidirectional Granger causality. However, that same folklore is flawed because it failed to recognize the possibility of part a. The folklore is further flawed because it failed to recognize the more serious reverse problem discussed below.

Proof of Theorem 7, Part a

We use the partitioned expressions in the discussion leading up to result 3. We also refer to the discussion leading up to theorem 6.

This allows us to write two decompositions. First, we write w_k=w_X,k +w_Y,k, where

$$w_{X,k}={\displaystyle {\sum }_1^m{A}^{m-i}{B}_X{\epsilon }_{X,km+i-1},}{w}_{Y,k}={\displaystyle {\sum }_1^m{A}^{m-i}{B}_Y{\epsilon }_{X,km+i-1}}.$$

From result 3 and the definition of dn-sgc,

$$w_{X,k}\text{is uncorrelated with}{w}_{Y,l}\text{for all}k,l.$$ (7.1)

The other decomposition is ${\overline{\epsilon }}_k=\left(\begin{array}{c}{\overline{\epsilon }}_{X,k}\\ {\overline{\epsilon }}_{Y,k}\end{array}\right)$, and

$${\overline{\epsilon }}_{X,k}\text{is uncorrelated with}{\overline{\epsilon }}_{Y,l}\text{for all}k,l.$$ (7.2)

Next we note from theorem 4 that

$$C_X{(L^{-1}I-A^m)}^{-1}{A}^p{B}_Y=C_X{\displaystyle {\sum }_1^{\infty }{A}^{m+r-1}{B}_Y{L}^r=0.}$$

for all p ≥ 0. Thus, we deduce

$$C_X{w}_{Y,k}=0,\text{for all}k.$$ (7.3)

We can now write

$$\begin{array}{l}{\overline{x}}_k=C_X{(L^{-1}I-A^m)}^{-1}{w}_k+{\overline{\epsilon }}_{X,k}\\ =C_X{(L^{-1}I-A^m)}^{-1}{w}_{X,k}+{\overline{\epsilon }}_{X,k}\\ {\overline{y}}_k=C_Y{(L^{-1}I-A^m)}^{-1}{w}_{X,k}+C_Y{(L^{-1}I-A^m)}^{-1}{w}_{Y,k}+{\overline{\epsilon }}_{Y,k}.\end{array}$$ (7.4)

Based on equation 7.4, we now introduce the ISS model for ${\overline{x}}_k$,

$${\overline{x}}_k=C_X{(L^{-1}I-A^m)}^{-1}{K}_{(X)}{\nu }_{X,k}+{\nu }_{X,k},$$

where ν_X,k is the innovations sequence. Using this, we introduce the estimator K_(X)ν_X,k of w_X,k and the estimation error ${\stackrel{\sim }{w}}_{X,k}=w_{X,k}-K_{(X)}{\nu }_{X,k}$. Below we show

$${\stackrel{\sim }{w}}_{X,k}\text{is uncorrelated with}{\nu }_{X,l}\text{for all}k,l.$$ (7.5)

We thus rewrite the model for ${\overline{y}}_k$ as

$$\begin{array}{l}{\overline{y}}_k=C_Y{(L^{-1}I-A^m)}^{-1}{K}_{(X)}{\nu }_{X,k}+{\zeta }_k,\\ {\zeta }_k=C_Y{(L^{-1}I-A^m)}^{-1}[w_{Y,k}+{\stackrel{\sim }{w}}_{X,k}]+{\overline{\epsilon }}_{Y,k}.\end{array}$$

Now we can construct an ISS model for ζ_k = (I + C_Y (L⁻¹ I − A^m)⁻¹K_(Y))ν_Y,k where ν_Y,k is the innovations sequence. In view of equations 7.1, 7.2, and 7.5, ν_X,k and ν_Y,l are uncorrelated for all k, l. Thus, we have constructed the joint ISS model:

$$\begin{array}{l}\left[\begin{array}{c}{\overline{x}}_k\\ {\overline{y}}_k\end{array}\right]=\overline{H}(z)\left[\begin{array}{c}{\nu }_{X,k}\\ {\nu }_{Y,k}\end{array}\right]\\ \overline{H}(z)=\left[\begin{array}{cc}I+C_X{(L^{-1}I-A^m)}^{-1}{K}_{(X)}& 0\\ C_Y{(L^{-1}I-A^m)}^{-1}{K}_{(X)}& I+C_Y{(L^{-1}I-A^m)}^{-1}{K}_{(Y)}\end{array}\right].\end{array}$$

From this we deduce that ${\overline{y}}_k$ dn-sgc ${\overline{x}}_k$ as required.

Proof of Equation 7.5

Consider then $E({\stackrel{\sim }{w}}_{X,k}{\nu }_{X,l}^T)=E(w_{X,k}-K_{(X)}{\nu }_{X,k}){\nu }_{X,l}^T)=E(w_{X,k}{\nu }_{X,l}^T-K_{(X)}E({\nu }_{X,k}{\nu }_{X,l}^T)$. The second term vanishes for k ≠ l. The first term vanishes for k > l since w_X,_k is uncorrelated with the past and hence ν_X,l; for l > k, it vanishes since ν_X,l is uncorrelated with the past. For k = l, it vanishes by the definition of K_(X) (Kailath et al., 2000).

Proof of Theorem 7, Part b

A perusal of the proof of theorem 7, part a, shows that we cannot construct the block lower triangular joint ISS model. In general, we obtain a full block ISS model.

8 Downsampling and Reverse Granger Causality

We now come to the more serious issue of how downsampling might distort GC. To establish distortion, we simply have to exhibit a numerical example, but that is not as simple as one might hope.

8.1 Simulation Design

Designing a procedure to generate a wide class of examples of spurious causality is not as simple as one might hope. We develop such a procedure for a bivariate vector autoregression of order one: a bivariate VAR(1). On the one hand, this is about the simplest example one can consider; on the other hand, it is general enough to generate important behaviors.

The bivariate VAR(1) model is then

$$\left(\begin{array}{c}{x}_t\\ y_t\end{array}\right)=A\left(\begin{array}{c}{x}_{t-1}\\ y_{t-1}\end{array}\right)+\left(\begin{array}{c}{\epsilon }_{X,t}\\ {\epsilon }_{Y,t}\end{array}\right),A=\left(\begin{array}{cc}{\varphi }_x& {\gamma }_x\\ {\gamma }_y& {\varphi }_y\end{array}\right),{\displaystyle \sum =\left(\begin{array}{cc}{\sigma }_a^2& \rho {\sigma }_a{\sigma }_b\\ \rho {\sigma }_a{\sigma }_b& {\sigma }_b^2\end{array}\right),}$$

Where Σ is the variance matrix of the zero mean white noise $\left(\begin{array}{c}{\epsilon }_{X,t}\\ {\epsilon }_{Y,t}\end{array}\right)$ and ρ is a correlation.

We note that this model can be written as an ISS model with parameters, A, I, −A, Σ. Hence, all the computations described above are easily carried out.

But the real issue is how to select the parameters. By a straightforward scaling argument, it is easy to see that we may set σ_a = 1 = σ_b without loss of generality. Thus, we need to choose only A, ρ.

Some reflection shows that there are two issues. First, we must ensure the process is stationary; for the eigenvalues λ₁, λ₂ of A, we must have |λ₁| < 1, |λ₂| < 1. Second, to design a simulation, we need to choose F_Y→X, F_X→Y, but these quantities depend on the parameters A, ρ in a highly nonlinear way, so it is not obvious how to do this. And five parameters are already too many to pursue this by trial and error.

For the first issue, we have trace(A) = λ₁ + λ₂=ϕ_x + ϕ_y and det(A) = λ₁λ 2 = ϕ_xϕ_y − γ_xγ_y. Our approach is to select λ₁, λ₂ and then find ϕ_x, ϕ_y to satisfy ϕ_x + ϕ_y = λ₁ + λ₂, ϕ_xϕ_y = λ₁λ₂ + γ_xγ_y. This requires solving a quadratic equation. If we denote the solutions as r₊, r₋, then we get two cases: (ϕ_x, ϕ_y) = (r₊, r₋) and (ϕ_y, ϕ_x) = (r₊, r₋). This leaves us to select γ_x, γ_y.

In appendix B we show that $F_{Y\to X}=\mathit{ln}\frac{{\sigma }_x^2}{{\sigma }_a^2}\ge \mathit{ln}(1+{\xi }_x)$ where ${\xi }_x={\gamma }_x^2(1-{\rho }^2)$. Similarly, F_X→Y ≥ ln(1 + ξ_y) where ${\xi }_y={\gamma }_y^2(1-{\rho }^2)$. But we also show that ξ_x = 0 ⇒ F_Y→X = 0 and ξ_y = 0 ⇒ F_X→Y = 0, so we select ξ_x, ξ_y, thereby setting a lower bounds to F_Y→X, F_X→Y. This seems to be the best one can do, and as we see below, it works quite well. So given ξ_x, ξ_y, compute ${\gamma }_x=\pm \frac{\sqrt{{\xi }_x}}{\sqrt{1-{\rho }^2}}$ and ${\gamma }_y=\pm \frac{\sqrt{{\xi }_y}}{\sqrt{1-{\rho }^2}}$. This gives four cases and multiplied by the two cases above yields eight cases.

This is not quite the end of the story since the γ_x, γ_y values need to be consistent with the ϕ_x, ϕ_y values. Specifically the quadratic equation to be solved for ϕ_x, ϕ_y must have real roots. Thus, the discriminant must be ≥ 0. So (ϕ_x + ϕ_y)² − 4(ϕ_xϕ_y) = (λ₁ + λ₂)² − 4(λ₁λ₂ + γ_xγ_y)=(λ₁− λ₂)² − 4γ_xγ_y ≥ 0. There are four cases: two with real roots and two with complex roots.

If λ₁, λ₂ are real, then we require ${({\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2)}^2\ge 4{\gamma }_x{\gamma }_y\Rightarrow {({\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2)}^2\ge 4\mathit{sign}({\gamma }_x{\gamma }_y)\frac{\sqrt{{\xi }_x{\xi }_y}}{1-\rho }$. This always holds if sign(γ_xγ_y) ≤ 0. If sign(γ_x γ_y) > 0, we have a binding constraint that restricts the sizes of ξ_x, ξ_y.

If λ₁, λ₂ are complex conjugates, then (λ₁−λ₂)² is negative. If sign(γ_xγ_y) ≥ 0, then the condition never holds. If sign(γ_xγ_y) < 0, then there is a binding constraint that restricts the sizes of ξ_x, ξ_y. In particular, note that if sign(γ_xγ_y) = 0, then one cannot have complex roots for A. We now use this design procedure to illustrate reverse causality.

8.2 Computation

We describe the steps used to generate the results below. We assume the state-space model for $z_t=\left(\begin{array}{c}{x}_t\\ y_t\end{array}\right)$ comes in ISS form. Since standard state-space subspace model-fitting algorithms (Larimore, 1983; van Overschee & de Moor, 1996; Bauer, 2005) generate ISS models, this is a reasonable assumption. Otherwise we use result 1 to generate the corresponding ISS model.

Given a sampling multiple m, we first use theorem 3 to generate the subsampled ISS model and, hence, ${\displaystyle {\sum }_{\epsilon }^{(m)}}$. To obtain the GEMs, we use theorem 1 to generate the marginal models for x_t, y_t yielding ${\mathrm{\Omega }}_X^{(m)}$, ${\mathrm{\Omega }}_Y^{(m)}$. And now $F_{Y\to X}^{(m)}$, $F_{X\to Y}^{(m)}$ are gotten from formulas 5.8 and 5.9 and the comment following theorem 5a.

8.3 Scenario Studies

We now illustrate the various results above with some bivariate simulations.

Example 1: GEMs Decline Gracefully

Here, for the underlying process, y pushes x much harder than x pushes y. This pattern is roughly preserved with slower sampling, but the relative strengths change as seen in Table 1.

Table 1.

GEMs for Various Sampling Intervals for (λ₁, λ₂, ξ_x, ξ_y, ρ) = (−.95 exp(j × .1), −.95 exp(− j × .1), 1.5, .2, .2) ⇒ $A=\left(\begin{array}{cc}-.204& -1.24\\ .452& -1.69\end{array}\right)$.

m	1	2	3	4	5	6	10	20	30	40
FY→X	1.38	1.66	1.41	1.17	0.99	0.86	0.551	0.15	0.00	0.01
FX→Y	0.20	0.25	0.29	0.31	0.32	0.32	0.29	0.11	0.00	0.01

Example 2: GEMs Reverse

In this case, the underlying processes push each other with roughly equal strength. But subsampling yields a false picture with x pushing y much harder than the reverse (see Table 2).

Table 2.

GEMs for Various Sampling Intervals for (λ₁, λ₂, ξ_x, ξ_y, ρ) = (.95 exp(j × .1), .95 exp(− j × .1), 1.5, .2, .2) ⇒ $A=\left(\begin{array}{cc}1.69& -1.24\\ .452& .204\end{array}\right)$.

m	1	2	3	4	5	6	10	20	30	40
FY→X	0.93	0.88	0.77	0.683	0.62	0.57	0.42	0.13	0.00	0.01
FX→Y	1.05	1.82	2.01	1.80	1.53	1.30	0.75	0.18	0.00	0.02

Example 3: Near Equal Strength Dynamics Becomes Nearly Unidirectional

In this case, the underlying relation is one of near equal strength feedback interconnection. But as Table 3 shows, almost immediately a very unequal relation appears under subsampling which soon decays to a near unidirectional relation.

Table 3.

GEMs for Various Sampling Intervals for (λ₁, λ₂, ξ_x, ξ_y, ρ) = (.995, −.7, 1, .5, .7) ⇒ $A=\left(\begin{array}{cc}-1.45& -1.18\\ -.84& -1.16\end{array}\right)$

m	1	2	3	4	5	6	10	20	30	40
FY→X	1.49	0.05	0.25	0.06	0.11	0.05	0.04	0.02	0.01	0.01
FX→Y	1.69	0.17	0.64	0.26	0.47	0.29	0.29	0.21	0.16	0.13

Example 4: Near Unidirectional Dynamics Becomes Near Equal Strength

In this case a near unidirectional dynamic relation immediately becomes one of significant but unequal strengths and then one of near equal strength (see Table 4).

Table 4.

GEMs for Various Sampling Intervals for (λ₁, λ₂, ξ_x, ξ_y, ρ) = (.99 exp(j × .25), .95 exp(− j × .25), .1, 3, −.8) ⇒ $A=\left(\begin{array}{cc}1.883& -0.408\\ 2.236& 0.036\end{array}\right)$.

m	1	2	3	4	5	6	10	20	30	40
FY→X	0.02	0.28	0.38	0.43	0.45	0.46	0.31	0.45	0.41	0.17
FX→Y	2.93	2.38	1.62	1.24	1.02	0.86	0.37	0.53	0.45	0.18

There is nothing pathological about these examples, and using the design procedure developed above, it is easy to generate other similar kinds of examples. They make it emphatically clear that GC cannot be reliably discerned from downsampled data.

In independent work, Seth et al. (2013) have shown simulations where downsampling distorts GC. But their work is purely empirical, and they do not have the theoretical framework developed here to design specific types of distortion as we have done.

9 Application to fMRI

In this section we apply the above results to fMRI, but to do so, we need to describe fMRI data generation schemes (dgs’s); we give three such schemes The following feature is common to all of them.

We suppose there is an underlying neural activity (NA) 2-node circuit operating on a fast timescale of order 50 ms and that it is described by a state-space model. Specifically, the (possibly vector) NA signals at each node are x_t, y_t, which we collect together into a joint NA vector signal $z_t=\left(\begin{array}{c}{x}_t\\ y_t\end{array}\right)$, which is described by a state-space model such as equation 2.1 or 2.3.

• Filter (F). The BOLD signal recorded at a particular voxel is generated as follows. The NA z_t is filtered by (a spatially varying) HRF to generate a fast BOLD signal ${\overline{z}}_{b,t}$—specifically

  $${\overline{z}}_{b,t}=\left(\begin{array}{c}{\overline{x}}_{b,t}\\ {\overline{y}}_{b,t}\end{array}\right)=\left[\begin{array}{cc}{H}_{\mathit{xx}}(L)& 0\\ 0& H_{\mathit{yy}}(L)\end{array}\right]z_t$$

• Filter then downsample (F-DS). The BOLD signal recorded at a particular voxel is generated in two stages. The first stage is the same as F. In the second stage, the scanner samples this signal delivering a downsampled (or slow) BOLD signal $z_{b,k}={\overline{z}}_{b,mt}$—for example, if the NA timescale is 50 ms and the downsampled time scale is 200 ms, then m = 4.

• Downsample then filter (DS-F). Here we suppose the NA z_t is down-sampled to a slow timescale giving a slow NA ${\overline{z}}_k=z_{\mathit{mt}}$. This is then filtered by (a slow spatially varying) HRF to generate the slow BOLD signal z_b,k.

Note that F is the limiting case of F-DS where fMRI is recorded on the same timescale as NA. Clearly F-DS makes physiological sense, whereas DS-F does not. Indeed F-DS is advocated by Deshpande et al. (2010), who provide further physiological references to back it up. However, below we will see that DS-F seems to be behind some of the processing methods used in practice.

The aim now is to try to solve the reverse GC problem; to determine the GCS of fast NA circuit z_t from the GCS of either the fast BOLD circuit ${\overline{z}}_i$ or the slow BOLD circuit z_b,k. To do this, we see from theorem 6, that we need to investigate the phase properties of the HRF.

9.1 HRFs Are Nonminimum Phase

We denote an HRF by h_r, r=1, 2,⋯ and its transfer function as $h(L)={\displaystyle {\sum }_1^{\infty }{h}_r{L}^r=}{\displaystyle {\sum }_1^{\infty }{h}_r{z}^{-r}=}H(z)$. We assume H(z) is bounded input, bounded output stable (Kailath et al., 2000), for which the necessary and sufficient condition is $B={\displaystyle {\sum }_1^{\infty }\left|h_r\right|<\infty }$.

In Figure 1 we show plots of canonical HRFs (with default parameter choices) used in SPM and Glover (1999). They exhibit three main features found in practice:

1. Refractory period: Characterized by a time to onset τ_o

2. Overshoot—characterized by a peak time τ_p

3. Undershoot

Figure 1.

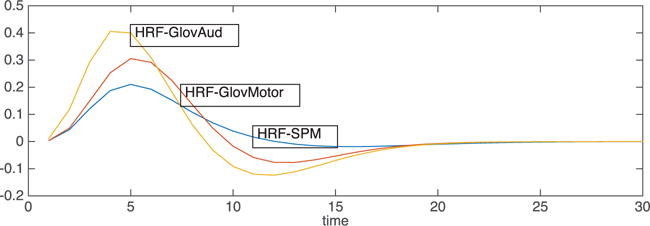
Canonical HRFs.

Also there are persistent reports in the literature of HRFs with an initial small dip immediately following the refractory period (e.g., Miezin, Maccotta, Ollinger, Petersen, & Buckner, 2000).

A number of results in the control engineering literature show how nonminimum phase (NMP) zeros of the transfer function imply overshoot and undershoot of an impulse response (see Damm & Muhirwa, 2014). But none of these works provide converse results, showing what impulse response shape implies about transfer function zeros.

We give a preliminary general result and then two converse results.

Theorem 8a

Any HRF with a refractory period is NMP.

Proof

We can write the transfer function as h(L) = L^τo g(L) where g(L) is a causal transfer function. Even if g(L) is MP, then h(L) is NMP because L^−τo is not a causal operator.

Certainly the time to onset can be estimated, and then the BOLD signal can be shifted in time to align the start time with the stimulus start time. This effectively corrects the HRF for the refractory period. But this makes sense only if it is known that the refractory period is due to information transmission delay. If it is due to the GCS, then such alignment, being noncausal, will destroy the GCS.

To continue, we now assume the HRF has been corrected for the refractory period so that the corrected transfer function is $H_c(z)=z{\displaystyle {\sum }_1^{\infty }{h}_r{z}^{-r}}$.

Theorem 8b

Dip: if h₁ < 0 and H(1) > 0, then the HRF is NMP.

Note that $H_c(1)=H(1)={\displaystyle {\sum }_1^{\infty }{h}_r=-\text{area above the dip}+\text{area under the overshoot}-\text{area above the undershoot}}$. The fact that the overshoot area (far) exceeds the sum of the other two areas (so that H(1) > 0) seems to be a universal property of actual HRFs.

Proof

We prove that H_c(z) has a real zero outside the UC. We can set z = R, which is real. Then consider that $H_c(R)=RH(R)=R{\displaystyle {\sum }_1^{\infty }{h}_r{R}^{-r}=h_1+}{\displaystyle {\sum }_2^{\infty }{h}_r{R}^{-(r-1)}}$. For R ≥ 1, the second term is bounded by $R^{-1}{\displaystyle {\sum }_2^{\infty }\left|h_r\right|}<R^{-1}B$ and → 0 as R → ∞. Since h₁ < 0, then for R large enough, RH(R) < 0 Since 1H(1) > 0, this means there must exist R_o > 1 with R_oH(R_o) = 0 as required.

Theorem 8c

No dip: if h₁ > 0 and H(−1) > 0, then the HRF is NMP.

Note that $H(-1)={\displaystyle {\sum }_1^{\infty }{(-1)}^r{h}_r={\displaystyle {\sum }_{m=1}^{\infty }(h_{2m}-h_{2m-1})}}$ and H(−1) > 0 is satisfied by the default canonical HRFs. Further, because HRFs are very smooth, the successive differences h_2m − h_2m−1 will be very small. H(−1) can be split into four pieces: a positive sum up to the peak time, a negative sum from there to the zero crossing, a positive sum to the trough of the undershoot, and a negative sum from there back up to the the time axis. We thus expect H(−1) to be small.

Proof

We prove H_c(z) has a complex zero outside the UC. Put z = Re^jπ = −R. Then consider that $-H_c(-R)=RH(-R)=R{\displaystyle {\sum }_1^{\infty }{h}_r}{(-R)}^{-r}=-h_1+{\displaystyle {\sum }_2^{\infty }{h}_r{(-1)}^r{R}^{-(r-1)}}$. For R ≥ 1, the second term is bounded by $R^{-1}{\displaystyle {\sum }_2^{\infty }\left|h_r\right|<R^{-1}B}$, which → 0 as R → ∞ and so since −h₁ < 0, then for R large enough, RH(−R) < 0. Since 1H (−1) > 0, there must thus exist R_o > 1 for which R_oH(−R_o) = 0 and the result is established.

Since the condition H(−1) > 0 and more generally the possibility of complex zeros outside the UC is so crucial, more flexible modeling of the HRF is called for. Recent approaches include Khalidov, Fadili, Lazeyras, Ville, and Unser (2011), Zafer, Blu, and Ville (2014), Wu et al. (2013), Sreenivasan, Havlicek, and Deshpande (2015) and our approach using Laguerre-polynomials (Cassidy, Long, Rae, & Solo, 2012).

9.2 Deconvolution

As noted in section 1, the current practice is to first apply a deconvolution to the BOLD signals before carrying out a GC analysis. As discussed in section 9.3, this makes sense only for DS-F.

We now see from the deconvolution example 6 C that even if Wiener deconvolution is applied to noise-free data z_b,k, it will distort the GCS because it necessarily involves noncausal filtering. This is discussed further in section 9.3.

9.3 Reverse GC Problem

We discuss approaches under F, F-DS, and DS-F.

F

There is only one approach possible here. If the HRF is minimum phase, then the fast filtering will not affect the GCS and the first stage would consist of a GC analysis of the fast BOLD data. That is, fit an SS model to ${\overline{z}}_{b,t}$; find submodels for ${\overline{x}}_{b,t}$, ${\overline{y}}_{b,t}$ using DARE (see theorem 1); and compute the GEMS F_Y→X, F_Y.X, F_X→Y using the expressions in theorem 5a. This would deliver the GCS of the fast BOLD circuit and, hence, of the NA circuit. But in practice, the BOLD data will be noisy, and an attempt to reduce the impact of the noise by deconvolution will distort the GCS. If the HRF is nonminimum phase, then this GCS would be distorted and nothing can be done to overcome that.

F-DS

Again there is only one approach possible here. If the HRF is minimum phase, then the fast filtering will not affect the GCS and the first stage would consist of a GC analysis of the slow BOLD data—that is, fit an SS model to z_b,k; find submodels for x_b,k, y_b,k using DARE (see theorem 1); and compute the GEMS F_Y→X, F_Y.X, F_X→Y using the expressions in theorem 5a. This would deliver the GCS of the slow BOLD circuit. The second stage is to try to get the GCS of the fast BOLD circuit. But now we see that it must fail since the results of the reverse GC study in section 8 demonstrate that we cannot use the GCS of the slow BOLD circuit to discern the GCS of the fast BOLD circuit. So we cannot get at the GCS of the fast NA circuit.

Notice that in F-DS there is no role for deconvolution.

If the HRF, is NMP then the GCS will be distorted and there is nothing we can do to overcome this. If we apply deconvolution, then the analysis above shows it must fail since the Wiener filter is NMP.

DS-F

There are two approaches here. The direct approach has two stages. If the HRF is minimum phase, then the slow filtering will not affect the GCS and the first stage would consist of a GC analysis of the slow BOLD data—that is, fit an SS model to z_b,k; find submodels for x_b,k, y_b,k using DARE (see theorem 1); and compute the GEMS F_Y→X, F_Y.X, F_X→Y using the expressions in theorem 5a. This would deliver the GCS of the slow NA circuit since by theorem 6, the GEMS would be the same as for the slow BOLD data. The second stage is to try to get the GCS of the fast NA circuit. But now we see that it must fail, since the results of the reverse GC study in section 8 demonstrate that we cannot use the GCS of the slow NA circuit to discern the GCS of the fast NA circuit.

The indirect approach has three stages. If the slow HRF is minimum phase, then in the zeroth stage, we could inverse filter (deconvolve) the slow BOLD data to obtain the slow NA. In the first stage, we obtain its GCS using the procedure described in the first stage of the direct approach. But for the second stage, we are in the same situation as in the direct approach and must fail to discern the GCS of the fast NA.

In practice, slow timescale deconvolution has gained favor recently. It is done using a Wiener filter (Glover, 1999) since this deals with possible noise (which we have ignored in our discussion). But as discussed above, this must fail since the Wiener filter is NMP.

We see here that only in DS-F is there a role for slow timescale deconvolution.

In sum we conclude that under any data-generating scheme, GC analysis must fail.

We note that there is an extensive discussion of GC in fMRI in Rodrigues and Andrade (2015). Unfortunately this work relies on the erroneous method of Chen et al. (2006) for computing GEMs (see the remarks following theorem 5b), and so its results are flawed.

10 Conclusion

This letter has given a theoretical and computational analysis of the use of Granger causality (GC) and applied the results to fMRI. There were two main issues: the effect of downsampling and the effect of hemodynamic filtering on Granger causal structure (GCS). To deal with these issues, a number of novel results in multivariate time series and Granger causality were developed via state-space methods as follows:

1. Computations of submodels via the DARE (see theorems 1 and 4)

2. Computation of downsampled models via the DARE (see theorem 3)

3. Reliable computation of GEMs via the DARE (see theorems 5a and 5b)

4. Effect of filtering on GEMs (see theorem 6)

Theorem 6 showed that nonminimum phase filters distort GCS. Using the results in the first three methods, we were able to develop, in section 8, a framework for generating downsampling-induced spurious Granger causality on demand and provided a number of illustrations.

In section 9 these results were applied to fMRI. To do this we described three data generating processes for fMRI:

1. F where fMRI time series are filtered neural activity (NA)

2. F-DS where NA is filtered, then downsampled to give fMRI time series

3. DS-F where NA is downsampled, then fitered to give fMRI time series

While F-DS has strong physiological justification, DS-F seems to be behind a number of approaches in the literature. We showed that HRFs are non-minimum phase due to a refractory period. If that period can be corrected for, the phase character of the HRF has to be checked on a case-by-case basis. Certainly default canonical HRFs are nonminimum phase, and so more flexible HRF modeling will be needed.

Then we discussed the reverse GC problem under each data-generating process. In each case, we concluded that GC analysis could not work.

All this leads to the conclusion that linear Granger causality analysis of fMRI data cannot be used to discern neuronal level–driving relationships. Not only is the timescale too slow, but even with faster sampling, the non-minimum phase aspect of the HRF and the noise will still compromise the method.

Future work would naturally include an extension of the Granger causality results to handle the presence of a third vector time series and extensions to deal with time-varying Granger causality. Nongaussian versions could mitigate the nonminimum phase problem to some extent, but there does not seem to be any evidence for the nongaussianity of fMRI data. Extensions to nonlinear Granger causality are currently of great interest but need considerable development.

Appendix A: Stabilizability, Detectability, and DARE

In this appendix we restate and modify for our purposes some standard state-space results. We rely mostly on Kailath et al. (2000, appendixes E and C).

We denote an eigenvalue of a matrix by λ and a corresponding eigenvector by q. We say λ is a stable eigenvalue if |λ| < 1; otherwise, λ is an unstable eigenvalue.

A.1 Stabilizability

The pair (A, B) is controllable if there exists a matrix G so that A−BG is stable (i.e., all eigenvalues of A−BG are stable). (A, B) is controllable iff any of the following conditons hold,

• Controllability matrix: C = [B, AB, …, Aⁿ⁻¹B] has rank n.

• Rank test: rank[λI − A, B] = n for all eigenvalues λ of A.

• PBH test: There is no left eigenvector of A that is orthogonal to B, that is, if q^TA = λq^T, then q^TB ≠ 0.

The pair (A, B) is stabilizable if rank[λI − A, B] = n for all unstable eigen-values of A. Three useful tests for stabilizability are:

• PBH test: (A, B) is stabilizable iff there is no left eigenvector of A corresponding to an unstable eigenvalue that is orthogonal to B, that is, if q^TA = λq^T and |λ| 1, then q^TB ≠ 0.

• (A, B) is stabilizable if (A, B) is controllable.

• (A, B) is stabilizable if A is stable.

A.2 Theorem DARE

See Kailath et al. (2000, theorem E6.1, lemma 14.2.1, section 14.7).

Under conditions N,St,De, the DARE has a unique positive semidefinite solution P, which is stabilizing (i.e., A_s − K_sC is a stable matrix). Further if we initialize P₀ = 0, then P_t is nondecreasing and P_t → P as t → ∞.

Remarks

1. “A_s − K_sC stable” means that A−KC is stable (see below), and this implies that (A, K) is controllable (see below).

2. Since V ≥ R, then N ⇒ V is positive definite.

Proof of Remark i

We first note (taking limits in) (Kailath et al., 2000, equation 9.5.12) K_s = K − SR⁻¹. We then have A_s−K_sC=A − SR⁻¹C − (K − SR⁻¹)C = A − KC. So A_s− K_sC is stable iff A−KC is stable. But then (A, K) is controllable.

A.3 Detectability

The pair (A,C) is detectable if (A^T,C^T) is stabilizable.

Remarks

1. If A_s is stable (all eigenvalues have modulus < 1), then St De automatically hold.

2. Condition De can be replaced with the detectability of (A,C) which is the way Kailath et al. (2000) state the result. We show equivalence below (this is also noted in a footnote in Kailath et al., 2000, section 14.7).

Proof of Remark ii

Suppose (A_s,C) is detectable but (A,C) is not. Then by the PBH test, there is a right eigenvector p of A corresponding to an unstable eigenvalue of A with Ap = λp,Cp = 0. But then A_sp = (A − SR⁻¹C)p = Ap = λp while Cp = 0 which contradicts the detectbility of (A_s,C). The reverse argument is much the same.

Proof of Result 1

Part a follows from the discussion leading to theorem DARE. Part b follows from the remarks after theorem DARE.

Appendix B: GEMs for Bivariate VAR(1)

Applying formula 5.5 and reading off H_XX from the VAR(1) model yields

$$\begin{array}{l}{f}_X(\mathrm{\lambda })=[(1+{\varphi }_y^2-2{\varphi }_y\cos (\mathrm{\lambda })){\sigma }_a^2+{\gamma }_x^2{\sigma }_b^2\\ -2\rho {\sigma }_a{\sigma }_b({\gamma }_x{\varphi }_y-{\gamma }_x\cos (\mathrm{\lambda }))]/|D(e^{j\mathrm{\lambda }}){|}^2\\ D(L)=(1-{\varphi }_{x}L)(1-{\varphi }_{y}L)-{\gamma }_x{\gamma }_y{L}^2.\end{array}$$

This can clearly be written as an ARMA(2,1) spectrum ${\sigma }_x^2|1-{\theta }_x{e}^{-j\mathrm{\lambda }}{|}^2/|D(e^{j\mathrm{\lambda }}){|}^2$ Equating coefficients gives

$$\begin{array}{l}{\gamma }_0={\sigma }_x^2(1+{\theta }_x^2)=(1+{\varphi }_y^2){\sigma }_a^2+{\sigma }_b^2{\gamma }_x^2-2\rho {\sigma }_a{\sigma }_b{\gamma }_x{\varphi }_y={\sigma }_a^2(1+{\xi }_x+d_x^2),\\ {\gamma }_1={\sigma }_x^2{\theta }_x={\sigma }_a^2{d}_x,\end{array}$$

where ${\xi }_x=(1-{\rho }^2){\gamma }_x^2{\sigma }_b^2$ and $d_x={\varphi }_y=\rho {\gamma }_x\frac{{\sigma }_b}{{\sigma }_a}$. We thus have ${\theta }_x^2={\gamma }_1^2/{\sigma }_x^4$, and using this in the first equation gives, ${\gamma }_0={\sigma }_x^2+{\gamma }_1^2/{\sigma }_x^2$ or ${\sigma }_x^4-{\sigma }_x^2{\gamma }_0+{\gamma }_1^2=0$. This has, of course, two solutions:

$$\begin{array}{l}{\sigma }_x^2=\frac{1}{2}\left({\gamma }_0\pm \sqrt{{\gamma }_0^2-4{\gamma }_1^2}\right),\\ \Rightarrow \frac{{\sigma }_x^2}{{\sigma }_a^2}=\frac{1}{2}\left(\frac{{\gamma }_0}{{\sigma }_a^2}\pm \sqrt{\frac{{\gamma }_0^2}{{\sigma }_a^4}-4\frac{{\gamma }_1^2}{{\sigma }_a^4}}\right)\\ =\frac{1}{2}\left(1+{\xi }_x+d_x^2\pm \sqrt{{(1+{\xi }_x+d_x^2)}^2-4d_x^2}\right).\end{array}$$

Note that if ξ_x = 0, this delivers $\frac{{\sigma }_x^2}{{\sigma }_a^2}=\frac{1}{2}(1+d_x^2+\sqrt{{(1-d_x^2)}^2}=1$.

We must choose the solution that ensures $|{\theta }_x|<1\equiv \frac{{\gamma }_1^2}{{\sigma }_x^4}<1\equiv \frac{{\gamma }_0}{{\sigma }_x^4}<2\equiv {\gamma }_0/{\sigma }_a^2<2{\sigma }_x^2/{\sigma }_a^2\equiv 1+{\xi }_x+d_x^2<1+{\xi }_x+d_x^2\pm \sqrt{{(1+{\xi }_x+d_x^2)}^2-4d_x^2}$. And so we must choose the + solution. Continuing, we now claim,

$$\begin{array}{l}\frac{{\sigma }_x^2}{{\sigma }_a^2}\ge \frac{1}{2}\left(1+{\xi }_x+d_x^2+\sqrt{{(1+{\xi }_x-d_x^2)}^2}\right)\\ =\frac{1}{2}(1+{\xi }_x+d_x^2+1+{\xi }_x-d_x^2)=1+{\xi }_x.\end{array}$$

This follows if ${(1+{\xi }_x+d_x^2)}^2-4d_x^2\ge {(1+{\xi }_x-d_x^2)}^2\equiv (1+{\xi }_x+d_x^2)-{(1+{\xi }_x-d_x^2)}^2\ge 4d_x^2\equiv 2(1+{\xi }_x)2d_x^2\ge 4d_x^2\equiv 1+{\xi }_x\ge 1$, which holds.

Appendix C: Spectral Factorization

Suppose ε_t is a white noise sequence with E(ε_t) = 0, var(ε_t)= Σ. Let G(L) be a stable causal, possibly nonminimum phase filter. Then ${\overline{z}}_t=G(L){\epsilon }_t$ has spectrum $f_{\overline{Z}}(\mathrm{\lambda })=G(L)V{G}^T(L^{-1})$ where L = exp(−jλ). We can then find a unique causal, stable minimum phase spectral factorization $f_{\overline{Z}}(\mathrm{\lambda })=G_o(L)V_o{G}_o^T(L^{-1})$. Let V, V_o have Cholesky factorizations V = JJ^T, $V_o=J_o{J}_o^T$ and set G_c(L) = G(L)J, G_o,c(L) = G_o(L)J_o. Then $f_{\overline{Z}}(\mathrm{\lambda })=G_c(L)G_c^T(L^{-1})=G_{o,c}(L)G_{o,c}^T(L^{-1})$. Since G_o,c(L) is minimum phase, we can introduce the causal filter $E(L)=G_{o,c}^{-1}(L)G_c(L)\Rightarrow E(L)E^T(L^{-1})=I$. Such a filter is called an all pass filter (Hannan & Deistler, 1988; Green, 1988). Now, G_c(L) = G_o,c(L)E(L) or G(L) = G_o(L)J_oE(L)J⁻¹ (i.e., a decomposition of a nonminimum phase (matrix) filter into a product of a minimum phase filter and an all-pass filter. We can also write this as $G_o(L)=G(L)J{E}^{-1}(L)J_o^{-1}=G(L)J{E}^T(L^{-1})J_o^{-1}$ showing how the nonminimum phase filter is transformed to yield a spectral factor.