The role of the Met²⁰ loop in the hydride transfer in Escherichia coli dihydrofolate reductase

Abstract

A key question concerning the catalytic cycle of Escherichia coli dihydrofolate reductase (ecDHFR) is whether the Met²⁰ loop is dynamically coupled to the chemical step during catalysis. A more basic, yet unanswered question is whether the Met²⁰ loop adopts a closed conformation during the chemical hydride transfer step. To examine the most likely conformation of the Met²⁰ loop during the chemical step, we studied the hydride transfer in wild type (WT) ecDHFR using hybrid quantum mechanics-molecular mechanics free energy simulations with the Met²⁰ loop in a closed and disordered conformation. Additionally, we investigated three mutant forms (I14X; X = Val, Ala, Gly) of the enzyme that have increased active site flexibility and donor-acceptor distance dynamics in closed and disordered Met²⁰ loop states. We found that the conformation of the Met²⁰ loop has a dramatic effect on the ordering of active site hydration, although the Met²⁰ loop conformation only has a moderate effect on the hydride transfer rate and donor-acceptor distance dynamics. Finally, we evaluated the pK_a of the substrate N5 position in closed and disordered Met²⁰ loop states and found a strong correlation between N5 basicity and the conformation of the Met²⁰ loop.

Introduction

Escherichia coli dihydrofolate reductase (ecDHFR)³ serves as a benchmark enzyme for the study of static and dynamic effects in biocatalysis (1). DHFR catalyzes the reduction of dihydrofolate (DHF or H₂folate) by nicotinamide adenine dinucleotide phosphate hydride (NADPH) to form tetrahydrofolate (H₄folate) and NADP⁺ (Scheme 1). Its principal function is to maintain intracellular pools of H₄folate, a compound essential for the biosynthesis of purines, thymine nucleotides, and several amino acids.

Scheme 1.

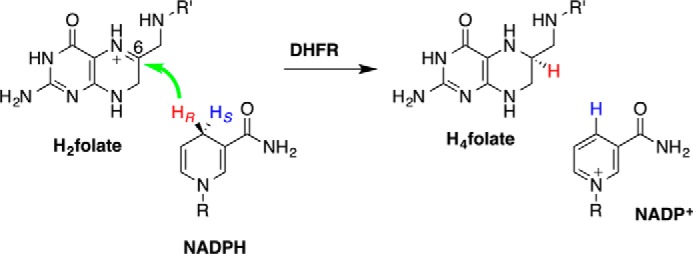
The DHFR-catalyzed hydride transfer. The green arrow marks the transfer of the hydride (H_R) from its donor to the acceptor. R, adenine dinucleotide 2′-phosphate; R′, p-aminobenzoyl-glutamate.

The Met²⁰ loop in ecDHFR is a flexible structural motif that closes and opens the active site cleft as ligands bind or dissociate from the enzyme. The Met²⁰ loop dynamics have been suggested to occur on the pico- to millisecond timescale (2), and an important question is whether any of its motions are coupled to catalysis (3–5). It has been proposed that the Met²⁰ loop (residues 9–23) may adopt three principle states, open, closed, and occluded (6), and the conformation of the Met²⁰ loop has been proposed to correlate with catalysis (6–11). For instance, Brooks and co-workers (12–14) suggested that rapid hydride transfer is correlated with a selected subset of Met²⁰ conformational states. This raises the question of whether the Met²⁰ loop is closed during the chemical step and more generally whether the Met²⁰ loop plays a role during hydride transfer.

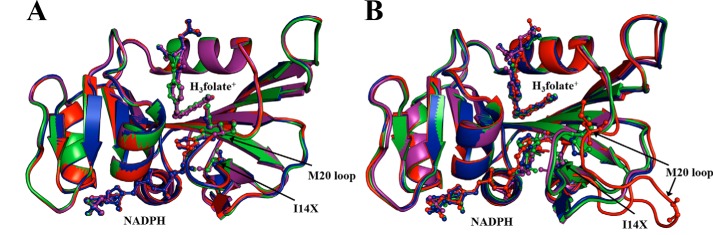
To investigate this question, we studied the hydride transfer in wild type (WT) ecDHFR and three Met²⁰ loop mutant enzymes, namely I14V, I14A, and I14G. These mutants have been shown to possess increased active site flexibility relative to the WT enzyme and, in particular, enhanced donor-acceptor distance (DAD) dynamics (15, 16). This DAD dynamics perturbation has a rather radical effect on the temperature dependence of the kinetic isotope effect (KIE) (15, 17). In the WT enzyme, the KIE is temperature-independent, whereas the KIE becomes increasingly temperature-dependent as the steric effect of the mutation becomes more pronounced. In the crystal structures of these mutant enzymes, the Met²⁰ loop adopts an increasingly open and disordered conformation as a function of the mutation (Fig. 1) (16). The analogous ternary complexes for all three mutations of Ile¹⁴ in ecDHFR were crystallized, and their structures were determined (16). In the I14A and I14V mutants, the structures were obtained in the P2₁ space group where the Met²⁰ loop is observed in a disordered conformation as this conformation is seemingly stabilized by crystal contacts. These structures are rather similar to the analogous WT structures of Sawaya and Kraut (6) in the C2 and P2₁ space groups. In contrast, the crystal structure of I14G ecDHFR was crystallized in the P2₁2₁2 space group where both the Met²⁰ loop and the F-G loop, which is in direct contact with the Met²⁰ loop (Fig. 1), are partially disordered. It is possible that a transient population of the open conformational state plays a role in the catalytic cycle because the open conformation enables both substrate binding and product release (3, 18–20). However, replacement of a part of the Met²⁰ loop (residues 16–19) with a single glycine residue still yields an enzyme that exhibits some catalytic activity (7), suggesting that the loop is not essential for basic catalytic activity. In our previous work, the above mentioned mutant crystal structures with a disordered Met²⁰ loop were not used for modeling purposes as we focused on the closed conformation. Indeed, it is not clear whether the Met²⁰ loop plays a role during the hydride transfer step in general (7) and whether it influences the DAD in particular.

Figure 1.

Superimposition of energy-minimized structures of WT ecDHFR (purple), I14V (green), I14A (blue), and I14G (red) (A) and WT* ecDHFR (purple), I14V* (green), I14A* (blue), and I14G* (red) (B).

In this work, we present free energy profiles along with structural and dynamic analyses for the hydride transfer in WT ecDHFR and three of its mutants (I14V, I14A, and I14G). The WT enzyme is treated in a closed conformation as is observed in the ternary complex crystal structure as well as with a disordered Met²⁰ loop conformation (6). The mutant enzymes are also constructed in both the closed and disordered Met²⁰ loop conformations. To quantify the effect of conformation on chemistry, we used a hybrid quantum mechanics (QM)/molecular mechanics (MM) Hamiltonian especially designed for the DHFR reaction (21). The free energy profiles were obtained from molecular dynamics (MD) umbrella sampling simulations and were compared with available experimental pre-steady-state single-turnover rates (15). Finally, we estimated the pK_a for the N5 position of the folate moiety with the Met²⁰ loop in the closed and disordered conformations.

Results

Free energy profiles

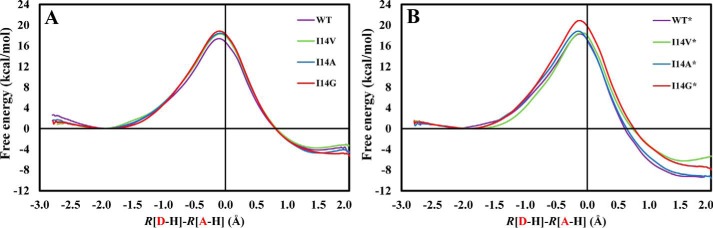
We obtained the classical mechanics potential of mean force (PMF) profiles at 25 °C for the catalyzed hydride transfer from NADPH to H₃folate⁺ (N5-protonated DHF) in the WT ecDHFR and three I14X mutant ecDHFRs, namely I14V, I14A, and I14G. In Fig. 2A, we present the PMFs for the WT enzyme as well as for the I14X mutant enzymes, all with the Met²⁰ loop in the closed conformation. The classical free energy of activation for the WT enzyme, ΔG^‡, is 17.4 ± 0.3 kcal/mol, whereas the reaction free energy, ΔG_r, is −4.5 ± 0.3 kcal/mol. The barrier obtained is similar to that obtained in our previous study (16.8 kcal/mol), although the reaction is less exergonic than previously observed (−9.7 kcal/mol) (16, 21). Possible sources for the slight differences are the different initial crystal structures used in the two studies, higher ionic concentration in the current work, and statistical uncertainty. We stress that addition of nuclear quantum effects on the hydride transfer typically reduces the barrier for this reaction by 2–3 kcal/mol (21, 22), bringing the computed value into agreement with the phenomenological value estimated from single-turnover rates and the Eyring equation (13.4–14.3 kcal/mol) (15, 23–25). We have previously shown that the nuclear quantum effects are similar for WT and the I14X mutants (16, 22). The presence of a slightly less bulky side chain in the I14V ecDHFR system causes an increase in the free energy barrier (18.3 ± 0.4 kcal/mol) relative to WT ecDHFR in mutant simulations with the Met²⁰ loop closed (Figs. 1A and 2A). Further truncation of the side chain brings about even higher free energy barriers as evident by the ΔG^‡ value for the I14A and I14G systems (18.4 ± 0.4 and 18.8 ± 0.4 kcal/mol, respectively). The effect of the mutations is similar to our earlier work and is generally in accord with the experimental trends, although the effect of mutation to Val is slightly overestimated (Table 1) (15–17). We note that the experimental single-turnover rates are pH-dependent and include conformationally induced fit during DHF binding, the protonation at N5, and the hydride transfer step, whereas the current simulations only account for the hydride transfer step. In Fig. 2B, we show an analogous plot but with the Met²⁰ loop in a disordered conformation (Fig. 1B). A similar trend in the PMFs is seen in these profiles (18.3 ± 0.4, 18.5 ± 0.1, 18.8 ± 0.4, and 20.9 ± 0.4 kcal/mol for WT*, I14V*, I14A*, and I14G*, respectively). The free energy barriers are somewhat higher for all models with the Met²⁰ loop in a disordered conformation than with the Met²⁰ loop in the ordered conformation (see supplemental Fig. S3). We ascribe this to the greater reorganization cost in climbing from the ground state (GS) to the transition state (TS) required for the more disordered structures. We note that the limited accuracy in our computed free energy barriers (approximately ±0.4 kcal/mol) precludes us from drawing quantitative conclusions regarding possible correlation between the effects of Met²⁰ loop conformation and I14X mutations, such as additivity or cooperativity.

Figure 2.

Potential of mean force profiles for WT ecDHFR and a series of I14X mutants in the closed (A) and disordered (B) Met²⁰ loop conformation.

Table 1.

Differences in computed activation free energies, ΔΔG^‡ (kcal/mol), for WT ecDHFR and I14X mutants (X = Val, Ala, Gly) relative to the WT with the Met²⁰ loop in the closed conformation at 25 °C

The enzyme models were constructed with the Met²⁰ loop either closed or disordered. The corresponding free energy barriers are compared with relative experimental pre-steady state single-turnover data at 25 °C. Calc., calculated; Exp., experimental.

Enzyme	ΔΔG‡ (kcal/mol)
	Calc.
	Met20 closed	Met20 disordered	Exp.a
WT	0.0	0.9	0.0
I14V	0.9	1.1	1.2
I14A	1.0	1.4	2.2
I14G	1.4	3.5	4.1

^a From Ref. 15.

Structural analysis

Conformational substates

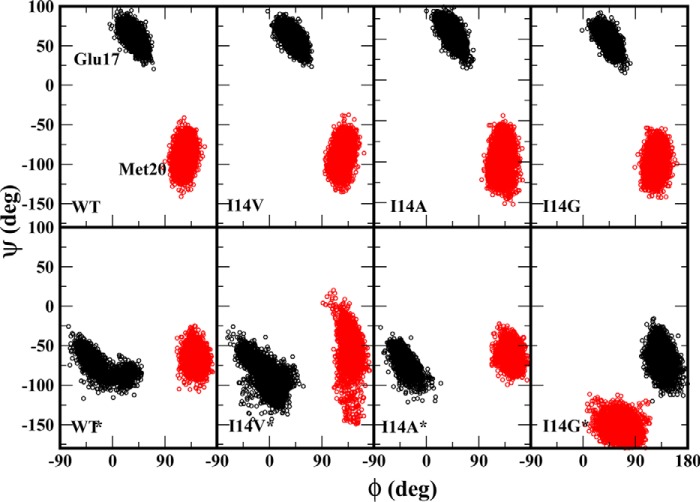
We examined different loop conformations that are sampled in each of the simulations using substate analyses. This was done by calculating the backbone dihedral angles of Met²⁰ loop residues (Glu¹⁷ and Met²⁰) as this can demonstrate the conformational flexibility in the loop. The dihedral angles, ϕ and ψ, of Glu¹⁷ show distinct Met²⁰ loop conformations for the closed and disordered state proteins (Fig. 3). These observations are consistent with those reported by Rod et al. (26). In the closed state protein, we note a clear clustering of ϕ/ψ values near 50°/50°, and these angles do not vary due to the I14X mutations as the H-bond between Asp¹²² and Glu¹⁷ was maintained in the closed state of Met²⁰ loop. However, in the disordered Met²⁰ conformation, the Asp¹²² and Glu¹⁷ contacts are lost, and the enzyme adopts another distinct conformation with dihedral values clustered near −20°/−70°. This conformation is similar to the open conformation reported by Rod et al. (26). In the I14G* mutant, the Met²⁰ loop is highly disordered with a wide distribution of ϕ/ψ angles.

Figure 3.

Distribution of backbone dihedral angles ϕ and ψ for ecDHFR residues Glu¹⁷ and Met²⁰ (colored black and red, respectively). The upper panel shows WT and I14X mutants in a closed state, and the bottom panel represents enzymes with disordered Met²⁰ conformations.

The impact of Met²⁰ on structure

The position of the GS stationary point of the PMF along the antisymmetric stretch coordinate for the WT enzyme in the closed conformation is approximately −1.8 Å, whereas for all other systems studied herein the value is greater, approximately −2.0 Å (Tables 2 and 3). There is, however, greater variability in the positions of the GS and TS for the mutant systems with a disordered Met²⁰ loop relative to the WT enzyme. For instance, the position of the TS ranges from −0.09 to −0.10 Å for the I14X systems (Table 2), whereas for the I14X* mutants the TS ranges from −0.05 to −0.16 Å (Table 3). Interestingly, the ensemble-averaged value of the DAD distance at the classical TS is nearly identical (2.63–2.66 Å) for all simulations. This invariability of the TS position with mutations is in agreement with earlier findings in our group (16, 27) and many other groups (28–34). However, the DADs in the GS show greater variability for the disordered structures than for the closed structures. The ensemble averaged D-H-A angle in the GS is rather similar for all systems with a closed Met²⁰ loop, ranging from 134–145°, whereas this range is widened to 109–149° in the disordered loop enzymes. However, ∡D-H-A at the TS is similar for all systems, ranging from 153 to 158° with similar standard deviations.

Table 2.

Ensemble-averaged structural properties of WT DHFR and I14X mutants with the Met²⁰ loop in a closed conformation at 25 °C in the ground and transition states

Standard deviations are shown in parentheses. The ensemble-averaged data were obtained from 250-ps simulations of the GS and TS. The position of the TS along the reaction coordinate was determined from the position of the maximum PMF value.

	WT		I14V		I14A		I14G
	GS	TS	GS	TS	GS	TS	GS	TS
ζasym (Å)a	−1.73 (0.28)	−0.09 (0.01)	−1.98 (0.29)	−0.09 (0.01)	−1.98 (0.33)	−0.10 (0.01)	−1.88 (0.24)	−0.09 (0.01)
C4N–C6 (DAD) (Å)	3.82 (0.21)	2.64 (0.07)	4.02 (0.21)	2.63 (0.07)	4.00 (0.21)	2.65 (0.07)	3.84 (0.23)	2.65 (0.07)
C4N–H4N–C6 (∡D-H-A) (°)	145.09 (15.33)	157.46 (7.69)	140.27 (13.87)	155.09 (7.97)	133.77 (15.58)	157.20 (7.94)	142.15 (17.68)	156.70 (7.75)
N5–S(Met20) (Å)	3.79 (0.34)	3.70 (0.37)	3.90 (0.33)	3.58 (0.29)	3.82 (0.28)	4.16 (0.44)	4.37 (0.56)	3.78 (0.44)
N7N–S(Met20) (Å)	3.67 (0.33)	3.72 (0.33)	3.60 (0.26)	3.71 (0.31)	4.09 (0.45)	4.45 (0.44)	4.66 (0.73)	4.10 (0.61)
N7N–O(Ala7) (Å)	2.78 (0.14)	2.82 (0.13)	2.88 (0.16)	2.90 (0.14)	2.84 (0.13)	2.84 (0.13)	2.91 (0.18)	2.87 (0.14)
N7N–O(Ile14) (Å)	3.02 (0.24)	2.93 (0.22)	3.07 (0.22)	3.13 (0.25)	3.20 (0.32)	3.15 (0.33)	3.21 (0.37)	2.93 (0.18)
O7N–N(Ala7) (Å)	3.19 (0.23)	2.90 (0.11)	3.41 (0.29)	2.92 (0.12)	3.15 (0.18)	2.99 (0.14)	3.30 (0.25)	2.99 (0.14)
N3–Oδ2(Asp27) (Å)	2.73 (0.17)	2.74 (0.17)	2.96 (0.26)	2.86 (0.18)	2.87 (0.20)	2.85 (0.16)	2.91 (0.22)	2.84 (0.17)
NA2–Oδ1(Asp27) (Å)	2.72 (0.11)	2.75 (0.12)	2.79 (0.12)	2.81 (0.12)	2.78 (0.11)	2.78 (0.11)	2.78 (0.11)	2.80 (0.12)

^a Determined from the stationary points along the PMF profile.

Table 3.

Ensemble-averaged structural properties of WT DHFR and I14X mutants with the Met²⁰ loop in a disordered conformation at 25 °C in the ground and transition states

Standard deviations are shown in parentheses. The ensemble-averaged data were obtained from 250-ps simulations of the GS and TS. The position of the TS along the reaction coordinate was determined from the position of the maximum PMF value.

	WT*		I14V*		I14A*		I14G*
	GS	TS	GS	TS	GS	TS	GS	TS
ζasym (Å)a	−2.09 (0.38)	−0.13 (0.01)	−1.77 (0.63)	−0.05 (0.01)	−2.02 (0.26)	−0.16 (0.01)	−1.88 (0.40)	−0.12 (0.01)
C4N–C6 (DAD) (Å)	5.28 (0.32)	2.65 (0.07)	4.74 (0.44)	2.65 (0.07)	3.90 (0.24)	2.65 (0.07)	3.97 (0.26)	2.64 (0.07)
C4N–H4N–C6 (∡D-H-A) (°)	112.95 (10.99)	157.99 (7.97)	108.67 (18.26)	156.91 (7.54)	148.71 (14.93)	157.93 (7.92)	130.60 (21.18)	152.71 (7.29)
N5–S(Met20) (Å)	10.18 (0.71)	9.97 (0.93)	8.90 (0.69)	8.03 (0.83)	8.29 (0.83)	9.07 (0.45)	7.16 (0.77)	15.00 (0.69)
N7N–S(Met20) (Å)	6.90 (0.82)	6.99 (0.82)	7.10 (1.15)	4.67 (0.49)	5.27 (0.52)	5.29 (0.47)	10.75 (0.77)	15.88 (0.74)
N7N–O(Ala7) (Å)	6.09 (0.50)	3.34 (0.38)	4.61 (0.67)	2.94 (0.20)	2.88 (0.14)	3.15 (0.55)	3.12 (0.26)	3.08 (0.20)
N7N–O(Ile14) (Å)	4.08 (0.75)	4.71 (0.44)	4.65 (1.03)	3.09 (0.29)	3.20 (0.33)	3.43 (0.47)	18.61 (0.45)	18.64 (0.48)
O7N–N(Ala7) (Å)	5.97 (0.35)	3.06 (0.19)	5.62 (0.89)	2.94 (0.12)	3.16 (0.26)	3.23 (0.75)	3.05 (0.17)	2.95 (0.13)
N3–Oδ2(Asp27) (Å)	3.17 (0.35)	2.91 (0.18)	2.94 (0.21)	2.84 (0.14)	2.94 (0.20)	2.88 (0.17)	2.87 (0.16)	2.86 (0.15)
NA2–Oδ1(Asp27) (Å)	2.80 (0.13)	2.78 (0.11)	2.79 (0.12)	2.80 (0.12)	2.78 (0.12)	2.77 (0.11)	2.77 (0.11)	2.82 (0.12)

^a Determined from the stationary points along the PMF profile.

In accordance with MD simulations of the GS in Ref. 15, the interaction between the pterin ring and Asp²⁷ remains tight throughout the reaction for all systems. Similarly, the hydrogen bonds between the nicotinamide carboxamide moiety and the amide backbone of Ala⁷ and Ile¹⁴ remain intact for all systems except for I14G*. In this latter system, a different binding mode is observed in the crystal structure where the carboxamide group interacts with the backbone of Thr¹²³ instead of Ile¹⁴. Additionally, the WT enzyme with the closed Met²⁰ loop conformation has the tightest hydrogen bonds to the cofactor and substrate at the TS. The greatest difference in the interaction pattern between the WT/I14X and WT*/I14X* mutant systems is found in the contact between the Met²⁰ residue and the substrate–cofactor complex (Fig. 1). In the WT and I14X systems, the Met²⁰ loop packs against the reactive complex. This is reflected in the distances between the Met²⁰ sulfur atom and key nitrogen atoms in the NAD(H) and pterin moieties that range between 3.6 and 4.7 Å (Tables 2 and 3). In contrast, in the WT* and I14X* systems, the Met²⁰ loop is not packed against the pterin ring, and the range of Met²⁰-nitrogen distances is 4.7–15.9 Å.

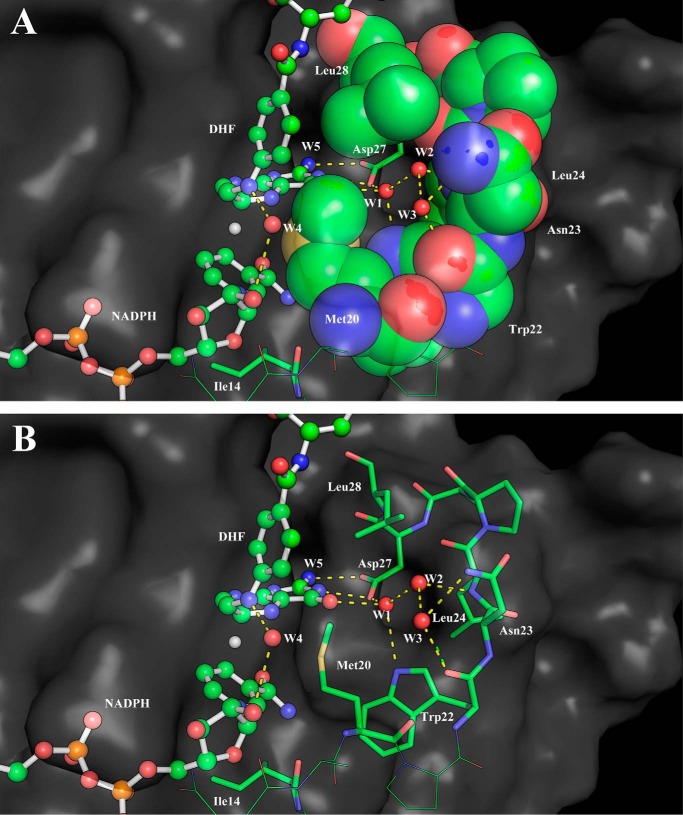
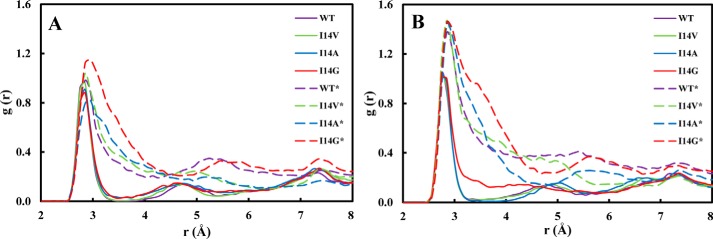
An additional interesting structural aspect that is greatly influenced by the conformation of the Met²⁰ loop is the active site hydration. It is well known that several conserved water molecules are located near the cofactor–substrate complex (6, 35–38). Particular attention has been devoted to the water molecule likely responsible for the N5 protonation (38). Here we focus on a triad of waters that are located near the pterin ring O4 oxygen and Asp²⁷ (W1–3; Fig. 4) whose detailed structure has been revealed by a high-resolution WT ecDHFR structure (38). These water molecules stabilize the reduced pterin and likely give greater weight to the polarized resonance structures (Scheme 2) (39, 40). These resonance structures facilitate charge–charge interactions with Asp²⁷. Indeed, Garcia-Viloca et al. (40) found that this resonance-assisted charge-separated moiety (Scheme 2) is the most polarized region of the substrate–cofactor entity. In Fig. 5, we present the radial distribution functions (RDFs) around O4 of the pterin ring in the GS and at the TS for all enzyme forms studied herein. There is a striking difference in the RDFs for the closed and disordered Met²⁰ loop forms. In the closed enzyme, there are distinct peaks with the first solvation shell corresponding to a highly organized water molecule. The maximum of this peak is located at ∼2.85 Å and corresponds to a water molecule that interacts with O4, Asp²⁷, and Trp²² (W1) and is highly conserved in DHFRs (Fig. 4). This water molecule is not exchanged throughout the simulations. A second peak in the RDFs is located at ∼4.6 Å, and a third peak is found at ∼7.5 Å, corresponding to the two water molecules W2 and W3 (see supplemental Fig. S4). In the simulations with the disordered Met²⁰ loop, the RDFs are much broader, suggesting less hydration structure with considerably more waters penetrating the active site. However, even in the case of the open Met²⁰ loop simulations, a water molecule is directly interacting with O4. Inspection of the identity of the water molecule closest to O4 revealed that in the open Met²⁰ loop simulations this water molecule is exchangeable. Notably, in the GS of the I14G* simulations, the maximum peak is shifted to 2.95 Å, suggesting a more disordered state. For the WT enzyme with a closed Met²⁰ loop at the TS, the maximum peak of the first hydration shell is shifted to 2.75 Å, suggesting TS stabilization.

Figure 4.

A snapshot of TS configuration of WT ecDHFR from molecular dynamics simulations. Water cavity-forming residues are shown as space-filling (A) and stick (B) models.

Scheme 2.

Possible resonance structures for the pterin ring in H₄folate. R′, p-aminobenzoyl-glutamate.

Figure 5.

Hydration radial distribution functions near the O4 oxygen of the pterin ring in the active site of ecDHFR. A, ground state. B, transition state.

The impact of Met²⁰ on N5 pK_a

We examined the pK_a of substrate N5 atom in the ternary Michaelis complex. Our calculated pK_a for the closed (WT) and disordered (WT*) state enzyme are 8.3 and 6.8, respectively, in excellent agreement with the values determined by Brooks and co-workers (14, 41).The pK_a obtained for the less ordered conformation (6.8) is similar to the experimentally reported pK_a (∼6.5 (42) or 6.7 (43)), suggesting that protonation occurs in a conformational state with the Met²⁰ loop accessible to bulk water. In contrast, the pK_a of N5 in the closed Met²⁰ conformation is observed to be less acidic (pK_a = 8.3), which is consistent with the recent experimental study by Liu et al. (43) These authors found DHF N5 to be partially protonated at pH values up to 11 based on kinetic studies (43). These kinetic studies showed that hydride transfer occurs even at such high pH values. Considering that in the current work we have established that hydride transfer occurs in the closed Met²⁰ loop state, we suggest that the elevated pK_a value reported by Liu et al. (43) corresponds to the closed Met²⁰ loop state. The role of Met²⁰ in modulating the N5 pK_a has been emphasized previously by Brooks and co-workers (14, 41), and the current findings fully support their findings. We suggest that different Met²⁰ loop conformations bring about changes to the active site electrostatics that might affect N5 acidity. Specifically, these changes are expected to be correlated with the active site hydration as will be shown below.

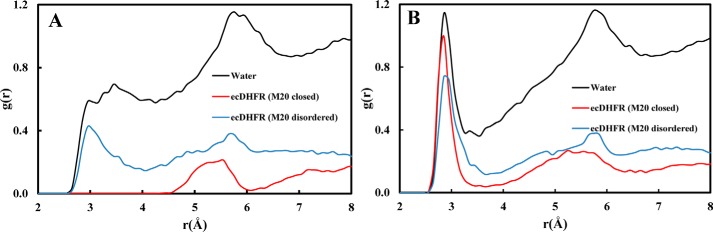
Next, we analyzed the hydration near DHF in the closed and disordered Met²⁰ conformations as well as in bulk water. We plotted the radial distribution function between the substrate N5 and the water oxygens for the two folate forms, i.e. H₃F⁺ and H₂F (Fig. 6). The broad peaks near the H₃F⁺ N5 (2.95 Å) in solution and WT* enzyme indicate specific hydration (Fig. 6A). In the closed WT complex, the Met²⁰ side chain packs against the pterin ring of the substrate (6, 10, 44, 45), and no first solvation shell is observed. A small peak near 5.5 Å in both ternary complexes represents a water molecule stabilized by Asp²⁷ and H₃F⁺ O4 interactions. In Fig. 6B, a sharp peak is observed at 2.85 Å, which shows that water tends to stabilize near N5 of H₂F via hydrogen bond interactions in all the systems. The Met²⁰ loop flexibility has been suggested to be responsible for allowing water access to the substrate. Interestingly, in crystal structures of the ternary complex of ecDHFR, a water molecule is also observed near N5 of H₂F (38). Seemingly, prior to N5 protonation, the packing of the Met²⁰ loop is somewhat loose, allowing access to water, whereas following N5 protonation the packing is tightened in preparation for the hydride transfer step, thereby excluding water molecules and hence raising the N5 pK_a.

Figure 6.

Radial distribution functions between the N5 atom of the pterin ring and water oxygens in solution and ternary complex at the end points of the physical states. A, H₃F⁺. B, H₂F. Substrate in solution colored as black and ternary ecDHFR complexes with the closed and disordered Met²⁰ loop conformations colored as red and blue, respectively.

The impact of Met²⁰ on dynamics

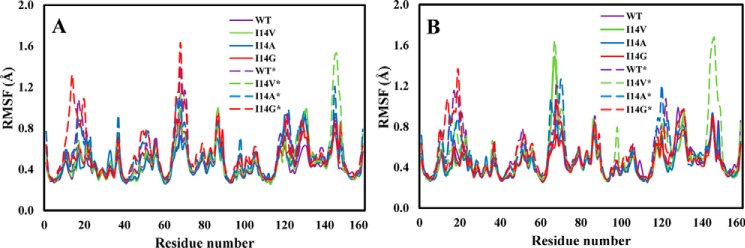
In Fig. 7, we present the root mean square fluctuations of the Cα atoms as a function of amino acid residue number in the GS and TS for WT and I14X mutant enzyme forms in the closed and disordered Met²⁰ loop conformations. The main characteristic that is apparent in the root mean square fluctuation plots is the increased flexibility in the systems with the disordered Met²⁰ loop. In particular, the Met²⁰ loop (residues 9–23) and F-G loop (residues 117–131) regions are considerably more flexible in the disordered than in the closed structures. This is likely due to changes in the contact between these two segments in the disordered structures. For instance, the contact between the side chain of Asp¹²² in the F-G loop and the backbone amide of Glu¹⁷ in the Met²⁰ loop is lost. We also note increased flexibility in the C-D loop (residues 64–71) for all the disordered systems, including the WT* enzyme. These fluctuations are slightly greater in some of the mutants. Finally, we note that there is great flexibility in Gln¹⁴⁶ in the I14V* mutant in the disordered conformation. This greater fluctuation in the I14V* mutant is the result of the loss of an intraloop hydrogen bond between Asp¹⁴⁴ and Gln¹⁴⁶ during the simulation. The general observations discussed above are in agreement with earlier experimental and theoretical studies (11, 46).

Figure 7.

Root mean square fluctuations (RMSF) of Cα atoms of ecDHFR in the ground state (A) and transition state (B).

Discussion

A crucial question regarding the chemical steps in enzyme reactions is to what extent global protein motions might participate in the reaction coordinate. In the case of ecDHFR, it has been argued that the Met²⁰ loop participates in the reaction coordinate. In the current study, we asked an even simpler question: whether the Met²⁰ loop is preferably closed during hydride transfer or not and whether this influences the DADs. Seemingly, based on the free energy profiles obtained in this work, the Met²⁰ loop is indeed likely to be in the closed conformation in the WT enzyme with the Met²⁰ residue packed against the pterin ring. In the case of the WT enzyme, we simulated both the closed and disordered Met²⁰ loop configurations and obtained a slightly higher free energy barrier with the disordered Met²⁰ loop (ΔΔG^‡ ∼ 1 kcal/mol). In the case of the I14X mutants (X = Val, Ala, Gly), we obtained best agreement with pre-steady-state single-turnover rates using the more disordered structures (Table 1), although the results are within statistical error for X = Val, Ala. A possible interpretation of these results is that the Met²⁰ loop in general and the Met²⁰ amino acid in particular are preferentially in the closed conformation during the hydride transfer step in WT ecDHFR but not necessarily so in the I14X mutants. That is, the I14X mutants can reach a reactive configuration similar to that of the WT enzyme but with a more disordered Met²⁰ loop. We note, however, that the effect of the Met²⁰ loop is small in agreement with experiments showing that the enzyme is active with significant parts of the Met²⁰ loop deleted (7). We did not observe any strong connection between the Met²⁰ loop conformation and the DADs.

Our simulations verify earlier results of Brooks and co-workers (41) relating to the crucial role of the Met²⁰ loop in determining the substrate N5 pK_a. The pK_a value computed for the disordered Met²⁰ loop (∼6.8) is comparable with the experimentally determined value (∼6.5 (42) or 6.7 (43)), whereas the pK_a computed for the closed conformation (8.3) is in agreement with the finding that hydride transfer occurs at basic pH values up to ∼11 (43). The difference in pK_a values for the two loop conformations is likely due to differences in active site hydration.

Additionally, the closed Met²⁰ loop conformation is also involved in ordering in the structure of several conserved water molecules in the vicinity of the pterin ring O4 position. It has been suggested previously that these water molecules are part of a proton relay (36, 37) or ligand recognition (6, 35, 38); here we suggest that these water molecules also play a classical enzyme catalytic role, TS stabilization. Indeed, these tightly bound waters likely facilitate substrate polarization as suggested by Garcia-Viloca et al. (40) and stabilize charge separation (Scheme 2). This in turn enhances substrate binding via interaction with Asp²⁷ and serves to mitigate hydride charge transfer by screening the Asp²⁷ charge (Fig. 4). Experimentally, mutation of Trp²², which forms part of this hydration motif, to His or Phe results in a non-negligible reduction in the rate of the hydride transfer step as determined by stopped flow kinetics (47). In the case of other DHFRs, this could be a similar requirement, such as in human DHFR where, instead of the Met²⁰ residue, Leu²² is packed against the substrate–cofactor complex and creates a similar water cavity.

Conclusions

A question concerning the catalytic cycle of ecDHFR that has garnered significant interest is whether the Met²⁰ loop motion is coupled to the hydride transfer step. In the current study, we examined whether the Met²⁰ loop is preferably closed during hydride transfer or not and whether this influences the DADs. To address this question, we studied the WT and three mutant forms (I14X; X = Val, Ala, Gly) of the enzyme and compared the finding with published experimental observations. These enzyme forms were modeled with the Met²⁰ loop in its closed and disordered conformations. Using hybrid QM/MM free energy simulations, we obtained optimal agreement with experimental pre-steady-state kinetics modeling the WT in the closed Met²⁰ form and the mutants in the disordered Met²⁰ form. Indeed, we found that the disordered conformation of the Met²⁰ loop causes a consistent slight increase in the activation free energy barrier for the WT and mutant enzymes. We conclude that a closed Met²⁰ loop is likely preferential for catalysis as it aids in the preorganization of several conserved water molecules, likely influencing both ligand binding and TS stabilization. The DADs at the TS, however, remain rather similar in the closed and disordered conformations. We also found a significant correlation between the substrate N5 pK_a and the Met²⁰ conformation. The open Met²⁰ loop conformation facilitates protonation prior to the hydride transfer. Closing of this loop reduces the acidity of the N5 proton, thereby stabilizing the H₃F⁺ state in preparation for hydride transfer.

Materials and methods

The X-ray crystal structures of WT ecDHFR (Protein Data Bank codes 4RGC and 1RB2) (6, 38) and mutant E. coli I14V, I14A, and I14G (Protein Data Bank codes 4QLG, 4QLE, and 4QLF, respectively) (16) with folate and the oxidized cofactor NADP⁺ were used to construct the initial configurations for the present study. The 4RGC structure corresponds to the closed ternary complex where the Met²⁰ residue is packed against folate (henceforth WT), whereas in 1RB2 the Met²⁰ loop is disordered (henceforth WT*; * = disordered). The crystal structure of I14G was missing a part of the cofactor and part of a loop (residues 122 and 123). The missing cofactor coordinates were obtained by superimposing the I14V structure on the I14G structure followed by extraction of the missing coordinates for I14G from I14V. The missing residues were modeled with Discovery Studio software (Biovia, Inc.). These mutant enzyme forms that have the Met²⁰ loop in a disordered conformation are termed I14X* (X = Val, Ala, Gly and * = disordered). Additionally, a second set of mutant structures that are similar to the WT were constructed in silico by changing the Ile¹⁴ residue in the original WT ecDHFR structure (Protein Data Bank code 4RGC) to Val, Ala, or Gly (termed I14X where X = Val, Ala, Gly).

The setup and MD heating and equilibration simulations of all systems were carried out using procedures similar to those used for the WT and mutant ecDHFRs in previous studies (16, 21, 48). Briefly, the protonation states of all polar amino acid residue side chains were adjusted to pH 7, and the protonation states of the His residues (either neutral tautomeric forms or positively charged form) were determined based on the hydrogen bonding patterns of the local environment. The N5 position of the pterin ring of the dihydrofolate was protonated (43, 49, 50). The HBUILD facility in the program CHARMM was used to add hydrogen atoms (51, 52). 29 sodium ions and 15 chlorine ions were added to all enzyme systems to neutralize the overall negative charge. This ionic concentration mimics experimental conditions (16) and effectively screens the charges in the system.

The potential energy surface in the current study is described by a hybrid QM/MM Hamiltonian (53) where the QM region is treated by a modified AM1 semiempirical Hamiltonian (54) denoted AM1-specific reaction parameter (55). This Hamiltonian was designed to reproduce high-level calculations for an assortment of electronic and thermodynamic properties for reactions involving various nicotinamide and pterin derivatives (21). The QM region includes significant fragments of DHF and NADPH, which are proximal to the reaction center, whereas the MM region contains the remaining ligand atoms, the entire protein, water molecules, and salt. The water molecules were represented by the three-point charge TIP3P model (56). Hydrogen link atoms were placed across the bonds intersecting the QM/MM boundary. The QM/MM interactions were treated by electrostatic embedding. A detailed QM/MM partitioning scheme and a thorough description of the development of the AM1-specific reaction parameter Hamiltonian are provided elsewhere (21). In modeling the MM region, we used the all-atom CHARMM36 force field (57–60).

Periodic boundary conditions were used to solvate the Michaelis complex using a pre-equilibrated cubic water box (∼65 × ∼65 × ∼65 Å) while treating long-range electrostatic interactions with the Ewald summation technique (64 × 64 × 64 fast Fourier transform grid, κ = 0.340 Å⁻¹) (61). All systems were fully minimized, heated up gradually to 298 K for 25 ps, and equilibrated at that temperature for 1 ns. All equilibrations were conducted in the isothermal-isobaric (NPT) ensemble at 1 atm, and the target temperature was controlled by the extended constant pressure/temperature method (62, 63) and a Hoover thermostat (64). The leapfrog integration scheme (65) was used to propagate the equations of motions, and the SHAKE algorithm (66) was applied to constrain all MM bonds involving hydrogen atoms, allowing a time step of 1 fs. During the initial stages of the equilibration, several nuclear Overhauser effect (NOE) restraints were imposed on key hydrogen bond interactions between the ligands and the surrounding residues as well as within the protein.

The umbrella sampling technique (67) was used to determine the classical-mechanical PMF for the hydride transfer reaction at 25 °C (i.e. the free energy profile along a predefined reaction coordinate). The reaction coordinate was defined as the antisymmetric reactive stretch coordinate, ζ_asym. Specifically, ζ_asym is defined as the difference between the lengths of the breaking C4N–H and forming H–C6 bonds. The reaction coordinate was discretized and divided into 16 evenly spaced regions, or “windows,” ranging from −2.00 to 1.5 Å. Each window was subjected to an appropriate harmonic restraint, which keeps ζ_asym in the desired region, and an umbrella potential (roughly the negative of the PMF) as a function of ζ_asym. The cumulative simulation time per window was 1 ns, and the statistics for the reaction coordinate were sorted into bins of width 0.01 Å. PMF profiles were computed using the weighted histogram analysis method (48, 68). The statistical error was estimated using the bootstrapping algorithm (1000 steps) combined with the weighted histogram analysis method (69). The resulting error analysis of the free energy profiles obtained is provided in the supplemental Fig. S1. The effect of bin size on the free energy profiles was also investigated (supplemental Fig. S2). We also plotted the free energy profiles computed for different time intervals in the same figure.

To evaluate the pK_a for H₂F at the N5 position, we carried out free energy perturbation (FEP) simulations of substrate molecule in bulk water and in two ternary complexes of the WT ecDHFR (with closed and disordered Met²⁰ loops). We used single-topology FEP QM/MM simulations where a molecule is transformed from one chemical state to another via a series of intermediates (70, 71). We used the λ-dynamics methodology where the potential energy function of system is defined as follows.

$$U\left(\lambda \right)=\left(1-\lambda \right)U_A+\lambda U_B$$ (Eq. 1)

The A and B states here correspond to the protonated substrate H₃F⁺ and its unprotonated analog H₂F, respectively, and λ is a coupling parameter. This approach entails annihilating the QM and classical force field terms for the proton attached to the DHF N5 position as a function of λ. In the present study, we chose Δλ = 0.1, and 10 windows were used to perturb λ = 0 → 0.1 → 0.2 … → 1.0. The cumulative simulation time per window was 1 ns. The double-wide sampling used here includes the FEP calculations in both forward and reverse directions. Therefore, for each sampling window (λ), the free energies for the forward and backward perturbations were obtained. We confirmed the convergence of these simulations by comparing the backward and forward perturbation free energies for each λ window. Finally, the protonation free energies for the full reaction were obtained by integrating all the sampling windows (λ).

The difference between the substrate protonation free energy in the enzyme and solution was used to compute the pK_a shift for each complex relative to that in bulk water (72). To compute estimates for the experimental pK_a values in the complexes, we added the corresponding computed ΔpK_a shift to the experimental pK_a value in bulk water (2.6) (41, 73).

Author contributions

D. T. M. designed and coordinated the study and wrote the paper. A. R. M. and A. V.-K. performed and analyzed the simulations. A. K. contributed to interpretation of the data and wrote the paper. All authors reviewed the results and approved the final version of the manuscript.