Finite Element Biomechanics of Optic Nerve Sheath Traction in Adduction

Abstract

Historical emphasis on increased intraocular pressure (IOP) in the pathogenesis of glaucoma has been challenged by the recognition that many patients lack abnormally elevated IOP. We employed finite element analysis (FEA) to infer contribution to optic neuropathy from tractional deformation of the optic nerve head (ONH) and lamina cribrosa (LC) by extraocular muscle (EOM) counterforce exerted when optic nerve (ON) redundancy becomes exhausted in adduction. We characterized assumed isotropic Young's modulus of fresh adult bovine ON, ON sheath, and peripapillary and peripheral sclera by tensile elongation in arbitrary orientations of five specimens of each tissue to failure under physiological temperature and humidity. Physical dimensions of the FEA were scaled to human histological and magnetic resonance imaging (MRI) data and used to predict stress and strain during adduction 6 deg beyond ON straightening at multiple levels of IOP. Young's modulus of ON sheath of 44.6 ± 5.6 MPa (standard error of mean) greatly exceeded that of ON at 5.2 ± 0.4 MPa, peripapillary sclera at 5.5 ± 0.8 MPa, and peripheral sclera at 14.0 ± 2.3 MPa. FEA indicated that adduction induced maximum stress and strain in the temporal ONH. In the temporal LC, the maximum stress was 180 kPa, and the maximum strain was ninefold larger than produced by IOP elevation to 45 mm Hg. The simulation suggests that ON sheath traction by adduction concentrates far greater mechanical stress and strain in the ONH region than does elevated IOP, supporting the novel concept that glaucomatous optic neuropathy may result at least partly from external traction on the ON, rather than exclusively on pressure on the ON exerted from within the eye.

Introduction

Historically, excessive intraocular pressure (IOP) has been considered the principal if not sole mechanism of glaucoma, and thus an initiator of blindness due to loss of retinal ganglion cells and optic nerve (ON) damage that interrupts transmission of electrical impulses from the retina to the brain [1]. Marked IOP elevation, especially acutely, undoubtedly causes optic neuropathy. However, many patients considered to have glaucomatous optic neuropathy do not have elevated IOP and are thus considered to have normal tension glaucoma (NTG). Patients with NTG have progressive ON damage and visual field loss, yet IOP within the normal range [2]. In East Asia, NTG is now the most prevalent form of glaucoma [2,3]. Numerous investigators have attempted to elucidate the etiology of NTG, considering among other factors the pressure, the pressure differential across the lamina cribrosa (LC) between IOP and intracranial pressure (ICP) of the cerebrospinal fluid. While optic nerve head (ONH) vascular compromise has also been considered [4], a clear etiology for NTG has not emerged.

Traction as Alternative Cause of Glaucoma.

The conventional view of the pathogenesis of glaucoma as mechanical damage produced by excessive IOP has recently been challenged by Demer's proposal that similar damage could arise from traction on the ONH exerted from outside the eye [5]. Traction is well known to injure nerve, with only 6% strain markedly altering electrophysiological properties in peripheral nerve [6] and 8% blocking conduction in the brachial plexus [7]. Demer employed magnetic resonance imaging (MRI) to demonstrate that the length of the ON and sheath is often insufficient for large ocular rotations toward the nose (adduction), where these tissues become straightened and develop progressively increasing tension as adduction continues (Fig. 1) [5]. The ON sheath mechanically loads globe, opposing the adducting force exerted by the medial rectus (MR) extraocular muscle (EOM). In large angle adduction, MR force is not simply opposed by lateral rectus force, but also by potentially much greater reaction force exerted by stretching the ON sheath. Moreover, while MR force is applied broadly on the eye at a tendon insertion some 11 mm wide, its reaction force is concentrated on a small area at the temporal edge of the ON canal, implying high local stress. Resulting strain in this region could damage the LC and peripapillary sclera, critical tissues damaged in glaucoma. Deformation of these tissues within their elastic limits might deform blood vessels or induce biological changes such as tissue stiffening or induced metabolic signaling. Strain exceeding elastic limits might occasionally cause an acute mechanical failure such as acute disinsertion of a part of the LC with disk hemorrhage [8], but gradual plastic deformation of the ONH and peripapillary region might also occur [9]. Young children seldom exhibit an ON cup and virtually never ONH tilting [10], peripapillary atrophy (atrophy or thinning in the layers of the retina and retinal pigment epithelium (RPE) around the optic nerve), or axial myopia, which is globe elongation associated with nearsightedness [11]. These features develop with age [12] and become common in myopia [13], which is progressive and exceeds 95% prevalence among young Asian adults [14]. Peripapillary atrophy, particularly at the temporal ON margin [15], is frequent with glaucoma [16] and progresses with age [17], myopia [18], and glaucoma progression [19] where it correlates with the topography [15] and degree of ON damage and visual field loss [20]. Peripapillary atrophy is closely associated with temporal and oblique (“torsion”) ONH, both of which correlate with visual field defects in NTG but not when glaucoma is associated with high IOP [21]. Sibony et al. have suggested that peripapillary subretinal hemorrhage may result in part from ocular motor forces and scleral thinning in myopic eyes [22].

Fig. 1.

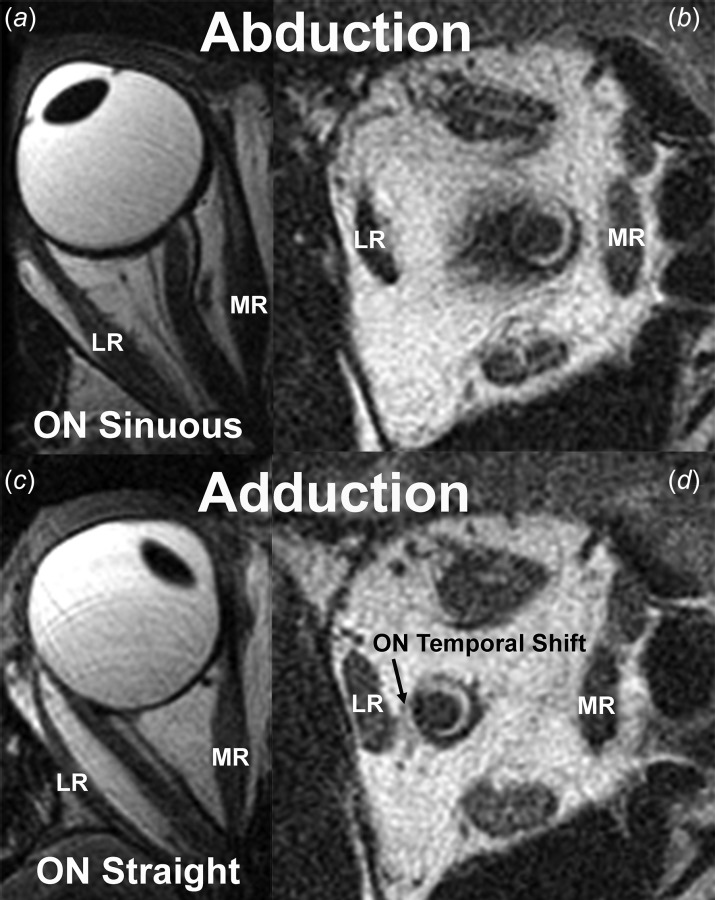
Previously unpublished T2-weighted axial (left) and quasi-coronal (right) MRI of a normal right adult orbit from the study of Demer [5] showing that the sinuous ON in abduction (a) straightens in adduction (c). Quasi-coronal images obtained in the same eye positions show that in adduction, the ON shifts temporally as the CSF (bright ring surrounding the dark ON) within the ON sheath (dark ring) shifts nasally. LR—lateral rectus muscle and MR—medial rectus muscle.

Biomechanics in Glaucoma.

Biomechanical properties of some the foregoing tissues have been characterized experimentally [23,24], including the sievelike LC [25]. Biomechanical techniques have been applied to define the behavior of EOM [26,27] orbital connective tissue and fat [28]. A helpful aid is finite element analysis (FEA). Useful reviews of concepts and terminology relevant to ocular biomechanics in glaucoma have recently been published [29].

Experimental [29,30] and simulation [31] studies have investigated the biomechanical effects of IOP and ICP variations on the LC, but have not considered possible contributions from other sources posterior to the globe. One prior application of FEA to the orbit and EOMs was limited by unrealistic guesses about material properties, geometric oversimplification, failure to implement constitutive models, and problems with modeling large eye rotations [32]. Recent FEA by Wang et al. motivated their proposal that horizontal eye movement induces strain in ONH region [33]. In the orbit imaged by Wang et al., even a modest 13 deg abduction for which MRI showed that the ON remained markedly redundant was predicted to induce greater strain in the LC and papillary sclera than produced by marked IOP elevation to 50 mm Hg.

Aims.

The current study aimed to employ modern biomechanical characterization methods to define tissue constitutive properties to build a realistic overall FEA model of the globe and associated tissues, including the critical juncture of the ON sheath with posterior sclera. This model was then used to evaluate the plausibility of the hypothesis that ON sheath traction in adduction might strain the ON and LC, and thus potentially cause the optic neuropathy by a repetitive strain analogous to that recognized in the musculoskeletal system [34].

Methods

Biomechanical Characterization.

Experiments employed a horizontally mounted microtensile load cell including a linear motor (Ibex Engineering, Newbury Park, CA) capable of high speed (100 mm/s) and 20 nm resolution, with a strain gauge (LSB200, FUTEK, Irvine, CA) having 5 mN force resolution permitting specimen testing in a physiological environment (Fig. 2) [35]. Within about 3 h slaughter of cows aged 20–30 months at a nearby abattoir (Manning Beef LLC, Pico Rivera, CA), fresh globes with contiguous ONs were isolated into lactated Ringer's solution. Four different tissues were evaluated: ON, ON sheath, peripheral sclera, and peripapillary sclera. The ON sheath and scleral specimens were trimmed by scalpel to rectangular shape, while isolated ON was cylindrical. Specimens were cyanoacrylate glued between 5-mm long layers of thin cardboard and anchored in serrated clamps (Fig. 2). Specimens were measured with digital calipers or optical coherence tomography (OCT) (Thorlabs Inc., Newton, NJ), and mean cross section along specimen length was employed for stress calculation. Specimen sizes (±standard deviation of length × width) were 18.6 ± 3.0 mm × 4.8 ± 0.2 mm for ON, 15.8 ± 1.2 mm × 9.3 ± 0.8 mm for ON sheath, and 14.2 ± 0.4 mm × 9.9 ± 0.1 mm for sclera. The aspect ratio of each tissue was 3.87, 1.69, and 1.43, respectively. The ON length exceeded that of other tissues to avoid experimental artifact by clamping its thick, circular ON cross section.

Fig. 2.

Tensile loading apparatus and specimen clamping. (a) The Linear motor on the left was connected to a strain gauge transmitting its measured tensile force through a frictionless air bearing and cylindrical shaft to the moveable specimen clamp to which one end of the specimen was affixed in an environmentally controlled chamber at right. The other clamp at right was rigidly anchored at the opposite end of the specimen. ON (b), ON sheath (c), and sclera (d) were similarly clamped at each end.

Control tensile elongation experiments with and without preconditioning in this and a prior study [36] demonstrated that preconditioning did not alter measured parameters. For example, in the current study, Young's modulus in the linear region for peripheral sclera was 15.9 ± 3.1 with versus 13.2 ± 3.5 MPa without preconditioning by cyclic loading (N = 5), and for ON sheath 38.8 ± 1.1 with versus 39.4 ± 4.1 MPa without preconditioning (N = 3). Representative preconditioning curves are illustrated in Fig. 3 showing that the stiffness is not significantly altered during cyclic loading. Therefore, preconditioning was omitted for the experiments reported here subsequently. Specimens were preloaded by 0.05 N in order to avoid slackness, then elongated at 0.1 mm/s under physiological conditions of temperature and 100% humidity until failure, during tensile force recorded by the strain gauge. Except for ON specimens, the loading direction was arbitrary relative to tissue orientation since material properties were assumed isotropic. Failure was indicated by abrupt tension decrease and was usually associated with visible rupture. Specimens were assumed linearly elastic, incompressible, and homogeneous.

Fig. 3.

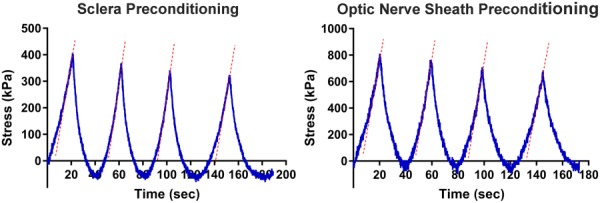
Representative preconditioning curves for human sclera and ON sheath. Cyclic loading was up to 5% of the initial length. Dotted lines illustrate the elastic stiffness of each loading cycle; slopes of these lines did not change significantly during cyclic loading.

Structure of the Finite Element Model (FEM).

Posterior ocular structures, including ON, ON sheath, sclera, and LC, were modeled using solidworks (Version 2015, Dassault Systèmes SolidWorks Corp., Waltham, MA, Fig. 4). Since the angle of the bony orbit diverges from the midsagittal plane, in central gaze, the eye may be considered rotated toward the nose (adducted) ∼17 deg relative to the long orbital axis. The ON straightens at and beyond ∼20 deg adduction from central gaze [5]. Consequently, the initial rotational configuration was taken as the sum of these angles at 37 deg, representing the position at which tension in the ON sheath resulting from adduction would just exceed zero.

Fig. 4.

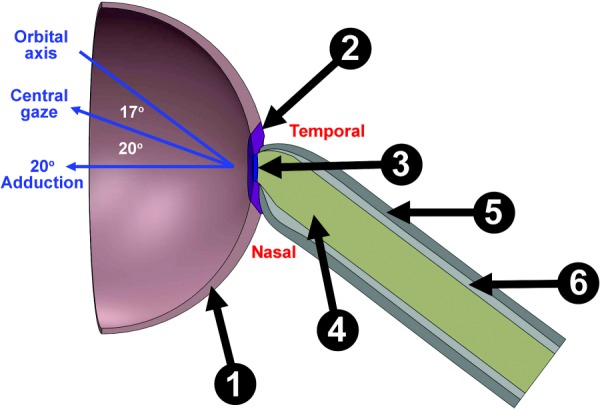
Hemisected axial view of FEM. The sclera is divided into peripheral (①) and peripapillary regions (②), with LC (③) attached to the ON (④) and posterior sclera attached to the ON sheath (⑤) that also contains CSF (⑥).

Globe diameter was set as 24 mm [37], and sclera was assigned nonuniform thickness ranging from 0.4 mm at the equator to 1 mm at the posterior pole [38]. The rim of the scleral canal is tapered approximately 30 deg to the sclera–LC junction [38,39]. For simplicity, the sclera was divided into the peripapillary sclera extending radially approximately 1.5–1.7 mm from the scleral canal and peripheral sclera elsewhere [40]. Circular LC diameter was taken as 1.84 mm, the mean value of horizontal and vertical optic disk dimensions [41], centered in the anterior scleral canal, with 0.3 mm thickness [39,42]. The ON was realistically modeled as encased by thick connective tissue pia layer surrounding neural tissue (optic nerve axons) intercalated with a finely grained matrix of connective tissue contiguous with the pia and constituting about 30% of total ON cross section in the immediately retrobulbar region [43], as illustrated in Fig. 5. This anatomically verified ON structure is clearly different from brain, which in contrast contains minimal internal connective tissue and only a thin and diaphanous pia. Also unlike the easily removal brain pia, we have never been able to separate ON pia from the ON by dissection, since the intrinsic connective tissue of the ON is so intimately connected to the pia. There is no realistic way to separate the axon bundles from the connective tissue for meaningful separate characterization of the ON or enveloping connective tissue.2 We, therefore, implemented the current FEA using an overall Young's modulus for the ON as a composite material as measured. The ON and its integrated pia were modeled as a composite material hereafter designated only as “ON” that abuts the LC. The possible mechanical implications of our preferred composite characterization of the ON were explored by separate FEA simulation in which that anatomically unrealistic configuration of an ON simply surrounded by a separable pia was assumed.

Fig. 5.

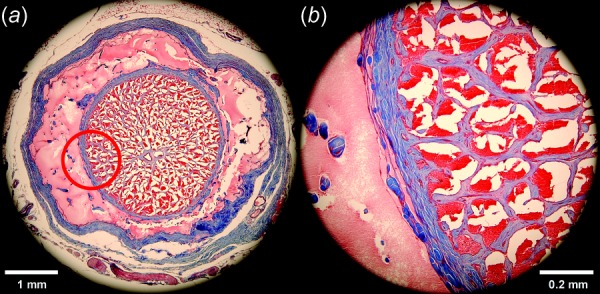
Masson's trichrome-stained transverse histological section of retrobulbar ON from a 57-year-old human 1.84 mm posterior to the globe. Collagen stains blue, nerve tissue purple, and acellular protein in the cerebrospinal space pink. (a) The ON sheath is the external blue ring surrounding the light pink of the CSF space that bathes the ON within it. (b) Magnified view of red circle area illustrating the intimate connection between pia and the dense blue network of connective tissue within the ON. It is thus reasonable to model the ON and its incorporated pia and connective tissue as one composite structure.

The ON was here modeled as bathed in cerebrospinal fluid (CSF) at defined pressure within the ON sheath. Based upon our published dimensions from human MRI, ON diameter was taken as 3.55 mm, ON length 28 mm, ON sheath thickness 0.74 mm, and CSF gap thickness 0.59 mm (Table 1) [5].

Table 1.

Anatomic parameters of FEM

Parameter	Units	Values	References
Initial rotational configuration of ON junction with globe	deg	37	[5]
Globe diameter	mm	24	[37]
Scleral thickness range (from equator to scleral canal)	mm	0.4–1.0	[38]
Scleral tapering angle at scleral canal rim	deg	30	[38,39]
Peripapillary scleral boundary from scleral canal	mm	1.5–1.7	[40]
LC diameter	mm	1.84	[41]
LC thickness	mm	0.3	[39,42]
ON diameter	mm	3.55	[5]
ON length	mm	28	[5]
ON sheath thickness	mm	0.74	[5]
CSF gap thickness	mm	0.59	[5]

Modeling described the mechanical changes resulting from adduction exceeding 20 deg (from central gaze) at which the ON first becomes straightened. This situation has been shown by MRI in many cases to shift CSF from the temporal to nasal side of the ON sheath (Fig. 1), causing the ON to approach the inner temporal surface of the sheath [5]. This structural asymmetry was therefore modeled as thin temporal but thick nasal CSF layers (Fig. 4). The posterior model includes six mutually interconnected tissues achieved by techniques including “split” and “Boolean subtraction” to achieve seamless unions. The “fillet” function avoided unrealistic sharp corners or other singularities at boundaries.

Finite Element Analysis.

Finite element analysis of the posterior ocular structures was solved using solidworks simulation (Version 2015, Dassault Systèmes SolidWorks Corp., Waltham, MA). In this FEA, ten node parabolic tetrahedral solid elements were employed. The size of most mesh elements in the sclera, ON, and sheath was set to 300 μm, but the ONH region (peripapillary sclera, ON, and ON sheath) was remeshed at 100 μm and the LC at 50 μm to keep mesh elements small relative to these biologically critical tissues. The mesh size was determined from convergence testing by incrementing mesh size by 10 μm steps to verify the appropriateness of the mesh. This approach permitted high resolution in the regions of interest, without elements too numerous for computation. Figure 6 illustrates the mesh convergence of maximum strain for the LC and ON sheath. Strains remained distinct for up to 50 μm mesh for the LC and 100 μm for the ON sheath; these values were therefore employed for meshing the full model. Since peripapillary sclera and ON did not significantly differ in mesh convergence, the mesh size was set to 100 μm for both. A 16-point Jacobian check was employed to avoid mesh element inversion. The ON and sheath were fixed posteriorly at the orbital apex boundary where connection to the bony optic canal is rigid. Experimentally varied model parameters included an angle of further adduction past the 20 deg point of ON straightening, IOP, and ICP. Based upon published reports in human, Young's modulus of a highly simplified LC was taken to be 0.3 MPa [39]. Other moduli were as measured in bovine tissues. Effects of the assumptions of linear elasticity, isotropy, and incompressibility were evaluated by repeating simulations using hyperelasticity and also by sensitivity analysis with simulations setting isotropic parameters to the most extreme plausible limits in any anisotropic direction.

Fig. 6.

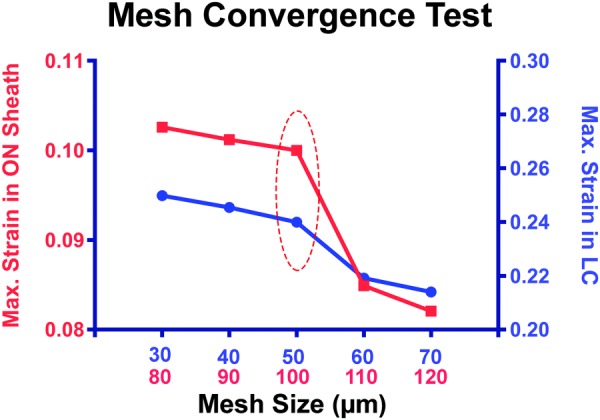
Mesh convergence. Strain simulations for LC and ON sheath were plotted from small (30 and 80 μm) to large (70 and 110 μm) mesh size by 10 μm increment. Appropriate mesh size was determined to be 50 μm for LC and 100 μm for ON sheath by balancing simulation accuracy against the computational load.

Results

Elastic Moduli of Posterior Eye Tissues.

Five specimens were subjected to tensile testing of each of four different bovine ocular tissues, and mean data are illustrated in Fig. 7. Elongation of the ON was along its long dimension, but the other tissues were elongated in arbitrary directions justified by assumed isotropy. A linear region in the strain–stress curve for each tissue was evident, and Young's modulus could be obtained by calculating the slope of the relationship between stress and strain. Young's modulus of the ON sheath exceeded all other tissues tested at 44.6 ± 5.6 (standard error of mean) MPa. By comparison, reported porcine ON sheath stiffness is linearly approximated as 4–5 MPa [33], about an order of magnitude less than the current bovine value. The modulus of bovine peripheral sclera (14.0 ± 2.3 MPa) measured approximately three times that of the peripapillary sclera (5.5 ± 0.8 MPa). The peripapillary sclera data are comparable with published modulus of ∼6 MPa for static loading of this bovine tissue [44]. Young's modulus of the composite ON was similar to the peripapillary sclera at 5.2 ± 0.4 MPa.

Fig. 7.

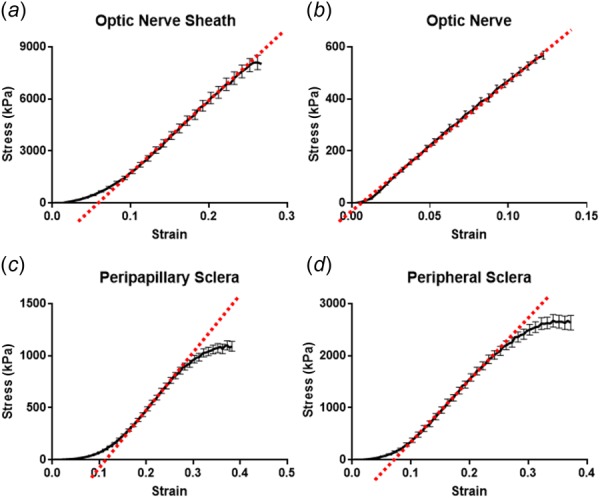
Mean tensile behavior of five samples of each of ON sheath (a), ON (b), peripapillary sclera (c), and peripheral sclera (d). Young's moduli were calculated from each linear regions as 44.6 ± 5.6 (standard error of mean) MPa for ON sheath, 5.2 ± 0.4 MPa for ON, 5.5 ± 0.8 MPa for peripapillary sclera, and 14.0 ± 2.3 MPa for peripheral sclera.

FEM Simulations.

Adduction 6 deg, implemented by 6 deg rotation of the scleral equator beyond the angle of ON straightening, was the input to each simulation. Initially, IOP and ICP were set to normal at 15 and 10 mm Hg (136 mm H₂O), respectively. The FEA for these normal conditions is illustrated in Fig. 8, a color map of simulated von Mises stress and strain, in which the adduction produced 4.3 MPa maximum stress in the ON sheath and 53% maximum strain at in the temporal peripapillary sclera. These values should be considered relative approximations and not absolute. It is a common pitfall of FEA that extreme values can be localized to only a few mesh elements representing mechanically unrealistic singularities. That was not the case here. Numerous mesh elements experienced lesser but still significant mechanical effects having maximal values of 1 MPa stress and 10% strain; higher strain values also map red (Fig. 8). Maximum stress occurred at the temporal junction of the ON, ON sheath, and sclera, and propagated to the temporal inner peripapillary sclera including the macular region. There was less stress on the nasal side of the ONH. Corresponding to the stress, the maximum strain was also greatest at temporal ONH border, but strain distribution differed slightly from stress because of variations in tissue Young's modulus. Marked strain occurred in two regions: the outer boundary layer at the junction of the ON sheath and sclera, and the inner boundary layer at the junction of the LC and peripapillary sclera. In the former case, the considerable strain was imposed by the stiff ON sheath on the relatively compliant sclera. Likewise, the outer peripapillary sclera transferred stress to the adjacent but relatively deformable LC, inducing large strain in the temporal LC rim.

Fig. 8.

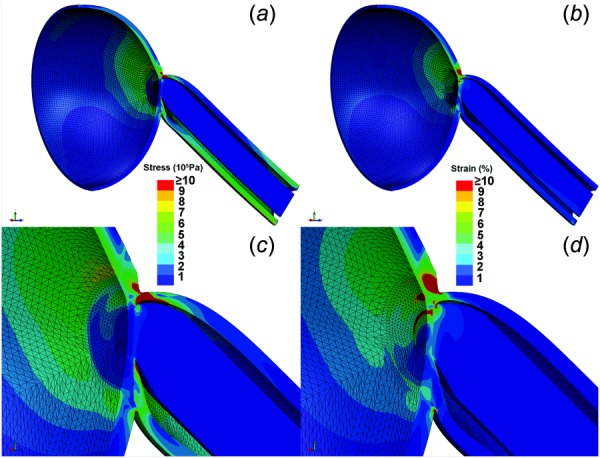
FEA of von Mises stress ((a) and (c)) and strain ((b) and (d)) in ON sheath and posterior sclera in adduction 6 deg past the point of ON straightening, assuming 15 mm Hg IOP and 136 mm H₂O ICP. For visualization, a hemisected view is shown with the temporal side oriented upward. (c) Magnified view showing maximum stress generated at the junction of ON, ON sheath, and sclera, propagating widely from the temporal peripapillary region to a wide zone of the temporal inner sclera, including the macular region. (d) Magnified view showing maximum strain is induced in two areas: temporal peripapillary sclera adjacent to the stiff ON sheath and temporal LC.

In addition to stress and strain analysis, the overall posterior ocular shape was compared before and after 6 deg adduction past the point of ON straightening overlapping resulting images (Fig. 9). Adduction caused a significant deformation and even thinning in the temporal peripapillary sclera, but a little change in nasal sclera.

Fig. 9.

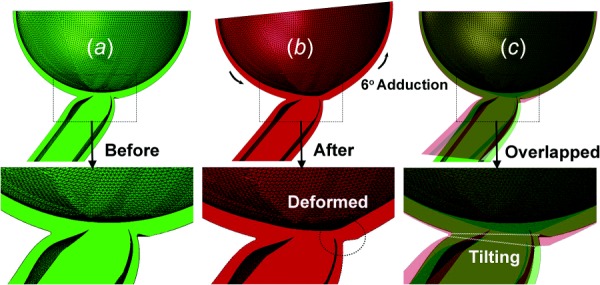
FEA of posterior globe before and after adduction 6 deg past the point of ON straightening. (a) Before adduction rendered in green. (b) After adduction, rendered in red, the temporal peripapillary sclera was deformed. (c) Overlay of (a) and (b), so that overlapping area is yellowish. The ONH tilted temporally in adduction.

Strain in LC.

Since LC strain may be important in axonal injury [45], the FEA was performed at a higher spatial resolution in this region. The maximum stress induced by 6 deg adduction past ON straightening was 180 kPa, associated with 18% maximum strain in temporal LC. For illustration, strain in a simplified LC was rendered in isolation from the complete FEA strain model shown in Fig. 8 and illustrated in Fig. 10 at high magnification before and after 6 deg adduction past ON straightening. While IOP-oriented strain is radially directed outward from the globe interior, strain induced by adduction is mainly tangent to the globe, and thus perpendicular to IOP-related strain. Adduction produced no change in shape of the nasal LC. However, the temporal LC exhibited the two different deformations in adduction: compression anteriorly and tension posteriorly. Transverse bending was evident as anterior LC diameter decreased by 1.1%, while posterior LC diameter increased by 2.1% in adduction 6 deg past the point of ON straightening.

Fig. 10.

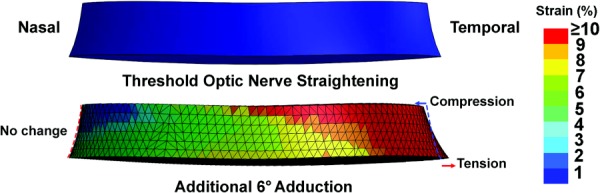
FEA of strain in the LC during adduction from the point of ON straightening (top) to an additional 6 deg adduction (bottom) assuming 15 mm Hg IOP and 136 mm H₂O ICP. While there is a little deformation of the nasal LC, the temporal side exhibits shear with compression anteriorly and elongation posteriorly.

Effect of Pressure on LC Strain in Adduction.

In this FEA sensitivity analysis, three inputs were varied: adduction, IOP, and ICP. A total of 18 FEA simulations was conducted, including all combinations of IOP at 5 (subnormal), 15 (normal), and 45 mm Hg (pathologically high); ICP at 68 (subnormal), 136 (normal), and 408 mm H₂O (pathologically high); and adduction at threshold of ON straightening, as well as 6 deg adduction beyond this point. Figure 11(a) illustrates the effects of varying IOP under while maintaining normal ICP and without eye movement; Fig. 11(b) illustrates the effects of varying ICP while maintaining constant normal IOP without eye movement; and Fig. 11(c) illustrates the effects of adduction at varying levels of IOP eye while maintaining constant, normal ICP. The sensitivity analysis in Fig. 11 indicates that adduction is by far the most influential factor on LC strain, followed distantly by IOP and least by ICP. Strain during adduction was mainly in the temporal LC where it exceeded 10% (Fig. 11(c)). While strain in the peripheral LC increased approximately 2% with IOP increasing to the markedly elevated value of 45 mm Hg (Fig. 11(a)), which is comparable with a maximum strain in monkey peripapillary sclera of 1.5% at 30 mm Hg IOP [30], the effect of IOP was much less than that of adduction. Increasing ICP had almost no effect on LC strain (Fig. 11(b)), in agreement with a report that concluded that acute ICP elevation has minimal impact on the LC [46].

Fig. 11.

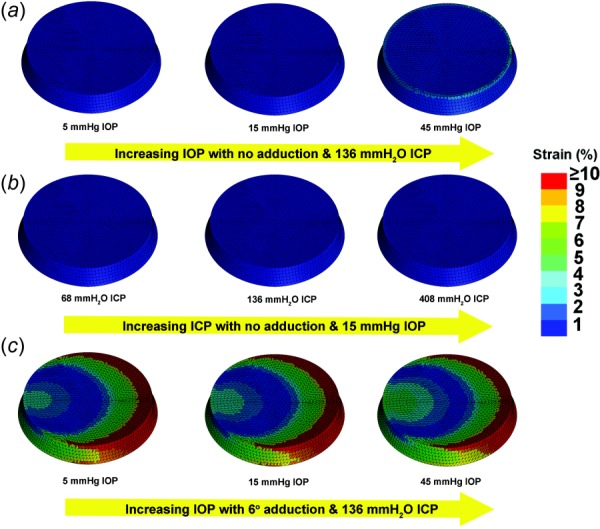
Sensitivity analysis of LC strain to variation in IOP, ICP, and adduction. (a) IOP was increased from 5 to 45 mm Hg with constant 136 mm H₂O ICP, without adduction. For the 45 mm Hg IOP, approximately 2% strain was induced around the inner LC rim. (b) ICP was increased from 68 to 408 mm H₂O while maintaining 15 mm Hg IOP, without adduction. There was no significant strain. (c) IOP was increased from 5 to 45 mm Hg with constant 136 mm H₂O ICP, and with 6 deg adduction past the point of ON straightening, inducing strain exceeding 10% in temporal LC that increased only slightly with increasing IOP.

Sensitivity to Young's Elastic Modulus of Individual Tissues.

Recognizing that bovine rather than human moduli were employed for some tissues in the FEA, additional FEA was performed to assess the strain sensitivity to tissue elastic moduli that might differ in humans. Rather than employing a different modulus for each individual tissue, the simulations were repeated assuming 3 MPa uniform modulus for all tissues in order to avoid possible artifacts from discontinuities of the modulus. As illustrated in Fig. 12(a), the strain concentration nevertheless was predicted by simulations at the temporal boundaries of ON sheath and peripapillary sclera, and in peripapillary sclera and LC. While strain magnitudes under the assumption of uniform modulus differed quantitatively from those produced by simulations employing individually measured or assumed tissue moduli (Fig. 12(b)), the relative strain distributions were similar. This finding supports the inference that the geometrical configuration of the ON sheath under tension in adduction is the main factor in localization of peripapillary and LC strain, rather than particular values of tissue elastic moduli. The generality of ON sheath tethering in adduction as a mechanical perturbation to the ONH irrespective of individual biomechanical tissue parameters is reassuring, since the published data on these parameters in humans are still sparse.

Fig. 12.

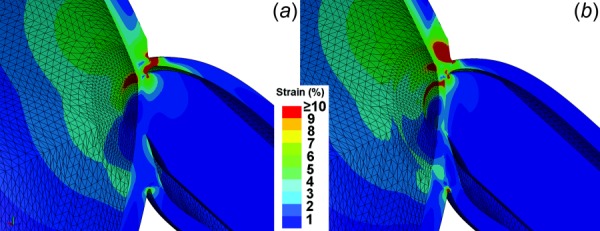
Hemisected axial rendering of the sensitivity of peripapillary and LC strain to variation in Young's elastic modulus of tissues in 6 deg adduction. Simulation input was 15 mm Hg IOP and 136 mm H₂O ICP. (a) Magnified strain distribution assuming identical 3 MPa elastic modulus for all tissues. (b) Magnified strain distribution with measured individual bovine parameters for various tissues. Note that the strain distributions in (a) and (b) localize in qualitatively similar temporal regions, implying that the general phenomenon of temporal peripapillary strain is independent of precise local biomechanical properties. However, in (b) there is a greater strain in the temporal LC.

Unique to the simulation in Fig. 12(b) is the stiffness differential between tissues. For example, in Fig. 12(b), the ON sheath is assigned much stiffer (44.6 MPa) value than adjacent peripapillary sclera (5.5 MPa), so that the majority of strain in adduction is imposed by the stiff ON sheath upon the compliant peripapillary sclera. The LC is yet much less stiff (0.3 MPa) than peripapillary sclera, and because the softer tissue is deformed more by the same force, the greater strain results in the temporal LC (Fig. 12(b)). Therefore, while ON sheath tension in adduction is predicted to concentrate strain on the temporal peripapillary sclera and LC regardless of the particular biomechanical properties of these tissues, the absolute degree and spatial extent of strain concentration may vary in the temporal LC and other nearby regions depending upon individual biomechanical parameters for each tissue.

FEA With Assumed Separate Pia and Neural Tissue.

The current study realistically modeled the ON as a composite material, although prior investigators have simulated the neural tissue in the ON to have the mechanical properties of the brain, and be mechanically and anatomically separable from the surrounding pia. In order to compare the effects of these alternative formulations, another FEA of 6 deg adduction past ON straightening was implemented under the foregoing assumption of separable ON pia and neural tissue. Pial thickness of 0.06 mm, pial elastic modulus of 3 MPa, and ON neural tissue modulus of 0.03 MPa were taken from published literature [39]. Figure 13 illustrates the resulting stress and strain for the separable ON and pial model in 6 deg adduction past the point of ON straightening, indicating stress and strain distributions nearly identical to those for the composite ON assumption in Figs. 8(c) and 8(d), except that there was a greater concentration of strain in the soft, temporal ON tissue due to the unrealistically assumed absence of internal connective tissue support within it.

Fig. 13.

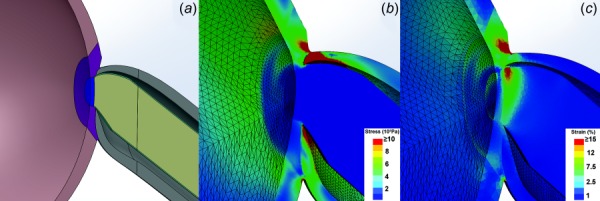
FEA of adduction 6 deg past the point of ON straightening, assuming mechanically distinguishable rather than composite ON pia and neural tissue. (a) Modified ON model with soft neural tissue surrounded by separable pia. Neural tissues enclosed by 0.06-mm thick pia are rendered as green. Stress (b) and strain (c) distributions are qualitatively similar to those in Figs. 7(c) and 7(d) that assumed ON and pia to be composite, except for greater strain in the temporal ONH in the mechanically distinguishable model due to the low elastic modulus of neural tissue when assumed to lack internal connective tissue support.

Hyperelasticity.

The present study simulated 6 deg incremental rotation past the point of ON straightening. This small deformation was assumed to warrant linear elasticity methods, but this assumption was tested by simulation repeated using a two-parameter Mooney–Rivlin hyperelastic model [47] having the form

$$\sigma =\left(2C_1+\frac{2C_2}{\lambda }\right)\left({\lambda }^2-\frac{1}{\lambda }\right)$$

where $\sigma$ is stress and $\lambda$ is the stretch ratio. Material parameters from four different tissues for Mooney–Rivlin analysis were extracted by curve fitting from uniaxial tensile loading experiments (Table 2). Experimental data and corresponding curve fittings are plotted in Fig. 14. Nonlinear FEA was performed using these fitted parameters. However, the stress and strain distributions with the hyperelastic model, as illustrated in Figs. 15(a) and 15(b), were qualitatively identical to those for the previously presented linear FEA (Figs. 8(c) and 8(d)).

Table 2.

Mooney–Rivlin hyperelastic model constants for posterior bovine tissues determined by curve fitting to uniaxial tensile loading data

Mooney–Rivlin parameter	ON sheath	ON	Peripapillary sclera	Peripheral sclera
C1 (MPa)	2.674	0.4392	0.0716	6.781
C2 (MPa)	4.918	0.2699	0.6741	−6.352

Fig. 14.

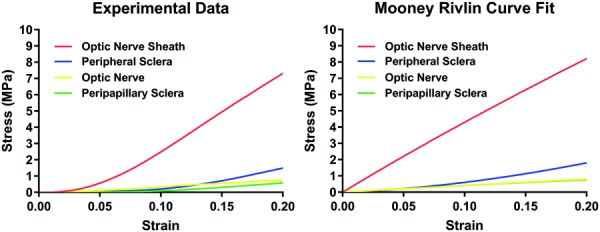
Tensile data compared with Mooney–Rivlin fits. Peripheral sclera, ON, and peripapillary sclera fitted experimental data reasonably, but the relatively linear Mooney–Rivlin model did not fit the ON sheath data well in the nonlinear, low-strain region.

Fig. 15.

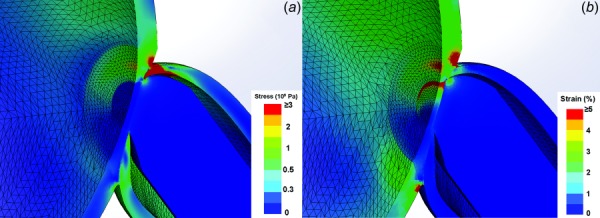
FEA using Mooney–Rivlin hyperelastic model. (a) Magnified view of stress distribution showing maximum stress at the temporal junction of ON, ON sheath, and sclera, which is similar to the linear FEA stress result in Fig. 8(c). (b) Magnified view showing maximum strain at the temporal sclera–ON sheath junction and outer rim of LC that is also similar to the linear FEA strain result in Fig. 8(d).

Discussion

Strain due to Eye Rotation.

The current study supports a novel hypothesis proposing repetitive strain injury to the ON during adduction as a component of the pathogenesis of NTG, a form of primary open angle glaucoma in which ON damage occurs at relatively low IOP. Computational simulations strongly suggest that ON sheath traction caused by adduction generates stress and strain in the temporal ONH and LC exceeding the effects of IOP, ICP, as well as differential values of IOP and ICP that correspond to translaminar pressure. Unlike elevated IOP, a large ocular adduction is not a continuous, steady-state phenomenon, yet it is an intense, transient phenomenon repeated ubiquitously. Humans make about three rapid eye movements—called saccades—each second [48], for about 183,000 daily [49], including saccades during sleep [50]. Saccades or binocular convergence during reading probably load the ON less than the largest and fastest adduction during tracking of visual targets or coordinated with self-generated head turns. Inner ear reflexes generate ocular counterrotations coordinated with head movement, particularly during large gaze shifts required during walking, running, and other common daily activities. Consequently, the large gaze shifts coordinated with head movement include eye movements averaging about 30 deg [51]. In one experiment, subjects who touched a series of targets within arms' length made saccades as large as 45 deg [52].

Nonlight-generated visual perceptions of light due to mechanical photoreceptor stimulation can be perceived during ordinary saccades, indicating strain in the retina adjacent the ONH [53]. The extraocular muscles generate high transient tensions during saccades, with the maximum isometric tension in human horizontal rectus muscles averaging 40 gm-f for a 20 deg and 52 gm-f for 30 deg saccades, higher than corresponding postsaccadic steady-state tensions of 26 and 33 gm-f, respectively [54].

An investigation by MRI indicates that any horizontal eye movement to a distant target exceeding 20 deg would probably exhaust ON sheath redundancy in the adducting eye [5], and a smaller gaze shifts would do so during convergence to near targets. Repetition of these strains many millions of times over years might plausibly induce ON damage, and so could contribute as to optic neuropathy. Moreover, since the current FEA simulations were static, they set only a lower bound on dynamic stresses and strains during rapid eye movements. The muscles and orbital connective tissues are viscoelastic [28,36]. Although viscosity is omitted from the current FEA, the elastic modulus of bovine sclera is reportedly five- to sixfold higher at for saccadic than static loading [44]. Intense transient strains during adducting saccades might cause repetitive strain to the ON, analogous to the effect of repetitive wrist motion in carpal tunnel syndrome [55]. Wrist extension at 15/min, 15 N force, and for 7 h daily for only 3 weeks provokes injury [56]. Nerve damage occurs after only 132,300 wrist extensions in 3 weeks, less than the daily average saccade number [51]. Moreover, even static FEA suggests that adduction tethering has two orders of magnitude larger mechanical effect on the ONH and LC than static IOP elevation. The foregoing implication is that dynamic effects during saccades might be much greater, although this remains presumptive.

Clinical Correlates.

While the similarities between Figs. 12(a) and 12(b) support the general thesis of temporal peripapillary strain in adduction, the differences highlight potential susceptibility to optic neuropathy in particular individuals. Foremost are the geometry and physical dimensions of the globe, ON sheath, and orbit of individuals. Regardless of these variables, under whatever conditions when the ON has exhausted its redundancy in adduction, the stress and strain are concentrated on the temporal edge of the ONH and LC (Fig. 8). It is probably no coincidence that direct clinical examination of the adult eye very frequently reveals “peripapillary atrophy,” a degeneration of this same crescent-shaped temporal region, in which the retina and retinal pigment epithelium around the ON become thin or absent [5]. Peripapillary atrophy is most common adjacent the temporal edge of the disk [15], consistent with the stress and strain distribution in current FEA.

Optical coherence tomography is a two-dimensional imaging technique that in living humans has demonstrated posterior displacement of the optic cup and temporal peripapillary RPE progressively increasing with adduction [57]. This OCT finding concords with the FEA shown in Fig. 9. Temporal ONH tilting amounts to a posterior displacement of the optic cup and temporal RPE. These deformations of the optic cup and peripapillary retinal pigment epithelium due to normal adduction are markedly larger than demonstrated by OCT due to severe IOP elevation in acute angle closure [58], or following surgical IOP reduction [59]. The observed greater effect of adduction than IOP elevation is also predicted by the FEA (Fig. 11).

Limitations.

While apparently reasonable, the current FEA is at most a proof of principle suggesting relative mechanical behavior. The current FEA is a static model employing the material properties of bovine tissues determined by uniaxial tensile loading and assumed isotropy within the homogeneous tissue. Human tissue data from multidirectional testing, including compressive and shear loading, could in the future provide more nuanced descriptions. Due to anatomical considerations, it was not possible to employ the same aspect ratio for all tissues. The variation in aspect ratio could influence measured values for Young's modulus. For example, it has been shown that the aspect ratio is positively correlated with tensile stiffness, so that as a specimen aspect ratio increases from 1 to 5, the stiffness increases by 36% [60]. Therefore, the low aspect ratios of some specimens tested here (1.4 for sclera and 1.7 for ON sheath) may have affected the apparent values of Young's modulus modestly, but by an amount probably within the range of intersample measurement variability. While the FEA assumed linear elasticity, Mooney–Rivlin simulation suggested that this assumption was noncritical. Dynamic data would be necessary to build a viscoelastic model [28,36]. However, an FEA simultaneously incorporating anisotropic, nonlinear viscoelasticity for all its tissue constituents would likely be computationally impractical, even if all of the required constitutive properties could be measured. A more practical approach would be to estimate the most important properties relevant to ON and LC strain, and model these realistically on appropriate spatial and temporal scales as a guide to future data acquisition. Of course, it is likely that many anatomic and mechanical properties may vary significantly among individual humans, so that the precise behavior of individual models would vary correspondingly.

The current simulation for static maintained adduction probably underestimated stresses and strains in the posterior sclera and peripapillary region for at least three reasons. First, EOM forces are much higher during dynamic saccades than during sustained fixations [61]. Second, during saccades, stress waves are magnified at the ONH [62]. Finally, scleral stiffness is greater during higher loading rates, such as during saccades, than during static loading, and increases nonlinearly with strain [63]. Therefore, the present simulations probably represent lower bounds for the deformations experienced by the peripapillary and LC region numerous times every day during eye movements.

The current study modeled the ON as a composite structure realistically incorporating integrated pia and neural tissue. A supplemental FEA using the alternative ON model with mechanically distinguishable pial and neural tissue exhibited qualitatively similar stress and strain distributions, but overestimated strain in the temporal ON (Figs. 13(b) and 13(c)). This is unsurprising since the Young's modulus of neural tissues was assumed to be the very low value typical of the brain at 0.03 MPa. In actuality, Fig. 5 shows that the neural tissue of the ON is not only intimately enclosed by pial connective tissue but the pia is also intimately connected with reinforcing struts of internal connective tissue intercalated throughout it that account for its considerably higher elastic modulus. The internal connective tissue of the ON would obviously mitigate strain within it. Nevertheless, in both composite and separable ON FEA, the temporal stress–strain concentration was predicted as a result of adduction tethering of the ON and sheath.

The current study does not deny that high IOP can be a pathogenic mechanism in glaucoma. However, FEA does suggest that mechanical effects of ocular adduction could be an alternative or supplemental pathogenic mechanism to elevated IOP in this blinding disease.

Funding Data

• National Eye Institute (Grant Nos. EY000331 and EY008313).

• Research to Prevent Blindness (Unrestricted Grant).

Nomenclature

Abduction =

rotation of the eye laterally, away from the midline

Adduction =

rotation of the eye medially, toward the midline

C_i =

Mooney–Rivlin hyperelastic parameters

CSF =

cerebrospinal fluid

EOM =

extraocular muscle

FEA =

finite element analysis

FEM =

finite element model

ICP =

intracranial pressure

LC =

lamina cribrosa of the optic nerve head

MR =

medial rectus extraocular muscle

MRI =

magnetic resonance imaging

NTG =

normal tension glaucoma

OCT =

optical coherence tomography

ON =

optic nerve

ONH =

optic nerve head

$\lambda$ =

stretch ratio

$\sigma$ =

stress