Experimental evaluation of the Liu–Beveridge dinucleotide step model of DNA structure

Abstract

Methods for predicting DNA curvature have many possible applications. Dinucleotide step models describe DNA shape by characterization of helical twist, deflection angles and the direction of deflection for nearest neighbor base pairs. Liu and Beveridge have extended previous applications of dinucleotide step models with the development and qualitative validation of a predictive method for sequence-dependent DNA curvature (the LB model). We tested whether the LB model accurately predicts experimentally deduced curvature angles and helical repeat parameters for DNA sequences not in its training set, particularly when challenged with quantitative data and subtle sequence phasings. We examined a series of 17 well-characterized DNA sequences to compare electrophoretic and computational results. The LB model is superior to two other models in the prediction of helical repeat parameters. We observed a strong linear correlation between curvature magnitudes predicted using the LB model and those determined by electrophoretic ligation ladder experiments, although the LB model somewhat underestimated apparent curvature. With longer electrophoretic phasing probes the LB model slightly overestimated gel mobility anomalies, with modest deviations in predicted helical repeat parameters. Overall, our analyses suggest that the LB model provides reasonably accurate predictions for the electrophoretic behavior of DNA.

INTRODUCTION

Since the initial characterization of intrinsically curved DNA from Leishmania tarentolae kinetoplasts (1) biologists have long sought both a biophysical understanding of the apparent intrinsic curvature of certain DNA sequences and an accurate basis for predicting such curvature. Gel electrophoresis is a commonly used technique that detects apparent intrinsic curvature as mobility retardation, but this technique lacks a rigorous physical theory and therefore relies on the behavior of empirical curvature standards (2). Such electrophoretic methods have  shown that DNA mobility anomalies in native polyacrylamide gels increase as the square of the degree of curvature for a given mass (3).

Solution measurements of DNA curvature have been more readily interpreted from first principles. DNA cyclization kinetics (4), minicircle competition (5) and T4 DNA ligase circle formation assays (6–8) have been used to detect both intrinsic DNA curvature and DNA bending induced by proteins. Alternative methods include spectroscopic tools such as transient electric birefringence (9) and fluorescence resonance energy transfer (10), but these methods are more laborious and expensive.

According to dinucleotide models of DNA curvature (11–12) each dinucleotide step is associated with a characteristic deflection of the local helix axis. These models attempt to describe DNA shape by characterization of helical twist, deflection angles and the direction of deflection. A now classic paper by Bolshoy et al. attempted to use DNA cyclization and electrophoretic mobility data to test experimentally theoretical predictions of a dinucleotide ‘wedge’ model (13). The authors solved a system of equations to minimize misfits between calculated and observed DNA curvature. The output was then used for prediction of sequence-dependent DNA trajectory.

This model, here termed BMHT, accounts well for data within its training set, but is not fully reconciled with many sequence motifs or with base pair step parameters derived from crystal structures (14). Liu and Beveridge have extended the BMHT model in a recent report describing the development and qualitative validation of a predictive method for sequence-dependent DNA curvature based on optimized dinucleotide step parameters (14). The work examines dinucleotide steps obtained from 54 DNA crystal structures utilizing an approach similar to that described in the BMHT model. The main advances introduced by the Liu–Beveridge (LB) model lie in the implementation of updated mathematical treatments of base pair step geometries and the use of simulated annealing protocols for parameter refinement (14). Liu and Beveridge thus attempted to develop a computational tool with improved predictive power that accounts for DNA gel retardation as a function of DNA sequence. These authors emphasize that the output of their model defines a ‘structural construct’ that predicts molecular behavior but may or may not correspond to a true molecular structure. A third model, DCS, has been derived from mean values of roll, tilt and twist angles from a database of dinucleotide crystal structures (14). It should be emphasized that dinucleotide models obtained from parameter fittings are effectively knowledge-based prediction schemes and are not necessarily amenable to physical interpretation. Their output reflects only whatever knowledge is implicit in the parameterization set.

The general predictive power of the LB model was previously demonstrated with a qualitative analysis of a series of well-characterized DNA structural motifs, including A_5/6 tracts, A₄T₄ and T₄A₄ motifs and kinetoplast DNA sequences (14). Although the LB model successfully differentiated ‘strongly curved’ from ‘uncurved’ DNA, it remains to be determined if the model predicts experimentally deduced curvature angles and helical repeat parameters derived for a variety of DNA sequence motifs.

We have therefore tested the LB model in a quantitative analysis of macroscopic DNA curvature data. Our goal is simply to provide a critical assessment of the LB prediction scheme, rather than provide detailed physical insight per se. This goal is fundamentally practical: molecular biologists frequently seek computational tools to provide insight into possible sequence-dependent DNA structure. We wished to determine if a convenient web-based tool implementing the LB model could serve this purpose. We examined a library of well-characterized DNA sequences to compare electrophoretic and computational results. We first show that the LB model is superior to the BMHT and DCS models, in terms of ability to predict correctly DNA helical repeat parameters in solution. We then analyzed data from a series of 17 short DNA duplexes. Each duplex represented two helical turns of DNA and was polymerized into a 147 bp molecule, both enzymatically and in silico. Our electrophoretic data for these molecules (ranging from straight to curved) have been previously published (15). We further examined the structures of longer (∼240 bp) electrophoretic phasing probes containing systematically spaced arrays of phased A₅ tracts (16).

We report a strong linear correlation between curvature magnitudes predicted using the LB model and those determined by electrophoretic methods for 147 bp duplexes, although the curvature estimates for A₅ tracts deduced from the LB model were found to be ∼20% lower than the standard estimate of 18°. On the other hand, using larger phasing probes we show that the LB model slightly overestimates gel mobility anomalies in these cases and the predicted helical repeat parameters also differ slightly from observed values. Overall, our quantitative analysis of the LB model extends the preliminary validation performed by Liu and Beveridge (14) and shows that the model provides reasonably accurate predictions for the electrophoretic behavior of DNA molecules not in its training set.

MATERIALS AND METHODS

DNA ligation ladders

Ligation ladder analyses were performed as described (15,17). Briefly, radiolabeled DNA duplexes (169 pmol, created by annealing enzymatically phosphorylated synthetic oligonucleotides) were assembled into 20 µl ligation reactions containing 400 U T4 DNA ligase (New England Biolabs) and incubated at 22°C for 30 min. In some cases BAL-31 exonuclease (New England Biolabs) was used to distinguish circular from linear ligation products. Ligation ladders were analyzed by electrophoresis through 5% native polyacrylamide gels (1:29 bisacrylamide:acrylamide) in 1× TBE buffer, with a voltage gradient of 10 V/cm at 22°C for 2.5 h. Molecular weight markers were created by labeling a 100 bp duplex DNA ladder (Gibco BRL) using T4 DNA polymerase (New England Biolabs) and [α-³²P]dATP as recommended by the ladder manufacturer. Gels were dried and exposed to storage phosphor screens for analysis using a Molecular Dynamics Storm 840 phosphorimager. Curve fitting was performed by a least squares method using Kaleidagraph software running on a power Macintosh computer.

Measurement of DNA relative curvature

Measurement of the relative curvature of 147 bp molecules from ligation ladder analyses was performed as described (17). Briefly, the distances migrated were measured manually for all radiolabeled bands in experimental lanes. An exponential equation was fitted by a least squares method to a plot of distance migrated (x) as a function of length (L) for 100 bp DNA ladder markers:

L = αe^βx 1

where L is DNA length (in bp), x is distance migrated (typically measured in mm) and α and β are fit parameters. Once determined, parameters α and β were fixed and substituted back into equation 1 and the resulting function was used to calculate the apparent length (L_app) for all bands in experimental ligation ladders. Electrophoresis of unligated samples allowed assignment of the monomer duplex band, permitting assignment of an actual length (L_act) to each gel band. Relative mobility, R_L, is defined as:

R_L = L_app/L_act 2

R_L was determined for each of the 147 bp ligation products obtained for test duplexes.

Molecular modeling of ligation ladder species

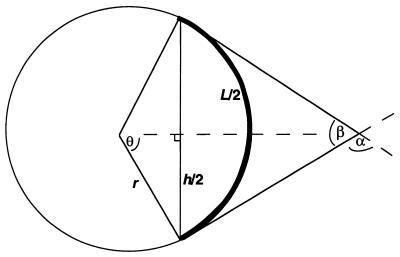
Molecules of 147 bp (representing seven copies each of test duplexes ligated end-to-end) were submitted for structure prediction using the LB, DCS and BMHT models as described in detail by Liu and Beveridge (14; http://ludwig.chem.wesleyan.edu/dna/). The predicted structures are generated in protein data bank (pdb) format and were analyzed using Insight II software (MSI) running on a Silicon Graphics O2 workstation. The molecular end-to-end distance was measured for each predicted structure. Conversion of end-to-end distance to relative DNA curvature was performed using the geometric derivation shown in Figure 1.

Figure 1.

Geometric model used to calculate DNA curvature predicted by the LB model. See text for a detailed description. The bold curve represents DNA trajectory. Total DNA curvature is given by angle α.

We assumed that the DNA contour length (L) formed an arc of a virtual circle (bold in Fig. 1), lying in a plane with both the initial and final vectors tangent to the circle. The end-to-end distance (h), determined from the coordinates generated from the LB model, was drawn as a chord of the circle, connecting the ends of the arc (vertical line in Fig. 1). The central angle of the circle describing half of the arc (θ) was then determined by:

sinθ = h/2r 3

r = h/2sinθ 4

where r refers to the radius of the circle. Geometric analysis of the circle indicates:

L = πθh/180sinθ 5

θ/sinθ = 180L/πh 6

Given a known DNA contour length (L) and the measured end-to-end distance (h), θ is then directly determined. The value of 2θ (equal to α in Fig. 1) represents the total DNA curvature, averaged over the total DNA contour length. We normalized this value to determine a modeled curvature value (M_C) by dividing 2θ by the number of helical turns in the DNA molecule:

M_C = 2θ/L/10.5 7

The helical repeat (bp/turn) of these molecules was previously determined to be 10.4–10.5 bp/turn (17; P.R.Hardwidge, R.B.Den and L.J.Maher, unpublished data).

Quantitative analyses of DNA phasing probe mobilities

A trimolecular ligation design to produce electrophoretic phasing probes has been presented in detail elsewhere (16). Ligation products (∼240 bp) were resolved on 8% native polyacrylamide gels (1:29 bisacrylamide:acrylamide) by electrophoresis at 10 V/cm in 0.5× TBE buffer at 22°C for 5 h. Electrophoretic mobilities (µ) were measured and normalized to the average mobility (µ) for each group of five probes involving the same test sequence at different distances relative to an A₅ tract array. The value of µ/µ was plotted against the spacing (bp) between the two sets of A₅ tracts and then fitted to a phasing function (16,18):

µ/µ = (A_PH/2)cos[2π(S – _ST)/_PPH] + 1 8

where A_PH is the amplitude of the phasing function, S is the normalized spacer length, S_T is the trans spacer length (the distance in bp such that the two elements of curvature most nearly cancel) and P_PH is the phasing period (set at 10.5 bp/helical turn).

RESULTS AND DISCUSSION

We wished to extend the analyses performed by Liu and Beveridge in validation of their dinucleotide step DNA structure prediction model (14). Rather than provide a detailed physical understanding of DNA curvature, our goal was to examine critically the utility of the LB model in the prediction of sequence-dependent DNA curvature. These authors applied their model to short sequences, did not examine helical repeat issues and used only limited quantitative comparisons.

Ligation ladder experiments

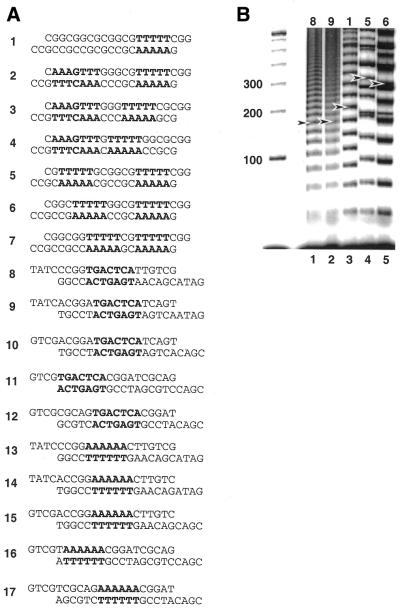
We first examined DNA structures predicted by various dinucleotide step models to compare predicted DNA curvature with that deduced from electrophoretic ligation ladder experiments (15,17). We compared the LB, DCS and BMHT models as implemented (http://ludwig.chem.wesleyan.edu/dna/). A detailed comparison of roll, tilt and twist angles among the three models has been published previously (14). In broad qualitative terms the main differences among the three models are as follows. In the LB model A tracts are straight, with bending occurring in the intervening sequences. In BMHT bending occurs at ApA wedges within A tracts. The DCS model comprises mean values of roll, tilt and twist angles from a database of dinucleotide crystal structures. We had previously determined relative curvature values for a series of 17 DNA duplexes measured in electrophoretic ligation ladder experiments. In particular, we focused on tandem repeats of 21-bp duplexes created by ligation of 17 DNA duplexes encompassing a wide range of relative curvatures (Fig. 2A).

Figure 2.

Comparative electrophoresis experiments. (A) DNA duplexes under investigation. The primary sequence elements of interest are indicated in bold. Top strands are written such that the 5′-terminus is at the left. (B) Image obtained after native PAGE of ligation products of duplexes 8, 9, 1, 5 and 6. Ladder markers (100 bp) are shown at left (M). Arrowheads indicate molecules containing seven duplexes ligated end-to-end (147 bp).

Electrophoretic data for a subset of these duplexes are presented in Figure 2B. Duplexes 8, 9, 1, 5 and 6 were electrophoresed through native polyacrylamide gels. Arrows in Figure 2B indicate molecules containing seven duplexes ligated end-to-end (147 bp). This assignment was made with reference to unligated controls and circular DNAs were distinguished by exonuclease treatment (data not shown). Pronounced mobility differences were observed, as expected. Duplexes 8 and 9 contained AP-1 sequences, with little intrinsic curvature (Fig. 2B, lanes 1 and 2). Duplex 1 contained a single A₅ tract (Fig. 2B, lane 3). Phased A_5/6 tracts are each estimated to provide ∼18° of curvature. Duplex 5 (Fig. 2B, lane 4) contained a second A₅ tract, whose orientation was phased in cis relative to the single A₅ tract found in duplex 1 (total predicted curvature ∼36°). Duplex 6 (Fig. 2B, lane 5) also contained a second A₅ tract, in this case oriented ortho (∼69° clockwise) with respect to the A₅ tract found in duplex 5.

The sensitivity of the ligation ladder assay to the different resulting DNA shapes is immediately apparent (Fig. 2B). Ligation of duplexes 8 and 9 resulted in product ladders with very little gel mobility anomaly (Fig. 2B, lanes 1 and 2). In contrast, ligation products involving duplex 1 displayed a marked reduction in gel mobility due to the curvature associated with the A₅ tract (Fig. 2B, lane 3). This effect was even more pronounced in duplex 5 (cis), where two A₅ tracts were phased, producing a highly curved duplex. The mobilities of duplex 6 ligation products were slightly increased because the A₅ tracts are not optimally phased (Fig. 2B, lanes 4 and 5).

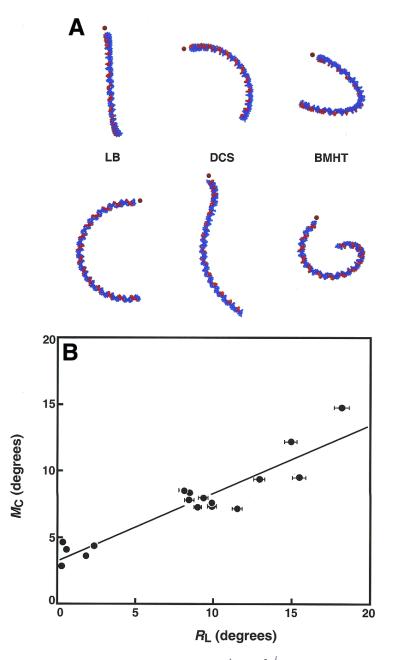
We then examined the predicted structures after in silico ligation of duplexes 1–17 into 147 bp molecules, followed by analysis of structures predicted by the LB, DCS and BMHT models (Fig. 3A, left, middle and right, respectively). End views (upper row) and side views (lower row) of the structures of duplex 5 are shown in Figure 3A. The predicted structures immediately reveal the qualitative superiority of the LB model compared to both the DCS and BMHT models in terms of the predicted helical repeat parameter. We had previously measured the helical repeat of duplex 5 (and related sequences), confirming a value of 10.4–10.5 bp/turn (17). Thus, tandem ligation products based on 21 bp duplexes must be approximately planar. Only the LB model successfully predicts a planar structure, while the DCS and BMHT models predict unobserved writhe (Fig. 3A).

Figure 3.

Analysis of comparative electrophoresis experiments. (A) End and side views of 147 bp ligation products of duplex 5, predicted from the dinucleotide models LB, DCS and BMHT, respectively. A₅ tracts are indicated in red. Dots indicate equivalent ends. These ends project towards the reader in top views. Only the LB model properly predicts a planar structure. (B) Relationship between modeled and measured DNA curvature. Data are plotted as the modeled curvature (M_C) versus relative curvature (R_L) measured in electrophoretic experiments. A₅ tracts were assigned a value of 18° of curvature.

Quantitative DNA shape information from electrophoresis experiments was then analyzed in a conventional manner by determining relative electrophoretic mobility (R_L) as described in Materials and Methods (data not shown). We plotted the modeled curvature (M_C, equation 7) versus the measured relative curvature (R_L) for duplexes 1–17, following conversion of R_L to a degree measure, assuming 18° of curvature per phased A₅ tract (19). This comparison is presented in Figure 3B. Overall, the LB model underestimates DNA curvature such that, based on the slope of the line in Figure 3B, the predicted curvature averages ∼50% of that deduced from our electrophoretic ligation ladder experiments. Figure 3B shows a striking clustering of data at ∼9° helical turn for all duplexes with one A tract per two helical turns. This result shows that neither predicted nor observed curvature is strongly affected by the various sequences separating A tracts. The overall correlation between the predicted and measured values was strong and the prediction differs by only ∼20% for duplex 5, which contains two phased A₅ tracts. The equation of the best fit linear correlation between the data sets is:

M_C = 3.24 + 0.52R_L; R² = 0.87 9

We also note that recent molecular dynamics simulations predict a curvature angle for A₅ tracts of 15.5°, less than that deduced from electrophoresis (20). In fact, for all duplexes containing at least one A₅ tract, predicted and observed curvature estimates differed by no more than ∼20%. Deviations for duplexes 8–12, which do not contain loci of significant intrinsic curvature, were more significant. These results might reflect the inability of ligation ladder experiments to detect sensitively very modest curvature in DNA.

Analysis of electrophoretic phasing probes

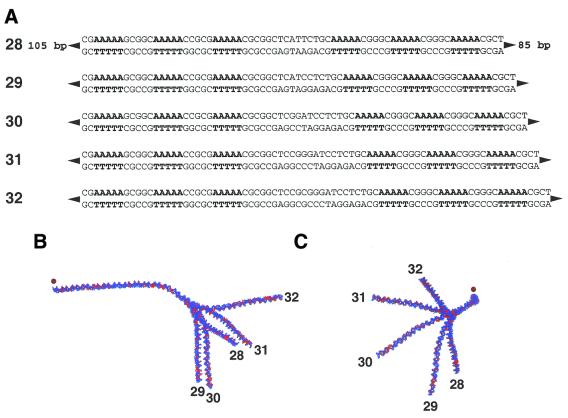
We extended our analysis to an independent set of experiments involving longer electrophoretic phasing probes, described in detail elsewhere (16). Each ∼240 bp probe contained either one (probes 18–22), two (23–27) or three (28–32) phased A₅ tracts, separated by 20–40 bp from another series of three phased A₅ tracts (Fig. 4A). Within each group of five probes the DNA sequences are identical, except for the spacing between the sets of phased A₅ tracts. The helical alignment is thus altered between the two sets of phased A₅ tracts, creating different global DNA shapes. Comparison of the relative mobilities of each probe within a group provides accurate quantitative information regarding the magnitude and direction of DNA curvature (3,16).

Figure 4.

Examples of electrophoretic phasing probes. (A) Phasing probes (designated 28–32) are ∼240 bp in length and differ only in the spacing between the two sets of three phased A₅ tracts. Phased A₅ tracts are in bold. Top strand sequences are shown 5′→3′ (left to right). Two additional groups of five phasing probes were also constructed such that either one (probes 23–27) or two (18–22) of the A₅ tracts were replaced with the sequence 5′-GCGGC-3′ (not shown). (B and C) Structures predicted from the LB model for phasing probes 28–32. Adenosine residues are indicated in red. (B) Side view. The 5′-ends of phasing probes 28–32 are oriented to the left of the figure (dot). (C) Bottom view. The overlaid 5′-ends of phasing probes 28–32 project out of the plane of the figure towards the reader (dot).

We examined the predicted structures for probes 18–32 (14; http://ludwig.chem.wesleyan.edu/dna/). Analyses were limited to the LB model, whose twist parameters had previously proven superior (see above). The predicted structures of probes 28–32 are displayed in Figure 4B (side view) and C (bottom view). Structures predicted by the LB model were analyzed further by measurement of end-to-end distance (h) and contour length (L), as described in Materials and Methods.

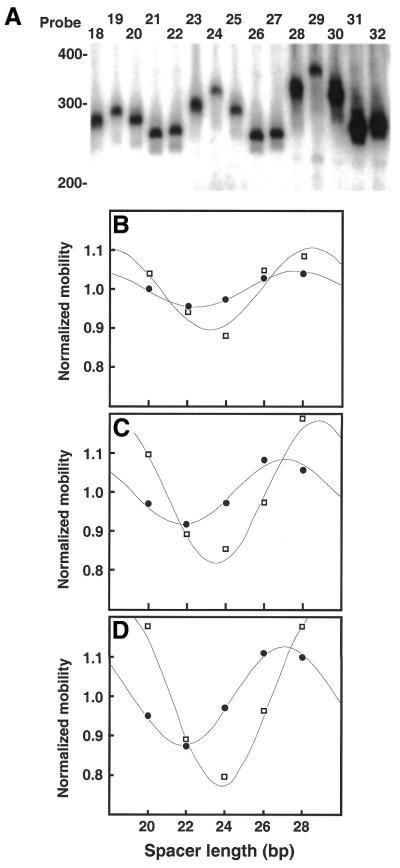
Probes 18–32 were electrophoresed through 8% native polyacrylamide gels. Representative data from electrophoretic analyses of probes 18–32 are shown in Figure 5A. As the spacing between the two sets of phased A₅ tracts changes, electrophoretic mobility is altered. When curvature loci are aligned in cis, gel mobility is minimized. The extent to which gel mobility is reduced in each probe is interpreted as a measure of the magnitude and direction of DNA curvature contributed by the DNA duplex insert.

Figure 5.

Analysis of electrophoretic phasing probes. (A) Image obtained after native PAGE of phasing probes 18–32. Mobilities of 100 bp ladder markers are indicated at the left. (B–D) Quantitative analysis of electrophoretic data for phasing probes 18–32. Normalized mobilities reflect the observed (µ/µ, circles) and predicted (q/q, squares) values for each of the five phasing probes in a given group. Data are plotted as a function of the spacing (bp) between the center of the third and fourth A₅ tracts, as counted from left to right in (A). Data are fitted to equation 8, as described in Materials and Methods. (B) Probes 18–22. (C) Probes 23–27. (D) Probes 28–32.

For probes 18–22 containing a single A₅ tract separated from a set of three phased A₅ tracts probe mobilities displayed an obvious dependence on the position of the single A₅ tract in relation to the set of three phased A₅ tracts (Fig. 5A). Mobility retardation was maximal for probe 19, indicating that the loci of curvature were most nearly in phase. Mobility retardation is minimized in probes 21 and 22, where the loci of curvature are out of phase.

Analysis of the two other groups of probes yielded similar information. Probes 23–27 contain an additional A₅ tract compared to 18–22. These probes displayed relative mobility anomaly differences almost twice those of 18–22, indicative of an additional phased locus of curvature. Probes 28–32 contained an additional A₅ tract and displayed even greater mobility differences. In each case the spacing at which the loci of curvature are aligned in either a cis or trans orientation remained constant, confirming that the A₅ tracts remain aligned on the same face of the DNA helix.

We then proceeded to analyze the structures of probes 18–32 predicted by the LB model. From measurements of end-to-end distance (h) and contour length (L) we computed the quotient q:

q = h²/L² 10

The value of q is predicted to correlate with electrophoretic mobility (21). Values of q were normalized to average values of q (q) for each group (q/q) such that normalized parameters oscillate around a value of 1.0, as for values of µ/µ. Values of µ/µ and q/q were then plotted against the spacing (bp) between the two sets of A₅ tracts and fitted to equation 8. Quantitative experimental and predicted mobility data are presented in Figure 5B–D. Perfect agreement between the model and the experimental data would be indicated if the two plots in each figure were superimposable.

For probes 18–22 (Fig. 5B) we observed that experimental phasing amplitudes were about half of those predicted by end-to-end distance measurements from the LB model (Table 1). Absolute differences between observed and predicted mobility differences among probes increased as the number of A₅ tracts was increased to two (Fig. 5C, probes 23–27) or three (Fig. 5D, probes 28–32), although relative differences remained fairly constant (∼45% for probes 23–27; ∼55% for probes 28–32). Interestingly, the overestimate of predicted mobility differences based on q (equation 10) relative to experimental measurements is very similar to that reported by Crothers and Drak based on a different data set (21).

Table 1. DNA phasing probes: observed and predicted behavior^a.

Probe	µ/µ̄	q/q̄	APH, obs	APH, pred	ST, obs	ST, pred
18	1.01 ± 0.02	1.04
19	0.96 ± 0.01	0.95
20	0.98 ± 0.01	0.88	0.11 ± 0.02	0.21	2.09 ± 0.19	2.20
21	1.04 ± 0.01	1.05
22	1.02 ± 0.02	1.09
23	0.97 ± 0.02	1.10
24	0.91 ± 0.01	0.89
25	0.98 ± 0.01	0.85	0.19 ± 0.02	0.36	1.80 ± 0.14	2.51
26	1.08 ± 0.01	0.97
27	1.06 ± 0.01	1.19
28	0.95 ± 0.01	1.18
29	0.86 ± 0.02	0.89
30	0.97 ± 0.01	0.80	0.29 ± 0.02	0.44	1.74 ± 0.03	2.80
31	1.12 ± 0.01	0.96
32	1.11 ± 0.03	1.18

^aData are presented as the means ± SD of at least three independent experiments.

Analysis of the positions of the peaks and troughs in the data fitted to equation 8 (Fig. 5) highlights another small discrepancy between the predicted and experimental data (Table 1). The experimentally observed value of S_T (equation 8, the position at which loci of curvature are in trans) was found to differ by 0.8 (probes 18–22), 1.7 (23–27) and 2.0 bp (28–32) from that predicted by equation 10. We interpret this discrepancy (5–10%) between the measured and predicted S_T values as indicative of slight errors in the DNA helical repeat as predicted by the LB model.

Drak and Crothers interpreted the overestimate of curvature as due to DNA straightening during migration through the gel matrix, noting that the percentage of polyacrylamide used in gel electrophoresis may influence mobility results (21). With 5% gels good agreement was seen between observed gel mobilities and predicted values calculated from end-to-end distances. Anomalies between observed and predicted values became evident as the gel percentage was increased (8–16%). Low percentage gels may have a large enough average pore size such that DNA may not need to rotate substantially during gel migration. Higher percentage gels, with smaller average pore diameters, may require rotation and subsequently complicate predictions. We considered this as a possible explanation as to why the LB model overestimates curvature with electrophoretic phasing probes. We therefore directly compared the relative mobilities of phasing probes 18–32 through 5% versus 8% gels (data not shown). We observed a slight reduction in relative mobility differences in 5% gels, relative to behavior in 8% gels. However, mobility differences as a function of gel percentage were not sufficient to account for the discrepancy between observed and predicted behavior in phasing experiments (Fig. 5 and Table 1). It remains unclear why the LB model somewhat underestimates curvature with ligation ladders (probes 1–17) while somewhat overestimating curvature with electrophoretic phasing probes (probes 18–32).

It is notable that the LB model bases its predictions on ApA dinucleotide steps without significant wedges, i.e. straight A tracts as observed in X-ray crystal structures (22). Regardless of the actual molecular shape of A tract sequences (11–12), we conclude that this dinucleotide model achieves reasonable success in predicting the overall electrophoretic behavior of the DNA molecules (∼150 and ∼250 bp) we have analyzed. The general predictive success of the LB dinucleotide step model is all the more noteworthy in that it was parameterized with data from DNA crystals obtained under a variety of solvent and solute conditions but is here applied to predict the electrophoretic behavior of DNA in dilute aqueous solution. The success of the LB model in this assessment proves that interpretation of results based on an essentially straight A tract model is not inconsistent with the experimental data. We emphasize that this result cannot be taken as conclusive evidence for or against the hypothesis that A tracts are straight.

CONCLUSIONS

We have applied the LB model to well-characterized ligation ladder (15) and electrophoretic phasing probes (16) in an attempt to analyze quantitatively the practical predictive power of the LB model for macroscopic DNA curvature. We find that the LB model is clearly superior to two other DNA structure models (DCS and BMHT), predominantly in its more realistic twist parameters. With ligation ladders we find a strong linear correlation between curvature magnitudes derived from the LB model and those estimated by electrophoresis, although the model somewhat underestimates curvature angles. In contrast, analysis of predicted versus observed data for longer electrophoretic phasing probes resulted in qualitative agreement but a modest overestimation of apparent curvature by the LB model. We also observe a small discrepancy in the predicted versus measured helical repeat parameters. The origin of these discrepancies remains unclear. Taken as a whole, the LB model provides moderately accurate predictions of DNA behavior in two kinds of electrophoretic experiments. We conclude that this model may therefore be applied (with proper caution) to the prediction of electrophoretic results and, as a first approximation, the actual molecular geometry of DNA. We emphasize that our goal was to provide a critical assessment of the LB prediction scheme, rather than to make conclusions about the fundamental origin of intrinsic DNA curvature. This ‘single blind’ assessment is an important validation step for any predictive method. Others are invited to analyze their electrophoretic data in an analogous fashion.