Photoinduced nanobubble-driven superfast diffusion of nanoparticles imaged by 4D electron microscopy

Direct visualization of superfast ballistic and diffusive gold nanoparticles driven by photoinduced nanobubbles.

Abstract

Dynamics of active or propulsive Brownian particles in nonequilibrium status have recently attracted great interest in many fields including artificial micro/nanoscopic motors and biological entities. Understanding of their dynamics can provide insight into the statistical properties of physical and biological systems far from equilibrium. We report the translational dynamics of photon-activated gold nanoparticles (NPs) in water imaged by liquid-cell four-dimensional electron microscopy (4D-EM) with high spatiotemporal resolution. Under excitation of femtosecond laser pulses, we observed that those NPs exhibit superfast diffusive translation with a diffusion constant four to five orders of magnitude greater than that in the absence of laser excitation. The measured diffusion constant follows a power-law dependence on the laser fluence and a linear increase with the laser repetition rate, respectively. This superfast diffusion of the NPs is induced by a strong random driving force arising from the photoinduced steam nanobubbles (NBs) near the NP surface. In contrast, the NPs exhibit a superfast ballistic translation at a short time scale down to nanoseconds. Combining with a physical model simulation, this study reveals a photoinduced NB propulsion mechanism for propulsive motion, providing physical insights into better design of light-activated artificial micro/nanomotors. The liquid-cell 4D-EM also provides the potential of studying other numerical dynamical behaviors in their native environments.

INTRODUCTION

Back in 1827, using an optical microscope, the botanist Robert Brown first observed the jittery motion of small suspended particles and found that each moving step of the particle was independent of the previous one (1). This random motion of the particles, now known as passive Brownian motion, was first interpreted by Einstein in 1905 as the amplification of thermal fluctuations: A Brownian particle receives momentum from the surrounding molecule collisions, but its movement is dissipated by the viscosity of the liquid (2).

Over the past decade, active Brownian motion far from equilibrium status (3–7) has attracted increasing interest due to the great potential of using autonomous micro/nanomachinery in biomedical applications (8). For a Brownian object, an external driving force could drive it out of equilibrium to realize the autonomous motion (9). Notable examples of these out-of-equilibrium systems range from biological entities, such as bacteria (10) and motile cells (11), to artificial micro/nanomotors (12–14). They present the potential as autonomous agents for delivering nanoscopic objects to targeted positions, such as in noninvasive microsurgery (15) and drug delivery (16, 17), where the interplay between the external activations and the internal fluctuations from the nature of the systems leads to a complex behavior of their dynamics. So far, a number of different propulsion mechanisms have been proposed for artificial micro/nanomotors. Most of these mechanisms are based on a scheme that the micro/nanomotors act as an engine and generate a propulsive force owing to the following: magnetic field (18), electric field (19), special flow field induced by a gradient of osmotic pressure or temperature (20–23), and catalytic decomposition (24). However, the diffusion process or the directional motion of the micro/nanomotors by these propulsion mechanisms is relatively slow, where the average speed is usually below several micrometers per second. It has been reported that the nucleation and growth of oxygen or hydrogen bubbles through a chemically catalytic reaction could lead to an efficient propulsion of tubular microjets (25–27), where the average speed could be up to 10 mm/s (28). As shown in the first experimental observation of the bubble propulsion and the instantaneous velocity damping due to liquid drag of the tubular microjets at low Reynolds number (25), the microjets presented discrete velocity peaks over time because of the cyclic formation and expansion of bubbles at the tube end, which was distinct from their counterparts at the macroscopic scale. This unique motion behavior at low Reynolds number makes the tubular microjets promising for applications in noninvasive microsurgery and micro-object delivery (29). This chemically powered gas bubble propulsion usually requires hydrogen peroxide fuel or highly acidic-/salt-rich environments, and real-time observation of the velocity peak evolution induced by a gas bubble requires high temporal resolution. On the other hand, the dynamical phenomenon of superfast propulsive motion of Brownian objects, especially nanoscale objects, is still far from being understood due to the lack of a proper liquid-phase imaging technique with high spatiotemporal resolution. The development of four-dimensional electron microscopy (4D-EM) provides the promising capability of imaging nanoscale objects at an ultrafast time scale (30–32). Recently, we have successfully extended 4D-EM to include liquid cells and made the liquid-phase 4D imaging no longer limited by the response of the detector (33). In that work, we demonstrated 4D imaging of the rotational dynamics of nanoparticle (NP) dimers in aqueous solution and studied the morphological asymmetry effect on their rotational behaviors.

Active Brownian particles generally engage in both translational and rotational motion, where the translational dynamics are particularly significant for applications of artificial micro/nanomotors. Here, we chose symmetric gold NPs and studied their translational dynamics in water under femtosecond laser pulse excitation in both diffusive and ballistic regimes by 4D-EM. We systematically investigated the laser fluence and repetition rate dependence of the particle translational dynamics. Under repetitive laser pulse excitation, the NPs exhibit a superfast diffusive translation with a diffusion constant following a power-law dependence on the fluence and a linear increase with the repetition rate, respectively. In contrast, the NPs exhibit a superfast ballistic translation at a short time scale down to nanoseconds. A full picture of rapid nucleation, expansion, detachment, and collapse of steam nanobubbles (NBs) around the gold NP was directly visualized during the particle translation. Combining with physical model simulation, a photoinduced NB propulsion mechanism for propulsive motion was revealed, in which the particles were propelled by strong random driving forces arising from the photoinduced steam NBs. In addition, the threshold laser fluence for explosive boiling (generation of steam) around a single gold NP was experimentally determined.

RESULTS

4D imaging of NPs in liquid

To image the translational dynamics of photon-activated gold NPs in liquid with high spatiotemporal resolution, the solution containing spherical gold NPs (~80 nm in diameter; with strong optical absorption at the excitation wavelength through localized surface plasmon enhancement) was sealed between two electron-transparent, 20-nm-thick silicon nitride membranes with a liquid thickness of ~300 nm. Details of the preparation protocol of the liquid cell are described in Materials and Methods and are also available elsewhere (33–35). The liquid cell was then integrated to our 4D-EM for dynamical measurement (see Fig. 1). In 4D-EM, green femtosecond laser pulses were used to trigger the dynamics, whereas precisely timed electron pulses were used to image the particle motion (see Materials and Methods), where the time resolution is not limited by the response of the detector inside the electron microscope. For the measurement at long times, repetitive femtosecond laser pulses (with wavelength of 520 nm and pulse duration of 350 fs) were used to activate a single NP, whereas a continuous electron beam with a low electron dose was presented to trace the trajectory of the NP motion. At a short time scale, single-pulse imaging methodology was used to capture the transient morphologies of the NP activated by a single femtosecond laser pulse, where the images were acquired by a single precisely timed electron pulse at specific delays. Details of the procedure are also available in the previous studies from this group (32, 33).

Fig. 1. Schematic of photon-activated gold NP diffusion in liquid imaged by 4D-EM.

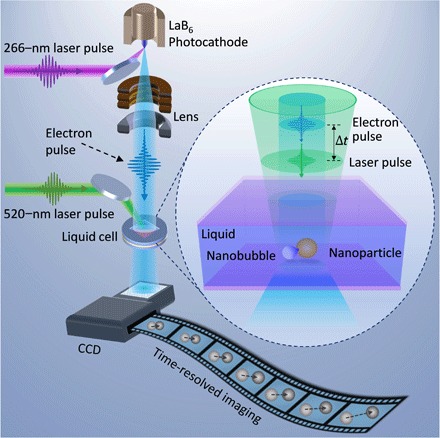
Infrared femtosecond laser pulses (1040 nm; pulse duration of 350 fs) were used to generate green femtosecond laser pulses (520 nm) via second harmonic generation, which were directed to the liquid cell integrated in the transmission electron microscope (TEM) to trigger the particle dynamics in liquid. Ultraviolet (UV) nanosecond laser pulses (266 nm; pulse duration of 10 ns) were directed to the photocathode inside the TEM to generate electron pulses, which were accelerated to 120 keV to image the particle dynamics. The femtosecond laser pump pulse and nanosecond electron probe pulse were synchronized by a digital delay generator, which controls the time delay between them. For the time-resolved imaging at long times, a continuous thermal emission electron beam with a low electron dose was present to image the NP diffusion under repetitive femtosecond laser pulse excitation, whereas for the time-resolved imaging at short time scale, a single femtosecond laser pulse triggered the NP motion and a precisely timed electron pulse was used to image the transient NP morphologies at specific time delays, where the time resolution was unlimited by the response of the charge-coupled device (CCD).

Superfast translational dynamics in diffusive regime

We traced the translational dynamics of a single photon-activated gold NP at a long time scale by continuous electron beam imaging mode (see Materials and Methods). A set of typical snapshots of the NP translational motion under repetitive femtosecond laser pulse excitation (fluence of 2.3 mJ/cm², repetition rate of 1 kHz) at different times is presented in Fig. 2A. Before excitation (0 s), the NP inside the thin-layer solution sandwiched in the liquid cell was weakly bound near the substrate surface by weak electrostatic interaction (36, 37). Upon excitation, the NP was activated to move randomly due to rapid nucleation, expansion, detachment, and collapse of the visible steam NBs around the particle surface (see Fig. 2A and movie S1). Note that the number, size, and nucleation position of the NBs were independent at different times. The long-time visibility of these steam NBs under repetitive laser pulse excitation will be discussed later. Two typical trajectories of the NP under repetitive laser pulse excitation with different fluences (2.0 and 2.3 mJ/cm²) are displayed in the left column of Fig. 2 (B and C), respectively, whereas their corresponding displacement distributions along x and y directions (with Gaussian distribution) are shown in the right column. These trajectories and Gaussian displacement distributions indicate that the particle translates in a manner of random walk and that the range of its displacements increases with the fluence, indicating the faster translation of the particle at the higher laser fluence.

Fig. 2. Typical snapshots and trajectories of photon-activated gold NP diffusion in liquid.

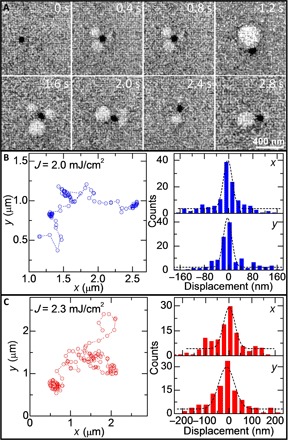
(A) Typical snapshots of a gold NP diffusion under 1-kHz laser pulse (fluence of 2.3 mJ/cm²) excitation at the different times. The NP was driven to move by rapid nucleation, expansion, detachment, and collapse of the photoinduced steam NBs near the particle surface (see the circles with white contrast). (B and C) Two typical trajectories (left column) of the gold NP diffusion and the corresponding displacement distributions along x and y (right column) at different laser fluences of 2.0 and 2.3 mJ/cm², respectively. The dashed black lines in the right column of (B) and (C) show the Gaussian fit, which indicate that the NP translates in a manner of random walk.

To understand the statistical properties of the translational dynamics of the photon-activated gold NP, its mean square displacements (MSDs) under different laser fluences (1.6 to 3.0 mJ/cm²; repetition rate of 1 kHz) are presented in Fig. 3A. The detailed calculation of MSDs is described in Materials and Methods. All the measured MSDs almost show a linear relation with time, that is, MSD ∝ t, following a substantial increase in the slope with increasing laser fluence. These linear MSDs demonstrate that the photon-activated gold NP exhibits a diffusive behavior, which is similar to conventional passive Brownian motion. However, the diffusion constant in our observations exhibits a power-law dependence on the laser fluence as D ∝ (J − J_c)^2.2 for J ≥ J_c (see the fit curve in Fig. 3B), and its value (1.2 × 10³ to 36 × 10³ nm²/s) is four to five orders of magnitude greater than that of the conventional Brownian motion of gold NPs without photon activation (36). The parameter J_c is the minimum laser fluence (threshold) required to raise water above its boiling temperature for the water molecule evaporation near the gold NP surface, namely, the threshold of explosive boiling around a single gold NP (38). The retrieved threshold value of the fluence from the fit is 1.25 mJ/cm², which agrees well with the experimental observation that, below a fluence of ~1.3 mJ/cm², the laser heating of the NP is insufficient to generate any steam to actuate the NP to move. Moreover, at a fixed laser fluence (J = 3.2 mJ/cm²), the diffusion of the gold NP becomes faster as the laser repetition rate increases (see the MSDs in Fig. 3C), and the diffusion constant is proportional to the repetition rate (see Fig. 3D). From these results, an intuitive mechanism for the superfast diffusion of the photon-activated NP under repetitive laser pulse excitation emerges. Owing to the strong local photothermal effect because of the localized surface plasmon–enhanced optical absorption of the gold NP at the laser wavelength, the particle is heated up in hundreds of picoseconds (39–41). This results in a rapidly raised temperature over the boiling point of the neighboring water molecules that evaporate into steam (42). This water steam would nucleate as NBs on the NP surface (38, 43, 44). Consequently, these steam NBs expand, detach, and collapse, inducing a random driving force on the NP to propel its motion, where the instantaneous velocity of the NP is damped by the fluid drag. Unlike the random force arising from the fluid molecule collisions in passive Brownian motion, it is the random force arising from the photoinduced steam and NBs near the NP surface that dominates the superfast diffusion. The radiation pressure or optical trapping force induced by the laser pulse is negligible compared to the strong driving force arising from the NBs. In our experiment, the NPs are much smaller than the size of the laser beam (diameter of ~35 μm); therefore, the radiation pressure along the z axis has negligible impact on the NP diffusion in the x-y plane, and the optical trapping due to a light intensity gradient in the x-y plane is insignificant. No motion of the gold NP was observed when the laser fluence was below the threshold for generating steam around the NP.

Fig. 3. Laser fluence and repetition rate dependence of the gold NP diffusion dynamics.

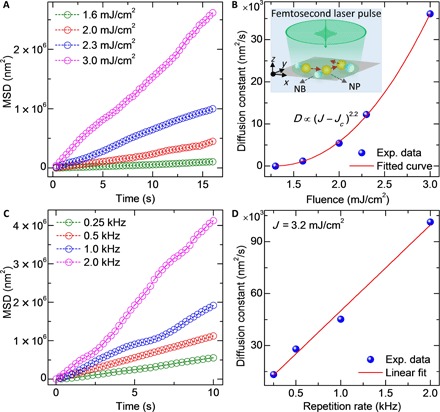
(A) MSDs of the gold NP diffusion under different laser fluences (repetition rate of 1.0 kHz). (B) Variation of the diffusion constant of the photon-activated NP as a function of laser fluence, which follows a power-law dependence with a retrieved threshold fluence for explosive boiling of J_c ~ 1.25 mJ/cm². Inset: Schematic of superfast diffusion (random walk) of a gold NP driven by the photoinduced steam NBs. (C) MSDs of a gold NP diffusion under a fixed laser fluence of 3.2 mJ/cm² with different repetition rates. (D) Variation of the diffusion constant as a function of the laser pulse repetition rate, which follows a linear dependence.

Translational dynamics in ballistic regime

Using the single-pulse imaging mode of 4D-EM, we further studied the transient dynamics of the photon-activated gold NPs at a short time scale down to nanoseconds. Figure 4A presents the typical imaging result of the transient translation process of a gold NP induced by a single femtosecond laser pulse excitation with a fluence of 7.8 mJ/cm². The first and second columns show the typical single-pulse images of the NP before the laser pulse and at specific delays (25, 40, and 60 ns; similar single-pulse images of more delay points are not shown here), respectively, whereas their corresponding difference images are shown in the third column. The red and blue dashed circles in the difference images indicate the initial position and the position of the NP at specific delays, respectively. Apparently, the displacement of the NP increases with the delay time. By considering the ballistic feature of the Brownian motion at a short time scale (45–48), we assume for simplicity that for each single-pulse imaging measurement on the same, single gold NP with the same laser fluence, (i) the driving force on the NP has similar magnitude (the direction of the force may be random), and (ii) the NP is in the same liquid environment. Therefore, we plotted the displacements of the same NP at different delays in Fig. 4B to evaluate its time-dependent displacement evolution in the ballistic regime. We only traced the magnitude of the displacement, not the direction of translation in each single-pulse imaging measurement. The displacement increases very slowly in the first 25 ns and then grows fast from 25 to 60 ns (nearly linear increase), followed by a very slow increase to a saturation level after about 80 ns. This result demonstrates that upon the femtosecond laser pulse excitation, the NP was accelerated and obtained a momentum in 20 to 30 ns due to the photoinduced steam and NBs near the particle surface, and then its velocity and translation were damped in hundreds of nanoseconds by the surrounding drag, including both the liquid friction and the interaction from the substrate. The velocity of the NP (from 20 to 60 ns) was estimated to be ~6 m/s, which is three orders of magnitude faster than that of the conventional passive Brownian motion in the ballistic regime (48). Therefore, the nature of the photon-activated Brownian motion is similar to the passive one at the short time range (both are ballistic), but the former one has a much higher velocity due to the strong impulsive driving force induced by the photoinduced steam NBs.

Fig. 4. Single-pulse imaging of a photon-activated gold NP in the ballistic regime.

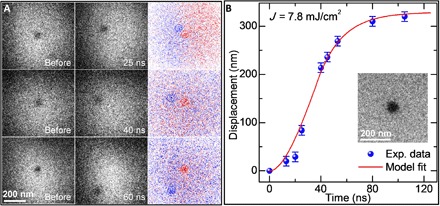
(A) Single-pulse images of the photon-activated NP at three specific delay times. The images in the first and second columns are the states of the NP before the laser pulse and at specific delays of 25, 40, and 60 ns after the laser pulse (fluence of 7.8 mJ/cm²), respectively. The third column shows the corresponding difference images obtained by subtracting the single-pulse image before the laser pulse from that at the short delay time. The red and blue dashed circles indicate the NP positions before the laser pulse and at short delays after the laser pulse, respectively. (B) Evolution of the displacement of the NP as a function of delay time with a physical model fit. The inset shows the image of the measured gold NP.

Visibility of NBs in the liquid cell

We showed experimentally that the translational motion of the NPs was propelled by strong random driving forces arising from the photoinduced steam NBs. In the continuous electron beam images (see Fig. 2A and movie S1), the steam NBs were visualized when the gold NP was under repetitive laser pulse excitation with a fluence above the threshold. However, it was difficult to distinguish NBs in the single-pulse images with only a single laser pulse excitation (Fig. 4A). The reasons are as follows: (i) There are only ~10⁵ electrons in one electron pulse, and the image contrast is low in the single-pulse imaging mode; (ii) the steam NBs with a single laser pulse excitation are initially very small and invisible and are difficult to grow into big visible NBs before collapse or dissolution. Nevertheless, under repetitive laser pulse excitation, which causes continuous heating accumulation, the small invisible steam NBs would coalesce with their neighboring ones and grow into big visible NBs. Therefore, the repetitive excitation–induced continuous heating accumulation is necessary to form the big visible steam NBs. Because of the continuous heating accumulation, these big visible NBs involve several subsequent processes: nucleation of small invisible steam NBs, merging of small NBs, detachment from NPs, and expansion of the merged NBs; thus, they were present for subseconds to seconds in the continuous electron beam images (Fig. 2A and movie S1). It should be noted that the duration of the impulsive forces is only involved in a portion of the whole process, namely, initial generation of steam, nucleation of small invisible NBs, and detachment/collapse from NPs.

Modeling of translational dynamics in diffusive regime

To unravel the underlying mechanism for the observed superfast diffusion of the photon-activated gold NPs, theoretical simulation was performed at both long and short time scales. On the basis of Einstein’s theory, the 1D translational dynamics of an active Brownian particle can be generally reformulated in terms of a Langevin equation (49) as

$$\frac{{\mathit{d}}^2}{\mathit{d}{\mathit{t}}^2}\mathit{x}+\mathrm{\gamma }\frac{\mathit{d}}{\mathit{d}\mathit{t}}\mathit{x}={\mathit{A}}_{\text{th}}(\mathit{t})+{\mathit{A}}_{\text{ext}}(\mathit{t})$$ (1)

where x is the particle displacement, γ is the damping factor due to surrounding friction force, A_th(t) is the acceleration induced by the random force arising from the liquid molecule collisions, and A_ext(t) is the acceleration executed by external activations. For the photon-activated gold NPs in our experiment, it is reasonable to consider that A_ext(t) ≫ A_th(t).

For the dynamics at the long time scale, we proposed a simple physical model to analyze the MSD directly from the Langevin equation, with the assumption that A_ext(t) consists of a comb of very short rectangular-shaped impulses that arise from the NBs induced by the repetitive laser pulse excitation with a duration of τ₀ and a time interval of T_p (repetition rate is $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\mathit{T}}_{\mathrm{p}}$}\right.$). For the kth impulse, A_ext(t) = A_k(0)(H(t − kT_p) − H(t − τ₀ − kT_p)), where H(t) is a Heaviside step function. The Langevin equation can be thus recast as

$$\frac{{\mathit{d}}^2}{\mathit{d}{\mathit{t}}^2}\mathit{x}+\mathrm{\gamma }\frac{\mathit{d}}{\mathit{d}\mathit{t}}\mathit{x}={\displaystyle \sum _{\mathit{k}=0}}{\mathit{A}}_{\mathit{k}}(0)(\mathit{H}(\mathit{t}-\mathit{k}{\mathit{T}}_{\mathrm{p}})-\mathit{H}(\mathit{t}-{\mathrm{\tau }}_0-\mathit{k}{\mathit{T}}_{\mathrm{p}}))$$ (2)

For simplicity, we assume the initial value x(0) = 0 and the velocity ${\mathit{u}}_0=\stackrel{.}{\mathit{x}}(0)\ne 0$. Because there is neither correlation between the initial velocity and the impulsive forces nor correlation between the directions of the impulsive forces in different excitation circles, one has 〈u₀A_k(0)〉 = 0 and $\langle {\mathit{A}}_{\mathit{k}}(0){\mathit{A}}_{\mathit{j}}(0)\rangle ={\mathrm{\delta }}_{\mathit{k}\mathit{j}}{\mathit{A}}_{\text{ave}}^2$, where A_ave (assumed to depend on the laser fluence) represents an average value of the comb of random impulses. Assuming that the damping constant γ is independent of liquid temperature and resolving the above Langevin equation (see Supplementary Text), we obtained a key formula for the MSD in the long time limit of $\mathit{t}\gg \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\gamma }$}\right.$ as

$$\text{MSD} \approx \frac{\mathit{t}}{{\mathit{T}}_{\mathrm{p}}}\frac{{\mathit{A}}_{\text{ave}}^2{\mathrm{\tau }}_0^2}{{\mathrm{\gamma }}^2}$$ (3)

Similarly, for a 2D case, $\text{MSD} \approx 2\frac{\mathit{t}}{{\mathit{T}}_{\mathrm{p}}}\frac{{\mathit{A}}_{\text{ave}}^2{\mathrm{\tau }}_0^2}{{\mathrm{\gamma }}^2}$, which is linear with respect to time t and agrees with our experimental results (Fig. 3, A and C). In analogy with Einstein’s linear law for a conventional 2D Brownian motion (MSD = 4Dt) (2), one can get an effective diffusion constant as $\mathit{D}=\frac{{\mathit{A}}_{\text{ave}}^2{\mathrm{\tau }}_0^2}{2{\mathit{T}}_{\mathrm{p}}{\mathrm{\gamma }}^2}$, which has a quadratic dependence on the strength of the average impulsive acceleration. Because A_ave is proportional to the laser fluence J − J_c (J_c is the threshold fluence required to raise the temperature to cause evaporation of the water molecules near the gold NP surface), the deduced effective diffusion constant should also follow a quadratic relation with the laser fluence, that is, D ∝ (J − J_c)² for J ≥ J_c. Our experimental observation, D ∝ (J − J_c)^2.2 (see Fig. 3B), agrees well with the simulation. The small discrepancy of the exponent is probably due to temperature dependence of the liquid viscosity (related to the damping constant γ in Eq. 2), which slightly decreases with the temperature change of the surrounding liquid and steam NBs around the water boiling point. Furthermore, the predicted diffusion constant linearly increases with the impulse repetition rate $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\mathit{T}}_{\mathrm{p}}$}\right.$at a given fluence, which is in line with the experimental result (see Fig. 3D). These agreements validate our hypothesis and the physical model for the photoinduced steam NB–driving mechanism.

Physical model of translational dynamics in ballistic regime

For the dynamics of the NP at a short time scale induced by a single femtosecond laser pulse, the impulsive acceleration is given for simplicity by a rectangular-shaped impulse function with a time duration of τ₀, namely, A_ext(t) = A(0)(H(t) − H(t − τ₀)), where A_ext(t) ≫ A_th(t). The dynamical equation of the NP translation after a single laser pulse excitation is given by

$$\frac{{\mathit{d}}^2}{\mathit{d}{\mathit{t}}^2}\mathit{x}+\mathrm{\gamma }\frac{\mathit{d}}{\mathit{d}\mathit{t}}\mathit{x}=\mathit{A}(0)(\mathit{H}(\mathit{t})-\mathit{H}(\mathit{t}-{\mathrm{\tau }}_0))$$ (4)

Solving the dynamical equation, one can obtain the analytical solution for x(t) as

$$\mathit{x}(\mathit{t})=\{-\frac{\mathit{A}(0)}{\mathrm{\gamma }}[\frac{{\mathit{e}}^{-\mathrm{\gamma }(\mathit{t}-{\mathrm{\tau }}_0)}-1}{\mathrm{\gamma }}+(\mathit{t}-{\mathrm{\tau }}_0)\left]\right\}\cdot \mathit{H}(\mathit{t}-{\mathrm{\tau }}_0)+\frac{\mathit{A}(0)}{{\mathrm{\gamma }}^2}({\mathit{e}}^{-\mathrm{\gamma }\mathit{t}}-1)+\frac{\mathit{A}(0)\mathit{t}}{\mathrm{\gamma }}$$ (5)

where the Heaviside step function H(t − τ₀) = 0 for 0 ≤ t ≤ τ₀, and H(t − τ₀) = 1 for τ₀ < t. Therefore, for 0 ≤ t ≤ τ₀, one has $\mathit{x}(\mathit{t})\approx \frac{\mathit{A}(0)}{2}{\mathit{t}}^2$, suggesting that, in such a short time range, the particle is still under acceleration; for τ₀ < t, the acceleration period ends, and because of the damping from the surrounding drag, the particle displacement levels off, following Eq. 5. This prediction captures well the single-pulse imaging result in our experiment (see the fit curve by Eq. 5 in Fig. 4B). The magnitude of the damping constant γ, which reflects the effective damping effect, was retrieved to be ~0.05 ns⁻¹. The acceleration period τ₀ due to the steam NB–driving effect was determined to be ~35 ns, which coincides with the lifetime range of the femtosecond pulse–induced plasmonic NBs around the gold NPs in water (50), further validating the hypothesis of our model. Therefore, the combined experimental results (Figs. 3 and 4) and model simulations at both long and short times elucidate the steam NB–driving mechanism for the superfast diffusion of the photon-activated gold NPs.

DISCUSSION

Here, we introduced the 4D imaging of translational dynamics of photon-activated gold NPs in water by liquid-cell 4D-EM. Our results revealed a type of highly efficient photoinduced steam NB propulsion mechanism of gold NPs under photon excitation. Because of strong steam NB–driving forces, the photon-activated gold NPs show a superfast diffusion at long times, with the diffusion constant being four to five orders of magnitude greater than that of passive Brownian motion, whereas they exhibit a superfast ballistic translation at the nanosecond time scale. The observed dynamical phenomena and their dependence on laser fluence and repetition rate agree with our physical model simulation. These results provide valuable insight into the fundamental dynamical behavior of nanoscale photon-active motion and demonstrate great potential for the future design of light-driven artificial micro/nanoscopic motors working in complex liquid environments (51), such as Janus micro/nanomotors with high propulsion efficiency and micro/nanomotors propelled by photoinduced steam NBs arising from specifically attached metallic NPs. The high spatiotemporal resolution of the liquid-cell 4D-EM would also permit the ability to image and study the dynamical behaviors of other out-of-equilibrium nano- or microscopic systems, such as active matter and even biological entities in their native environments.

MATERIALS AND METHODS

Preparation of liquid cell

Standard TEM silicon nitride windows (250 × 250 μm²) on a 200-μm-thick silicon frame (customized from Norcada Inc.; circular shape that fits the standard TEM holder) with a thin layer of pre-prepared gold film spacer (~200 nm; customized from Norcada Inc.) were used. The ultrathin low-stress silicon nitride membrane (~20 nm) deposited by low-pressure chemical vapor deposition guarantees the spatial resolution of the liquid cell to be in a nanometer range. The gold film spacer was deposited at the edge of the silicon frame without blocking the electron-transparent silicon nitride window.

The silicon nitride membrane was rinsed with acetone, isopropyl alcohol, and deionized water, followed by plasma cleaning (P ~ 3.5 W; t ~ 30 s) to make the silicon nitride membrane hydrophilic to aqueous solution. A drop of ~5 μl of the aqueous solution with citrate-stabilized spherical gold NPs (~80 nm in diameter; purchased from nanoComposix Inc.) was loaded on a bottom chip with spacer, and another top chip without spacer was put on the surface of the liquid. Because of the liquid tension, the top silicon nitride window would rotate freely and align well with the bottom one. Then, these two well-aligned silicon nitride window chips were clamped by a tweezer, and the superfluous liquid was absorbed by a small piece of filter paper from the side. Between the two silicon nitride membranes, there was a thin layer of liquid, with its thickness approximately equivalent to the spacer thickness. An epoxy adhesive (Ted Pella Inc.) was quickly used to seal the side of the liquid cell. The liquid cell was loaded in our 4D-EM for measurements after the sealing was dried. In the measurement, we carefully checked each liquid cell by tilting it to different view angles to exclude the bad one with apparent bulges or gas bubbles. For the good liquid cell filled with liquid, it may have a little bulge when put in the high vacuum of TEM. Nevertheless, such a small bulge should not significantly influence the observed diffusion dynamics of the NPs in the liquid cell.

Time-resolved imaging measurements

We performed the measurements in our 4D-EM instrument (UEM-1 at California Institute of Technology), which integrated liquid cell technology. Infrared femtosecond laser pulses (1040 nm; pulse duration of 350 fs) were used to generate the visible pump femtosecond laser pulses (520 nm) via second harmonic generation, and the green femtosecond pulses were directed to the liquid cell sample inside the microscope to activate the particle dynamics. Precisely synchronized UV nanosecond laser pulses (266 nm; pulse duration of 10 ns) were directed to the photocathode inside the TEM to generate nanosecond electron pulses, which were accelerated to 120 keV to probe the particle dynamics through the silicon nitride window. A digital delay generator was used to synchronize the nanosecond electron probe pulse and the femtosecond laser excitation pulse and to control the time delay between them. For the time-resolved imaging measurement at long times, the sample in the liquid cell was excited by repetitive green femtosecond laser pulses. A continuous electron beam (regular TEM mode) with a low electron dose was present to capture the dynamics. We used the video collection mode to trace the NP diffusion process, where the frame rate is 5 frames/s, and the espouse time of each frame is 0.05 s, whereas for the time-resolved imaging measurement at a short time scale (that is, the single-pulse imaging mode), a single green femtosecond laser pulse was used to trigger the dynamics, and a precisely timed nanosecond electron pulse was used to probe the subsequent transient dynamics at specific time delays. The time resolution of our 4D-EM instrument is ~10 ns (33). The nanosecond electron pulses (~10⁵ electrons per pulse) used for the real-time imaging in our 4D-EM are too weak to generate any bubbles in the liquid.

Calculation of MSD for the NPs

For the analysis of the statistical properties of the translational dynamics of a photon-activated gold NP, we utilized the widely used statistical method (48) to calculate its time-dependent MSD based on Einstein’s model. A set of snapshots at t₀, t₁, t₃, …, and t_N of the NP was extracted from the recorded movie of its translational dynamics with a time interval of Δt, where Δt = 0.2 s in our analysis. The displacement of the NP at each time point relative to its initial position at t₀ can be determined as r(t₀), r(t₁), r(t₃), …, and r(t_N), respectively. Then, the MSD at t = Δt is given by

$$\text{MSD}(\mathit{t}=\mathrm{\Delta }\mathit{t})=\frac{{\displaystyle \sum _{\mathit{k}=1}^{\mathit{N}}}{[\mathit{r}({\mathit{t}}_{\mathit{k}})-\mathit{r}({\mathit{t}}_{\mathit{k}-1})]}^2}{\mathit{N}}$$ (6)

likewise, at t = nΔt

$$\text{MSD}(\mathit{t}=\mathit{n}\mathrm{\Delta }\mathit{t})=\frac{{\displaystyle \sum _{\mathit{k}=\mathit{n}}^{\mathit{N}}}{[\mathit{r}({\mathit{t}}_{\mathit{k}})-\mathit{r}({\mathit{t}}_{\mathit{k}-\mathit{n}})]}^2}{\mathit{N}-(\mathit{n}-1)}$$ (7)

where n is a number from 0 to N. The calculated MSD is, in principle, proportional to time, and the diffusion constant of the NP is determined by the slope of the linear curve of MSD versus time.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/8/e1701160/DC1

Supplementary Text

movie S1. Translation of a gold NP induced by repetitive femtosecond laser pulse excitation (fluence of 2.3 mJ/cm²; repetition rate of 1 kHz) under continuous electron beam imaging mode.