Observation of prethermalization in long-range interacting spin chains

Many-body interactions could lead to quantum thermalization, but long-range interactions provide an alternative.

Abstract

Although statistical mechanics describes thermal equilibrium states, these states may or may not emerge dynamically for a subsystem of an isolated quantum many-body system. For instance, quantum systems that are near-integrable usually fail to thermalize in an experimentally realistic time scale, and instead relax to quasi-stationary prethermal states that can be described by statistical mechanics, when approximately conserved quantities are included in a generalized Gibbs ensemble (GGE). We experimentally study the relaxation dynamics of a chain of up to 22 spins evolving under a long-range transverse-field Ising Hamiltonian following a sudden quench. For sufficiently long-range interactions, the system relaxes to a new type of prethermal state that retains a strong memory of the initial conditions. However, the prethermal state in this case cannot be described by a standard GGE; it rather arises from an emergent double-well potential felt by the spin excitations. This result shows that prethermalization occurs in a broader context than previously thought, and reveals new challenges for a generic understanding of the thermalization of quantum systems, particularly in the presence of long-range interactions.

INTRODUCTION

In the classical world, thermalization is expected in all but special cases where conserved quantities or hidden symmetries prevent the ergodic exploration of phase space. Because the classical world is ultimately composed of quantum systems, we therefore expect that a closed quantum system will also reach thermal equilibrium (1–9). Although quantum dynamics are unitary, measurements made within a subsystem trace over the rest of the system and appear thermal because the rest of the system acts as a thermal bath (10–13).

However, this is not always the case. For integrable models, an extensive number of conserved quantities prevent the efficient exploration of phase space (14), and the system relaxes to a steady state predicted by a generalized Gibbs ensemble (GGE) (4, 15–18) specified by the initial values of the integrals of motion. For near-integrable systems, such as weakly interacting ultracold gases, thermalization can still occur but only over extremely long time scales beyond current experimental reach (16, 17). However, it is possible to observe quasi-stationary states, often called prethermal (19), which emerge within an experimentally accessible time scale.

Previous observations of prethermal states have focused on those described by a GGE associated with the integrable part of the model (16, 17). Here, we observe a different type of prethermalization (20), where a system of interacting spins rapidly evolves to a quasi-stationary state that cannot be predicted by a standard GGE. This type of prethermal state arises, even in the thermodynamic limit, when a system has long-range interactions and open boundaries such that the translational invariance is broken. As a result, spin excitations feel an emergent double-well potential whose depth grows with interaction range (Fig. 1). Memory of the initial state is preserved by this emergent potential but is eventually lost because of weak quantum tunneling between the two wells and the interactions between spin excitations.

Fig. 1. Emergent double-well potential.

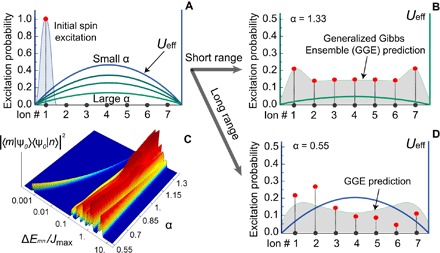
Calculated spin excitation probability after a quantum quench. (A) The spin chain starts with a single-spin excitation on the left end in an effective double-well potential, U_eff, whose barrier height is determined by the range α of the interactions. The black dots represent the positions of the ions, whereas the red dots represent the simulated spin excitation probabilities. (B) For short-range interactions (α = 1.33), we map the system to a particle in a 1D square well, where the excitation becomes symmetrically distributed across the chain as predicted by the GGE, ${\langle {\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}\rangle }_{\text{GGE}}$. (D) However, for long-range interactions (α = 0.55), there is an emergent double-well potential, which prevents the efficient transfer of the spin, and the excitation location retains memory of the initial state, in contrast to ${\langle {\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}\rangle }_{\text{GGE}}$. (C) The double-well gives rise to near-degenerate eigenstates as α is decreased, as seen in the calculated energy difference between all pairs of eigenstates versus α. The height of the plot quantifies the off-diagonal density matrix elements of the initial state.

RESULTS

Effective spin-1/2 particles are encoded in the ²S_1/2 |F = 0, m_F = 0〉 and |F = 1, m_F = 0〉 hyperfine “clock” states of a ¹⁷¹Yb⁺ ion, denoted | ↓ 〉_z and | ↑ 〉_z (21). We confine a chain of ions in a linear radio frequency Paul trap and apply optical dipole forces to generate the effective spin-spin coupling (22, 23) of an Ising Hamiltonian

$$\mathit{H}={\displaystyle {\sum }_{\mathit{i}<\mathit{j}}{\mathit{J}}_{\mathit{i}\mathit{j}}{\mathrm{\sigma }}_{\mathit{i}}^{\mathit{x}}{\mathrm{\sigma }}_{\mathit{j}}^{\mathit{x}}}+\mathit{B}{\displaystyle {\sum }_{\mathit{i}}}{\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}$$ (1)

where ${\mathrm{\sigma }}_{\mathit{i}}^{\mathrm{\gamma }}(\mathrm{\gamma }=\mathit{x},\mathit{z})$ are the Pauli matrices acting on the ith spin, J_ij is the coupling between spins i and j, and B/(2π) = 10 kHz is a uniform effective transverse field. We use units in which Planck’s constant equals 1. The spin-spin interaction is long-range and can be described by a power-law decay, ${\mathit{J}}_{\mathit{i}\mathit{j}}\approx \frac{{\mathit{J}}_{\text{max}}}{{|\mathit{i}-\mathit{j}|}^{\mathrm{\alpha }}}$, where J_max is the maximum coupling strength, which ranges from 0.45 to 0.98 kHz. We tune the power-law exponent α between 0.55 and 1.33 by changing the axial confinement of the ions. With long-range interactions, H is, in general, nonintegrable [in contrast to the nearest-neighbor case where the one-dimensional (1D) model is integrable (24)], and thermalization is anticipated in the long-time limit according to the eigenstate thermalization hypothesis (25–28). However, we can map each spin excitation along the z direction into a bosonic particle to turn Eq. 1 into a bosonic model with two parts: An integrable part made from noninteracting bosons that will be used to construct a GGE, and an integrability-breaking part consisting of interactions among the bosons, which is responsible for the eventual thermalization (see the Supplementary Materials for details). When the initial state has a low spin/bosonic excitation density, we expect the bosonic model to be near-integrable because the interactions are weak.

We initialize the chain of seven spins by optically pumping all spins to the |↓〉_z state, and then use a tightly focused individual-ion addressing laser to excite a single spin on one end of the chain to the | ↑ 〉_z state as seen in Fig. 1A (29). The spins then evolve under Eq. 1, and we measure the time evolution of the spin projection in the z-basis. For the shortest-range interactions we realize (α = 1.33), the system rapidly evolves to a prethermal state predicted by the GGE associated with the integrals of motion corresponding to the eigenmode occupation numbers of the noninteracting bosons, which does not preserve memory of the initial spin excitation location (Fig. 1B).

However, in the long-range interacting case (α = 0.55), we see that the position of the spin excitation reaches an equilibrium value that retains a memory of the initial state (Fig. 1D) out to the longest experimentally achievable time of 25/J_max. This prethermal state is in obvious disagreement with both a thermal state and the GGE prediction, which both maintain the right-left symmetry of the system.

The dynamics of the spin-wave boson model for short-range interactions are similar to those of a free particle in a square-well potential. However, the presence of long-range interactions distorts the square-well into a double-well potential (Fig. 1A). Here, we emphasize that the double-well potential emerges, despite the fact that our model (Eq. 1) is transitionally invariant without boundaries. The spin-wave boson model has an extensive number of near-degenerate eigenstates that are symmetric and antisymmetric superpositions of spin excitations in the left and right potential wells. For seven spins, we calculate the energy difference, ΔE_mn, between all pairs of eigenstates and plot them with respect to α in Fig. 1C, where the amplitudes, |〈m|ψ₀〉〈ψ₀|n〉|², are products of the overlaps of the eigenstates |m〉 and |n〉 with the initial state |ψ₀〉. With α = 0.55, the two lowest energy states are almost degenerate, with an energy difference approximately 1000 times smaller than J_max. This is due to the tunneling rate between the ground states of each well, which is exponentially small in the barrier height. As a result, the spin excitation will remain in its initial well until it tunnels across the potential barrier at much longer times. Note that even for α = 1.33 (Fig. 1B), a small potential still exists, but tunneling already happens during the experiment.

To better characterize the “location” of the spin excitation, we construct the observable

$$\mathit{C}={\displaystyle \sum _{\mathit{i}}}\frac{2\mathit{i}-\mathit{N}-1}{\mathit{N}-1}\frac{{\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}+1}{2}$$ (2)

where N is the number of ions. The expectation value of C varies between −1 and 1 for a spin excitation on the left and right ends, respectively. Because of the spatial inversion symmetry of the spin-wave boson model and Eq. 1, both the GGE predicted and thermal values of 〈C〉 are zero. In Fig. 2, we plot 〈C〉 along with its cumulative time average $\langle \overline{\mathit{C}}\rangle =\frac{1}{\mathit{t}}{\displaystyle {\int }_0^{\mathit{t}}}\langle \mathit{C}(\mathrm{\tau })\rangle \mathit{d}\mathrm{\tau }$ for α = 1.33 (short range) and α = 0.55 (long range). This averaging smooths out fast temporal fluctuations in our small systems. To further accentuate the asymmetry of the prethermalization, we prepare initial states with a single-spin excitation on the left or right ends of the chain.

Fig. 2. Measured location of spin excitation.

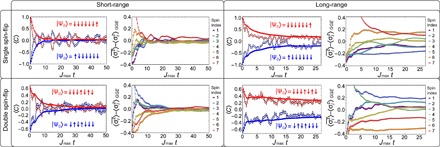
The average position of the spin excitation, 〈C〉, is plotted for an initial excitation on the left (dark blue unfilled squares) and right (dark red unfilled circles) along with their cumulative time average (blue and red filled circles and squares) for short-range (α = 1.33) and long-range (α = 0.55) interactions with initial states with one spin excitation (top panels) and two spin excitations (bottom panels). The cumulative time average of the deviation of the postselected individual spin projections from the GGE, $\langle {\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}\rangle -{\langle {\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}\rangle }_{\text{GGE}}$, is also plotted. For short-range interactions, the spins quickly thermalize to a value predicted by the GGE, but for the long-range interacting system, a new type of prethermal state emerges. Error bars are statistical, calculated on the basis of quantum projection noise and calibrated detection errors (38).

With short-range interactions, the system quickly relaxes to the prethermal value predicted by the GGE, where 〈C〉 is near zero irrespective of the initial state. But with long-range interactions, the prethermal state that emerges retains a clear memory of the initial conditions and is different than both the thermal and GGE predictions.

In addition to showing the relaxation behavior of the global observable 〈C〉, we also observe the dynamics of local observables with single-site resolution. In Fig. 2, we plot the cumulative time average of the deviation of the single-spin magnetizations, $\langle {\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}\rangle$, from the equilibrium value predicted by the GGE. Here, we postselect the data for the correct number of spin excitations to eliminate the effects of imperfect state preparation and small deviations from our model Hamiltonian due to unwanted excitations of the phonon modes (see Supplementary Materials). For the short-range interactions, we see that the cumulative time average for each spin quickly converges to the GGE predicted value. However, with the long-range interactions, we see that the individual spins reach a steady state that does not match the GGE because the emergent double well prevents the efficient transfer of the excitation across the chain.

We show the prethermal state’s robustness to weak interactions, similar to how many-body localization is robust to interactions (7, 30), by preparing initial states with two spin excitations. In this case, the multiple spin flips increase the size of the integrability-breaking part of the Hamiltonian, which represents weak interactions between the spin-wave bosons. However, the prethermal state still persists. For better contrast between the prethermal and GGE predicted values of 〈C〉, we flip the second and fourth spins such that |ψ₀〉 = | ↓↑↓↑↓↓↓ 〉. We emphasize that the observed prethermalization and departure from the GGE prediction are not sensitive to the specific choice of initial state in the thermodynamic limit, as long as the initial state is not symmetric. But for a small-sized system, these initial states offer us the maximum signal. As before, we also prepare the mirror image of the initial state by exciting the fourth and sixth ions ($|\mathrm{\psi }0\rangle$ = | ↓↓↓↑↓↑↓ 〉). We observe relaxation to the value predicted by the GGE for short-range interactions, but with long-range interactions, we see a prethermal state that strongly deviates from the GGE (bottom panel of Fig. 2).

In Fig. 3, we plot the experimental evolution of the prethermal state for both the double and single spin flip initial states along with a long-time numerical simulation under Eq. 1, accounting for known experimental noise. The plots demonstrate excellent agreement between numerical simulations and experimental data and confirm that the prethermal states persist well beyond the current experimental time limit. Because of the nonconservation of the number of spin-wave bosons for any finite B and the interactions between them, the system will eventually relax to the thermal equilibrium in the thermodynamic limit; however, relaxation to the GGE may or may not be seen depending on the range of interactions.

Fig. 3. Long-time dynamics.

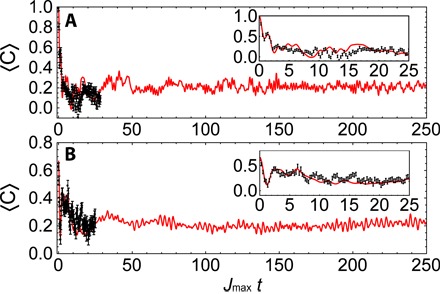
Comparison between a numerical simulation (red line; with laser power fluctuations included) of the transverse-field Ising model and experimental data (black dots) for single (A) and double (B) initial spin excitations. The inset shows good agreement between experiment and numerics for 〈C〉. For both the single and double spin flip cases, the prethermal state persists for much longer than the experimental time scale and eventually relaxes to the thermal state. Error bars, 1 SD.

To demonstrate that the prethermal state we observe is not sensitive to system size, we repeat the experiment in a chain of 22 ions, the largest ion chain used for quantum simulation in the literature to date. The power-law interaction range is α ≈ 0.9. The time evolution and cumulative time average of 〈C〉 are depicted in Fig. 4. Experimentally, as well as in the analytic result in the thermodynamic limit (see the Supplementary Materials), we see that the system relaxes to a similar quasi-equilibrium state as before that clearly has memory of the initial state. This is because the number of near-degenerate pairs of (localized) eigenstates is an extensive quantity, and the observed prethermalization will not disappear as the system size grows.

Fig. 4. Scaling to larger system size.

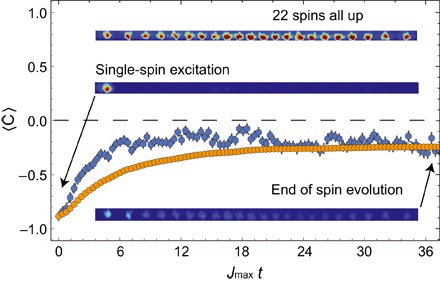
Time evolution (light blue) and cumulative time average (orange) of 〈C〉 with false color images of the 22-ion chain, where the brightness of each ion is determined by the value of $\langle {\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}\rangle$. The ions fluoresce during detection when in the | ↑ 〉_z state (top image). We initialize the spins with a single spin excitation on the left end (middle image). After evolving for 36 J_max, the spin excitation is delocalized, but its average position remains on the left half of the chain (bottom image). Effective range of the interaction is α ≈ 0.9. Error bars, 1 SD.

DISCUSSION

We point out that the observed prethermalization and deviation from the GGE should disappear if the system is subject to periodic boundary conditions, regardless of system size. Here, we emphasize that the long-range interactions make the boundary conditions relevant for bulk properties, and thus, changing the boundary conditions can affect an extensive number of eigenstates (31). The effects of long-range interactions on many-body dynamics are far richer than the effect discussed in the current experiment. For sufficiently long-range interactions, the notion of locality breaks down and quasi-particles in the system can travel at divergent velocities for thermodynamic systems, potentially leading to markedly different thermalization/prethermalization time scales in certain systems (32–34). We believe that the current experiment, as well as the platform it is built upon, will pave the way to a more complete understanding of the fundamental role long-range interactions play in the quench dynamics and emergent statistical physics of quantum many-body systems.

MATERIALS AND METHODS

Effective Hamiltonian generation

We generated spin-spin interactions by applying spin-dependent optical dipole forces to ions confined in a three-layer linear Paul trap with a 4.8-MHz radial frequency. Two off-resonant laser beams with a wave vector difference δk along a principal axis of transverse motion globally address the ions and drive stimulated Raman transitions. The two beams contain a pair of beat note frequencies symmetrically detuned from the resonant transition at ν₀ = 12.642819 GHz by a frequency μ, comparable to the transverse motional mode frequencies. In the Lamb-Dicke regime, this results in the Ising-type Hamiltonian in Eq. 1 (22, 23, 35) with

$${\mathit{J}}_{\mathit{i}\mathit{j}}=\frac{\mathrm{\hslash }{(\mathrm{\delta }\mathit{k})}^2{\mathrm{\Omega }}^2}{2\mathit{M}}{\displaystyle \sum _{\mathit{m}=1}^{\mathit{N}}}\frac{{\mathit{V}}_{\mathit{i},\mathit{m}}{\mathit{V}}_{\mathit{j},\mathit{m}}}{{\mathrm{\mu }}^2-{\mathrm{\omega }}_{\mathit{m}}^2}$$ (3)

where Ω is the global Rabi frequency, ħ is the reduced Planck’s constant, V_i,m is the normal-mode matrix (36), and ω_m are the transverse mode frequencies. The coupling profile may be approximated as a power-law decay J_ij ≈ J_max/|i − j|^α, where, in principle, α can be tuned between 0 and 3 by varying the laser detuning μ or the bandwidth of ω_m (23, 35). For the seven-ion data in this work, α was tuned to 0.55 (long-range interactions) and 1.33 (short-range interactions) by changing the bandwidth of ω_m. By asymmetrically adjusting the laser beat note detuning μ about the carrier by a value of 2B, we apply a uniform effective transverse magnetic field of $\mathit{B}{\mathrm{\sigma }}_{\mathit{i}}^{\mathit{z}}$ (37).

Single spin flip initialization and site-resolved detection

We initialized individual spin excitations using a tightly focused laser beam to imprint a fourth-order ac Stark shift (29) in conjunction with a Ramsey or Rabi sequence. When the ion spacing is larger than the beam waist of the individual-ion addressing laser as is the case for the seven-ion short-range data, we used a Ramsey method. This consists of first optically pumping the spins to | ↓ 〉_z. Then, we globally performed a π/2 rotation so that all of the spins are in | ↓ 〉_x. Using the individual-ion addressing beam, we applied a Stark shift to the spins to be flipped, and then we allowed the chain to evolve until these spins are π out of phase compared to the spins without an applied Stark shift. Afterward, a global π/2 rotation brings the spins back into the z-basis. With this method, individual spin flips can be prepared with a fidelity of ~0.97, whereas N spin flips can be achieved with a fidelity of ~(0.97)^N.

We used the Rabi method for the long-range interacting data because site-resolved Stark shifts can no longer be applied as the ion separation is smaller than the beam waist. Here, we applied a large Stark shift to all of the spins, except the ones to be flipped, and a global π pulse at the hyperfine splitting between the two effective spin levels. Thus, only the ions without an applied Stark shift were flipped. This approach has a single and N spin flip fidelity of ~0.85 and ~(0.85)^N, respectively.

After quenching to and allowing time evolution under our spin Hamiltonian, we measured the spin projections of each ion along the z direction of the Bloch sphere. We exposed the ions to a laser beam that addresses the cycling transition ²S_1/2 |F = 1〉 to ²P_1/2|F = 0〉 for 3 ms. Ions fluoresce only if they are in the state | ↑ 〉_z. This fluorescence was collected through an NA (numerical aperture) = 0.23 objective and imaged using an intensified charge-coupled device (CCD) camera with single-site resolution.

To discriminate between “bright” and “dark” states (| ↑ 〉_z and | ↓ 〉_z, respectively), we begin by calibrating the camera with 1000 cycles each of all-bright and all-dark states. For the bright states, the projection of the 2D CCD image onto a 1D row gives a profile composed of Gaussian distributions at each ion location. We performed fits to locate the center and fluorescence width of each ion.

We achieved single-shot discrimination of individual ion states in the experimental data by fitting the captured 1D profile to a series of Gaussian distributions with calibrated widths and positions but freely varying amplitudes. These extracted values for each ion were then compared with a threshold found via Monte Carlo simulation to determine whether the measured state was bright or dark. Our discrimination protocol also gives an estimate of the detection error (for example, misdiagnosing a bright ion as dark), which is typically of order ~5%. Corrected state probabilities (along with their respective errors) were found following the method outlined by Shen and Duan (38), which also takes into account errors due to quantum projection noise.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/8/e1700672/DC1

Experimental noise sources and their influence on the thermalization dynamics

Measuring the spin-spin coupling matrix

Justification for postselection

The spin-boson mapping and the GGE

Single-particle properties of H₀

Discussion

fig. S1. We directly measure the spin-spin coupling matrix with seven ions for both short-range (left matrix) and long-range (right matrix) interactions and see if it is symmetric.

fig. S2. Numerical calculation to illustrate the origin of the double-well potential.

Reference (39)