Abstract
The KV1.5 potassium channel, which underlies the ultra-rapid delayed-rectifier current (IKur) and is predominantly expressed in atria vs. ventricles, has emerged as a promising target to treat atrial fibrillation (AF). However, while numerous KV1.5-selective compounds have been screened, characterized, and tested in various animal models of AF, evidence of antiarrhythmic efficacy in humans is still lacking. Moreover, current guidelines for pre-clinical assessment of candidate drugs heavily rely on steady-state concentration-response curves or IC50 values, which can overlook adverse cardiotoxic effects. We sought to investigate the effects of kinetics and state-dependent binding of IKur-targeting drugs on atrial electrophysiology in silico and reveal the ideal properties of IKur blockers that maximize anti-AF efficacy and minimize pro-arrhythmic risk. To this aim, we developed a new Markov model of IKur that describes KV1.5 gating based on experimental voltage-clamp data in atrial myocytes from patient right-atrial samples in normal sinus rhythm. We extended the IKur formulation to account for state-specificity and kinetics of KV1.5-drug interactions and incorporated it into our human atrial cell model. We simulated 1- and 3-Hz pacing protocols in drug-free conditions and with a [drug] equal to the IC50 value. The effects of binding and unbinding kinetics were determined by examining permutations of the forward (kon) and reverse (koff) binding rates to the closed, open, and inactivated states of the KV1.5 channel. We identified a subset of ideal drugs exhibiting anti-AF electrophysiological parameter changes at fast pacing rates (effective refractory period prolongation), while having little effect on normal sinus rhythm (limited action potential prolongation). Our results highlight that accurately accounting for channel interactions with drugs, including kinetics and state-dependent binding, is critical for developing safer and more effective pharmacological anti-AF options.
Current pharmacological therapy against atrial fibrillation, the most common cardiac arrhythmia, is limited by low efficacy and adverse side effects of available anti-arrhythmic agents, which often actually increase the propensity for developing life-threatening ventricular arrhythmias. One way to circumvent the latter is to target ion channels that are predominantly expressed in atria vs. ventricles, such as the ultra-rapid delayed rectifier K+ channel, carried by KV1.5.
In this paper, we propose an in silico strategy to define optimal KV1.5-targeting drug characteristics to treat atrial fibrillation. We utilize kinetic models of ion channel gating and channel-drug interaction to determine the binding state-dependence and kinetics properties that allow achieving a positive rate-dependence, i.e., maximal effect on anti-arrhythmic indices at fast atrial rates and minimal effect on atrial electrophysiology during normal sinus rhythm.
The results show that IKur inhibitors that bind to the open or open and inactivated states of the KV1.5 channels have the potential to display a positive rate-dependence. Drug binding and unbinding kinetics strongly affect the impact of these blockers on atrial electrophysiological parameters. Drug effects are most prominent when binding and unbinding rates are in the range of the channel's activation and deactivation kinetics, which dictates IKur dynamics during the cardiac cycle.
We propose that in silico strategies such as that presented here could be coupled to in vitro and in vivo assays to facilitate the ongoing search for novel agents against atrial fibrillation.
I. INTRODUCTION
The voltage-gated K+ channel alpha subunit KV1.5 (encoded by KCNA5) underlies the ultra-rapid delayed-rectifier K+ current (IKur). KV1.5 is expressed in many organs, including skeletal muscle, brain, and pulmonary arteries,32,46,51 but it has drawn attention as an atrial-selective pharmacological target against atrial fibrillation (AF), the most common cardiac arrhythmia, given its predominant expression in human atrial vs. ventricular myocytes.22,38 Like most other voltage-gated ion channels, KV1.5 can exist in three distinct conformational states: open, closed, and inactivated, where the transitions between these states are membrane potential (Em) and temperature dependent.38 Upon depolarization, IKur activates more rapidly than other repolarization currents, such as IKs and IKr, and inactivates very slowly (in seconds). The block of IKur could result in prolongation of the human atrial action potential (AP) duration (APD) and effective refractory period (ERP), although findings reveal variable response to the IKur blockade.22 Our group and others have hypothesized that the extent of AP and ERP prolongation due to the IKur blockade depends on the degree of AF-induced remodeling of other K+ currents, such as the small conductance Ca2+-activated K+ current, and relative strengths of ICaL and IKr.22,35,53 As AP prolongation augments the Ca2+ transient amplitude, the inhibition of IKur enhances the force of contraction of isolated human atrial trabeculae both in patients in normal sinus rhythm (nSR) and chronic AF (cAF).42,43,53 However, prolongation and elevation of the AP plateau can lead to an increased risk of early afterdepolarizations (EADs) that can trigger and/or maintain AF.23 For these reasons, KV1.5 could be a useful atrial-specific target to prolong refractoriness and counteract the hypocontractility associated with cAF and, like the block of IKr, could be of regulatory concern if drug binding leads to EADs and arrhythmias.
Although many KV1.5 blockers have been studied both in vitro and in vivo, the anti-AF efficacy of IKur-targeting compounds remains to be confirmed in patients.37 As the effects of the IKur block on atrial repolarization, refractoriness, and Ca2+ dynamics are potentially complex, a modeling approach could help to identify the net impact of IKur inhibition on atrial electrophysiological parameters.5 Currently, guidelines for pre-clinical assessment of candidate antiarrhythmic drugs (and their effect on cardiac ionic channels such as KV1.5) heavily rely on steady-state concentration-response curves or IC50 values, which can overestimate or underestimate adverse cardiotoxic effects. However, recent work in ion channel pharmacology has highlighted the importance for accounting for channel interactions with drugs, including state-dependent binding and complex binding kinetics, and how they are related to electrophysiological properties such as APD, ERP, and propensity for triggered activity, alternans, and reentry.2,3,26,33,35,48 Drugs that interact with KV1.5 have been shown to bind to multiple channel conformational states,6,12,14,19,24,29,47 and the kinetics of drug binding and unbinding vary significantly for IKur-targeting compounds. In the spirit of the FDA Comprehensive in vitro Proarrhythmia (CiPA) initiative, which aims at moving from a predominantly traditional pharmacodynamics approach to an in silico and in vitro drug toxicity assessment of overall pro-arrhythmic risk,11 we sought to investigate in silico the effects of kinetics and state-dependent binding of IKur blockers on atrial electrophysiology. To avoid malignant adverse effects on the ventricular function, an effective AF-selective drug should exert potent effects on fibrillating atria (e.g., fast-rate electrical activity) without significantly impacting ventricular or atrial tissue during normal sinus rhythm. Here, we utilized the Grandi et al. human atrial myocyte model23,36 and incorporated a new Markov formulation of IKur, based on experimental voltage-clamp data in atrial myocytes from patient right-atrial samples, to reveal the ideal kinetic and state-dependent binding properties of IKur-blocking drugs that maximize anti-AF efficacy and minimize pro-arrhythmic risk.
II. METHODS
A. KV1.5 gating and drug binding model
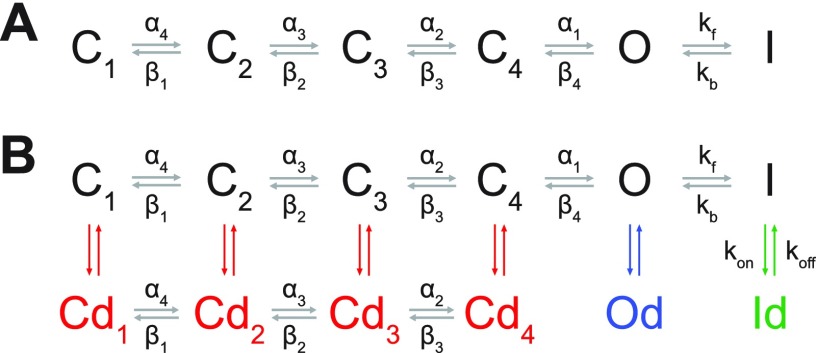
Human atrial IKur was simulated using a 6-state Markov chain derived from the study by Zhou et al.55 to replace our existing Hodgkin and Huxley formulation and integrated into our computational framework of human atrial myocyte electrophysiology.23,36 The Markov model [Fig. 1(a)] includes four closed states (C1, C2, C3, and C4), an open conducting state (O), and an inactivated state (I). Parameters describing the transition rates between each state (equations can be found in the supplementary material) were fit to experimental voltage-clamp data in human atrial myocytes.17,18,52 Several voltage-clamp protocols were simulated for parameterization, including steady-state activation and inactivation [Fig. 2(a)], time constants of inactivation [Fig. 2(c)], and recovery from inactivation [Fig. 2(d)].
FIG. 1.
Markov scheme of IKur. (a) Drug-free Markov model of IKur derived from the study by Zhou et al.55 The model has 4 closed states (C1, C2, C3, and C4), a conducting open state (O), and an inactivated state (I). (b) Extended model showing drug-bound states (Cd1, Cd2, Cd3, Cd4, Od, and Id) where an IKur inhibitor can bind to the closed, open, and inactivated states, with various kon and koff rates.
FIG. 2.
IKur model fitting to experimental data. (a) Simulated (solid lines) and measured (symbols and dashed lines) Em-dependence of activation and inactivation after 1-s and 50-s inactivating pulses. (b) Simulated IKur-voltage relationships are compared to experimental data (inset). Current densities at room temperature are converted into physiological temperature using Q10 = 2.5.18,39 (c) Simulated (solid line) and experimental (symbols) inactivation studied with the voltage protocol in the inset. (d) Simulated and experimental recovery from inactivation studied with the voltage protocol in the inset.
We further expanded the new IKur Markov formulation to describe various drug-KV1.5 channel binding schemes [Fig. 1(b)]. We simulated a variety of likely combinations of drug-channel interactions, including drugs that exclusively bind to the closed, open, or inactivated states and drugs that can bind multiple states of the channel. To investigate the effect of binding and unbinding kinetics on the characteristics of the IKur block, we used the approach designed by the Hill group.26 We considered different theoretical drugs with variable forward (kon) and reverse (koff) drug binding rates to the closed, open, and inactivated states of the KV1.5 channel in the predicted physiological range24 of 0.01–100 s−1 using half-logarithmic increments resulting in nine transition rates for each drug state transition (0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, and 100 s−1). For a particular state of the channel, dissociation constants (Kd) for our drug scenarios were calculated as koff/kon, and affinity constants were calculated as kon/koff. To investigate the effects of these drug characteristics, for a given state-dependent binding inhibitor, we varied kon and koff together (kon = koff) or considered all permutations of the nine different rates of drug binding (producing a total of 81 different drug scenarios). For drugs that could bind to multiple states of the KV1.5 channel, we also varied the relative affinity to open (KO) vs. inactivated state (KI).
IC50 values were computed by assessing the extent of the block of peak IKur after the application of different drug doses from 1 nM to 1 M. We calculated IC50 values using a typical experimental protocol, consisting of a train of 200-ms long voltage-steps from −60 mV to +50 mV,12,14,21,24 and with a 200-ms down-ramp voltage-clamp protocol from +30 mV to −60 mV. After the application of a given drug concentration, we allowed sufficient time for the degree of blocking to reach equilibrium. IC50 values were calculated at 1- and 3-Hz pacing rates as the drug concentration causing a 50% reduction in peak IKur compared to drug-free conditions.
B. Atrial AP simulations
The Grandi et al. human atrial cellular model was used to simulate the AP of a single atrial myocyte at 37 °C.23,36 The IKur Markov model described above was included, and its maximal conductance (gKur) scaled to mimic the same peak IKur value as the original Grandi et al. model at 1- and 3-Hz pacing. We only evaluated drugs that bound solely to the KV1.5 channel, i.e., no off-target drug effects on other ion channels (or K+ channel sub-types) were considered for this investigation. Simulations were equilibrated for 300 beats for 1-Hz pacing or 900 beats for 3-Hz pacing. After the 300th or 900th beat, the time to 90% repolarization of the AP (APD90) and the change in channel state occupancy were used as the initial AP metrics of analysis for the individual drugs.
The atrial ERP was determined using a standard S1-S2 premature stimulation protocol,12,44,50,54 where the S1 basal stimulus (5 ms in duration) was applied to a steady-state human atrial myocyte model. ERP was determined by applying the premature S2 stimulus (5 ms in duration, 2-fold the diastolic threshold of excitation) at progressively smaller S1-S2 intervals from 700 ms to refractoriness by decrements of 2 ms. The longest S1-S2 interval that failed to elicit an AP was taken as the local ERP (i.e., maximum upstroke velocity of ≥5 V/s and AP with an amplitude of ≥50% of the amplitude of the preceding AP elicited by S1).
All simulations and analysis were performed with MATLAB (The MathWorks, Natick, MA, USA) using the stiff ordinary differential equation solver ode15s. The model code is available for download at the following webpages: https://somapp.ucdmc.ucdavis.edu/Pharmacology/bers/ and http://elegrandi.wixsite.com/grandilab/downloads.
III. RESULTS
A. IKur gating model and state occupancies during the human atrial AP
Figure 2 shows experimental data and simulations confirming the adequacy of the IKur Markov model. Table I summarizes the sources of experimental data used to fit the model parameters. To assess the voltage dependence of IKur activation [Fig. 2(a)], tail current amplitudes were measured upon repolarization to −10 mV after 500-ms long test pulses from a holding Em of −50 mV to Em between −60 mV and +50 mV (the latter used for normalization). A 300-ms pre-pulse to +50 mV was used 10 ms before each test pulse, as this is used experimentally to inactivate the transient outward K+ current (Ito). The voltage-dependent inactivation of IKur was measured with test pulses to +40 mV (2 s in duration) after conditioning pulses (1 or 50 s in duration) to various Em values from a holding Em of −60 mV [Fig. 2(a)]. Inactivation kinetics [Fig. 2(c)] was studied with conditioning pulses of varying duration, followed 5 ms later by a 100-ms pre-pulse (to inactivate Ito) and then a 100-ms test pulse to +40 mV. An exemplary fit of the model to experimental data is displayed in Fig. 2(c) corresponding to a voltage step to +40 mV. The time constant of inactivation was rather Em-independent in both experiments and model. Recovery from inactivation [Fig. 2(d)] was investigated using a pair of 50-s pulses (P1 and P2) from −80 mV to +40 mV (preceded again by an Ito-inactivating 100-ms pre-pulse) at varying coupling intervals. Figure 2(b) displays the simulated IKur-voltage relationship compared to experiments from five different sources. The flattening of the simulated IKur-voltage curve at higher potentials, in contrast to most experiments showing a linearly increasing current, might be due to differences in recording vs. simulated conditions (e.g., physiological vs. room temperature).
TABLE I.
Experimental data used for IKur model parameterization.
| Measure | Source | Experiment |
|---|---|---|
| Activation Em-dependence | Fedida et al.17 | Human atrial myocytes, room temperature, whole-cell patch clamp |
| Inactivation Em-dependence | Feng et al.,18 Wang et al.52 | Human atrial myocytes, room temperature52 and physiological temperature,18 whole-cell patch clamp |
| Inactivation kinetics | Feng et al.18 | Human atrial myocytes, 37 °C, whole-cell patch clamp |
| Recovery kinetics | Feng et al.18 | Human atrial myocytes, 37 °C, whole-cell patch clamp |
| IKur-Em relationship (used to validate maximal conductance, Q10 adjusted) | Fedida et al.,17 Amos et al.,4 Wang et al.,52 Tessier et al.,47 Gluais et al.20 | Human atrial myocytes, room temperature, whole-cell patch clamp |
B. Optimization of IC50 value calculations using a down-ramp voltage-clamp protocol
Simulated IKur during a human atrial AP at a pacing rate of 1-Hz is depicted in Fig. 3(b). Notably, the channel opens rapidly upon depolarization and deactivates (closes) within 100 ms, with little or no inactivation, as shown in the time courses of state occupancies, and confirmed in a recent in silico study.1 We noted that the rather long depolarization steps used for IC50 determination underestimate the closed state occupancy and cause significant inactivation [Fig. 3(a)], which is not seen during a physiologic AP [Fig. 3(b)]. Note that although the channel does not inactivate much during a depolarization step, build-up in the inactivation state occurs over several beats (simulations are run to the steady state). Thus, we modified the IC50 protocol using a voltage waveform that more closely resembles the atrial AP shape and allows for comparable time courses of channel state occupancies [Fig. 3(c)].
FIG. 3.
IKur, channel state occupancy, and IC50 during a square voltage step, an atrial AP, and a triangular pulse. Time courses of Em (top), IKur (middle), and closed, open, inactivated state occupancy (bottom) during (a) a 200-ms long voltage step to +50 mV, (b) an atrial AP, and (c) a 200-ms long triangular pulse to +30 mV (1 Hz). Simulations are run to the steady-state. (d) IC50 values obtained for closed (left), open (center), and inactivated (right) state blocker with a square or triangular voltage pulse at 1- and 3-Hz pacing rates.
As shown in Fig. 3(d), even when a drug has the same binding/unbinding kinetics and overall affinity for the KV1.5 channel (Kd = 1 μM), its efficacy at blocking IKur greatly depends (by orders of magnitude) on the conformational state specificity of binding. Moreover, it is worth noting that if we were to use the square voltage step protocol [Fig. 3(a)], which overestimated the state occupancy of the inactivated state and underestimated the state-occupancy of the closed states, we would overestimate the potency of the inactivated state blocker and underestimate the potency of a closed state blocker [Fig. 3(d)].
C. Effect of conformational state specificity and binding/unbinding kinetics on IC50 at normal and fast pacing rates
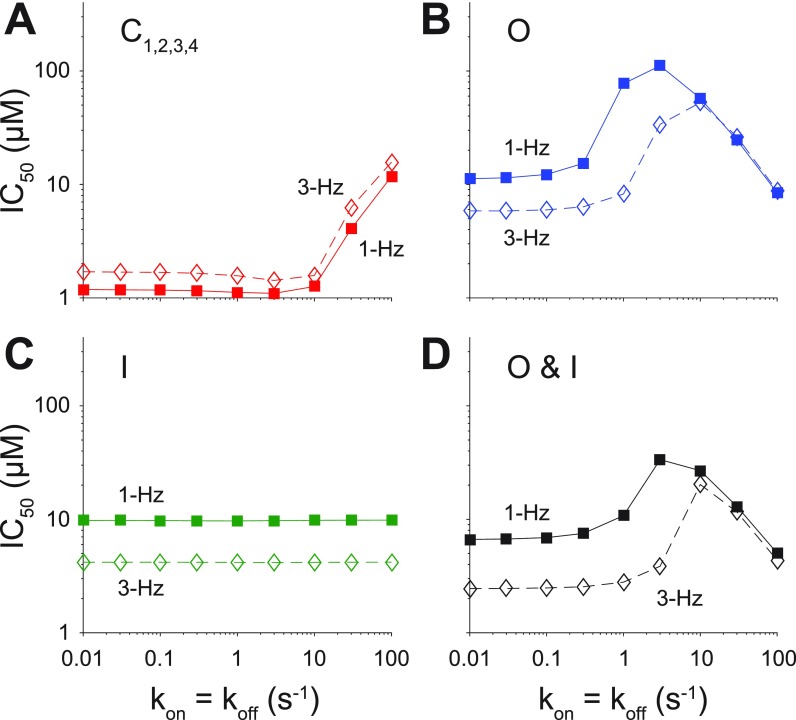
We next investigated the effect of state-specific affinity, binding kinetics, and pacing rate-dependence of KV1.5-selective theoretical drugs with the same kinetics of association/dissociation (koff = kon and Kd = 1 μM). We used nine different rates of binding kinetics between 0.01 and 100 s−1 using half-logarithmic increments (0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, and 100 s−1). Using the Markov schemes shown in Fig. 1(b), we considered six different scenarios for each hypothetical IKur blocker where the drug could interact exclusively with the O, I, and C, O and I, O and C, or all states of the channel.
A drug that could only bind the closed states of the KV1.5 channel (i.e., closed state blocker) was the most potent type of blocker and rather insensitive to binding kinetics at both 1- and 3-Hz pacing for koff = kon ≤ 10 s−1. At faster kinetics, the closed state blocker loses potency [Fig. 4(a)]. Notably, across the entire range of drug-binding kinetics, a closed state blocker is more potent at 1-Hz pacing than at 3-Hz pacing, i.e., opposite to the desired characteristic for a drug designed to treat AF.
FIG. 4.
Effect of the state-dependence and kinetics of drug binding on IC50. IC50 values were obtained using a down-ramp voltage-clamp protocol at 1- and 3-Hz pacing rates for a closed state blocker (a), open state blocker (b), inactivated state blocker (c), and open and inactivated state blocker (d) given nine different rates of binding kinetics between 0.01 and 100 s−1 using half-logarithmic increments, whereby koff = kon and Kd = 1 μM.
Drugs that only bind to the open state of the KV1.5 channel are the least potent [Fig. 4(b)]. Their IC50 values are rather insensitive to slow binding kinetics (<1 s−1) but display a biphasic relationship with hastening kinetics. Open state blockers are more potent at faster pacing rates (i.e., fast pacing-rate selectivity, compare IC50 at 3 vs. 1 Hz), but this fast pacing-rate selectivity is lost at binding rates greater than 10 s−1.
IC50 values were independent of drug-binding kinetics for inactivated state blockers [Fig. 4(c)], which resulted quite more potent at 3-Hz pacing as compared to 1-Hz pacing, thus displaying fast-rate selectivity.
Open and closed state blockers and drugs that could bind equally to any state did not display favorable fast pacing-rate selectivity (not shown), whereas open and inactivated state blockers did [Fig. 4(d)], and thus, we considered this type of inhibitor and the open state blocker for subsequent analysis.
D. Effect of conformational state specificity and binding/unbinding kinetics on human atrial APD at normal and fast pacing rates
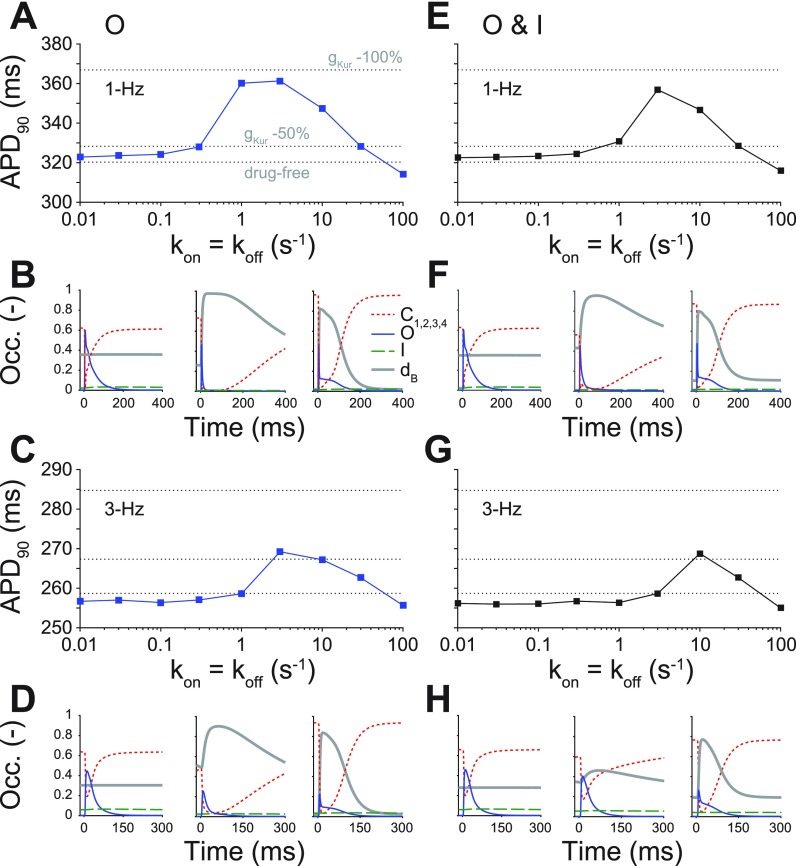
To assess the effect of conformational state specificity and binding/unbinding kinetics on human atrial APD at normal and fast pacing rates, we considered three types of blockers: an open [Figs. 5(a)–5(d)], an inactivated (Fig. S1 in the supplementary material), and an open and inactivated state blocker [Figs. 5(e)–5(h)]. These were the inhibitors that displayed fast pacing-rate selectivity when looking at their effects on IKur. For each of these types of blockers, we examined the relationship between APD and drug-binding kinetics using the IC50 values calculated previously and using the same range as used for the calculation of the IC50 values (0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, and 100 s−1). Changes in APD are compared to no block, 50%, and 100% reduction in gKur.
FIG. 5.
Effect of the state-dependence and kinetics of drug binding on APD90. APD90 was determined for open (1-Hz [a] and 3-Hz [c] pacing rates) and open and inactivated (1-Hz [e] and 3-Hz [g] pacing rates) state blockers given nine different rates of binding kinetics between 0.01 and 100 s−1 using half-logarithmic increments, whereby koff = kon and Kd = 1 μM. These simulations were also run in drug-free conditions, given a 50% and 100% reduction in gKur (dashed lines in a, c, e, and g). Simulations were equilibrated for 300 beats at 1-Hz pacing or 900 beats at 3-Hz pacing using a [drug] equal to the IC50 value. (b), (d), (f), and (h) show the closed, open, inactivated, and drug-bound (dB, i.e., Od or Od + Id) state occupancies during an AP for three different drug-binding kinetics (koff = kon = 0.01, 3, and 100 s−1).
A drug that can only bind to the KV1.5 open state displays a biphasic relationship between APD and drug-binding kinetics at both 1- and 3-Hz pacing [Figs. 5(a) and 5(c)], whereby APD prolongation is only seen for intermediate binding kinetics (1 to 10 s−1 for 1-Hz pacing and 3 to 30 s−1 for 3-Hz pacing). For both slow (≤0.3 s−1 for 1-Hz pacing and ≤1 s−1 for 3-Hz pacing) and fast (100 s−1) drug-binding kinetics, APD in the presence of drug is comparable to drug-free conditions. Notably, APD prolongation with an IC50 concentration of the drug reaches values well above a constant 50% reduction in gKur at 1-Hz pacing, but more closely resembles it at 3-Hz pacing. Figure 5(b) (1-Hz pacing) and Fig. 5(d) (3-Hz pacing) display the closed, open, and inactivated state occupancies during a steady-state AP for the slowest (0.01 s−1), intermediate (3 s−1), and fastest (100 s−1) drug-binding rates. For the slowest drug-binding kinetics, the inhibitor does not bind readily during the AP, and the drug-bound state stays level below 0.4. At intermediate drug-binding kinetics, the open state blocker binds readily during the AP, thus significantly shrinking the open state occupancy. In addition, the off-rate of drug binding is slow enough to achieve maintenance in the drug-bound state during the AP. This allows for considerable AP prolongation, almost mimicking 100% reduction in gKur. Finally, for the fastest drug-binding kinetics, the IKur-blocker again binds readily during the AP, but the off-rate of drug binding is so fast as to cause cycling between the drug-free open state and the drug-bound open state during a single AP, resulting in prolongation of the drug-free open state occupancy later in the AP and slight AP shortening.
For an open and inactivated state blocker, a biphasic relationship between APD and drug-binding kinetics is also seen at 1- and 3-Hz pacing [Figs. 5(e) and 5(g)]. Slow (≤0.3 s−1 for 1-Hz pacing and ≤3 s−1 for 3-Hz pacing) and fast (100 s−1) drug-binding kinetics yield an APD that is comparable to no IKur block. At 1-Hz pacing, we observe significant APD prolongation at drug-binding kinetics equal to 3 or 10 s−1, while we only see significant AP prolongation at 3-Hz pacing for drug-binding kinetics equal to 10 s−1. Figures 5(f)–5(h) show the state occupancies of the closed, open, and inactivated states during a steady-state AP for the slowest (0.01 s−1), intermediate (3 s−1), and fastest (100 s−1) drug-binding rates at 1- and 3-Hz pacing. They closely resemble the state occupancies observed at these drug-binding rates for the open state blocker, except for the intermediate binding rate, which results in less drug bound state occupancy [Figs. 5(h) vs. 5(d), middle] and produces little AP prolongation.
E. Effect of conformational state specificity and binding/unbinding kinetics on human atrial ERP at normal and fast pacing rates
Since a desired effect of IKur inhibitors is the prolongation of atrial refractoriness,4,12,19,29,41 we assessed the effects of binding/unbinding kinetics on the ERP for open state [Figs. 6(a) and 6(b)] and open and inactivated state blockers [Figs. 6(c) and 6(d)] at 1- and 3-Hz pacing. We used the IC50 values calculated previously (Fig. 4) and compared our results to no block, 50%, and 100% reduction in gKur. Figure 6 shows a similar biphasic relationship between ERP and drug-binding kinetics for both types of blockers, as observed in Fig. 5 for APD: when APD increases for a particular IKur inhibitor, we also find ERP prolongation.
FIG. 6.
Effect of the state-dependence and kinetics of drug binding on ERP. ERP was determined for open (1-Hz [a] and 3-Hz [b] pacing rates) and open and inactivated (1-Hz [c] and 3-Hz [d] pacing rates) state blockers given nine different rates of binding kinetics between 0.01 and 100 s−1 using half-logarithmic increments, whereby koff = kon, Kd = 1 μM. These simulations were also run in drug-free conditions, given a 50% and 100% reduction in gKur (dashed lines).
For the open state blocker [Figs. 6(a) and 6(b)], we see modest ERP prolongation at slow drug-binding rates (≤0.3 s−1) at either 1- or 3-Hz pacing. Drugs with intermediate binding rates cause more substantial ERP prolongation (>0.3 s−1 and ≤10 s−1) at 1 Hz, mirroring their effects on APD. At 3-Hz pacing, both intermediate and fast drug-binding kinetics lead to ERP prolongation (>1 s−1). Thus, drugs with the fastest drug-binding kinetics (30 and 100 s−1) cause ERP prolongation at 3-Hz pacing, while having a lesser effect at 1-Hz pacing, i.e., they show a positive frequency-dependence that is desirable for an AF-selective drug.
For the open and inactivated state blocker [Figs. 6(c) and 6(d)], we again predict a biphasic relationship between ERP and drug-binding kinetics. Once more, drugs with slow binding kinetics do not exhibit substantial ERP prolongation, and drugs with fast binding rates (>30 s−1) cause more ERP prolongation at 3-Hz pacing as compared to 1-Hz pacing.
For an inactivated state blocker, APD and ERP changes are independent of the drug-binding kinetics at both 1- and 3-Hz pacing (Figs. S1 and S2 in the supplementary material), APD closely resembles that in drug-free conditions, and the ERP is decreased compared to no IKur block. For these reasons, an inactivated-state-only blocker was excluded in our subsequent analysis.
F. Effects of drug binding/unbinding kinetics with variable Kd on APD and ERP
We have shown drug scenarios where the on- and off-rates of drug binding are equal to each other (kon = koff and Kd = 1 μM). However, even closely related IKur inhibitors can have dissimilar Kd values.24 Thus, we simulated all permutations of the nine different rates of drug binding (0.01 to 100 s−1), yielding 81 different combinations of kon and koff. We assessed the effects of these drugs using their IC50 values by looking at AP prolongation at 1 Hz [Fig. 7(a)] and ERP prolongation at 3 Hz [Fig. 7(b)]. The output of the simulations for an open and inactivated state blocker is displayed as a heatmap, where the diagonals of the squares from the bottom left to the top right corner in Figs. 7(a) and 7(b) correspond to the drug scenarios in Figs. 5(e) and 6(b), respectively. Drugs with slow drug-binding kinetics (kon and koff ≤ 0.3 s−1) cause little prolongation of APD and ERP, as well as drugs with a large Kd (koff ≫ kon). In addition, holding kon constant, we see that APD and ERP are not very sensitive to changes in koff. The drugs with a fast kon rate (≥30 s−1) display favorable pacing-rate selectivity (boxes in Fig. 7), as they produce ERP prolongation at 3-Hz pacing while having little effect on APD at 1-Hz pacing.
FIG. 7.
Effect of drug binding kinetics on APD90 and ERP for an open and inactivated state blocker. (a) APD90 (at 1 Hz) and (b) ERP (at 3 Hz) are plotted for open and inactivated state blockers with varying binding kinetics, which were simulated via permutations of nine different drug-binding rates of (from 0.01 to 100 s−1) while keeping kon,O = kon,I and koff,O = koff,I.
G. Effect of relative state-specific drug binding
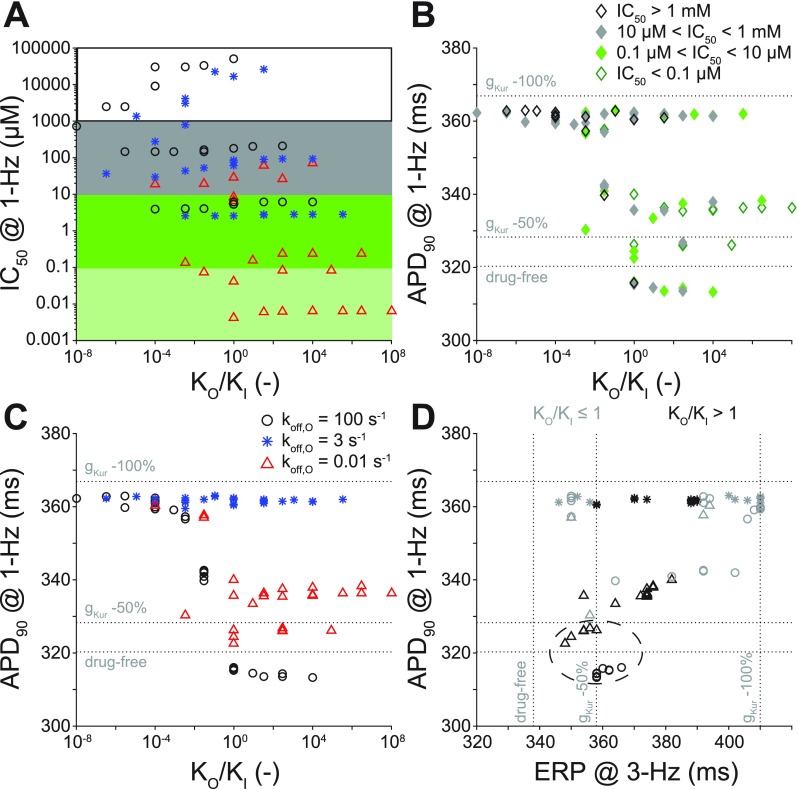
We further studied the open and inactivated state blocker by investigating the effects of its relative affinity to the open and inactivated states (Ko/Ki) on IKur (IC50) and electrophysiology (APD and ERP). Previously, we only changed the overall affinity to the open and inactivated states of the channel (variable Kd), but KO was always equal to KI (KO/KI = 1). In Fig. 8, we summarize our findings when we allow kon, koff, Kd, and Ko/Ki to vary. Specifically, we allowed kon for the open state (kon,O), koff for the open state (koff,O), kon for the inactivated state (kon,I), and koff for the inactivated state (koff,I) to have any of three binding rates (0.01, 3, and 100 s−1) and varied them independently to yield 81 different drug combinations. Again, we compare our outputs of APD and ERP to drug-free conditions, 50%, and 100% reduction in gKur (dashed lines).
FIG. 8.
Effect of conformational state affinity and drug-binding kinetics of an open and inactivated state blocker on IC50, APD90, and ERP. Open and inactivated state blockers with varying affinities to the open and inactivated states were simulated via permutations of three different rates of binding kinetics (0.01, 3, and 100 s−1). (a) IC50 and (b and c) APD90 are plotted as a function of the ratio of the open to the inactivated state affinity (KO/KI). (d) APD90 at 1 Hz and ERP at 3 Hz are plotted for each KO/KI. In (a) and (b), shades code for IC50 concentration levels. In (b), (c), and (d), symbols code for various koff,O. Shades in (d) reflect either higher affinity to the open or the inactivated state. Dashed lines represent APD90 and ERP in drug-free conditions and 50% and 100% reduction in gKur. The best theoretical drugs are circled in (d). Simulations were equilibrated for 300 beats at 1-Hz pacing or 900 beats at 3-Hz pacing using a [drug] equal to the IC50 value.
Figure 8(a) displays the relationship between IC50 (at 1-Hz pacing) and KO/KI. The panel is shaded according to IC50 value cutoffs of 0.1 μM, 10 μM, and 1 mM, and the symbols indicate different koff,O. Overall, there is a trend whereby increasing KO/KI and decreasing koff,O increase the potency of the drug (i.e., decrease the IC50 value). Thus, the most potent drugs have KO > KI and the slowest koff,O. Figures 8(b) and 8(c) show APD (at 1-Hz pacing) as a function of KO/KI. Data points are separated by IC50 cutoffs [Fig. 8(b)] or koff,O [Fig. 8(c)]. When KO/KI < 1, we almost always obtain maximal AP prolongation (this also corresponds to larger IC50). When KO/KI > 1, we only obtain close to maximal AP prolongation when koff,O is equal to 3 s−1 (intermediate drug-binding rate). In Fig. 8(d), we plotted APD at 1 Hz vs. ERP at 3 Hz for various KO/KI ratios (light gray symbols correspond to KO/KI ≤ 1, and dark symbols correspond to KO/KI > 1). The open and inactivated state blockers displaying favorable pacing-rate selectivity, i.e., producing ERP prolongation at 3-Hz pacing while having moderate effects on APD (and ERP) at 1-Hz pacing, are ones with KO/KI > 1, except if koff,O equals 3 s−1 (dashed circle).
IV. DISCUSSION
In this in silico study, we sought to determine how a KV1.5-targeting drug's kinetics and state-dependent binding properties influence the degree of IKur inhibition (IC50) and extent of electrophysiological parameter (APD and ERP) changes. Inspired by the approach recently utilized by the Hill group in the study of hERG-binding compounds,26 we simulated a new Markov model of IKur, which describes KV1.5 gating based on experimental data in human atrial myocytes and allows for state-specific KV1.5-drug interactions, into our human atrial myocyte model.23,36 We then compared theoretical IKur inhibitors in single cell simulations utilizing their IC50 drug concentrations. Our study revealed that (i) use-dependent inhibition of IKur is achieved with open, inactivated, and open and inactivated state inhibitors over a broad range of drug-binding rates; (ii) intermediate drug-binding kinetics (comparable to AP dynamics) cause potentially harmful APD prolongation; (iii) inhibitors with increased affinity for the open vs. inactivated state and drug-binding kinetics faster or slower than AP kinetics exert anti-AF effects on electrophysiological parameters at fast pacing rates (ERP prolongation), while having moderate effects on nSR (limited AP prolongation), and might represent a subset of ideal drugs. Overall, our results emphasize the importance of accurately accounting for channel interactions with drugs, namely, kinetics and state-dependent binding, when developing safe and effective KV1.5-selective anti-AF compounds.
A. IC50 values vary considerably depending on the specific voltage-clamp protocol
We found that even if a drug has the same binding/unbinding kinetics and overall affinity to the KV1.5 channel, its potency largely depends on the state-specificity of binding [Fig. 3(d)]. When simulating IKur during a normal human atrial AP, we noted that the current undergoes very little inactivation, even at fast pacing rates (Fig. S3 in the supplementary material), compared to more substantial inactivation during long depolarization steps commonly used for IC50 value determination4,12,14,19 [Fig. 3(b) vs. 3(a)]. Using these typical square depolarization steps overestimates the KV1.5 channel open state occupancy and underestimates the closed state occupancy during an AP. Thus, we proposed that using a waveform (such as a triangular down-ramp voltage-step) that more closely resembles the AP leads to more accurate representation of the channel state occupancies in a beating atrial myocyte and IC50 calculations. Indeed, we showed that square vs. down-ramp voltage step protocols lead to remarkably different IC50 values [Fig. 3(d)]. While an AP-clamp protocol might yield even more precise estimates, down-ramp protocols can easily be standardized in a high-throughput drug-screening process.
B. Drug-binding kinetics and state-dependence influence rate-dependence of the IKur block
We found that the potency of KV1.5 inhibitors varies with the stimulation rate, depending on the binding state-specificity and kinetics (Fig. 4). Closed state blockers display lower IC50 values at normal vs. fast pacing rates over the full range of kinetics (reverse pacing-rate dependent block), and their potency decreases with hastening binding and unbinding rates. Inactivated state blockers, on the other hand, always produce a greater block at fast vs. normal pacing rates (where inactivation is increased), but the degree of frequency-dependent blocking is independent of the drug-binding kinetics. Open and open and inactivated state inhibitors exhibited fast pacing-rate selectivity (lower IC50 values at 3-Hz pacing compared to 1-Hz pacing) over a broad range of binding kinetics. Positive fast pacing-rate selectivity (or use-dependence) is a favorable quality for a potential anti-AF drug: an ideal IKur inhibitor would obstruct IKur at fast pacing rates (causing ERP prolongation), while having little effect during nSR, as excessive AP prolongation could lead to arrhythmia. Frequency-dependent block has been a hallmark of the best performing KV1.5-selective compounds such as XEN-D0103,19 and many of these compounds have been confirmed to bind to the open state.9,12,24 By simulating a simple pore block (i.e., fixed reduction in the maximal conductance of IKur), Aguilar et al. have recently suggested that positive pacing-rate dependent AP prolongation occurs as a result of differential IKr activation at slow versus rapid pacing rates, as the AP plateau potential moves to more positive voltages with IKur inhibition.1 Here, we extend these findings to show for the first time that the fast pacing-rate selectivity of an open state blocker and an open and inactivated state blocker is significantly affected by its binding kinetics.
C. Drug-binding kinetics influences rate-dependent APD and ERP prolongation
The properties of the drug block described above lead to marked binding kinetics-dependent differences in APD and ERP changes in our whole-cell simulations, even when always using a [drug] equal to the IC50 value (Figs. 5 and 6). Overall, (i) slow drug-binding kinetics caused minimal AP changes and modest ERP prolongation; (ii) intermediate drug-binding kinetics led to substantial AP and ERP prolongation; and (iii) fast drug-binding kinetics failed to produce substantial AP or ERP prolongation at a normal pacing rate but increased the ERP at 3-Hz pacing. IKur inhibitors that exist in the parameter space (i) and (iii) would likely be the best candidates for anti-AF therapy. However, it is worth noting that by simulating each drug at the IC50 calculated at the given pacing rate, for slow and intermediate kinetics, we overestimate the effects that a given [drug] would exert at slow vs. fast pacing (see, e.g., Fig. S4 in the supplementary material).
To understand the biphasic relationship between drug-binding kinetics and APD, we took a closer look at the occupancy of drug-bound states during the atrial AP for slow, intermediate, and fast kinetics (Fig. 5). For the slowest drug-binding rate, the IKur inhibitor does not bind readily during the AP, leading to little AP prolongation. For intermediate and fast drug-binding rates, IKur inhibitors bind readily during the AP. While for intermediate binding rates, they do not leave the drug-bound state during the cardiac cycle, favoring AP prolongation, a fast koff leads to cycling between the drug-free and the drug-bound open states during a single AP, thus lengthening the drug-free open state occupancy later in the cardiac cycle and preventing AP prolongation. These observations parallel the findings by Lee et al. on KV11.1 (hERG) inhibitors.26 The authors found that drugs with slow overall binding kinetics (slower than the rates of inactivation/recovery from inactivation) lead to drug-bound states that are only transiently populated during the cardiac cycle (i.e., drugs with slow binding kinetics never reach true equilibrium). For KV1.5, channel activation/deactivation kinetics mostly impact IKur dynamics during the AP (as also reported by Aguilar et al.1) and the effect of varying binding kinetics on atrial parameters.
We also accounted for the complexity of drug-binding kinetics by allowing our theoretical drugs to have any combination of kon and koff over a likely physiological range24 (Fig. 7). Adding this dimension revealed that APD and ERP are rather insensitive to changes in koff and confirmed the overall dependence on binding kinetics.
D. Increasing the affinity to the open vs. inactivated state increases the potency of multi-state IKur blockers
We extended our analysis and expanded the parameter space to simulate drugs that can bind to both open and inactivated states of the KV1.5 channel with variable affinity. We found that increasing the relative affinity to the open state (KO/KI) generally increases the potency of the drug (especially when also decreasing koff,O). When KO/KI < 1, we almost always obtain maximal AP prolongation (corresponding to larger IC50 values), whereas when KO/KI > 1, we only obtain nearly maximal AP prolongation when koff,O is equal to the intermediate binding rate. To reveal KV1.5-binding properties with a favorable (positive) heart rate-dependence, we plotted the APD at 1 Hz vs. ERP at 3 Hz [Fig. 8(d)] and looked for binding kinetics permutations producing ERP prolongation at 3-Hz pacing while having moderate effects on APD (and ERP) at a normal pacing rate. These are ones with KO/KI > 1 and either slow or fast (i.e., not intermediate) koff,O.
E. Limitations and future directions
We presented a purely theoretical study to analyze the parameter space defining state-dependence and kinetics of KV1.5-binding drugs. A major strength here is that the properties of potential drugs are explored under many different conditions, including on and off binding rates that vary over 4 orders of magnitude. Although it was impossible for us to relate the results to the effects of real drugs on native human atrial IKur currents, the range of the on and off rates of drug binding chosen here represents a plausible physiological range as shown for some IKur inhibitors in heterologous systems expressing the human KV1.5 channel.24 Our results could be further informed by IC50 values, kon, koff, and affinity ratios that can be measured using in vitro assays for real candidate compounds and then mapped to our computed parameter space for validation. Furthermore, this type of analysis can be applied to other multi-state blockers, as successfully done for hERG inhibitors.26,40 Future analysis should also consider multi-channel effects of drugs, which we have not accounted for here.28
Our drug-binding scheme for the open state inhibitor reflects the so-called “foot-in-the-door” mechanism, whereby returning to the open or closed states requires that the bound drug disassociates from its binding site, as described for several KV1.5 open state inhibitors including AVE0118.14 However, when simulating a multi-state IKur blocker (i.e., O and I), the assumption that there are no channel transitions between drug-bound open and inactivated states, i.e., a drug must dissociate from the binding site to allow the channel to enter the inactivated state, might not be correct. Nevertheless, if the kinetics of inactivation and recovery thereof are slower than the drug kon and koff rates, drug binding and unbinding are expected to be more frequent than transitions between drug-bound open and inactivated states. We compared our results with those obtained with the alternative binding scheme in Fig. S5(a) in the supplementary material, where we assumed for simplicity that transition rates from drug-bound open and inactivated states equal those from drug-free open and inactivated states. The predicted changes in IC50 [Fig. S5(b) in the supplementary material], APD90 [Fig. S5(c) in the supplementary material], and ERP [Fig. S6(d) in the supplementary material] with binding kinetics are indistinguishable at both 1- and 3-Hz pacing. Thus, the conclusions drawn from Figs. 4, 5, and 6 are valid with either binding scheme. Note that with the scheme in Fig. S5(a) in the supplementary material, microscopy reversibility requires affinities for the open and inactive state be equal (KO = KI). To consider situations where KO ≠ KI (as in Figs. 7 and 8), we would need to assume transition rates between the drug-bound open and inactivated states to be different from drug-free transitions and allow one to vary based on microscopic reversibility. Although this scenario is more realistic, because the drug-bound conformational changes would be expected to be different in the absence of a drug, new transition rates would need to be introduced, thus making the analysis even more complex and system identification from experimental data more demanding.
This study used single cell APD and ERP as its main metrics of analysis. Other arrhythmia indices and integration of such simulations into tissue and organ level models would provide additional details that could be used to assess the antiarrhythmic efficacy of candidate IKur inhibitors. For example, recently, Lancaster and Sobie combined AP simulations to compute a variety of metrics from both the AP and intracellular Ca2+ dynamics, with statistical and machine-learning methods to predict the torsadogenic risk of drugs and reveal which cardiac ion channels may have the largest impact on such risk.25
Our investigation aimed at revealing the effects of drugs in an average human atrial myocyte in nSR conditions. IKur is diminished in cAF,7,10,12,16,49 and thus, IKur inhibitors may have limited efficacy when extensive ionic remodeling has occurred.1 Their therapeutic potential might be better exploited in paroxysmal AF, although the expression of the KV1.5 channel subunit is decreased also in this patient population.8,9 Nevertheless, there may be instances where IKur-targeting drugs prolong AP and ERP in paroxysmal and chronic AF but not in atrial myocytes from sinus rhythm patients (as observed in Ref. 19) Thus, similar in silico examination of optimal drug characteristics can be extended to models of cAF. Furthermore, population-based computational approaches have been established and proven valuable for understanding inter-subject variability in electrophysiological properties and cardiotoxicity. The best performing drugs identified here could be simulated in a population of human atrial myocyte models as in Refs. 15, 27, 34, and 45 to identify via sensitivity analysis what atrial cell characteristics lead to more favorable responses to drug therapy,13 e.g., positive heart rate-dependence.
Experimental data on drug-binding kinetics to various currents in the heart continue to grow as we realize modifying certain channel properties can have specific (favorable) effects on arrhythmia dynamics. In addition, a natural symbiosis between patch-clamp and in silico experiments has continued to strengthen, especially when trying to identify new antiarrhythmic strategies.31 In particular, combining the dynamic patch-clamp technique and computational models shows great promise as a tool for drug discovery of novel agents, as one can look at the effects of changing ion channel gating on antiarrhythmic efficacy.30 This is because, as this study highlights, the effects of the current block on repolarization and refractoriness are complex, and modeling approaches are crucial for understanding their net impact in various conditions.
V. CONCLUSIONS
This study employed an in silico approach to identify ideal therapeutic properties of IKur-targeting drugs that maximize AF selectivity. Currently, guidelines for the pre-clinical assessment of candidate drugs heavily rely on steady-state metrics such as IC50 values, which do not yield enough information to draw conclusions about AP or ERP prolongation on their own. Our results demonstrate that thoroughly accounting for channel interactions with drugs, including kinetics and state-dependent binding, is critical for developing safer and more effective pharmacological anti-AF options. This study also confirms that in silico models can be useful tools for screening IKur-blockers during the pre-clinical drug development process.
VI. SUPPLEMENTARY MATERIAL
See supplementary material for IKur model equations and supplementary figures.
ACKNOWLEDGMENTS
This work was supported by the National Institutes of Health grant R01-HL131517 (to EG), the American Heart Association grant 15SDG24910015 (EG), the Heart Rhythm Society post-doctoral fellowship 16OA9HRS (SM), and the Bill Bertken Sudden Death Prevention Fund.
References
- 1. Aguilar M., Feng J., Vigmond E., Comtois P., and Nattel S., “ Rate-dependent role of IKur in human atrial repolarization and atrial fibrillation maintenance,” Biophys. J. 112, 1997–2010 (2017). 10.1016/j.bpj.2017.03.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Aguilar M., Xiong F., Qi X. Y., Comtois P., and Nattel S., “ Potassium channel blockade enhances atrial fibrillation-selective antiarrhythmic effects of optimized state-dependent sodium channel blockade,” Circulation 132, 2203–2211 (2015). 10.1161/CIRCULATIONAHA.115.018016 [DOI] [PubMed] [Google Scholar]
- 3. Aguilar-Shardonofsky M., Vigmond E. J., Nattel S., and Comtois P., “ In silico optimization of atrial fibrillation-selective sodium channel blocker pharmacodynamics,” Biophys. J. 102, 951–960 (2012). 10.1016/j.bpj.2012.01.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Amos G. J., Wettwer E., Metzger F., Li Q., Himmel H. M., and Ravens U., “ Differences between outward currents of human atrial, and subepicardial ventricular myocytes,” J. Physiol. - London 491, 31–50 (1996). 10.1113/jphysiol.1996.sp021194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Bers D. M. and Grandi E., “ Human atrial fibrillation: Insights from computational electrophysiological models,” Trends Cardiovasc. Med. 21, 145–150 (2011). 10.1016/j.tcm.2012.04.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Bouchard R. and Fedida D., “ Closed- and open-state binding of 4-aminopyridine to the cloned human potassium channel Kv1.5,” J. Pharmacol. Exp. Ther. 275, 864–876 (1995). [PubMed] [Google Scholar]
- 7. Brandt M. C., Priebe L., Bohle T., Sudkamp M., and Beuckelmann D. J., “ The ultrarapid and the transient outward K+ current in human atrial fibrillation. Their possible role in postoperative atrial fibrillation,” J. Mol. Cell Cardiol. 32, 1885–1896 (2000). 10.1006/jmcc.2000.1221 [DOI] [PubMed] [Google Scholar]
- 8. Brundel B. J., Van Gelder I. C., Henning R. H., Tieleman R. G., Tuinenburg A. E., Wietses M., Grandjean J. G., Van Gilst W. H., and Crijns H. J., “ Ion channel remodeling is related to intraoperative atrial effective refractory periods in patients with paroxysmal and persistent atrial fibrillation,” Circulation 103, 684–690 (2001). 10.1161/01.CIR.103.5.684 [DOI] [PubMed] [Google Scholar]
- 9. Brundel B. J., Van Gelder I. C., Henning R. H., Tuinenburg A. E., Wietses M., Grandjean J. G., Wilde A. A., Van Gilst W. H., and Crijns H. J., “ Alterations in potassium channel gene expression in atria of patients with persistent and paroxysmal atrial fibrillation: Differential regulation of protein and mRNA levels for K+ channels,” J. Am. Coll. Cardiol. 37, 926–932 (2001). 10.1016/S0735-1097(00)01195-5 [DOI] [PubMed] [Google Scholar]
- 10. Caballero R., de la Fuente M. G., Gomez R., Barana A., Amoros I., Dolz-Gaiton P., Osuna L., Almendral J., Atienza F., Fernandez-Aviles F., Pita A., Rodriguez-Roda J., Pinto A., Tamargo J., and Delpon E., “ In humans, chronic atrial fibrillation decreases the transient outward current and ultrarapid component of the delayed rectifier current differentially on each atria and increases the slow component of the delayed rectifier current in both,” J. Am. Coll. Cardiol. 55, 2346–2354 (2010). 10.1016/j.jacc.2010.02.028 [DOI] [PubMed] [Google Scholar]
- 11. Cavero I. and Holzgrefe H., “ Comprehensive in vitro Proarrhythmia Assay, a novel in vitro/in silico paradigm to detect ventricular proarrhythmic liability: A visionary 21st century initiative,” Expert Opin. Drug Saf. 13, 745–758 (2014). 10.1517/14740338.2014.915311 [DOI] [PubMed] [Google Scholar]
- 12. Christ T., Wettwer E., Voigt N., Hala O., Radicke S., Matschke K., Varro A., Dobrev D., and Ravens U., “ Pathology-specific effects of the IKur/Ito/IK,ACh blocker AVE0118 on ion channels in human chronic atrial fibrillation,” Br. J. Pharmacol. 154, 1619–1630 (2008). 10.1038/bjp.2008.209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Cummins M. A., Dalal P. J., Bugana M., Severi S., and Sobie E. A., “ Comprehensive analyses of ventricular myocyte models identify targets exhibiting favorable rate dependence,” PLoS Comput. Biol. 10, e1003543 (2014). 10.1371/journal.pcbi.1003543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Decher N., Kumar P., Gonzalez T., Pirard B., and Sanguinetti M. C., “ Binding site of a novel Kv1.5 blocker: A ‘foot in the door’ against atrial fibrillation,” Mol. Pharmacol. 70, 1204–1211 (2006). 10.1124/mol.106.026203 [DOI] [PubMed] [Google Scholar]
- 15. Devenyi R. A. and Sobie E. A., “ There and back again: Iterating between population-based modeling and experiments reveals surprising regulation of calcium transients in rat cardiac myocytes,” J. Mol. Cell Cardiol. 96, 38–48 (2016). 10.1016/j.yjmcc.2015.07.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Dobrev D. and Ravens U., “ Remodeling of cardiomyocyte ion channels in human atrial fibrillation,” Basic Res. Cardiol. 98, 137–148 (2003). 10.1007/s00395-003-0409-8 [DOI] [PubMed] [Google Scholar]
- 17. Fedida D., Wible B., Wang Z., Fermini B., Faust F., Nattel S., and Brown A. M., “ Identity of a novel delayed rectifier current from human heart with a cloned K+ channel current,” Circ. Res. 73, 210–216 (1993). 10.1161/01.RES.73.1.210 [DOI] [PubMed] [Google Scholar]
- 18. Feng J., Xu D., Wang Z., and Nattel S., “ Ultrarapid delayed rectifier current inactivation in human atrial myocytes: Properties and consequences,” Am. J. Physiol. 275, H1717–H1725 (1998). [DOI] [PubMed] [Google Scholar]
- 19. Ford J., Milnes J., El Haou S., Wettwer E., Loose S., Matschke K., Tyl B., Round P., and Ravens U., “ The positive frequency-dependent electrophysiological effects of the IKur inhibitor XEN-D0103 are desirable for the treatment of atrial fibrillation,” Heart Rhythm 13, 555–564 (2016). 10.1016/j.hrthm.2015.10.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Gluais P., Bastide M., Grandmougin D., Fayad G., and Adamantidis M., “ Risperidone reduces K+ currents in human atrial myocytes and prolongs repolarization in human myocardium,” Eur. J. Pharmacol. 497, 215–222 (2004). 10.1016/j.ejphar.2004.06.046 [DOI] [PubMed] [Google Scholar]
- 21. Gogelein H., Brendel J., Steinmeyer K., Strubing C., Picard N., Rampe D., Kopp K., Busch A. E., and Bleich M., “ Effects of the atrial antiarrhythmic drug AVE0118 on cardiac ion channels,” Naunyn-Schmiedeberg's Arch. Pharmacol. 370, 183–192 (2004). 10.1007/s00210-004-0957-y [DOI] [PubMed] [Google Scholar]
- 22. Grandi E. and Maleckar M. M., “ Anti-arrhythmic strategies for atrial fibrillation: The role of computational modeling in discovery, development, and optimization,” Pharmacol. Ther. 168, 126–142 (2016). 10.1016/j.pharmthera.2016.09.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Grandi E., Pandit S. V., Voigt N., Workman A. J., Dobrev D., Jalife J., and Bers D. M., “ Human atrial action potential and Ca2+ model: Sinus rhythm and chronic atrial fibrillation,” Circ. Res. 109, 1055–1066 (2011). 10.1161/CIRCRESAHA.111.253955 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Lagrutta A., Wang J., Fermini B., and Salata J. J., “ Novel, potent inhibitors of human Kv1.5 K+ channels and ultrarapidly activating delayed rectifier potassium current,” J. Pharmacol. Exp. Ther. 317, 1054–1063 (2006). 10.1124/jpet.106.101162 [DOI] [PubMed] [Google Scholar]
- 25. Lancaster M. C. and Sobie E. A., “ Improved prediction of drug-induced Torsades de Pointes through simulations of dynamics and machine learning algorithms,” Clin. Pharmacol. Ther. 100, 371–379 (2016). 10.1002/cpt.367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Lee W., Mann S. A., Windley M. J., Imtiaz M. S., Vandenberg J. I., and Hill A. P., “ In silico assessment of kinetics and state dependent binding properties of drugs causing acquired LQTS,” Prog. Biophys. Mol. Biol. 120, 89–99 (2016). 10.1016/j.pbiomolbio.2015.12.005 [DOI] [PubMed] [Google Scholar]
- 27. Lee Y. S., Liu O. Z., Hwang H. S., Knollmann B. C., and Sobie E. A., “ Parameter sensitivity analysis of stochastic models provides insights into cardiac calcium sparks,” Biophys. J. 104, 1142–1150 (2013). 10.1016/j.bpj.2012.12.055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Li Z., Dutta S., Sheng J., Tran P. N., Wu W., Chang K., Mdluli T., Strauss D. G., and Colatsky T., “ Improving the in silico assessment of proarrhythmia risk by combining hERG (Human Ether-a-go-go-Related Gene) channel-drug binding kinetics and multichannel pharmacology,” Circ. Arrhythmia Electrophysiol. 10, e004628 (2017). 10.1161/CIRCEP.116.004628 [DOI] [PubMed] [Google Scholar]
- 29. Loose S., Mueller J., Wettwer E., Knaut M., Ford J., Milnes J., and Ravens U., “ Effects of IKur blocker MK-0448 on human right atrial action potentials from patients in sinus rhythm and in permanent atrial fibrillation,” Front. Pharmacol. 5, 26 (2014). 10.3389/fphar.2014.00026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Madhvani R. V., Angelini M., Xie Y. F., Pantazis A., Suriany S., Borgstrom N. P., Garfinkel A., Qu Z. L., Weiss J. N., and Olcese R., “ Targeting the late component of the cardiac L-type Ca2+ current to suppress early afterdepolarizations,” J. Gen. Physiol. 145, 395–404 (2015). 10.1085/jgp.201411288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Mahajan A., Sato D., Shiferaw Y., Baher A., Xie L. H., Peralta R., Olcese R., Garfinkel A., Qu Z., and Weiss J. N., “ Modifying L-type calcium current kinetics: Consequences for cardiac excitation and arrhythmia dynamics,” Biophys. J. 94, 411–423 (2008). 10.1529/biophysj.106.98590 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Matsubara H., Liman E. R., Hess P., and Koren G., “ Pretranslational mechanisms determine the type of potassium channels expressed in the rat skeletal and cardiac muscles,” J. Biol. Chem. 266, 13324–13328 (1991). [PubMed] [Google Scholar]
- 33. Moreno J. D., Zhu Z. I., Yang P. C., Bankston J. R., Jeng M. T., Kang C., Wang L., Bayer J. D., Christini D. J., Trayanova N. A., Ripplinger C. M., Kass R. S., and Clancy C. E., “ A computational model to predict the effects of class I anti-arrhythmic drugs on ventricular rhythms,” Sci. Transl. Med. 3, 98ra83 (2011). 10.1126/scitranslmed.3002588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Morotti S. and Grandi E., “ Logistic regression analysis of populations of electrophysiological models to assess proarrythmic risk,” MethodsX 4, 25–34 (2017). 10.1016/j.mex.2016.12.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Morotti S., Koivumäki J. T., Maleckar M. M., Chiamvimonvat N., and Grandi E., “ Small-conductance Ca2+-activated K+ current in atrial fibrillation: Both friend and foe,” Biophys. J. 110, 274a (2016). 10.1016/j.bpj.2015.11.1487 [DOI] [Google Scholar]
- 36. Morotti S., McCulloch A. D., Bers D. M., Edwards A. G., and Grandi E., “ Atrial-selective targeting of arrhythmogenic phase-3 early afterdepolarizations in human myocytes,” J. Mol. Cell Cardiol. 96, 63–71 (2016). 10.1016/j.yjmcc.2015.07.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Ravens U., Poulet C., Wettwer E., and Knaut M., “ Atrial selectivity of antiarrhythmic drugs,” J. Physiol. 591, 4087–4097 (2013). 10.1113/jphysiol.2013.256115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Ravens U. and Wettwer E., “ Ultra-rapid delayed rectifier channels: Molecular basis and therapeutic implications,” Cardiovasc. Res. 89, 776–785 (2011). 10.1093/cvr/cvq398 [DOI] [PubMed] [Google Scholar]
- 39. Rich T. C., Yeola S. W., Tamkun M. M., and Snyders D. J., “ Mutations throughout the S6 region of the hKv1.5 channel alter the stability of the activation gate,” Am. J. Physiol. Cell Physiol. 282, C161–C171 (2002). 10.1152/ajpcell.00232.2001 [DOI] [PubMed] [Google Scholar]
- 40. Romero L., Trenor B., Yang P. C., Saiz J., and Clancy C. E., “ In silico screening of the impact of hERG channel kinetic abnormalities on channel block and susceptibility to acquired long QT syndrome,” J. Mol. Cell Cardiol. 87, 271–282 (2015). 10.1016/j.yjmcc.2015.08.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Sanchez C., Corrias A., Bueno-Orovio A., Davies M., Swinton J., Jacobson I., Laguna P., Pueyo E., and Rodriguez B., “ The Na+/K+ pump is an important modulator of refractoriness and rotor dynamics in human atrial tissue,” Am. J. Physiol. - Heart Circ. Physiol. 302, H1146–H1159 (2012). 10.1152/ajpheart.00668.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Schotten U., de Haan S., Verheule S., Harks E. G., Frechen D., Bodewig E., Greiser M., Ram R., Maessen J., Kelm M., Allessie M., and Van Wagoner D. R., “ Blockade of atrial-specific K+-currents increases atrial but not ventricular contractility by enhancing reverse mode Na+/Ca2+-exchange,” Cardiovasc. Res. 73, 37–47 (2007). 10.1016/j.cardiores.2006.11.024 [DOI] [PubMed] [Google Scholar]
- 43. Shibata E. F., Drury T., Refsum H., Aldrete V., and Giles W., “ Contributions of a transient outward current to repolarization in human atrium,” Am. J. Physiol. 257, H1773–H1781 (1989). [DOI] [PubMed] [Google Scholar]
- 44. Shinagawa K., Mitamura H., Takeshita A., Sato T., Kanki H., Takatsuki S., and Ogawa S., “ Determination of refractory periods and conduction velocity during atrial fibrillation using atrial capture in dogs: Direct assessment of the wavelength and its modulation by a sodium channel blocker, pilsicainide,” J. Am. Coll. Cardiol. 35, 246–253 (2000). 10.1016/S0735-1097(99)00488-X [DOI] [PubMed] [Google Scholar]
- 45. Sobie E. A., “ Parameter sensitivity analysis in electrophysiological models using multivariable regression,” Biophys. J. 96, 1264–1274 (2009). 10.1016/j.bpj.2008.10.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Swanson R., Marshall J., Smith J. S., Williams J. B., Boyle M. B., Folander K., Luneau C. J., Antanavage J., Oliva C., Buhrow S. A. et al. , “ Cloning and expression of cDNA and genomic clones encoding three delayed rectifier potassium channels in rat brain,” Neuron 4, 929–939 (1990). 10.1016/0896-6273(90)90146-7 [DOI] [PubMed] [Google Scholar]
- 47. Tessier S., Karczewski P., Krause E. G., Pansard Y., Acar C., Lang-Lazdunski M., Mercadier J. J., and Hatem S. N., “ Regulation of the transient outward K+ current by Ca2+/calmodulin-dependent protein kinases II in human atrial myocytes,” Circ. Res. 85, 810–819 (1999). 10.1161/01.RES.85.9.810 [DOI] [PubMed] [Google Scholar]
- 48. Tsujimae K., Murakami S., and Kurachi Y., “ In silico study on the effects of IKur block kinetics on prolongation of human action potential after atrial fibrillation-induced electrical remodeling,” Am. J. Physiol. Heart Circ. Physiol. 294, H793–H800 (2008). 10.1152/ajpheart.01229.2007 [DOI] [PubMed] [Google Scholar]
- 49. Van Wagoner D. R. and Nerbonne J. M., “ Molecular basis of electrical remodeling in atrial fibrillation,” J. Mol. Cell Cardiol. 32, 1101–1117 (2000). 10.1006/jmcc.2000.1147 [DOI] [PubMed] [Google Scholar]
- 50. Wang D., Shryock J. C., and Belardinelli L., “ Cellular basis for the negative dromotropic effect of adenosine on rabbit single atrioventricular nodal cells,” Circ. Res. 78, 697–706 (1996). 10.1161/01.RES.78.4.697 [DOI] [PubMed] [Google Scholar]
- 51. Wang J., Juhaszova M., Rubin L. J., and Yuan X. J., “ Hypoxia inhibits gene expression of voltage-gated K+ channel alpha subunits in pulmonary artery smooth muscle cells,” J. Clin. Invest. 100, 2347–2353 (1997). 10.1172/JCI119774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Wang Z., Fermini B., and Nattel S., “ Sustained depolarization-induced outward current in human atrial myocytes. Evidence for a novel delayed rectifier K+ current similar to Kv1.5 cloned channel currents,” Circ. Res. 73, 1061–1076 (1993). 10.1161/01.RES.73.6.1061 [DOI] [PubMed] [Google Scholar]
- 53. Wettwer E., Hala O., Christ T., Heubach J. F., Dobrev D., Knaut M., Varro A., and Ravens U., “ Role of IKur in controlling action potential shape and contractility in the human atrium: Influence of chronic atrial fibrillation,” Circulation 110, 2299–2306 (2004). 10.1161/01.CIR.0000145155.60288.71 [DOI] [PubMed] [Google Scholar]
- 54. Zhao Q., Tang Y., Okello E., Wang X., and Huang C., “ Changes in atrial effective refractory period and IKACh after vagal stimulation plus rapid pacing in the pulmonary vein,” Rev. Esp. Cardiol. 62, 742–749 (2009). 10.1016/S0300-8932(09)71687-2 [DOI] [PubMed] [Google Scholar]
- 55. Zhou Q., Bett G. C., and Rasmusson R. L., “ Markov models of use-dependence and reverse use-dependence during the mouse cardiac action potential,” PLoS One 7, e42295 (2012). 10.1371/journal.pone.0042295 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for IKur model equations and supplementary figures.