Deriving depth‐dependent light escape efficiency and optical Swank factor from measured pulse height spectra of scintillators

Abstract

Purpose

Pulse height spectroscopy has been used by investigators to deduce the imaging properties of scintillators. Pulse height spectra (PHS) are used to compute the Swank factor, which describes the variation in scintillator light output per x‐ray interaction. The spread in PHS measured below the K‐edge is related to the optical component of the Swank factor, i.e., variations in light escape efficiency from different depths of x‐ray interaction in the scintillator, denoted $\overline{\mathit{\epsilon }}(z)$. Optimizing scintillators for medical imaging applications requires understanding of these optical properties, as they determine tradeoffs between parameters such as x‐ray absorption, light yield, and spatial resolution. This work develops a model for PHS acquisition such that the effect of measurement uncertainty can be removed. This method allows $\overline{\mathit{\epsilon }}(z)$ to be quantified on an absolute scale and permits more accurate estimation of the optical Swank factor of scintillators.

Methods

The pulse height spectroscopy acquisition chain was modeled as a linear system of stochastic gain stages. Analytical expressions were derived for signal and noise propagation through the PHS chain, accounting for deterministic and stochastic aspects of x‐ray absorption, scintillation, and light detection with a photomultiplier tube. The derived expressions were used to calculate PHS of thallium‐doped cesium iodide (CsI) scintillators using parameters that were measured, calculated, or known from literature. PHS were measured at 25 and 32 keV of CsI samples designed with an optically reflective or absorptive backing, with or without a fiber‐optic faceplate (FOP), and with thicknesses ranging from 150–1000 μm. Measured PHS were compared with calculated PHS, then light escape model parameters were varied until measured and modeled results reached agreement. Resulting estimates of $\overline{\mathit{\epsilon }}(z)$ were used to calculate each scintillator's optical Swank factor.

Results

For scintillators of the same optical design, only minor differences in light escape efficiency were observed between samples with different thickness. As thickness increased, escape efficiency decreased by up to 20% for interactions furthest away from light collection. Optical design (i.e., backing and FOP) predominantly affected the magnitude and relative variation in $\overline{\mathit{\epsilon }}(z)$. Depending on interaction depth and scintillator thickness, samples with an absorptive backing and FOP were estimated to yield 4.1–13.4 photons/keV. Samples with a reflective backing and FOP yielded 10.4–18.4 keV⁻¹, while those with a reflective backing and no FOP yielded 29.5–52.0 keV⁻¹. Optical Swank factors were approximately 0.9 and near‐unity in samples featuring an absorptive or reflective backing, respectively.

Conclusions

This work uses a modeling approach to remove the noise introduced by the measurement apparatus from measured PHS. This method allows absolute quantification of $\overline{\mathit{\epsilon }}(z)$ and more accurate estimation of the optical Swank factor of scintillators. The method was applied to CsI scintillators with different thickness and optical design, and determined that optical design more strongly affects $\overline{\mathit{\epsilon }}(z)$ and Swank factor than differences in CsI thickness. Despite large variations in $\overline{\mathit{\epsilon }}(z)$ between optical designs, the Swank factor of all evaluated samples is above 0.9. Information provided by this methodology can help validate Monte Carlo simulations of structured CsI and optimize scintillator design for x‐ray imaging applications.

1. Introduction

Flat panel imagers (FPIs) are widely used in medical imaging systems, and are generally classified as either indirect or direct.¹ Indirect FPIs use scintillators to convert energy of x‐ray interactions into bursts of optical light, and collect this light to form images using a 2D array of a‐Si:H photodiodes and thin‐film transistors. Direct FPIs replace the scintillator and photodiode components with a biased x‐ray photoconductor, which directly converts the incident x‐rays into a charge image for readout.

Swank^{2, 3} showed that fluctuations in the conversion gain of x‐ray converters (i.e., scintillators or photoconductors) adds to the noise of such imaging systems. This phenomenon is studied using pulse height spectroscopy,⁴ which characterizes the probability distribution of the number of quanta output by the converter per x‐ray interaction. Pulse height spectroscopy has been used by investigators to evaluate x‐ray conversion in x‐ray image intensifiers,^{2, 5} scintillators used in screen‐film,^{6, 7, 8, 9} computed radiography¹⁰ and digital radiography systems,^{11, 12, 13, 14, 15, 16} photoconductors used in direct FPIs such as a‐Se,^{17, 18, 19} and photon counting detectors for mammography^{20, 21} and computed tomography.^{22, 23}

The spread in a pulse height spectrum is quantified by the Swank factor A _s , which plays a large role in determining the converter's ability to efficiently transfer large‐area information. This aspect of performance is represented by the zero‐frequency detective quantum efficiency DQE(0). In an energy‐integrating detector, DQE(0) is calculated by the product of the converter's x‐ray quantum efficiency A _Q and A _s ^{2, 3}:

$$DQE(0)=A_Q{A}_s.$$ (1)

The Swank factor of a scintillator may be separated into an optical Swank factor (I _OPD ) and x‐ray Swank factor (I _AED ), according to^{2, 3}:

$$A_s=I_{OPD}{I}_{AED}$$ (2)

The x‐ray Swank factor I _AED describes variations in the energy deposited in the scintillator per x‐ray interaction. These variations not only affect DQE(0) of energy‐integrating detectors, but are also an important consideration in the precision of energy measurements in single‐photon counting detectors.²⁴ Factors that degrade I _AED include spread in the incident x‐ray energy distribution and the escape of characteristic fluorescence or Compton scattered photons from the scintillator.^{3, 25} Hajdok et al.²⁵ and more recently Yun et al.²⁶ have described comprehensive analytical models which consider these effects and allow calculation of I _AED in x‐ray converters.

Below the K‐edge of scintillators typically used in indirect FPIs (e.g., CsI:Tl), x‐ray interaction is dominated by the photoelectric effect.²⁷ For monoenergetic x‐rays below the K‐edge, I _AED approaches unity and A _s is determined solely by I _OPD , which depends on random variations in x‐ray conversion gain and the inherent optical properties of the scintillator. Consequently, pulse height spectra (PHS) measured under these conditions may be interpreted to assess scintillator optical properties, such as how efficiently light escapes from different depths of x‐ray interaction.¹² The light escape properties of a scintillator may be influenced by optical design factors such as an optically absorptive or reflective backing to improve different aspects of performance (e.g., high spatial resolution or high light output, respectively).²⁸ Understanding how design factors influence scintillator optical properties is crucial for indirect detector optimization. Drangova and Rowlands⁸ first demonstrated this by showing how reflective and absorptive backings in various powder phosphors change PHS shape and affect the Swank factor and DQE(0).

Previous work by Lubinsky et al.¹² showed how PHS can be analyzed to estimate the depth dependence of relative light escape from a scintillator. Their approach has improved the understanding of the Swank factor and optical transport within scintillators, although it has two inherent limitations: (a) it is susceptible to errors from uncertainty in PHS measurement and; (b) no information on the absolute light escape efficiency is determined. Other investigators, such as Badano et al.,^{14, 29} Freed et al.^{30, 31} and Sharma et al.³² have used Monte Carlo simulations to investigate scintillator imaging properties, using experimental data such as Swank factor to validate simulation parameters. Such simulations are advantageous for estimating scintillator properties that are not readily studied experimentally, such as depth‐dependent blur,³³ but rely heavily on measured data for validation. Accurate estimation of depth‐dependent light escape efficiency and Swank factor directly from measurements of PHS will be useful for further validation of Monte Carlo simulations of scintillator optics, though to the best of our knowledge such methods do not currently exist. A more complete understanding of light propagation in scintillators will facilitate their optimization for medical imaging applications, as these properties affect tradeoffs between parameters such as x‐ray absorption, light yield, and spatial resolution.

In the present work, we develop a method to remove the effect of noise introduced by the PHS measurement apparatus and derive the absolute depth‐dependent light escape efficiency of a scintillator, which enables more accurate estimation of its optical Swank factor. In our approach, the PHS are modeled by accounting for the stochastic gain processes of x‐ray absorption, scintillation and optical detection with a photomultiplier tube (PMT). This is achieved using analytical expressions for signal and noise propagation through each stage of the pulse height spectroscopy chain. Measured PHS of various thallium‐doped CsI scintillators, which we hereafter refer to as CsI, are compared with modeled PHS to deduce their depth‐dependent light escape efficiency. This analysis is used to investigate how scintillator thickness and optical design affect light escape efficiency and the Swank factor of CsI scintillators used in flat panel detectors.

2. Materials and methods

2.A. Analytical model of the noise‐free pulse height spectrum: $\mathit{\phi }({\overline{N}}_{phe})$

An analytical expression for PHS was derived based on x‐ray absorption, scintillation and light escape processes as a function of x‐ray interaction depth. Here, these processes are treated as deterministic, that is, noiseless, however we extend our analysis in Section 2.B.. to determine how statistical variations in these processes also affect PHS.

We consider the case where x‐rays are monoenergetic and below the scintillator K‐edge. We assume that x‐ray attenuation in the scintillator is solely due to photoelectric interactions, which is a reasonable approximation in high‐Z scintillators (e.g., CsI). For example, Compton scatter events occur in less than 1.5% of x‐ray interactions in CsI below the K‐edge of I.²⁷ Coherent scatter also occurs in less than 10% of x‐ray interactions at these energies, however, these events do not deposit energy in the scintillator and thus do not contribute to PHS; therefore, they are ignored.

The detector geometry used in our analysis, shown in Fig. 1, matches the typical geometry of experimental measurements, where x‐rays are orthogonally incident to a scintillator with thickness L.

Figure 1.

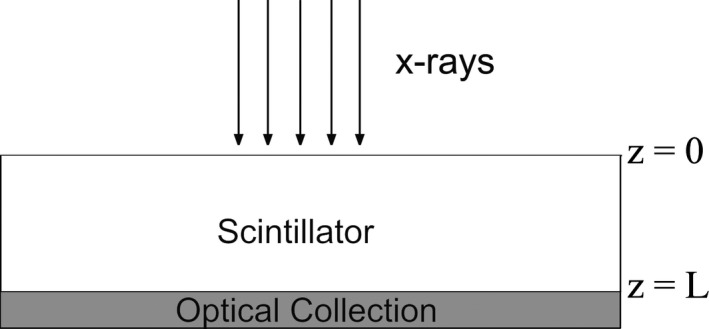
Depth within the scintillator is defined by z = 0 at the x‐ray entrance and z = L at the exit plane toward optical collection. Ideal (100%) optical coupling efficiency is assumed at the interface of the scintillator and optical sensor.

2.A.1. X‐ray absorption and conversion gain

For N ₀ monoenergetic x‐rays incident on a scintillator with photoelectric linear attenuation coefficient μ, the number absorbed from depth 0 to z is:

$$N_A(z)=N_0-N_0{e}^{-\mathit{\mu }z},$$ (3)

and the total number of absorption events is:

$$N_T=N_A(L).$$ (4)

Each interaction results in scintillation with a conversion gain of $\overline{g}$, which is determined by the absorbed energy E and the energy required to produce one scintillation photon W:

$$\overline{g}=\frac{E}{W}.$$ (5)

We assume E is equal to the incident x‐ray energy, which is reasonable in the case we have considered here where: (a) x‐ray energy is below the scintillator K‐edge, such that there are no variations in energy absorption due to the generation and escape of K‐fluorescence and; (b) variations in E due to Compton scatter are improbable and can be neglected.²⁷ More detailed models^{25, 26} should be considered in cases where characteristic fluorescence or Compton interactions cannot be avoided or neglected, e.g., with low‐Z scintillators.⁴

2.A.2. Optical photon escape

A fraction of the optical photons generated by an absorbed x‐ray escape the scintillator with probability $\overline{\mathit{\epsilon }}$, which depends on the depth of interaction z. For consistency with previous work, we refer to this fraction as the escape efficiency^{12, 34} $\overline{\mathit{\epsilon }}(z)$. Others have referred to this quantity as the optical escape fraction^{15, 29} and optical collection efficiency.³¹ Escape efficiency is expected to increase with depth, e.g., interactions closer to optical collection will have higher escape efficiency than those occurring further away. The number of photons that escape the scintillator per x‐ray interaction, ${\overline{N}}_{phe}$, is the product of the conversion gain $\overline{g}$ and the depth‐dependent escape efficiency:

$${\overline{N}}_{phe}(z)=\overline{g}\overline{\mathit{\epsilon }}(z).$$ (6)

As illustrated in Fig. 2(a), light escape from different depths of the scintillator is weighted by non‐uniform x‐ray absorption, which results in a probability density function of ${\overline{N}}_{phe}$ represented generically in Fig. 2(b). The following analysis was used to derive an expression for this function, denoted as $\mathit{\phi }({\overline{N}}_{phe})$.

Figure 2.

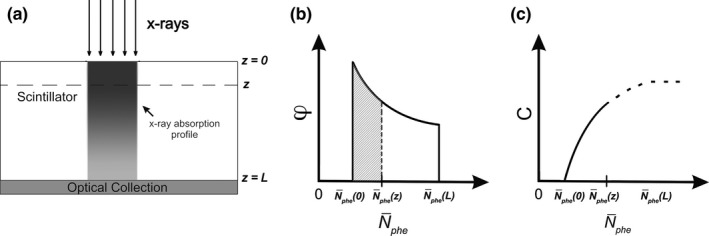
(a) X‐ray attenuation is exponential within the scintillator, with absorption weighted toward the entrance plane z = 0. (b) Non‐uniform x‐ray absorption and light escape efficiency with depth result in a probability density function φ of the light output per x‐ray interaction. (c) Integrating φ with respect to ${\overline{N}}_{phe}$ [bounds represented by the shaded region in (b)] computes the cumulative distribution function $C({\overline{N}}_{phe})$, which may be related to the total x‐ray absorption from depth 0 to z.

2.A.3. Derivation of $\mathit{\phi }({\overline{N}}_{phe})$

The PHS experiment consists of a series of N _T observations of the number n escaping photons per absorption event. We denote the probability $P\left\{n\le {\overline{N}}_{phe}\left(z\right)\right\}$ by the cumulative distribution function $C\left[{\overline{N}}_{phe}\right]$ which is represented generically in Fig. 2(c). The probability density function $\mathit{\phi }\left({\overline{N}}_{phe}\right)$ is related to this by:

$$C\left[{\overline{N}}_{phe}\left(z\right)\right]={\int }_{{\overline{N}}_{phe}(0)}^{{\overline{N}}_{phe}(z)}\mathit{\phi }\left[{\overline{N}}_{phe}\left(z\right)\right]d{\overline{N}}_{phe}.$$ (7)

The product of the total number of observed events and the probability $P\left\{n\le {\overline{N}}_{phe}\left(z\right)\right\}$ is equal to the number of absorption events in the scintillator from depth 0 to z:

$$N_{T}C\left[{\overline{N}}_{phe}(z)\right]=N_A(z)=N_0-N_0{e}^{-\mathit{\mu }z}.$$ (8)

Applying the fundamental theorem of calculus to Eq. (7), we may write:

$$\mathit{\phi }[{\overline{N}}_{phe}(z)]=\frac{dC}{d{\overline{N}}_{phe}}.$$ (9)

Noting that ${\overline{N}}_{phe}$ is a function of z, we apply the chain rule to derive:

$$\frac{dC}{dz}=\frac{dC}{d{\overline{N}}_{phe}}\frac{d{\overline{N}}_{phe}}{dz}.$$ (10)

Rearranging Eq. (10) and substituting into Eq. (9) yields:

$$\mathit{\phi }[{\overline{N}}_{phe}(z)]=\frac{\frac{dC}{dz}}{\frac{d{\overline{N}}_{phe}}{dz}}.$$ (11)

The numerator and denominator on the right side of Eq. (11) are determined by recalling Eqs. (8) and (6), respectively:

$$\mathit{\phi }\left[{\overline{N}}_{phe}\left(z\right)\right]=\frac{\frac{N_0}{N_T}\mathit{\mu }{e}^{-\mathit{\mu }z}}{\overline{g}\frac{d\overline{\mathit{\epsilon }}}{dz}}.$$ (12)

Note that φ describes photons⁻¹, which is unitless. Eq. (12) can be written in terms of ${\overline{N}}_{phe}$ in cases where the relation (6) between ${\overline{N}}_{phe}$ and z is invertible, using:

$$z={\overline{\mathit{\epsilon }}}^{-1}\left(\frac{{\overline{N}}_{phe}}{\overline{g}}\right).$$ (13)

2.A.4. Calculating PHS from $\mathit{\phi }({\overline{N}}_{phe})$ : linear $\overline{\mathit{\epsilon }}\text{(z)}$

Equation (12) can be used to calculate PHS when a particular form of $\overline{\mathit{\epsilon }}(z)$ is assumed. As an example, we consider the case where $\overline{\mathit{\epsilon }}$ is linear with depth:

$${\overline{N}}_{phe}(z)=\overline{g}\left[\overline{\mathit{\epsilon }}\left(0\right)+\frac{\overline{\mathit{\epsilon }}\left(L\right)-\overline{\mathit{\epsilon }}\left(0\right)}{L}z\right],$$ (14)

although cases of non‐linear $\overline{\mathit{\epsilon }}(z)$ may also be treated using the same approach. Inverting Eq. (14) yields:

$$z=\frac{{\overline{N}}_{phe}-{\overline{N}}_{phe}(0)}{{\overline{N}}_{phe}(L)-{\overline{N}}_{phe}(0)}L.$$ (15)

Differentiating $\overline{\mathit{\epsilon }}(z)$ with respect to z results in:

$$\frac{d\overline{\mathit{\epsilon }}}{dz}=\frac{\overline{\mathit{\epsilon }}(L)-\overline{\mathit{\epsilon }}(0)}{L}.$$ (16)

Substituting Eqs. (15) and (16) into Eq. (12) yields the final expression:

$$\mathit{\phi }\left[{\overline{N}}_{phe}\right]=\frac{N_0\mathit{\mu }L}{N_T\left[{\overline{N}}_{phe}(L)-{\overline{N}}_{phe}\left(0\right)\right]}{e}^{-\mathit{\mu }L\left[\frac{{\overline{N}}_{phe}-{\overline{N}}_{phe}\left(0\right)}{{\overline{N}}_{phe}\left(L\right)-{\overline{N}}_{phe}\left(0\right)}\right]}.$$ (17)

This analytical expression can be used to calculate the noise‐free (i.e., no quantum or electronic noise) PHS of a scintillator as a function of ${\overline{N}}_{phe}$, for the case of linear $\overline{\mathit{\epsilon }}(z)$. The minimum number of photons escaping the scintillator is ${\overline{N}}_{phe}(0)=\overline{g}\overline{\mathit{\epsilon }}(0)$, and the maximum number ${\overline{N}}_{phe}(L)=\overline{g}\overline{\mathit{\epsilon }}(L)$; therefore, $\mathit{\phi }({\overline{N}}_{phe})$ is given by Eq. (17) over the range $\left[{\overline{N}}_{phe}(0),{\overline{N}}_{phe}(L)\right]$, and is zero elsewhere. In this example, Eq. (17) shows that $\overline{\mathit{\epsilon }}(0)$ and $\overline{\mathit{\epsilon }}(L)$ are sufficient to calculate φ if $\overline{g}$, μ and L are known.

Calculations of φ may be compared to measured PHS by noting that experimental observations sort φ into bins of width ΔN, which is a measurement system parameter expressed as a number of photons. The bounds of the j‐th bin of the PHS are [jΔN, (j+1)ΔN] _, where j is a non‐negative integer and the event count in the bin is:

$$Counts(j)=N_T{\int }_{j\mathrm{\Delta }N}^{(j+1)\mathrm{\Delta }N}\mathit{\phi }({\overline{N}}_{phe})d{\overline{N}}_{phe}.$$ (18)

2.B. Modeling measured PHS with noise: linear system analysis

Cascaded linear system analysis was used to determine how $\mathit{\phi }({\overline{N}}_{phe})$ is degraded by stochastic effects in the PHS measurement chain shown in Fig. 3. The stages of x‐ray conversion gain, light escape, detection by a PMT and dynode amplification were modeled as a cascade of stochastic amplification processes.

Figure 3.

The pulse height spectroscopy chain begins with absorption of an x‐ray at a given depth z. This primary quantum is amplified by the scintillator conversion gain, and a fraction of the generated optical photons are able to escape. A portion of the escaped photons interact with the PMT photocathode, generating photoelectrons that undergo dynode amplification before pulse height analysis.

The signal and noise propagation through each stage was determined using^{35, 36}:

$${\overline{N}}_{out}=\overline{m}{\overline{N}}_{in}$$ (19)

$${\mathit{\sigma }}_{out}^2={\overline{m}}^2{\mathit{\sigma }}_{in}^2+{\mathit{\sigma }}_m^2{\overline{N}}_{in}$$ (20)

where ${\overline{N}}_{in}$ and ${\overline{N}}_{out}$ represent the mean numbers of input and output quanta, $\overline{m}$ and ${\mathit{\sigma }}_m^2$ denote the mean and variance of the stochastic gain, and ${\mathit{\sigma }}_{in}^2$ and ${\mathit{\sigma }}_{out}^2$ are the variances in N _in and N _out , respectively. Detailed expressions for the mean and variance in the number of quanta at each stage of Fig. 3 are given in Appendix A. Briefly, the total variance in measurements of ${\overline{N}}_{phe}$, which includes noise due to the measurement apparatus, was derived to be:

$${\mathit{\sigma }}_{tot}^2\left({\overline{N}}_{phe}\right)=\frac{{\overline{N}}_{phe}\left(\frac{\overline{\mathit{\delta }}}{\overline{\mathit{\delta }}-1}\right)}{{\overline{\mathit{\eta }}}_{eff}},$$ (21)

where $\overline{\mathit{\delta }}$ denotes the average gain of each PMT dynode and ${\overline{\mathit{\eta }}}_{eff}$ represents the mean quantum efficiency of the PMT to scintillation light, defined by:

$${\overline{\mathit{\eta }}}_{eff}=\frac{{\int }_0^{\infty }I(\mathit{\lambda })\mathit{\eta }(\mathit{\lambda })d\mathit{\lambda }}{{\int }_0^{\infty }I(\mathit{\lambda })d\mathit{\lambda }},$$ (22)

where I(λ) represents the emission spectrum of the scintillator and η(λ) is the spectral response of the photocathode.

Figure 4 illustrates conceptually how the measurement chain degrades the PHS. Shown in Fig. 4(a) is a representation of a noise‐free PHS, which is determined by calculating and sorting $\mathit{\phi }({\overline{N}}_{phe})$ into bins using Eqs. (17) and (1), respectively. In Fig. 4(b), the total stochastic noise in x‐ray conversion gain, light escape, PMT detection and dynode amplification is introduced to degrade the PHS. This is calculated using Gaussian distributions centered at each ${\overline{N}}_{phe}$ bin, with variances determined by Eq. (4). The contributions of these distributions to each bin are summed, as shown in Fig. 4(c), to model the measured PHS.

Figure 4.

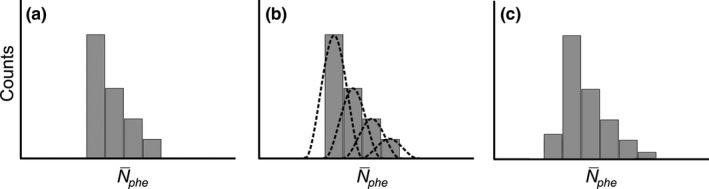
(a) $\mathit{\phi }({\overline{N}}_{phe})$ is calculated based on x‐ray energy, scintillator thickness, conversion gain, and an assumption of $\overline{\mathit{\epsilon }}(z)$, and is sorted into bins of width ΔN defined by the experimental apparatus. (b) The total variance in measurements of ${\overline{N}}_{phe}$ is calculated according to Eq. (4) and used to calculate normal distributions centered at each bin of $\mathit{\phi }({\overline{N}}_{phe})$. (c) The calculated distributions are then summed to model measured PHS.

2.C. PHS measurement and calibration

Commercial CsI scintillator samples were obtained from Hamamatsu Photonics K.K, with design types FOS HR, FOS HL and GPXS. FOS designs have CsI deposited on a fiber‐optic faceplate (FOP) and are coated with an optically absorptive or reflective backing in HR or HL type, respectively.³⁷ The FOP is always in contact with the optical sensor, as shown in Fig. 5(a). In the GPXS structure, CsI is deposited on a highly reflective aluminum substrate, as shown in Fig. 5(b), with a transparent protective coating on the surface to be coupled to the optical sensor. The nominal thickness of the FOS and GPXS samples ranged from 150 to 1000 μm.

Figure 5.

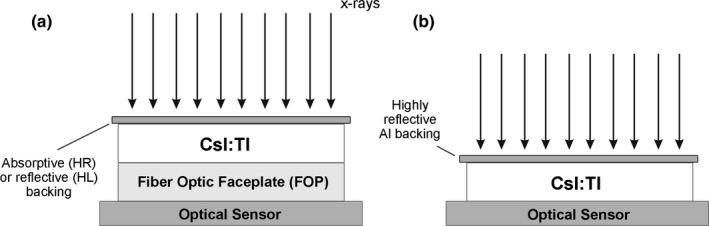
(a) In the FOS design, CsI is deposited on an FOP, which is in contact with the optical sensor. FOS designs feature an optically absorbing backing in HR type, and a reflective backing in HL type. (b) GPXS type samples feature CsI deposited on a reflective aluminum backing, and the sensor‐coupled surface is coated with a transparent protective film. Samples of FOS HR, FOS HL, and GPXS with 150 #bib200 #bib600, and 1000 μm thickness were studied.

PHS were measured at energies below the K‐edges of Cs and I using the apparatus sketched in Fig. 6, with acquisition parameters reported in Table 1. Monoenergetic x‐rays at 25.2 keV and 32.1 keV were generated via K _α fluorescence of tin (Sn) and barium (Ba) metallic targets, with K _β emissions of the targets filtered by silver (Ag) and I, respectively. The monochromatic x‐rays were collimated using a lead pinhole to expose the samples, which were coupled to a PMT (R1450, Hamamatsu Photonics K.K.) for light collection. The PMT output was fed to a charge amplifier (A1424, CAEN S.p.A.) with a decay time constant of 50 μs. The output of the charge amplifier was fed to a fast digitizer (V1724, CAEN S.p.A.) for pulse height analysis using a digital trapezoid shaper with 10 μs rise time and 16 μs peaking time.³⁸ Shaper rise time was made substantially longer than the temporal decay time constants of CsI³⁹ (primary decays τ ₁ = 0.68 μs #bib63.7% and τ ₂ = 3.34 μs #bib36.1%) to maximize the collection of light photons generated from each x‐ray interaction. X‐ray source intensity was limited (~1000 counts/s) in the experiments to reduce the probability of pulse pileup resulting from the long shaping time. The total acquisition time for each spectrum was less than 5 minutes.

Figure 6.

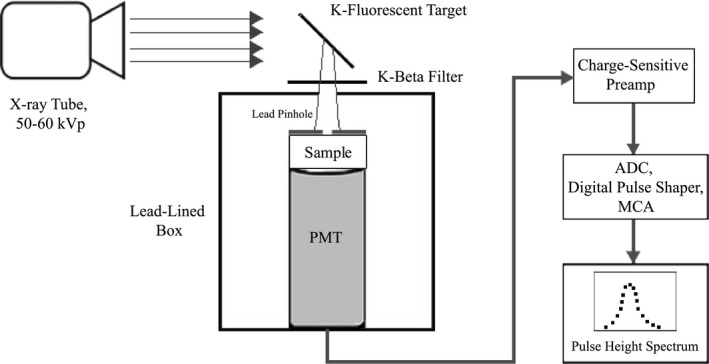
Schematic of the pulse height spectroscopy apparatus used in our experiments. Monoenergetic x‐rays produced via K‐fluorescence excited the sample, which was coupled to a PMT. PMT output was fed to a digital pulse height analysis module.

Table 1.

PHS acquisition parameters used in calibration and CsI measurements

PMT Gain	2–4 × 106
Charge amplifier sensitivity	3–10 mV/pC
Charge amplifier decay	50 μs
Trapezoid shaping (rise time)	10 μs
Peaking time	16 μs

Abscissae of measured PHS were calibrated to relate measurement channel number to the number of optical photons detected per x‐ray interaction (i.e., ${\overline{N}}_{phe}$) using methodology described in detail by Watt et al.¹⁰ The calibration apparatus is shown in Fig. 7, in which a green LED source was pulsed in 0.75–2 μs intervals toward the PMT to produce PHS of the detected light bursts. Calibration measurements were acquired with parameters reported in Table 1.

Figure 7.

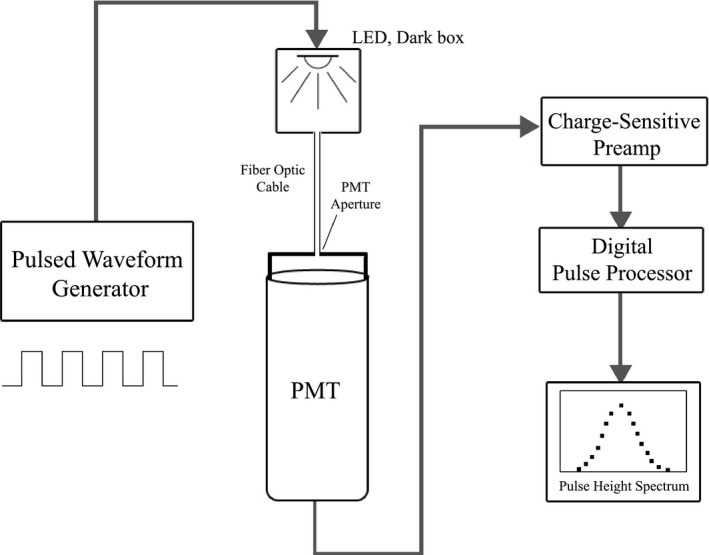
A waveform generator with variable duty cycle was used to drive a green (λ = 525 nm) LED at various pulse durations. LED light was sent to the PMT via fiber optic cable, and PMT output was fed to the charge amplifier and pulse height analysis module used in experiments.

The duration of LED pulses was varied to control the number of photons reaching the PMT photocathode. Photon detection is Poisson distributed, therefore, the variance in PHS channel number ${\mathit{\sigma }}_k^2$ is related to the peak PHS channel number k _p by:

$${\mathit{\sigma }}_k^2=a{k}_p.$$ (23)

The constant a represents the system's constant of proportionality between channel number and generated photoelectrons, which was determined by the slope of the best‐fit line between ${\mathit{\sigma }}_k^2$ and k _p for the ensemble of LED PHS.

Dynode amplification adds noise to the PMT input signal, due to the statistical nature of each dynode's gain δ.^{4, 10, 12} We derive expressions that describe how noise propagates in a multi‐dynode PMT in Appendix B. We show that, given certain reasonable assumptions, the noise contribution from dynode amplification reduces to a multiplicative noise factor NF given by:

$$NF=\left(\frac{\overline{\mathit{\delta }}}{\overline{\mathit{\delta }}-1}\right).$$ (24)

This factor scales the variance of the PMT input, therefore the measured PHS variance was divided by NF prior to the calculation of a.

Once determined, a was multiplied by the effective quantum efficiency ${\overline{\mathit{\eta }}}_{eff}$ of the PMT to CsI scintillation light. A final correction factor accounting for light transmission through the PMT window⁴⁰ was applied to the product of a and ${\overline{\mathit{\eta }}}_{eff}$ to determine the relationship between channel number (i.e., measured PHS abscissae) and the number of optical photons exiting the CsI scintillators.

2.D. Deriving depth‐dependent light escape from measured PHS

PHS of various CsI scintillators were calculated using the method outlined in Section 2.B.. and illustrated by Fig. 4. The mean conversion gain in CsI was assumed to be 58.8 keV⁻¹ (W = 17 eV) based on literature,^{4, 40, 41, 42, 43, 44} and mean dynode gain was determined from the k‐th root of PMT gain (k = 10 in R1450 PMT). Previous investigations have shown that light escape in CsI varies approximately linearly with depth.^{12, 29, 31} Following these results, $\overline{\mathit{\epsilon }}(z)$ was modeled using

$$\overline{\mathit{\epsilon }}(z)=\overline{\mathit{\epsilon }}(0)+\frac{\overline{\mathit{\epsilon }}(L)-\overline{\mathit{\epsilon }}(0)}{L}z,$$ (25)

making $\overline{\mathit{\epsilon }}(0)$ and $\overline{\mathit{\epsilon }}(L)$ the only variable parameters in PHS model calculations.

Various combinations of $\overline{\mathit{\epsilon }}(0)$ and $\overline{\mathit{\epsilon }}(L)$ were used to calculate PHS, and the process was repeated until modeled and measured PHS reached agreement. The quality of agreement was quantified by the objective function

$$F=\sum \left|PH{S}_{calculated}\left({\overline{N}}_{phe}\right)-PH{S}_{measured}\left({\overline{N}}_{phe}\right)\right|.$$ (26)

The values of $\overline{\mathit{\epsilon }}(0)$ and $\overline{\mathit{\epsilon }}(L)$ that minimized F were used in Eq. (8) to calculate the light escape efficiency as a function of depth in each sample.

2.E. Measured estimate vs. true optical Swank factor I _OPD

An estimate of the Swank factor A _s , which is equivalent to I _OPD in our experiments, can be calculated directly from the measured PHS using:^{2, 3}

$$A_s=\frac{m_1^2}{m_0{m}_2},$$ (27)

where m _i represents the i‐th moment of the spectrum; however, this method underestimates the true optical Swank factor of the scintillator, as the PHS are degraded by noise introduced by the measurement apparatus.^{5, 12} A more accurate estimate of I _OPD was obtained for each sample using the following method: First an estimate of $\overline{\mathit{\epsilon }}(z)$ was obtained using the iterative methods outlined in the previous section. Then the corresponding light escape parameters were used in Eqs. (17) and (4) to calculate the scintillator's PHS under ideal measurement conditions, i.e., ${\overline{\mathit{\eta }}}_{eff}$ = 100% and $\overline{\mathit{\delta }}\to \infty$. Finally, the moments of the resulting PHS were used to calculate the true I _OPD without noise contributions from the measurement apparatus.

3. Results

3.A. Modeling PHS with noise: linear system analysis

Figure 8 shows calculated PHS of a scintillator using the expressions (17) and (4) and methods described in Sections 2.A.. and 2.B.. B. Shown in Fig. 8(a) is the noise‐free PHS $\mathit{\phi }({\overline{N}}_{phe})$ for a 600 μm CsI scintillator with 32 keV x‐ray energy and an example set of escape efficiency parameters. The x‐axis position and width of φ are determined by the values and range of $\overline{\mathit{\epsilon }}(z)$, respectively, while the shape of the distribution depends on x‐ray attenuation and scintillator thickness.

Figure 8.

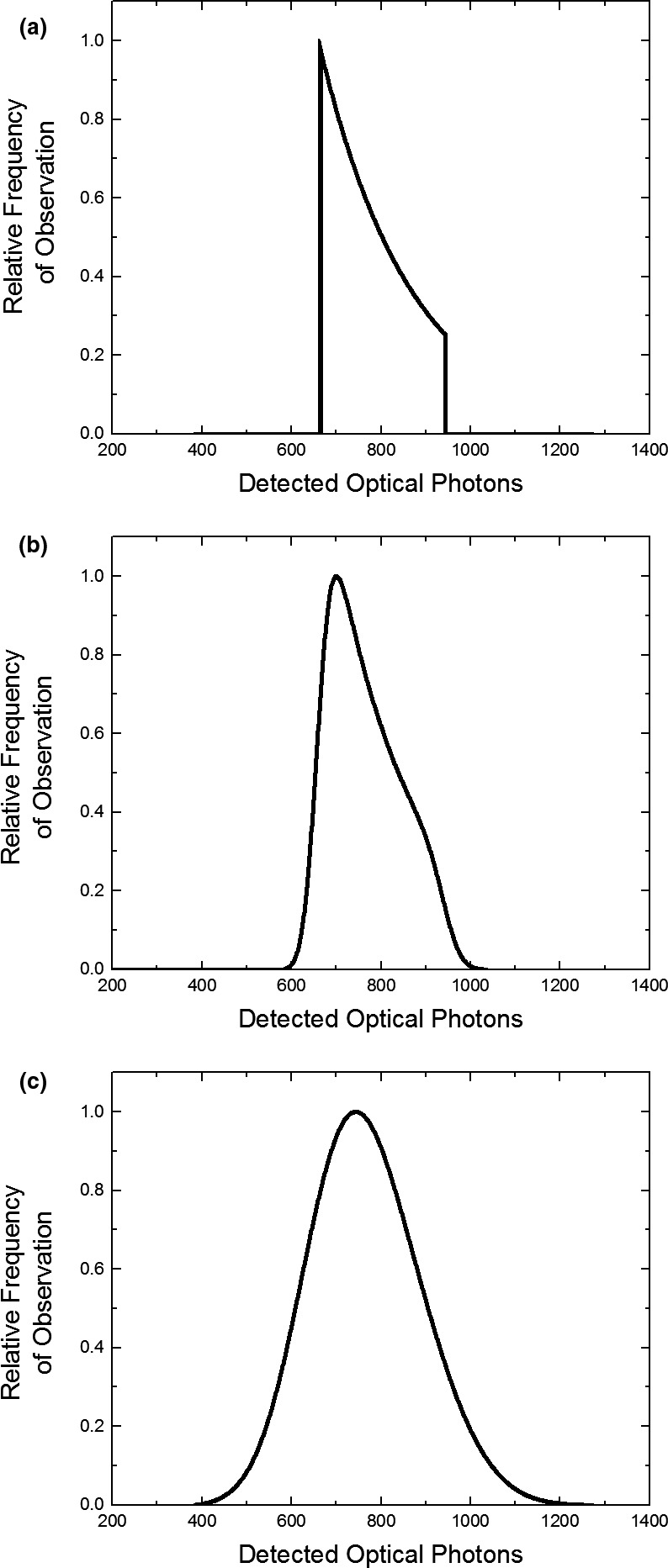
Calculated PHS of scintillators, including various sources of noise and measurement conditions. (a) An example $\mathit{\phi }({\overline{N}}_{phe})$ of a 600 μm CsI scintillator with $\overline{\mathit{\epsilon }}(0)=0.35$, $\overline{\mathit{\epsilon }}(L)=0.5$ with 32 keV excitation. (b) The same PHS, accounting for stochastic effects in photon generation and escape, but with idealized measurement, i.e. #bib100% detection efficiency and $\overline{\mathit{\delta }}\to \infty$. (c) The same spectrum, including noise due to finite PMT quantum efficiency and dynode gain – a “realistic example” of the measured PHS. Note that each PHS is normalized to its maximum value; in practice the ordinate expresses a number of counts.

Figure 8(b) shows how φ is degraded when stochastic effects in photon creation and light escape are introduced. The plotted spectrum represents the PHS measured with an idealized system, where the detection efficiency of the PMT is unity and dynode gain approaches infinity. Following Eq. (4), the total variance in measurements of ${\overline{N}}_{phe}$ is:

$${\mathit{\sigma }}_{tot}^2({\overline{N}}_{phe})={\overline{N}}_{phe}.$$ (28)

The calculated PHS shown in Fig. 8(c) represents a realistic example of the measured PHS, which includes the additional stochastic effects of finite PMT detection efficiency and noise associated with finite dynode gain. The total variance in measurements of ${\overline{N}}_{phe}$ is given by Eq. (4). Although ${\overline{\mathit{\eta }}}_{eff}$ is reduced from unity in Fig. 8(c), the PHS abscissa represents the number of photons detected in a calibrated measurement, which does not change; however, the low efficiency of PMT detection broadens the measured PHS substantially according to the inverse relationship between ${\overline{\mathit{\eta }}}_{eff}$ and ${\mathit{\sigma }}_{tot}^2$ in Eq. (4).

3.B. Light output calibration

The measured data for PHS calibration are shown in Fig. 9. Figure 9(a) shows the measured PHS with 1–2 μs LED pulses, which demonstrate a linear relationship between pulse length (i.e., number of incident photons) and peak channel number k _p , with a small offset due to the finite response time of the LED. Figure 9(b) shows the variation in channel variance ${\mathit{\sigma }}_k^2$ as a function of k _p for the various LED pulse lengths. The slope of the best‐fit line between k _p and ${\mathit{\sigma }}_k^2$, also shown in Fig. 9(b), was the constant of proportionality a = 29.6 channels per photoelectron. Figure 9(c) shows the emission spectrum of CsI and the quantum efficiency of our PMT, which were used to calculate ${\overline{\mathit{\eta }}}_{eff}$ = 9.3% following Eq. (5). The product of a and ${\overline{\mathit{\eta }}}_{eff}$ was corrected for light transmission (92%) through the PMT window to relate 3.06 measurement channels to each optical photon emitted from CsI.

Figure 9.

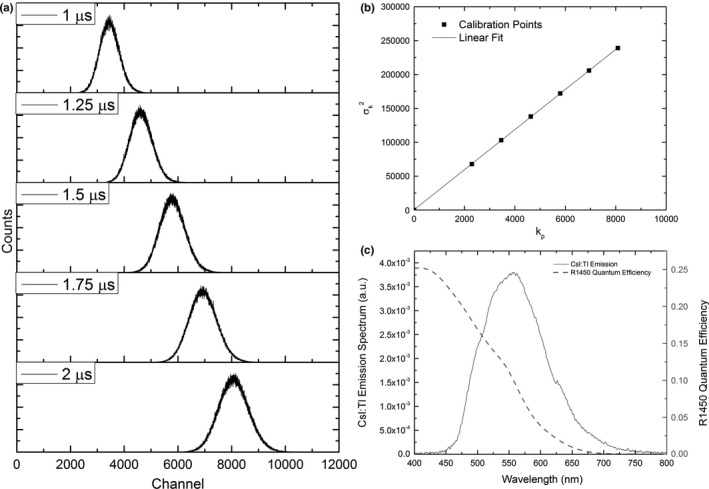
(a) Measured PHS of light collected from an LED driven at 1–2 μs intervals. (b) The relationship between channel variance and peak channel number is linear through the origin. The slope of their best‐fit line was determined and scaled to relate channel number to optical photons escaping CsI in experiments. (c) The spectral quantum efficiency of the PMT used in experiments and the measured emission spectrum of investigated CsI samples (SM240, Spectral Products).

3.C. Measured and modeled PHS of CsI scintillators

Measured PHS of the 600 μm thick FOS (HR and HL) and GPXS scintillators are shown in Fig. 10. Their comparison shows that light yield per x‐ray interaction varied by almost an order of magnitude between different scintillator optical designs. The FOS HR sample emitted the fewest number of photons per interaction, due to the optically absorptive backing and light attenuation by the FOP.³⁷ The reflective backing used in the FOS HL sample improved this yield by a factor of 3, by enabling light generated deep within the scintillator to be reflected back toward the optical detector. The GPXS design yielded approximately three times more light than FOS HL and nine times more than FOS HR, due to both its highly reflective backing and the absence of an FOP.

Figure 10.

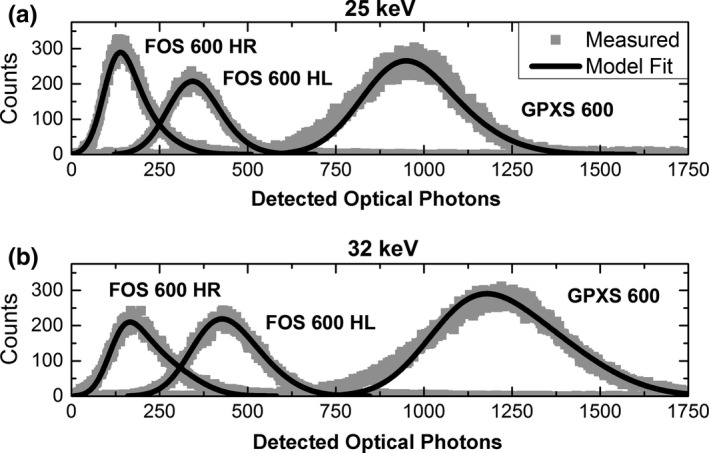
Measured PHS of 600 μm FOS HR, FOS HL, and GPXS scintillator at (a) 25 keV and (b) 32 keV, with best fits determined by iterative calculation. Calculated PHS of thinner and thicker samples show comparable agreement with measurements, and are not shown due to space considerations.

Figure 10 also shows a comparison between measured PHS and the best‐fit PHS model results after iterative fitting. Modeled PHS showed reasonable agreement with all measurements. All estimates of $\overline{\mathit{\epsilon }}(0)$ and $\overline{\mathit{\epsilon }}(L)$ from measurements at 25 and 32 keV were within 7% root‐mean‐square (RMS) error.

Figure 11 shows the estimates of $\overline{\mathit{\epsilon }}(z)$ in the 600 μm samples determined through PHS fitting. Light escape efficiency ranged from 6.9 to 20.7% #bib20.1 to 31.1% and 57.5 to 81.4% from the back (z = 0) to the front (z = L) of the FOS HR, FOS HL, and GPXS samples, respectively. The low light, right‐skewed PHS of FOS HR is due to the low values of $\overline{\mathit{\epsilon }}(z)$ with relatively large variations over x‐ray interaction depth. Similarly, the brighter and more symmetric PHS observed in FOS HL and GPXS corresponds to higher values of $\overline{\mathit{\epsilon }}(z)$ with smaller depth‐dependent variations.

Figure 11.

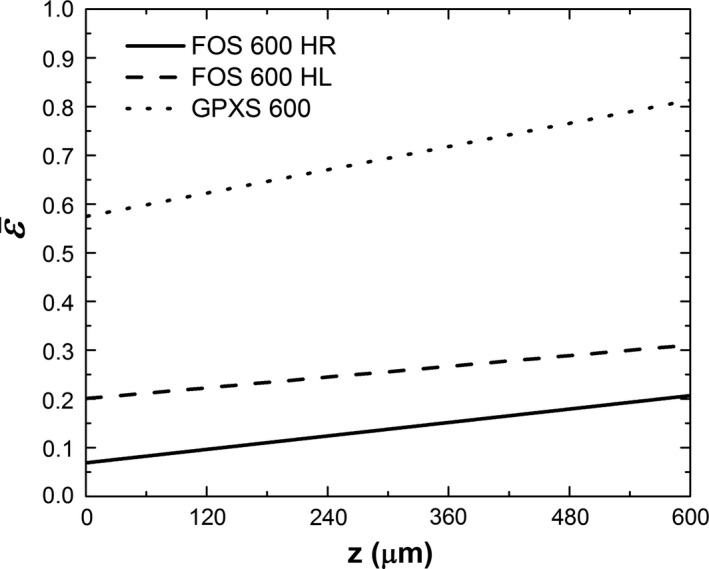
Estimated light escape efficiency vs. depth in the 600 μm samples of the FOS HR, FOS HL and GPXS scintillators. These estimates of $\overline{\mathit{\epsilon }}(z)$ yield the best agreement between calculated and measured PHS.

Table 2 reports the estimated light escape efficiency minima and maxima for all of the investigated samples. These data are also scaled by the inherent W of CsI to the unit of keV⁻¹, and provide upper and lower bounds to each scintillator's effective conversion gain, i.e., the number of photons emitted per unit energy of excitation.

Table 2.

Estimated escape efficiency and light output (keV⁻¹) for interactions at the back (z = 0) and front (z = L) of the investigated samples. Light output values are determined by dividing escape efficiency estimates by W = 17 eV

	Back		Front
	$\overline{\mathit{\epsilon }}(0)$	keV−1	$\overline{\mathit{\epsilon }}(L)$	keV−1
FOS 150 HR	0.073	4.3	0.228	13.4
FOS 600 HR	0.069	4.1	0.207	12.2
FOS 200 HL	0.222	13.1	0.313	18.4
FOS 600 HL	0.201	11.8	0.311	18.3
FOS 1000 HL	0.176	10.4	0.293	17.2
GPXS 200	0.600	35.3	0.810	47.6
GPXS 600	0.575	33.8	0.814	47.9
GPXS 1000	0.501	29.5	0.884	52.0

The data reported in Fig. 11 and Table 2 can be used to compare the evaluated samples as a function of thickness or optical design. For the same optical design, thicker samples are shown to yield less light, with greater variation in $\overline{\mathit{\epsilon }}(z)$ compared to thinner samples. The amount of light escaping from interactions furthest from the optical collection is reduced by 5.5% #bib20.7%, and 16.5% from the thinnest to the thickest samples of FOS HR, FOS HL, and GPXS, respectively. In comparison, scintillator optical design is shown to be the dominant factor in determining the values of $\overline{\mathit{\epsilon }}(z)$, which varied up to an order of magnitude between samples.

3.D. Optical Swank factor

Table 3 reports measured estimates of the optical Swank factor which were computed directly from measured PHS, as well as the estimated true optical Swank factor (I _OPD ) determined from PHS calculated with measurement noise removed. Optical design (i.e., backing and FOP) is shown to be the dominant factor affecting I _OPD , which is estimated to be greater than 0.9 in all samples. The FOS HL and GPXS scintillators, which exhibit smaller variations in $\overline{\mathit{\epsilon }}(z)$, are shown to have I _OPD approaching unity. This result agrees well with estimates that others have provided through experiments^{5, 11, 12} and Monte Carlo simulations^{15, 32, 45} of CsI. The FOS HR scintillators, despite having poorer light escape properties, maintain high I _OPD of approximately 0.9.

Table 3.

Optical Swank factors calculated directly from measured PHS, which include measurement noise, and from PHS corrected for measurement effects, which represent the inherent performance of the scintillator

	Measured estimate of the optical Swank factor (measurement noise included)		True optical Swank factor I OPD (measurement effects removed)
	25 keV	32 keV	25 keV	32 keV
FOS 150 HR	0.828	0.844	0.900	0.903
FOS 600 HR	0.847	0.821	0.911	0.906
FOS 200 HL	0.958	0.948	0.988	0.988
FOS 600 HL	0.944	0.936	0.985	0.983
FOS 1000 HL	0.940	0.936	0.985	0.979
GPXS 200	0.968	0.964	0.998	0.995
GPXS 600	0.966	0.954	0.999	0.998
GPXS 1000	0.955	0.946	0.984	0.976

4. Discussion

4.A. Light transport in CsI scintillators: optical design

Results shown in Fig. 11 and Table 2 indicated that detector optical design parameters, i.e., backing and FOP, are the dominant factors determining the light escape properties of the CsI samples. Samples featuring a reflective backing and no FOP yielded appreciably more light than samples with an absorptive backing, FOP, or both. While it is desirable to maximize light yield (i.e., signal) to overcome electronic noise limitations in FPI readout, other imaging performance parameters need to be taken into consideration. For example, Zhao et al.¹¹ showed that the absorptive optical backing of the FOS HR design reduces overall light yield to enhance spatial resolution. Alternatively, an FOP not only attenuates visible light, but also attenuates undetected x‐rays to minimize radiation absorption or damage in underlying electronics, e.g., CMOS sensor.³⁷

4.B. Light transport in CsI scintillators: thickness

Results in Tables 2 and 3 showed how thickness variations affect light escape and the Swank factor of CsI scintillators. In each of the sample designs, large differences in thickness (e.g., from 200 to 1000 μm) only resulted in minor changes in $\overline{\mathit{\epsilon }}(z)$. This indicates that light photons escape efficiently from CsI layers with thickness up to 1 mm. The small variations in $\overline{\mathit{\epsilon }}(z)$ exhibited by CsI scintillators result in optical Swank factors that approach unity.^{5, 11, 12, 13, 14, 32} In contrast, isotropic powder phosphors such as Gd₂O₂S:Tb, are known to exhibit larger variations in $\overline{\mathit{\epsilon }}(z)$ and lower Swank factors.^{6, 7, 8, 15} This inherent advantage of CsI can be used to improve the DQE(0) of indirect FPIs, particularly in high‐energy applications such as cone‐beam CT. Using a thicker CsI layer (up to 1 mm) for these applications can enhance DQE(0) by improving x‐ray absorption while maintaining a high Swank factor.¹³

4.C. Intrinsic x‐ray conversion gain: W of CsI

All parameters used in PHS modeling were either well‐known or directly measured, with the exception of the energy required to create one optical photon, W. Extensive efforts^{4, 40, 41, 42, 43, 44} have been devoted to estimate the intrinsic conversion gain in CsI. The gain value used in the present work (58.8 keV⁻¹, or W = 17 eV) is a conservative estimate based on previous investigations, which reported W values ranging from 13.3 to 22 eV with an average of approximately 17 eV. The choice of W directly affects the absolute values of light escape efficiency deduced from the PHS. This should be considered when comparing scintillators without well‐defined W values. In this investigation, W was assumed to be constant between samples, which were prepared by the same manufacturer.

4.D. Precision in estimating and $\overline{\mathit{\epsilon }}(0)$ and $\overline{\mathit{\epsilon }}(L)$

The quality of agreement between measured and modeled PHS is most sensitive to the value of $\overline{\mathit{\epsilon }}(0)$ used in calculations, and is less sensitive to $\overline{\mathit{\epsilon }}(L)$. Consequently, measured PHS estimate $\overline{\mathit{\epsilon }}(0)$ more precisely than $\overline{\mathit{\epsilon }}(L)$. Figure 12 shows an example of how the agreement between measured PHS and modeled PHS changes when one fitting parameter (i.e., $\overline{\mathit{\epsilon }}(0)$ or $\overline{\mathit{\epsilon }}(L)$) is varied while the other is fixed. Figure 12(a) shows PHS calculated when $\overline{\mathit{\epsilon }}(L)$ is fixed and $\overline{\mathit{\epsilon }}\left(0\right)$ is varied by 10% of its estimated value in the FOS 600 HL scintillator. Different values of $\overline{\mathit{\epsilon }}(0)$ shift the position of modeled PHS peaks, which strongly affects the agreement with measurement. Figure 12(b) shows the PHS calculated with fixed $\overline{\mathit{\epsilon }}(0)$ and 10% variation in $\overline{\mathit{\epsilon }}(L)$. Differences in $\overline{\mathit{\epsilon }}(L)$ elongate the upper tails of modeled PHS, but the change is much less in comparison with the effect of $\overline{\mathit{\epsilon }}(0)$.

Figure 12.

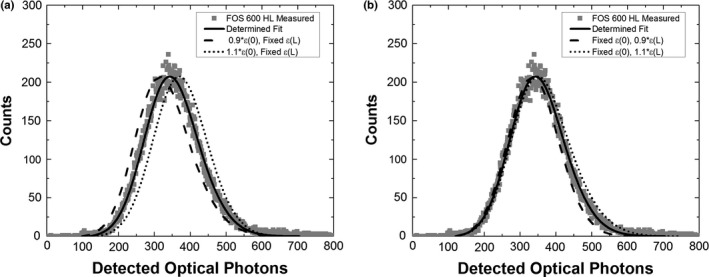
(a) Comparison of a measured PHS (FOS 600 HL #bib25 keV) and calculated PHS when $\overline{\mathit{\epsilon }}(0)$ is varied by ± 10% of its estimated value. Agreement between the modeled and measured PHS is strongly affected by $\overline{\mathit{\epsilon }}(0)$, which shifts the position of the modeled PHS peak. (b) PHS calculated when $\overline{\mathit{\epsilon }}(0)$ is fixed and $\overline{\mathit{\epsilon }}(L)$ varied by ± 10%. Agreement between the modeled and measured PHS is less sensitive to changes in $\overline{\mathit{\epsilon }}(L)$, which primarily affect the upper PHS tail.

Modeled PHS change unequally with respect to $\overline{\mathit{\epsilon }}(0)$ and $\overline{\mathit{\epsilon }}(L)$ due to our measurement geometry (Fig. 1) and exponential x‐ray attenuation in the scintillator. At low energies, e.g., 25 keV, most x‐ray interactions occur near the entrance plane (z = 0). These events, which have lower escape efficiency of light, contribute most to the PHS. Conversely, only a small portion of x‐ray interactions occur near the exit (z = L), and their contribution to the PHS is much less. This asymmetry is most evident in thick or high‐attenuating scintillators, where the difference in x‐ray absorption at z = 0 and z = L is the largest.

Escape efficiency estimates may also be affected by nonlinearity in $\overline{\mathit{\epsilon }}(z)$, which is not considered in this work. Previous estimates of light escape efficiency in CsI using measured PHS¹² have shown that it varies approximately linearly with depth. Monte Carlo simulations by Badano et al.²⁹ and Freed et al.³¹ have also shown that $\overline{\mathit{\epsilon }}(z)$ in CsI can be approximated by a linear function. PHS interpretation with non‐linear $\overline{\mathit{\epsilon }}(z)$ is possible with the presented model using the approach described in Section 2.A.. This may be explored in future work; however, its impact on imaging performance parameters, e.g., Swank factor, is expected to be small.

5. Conclusions

In this paper, we developed a new approach to deriving depth‐dependent light escape efficiency and more accurately estimating the true optical Swank factor of scintillators from measured PHS, using a model that removes the effects of added noise in the measurement chain. This method was used to investigate CsI scintillators with various thickness and optical design used in indirect FPIs. Our results showed that light escape varies almost an order of magnitude between scintillators with different optical designs, and varies considerably less with changes in CsI thickness. After removing the effect of measurement noise, the optical Swank factor of the scintillators with the lowest light escape properties still exceeds 0.9, and approaches unity in scintillators with reflective backings. Estimates of the depth‐dependent light escape efficiency and Swank factor provided by the present work can help validate Monte Carlo simulations of structured CsI and can be used to optimize scintillator design for different x‐ray imaging applications.

Conflicts of interest

The authors have no conflicts of interest to disclose.

Appendix A. Variance in the number of optical photons detected per X‐ray interaction

A.1.

Here, we propagate the mean and variance in the number of quanta generated by an x‐ray (absorbed at a given depth z) through the stochastic amplification stages of PHS shown in Fig. 3. This analysis determines how each stage contributes to the total variance in measurements of ${\overline{N}}_{phe}$ given by Eq. (4).

A.1.1. Scintillation

The absorbed x‐ray is converted to N _ph optical photons through conversion with mean gain $\overline{g}$. The variance ${\mathit{\sigma }}_{ph}^2$ in N _ph is assumed to be proportional to $\overline{g}$ by a constant γ ²:

$${\overline{N}}_{ph}=\overline{g}$$ (A1)

$${\mathit{\sigma }}_{ph}^2={\mathit{\gamma }}^2\overline{g}.$$ (A2)

A.1.2. Optical photon escape

Photon escape from the scintillator is modeled as a binary selection process,⁴⁶ which is a special case of a stochastic amplification stage, wherein the gain in each quantum is either 1 or 0 for successful or unsuccessful escape, respectively. The mean gain of this stage is the escape efficiency $\overline{\mathit{\epsilon }}$, which corresponds to the interaction depth under consideration, and its variance is given by ${\mathit{\sigma }}_{\mathit{\epsilon }}^2=\overline{\mathit{\epsilon }}(1-\overline{\mathit{\epsilon }})$. The mean number of escaped photons ${\overline{N}}_{phe}$ and the variance ${\mathit{\sigma }}_{phe}^2$ in N _phe are:

$${\overline{N}}_{phe}=\overline{g}\overline{\mathit{\epsilon }}$$ (A3)

$${\mathit{\sigma }}_{phe}^2={\overline{\mathit{\epsilon }}}^2{\mathit{\sigma }}_{ph}^2+{\mathit{\sigma }}_{\mathit{\epsilon }}^2{\overline{N}}_{ph}$$ (A4)

$$={\overline{\mathit{\epsilon }}}^2{\mathit{\gamma }}^2\overline{g}+\overline{\mathit{\epsilon }}[1-\overline{\mathit{\epsilon }}]\overline{g}$$ (A5)

$$={\overline{\mathit{\epsilon }}}^2({\mathit{\gamma }}^2-1)\overline{g}+\overline{g}\overline{\mathit{\epsilon }}.$$ (A6)

A.1.3. Optical photon detection

Optical photon interaction with the PMT photocathode is also modeled as a binary selection process, with average gain equal to the effective quantum efficiency ${\overline{\mathit{\eta }}}_{eff}$ defined in Eq. (5). The mean number of generated photoelectrons ${\overline{N}}_e$ and variance ${\mathit{\sigma }}_e^2$ in N _e is:

$${\overline{N}}_e={\overline{\mathit{\eta }}}_{eff}\overline{g}\overline{\mathit{\epsilon }}$$ (A7)

$${\mathit{\sigma }}_e^2={\overline{\mathit{\eta }}}_{eff}^2{\mathit{\sigma }}_{phe}^2+{\mathit{\sigma }}_{\mathit{\eta }}^2{\overline{N}}_{phe}$$ (A8)

$$={\overline{\mathit{\eta }}}_{eff}^2\left[{\overline{\mathit{\epsilon }}}^2\left({\mathit{\gamma }}^2-1\right)\overline{g}+\overline{g}\overline{\mathit{\epsilon }}\right]+{\overline{\mathit{\eta }}}_{eff}\left[1-{\overline{\mathit{\eta }}}_{eff}\right]\overline{g}\overline{\mathit{\epsilon }}$$ (A9)

$$={\overline{\mathit{\eta }}}_{eff}^2\left({\mathit{\gamma }}^2-1\right)\overline{g}{\overline{\mathit{\epsilon }}}^2+{\overline{\mathit{\eta }}}_{eff}\overline{g}\overline{\mathit{\epsilon }}.$$ (A10)

A.1.4. Dynode amplification

The amplification of photoelectrons over k dynodes of a PMT is modeled as a serial cascade of k stochastic gain stages, each with mean gain $\overline{\mathit{\delta }}$ and gain variance ${\mathit{\sigma }}_{\mathit{\delta }}^2$.⁴, ⁴⁷, ⁴⁸ The entire dynode chain has average gain $\overline{G}={\overline{\mathit{\delta }}}^k$, with variance ${\mathit{\sigma }}_G^2$. The mean number of output photoelectrons ${\overline{N}}_{em}$ and the variance ${\mathit{\sigma }}_{em}^2$ in N _em are given by:

$${\overline{N}}_{em}=\overline{G}{\overline{N}}_e=\overline{G}{\overline{\mathit{\eta }}}_{eff}\overline{g}\overline{\mathit{\epsilon }}$$ (A11)

$${\mathit{\sigma }}_{em}^2={\overline{G}}^2{\mathit{\sigma }}_e^2+{\mathit{\sigma }}_G^2{\overline{N}}_e.$$ (A12)

In Appendix B, we derive expressions for variance transfer in a multi‐dynode PMT to determine the form of ${\mathit{\sigma }}_G^2$. Briefly, ${\mathit{\sigma }}_G^2$ is determined by two assumptions made in this work: (a) We consider the number of photons generated in the scintillator to be Poisson distributed, i.e., γ ² = 1. This is an approximate but reasonable assumption in the study of various scintillators, including CsI.⁴⁹ (b) We also consider the variance in each dynode's gain to be Poisson distributed, i.e., ${\mathit{\sigma }}_{\mathit{\delta }}^2=\overline{\mathit{\delta }}$, which is a common approximation made in PMT literature.⁴, ⁴⁷ Given these assumptions, ${\mathit{\sigma }}_e^2$ reduces to

$${\mathit{\sigma }}_e^2={\overline{\mathit{\eta }}}_{eff}\overline{g}\overline{\mathit{\epsilon }},$$ (A13)

and following Eq. (B19) derived in Appendix B:

$${\mathit{\sigma }}_{em}^2=\frac{{\overline{\mathit{\delta }}}^k\left({\overline{\mathit{\delta }}}^{k+1}-1\right)}{\overline{\mathit{\delta }}-1}{\mathit{\sigma }}_e^2$$ (A14)

$$=\frac{{\overline{\mathit{\delta }}}^k\left({\overline{\mathit{\delta }}}^{k+1}-1\right)}{\overline{\mathit{\delta }}-1}{\overline{\mathit{\eta }}}_{eff}\overline{g}\overline{\mathit{\epsilon }}.$$

A.1.5. Pulse height analysis

In measured (and calibrated) PHS, ${\overline{N}}_{em}$ is scaled by $\overline{G}$ and ${\overline{\mathit{\eta }}}_{eff}$ to represent the number of optical photons escaping the scintillator ${\overline{N}}_{phe}$:

$$\frac{{\overline{N}}_{em}}{\overline{G}{\overline{\mathit{\eta }}}_{eff}}=\overline{g}\overline{\mathit{\epsilon }}={\overline{N}}_{phe}.$$ (A15)

However, the total variance in this quantity ${\mathit{\sigma }}_{tot}^2$ does not reduce to ${\mathit{\sigma }}_{phe}^2$ but rather to:

$${\mathit{\sigma }}_{tot}^2=\frac{{\mathit{\sigma }}_{em}^2}{{\overline{G}}^2{\overline{\mathit{\eta }}}_{eff}^2}$$ (A16)

$$=\frac{\left(\overline{\mathit{\delta }}-\frac{1}{{\overline{\mathit{\delta }}}^k}\right)}{{\overline{\mathit{\eta }}}_{eff}\left(\overline{\mathit{\delta }}-1\right)}{\overline{N}}_{phe}.$$ (A17)

In cases where the total dynode gain ${\overline{\mathit{\delta }}}^k$ is much greater than 1, which is true in our experiments (Table 1):

$${\mathit{\sigma }}_{tot}^2\approx \frac{{\overline{N}}_{phe}\left(\frac{\overline{\mathit{\delta }}}{\overline{\mathit{\delta }}-1}\right)}{{\overline{\mathit{\eta }}}_{eff}},$$ (A18)

which is the relation (4) used in all calculations. In addition, Eq. (A18) shows that the multiplicative noise factor NF (24) described in Section 2.C. arises in the case that PMT input variance and dynode gain variance are Poisson distributed.

Appendix B. Variance transfer through a multi‐dynode photomultiplier tube

B.1.

In this Appendix, we derive expressions for the mean and variance in the number of photoelectrons at each dynode of a photomultiplier tube. A PMT with k dynodes is modeled as a serial cascade of k stochastic gain stages, with mean and variance transfer determined by Eqs. (2) and (3). We first derive a general expression for variance transfer over k dynodes, making no assumptions of the PMT input variance or dynode gain variance. We then derive an expression for the case where both the PMT input variance and dynode gain variance are Poisson distributed, which are the assumptions applied in this work.

Consider an average of ${\overline{N}}_0$ photoelectrons generated at a PMT photocathode with variance ${\mathit{\sigma }}_0^2$. When amplified by a dynode with mean gain $\overline{\mathit{\delta }}$ and gain variance ${\mathit{\sigma }}_{\mathit{\delta }}^2$, the mean ${\overline{N}}_1$ and variance ${\mathit{\sigma }}_1^2$ in the number of photoelectrons after amplification are:

$${\overline{N}}_1=\overline{\mathit{\delta }}{\overline{N}}_0$$ (B1)

$${\mathit{\sigma }}_1^2={\overline{\mathit{\delta }}}^2{\mathit{\sigma }}_0^2+{\overline{N}}_0{\mathit{\sigma }}_{\mathit{\delta }}^2.$$ (B2)

When these photoelectrons are amplified by a second identical dynode, the mean ${\overline{N}}_2$ and variance ${\mathit{\sigma }}_2^2$ in the resulting number of photoelectrons are:

$${\overline{N}}_2={\overline{\mathit{\delta }}}^2{\overline{N}}_0$$ (B3)

$$\begin{array}{cc}\hfill {\mathit{\sigma }}_2^2& ={\overline{\mathit{\delta }}}^2\left({\overline{\mathit{\delta }}}^2{\mathit{\sigma }}_0^2+{\overline{N}}_0{\mathit{\sigma }}_{\mathit{\delta }}^2\right){\mathit{\sigma }}_0^2+\overline{\mathit{\delta }}{\overline{N}}_0{\mathit{\sigma }}_{\mathit{\delta }}^2\hfill \\ & ={\overline{\mathit{\delta }}}^4{\mathit{\sigma }}_0^2+\left({\overline{\mathit{\delta }}}^2+\overline{\mathit{\delta }}\right){\overline{N}}_0{\mathit{\sigma }}_{\mathit{\delta }}^2.\hfill \end{array}$$ (B4)

Repeating this process for a third dynode gives:

$${\overline{N}}_3={\overline{\mathit{\delta }}}^3{\overline{N}}_0$$ (B5)

$${\mathit{\sigma }}_3^2={\overline{\mathit{\delta }}}^6{\mathit{\sigma }}_0^2+\left({\overline{\mathit{\delta }}}^4+{\overline{\mathit{\delta }}}^3+{\overline{\mathit{\delta }}}^2\right){\overline{N}}_0{\mathit{\sigma }}_{\mathit{\delta }}^2.$$ (B6)

For k iterations of this process, i.e., amplification over k dynodes, the pattern emerges that:

$${\overline{N}}_k={\overline{\mathit{\delta }}}^k{\overline{N}}_0$$ (B7)

$${\mathit{\sigma }}_k^2={\overline{\mathit{\delta }}}^{2k}{\mathit{\sigma }}_0^2+\left({\overline{\mathit{\delta }}}^{2k-2}+{\overline{\mathit{\delta }}}^{2k-3}+\dots +{\overline{\mathit{\delta }}}^{k-1}\right){\overline{N}}_0{\mathit{\sigma }}_{\mathit{\delta }}^2.$$ (B8)

In the case that amplification at each dynode is Poisson distributed, ${\mathit{\sigma }}_{\mathit{\delta }}^2=\overline{\mathit{\delta }}$ and:

$${\mathit{\sigma }}_1^2={\overline{\mathit{\delta }}}^2{\mathit{\sigma }}_0^2+{\overline{N}}_0\overline{\mathit{\delta }}$$ (B9)

$${\mathit{\sigma }}_2^2={\overline{\mathit{\delta }}}^4{\mathit{\sigma }}_0^2+\left({\overline{\mathit{\delta }}}^3+{\overline{\mathit{\delta }}}^2\right){\overline{N}}_0$$ (B10)

$${\mathit{\sigma }}_3^2={\overline{\mathit{\delta }}}^6{\mathit{\sigma }}_0^2+\left({\overline{\mathit{\delta }}}^5+{\overline{\mathit{\delta }}}^4+{\overline{\mathit{\delta }}}^3\right){\overline{N}}_0$$ (B11)

$\dots$

$${\mathit{\sigma }}_k^2={\overline{\mathit{\delta }}}^{2k}{\mathit{\sigma }}_0^2+\left({\overline{\mathit{\delta }}}^{2k-1}+{\overline{\mathit{\delta }}}^{2k-2}+\dots +{\overline{\mathit{\delta }}}^k\right){\overline{N}}_0.$$ (B12)

Further, if the number of photoelectrons at the PMT input is Poisson distributed, ${\mathit{\sigma }}_0^2={\overline{N}}_0$ and:

$${\mathit{\sigma }}_1^2=\left({\overline{\mathit{\delta }}}^2+\overline{\mathit{\delta }}\right){\mathit{\sigma }}_0^2$$ (B13)

$${\mathit{\sigma }}_2^2=\left({\overline{\mathit{\delta }}}^4+{\overline{\mathit{\delta }}}^3+{\overline{\mathit{\delta }}}^2\right){\mathit{\sigma }}_0^2$$ (B14)

$${\mathit{\sigma }}_3^2=\left({\overline{\mathit{\delta }}}^6+{\overline{\mathit{\delta }}}^5+{\overline{\mathit{\delta }}}^4+{\overline{\mathit{\delta }}}^3\right){\mathit{\sigma }}_0^2,$$ (B15)

$\dots$

$${\mathit{\sigma }}_k^2=\left({\overline{\mathit{\delta }}}^{2k}+{\overline{\mathit{\delta }}}^{2k-1}+\dots +{\overline{\mathit{\delta }}}^k\right){\mathit{\sigma }}_0^2.$$ (B16)

Factoring out ${\overline{\mathit{\delta }}}^k$ from Eq. (B16) gives:

$${\mathit{\sigma }}_k^2={\overline{\mathit{\delta }}}^k\left({\overline{\mathit{\delta }}}^k+{\overline{\mathit{\delta }}}^{k-1}+\dots +1\right){\mathit{\sigma }}_0^2.$$ (B17)

Noting the geometric series:

$$\left({\overline{\mathit{\delta }}}^k+{\overline{\mathit{\delta }}}^{k-1}+\dots +1\right)=\frac{{\overline{\mathit{\delta }}}^{k+1}-1}{\overline{\mathit{\delta }}-1},$$ (B18)

we simplify Eq. (B17) to:

$${\mathit{\sigma }}_k^2=\frac{{\overline{\mathit{\delta }}}^k\left({\overline{\mathit{\delta }}}^{k+1}-1\right)}{\overline{\mathit{\delta }}-1}{\mathit{\sigma }}_0^2.$$ (B19)

Equation (B19) shows that for Poisson distributed input variance and dynode gain, the variance in the output of a multi‐dynode PMT is directly proportional to the variance in its input, and thus can be described by a multiplicative factor.