Abstract
The combined effects of anthropogenic and biological CO2 inputs may lead to more rapid acidification in coastal waters compared to the open ocean. It is less clear, however, how redox reactions would contribute to acidification. Here we report estuarine acidification dynamics based on oxygen, hydrogen sulfide (H2S), pH, dissolved inorganic carbon and total alkalinity data from the Chesapeake Bay, where anthropogenic nutrient inputs have led to eutrophication, hypoxia and anoxia, and low pH. We show that a pH minimum occurs in mid-depths where acids are generated as a result of H2S oxidation in waters mixed upward from the anoxic depths. Our analyses also suggest a large synergistic effect from river–ocean mixing, global and local atmospheric CO2 uptake, and CO2 and acid production from respiration and other redox reactions. Together they lead to a poor acid buffering capacity, severe acidification and increased carbonate mineral dissolution in the USA’s largest estuary.
The potential contribution of redox reactions to acidification in coastal waters is unclear. Here, using measurements from the Chesapeake Bay, the authors show that pH minimum occurs at mid-depths where acids are produced via hydrogen sulfide oxidation in waters mixed upward from anoxic depths.
Introduction
Anthropogenic carbon dioxide (CO2) has increased more rapidly in the atmosphere since the Industrial Revolution than natural CO2 increase in any period of the last ~800,000 years1, 2; consequently, it has been known that the uptake of CO2 by the ocean has altered surface seawater acid-based chemistry lowering pH by about 0.1 unit and calcium carbonate saturation state by roughly 0.5. This process, known popularly as ocean acidification (OA) for over a decade, will continue to decrease seawater pH by about 0.3 units by the end of the century3, 4. It is likely that OA will cause detrimental effects on the health of marine organisms and ecosystems and alter the associated biogeochemical processes5–7.
Recent research indicates that eutrophication can exacerbate OA, where respiratory processes contribute a far greater acidification in the coastal oceans relative to the open ocean8–13. Coastal eutrophication occurs with increased inputs of nutrients from the application of chemical fertilizers, discharges of human and animal wastes, and atmospheric NOx inputs from fossil fuel burning, which have fueled large algal blooms in many coastal water bodies, especially those near population centers14. It is well known that decomposition of algal organic matter from highly productive surface water leads to the development of seasonally low oxygen (hypoxic) or even zero oxygen (anoxic) bottom waters in many coastal water bodies in the world15, 16. However the coupling between redox and acid–base chemistry has not been explored extensively in seasonally anoxic and partially mixed estuaries nor in permanently anoxic deep basins although redox chemistry and pH have been reported before in the latter13, 17–22. Specifically, it is not known how subsurface water pH dynamics are influenced by anaerobic respiration and the oxidation of reduced chemical species (notably H2S) in seasonally low oxygen (O2) estuaries around the world let alone the interaction of these processes with the anthropogenic CO2 induced OA.
The Chesapeake Bay is the largest estuary in the United States with a well-documented history of eutrophication over the past half century23–25. A recent report demonstrates that some regions of the bay have suffered a long-term pH decline related to eutrophication26. However, few process studies have examined the CO2 system and pH in the Chesapeake, and those that exist have focused on tributaries in the southern reaches of the estuary27, 28. To address the coupling between acid–base chemistry and redox chemistry and its contribution to coastal OA, we sampled the water column repeatedly for several days within a deep basin of the main-stem bay in August 2013 and 2014, a time of peak hypoxia and anoxia, and these data were supplemented with an April 2015 (pre-hypoxia) study. In this paper, we report and explain the occurrence of a pH minimum at and above the oxic–anoxic boundary due to H2S oxidation. We further demonstrate how a combination of processes drives down pH and aragonite mineral saturation state, leading to CaCO3 mineral dissolution in subsurface waters. Finally, we present a general geochemical model to explain why large eutrophic estuaries, exemplified by the Chesapeake Bay, are particularly vulnerable to the acidification stresses caused by the increase of anthropogenic atmospheric CO2 and aquatic eutrophication and respiration.
Results
Acidification due to eutrophication-induced local CO2 uptake
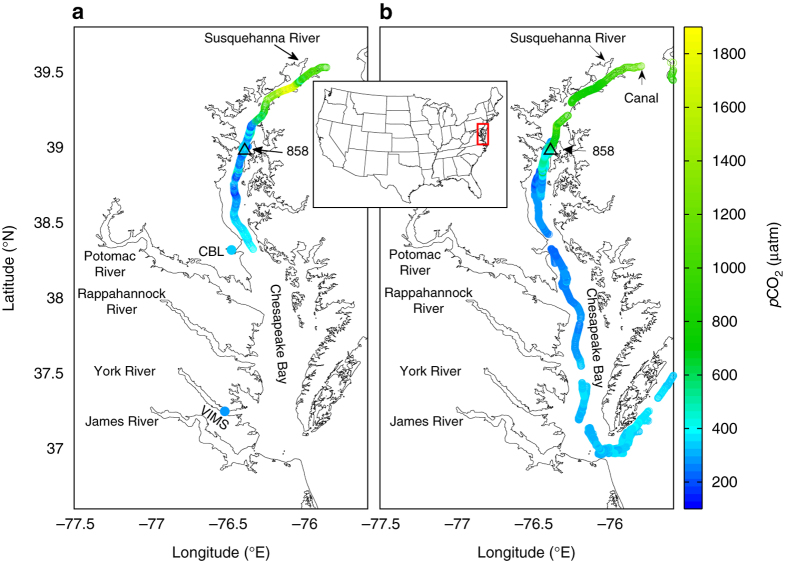
Partial pressure of carbon dioxide (pCO2) in surface waters of the Chesapeake Bay exceeded 1600 μatm in its upper reach and was below the atmospheric level (~ 390 μatm) in the mid-bay for all three cruises between spring and summer (Fig. 1a, b, Table 1, Supplementary Fig. 1, and Methods). The low pCO2 was accompanied by high chlorophyll-a, a phytoplankton biomass proxy, and supersaturated dissolved O2 for much of the year in the mid- and lower-bay (Supplementary Figs. 2–5), indicating net biological production fueled by high riverine nutrient loading. The low surface pCO2 should lead to atmospheric CO2 invasion and may contribute to water column CO2 accumulation and acidification, particularly given atmospheric concentrations are ∼40% greater than the pre-industrial and bay has a long water residence time of 100 days24. While complete water column mixing and destratification occurs occasionally during storms29, 30, smaller wind events more frequently mix water and chemical species down to middle depths (Fig. 2a, Supplementary Figs. 6 and 7). Turbulence in the tidally driven bottom boundary layer will then mix the chemical species in the bottom water31. We have estimated the air-to-water CO2 flux and its impact on water column total dissolved inorganic carbon (DIC) and pH over the period of spring to summer (Table 1). To calculate the effect of DIC increase on bottom water pH decrease, we have modified the popularly used CO2SYS program to include H2S–HS− and NH3–NH4 + species in the acid–base equilibrium calculations as the bottom water in August contains these reduced chemical species (Methods). The resulting bottom-water pH decreases (0.08–0.13 over the spring-summer period; Table 1) are significant when compared with pH decrease due to CO2 uptake from the atmosphere in the open ocean (0.11). However the time scales of acidification due to local CO2 uptake (months) are much shorter than open ocean uptake (decadal to centennial).
Fig. 1.
Measured surface water pCO2 overlapped on a site map of the Chesapeake Bay. a 8–15 August 2013 and b 11–16 April 2015. Data were collected underway aboard R/V Sharp and supplemented with dockside measurements at the Chesapeake Biological Laboratory (CBL) and Virginia Institute of Marine Science (VIMS) during the August cruise. The inserted map shows the general location of the bay. Station 858 is our focused study site. The cruise average of atmospheric and surface water pCO2 values and monthly wind speed are given in Table 1. The pCO2 range was 340–590 µatm near CBL and 290–550 µatm near VIMS, with the lower ends represent incoming bay water during high tides and the high ends representing outgoing sub-estuarine waters during low tides
Table 1.
Air–sea CO2 flux and its impact on bottom-water DIC and pH in the middle Chesapeake Bay
| Month Year | Air pCO2 | Water pCO2 | Wind speed | CO2 flux | ΔDIC | ΔpH |
|---|---|---|---|---|---|---|
| µatm | µatm | m s−1 | mmol m−2 d−1 | μmol kg−1 | ||
| August 2013 | 380.2 ± 11.2 | 309.1 ± 99.3 | 4.4 ± 2.3 | −4.3 ± 0.4 | 21.2 | −0.081 |
| August 2014 | 373.1 ± 9.1 | 251.6 ± 70.9 | 4.2 ± 2.2 | −6.7 ± 0.7 | 33.1 | −0.13 |
| April 2015 | 409.1 ± 8.8 | 341.3 ± 116.6 | 5.8 ± 3.6 | −6.6 ± 0.9 | 32.6 | – |
The mid-bay region is defined as the area between 37.9 and 39.0° N. Monthly averaged wind data were calculated from National Data Buoy Center station# COVM2-8577018 at Cove Point LNG Pier, MD
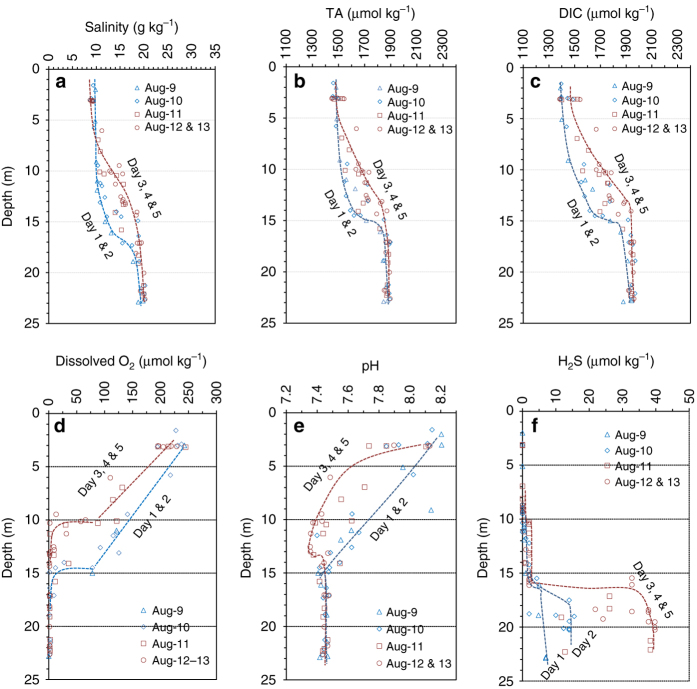
Fig. 2.
Vertical distributions of measured chemical properties at the focused study site in August 2013. a Salinity, b total alkalinity (TA), c dissolved inorganic carbon (DIC), d dissolved oxygen, e pH (25 °C and NBS scale), and f H2S concentration. See Fig. 1 for location (station 858). The lines are the lower and upper boundaries between days 1 and 2 and days 3–5, respectively. August 2014 data are presented in Supplementary Fig. 8 for comparison and affirmation of the 2013 observations
We also note that acidification induced by local CO2 uptake is caused by both increased atmospheric CO2 and coastal eutrophication. This is in sharp contrast with the CO2 uptake in the open ocean where atmospheric forcing is comparable to the coastal ocean but biological CO2 removal and physical mixing are less intense or frequent. Clearly, climate change, anthropogenic inputs, and natural processes have jointly altered the carbon cycle and stressed aquatic environments in the coastal zone.
The spatial gradients of pCO2 observed here and inferred net autotrophy are consistent with prior investigations using oxygen-based approaches to measuring primary production and respiration. Kemp et al.25 concluded that the Chesapeake Bay was net autotrophic overall, but heterotrophic conditions (where respiration exceeded photosynthesis) prevailed in low-salinity regions where we measured supersaturated pCO2 (Fig. 1a, b, Supplementary Fig. 1) and O2 was consistently under saturated (Supplementary Figs. 2b, 3–5). Dissolved O2 tends to be undersaturated in northern regions of the bay given high respiration rates associated with external loads of organic carbon32.
These heterotrophic conditions gave way to a near balanced and an autotrophic metabolism in the mid- and lower-bay, leading to a mean, bay-wide net ecosystem production, which is consistent with strong under saturation of pCO2 in these seaward regions (Fig. 1a, b and Supplementary Fig. 1). The mid- and lower-bay stations (CB3.3C and south) tended towards O2 supersaturation during most months of the year, especially during the warmer months (Supplementary Figs. 2b, 4 and 5). Despite some interannual variability in the seasonal pattern of dissolved O2 saturation, the years of 2013–2015 indicate similar seasonal patterns. Oxygen-based estimates of metabolism showed consistent surface-layer net O2 production and bottom-layer net O2 consumption, the rates of which were highly correlated32. Although oxygen-based methods could not be applied under oxygen-depleted conditions, independent measures of sulfate reduction (SR) in sediments, which dominated the benthic metabolism during warm months and led to significant sediment–water sulfide fluxes in the mid-bay33, 34, clearly support the accumulation of sulfide observed in August 2013 (Fig. 2f).
Subsurface pH minimum due to oxidation of reduced chemicals
Repeated vertical profiles during both summers revealed a consistent pH minimum below the surface mixed layer at our focused study station, a deep site in the upper part of the mid-bay. Salinity profiles at this site (Fig. 2a) combined with a time series of wind speed indicate a physical mixing event before our first sampling on August 9, 2013. Stratification quickly re-established when wind speed reduced and the wind direction switched from favoring mixing to favoring stratification (Supplementary Fig. 6a, b). Total alkalinity (TA) and DIC were lower in the surface, but became higher in the bottom water (Fig. 2b, c). Dissolved O2 was at saturation or supersaturation in the surface due to gas exchange and biological production and was not detectable below 10–15 m depths due to respiration (Fig. 2d).
On day 1, the mixed layer depth was still as deep as 15–18 m, but within 2 days, it shoaled to 10 m (Fig. 2a). Following this dynamic change, the O2 penetration depth changed from about 15 m on day 1 to about 10 m on days 3–5 (Fig. 2d). Simultaneously, water column pH (25 °C and NBS scale) decreased greatly over this period (Fig. 2e). For example, at the depth of 6 m, pH decreased from nearly 8.0 on day 1 to ~ 7.5 on days 3–5. A pH minimum (7.35 ± 0.03) occurred at 11–13 m depth in the low O2 zone (<10 μmol kg−1), below which pH increased slightly and then became constant at 7.45 ± 0.02. This pH minimum and the associated rapid pH decrease above it within a short period of <2 days have not been previously documented, although large pH changes were observed or expected in many strongly productive or stratified shallow water systems35–37. Such dramatic decreases in both O2 and pH over just 2 days could likely put the biological system under stress38. This pH minimum was also observed in August 2014, though water column O2 and pH profiles in August 2014 were relatively stable before and during the 5-days cruise, as wind speeds were less strong and less variable than those of the 2013 (Supplementary Fig. 7a, b), the oxycline (where O2 decreases rapidly) and the pH minimum were even sharper and shallower, and bottom-water pH, DIC and TA were lower in 2014 than 2013 (Supplementary Fig. 8).
We suggest the oxidation of reduced chemicals is responsible for the pH minimum in the low O2 zone and the rapid pH decrease above it where declining O2 gradients were steepest (Fig. 2e). The coupling between acid–base and redox chemistry is described by the following formula:
| 1 |
| 2 |
| 3 |
| 4 |
In August 2013, because of the strong mixing event prior to our cruise, the total concentration of H2S was only 5 μmol kg−1 at the 20 m depth on day 1, but it rapidly increased to 30–40 μmol kg−1 on days 3–5 when the water column was restratified (Fig. 2f)39. Oxidation of other reduced chemicals accumulating in the bottom water could also have contributed to the formation of the pH minimum. NH4 + concentration measured near our site was 15–20 μmol kg−1 at 20 m (Supplementary Fig. 9). Also, during days 3–5, bottom water [Mn2+] and [Fe2+] became as high as 7 and 2 μmol kg−1, respectively39. When these reduced species (total concentration ~ 60 μmol kg−1) were mixed upward into oxygenated water, they were oxidized, hydrogen ions were generated, TA was decreased and thus the water became more acidified (see Eqs. (1)–(4)). However, we recognize the oxidation of reduced species are often complex involving many intermediate steps and side products40 and could have different H+ production ratios.
It has been shown that oxidation of H2S by O2 is sufficiently slow that H2S can be brought near to the surface during vigorous mixing events and lead to fish kills in coastal waters20, 36, 41. Similarly, ammonia oxidation is not instantaneous12, 17, 41. We suggest that the slow oxidation kinetics and rapid mixing facilitate the transport of reduced species and can subsequently result in acidification of the oxygenated near- and sub-surface waters, potentially resulting in a negative impact on aquatic organisms38. If, for example, one volume of bottom water of 60 μmol kg−1 of reduced chemicals is mixed with one volume of sufficiently oxygenated water, the resulting mixed water has the total concentration of the reduced chemicals halved to 30 μmol kg−1, and eventually ~ 60 μmol kg−1 of acid (or −ΔTA) would be generated due to the oxidation of the reduced chemical species (Eqs. (1)–(4)). Based on CO2SYS simulations, the predicted pH decrease due to these oxidation reactions can be up to 0.20 pH units in Chesapeake Bay waters, although other mixing ratios and incomplete reactions due to slow kinetics may generate less of a pH decrease (Methods). This pH decrease is substantial and is consistent with our observations (Fig. 2e; also see a model simulation of TA, DIC, O2, and pH evolving loci below). Note that while the size and location of this pH minimum may vary depending on the strength of the physical mixing and [H2S] in the bottom water, it occurs whenever bottom-water anoxia exists regardless of whether a prior severe mixing event has occurred as in our 2013 study, because moderate mixing occurs constantly in the bay (Supplementary Fig. 7).
In sediment porewater, a pH minimum was reported at and above the O2 penetration depths as a result of oxidation of reduced chemicals, which diffused upward from deeper, anoxic depths42, 43 and was predicted by sediment diagenetic models44, 45. Such a pH minimum was also seen in low O2 waters of permanently stratified and anoxic deep basins including the Baltic Sea13, 17, the Black Sea18, 19, the Framvaren Fjord21, the Hunnbunn Fjord20, and the Cariaco Basin22 though no one has pointed out this phenomenon except Yao and Millero21 who commented that “the low pH is difficult to explain”. The pH minimum is an interesting feature that results from the decrease in TA:DIC ratio due to acid production during oxidation of reduced chemicals when encountering free O2 due to vigorous physical mixing. To our knowledge, this is the first time that such a pH minimum has been reported and properly interpreted in the water column. We predict that the pH minimum should occur in all oceanic systems that have seasonally or permanently occurring oxic–anoxic boundaries, including the above mentioned cases as well as in the dead-end canals of Delaware Inland Bays36, Lake Grevelingen (the Netherlands)12, the Saanich Inlet46, and estuaries and bays elsewhere17, 20. We further argue that the pH minimum is likely more dynamic in seasonally anoxic coastal systems than permanently anoxic deep basins, due to the shallower water depth and higher frequency of physical disturbances. Physical disturbances such as winds and tides occur regularly in the Chesapeake Bay (Supplementary Fig. 7a, b) and other seasonally stratified coastal waters12, 36. Therefore, their chemical and biological consequences, in the context of coastal OA and deoxygenation, deserve further attention.
Geochemical drivers and carbonate dissolution
To separate biological processes from physical mixing and to explore the biogeochemical control mechanisms in a broader context, we examine TA and DIC vs. salinity relationships at this site together with data from other areas of the bay and the river and offshore endmembers (Fig. 3a). Between the river and ocean endmembers, as expected, TA and DIC increased with salinity. However, at our focused study station, all subsurface and bottom-water samples were located well above the mixing lines, indicating net release of CO2 and accumulation of DIC and TA. In addition, both DIC and TA data collected at the Chesapeake Biological Laboratory (CBL) dock, downstream of our focused study site at the lower end of the mid-bay, were also above the mixing lines. Those from the Virginia Institute of Marine Science (VIMS) dock, farther downstream near the bay mouth, however, showed the least enrichment relative to the conservative mixing lines. We also calculated the acid–base buffer factors from TA, DIC, and nutrients (PO4 3−, H2S, and NH4 +) (Methods). It is clear the bay waters are poorly buffered as indicated by their much lower buffer factors compared to offshore waters here and elsewhere (Fig. 3b; also see next section for definitions and explanations).
Fig. 3.
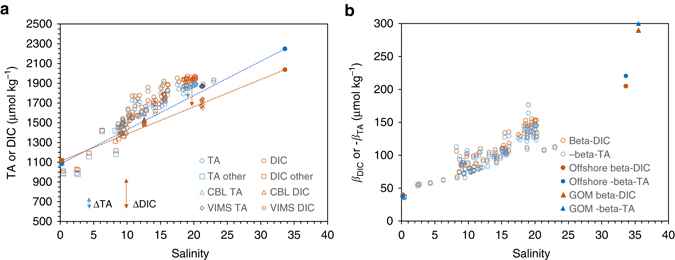
Total alkalinity and dissolved inorganic carbon as well as buffer factor distributions against salinity in August 2013. a Total alkalinity (TA) and dissolved inorganic carbon (DIC) and b buffer factors (see definitions in Eqs. (6) and (7)). Most data were collected at the focused study site over a 5-day period, as marked in Fig. 1 (station 858). Those marked as TA other or DIC other were collected in waters between station 858 and the Chesapeake–Delaware Canal in the upper bay (Fig. 1). Data were also collected in the mid- and lower-bays at the CBL dock and the VIMS dock shortly after the main cruise
TA is usually a good conservative tracer of river–ocean mixing within an estuary because it is not influenced by CO2 addition and removal. Because TA and DIC share a common major component (HCO3 −), deviations of DIC from the nearly conservative behavior defined by TA and salinity provide a measure of biological use or release of CO2 47. Bottom waters in the Chesapeake Bay, however, are conspicuously different from this general geochemical behavior normally encountered in oxygenated or moderately low oxygen environments8, 9, 47. DIC not only show a large enrichment against the conservative mixing line, but TA is also substantially enriched; with the excess DIC and TA reaching 275.3 ± 59.5 and 167.3 ± 54.2 μmol kg−1 respectively (Fig. 3a, Methods).
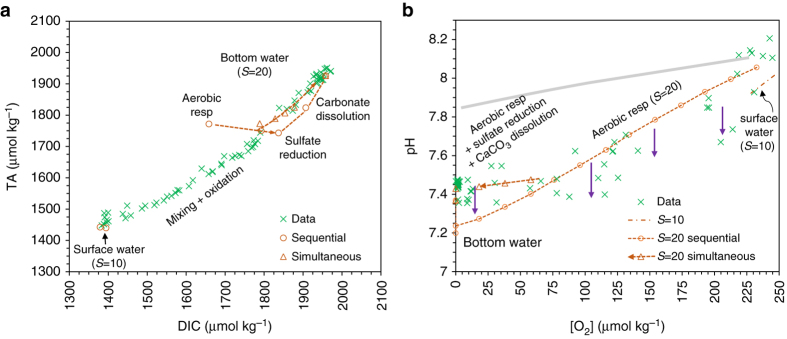
In any estuary, the most important internal sources of TA and DIC are aerobic respiration (AR), SR, and carbonate dissolution (CD)12, 13, 21, 45 (Fig. 4a, Table 2). Because each of these processes has a distinctly different ΔTA to ΔDIC ratio and involves a different pH change (Table 2), ΔTA:ΔDIC ratio and pH change become diagnostic of the geochemical processes. Based on the mixing line prediction, we can calculate the initial DIC and TA values at salinity (S) = 10 g kg−1 for surface water and S = 20 g kg−1 for bottom water. From the solubility constants we can also determine the initial concentrations of O2 in S = 10 and 20 g kg−1 waters. Assuming the bottom water starts with a fully saturated dissolved O2, we can then derive DIC and TA generations and pH change for each step (Table 2). In this poorly buffered water (Fig. 3b), the complete use of O2 solely for AR would drive bottom-water TA and pH lower than the observed values (Fig. 4a, b). Sulfate reduction and CaCO3 dissolution must then be invoked to explain the observed TA and pH. The effects of SO4 2− reduction on TA and DIC can be estimated from the observed [H2S] (Table 2) and the rest is made up by CaCO3 dissolution (Methods). We envision that these three processes can occur either sequentially (Table 2) or simultaneously when O2, pH, carbonate mineral saturation state are sufficiently low. While the sequential pathway simulates the general patterns of the TA and DIC relationship (Fig. 4a) and the pH and O2 relationship (Fig. 4b) reasonably well, it appears that CaCO3 dissolution must have proceeded and occurred simultaneously with AR and SR as the simultaneous pathway simulates the observation better (Fig. 4a, b) and as is justified by the very low aragonite carbonate saturation state once more than 50% of O2 is consumed (Table 2).
Fig. 4.
Model simulations of the evolution of total alkalinity, dissolved inorganic carbon, pH, and O2 during biogeochemical processes. a Total alkalinity (TA) and dissolved inorganic carbon (DIC) relationship and b pH (25 °C and NBS scale) and [O2] relationship. The biogeochemical pathway, or TA and DIC loci, includes aerobic respiration (AR), sulfate reduction (SR) and CaCO3 dissolution (CD). Predicted pH or TA values are provided together with observed pH or TA (calculated from pH and DIC data from August 2013). Both sequential (open circles) and simultaneous (triangles) pathways are presented. Purple arrows represent acidification generated by oxidation of reduced chemicals (H2S). The light shaded line at the top indicates the pH and [O2] relationship from the Gulf of Mexico reflecting aerobic respiration
Table 2.
O2 consumption and DIC and TA production during sequential aerobic respiration, sulfate reduction and carbonate mineral dissolution in bottom waters45, 83
| Redox | Δ[O2] ( μmol kg−1) | ΔDIC ( μmol kg−1) | ΔTA ( μmol kg−1) | ΔTA/ΔDIC | pH | Ωarag |
|---|---|---|---|---|---|---|
| AR | (CH2O)106(NH3)16(H3PO4) + 106O2 ↔ 106CO2 + 16HNO3 + H3PO4 + 122H2O | −(16+1)/106 = −0.16 | ||||
| 0 (100%) | 0 | 0 | 8.055 | 1.56 | ||
| −58 (75%) | +45 | −7.2 | 7.859 | 1.05 | ||
| −117(50%) | +90 | −14.4 | 7.629 | 0.65 | ||
| −174(25%) | +134 | −21.5 | 7.421 | 0.40 | ||
| −231.7(0%) | +178.0 | −28.5 | 7.237 | 0.26 | ||
| SR | (CH2O)106(NH3)16(H3PO4) + 53SO4 2− → 106HCO3 − + 53H2S + 16NH3 + H3PO4 | (106+16−1)/106 = 1.142 | ||||
| 0 | +70.0 | +80.6 | 7.199 | 0.25 | ||
| CD | CaCO3 + CO2 + H2O → Ca2+ + 2HCO3 − | 2/1 | ||||
| 0 | +57.6 | +115.3 | 7.368 | 0.38 | ||
| Total | −231.7 | +305.6 | +167.3 | |||
AR, aerobic respiration; CD, carbonate dissolution; DIC, dissolved inorganic carbon; SR, sulfate reduction; TA, total alkalinity. The last columns listed the expected pH and aragonite mineral saturation state (Ωarag) values at the end of each step. pH and Ωarag values are also calculated at the initial and mid-points of O2 consumption (or % of O2 saturation). For simultaneous reactions at low pH and Ωarag, see the text. The calculation steps and results are detailed in the Methods. Note for a more stable carbonate mineral, calcite, Ωcalcite = 1.5 × Ωarag
From the above simulations, we conclude that up to ~70% of the bottom-water TA production comes from CaCO3 dissolution, which raises bottom-water pH from expected 7.25 to 7.45 and provides an important buffer mechanism in bottom waters (Methods). It has been reported that eutrophication led to lower pH in the polyhaline (S > 18 g kg−1) part of the bay between 1985 and 200826. Based on our data and model simulations, we suggest that eutrophication in the bay has led to more O2 consumption, SO4 2− reduction, pH decrease, and dissolution of CaCO3 shells and abiotic minerals in subsurface and bottom waters, consequently leading to possibly more TA and DIC export to the coastal ocean.
While shellfish calcification can represent a significant store of CaCO3 in the Chesapeake Bay26, 48, much of the CD present in the current study likely also comes from abiotic precipitation in surface waters, a mechanism noted before in the Loire estuary49. The extent of CD in deep waters estimated here could be supported by independently estimated CaCO3 production in surface waters from deviations from conservative mixing (Supplementary Fig. 10)48, which is consistent with the TA deficit observed here in low-salinity surface waters (Fig. 3a). While the precipitation may largely be driven by seasonal dynamics in primary production enhanced by estuarine eutrophication49, importantly, current and future increasing atmospheric CO2 due to fossil fuel production may lower surface water carbonate saturation state enough to decrease mineral formation and thus delivery below the pycnocline. If so, the bay’s deep water would have a reduced capacity to neutralize metabolically generated CO2, further enhancing eutrophication driven acidification.
Another important metabolic pathway is denitrification which uses NO3 − as the oxidant for organic matter decomposition50, 51. Note that [NO3 −] is generally low in the mid-bay (<1 μmol kg−1). However, denitrification is often coupled to nitrification at the sediment water interface. System-wide integrated denitrification rate has been estimated to be about 70 μmol m−2 h−1 in the Chesapeake Bay (summer time)52, although other estimations are lower. Taking this value as the upper end, we estimate that denitrification can contribute to a DIC production of up to 17 μmol kg−1 and TA production of up to 16 μmol kg−1 in a 10 m bottom-water column and over a 100-day period. This amount is only up to about 8% of the total TA production in the bottom water observed here. Finally, while organic matter decomposition using metal oxides as oxidants is important intermediate steps for biogeochemical cycles, the contributions to alkalinity production must be lower in the bay as recycled [Mn2+] (<7 μmol kg−1) and [Fe2+] (<2 μmol kg−1)39 are much lower than the observed TA production in the bottom water; a conclusion similar to that derived in the Baltic Sea13, 21.
Discussion
The buffering capacity reflects the marine carbonate system’s ability to resist changes in pH (or pCO2) when DIC and/or TA are altered by physical and biogeochemical processes and when relevant thermodynamic constants are altered by temperature (T) and salinity (S) changes53–58. Mathematically, an aquatic system’s ability to resist pH change can be deconstructed into its sensitivity to changes in T, S, DIC, and TA.
| 5 |
Here the first and second terms represent the effects of change in thermodynamic constants as a function of T and S. The third term reflects the pH change when DIC is added while keeping T, S, and TA constant and the fourth term reflects the pH change when a strong acid (H+ or –ΔTA) is added while keeping T, S, and DIC constant. The slopes in the third and fourth terms are directly related to the buffer factors β DIC and β TA defined before53, 54 with
| 6 |
and
| 7 |
In estuarine conditions, because β DIC and β TA are similar in magnitude54 (also see Fig. 3b), the overall contribution to acidification or pH decrease is largely decided by changes in DIC and TA during physical and biogeochemical processes (e.g., at constant T and S) and also by the initial buffering capacity (e.g., at variable T and S).
The pH and [O2] relationship in Chesapeake Bay waters differs greatly from that observed in northern Gulf of Mexico (nGOM) waters (shaded line in Fig. 4b)9. It appears that Chesapeake Bay waters are more vulnerable to both anthropogenic CO2 and biological induced acidifications because they have a lower buffering capacity than that of the offshore waters, in particular, in the nGOM as TA and DIC are lower in the Susquehanna River and US eastern margin waters than those of the Mississippi River and nGOM seawater (Figs. 3b, 4b and 5a)9, 59, 60. However, our simulations and those of the previous studies12, 53–57 suggest that lower buffering capacity itself does not necessarily lead to low pH (Fig. 5a); rather, it allows a much greater pH decrease when other sources of CO2 or strong acids are added (Fig. 5b). Similar amounts of AR (Table 2) would lead to a pH decrease of only 0.4 units in the strongly buffered nGOM waters whereas a larger decrease of nearly 0.8 units would occur in the poorly buffered Chesapeake Bay waters at the present day conditions (at S = 34 and 20 g kg−1, respectively, Figs. 4b and 5c).
Fig. 5.
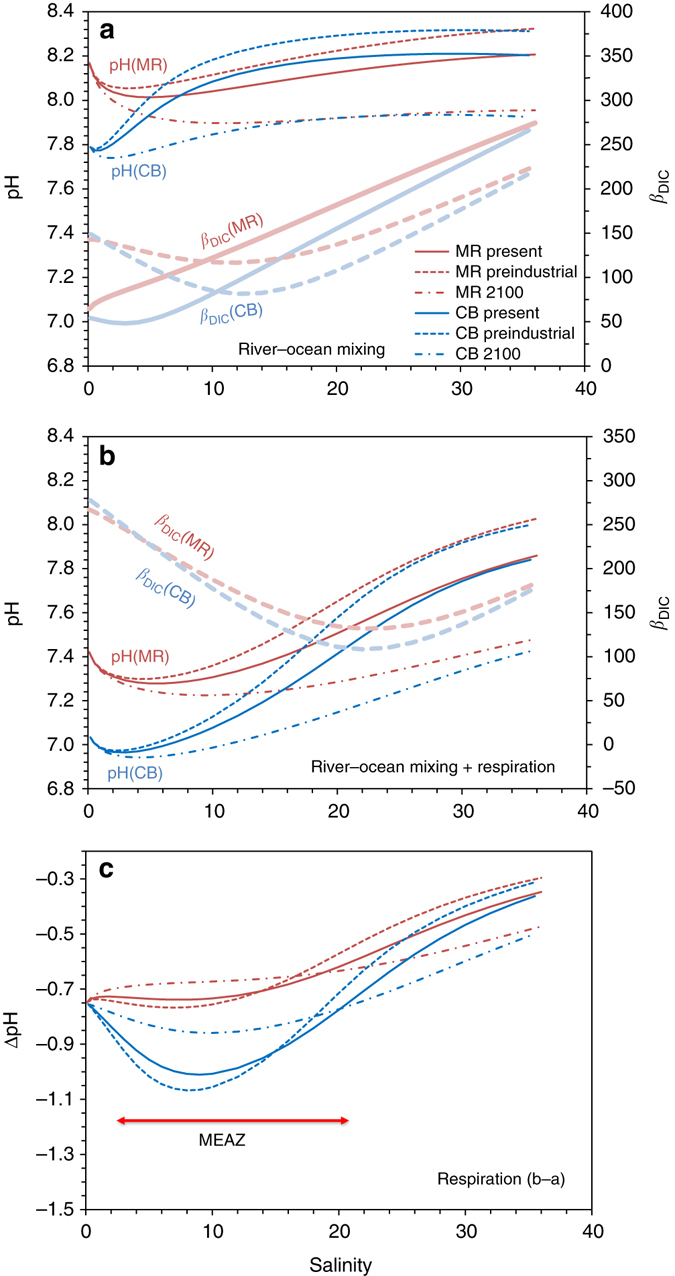
Simulations of pH and pH decrease and the evolution of the buffer factor β DIC in Chesapeake Bay (CB) waters and Mississippi River (MR) coastal waters. a pH curves (thin lines) during estuarine mixing under three scenarios (preindustrial era, present day, and year 2100). Buffer factor β DIC for the present day condition (thick solid lines) and the present day condition plus 100 μmol kg−1 (thick dashed lines) are also presented for both estuaries. b pH curves and β DIC curves plus full O2 consumption (respiration) during estuarine mixing. (c) pH decrease (−ΔpH) as a result of full O2 consumption during estuarine mixing (a difference between b and a). The red arrows represents the Maximum Estuarine Acidification Zone (MEAZ). Note that β DIC presented here does not match that from the real data (Fig. 3b) at low salinities as a stratified and O2 depleted state does not exist for the very low salinity part of the Chesapeake Bay
While the OA signal due to CO2 uptake in the open ocean regions is similar across middle and lower latitudes, the manifestation of this anthropogenic CO2 signal through ocean–river mixing in estuaries is dependent on the river TA and DIC values, which are highly variable among the world’s rivers61, and whether CO2 is also introduced via microbial respiration11, 60. Due to the very high river TA and DIC and the resulting strong buffering capacity over the entire salinity range in the Mississippi River impacted coastal waters, pH change due to OA is proportional to the open ocean OA source signal and salinity and decreases toward zero salinity (Fig. 5a)9, 60, 62. In the Chesapeake Bay where average river TA, DIC, and buffering capacity are low, however, the oceanic OA signal is amplified in the low and middle salinity zone. Here the combination of reduced buffering capacity (with decreasing salinity) and a still sufficiently strong open ocean OA signal generates a minimum buffer zone60 and thus a Maximum Estuarine Acidification Zone (MEAZ) (Fig. 5c). The existence of a MEAZ and its salinity range depend not only on the river TA value, but also the TA:DIC ratio60. When CO2 addition from AR increases from 0 to 100 and finally to ~200 μmol kg−1 (or 0 to roughly half or to a full O2 consumption depending on the salinity and temperature), the minimum buffer zone shifted from salinity ~4 to ~13 (Fig. 5a) and finally to ~23 (Fig. 5b)60. Note that local CO2 uptake, carbonate mineral dissolution and SR are not included in this discussion (Fig. 5) and would further modify the estuarine buffering capacity as they would modify the TA to DIC ratio in estuarine waters (Table 2, Figs. 3b, 4a, b).
Below we further discuss the effects of anthropogenic CO2 and biological CO2 and acid additions on estuarine pH buffering capacity53, 54. The marine carbonate system has a minimum buffering or maximum pH change point when DIC increases approximately equal to that of TA (or TA:DIC ≈ 1) where [CO2] = [CO3 2−] + [B(OH)4 −] (if we ignore all other weak acid–base species). At this point, any addition or removal of CO2 or acids will result in a maximum pH decrease or increase. Because DIC is slightly higher than or nearly equal to TA in rivers47, 62, 63 and is lower than TA in seawater, there may exist a small crossover of DIC and TA at the very low-salinity zone. A peculiar pH minimum occurring in the low-salinity zone of estuaries is related to this mixing feature as was noticed a long time ago in both closed64 and open65 system simulations. Furthermore, how CO2 is added to the estuarine waters affect how the crossover point will move. First we contend anthropogenic CO2 does not directly add to the high pCO2 river water but is mixed into the estuary via river–ocean mixing60. In contrast, respiratory CO2 is nearly equally added to the bottom water based on O2 consumption regardless of the mixing index or salinity (except that O2 solubility increases when salinity decreases, but it is a small correction). In Fig. 6, we summarize several scenarios illustrating how the crossover point of the TA and DIC to salinity lines or the point of TA:DIC ratio = 1 moves along the TA-salinity line. Adding anthropogenic CO2 to the seawater endmember would move this crossover point to only a slightly higher salinity. Adding biological CO2 (for example 100 μmol kg−1) to both the river and ocean endmembers would, however, shift the DIC line to a much higher position (parallel to the original line) creating a crossover point located at a salinity substantially higher than the original one. Finally the combined effect of anthropogenic CO2 and biological CO2 from respiration moves the crossover point to an even higher salinity. These crossover points are consistent with the progressive shift of the minimum buffer factor (β DIC), the pH minimum, and the maximum acidification zone (–ΔpH) presented in Fig. 5. However there appears a difference in the location (salinity) between the minimum buffer factor (β DIC) and the maximum acidification (–ΔpH). This is because ΔpH represents the accumulative pH change between an end point and a beginning point while the buffer factor reflects the pH sensitivity at a specific point if additional DIC is added to the system.
Fig. 6.
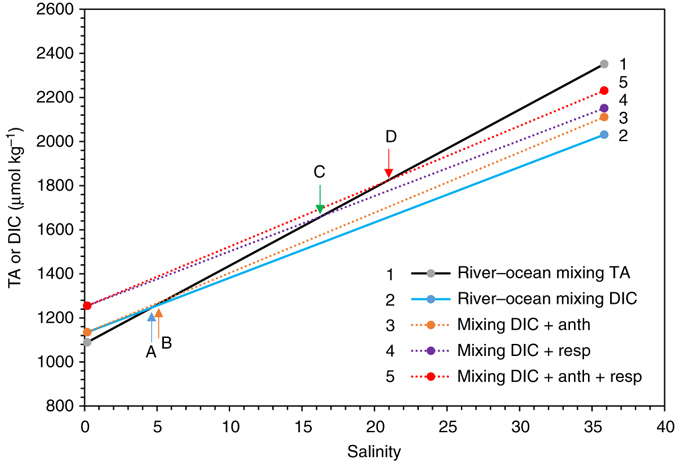
Estuarine TA or DIC mixing lines between the river and ocean endmembers with additional CO2 added in from anthropogenic sources and respiration. Line 1 is river-ocean mixing of TA, line 2 is river-ocean mixing of DIC, line 3 is mixing DIC plus anthropogenic CO2 addition, line 4 is mixing DIC plus respiratory CO2 addition, and line 5 is mixing DIC plus both anthropogenic and biological CO2 additions. The crossover points are river–ocean mixing lines of TA with A river–ocean mixing lines of DIC, B mixing plus anthropogenic CO2, C mixing plus CO2 from respiration, and D mixing plus CO2 from both B and C
In summary, large estuarine water bodies, exemplified by the Chesapeake Bay, are particularly vulnerable to the anthropogenic CO2 and eutrophication-induced coastal OA. In this paper we emphasize that subsurface H2S oxidation (~0.2 pH units) and local surface CO2 uptake (~0.1 pH units) work together with known organic matter respiration and the open-ocean OA source signal to drive substantial acidification and CaCO3 dissolution in estuarine subsurface waters. Currently, acidification due to CO2 input from AR (up to 0.8 pH units) in the bay exceeds that from the atmospheric CO2 increase in the open ocean (~0.1 pH units in surface waters and the signal is mixed into estuaries proportional to salinity) and local estuarine uptake; but towards the end of this century the latter will approach or exceed the former and the synergy between them will also increase. In addition, future increasing atmospheric CO2 due to fossil fuel production may lower carbonate saturation state enough to decrease mineral formation in surface water and thus delivery below the pycnocline, where we have currently demonstrated that CaCO3 dissolution offsets a significant proportion of the metabolic CO2 effect on acidification. We further recognize that natural and anthropogenic acidification mechanisms most relevant to estuarine acidification are characterized by various time scales. They range from nearly instantaneous for acid–base equilibrium66, to minutes for CO2 hydration66, and to minutes to hours for H2S oxidation36, 41, 67. In contrast, time scales for physical mixing are on the order of tidal or less, to daily and seasonal30, 31, 68 while local CO2 uptake from the atmosphere and its accumulation in the water column and acidification of the bottom water as well as pelagic and benthic respirations operate over tidal to seasonal scales12, 13, 35, 37, 69. Although anthropogenic changes in external forcing due to variability in river and ocean endmembers may also have a seasonal component, decadal and centennial variation is more important5, 35, 70, 71. This mosaic of processes with different time and space scales poses a great challenge in our ability to understand and predict coastal OA.
Methods
Site and cruise descriptions
The Chesapeake Bay is the largest estuary in the US. The August 2013 survey started from the upper estuary near the Susquehanna River mouth (Fig. 1a). The upper and middle Chesapeake Bay were surveyed during 9–14 August 2013 by RV Hugh R. Sharp. The water column survey focused mainly at one site south of the Bay Bridge (38°58.8 N, 76°22 W), where a field study of redox chemistry39 and water column inorganic carbon and pH were carried out. We consider this site as the up end of the mid-bay. We repeatedly sampled the water column at high slack tide and low slack tide. During this 5-day survey, an excursion was made south to the middle bay near Solomons Island. After the completion of the cruise, we set up two 24-h dockside measurements, one at the dock of the Chesapeake Biological Laboratory (CBL; 38.317317° N, 76.450980° W) on Solomons Island near the southern end of our ship-based survey and another further south at a pier of the Virginia Institute of Marine Science (VIMS; 37.2473° N, 76.4994° W) near the bay mouth. A similar study was conducted during 18–24 August 2014 (Supplementary Fig. 1). We also conducted a spring survey (11–16 April 2015) to get an initial condition before the hypoxia season (Fig. 1b).
Sample and analytical methods
Salinity, temperature, and O2 were obtained from the CTD Rosette system. Total sulfide (H2S and HS−) was determined by voltammetry using solid state Au/Hg electrodes36, 39, 43. Surface water partial pressure of CO2 (pCO2), position, temperature, and salinity information were measured underway while the ship was sailing or anchored by pumping surface water from under the ship to the shipboard laboratory using an underway pCO2 system72. TA and DIC water samples were taken from Niskin bottles and were preserved and stored in 250 ml borosilicate glass bottles with 100 μl saturated HgCl2 solution73. TA and DIC samples were stored at refrigerated temperature (~5 °C) before being measured (within 4 weeks). TA samples were measured by open-cell Gran titration with a precision better than ±0.1% using an Apollo Scitech Seawater Total Alkalinity titration system73. DIC samples were analyzed by adding phosphoric acid into sample waters to release CO2, which was measured by an infrared CO2 analyzer (LI-COR 7000) with an overall precision of ±0.1% using an Apollo Scitech DIC Analyzer73. Both TA and DIC measurements were quality controlled by Certified Reference Materials from Andrew Dickson of the University of California at San Diego. pH samples were taken by the same Niskin bottle and were measured by an Orion Ross glass electrode within 1 h after the water temperature was stable in a 25.0 ± 0.1 °C thermal bath on the research vessel. The electrode was calibrated against three NBS (NIST) standards and pH values are reported in NBS scale and at 25 °C. Note that pH values in NBS scale are about 0.1 pH unit higher than those reported in total H+ scale (pHT) elsewhere.
Uncertainty in determining DIC and TA enrichment
We averaged all subsurface and bottom waters (S > 11 g kg−1) to derive a DIC enrichment of 275.3 ± 59.5 and a TA enrichment of 127.3 ± 54.2 μmol kg−1 , with respect to their expected conservative behaviors. The TA enrichment is underestimated because of a technical challenge caused by HgS precipitation, which releases H+ when HgCl2 was used to stop microbial activity18, and/or oxidation of H2S and NH4 + during sample storage and/or analysis (which also generate H+). TA values calculated from DIC and pH analyzed onboard (neither is subject to the sample preservation and storage problems) agree well with measured TA except in the bottom waters (Supplementary Fig. 11a), and the disagreement increases as [H2S] increases (Supplementary Fig. 11b). The internal consistency analysis suggests that TA reduction due to sample preservation and storage is 40 ± 20 μmol kg−1; thus, the most likely TA enrichment in the bottom water is (127.3 ± 54.2) + (40 ± 20) = 167.3 ± 57.6 μmol kg−1.
Determination of the endmembers and mixing lines
Lowest salinity values (from the station immediately downstream of the Susquehanna River) were selected as the river endmember values (S, TA, and DIC were measured as 0.189 g kg−1, 1089.2 μmol kg−1, and 1115.1 μmol kg−1 , respectively), though the station near the canal had the lowest TA and DIC due to mixing of water from the Delaware Bay. The offshore end-member data were collected at Latitude and Longitude of 37.13333° N and 73.32533° W on August 14 at the end of the cruise. We took the average values of the surface 45 m as the ocean endmember (S = 33.618 ± 0.139 g kg−1, TA = 2248.4 ± 78.4 μmol kg−1, and DIC = 2037.9 ± 72.4 μmol kg−1). So, the TA conservative mixing line is TA = 34.676 × S + 1082.7 and the DIC line is DIC = 27.607 × S + 1109.9.
Calculation of air–sea CO2 flux and the DIC increase
Water surface pCO2 was measured every 1–1.5 min with calibrations every 6–12 h (August 2013, August 2014, and April 2015). Atmospheric pCO2 values were also measured every 2–4 h during these cruises. Both atmosphere and water CO2 values were measured in a dry condition (xCO2) and were converted to pCO2 in 100% water saturated conditions inside the equilibrator (pCO2(eq)) by considering water vapor pressure:
| 8 |
where P b is barometric pressure and P weq is water vapor pressure in the equilibrator. For water data, the pCO2(eq) is further converted to estuarine surface water pCO2 (pCO2(water)) by considering temperature changes between the surface water and the equilibrator through the following equation72:
| 9 |
where SST is sea surface temperature (°C) and T eq is temperature in the equilibrator. Our measured atmospheric xCO2 values were also converted from dry condition to near sea surface wet condition (pCO2(air)) by Eq. (10):
| 10 |
Here P b is barometric pressure and P w is water vapor pressure at the sea surface. Each pCO2(water) and its corresponding pCO2(air) were used to calculate the gas exchange flux (F CO2) between atmosphere and water by Eq. (11).
| 11 |
where k represents the gas transfer velocity and K 0 is the solubility of CO2 74. We adopted Ho et al.75 as the gas transfer velocity and an ensemble of gas transfer parameters to evaluate the uncertainty range following the previous practice72, 76. Finally, the coefficient C2 corrects the non-symmetrical distribution of wind76. A negative air–sea CO2 flux means an uptake of atmospheric CO2 for the water.
Over at least a 100-day water residence period (from May to August) and over a water column of 20 m, this CO2 flux can be converted into an increase in DIC of, 4.3–6.7 (mmol m−2 d−1) × 100d/20 m ≈ 21.5–33.5 mmol m−3 or 21.2–33.1 μmol kg−1 (here a density of 1012.09 kg m−3 is used). We used the entire water column rather than the surface mixed layer because the main concern here is how local CO2 uptake, via internal mixing, contributes to acidification of the especially vulnerable bottom waters.
Calculation of pH decrease due to local CO2 uptake
With H2S included, the calculation of pH (in NBS scale and at 25 °C) decrease was performed using the modified CO2SYS program. Note another program, AquaEnv, also has such a capacity77. We used day 4 data with S = 18.618 g kg−1, T = 25.28 °C, depth = 17 m, DIC = 1933.8 μmol kg−1, total [H2S] = 37.79 μmol kg−1, [NH3+NH4 +] = 13.6 μmol kg−1, T-PO4 = 3.5 μmol kg−1, and pH = 7.476 to calculate a TA = 1934.1 μmol kg−1. Then, we subtracted the summer DIC by 21.2–33.1 μmol kg−1 (=1912.6–1900.7 μmol kg−1) to calculate a new pH (7.557–7.604). Thus, the pH decrease by an increase of DIC derived from local uptake of atmospheric CO2 is 0.081–0.128 pH unit over the entire period from spring to summer.
pH decrease due to oxidation of reduced chemicals
We used day 4 data with S = 15.145 g kg−1, T = 25.36 °C, depth = 12.54 m, DIC = 1767.7 μmol kg−1, [H2S] = 2 μmol kg−1, and pH = 7.354 to calculate a TA = 1698.8 μmol kg−1. Then, we subtracted a 30–60 μmol kg−1 from TA to calculate a new pH (7.152–7.246). Thus, the pH decrease by a 30–60 μmol kg−1 of TA reduction is 0.108–0.202 pH units (represented by the purple arrows in Fig. 4b). The modified version of CO2SYS was used for all the CO2 and pH calculations. Note, adding a <3 μmol kg−1 of T-PO4 would only lead to <0.005 pH unit decrease in the calculation. Thus, its infleunce is ignored here.
Modification of the CO2SYS program
The modifications were done on the Excel version 2.1 of the program78, which is available for download from CDIAC (http://cdiac.ornl.gov/ftp/co2sys/). A Matlab version is available from the corresponding author. In addition to the total Phosphate and Silicate, the program now accepts the total NH3 and total H2S in µmol (kg of SW)−1. The contribution of each to the alkalinity is given by:
| 12 |
and
| 13 |
where and K H2S are the dissociation constants of ammonium (NH4 +) and hydrogen sulfide (H2S).
The dissociation constant for NH4 + was taken from Clegg and Whitfield79 and is valid for S = 0–40 g kg−1 and t = −2 to 40 °C (note ref. 21 essentailly provided the same constant). The constant for H2S was taken from Millero et al.80 and is valid for S = 0–40 g kg−1 and t = 0–35 °C. When the pressure is not zero, a correction is applied according to Millero81. A comparison with AquaEnv under [H2S] <50 (or 300) μmol kg−1 shows a good agreement of calculated pH (in free scale) within 0.0003 (or 0.0026) from known TA and DIC. We have further tested the calculations with waters containing high concentrations of H2S and posted this modified version of the CO2SYS program on the CDIAC website for public access82.
Simulation of bottom-water geochemical pathways
We present here the calculation methods for Table 2 and Fig. 4a, b. For the bottom-water condition (S = 19.87 g kg−1 and T = 25 °C), we have a saturated [O2] = 231.7 μmol kg−1, and, from the mixing line at S = 19.87 g kg−1, TA = 1771.1 μmol kg−1 and DIC = 1658.5 μmol kg−1, we have pH = 8.066. If all dissolved O2 is used by heterotrophic bacteria for organic carbon respiration via Redfield stoichiometry45, 83, it would increase DIC by 178.0 μmol kg−1 and decrease TA by 28.5 μmol kg−1. To be consistent with our observation, SR and CaCO3 dissolution must have increased bottom-water TA by a total of 195.9 μmol kg−1 (i.e., observed 167.3 μmol kg−1 plus expected −28.5 μmol kg−1) beyond conservative mixing. We estimate TA increase from SO4 2− reduction as 80.6 μmol kg−1 from the total concentration of H2S (35 μmol kg−1)39 by the following equation:
| 14 |
where 2 × [H2S] represents an equal amount of HCO3 − and HS− production during SO4 2− reduction and 16/53 × [H2S] represents NH3 production (and contribution to TA) based on stoichiometry (see Table 2). Then the TA generated from CaCO3 dissolution must be as high as 115.3 ± 20.0 μmol kg−1 by the difference (195.9–80.6) and contributes up to 70% of total amount of TA production. The amount of DIC production following these steps is 305.6 ± 10.0 μmol kg−1. This is within the uncertainty of the observed value of 275.3 ± 59.5 (Fig. 3). The 10% difference (30 μmol kg−1) can be explained either by TA increase due to organic matter respiration using nitrate (denitrification) and metal oxides13, 45 and/or the deviation of C/N ratio from the Redfield ratio13, 84, 85 as well as probably organic alkalinity contribution86. Indeed if a lower C to −O2 ratio (106/154 = 0.688) given in ref. 84 is used, the produced DIC would be close to the observation.
From the resulting pH and Ωarag (Table 2), it is clear when O2 is partially consumed aragonite mineral becomes undersaturated (starting at 75% O2 saturation) and CaCO3 dissolution can proceed together with AR. To simulate the observed DIC (measured) and TA (calculated from DIC and pH) data, we assume the dissolution does not occur until a sufficiently low Ωarag in waters and that the first 20% of CaCO3 dissolution occurs before or at DO = 33%. Then the second, third and fourth 20% of the CaCO3 dissolution occurs before or at DO = 16%, 8%, and 0%, respectively. The last 20% of the CaCO3 dissolution occurs together with SR.
Simulation of pH changes
We present here the calculation methods for Fig. 5a, b. Although each term in Eq. (5) may be derived analytically, in this paper, we obtain the overall pH change, ΔpH (presented in Fig. 5c), numerically using the updated CO2SYS program. Conditions used are given below.
We assume a present day atmospheric dry CO2 fraction (xCO2) as of 396.2 ppm and the corresponding water pCO2 = 384.0 μatm at 25 °C and salinity = 36.0 g kg−1. xCO2 is set to 281.3 ppm for the pre-industrial era and 798.0 ppm for year 2100.
For the Chesapeake Bay simulation, we take TA from the offshore water at 74.9 m, S = 35.839 g kg−1, and TA = 2351.5 μmol kg−1. Equilibrium of this water with the atmosphere yield a DIC = 2030.3 μmol kg−1 and pH = 8.198 (in NBS scale) at 25 °C and 1 m of water depth. For the Gulf of Mexico water, we take the endmember values from Cai et al.9 and adjust the present condition slightly to the above pCO2. The present day conditions are S = 36.3, TA = 2398.1 μmol kg−1, DIC = 2065.2 μmol kg−1, pH = 8.203 at 25 °C and 1 m water depth.
For the Mississippi River end-member conditions, we have S = 0.1 g kg−1, TA = 2400 μmol kg−1, DIC = 2430 μmol kg−1, and pCO2 = 1388.9 μatm. For the Susquehanna River, we have S = 0.189 g kg−1, TA = 1089.2 μmol kg−1, DIC = 1135 μmol kg−1, and pCO2 = 1514.9 μatm.
For Mississippi/GOM bottom water, at S = 34 g kg−1, T=25 °C, and [O2] = 216.0 μmol kg−1, complete O2 consumption would lead to a DIC increase of 216 × 106/138 = 165.9 μmol kg−1 and a TA decrease of 26.6 μmol kg−1. For Chesapeake Bay bottom water, at S = 20 g kg−1, T = 25 °C, and [O2] = 232.6 μmol kg−1, complete O2 consumption would lead to a DIC increase of 216 × 106/138 = 178.7 μmol kg−1 and a TA decrease of 28.7 μmol kg−1.
Buffer factor calculation
We calculate these buffer factors (Fig. 5) following the analytical formula provided by Egleston et al.54 with a typo corrected87. Specifically, we extract out species concentrations and thermodynamic constants from the updated version of CO2SYS. We also compare results with those calculated with two other programs AquaEnv and SEACARB (http://CRAN.R-project.org/package=seacarb) and the agreement is reasonable (within 8 μmol kg−1 or 3%) as is expected. Although H2S and NH4 are not included in the analytical equations, as our equilibrium calculation already include these acid–base species and [H2S] and [NH4] are not high in the bay, the calculated results are similar to those from the AquaEnv which includes fully these reduced chemical species. Finally, in Fig. 3b, for the real system buffer factors, we directly use AquaEnv. Given the low [H2S] in the bay, with or without H2S have only resulted in a minor difference in buffer factor calculation.
Computer program availability
The modified CO2SYS program on Excel version 2.1 is available for download from CDIAC (http://cdiac.ornl.gov/ftp/co2sys/). The Matlab version is available from the corresponding author upon reasonable request.
Data availability
All data are available from the corresponding author upon reasonable request and will be deposited at the US National Centers for Environmental Information (https://www.nodc.noaa.gov/oceanacidification/).
Electronic supplementary material
Acknowledgements
This work was supported by internal funds from the University of Delaware Provost’s office and the College of Earth, Ocean and Environment Dean’s office to W.-J.C., by grants from the National Science Foundation (NSF OCE-1559312) and NASA (NNX14AM37G) to W.-J.C., by grants from NSF (OCE-1155385) and the U.S. National Oceanic and Atmospheric Administration (NOAA) Sea Grant program (NA14OAR4170087) to G.W.L., and a NOAA grant to J.T., W.-J.C., M.L., G.G.W., J.C., and W.M.K. (NA15NOS4780190, publication # 17-001). We thank Xinping Hu for discussion and the Chesapeake Bay Program and the Maryland Department of Natural Resources for the monitoring data. This is UMCES publication number 5369.
Author contributions
W.-J.C. and G.W.L. are responsible for the design of the fieldwork. W.-J.C. is responsible for data analysis and writing of the paper. W.-J.H., M.X., A.J., R.M., J.B., N.H. are responsible for data collection and sample analysis. Y.-Y.X. contributes to buffer factor calculation. M.L. contributes to physical mixing part. J.T. and W.M.K. contribute to the biological production part. All authors have contributed to discussion and revision of the paper.
Competing interests
The authors declare no competing financial interests.
Footnotes
Electronic supplementary material
Supplementary Information accompanies this paper at doi:10.1038/s41467-017-00417-7.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.IPCC. Climate Change 2013. The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (2014).
- 2.Sabine CL, et al. The oceanic sink for anthropogenic CO2. Science. 2004;305:367–371. doi: 10.1126/science.1097403. [DOI] [PubMed] [Google Scholar]
- 3.Orr JC, et al. Anthropogenic ocean acidification over the twenty-first century and its impact on calcifying organisms. Nature. 2005;437:681–686. doi: 10.1038/nature04095. [DOI] [PubMed] [Google Scholar]
- 4.Caldeira K, Wickett ME. Anthropogenic carbon and ocean pH. Nature. 2003;425:365–365. doi: 10.1038/425365a. [DOI] [PubMed] [Google Scholar]
- 5.Doney SC. The growing human footprint on coastal and open-ocean biogeochemistry. Science. 2010;328:1512–1516. doi: 10.1126/science.1185198. [DOI] [PubMed] [Google Scholar]
- 6.Hoegh-Guldberg O, Bruno JF. The impact of climate change on the world’s marine ecosystems. Science. 2010;328:1523–1528. doi: 10.1126/science.1189930. [DOI] [PubMed] [Google Scholar]
- 7.Riebesell U, Gattuso J-P. Lessons learned from ocean acidification research. Nat. Clim. Change. 2015;5:12–14. doi: 10.1038/nclimate2456. [DOI] [Google Scholar]
- 8.Feely RA, et al. The combined effects of ocean acidification, mixing, and respiration on pH and carbonate saturation in an urbanized estuary. Estuar., Coast. Shelf Sci. 2010;88:442–449. doi: 10.1016/j.ecss.2010.05.004. [DOI] [Google Scholar]
- 9.Cai W-J, et al. Acidification of subsurface coastal waters enhanced by eutrophication. Nat. Geosci. 2011;4:766–770. doi: 10.1038/ngeo1297. [DOI] [Google Scholar]
- 10.Wallace RB, Baumann H, Grear JS, Aller RC, Gobler CJ. Coastal ocean acidification: the other eutrophication problem. Estuar., Coast. Shelf Sci. 2014;148:1–13. doi: 10.1016/j.ecss.2014.05.027. [DOI] [Google Scholar]
- 11.Sunda WG, Cai W-J. Eutrophication induced CO2-acidification of subsurface coastal waters: interactive effects of temperature, salinity, and atmospheric PCO2. Environ. Sci. Technol. 2012;46:10651–10659. doi: 10.1021/es300626f. [DOI] [PubMed] [Google Scholar]
- 12.Hagens M, et al. Biogeochemical processes and buffering capacity concurrently affect acidification in a seasonally hypoxic coastal marine basin. Biogeosciences. 2015;12:1561–1583. doi: 10.5194/bg-12-1561-2015. [DOI] [Google Scholar]
- 13.Ulfsbo A, Hulth S, Anderson LG. pH and biogeochemical processes in the Gotland Basin of the Baltic Sea. Mar. Chem. 2011;127:20–30. doi: 10.1016/j.marchem.2011.07.004. [DOI] [Google Scholar]
- 14.Galloway JN, et al. Transformation of the nitrogen cycle: recent trends, questions, and potential solutions. Science. 2008;320:889–892. doi: 10.1126/science.1136674. [DOI] [PubMed] [Google Scholar]
- 15.Diaz RJ, Rosenberg R. Spreading dead zones and consequences for marine ecosystems. Science. 2008;321:926–929. doi: 10.1126/science.1156401. [DOI] [PubMed] [Google Scholar]
- 16.Rabalais NN, et al. Eutrophication-driven deoxygenation the coastal ocean. Oceanography. 2014;27:172–183. doi: 10.5670/oceanog.2014.21. [DOI] [Google Scholar]
- 17.Edman M, Omstedt A. Modeling the dissolved CO2 system in the redox environment of the Baltic Sea. Limnol. Oceanogr. 2013;58:74–92. doi: 10.4319/lo.2013.58.1.0074. [DOI] [Google Scholar]
- 18.Hiscock WT, Millero FJ. Alkalinity of the anoxic waters in the Western Black Sea. Deep Sea Res. Part II: Top. Stud. Oceanogr. 2006;53:1787–1801. doi: 10.1016/j.dsr2.2006.05.020. [DOI] [Google Scholar]
- 19.Konovalov SK, Murray JW, Luther GW, Tebo BM. Processes controlling the redox budget for the oxic/anoxic water column of the Black Sea. Deep Sea Res. Part II: Top. Stud. Oceanogr. 2006;53:1817–1841. doi: 10.1016/j.dsr2.2006.03.013. [DOI] [Google Scholar]
- 20.Pakhomova S, Braaten HFV, Yakushev E, Skei J. Biogeochemical consequences of an oxygenated intrusion into an anoxic fjord. Geochem. Trans. 2014;15:1–12. doi: 10.1186/1467-4866-15-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yao W, Millero FJ. The chemistry of the anoxic waters in the Framvaren Fjord, Norway. Aquat. Geochem. 1995;1:53–88. doi: 10.1007/BF01025231. [DOI] [Google Scholar]
- 22.Zhang J-Z, Millero FJ. The chemistry of the anoxic waters in the Cariaco Trench. Deep Sea Res. Part I: Oceanogr. Res. Pap. 1993;40:1023–1041. doi: 10.1016/0967-0637(93)90088-K. [DOI] [Google Scholar]
- 23.Kemp WM, et al. Eutrophication of Chesapeake Bay: historical trends and ecological interactions. Mar. Ecol.-Prog. Ser. 2005;303:1–29. doi: 10.3354/meps303001. [DOI] [Google Scholar]
- 24.Boynton WR, Garber JH, Summers R, Kemp WM. Inputs, transformations, and transport of nitrogen and phosphorus in Chesapeake Bay and selected tributaries. Estuaries. 1995;18:285–314. doi: 10.2307/1352640. [DOI] [Google Scholar]
- 25.Kemp WM, Smith EM, Marvin-DiPasquale M, Boynton WR. Organic carbon balance and net ecosystem metabolism in Chesapeake Bay. Mar. Ecol. Prog. Ser. 1997;150:229–248. doi: 10.3354/meps150229. [DOI] [Google Scholar]
- 26.Waldbusser G, Voigt E, Bergschneider H, Green M, Newell RE. Biocalcification in the Eastern Oyster (Crassostrea virginica) in relation to long-term trends in Chesapeake Bay pH. Estuar. Coasts. 2011;34:221–231. doi: 10.1007/s12237-010-9307-0. [DOI] [Google Scholar]
- 27.Raymond PA, Bauer JE, Cole JJ. Atmospheric CO2 evasion, dissolved inorganic carbon production, and net heterotrophy in the York River Estuary. Limnol. Oceanogr. 2000;45:1707–1717. doi: 10.4319/lo.2000.45.8.1707. [DOI] [Google Scholar]
- 28.Wong GTF. Alkalinity and pH in the Southern Chesapeake Bay and and the James River Estuary. Limnol. Oceanogr. 1979;24:970–977. doi: 10.4319/lo.1979.24.5.0970. [DOI] [Google Scholar]
- 29.Li M, Zhong L, Boicourt WC, Zhang S, Zhang D-L. Hurricane-induced destratification and restratification in a partially-mixed estuary. J. Mar. Res. 2007;65:169–192. [Google Scholar]
- 30.Goodrich DM, Boicourt WC, Hamilton P, Pritchard DW. Wind-induced destratification in Chesapeake Bay. J. Phys. Oceanogr. 1987;17:2232–2240. doi: 10.1175/1520-0485(1987)017<2232:WIDICB>2.0.CO;2. [DOI] [Google Scholar]
- 31.Li M, Zhong L. Flood–ebb and spring–neap variations of mixing, stratification and circulation in Chesapeake Bay. Cont. Shelf Res. 2009;29:4–14. doi: 10.1016/j.csr.2007.06.012. [DOI] [Google Scholar]
- 32.Smith EM, Kemp WM. Seasonal and regional variations in plankton community production and respiration for Chesapeake Ba. Mar. Ecol. Prog. Ser. 1995;116:217–231. doi: 10.3354/meps116217. [DOI] [Google Scholar]
- 33.Marvin-DiPasquale MC, Capone DG. Benthic sulfate reduction along the Chesapeake Bay central channel. I. Spatial trends and controls. Mar. Ecol. Prog. Ser. 1998;168:213–228. doi: 10.3354/meps168213. [DOI] [Google Scholar]
- 34.Roden EE, Tuttle JH. Sulfide release from estuarine sediments underlying anoxic bottom water. Limnol. Oceanogr. 1992;37:725–738. doi: 10.4319/lo.1992.37.4.0725. [DOI] [Google Scholar]
- 35.Duarte C, et al. Is ocean acidification an open-ocean syndrome? Understanding anthropogenic impacts on seawater pH. Estuar. Coasts. 2013;36:221–236. doi: 10.1007/s12237-013-9594-3. [DOI] [Google Scholar]
- 36.Luther GW, et al. The roles of anoxia, H2S, and storm events in fish kills of dead-end canals of Delaware Inland Bays. Estuaries. 2004;27:551–560. doi: 10.1007/BF02803546. [DOI] [Google Scholar]
- 37.Dai M, et al. Diurnal variations of surface seawater CO2 in contrasting coastal environments. Limnol. Oceanogr. 2009;54:735–745. doi: 10.4319/lo.2009.54.3.0735. [DOI] [Google Scholar]
- 38.Breitburg DL, et al. And on top of all that… coping with ocean acidification in the midst of many stressors. Oceanography. 2015;28:48–61. doi: 10.5670/oceanog.2015.31. [DOI] [Google Scholar]
- 39.Oldham VE, Owings SM, Jones MR, Tebo BM, Luther GW., III Evidence for the presence of strong Mn(III)-binding ligands in the water column of the Chesapeake Bay. Mar. Chem. 2015;171:58–66. doi: 10.1016/j.marchem.2015.02.008. [DOI] [Google Scholar]
- 40.Findlay AJ, et al. Distribution and size fractionation of elemental sulfur in aqueous environments: the Chesapeake Bay and Mid-Atlantic Ridge. Geochim. Cosmochim. Acta. 2014;142:334–348. doi: 10.1016/j.gca.2014.07.032. [DOI] [Google Scholar]
- 41.Lee DY, Owens MS, Crump BC, Cornwell JC. Elevated microbial CO2 production and fixation in the oxic/anoxic interface of estuarine water columns during seasonal anoxia. Estuar., Coast. Shelf Sci. 2015;164:65–76. doi: 10.1016/j.ecss.2015.07.015. [DOI] [Google Scholar]
- 42.Cai WJ, Reimers CE. The development of pH and pCO2 microelectrodes for studying the carbonate chemistry of pore waters near the sediment-water interface. Limnol. Oceanogr. 1993;38:1762–1773. doi: 10.4319/lo.1993.38.8.1762. [DOI] [Google Scholar]
- 43.Luther GW, Reimers C, Nuzzio DB, Lovalvo D. In situ deployment of voltammetric, potentiometric, and amperometric microelectrodes from a ROV to determine dissolved O2, Mn, Fe, S(-2), and pH in porewaters. Environ. Sci. Technol. 1999;33:4352–4356. doi: 10.1021/es9904991. [DOI] [Google Scholar]
- 44.Boudreau BP. A method-of-line code for carbon and nutrient daigenesis in aquatic sediments. Comput. Geosci. 1996;22:479–496. doi: 10.1016/0098-3004(95)00115-8. [DOI] [Google Scholar]
- 45.Wang Y, Van Cappellen P. A multicomponent reaction transport model of early diagenesis: application to redox cycling in coastal marine sediments. Geochim. Cosmochim. Acta. 1996;60:2993–3014. doi: 10.1016/0016-7037(96)00140-8. [DOI] [Google Scholar]
- 46.Emerson S, Cranston RE, Liss PS. Redox species in a reducing fjord: equilibrium and kinetic considerations. Deep Sea Res. 1979;26A:859–878. doi: 10.1016/0198-0149(79)90101-8. [DOI] [Google Scholar]
- 47.Cai WJ, et al. The biogeochemistry of inorganic carbon and nutrients in the Pearl River estuary and the adjacent Northern South China Sea. Cont. Shelf Res. 2004;24:1301–1319. doi: 10.1016/j.csr.2004.04.005. [DOI] [Google Scholar]
- 48.Waldbusser GG, Powell EN, Mann R. Ecosystem effects of shell aggregations and cycling in coastal waters: an example of Chesapeake Bay oyster reefs. Ecology. 2013;94:895–903. doi: 10.1890/12-1179.1. [DOI] [Google Scholar]
- 49.Abril G, Etcheber H, Delille B, Frankignoulle M, Borges AV. Carbonate dissolution in the turbid and eutrophic Loire estuary. Mar. Ecol.-Prog. Ser. 2003;259:129–138. doi: 10.3354/meps259129. [DOI] [Google Scholar]
- 50.Middelburg JJ, Soetaert K, Herman PMJ, Heip CHR. Denitrification in marine sediments: a model study. Glob. Biogeochem. Cycles. 1996;10:661–673. doi: 10.1029/96GB02562. [DOI] [Google Scholar]
- 51.Hu X, Cai W-J. The impact of denitrification on the atmospheric CO2 uptake potential of seawater. Mar. Chem. 2011;127:192–198. doi: 10.1016/j.marchem.2011.09.008. [DOI] [Google Scholar]
- 52.Kana TM, Cornwell JC, Zhong L. Determination of denitrification in the Chesapeake Bay from measurements of N2 accumulation in bottom water. Estuar. Coasts. 2006;29:222–231. doi: 10.1007/BF02781991. [DOI] [Google Scholar]
- 53.Frankignoulle M. A complete set of buffer factors for acid-base CO2 system in seawater. J. Mar. Syst. 1994;5:111–118. doi: 10.1016/0924-7963(94)90026-4. [DOI] [Google Scholar]
- 54.Egleston ES, Sabine CL, Morel FMM. Revelle revisited: buffer factors that quantify the response of ocean chemistry to changes in DIC and alkalinity. Glob. Biogeochem. Cycles. 2010;24:GB1002. doi: 10.1029/2008GB003407. [DOI] [Google Scholar]
- 55.Hofmann AF, Middelburg JJ, Soetaert K, Wolf-Gladrow DA, Meysman FJR. Proton cycling, buffering, and reaction stoichiometry in natural waters. Mar. Chem. 2010;121:246–255. doi: 10.1016/j.marchem.2010.05.004. [DOI] [Google Scholar]
- 56.Hofmann AF, Middelburg JJ, Soetaert K, Meysman FJR. pH modelling in aquatic systems with time-variable acid-base dissociation constants applied to the turbid, tidal Scheldt estuary. Biogeosciences. 2009;6:1539–1561. doi: 10.5194/bg-6-1539-2009. [DOI] [Google Scholar]
- 57.Hagens M, Middelburg JJ. Generalised expressions for the response of pH to changes in ocean chemistry. Geochim. Cosmochim. Acta. 2016;187:334–349. doi: 10.1016/j.gca.2016.04.012. [DOI] [Google Scholar]
- 58.Hagens M, Hunter KA, Liss PS, Middelburg JJ. Biogeochemical context impacts seawater pH changes resulting from atmospheric sulfur and nitrogen deposition. Geophys. Res. Lett. 2014;41:935–941. doi: 10.1002/2013GL058796. [DOI] [Google Scholar]
- 59.Wang ZA, et al. The marine inorganic carbon system along the Gulf of Mexico and Atlantic coasts of the United States: insights from a transregional coastal carbon study. Limnol. Oceanogr. 2013;58:325–342. doi: 10.4319/lo.2013.58.1.0325. [DOI] [Google Scholar]
- 60.Hu X, Cai W-J. Estuarine acidification and minimum buffer zone—a conceptual study. Geophys. Res. Lett. 2013;40:5176–5181. doi: 10.1002/grl.51000. [DOI] [Google Scholar]
- 61.Cai W-J, et al. A comparative overview of weathering intensity and HCO3- flux in the world’s major rivers with emphasis on the Changjiang, Huanghe, Zhujiang (Pearl) and Mississippi Rivers. Cont. Shelf Res. 2008;28:1538–1549. doi: 10.1016/j.csr.2007.10.014. [DOI] [Google Scholar]
- 62.Guo X, et al. Carbon dynamics and community production in the Mississippi River plume. Limnol. Oceanogr. 2012;57:1–17. doi: 10.4319/lo.2012.57.1.0001. [DOI] [Google Scholar]
- 63.Guo X, et al. Seasonal variations in the inorganic carbon system in the Pearl River (Zhujiang) estuary. Cont. Shelf Res. 2008;28:1424–1434. doi: 10.1016/j.csr.2007.07.011. [DOI] [Google Scholar]
- 64.Mook WG, Koene BKS. Chemistry of dissolved inorganic carbon in estuarine and coastal brackish waters. Estuar. Coast. Mar. Sci. 1975;3:325–336. doi: 10.1016/0302-3524(75)90032-8. [DOI] [Google Scholar]
- 65.Whitfield M, Turner DR. The carbon dioxide system in estuaries—An inorganic perspective. Sci. Total Environ. 1986;49:235–255. doi: 10.1016/0048-9697(86)90243-3. [DOI] [Google Scholar]
- 66.Morel, F. M. M. & Hering, J. G. Principles and Applications of Aquatic Chemistry 2nd edn, (John Wiley and Sons, 1992).
- 67.Luther, G. W. et al. Thermodynamics and kinetics of sulfide oxidation by oxygen: a Look at inorganically controlled reactions and biologically mediated processes in the environment. Front. Microbiol. 2, Article 62 (2011). [DOI] [PMC free article] [PubMed]
- 68.Geyer WR, MacCready P. The estuarine circulation. Annu. Rev. Fluid Mech. 2014;46:175–197. doi: 10.1146/annurev-fluid-010313-141302. [DOI] [Google Scholar]
- 69.Kemp W, Testa J. Metabolic balance between ecosystem production and consumption. Treatise Estuar. Coast. Sci. 2011;7:83–118. doi: 10.1016/B978-0-12-374711-2.00706-3. [DOI] [Google Scholar]
- 70.Bauer JE, et al. The changing carbon cycle of the coastal ocean. Nature. 2013;504:61–70. doi: 10.1038/nature12857. [DOI] [PubMed] [Google Scholar]
- 71.Borges AV, Gypens N. Carbonate chemistry in the coastal zone responds more strongly to eutrophication than ocean acidification. Limnol. Oceanogr. 2010;55:346–353. doi: 10.4319/lo.2010.55.1.0346. [DOI] [Google Scholar]
- 72.Huang W-J, Cai W-J, Wang Y, Lohrenz SE, Murrell MC. The carbon dioxide system on the Mississippi River-dominated continental shelf in the northern Gulf of Mexico: 1. Distribution and air-sea CO2 flux. J. Geophys. Res.: Oceans. 2015;120:1429–1445. doi: 10.1002/2014JC010498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Huang W-J, Wang Y, Cai W-J. Assessment of sample storage techniques for total alkalinity and dissolved inorganic carbon in seawater. Limnol. Oceanogr. Methods. 2012;10:711–717. doi: 10.4319/lom.2012.10.711. [DOI] [Google Scholar]
- 74.Weiss RF. Carbon dioxide in water and seawater: the solution of a non-ideal gas. Mar. Chem. 1974;2:203–215. doi: 10.1016/0304-4203(74)90015-2. [DOI] [Google Scholar]
- 75.Ho DT, et al. Measurements of air-sea gas exchange at high wind speeds in the Southern Ocean: implications for global parameterizations. Geophys. Res. Lett. 2006;33:L16611. doi: 10.1029/2006GL026817. [DOI] [Google Scholar]
- 76.Wanninkhof R. Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr.: Methods. 2014;12:351–362. doi: 10.4319/lom.2014.12.351. [DOI] [Google Scholar]
- 77.Hofmann A, Soetaert K, Middelburg J, Meysman FR. AquaEnv: an aquatic acid–base modelling environment in R. Aquat. Geochem. 2010;16:507–546. doi: 10.1007/s10498-009-9084-1. [DOI] [Google Scholar]
- 78.Pierrot, D., Lewis, E. & Wallace, D. W. R. MS Excel Program Developed for CO2System Calculations (Oak Ridge National Laboratory, 2006).
- 79.Clegg SL, Whitfield M. A chemical model of seawater including dissolved ammonia and the stoichiometric dissociation constant of ammonia in estuarine water and seawater from −2 to 40 °C. Geochim. Cosmochim. Acta. 1995;59:2403–2421. doi: 10.1016/0016-7037(95)00135-2. [DOI] [Google Scholar]
- 80.Millero FJ, Plese T, Fernandez M. The dissociation of hydrogen sulfide in seawater. Limnol. Oceanogr. 1988;33:269–274. doi: 10.4319/lo.1988.33.2.0269. [DOI] [Google Scholar]
- 81.Millero FJ. Thermodynamics of the carbon-dioxide system in the oceans. Geochim. Cosmochim. Acta. 1995;59:661–677. doi: 10.1016/0016-7037(94)00354-O. [DOI] [Google Scholar]
- 82.Xu, Y.-Y., Cai, W.-J., Pierrot, D. Ocean carbonate system computation for anoxic waters using an updated CO2SYS program. Mar. Chem.https://doi.org/10.1016/j.marchem.2017.07.002 (2017).
- 83.Cai W-J, Luther G, III, Cornwell J, Giblin A. Carbon cycling and the coupling between proton and electron transfer reactions in aquatic sediments in Lake Champlain. Aquat. Geochem. 2010;16:421–446. doi: 10.1007/s10498-010-9097-9. [DOI] [Google Scholar]
- 84.Hedges JI, et al. The biochemical and elemental compositions of marine plankton: a NMR perspective. Mar. Chem. 2002;78:47–63. doi: 10.1016/S0304-4203(02)00009-9. [DOI] [Google Scholar]
- 85.Chen C-TA, Lin C-M, Huang B-T, Chang L-F. Stoichiometry of carbon, hydrogen, nitrogen, sulfur and oxygen in the particulate matter of the western North Pacific marginal seas. Mar. Chem. 1996;54:179–190. doi: 10.1016/0304-4203(96)00021-7. [DOI] [Google Scholar]
- 86.Cai W-J, Wang Y, Hodson RE. Acid-base properties of dissolved organic matter in the estuarine waters of Georgia. Geochim. Cosmochim. Acta. 1998;62:473–483. doi: 10.1016/S0016-7037(97)00363-3. [DOI] [Google Scholar]
- 87.Álvarez M, et al. The CO2 system in the Mediterranean Sea: a basin wide perspective. Ocean Sci. 2014;10:69–92. doi: 10.5194/os-10-69-2014. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data are available from the corresponding author upon reasonable request and will be deposited at the US National Centers for Environmental Information (https://www.nodc.noaa.gov/oceanacidification/).