Understanding the mTOR signaling pathway via mathematical modeling

Abstract

The mechanistic target of rapamycin (mTOR) is a central regulatory pathway that integrates a variety of environmental cues to control cellular growth and homeostasis by intricate molecular feedbacks. In spite of extensive knowledge about its components, the molecular understanding of how these function together in space and time remains poor and there is a need for Systems Biology approaches to perform systematic analyses. In this work, we review the recent progress how the combined efforts of mathematical models and quantitative experiments shed new light on our understanding of the mTOR signaling pathway. In particular, we discuss the modeling concepts applied in mTOR signaling, the role of multiple feedbacks and the crosstalk mechanisms of mTOR with other signaling pathways. We also discuss the contribution of principles from information and network theory that have been successfully applied in dissecting design principles of the mTOR signaling network. We finally propose to classify the mTOR models in terms of the time scale and network complexity, and outline the importance of the classification toward the development of highly comprehensive and predictive models. WIREs Syst Biol Med 2017, 9:e1379. doi: 10.1002/wsbm.1379

For further resources related to this article, please visit the WIREs website.

INTRODUCTION

Mammalian target of rapamycin (mTOR) is a central regulator of translation, transcription, differentiation, and metabolism thereby controlling cell growth, survival and stress.1 The mTOR pathway responds to diverse environmental signals such as growth factors, nutrients, hormones and stress, and regulates cellular energy and nutrients required for execution of cell growth and proliferation.2 Therefore, it has attracted a broad research interest as it is involved in many research fields, such as cancer, type II diabetes, obesity, neurodegeneration,1 and aging.3, 4, 5 While the extent of the mTOR signaling pathway, involving almost 1000 molecules, has been elucidated and summarized into static interaction networks (see e.g., Caron et al.,6 BioModels Database,7 IDs MODEL1012220002‐4) the pathway topology alone was shown to be insufficient to capture the dynamics of mTOR regulation at a molecular level. For example, rapamycin is the best‐known mTOR inhibitor used in cancer therapy. However, limited success has been achieved in clinical applications of rapamycin and other drugs.8 Apparently, the effect of drugs on mTOR signaling are quite complex, thus requiring a better understanding of its dynamic regulation. At this stage, a Systems Biology approach can assist the understanding of this complex pathway beyond mere intuition by transforming experimental knowledge into a coherent mathematical model and testing hypotheses in silico.9 In contrast to other signaling pathways such as MAPK,10 TGFβ,11 JAK‐STAT,12 and NF‐κB,13 for which mathematical models have provided many insights, dynamic mTOR pathway models have received less attention. One reason is the diversity of upstream signals it senses. The mTOR pathway integrates inputs from at least five major intracellular and extracellular cues such as growth factors, energy status, stress, oxygen, and amino acids.2 The other reason lies in the multiple effects the mTOR signaling exerts on multiple time scales. Therefore, currently developed mathematical models of this pathway differ with respect to the complexity and time scale which they cover.

The aim of this review is to introduce the molecular basis of the mTOR pathway that lays the ground for the challenges of Systems Biology. Next, we describe different modeling approaches and model analysis methods applied to dynamic processes on the subcellular level. Furthermore, we discuss the effect of molecular feedbacks in the stability of the pathway outcome, as well as the crosstalk mechanisms that have been identified using modeling approaches. We discuss the design principles of the mTOR signaling pathway using methods from information and network theory and how the application of these methods impacted on our understanding of mTOR signaling. Lastly, we discuss the impact of time scales and the degree of complexity on the design principles of mTOR signaling and will conclude with the integrative modeling challenges that are still open for the mTOR pathway.

THE OVERVIEW OF MTOR SIGNALING PATHWAY

mTOR is a serine/threonine protein kinase which belongs to the phosphoinositide 3‐kinase (PI3K)‐related family and interacts with several proteins to form two distinct complexes, named mTOR complex 1 (mTORC1) and mTOR complex 2 (mTORC2).8 mTORC1 and mTORC2 are known to comprise six and seven protein components, respectively. They share the catalytic mTOR subunit, mammalian lethal with sec‐13 protein 8 (mLST8),14, 15 DEP domain including mTOR‐interacting protein (DEPTOR)16 and the Tti1/Tel2 complex.17 The protein components specific to mTORC1 are the regulatory‐associated protein of mammalian target of rapamycin (raptor)18, 19 and proline‐rich AKT substrate 40 kDa (PRAS40).20, 21, 22, 23

The proteins specific to mTORC2 comprise rapamycin‐insensitive companion of mTOR (rictor),14, 24 mammalian stress activated map kinase‐interacting protein 1 (mSin1) and protein observed with rictor 1 and 2 (protor 1/2).25 mTORC1 is generally known to control cellular growth, translation, transcription, and autophagy, while mTORC2 is associated with the coordination of spatial growth by regulating the actin cytoskeleton.2

The key signaling nodes of the core mTOR network are depicted in Figure 1. Illustrated are the important signaling pathways that promote the activation of mTOR signaling. Insulin induces a kinase signaling cascade through the insulin receptor (IR), insulin receptor substrate (IRS), class I phosphoinositide 3‐kinases (PI3Ks), phosphoinositide dependent protein kinase 1 (PDK1), and AKT kinase. AKT activates mTORC1 by inhibiting the tuberous sclerosis complex 1/2 (TSC1/TSC2) and PRAS40, which are negative regulators of mTORC1.2 AKT also activates mTORC1 in a TSC1/2 independent manner by phosphorylating PRAS40.20, 21, 22, 23 In response to insulin stimulation, mTORC2 phosphorylates AKT in Drosophila and several human cell lines.26 Recent evidence in HEK293 and Hela cells suggested the activation of mTORC2 via insulin, which in turn phosphorylates AKT.20

Figure 1.

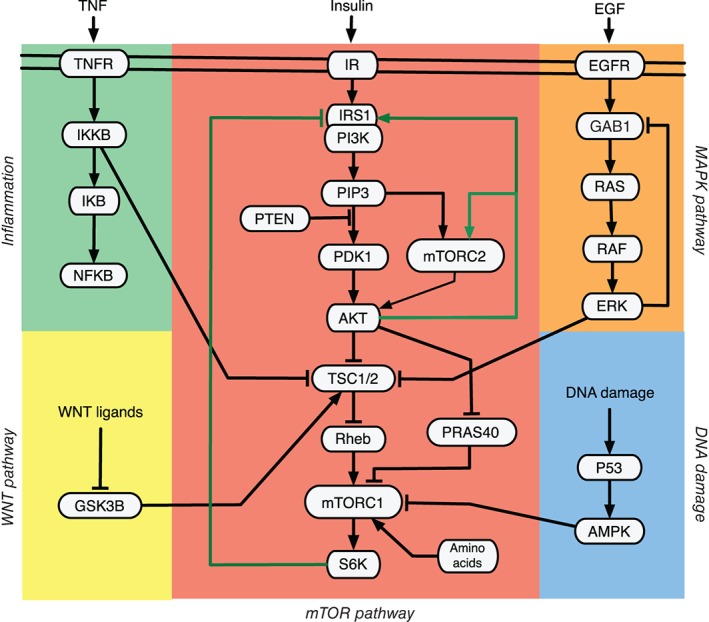
Overview of the major mTOR signaling network. Shown are core components of PI3K/AKT/mTOR pathways and the pathways that influence the mTOR signaling pathway.2 Depicted are also critical inputs regulating mTORC1 and mTORC2 including growth factors such as insulin, epidermal growth factor (EGF), tumor necrosis factor (TNF), wingless type integration site family (WNT) ligands and amino acids. Once active, mTORC1 regulates protein synthesis, energy metabolism, lipogenesis, and inhibits autophagy and lysosome biogenesis. mTORC2 promotes cytoskeletal organization, cell survival, and longevity. Green edges denote feedback loops in the core mTOR signaling pathway. For more information, see the text.

mTOR activation by the MAP kinase pathway occurs at the level of TSC1/2, where ERK activates mTORC1 via TSC1/2 inhibition.27 The proinflammatory cytokine TNFα activates mTORC1 through a similar mechanism, where IKKβ phosphorylates TSC1/2 by causing its inhibition.28 The canonical WNT pathway, a major regulator of cell growth, proliferation, polarity and differentiation, and development, also activates mTORC1 via suppressing glycogen synthase kinase 3β (GSK3‐β). GSK3‐β itself phosphorylates and promotes TSC1/2 activity.29 DNA damage downregulates mTORC1 via p53‐dependent transcription of Sestrin1/2, which activates AMPK and thus leads to TSC1/2 activation and mTORC1 inactivation.30 Less clear, but independent from TSC1/2 is the activation of mTORC1 by amino acids.31 Omitting leucine and arginine in culture media is as effective as complete amino acid withdrawal and leads to inactivation of mTORC1.32 In amino acid bound state the GTPases of the Rag family and Rheb play an important role in recruiting the mTORC1 to the lysosome where these components are anchored by the regulator complex and brought into close contact.33, 34 Many other components are discussed here35 in detail as part of an amino acid sensing complex.

There are several known feedback loops in the core mTOR signaling (Figure 1, green lines). The first one is the positive feedback from AKT to insulin receptor substrate‐1 (IRS1).36 It was shown that the activation of AKT in response to insulin propagates insulin signaling and promotes the phosphorylation of IRS1 on specific sites and downregulates its functions.37 This phosphorylation prevents dephosphorylation of IRS1 by tyrosine phosphatases and maintains IRS1 in the active form.36 The second one is the widely observed negative feedback from S6K to IRS1. Once active, S6K phosphorylates and inhibits IRS1, which prevents the activation of PI3K in response to insulin.38 S6K inhibition also activates the ERK‐signaling cascade in metastatic cancer patients and in a mouse model of prostate cancer.39 The third one is a recently reported positive feedback from AKT to mTORC2, where AKT phosphorylates the mTORC2 subunit SIN1 thereby enhancing mTORC2 activity.40

MODELING CONCEPTS RELEVANT FOR MTOR SIGNALING PATHWAY

Dynamic Modeling of mTOR Signaling

The use of mathematical modeling in understanding the complex dynamics of biochemical signaling cascades, such as the mTOR pathway, has become standard in Biology. Iteration between wet‐lab experiments and dry‐lab computer simulations is generally known as Systems Biology approach to life sciences.41 Systems Biology tries to quantify and predict dynamic biological processes through mathematical modeling approaches to understand the underlying regulatory concepts and unravel biocomplexity as described below. In general, modeling is a simplified and abstract representation of naturally occurring processes to discern their core principles and to predict their behavior. Moreover, it allows to test many scenarios, which are either experimentally not accessible or affordable and results, if successful, in testable predictions. Depending on the degree of complexity and the scope of modeling, signaling pathway models are based on different mathematical formalism. The choice of a particular modeling approach depends on various factors: (i) the biological question, (ii) the extent of mechanistic detail, (iii) data availability and data type.^42,9 Usually, biological experiments are described by continuous measurements such as reaction rates, cell mass, protein concentrations and gene expression intensities which can be further combined with various modeling formalisms. In the following, we briefly overview the modeling approaches that are mainly used in modeling mTOR signaling pathway. The mTOR models and the corresponding modeling approaches are summarized in Table 1.

Table 1.

Summary of Published mTOR Models

mTOR Models	Biological Context	Model Type	Model Size	Timescale
Dalle Pezze et al.43	Mechanisms of mTORC2 regulation	ODE	25–33	0–120 min
Sonntag et al.44	mTOR‐AMPK crosstalk	ODE	26–28	0–120 min
Kubota et al.45	Decoding insulin signal in the mTOR pathway	ODE	11	0–600 min
Toyoshima et al.46	Signal transfer in the mTOR pathway	ODE	3–4	0–120 min
Noguchi et al.47	Metabolism regulation by the mTOR pathway	ODE	15	0–480 min
Borisov et al.48	MAPK‐mTOR crosstalk	ODE	78	0–30 min
Fujita et al.49	Signal transfer in the mTOR pathway	ODE	3–8	0–120 min
Jain et al.50	BDNF‐mTOR crosstalk	ODE	130	0–30 min
Wu et al.51	mTOR‐MAPK‐PKC crosstalk	Boolean	19–22	0–60 min
Hatakeyama et al.52	mTOR‐MAPK crosstalk	ODE	33–34	0–30 min
Sedaghat et al.53	Metabolic insulin signaling	ODE	21	0–60 min
Faratian et al.54	mTOR‐MAPK crosstalk	ODE	56	0–60 min
Brännmark et al.55	Mechanisms of receptor internalization	ODE	5	0–30 min
Brännmark et al.56	Mechanisms of insulin resistance	ODE	26–27	0–30 min
Vinod et al.57	mTOR regulation via amino acids	ODE	10–13	0–30 min
Araujo et al.58	Feedback characterization in the mTOR pathway	ODE	4–5	a.u.
Giri et al.59	Input–output characterization in metabolic insulin signaling	Algebraic	22	a.u.
Tian and Wu60	Robustness property of the mTOR pathway	ODE	16	a.u.
Wang and Krueger61	Bifurcation analysis of the mTOR pathway	Algebraic	2	a.u.
Nguyen and Kholodenko62	Feedback regulation in the mTOR‐MAPK pathways	ODE	29	a.u.
Kriete et al.63	Metabolism regulation by the mTOR and NF‐kB pathways	Fuzzy‐logic	34	a.u.
Mosca et al.64	Metabolism regulation by the mTOR pathway	ODE, Algebraic	25	a.u.

a.u., arbitrary units. Model size represents (i) the number of equations in ODEs and algebraic equations, (ii) the number of nodes in Boolean models and (iii) the number of reactions in fuzzy‐logic models (rule‐based).

Most models of mTOR signaling have been encoded using ordinary differential equations (ODEs; Figure 2(a)) which belong to a class of mechanistic models and provide detailed information about the network dynamics. Applications of ODEs have allowed to specify the network topology and kinetic mechanisms of the mTOR signaling pathway. In particular, an application of this method with a combination of time‐course measurements has been crucial in dissecting feedback mechanisms in mTOR signaling.43, 45, 56, 58 ODEs with real valued parameters over a continuous time‐scale allow a comparison of the global state and experimental data, which can be mathematically more accurate.65 ODEs are derived from the law of mass action or Michaelis‐Menten kinetics, and describe the change of a system in continuous time. They assume a homogenous reaction volume inside the components of the cell, and that active transport and diffusion are fast compared to the reaction rates of molecular interactions and the spatial extent of the compartment.66 Modeling using ODEs provides causal information on the chemical reaction dynamics, but it also requires to estimate kinetic parameters based on quantitative data.65 The main challenge in exploiting ODEs is that they require a substantial amount of prior information about initial concentrations of species and kinetic parameters from experimental measurements. Taking into account the limitation of available quantitative data, it is important to specify the model size such that model predictions can be experimentally supported. Because the amount of quantifiable data is currently limited or cost and labor prohibitive, the size of the ODE models is nowadays restricted to few variables and parameters in the order of $\mathcal{O}\left({10}^1-{10}^2\right)$. However, this might change in the future with advances in multiplex protein assays or mass spectrometry.

Figure 2.

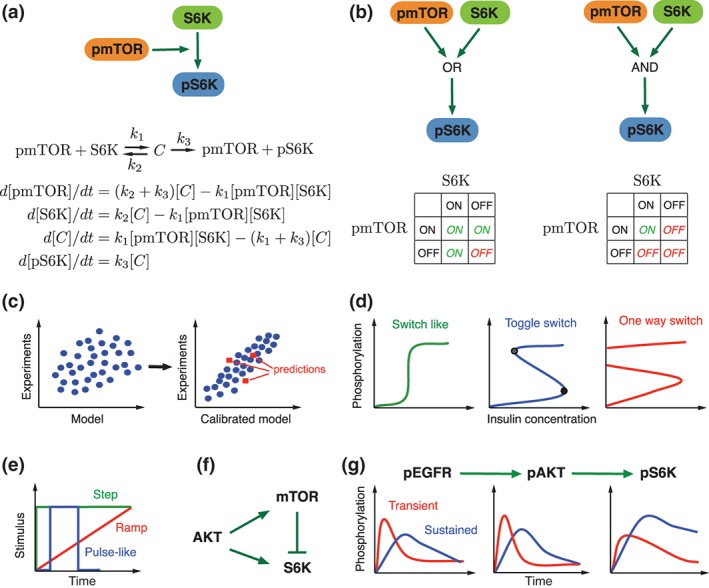
Methods used in mTOR signaling network modeling. (a) Converting a network into ODEs. At the first step, the network is converted into biochemical reactions and further into a set of ODEs, assuming mass action kinetics. (b) Modeling networks using two state Boolean logic. (c) Steps required to get a useful model. Before the model calibration, there is a poor correlation between the data obtained by the model and the experimental data. The calibrated model can successfully reproduce experimental data and gives more accurate predictions than the uncalibrated model. (d) Types of bifurcation observed in biological systems. Illustrative example is given in term of sensitivity of protein phosphorylation to insulin concentrations. Drug treatment may drive the system to one of these modes. Insulin controllable modes: switch like (left) and toggle switch (middle) and uncontrollable one switch mode (right). (e) Three temporal patterns of the stimuli that have widely been used to elucidate the properties of mTOR pathway are illustrated. (f) IFFL (incoherent feed‐forward loop) has been found as an optimal mechanism to explain S6K activation by AKT.45 (g) Example of the pathway that exhibits a low‐pass filter property that could transmits slowly occurring changes in upstream regulators to downstream effectors more efficiently than fast occurring changes in upstream regulators.49

A Boolean or logic‐based approach is another type of modeling used in mTOR signaling.51, 63 If the exact kinetic parameters and type of molecular interactions are less important as compared to the topology of the reaction network, logic‐based models provide a viable approach in case of insufficient time resolved quantitative data (Figure 2(b)). Boolean models are discrete two‐state logic‐based models in which each component is represented by on and off states.67 Importantly, Boolean models have no free parameters and the models covering the same set of components differ only in topology.68 Since most experimental data is continuous, it is required to binarize the data that is used in Boolean models.65 This modeling approach has been successfully applied for diverse systems such as gene regulatory networks69, 70, 71 and EGFR signaling,72 etc. A limitation of Boolean models is that they contain a limited number of states and require binarization of data which reduces the accuracy of predictions. However, fuzzy logic‐based methods that allow for multiple states can partially overcome these drawbacks.73 For example, Kriete et al.63 modeled mTOR, NF‐κB and cellular processes that play a role in aging via a fuzzy‐logic framework based on assembled interaction rules.

mTOR signaling has also been modeled using steady state or algebraic equations based on ODEs that arise from switch‐like input–output relationships.74 Goldbeter and Koshland showed that in signal transduction pathways, a simple mechanism can create switch‐like response relationships.75 This mechanism termed as zero‐order ultrasensitivity emerges, when phosphorylation and dephosphorylation reactions are modeled with Michaelis‐Menten kinetics. In this case, the steady‐state response of the system is described by Goldbeter–Koshland equations.75 For example, Giri et al. modeled the metabolic insulin signaling and the mTOR signaling at steady state using the Goldbeter–Koshland framework.59

Other modeling formalisms can also be useful in modeling the mTOR signaling. Recent advances in flow cytometry and microfluidics technology allow now to measure the protein abundance on the single cell level, when protein molecules are present in small numbers, only.76 When molecule numbers are low (typically less than 100), random fluctuations need to be accounted for through stochastic modeling rather than using ODEs.67 Stochastic simulations provide a more detailed description of the discrete molecule dynamics by estimating the mean abundance as well as its fluctuations.9 They are widely used in modeling gene expression to account for extrinsic and intrinsic noise in transcription and translation processes.9, 77 The above mentioned modeling approaches can be implemented and simulated using publicly available Systems Biology tools. ODEs and stochastic models can be simulated via user‐friendly tools such as CellDesigner,78 COPASI,79 and PyBioS,80 all of which include methods for parameter estimation and model analysis. Boolean or logic‐based models can be created and simulated by, e.g., CellNetOptimizer,81 a software suite which allows to train a set of possible logical models against experimental data.

Modeling with High‐throughput Measurements

Until recently, experimental data for parameter estimation of signaling pathway models mainly came from low‐throughput experiments such as assays, protein western blotting and microscopy.82 For mechanistic modeling approaches using ODEs this is a limiting factor, which restricts the accuracy of parameter estimates and scalability of ODEs to larger systems. Recent progress in high‐throughput technologies such as kinase arrays and mass spectrometry now makes large‐scale dynamic modeling possible. These technologies allow to quantify a large number of proteins in a single experiment.83 This will result in more detailed models of the mTOR signaling pathway and will improve the quality of parameter estimates. However, with an increasing number of proteins and kinetic parameters, the parameter estimation becomes more difficult irrespective of any optimization algorithm used because of the ‘combinatorial explosion’ problem.84 An alternative to ODEs in this case will be to exploit logic‐based ODEs, also known as piecewise linear ODEs that reduce the complexity of the model calibration task.85, 86, 87 Logic‐based ODEs do not represent a mechanistic model, but they explain and predict the quantitative and dynamic behavior of the system, which is not possible with discrete Boolean models. Several studies showed how to transform discrete Boolean models into logic‐based ODE models through multivariate polynomial interpolation and Hill functions, where the resulting ODE models preserve important properties of the original system such as steady‐state behavior.87, 88 Another alternative is to exploit partial correlation methods, which are based on the conditional independence concept and are able to perform network inference from high‐throughput data efficiently.89 Popular approaches are regularization based Lasso methods that induce the sparsity in the estimated network.90 However, these models just infer the undirected network of proteins and cannot deduce a causality structure between the proteins. Such a structure can be learned using Bayesian networks which are a probabilistic graphical model of random variables and their conditional dependencies. A dynamic version of Bayesian network (DBN) is able to incorporate the time‐course data and complement ODE‐based approaches by providing a feasible way to explore a large space of various network topologies from the data.91

Computational Methods to Analyze mTOR Models

An important step towards a useful dynamic mTOR model is its calibration against experimental data. This procedure is known also as parameter estimation, model fitting or model training. In model calibration, the aim is to match model performance to experimental data via adjusting model parameters. In case of ODEs, the model parameters are rate constants and/or initial conditions, whereas in Boolean models model calibration refers to adjusting the network topology and the combination of logic ‘and’/‘or’ gates. A key to model calibration is to define an objective function (known also as cost function and error function), which is the squared difference between model predictions and experimental data, also known as the method of least squares. The objective function can also be defined in terms of Bayesian framework where the model parameters are considered as random variables and defined in terms of a probability distribution. For more information, we refer to Klipp et al.9 The goal is to minimize the objective function in terms of model parameters, which can be done by variety optimization algorithms. After model calibration, a trained model can successfully reproduce experimental data and make predictions in agreement with measured data (Figure 2(c)). Partly calibrated or noncalibrated models are still useful for simulation purposes, however, informative conclusions about the rate constants and concentrations are difficult.92 Another important prerequisite for model calibration is the identifiability of model parameters that are estimated from experimental data. A model parameter is identifiable, if it can be determined from the data. Biological questions are not addressable, if the model parameters cannot be estimated from the experimental data and thus are simply nonidentifiable.93 Identifiability of parameters can help to infer feasible model predictions. Identifiability of model parameters can be applied before or after the model calibration. There are two types of identifiability analyses for a system of ODEs. Structural identifiability analysis is applied before the availability of experimental data, while practical identifiability analysis is applied if actual experimental data is available. For instance, the mTOR models of Dalle Pezze et al.43 and Sonntag et al.44 have been subject to model calibration and both structural and practical identifiability analyses, whereas the model predictions and simulations have been conducted on a set of identifiable parameters.

The influence of model parameters on model output is of particular interest and can be approached using sensitivity analysis. Sensitivity analysis is a method for quantifying uncertainty and how input uncertainty impacts model outcome.94 This analysis identifies, which outputs are sensitive to variation of a particular parameter of interest and can be considered computationally equivalent to protein knock down or overexpression experiments.67 Sensitivity analysis reveals fragile points in the network that exhibit major sensitivity to small perturbations and identifies possible targets for therapeutic intervention. For example, sensitivity analysis on the ODE model of the AKT pathway (upstream of mTOR pathway), identified critical parameters for the cutoff frequency at which the transfer efficiency of proteins in the pathway change.49

Robustness analysis is another method of model analysis. Robustness is defined as the ability of a system to function correctly in the presence of both internal and external perturbations.95 Robustness is a ubiquitously observed property of biological systems and this property has been widely applied as an important measure to filter the optimal network structure.60 Thus, this method can be used for validation of models of biological systems.96 For instance, Tian and Wu60 have examined the robustness properties of an upstream model for the mTOR pathway. The behavior of dynamical models can be further analyzed using the bifurcation analysis, which is the study of qualitative changes in the behavior of nonlinear dynamical systems when parameters of the system are varied.97 Parameters can be considered as signal strength that is controllable by experiments. The points at which systems output changes discontinuously leading to a different dynamic behavior are called bifurcation points.98 Bifurcation analysis is very useful when analyzing the input–output behavior and summarizes the behavior of the biological system. This method further enables to study critical decisions made by biological systems in terms of mathematical modeling and identification of suitable targets for a drug intervention. Araujo et al.58 applied bifurcation analysis on the mTOR pathway model, and characterized the dependence of pIRS1 on different inhibitors. Moreover, by employing bifurcation analysis, Wang and Krueger analyzed the dependence of pAKT on the insulin level and examined the conditions under which this dependence produces a bistable behavior.61

FEEDBACKS AND CROSSTALK IN THE MTOR PATHWAY

Multiple Feedbacks in the mTOR Pathway

Signaling pathways are highly interconnected via positive and negative feedback loops. Feedback occurs when the output of a system serves as an input to the same system resulting in a loop structure. Because the effect of feedback loops on the dynamic behavior of a system is difficult to examine experimentally, mathematical models have proven a powerful tool to study this problem. Positive feedbacks may create a discontinuous bistable switch such that the cellular response changes abruptly and irreversibly as signal strength crosses a critical threshold.98 Negative feedback enables the system to respond robustly to external and internal perturbations.95 The interplay of these two feedbacks can drive the system into bistable, toggle and one‐way switches (Figure 2(d)). A stronger positive feedback compared to its negative counterpart facilitates a bistable and one‐way switch. Once the signal crosses a certain threshold, it remains at the high steady state despite complete removal of the stimulus thereby creating the one‐way switch.58 A one‐way switch is characterized by a point‐of‐no‐return. A toggle switch is the two‐way switch that is capable of exhibiting two stable steady states.99 If the input signal in the toggle switch is weak enough, the switch will go back from the high to the lower steady state.98

In the core mTOR signaling pathway, there are currently two positive and one negative feedback loops identified (Figure 1, green edges). The first positive feedback loop descends from AKT and connects to IRS1.36 Another positive feedback loop results from AKT to mTORC2 via SIN1 phosphorylation.40 The negative feedback emerges from S6K and leads back to IRS1.38 The interplay of the positive feedback loop from AKT to IRS1 and negative feedback from S6K to IRS1 was investigated theoretically.58 By using a simple mTOR pathway model, the authors suggested that inhibiting the mTOR complex downregulates the downstream effectors eukaryotic translation initiation factor 4E binding protein 1 (4EBP1) and S6K. The inhibitor, however, also disrupts the negative feedback and increases IRS1 and AKT activation, which ultimately leads to the high mTOR activity. They further demonstrated that an imbalance in favor of the positive feedback, while weakening the negative counterpart, creates the dangerous one‐way switch that could cause constitutive activation of effectors downstream of mTOR. In their simulations, additional inhibition of AKT converted this one‐way switch into a two‐way toggle switch. Only a joint blockage of IRS1, AKT, and mTOR removed the switch and allowed a graded response to input stimuli. Several experimental studies supported this prediction in which the mTOR inhibitor, rapamycin, released the S6K dependent negative feedback and activated AKT in human tumors as well as in tumor cell lines.100, 101, 102

The role of the negative feedback from S6K to IRS1 was further investigated by several groups. The combination of modeling and experiments revealed that this negative feedback does not affect mTORC2 in Hela cells, although the latter depends on PI3K levels43 (Figure 3, label 1). A similar observation was found in Fao cells (hepatic‐derived cell line), where the disruption of this negative feedback by rapamycin could not restore pAKT levels completely.45 The role of the feedback from mTORC1 to IRS1 was shown to be crucial in explaining mechanistic differences between healthy and diabetic cells.56 This work suggested that attenuated activity of mTORC1 to IRS1 is a key mechanism in insulin resistance in Type 2 diabetes and helped to explain the reduced sensitivity to insulin and glucose uptake. Kubota et al. demonstrated the existence of a delayed negative feedback, different from the negative feedback discussed above. The delayed negative feedback is sufficient to explain the adaptation of S6K levels to insulin in Fao cells, indicating the presence of unidentified pathways regulating S6K45 (Figure 3, label 3). This work proposed the negative feedback from mTORC1 to S6K, which could explain the dynamics of S6K. However, this still remains to be verified experimentally. There is also a reported negative cross‐pathway feedback between mTOR and MAPK pathways.103, 104 Chandarlapaty et al.103 reported FOXO‐dependent activation of RTK receptors such as HER3, IGF‐1R, and IR under inhibition of AKT in breast cancer cell lines. According to these findings, AKT inhibits FOXO which in turn activates HER3 that leads to an activation of the mTOR pathway. Based on this observation, Nguyen et al.62 developed a mechanistic cross‐talk model of mTOR/RTK/ERK pathways, analyzed qualitatively the functional role of feedback loops and performed feedback‐related therapeutic simulations.

Figure 3.

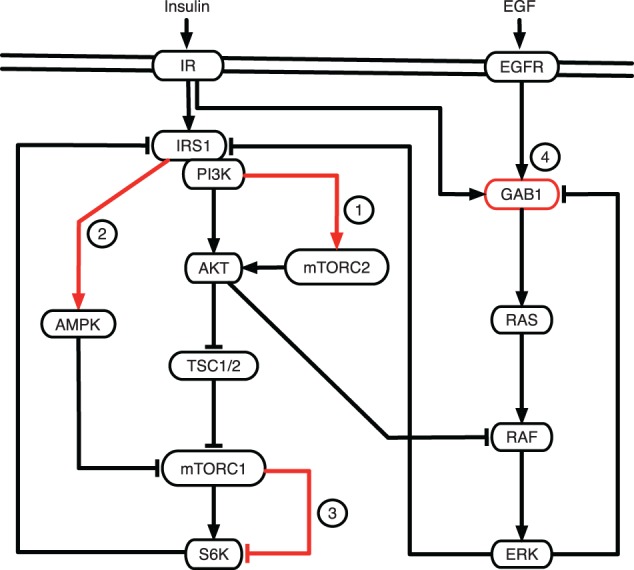
Simplified mTOR signaling network with interactions inferred from modeling approaches. Depicted is the crosstalk of mTOR with MAPK signaling pathway. Red dashed edges numbered as circled labels represent the interactions and nodes inferred from modeling approaches. Label 1: PI3K dependent regulation of mTORC2 which is independent of negative feedback from S6K to IRS1.43 Label 2: Positive regulation of AMPK by IRS1.44 Label 3: Negative regulation of S6K by mTORC1.45 Label 4: Gab1 was found to be an important adaptor protein between insulin and MAPK signaling that plays a role of a nonlinear amplifier of mitogenic responses.48

Crosstalk Between mTOR Signaling and Other Pathways

Cells can convert multiple external clues into distinct cellular decisions via a limited number of signaling pathways. mTOR signaling senses and integrates a variety of environmental signals to regulate the growth and homeostasis.2 But it is currently not well understood how the mTOR signaling pathway integrates all these signals. Borisov et al. investigated the crosstalk between insulin/mTOR signaling and MAPK signaling pathways using a combined approach of modeling and experiments.48 To explore how these two signaling networks are linked together, the authors built a large‐scale ODE model comprising 78 variables and 200 parameters. This work showed that co‐activation by low insulin and high EGF led to increased RAF activity due to increased RAS activity and suggested that the net effect of insulin and EGF stimulation on RAF is positive in the human embryonic kidney (HEK293) cells. The model predicted that insulin cannot enhance ERK and MEK upon PI3K inhibition, which was validated experimentally by treating HEK293 cells with the PI3K inhibitor, wortmannin. In the same study, the quantitative experimental data on the dynamics of GAB1‐PI3K complexes upon insulin and EGF co‐stimulation suggested that GAB1 is one of the key mediators of insulin‐EGF crosstalk (Figure 3, label 4). Another link between insulin stimulated mTOR and ERK signaling was observed by Wu et al., where a three state Boolean model predicted that the ERK feedback to IRS1 does not affect IRS1 tyrosine phosphorylation levels.51 Experimental validation was done by applying the ERK inhibitor to human liver carcinoma (HepG2) cells. This work also experimentally demonstrated that the JNK inhibitor significantly upregulated IRS1 tyrosine phosphorylation thereby highlighting the importance of the feedback from JNK pathway to insulin signaling via IRS1. Hatakeyama et al. experimentally confirmed in WebB4 expressing Chinese hamster ovary (CHO) cells that PI3K‐AKT pathway activation suppresses the ERK pathway by negatively regulating RAF.52 This was independently confirmed in other cell lines.105, 106 The established model in the same work,52 including RAF‐AKT crosstalk and protein phosphatase 2A (PP2A), accounted for the experimental data better than the model without crosstalk. The findings indicate that a dual regulation by the crosstalk and PP2A is necessary for the kinetic regulation of ERK activity.

Faratian et al. developed an mTOR‐ERK crosstalk model to study the consequences of anti‐HER2 antibody therapeutic intervention in ovarian carcinoma (PE04) and breast cancer cells (BT474).54 In this work, the authors revealed that PTEN, a negative regulator of PI3K and mTOR, is the dominant resistance factor to receptor tyrosine kinase (RTK) inhibition, which suggested that PI3K inhibition in tumors with low PTEN levels should be combined with RTK inhibitors. The effect of combined adenosine monophosphate dependent kinase (AMPK) and mTORC1 inhibition was studied experimentally and through modeling.107 The authors investigated the impact of AMPK on mTOR in response to energy deprivation. AMPK activated pathways that led to the generation of ATP and suppressed ATP consuming anabolic processes, such as ribosome biogenesis and translation.108 Upon activation, AMPK phosphorylated the TSC1–TSC2 complex, which eventually suppressed mTORC1. By extending the previous model43 and combining it with new experiments, Sonntag et al. investigated how AMPK is linked to mTOR signaling.44 Their model predicted a mechanism, in which IRS1 activated AMPK upon stimulation (Figure 3, label 2), which was then experimentally validated with western blot analysis from Hela cells by overexpressing IRS1 and PTEN.

Another crosstalk is observed between the mTOR and SIRT1 pathways. Both mTOR and SIRT1 regulate a number of metabolic pathways and play an important role in promoting longevity.109 However, it remains less well understood how their interplay might contribute to longevity. Several studies suggested a mechanism wherein SIRT1 negatively regulates mTOR signaling through the TSC1/2 complex.110, 111 Based on experimental results, Auley et al. suggested a mathematical model of metabolic regulation in aging.109 Jain et al. modeled the crosstalk of the brain‐derived neurotrophic factor (BDNF) and mTOR pathways, analyzed the stability properties of the combined model and explored the impact of input combinations and feedbacks on the behavior of the BDNF‐mTOR crosstalk.50

mTOR Models in Metabolic Insulin Signaling

Insulin is the major controller of energy homeostasis in the human body and is therefore closely linked to mTOR signaling on the cellular level. Major metabolic action of insulin is catalyzing glucose uptake into skeletal muscle and adipose tissue.112 Because the insulin signaling is a highly complex process and involves several layers of regulation, mathematical models have proven to be very useful to uncover these complexities. Extensive modeling has been carried out to uncover mechanistic insights starting from the insulin binding to the insulin signaling and eventually to cellular responses. Based on the available models of IR binding, Sedaghat et al. developed an ODE model of the metabolic insulin signaling.53 This model includes upstream regulators of mTORC1 such as PI3K and AKT and predicted that the negative feedback from protein kinase C (PKC) to IRS1 is sufficient to explain PKC activation dynamics in response to insulin. A steady‐state model that used parameters from Sedaghat et al.53 showed that insulin stimulated GLUT4 can operate as a bistable switch.59 The model of Sedaghat et al.53 was extended to study the effect of amino acids in presence of insulin.57 Their model proposed that GLUT4 translocation is more sensitive to higher amino acid concentrations and produced a bistable behavior under various insulin concentrations at steady state. The insulin stimulated PI3K/AKT/mTOR pathway model was linked to metabolic pathways to study how metabolic processes are regulated by the mTOR pathway.47, 64 mTOR models have been successfully applied in untangling complex mechanisms of insulin resistance, which is the main cause of Type 2 diabetes. Insulin resistance is characterized by dysfunction in the insulin control that involves several layers of regulation, different cell types and different organs.113 Brännmark et al. developed an ODE model and examined the phosphorylation of the IR, IRS1 and its endocytosis that were measured under various experimental perturbations in primary human adipocytes.55 By testing several activation mechanisms, this work proposed that both the receptor internalization and feedback from IRS1 to IR are most plausible mechanisms that explain experimental observations. Later, the same authors built an extended ODE model comprising mTORC1 and its downstream effectors and combined it with the experimental data to explore mechanistic differences between healthy and diabetic cells.56 Experiments performed by these authors showed attenuated activity of mTORC1 as a key feature of insulin resistance in diabetic condition. Integration of these experiments with the mathematical model predicted that attenuation of the feedback from mTORC1 to IRS1 is a key mechanism in insulin resistance in Type 2 diabetes.

DISSECTING MTOR SIGNALING USING THE PRINCIPLES FROM INFORMATION THEORY AND NETWORK MOTIFS

Signaling pathways have a remarkable property to code multiple cellular information via few common signaling pathways.114 This cellular information is coded in certain temporal patterns of stimuli such as growth factors that are translated into specific temporal patterns in signaling pathways.115 Eventually, encoded information in signaling pathways is selectively decoded by various downstream molecules. For instance, pulsative dynamics of a stimulus may produce an increasing or pulsatile response in the molecules of signaling pathways.49 Overall, there are three types of temporal patterns of a stimulus that have been extensively studied in signaling pathways both theoretically and experimentally (Figure 2(e)). Encoding and decoding the temporal patterns is highly dependent on the network structure and this dependency has been studied in detail in terms of network motifs. Network motifs are recurring circuits of interactions, from which networks are constructed and were shown to be the building blocks of transcriptional and signal transduction networks.116 Based on these ideas, there have been series of studies to uncover the mechanisms of the mTOR pathway using the principles from information theory and network motifs. By measuring and translating the temporal profiles of pAKT and its downstream effector S6K into an ODE model, Kubota et al. revealed that the activation kinetics of S6K were best explained by an incoherent feed‐forward loop (IFFL)45 (Figure 2(f)). An IFFL consists of three nodes, wherein the first node regulates the other nodes positively and the second node regulates the third node negatively.116 This motif structure explained why S6K levels return to the basal level despite continuous stimulation. In their model, S6K is activated through an IFFL that involves rapid activation followed by delayed inactivation through mTOR. This property is known as perfect adaptation, where upon the stimulation the system's response returns to the prestimulus level.117, 118 Different insights in temporal patterns have been obtained in PC12 cells, where the cells were stimulated by step, pulse and ramp type patterns of EGF stimuli.49 The authors investigated how the AKT/mTOR pathway transmits temporal information from distinct upstream EGF stimulus patterns to downstream effectors (Figure 2(g)). They modeled the mTOR pathway using a simple three component ODE model and applied frequency response analysis, which allows to study how the system responds to inputs over a wide range of time scales.119 The authors showed that the AKT/mTOR pathway functions as a low‐pass filter despite the different temporal patterns of phosphorylated EGF receptors in PC12 cells. Low‐pass filters transmit slowly occurring changes from upstream signals to downstream effectors more efficiently than rapidly occurring ones. This property of the AKT pathway suggested that the EGFR inhibitor, lapatinib, converts strong transient pAKT into weak sustained pAKT signals, which led to a stronger S6 phosphorylation.

Following this study, Toyoshima et al. examined signal transfer efficiencies of various pathways, including AKT, in different cell lines using both theoretical and experimental approaches.46 By modeling the pathways using ODEs they revealed that the signal transfer efficiency of the transient peak amplitude from upstream to downstream signals is attenuated proportionally to the negative regulation within the signaling network. Global analysis of about 568 sets of upstream and downstream time courses of signaling pathways demonstrated that the attenuation of the signal transfer efficiency is a global property of signaling pathways, where about 169 sets including the AKT/mTOR pathway met this criterion. This property was found to be conserved not only in PC12 cells, but also in other cell lines such as human umbilical vein endothelial cells (HUVECs), Swiss 3T3 and HeLa cells. Owing to this property, downstream molecules show higher sensitivity to the activator and lower sensitivity to the inhibitor compared to the upstream molecules. Experiments revealed that in the mTOR pathway, S6 which is a downstream molecule, shows lower sensitivity to the EGFR inhibitor than AKT. Overall, this study revealed that through this remarkable mechanism the cells can control the sensitivity of mTOR pathway molecules to both activators and inhibitors of the pathway.

TIME SCALE AND DEGREE COMPLEXITY IN THE MTOR MODELS

mTOR signaling exerts multiple effects on multiple time scales. Based on this fact, the mathematical models of the mTOR pathway differ with respect to the time scale and the complexity which they cover. In this section, we will discuss the impact of the time scale of observation on the design principles of the mTOR signaling pathway by providing some recent examples.

Figure 4 maps the different mathematical models of the mTOR pathway onto the time‐scale versus complexity plane. The corresponding table that summarizes the mTOR models is given in Table 1. The models on the time scale of minutes are typically valid for protein signaling networks. To study the relation between the receptor internalization and the activation of downstream insulin network components in response to insulin stimulus, it was necessary to perform measurements within the first hour of stimulation.55, 56 Detailed measurements on this early time scale allowed to model the early phase of insulin signaling thereby enabling for a better understanding of insulin resistance in human adipocytes. In the work of Kubota et al., the authors measured the response of Fao cells to different temporal patterns of insulin stimulation.45 In this case, monitoring the system dynamics for a longer time period was essential, because the effects of step and ramp stimulation on protein phosphorylation lasted over hours and protein activation remained dynamic. Monitoring the dynamics over longer time is also important to properly differentiate, whether the activation follows transient or sustained behavior, which significantly affects the design principles of the underlying network. In the same work, by conducting experiments for 4–8 h and quantifying transient as well as sustained responses, the authors revealed the dependence of pAKT on the increasing rate and final concentration of insulin, whereas pS6K was dependent on the increasing rate of insulin, only. Based on these observations, they could reconstruct the underlying mechanism on the molecular level. Without long time analysis it would have been impossible to reveal such dependencies and would have resulted in an improper and incomplete network design.

Figure 4.

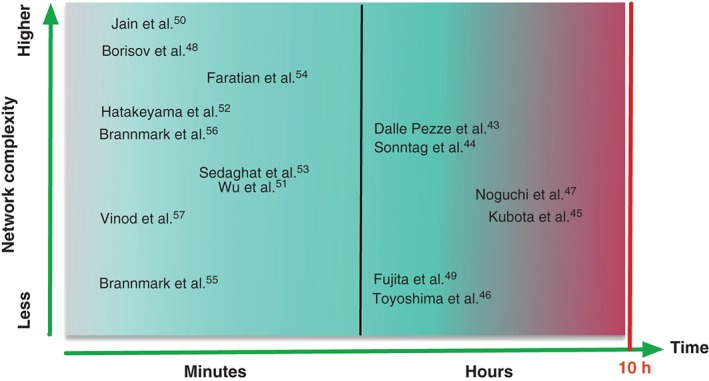
Scatter plot of mTOR models according to their complexity and time window of observation. The complexity axis refers to the number of molecules and/or genes considered in the model. Depicted are only models supported by experimental time series data. The fast time scale from seconds to minutes is associated with activation and deactivation mechanisms based on post‐translational modifications, while the longer time scales incorporate processes such as protein synthesis and degradation. Most models of mTOR signaling pathways are valid in time scale of minutes and mainly describe the early phase of the mTOR signaling. Interestingly, majority of crosstalk models are grouped in this range and belong to the models with higher complexity. Most models that exploit information‐theory approaches belong to the long time scale group.

Long term observation was also important in establishing the link between mTOR signaling and metabolism.47 In particular, this study showed that pAKT can encode the information over a wide dynamic range of insulin concentrations in both transient and sustained phases, and control the glucose metabolism. The most complex mTOR models so far have been established by Jain et al.50 and Borisov et al.48 The latter model is one of the successful examples that integrates detailed pathway information with mechanistic modeling. This model was developed to dissect how the multiple crosstalk mechanisms in insulin and EGF stimulated pathways function together in a cell‐dependent context. Despite many mechanisms of IR‐EGFR crosstalk being well characterized at the molecular level, is not well understood how cell responds to combined EGF and insulin stimulation due to the many pathway interactions and feedback loops. With the aid of this detailed model, the authors predicted that GAB1 behaves like a nonlinear amplifier for mitogenic responses and insulin provides EGF signaling with the stability to GAB1 suppression.

Another example is the crosstalk model by Faratian et al.,54 in which the detailed modeling enabled the authors to closely examine therapeutic responses to RTK inhibitors and finally allowed for improved selection of treated patients. We think that the classification of the models with respect to the time and degree of complexity can guide the reader to select appropriate model of interest depending on the details and the time scale, in which the experiments were conducted. Since there is a number of different models available, this approach can simplify the model selection depending on the experimental data measured in certain time scales.

Bridging mTOR Models with Different Time Scales

The classification of mTOR models according to their time scale raises the question of constructing an integrated model bridging various processes running on different time scales. Since most mTOR models are ODE based and thus share the same model formalism it is in principle possible to integrate the various descriptive levels into one large differential equation model. However, apart from the problem of defining proper biological boundary conditions between the different processes evolving on different times, the resulting ODEs which will be very stiff due to large differences in time scales. Numerical integration of stiff ODEs is computationally challenging and requires suitable numerical methods and might lead to precision loss.120 One solution is the use of a quasi steady‐state approximation. It is possible to reduce the dimensionality of the ODE system, thereby allowing to speed up numerical simulations. The quasi steady‐state approximation is based on the assumption that enzyme mediated substrate conversion quickly reaches and remains in a quasi steady‐state.121 These assumptions allow to separate fast and slow time scales. Since the fast time scale is neglected in this setting, it is, however, not possible to analyze feedbacks that arise in fast time scales. In order to study feedbacks that are present both in fast and slow time scales, one could model them using different modeling formalisms. For example, some studies recommend to model fast processes by ODEs and slow processes by flux balance analysis (FBA), and to integrate them using advanced approaches such as iFBA (integrated FBA)122 and integrated dynamic FBA (idFBA).123 In addition, these approaches are capable of integrating Boolean models with ODEs and FBA. The first integrated whole‐cell model of Mycoplasma genitalium was constructed using these advanced approaches that allowed to capture a diverse types of cellular processes which was not possible by a single formalism alone.124

CONCLUSIONS

The mTOR pathway has attracted much scientific interest over the last decade and many things continue to be discovered as we learn more about this pathway. In this review, we discussed the contribution of Systems Biology approaches to the understanding of mTOR signaling. Overall, combined efforts of experiments and mathematical models shed light onto the mechanisms regulating mTOR signaling. Most mTOR models simulations are in a close agreement with the time course of experimental data, which indicates a predictive power of the models. Mathematical modeling has explained the role of negative feedback in the presence of opposing positive feedbacks58 in mTOR signaling and showed the importance of this feedback in elucidating the molecular differences between healthy and diabetic cells.45 Moreover, modeling efforts have been crucial in identifying the negative feedback in mTOR signaling that has been inferred from experimental data in Fao cells.45 Applying principles from information theory also helped to elucidate the dynamics of mTOR signaling components in terms of network motifs.46, 49 These studies provided an alternative explanation as to why downstream components are less sensitive to the inhibitor than the upstream components in the mTOR pathway. Modeling was also successful in providing significant insights into the crosstalk of mTOR with other pathways. In particular, modeling provided a quantitative explanation about crosstalk mechanisms at different levels between mTOR and MAPK pathways such as the crosstalk upstream of Ras,48 the RAF‐AKT crosstalk,52 the crosstalk at the level of ERK and IRS1,51 and the crosstalk between mTOR and AMPK pathways.44 Mathematical models of the mTOR pathway may provide rational drug targeting predictions. For instance, the low‐pass filter property of the AKT pathway helped to elucidate why the EGFR inhibitor lapatinib leads to strong S6K phosphorylation.49 Furthermore, modeling efforts revealed that PI3K inhibition in tumors with low PTEN levels should be combined with RTK inhibitors.54 Theoretical analysis on feedback loops in the mTOR pathway proposed the administration of additional inhibitors that target PI3K and AKT together with rapamycin to achieve a better treatment efficacy.58 Mathematical and computational models have been shown to be extremely useful in characterizing how the multiple feedback loops work together and how mTOR signaling is linked to further signaling pathways. The impact of the different time scales on the design of mTOR pathway should be noted as well. Different time scales include time‐sequential events involving protein signaling and gene regulation in feedback entangled processes that last for several hours.71 Based on this, the design principles of mTOR network on different time scales might be largely affected. The degree complexity of models should be increased depending on the amount and quality of the experimental data, because the predictive power of the model relies on the identifiability of model parameters, which can be estimated from the data.93

One important challenge that remains to be explored is how mTOR as a single protein and even the multisubunit complex mTORC1 can integrate and translate these signals into different cell fate decisions. It is also less understood how mTORC1 and mTORC2 signaling pathways regulate each other. It is known that mTORC1 and mTORC2 function as scaffold proteins for integrating the complexes and for binding substrates and regulators.8 The function of scaffold proteins has been well characterized by mathematical modeling and engineered scaffold proteins. In particular, both approaches have shown that scaffold proteins can modify signaling pathways by coordinating positive and negative feedback signals.125 In addition, scaffold proteins are capable of creating signaling thresholds and various signaling behaviors ranging from graded to oscillatory signalings.126 Given the current knowledge of the mTOR signaling, it is feasible to verify these questions via mathematical modeling by generating various hypotheses in silico which might give a better idea about possible regulation mechanisms that are amenable for experimental validation.

One of the bottlenecks in the development of accurate predictive mathematical models for signaling networks is the lack of experimental data on initial conditions and rate constants. This is certainly true for the mTOR pathway as well. Signaling components have been largely identified, but relatively little is known about their quantitative values like abundance and rate constants. These values can only be determined when recombinant proteins are available.11 Additionally, direct measurement of the rate constants for different signaling reactions is still experimentally challenging. Since there is a number of mTOR models which were developed for different cell lines and in different context, the next challenge will be to merge them to get a more comprehensive model with presumably higher predictive power. For example, such a consensus model was developed for the NF‐kB signaling network13 which shows an increased predictive power over the formerly used small networks. On the other hand, mathematical models can be combined with network inference algorithms that have been successfully applied to identify principal drivers of the molecular differences between the genetic and pharmacological perturbations.127

In summary, application of mathematical modeling to mTOR signal transduction is still at the beginning with many conceptual and technical challenges. So far, despite extensive biochemical knowledge about mTOR signaling, only a subset of known information has been subjected to computational modeling. In order to gain a more global understanding of the mTOR pathway, new mechanistic and logical models are needed. They will allow us to tackle yet unresolved questions such as the exact contribution of the mTOR pathway on aging, on other signaling pathways and suitable targets for drug intervention. Therefore, computational modeling will continue to play an important role as experimental research uncovers new mechanistic knowledge and tackles new questions about mTOR signaling.