The forecasting of menstruation based on a state‐space modeling of basal body temperature time series

Abstract

Women's basal body temperature (BBT) shows a periodic pattern that associates with menstrual cycle. Although this fact suggests a possibility that daily BBT time series can be useful for estimating the underlying phase state as well as for predicting the length of current menstrual cycle, little attention has been paid to model BBT time series. In this study, we propose a state‐space model that involves the menstrual phase as a latent state variable to explain the daily fluctuation of BBT and the menstruation cycle length. Conditional distributions of the phase are obtained by using sequential Bayesian filtering techniques. A predictive distribution of the next menstruation day can be derived based on this conditional distribution and the model, leading to a novel statistical framework that provides a sequentially updated prediction for upcoming menstruation day. We applied this framework to a real data set of women's BBT and menstruation days and compared prediction accuracy of the proposed method with that of previous methods, showing that the proposed method generally provides a better prediction. Because BBT can be obtained with relatively small cost and effort, the proposed method can be useful for women's health management. Potential extensions of this framework as the basis of modeling and predicting events that are associated with the menstrual cycles are discussed. © 2017 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.

1. Introduction

The menstrual cycle is the periodic changes that occur in the female reproductive system that make pregnancy possible. Throughout the menstrual cycle, basal body temperature (BBT) also follows a periodic pattern. The menstrual cycle consists of two phases, the follicular phase followed by the luteal phase, with ovulation occurring at the transition between the two phases. During the follicular phase, BBT is relatively low with the nadir occurring within 1 to 2 days of a surge in luteinizing hormone that triggers ovulation. After the nadir, the cycle enters the luteal phase and BBT rises by 0.3°C to 0.5°C 1.

Considerable attention has been paid to the development of methods to predict the days of ovulation and the day of onset of menstruation; currently available methods include urinary and plasma hormone analyses, ultrasound monitoring of follicular growth, and monitoring of changes in the cervical mucus or BBT. Monitoring the change in BBT is straightforward because it requires neither expensive instruments nor medical expertise. However, of the currently available methods, BBT measurement is the least reliable because it has an inherently large day‐to‐day variability 1; therefore, statistical analyses are required to improve predictions of events associated with the menstrual cycle based on BBT.

Many statistical models of the menstrual cycle length have been proposed, with the majority explaining the marginal distribution of menstrual cycle length, which is characterized by a long right tail. To explain within‐individual heterogeneity, which is an important source of variation in menstrual cycle length, Harlow and Zeger 2 made the biological assumption that a single menstrual cycle is composed of a period of ‘waiting’ followed by the ovarian cycle. They classified menstrual cycles into standard, normally distributed cycles that contained no waiting time and into nonstandard cycles that contained waiting time. Guo et al. 3 extended this idea and proposed a mixture model consisting of a normal distribution and a shifted Weibull distribution to explain the right‐tailed distribution. By accommodating covariates, they also investigated the effect of an individual's age on the moments of the cycle length distribution. Lin et al. 4 described a linear mixed model that can explain heterogeneous variances of within‐woman cycle length. Huang et al. 5 attempted to model the changes in the mean and variance of menstrual cycle length that occur during the approach of menopause. By using a change‐point model, they found changes in the annual rate of change of the mean and variance of menstrual cycle length, which indicate the start of early and late menopausal transition. In contrast, Bortot et al. 6 focused on the dynamic aspect of menstrual cycle length over time. By using a state‐space modeling approach, they derived a predictive distribution of menstrual cycle length that was conditional on past time series. By integrating a fecundability model into their time series model, they also developed a framework that estimates the probability of conception that is conditional on the within‐cycle intercourse behavior. A related joint modeling of menstrual cycle length and fecundability has been attained more recently 7, 8.

Although daily fluctuations in BBT are associated with the events of the menstrual cycle, and therefore BBT time series analyses likely provide information regarding the length of the current menstrual cycle, there have been no previous studies modeling BBT data to predict menstrual cycle length. Thus, in the present study, we developed a statistical framework that provides a predictive distribution of menstrual cycle length (which, by extension, is a predictive distribution of the next day of onset of menstruation) that is sequentially updated with daily BBT data. We used a state‐space model that includes a latent phase state variable to explain daily fluctuations in BBT and to derive a predictive distribution of menstrual cycle length that is dependent on the current phase state.

This paper is organized as follows: in Section 2, we briefly describe the data required for the proposed method and how the test dataset was obtained. In Section 3, we provide the formulation of the proposed state‐space model for menstrual cycle and give an overview of the filtering algorithms that we use to estimate the conditional distributions of the latent phase variable given the model and dataset. In the same section, we also describe the predictive probability distribution for the next day of onset of menstruation that was derived from the proposed model and the filtering distribution for the menstrual phase. In Section 4, we apply the proposed framework to a real dataset and compare the accuracy of the point prediction of the next day of onset of menstruation among the proposed method and previous methods. In Section 5, we discuss the practical utility of the proposed method with respect to the management of women's health and examine the potential challenges and prospects for the proposed framework.

2. Data

We assumed that for a given female subject, a dataset containing a daily BBT time series and days of onset of menstruation was available. The BBT could be measured with any device (e.g., a conventional thermometer or a wearable sensor), although different model parameters may be adequate for different measurement devices. In the application of the proposed framework described in Section 4, we used real BBT time series and menstruation onset data that was collected via a website called Ran's story (QOL Corporation, Ueda, Japan), which is a website that allows registered users to upload their self‐reported daily BBT and days of menstruation onset to QOL Corporation's data servers. At the time of registration to use the service, all users of Ran's story agree to the use of their data for academic research. Although no data regarding the ethnic characteristics of the users were available, it is assumed that the majority of, if not all, the users were ethnically Japanese because Ran's story is provided only in the Japanese language.

3. Model description and inferences

3.1. State‐space model of the menstrual cycle

Here we develop a state‐space model for a time series of observed BBT, y _t, and an indicator of the onset of menstruation, z _t, obtained for a subject for days t=1,…,T. By z _t=1, we denote that menstruation started on day t, whereas z _t=0 indicates that day t is not the first day of menstruation. We denote the BBT time series and menstruation data obtained until time t as Y _t=(y ₁,…,y _t) and Z _t=(z ₁,…,z _t), respectively.

We considered the phase of the menstrual cycle, ${\theta }_t\in \mathbb{R}(t=0,1,\dots ,T)$, to be a latent state variable. We let ϵ _t as the daily advance of the phase and assume that it is a positive random variable that follows a gamma distribution with shape parameter α and rate parameter β, which leads to the following system model:

$${\theta }_t={\theta }_{t-1}+{ϵ}_t$$ (1)

$${ϵ}_t\sim \text{Gamma}(\alpha ,\beta ).$$ (2)

Under this assumption, the conditional distribution of θ _t, given θ _t−1, is a gamma distribution with a probability density function:

$$\begin{array}{ccc}\hfill p\left({\theta }_t\right|{\theta }_{t-1})& =\text{Gamma}(\alpha ,\beta )\hfill & \hfill \\ \hfill & =\frac{{\beta }^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}{({\theta }_t-{\theta }_{t-1})}^{\alpha -1}\exp \left\{-\beta ({\theta }_t-{\theta }_{t-1})\right\}.\hfill \end{array}$$ (3)

It is assumed that the distribution for the observed BBT y _t is conditional on the phase θ _t. As periodic oscillation throughout each phase is expected for BBT, a finite trigonometric series is used to model the average BBT. Assuming a Gaussian observation error, we expressed the observation model for BBT as

$$y_t=a+\sum _{m=1}^M(b_m\cos 2m\pi {\theta }_t+c_m\sin 2m\pi {\theta }_t)+e_t$$ (4)

$$e_t\sim \text{Normal}(0,{\sigma }^2),$$ (5)

where M is the maximum order of the series. Conditional on θ _t,y _t then follows a normal distribution with a probability density function:

$$\begin{array}{ccc}\hfill p\left(y_t\right|{\theta }_t)& =\text{Normal}\left\{\mu \left({\theta }_t\right),{\sigma }^2\right\}\hfill & \hfill \\ \hfill & =\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{{\left\{y_t-\mu \left({\theta }_t\right)\right\}}^2}{2{\sigma }^2}\right],\hfill \end{array}$$ (6)

where $\mu \left({\theta }_t\right)=a+{\sum }_{m=1}^M(b_m\cos 2m\pi {\theta }_t+c_m\sin 2m\pi {\theta }_t)$. By this definition, μ(θ _t) is periodic in terms of θ _t with a period of 1.

For the onset of menstruation, we assume that menstruation starts when θ _t ‘steps over’ the smallest following integer. This is represented as follows:

$$z_t=0\text{when}\lfloor {\theta }_t\rfloor =\lfloor {\theta }_{t-1}\rfloor$$ (7)

$$=1\text{when}\lfloor {\theta }_t\rfloor >\lfloor {\theta }_{t-1}\rfloor ,$$ (8)

where ⌊x⌋ is the floor function that returns the largest previous integer for x. Writing this deterministic allocation in a probabilistic manner, which is conditional on (θ _t,θ _t−1),z _t follows a Bernoulli distribution:

$$p\left(z_t\right|{\theta }_t,{\theta }_{t-1})=(1-z_t)\left\{I(\lfloor {\theta }_t\rfloor =\lfloor {\theta }_{t-1}\rfloor )\right\}+z_t\left\{I(\lfloor {\theta }_t\rfloor >\lfloor {\theta }_{t-1}\rfloor )\right\},$$ (9)

where I(x) is the indicator function that returns 1 when x is true or 0 otherwise.

Let $\mathit{\xi }=(\alpha ,\beta ,\sigma ,a,b_1,\dots ,b_M,c_1,\dots c_M)$ be a vector of the parameters of this model. Given a time series of BBT, Y _T=(y ₁,…,y _T), an indicator of menstruation, Z _T=(z ₁,…,z _T), and a distribution specified for initial states, p(θ ₁,θ ₀), these parameters can be estimated by using the maximum likelihood method. The log‐likelihood of this model is expressed as

$$\begin{array}{c}\hfill l(\mathit{\xi };Y_T,Z_T)=logp(y_1,z_1|\mathit{\xi })+\sum _{t=2}^{T}logp(y_t,z_t|Y_{t-1},Z_{t-1},\mathit{\xi }),\end{array}$$ (10)

where

$$\begin{array}{c}\hfill logp(y_1,z_1|\mathit{\xi })=log\int \int p(y_1\left|{\theta }_1\right)p\left(z_1\right|{\theta }_1,{\theta }_0\left)p\right({\theta }_1,{\theta }_0)d{\theta }_{1}d{\theta }_0,\end{array}$$ (11)

and for t=2,…,T,

$$\begin{array}{c}\hfill logp(y_t,z_t|Y_{t-1},Z_{t-1},\mathit{\xi })=log\int \int p(y_t\left|{\theta }_t\right)p\left(z_t\right|{\theta }_t,{\theta }_{t-1}\left)p\right({\theta }_t,{\theta }_{t-1}|Y_{t-1},Z_{t-1})d{\theta }_{t}d{\theta }_{t-1},\end{array}$$ (12)

which can be sequentially obtained by using the Bayesian filtering technique described later. Note that although p(y _t|θ _t)(t⩾1) and p(θ _t,θ _t−1|Y _t−1,Z _t−1)(t⩾2) depend on ξ, this dependence is not explicitly described for notational simplicity.

3.2. State estimation and calculation of log‐likelihood by using the sequential Bayesian filtering

Given the state‐space model of menstrual cycle described earlier and its parameters and data, the conditional distribution of an unobserved menstrual phase can be obtained by using recursive formulae for the state estimation problem, which are referred to as the Bayesian filtering and smoothing equations 9. We describe three versions of this sequential procedure, that is, prediction, filtering, and smoothing, for the state‐space model described earlier.

Let p(θ _t,θ _t−1|Y _t,Z _t) be the joint distribution for the phase at successive time points t and t−1, which is conditional on the observations obtained by time t. This conditional distribution accommodates all the data obtained by time t and is called the filtering distribution. Similarly, the joint distribution for the phase of successive time points t and t−1 conditional on the observations obtained by time t−1,p(θ _t,θ _t−1|Y _t−1,Z _t−1), is referred to as the one‐step‐ahead predictive distribution. For t=1,…,T, these distributions are obtained by sequentially applying the following recursive formulae:

$$\begin{array}{ccc}\hfill p({\theta }_t,{\theta }_{t-1}|Y_{t-1},Z_{t-1})& =p\left({\theta }_t\right|{\theta }_{t-1}\left)p\right({\theta }_{t-1}|Y_{t-1},Z_{t-1})\hfill & \hfill \\ \hfill & =p\left({\theta }_t\right|{\theta }_{t-1})\int p({\theta }_{t-1},{\theta }_{t-2}|Y_{t-1},Z_{t-1})d{\theta }_{t-2},\hfill \end{array}$$ (13)

$$\begin{array}{ccc}\hfill p({\theta }_t,{\theta }_{t-1}|Y_t,Z_t)& =\frac{p(y_t,z_t|{\theta }_t,{\theta }_{t-1}\left)p\right({\theta }_t,{\theta }_{t-1}|Y_{t-1},Z_{t-1})}{\int \int p(y_t,z_t|{\theta }_t,{\theta }_{t-1}\left)p\right({\theta }_t,{\theta }_{t-1}|Y_{t-1},Z_{t-1})d{\theta }_{t}d{\theta }_{t-1}}\hfill & \hfill \\ \hfill & =\frac{p\left(y_t\right|{\theta }_t\left)p\right(z_t|{\theta }_t,{\theta }_{t-1})p({\theta }_t,{\theta }_{t-1}|Y_{t-1},Z_{t-1})}{\int \int p\left(y_t\right|{\theta }_t\left)p\right(z_t|{\theta }_t,{\theta }_{t-1})p({\theta }_t,{\theta }_{t-1}|Y_{t-1},Z_{t-1})d{\theta }_{t}d{\theta }_{t-1}},\hfill \end{array}$$ (14)

where for t=1, we set p(θ ₁,θ ₀|Y ₀,Z ₀) as p(θ ₁,θ ₀), which is the specified initial distribution for the phase. Equations (13) and (14) are the prediction and filtering equations, respectively. Note that the denominator in Equation (14) is the likelihood for data at time t(Equations (11) and (12)). Hence, the log‐likelihood of the state‐space model is obtained through application of the Bayesian filtering procedure. Missing observations can be handled in the filtering equation (14) by marginalizing likelihood over the missing values.

The joint distribution for the phase, which is conditional on the entire set of observations, p(θ _t,θ _t−1|Y _T,Z _T), is referred to as the (fixed‐interval type) smoothed distribution. With the filtering and the one‐step‐ahead predictive distributions, the smoothed distribution is obtained by recursively using the following smoothing formula:

$$\begin{array}{ccc}\hfill p({\theta }_t,{\theta }_{t-1}|Y_T,Z_T)& =p({\theta }_t,{\theta }_{t-1}|Y_t,Z_t)\int \frac{p({\theta }_{t+1},{\theta }_t|Y_T,Z_T\left)p\right({\theta }_{t+1}\left|{\theta }_t\right)}{p({\theta }_{t+1},{\theta }_t|Y_t,Z_t)}d{\theta }_{t+1}\hfill & \hfill \\ \hfill & =\frac{p({\theta }_t,{\theta }_{t-1}|Y_t,Z_t)\int p({\theta }_{t+1},{\theta }_t|Y_T,Z_T)d{\theta }_{t+1}}{p\left({\theta }_t\right|Y_t,Z_t)}\hfill \\ \hfill & =\frac{p({\theta }_t,{\theta }_{t-1}|Y_t,Z_t)\int p({\theta }_{t+1},{\theta }_t|Y_T,Z_T)d{\theta }_{t+1}}{\int p({\theta }_t,{\theta }_{t-1}|Y_t,Z_t)d{\theta }_{t-1}}.\hfill \end{array}$$ (15)

In general, these recursive formulae are not analytically tractable for non‐linear, non‐Gaussian, state‐space models. However, the conditional distributions, as well as the log‐likelihood of the state‐space model, can still be approximated by using filtering algorithms for general state‐space models. We use Kitagawa's non‐Gaussian filter 10, where the continuous state space is discretized into equally spaced grid points at which the probability density is evaluated. We describe the numerical procedure to obtain these conditional distributions by using the non‐Gaussian filter in Appendix A.1.

3.3. Predictive distribution for the day of onset of menstruation

A predictive distribution for the day of onset of menstruation is derived from the assumptions of the model and the filtering distribution of the state.

We denote the distribution function and the probability density function of the gamma distribution with shape parameter s and rate parameter r as G(·;s,r) and g(·;s,r), respectively. Let the accumulated advance of the phase be denoted by Δ_k(t), which is then calculated as ${\mathrm{\Delta }}_k\left(t\right)={\sum }_{r=t+1}^{t+k}{ϵ}_r,k=1,2,\dots$. We consider the conditional probability that the next menstruation has occurred before day k+t given the phase state θ _t. We denote this conditional probability as $F\left(k\right|{\theta }_t)=\mathrm{Pr}\left\{{\mathrm{\Delta }}_k\left(t\right)⩾\lceil {\theta }_t\rceil -{\theta }_t\right\}$, where ⌈x⌉ is the ceiling function that returns the smallest following integer for x. Therefore, F(k|θ _t) represents the conditional distribution function for the onset of menstruation. Under the assumption of the state‐space model described earlier, F(k|θ _t) is given as

$$\begin{array}{ccc}\hfill F\left(k\right|{\theta }_t)& ={\int }_{\lceil {\theta }_t\rceil -{\theta }_t}^{\infty }g(x;k\alpha ,\beta )dx\hfill & \hfill \\ \hfill & =1-G(\lceil {\theta }_t\rceil -{\theta }_t;k\alpha ,\beta ).\hfill \end{array}$$ (16)

The conditional probability function for the day of onset of menstruation, denoted as f(k|θ _t), is then given as

$$\begin{array}{ccc}\hfill f\left(k\right|{\theta }_t)& =F\left(k\right|{\theta }_t)-F(k-1\left|{\theta }_t\right)\hfill & \hfill \\ \hfill & =\left\{1-G(\lceil {\theta }_t\rceil -{\theta }_t;k\alpha ,\beta )\right\}-\left[1-G\left\{\lceil {\theta }_t\rceil -{\theta }_t;(k-1)\alpha ,\beta \right\}\right]\hfill \\ \hfill & =G\left\{\lceil {\theta }_t\rceil -{\theta }_t;(k-1)\alpha ,\beta \right\}-G(\lceil {\theta }_t\rceil -{\theta }_t;k\alpha ,\beta ),\hfill \end{array}$$ (17)

where we set F(0|θ _t)=0.

The marginal distribution for the day of onset of menstruation, denoted as h(k|Y _t,Z _t), can also be obtained with the marginal filtering distribution for the phase state, p(θ _t|Y _t,Z _t). It is given as

$$h\left(k\right|Y_t,Z_t)=\int f(k\left|{\theta }_t\right)p\left({\theta }_t\right|Y_t,Z_t)d{\theta }_t.$$ (18)

Note that this distribution is conditional on the data obtained by time t, and therefore, it provides a predictive distribution for the day of onset of menstruation that accommodates all the available information. The point prediction for the day of onset of menstruation can also be obtained from h(k|Y _t,Z _t) and a natural choice for it would be the k that gives the highest probability, $\max h\left(k\right|Y_t,Z_t)$.

In Appendix A, we describe the numerical procedure for the non‐Gaussian filtering that we used to obtain these predictive distributions.

4. Application

We used the BBT time series and menstruation onset data provided by 20 users of the Ran's story website (QOL Corporation). Data were collected through the course of 44 to 91 consecutive menstrual cycles (see Table 1 for a summary of the data). Data of each subject's first 29 consecutive menstrual cycles were used to fit the state‐space model described earlier and to obtain maximum likelihood estimates of the parameters. For the order of the trigonometric series to be determined, models with M=1,2,…,12(referring to models M1, M2, …, and M12, respectively) were fitted and then compared based on the Akaike information criterion (AIC) for each subject. The best AIC model and the remaining menstrual cycle data (i.e., the data that were not used for the parameter estimations) were then used to evaluate the accuracy of the prediction of the next day of onset of menstruation based on the root mean square error (RMSE) and the mean absolute error (MAE) for each subject. We compared accuracy of the sequential prediction, obtained by using the proposed method, with that of prediction based on two previous methods: (i) the conventional calendar calculation method, which predicts the upcoming menstruation day as the day after a fixed number of days from the onset of preceding menstruation, and (ii) the sequential predictive method proposed by Bortot et al. 6, which utilizes the time series of past cycle length to yield a model‐based prediction of the length of the current cycle. The technical details for this comparison are described in Appendix B.1.

Table 1.

Summary of self‐reported menstrual cycle data obtained from 20 subjects.

	Subject
	1	2	3	4	5	6	7	8	9	10
All data
No. of consecutive cycles	46	45	48	54	52	57	56	52	45	44
Range of cycle length	[28, 59]	[23, 45]	[19, 61]	[26, 59]	[18, 47]	[25, 49]	[25, 36]	[26, 56]	[30, 51]	[27, 48]
Mean of cycle length	39.4	33.2	32.8	31.2	27.2	29.7	30.1	31.7	34.1	33.4
Median of cycle length	38	33	32.5	30.5	26	29	30	31	32	33
SD of cycle length	6.7	4.1	5.6	4.7	4.9	3.9	2.6	5.2	4.7	4.6
Initial age	29.6	24.9	23.2	26.3	30.5	33.2	34.9	29.9	33.9	31.4
Final age	34.5	29.0	27.6	30.9	34.4	37.8	39.5	34.4	38.1	35.4
Length of time series	1812	1495	1576	1687	1418	1693	1687	1647	1534	1470
No. of missing observations	80	0	96	31	43	33	21	85	38	60
Data for parameter estimation
No. of consecutive cycles	29	29	29	29	29	29	29	29	29	29
Range of cycle length	[31, 59]	[23, 43]	[19, 39]	[26, 59]	[22, 37]	[25, 49]	[27, 36]	[26, 56]	[30, 51]	[27, 42]
Mean of cycle length	41.3	33.7	31.5	30.6	26.7	30.4	30.9	33.0	34.7	32.1
Median of cycle length	41	34	32	29	26	30	31	32	32	31
SD of cycle length	7.2	4.0	3.9	5.8	3.3	4.8	2.5	5.9	5.8	3.5
Length of time series	1199	978	914	888	776	882	897	958	1007	933
No. of missing observations	24	0	52	21	20	22	8	5	19	34
Data for predictive
accuracy estimation
No. of consecutive cycles	17	16	19	25	23	28	27	23	16	15
Range of cycle length	[28, 44]	[28, 45]	[26, 61]	[28, 39]	[18, 47]	[26, 36]	[25, 36]	[26, 39]	[31, 35]	[27, 48]
Mean of cycle length	36.1	32.3	34.8	32.0	27.9	29.0	29.3	30.0	32.9	35.8
Median of cycle length	35	32	33	32	27	28	30	29	33	35
SD of cycle length	4.2	4.2	7.2	2.7	6.5	2.5	2.5	3.6	1.4	5.6
Length of time series	613	517	662	799	642	811	790	689	527	537
No. of missing observations	56	0	44	10	23	11	13	80	19	26
	Subject
	11†	12†	13†	14†	15†	16†	17†	18†	19†	20†
All data
No. of consecutive cycles	80	91	50	49	57	55	44	46	46	55
Range of cycle length	[24, 39]	[23, 31]	[22, 42]	[22, 41]	[24, 56]	[21, 55]	[14, 50]	[23, 43]	[9, 53]	[22, 51]
Mean of cycle length	29.0	26.6	27.2	31.0	27.8	27.9	28.7	26.6	31.4	27.6
Median of cycle length	28	26	27	31	27	25	29	26	31	27
SD of cycle length	3.3	1.8	3.1	3.5	4.1	7.7	4.7	3.0	6.2	3.9
Initial age	32.8	32.7	23.8	26.5	23.6	34.1	34.2	27.8	28.1	24.5
Final age	39.8	39.7	27.9	31.3	28.4	38.7	38.1	32.3	32.1	28.9
Length of time series	2318	2426	1361	1521	1584	1536	1265	1224	1447	1521
No. of missing observations	25	226	334	189	319	527	189	279	50	295
Data for parameter estimation
No. of consecutive cycles	29	29	29	29	29	29	29	29	29	29
Range of cycle length	[26, 39]	[23, 30]	[22, 31]	[22, 39]	[25, 56]	[21, 55]	[22, 31]	[23, 43]	[9, 53]	[22, 51]
Mean of cycle length	30.4	27.4	26.5	30.9	28.4	28.6	28.5	26.7	31.0	27.8
Median of cycle length	29	28	26	31	28	26	29	26	31	27
SD of cycle length	3.2	1.7	2.6	3.1	5.5	8.8	1.9	3.7	7.3	5.0
Length of time series	883	796	769	898	825	831	828	774	899	806
No. of missing observations	4	20	201	105	117	273	135	149	32	142
Data for predictive
accuracy estimation
No. of consecutive cycles	51	62	21	20	28	26	15	17	17	26
Range of cycle length	[24, 38]	[24, 31]	[25, 42]	[26, 41]	[24, 31]	[21, 53]	[14, 50]	[24, 29]	[26, 40]	[24, 32]
Mean of cycle length	28.1	26.3	28.2	31.1	27.1	27.1	29.1	26.5	32.2	27.5
Median of cycle length	27	26	27	30	27	25	29	26	32	27
SD of cycle length	3.1	1.7	3.6	4.0	1.5	6.3	7.7	1.5	3.8	2.2
Length of time series	1435	1630	592	623	759	705	437	450	548	715
No. of missing observations	21	206	133	84	202	254	54	130	18	153

^† Original data contain a small amount of extremely short cycles. We assumed that cycles less than or equal to 5 days have been arisen owing to menstruation records that were wrongly reported, and have corrected them before the analyses.

Parameter estimates in the best AIC model for the 20 subjects are shown in Table 2. The selected order of the trigonometric series ranged from 2 to 12. The estimated relationship between expected BBT and menstrual phase, and the estimated probability density distribution for phase advancement for each subject are shown in Figure 1. Although the estimated temperature‐phase regression lines were ‘squiggly’ owing to the high order of the trigonometric series, they in general exhibited two distinct stages: the temperature tended to be lower in the first half of the cycle and higher in the second half, which is consistent with the well‐known periodicity of BBT through the menstrual cycle 1. Figure 2 shows examples of the estimated conditional distributions for menstrual phase and the associated predictive distributions for the day of onset of menstruation.

Table 2.

Results of fitting the state‐space model by using the maximum likelihood method.

	Subject
	1	2	3	4	5	6	7	8	9	10
Best model	M10	M8	M9	M6	M11	M8	M11	M12	M10	M5
α	0.210	0.953	0.344	1.520	0.318	1.971	0.630	0.172	0.150	0.201
	[0.151,0.292]	[0.628,1.439]	[0.253,0.467]	[1.015,2.266]	[0.233,0.435]	[1.329,2.905]	[0.449,0.882]	[0.128,0.231]	[0.106,0.211]	[0.140,0.288]
β	8.915	32.131	10.916	45.146	8.536	59.929	19.510	5.886	5.284	6.544
	[6.303,12.610]	[21.157,48.798]	[7.883,15.115]	[30.420,67.002]	[6.094,11.955]	[40.536,88.601]	[13.806,27.572]	[4.236,8.178]	[3.595,7.766]	[4.429,9.669]
σ	0.112	0.161	0.119	0.121	0.093	0.152	0.108	0.101	0.116	0.209
	[0.103,0.121]	[0.150,0.173]	[0.109,0.130]	[0.113,0.129]	[0.085,0.102]	[0.142,0.163]	[0.098,0.120]	[0.094,0.109]	[0.109,0.123]	[0.195,0.224]
a	36.299	36.203	36.485	36.384	36.632	36.522	36.518	36.519	36.645	36.123
	[36.247,36.351]	[36.187,36.219]	[36.466,36.504]	[36.370,36.397]	[36.614,36.650]	[36.509,36.535]	[36.501,36.536]	[36.492,36.546]	[36.620,36.670]	[36.087,36.160]
b 1	0.193	0.197	0.174	0.098	−0.034	0.107	0.130	0.141	0.129	0.138
	[0.153,0.232]	[0.179,0.216]	[0.147,0.200]	[0.074,0.122]	[−0.072,0.003]	[0.088,0.126]	[0.101,0.159]	[0.114,0.169]	[0.099,0.159]	[0.082,0.193]
b 2	0.015	0.024	−0.028	−0.079	0.115	−0.063	−0.001	−0.370	−0.012	0.002
	[−0.021,0.050]	[−0.010,0.058]	[−0.061,0.006]	[−0.096,−0.061]	[0.063,0.167]	[−0.081,−0.046]	[−0.024,0.022]	[−0.416,−0.323]	[−0.067,0.043]	[−0.082,0.085]
b 3	0.009	−0.057	0.027	0.032	−0.098	0.018	0.025	−0.089	−0.087	−0.126
	[−0.112,0.130]	[−0.085,−0.029]	[−0.001,0.056]	[0.012,0.051]	[−0.148,−0.048]	[−0.003,0.039]	[0.001,0.049]	[−0.132,−0.045]	[−0.136,−0.038]	[−0.192,−0.060]
b 4	−0.039	0.021	−0.023	0.007	0.124	−0.028	−0.032	0.167	−0.078	−0.153
	[−0.075,−0.003]	[−0.010,0.053]	[−0.051,0.005]	[−0.017,0.030]	[0.094,0.153]	[−0.054,−0.001]	[−0.061,−0.003]	[0.105,0.229]	[−0.125,−0.030]	[−0.250,−0.056]
b 5	0.058	−0.046	0.013	−0.020	−0.129	−0.030	0.029	0.174	0.049	−0.003
	[−0.006,0.121]	[−0.097,0.005]	[−0.028,0.054]	[−0.039,−0.002]	[−0.165,−0.092]	[−0.061,0.000]	[0.001,0.057]	[0.137,0.212]	[−0.040,0.139]	[−0.153,0.148]
b 6	−0.014	0.046	−0.065	−0.022	0.097	0.028	−0.001	−0.038	0.100	NA
	[−0.230,0.202]	[−0.005,0.098]	[−0.106,−0.024]	[−0.051,0.006]	[0.045,0.149]	[−0.001,0.058]	[−0.030,0.029]	[−0.122,0.047]	[0.040,0.160]
b 7	−0.024	0.019	0.006	NA	−0.078	−0.026	0.024	−0.112	−0.003	NA
	[−0.485,0.437]	[−0.030,0.068]	[−0.034,0.046]		[−0.124,−0.032]	[−0.068,0.016]	[−0.015,0.062]	[−0.149,−0.075]	[−0.104,0.099]
b 8	0.037	0.034	−0.063	NA	0.088	0.037	0.060	−0.098	−0.058	NA
	[−0.256,0.331]	[−0.037,0.105]	[−0.145,0.020]		[0.047,0.129]	[−0.011,0.085]	[0.011,0.109]	[−0.180,−0.017]	[−0.171,0.056]
b 9	−0.086	NA	−0.045	NA	−0.060	NA	0.007	0.010	−0.036	NA
	[−0.231,0.060]		[−0.142,0.051]		[−0.090,−0.029]		[−0.019,0.033]	[−0.033,0.053]	[−0.136,0.064]
b 10	0.061	NA	NA	NA	0.101	NA	0.050	0.120	0.053	NA
	[−0.170,0.293]				[0.062,0.140]		[0.002,0.097]	[0.062,0.178]	[−0.036,0.141]
b 11	NA	NA	NA	NA	−0.058	NA	0.031	0.023	NA	NA
					[−0.100,−0.016]		[−0.032,0.094]	[−0.023,0.069]
b 12	NA	NA	NA	NA	NA	NA	NA	−0.114	NA	NA
								[−0.145,−0.082]
c 1	−0.193	−0.108	−0.182	−0.270	−0.184	−0.170	−0.254	−0.417	−0.172	−0.276
	[−0.304,−0.081]	[−0.140,−0.075]	[−0.218,−0.146]	[−0.289,−0.252]	[−0.204,−0.164]	[−0.190,−0.150]	[−0.274,−0.233]	[−0.463,−0.371]	[−0.218,−0.126]	[−0.334,−0.217]
c 2	−0.051	−0.131	−0.130	−0.034	−0.107	−0.058	−0.038	−0.216	−0.035	−0.057
	[−0.085,−0.018]	[−0.154,−0.108]	[−0.159,−0.101]	[−0.058,−0.010]	[−0.133,−0.080]	[−0.082,−0.035]	[−0.059,−0.017]	[−0.263,−0.169]	[−0.069,−0.001]	[−0.107,−0.006]
c 3	−0.089	−0.029	−0.022	−0.056	0.006	−0.023	−0.021	0.062	−0.070	−0.019
	[−0.120,−0.059]	[−0.065,0.008]	[−0.051,0.006]	[−0.076,−0.037]	[−0.041,0.052]	[−0.046,−0.000]	[−0.044,0.002]	[0.018,0.106]	[−0.126,−0.014]	[−0.096,0.059]
c 4	−0.030	−0.001	−0.035	0.005	−0.016	−0.012	0.016	0.248	−0.047	0.042
	[−0.174,0.114]	[−0.042,0.041]	[−0.063,−0.007]	[−0.014,0.025]	[−0.077,0.046]	[−0.038,0.014]	[−0.013,0.044]	[0.202,0.295]	[−0.118,0.024]	[−0.065,0.148]
c 5	−0.003	−0.058	0.027	−0.017	0.010	−0.037	−0.016	−0.040	−0.082	−0.126
	[−0.256,0.250]	[−0.117,0.001]	[−0.007,0.062]	[−0.040,0.007]	[−0.047,0.067]	[−0.067,−0.007]	[−0.044,0.011]	[−0.099,0.019]	[−0.134,−0.029]	[−0.186,−0.066]
c 6	−0.053	−0.003	0.023	−0.034	−0.007	−0.025	−0.010	−0.277	0.004	NA
	[−0.143,0.037]	[−0.055,0.050]	[−0.030,0.076]	[−0.059,−0.008]	[−0.052,0.038]	[−0.062,0.013]	[−0.036,0.015]	[−0.312,−0.243]	[−0.107,0.114]
c 7	0.068	−0.030	−0.031	NA	0.010	−0.040	−0.052	−0.075	0.059	NA
	[−0.040,0.176]	[−0.080,0.020]	[−0.073,0.012]		[−0.038,0.057]	[−0.086,0.006]	[−0.081,−0.023]	[−0.136,−0.015]	[0.014,0.104]
c 8	−0.050	0.044	0.067	NA	−0.044	0.027	0.027	0.214	0.074	NA
	[−0.324,0.223]	[−0.002,0.089]	[0.006,0.127]		[−0.102,0.013]	[−0.028,0.082]	[−0.014,0.068]	[0.171,0.257]	[−0.009,0.157]
c 9	−0.027	NA	−0.085	NA	0.006	NA	0.007	0.079	−0.067	NA
	[−0.675,0.620]		[−0.134,−0.036]		[−0.059,0.071]		[−0.049,0.063]	[0.036,0.122]	[−0.169,0.034]
c 10	0.025	NA	NA	NA	−0.019	NA	0.013	−0.107	−0.057	NA
	[−0.494,0.543]				[−0.088,0.050]		[−0.032,0.058]	[−0.172,−0.041]	[−0.156,0.042]
c 11	NA	NA	NA	NA	0.041	NA	0.067	−0.022	NA	NA
					[−0.011,0.093]		[0.025,0.108]	[−0.057,0.014]
c 12	NA	NA	NA	NA	NA	NA	NA	0.012	NA	NA
								[−0.053,0.077]
Log‐	468.905	164.278	206.631	415.909	343.887	234.46	354.47	408.464	330.137	−178.022
likelihood
	Subject
	11	12	13	14	15	16	17	18	19	20
Best model	M12	M12	M5	M7	M6	M9	M5	M2	M10	M10
α	0.452	0.439	3.626	3.246	12.593	1.000	9.367	2.084	0.456	0.360
	[0.329,0.620]	[0.331,0.580]	[2.249,5.744]	[1.984,5.224]	[6.756,21.022]	†	[5.696,14.622]	[1.258,3.414]	[0.326,0.638]	[0.265,0.487]
β	13.791	12.092	96.044	100.347	345.852	25.939	267.147	55.485	14.223	9.981
	[9.918,19.178]	[8.985,16.274]	[59.924,153.936]	[61.670,163.280]	[194.670,614.443]	†	[166.127,429.594]	[33.748,91.222]	[10.062,20.106]	[7.205,13.827]
σ	0.098	0.090	0.169	0.185	0.109	0.088	0.127	0.144	0.126	0.092
	[0.090,0.108]	[0.081,0.100]	[0.159,0.180]	[0.174,0.197]	[0.103,0.116]	†	[0.120,0.134]	[0.135,0.153]	[0.115,0.137]	[0.082,0.104]
a	36.536	36.741	36.715	36.393	36.687	36.407	36.512	36.280	36.529	36.439
	[36.520,36.553]	[36.722,36.760]	[36.699,36.730]	[36.378,36.407]	[36.678,36.696]	[36.393,36.421]	[36.501,36.522]	[36.266,36.294]	[36.512,36.547]	[36.423,36.455]
b 1	0.014	0.113	−0.000	0.142	0.011	0.091	0.028	0.100	0.085	0.121
	[−0.014,0.042]	[0.090,0.136]	[−0.025,0.025]	[0.121,0.164]	[−0.004,0.025]	[0.073,0.110]	[0.012,0.045]	[0.077,0.122]	[0.058,0.112]	[0.088,0.153]
b 2	0.055	−0.150	−0.026	−0.059	−0.019	−0.058	−0.041	−0.024	−0.103	−0.021
	[0.029,0.082]	[−0.188,−0.112]	[−0.051,−0.001]	[−0.081,−0.037]	[−0.032,−0.007]	[−0.079,−0.038]	[−0.057,−0.026]	[−0.043,−0.004]	[−0.129,−0.077]	[−0.052,0.011]
b 3	−0.042	0.148	−0.006	0.009	−0.013	−0.012	0.021	NA	0.005	−0.023
	[−0.088,0.004]	[0.109,0.187]	[−0.031,0.019]	[−0.016,0.034]	[−0.026,−0.000]	[−0.036,0.012]	[0.004,0.038]		[−0.026,0.036]	[−0.052,0.006]
b 4	0.001	−0.011	−0.011	−0.011	−0.009	−0.027	−0.005	NA	−0.001	−0.059
	[−0.080,0.083]	[−0.063,0.041]	[−0.040,0.018]	[−0.038,0.015]	[−0.023,0.006]	[−0.053,−0.000]	[−0.021,0.011]		[−0.031,0.029]	[−0.092,−0.027]
b 5	0.004	−0.081	−0.017	−0.012	−0.031	0.031	0.011	NA	0.019	0.008
	[−0.083,0.091]	[−0.108,−0.054]	[−0.049,0.015]	[−0.048,0.024]	[−0.045,−0.016]	[0.000,0.061]	[−0.007,0.029]		[−0.026,0.064]	[−0.033,0.049]
b 6	−0.015	0.058	NA	0.010	−0.027	0.021	NA	NA	−0.041	−0.039
	[−0.074,0.044]	[0.013,0.104]		[−0.041,0.062]	[−0.042,−0.011]	[−0.030,0.071]			[−0.085,0.002]	[−0.077,−0.002]
b 7	0.074	0.051	NA	−0.043	NA	0.001	NA	NA	0.002	−0.056
	[0.036,0.112]	[−0.027,0.129]		[−0.081,−0.005]		[−0.043,0.046]			[−0.032,0.036]	[−0.102,−0.010]
b 8	−0.097	−0.108	NA	NA	NA	−0.015	NA	NA	0.016	0.001
	[−0.121,−0.072]	[−0.170,−0.045]				[−0.097,0.066]			[−0.017,0.049]	[−0.047,0.049]
b 9	0.043	−0.025	NA	NA	NA	−0.057	NA	NA	0.030	−0.030
	[−0.005,0.090]	[−0.081,0.032]				[−0.109,−0.004]			[−0.038,0.098]	[−0.064,0.003]
b 10	−0.014	0.031	NA	NA	NA	NA	NA	NA	−0.075	0.012
	[−0.063,0.036]	[−0.019,0.082]							[−0.114,−0.036]	[−0.122,0.145]
b 11	−0.012	−0.061	NA	NA	NA	NA	NA	NA	NA	NA
	[−0.153,0.129]	[−0.180,0.058]
b 12	−0.035	−0.047	NA	NA	NA	NA	NA	NA	NA	NA
	[−0.187,0.116]	[−0.194,0.100]
c 1	−0.238	−0.071	−0.235	−0.164	−0.225	−0.181	−0.228	−0.198	−0.171	−0.200
	[−0.260,−0.216]	[−0.105,−0.036]	[−0.255,−0.214]	[−0.187,−0.140]	[−0.236,−0.213]	[−0.202,−0.160]	[−0.242,−0.214]	[−0.219,−0.178]	[−0.200,−0.143]	[−0.228,−0.172]
c 2	0.000	−0.173	0.004	−0.076	−0.009	−0.097	−0.012	−0.036	−0.059	−0.017
	[−0.028,0.029]	[−0.215,−0.131]	[−0.018,0.025]	[−0.101,−0.052]	[−0.021,0.003]	[−0.120,−0.074]	[−0.028,0.003]	[−0.057,−0.015]	[−0.097,−0.022]	[−0.039,0.004]
c 3	−0.116	−0.099	−0.053	−0.010	−0.031	−0.047	−0.062	NA	−0.061	−0.043
	[−0.147,−0.086]	[−0.150,−0.048]	[−0.078,−0.029]	[−0.033,0.013]	[−0.043,−0.018]	[−0.066,−0.028]	[−0.077,−0.047]		[−0.091,−0.031]	[−0.078,−0.007]
c 4	0.121	0.088	−0.029	−0.024	0.029	−0.046	−0.003	NA	−0.025	0.022
	[0.095,0.147]	[0.059,0.118]	[−0.055,−0.003]	[−0.051,0.002]	[0.015,0.043]	[−0.066,−0.026]	[−0.019,0.013]		[−0.054,0.004]	[−0.030,0.075]
c 5	−0.130	−0.033	−0.040	−0.046	0.007	−0.031	−0.030	NA	0.035	0.022
	[−0.166,−0.093]	[−0.090,0.024]	[−0.069,−0.012]	[−0.075,−0.016]	[−0.008,0.022]	[−0.067,0.005]	[−0.045,−0.011]		[−0.006,0.076]	[−0.007,0.051]
c 6	0.051	−0.078	NA	0.061	−0.009	0.039	NA	NA	−0.033	0.014
	[0.020,0.083]	[−0.124,−0.031]		[0.028,0.094]	[−0.025,0.007]	[0.004,0.074]			[−0.083,0.017]	[−0.024,0.052]
c 7	−0.017	0.088	NA	−0.020	NA	−0.031	NA	NA	−0.009	0.010
	[−0.104,0.070]	[0.036,0.139]		[−0.065,0.024]		[−0.051,−0.012]			[−0.048,0.030]	[−0.040,0.061]
c 8	−0.003	0.060	NA	NA	NA	0.052	NA	NA	0.004	0.017
	[−0.117,0.112]	[−0.015,0.135]				[0.023,0.082]			[−0.051,0.059]	[−0.025,0.060]
c 9	0.021	−0.057	NA	NA	NA	−0.034	NA	NA	0.036	−0.017
	[−0.050,0.091]	[−0.092,−0.022]				[−0.101,0.034]			[−0.031,0.103]	[−0.064,0.029]
c 10	−0.023	−0.032	NA	NA	NA	NA	NA	NA	0.007	−0.093
	[−0.061,0.014]	[−0.100,0.036]							[−0.123,0.136]	[−0.132,−0.053]
c 11	0.087	0.101	NA	NA	NA	NA	NA	NA	NA	NA
	[0.046,0.128]	[0.049,0.153]
c 12	−0.092	−0.111	NA	NA	NA	NA	NA	NA	NA	NA
	[−0.143,−0.040]	[−0.156,−0.067]
Log‐	343.440	287.380	111.443	88.146	479.948	267.320	365.655	217.357	266.617	253.890
likelihood

Parameter estimates and their 95% confidence intervals (in brackets) of the best Akaike information criterion model are shown for each subject. Log‐likelihood was approximated by using the non‐Gaussian filter with the state space discretized with 512 intervals.

^† Confidence intervals were not calculated because the Hessian of log‐likelihood was singular.

Figure 1.

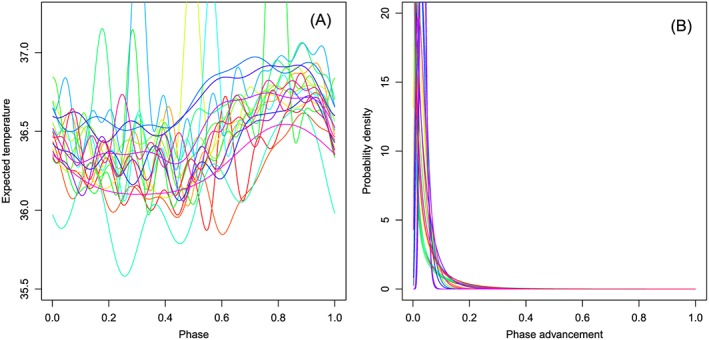
Model components for each subject. Each color represents a different subject. Lines show the best Akaike information criterion model associated with the maximum likelihood estimates for each subject. (A) Relationship between expected temperature and menstrual phase. The x‐axis represents θ _tmod1. (B) Probability density distribution for the advancement per day of the menstrual phase.

Figure 2.

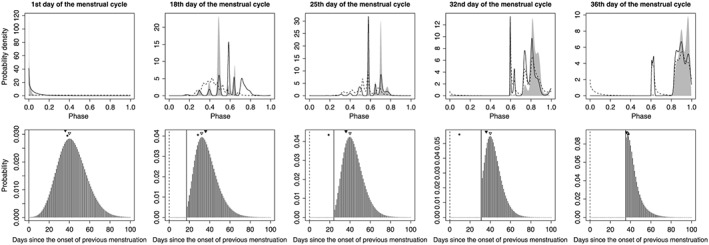
Example estimated conditional distributions for menstrual phase (top panels) and the associated predictive distributions for the day of onset of menstruation (bottom panels). In the top panels, predictive and filtering distributions are shown as dashed and solid lines, respectively, and smoothed distributions are represented by gray shading. x‐axes represent θ _tmod1. In the bottom panels, the marginal probabilities of the onset of menstruation h(k|Y _t,Z _t) are shown. Dashed and solid vertical lines indicate the day of onset of the previous menstruation and the current day, respectively. Filled circles indicate the actual day of onset of the next menstruation. Filled and open triangles indicate the best conventional prediction for the subject and the model‐based prediction, respectively. These results were obtained by applying the best Akaike information criterion model to the first menstrual cycle of the test data of subject 1. From left to right, panels correspond to 38, 21, 14, 7, and 3 days before the upcoming day of onset of menstruation, respectively.

The RMSE of prediction of the next day of onset of menstruation provided by each method is shown in Figure 3 and Table 3. In the proposed method, the RMSE tended to decrease as the day approached the next day of onset of menstruation, suggesting that accumulation of the BBT time series data contributed to increasing the accuracy of the prediction. Except for subjects 9 and 20, the proposed method exhibited a better predictive performance than the calendar calculation and the method of Bortot et al. 6, for at least one of the time points of prediction we considered (i.e., the day preceding the next day of onset of menstruation) (Figure 3). Compared with the best prediction provided by the calendar calculation method, the range, mean, and median of the rate of the maximum reduction in the RMSE for each subject in the sequential method were 0.066–1.481, 0.581, and 0.488, respectively.

Figure 3.

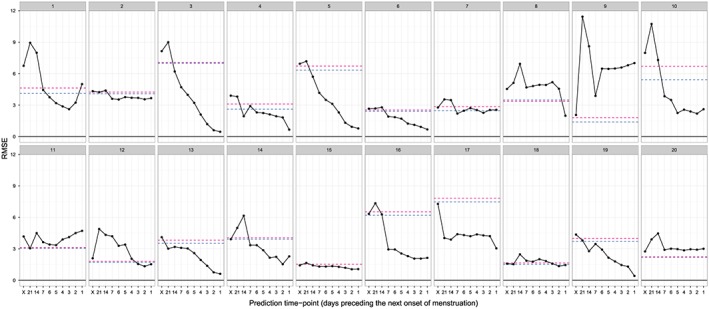
Root mean square error (RMSE) of the prediction of the day of onset of the next menstruation. Solid lines indicate the RMSE of the sequential prediction (based on the best Akaike information criterion model for each subject), and horizontal dashed lines indicate the lowest RMSE of the conventional prediction (blue) and the RMSE of prediction based on the method of Bortot et al. 6 (red) for each subject. On the horizontal axis, ‘X’ indicates the prediction obtained at the day of onset of the previous menstruation. Each panel shows the results for one subject.

Table 3.

Root mean square error of prediction of the next day of onset of menstruation based on the calendar calculation method.

Subject	Predicted cycle length
	25	26	27	28	29	30	31	32	33	34	35	36	37
1	11.797	10.865	9.947	9.046	8.167	7.320	6.517	5.775	5.122	4.595	4.243	4.109	4.215
2	8.370	7.512	6.694	5.932	5.250	4.684	4.279	4.085	4.131	4.409	4.880	5.494	6.210
3	12.068	11.267	10.501	9.776	9.105	8.498	7.970	7.539	7.222	7.034	6.985	7.079	7.309
4	7.435	6.508	5.607	4.746	3.950	3.268	2.786	2.615	2.814	3.317	4.010	4.812	5.678
5	6.975	6.620	6.403	6.338	6.430	6.672	7.050	7.541	8.127	8.787	9.507	10.274	11.079
6	4.641	3.822	3.111	2.598	2.413	2.625	3.157	3.878	4.702	5.584	6.500	7.438	8.390
7	4.918	4.082	3.339	2.762	2.472	2.568	3.012	3.682	4.476	5.340	6.245	7.175	8.122
8	6.065	5.279	4.578	4.005	3.624	3.495	3.648	4.049	4.634	5.345	6.136	6.981	7.863
9	8.058	7.075	6.098	5.130	4.176	3.250	2.385	1.677	1.392	1.750	2.487	3.363	4.294
10	12.083	11.198	10.334	9.497	8.695	7.937	7.239	6.618	6.099	5.710	5.477	5.422	5.550
11	4.384	3.734	3.266	3.065	3.181	3.584	4.191	4.929	5.746	6.614	7.515	8.438	9.377
12	2.118	1.704	1.823	2.396	3.188	4.072	5.000	5.951	6.917	7.890	8.870	9.854	10.840
13	4.756	4.152	3.723	3.532	3.619	3.964	4.509	5.192	5.964	6.796	7.669	8.569	9.489
14	7.290	6.469	5.705	5.025	4.467	4.080	3.918	4.006	4.330	4.843	5.491	6.233	7.039
15	2.598	1.880	1.524	1.763	2.428	3.268	4.179	5.123	6.086	7.058	8.038	9.022	10.009
16	6.549	6.297	6.199	6.260	6.478	6.836	7.314	7.891	8.546	9.263	10.029	10.833	11.667
17	8.540	8.103	7.772	7.559	7.474	7.523	7.703	8.004	8.414	8.918	9.501	10.149	10.850
18	2.044	1.495	1.515	2.086	2.900	3.804	4.747	5.709	6.682	7.662	8.647	9.634	10.625
19	8.128	7.252	6.412	5.626	4.917	4.325	3.903	3.710	3.781	4.102	4.621	5.280	6.034
20	3.288	2.609	2.193	2.193	2.609	3.288	4.100	4.981	5.900	6.842	7.798	8.764	9.737

The lowest value for each subject, which is shown in Figure 3, is in italics.

The predictive performance tended to be even better when the accuracy was measured by using the MAE; the MAE of the predictions of the next day of onset of menstruation provided by each method is shown in Figure 4 and Table 4. Compared with the best prediction provided by the calendar calculation method, the range, mean, and median of the rate of the maximum reduction in the MAE for each subject by using the sequential method was 0.056–1.368, 0.461, and 0.361, respectively.

Figure 4.

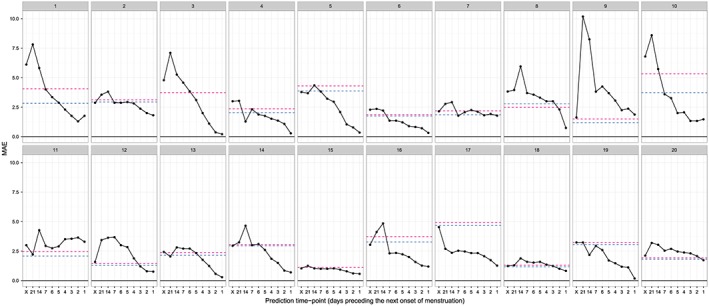
Mean absolute error (MAE) of the prediction of the day of onset of the next menstruation. Solid lines indicate the MAE of the sequential prediction (based on the best Akaike information criterion model for each subject), and horizontal dashed lines indicate the lowest MAE of the conventional prediction (blue) and the MAE of prediction based on the method of Bortot et al. 6 (red) for each subject. On the horizontal axis, ‘X’ indicates the prediction obtained at the day of onset of the previous menstruation. Each panel shows the results for one subject.

Table 4.

Mean absolute error of prediction of the next day of onset of menstruation based on the calendar calculation method.

Subject	Predicted cycle length
	24	25	26	27	28	29	30	31	32	33	34	35	36
1	12.059	11.059	10.059	9.059	8.059	7.176	6.294	5.412	4.529	3.765	3.118	2.824	3.000
2	8.312	7.312	6.312	5.312	4.312	3.688	3.188	3.062	2.938	2.938	3.312	3.938	4.812
3	10.842	9.842	8.842	7.947	7.053	6.158	5.263	4.368	4.000	3.737	3.789	4.158	4.737
4	7.960	6.960	5.960	4.960	3.960	3.040	2.440	2.080	2.040	2.400	2.840	3.520	4.280
5	4.696	4.217	3.913	3.870	4.174	4.739	5.391	6.130	6.870	7.609	8.348	9.087	9.826
6	4.964	3.964	2.964	2.179	1.750	1.893	2.250	2.821	3.464	4.321	5.179	6.107	7.036
7	5.259	4.259	3.481	2.778	2.222	1.889	1.852	2.333	3.111	3.963	4.889	5.815	6.741
8	5.957	4.957	3.957	3.130	2.826	2.783	2.826	3.130	3.522	4.087	4.826	5.565	6.391
9	8.938	7.938	6.938	5.938	4.938	3.938	2.938	1.938	1.312	1.188	1.438	2.062	3.062
10	11.800	10.800	9.800	8.800	7.933	7.200	6.600	6.000	5.400	4.800	4.200	3.733	3.800
11	4.137	3.216	2.373	2.078	2.216	2.627	3.157	3.804	4.529	5.373	6.216	7.098	7.980
12	2.290	1.484	1.290	1.484	2.129	2.871	3.774	4.710	5.710	6.710	7.710	8.710	9.710
13	4.190	3.190	2.476	2.143	2.190	2.429	2.952	3.857	4.762	5.667	6.571	7.476	8.381
14	7.150	6.150	5.150	4.250	3.650	3.250	2.950	2.950	3.150	3.550	4.150	4.950	5.750
15	3.107	2.179	1.464	1.107	1.393	2.107	2.964	3.893	4.893	5.893	6.893	7.893	8.893
16	3.731	3.269	3.423	3.808	4.346	4.885	5.500	6.192	6.962	7.731	8.500	9.346	10.192
17	7.000	6.267	5.533	5.067	4.733	4.667	4.867	5.200	5.800	6.533	7.267	8.000	8.733
18	2.471	1.706	1.176	1.235	1.647	2.529	3.529	4.529	5.529	6.529	7.529	8.529	9.529
19	8.235	7.235	6.235	5.353	4.588	3.824	3.176	3.118	3.059	3.235	3.529	3.941	4.471
20	3.500	2.654	1.962	1.808	1.885	2.192	2.731	3.577	4.500	5.500	6.500	7.500	8.500

The lowest value for each subject, which is shown in Figure 4, is in italics.

5. Discussion

Here we constructed a statistical framework that provides a model‐based prediction of the day of onset of menstruation based on a state‐space model and an associated Bayesian filtering algorithm. The model describes the daily fluctuation of BBT and the history of menstruation. The filtering algorithms yielded a filtering distribution of menstrual phase that was conditional on all of the data available at that point in time, which was used to derive a predictive distribution for the next day of onset of menstruation.

The predictive framework we developed has several notable characteristics that make it superior to previous methods for predicting the day of onset of menstruation. State‐space modeling and Bayesian filtering techniques enable the proposed method to yield sequential predictions of the next day of onset of menstruation based on daily BBT data. Even though menstrual cycle length fluctuates stochastically, the prediction of day of onset of menstruation is automatically adjusted based on the daily updated filtering distribution, yielding a flexible yet robust prediction of the next day of onset of menstruation. This is markedly different from the conventional calendar calculation method that yields only a fixed prediction that is never adjusted. In a study similar to the present study, Bortot et al. 6 constructed a predictive framework for menstrual cycle length by using the state‐space modeling approach. However, in their model, the one‐step‐ahead predictive distribution for menstrual cycle length is obtained based on the past time series of cycle length, and within‐cycle information is not taken into account in the prediction.

Furthermore, compared with previous methods, the proposed method generally yielded a more accurate prediction of day of onset of menstruation. As the day approaches the next onset of menstruation and more daily temperature data are accumulated, the proposed method produced a considerably improved prediction (Figures 3 and 4). During earlier stages of the cycle, however, previous methods tended to give better predictions. One of the reasons for this result is that we used the best possible prediction for each subject for the calendar calculation method as a baseline for comparison. Another reason is that, not being similar to the method proposed by Bortot et al. 6, the proposed method benefits little from the information about the lengths of previous cycles: the predictive distribution for upcoming menstruation does not vary largely (i.e., not being adjusted) at the days of onset of menstruation. Therefore, in practice, a combination of previous methods and the proposed method (e.g., using previous methods in earlier stages of the cycle, and then switching to the proposed method at some point in time) might result in a further improvement of prediction.

As measuring BBT is a simple and inexpensive means of determining the current phase of the menstrual cycle, the proposed framework can provide predictions of the next onset of menstruation that can easily be implemented for the management of women's health. In order to facilitate practitioners to implement and use the proposed method, we provide an r script for non‐Gaussian filtering and prediction, along with a simulated menstrual cycle dataset as a supporting web material. Although the non‐Gaussian filtering technique may be computationally impractical for a state‐space model with a high‐dimensional state vector 10, our proposed model only involves a two‐dimensional state vector so the computational cost required for filtering single data is negligible for a contemporary computer. We suggest that the proposed method will not be applicable to women using oral contraceptives because oral contraceptives can artificially control BBT and the onset of the menstruation. As long as the cycle is not under‐controlled by oral contraceptives and BBT shows the biphasic pattern, however, we suppose that the proposed prediction tool can be useful even for women with irregular cycle length (but see later for a difficulty in parameter estimation using data that include irregular cycle length).

The conditional probability density distribution for menstrual phase obtained with the sequential Bayesian filter may also be used for predicting other events that are related to the menstrual cycle. For example, the conditional probability of the menstrual phase being below or above a ‘change point’ of expected temperature could be used as a model‐based probability of the subject being in the follicular phase (before ovulation) or the luteal phase (after ovulation). These probabilities may also be used to estimate the timing of ovulation, for which BBT‐based estimates are error prone 11. Combined with a fecundability model that provides the probability of conception within a menstrual cycle that is conditional on daily intercourse behavior, the model might also be used to predict the probability of conception 6, 7, 8. As the Bayesian filtering algorithm can yield predictive and smoothed distributions (Equations (13) and (15)), these predictions could be obtained in both a prospective manner and a retrospective manner. Another possible extension of the model may be the addition of a new observation model for the physical condition of subjects, which may help to estimate the menstrual phase more precisely or to provide a forecast of the physical condition of subject as their menstrual cycle progresses.

We note that the state‐space model proposed in the present study may not be sufficiently flexible to describe the full variation in menstrual cycle length. In the present study, we fitted our model only to data from 20 subjects, and these data did not include extremely short or extremely long cycles because a preliminary investigation suggested that inclusion of such data could result in unreasonable parameter estimates (results not shown). Specifically, the estimates of α and β may become extremely small, leading to an almost flat probability density distribution for menstrual phase advancement. Under these parameter values, the predictive distribution for the onset of menstruation also becomes flat, preventing a useful prediction from being obtained. These results suggest that with a single set of parameter values, the proposed state‐space model does not capture the whole observed variation in cycle length. It is known that the statistical distribution of menstrual cycle length is characterized by a mixture distribution that comprises standard and nonstandard cycles, where, for the latter, a skewed distribution may well represent the observed pattern [e.g., 2, 3, 7, 8]. Our proposed model, however, does not provide such a mixture‐like marginal distribution for the day of onset of menstruation. It is also known that the mean and variance of the marginal distribution of cycle length can vary depending on subjects' age 3, 5, 6, 7. Therefore, we assume that modeling variations in the system model parameters (i.e., α and β), by including covariates such as age or within‐subject and among‐subject random effects, or both, may be a promising extension of the proposed framework. To this end, the model should be extended to treat longitudinal data (Y _it,Z _it), where time series is available for unit (i.e., subject or cycle) i. Then, differences in parameters among units can be modeled, for example, as $log{\alpha }_i={\gamma }_0+{\sum }_j{\gamma }_j{x}_{ij}+u_i$, where x _ij and u _i are covariate (e.g., age) and random effect, respectively. To explain the skewed marginal distribution of menstrual cycle length, Sharpe and Nordheim 12 considered a rate process in which the development rate fluctuates randomly. Inclusion of random effects for the system model parameters would allow us to accommodate this idea. Although the inclusion of random effects will increase the flexibility of the framework, it would also considerably complicate the likelihood calculation and make parameter estimation more challenging.

The state‐space model proposed here provides a conceptual description of the menstrual cycle. We explain this perspective by using the analogy of a clock that makes one complete revolution in each menstrual cycle. The system model expresses the hand of the clock (i.e., the latent phase variable) moving forward with an almost steadily, yet slightly variable, pace. Observation models describe observable events that are imprinted on the clock's dial; for example, menstruation is scheduled to occur when the hand of this clock arrives at a specific point on the dial. The fluctuation in BBT, as well as other possibly related phenomena such as ovulation, would also be marked on the dial. Even though the position of the hand of the clock is unobservable, we can estimate it as a conditional distribution of the latent phase variable by using the Bayesian filtering technique, which enables us to make a sequential, model‐based prediction of menstruation. Although this is a rather phenomenological view of the menstrual cycle, it is useful for developing a rigorous and extendable modeling framework for predicting and studying phenomena that are associated with the menstrual cycle.

Supporting information

Supporting info item

Appendix A. State estimation, likelihood calculation, and prediction using the non‐Gaussian filter

A.1.

The statistical inferences described in Section 3 of the main text were based on an estimation of the conditional distribution of the latent menstrual phase. Although the conditional distribution can be obtained by using the recursive equations described in Section 3.2, the integrals in those formulae are generally not analytically tractable for non‐linear, non‐Gaussian, state‐space models. Therefore, to obtain approximate conditional distributions, filtering algorithms for general state‐space models are required. We use the non‐Gaussian filter proposed by Kitagawa 10, in which the continuous state space is discretized with equally spaced fixed points at which the conditional probability density is evaluated. With these discretized probability density functions, integrals are evaluated by using numerical integration. This filtering algorithm also yields an approximate log‐likelihood, making the maximum likelihood estimation of the model parameters possible. Detailed descriptions for this numerical procedure are provided, for example, in Kitagawa 10, 13 and de Valpine and Hastings 14.

To apply non‐Gaussian filtering to the state‐space model described in Section 3.1, it is computationally more convenient to consider the state space of a circular phase variable rather than a linear phase variable described in the main text, because the latter requires discretization of unbounded real space. Hence, in the following, we first reformulate the statistical modeling framework in terms of a circular latent phase variable. The reformulated model conceptually agrees with the original formulation, given the probability that the menstrual phase advancement per day being more than 1 (i.e., Pr(ϵ _t>1)) is negligible. In practice, this condition is naturally attained in the estimation of the model parameters as long as unusually short menstrual cycles (e.g., 3 to 4 days) are not included in the dataset. Later, we provide a numerical procedure to obtain the conditional distributions, log‐likelihood, and the predictive distribution of the next day of onset of menstruation based on the non‐Gaussian filtering technique (note, all definitions and notations are the same as those used in Section 3 of the main text).

A1. Model with a circular state variable

Instead of using the real latent state variable for the menstrual phase, ${\theta }_t\in \mathbb{R}$, we reformulate the model with a circular latent variable of period 1, denoted by ω _t∈[0,1). We consider that the correspondence between these two variables is characterized by the following projection: ω _t=f(θ _t)=θ _tmod1. The system model for this circular variable is then expressed as

$${\omega }_t=\left({\omega }_{t-1}+{ϵ}_t\right)mod1$$ (A.1)

$${ϵ}_t\sim \text{Gamma}(\alpha ,\beta ).$$ (A.2)

Under this assumption, given ω _t−1, the conditional distribution of ω _t is a wrapped gamma distribution with a probability density function:

$$\begin{array}{ccc}\hfill p\left({\omega }_t\right|{\omega }_{t-1})& =\text{wGamma}(\alpha ,\beta )\hfill & \hfill \\ \hfill & =\frac{{\beta }^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}\exp \left\{-\beta \delta ({\omega }_t,{\omega }_{t-1})\right\}\mathrm{\Phi }\left\{\exp (-\beta ),1-\alpha ,\delta ({\omega }_t,{\omega }_{t-1})\right\},\hfill \end{array}$$ (A.3)

where $\delta ({\omega }_t,{\omega }_{t-1})={({\omega }_t-{\omega }_{t-1})}^{I({\omega }_t>{\omega }_{t-1})}{(1+{\omega }_t-{\omega }_{t-1})}^{I({\omega }_t⩽{\omega }_{t-1})}$ is the advancement of the menstrual phase on the circular scale and $\mathrm{\Phi }(z,s,a)={\sum }_{k=0}^{\infty }\frac{z^k}{{(a+k)}^s}$ is Lerch's transcendental function 15.

The observation model for BBT, which is conditional on ω _t, is expressed as

$$y_t=a+\sum _{m=1}^M(b_m\cos 2m\pi {\omega }_t+c_m\sin 2m\pi {\omega }_t)+e_t$$ (A.4)

$$e_t\sim \text{Normal}(0,{\sigma }^2),$$ (A.5)

leading to a normal conditional distribution of y _t with a probability density function:

$$\begin{array}{ccc}\hfill p\left(y_t\right|{\omega }_t)& =\text{Normal}\left\{\mu \left({\omega }_t\right),{\sigma }^2\right\}\hfill & \hfill \\ \hfill & =\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{{\left\{y_t-\mu \left({\omega }_t\right)\right\}}^2}{2{\sigma }^2}\right],\hfill \end{array}$$ (A.6)

where $\mu \left({\omega }_t\right)=a+{\sum }_{m=1}^M(b_m\cos 2m\pi {\omega }_t+c_m\sin 2m\pi {\omega }_t)$.

Assuming that Pr(ϵ _t>1) is negligible, we consider menstruation to have started when ω _t ‘steps over’ 1. This is represented as

$$z_t=0\text{when}{\omega }_t>{\omega }_{t-1}$$ (A.7)

$$=1\text{when}{\omega }_t⩽{\omega }_{t-1}.$$ (A.8)

We can write this deterministic allocation in a probabilistic manner that is conditional on (ω _t,ω _t−1), where z _t follows a Bernoulli distribution:

$$p\left(z_t\right|{\omega }_t,{\omega }_{t-1})=(1-z_t)\left\{I({\omega }_t>{\omega }_{t-1})\right\}+z_t\left\{I({\omega }_t⩽{\omega }_{t-1})\right\}.$$ (A.9)

The log‐likelihood of this model can then be expressed as

$$\begin{array}{c}\hfill l(\mathit{\xi };Y_T,Z_T)=logp(y_1,z_1|\mathit{\xi })+\sum _{t=2}^{T}logp(y_t,z_t|Y_{t-1},Z_{t-1},\mathit{\xi }),\end{array}$$ (A.10)

where

$$\begin{array}{c}\hfill logp(y_1,z_1|\mathit{\xi })=log{\int }_0^1{\int }_0^{1}p(y_1\left|{\omega }_1\right)p\left(z_1\right|{\omega }_1,{\omega }_0\left)p\right({\omega }_1,{\omega }_0)d{\omega }_{1}d{\omega }_0,\end{array}$$ (A.11)

and for t=2,…,T,

$$\begin{array}{c}\hfill logp(y_t,z_t|Y_{t-1},Z_{t-1},\mathit{\xi })=log{\int }_0^1{\int }_0^{1}p(y_t\left|{\omega }_t\right)p\left(z_t\right|{\omega }_t,{\omega }_{t-1}\left)p\right({\omega }_t,{\omega }_{t-1}|Y_{t-1},Z_{t-1})d{\omega }_{t}d{\omega }_{t-1}.\end{array}$$ (A.12)

For t=1,…,T, the prediction, filtering, and smoothing equations for the aforementioned model are expressed as follows:

$$\begin{array}{ccc}\hfill p({\omega }_t,{\omega }_{t-1}|Y_{t-1},Z_{t-1})& =p\left({\omega }_t\right|{\omega }_{t-1}\left)p\right({\omega }_{t-1}|Y_{t-1},Z_{t-1})\hfill & \hfill \\ \hfill & =p\left({\omega }_t\right|{\omega }_{t-1}\left){\int }_0^{1}p\right({\omega }_{t-1},{\omega }_{t-2}|Y_{t-1},Z_{t-1})d{\omega }_{t-2}\hfill \end{array}$$ (A.13)

$$\begin{array}{ccc}\hfill p({\omega }_t,{\omega }_{t-1}|Y_t,Z_t)& =\frac{p(y_t,z_t|{\omega }_t,{\omega }_{t-1}\left)p\right({\omega }_t,{\omega }_{t-1}|Y_{t-1},Z_{t-1})}{{\int }_0^1{\int }_0^{1}p(y_t,z_t|{\omega }_t,{\omega }_{t-1}\left)p\right({\omega }_t,{\omega }_{t-1}|Y_{t-1},Z_{t-1})d{\omega }_{t}d{\omega }_{t-1}}\hfill & \hfill \\ \hfill & =\frac{p\left(y_t\right|{\omega }_t\left)p\right(z_t|{\omega }_t,{\omega }_{t-1})p({\omega }_t,{\omega }_{t-1}|Y_{t-1},Z_{t-1})}{{\int }_0^1{\int }_0^{1}p\left(y_t\right|{\omega }_t\left)p\right(z_t|{\omega }_t,{\omega }_{t-1})p({\omega }_t,{\omega }_{t-1}|Y_{t-1},Z_{t-1})d{\omega }_{t}d{\omega }_{t-1}}\hfill \end{array}$$ (A.14)

$$\begin{array}{ccc}\hfill p({\omega }_t,{\omega }_{t-1}|Y_T,Z_T)& =p({\omega }_t,{\omega }_{t-1}|Y_t,Z_t){\int }_0^1\frac{p({\omega }_{t+1},{\omega }_t|Y_T,Z_T\left)p\right({\omega }_{t+1}\left|{\omega }_t\right)}{p({\omega }_{t+1},{\omega }_t|Y_t,Z_t)}d{\omega }_{t+1}\hfill & \hfill \\ \hfill & =\frac{p({\omega }_t,{\omega }_{t-1}|Y_t,Z_t\left){\int }_0^{1}p\right({\omega }_{t+1},{\omega }_t|Y_T,Z_T)d{\omega }_{t+1}}{p\left({\omega }_t\right|Y_t,Z_t)}\hfill \\ \hfill & =\frac{p({\omega }_t,{\omega }_{t-1}|Y_t,Z_t\left){\int }_0^{1}p\right({\omega }_{t+1},{\omega }_t|Y_T,Z_T)d{\omega }_{t+1}}{{\int }_0^{1}p({\omega }_t,{\omega }_{t-1}|Y_t,Z_t)d{\omega }_{t-1}},\hfill \end{array}$$ (A.15)

where for t=1, we set p(ω ₁,ω ₀|Y ₀,Z ₀) as p(ω ₁,ω ₀), which is the specified initial distribution for the phase.

We consider the conditional probability that the next menstruation has started by day k+t, given the phase state ω _t, to be $F\left(k\right|{\omega }_t)=\mathrm{Pr}\left\{{\mathrm{\Delta }}_k\left(t\right)⩾1-{\omega }_t\right\}$. Then, F(k|ω _t) represents the conditional distribution function for the onset of menstruation, and under the assumption of the state‐space model described earlier, this is given as

$$\begin{array}{ccc}\hfill F\left(k\right|{\omega }_t)& ={\int }_{1-{\omega }_t}^{\infty }g(x;k\alpha ,\beta )dx\hfill & \hfill \\ \hfill & =1-G(1-{\omega }_t;k\alpha ,\beta ).\hfill \end{array}$$ (A.16)

The conditional probability function for the day of onset of menstruation, f(k|ω _t), is then given as

$$\begin{array}{ccc}\hfill f\left(k\right|{\omega }_t)& =F\left(k\right|{\omega }_t)-F(k-1\left|{\omega }_t\right)\hfill & \hfill \\ \hfill & =\left\{1-G(1-{\omega }_t;k\alpha ,\beta )\right\}-\left[1-G\left\{1-{\omega }_t;(k-1)\alpha ,\beta \right\}\right]\hfill \\ \hfill & =G\left\{1-{\omega }_t;(k-1)\alpha ,\beta \right\}-G(1-{\omega }_t;k\alpha ,\beta ),\hfill \end{array}$$ (A.17)

where we set F(0|ω _t)=0.

The marginal distribution for the day of onset of menstruation, h(k|Y _t,Z _t), is then obtained with the marginal filtering distribution for the phase state, p(ω _t|Y _t,Z _t), which is given as

$$h\left(k\right|Y_t,Z_t)={\int }_0^{1}f(k\left|{\omega }_t\right)p\left({\omega }_t\right|Y_t,Z_t)d{\omega }_t,$$ (A.18)

which is used to provide a point prediction for the day of onset of menstruation by finding the value of k that gives the highest probability, $\max h\left(k\right|Y_t,Z_t)$.

A2. Numerical procedure for non‐Gaussian filtering

We let ω(i),i=1,…,N be equally spaced grid points with interval [0,1). We denote the approximate probability density of the predictive, filtering, and smoothed distributions evaluated at these grid points on the state space by ${\tilde{p}}_{\mathrm{p}}(i,j,t),{\tilde{p}}_{\mathrm{f}}(i,j,t)$, and ${\tilde{p}}_{\mathrm{s}}(i,j,t)$, which are defined respectively as

$${\tilde{p}}_{\mathrm{p}}(i,j,t)=p\left\{{\omega }_t=\omega \left(i\right),{\omega }_{t-1}=\omega \left(j\right)|Y_{t-1},Z_{t-1}\right\}$$ (A.19)

$${\tilde{p}}_{\mathrm{f}}(i,j,t)=p\left\{{\omega }_t=\omega \left(i\right),{\omega }_{t-1}=\omega \left(j\right)|Y_t,Z_t\right\}$$ (A.20)

$${\tilde{p}}_{\mathrm{s}}(i,j,t)=p\left\{{\omega }_t=\omega \left(i\right),{\omega }_{t-1}=\omega \left(j\right)|Y_T,Z_T\right\},$$ (A.21)

where for i,j=1,…,N and t=1,…,T. As the initial distribution, we also specify the probability density ${\tilde{p}}_{\mathrm{p}}(i,j,0)$. We define the probability density function of the system model (Equation (A.3)) evaluated at each grid point as ${\tilde{p}}_{\mathrm{m}}(i,j)=p\left\{{\omega }_t=\omega \left(i\right)|{\omega }_{t-1}=\omega (j)\right\}$. Then, the prediction, filtering, and smoothing equations, respectively, are expressed as

$${\tilde{p}}_{\mathrm{p}}(i,j,t)={\tilde{p}}_{\mathrm{m}}(i,j){\tilde{p}}_{\mathrm{f}}^{\prime }(j,t-1)$$ (A.22)

$${\tilde{p}}_{\mathrm{f}}(i,j,t)=\frac{p\left\{y_t|{\omega }_t=\omega (i)\right\}p\left\{z_t|{\omega }_t=\omega (i),{\omega }_{t-1}=\omega (j)\right\}{\tilde{p}}_{\mathrm{p}}(i,j,t)}{\frac{1}{N^2}\sum _{i=1}^N\sum _{j=1}^{N}p\left\{y_t|{\omega }_t=\omega (i)\right\}p\left\{z_t|{\omega }_t=\omega (i),{\omega }_{t-1}=\omega (j)\right\}{\tilde{p}}_{\mathrm{p}}(i,j,t)}$$ (A.23)

$${\tilde{p}}_{\mathrm{s}}(i,j,t)={\tilde{p}}_{\mathrm{f}}(i,j,t){\tilde{p}}_{\mathrm{s}}^{\prime }(i,t+1)/{\tilde{p}}_{\mathrm{f}}^{\prime }(i,t),$$ (A.24)

where ${\tilde{p}}_{\mathrm{f}}^{\prime }(i,t)$ and ${\tilde{p}}_{\mathrm{s}}^{\prime }(i,t+1)$ are the marginalized filtering and smoothed distributions, respectively, which are obtained as ${\tilde{p}}_{\mathrm{f}}^{\prime }(i,t)={\sum }_{k=1}^N{\tilde{p}}_{\mathrm{f}}(i,k,t)/N$ and ${\tilde{p}}_{\mathrm{s}}^{\prime }(i,t+1)={\sum }_{k=1}^N{\tilde{p}}_{\mathrm{s}}(k,i,t+1)/N$, respectively. Note in practice that the predictive and smoothed distributions should be normalized so that the value of the integral over the whole interval becomes 1 13.

The denominator of Equation (A.23) provides the approximate likelihood for an observation at time t. Therefore, the log‐likelihood of the model is approximated as

$$\begin{array}{ccc}\hfill & l(\mathit{\xi };Y_T,Z_T)=\hfill & \hfill \\ \hfill & \sum _{t=1}^{T}log\left[\sum _{i=1}^N\sum _{j=1}^{N}p\left\{y_t|{\omega }_t=\omega (i)\right\}p\left\{z_t|{\omega }_t=\omega (i),{\omega }_{t-1}=\omega (j)\right\}{\tilde{p}}_{\mathrm{p}}(i,j,t-1)\right]-2TlogN.\hfill \end{array}$$ (A.25)

Finally, the marginal distribution for the day of initiation of menstruation is approximated as

$$h\left(k\right|Y_t,Z_t)=\frac{1}{N}\sum _{i=1}^{N}f\left\{k|{\omega }_t=\omega (i)\right\}{\tilde{p}}_{\mathrm{f}}^{\prime }(i,t).$$ (A.26)

Appendix B. Details for comparing accuracy of the prediction for the day of onset of menstruation

B.1.

We compared the root mean square error (RMSE) and the mean absolute error (MAE) of prediction of the next day of onset of menstruation among the proposed method, calendar calculation method, and the method proposed in Bortot et al. 6.

As described in the main text, the proposed method can adaptively adjust the prediction using the within‐cycle information (i.e., daily BBT records). Thus, we estimated RMSE and MAE of the proposed method for several points in time within the cycle. Specifically, we calculated RMSE and MAE of the prediction obtained at the day of onset of the previous menstruation, as well as those obtained at 21, 14, 7, 6, 5, 4, 3, 2, and 1 day(s) before the upcoming day of onset of menstruation.

In the calendar calculation method, RMSE and MAE depend on the fixed number of days used for prediction. Thus, for each subject, we calculated RMSE and MAE over a range of parameter values and used the lowest value as a baseline for comparison (Tables 3 and 4).

The method proposed by Bortot et al. 6 uses state‐space modeling framework to predict the length of the cycle. The predictive distribution of menstrual cycle length is obtained conditional on past time series of cycle length. In contrast to the proposed method, the prediction does not vary within the cycle.

In order to implement the prediction method of Bortot et al. 6, we first fitted state‐space models to data for parameter estimation (Table 1). Samples from the joint posterior distribution of parameters and state variables were obtained by using the Markov chain Monte Carlo (MCMC) method run on jags software 16. Then, the ensemble Kalman filter was applied to obtain one‐step‐ahead predictive distributions of cycle length. The MCMC outputs were used for parameters and initial distributions of state variables that are required for the ensemble Kalman filter to work.

We tested several model variants that were simplified versions of the original state‐space model described in Bortot et al. 6. Among model variants in which convergent MCMC samples were obtained, we identified a model that provides, on average, the most accurate predictions and used it as a baseline for the comparison (Figures 3 and 4).

Fukaya, K. , Kawamori, A. , Osada, Y. , Kitazawa, M. , and Ishiguro, M. (2017) The forecasting of menstruation based on a state‐space modeling of basal body temperature time series. Statist. Med., 36: 3361–3379. doi: 10.1002/sim.7345.