Optimal design of longitudinal data analysis using generalized estimating equation models

Abstract

Longitudinal studies are often applied in biomedical research and clinical trials to evaluate the treatment effect. The association pattern within the subject must be considered in both sample size calculation and the analysis. One of the most important approaches to analyze such a study is the generalized estimating equation (GEE) proposed by Liang and Zeger, in which “working correlation structure” is introduced and the association pattern within the subject depends on a vector of association parameters denoted by ρ. The explicit sample size formulas for two-group comparison in linear and logistic regression models are obtained based on the GEE method by Liu and Liang. For cluster randomized trials (CRTs), researchers proposed the optimal sample sizes at both the cluster and individual level as a function of sampling costs and the intracluster correlation coefficient (ICC). In these approaches, the optimal sample sizes depend strongly on the ICC. However, the ICC is usually unknown for cluster randomized and multicenter trials. To overcome this shortcoming, Van Breukelen et al consider a range of possible ICC values identified from literature reviews and present Maximin designs (MMDs) based on relative efficiency (RE) and efficiency under budget and cost constraints. In this paper, the optimal sample size and number of repeated measurements using GEE models with an exchangeable working correlation matrix is proposed under the considerations of fixed budget, where “optimal” refers to maximum power for a given sampling budget. The equations of sample size and number of repeated measurements for a known parameter value ρ are derived and a straightforward algorithm for unknown ρ is developed. Applications in practice are discussed. We also discuss the existence of the optimal design when an AR(1) working correlation matrix is assumed. Our proposed method can be extended under the scenarios when the true and working correlation matrix are different.

1 Introduction

Longitudinal studies are often applied in biomedical research and clinical trials. Methods for analyzing such correlated data have been extensively developed in recent years. One of the most important approaches is generalized estimating equation (GEE) proposed by Liang and Zeger (Liang et al., 1986), which fits a marginal model. In order to describe the association pattern within the subject, the idea of a “working correlation structure” is introduced and the pattern depends on a vector of association parameters denoted by ρ. The advantage of this approach is that consistent estimates are provided when the marginal model is correctly specified, even if the working correlation matrix is incorrectly assumed. Therefore, GEE has been popularly applied (Dahmen et al., 2004; Sanda et al., 2008; Lin et al., 2015; Park et al., 2015; Toriola et al., 2015; Jeffe et al., 2016).

Sample size calculation or power estimation is an important topic in study design for investigators. For a two-group comparison with continuous or categorical outcomes, sample size formula have been extensively proposed (Schlesselman, 1982; Self et al., 1988; Self et al., 1992; Shuster, 1993; Dahmen et al., 2004; Dahmen et al., 2004). For longitudinal studies, Liu and Liang (Liu et al., 1997) propose a statistic based on the GEE method and present the asymptotic distribution. They derive the sample size calculation formula for correlated observations based on the score statistic. For special cases, e.g., two-group comparison in linear and logistic regression models, the explicit formulas are obtained. With the assumption of the exchangeable working correlation R(ρ), i.e., 1 for diagonal entries and ρ otherwise, their sample size formula for continuous outcomes is identical to the one developed by Diggle et al (Diggle et al., 1994) (p.31) and for a binary outcome is similar to that of Lee and Dubin (Lee et al., 1994).

Cluster randomized trials (CRTs) are performed when randomization at the individual-level is practically infeasible or may lead to severe estimation bias of the treatment effect. In recent years, there has been growing interest in conducting cluster randomized trials (Campbell et al., 2000; Gulliford et al., 2014; Gravenstein et al., 2016; Kalfon et al., 2016; Mehring et al., 2016; Nagayama et al., 2016; Yamagata et al., 2016). Individuals within a cluster may share similar characteristics or be exposed to common factors. The degree of such a similarity needs to be considered in the analysis and is commonly quantified by the intracluster correlation coefficient (ICC). The equations of sample size for cluster randomized trials have been published as a function of the ICC or the coefficient of variation (CV) of cluster sizes (Donner et al., 1981; Rosner et al., 2003; Eldridge et al., 2006; Austin, 2007; Rosner et al., 2011; Amatya et al., 2013). Additionally, cost is an important factor since it is associated with recruiting an additional cluster instead of an additional subject in an individually randomized trial. Therefore, sample size estimation is particularly important due to the large cost in such a design. Researchers have proposed the optimal sample sizes at both the cluster and individual level as a function of sampling costs and the ICC (Raudenbush, 1997; Raudenbush et al., 2000; Moerbeek et al., 2001; Moerbeek et al., 2001; Connelly, 2003; Liu, 2003; Headrick et al., 2005). Optimal means maximum power and precision for a given sampling budget, or minimum sampling costs for a given power and precision. In these approaches, the optimal sample sizes depend strongly on the ICC. However, the ICC is usually unknown for cluster randomized and multicenter trials. To overcome this shortcoming, Van Breukelen et al (Van Breukelen et al., 2015) consider a range of possible ICC values identified from literature reviews and present Maximin designs (MMDs) based on relative efficiency (RE) and efficiency under budget and cost constraints. Using the linear regression model and the variance of the maximum likelihood estimator, they give a practical expression for the optimal design (number of clusters, number of persons per cluster). They also show that the MMD has a high minimum RE for the realistic ICC ranges and cost ratios and can thus be recommended for practical use.

For longitudinal studies, selecting the optimal number of repeated measures is also a major concern for researchers in order to decrease intra-patient variability and thus increase statistical power (Vickers, 2003). Therefore, the guidance related to how researchers should select the number of repeated measures deserves more attention. Additionally, the cost spent on this kind of study includes the enrollment cost and the cost of repeated measures per subject. The total cost may dramatically increase when either the total sample size or the number of repeated measures per subject rises. Under a given total budget, finding the optimal design that maximizes the power is a practical issue for longitudinal studies. On the other hand, the association parameter (ρ) within the subject is unknown in most cases when the study is designed.

In this paper, we will discuss how many subjects need to be enrolled and how many repeated measures are sufficient under the budget constraint for known and unknown association parameter (ρ) in the working correlation structure within the subject. Given that GEE method provides consistent estimation regardless of the working correlation matrix, we will propose the optimal sample size based on the GEE under a fixed budget. The exchangeable correlation matrix is used in our proposed method and other correlation structures including working correlation matrix misspecification is discussed.

The outline of this article is as follows. In section 2, we briefly summarize the GEE method developed by Liang and Zeger (Liang and Zeger, 1986) and the sample size formula for two-group comparison in linear and logistic regression models proposed by Liu and Liang (Liu and Liang, 1997). Section 3 presents the locally optimal design (LOD) for known parameter value ρ in the working correlation matrix. Section 4 shows the optimal designs (ODs) for unknown parameter value ρ. In section 5, we discuss the existence of optimal design when the first-order autoregressive (AR(1)) is assumed to be the working correlation matrix and later consider several scenarios in which the true and working correlation structures are different. We discuss how the proposed method applies to the real world in section 6, followed by discussion of the limitations and directions for future research.

2 Generalized estimating equation model and sample size calculations

Let γ_i = (γ_i1, γ_i2, ··· γ_ini)′ be a vector of responses from the ith subject, i = 1, ···, m. The responses are assumed to be independent across subjects but correlated within each subject. Liu and Liang (Liu and Liang, 1997) consider the marginal model

$$g({\mu }_{ij})={\mathbf{X}}_{ij}^{\prime }\mathit{\phi }+{\mathbf{Z}}_{\mathit{ij}}^{\prime }\mathit{\lambda },i=1,\cdots ,m;\mathrm{j}=1,\cdots ,{\mathrm{n}}_i,$$ (1)

where μ_ij = E(γ_ij) and g(·) is a linking function. A p × 1 vector φ represents fixed effect and parameters of interests, whereas a q × 1 vector λ is nuisance parameters. The mean of γ_i is denoted by μ_i = E(γ_i) and the variance-covariance matrix for γ_i is denoted by ${\mathit{V}}_i=\theta {\mathit{A}}_{\mathit{i}}^{\mathbf{1}/\mathbf{2}}{\mathit{R}}_{\mathit{i}}(\mathrm{\rho }){\mathit{A}}_{\mathit{i}}^{\mathbf{1}/\mathbf{2}}$, where A_i = diag {γ(μ_i1), ···, γ(μ_ini)} and working correlation structure R_i(ρ) describes the association pattern within the subject. R_i(ρ) is a n_i × n_i matrix and depends on a vector of association parameters denoted by ρ. Both γ and θ are dependent on the distribution of responses. For instance, if γ_ij is binary, $\gamma ({\mu }_{ij})=\frac{{\mu }_{ij}(1-{\mu }_{ij})}{m}$ and θ=1; If γ_ij is continuous, γ(μ_ij) = 1 and θ is the random error variance.

The hypothesis are H₀: φ = φ₀ versus H₁: φ = φ₁. The quasi-score statistic based on the GEE is

$$T={\mathbf{S}}_{\mathit{\phi }}{({\mathit{\phi }}_{\mathbf{0}},{\widehat{\mathit{\lambda }}}_0,\mathrm{\rho })}^{\prime }{\mathbf{\sum }}_{\mathbf{0}}^{-\mathbf{1}}{\mathbf{S}}_{\mathit{\phi }}({\mathit{\phi }}_{\mathbf{0}},{\widehat{\mathit{\lambda }}}_0,\mathrm{\rho }),$$

where

$$\begin{array}{c}{\mathbf{S}}_{\mathit{\phi }}\left({\mathit{\phi }}_{\mathbf{0}},{\widehat{\mathit{\lambda }}}_0,\mathrm{\rho }\right)=\sum _{i=1}^m{\left(\frac{\partial {\mathit{\mu }}_i}{\partial \mathit{\phi }}\right)}^{\prime }{\mathbf{V}}_{\mathit{i}}^{-\mathbf{1}}({\mathbf{y}}_i-{\mathit{\mu }}_i),\\ {\mathbf{\sum }}_0={cov}_{{\mathrm{H}}_0}[{\mathbf{S}}_{\mathit{\phi }}({\mathit{\phi }}_{\mathbf{0}},{\widehat{\mathit{\lambda }}}_0,\mathrm{\rho })],\end{array}$$

and λ̂₀ is an estimator of λ under H₀ and estimated by solving the following equation

$${\mathbf{S}}_{\mathit{\lambda }}({\mathit{\phi }}_{\mathbf{0}},\mathit{\lambda },\mathrm{\rho })=\sum _{i=1}^m{\left(\frac{\partial {\mathit{\mu }}_i}{\partial \mathit{\lambda }}\right)}^{\prime }{\mathbf{V}}_{\mathit{i}}^{-\mathbf{1}}({\mathbf{y}}_i-{\mathit{\mu }}_i)=0.$$

Under H₀ and H₁, ${\mu }_{ij}=g^{-1}({\mathbf{X}}_{ij}^{\prime }{\mathit{\phi }}_{\mathbf{0}}+{\mathbf{Z}}_{\mathit{ij}}^{\prime }{\mathit{\lambda }}_{\mathbf{0}})$ and $g^{-1}({\mathbf{X}}_{ij}^{\prime }{\mathit{\phi }}_{\mathbf{1}}+{\mathbf{Z}}_{\mathit{ij}}^{\prime }{\mathit{\lambda }}_{\mathbf{1}})$, respectively. They show that T follows a non-central chi-square distribution asymptotically under the φ = φ₁ and λ = λ₁ with the non-central parameter ${\mathit{\epsilon }}^{\prime }{\mathbf{\sum }}_{\mathbf{1}}^{-\mathbf{1}}\mathit{\epsilon }$, where ε is the expectation of S_φ(φ_0,λ̂₀, ρ) and Σ₁ the covariance of S_φ(φ_0,λ̂₀, ρ) under H₁. Both the expectation and covariance can be approximately estimated. Therefore, the statistical power, equivalently the sample size calculation, can be approximated from the non-central chi-square distribution. Please note that this approach assumes that ρ is known.

For simplicity, the number of repeated measures is assumed to be identical across the subjects, i.e., n_i = n for all i. A special case is considered where p = q = 1 with Z_ij ≡ 1 and X_ij ≡ X_i = 1 for treatment or 0 for control group. Let π₀ be the proportion of control group and π₁ = 1 − π₀. Liu and Liang (Liu and Liang, 1997) obtain the explicit sample size formulas for a two-group study with binary and continuous responses.

For binary outcome, the null hypothesis is p₀ = p₁. The total sample size m is calculated by

$$m=\frac{{\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2\times ({\pi }_1{p}_0(1-p_0)+{\pi }_0{p}_1(1-p_1))}{{\pi }_0{\pi }_1{(p_1-p_0)}^2({\mathbf{1}}^{\prime }\mathit{R}{(\mathrm{\rho })}^{-1}\mathbf{1})},$$

where α is a pre-specified significance level, z_α is the 100×α percentile of a standard normal distribution, 1-β is the nominal power, and 1 is an n × 1 vector of 1’s. With the assumption of exchangeable correlation matrix,

$${\mathbf{1}}^{\prime }\mathit{R}{(\mathrm{\rho })}^{-1}\mathbf{1}=\frac{1+(n-1)\rho }{n},$$ (2)

the total sample size m is simplified to

$$m=\frac{{\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2\times ({\pi }_1{p}_0(1-p_0)+{\pi }_0{p}_1(1-p_1))(1+(n-1)\rho )}{n{\pi }_0{\pi }_1{(p_1-p_0)}^2}.$$

The factor 1 + (n − 1)ρ is known as the inflation factor or design effect (Neuhaus et al., 1993). Define

$${\mathrm{\Delta }}_1=\frac{{\pi }_1{p}_0(1-p_0)+{\pi }_0{p}_1(1-p_1)}{{\pi }_0{\pi }_1{(p_1-p_0)}^2},$$ (3)

the total sample size can be re-written as

$$m={\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2\frac{1+(n-1)\rho }{n}{\mathrm{\Delta }}_1.$$ (4)

Alternatively,

$$z_{1-\beta }=\sqrt{\frac{n}{1+(n-1)\rho }\frac{m}{{\mathrm{\Delta }}_1}}-z_{1-\alpha /2}.$$ (5)

Consequently, the power (1 − β) is calculated by φ⁻¹(z_{1 − β}), where φ is cumulative density function of standard normal distribution.

For a two-group study with continuous outcomes, the linear regression model for repeated measurements is considered, where the error term follows a multivariate normal distribution with mean 0 and covariance matrix σ²R(ρ). The hypothesis is H₀: φ = 0 versus H₁: φ = φ₁. The total sample size formula is

$$m=\frac{{\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2{\sigma }^2}{{\pi }_0{\pi }_1{\phi }_1^2({\mathbf{1}}^{\prime }\mathit{R}{(\mathrm{\rho })}^{-1}\mathbf{1})}.$$

Again, assuming that exchangeable correlation matrix, the total sample size formula reduces to

$$m=\frac{{\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2{\sigma }^2(1+(n-1)\rho )}{n{\pi }_0{\pi }_1{\phi }_1^2},$$

and the factor 1 + (n − 1)ρ is known as the inflation factor or design effect (Scott et al., 1982). As noted, it is identical to the one developed by Diggle et al (Diggle, Liang, et al., 1994) (p.31). Define

$${\mathrm{\Delta }}_1=\frac{{\sigma }^2}{{\pi }_0{\pi }_1{\phi }_1^2},$$ (6)

the sample size and power formula for two-group comparison with continuous outcome have the same format as equations (4) and (5). Therefore, we will use these two formulas throughout the paper, regardless of the binary or continuous outcome.

Van Breukelen et al (Van Breukelen and Candel, 2015) define the total budget B in CRTs. We will use the same idea in longitudinal studies. Assume the study cost per subject in the enrollment stage is c currency units (e.g. USD), and each repeated measurement costs s currency units. Total budget B includes m subjects and n repeated measurements per subject,

$$B=m(c+sn).$$ (7)

The term “optimal” refers to maximum power for a given sampling budget in this paper. The research question is to find the design which maximizes the power (1 − β) in equation (5) given the constraint in (7).

3 Known parameter value ρ in working correlation matrix

In this section we assume ρ is a known value. As noted that π₀, Δ₁, and α in the equation (5) are pre-determined values under null and alternative hypothesis. Maximizing the power means maximizing

$$K=\frac{nm}{1+(n-1)\rho }.$$

Substituting $m=\frac{B}{c+sn}$ gives

$$K=\frac{Bn}{c(1-\rho )+[c\rho +s(1-\rho )]n+s\rho n^2}.$$

Taking the partial derivatives with respect to n gives

$$\frac{\partial K}{\partial n}\propto Bc(1-\rho )-Bs\rho n^2.$$

It can be shown that when

$$n=\sqrt{\frac{c(1-\rho )}{s\rho }},$$ (8)

the derivatives equals 0. When $n>\sqrt{\frac{c(1-\rho )}{s\rho }},\frac{\partial K}{\partial n}$ is negative while when $n<\sqrt{\frac{c(1-\rho )}{s\rho }},\frac{\partial K}{\partial n}$ is positive. Therefore, $n=\sqrt{\frac{c(1-\rho )}{s\rho }}$ maximizes K. The locally optimal design (LOD) is reached for a known value ρ and n in equation (8) is denoted by n_LOD. Let $\theta =\frac{1-\rho }{\rho }$, the parameters in LOD are given by

$$n_{\text{LOD}}=\sqrt{\frac{\theta c}{s}},m_{\text{LOD}}=\frac{B}{\sqrt{\theta sc}+c}.$$ (9)

We also note that it is identical to the optimal designs (Raudenbush, 1997; Moerbeek et al., 2000; Van Breukelen and Candel, 2015), in which the variance of the treatment effect estimator in the linear regression model is minimized under the cost constraints.

Table 1 shows an example to determine the locally optimal design for binary outcome in a two-group study with p₀ = 0.1 and p₁ = 0.3 under two different fixed budgets (15,000$ and 20,000$) assuming c = 100, and s = 50. The equal sample size between treatment and control group is considered (π₀ = 0.5). For each ρ value between 0.1 and 0.9, the locally optimal design estimated by (9) and the maximized power are illustrated in the table.

Table 1.

Locally optimal design (LOD) at known parameter value ρ in working correlation matrix for two-sample study with c = 100, and s = 50

ρ	nLOD	mLOD	(1 − β)LOD	nup	mup	(1 − β)up	Bup	ndown	mdown	(1 − β)down	Bdown
B = 15,000$; p0 = 0.1, p1 = 0.3
0.1	4.2	48.1	0.893	5	42	0.885	14700	4	50	0.893	15000
0.2	2.8	62.1	0.834	3	60	0.833	15000	2	75	0.823	15000
0.3	2.2	72.1	0.793	3	60	0.782	15000	2	75	0.792	15000
0.4	1.7	80.4	0.764	2	75	0.762	15000	1	100	0.733	15000
0.5	1.4	87.9	0.745	2	75	0.733	15000	1	100	0.733	15000
0.6	1.2	95.1	0.735	2	75	0.705	15000	1	100	0.733	15000
0.7	0.9	102.5	0.734	1	100	0.733	15000	NA
0.8	0.7	110.8	0.743	1	100	0.733	15000	NA
0.9	0.5	121.4	0.770	1	100	0.733	15000	NA
B = 20,000$; p0 = 0.1, p1 = 0.3
0.1	4.2	64.1	0.959	5	57	0.958	19950	4	66	0.957	19800
0.2	2.8	82.8	0.923	3	80	0.922	20000	2	100	0.915	20000
0.3	2.2	96.1	0.893	3	80	0.885	20000	2	100	0.893	20000
0.4	1.7	107.2	0.872	2	100	0.870	20000	1	133	0.846	19950
0.5	1.4	117.2	0.857	2	100	0.846	20000	1	133	0.846	19950
0.6	1.2	126.8	0.848	2	100	0.823	20000	1	133	0.846	19950
0.7	0.9	136.7	0.847	1	133	0.846	19950	NA
0.8	0.7	147.8	0.855	1	133	0.846	19950	NA
0.9	0.5	161.9	0.876	1	133	0.846	19950	NA

n_up = int(n_LOD) + 1, $m_{\text{up}}=int(\frac{B}{c+s{n}_{\text{up}}})$; n_down = int(n_LOD), $m_{\text{down}}=int(\frac{B}{c+s{n}_{\text{down}}})$; int=an integer part of a number; (1 − β)_up and B_up, (1 − β)_down and B_down are actual power and needed budget based on (n_up, m_up) and (n_down, m_down), respectively; Bold refers to the proposed optimal sample size and number of repeated measures with larger power between (n_up, m_up) and (n_down, m_down); NA = Not Applicable.

Obviously n_LOD may be non-integer. In reality we need to choose an integer value for number of repeated measures with either n_up = int (n_LOD) + 1 or n_down = int (n_LOD), where int refers to an integer part of a number. For both integers, we calculate m_up and m_down from $m=\frac{B}{c+sn}$, and then calculate the corresponding power using equation (5). The proposed optimal number of repeated measures is the one with the larger power. Similarly, m_up and m_down are non-integers most likely. In order to meet within the limit of budget, the integer parts for m_up and m_down are taken as the values of corresponding sample sizes. Table 1 also shows the values of possible optimal design (n_up, m_up) and (n_down, m_down). The corresponding power and budget are given to show the actual power and needed budget. The proposed sample size and number of repeated measures ≥ 2 for the study are in bold.

Equation (9) shows that optimal number of repeated measures n_LOD is also dependent on the ratio of cost per subject to cost per repeat $\left(\frac{c}{s}\right)$. Using ρ = 0.5, c = 100, and s = 50 in table 1 as an example, it leads to $\frac{\theta c}{s}=2$ and n_LOD = 1.4. Consequently, n_up = 2 and n_down = 1, in which n_down = 1 has the larger power for the budget 15,000$. However, n > 1 should be expected for a longitudinal study. Additionally, we replace c = 100, and s = 50 by c = 100, and s = 10 and the other parameters are same as those in table 1. The results of locally optimal design are shown in table 2. For any ρ ≤ 0.7, both n_up and n_down > 1; For ρ > 0.7, $\frac{\theta c}{s}\le 4$. In order to design a feasible longitudinal study, we need to ensure that $\frac{\theta c}{s}$ is equal to or larger than 4 resulting in n_LOD ≥ 2.

Table 2.

Locally optimal design (LOD) at known parameter value ρ in working correlation matrix for two-sample study with c = 100, and s = 10

ρ	nLOD	mLOD	(1 − β)LOD	nup	mup	(1 − β)up	Bup	ndown	mdown	(1 − β)down	Bdown
B = 15,000$; p0 = 0.1, p1 = 0.3
0.1	9.5	77.0	0.999	10	75	0.999	15000	9	78	0.999	14820
0.2	6.3	91.9	0.991	7	88	0.991	14960	6	93	0.991	14880
0.3	4.8	101.1	0.973	5	100	0.973	15000	4	107	0.972	14980
0.4	3.9	108.1	0.950	4	107	0.950	14980	3	115	0.947	14950
0.5	3.2	114.0	0.925	4	107	0.922	14980	3	115	0.924	14950
0.6	2.6	119.2	0.901	3	115	0.899	14950	2	125	0.898	15000
0.7	2.1	124.3	0.879	3	115	0.872	14950	2	125	0.879	15000
0.8	1.6	129.5	0.863	2	125	0.861	15000	1	136	0.853	14960
0.9	1.1	135.7	0.854	2	125	0.842	15000	1	136	0.853	14960
B = 20,000$; p0 = 0.1, p1 = 0.3
0.1	9.5	102.6	1	10	100	1	20000	9	105	1	19950
0.2	6.3	122.5	0.999	7	117	0.999	19890	6	125	0.999	20000
0.3	4.8	134.9	0.994	5	133	0.994	19950	4	142	0.994	19880
0.4	3.9	144.2	0.986	4	142	0.986	19880	3	153	0.985	19890
0.5	3.2	151.9	0.975	4	142	0.973	19880	3	153	0.975	19890
0.6	2.6	159.0	0.963	3	153	0.962	19890	2	166	0.961	19920
0.7	2.1	165.7	0.951	3	153	0.946	19890	2	166	0.950	19920
0.8	1.6	172.7	0.941	2	166	0.939	19920	1	181	0.935	19910
0.9	1.1	180.9	0.936	2	166	0.927	19920	1	181	0.935	19910

n_up = int(n_LOD) + 1, $m_{\text{up}}=int(\frac{B}{c+s{n}_{\text{up}}})$; n_down = int(n_LOD), $m_{\text{down}}=int(\frac{B}{c+s{n}_{\text{down}}})$; int=an integer part of a number; (1 − β)_up and B_up, (1 − β)_down and B_down are actual power and needed budget based on (n_up, m_up) and (n_down, m_down), respectively; Bold refers to the proposed optimal sample size and number of repeated measures with larger power between (n_up, m_up) and (n_down, m_down).

Provided that ρ, c, and s are fixed, the number of total sample size is completely dependent on the given budget B. For instance, under the scenario of c = 100, s = 50, and ρ = 0.2, n_LOD = 2.8 for B = 15,000$ and B = 20,000$ but m_LOD = 62.1 and m_LOD = 82.8 for B = 15,000$ and B = 20,000$, respectively. The same findings are observed for all the cases in tables 1 and 2.

Equation (9) also shows that as ρ increases, that is, θ decreases, the number of repeated measurements n_LOD must decrease while the total sample size m_LOD must increase. Simultaneously,

$$n_{\text{LOD}}\times m_{\text{LOD}}=\sqrt{\frac{\theta c}{s}}\times \frac{B}{\sqrt{\theta sc}+c}=\frac{B}{\sqrt{s}(\sqrt{s}+\frac{\sqrt{c}}{\sqrt{\theta }})}=\frac{\frac{B}{s}}{1+\sqrt{\frac{c}{s\theta }}},$$

and

$$1+(n_{\text{LOD}}-1)\rho =1+\frac{\sqrt{\frac{\theta c}{s}}-1}{1+\theta }.$$

Therefore,

$$K_{\text{LOD}}(\theta )=\left\{\frac{\frac{B}{s}}{1+\sqrt{\frac{c}{s\theta }}}\right\}/\left\{1+\frac{\sqrt{\frac{\theta c}{s}}-1}{1+\theta }\right\}.$$

Set ρ₁ > ρ₂, that is, θ₁ < θ₂,

$$\frac{K_{\text{LOD}}({\rho }_1)}{K_{\text{LOD}}({\rho }_2)}=\frac{K_{\text{LOD}}({\theta }_1)}{K_{\text{LOD}}({\theta }_2)}=\frac{1+\sqrt{\frac{c}{s{\theta }_2}}}{1+\sqrt{\frac{c}{s{\theta }_1}}}\times \frac{1+\frac{\sqrt{\frac{{\theta }_{2}c}{s}}-1}{1+{\theta }_2}}{1+\frac{\sqrt{\frac{{\theta }_{1}c}{s}}-1}{1+{\theta }_1}}.$$ (10)

Let $f(\theta )=\left(1+\sqrt{\frac{c}{s\theta }}\right)\left(1+\frac{\sqrt{\frac{\theta c}{s}}-1}{1+\theta }\right)$, the mathematical computation shows f(θ) is a decreasing function of θ when $\sqrt{\frac{\theta c}{s}}>1$. Finally, $\frac{K_{\text{LOD}}({\theta }_1)}{K_{\text{LOD}}({\theta }_2)}=\frac{f({\theta }_2)}{f({\theta }_1)}<1$. It means, as ρ increases, the maximized power (1 − β)_LOD decreases for n_LOD > 1. Both tables 1 and 2 demonstrate these points well. The results above show the locally optimal design for known parameter value ρ given the cost.

4 Unknown parameter value ρ in working correlation matrix

Obviously n_LOD in the equation (9) requires the prior information of ρ. As shown in tables 1 and 2, the incorrect input of ρ will have the different optimal estimates (m_LOD, n_LOD), which maximize the power given the budget constraint. In the scenario of unknown parameter value of ρ, we assume to have the possible range of ρ from previous studies, (ρ_min, ρ_max), called parameter space (Atkinson et al., 2007; Berger et al., 2009). Also we define the range of sample size based on the practical feasibility, (m_min, m_max), called design space. The major research question is thus to identify OD within parameter and design space. One of solution is MMD approach (Mario et al., 2002; Winkens et al., 2007; Berger and Wong, 2009; Maus et al., 2010). It includes three steps. Step 1 defines the parameter and design space; the relative efficiency (RE) is computed in step 2 and finds its smallest RE value in each design within the design space; step 3 selects the design which maximizes the minimum RE among all designs in the design space.

Our algorithm of finding OD for unknown parameter value ρ in working correlation matrix is similar to the MMD approach. It also includes three steps and the optimal design will be chosen from step 3. The difference is that the power is computed in step 2 and the design which minimizes the maximum power is selected. Obviously these steps demonstrate the most robust power estimation even if the parameter value ρ is wrongly assumed.

• Step 1, Define the parameter and design space, (ρ_min, ρ_max) and (m_min, m_max), respectively.

• Step 2, For each ρ in the parameter space, calculate m_LOD using equation (9).

  1. If it is within the range (m_min, m_max), then set $m_{\text{LOD}}^{\prime }=m_{\text{LOD}}$.

  2. If it is outside of (m_min, m_max), then for any possible sample size m ∈(m_min, m_max) the number of repeats per subject n is calculated from $\left(\frac{B}{m}-c\right)/s$. Choose the design of (m, n) has the largest power within design space, denoted by ( $m_{\text{LOD}}^{\prime },n_{\text{LOD}}^{\prime }$). This choice has locally optimal design.

• Step 3, Select the design which minimizes the maximum power in step 2.

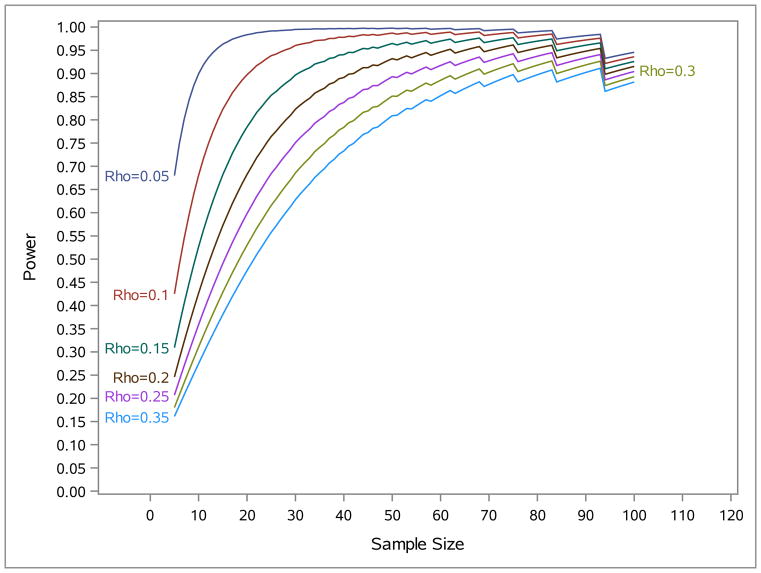
Table 3 shows an example to determine the optimal design for binary outcome in a two-group study with p₀ = 0.1 and p₁ = 0.3 under the fixed budgets of 15,000$, c = 100, and s = 20. We still assume the equal sample size between treatment and control group, and consider the parameter space of (0.05, 0.35) and design space of (5, 100). The locally optimal designs estimated by (5) fall within the design space and LODs are reached for each ρ within the parameter space. Figure 1 shows the power estimate for each different sample size and it clearly demonstrates the power is maximized within design space under the different ρ. Please note that $n_{\text{LOD}}^{\prime }$ and $m_{\text{LOD}}^{\prime }$ should be integers in practice, the similar approach in section 3 need to be adopted. Table 3 presents the proposed ( $m_{\text{LOD}}^{\prime },n_{\text{LOD}}^{\prime }$) for each ρ. Therefore, we choose 93 as the total sample size and 3 as number of repeated measurements (m_OD, n_OD) = (93, 3) as the optimal design, which gives the power of 91.1%.

Table 3.

Optimal design (OD) at unknown parameter value ρ in working correlation matrix for two-sample study with B = 15,000$, c = 100, and s = 20

ρ	nLOD	mLOD	(1 − β)LOD	nup	mup	(1 − β)up	ndown	mdown	(1 − β)down	$n_{\text{LOD}}^{\prime }$	$m_{\text{LOD}}^{\prime }$	${(1-\beta )}_{\text{LOD}}^{\prime }$
0.05	9.7	50.9	0.998	10	50	0.998	9	53	0.997	10	50	0.998
0.1	6.7	64.1	0.990	7	62	0.989	6	68	0.989	6	68	0.989
0.15	5.3	72.7	0.977	6	68	0.976	5	75	0.977	5	75	0.977
0.2	4.5	79.2	0.962	5	75	0.961	4	83	0.961	5	75	0.961
0.25	3.9	84.5	0.946	4	83	0.945	3	93	0.941	4	83	0.945
0.3	3.4	89.1	0.929	4	83	0.927	3	93	0.926	4	83	0.927
0.35	3.0	93.2	0.913	4	83	0.908	3	93	0.911	3	93	0.911

(ρ_min, ρ_max) = (0.05, 0.35) and (m_min, m_max) = (5, 100).

Figure 1.

Power of the treatment effect as a function of sample size (5, 100) for several values of Rho

If m_LOD is within the range (m_min, m_max) for all the values of ρ in the parameter space, as shown in table 3, then the maximized powers are reached under LOD. Section 3 shows that the maximized power is a decreasing function of ρ under LOD. It means that the algorithm finds the optimal design at ρ = ρ_max.

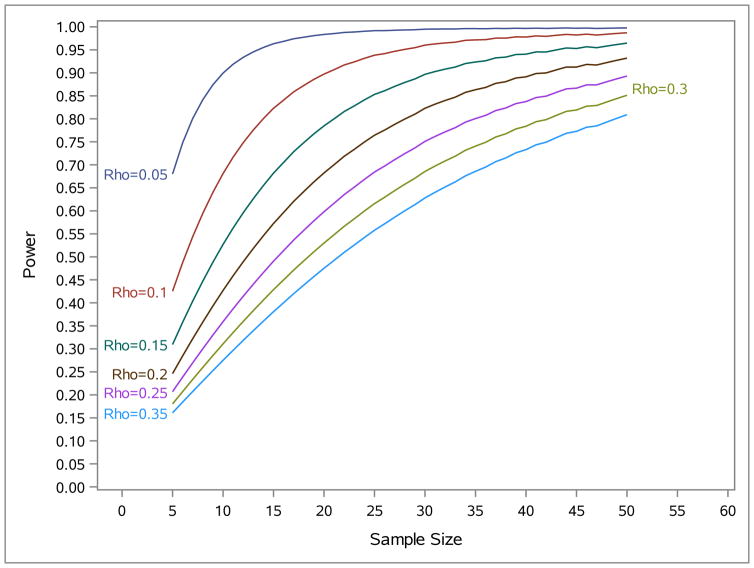
Table 4 shows the same study design as in table 3 but with the feasible sample size of (5, 50). Obviously the locally optimal designs are not reached for each ρ within the parameter space. Figure 2 shows the power estimate for the different sample sizes under the different ρ within design space. The power goes up with the increase of sample size. Table 4 presents LODs, the number of repeated measurements and actual power at the boundary of sample size: m_min and m_max for each ρ. Finally, (m_OD, n_OD) = (50, 10) is the optimal design with the power of 80.9%.

Table 4.

Optimal design (OD) at unknown parameter value ρ in working correlation matrix for two-sample study with B = 15,000$, c = 100, and s = 20

ρ	nLOD	mLOD	(1 − β)LOD	nmin	mmin	(1 − β)min	nmax	mmax	(1 − β)max	$n_{\text{LOD}}^{\prime }$	$m_{\text{LOD}}^{\prime }$	${(1-\beta )}_{\text{LOD}}^{\prime }$
0.05	9.7	50.9	0.998	145	5	0.680	10	50	0.998	10	50	0.998
0.1	6.7	64.1	0.990	145	5	0.426	10	50	0.987	10	50	0.987
0.15	5.3	72.7	0.977	145	5	0.309	10	50	0.965	10	50	0.965
0.2	4.5	79.2	0.962	145	5	0.246	10	50	0.932	10	50	0.932
0.25	3.9	84.5	0.946	145	5	0.207	10	50	0.893	10	50	0.893
0.3	3.4	89.1	0.929	145	5	0.180	10	50	0.851	10	50	0.851
0.35	3.0	93.2	0.913	145	5	0.161	10	50	0.809	10	50	0.809

(ρ_min, ρ_max) = (0.05, 0.35) and (m_min, m_max) = (5, 50).

Figure 2.

Power of the treatment effect as a function of sample size (5, 50) for several values of Rho

If m_LOD is outside of the range (m_min, m_max) for all the values of ρ in the parameter space, as shown in table 4, that is, m_max < m_LOD. Section 3 shows that K is maximized at (m_LOD, n_LOD). If m < m_LOD, then n > n_LOD from $m=\frac{B}{c+sn}$. Since K is a decreasing function of n for n > n_LOD, the power will be maximized at m = m_max. Let n_max denote the corresponding the number of repeated measurement at m_max. Obviously, $K=\frac{nm}{1+(n-1)\rho }$ at m_max is a decreasing function of ρ. Therefore, the algorithm also finds the optimal design at ρ = ρ_max.

Table 5 shows the same study design as in table 3 but with the feasible sample size of (5, 80). The locally optimal designs are reached for smaller values of ρ while those are not for larger values of ρ within the parameter space. Table 5 presents LODs, the number of repeated measurements and actual power at the boundary of sample size: m_min and m_max, ( $m_{\text{LOD}}^{\prime },n_{\text{LOD}}^{\prime }$) for each ρ. Finally, (m_OD, n_OD) = (80, 4) is the optimal design with the power of 89.7%.

Table 5.

Optimal design (OD) at unknown parameter value ρ in working correlation matrix for two-sample study with B = 15,000$, c = 100, and s = 20

ρ	nLOD	mLOD	(1 − β)LOD	$n_{\mathit{min}}^{\ast }$	$m_{\mathit{min}}^{\ast }$	${(1-\beta )}_{\mathit{min}}^{\ast }$	$n_{\mathit{max}}^{\ast }$	$m_{\mathit{max}}^{\ast }$	${(1-\beta )}_{\mathit{max}}^{\ast }$	$n_{\text{LOD}}^{\prime }$	$m_{\text{LOD}}^{\prime }$	${(1-\beta )}_{\text{LOD}}^{\prime }$
0.05	9.7	50.9	0.998	10	50	0.998	9	53	0.997	10	50	0.998
0.1	6.7	64.1	0.990	7	62	0.989	6	68	0.989	6	68	0.989
0.15	5.3	72.7	0.977	6	68	0.976	5	75	0.977	5	75	0.977
0.2	4.5	79.2	0.962	5	75	0.961	4	83	0.961	5	75	0.961
0.25	3.9	84.5	0.946	145	5	0.207	4	80	0.937	4	80	0.937
0.3	3.4	89.1	0.929	145	5	0.180	4	80	0.918	4	80	0.918
0.35	3.0	93.2	0.913	145	5	0.161	4	80	0.897	4	80	0.897

(ρ_min, ρ_max) = (0.05, 0.35) and (m_min, m_max) = (5, 80).

For m_LOD ∈ (m_min, m_max), $n_{\mathit{min}}^{\ast }=n_{\text{up}},m_{\mathit{min}}^{\ast }=m_{\text{up}},n_{\mathit{max}}^{\ast }=n_{\text{down}}$ and $m_{\mathit{max}}^{\ast }=m_{\text{down}};n_{\mathit{min}}^{\ast }=n_{min},m_{\mathit{min}}^{\ast }=m_{min},n_{\mathit{max}}^{\ast }=n_{max}$ and $m_{\mathit{max}}^{\ast }=m_{max}$.

If m_LOD is within the range (m_min, m_max) for smaller values of ρ and outside of the range (m_min, m_max) for larger values of ρ in the parameter space, as shown in table 5, then the maximized powers are reached under LOD for smaller values of ρ and at m = m_max for larger values of ρ. Combining the properties in tables 3 and 4, we can show that the algorithm finds the optimal design at ρ = ρ_max for this scenario as well.

In conclusion, the maximized power in the design space is a decreasing function of ρ in the parameter space. Therefore, we can simplify the above algorithm as follows.

• Step 1, Define the parameter and design space, (ρ_min, ρ_max) and (m_min, m_max), respectively.

• Step 2, Consider ρ = ρ_max, calculate m_LOD using equation (9).

  1. If it is within the range (m_min, m_max), then set m_OD = m_LOD.

  2. If it is outside of (m_min, m_max), then set m_OD = m_max. The number of repeats per subject n_OD is calculated by $\left(\frac{B}{m_{\text{OD}}}-c\right)/s$.

When comparing the algorithm in Maximin designs (MMDs) based on relative efficiency (RE) and efficiency (Van Breukelen and Candel, 2015), we notice that our finalized algorithm is simpler because the unique characteristics of power-the maximized power decreases as ρ increases, shown in equation (10). Source code to reproduce the results is available as Supporting Information on the journal’s web page (http://onlinelibrary.wiley.com/doi/xxx/suppinfo).

5 Working correlation matrix misspecification

We assume the exchangeable working correlation matrix in equations (2), (4), (5), and sections 3–4. If assuming the first-order autoregressive (AR(1)) to be working correlation matrix, which considers two adjacent measurements in time are more correlated than two measurements with increasing distance between time points, one has

$${\mathbf{1}}^{\prime }\mathit{R}{(\mathbf{\rho })}^{-\mathbf{1}}\mathbf{1}=\frac{1}{1+\mathrm{\rho }}[2\mathrm{\rho }+n(1-\mathrm{\rho })].$$ (11)

Thus the total sample size m for binary outcome is $\mathit{m}=\frac{{\left({\mathit{z}}_{1-\mathit{\alpha }/\mathbf{2}}+{\mathit{z}}_{1-\mathit{\beta }}\right)}^{\mathbf{2}}\times ({\mathit{\pi }}_{\mathbf{1}}{\mathit{p}}_{\mathbf{0}}(\mathbf{1}-{\mathit{p}}_{\mathbf{0}})+{\mathit{\pi }}_{\mathbf{0}}{\mathit{p}}_{\mathbf{1}}(\mathbf{1}-{\mathit{p}}_{\mathbf{1}}))(\mathbf{1}+\mathit{\rho })}{{\mathit{\pi }}_{\mathbf{0}}{\mathit{\pi }}_{\mathbf{1}}{({\mathit{p}}_{\mathbf{1}}-{\mathit{p}}_{\mathbf{0}})}^{\mathbf{2}}[\mathbf{2}\rho +\mathit{n}(\mathbf{1}-\rho )]}$ and for continuous outcome is $\mathit{m}=\frac{{({\mathit{z}}_{\mathbf{1}-\mathit{\alpha }/\mathbf{2}}+{\mathit{z}}_{\mathbf{1}-\mathit{\beta }})}^{\mathbf{2}}{\mathit{\sigma }}^{\mathbf{2}}(\mathbf{1}+\mathit{\rho })}{{\mathit{\pi }}_{\mathbf{0}}{\mathit{\pi }}_{\mathbf{1}}{\mathit{\phi }}_{\mathbf{1}}^{\mathbf{2}}[\mathbf{2}\rho +\mathit{n}(\mathbf{1}-\rho )]}$. Therefore, ${\mathit{z}}_{\mathbf{1}-\mathit{\beta }}=\sqrt{\frac{[\mathit{z}\rho +\mathit{n}(\mathbf{1}-\rho )]}{\mathbf{1}+\rho }\frac{\mathit{m}}{{\Delta }_{\mathbf{1}}}}-{\mathit{z}}_{\mathbf{1}-\frac{\mathit{\alpha }}{\mathbf{2}}}$, where Δ₁ is defined in equations (3) and (6), respectively. Maximizing the power means maximizing $\mathit{K}=\frac{[\mathbf{2}\rho +\mathit{n}(\mathbf{1}-\rho )]\mathit{m}}{\mathbf{1}+\mathit{\rho }}$. Substituting $\mathit{m}=\frac{\mathit{B}}{\mathit{c}+\mathit{sn}}$ and taking the partial derivatives with respect to n gives $\frac{\mathit{\partial }\mathit{K}}{\mathit{\partial }\mathit{n}}\propto (\mathbf{1}-\mathit{\rho })\mathit{c}-\mathbf{2}\mathit{\rho }\mathit{s}$. If $\mathit{\rho }<\frac{\mathit{c}}{\mathit{c}+\mathbf{2}\mathit{s}}$, then K is an increasing function of n. That is, the power increases when n increases; If $\mathit{\rho }>\frac{\mathit{c}}{\mathit{c}+\mathbf{2}\mathit{s}}$, then K is an decreasing function of n. Therefore no local optimal design exists for GEE models with AR(1) working correlation matrix.

In sample size calculation or power estimation, we need to specify the correlation structure and thus can use it as the working correlation. The advantage of GEE is that the estimator φ is still consistent even when the working correlation matrix is incorrectly assumed based on Liang and Zeger (Liang and Zeger, 1986). In this section, we also discuss the situations when a working correlation matrix is misspecified, even if we may not know the true correlation structure. Let R_t and R_w denote the true and working correlation structure, respectively. We still assume that the number of repeated measures is assumed to be identical across the subjects, i.e., n_i = n for all i.

For binary outcomes, Pan (Pan, 2001) shows that the robust variance estimator of $\sqrt{m}(\widehat{\mathit{\phi }}-\mathit{\phi })$ is

$$c\left[\frac{1}{{\pi }_1{p}_0(1-p_0)}+\frac{1}{{\pi }_0{p}_1(1-p_1)}\right],$$

where

$$c=\frac{{\mathbf{1}}^{\prime }{\mathit{R}}_{\mathit{w}}^{-\mathbf{1}}{\mathit{R}}_{\mathit{t}}{\mathit{R}}_{\mathit{w}}^{-\mathbf{1}}\mathbf{1}}{{({\mathbf{1}}^{\prime }{\mathit{R}}_{\mathit{w}}^{-\mathbf{1}}\mathbf{1})}^2}$$

If R_t = R_w are exchangeable matrices, or R_t is an exchangeable matrix and R_w is an independence model, then

$$c=\frac{1+(n-1)\rho }{n}.$$

It is exactly the same as equation (2). Therefore, the algorithm in section 3 and 4 works for such situations. If R_t = R_w are AR(1), c is same as equation (11) resulting in the fact that no optimal design exists.

For continuous outcomes, Wang and Carey (Wang et al., 2003) investigate the asymptotic relative efficiency of GEE when the working correlation structure and true correlation structure are different. If R_t is exchangeable and R_w is independence model, then the asymptotic relative efficiency is 1. That is, the discrepancies between working and true correlation matrix under this scenario has no impact on regression estimator. In conclusion, under the scenarios in which R_t = R_w are exchangeable matrices or R_t is an exchangeable matrix and R_w is an independence model, our algorithm in section 3 and 4 works for either binary or continuous outcomes.

6 Application

The estimates of (m_OD, n_OD) are dependent on c, s and B besides the parameter and design space. The parameter space may come from the literature review and design space is from the feasibility in a real world setting. We assume that c and s are fixed cost and can be known in advance. Therefore, it is particularly easy and straightforward to calculate the sample size and number of repeated measurements in section 3 for a known parameter value ρ and apply the algorithm in section 4 for unknown ρ in order to have an optimal design in the longitudinal study.

A key practical issue for researchers is budget setting at the stage of study design. Obviously, the total budget decides the possible total sample size and the possible number of repeated measurements. If the budget is too limited, the actual power is still very small even if using the optimal design. Here is an example showing budget estimates which may be useful in practice. The total sample size m′ is calculated assuming only one measurement per subject and then the budget is estimated by m′× c. Finally, the proposed budget in the longitudinal study needs to be larger than this estimated budget. Again, using the example in table 1 as an illustration, the total sample size is 124 if we assume there is only one measurement per subject under the type I error of 0.05 and power of 0.8. c = 100$ per subject cost results in the estimated budget is 12,400$. Therefore, we use 15,000$ and 20,000$ as the given budgets. The minimum of optimal power is more than 70% for c = 100 and s = 50, shown in table 1, and at least 80% for c = 100 and s = 10 in table 2.

The other issue in practice is the sample size calculation for each group. To find an appropriate total sample size m with the largest power in both equation (9) and the algorithm are needed to guarantee that mπ₀ and mπ₁ are integers for a two-group study.

7 Discussion

The equations and algorithm for sample size calculations (total sample size and the number of repeated measurements) were proposed in the longitudinal study under the considerations of a given budget. For a known parameter value ρ in the working correlation structure, the proposed formulas of (m_LOD, n_LOD) give the maximum of power under the constraints. While for the unknown parameter value ρ, the design space and parameter space need to be defined and the proposed algorithm finds the optimal design (m_OD, n_OD) which provides the minimum of maximized power for all the possible values of ρ within the parameter space.

In the paper (Van Breukelen and Candel, 2015), the efficient design was proposed for cluster randomized and multicentre trials with unknown intraclass correlation. However, there is no closed form for binary outcomes and the variance from binary outcome needs to be transformed to that of continuous outcomes. The rationals of our proposed method is the sample size formula based on GEE approach for continuous or binary responses (Liu and Liang, 1997). We derived the close form of optimal design and note that they have the similar format for two different type of outcomes. Van Breukelen et al (Van Breukelen and Candel, 2015) also considered the assumption of equal cluster size is not realistic. However, it is feasible and acceptable for longitudinal study to measure the same number of repeats for each subject.

There are several limitations to this approach. The first limitation is that the covariates were not included in the consideration. If we include the covariates in GEE model, the sample size formula is not shown to be simple as equation (4). Moreover, the performance of the sample size formula is sensitive to the distribution of the covariates (Liu and Liang, 1997). However, it is reasonable to calculate the sample size without the consideration of covariates in the design stage in general. The next limitation is, if ρ is a large number or the upper boundary in the parameter space, e.g. >0.7, the power in the optimal design may be low. In such a case, the budget needs to increase to a reasonable number. Section 6 illustrates how to set the budget in the design stage. The third limitation is that our proposed method is based on exchangeable working correlation matrix only. The key assumption is that both the true and working correlation matrices in sections 3 and 4 are the same and they are compound symmetry (CS). It may not hold in a real world application. When the working structure is incorrectly specified, the GEE moment estimator of the correlation matrix and “sandwich” based estimator of the asymptotic covariance matrix of the GEE estimator of the regression parameter may fail to be consistent (Crowder, 1995; Sutradhar et al., 1999). However, our proposed method still works under the scenario when the true and working correlation matrices are different, shown in section 5. The last limitation, or the direction of future research, is that only continuous and binary outcome are considered. We will consider optimal design for the count outcome using GEE model in the future.

In conclusion, it is easy for the researchers to design the longitudinal study using the method proposed in this paper. We believe that the proposed method is very useful, especially for designing the early stage studies when ρ is unknown and under the constraints of given budget.