Abstract
The treatment of cancer has progressed dramatically in recent decades, such that it is no longer uncommon to see a cure or log-term survival in a significant proportion of patients with various types of cancer. To adequately account for the cure fraction when designing clinical trials, the cure models should be used. In this article, a sample size formula for the weighted log-rank test is derived under the fixed alternative hypothesis for the proportional hazards cure models. Simulation showed that the proposed sample size formula provides an accurate estimation of sample size for designing clinical trials under the proportional hazards cure models.
Keywords: clinical trial, cure model, proportional hazards model, log-rank test, sample size calculation, survival analysis
1 Introduction
The treatment of cancer has progressed dramatically in recent decades, such that it is no longer uncommon to see a cure or long-term survival in a significant proportion of patients with various types of cancer, e.g., breast cancer, non-Hodgkin lymphoma, leukemia, prostate cancer, melanoma, and head and neck cancer [1]. To adequately account for cured patients in survival data from clinical trials, the cure models are increasingly useful. Various parametric and semiparametric cure models have been proposed by Farewell [2], Peng et al. [3] and Kuk and Chen [4], among others, and a maximum-likelihood EM algorithm for parametric and semiparametric cure models has been proposed by Peng and Dear [5] and Sy and Taylor [6]. A SAS macro PSPMCM developed by Corbiere and Joly [7] is available to fit both parametric and semiparametric cure models.
The traditional methods for designing survival trials may not be appropriate when there is a cure fraction. Sample size calculations have been developed for clinical trial designs under the cure models. For example, Halpern and Brown [8] developed a computer program to calculate the power and sample size for exponential cure models based on Monte Carlo simulation. Ewell and Ibrahim [1] provided a power formula for exponential cure models by considering a general alternative that allows for the effects of treatment on both short- and long-term survival. Recently, Wang et al. [9] considered a proportional hazards (PH) cure model, a special case of the general alternative proposed by Ewell and Ibrahim [1], and derived a sample size formula for the weighted log-rank test under a series of local alternatives. However, Wu [10] has pointed out that Wang’s formula does not provide adequate sample size or power for clinical trial designs. A series of local alternatives is that the alternative need to change along with the sample size such that the difference in parameter to be detected under the alternative need to diminish towards 0 in a rate of as the sample size n getting large towards infinity. The fixed alternative is that the difference in parameter to be detected under the alternative is fixed and not depending on the sample size. A sample size established under a series of local alternatives works well only when the value of parameter under the alternative is very close to the one under the null hypothesis, whereas no such restriction for the fixed alternative.
In this paper, we derived a novel sample size formula for the weighted log-rank test under the PH cure model. The rest of the paper is organized as follows. The PH cure models are introduced in section 2. The sample size formula is presented in section 3. Simulations are conducted in section 4 to study the performance of the proposed sample size formula and compared with Wang’s formula. Section 5 illustrates clinical trial design using the proposed methods. The conclusion and additional remarks are presented in section 6.
2 Proportional Hazards Cure Models
The failure time, T*, is assumed to be T* = vT + (1 − v)∞, where v is an indicator of whether a subject will eventually (v = 1) or never (v = 0) experience treatment failure, and T denotes the failure time if the subject is not cured, with a survival distribution S(t), which is the conditional distribution for patients who will experience failure, and is often called the latency distribution. Thus, the overall survival distribution of T* is a mixture model of a cure rate π = P(v = 0) and a latency distribution S(t) given by
For a two-arm randomized survival trial, let denote the overall survival function and let denote its corresponding hazard function for group j, where j = 0, 1 represents control group and treatment group, respectively. Similarly, let Sj(t) denote the survival function in uncured patients and let λj(t) denote its hazard function. The cure rate in group j is defined by πj, where 0 ≤ πj ≤ 1. For the mixture cure model, we have
and
for j = 0, 1. To derive the sample size calculation, we consider a class of PH cure models [1][9] in which
| (1) |
where η is the log-hazard ratio of treatment vs. control for uncured patients and γ is the log-odds ratio of the cure rates for the two groups. Note that π0 = π1 = 0 corresponds to the standard PH model. However, if either π0 ≠ 0 or π1 ≠ 0, the PH cure model does not satisfy the proportional hazards condition. For a survival trial in which a proportion of patients are cured, we are interested in testing the following null hypothesis:
which is equivalent to H0: η = γ = 0. Various alternative hypotheses are of interest: H1a : η ≠ 0, γ ≠ 0, with differences in both the short-term survival and the cure fraction; H1b : η ≠ 0, γ = 0, with a difference in the short-term survival but not in the cure fraction; and H1c : η = 0, γ ≠ 0, with difference in the cure fraction but not in the short-term survival.
3 Sample Size Formula
Consider a class of PH cure models as defined by the equations in (1). The sample size calculation is based on testing the null hypothesis
| (2) |
against one of the three alternative hypotheses, H1a, H1b, and H1c, defined in the previous section. The weighted or unweighted log-rank test can be used for testing this hypothesis. It is well known that the log-rank test is asymptotically normal distributed. To derive the asymptotic distribution of the log-rank test statistic under the alternatives hypotheses, suppose a survival trial involving n subjects, and let Ti and Ci denote the survival and censoring times of patient i, respectively, and Zi = 0/1 denote the treatment group indicator (0 for control group and 1 for treatment group). The observed data then consist of {Xi, Δi, Zi, i = 1, …, n}, where Xi = min(Ti, Ci) and Δi = I(Ti ≤ Ci). Let Ni(t) = ΔiI(Xi ≤ t) and Yi(t) = I(Xi ≥ t) be the failure and at-risk processes for i = 1, …, n. The weighted log-rank test statistic can then be written as
where τ is the study duration and and wi = W(ti) with W(t) as a weight function that converges to w(t). Under the PH cure models (1), the hazard function of patient i is given by
Given a type I error of α and power of 1−β under a series of local alternatives, the sample size formula derived by Wang et al. [9] is given by
| (3) |
where p is the proportion of sample size allocation for the control group, G(t) is the common survival distribution of censoring time of two groups and with Λ0(t) = − log S0(t) and .
There are two issues relating to the approach of sample size calculation based on a series of local alternatives. The theoretical issue is that the accuracy of the formula derived under the local alternative is not guaranteed when the alternative departures from the null. The practical issue is that the alternative hypothesis in application is always fixed, which does not change as the sample size changes. Thus, it is expected that the formula performances well only when the alternative is close to the null. Our simulation will show (see section 4) that this formula becomes practically unfitting when the alternative departs reasonably away from the null.
To overcome the inaccuracy of the formula (3), here we derive the asymptotic distribution of the log-rank test under the fixed alternative hypothesis by using a novel approach developed by Xiong [11] in which a theoretic development has showed that the log-rank test is not limited to the tests of proportional hazards model but can be used for more general survival models including the PH cure model. The details of the derivation are very complicated and tedious, and out of scope of this paper. Thus, we present the results in here and omit the details. It can be shown that , as n → ∞, where
| (4) |
| (5) |
where q1(t) and q2(t) are two functions given by equations (8) and (9) below. Thus, given a two-sided type I error of α, to achieve a power of 1 − β under the alternative, the total sample size n of the two groups must approximately satisfy the following equation:
The total sample size required for the study can then be determined as
| (6) |
Substituting equations (4) and (5) into (6), the formula of the total sample size is given by
| (7) |
where
| (8) |
| (9) |
where δ = eη is the hazard ratio of group 1 vs. group 0 as defined by (1), and
For the sample size calculation, assume subjects are accrued over an accrual period of duration ta and an additional follow-up time tf, that gives a total study duration of τ = ta + tf. For simplicity, we assume that the only censoring is administrative censoring at time τ, and that there is no loss to follow-up. The censoring distribution G(t) considered in the trial designs can then be uniform (the distribution of enrollment H(t) with density of h(t) = 1/ta on [0, ta]). This leads to the censoring distribution G(t) = H(τ − t) = 1 if t ≤ tf; = (ta + tf − t)/ta if tf ≤ t ≤ ta + tf; = 0 otherwise. Then the integrations in the sample size formula (6) can be calculated by numeric integrations, for example by using the R function integrate.
4 Simulation
We conducted simulation studies to investigate three important issues: 1) whether the proposed sample size formula provides an accurate estimation of sample size under the PH cure model; 2) what is the relative efficiency of the weighted log-rank test vs. the standard log-rank test; and 3) how is the accuracy of the proposed formula compared with the formula derived by Wang et al. [9].
To answer the first question, we assumed a PH cure model with a latency distribution of Weibull . The hazard rates of uncured patients and the cure rates were varied to examine three scenarios: (1) where there were differences in both hazard rates and cure rates, that is, η ≠ 0, γ ≠ 0; (2) where there were differences only between hazard rates, that is, η ≠ 0, γ ≠ 0; and (3) where there were differences only between cure rates, that is, η = 0, γ ≠ 0. The hazard rate of control was set to λ = 0.1 and shape parameter was set to κ = 0.5, 1 and 2, and the cure rate of control was set to π0 = 0.1. The hazard ratio δ = eη under the alternative was set in a range of 1.4−1 to 2−1, and the log-odds ratio of cure rate γ was set in a range of 0 to 1.6. It was assumed in simulations that the treatment group would have a lower hazard rate and a higher cure rate than the control group if there were differences. In addition, we considered a uniform accrual with accrual period ta of 1 year and a follow-up period tf of 10 years. Under each scenario, we calculated sample sizes under equal allocation (p = 0.5) for the standard log-rank test (w(t) = 1) under various parameter configurations, and the corresponding empirical powers via simulations with 10,000 replicates. The results (Table 1) showed that the empirical powers were almost identical to the nominal power of 90% for all three scenarios under all parameter configurations. Therefore, we can conclude that the formula (7) provided accurate sample size estimations.
Table 1.
Sample sizes were calculated under the Weibull cure model for the standard log-rank test with a nominal level of 0.05 and power of 90% (two-sided test, uniform accrual and equal allocation). The corresponding empirical type I errors and powers were estimated based on 10,000 simulation runs.
| δ−1/γ | n |
|
EP | n |
|
EP | n |
|
EP | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| Design | κ = 0.5 | κ = 1 | κ = 2 | ||||||||||
| Scenario 1: η ≠ 0 γ ≠ 0 | |||||||||||||
|
| |||||||||||||
| π0 = 0.1 | 1.2/0.4 | 3445 | .050 | .903 | 1385 | .050 | .902 | 1075 | .047 | .897 | |||
| λ0 = 0.1 | 1.3/0.5 | 1818 | .047 | .902 | 734 | .051 | .901 | 599 | .052 | .902 | |||
| ta = 1 | 1.4/0.6 | 1165 | .052 | .904 | 469 | .053 | .898 | 389 | .052 | .901 | |||
| tf = 10 | 1.5/0.7 | 833 | .048 | .902 | 333 | .052 | .897 | 276 | .049 | .905 | |||
| 1.6/0.8 | 638 | .053 | .899 | 253 | .051 | .905 | 208 | .048 | .897 | ||||
| 1.7/0.9 | 512 | .053 | .900 | 202 | .051 | .906 | 164 | .050 | .900 | ||||
| 1.8/1.0 | 426 | .049 | .909 | 166 | .052 | .900 | 133 | .053 | .903 | ||||
|
| |||||||||||||
| Scenario 2: η ≠ 0 γ = 0 | |||||||||||||
|
| |||||||||||||
| π0 = 0.1 | 1.4/0 | 1783 | .049 | .900 | 801 | .048 | .900 | 1335 | .048 | .902 | |||
| π1 = 0.1 | 1.5/0 | 1266 | .044 | .904 | 562 | .052 | .902 | 927 | .052 | .900 | |||
| λ0 = 0.1 | 1.6/0 | 970 | .049 | .903 | 425 | .048 | .903 | 696 | .049 | .900 | |||
| ta = 1 | 1.7/0 | 783 | .048 | .907 | 340 | .049 | .904 | 551 | .051 | .902 | |||
| tf = 10 | 1.8/0 | 655 | .053 | .904 | 281 | .052 | .897 | 454 | .050 | .901 | |||
| 1.9/0 | 563 | .052 | .911 | 240 | .053 | .904 | 385 | .054 | .896 | ||||
| 2.0/0 | 495 | .051 | .904 | 209 | .050 | .908 | 333 | .052 | .905 | ||||
|
| |||||||||||||
| Scenario 3: η = 0 γ ≠ 0 | |||||||||||||
|
| |||||||||||||
| π0 = 0.1 | 1/1.0 | 5627 | .049 | .900 | 1489 | .050 | .899 | 427 | .052 | .905 | |||
| λ0 = 0.1 | 1/1.1 | 4306 | .049 | .904 | 1148 | .050 | .904 | 338 | .047 | .902 | |||
| λ1 = 0.1 | 1/1.2 | 3356 | .047 | .897 | 902 | .052 | .900 | 272 | .052 | .901 | |||
| ta = 1 | 1/1.3 | 2657 | .052 | .903 | 720 | .049 | .897 | 222 | .050 | .899 | |||
| tf = 10 | 1/1.4 | 2133 | .050 | .900 | 583 | .047 | .903 | 184 | .051 | .908 | |||
| 1/1.5 | 1734 | .053 | .895 | 478 | .050 | .902 | 154 | .049 | .902 | ||||
| 1/1.6 | 1425 | .046 | .908 | 396 | .050 | .898 | 131 | .051 | .911 | ||||
To investigate the relative efficiency of the weighted log-rank test vs. the standard log-rank test, we consider a class of Harrington-Fleming weight functions , where is the left-continues version of the Kaplan-Meier estimate computed from the pooled sample of two groups [12]. Sample sizes were calculated for both weighted log-rank test and standard log-rank test under same scenarios as above. The results (Table 2) showed: a) the weighted log-rank test was not as efficient as the standard log-rank test (with weight function ) for scenarios 1 and 2; b) the weighted log-rank test with weight function was more efficient than the standard log-rank test for scenario 3. In fact, the weight function is the optimal weight function in scenario 3 as shown by Gray and Tsiatis [13] and Wu [14].
Table 2.
Comparison efficiency of the weighted log-rank test versus the standard log-rank test based on calculated sample sizes under the exponential cure model with a nominal type I error of 0.05 and power of 90% (two-sided test, uniform accrual and equal allocation).
| Weight function | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| Design | δ−1/γ |
|
|
|
|
|
|
||||||
| Scenario 1: η ≠ 0 γ ≠ 0 | |||||||||||||
|
| |||||||||||||
| π0 = 0.1 | 1.2/0.4 | 1385 | 1810 | 1460 | 1620 | 1446 | 2101 | ||||||
| λ0 = 0.1 | 1.3/0.5 | 734 | 966 | 769 | 866 | 765 | 1115 | ||||||
| ta = 1 | 1.4/0.6 | 469 | 617 | 490 | 556 | 487 | 708 | ||||||
| tf = 10 | 1.5/0.7 | 333 | 438 | 347 | 395 | 345 | 499 | ||||||
| 1.6/0.8 | 253 | 332 | 264 | 301 | 261 | 376 | |||||||
| 1.7/0.9 | 202 | 263 | 210 | 240 | 207 | 296 | |||||||
| 1.8/1.0 | 166 | 216 | 173 | 197 | 170 | 242 | |||||||
|
| |||||||||||||
| Scenario 2: η ≠ 0 γ = 0 | |||||||||||||
|
| |||||||||||||
| π0 = 0.1 | 1.4/0.0 | 801 | 1130 | 819 | 990 | 858 | 1337 | ||||||
| λ0 = 0.1 | 1.5/0.0 | 562 | 788 | 574 | 694 | 598 | 925 | ||||||
| ta = 1 | 1.6/0.0 | 425 | 594 | 435 | 525 | 451 | 692 | ||||||
| tf = 10 | 1.7/0.0 | 340 | 472 | 348 | 419 | 359 | 547 | ||||||
| 1.8/0.0 | 282 | 389 | 288 | 347 | 296 | 449 | |||||||
| 1.9/0.0 | 240 | 330 | 246 | 295 | 251 | 379 | |||||||
| 2.0/0.0 | 209 | 287 | 214 | 257 | 218 | 327 | |||||||
|
| |||||||||||||
| Scenario 3: η = 0 γ ≠ 0 | |||||||||||||
|
| |||||||||||||
| π0 = 0.1 | 1.0/1.0 | 1489 | 1554 | 1720 | 1495 | 1414 | 1687 | ||||||
| λ0 = 0.1 | 1.0/1.1 | 1148 | 1202 | 1321 | 1156 | 1092 | 1304 | ||||||
| ta = 1 | 1.0/1.2 | 902 | 948 | 1033 | 910 | 859 | 1027 | ||||||
| tf = 10 | 1.0/1.3 | 720 | 759 | 821 | 728 | 687 | 822 | ||||||
| 1.0/1.4 | 583 | 617 | 662 | 591 | 557 | 667 | |||||||
| 1.0/1.5 | 478 | 507 | 540 | 486 | 457 | 548 | |||||||
| 1.0/1.6 | 396 | 422 | 446 | 404 | 379 | 455 | |||||||
Finally, the accuracy of the proposed formula (7) was compared to Wang’s formula. We calculated the sample sizes and the empirical powers for both formulae (Table 3) under the exponential cure model with three scenarios similar to the Table 1 for a relative longer follow-up time (similar results were obtained for a relative shorter follow-up time with tf = 4 and results are not presented in the paper). The proposed formula (7) gave the accurate estimation of sample sizes for all the scenarios, while Wang’s formula could either overestimate or underestimate the sample sizes when the hazard ratio δ departures from 1. Thus, the formula derived by Wang et al. failed to provide the correct sample size estimation and should not be used for the trial designs in practice.
Table 3.
Comparison sample sizes calculated the exponential cure model using Wang’s formula and the new formula (6) with a nominal type I error of 0.05 and power of 90%: (two-sided test, uniform accrual and equal allocation).
| Wang | Formula (6) | Wang | Formula (6) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| Design | δ−1/γ | nW | EPW | nX | EPX | Design | δ−1/γ | nW | EPW | nX | EPX |
| Scenario 1: η ≠ 0 γ ≠ 0 | |||||||||||
|
| |||||||||||
| π0 = 0.4 | 1.2/0.4 | 927 | 0.887 | 972 | 0.903 | π0 = 0.1 | 1.2/0.4 | 1377 | 0.893 | 1385 | 0.906 |
| λ0 = 0.1 | 1.3/0.5 | 527 | 0.881 | 570 | 0.906 | λ0 = 0.1 | 1.3/0.5 | 714 | 0.894 | 734 | 0.899 |
| ta = 1 | 1.4/0.6 | 345 | 0.875 | 383 | 0.903 | ta = 1 | 1.4/0.6 | 448 | 0.884 | 469 | 0.899 |
| tf = 10 | 1.5/0.7 | 246 | 0.857 | 284 | 0.903 | tf = 10 | 1.5/0.7 | 313 | 0.878 | 333 | 0.904 |
| 1.6/0.8 | 186 | 0.853 | 221 | 0.904 | 1.6/0.8 | 234 | 0.886 | 253 | 0.903 | ||
| 1.7/0.9 | 147 | 0.849 | 180 | 0.908 | 1.7/0.9 | 184 | 0.877 | 202 | 0.900 | ||
| 1.8/1.0 | 119 | 0.834 | 152 | 0.912 | 1.8/1.0 | 150 | 0.870 | 166 | 0.902 | ||
|
| |||||||||||
| Scenario 2: η ≠ 0 γ = 0 | |||||||||||
|
| |||||||||||
| π0 = 0.4 | 1.4/0.0 | 1657 | 0.895 | 1668 | 0.902 | π0 = 0.1 | 1.4/0.0 | 745 | 0.885 | 801 | 0.904 |
| λ0 = 0.1 | 1.5/0.0 | 1141 | 0.903 | 1156 | 0.904 | λ0 = 0.1 | 1.5/0.0 | 513 | 0.875 | 562 | 0.900 |
| ta = 1 | 1.6/0.0 | 850 | 0.892 | 867 | 0.904 | ta = 1 | 1.6/0.0 | 382 | 0.871 | 425 | 0.903 |
| tf = 10 | 1.7/0.0 | 667 | 0.894 | 686 | 0.904 | tf = 10 | 1.7/0.0 | 300 | 0.869 | 340 | 0.904 |
| 1.8/0.0 | 543 | 0.888 | 565 | 0.906 | 1.8/0.0 | 245 | 0.853 | 282 | 0.901 | ||
| 1.9/0.0 | 456 | 0.890 | 478 | 0.909 | 1.9/0.0 | 205 | 0.854 | 240 | 0.900 | ||
| 2.0/0.0 | 391 | 0.889 | 414 | 0.910 | 2.0/0.0 | 176 | 0.855 | 209 | 0.907 | ||
|
| |||||||||||
| Scenario 3: η = 0 γ ≠ 0 | |||||||||||
|
| |||||||||||
| π0 = 0.4 | 1.0/1.0 | 420 | 0.941 | 360 | 0.906 | π0 = 0.3 | 1.0/1.0 | 255 | 0.952 | 209 | 0.904 |
| λ0 = 0.1 | 1.0/1.1 | 347 | 0.943 | 297 | 0.902 | λ0 = 0.3 | 1.0/1.1 | 211 | 0.953 | 171 | 0.904 |
| ta = 1 | 1.0/1.2 | 292 | 0.942 | 250 | 0.905 | ta = 1 | 1.0/1.2 | 177 | 0.948 | 143 | 0.905 |
| tf = 10 | 1.0/1.3 | 249 | 0.942 | 214 | 0.910 | tf = 10 | 1.0/1.3 | 151 | 0.959 | 121 | 0.908 |
| 1.0/1.4 | 214 | 0.944 | 186 | 0.910 | 1.0/1.4 | 130 | 0.956 | 105 | 0.910 | ||
| 1.0/1.5 | 187 | 0.945 | 164 | 0.912 | 1.0/1.5 | 114 | 0.956 | 91 | 0.910 | ||
| 1.0/1.6 | 164 | 0.940 | 146 | 0.912 | 1.0/1.6 | 100 | 0.954 | 81 | 0.908 | ||
abbreviation nW and EPW : sample size and empirical power calculated by formula derived by Wang at al.; abbreviation nX and EPX: sample size and empirical power calculated by formula (6).
5 Example
We illustrate the application of the proposed sample size formula with the use of data from the Eastern Cooperative Oncology Group (ECOG) trial e1684 [7]. The ECOG trial e1684 was a randomized two-arm phase III trial comparing an arm treated with high-dose interferon alpha-2b with an observation arm. The primary endpoint was relapse-free survival (RFS), with RFS defined as the time interval from the date of randomization to the date of disease relapse or death. The trial was originally designed to detect a 50% improvement in median RFS from 1.5 to 2.25 years, with an accrual period of 4 years and a follow-up period of 3 years. A sample size of 286 patients was considered, which was expected to yield a power of 83% based on the standard PH model [9].
Let us now design a randomized two-arm phase III trial similar to the ECOG trial by using the treatment arm of the ECOG trial as the preliminary data for the control arm of the new trial design. As shown by Kaplan-Meier estimate of this survival data in Fig. 1A, the relapse events had occurred almost within 4.3 years after the start of treatment, and approximately 35% of patients were cured (in the sense that they survived throughout the study period). We fitted survival data of all patients with the Weibull distribution, as shown in Fig. 1B. The fitted parametric survival model obviously did not match well the survival data, especially as the parametric model failed to present the later plateau of the empirical survival curve. The Kaplan-Meier estimate in Fig. 1A suggests that the patient cohort consisted of two parts: patients who would probably experience relapse within 4.3 years after the start of treatment and patients who would be cured in the sense that they would relapse-free for 7 years after the start of treatment. Thus, a cure model is appropriate. The SAS macro PSPMCM was applied to this data to fit the treatment arm data under the Weibull cure model, with an estimated shape parameter κ = 1.018, scale parameter λ = 0.836, and cure rate of 35%. Then, we have the Weibull cure model for the control group which matches well with the Kaplan-Meier survival curve, where π0 = 0.35 and S0(t) = exp(−0.836t1.018) (Fig. 1C and 1D).
Figure 1. KM curves (step function) and fitted Weibull models (solid curve) for the treatment arm of ECOG trial e1684 data.
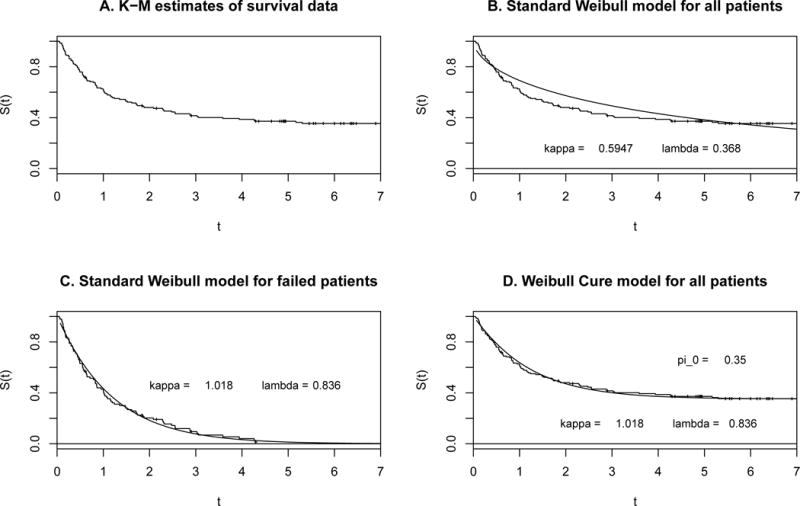
Fig. 1A: KM curve for all patients; Fig. 1B: KM curve and Weibull model for all patients; Fig. 1C: KM curve and Weibull model for failed patients; Fig. 1D: KM curve and Weibull cure model for all patients.
For the trial design under the PH cure model, assume the alternatives for the three scenarios are as follows: 1) π1 > π0 and δ < 1: to detect a hazard ratio δ = 1.5−1 (δ = eη) and a 10% increase in cure rate (i.e., π1 = 0.45); 2) π1 = π0 and δ < 1: to detect a hazard ratio δ = 2.0−1 and identical 35% cure rates for the two groups; and 3) π1 > π0 and δ = 1: to detect a 15% increase in cure rate (i.e., π1 = 0.50) and keep the hazard rates the same for the two groups (i.e., δ = 1). With equal allocation (p = 0.5) and uniform accrual with ta = 4, tf = 3, η = log(δ), and , we can calculate the sample sizes by using the sample size formula (7). To achieve a power of 90% with a two-sided type I error of 0.05 under the Weibull PH cure model, sample sizes of 468, 762, and 505 are required for scenarios 1, 2, and 3, respectively, and corresponding empirical powers based on 10,000 simulation runs are 0.902, 0.903 and 0.904, respectively. The corresponding sample sizes calculated by Wang’s formula are 473, 1135, and 557 for scenarios 1, 2, and 3, respectively, and corresponding empirical powers based on 10,000 simulation runs are 0.902, 0.977 and 0.926, respectively. The R code for the sample size calculation is given in Appendix.
6 Conclusion
In this paper, we have derived a new sample size formula for the log-rank test under the PH cure model. The simulations have shown that the proposed formula provides an accurate estimation of sample size under the PH cure models and corrects the sample size calculation proposed by Wang et al. [9]. The efficiency of a class of Harrington-Fleming weighted log-rank test is explored. For both scenarios 1 and 2, the weighted log-rank test may not be as efficient as the standard log-rank test. However, the weighted log-rank test with weight function is more efficient than the standard log-rank test for the scenario 3. It is interested to investigate the optimal weight function for the scenarios 2 and 3. This will be a future research topic.
Acknowledgments
This work was supported in part by National Cancer Institute support grant CA21765 and ALSAC.
Appendix: R code for the sample size calculations of the example
Size=function(kappa, lambda0, pi0, pi1, p, ta, tf, HR, alpha, power)
{z0=qnorm(1−alpha/2); z1=qnorm(power)
tau=ta+tf; delta=1/HR
gamma=log(pi1/(1−pi1))−log(pi0/(1−pi0))
q=function(t){num=pi0*exp(gamma)+(1−pi0)*S0(t)^delta
den=(pi0*exp(gamma)+(1−pi0))*(pi0+(1−pi0)*S0(t))
ans=num/den; return(ans)}
S0=function(t){exp(−lambda0*t^kappa)}
h0=function(t){kappa*lambda0*t^(kappa−1)}
G=function(t){1−punif(t, tf, tau)}
q1=function(t){den=(p+(1−p)*q(t))^2
num=q(t)*(p*(1−pi0+pi0*exp(gamma))+(1−p)*delta*S0(t)^(delta−1))
ans=num/den; return(ans)}
q2=function(t){den=p+(1−p)*q(t)
num=q(t)*(delta*S0(t)^(delta−1)/(q(t)*(1−pi0+pi0*exp(gamma)))−1)
ans=num/den; return(ans)}
f1=function(t){q1(t)*G(t)*S0(t)*h0(t)}
f2=function(t){q2(t)*G(t)*S0(t)*h0(t)}
A=integrate(f1, 0, tau)$value
B=integrate(f2, 0, tau)$value
nX=(z0+z1)^2*A/(p*(1−p)*(1−pi0)*(1−pi0+pi0*exp(gamma))*B^2)
m=function(t){pi0*(gamma−log(delta)*log(S0(t)))/(pi0+(1−pi0)*S0(t))−log(delta)}
g1=function(t){G(t)*S0(t)*h0(t)}
g2=function(t){m(t)*G(t)*S0(t)*h0(t)}
C=integrate(g1, 0, tau)$value
D=integrate(g2, 0, tau)$value
nW=(z0+z1)^2*C/(p*(1−p)*(1−pi0)*D^2)
ans=ceiling(c(nX, nW)); return(ans)}
Size(kappa=1.018,lambda0=0.836,pi0=0.35,pi1=0.45,p=0.5,ta=4,tf=3, HR=1.5,alpha=0.05,power=0.90)
468 473
Size(kappa=1.018,lambda0=0.836,pi0=0.35,pi1=0.35,p=0.5,ta=4,tf=3, HR=2.0,alpha=0.05,power=0.90)
762 1135
Size(kappa=1.018,lambda0=0.836,pi0=0.35,pi1=0.50,p=0.5,ta=4,tf=3, HR=1.0,alpha=0.05,power=0.90)
505 557
References
- 1.Ewell M, Ibrahim JG. The large sample distribution of the weighted log rank statistic under general local alternatives. Lifetime Data Analysis. 1997;3:5–12. doi: 10.1023/a:1009690200504. [DOI] [PubMed] [Google Scholar]
- 2.Farewell VT. The use of mixture models for the analysis of survival data with long-term survivors. Biometrics. 1982;38:1041–1046. [PubMed] [Google Scholar]
- 3.Peng Y, Dear KBG, Denham JW. A generalized F mixture model for cure rate estimation. Statistics in Medicine. 1998;17:813–830. doi: 10.1002/(sici)1097-0258(19980430)17:8<813::aid-sim775>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 4.Kuk AYC, Chen CH. A mixture model combining logistic regression with proportional hazards regression. Biometrika. 1992;79:531–541. [Google Scholar]
- 5.Peng Y, Dear KBG. A nonparametric mixture model for cure rate estimation. Biometrics. 2000;56:237–243. doi: 10.1111/j.0006-341x.2000.00237.x. [DOI] [PubMed] [Google Scholar]
- 6.Sy JP, Taylor JMG. Estimation in a Cox proportional hazards cure model. Biometrics. 2000;56:227–236. doi: 10.1111/j.0006-341x.2000.00227.x. [DOI] [PubMed] [Google Scholar]
- 7.Corbiere F, Joly P. A SAS macro for parametric and semiparametric mixture cure models. Computer Methods and Programs in Biomedicine. 2007;85:173–180. doi: 10.1016/j.cmpb.2006.10.008. [DOI] [PubMed] [Google Scholar]
- 8.Halpern J, Brown BW. Designing clinical trials with arbitrary specification of survival functions and for the log rank or generalized Wilcoxon test. Controlled Clinical Trials. 1987;8:177–189. doi: 10.1016/0197-2456(87)90043-2. [DOI] [PubMed] [Google Scholar]
- 9.Wang S, Zhang J, Lu W. Sample size calculation for the proportional hazards cure model. Statistics in Medicine. 2012;31:3959–3971. doi: 10.1002/sim.5465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wu J. Sample size calculation for the proportional hazards cure model, Letter to the editor. Statistics in Medicine. 2015 doi: 10.1002/sim.5465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Xiong X. A precise approach for sequential test design on comparing survival distributions by log-rank test. 2014 Un-published Manuscript. [Google Scholar]
- 12.Harrington DP, Fleming TR. A class of rank test procedures for censored survival data. Biometrika. 1982;69:553–566. [Google Scholar]
- 13.Gray RJ, Tsiatis AA. A linear rank test for use when the main interest is in differences in cure rates. Biometrics. 1989;45:899–904. [PubMed] [Google Scholar]
- 14.Wu J. Sample size calculation for testing differences between cure rates with the optimal log-rank test. Journal of Biopharmaceutical Statistics. 2016 Feb; doi: 10.1080/10543406.2016.1148711. [DOI] [PMC free article] [PubMed] [Google Scholar]


