Abstract
The tendon-to-bone attachment (enthesis) is a complex hierarchical tissue that connects stiff bone to compliant tendon. The attachment site at the micrometer scale exhibits gradients in mineral content and collagen orientation, which likely act to minimize stress concentrations. The physiological micromechanics of the attachment thus define resultant performance, but difficulties in sample preparation and mechanical testing at this scale have restricted understanding of structure-mechanical function. Here, microscale beams from entheses of wild type mice and mice with mineral defects were prepared using cryo-focused ion beam milling and pulled to failure using a modified atomic force microscopy system. Micromechanical behavior of tendon-to-bone structures, including elastic modulus, strength, resilience, and toughness, were obtained. Results demonstrated considerably higher mechanical performance at the micrometer length scale compared to the millimeter tissue length scale, describing enthesis material properties without the influence of higher order structural effects such as defects. Micromechanical investigation revealed a decrease in strength in entheses with mineral defects. To further examine structure-mechanical function relationships, local deformation behavior along the tendon-to-bone attachment was determined using local image correlation. A high compliance zone near the mineralized gradient of the attachment was clearly identified and highlighted the lack of correlation between mineral distribution and strain on the low-mineral end of the attachment. This compliant region is proposed to act as an energy absorbing component, limiting catastrophic failure within the tendon-to-bone attachment through higher local deformation. This understanding of tendon-to-bone micromechanics demonstrates the critical role of micrometer scale features in the mechanics of the tissue.
Keywords: Enthesis, Micromechanics, Image correlation, Tensile testing, Gradient, AFM
1. Introduction
The enthesis is a specialized tissue at the tendon-to-bone interface that connects two mechanically dissimilar materials: tendon, a compliant proteinaceous material with high toughness, and bone, a hard mineralized tissue with a significantly higher modulus. Dissimilar interfaces such as the tendon-to-bone attachment are prone to stress concentrations that increase failure risk. When two materials with differing mechanical properties and a sharp interface are exposed to external applied loads, they will exhibit non-uniform deformation. The mismatch in the deformation between the two phases will cause a stress singularity to arise locally increasing the risk of crack propagation and failure. Certain materials, such as metals, can use plasticity to minimize stress concentrations; however, the unique properties of biological tissues make then especially prone to interfacial singularities [1]. To alleviate these stress concentrations and allow for effective stress transfer, the healthy enthesis exhibits a complex hierarchical structure across multiple length scales. At the tissue level, tendons attach to bone with a splayed morphology and a large attachment area to minimize stress at the interface [2,3]. At a lower micrometer scale, the tissue is graded in composition and organization, with gradients in mineral content, collagen orientation, and protein type across the interface [4–7]. The presence of a toughening compliant zone between the tendon and bone has been predicted at this scale, but never clearly measured experimentally [5]. At the nanometer scale, the mineral organization relative to the collagen, whether intrafibrillar or extrafibrillar, varies along the interface, theoretically shifting the load-sharing mechanism among the components [8]. Compositional and structural features of the tendon-to-bone attachment at the micrometer scale are relatively well understood, but corresponding mechanics, especially in physiologically relevant tension loading, is lacking.
Modelling efforts have suggested that the gradient structures at the tendon-to-bone attachment result in unique mechanical behaviors, such as the presence of a region of increased compliance near the interfacial region [5]. However, due to the difficulty in preparing small, mechanically testable samples of the attachment containing both mineralized and unmineralized tissue, information on the attachment mechanics at the micrometer scale during physiologically relevant loading conditions have been impossible to obtain. Recently developed techniques using sample preparation via cryo-focused ion beam (FIB) and mechanical testing using a custom atomic force microscopy (AFM) system provide a unique opportunity to prepare and test micrometer-scale biological samples. Such a technique has been used previously to examine homogeneous mineralized tissues such as bones and teeth [9,10] and compliant materials such as polymers [11]. The current study represents the first time that this technique has been used on a heterogeneous biological tissue to examine deformation at the micrometer length scale. The goal is to obtain information about the micrometer-scale contributions to attachment deformation during loading. Specifically, the objective is to determine how the micrometer gradient structure at the attachment site participates in dissipation of applied forces and stress concentrations in healthy and pathological tissues. This understanding will create a foundation of knowledge for creating graded scaffolds on the micrometer scale for future treatment and repair of attachment sites [12–16].
2. Methods
2.1. Animals
The use of animals and procedures for this study were approved by the animal studies committee at Washington University (Protocol Number: 20100091). Female CD-1 wild type (WT) mice (Charles River lab. Int., Inc.) 14–18 weeks of age were used as healthy controls. Animals with mineral defects at the enthesis were used as a comparison group (KO group); specifically, hedgehog (Hh) signaling was deleted in scleraxis expressing cells [17–19] and samples were prepared from 8 week old mice. Hh signaling has been shown to play a role in attachment site development and maturation [19]. The ScxCre;Smofl/fl mice exhibit conditional knockout of smoothened, a molecule required for Hh responsiveness, at the tendon-to-bone attachment. These mice exhibited impaired enthesis mineralization and compromised tissue-level mechanics [19]. Three WT mice and three KO mice were used in the current study.
2.2. Preparation of micrometer-scale enthesis beams
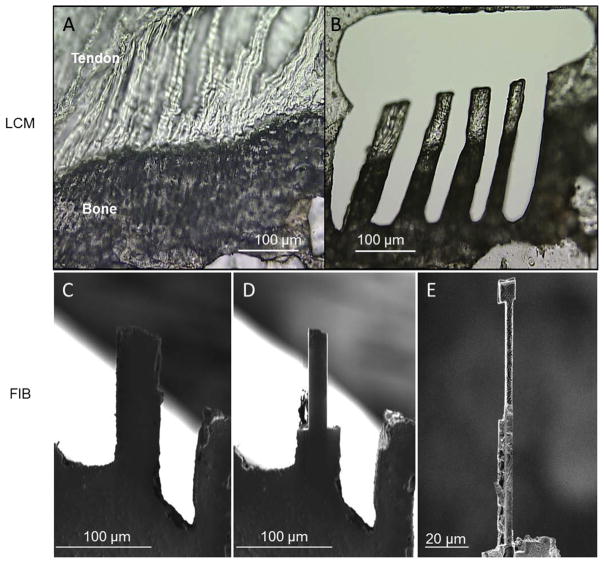
Right and left supraspinatus tendon-humeral head complexes were dissected from each animal immediately after sacrifice. Care was taken to maintain the integrity of the supraspinatus tendon-to-humeral head attachment site. This complex, which includes the tendon enthesis, was mounted in Optimal Cutting Temperature (OCT) compound and frozen at −80 °C. The OCT-embedded samples were cut into 20 μm thick sections and deposited onto Laser Capture Microscopy (LCM) tape (Fig. 1A). Slides were maintained at −80 °C after sectioning. The frozen sections were then thawed and imaged under an optical microscope to identify the tendon-to-bone attachment. Beams were cut using the LCM laser to ensure that the long axis of the beams was parallel to the collagen fibrils and spanned the mineralized and unmineralized fibrocartilage (Fig. 1B). This preparation resulted in beams with dimensions of 150–200 μm in length and ~30 μm in width. In order to facilitate access to the beams for subsequent FIB cutting, a relatively large hole (>1.5 mm) was cut around the beams to allow manipulation of the tendon-to-bone attachment section. Two to four beams spanning the mineralized and unmineralized fibrocartilage for each tendon-to-bone attachment section were prepared, depending on the dimension and quality of the section (Fig. 1B). Samples were subsequently refrozen at −80 °C. The beams prepared using LCM were noted as being irregular in width, as shown in Fig. 1B, and thus required further FIB preparation to produce regular beam structures. Regular beam structures were deemed necessary to avoid localized stress concentrations produced at irregular sample edges.
Fig. 1.
Murine tendon-to-bone attachment sites were cut and milled into beams measuring approximately 60 μm long and 4.5 by 4.5 μm in diameter. (A) Dissected supraspinatus-to-humeral head complexes were fresh frozen and sectioned into 20–30 μm thick slices. (B) LCM was used to cut large beams, ~250 μm by 50 μm by 20–30 μm, in the fibrocartilaginous region of the attachment where there is a gradient in mineralization. (C–E) The LCM cut beams were further milled down to the final small beams via cryo-FIB.
FIB fabrication of tendon enthesis beam samples was performed under cryogenic conditions using the FIB-SEM dual-beam system (Quanta 3D, FEI Company, USA/EU). Sample beams were mounted onto the sample stage of the FIB-SEM with a 60° pre-tilt using OCT solution such that the beams extended beyond the edge of the pre-tilt stage and perpendicular to the direction of the tilt. The cryo-stage with sample was then brought to cryo-temperatures by dipping into liquid nitrogen slush. The cryo-stage was continuously rotated in the slush for 2 min to reduce the stage temperature to −130 °C. The sample was then inserted into the pre-chamber of the FIB-SEM and brought to −90 °C to allow ice sublimation from the surface of the sample. Argon was then pumped into the chamber and a thin layer of platinum/gold was deposited on the sample through plasma sputtering to limit charging effects. Once coated, the sample was further inserted into the main cryo-chamber for FIB processing.
Regular beam structures were prepared by FIB by first positioning the sample such that the top surface of the LCM-fabricated beams was perpendicular to the direction of the ion beam. In this orientation, the left and right sides of the beam could be removed with the ion beam at a voltage of 16 kV and current of 3 nA for initial milling (Fig. 1C–D). A lower voltage (16 kV) was applied here compared with the voltage (30 kV) applied for previous work preparing bone in order to minimize potential FIB damage to this softer tissue sample [10]. The width of the beam was subsequently reduced to ~4 μm by the action of the FIB removing sample volume (Fig. 1D). The sample was subsequently removed from the cryo-chamber and the stage rotated 90°. The sample was then reinserted into the cryo-chamber and ice sublimated, as described above. Deposition of platinum/gold coating onto the sample was avoided in this second configuration such that the final sample would not contain any metal deposits. The side surface of the beam was positioned perpendicular to the direction of FIB to remove the top and bottom parts of the beam. This step was carried out in the same manner as described when dealing with the left and right sides except that the beam was given a dumbbell shape. During this process, the LCM tape (attached to the bottom of the beam) and the platinum/gold coating were removed. After this step, the gauge section of the beam had a resultant square cross-section of ~4 × 4 μm2 with wider sections at either end to facilitate gripping (Fig. 1E). The samples were then removed from the SEM chamber for AFM mechanical testing. A cross-sectional area of ~16 μm2 was selected such that the samples could be loaded to failure at the loads attainable in the AFM system (10 mN) while maintaining the integrity of the attachment structure.
2.3. Compositional study using X-ray energy dispersive spectroscopy
X-ray energy dispersive spectroscopy (EDS) microanalysis within an SEM (Inspect SEM, FEI Company, EU/USA) was used to investigate the proportion of the mineralized and unmineralized tissue in each FIB-fabricated tendon enthesis beam. EDS measurements were made at eleven equally spaced points along the length of each beam in order to determine the calcium content along the beam (Fig. 2). Interaction volume depths calculated using [20] indicate that the interaction depths are larger than the beam thickness and that as a result the EDS measurements provide accurate average values of the beam composition as a function of position while maintaining the beam integrity.
Fig. 2.
Micrometer scale beams of attachment tissue exhibiting a gradient in mineral content were attached to a modified AFM system. The mineralized end of the beam was attached to a motorized stage. The unmineralized end of the beam was attached to a blunted AFM tip with electron beam radiation-cured glue. The AFM tip was then retracted to apply a tensile load on the beam to failure.
2.4. AFM tensile testing
Mechanical testing of the tendon enthesis beams was conducted using AFM. Samples taken from the FIB preparation were rehydrated using the same methodology applied to bone samples in previous work [9]. Briefly, the FIB-sectioned beam samples were placed in a water vapor environment to replace any hydration lost during the beam milling process. After hydration, the sample complex was attached with carbon tape to the sample stage of an in situ AFM system situated within the FIB-SEM, as described previously [21,22]. The sample was attached such that the FIB-fabricated beams extended beyond the edge of the sample stage in order to perform tensile tests. A high-vacuum compatible electron beam-cured adhesive, SEMGLU (Kleindiek Nanotechnik GmbH, Germany), was used to attach the free end of the beam to the AFM tip in order to perform the tensile test. A small bead of SEMGLU was mounted on the tip of a thin wire placed besides and parallel to the beam. A FIB-flattened AFM tip with spring constant of 40 N·m−1 was placed 30 μm ahead of the initial position so that the AFM tip could retract backwards for tensile testing once attached firmly to the sample. The sample stage was then moved towards the AFM tip such that the apex of the tip contacted and picked up a relatively small volume of glue. The stage was then moved to bring the free end of the FIB-fabricated beam into contact with the glue on the AFM tip. All the steps were performed under an electron current of 93 pA to prevent the glue from hardening. The electron beam was then focused onto the glue drop under a high electron current of 1.5 nA for approximately 10 min to ensure solidification and a strong bond between the tip and the beam. In this way, the FIB-fabricated tendon enthesis beam was firmly attached to the AFM tip prior to the AFM tensile test (Fig. 2). Uniaxial tensile testing to failure of the samples was then performed by retracting the AFM tip in a quasi-static manner at a loading rate of 0.1 μm·s−1 while imaging using the secondary electron detection mode of the SEM.
2.5. Modelling the mechanical behavior of the composite beam
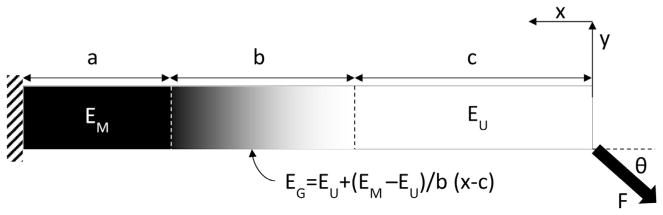
A model was developed to describe the mechanical behavior of the tendon enthesis beams. The model aimed to account for the variability in the composition of the beams and describe the average modulus of an idealized beam with varying amounts of mineralized, graded, and unmineralized tissue (Fig. 3). A force, F, was applied to the end of a beam (length L, cross-sectional area A) at an angle θ. The angle for each beam was determined from images of the mechanical tests nominally taken in the plane including the length and thickness of the beam (xy-plane). The angle θ in the xy-plane is expected to be the maximum off-axis angle due to difficulty in manually adjusting the beams in this direction and therefore represent the bulk contribution to off-axis loading. The axis, x, was defined along the length of the beam, with a value of 0 at the free end. The beam was composed of three sections: mineralized, graded, and unmineralized, with lengths of a, b, and c, respectively (note that a + b + c = L). The corresponding moduli of these sections were defined as EM, EG, and EU, respectively. The value of EG was determined as a linear interpolation between the mineralized and unmineralized moduli. The average modulus, E, can then be determined by satisfying the boundary and continuity conditions to be:
| (1) |
as shown in Appendix A.
Fig. 3.
A beam bending model was developed to determine the effect of changes in composition on the beam modulus. The beam was modelled as a three phase composite in series. The modulus of the gradient region is defined as a linear extrapolation between the mineralized and unmineralized regions (EG(x)). Values for the mineralized (EM) and unmineralized (EU) moduli were optimized to minimize error between the calculated and experimental beam moduli.
2.6. Local strain analysis
Experimental determination of the deformation field within tendon-to-bone attachments is instructive in relating mechanical behavior to composition. Local strains along the length of the specimen were calculated by considering the prepared beams as a one-dimensional manifold in two-dimensional space. Five locations along the length of each specimen were chosen based on identification of distinct features that were tracked using an image registration algorithm. For each successive frame, the regions were tracked using a Newton-Raphson-like method that computes pixel displacements [23]. The manifold was broken into individual segments bounded by a tracked region on either side for 1-dimensional strain calculations. Segment lengths were calculated by the Euclidian distance formula using pixel displacements of the tracked regions. Lagrangian strains were determined by comparing the lengths of the segments at the start of the test to the length of the segment at each successive frame, resulting in a single measure of Lagrangian strain for each segment at each frame. Aberrations and distortions caused by the SEM were determined to minimally affect the image at the energy, magnification, and raster rate used here and were therefore ignored.
2.7. Statistics
For all outcomes, the values from multiple beams prepared from a particular mouse were averaged for each mouse: WT1, WT2, WT3, KO1, KO2, KO3. Values reported for the WT and KO mice are averages of the values measured for each mouse. The reported errors are the standard deviations measured between the mice, not the individual beams. Student’s t-tests were performed (independent samples with equal variance) to compare WT to KO. Significance was defined as p < 0.05.
3. Results
3.1. Sample preparation
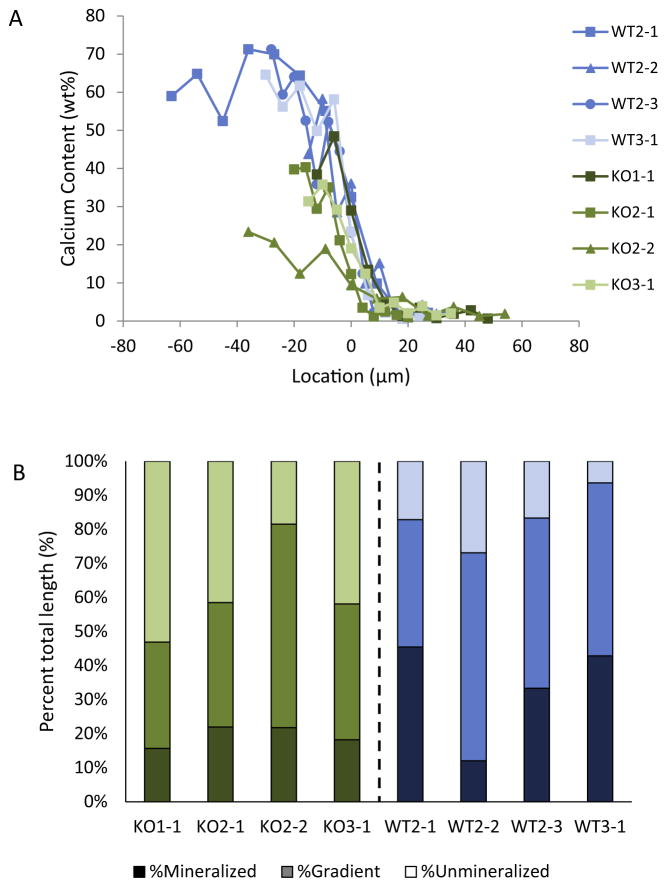
A total of 11 tendon enthesis beams were successfully prepared and tested, consisting of 7 samples from 3 KO mice and 4 samples from 3 WT mice. The beam lengths spanned from 41 to 99 μm, with an average of 64.8 ± 6.4 μm (Fig. 4A). The difference in the length of the beams was not significantly different when comparing WT and KO samples. The cross-sectional area of the beams ranged from 7.2 to 45.2 μm2, with an average of 23.5 ± 10.1 μm2. Beam cross-sectional areas were not significantly different between WT and KO samples.
Fig. 4.
The length and composition of the beams varied between beams. (A) Plot of calcium content as a function of position along the beams, with zero set as the center of the gradient region. The length of the beams ranged from 41 to 99 μm. (B) The length of the mineralized, unmineralized, and graded regions were determined from the plot in A and are shown normalized to beam length. Dark shades represent mineralized, medium shades represent graded, and light shades represent unmineralized. These variations in the amount of each phase between beams are expected to have mechanical consequences.
One goal when preparing beams was to obtain equivalent lengths of unmineralized, graded, and mineralized regions in each beam. However, due to variations in the samples themselves and difficulties in preparing the beams, the relative amounts of each tissue type varied from sample to sample (Fig. 4B). The average gradient length in the beams was 27.9 ± 8.5 μm, representing 43.9 ± 8.3% of the total beam length. The gradient length did not differ significantly between groups. Similarly, the amount of unmineralized tissue did not vary between WT and KO samples. However, the KO samples exhibited shorter lengths of mineralized tissue than for the WT samples, as expected based on previous results [19].
3.2. Micromechanical testing
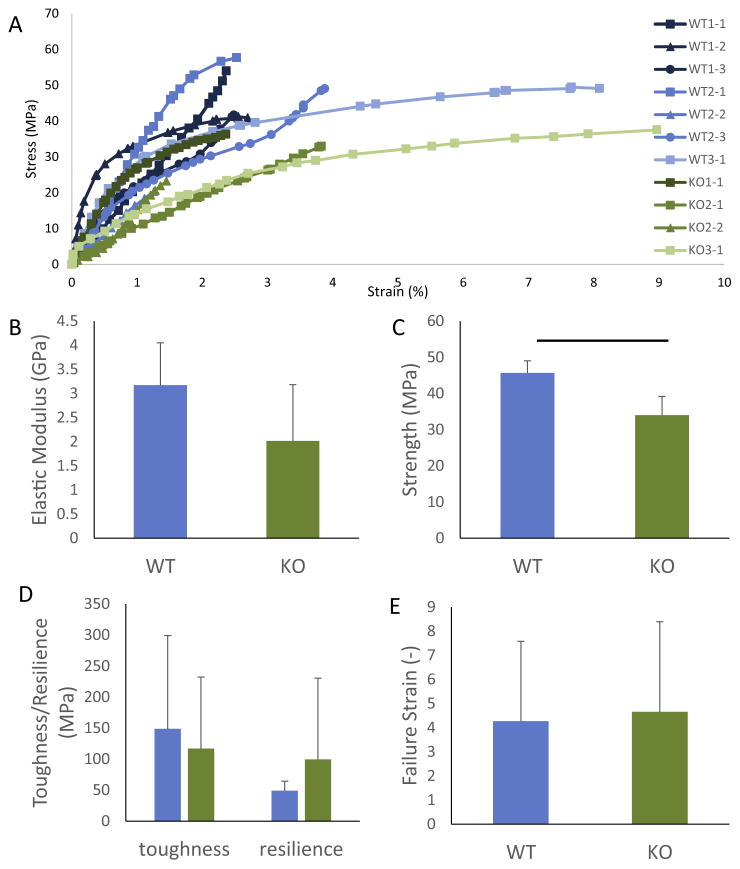
Fig. 5A shows the stress-strain curves for all eleven tensile tests. The average strength of the samples was 45.7 ± 3.4 and 34.0 ± 5.1 MPa for the WT and KO, respectively (Fig. 5B). The strength of the WT samples was significantly higher than that of the KO samples. Visual inspection of videos of the samples during loading indicates that none of the samples failed at the grip sites. All failures occurred between 30 and 98% of the length of the beam, as measured from the mineralized end of the beam, and with mean and median values around 70% of the length. The average beam moduli determined from the slopes of the stress-strain curves in the elastic regimes were 3.1 ± 0.9 and 2.0 ± 1.2 GPa for the WT and KO samples, respectively (Fig. 5C). The moduli were not statistically different between the WT and KO samples (p = 0.24), although the comparison was likely underpowered based on the small sample size. Beam stress-strain behavior beyond the elastic regime varied, as indicated in Fig. 5. Specifically, some samples displayed large plastic deformations up to 9% (e.g., WT3-1 and KO3-1) while other beams displayed linear elastic behavior with brittle failure (e.g., KO2-2 and WT2-2). The average strain at failure was 4.3 ± 3.3 and 4.7 ± 3.7% for WT and KO, respectively (Fig 5D). The average toughness and resilience for the WT samples were 148.8 ± 150 and 49.1 ± 12 MPa. The KO sample had toughness and resilience values of 117.1 ± 115 and 99.5 ± 131.0 MPa, which were not significantly different from those measured for the WT (Fig 5E).
Fig. 5.
(A) Stress vs. strain curves for the 11 micromechanical tests. There was no apparent difference between the WT and KO samples in terms of curve shape. Plots of elastic modulus (B), strength (C), toughness and resilience (D), and failure strain (E) are shown for the WT and KO beams. Strength was significantly decreased with in KO samples compared to WT samples. There was no significant change in modulus, toughness, resilience, or failure strain between the WT and KO samples.
3.3. Modelling
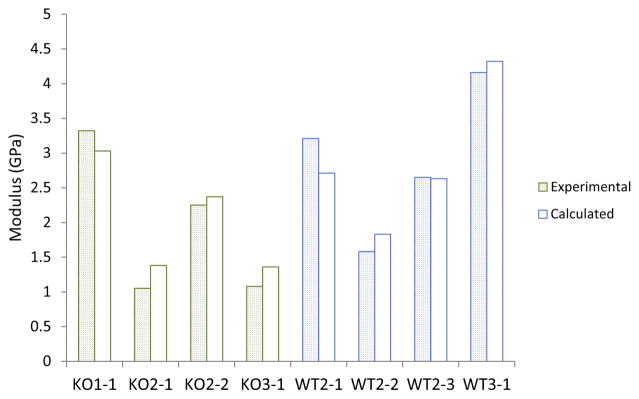
A beam model was developed to determine the relationship between the measured effective moduli and beam compositions, as measured by EDS (Fig. 3 and Appendix A). The model assumed that each beam was a three phase composite (mineralized, gradient, and unmineralized) in series undergoing tensile loading at an angle determined from the experimental images. The moduli for each phase were calculated using a simplex direct search optimization method [24] such that the error between the model and the experimental overall beam modulus was minimized for all samples. This optimization resulted in a modulus of the mineralized region equal to 15.7 GPa and modulus of the unmineralized region equal to 0.66 GPa. Using the optimized phase moduli, the model was able to predict the beam modulus with an error of 14.6% (Fig. 6). The average errors between the calculated and experimental moduli were equal to 9.9 ± 8.5% and 17.7 ± 8.6% for the WT and KO groups, respectively. The relative accuracy of the model suggests that the variations in beam composition account for the variations in the experimentally observed effective moduli.
Fig. 6.
Comparison of the experimental and modelled moduli for each beam. The error was small for all beams, with an average of 14.6%. The errors were not significantly different for the WT and KO beams, suggesting that the mineral defect had little effect on the micromechanics of the tissue.
3.4. Local strains
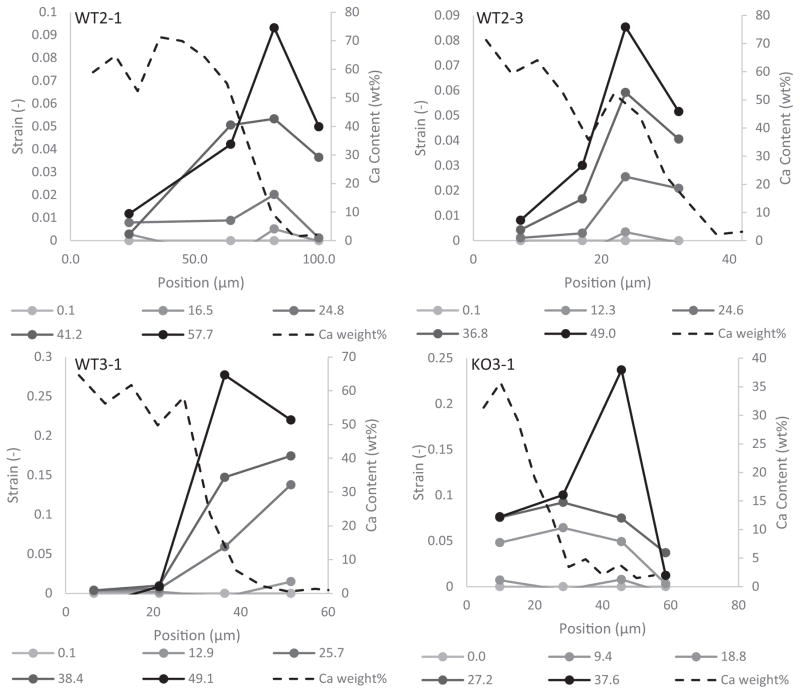
Local strains were measured for 9 out of the 11 beams that were imaged in situ with the SEM during loading. Of these 9 samples, 4 beams (3 WT and 1 KO) exhibited measurable local strains above 7%. Notably, the position of maximum strain was not located in the unmineralized region, but rather consistently appeared in between the mineralized and unmineralized regions in the area associated with the mineral gradient (Fig. 7). Monitoring the exact determination of high compliance locations along the tendon-to-bone gradient was limited by the relatively low spatial resolution of the local strain analysis. However, all samples clearly displayed a high-strain region associated with the transition from mineralized to unmineralized (Fig. 7).
Fig. 7.
Plots of local strain vs. position at multiple stresses (legend) for all of the samples for which local strains were measured. Dotted lines represent the calcium content as a function of position for each sample. The highest strain levels were not localized to the region closest to the tendon but instead within the beam near the gradient region. This indicates the presence of a region of high deformation within the enthesis.
4. Discussion
The tendon-to-bone attachment is a hierarchical tissue exhibiting spatially varying composition and structure across multiple length scales [3,25,26]. Variations at the nanometer, micrometer, and millimeter scale all contribute to the overall tissue mechanics [25,27]. Examining the mechanics of tissues across multiple length scales is critical for elucidating structure-function relationships that lead to an effective attachment between tendon and bone. Previous research has examined tissue mechanics for the tendon enthesis under uniaxial loading [7,19,28–33]. Although a few of these studies used visual markers and image correlation techniques in attempts to identify micrometer-scale local strains during tissue loading [29,32,34,35], no tensile mechanical tests to determine material performance have been directly performed at the micrometer scale. Indentation studies that have examined soft-to-hard tissue attachment sites, which probe the micrometer scale, measured the mechanical properties in the direction perpendicular to the physiological loading direction [36–38]. Useful relative information can be gathered from these experiments; however, the high level of anisotropy in these tissues limits the ability of these studies to obtain physiologically relevant values. The study presented here is the first to successfully conduct tensile micromechanical testing of the tendon enthesis. Using LCM and cryo-FIB, supraspinatus-humeral head complexes were cut into micrometer-sized beams, allowing for micrometer-scale mechanical testing. A better understanding of how local micrometer scale mineral variations lead to changes in mechanical behavior will allow for improved biomaterial design for enhanced tendon-to-bone repair.
The micrometer-sized beams of the tendon-to-bone attachment tissue employed in this study represent the first manufactured specimens of inhomogeneous biological tissue containing both mineralized and unmineralized tissue. The FIB-based technique has been used extensively in the field of nano- and micro-machining in the semiconductor industry, primarily working with silicon and germanium [39]. More recently, such techniques have been used to machine samples of homogeneous biological samples such as bone and limpet teeth to determine their micrometer-scale mechanical properties [9,10]. In the current study, cryo-FIB allowed for the machining of hydrated and inhomogeneous tendon-to-bone attachment samples into micrometer-sized beams while maintaining the overall tissue’s native structure and hydration level (Fig. 1). Since FIB is an inherently destructive process, there was concern that the remaining tissue was damaged during preparation. However, studies on soft materials have shown that FIB damage is localized and has limited effects on the mechanics and composition of the machined material [11]. In addition, a relatively low voltage was employed in the current study to minimize damage to the tissue during preparation. Therefore, this technique was considered to be ideal for the manufacture of hydrated, mechanically unaltered, beams of the attachment site with a controlled geometry at the micrometer scale.
Local strain analyses of the micromechanical tests indicated that local mechanical properties do not correlate directly to mineral content, but that the beams exhibited a region of high deformation near the mineral gradient. Consideration of the change in mineral content as the only contributor to tissue modulus would provide an expected highest modulus in the mineralized region, a decrease in the graded region, and the lowest in the unmineralized region [40]. However, a number of studies have suggested a region of increased deformation within the enthesis compared to the fully unmineralized regions [7,41]. The local strain measurements made on the beams in this study using deformable image correlation confirm the presence of a compliant zone in the graded region (Fig. 7). Observation of this high deformation region at the micrometer scale indicates that the increased compliance is not controlled solely by macro-level features. Although collagen fiber orientation and protein composition were not measured in the current study, the results indirectly support previous theories that the local increase in deformation is caused by changes in collagen orientation or protein composition rather than changes in mineral content [5,7]. Increased applied load and deformation will lead to collagen recruitment and realignment via affine deformation. This inelastic deformation is only reached at high physiological loads where the activation energy is exceeded and the deformation becomes localized to this region. This explains why the region of high deformation often only appears at higher applied loads as in WT3-1 and KO3-1. Variations in the initiation of the high deformation zone may be due to challenges in cutting the beams exactly along the collagen fiber direction. Small off-axis loading of the collagen fibrils may lead to shifts in when localized deformation is activated. The increase in local deformation at the gradient region potentially facilitates energy absorption during loading by dissipating applied stresses within this area of high compliance. Thus, the tissue can avoid failure to maintain function and overall integrity.
The toughness and resilience of the enthesis beams measured using uniaxial loading with a modified AFM system were significantly higher than those found for mechanical testing at the millimeter (i.e. tissue) scale. The beam toughness was approximately 20-fold larger than that reported for the whole tissue [19]. Similarly, the beams also exhibited a 20-fold increase in resilience. In both cases, the beam properties exhibited no difference between the WT and KO samples. The increase in toughness and resilience in the beams compared to the entire enthesis complex supports the idea that the region of increased deformation participates in increased sample toughness. Larger samples may contain structures that increase the failure risk by decreasing the tissue toughness. However, at the micrometer scale the toughness is enhanced due to the deformation zone, thus decreasing the failure risk.
The beam moduli were also dramatically higher than moduli measured for the entire supraspinatus tendon-to-humerus complex [28]. This difference in modulus is expected to be due to scaling effects and the elimination of measurement artefacts such as geometry and tissue interference, which may artificially decrease the stiffness of whole-complex mechanical test. Scaling effects have been shown for many materials, where a decrease in size results in an increase in modulus due to increases in residual strain, surface tension, interfacial effects, or loss of deformation mechanisms such as grain boundary movement [42]. The change in modulus seen here may also be due to factors such as decreased interfibrillar sliding or surface tension effects caused by the decrease in specimen size. Furthermore, the strength of the beams was twice the strength measured in the whole tissue mechanical tests [19,28], consistent with the higher modulus values recorded. This outcome is likely due to a decrease in the number of flaws that would result from smaller specimens, resulting in fewer sites for crack initiation and propagation, as seen in other materials [43,44]. These results suggest that at the micromechanics of the tendon-to-bone attachment exhibit high modulus and strength.
Analysis of the stress-strain plots indicated few statistically significant differences in the mechanical properties of the WT and KO. This suggests that the previously reported enthesis mineralization defects [19] did not dramatically affect the mechanics of the enthesis at the micrometer scale, with the exception of a decrease in strength. This is in contrast to whole tissue mechanics in these mice, which showed significant decreases in most mechanical properties compared to WT mice [19]. Changes in the amount of mineralized fibrocartilage at a higher hierarchical scale is therefore expected to be responsible for the compromised mechanical properties at the tissue level in the KO mice [19], as the material properties at the micrometer scale were relatively unaltered (Fig. 5). However, the sample sizes used in the current study were small compared to the potential effect size of the differences between groups, raising the possibility of an underpowered comparison and a type II statistical error.
A beam bending model was developed to predict the effective structural modulus of the bone-to-tendon beam samples using the variations in mineral content along the beam. Previous work has established the significance of mineral content on the elastic modulus of tissues [40,45–49]. Therefore, mineral content changes along the beam were considered for estimating the modulus. A predicted modulus was calculated for each beam using the relative local levels of mineral, as determined by EDS, the angle of loading determined from the in situ imaging and optimized values for the modulus of the mineralized and unmineralized phase (based on literature values [24,45,46,50–53]). The model successfully predicted the moduli of the beams, suggesting that the observed variations in mineral composition were indeed responsible for the experimentally measured moduli (Fig. 6). The predictive success of the model suggests that, in the elastic regime, the tendon-to-bone attachment can be described as a functionally graded multi-phase composite in series. The optimized values of 15 and 0.66 GPa for the mineralized and unmineralized sections are in agreement with the literature [45,46,52]. The consistency of these values implies that the mineral defects in the KO samples had only minor effects on the microscale mechanics. However, this does not preclude the possibility that larger scale structural changes may be responsible for the mechanical changes reported at the macroscale [19].
5. Conclusions
The tendon enthesis is a complex hierarchical tissue. Although the attachment site exhibits unique compositional and structural features at the micrometer scale, mechanical tests have never been performed at this scale due to difficulty in preparing and testing small samples. Micrometer-scale beams of the tendon enthesis were prepared and tested under uniaxial tension to failure using LCM, cryo-FIB, SEM and a modified AFM system. The samples exhibited elastic moduli and strengths that were dramatically higher than those measured in testing performed on the entire humerus-supraspinatus complex. These mechanical properties are expected to be a result of scaling effects that eliminate certain deformation modes. Beam moduli were found to be dependent on local composition using a beam bending model that incorporated spatial variations in beam composition. Image correlation analysis of local strains indicated the presence of a compliant region near the mineral gradient. This region, whose existence had been previously proposed [7,41], must be caused by micrometer-scale structures such as changes in collagen orientation rather than mineral content or macroscale features. Importantly, by increasing local deformation at the interface between the dissimilar materials, the tissue is able to absorb greater amounts of energy without failing, thus maintaining its integrity.
Statement of Significance.
The tendon-to-bone attachment (enthesis) is a complex hierarchical tissue with features at a numerous scales that dissipate stress concentrations between compliant tendon and stiff bone. At the micrometer scale, the enthesis exhibits gradients in collagen and mineral composition and organization. However, the physiological mechanics of the enthesis at this scale remained unknown due to difficulty in preparing and testing micrometer scale samples. This study is the first to measure the tensile mechanical properties of the enthesis at the micrometer scale. Results demonstrated considerably enhanced mechanical performance at the micrometer length scale compared to the millimeter tissue length scale and identified a high-compliance zone near the mineralized gradient of the attachment. This understanding of tendon-to-bone micromechanics demonstrates the critical role of micrometer scale features in the mechanics of the tissue.
Acknowledgments
The authors would like to acknowledge use of the facilities at The NanoVision Centre, Queen Mary University of London. A.C. Deymier was funded in part by the NSBRI First Award Fellowship NSBRI PD13-0019. Additional funding was provided by NIH U01 EB016422.
Appendix A
To model misalignment between the specimen and loading apparatus, we studied a straight, prismatic Euler-Bernoulli beam of length L, cross-sectional area A, and second moment of the cross-sectional area Izz. The force F was applied in the loading apparatus (XY) reference frame, which was rotated an angle θ from the beam (xy) reference frame (Fig. 3), so that the force applied at the end is:
| (1) |
where î and ĵ are unit vectors in the xy coordinate frame, and Î is a unit vector in the X-direction. The goal is to estimate the average modulus of elasticity of the beam from the relationship between the load F and the measured displacement of the free end.
The displacement vector v⃑ is the sum of the displacement vectors v⃑U of the unmineralized region, v⃑G of the graded region, and v⃑M of the unmineralized region:
| (2) |
As is obvious from Fig. 3, the vertical and horizontal components of the force are:
| (3) |
| (4) |
This force will cause a displacement of the loaded end that is denoted by v1 in the horizontal direction and v2 in the vertical direction. The total displacement, Δ, is equal to
| (5) |
The beam is composed of three sections: mineralized, graded, and unmineralized, with lengths a, b, and c, respectively (where a + b + c = L). The corresponding moduli of these sections are EM, EG, and EU respectively. We assume that the value of EG is a linear interpolation between the mineralized and unmineralized moduli such that:
| (6) |
The displacement in the horizontal direction v1, is the sum of the displacements in the unmineralized, vU, graded, vG, and mineralized, vM, sections of the beam, i.e.,
| (7) |
The horizontal displacements in the unmineralized and mineralized sections are
| (8) |
| (9) |
The horizontal displacement in the graded region can be found as
| (10) |
| (11) |
The total horizontal displacement can be found by substituting Eqs. (8), (9) and (11) into Eq. (7):
| (12) |
or
| (13) |
The vertical displacement of the beam is found below accounting for the boundary conditions and the continuity conditions between the three regions of the beam. In the following, the displacement within the unmineralized region is defined as y1, the displacement in the graded region is defined as y2, and the displacement in the mineralized region is defined as y3. The total vertical displacement of the beam at the free end of the beam, where x = 0 is
| (14) |
The solution must satisfy the following boundary and continuity conditions:
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
The vertical displacements in the unmineralized and mineralized sections are found by integrating the bending equations:
| (21) |
| (22) |
| (23) |
The bending equation for the graded tissue is more complicated involving a variable coefficient:
| (24) |
| (25) |
Let and so that
| (26) |
| (27) |
| (28) |
The vertical displacement can be calculated by solving for k2:
| (29) |
where k2 is found from the system of algebraic Eq. (15) through (20) with respect to the constants of integration k1 through k6. The total displacement can then be calculated by inserting Eqs. (29) and (13) into Eq. (5).
The average modulus of an equivalent homogeneous beam, E, is now available assuming that this beam experiences the same total displacement under the applied force as the actual beam. The total horizontal and vertical displacements in such equivalent beam are
| (30) |
| (31) |
The total displacement is therefore
| (32) |
Solving for the average modulus:
| (33) |
The resultant average modulus of each beam can be determined by inserting the total displacement from Eqs. (5), (13) and (29) into Eq. (33).
Footnotes
Part of the Gradients in Biomaterials Special Issue, edited by Professors Brendan Harley and Helen Lu.
References
- 1.Structural Interfaces and Attachments in Biology. Springer; New York, NY: 2013. [Google Scholar]
- 2.Thomopoulos S, Marquez JP, Weinberger B, Birman V, Genin GM. Collagen fiber orientation at the tendon to bone insertion and its influence on stress concentrations. J Biomech. 2006;39(10):1842–1851. doi: 10.1016/j.jbiomech.2005.05.021. [DOI] [PubMed] [Google Scholar]
- 3.Deymier-Black AC, Pasteris JD, Genin GM, Thomopoulos S. Allometry of the tendon enthesis: mechanisms of load transfer between tendon and bone. J Biomech Eng. 2015;137(11):111005–111005. doi: 10.1115/1.4031571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wopenka B, Kent A, Pasteris JD, Yoon Y, Thomopoulos S. The tendon-to-bone transition of the rotator cuff: a preliminary raman spectroscopic study documenting the gradual mineralization across the insertion in rat tissue samples. Appl Spectrosc. 2008;62(12):1285–1294. doi: 10.1366/000370208786822179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Genin GM, Kent A, Birman V, Wopenka B, Pasteris JD, Marquez PJ, Thomopoulos S. Functional grading of mineral and collagen in the attachment of tendon to bone. Biophys J. 2009;97(4):976–985. doi: 10.1016/j.bpj.2009.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schwartz AG, Pasteris JD, Genin GM, Daulton TL, Thomopoulos S. Mineral distributions at the developing tendon enthesis. PLoS One. 2012;7(11):9. doi: 10.1371/journal.pone.0048630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Thomopoulos S, Williams GR, Gimbel JA, Favata M, Soslowsky LJ. Variation of biomechanical, structural, and compositional properties along the tendon to bone insertion site. J Orthop Res. 2003;21(3):413–419. doi: 10.1016/S0736-0266(03)00057-3. [DOI] [PubMed] [Google Scholar]
- 8.Alexander B, Daulton TL, Genin GM, Lipner J, Pasteris JD, Wopenka B, Thomopoulos S. The nanometre-scale physiology of bone: steric modelling and scanning transmission electron microscopy of collagen-mineral structure. J R Soc Interface. 2012;9(73):1774–1786. doi: 10.1098/rsif.2011.0880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lu D, Barber AH. Optimized nanoscale composite behaviour in limpet teeth. J R Soc Interface. 2012;9(71):1318–1324. doi: 10.1098/rsif.2011.0688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jimenez-Palomar I, Shipov A, Shahar R, Barber AH. Influence of SEM vacuum on bone micromechanics using in situ AFM. J Mech Behav Biomed Mater. 2012;5(1):149–155. doi: 10.1016/j.jmbbm.2011.08.018. [DOI] [PubMed] [Google Scholar]
- 11.Bailey RJ, Geurts R, Stokes DJ, de Jong F, Barber AH. Evaluating focused ion beam induced damage in soft materials. Micron. 2013;50:51–56. doi: 10.1016/j.micron.2013.04.005. [DOI] [PubMed] [Google Scholar]
- 12.Smith L, Xia Y, Galatz LM, Genin GM, Thomopoulos S. Tissue engineering strategies for the tendon/ligament-to-bone insertion. Connect Tissue Res. 2012;53(2):95–105. doi: 10.3109/03008207.2011.650804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Smith LJ, Deymier AC, Boyle JJ, Li Z, Linderman SW, Pasteris JD, Xia Y, Genin GM, Thomopoulos S. Tunability of collagen matrix mechanical properties via multiple modes of mineralization. Interface Focus. 2016;6(1) doi: 10.1098/rsfs.2015.0070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Thomopoulos S, Das R, Birman V, Smith L, Ku K, Elson EL, Pryse KM, Marquez JP, Genin GM. Fibrocartilage tissue engineering: the role of the stress environment on cell morphology and matrix expression. Tissue Eng Part A. 2011;17(7–8):1039–1053. doi: 10.1089/ten.tea.2009.0499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li X, Xie J, Lipner J, Yuan X, Thomopoulos S, Xia Y. Nanofiber scaffolds with gradations in mineral content for mimicking the tendon-to-bone insertion site. Nano Lett. 2009;9(7):2763–2768. doi: 10.1021/nl901582f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xie J, Li X, Lipner J, Manning CN, Schwartz AG, Thomopoulos S, Xia Y. “Aligned-to-random” nanofiber scaffolds for mimicking the structure of the tendon-to-bone insertion site. Nanoscale. 2010;2(6):923–926. doi: 10.1039/c0nr00192a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Blitz E, Viukov S, Sharir A, Shwartz Y, Galloway JL, Pryce BA, Johnson RL, Tabin CJ, Schweitzer R, Zelzer E. Bone ridge patterning during musculoskeletal assembly is mediated through SCX regulation of Bmp4 at the tendon-skeleton junction. Dev Cell. 2009;17(6):861–873. doi: 10.1016/j.devcel.2009.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Long F, Zhang XM, Karp S, Yang Y, McMahon AP. Genetic manipulation of hedgehog signaling in the endochondral skeleton reveals a direct role in the regulation of chondrocyte proliferation. Development (Cambridge, England) 2001;128(24):5099–5108. doi: 10.1242/dev.128.24.5099. [DOI] [PubMed] [Google Scholar]
- 19.Schwartz AG, Long F, Thomopoulos S. Enthesis fibrocartilage cells originate from a population of Hedgehog-responsive cells modulated by the loading environment. Development. 2015;142(1):196–206. doi: 10.1242/dev.112714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Stokes D. Principles and Practice of Variable Pressure: Environmental Scanning Electron Microscopy (VP-ESEM) Wiley; 2008. [Google Scholar]
- 21.Hang F, Barber AH. Nano-mechanical properties of individual mineralized collagen fibrils from bone tissue. J R Soc Interface. 2011;8(57):500–505. doi: 10.1098/rsif.2010.0413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Barber AH, Lu D, Pugno NM. Extreme strength observed in limpet teeth. J R Soc Interface. 2015;12(105) doi: 10.1098/rsif.2014.1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Boyle JJ, Kume M, Wyczalkowski MA, Taber LA, Pless RB, Xia Y, Genin GM, Thomopoulos S. Simple and accurate methods for quantifying deformation, disruption, and development in biological tissues. J R Soc Interface. 2014;11(100):20140685. doi: 10.1098/rsif.2014.0685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J Optim. 1998;9(1):112–147. [Google Scholar]
- 25.Liu Y, Birman V, Chen C, Thomopoulos S, Genin GM. Mechanisms of bimaterial attachment at the interface of tendon to bone. J Eng Mater Technol. 2011;133(1):011006. doi: 10.1115/1.4002641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu Y, Thomopoulos S, Chen C, Birman V, Buehler MJ, Genin GM. Modelling the mechanics of partially mineralized collagen fibrils, fibres and tissue. J R Soc Interface. 2014;11(92):20130835. doi: 10.1098/rsif.2013.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Deymier-Black AC, Pasteris JD, Genin GM, Thomopoulos S. Allometry of the Tendon Enthesis: Mechanisms of Load Transfer Between Tendon and Bone. J Biomech Eng. 2015;137(11) doi: 10.1115/1.4031571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schwartz AG, Lipner JH, Pasteris JD, Genin GM, Thomopoulos S. Muscle loading is necessary for the formation of a functional tendon enthesis. Bone. 2013;55(1):44–51. doi: 10.1016/j.bone.2013.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Thomopoulos S, Zampiakis E, Das R, Silva MJ, Gelberman RH. The effect of muscle loading on flexor tendon-to-bone healing in a canine model. J Orthopaed Res. 2008;26(12):1611–1617. doi: 10.1002/jor.20689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Miller KS, Connizzo BK, Feeney E, Soslowsky LJ. Characterizing local collagen fiber re-alignment and crimp behavior throughout mechanical testing in a mature mouse supraspinatus tendon model. J Biomech. 2012;45(12):2061–2065. doi: 10.1016/j.jbiomech.2012.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gimbel JA, Van Kleunen JP, Mehta S, Perry SM, Williams GR, Soslowsky LJ. Supraspinatus tendon organizational and mechanical properties in a chronic rotator cuff tear animal model. J Biomech. 2004;37(5):739–749. doi: 10.1016/j.jbiomech.2003.09.019. [DOI] [PubMed] [Google Scholar]
- 32.Stouffer DC, Butler DL, Hosny D. The relationship between crimp pattern and mechanical response of human patellar tendon-bone units. J Biomech Eng. 1985;107(2):158–165. doi: 10.1115/1.3138536. [DOI] [PubMed] [Google Scholar]
- 33.Soslowsky LJ, Carpenter JE, Bucchieri JS, Flatow EL. Biomechanics of the rotator cuff. Orthop Clin North Am. 1997;28(1):17–30. doi: 10.1016/s0030-5898(05)70261-3. [DOI] [PubMed] [Google Scholar]
- 34.Moffat KL, Sun WH, Chahine NO, Pena PE, Doty SB, Hung CT, Ateshian GA, Lu HH. Characterization of the mechanical properties and mineral distribution of the anterior cruciate ligament-to-bone insertion site. Conference proceedings: Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 1, IEEE Engineering in Medicine and Biology Society; 2006; pp. 2366–2369. Annual Conference. [DOI] [PubMed] [Google Scholar]
- 35.Moffat KL, Sun WH, Pena PE, Chahine NO, Doty SB, Ateshian GA, Hung CT, Lu HH. Characterization of the structure-function relationship at the ligament-to-bone interface. Proc Natl Acad Sci USA. 2008;105(23):7947–7952. doi: 10.1073/pnas.0712150105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ferguson VL, Bushby AJ, Boyde A. Nanomechanical properties and mineral concentration in articular calcified cartilage and subchondral bone. J Anat. 2003;203(2):191–202. doi: 10.1046/j.1469-7580.2003.00193.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Campbell SE, Ferguson VL, Hurley DC. Nanomechanical mapping of the osteochondral interface with contact resonance force microscopy and nanoindentation. Acta Biomater. 2012;8(12):4389–4396. doi: 10.1016/j.actbio.2012.07.042. [DOI] [PubMed] [Google Scholar]
- 38.Abraham AC, Pauly HM, Donahue TLH. Deleterious effects of osteoarthritis on the structure and function of the meniscal enthesis. Osteoarthritis and Cartilage. 2014;22(2):275–283. doi: 10.1016/j.joca.2013.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yao N. Focused Ion Beam Systems: Basics and Applications. Cambridge University Press; Cambridge, UK: 2011. [Google Scholar]
- 40.Currey JD. The mechanical consequences of variation in the mineral content of bone. J Biomech. 1969;2(1):1–11. doi: 10.1016/0021-9290(69)90036-0. [DOI] [PubMed] [Google Scholar]
- 41.Sano H, Saijo Y, Kokubun S. Non-mineralized fibrocartilage shows the lowest elastic modulus in the rabbit supraspinatus tendon insertion: measurement with scanning acoustic microscopy. J Shoulder Elbow Surg. 2006;15(6):743–749. doi: 10.1016/j.jse.2005.12.008. [DOI] [PubMed] [Google Scholar]
- 42.Handbook of Nanomechanics and Mincromechanics. Taylor and Francis Group; Boca Raton, Fl: 2013. [Google Scholar]
- 43.Weibull W. A statistical distribution function of wide applicability. J Appl Mech. 1951;73:293. [Google Scholar]
- 44.Bazant ZP. Scaling of Structural Strength. Elsevier Butterworth-Heinemann; Burlington, MA: 2002. [Google Scholar]
- 45.Currey JD. The effect of porosity and mineral-content on the Youngs modulus of elasticity of compact-bone. J Biomech. 1988;21(2):131–139. doi: 10.1016/0021-9290(88)90006-1. [DOI] [PubMed] [Google Scholar]
- 46.Currey JD. What determines the bending strength of compact bone? J Exp Biol. 1999;202(18):2495–2503. doi: 10.1242/jeb.202.18.2495. [DOI] [PubMed] [Google Scholar]
- 47.Weiner S, Wagner HD. The material bone: structure mechanical function relations. Annu Rev Mater Sci. 1998;28:271–298. [Google Scholar]
- 48.Bala Y, Depalle B, Douillard T, Meille S, Clement P, Follet H, Chevalier J, Boivin G. Respective roles of organic and mineral components of human cortical bone matrix in micromechanical behavior: an instrumented indentation study. J Mech Behav Biomed Mater. 2011;4(7):1473–1482. doi: 10.1016/j.jmbbm.2011.05.017. [DOI] [PubMed] [Google Scholar]
- 49.Chen PY, McKittrick J. Compressive mechanical properties of demineralized and deproteinized cancellous bone. J Mech Behav Biomed Mater. 2011;4(7):961–973. doi: 10.1016/j.jmbbm.2011.02.006. [DOI] [PubMed] [Google Scholar]
- 50.Calvert P, Kempf J-F, Bonnomet F, Boutemy P, Marcelin L, Kahn J-L. Effects of freezing/thawing on the biomechanical properties of human tendon. Surg Radiol Anat. 2001;23:259–262. doi: 10.1007/s00276-001-0259-8. [DOI] [PubMed] [Google Scholar]
- 51.Sasaki N, Odajima S. Stress-strain curve and Young’s modulus of a collagen molecule as determined by the X-ray diffraction technique. J Biomech. 1996;29(5):655–658. doi: 10.1016/0021-9290(95)00110-7. [DOI] [PubMed] [Google Scholar]
- 52.Robinson PS, Huang TF, Kazam E, Iozzo RV, Birk DE, Soslowsky LJ. Influence of decorin and biglycan on mechanical properties of multiple tendons in knockout mice. J Biomech Eng. 2005;127(1):181–185. doi: 10.1115/1.1835363. [DOI] [PubMed] [Google Scholar]
- 53.Lake SP, Miller KS, Elliott DM, Soslowsky LJ. Tensile properties and fiber alignment of human supraspinatus tendon in the transverse direction demonstrate inhomogeneity, nonlinearity, and regional isotropy. J Biomech. 2010;43(4):727–732. doi: 10.1016/j.jbiomech.2009.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]