Dorsal hippocampus contributes to model-based planning

Abstract

Planning can be defined as action selection that leverages an internal model of the outcomes likely to follow each possible action. Its neural mechanisms remain poorly understood. Here, we adapt for rodents recent advances from human research, presenting for the first time an animal task that produces many trials of planned behavior per session, making multitrial rodent experimental tools available to study planning. We use part of this toolkit to address a perennially controversial issue in planning: the role of the dorsal hippocampus. Although prospective hippocampal representations have been proposed to support planning, intact planning in hippocampally-damaged animals has been repeatedly observed. Combining formal algorithmic behavioral analysis with muscimol inactivation, we provide the first causal evidence directly linking dorsal hippocampus with planning behavior. Our results and methods open the door to new and more detailed investigations of the neural mechanisms of planning, in the hippocampus and throughout the brain.

Introduction

Imagine a game of chess. As the players think about their next moves, they consider the outcome each action would have on the board, as well as the opponent’s likely reply. The players’ knowledge of the board and the rules constitutes an internal model of chess, a knowledge structure that links actions to their likely outcomes. The process of using such an “action-outcome” model to inform behavior is defined within reinforcement learning theory as the act of planning¹. Planning, so defined, has been an object of scientific investigation for many decades, and this research has generated important insights into the planning abilities of both humans and other animals^2–5.

Despite this progress, the neural mechanisms that underlie planning remain frustratingly obscure. One important reason for this continuing uncertainty lies in the behavioral assays that have traditionally been employed. Until recently, research on planning has largely employed behavioral tests (e.g. outcome devaluation) in which the subject is put through a sequence of training stages then makes just one single decision to demonstrate planning (or an absence thereof)^2,6,7. While the same animal can be tested multiple times⁸, at most one behavioral measure is obtained per session. Seminal studies using these assays have established the relevance of several neural structures^3,4, and they continue to be fundamental for many experimental purposes, but these assays are constrained by the small number of planned decisions they elicit. In an important recent breakthrough, new tasks have been developed that lift this constraint^9–12, allowing the collection of many repeated trials of planned behavior. These tasks provide an important complement to existing behavioral assays, promising to allow both a detailed evaluation of competing models as well as new opportunities for experiments investigating the neural mechanisms of planning. They have, however, so far been applied only to human subjects, limiting the range of experimental techniques available.

Here, we have adapted one of these tasks (the “two-step” task⁹) for rats, combining for the first time a multi-trial decision task with the experimental toolkit available for rodents. In a first experiment, we conducted a set of detailed computational analyses on a large behavioral dataset, and confirmed that rats, like humans, employ model-based planning to solve the task. In a second experiment, we employed causal neural techniques not available in humans to address an important open question in the neuroscience of planning: the role of the dorsal hippocampus.

A long-standing theory of hippocampal function holds that it represents a “cognitive map” of physical space used in support of navigational decision-making¹³. Classic experiments demonstrate hippocampal involvement in navigation tasks^14,15, as well as the existence of “place cells” which both encode current location¹⁶ and “sweep out” potential future paths at multiple timescales^17,18. These findings have given rise to computational accounts of hippocampal function that posit a key role for the region in model-based planning^19–21. However, support for these theories from experiments employing causal manipulations has been equivocal. Studies of both spatial navigation and instrumental conditioning have shown intact action-outcome behaviors following hippocampal damage^22–27. At the same time, tasks requiring relational memory do show intriguing impairments following hippocampal damage^28–30. The latter tasks assay whether behavior is guided by knowledge of relationships between stimuli (stimulus-stimulus associations), which plausibly involve similar representations and structures as the action-outcome associations that underlie planning, but they do not focus on action-outcome associations. Here, with the two-step task, we isolate these latter types of associations specifically.

Using rats performing the two-step task, we performed reversible inactivation experiments in both dorsal hippocampus (dH) and in orbitofrontal cortex (OFC), a brain region widely implicated in model-based control in traditional assays^31–33. The repeated-trials nature of the task allows us to use computational modeling to identify a set of separable behavioral patterns which jointly explain observed behavior, and to quantify the relative strength of each pattern. We find that the behavior of our animals is dominated by a pattern consistent with model-based planning, with important influences of novelty aversion, perseveration, and bias. The model-based pattern is selectively impaired by inactivation of OFC or dH, while other patterns are unaffected.

Importantly, model-based planning depends on a number of computations – behaviorally observed planning impairments might be caused by impairments to the planning process itself or instead by impairments to learning and memory processes upon which planning depends. Computational modeling analysis indicates that our effects are not well-described as an impairment in learning or memory in general, but as a specific attenuation of planned behavior. We therefore conclude that these regions either perform computations integral to the planning process itself (i.e. use of the action-outcome model to inform choice) or represent inputs that are used specifically by the planning process. This provides what is, to our knowledge, the first causal evidence that dorsal hippocampus contributes to model-based planning.

Results

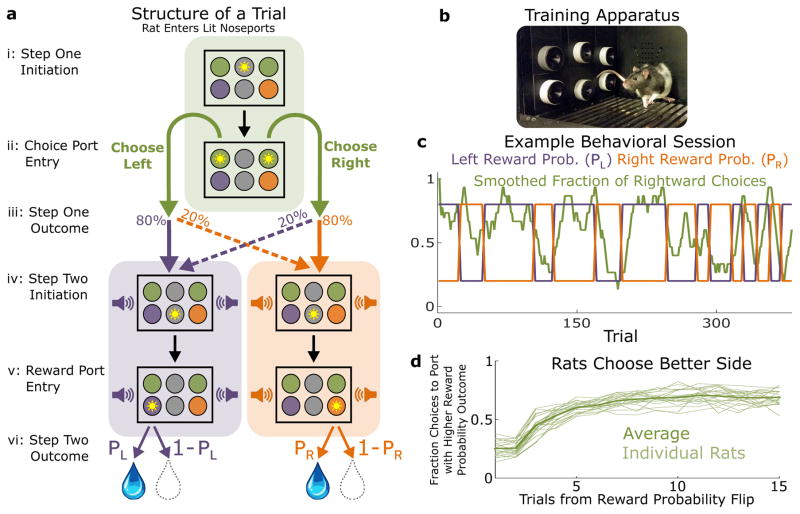
We trained rats to perform a multi-trial decision making task⁹, adapted from the human literature, designed to distinguish model-based versus model-free behavioral strategies (the “two-step” task; Fig. 1). In the first step of the task, the rat chooses between two choice ports, each of which leads to one of two reward ports becoming available with probability 80% (common transition), and to the other reward port with probability 20% (uncommon transition). In the second step, the rat does not have a choice, but is instead instructed as to which reward port has become available, enters it, and either receives (reward) or does not receive (omission) a bolus of water. Reward ports differ in the probability with which they deliver reward, and reward probability changes at unpredictable intervals (see Methods). Optimal performance requires learning which reward port currently has the higher reward probability, and selecting the choice port more likely to lead to that port. This requires using knowledge of the likely outcomes that follow each possible chosen action – that is, it requires planning.

Figure 1.

Two-Step Decision Task for Rats. A) Structure of a single trial of the two-step task. i) Top center port illuminates to indicate trial is ready, rat enters it to initiate the trial. ii) Choice ports illuminate, rat indicates decision by entering one of them. iii) Probabilistic transition takes place, with probability depending on the choice of the rat. Sound begins to play, indicating the outcome of the transition. iv) Center port in the bottom row illuminates, rat enters it. v) The appropriate reward port illuminates, rat enters it. vi) Reward is delivered with the appropriate probability. B) Photograph of behavioral apparatus, consisting of six nose-ports with LEDs and infrared beams, as well as a speaker mounted in the rear wall. C) Example behavioral session. Rightward choices are smoothed with a 10-trial boxcar filter. At unpredictable intervals, reward probabilities at the two ports flip synchronously between high and low. Rats adapt their choice behavior accordingly. D) Choice data for all rats (n = 21). The fraction of trials on which the rat selected the choice port whose common (80%) transition led to the reward port with currently higher reward probability, as a function of the number of trials that have elapsed since the last reward probability flip.

Rats performed the two-step task in a behavioral chamber outfitted with six nose ports arranged in two rows of three (Fig. 1B). Choice ports were the left and right side ports in the top row, and reward ports were the left and right side ports in the bottom row. Rats initiated each trial by entering the center port on the top row, and then indicated their choice by entering one of the choice ports. An auditory stimulus then indicated which of the two reward ports was about to become available. Before entering the reward port, however, the rat was required to enter the center port on the bottom row. This kept motor acts relatively uniform across common and uncommon trial types. For some animals, the common transition from each choice port led to the reward port on the same side (as in Figure 1A; “common-congruent” condition), while for others, it led to the reward port on the opposite side (“common-incongruent”). These transition probabilities constitute stable relationships between actions (choice ports) and their likely outcomes (reward ports). Subjects therefore have the opportunity to incorporate these action-outcome relationships into an internal model and to use them in order to plan.

Two analysis methods to characterize behavior and quantify planning

We trained 21 rats to perform the two-step task in daily behavioral sessions (n=1959 total sessions), using a semi-automated training pipeline which enabled us to run large numbers of animals in parallel with minimal human intervention (see Methods, Behavioral Training Pipeline). Although optimal performance in the two-step task requires planning, good performance can be achieved by both planning and model-free strategies (Fig S1). Critically, however, each type of strategy gives rise to a different patterns of choices⁹. Model-free strategies tend to repeat choices that resulted in reward, and to avoid choices that led to omission, regardless of whether the transition after the choice was a common or an uncommon one. Planning strategies, in contrast, are by definition aware of these action-outcome probabilities. Thus, after an uncommon transition, planning strategies tend to avoid choices that led to a reward, because the best way to reach the rewarding port again is through the common transition that follows the opposite choice. Similarly, after an uncommon transition planning strategies tend to repeat choices that led to a reward omission, because the best way to avoid the unrewarding port is through the common transition likely to occur after repeating the choice. Following this logic, Daw et al. (2011) examined how humans’ choices in a given trial depend on the immediately previous trial, and concluded that humans appear to use a mixture of model-free strategies and model-based planning⁹.

To assess the extent to which rat subjects were using a planning strategy, we extended the analysis of Daw et al. (2011), which considered the influence of the immediately preceding trial on present-trial behavior, to use information from multiple trials in the past (Fig S2). We have shown separately that that this many-trials-back approach is robust to some potential artifacts (e.g. due to slow learning rates; Miller, Brody, and Botvinick, 2016, bioRxiv³⁴). The many-trials-back approach consists of a logistic regression model that predicts the choice of the rat on each trial, given the history of recent trials and their outcomes. A trial that occurred τ trials ago can be one of four types: common-rewarded, uncommon-rewarded, common-omission, and uncommon-omission. For each τ, each of these trial types is assigned a weight (β_CR(τ), β_UR(τ), β_CO(τ), β_UO(τ) respectively). Positive weights correspond to greater likelihood to make the same choice that was made on a trial of that type which happened τ trials in the past, while negative weights correspond to greater likelihood to make the other choice. The weighted sum of past trials’ influence then dictates choice probabilities (see Methods, Behavior Analysis, equation one). Importantly, because model-free strategies do not distinguish between common and uncommon transitions, model-free strategies will tend to have β_CR ≈ β_UR and β_CO ≈ β_UO. In contrast, model-based strategies tend to change their behavior in different ways following common versus uncommon transitions, and will therefore have β_CR > β_UR and β_CO < β_UO.

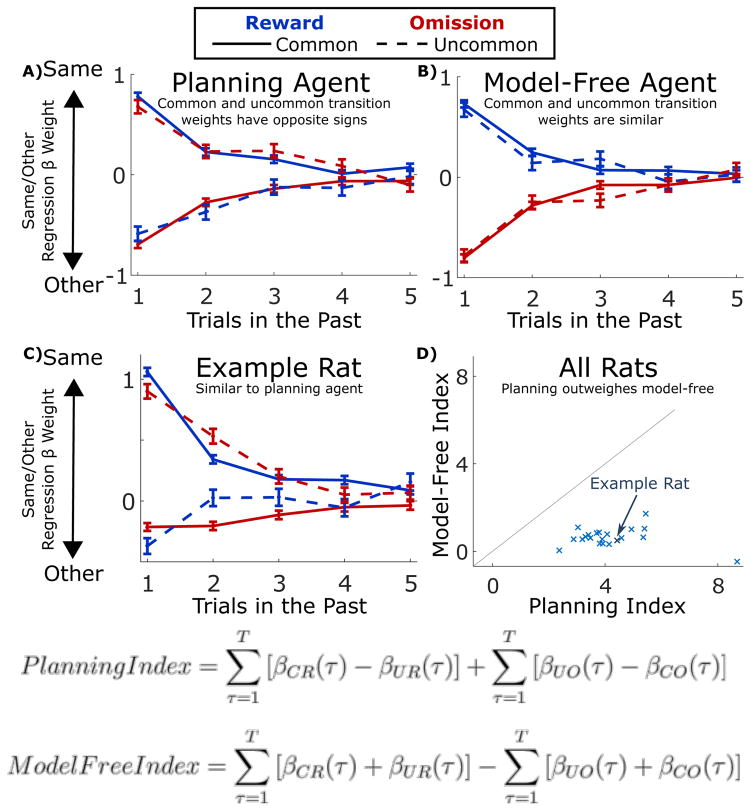
Applying this approach to synthetic data from artificial reinforcement learning agents using planning or model-free strategies (see Methods: Synthetic Behavioral Data) yields the expected patterns (Fig. 2A,B). For the planning agent (Fig. 2A), trials with common (solid) and uncommon (dashed) transitions have opposite effects on the current choice (compare e.g. blue solid versus blue dashed curves). In contrast, for the model-free agent (Fig. 2B), common and uncommon transition trials have the same effect (solid and dashed curves overlap), and only reward versus omission is important (red versus blue curves). Figure 2C shows the result of fitting the regression model to data from an example rat. The behavioral patterns observed are broadly similar to those expected of a model-based agent (compare 2A to 2C).

Figure 2.

Behavior Analysis Overview. A) Results of the trial-history regression analysis applied to simulated data from a model-based planning agent. Error bars indicate standard errors of the fit regression weights. B) Results of the same analysis applied to a model-free temporal difference learning agent. C) Results of the analysis applied to data from an example rat. D) Model-free and planning indices computed from the results of the regression analysis, shown for all rats in the dataset (n=21).

$$\begin{array}{c}\mathit{PlanningIndex}=\sum _{\tau =1}^T[{\beta }_{CR}(\tau )-{\beta }_{UR}(\tau )]+\sum _{\tau =1}^T[{\beta }_{UO}(\tau )-{\beta }_{CO}(\tau )]\\ \mathit{ModelFreeIndex}=\sum _{\tau =1}^T[{\beta }_{CR}(\tau )+{\beta }_{UR}(\tau )]-\sum _{\tau =1}^T[{\beta }_{UO}(\tau )+{\beta }_{CO}(\tau )]\end{array}$$

We next applied this approach to the behavior of each rat in our dataset (Figure S3) to reveal the nature of that animal’s choice strategy. To quantify the overall extent to which each rat showed evidence of planning vs. a model-free strategy, we defined a “planning index” and a “model-free index” by summing over the regression weights consistent with each pattern (see Fig. 2; Methods, Behavior Analysis). We have found that these measures provide a more reliable guide to behavioral strategy than standard measures, which consider only the immediately previous trial (see Miller, Brody, & Botvinick, 2016, bioRxiv, for details³⁴). We found that trained rats overwhelmingly showed large positive planning indices (see Figure 2; mean over rats: 4.2, standard error 0.3), and small positive model-free indices (mean: 0.6, standard error 0.1), consistent with their having adopted a planning strategy. Similarly, we found that movement times from the bottom center port to the reward port were faster for common vs. uncommon transition trials (average median movement time 700 ms for common and 820 ms for uncommon, p < 10⁻⁵; Figure S4), further indicating that rats used knowledge of the transition probabilities to inform their behavior. These results were similar between rats in the common-congruent condition (common outcome for each choice port is the reward port on the same side, as in Figure 1A) and those in the common-incongruent condition (common outcome is the port on the opposite side; p > 0.2).

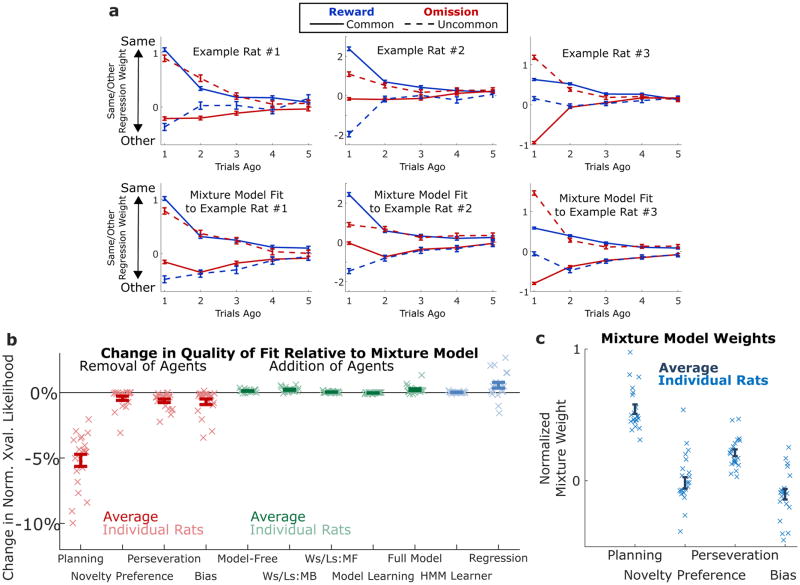
This regression analysis also revealed first, that there is substantial rat-by-rat variability (Figure 3A, top panel), and second, that there are important deviations from the predicted model-based pattern (Figure 3A; Figure S4). For example, the rat in the top left panel of Fig. 3A (same rat as in Fig. 2C) shows the overall pattern of regression weights expected for a model-based strategy, but in addition all weights are shifted in the positive direction (i.e. the “repeat choice” direction). This particular rat’s behavior can thus be succinctly described as a combination of a model-based strategy plus a tendency to repeat choices; we refer to the latter behavioral component as “perseveration”. While the regression analysis’ rich and relatively theory-neutral description of each rat’s behavioral patterns is useful for identifying such deviations from a purely model-based strategy, it is limited in its ability to disentangle the extent to which each individual deviation is present in a dataset. The regression analysis suffers from several other disadvantages as well – it requires a relatively large number of parameters, and it is implausible as a generative account of the computations used by the rats to carry out the behavior (requiring an exact memory of the past five trials). We therefore turned to a complementary analytic approach: trial-by-trial model fitting using mixture-of-agents models.

Figure 3.

Model-Fitting Analysis. A) Results of the trial-history regression analysis applied to data from three example rats (above) and simulated data produced by the agent model with parameters fit to the rats (below). Error bars indicate standard errors of the fit regression weights. B) Change in quality of fit resulting from removing (red) or adding (green) components to the reduced behavioral model (n=21 rats), error bars indicate standard error of the mean. C) Normalized mixture weights resulting from fitting the model to rats’ behavior, error bars indicate standard error of the mean.

Mixture-of-agents models provide both more parsimonious descriptions of each rat’s dataset (involving fewer parameters) and more plausible hypotheses about the underlying generative mechanism. Each model comprises a set of agents, each deploying a different choice strategy. Rats’ observed choices are modeled as reflecting the weighted influence of these agents, and fitting the model to the data means setting these weights, along with other parameters internal to the agents, so as to best match the observed behavior. We found that a good qualitative match to rats’ behavior could be achieved with a mixture of only four simple agents, representing four patterns – we call these patterns planning, choice perseveration, novelty preference, and choice bias (compare top row to bottom row, Fig. 3A; Figure S3). The four agents implementing these four patterns were a model-based reinforcement learning agent (planning), an agent which repeated the previous trial’s choice (perseveration), an agent which repeated or avoided choices which led to a common vs. an uncommon transition (novelty preference), and an agent which prefered the left or the right choice port on each trial (choice bias; see Methods, Behavioral Models). In all, this model contained five free parameters: four mixing weights, β_plan, β_np, β_persev, and β_bias, associated with each of the four agents, as well as a learning rate, α_plan, internal to the planning agent. We arrived at these four particular patterns as the necessary components because removing any of the four agents from the mixture resulted in a large decrease in quality of fit (assessed by cross-validated likelihood: Fig 3B, red; Methods, Model Comparison), and because adding a variety of other additional patterns (model-free reinforcement learning, model-based and model-free win-stay/lose-switch, transition learning, or all of the above; Methods, Behavioral Models) resulted in only negligible improvements (Fig 3B, green), as did substituting an alternate learning mechanism based on Hidden Markov Models into the planning agent (Fig 3B, blue; Methods, Behavioral Models). We found that the mixture model performed similarly in quality of fit to the regression-based model, for all but a minority of rats (Fig 3B, blue). The planning agent earned on average the largest mixing weights of any agent, indicating that model-based planning is the dominant component of behavior on our task (Fig 3C). Taken together, these findings indicate that this mixture model is an effective tool for quantifying patterns present in our behavioral data, and that well-trained rats on the two-step task exhibit perseveration, novelty preference, and bias, but predominantly exhibit model-based planning.

Pharmacological inactivation of hippocampus or orbitofrontal cortex impairs planning

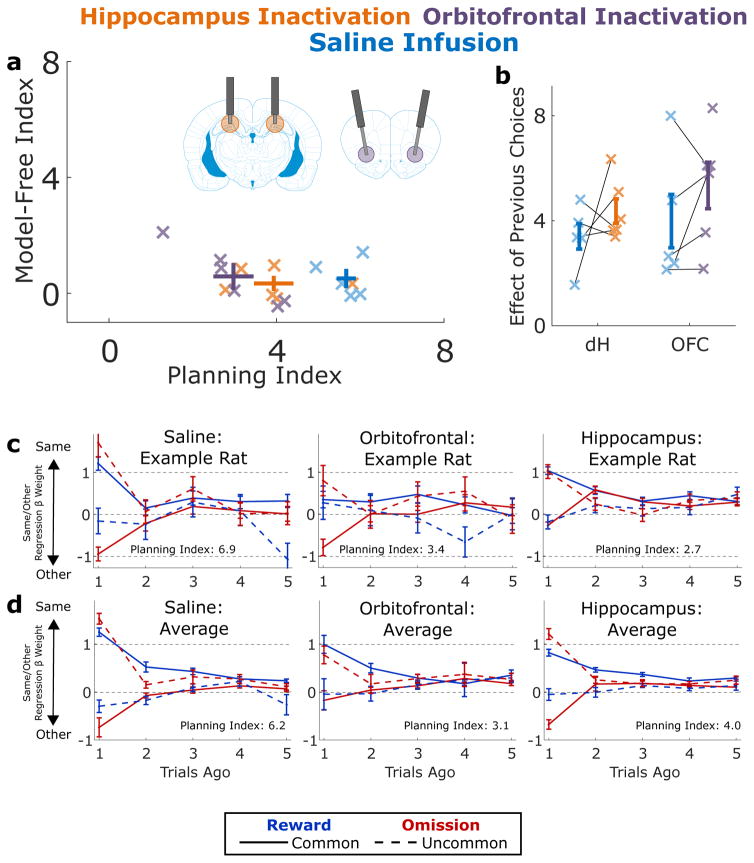
In the next phase of this work, we took advantage of both the regression analysis and the mixture-of-agents model to investigated the causal contribution of OFC and dH to planning behavior. We implanted six well-trained rats with infusion cannulae targeting each region bilaterally (Fig S5), and used these cannulae to perform reversible inactivation experiments. In these experiments, we infused the GABA-A agonist muscimol into a target brain region bilaterally, then allowed the animals to recover for a short time before placing them in the behavioral chamber to perform the task (see Methods, Inactivation Experiments). We compared behavior during muscimol sessions to behavior during control sessions performed the day before and after inactivation, as well as to sessions before which we infused saline into the target region (Fig S6, S7, and S8). We found that inactivation of either region substantially reduced the magnitude of the planning index relative to both each region’s control sessions (Figure 4; OFC p=0.001, dH p=0.01, see Methods, Analysis of Inactivation Data), and to pooled saline sessions (OFC p=0.004, dH, p=0.04). We found no effect of inactivation on the model-free index (all p > 0.5). We also found that inactivation of dH resulted in decrease in task performance, as measured by the fraction of times the choice ports whose common transition led to the reward port with larger reward probability (p=0.003; Fig S9). For completeness, we also present results of the traditional one-trial-back analysis on the inactivation dataset (Figs S10 and S11). The impact of inactivation on model-based behavioral patterns was not simply due to an overall reduction of the modulation of past trials on current trial choices: we computed the aggregate main effect of past choices on future choices (β_CR + β_UR + β_CO + β_UO, see Methods) for each rat for each type of session, and found that this measure was insensitive to inactivation of either region (Figure 4B; OFC p=0.4, dH p=0.7). Together, these results suggest that inactivation of OFC or dH reduces the extent to which behavior shows evidence of planning, but does not affect evidence for perseveration or model-free patterns.

Figure 4.

Effects of Muscimol Inactivation. A) Planning index and model-free index for implanted rats (n=6) performing the task on OFC inactivation sessions (purple), dH inactivation sessions (orange) and pooled saline infusions (blue; pooled for display). Inactivation of either region significantly decreases the planning index. Error bars show mean across rats and standard error. B) Main effect of past choice on future choice during the same sessions (saline session unpooled). Inactivation has no significant effect on this measure. Error bars show mean across rats and standard error. C) Results of the same/other regression analysis applied to data from an example rat on saline sessions (left), OFC infusions (middle), and dH infusions (right). D) Average over all rats of the results of the same/other regression analysis.

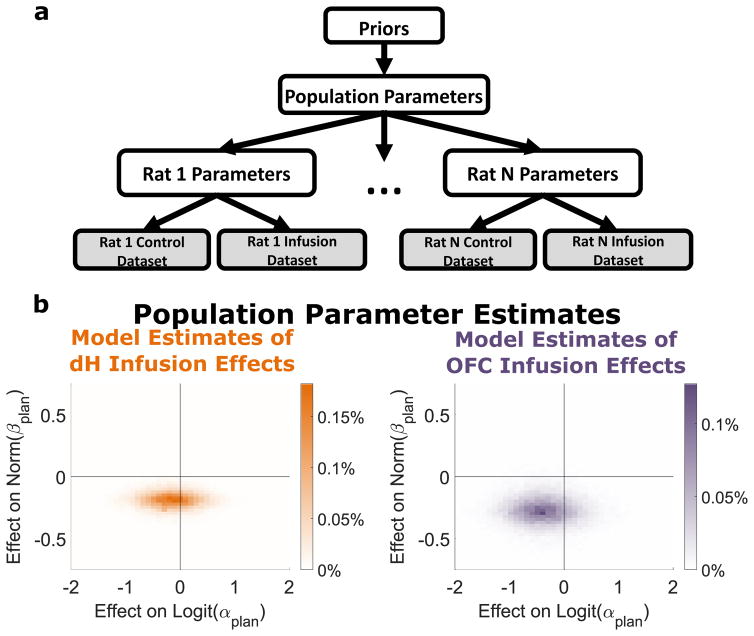
To determine the extent to which these muscimol-induced behavioral changes were specific to planning, we applied our mixture-of-agents model to the inactivation datasets (Figure 5A; Methods, Modeling Inactivation Data). To make the most efficient use of our data, we adopted a hierarchical modeling approach, simultaneously estimating parameters for both each rat individually as well as for the population of rats as a whole. For each rat, we estimated the mixture-of-agents model parameters (β_plan, α_plan, β_np, β_persev, and β_bias) for control and inactivation sessions. For the population, we estimated the distribution of each of the rat-level parameters across animals, as well as the effect of inactivation on each parameter. To perform Bayesian inference with this model, we conditioned it on the observed datasets and used Hamiltonian Markov Chain Monte Carlo to estimate the posterior distribution jointly over all model parameters (see Methods, Modeling Inactivation Data; Figures S12 and S13). We summarize this distribution by reporting the median over each parameter, taking this as our estimate for that parameter. Estimates for parameters governing behavior on control sessions were similar to those produced by fitting the model to unimplanted rats (compare Figures 5B and Table 1). Estimates for parameters governing the effect of inactivation on performance suggested large and consistent effects on the planning parameter β_plan, with weak and/or inconsistent effects on other parameters. To test whether inactivation affected behavior at the population level, we computed for each population-level parameter the fraction of the posterior in which that parameter has the opposite sign as its median – the Bayesian analogue of a p-value. We found that this value was small only for the parameter corresponding to the planning weight (β_plan; OFC, p = 0.01; dH, p = 0.01), and large for all other parameters (all p > 0.1). To determine whether this was robust to tradeoff in parameter estimates between β_plan and other parameters, we inspected plots of the density of posterior samples as a function of several parameters at once. Figure 5C shows a projection of this multidimensional density onto axes that represent the change in β_plan (planning agent’s weight) and the change in α_plan (planning agent’s learning rate) due to the infusion. We found that no infusion-induced change in α_plan would allow a good fit to the data without a substantial reduction in the β_plan parameter (all of the significant density is below the “effect on β_plan = 0” axis). We find similar robustness with respect to the other population-level parameters (Figure S14).

Figure 5.

Effects of Muscimol Inactivation on Mixture Model Fits. A) Schematic showing hierarchical Bayesian framework for using the agent model for parameter estimation. Each rat is characterized by a set of control parameters governing performance in saline sessions, as well as a set of infusion effect parameters governing the change in behavior following infusion. The population of rats is characterized by the means and standard deviations of each of the rat-level parameters. These population parameters are subject to weakly informative priors. B) Posterior belief distributions produced by the model over the parameters governing the effect of inactivation on planning weight (β_plan) and learning rate(α_plan).

Table 1.

Parameter estimates produced by the hierarchical Bayesian model for population parameters. Column one shows parameters governing behavior on saline sessions. Columns two and three show parameters governing the change in performance due to OFC or dH inactivation. In columns two and three, asterisks indicate parameters for which 95% or more of the posterior distribution shares the same sign.

	Saline	OFC Effects	dH Effects
Norm. Planning (βplan)	0.73	−0.28*	−0.19*
Norm. Novelty Pref. (βnp)	0.09	−0.13	0.02
Norm. Perseveration (βpersev)	0.21	−0.02	−0.04
Bias (βbias)	0.09	0.17	0.05
Logit Learning Rate (αplan)	−0.38	−0.39	−0.34

To test the hypothesis that the effects of inactivation were specific to planning, we constructed several variants of our model and compared them to one another using cross-validation. The first of these was designed to simulate a global effect of inactivation on memory, and constrained any effect on β_plan, β_np, and β_persev to be equal. The second was designed to simulate an effect specifically on memory for more remote past events, and allowed inactivation to affect only the influence of outcomes which occurred two or more trials in the past. The third was a combination of these two, allowing inactivation to have different effects on the recent and the remote past, but constraining it to affect all agents equally. We found that in all cases model comparison strongly dispreferred these alternative models, favoring a model in which inactivation has different effects on different components of behavior (log posterior predictive ratio of 42, 56, and 47 for OFC in the first, second, and third alternative models; lppr of 26, 43, and 26 for dH; see Methods, Inactivation Model Comparison). Taken together, these findings indicate that both OFC and dH play particular roles in supporting particular behavioral patterns, and that both play a specific role in model-based planning behavior. We find no evidence that either region plays a consistent role in supporting any behavioral component other than planning.

Discussion

We report the first successful adaptation of the two-step task – a repeated-trial, multi-step decision task widely used in human research – to rodents. This development, along with parallel efforts in other labs (Miranda, Malalasekera, Dayan, & Kennerly, 2013, Society for Neuroscience Abstracts; Akam, Dayan, & Costa, 2013, Cosyne Abstracts; Groman, Chen, Smith, Lee, & Taylor, 2014, Society for Neuroscience Abstracts; Dezfouli, 2015, unpublished doctoral thesis; Hasz & Redish, 2016, Society for Neuroscience Abstracts) provides a broadly applicable tool for investigating the neural mechanisms of planning. While existing planning tasks for rodents are well-suited to identifying the neural structures involved, and expose for study the process of model learning itself, the two-step task provides important complementary advantages. By eliciting many planned decisions in each behavioral session, it opens the door to a wide variety of new experimental designs, including those employing neural recordings to characterize the neural correlates of planning, as well as those, like ours, employing trial-by-trial analysis to quantify the relative influence of planning vs. other behavioral strategies.

Analysis of choice behavior on our task reveals a dominant role for model-based planning. Strikingly, our analysis reveals little or no role for model-free reinforcement learning, in contrast with the performance of human subjects on the same task⁹. One possible reason for this is the extensive experience our rat subjects have with the task – human subjects given several sessions of training tend, like our rats, to adopt a predominantly model-based strategy³⁵. These data stand in tension with theoretical accounts suggesting that model-based control is a slower, more costly, or less reliable alternative to model-free, and should be avoided when it does not lead to a meaningful increase in reward rates^5,36. They are in accord with data showing that human subjects adopt model-based strategies even when this does not result in an increase in reward rate³⁷. Together, these data suggest that model-based control may be a default decision-making strategy adopted in the face of complex environments. Importantly, rats also reveal knowledge of action-outcome contingencies in their movement times (Figure S3), making it unlikely that they are using any model-free strategy, including one which might use an alternative state space to allow it to mimic model-based choice³⁸ (see supplementary discussion).

We found that reversible inactivation of orbitofrontal cortex selectively impaired model-based choice, consistent with previous work indicating causal roles for this region in model-based control^31–33, as well as theoretical accounts positing a role for this structure in model-based processing and economic choice^39–41. That we observe similar effects in the rat two-step task is an important validation of this behavior as an assay of planning in the rat. Not all accounts of OFC’s role in model-based processing are consistent with a causal role in instrumental choice⁴². Our findings here are therefore not merely confirmatory, but also help adjudicate between competing accounts of orbitofrontal function.

Inactivation of dorsal hippocampus also selectively impaired model-based control, leaving other behavioral patterns unchanged. This finding offers the first causal demonstration, using a well-controlled task where planning can be clearly identified, of a long-hypothesized role in planning for hippocampus. Long-standing theories of hippocampal function¹³ hold that it represents a “cognitive map” of physical space, and that this map is used in navigational planning. Classic causal data indicate that hippocampus is necessary for tasks that require navigation^14,15, but do not speak to the question of its involvement specifically in planning. Such data are consistent with theoretical accounts in which hippocampus provides access to abstract spatial state information (i.e., location) as well as abstract spatial actions (e.g. ‘run south,’ independent of present orientation)⁴³. This information might be used either by a strategy based on action-outcome associations (i.e., a planning strategy), or on stimulus-response associations (a model-free strategy). An example of this comes from experiments using the elevated plus-maze¹⁴, in which a rat with an intact hippocampus might adopt a strategy of running south at the intersection, independent of starting location, either because it knows that this action will lead to a particular location in the maze (planning) or because it has learned a stimulus-response mapping between this location and this spatial action. A related literature argues that the hippocampus is important for working memory, citing hippocampal impairments in tasks such as delayed alternation and foraging in radial arm mazes^44,45, in which decisions must be made on the basis of recent past events. Impairments on these tasks are consistent both with accounts in which information about the recent past is used in model-free learning (i.e. generalized stimulus-response learning in which the “stimulus” might be a memory) as well as with accounts in which it supports action-outcome planning in particular. We find that our data are less well explained by models in which inactivation impairs memory in general. This indicates that if hippocampus’ role in our task is to support memory, then this is a particular type of memory that is specifically accessible for the purposes of planning.

Our results are in accord with theoretical accounts which posit a role for the hippocampus in planning^19–21, but stand in tension with data from classic causal experiments. These experiments have demonstrated intact action-outcome behaviors following hippocampal damage in a variety of spatial and non-spatial assays. One prominent example is latent learning, in which an animal that has previously been exposed to a maze learns to navigate a particular path through that maze more quickly than a naive animal – whether or not it has an intact hippocampus^22,23,27. Hippocampal damage also has no impact on classic assays of an animal’s ability to infer causal structure in the world, including contingency degradation, outcome devaluation, and sensory preconditioning^24–26. A comparison of these assays to our behavior reveals one potentially key difference: only the two-step task requires the chaining together of multiple action-outcome associations. Outcome devaluation, for example, requires one A-O association (e.g. lever–food), as well as the evaluation of an outcome (food–utility). Our task requires two A-O associations (e.g. top-left poke – bottom-right port lights; bottom-right poke – water) as well an evaluation (water–utility). This difference suggests a possible resolution: perhaps the hippocampus is necessary specifically in cases where planning requires linking actions to outcomes over multiple steps. This function may be related to the known causal role of hippocampus in relational memory tasks^28,29, which require chaining together multiple stimulus-stimulus associations. It may also be related to data indicating a role in second-order classical conditioning⁴⁶ and as well as in trace conditioning⁴⁷. Future work should investigate whether it is indeed the multi-step nature of the two-step task, rather than some other feature, that renders it hippocampally dependent.

Another contentious question about the role of hippocampus regards the extent to which it is specialized for spatial navigation⁴⁸ as opposed to playing some more general role in cognition^49,50. While performing the two-step task does require moving through space, the key relationships necessary for planning on this task are non-spatial, namely the causal relationships linking first-step choice to second-step outcome. Once the first-step choice was made, lights in each subsequent port guided the animal through the remainder of the trial – apart from the single initial left/right choice, no navigation or knowledge of spatial relationships was necessary. Taken together with the literature, our results suggest that multi-step planning specifically may depend on the hippocampus, in the service of both navigation and other behaviors.

Model-based planning is a process that requires multiple computations. Importantly, our results do not reveal the particular causal role within the model-based system that is played by either hippocampus or OFC. An important question which remains open is whether these regions perform computations involved in the planning process per se (i.e. actively using an action-outcome model to inform choice), or instead perform computations which are specifically necessary to support planning (e.g. planning-specific forms of learning or memory). It is our hope that future studies employing the rat two-step task, perhaps in concert with electrophysiology and/or optogenetics, will be able to shed light on these and other important questions about the neural mechanisms of planning.

Methods

Subjects

All subjects were adult male Long-Evans rats (Taconic Biosciences, NY), placed on a restricted water schedule to motivate them to work for water rewards. Some rats were housed on a reverse 12-hour light cycle, and others on a normal light cycle – in all cases, rats were trained during the dark phase of their cycle. Rats were pair housed during behavioral training and then single housed after being implanted with cannula. Animal use procedures were approved by the Princeton University Institutional Animal Care and Use Committee and carried out in accordance with NIH standards. One infusion rat was removed from study before completion due to health reasons – this rat did not complete any saline sessions.

The number of animals used in the inactivation experiment was determined informally by comparison to similar previous studies and by resources available. Particular animals were selected for inclusion informally – they were the first three in each transition probability condition to complete training on the present version of the task, with high trial counts per session. Example animals (figures 2c 3a, and 4c) were selected on the basis of cleanly demonstrating effects that were consistent in the population. Corresponding plots for all animals can be found in supplemental figures S4 and S6.

Behavioral Apparatus

Rats performed the task in custom behavioral chambers (Island Motion, NY) located inside sound- and light-attenuated boxes (Coulborn Instruments, PA). Each chamber was outfitted with six “nose ports” arranged in two rows of three, and with a pair of speakers for delivering auditory stimuli. Each nose port contained a white light emitting diode (LED) for delivering visual stimuli, as well as an infrared LED and infrared phototransistor for detecting rats’ entries into the port. The left and right ports in the bottom row also contained sipper tubes for delivering water rewards. Rats were placed into and removed from training chambers by technicians blind to the experiment being run.

Training Pipeline

Here, we outline a procedure suitable for efficiently training naive rats on the two-step task. Automated code for training rats using this pipeline via the bControl behavioral control system can be downloaded from the Brody lab website. This formalization of our training procedure into a software pipeline should also facilitate efforts to replicate our task in other labs, as the pipeline can readily be downloaded and identically re-run.

Phase I: Sipper Tube Familiarization

In this phase, rats become familiar with the experimental apparatus, and learn to approach the reward ports when they illuminate. Trials begin with the illumination of the LED in one of the two reward ports, and reward is delivered upon port entry. Training in this phase continues until the rat is completing an average of 200 or more trials per day.

Phase II: Trial Structure Familiarization

In this phase, rats must complete all four actions of the complete task, with rewards delivered on each trial. Trials begin with the illumination of the LED in the top center port, which the rat must enter. Upon entry, one of the side ports (chosen randomly by the computer) will illuminate, and the rat must enter it. Once the rat does this, the LED in the bottom center port illuminates, and a sound begins to play indicating which of the bottom side ports will ultimately be illuminated (according to the 80%/20% transition probabilities for that rat). The rat must enter the lit bottom center port, which will cause the appropriate bottom side port to illuminate. Upon entry into this side port, the rat receives a reward on every trial. For rats in the “congruent” condition, the reward port available will be on the same side as the choice port selected 80% of the time, while for rats in the “incongruent” condition, ports will match in this way 20% of the time. “Violation trials” occur whenever the rat enters a port that is not illuminated, and result in a five second timeout and an aversive white noise sound. Training in this phase continues until the rat is completing an average of 200 or more trials per day with a rate of violation trials less than 5%.

Phase IIIa: Performance-Triggered Flips

In this phase, probabilistic dynamic rewards are introduced, and rats must learn to choose the choice port that is associated with the reward port which currently has higher reward probability. Trial structure is as in phase II, except that in 90% of trials both choice ports illuminate after the rat enters the top center port, and the rat must decide which choice port to enter. The rat then receives an auditory cue, and LED instructions to enter the bottom center port and one of the reward ports, as above. This phase consists of blocks, and in each block, one of the reward ports is “good” and the other is “bad”. If the good reward port is illuminated, the rat will receive a water reward for entering it 100% of the time. If the bad reward port is illuminated, the rat must enter it to move on to the next trial, but no water will be delivered. Which reward port is good and which is bad changes in blocks, and the change in blocks is enabled by the rat’s performance. Each block lasts a minimum of 50 trials, after this, the block switch is “enabled” if the rat has selected the choice port which leads most often to the “good” reward port on 80% of free choices in the last 50 trials. On each trial after the end is enabled, there is a 10% chance per trial that the block will actually switch, and the reward ports will flip their roles. Phase IIIa lasts until rats achieve an average of three to four block switches per session for several sessions in a row. Rats which show a decrease in trial count during this phase can often be re-motivated by using small rewards (~10% of the usual reward volume) in place of reward omissions at the “bad” port.

Phases IIIb and IIIc

The same as phase IIIa, except that the “good” and “bad” reward ports are rewarded 90% and 10%, respectively, in phase IIIb, and 80% and 20% of the time in phase IIIc. Block flips are triggered by the rat’s performance, as above. Each of these phases lasts until the rat achieves an average of two to three block changes per session for several sessions in a row.

Phase IV: Final Task

The same as phase IIIc, except that changes in block are no longer triggered by the performance of the rat, but occur stochastically. Each block has a minimum length of 10 trials, after which the block has a 2% chance of switching on each trial. In our experience, approximately 90% of rats will succeed in reaching the final task.

Behavior Analysis

We quantify the effect of past trials and their outcomes on future decisions using a logistic regression analysis based on previous trials and their outcomes⁵⁵. We define vectors for each of the four possible trial outcomes: common-reward (CR), common-omission (CO), uncommon-reward (UR), and uncommon-omission (UO), each taking on a value of +1 for trials of their type where the rat selected the left choice port, a value of −1 for trials of their type where the rat selected the right choice port, and a value of 0 for trials of other types. We define the following regression model:

$$\begin{array}{c}log\left(\frac{P_{\mathit{left}}(t)}{P_{\mathit{right}}(t)}\right)=\sum _{\tau =1}^T{\beta }_{CR}(\tau )\ast CR(t-\tau )+\sum _{\tau =1}^T{\beta }_{CO}(\tau )\ast CO(t-\tau )+\\ \sum _{\tau =1}^T{\beta }_{UR}(\tau )\ast UR(t-\tau )+\sum _{\tau =1}^T{\beta }_{UO}(\tau )\ast UO(t-\tau )+\end{array}$$ (1)

where β_cr, β_co, β_ur, and β_uo are vectors of regression weights which quantify the tendency to repeat on the next trial a choice that was made τ trials ago and resulted in the outcome of their type, and T is a hyperparameter governing the number of past trials used by the model to predict upcoming choice. Unless otherwise specified, T was set to 5 for all analyses (see Figure S15).

We expect model-free agents to show a pattern of repeating choices which lead to reward and switching away from those which lead to omissions, so we define a model-free index for a dataset as the sum of the appropriate weights from a regression model fit to that dataset:

$$\mathit{ModelFreeIndex}=\sum _{\tau =1}^T[{\beta }_{CR}(\tau )+{\beta }_{UR}(\tau )]-\sum _{\tau =1}^T[{\beta }_{UO}(\tau )+{\beta }_{CO}(\tau )]$$ (2)

We expect that planning agents will show the opposite pattern after uncommon transition trials, since the uncommon transition from one choice is the common transition from the other choice. We define a planning index:

$$\mathit{PlanningIndex}=\sum _{\tau =1}^T[{\beta }_{CR}(\tau )-{\beta }_{UR}(\tau )]+\sum _{\tau =1}^T[{\beta }_{UO}(\tau )-{\beta }_{CO}(\tau )]$$ (3)

We test for significant model-free and planning indices using a one-sample t-test across rats. We test for significant differences between rats in the common-congruent and the common-incongruent conditions using a two-sample t-test.

Behavior Models

We model our rats behavior using a mixture-of-agents approach, in which each rat’s behavior is described as resulting from the influence of a weighted average of several different “agents” implementing different behavioral strategies to solve the task. On each trial, each agent A computes a value, Q_A(a), for each of the two available actions a, and the combined model makes a decision according to a weighted average of the various strategies’ values, Q_total(a):

$$\begin{array}{c}{Q}_{\mathit{total}}(a)=\sum _{A\in \{\mathit{agents}\}}{\beta }_A{Q}_A(a)\\ \pi (a)=\frac{e^{Q_{\mathit{total}}(a)}}{{\sum }_{a^{\prime }}{e}^{Q_{\mathit{total}}(a^{\prime })}}\end{array}$$ (4)

where the β’s are weighting parameters determining the influence of each agent, and Q(a) is the probability that the mixture-of-agents will select action a on that trial. We considered models consisting of subsets of the seven following agents: model-based temporal difference learning, model-free temporal difference learning, model-based win-stay/lose switch, model-free win-stay/lose-switch, common-stay/uncommon-switch, perseveration, and bias. The “full model” consists of all of these agents, while the “reduced model” consists of four agents which were found to be sufficient to provide a good match to rat behavior. These were model-based temporal difference learning (without transition updating), novelty preference, perseveration, and bias.

Model-Based Temporal Difference Learning

Model-based temporal difference learning is a planning strategy, which maintains separate estimates of the probability with which each action (selecting the left or the right choice port) will lead to each outcome (the left or the right reward port becoming available), T(a,o), as well as the probability, R_plan(o), with which each outcome will lead to reward. This strategy assigns values to the actions by combining these probabilities to compute the expected probability with which selection of each action will ultimately lead to reward:

$$Q_{\mathit{plan}}(a)={\sum }_o{R}_{\mathit{plan}}(o)\ast T(a,o)$$ (6)

At the beginning of each session, the reward estimate R_plan(o) is initialized to 0.5 for both outcomes, and the transition estimate T(a,o) is initialized to the true transition function for the rat being modeled (0.8 for common and 0.2 for uncommon transitions). After each trial, the reward estimate for both outcomes is updated according to

$$R_{\mathit{plan}}(o)\leftarrow \{\begin{array}{ll}{R}_{\mathit{plan}}(o)+{\alpha }_{\mathit{plan}}\left(r_t-R_{\mathit{plan}}(o)\right),\hfill & o=o_t\hfill \\ R_{\mathit{plan}}(o)+{\alpha }_{\mathit{plan}}\left(1-r_t-R_{\mathit{plan}}(o)\right),\hfill & o\ne o_t\hfill \end{array}$$ (7)

where o_t is the outcome that was observed on that trial, r_t is a binary variable indicating reward delivery, and α_plan is a learning rate parameter. The full model (but not the reduced model) also included transition learning, in which the function T(a,o) is updated after each outcome according to

$$T(a_t,o)\leftarrow \{\begin{array}{ll}T(a_t,o)+{\alpha }_T\left(1-T(a_t,o)\right),\hfill & o=o_t\hfill \\ T(a_t,o)+{\alpha }_T\left(0-T(a_t,o)\right),\hfill & o\ne o_t\hfill \end{array}$$ (8)

where a_t is the action taken, and α_T is a learning rate parameter.

Model-Free Temporal Difference Learning

Model-free temporal difference learning is a non-planning reward-based strategy. It maintains an estimate of the value of the choice ports, Q_MF(a), as well as an estimate of the values of the reward ports, R_MF(o). After each trial, these quantities are updated according to

$$\begin{array}{c}{Q}_{mf}(a_t)\leftarrow Q_{mf}(a_t)+{\alpha }_{mf}\left(R_{mf}(o_t)-Q_{mf}(a_t)\right)+{\alpha }_{mf}\lambda \left(r_t-R_{mf}(o_t)\right)\\ R_{mf}(o)\leftarrow \{\begin{array}{ll}{R}_{mf}(o)+{\alpha }_{mf}\left(r_t-R_{mf}\left(o\right)\right),\hfill & o=o_t\hfill \\ R_{mf}(o)+{\alpha }_{mf}\left(1-r_t-R_{mf}(o)\right),\hfill & o\ne o_t\hfill \end{array}\end{array}$$ (9)

where α_mf and λ are learning rate and eligibility trace parameters affecting the update process.

Model-Free Win-Stay/Lose Switch

Win-stay lose-switch is a pattern that tends to repeat choices that led to rewards on the previous trial and switch away from choices that led to omissions. It calculates its values on each trial according to the following

$$\begin{array}{c}{Q}_{\mathit{wsis}-mf}(a_t)\leftarrow r_t\\ Q_{\mathit{wsis}-mf}(a\ne a_t)\leftarrow 1-r_t\end{array}$$ (10)

Model-Based Win-Stay/Lose-Switch

Model-based win-stay lose switch follows the win-stay lose-switch pattern after common transition trials, but inverts it after uncommon transition trials.

$$\begin{array}{c}{Q}_{\mathit{wsis}-mb}(a_t)\leftarrow \{\begin{array}{ll}\hfill r_t,\hfill & \text{common}\text{transition}\text{trials}\hfill \\ \hfill 1-r_t,\hfill & \text{uncommon}\text{transition}\text{trials}\hfill \end{array}\\ Q_{\mathit{wsis}-mb}(a\ne a_t)\leftarrow 1-Q_{\mathit{wsis}-mb}(a_t)\end{array}$$ (11)

Novelty Preference

The novelty preference agent follows an “uncommon-stay/common switch” pattern, which tends to repeat choices when they lead to uncommon transitions on the previous trial, and to switch away from them when they lead to common transitions. Note that some rats have positive values of the β_np parameter weighting this agent (novelty preferring) while others have negative values (novelty averse; see Fig 3C):

$$\begin{array}{c}{Q}_{np}(a_t)\leftarrow \{\begin{array}{rr}\hfill 1,& \hfill \text{common}\text{transition}\text{trials}\\ \hfill 0,& \hfill \text{uncommon}\text{transition}\text{trials}\end{array}\\ Q_{np}(a\ne a_t)\leftarrow 1-Q_{np}(a_t)\end{array}$$ (12)

Perseveration

Perseveration is a pattern which tends to repeat the choice that was made on the previous trial, regardless of whether it led to a common or an uncommon transition, and regardless of whether or not it led to reward.

$$\begin{array}{c}{Q}_{\mathit{persev}}(a_t)\leftarrow 1\\ Q_{\mathit{persev}}(a\ne a_t)\leftarrow 0\end{array}$$ (13)

Bias

Bias is a pattern which tends to select the same choice port on every trial. Its value function is therefore static, with the extent and direction of the bias being governed by the magnitude and sign of this strategy’s weighting parameter β_bias.

$$\begin{array}{c}{Q}_{\mathit{bias}}(\text{left})\leftarrow 1\\ Q_{\mathit{bias}}(\text{right})\leftarrow -1\end{array}$$ (14)

Model Comparison and Parameter Estimation: Unimplanted Rats

We implemented the model described above using the probabilistic programming language Stan^56,57, and performed maximum-a-posteriori fits using weakly informative priors on all parameters⁵⁸ The prior over the weighting parameters β was normal with mean 0 and sd 0.5, and the prior over α_mf, α_mb, and λ was a beta distribution with a=b=3.

To perform model comparison, we used two-fold cross validation, dividing our dataset for each rat into even- and odd-numbered sessions, and computing the log-likelihood of each partial dataset using parameters fit to the other. For each model for each rat, we computed the “normalized cross-validated likelihood” by summing the log-likelihoods for the even- and odd-numbered sessions, dividing by the total number of trials, and exponentiating. This value can be interpreted as the average per-trial likelihood with which the model would have selected the action that the rat actually selected. We define the “reduced model” to be the full model defined above, with the parameters β_MF, β_WSLS-MF, β_WSLS-MB, and α_T all set to zero, leaving as free parameters β_plan, α_plan, β_np, β_persev, and β_bias (note that α_mf and λ become undefined when β_MF = 0). We compared this reduced model to nine alternative models: four in which we allowed one of the fixed parameters to vary freely, four in which we fixed one of the free parameters β_plan, β_np, β_persev, or β_bias to zero, and the full model in which all parameters are allowed to vary.

We performed parameter estimation by fitting the reduced model to the entire dataset generated by each rat (as opposed to the even/odd split used for model comparison), using maximum-a-posteriori fits under the same priors. For ease of comparison, we normalize the weighting parameters β_plan, β_np, and β_persev, dividing each by the standard deviation of its agent’s associated values (Q_plan, Q_np, and Q_persev) taken across trials. Since each weighting parameter affects behavior only by scaling the value output by its agent, this technique brings the weights into a common scale and facilitates interpretation of their relative magnitudes, analogous to the use of standardized coefficients in regression models.

Synthetic Behavioral Datasets: Unimplanted Rats

To generate synthetic behavioral datasets, we took the maximum-a-posteriori estimates parameter estimates for each rat, and used the reduced model in generative mode. The model matched to each rat received the same number of trials as that rat, as well as the same sequence of reward probabilities. We used these synthetic datasets for qualitative model-checking: if the reduced model does a good job capturing patterns in behavior, applying the regression analysis to both real and synthetic datasets should yield similar results.

Surgery

We implanted six rats with infusion cannula targeting dorsal hippocampus, orbitofrontal cortex, and prelimbic cortex, using standard stereotaxic techniques (data from PL are not reported in this paper). Anesthesia was induced using isoflurane, along with injections of ketamine and buprenorphine, the head was shaved, and the rat was placed in a stereotax (Kopf instruments) using non-puncture earbars. Lidocaine was injected subcutaneously under the scalp for local anesthesia and to reduce bleeding. An incision was made in the scalp, the skull was cleaned of tissue and bleeding was stopped. Injection cannula were mounted into guide cannula held in stereotax arms (dH & OFC: 22ga guide, 28ga injector; PL: 26ga guide, 28ga injector; Plastics One, VA), while a separate arm held a fresh sharp needle. The locations of bregma and interaural zero were measured with the tip of each injector and with the needle tip. Craniotomies were performed at each target site, and a small durotomy was made by piercing the dura with the needle. The skull was covered with a thin layer of C&B Metabond (Parkell Inc., NY), and the cannula were lowered into position one at a time. Target locations relative to bregma were AP −3.8, ML +−2.5, DV −3.1 for dorsal hippocampus, AP +3.2, ML +−0.7, DV −3.2 for prelimbic, and AP + 3.5, ML +−2.5, DV - 5 for orbitofrontal cortex. Orbitofrontal cannula were implanted at a 10 degree lateral angle to make room for the prelimbic implant. Cannula were fixed to the skull using Absolute Dentin (Parkell Inc, NY), and each craniotomy was sealed with Kwik-Sil elastomer (World Precision Instruments, FL). One all cannula were in place, Duralay dental acrylic (Reliance Dental, IL) was applied to secure the implant. The injector was removed from each guide cannula, and replaced with a dummy cannula. Rats were treated with ketofen 24 and 48 hours post-operative, and allowed to recover for at least seven days before returning to water restriction and behavioral training.

Inactivation Experiments

Each day of infusions, an injection system was prepared with the injection cannula for one brain region. The injection cannula was attached to a silicone tube, and both were filled with light mineral oil. A small amount of distilled water was injected into the other end of the tube to create a visible water-oil interface, and this end was attached to a Hamilton syringe (Hamilton Company, NV) filled with distilled water. This system was used to draw up and let out small volumes of muscimol solution, and inspected to ensure that it was free of air bubbles.

Rats were placed under light isoflurane anesthesia, and the dummy cannula were removed from the appropriate guide cannula. The injector was placed into the guide, and used to deliver 0.3 uL of 0.25 mg/mL muscimol^59,60 solution over the course of 90 seconds. The injector was left in place for four minutes for solution to diffuse, and then the procedure was repeated in the other hemisphere. For saline control sessions, the same procedure was used, but sterile saline was infused in place of muscimol solution. The experimenter was not blind to the region (OFC, dH, PL) or substance (muscimol, saline) being infused. After the completion of the bilateral infusion, rats were taken off of isoflurane and placed back in their home cages, and allowed to recover for 30–60 minutes before being placed in the behavioral chamber to perform the task.

Analysis of Inactivation Data

For each rat, we considered five types of sessions: OFC muscimol, dH muscimol, OFC control, dH control, and saline. Control sessions were performed the day before and the day after each infusion session, and saline sessions were pooled across OFC saline infusions and dH saline infusions (OFC musc., 18 sessions, OFC cntrl, 36 sessions, OFC sal. 6 sessions, dH musc. 33 sessions, dH cntrl, 64 sessions, dH sal. 10 sessions). Our dataset for each session consisted of up to the first 400 trials of each session in which at least 50 trials were performed. We perform the regression analysis (equation one), and compute the model-free index and planning index (equations two and three) for each dataset. To compute p-values, we performed a paired t-test across rats on the difference between muscimol and control datasets for each region, and on the difference between muscimol infusion in each region and the pooled saline infusion datasets.

Modeling Inactivation Data

We constructed a hierarchical Bayesian version of our reduced model, using the probabilistic programming language Stan^56,57,61,62. This model considered simultaneously two datasets from each rat: an inactivation and a control dataset. Each of these datasets is modeled as the output of the reduced model (see Behavior Models, above), which take the five parameters β_plan, α_plan, β_np, β_persev, and β_bias, giving each rat ten parameters: five for the control dataset, and five for the infusion dataset. For the purpose of the hierarchical model, we reparameterize these, characterizing each rat R by ten parameters organized into two vectors, ${\mathit{\theta }}_{\mathbf{R}}={\theta }_R^1\dots {\theta }_R^5$ and ${\mathbf{\Delta }}_{\mathbf{R}}={\mathrm{\Delta }}_R^1\dots {\mathrm{\Delta }}_R^5$ according to the following mapping:

	Rat R Control Dataset	Rat R Infusion Dataset
Norm(βplan)	${\theta }_R^1$	${\theta }_R^1+{\mathrm{\Delta }}_R^1$
Logit(αplan)	${\theta }_R^2$	${\theta }_R^2+{\mathrm{\Delta }}_R^2$
Norm(βnp)	${\theta }_R^3$	${\theta }_R^3+{\mathrm{\Delta }}_R^3$
Norm(βpersev)	${\theta }_R^4$	${\theta }_R^4+{\mathrm{\Delta }}_R^4$
βbias	${\theta }_R^5$	${\theta }_R^5+{\mathrm{\Delta }}_R^5$

where Norm indicates normalization of the weight (see Parameter Estimation, above), and Logit indicates the inverse-sigmoid logit function, which transforms a parameter bounded at 0 and 1 into a parameter with support over all real numbers.

The values in θ_R and Δ_R adopted by a particular rat are modeled as draws from a gaussian distribution governed by population-level parameter vectors θ_μ, θ_σ, Δ_μ, and Δ_σ giving the mean and standard deviation of the distribution of each of the rat-level parameters in the population:

$${\theta }_R^m~\text{Normal}({\theta }_{\mu }^m,{\theta }_{\sigma }^m)\text{and}{\mathrm{\Delta }}_R^m~\text{Normal}({\mathrm{\Delta }}_{\mu }^m,{\mathrm{\Delta }}_{\sigma }^m)$$

for each rat R, for each value of m indexing the various parameter vectors.

These population-level parameters are themselves modeled as draws from weakly informative prior distributions⁵⁸ chosen to enforce reasonable scaling and ensure that all posteriors were proper:

$$\begin{array}{ll}{\mathit{\theta }}_{\mathit{\mu }}~\text{Normal}(0,1)\hfill & {\mathrm{\Delta }}_{\mathit{\mu }}~\text{Normal}(0,1)\hfill \\ {\mathit{\theta }}_{\mathit{\sigma }}~\text{Cauchy}(0,1)\hfill & {\mathrm{\Delta }}_{\mathit{\sigma }}~\text{Cauchy}(0,1)\hfill \end{array}$$

Having established this generative model, we perform inference by conditioning it on the observed datasets (control and inactivation) for each rat, and approximating the joint posterior over all parameters by drawing samples using Hamiltonian Markov Chain Monte Carlo (H-MCMC)^58,63. To obtain estimated values for each parameter, we take the median of these samples with respect to that parameter. To test whether inactivation produced effects on behavior that were consistent at the population level, we computed a “p-value” for each parameter in Δ_μ given by the fraction of samples having the opposite sign as the median sample.

Inactivation Model Comparison

We performed a series of model comparisons between models like the above and alternative models in which inactivation affected memory in general, memory for distant past trials specifically, or a combination of these. In the first alternative model, inactivation was constrained to affect equally all of the agents which depend on the history of previous trials (planning, perseveration, and novelty preference). This alternative model contains a new parameter, the “memory multiplier”, m, which scales the weights of these agents, in this revised version of eq. 4:

$$Q_{\mathit{total}}(a)={\beta }_{\mathit{bias}}{Q}_{\mathit{bias}}+\sum _{A\in \{\mathit{plan},\mathit{persev},np\}}m{\beta }_A{Q}_A(a)$$

This memory multiplier is fixed to 1 for control sessions, but allowed to vary freely for each rat in infusion sessions. It has it’s own population-level mean and variance parameters, which are given weakly informative priors (see Methods, Modeling Inactivation Data). In the alternative version of the model, the β_A parameters are fixed between control and inactivation sessions. Since bias does not require memory, β_bias is allowed to vary. We implement this by fixing the parameters ${\mathrm{\Delta }}_R^1$ through ${\mathrm{\Delta }}_R^4$ to zero for each rat R (see Methods, Modeling Inactivation Data), and allowing the effects of inactivation to be described by ${\mathrm{\Delta }}_R^5$ and the new parameter m_R.

We compare this model to the model above using two-fold cross validation of H-MCMC fits. To compare these models quantitatively, we compute the log posterior predictive ratio (lppr):

$$log\frac{P(\mathit{testdata}\mid M1,\mathit{traindata})}{P(\mathit{testdata}\mid M2\mathit{traindata})}$$

In the next model comparisons, we separate the influence of the most recent trial’s outcome from the influence of all trials further back in time. We implement this by replacing the model-based reinforcement learning agent (equations 6 & 7) with both a model-based win-stay/lose-switch agent (equation 11), and a new “lagged model-based” agent constructed by taking the value of Q_plan from one trial in the past and using it to guide decision-making on the current trial, so that the value of Q_lagged–mb used on each trial contains information about the outcomes of all past trials except the most recent one. Fits of this model therefore contain two parameters to quantify planning: β_ws/ls–mb for the influence of the most recent outcome, and β_lagged–mb for the influence of all trials further into the past.

For the second model comparison, we limit the influence of inactivation to only affect β_lagged–mb and β_bias– that is, to only affect the influence of distant past trials on choice behavior, as well as choice bias. For the this model comparison, we also allow inactivation to affect the memory multiplier m, allowing it to have separate effects on memory for distant past trials and on memory for the immediately previous trial. We compare both of these models to a model in which inactivation can have separate effects on the each of the components of behavior. We compute the log posterior predictive ratio using leave-one-out cross validation over sessions (i.e., we compute posteriors based on all of the dataset except for one session, and compute the lppr for that session using those posteriors, then repeat for all sessions).

Synthetic Behavioral Datasets: Inactivation Data

To generate synthetic behavioral datasets, we took the parameter estimates produced by the hierarchical model for each rat for orbitofrontal, hippocampus, and saline infusions. Parameters used for synthetic saline datasets were the average of the saline parameters produced by fitting the model to saline/hippocampus data and to saline/orbitofrontal (note that rat #6 did not complete any saline sessions – parameter estimates for this rat are still possible in the hierarchical model since they can be “filled in” based on infusion data and data from other rats). We used the reduced model in generative mode with these parameters, applying each parameter set to a simulated behavioral session consisting of 10,000 trials. We then applied the trial-history regression analysis to these synthetic datasets, and used the results for qualitative model checking, comparing them to the results of the same analysis run on the actual data.

Code and Data Availability

All software used for behavioral training will be available on the Brody lab website. Software used for data analysis, as well as raw and processed data, are available from the authors upon request.