Skip to main content
PMC home page
The Journal of Experimental Biology logoLink to The Journal of Experimental Biology
. 2017 Aug 15;220(16):2993–3000. doi: 10.1242/jeb.149450

Changes in mechanical work during neural adaptation to asymmetric locomotion

Brian P Selgrade 1,*, Montakan Thajchayapong 1,*, Gloria E Lee 1,*, Megan E Toney 1, Young-Hui Chang 1,‡
PMCID: PMC5576064  PMID: 28596214

ABSTRACT

Minimizing whole-body metabolic cost has been suggested to drive the neural processes of locomotor adaptation. Mechanical work performed by the legs should dictate the major changes in whole-body metabolic cost of walking while providing greater insight into temporal and spatial mechanisms of adaptation. We hypothesized that changes in mechanical work by the legs during an asymmetric split-belt walking adaptation task could explain previously observed changes in whole-body metabolic cost. We predicted that subjects would immediately increase mechanical work performed by the legs when first exposed to split-belt walking, followed by a gradual decrease throughout adaptation. Fourteen subjects walked on a dual-belt instrumented treadmill. Baseline trials were followed by a 10-min split-belt adaptation condition with one belt running three times faster than the other. A post-adaptation trial with both belts moving at 0.5 m s−1 demonstrated neural adaptation. As predicted, summed mechanical work from both legs initially increased abruptly and gradually decreased over the adaptation period. The initial increase in work was primarily due to increased positive work by the leg on the fast belt during the pendular phase of the gait cycle. Neural adaptation in asymmetric split-belt walking reflected the reduction of pendular phase work in favor of more economical step-to-step transition work. This may represent a generalizable framework for how humans initially and chronically learn new walking patterns.

KEY WORDS: Biomechanics, Motor control, Locomotor adaptation, Mechanical work, Split-belt treadmill

Summary: Minimizing mechanical work performed by the legs may drive locomotor adaptation, with wide relevance for the control of legged locomotion and motor learning in novel environments.

INTRODUCTION

In walking animals, each leg uses muscular activation to perform mechanical work to propel the body forward and maintain upright posture. In doing so, the work of walking can be done more economically depending upon when in the gait cycle mechanical work is performed by the legs on the center of mass (COM). In humans, the walking gait cycle can be broken down into a pendular phase and a step-to-step transition phase. In the pendular phase of gait, which roughly coincides with single-limb support, the dynamics of the COM are analogous to that of an inverted pendulum. The step-to-step transition is when the COM is redirected from one pendular arc to the next and roughly coincides with the double-support phase of gait. Both the pendular and step-to-step transition phases are defined by the transitions observed in the trajectory of the vertical COM velocity. The step-to-step transition is the portion of the gait cycle when the COM is redirected upward from the previous pendular phase onto the contralateral leg and into the pendular phase of the next step (Kuo, 2007). Under ideal conditions, steady-state walking minimally requires positive work to counteract the negative work of the lead leg as it strikes the ground during the step-to-step transition (Ruina et al., 2005). In walking simulations, the energetically optimal manner in which to replace this negative work and redirect the COM is to pre-emptively perform positive work on the COM with the trail leg just before the lead leg contacts the ground (Kuo et al., 2005). This general strategy has also been demonstrated in human walking, where the trail leg begins to generate positive work on the COM just before and in opposition to the negative work performed by the lead leg throughout the step-to-step transition (Donelan et al., 2002a,b). Modeling of overground walking demonstrates the theory that this strategy of pre-emptive work and COM redirection performed by the trail leg is the most economical walking strategy, requiring only a quarter of the mechanical work compared with doing work during the pendular phase of gait (Kuo, 2002). Despite the energetic benefits of this preemptive push-off, it is not well understood how the human body adapts and utilizes this economical walking strategy during novel walking conditions that result in an inappropriate amount of trail-leg push-off work.

A novel walking task that challenges the ability of the trail leg to perform the appropriate amount of work to compensate for the negative work of the lead leg can provide insights into strategies for minimizing walking energetics under both steady and non-steady conditions (e.g. Soo and Donelan, 2012). Human walkers are observed to abandon the aforementioned more economical pre-emptive trail-leg work strategy during continuous acceleration (Oh et al., 2012). In this case, humans use the more energetically costly strategy of performing work during the pendular phase to meet the immediate, increased energy demand to accelerate the body forward. This result indicates that a single general control strategy is not used across all walking conditions and that minimizing energy cost is not always the prevailing control strategy, particularly when there is an immediate need to maintain walking mechanics.

Little is known about how the mechanical energy cost of walking is minimized when the locomotor system must adapt to a novel walking condition. A recent study by Finley and colleagues (2013) utilized a split-belt walking task to suggest that minimizing whole-body metabolic energy was a major driver of locomotor adaptation. During split-belt treadmill walking, subjects simultaneously walk with each leg on a separate, mechanically isolated treadmill belt where one belt moves faster than the other belt. Even though the optimality of preemptive push-off work from the trail leg may not extend from overground to split-belt walking, reductions in metabolic cost during split-belt adaptation scale with the magnitude of step-parameter adaptation and concomitant decreases in muscle activation (Finley et al., 2013). Although the mechanical work performed by the muscles of each leg is likely responsible for the major changes observed in whole-body metabolic energy and step symmetry, it is not known how work performed by each leg changes during split-belt treadmill walking. The mechanics of walking are intimately linked with its metabolic cost, and knowing how mechanical work of the legs changes during split-belt treadmill walking will provide more spatial and temporal details of the biomechanical and physiological principles dictating neural adaption during legged locomotion.

The peculiar condition of split-belt treadmill walking is further revealed when we consider its mechanics relative to steady-speed level walking either over ground or on a regular tied-belt treadmill. On average, in all three cases there is zero net mechanical work done on the COM and zero net horizontal (anteroposterior) force acting on the COM for a person walking at constant velocity. In the overground and tied-belt treadmill cases, the legs must perform zero net work on the ground or treadmill belt to satisfy these two requirements. When belt speeds for each leg are unequal, as in the split-belt condition, however, a large force generated on the fast belt can be matched with a relatively small force on the slow belt while satisfying the condition of zero net work and zero net horizontal force acting on the COM. So, in the special case of split-belt treadmill walking, there is a divergence in how we can account for the net work done by the legs on the COM and the net work done by each leg on each treadmill belt that is moving at different speeds. When we consider the physiology of walking, however, we are more concerned with the mechanical work done by the legs on the belt because this is likely to be a better indicator of work done by the leg muscles than net work done on the COM. In summary, the physics of walking on a split-belt treadmill allow for a walker's legs to perform positive, negative or zero net mechanical work on the treadmill belt while still fulfilling the requirements of zero net horizontal force and zero net mechanical work on the COM.

In the current study, we addressed two general questions related to the biomechanics of locomotor adaptation. First, we asked whether the walking patterns adopted immediately upon exposure to split-belt treadmill walking would reflect an energy-minimization strategy. Second, we asked whether changes in mechanical work by each leg over the course of adaptation would reflect the known reductions in metabolic cost associated with adaptation to split-belt treadmill walking. It has been demonstrated that, under non-steady conditions, more energetically costly walking patterns may be selected over more economical ones (Oh et al., 2012), and reaching an energetically optimum gait under novel conditions can take several minutes (Selinger et al., 2015). Therefore, we hypothesized that the immediate response to split-belt treadmill walking would be a less economical walking pattern that does not minimize energy cost. Because metabolic cost is high at the beginning of split-belt treadmill walking (Finley et al., 2013), we hypothesized that the summed mechanical work performed by both legs would be high during early split-belt treadmill walking. Furthermore, we hypothesized that this high initial work would be due to a strategy that favored mechanical work during the pendular phase over the step-to-step transition. We further hypothesized that the amount of mechanical work during the pendular phase would gradually decrease over the course of locomotor adaption as subjects gradually shifted to the more economical strategy of generating positive work during the step-to-step transition. These hypotheses suggest that, when exposed to a novel walking condition, subjects initially maintain the baseline motor behavior, which is energetically expensive under the novel conditions. However, they then adapt by gradually shifting to an economical walking pattern.

MATERIALS AND METHODS

Subjects

Thirteen healthy subjects participated in this study (age: 25.1±4.2 years; height: 174.8±9.5 cm; body mass: 70.7±12.4 kg; 7 females, 6 males). All subjects gave informed written consent prior to participation according to a protocol approved by the Georgia Institute of Technology Institutional Review Board. We excluded participants with any history of neuromuscular impairments or musculoskeletal conditions. Additionally, all subjects had no prior experience walking on a split-belt treadmill.

Procedure

Subjects walked on a dual-belt instrumented treadmill (Toney and Chang, 2013, 2016), with each side having the same design as a previously developed instrumented treadmill (Kram et al., 1998; Collins et al., 2009), where the speeds of two mechanically isolated belts were controlled independently. Throughout the experiment, the treadmill belts were set at either the same speed (tied-belt condition during baseline and post-adaptation periods) or at different speeds, with one belt running at a speed three times higher than the other (3:1 ratio, split-belt condition during adaptation period). We assigned subjects to have their dominant leg on the fast speed belt during the adaptation period. We defined leg dominance as the preferred leg subjects used to perform at least two of three skilled activities with their feet (kicking a soccer ball, picking up a marble and tracing a shape with the toe) (Schneiders et al., 2010). Subjects wore a safety harness and began each trial by stepping onto the treadmill once full speed was attained while holding lightly onto a safety rail in front of them and immediately releasing their hold as walking trials began. At the end of each trial, subjects were instructed to step off to the side and rest until the next trial's treadmill speeds were set.

Subjects first walked at a slow speed (0.5 m s−1) for 5 min in the tied-belt condition. This warm-up period occurred prior to data collection to ensure that subjects were familiarized with treadmill walking (Zeni and Higginson, 2010). Subjects then started the experiment walking in five tied-belt baseline conditions for 2 min each (0.5, 1.5, 0.5, 1.0 and 0.5 m s−1), which represented slow (0.5 m s−1), fast (1.5 m s−1) and intermediate (1.0 m s−1) walking speeds. During the adaptation period, subjects walked continuously for 10 min in the split-belt condition (slow belt at 0.5 m s−1, fast belt at 1.5 m s−1). The study ended with a post-adaptation period where subjects walked for 6 min in a tied-belt condition at the slow speed (0.5 m s−1). Our protocol was consistent with previous split-belt adaptation studies and the split-belt speed ratio exactly matched the one used by Finley and colleagues to measure changes in metabolic cost (Reisman et al., 2005; Finley et al., 2013).

Data collection

We used a six-camera motion-analysis system to record lower-limb kinematics (120 Hz, Vicon Motion Systems, Oxford, UK). Reflective markers were placed on each subject's second metatarsophalangeal joint, lateral malleolus, lateral condyle, anterior superior iliac spine, posterior superior iliac spine, shank segment and thigh segment. Data were collected intermittently during each of the three phases of the experiment. For the baseline phase, data from the first slow, the fast and the moderate speed trials were analyzed. During the adaptation phase, we collected data at four different time points within the 10-min split-belt walking task. Collection time points corresponded to the first 2 min at the start of adaptation (early adaptation), the fourth minute of adaptation, the seventh minute of adaptation and the tenth minute of adaptation (late adaptation). We collected data during two time points of post-adaptation: during the first 2 min (early post-adaptation) and during the sixth minute (late post-adaptation). Ground reaction force (GRF) data were collected from two side-by-side force platforms (1080 Hz, Advanced Mechanical Technology Incorporated, Watertown, MA, USA) with a custom-built treadmill mounted on top of each one (Kram et al., 1998).

Data processing

We filtered marker and force data with a zero-phase lag fourth-order Butterworth low-pass filter with a 10 Hz cut-off frequency for camera data and with a 25 Hz cut-off frequency for GRF. Heel-strike and toe-off times were identified when vertical force crossed a threshold of 32 N (Giest and Chang, 2016; Selgrade and Chang, 2015).

Mechanical work performed by the leg

The mechanical work performed by each leg is equal to the cumulative time integral of the mechanical power generated by each leg over the course of a stride cycle. We used a modification of the individual-limbs method to calculate the power generated by each leg (Donelan et al., 2001, 2002a). The individual-limbs method assumes that the leg is a massless piston applying equal and opposite forces to the ground and COM (Kuo, 2002). With overground walking, the leg only applies power to the COM because the ground has zero velocity. Treadmill walking, however, involves the leg applying force to a moving belt (Fig. 1A). Thus, we included the power applied to the belt by the leg as well. We determined integration constants by requiring average vertical and anterior–posterior velocity over a stride to both equal zero. All calculations were in a fixed reference frame in the sagittal plane. Mathematically, this work calculation gave the same result as the traditional individual-limbs method would if COM velocity were calculated relative to the treadmill belt (Selgrade et al., 2017) but avoids the confusing abstraction of placing the COM in two reference frames simultaneously when the belts moved at different speeds. Limb work calculations were performed based on the following time periods of interest: full stride; pendular phase; and the step-to-step transition. A complete stride is defined from heel contact to the next ipsilateral heel contact. The boundaries separating pendular and step-to-step transition phases were defined by the times of minimum and maximum vertical COM velocity (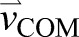Inline graphic), respectively (Adamczyk and Kuo, 2009).

Fig. 1.

Fig. 1.

Open in a new tab

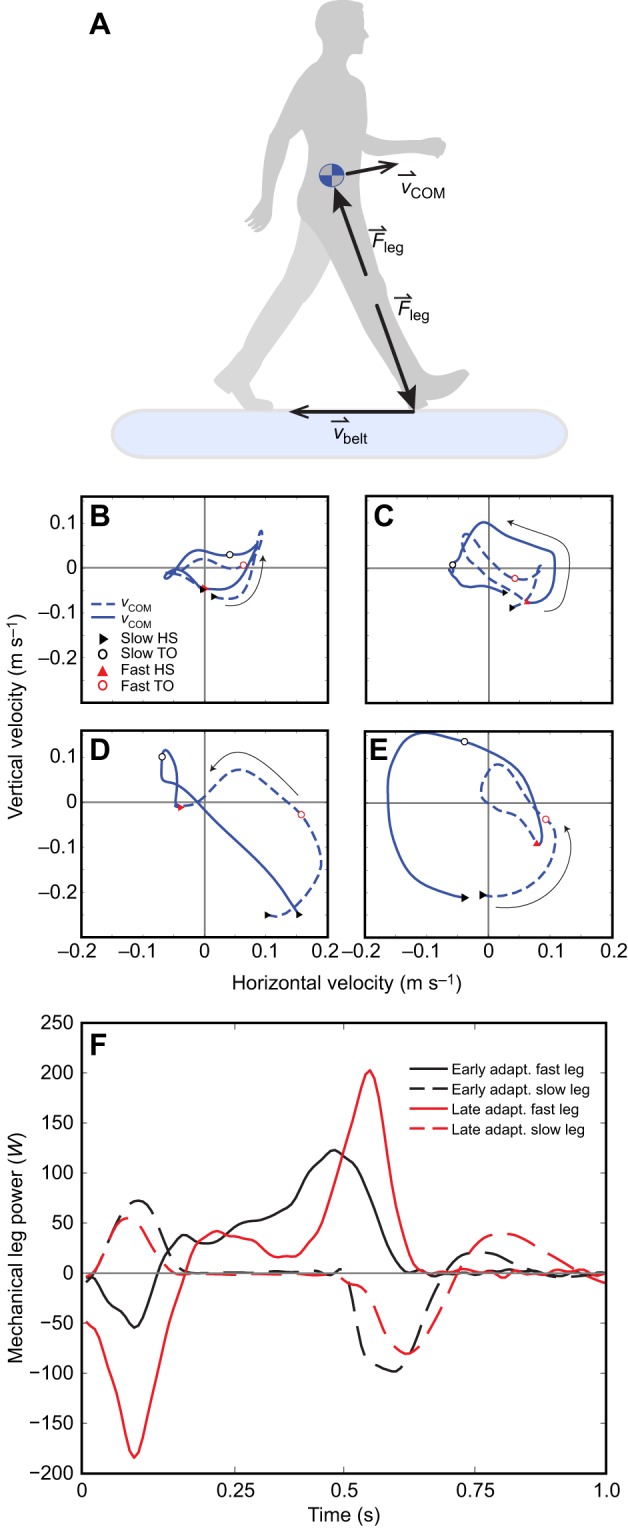
Conceptual diagram of leg work during split-belt walking and representative data. (A) Work done by the leg is calculated based on leg force [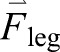Inline graphic; equivalent to ground reaction force (GRF)], COM velocity (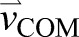Inline graphic) and belt velocity (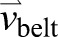Inline graphic). (B–D) COM velocity for one stride during slow (dashed line) and fast (solid line) leg stance phases during the slow baseline condition (B), early post-adaptation (C), early adaptation (D) and late adaptation (E) for a typical subject. (B,C) Correspond to trials with tied belts moving at 0.5 m s−1; (D,E) correspond to the split-belt condition. All velocities are with respect to a fixed, global reference frame. Early adaptation and post-adaptation data are the first complete stride under each condition. HS, heel strike; TO, toe off. (F) Mechanical power performed by the fast leg (solid lines) and slow leg (dashed lines) during early (black lines) and late (red lines) adaptation. All trajectories begin with heel strike of the fast leg.

We calculated mechanical work (W) done by each leg with the leg denoted by the belt on which it makes contact as ‘fast’ and ‘slow’ in Eqns 1 and 2, respectively. Note that, even during tied-belt conditions, we use the ‘fast’ and ‘slow’ notation to distinguish between the two legs. We separately integrated the mechanical work over the positive (denoted by POS) and negative (denoted by NEG) integrands for each particular time interval. Within each integrand, the first term denotes leg power, where force (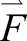Inline graphic) is the ground reaction force vector, and the second term denotes leg power applied to the treadmill belt:

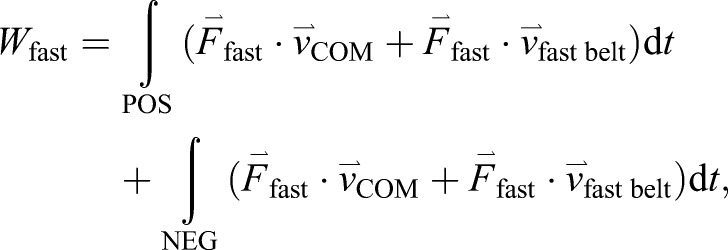graphic file with name jexbio-220-149450-e1.jpg (1)
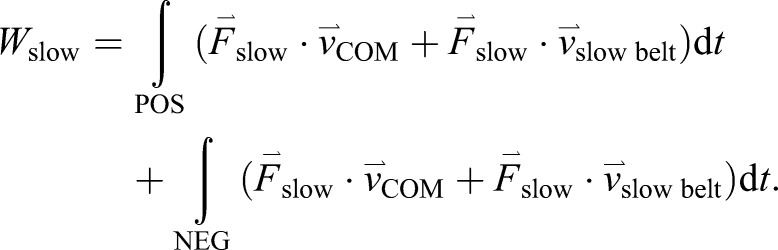graphic file with name jexbio-220-149450-e2.jpg (2)

In Eqns 1 and 2, the second integral is always less than zero and therefore acts in opposition to the first integral even though they are summed. We also calculated the sum of the mechanical work performed by both limbs (Eqn 3):

graphic file with name jexbio-220-149450-e3.jpg (3)

Adaptation parameters

We used step length symmetry (SLS) as an indicator to confirm locomotor adaptation in our subjects. Previous studies have shown that individuals adapt their step lengths while walking at various split-belt treadmill speeds (Finley et al., 2013; Reisman et al., 2005, 2007; Malone and Bastian, 2010). We defined SLS as the normalized difference between step lengths (Lstep) of fast (f) and slow (s) legs (Reisman et al., 2005):

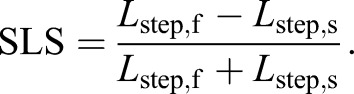graphic file with name jexbio-220-149450-e4.jpg (4)

Lstep was measured as the anterior–posterior distance between the two feet at the time of heel strike. Lstep,f and Lstep,s corresponded to the lead leg being on the fast or slow belt, respectively, at heel strike.

Statistical analysis

We performed a repeated-measures ANOVA to test for significant differences across all conditions of the experiment. When significance was found, we used a Bonferroni post hoc analysis to assess the adaptation by comparing early adaptation versus baseline values and by comparing early adaptation (the first 10 steps of adaptation) to late adaptation (the final 10 steps). We also performed a Student's one-sample t-test to test the null hypothesis of a non-significant difference between the SLS during late adaptation compared with baseline. All statistical analyses were done at an alpha level of 0.05 using Statview (SAS, NC, USA).

RESULTS

SLS and COM velocity

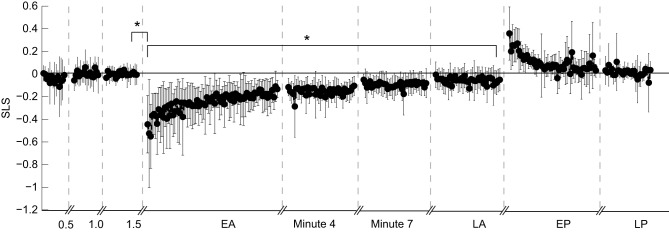
COM velocity (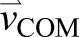Inline graphic) was qualitatively different between baseline, early post-adaptation and adaptation (Fig. 1B–E) but also changed as subjects adapted to split-belt walking. During early adaptation, the direction of each subject's COM velocity abruptly changed after both fast heel strike and slow toe off (Fig. 1D). During baseline walking, SLS remained near zero throughout each tied-belt walking condition, indicating that our subjects walked with a near-symmetric gait (Fig. 2). We observed an abrupt change in SLS, however, during early adaptation, when the SLS became negative, indicating that step lengths were larger when the slow leg was leading compared to when the fast-belt leg was leading. SLS gradually returned to a baseline level of symmetry by late adaptation (Fig. 2). Once the belt speeds were tied again during the post-adaptation period, a large asymmetry in step length was again observed initially, but with the opposite trend compared with early adaptation. The positive SLS returned to a baseline level by the end of post-adaptation. Mean SLS during the first 10 steps of early adaptation was significantly different compared with the mean of the last 10 steps during late adaptation (P<0.001). We found no difference between the last 10 steps of late adaptation compared to each of the baseline tied-condition means (P>0.05). We also found a significant difference between mean SLS during the first 10 steps of early post-adaptation and the mean of the last 10 steps during late post-adaptation (P<0.001). No difference was found when comparing the last 10 steps of late post-adaptation to each of the baseline tied-condition means (P>0.05).

Fig. 2.

Fig. 2.

Open in a new tab

Mean step length symmetry (SLS) across walking conditions. Positive SLS indicates that the step length when the fast limb is leading is larger than when the slow limb is leading, or vice versa (see Eqn 4). Each data point represents each walking step averaged across 13 subjects (error bars are 1 s.d.). The dashed vertical lines separate data collections from each different walking condition and include periods of rest and walking without data collection. The numbers on the x-axis represent the belt speeds in m s−1 for baseline conditions. EA, early adaptation; minute 4, the fourth minute of the adaptation phase; minute 7, the seventh minute of the adaptation phase; LA, late adaptation; EP, early post-adaptation; LP, late post-adaptation. *P<0.05 in comparison to early adaptation.

Mechanical work over the entire stride

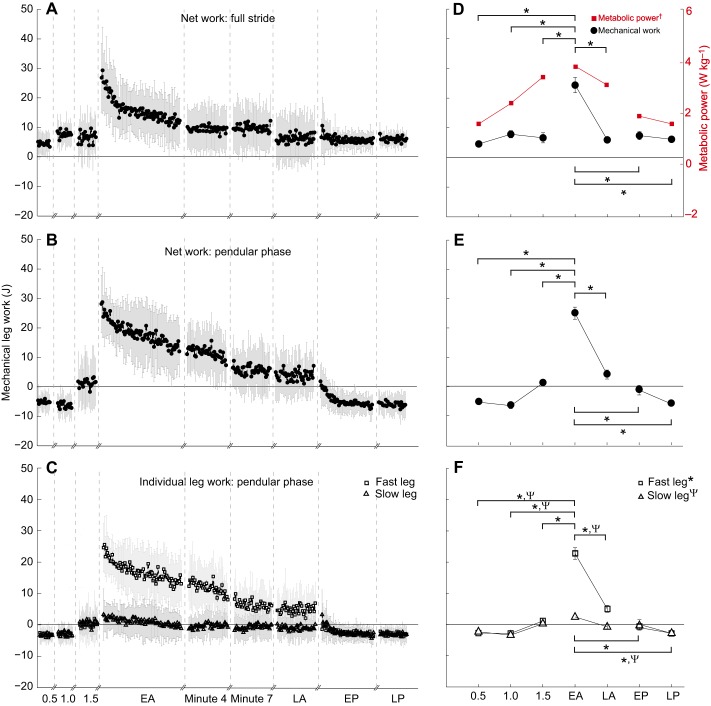
The summed mechanical work performed by both legs over the entire stride during early adaptation was significantly greater than all baseline and late-adaptation trials (Fig. 3A,D). By late adaptation, the summed mechanical work by the legs had decreased to the point of exhibiting no significant difference compared to each of the baseline trials (P>0.05; Fig. 3A,D). There was a clear increase in mechanical work during the first few steps of the post-adaptation phase; however, this was not significantly different from baseline when averaged over 10 steps, indicating a rapid decrease in leg work. For the rest of the post-adaptation phase, the mechanical work remained at baseline level.

Fig. 3.

Fig. 3.

Open in a new tab

Mechanical leg work measurements. Mean mechanical work performed by the legs calculated over the full stride (A,D), summing over two successive pendular phases from both legs (B,E) and for the pendular phase of each leg individually (C,F). Data are means (±s.d.) across all 13 subjects for each step (A–C), or means of the first 10 steps from each trial (D–F). Changes in metabolic power (D, red squares) are taken from Finley et al. (2013) and reflect the changes in total mechanical work from the fast leg during single-limb support observed here (C). *,ΨP<0.05 in comparison to early adaptation. The numbers on the x-axis represent the belt speeds in m s−1 for baseline conditions. EA, early adaptation; minute 4, the fourth minute of the adaptation phase; minute 7, the seventh minute of the adaptation phase; LA, late adaptation; EP, early post-adaptation; LP, late post-adaptation.

Mechanical work during the pendular phase versus step-to-step transition

If we isolate only the mechanical work done by the two legs over both of the two pendular phases occurring within a stride, the changes in pendular phase work during early adaptation mirrored the changes we observed for work done over the full stride (Fig. 3B,E). If we further distinguish pendular phase work done by each leg, the leg walking on the fast belt demonstrated the greatest increase and accounted for nearly all of the changes in work from both legs during adaptation. In contrast, the slow leg showed only a small, but significant, change in work performed compared with baseline (Fig. 3C,F).

During all baseline trials, a larger percentage of the subjects' positive work over the whole stride was performed during the step-to-step transition than during the pendular phase (Fig. 4). In early adaptation, there was an abrupt, significant increase in the relative positive work done during the pendular phase (P<0.001) and a significant decrease in step-to-step transition compared with baseline (P<0.001; Fig. 4). Over the course of split-belt adaptation, the pendular phase positive work significantly decreased and the step-to-step-transition positive work significantly increased (P=0.002 for both), although not back to fast baseline levels (Fig. 4). In early post-adaptation, there was a small abrupt increase in pendular phase work, although this was not significantly different compared to work in the slow baseline trial (P=0.053). By late post-adaptation, we observed a small, significant decrease that returned pendular phase work to slow baseline levels (P=0.048; Fig. 4).

Fig. 4.

Fig. 4.

Open in a new tab

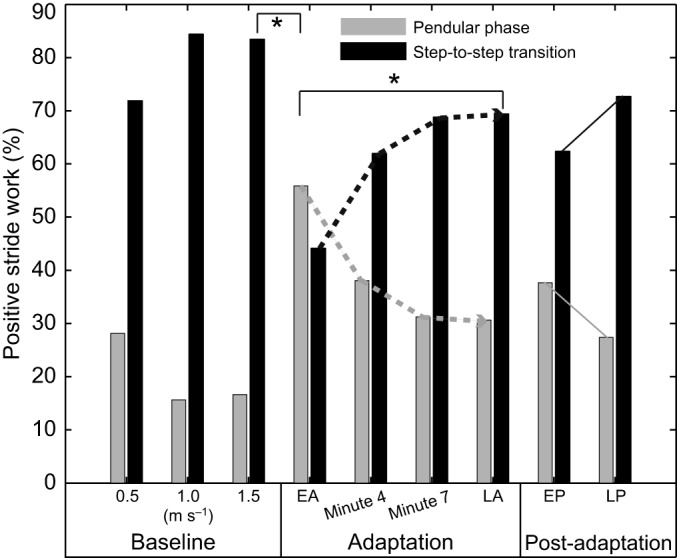
Positive work performed during the pendular phase and the step-to-step transition as a percentage of the full-stride positive mechanical work. Data are means across all 13 subjects for the first 10 steps from each trial. The numbers on the x-axis represent the belt speeds for baseline periods. *P<0.05 in comparison to early adaptation. EA, early adaptation; minute 4, the fourth minute of the adaptation phase; minute 7, the seventh minute of the adaptation phase; LA, late adaptation; EP, early post-adaptation; LP, late post-adaptation.

DISCUSSION

The primary goal of this study was to investigate how humans adapt the mechanical work done by the legs when exposed to a novel asymmetric walking perturbation by a split-belt treadmill. We used a nearly identical adaptation protocol to previous studies measuring whole-body metabolic work (Finley et al., 2013) with a 1.5:0.5 m s−1 ratio in the belt speeds used for the split-belt adaptation and observed very similar results in the adaptation of SLS (Fig. 2). We further showed that the decrease in summed mechanical work done by the legs over the entire stride during split-belt treadmill adaptation mirrored these kinematic changes in SLS, supporting our initial hypothesis. Notably, these changes in mechanical work adaptation by the legs also followed the same trends observed for whole-body metabolic power by Finley and colleagues (Finley et al., 2013). Moreover, we were able to isolate the primary source of these mechanical work changes occurring during split-belt treadmill adaptation to the changes in work done by the leg on the fast belt. We show that the changes in mechanical work combined with the previously observed changes in whole-body metabolic power can be explained by a shift in the control strategy dictating when in the gait cycle the legs perform work on the COM.

Adaptation is a sensorimotor learning process that involves the ability to predict changes in the environment. Subjects returning to common, tied-belt walking after split-belt treadmill walking display an over-compensation in gait asymmetry (Fig. 2). This kinematic aftereffect demonstrates that a neural adaptive change in predictive locomotor control has occurred because the subject is inappropriately responding to a difference in belt velocities that no longer exists. Several studies indicate that humans adapt their locomotor patterns to minimize whole-body metabolic energy cost (Donelan et al., 2002b; Finley et al., 2013; Farris and Sawicki, 2012; Ellis et al., 2013), but the biomechanical mechanisms underlying the reduction in metabolic power during adaptation have been sparsely studied. Despite the importance of minimizing whole-body energetics during split-belt walking adaptation, this is the first study to quantify the changes in mechanical work performed by the legs and to identify a shift in mechanical work strategy that explains the decreased energetic cost of walking during locomotor adaptation.

Mechanical work done by the fast leg likely drives change in metabolic power

Our findings suggest that mechanical work done by the leg on the fast belt is the primary driver of the reduction in metabolic power during split-belt treadmill walking adaptation. Subjects initially display a large increase in leg work during early adaptation. The majority of this initial increase is due to an increase in pendular phase work by the leg on the fast belt, with only a small increase on the slow belt. The subsequent gradual decrease in fast-leg mechanical work over adaptation reflects the decreasing metabolic power previously observed (Finley et al., 2013). Additionally, Finley and colleagues observed a disproportionate, asymmetric increase in activity of leg muscles on the fast belt, which agrees with our findings on the asymmetric mechanical work output across the two legs. Our empirical observations of mechanical work, therefore, agree with independent observations of metabolic cost and muscle activity under very similar experimental conditions of locomotor adaptation.

Switch from step-to-step transition work to pendular work during early adaptation

The initial changes in mechanical work during early adaptation to split-belt treadmill walking demonstrate a switch to a less economical strategy of performing more leg work during the pendular phase of gait. Under ideal conditions of steady, constant-speed walking, the most economical way to walk would be to perform work to redirect the COM velocity during the step-to-step transition (Donelan et al., 2002a,b; Kuo et al., 2005). Simulations of idealized bipedal walkers predict that mechanical work performed during the pendular phase of gait is four times more energetically costly than work done to redirect the COM during a step-to-step transition (Kuo, 2002; Ruina et al., 2005). This switch to the pendular work strategy likely explains the initial increase in metabolic cost during early split-belt treadmill adaptation. Our findings also agree with others that have observed human subjects to switch to the pendular phase work strategy when walking with constant acceleration (Oh et al., 2012) or when an asymmetric stepping pattern is enforced through a metronome (Ellis et al., 2013).

Given that humans move more economically as they adapt to new environments in a variety of experiments (Huang et al., 2012; Emken et al., 2007; Selinger et al., 2015), it is, perhaps, unsurprising to observe that humans reduce both mechanical work overall and pendular phase work as they adapt to split-belt treadmill walking. What is less clear is the subjects' early adaptation to the split-belt condition; subjects must learn to move away from their baseline behavior toward a response that is more economical in the new environment (Donelan, 2016), but they also must avoid falling, which may be a higher priority initially. Ogawa and colleagues recently suggested that changes in the forces generated by the slow leg during early split-belt adaptation reflect a strategy that favors maintaining balance (Ogawa et al., 2014). It could be that the increased pendular work of the fast leg is necessary to overcome high slow-leg braking in early adaptation. Additionally, after experiencing a slip, people will respond by walking with increased muscle co-contraction (Chambers and Cham, 2007). Because co-contraction is metabolically expensive, this demonstrates that humans will prioritize avoiding falls over reducing expended energy in response to a perturbation. This may be the case in early split-belt adaptation, where subjects can often exhibit an awkward stumbling response upon abrupt exposure to the different belts speeds, which would be consistent with an initially high energetic cost in order to maintain balance and stability.

Limitations and future work

It is difficult to make definitive conclusions on what subjects prioritized in early adaptation because we did not quantify balance during split-belt walking, which subjects may improve to prevent falls before reducing energetic cost. Subjects did, however, clearly make a shift in their locomotor strategy to prioritize economy of work in late adaptation. We previously observed that humans adapting leg force control during hopping initially adopt a control strategy favoring performance improvement, but later shift to a control strategy favoring performance maintenance (Selgrade and Chang, 2015). It is plausible to speculate that the shift in the timing of fast-leg work to return to the more economical step-to-step transition strategy occurred once subjects had achieved some minimal level of performance in anticipating the belt speed transitions. Future work to identify the optimization parameters in early adaptation would benefit our larger understanding of the prioritization of different drivers of locomotor control and adaptation.

One unexpected result was that net work, which should be zero if subjects maintain position on a tied-belt treadmill, was non-zero in the baseline conditions. We determined that a small amount of energy was being lost to the treadmill owing to slipping of the treadmill belt over the rollers causing a momentary deceleration (<5% of belt speed) with each heel strike and slight acceleration upon approaching toe off. The result was that the force plate under the treadmill underestimated posterior braking force at heel strike, some of which was dissipated by the belt deceleration, and similarly overestimated push-off force at toe off. Upon inspection of GRFs, these slight differences were unnoticeable but, when integrated over time to calculate work, it resulted in a non-zero net work during the baseline conditions. The effect of belt deceleration on force measurement, however, was consistent across conditions. Thus, it did not affect the trends we observed in the changes in work across different conditions and does not change our conclusions, which are based on comparisons between conditions.

Although changes in mechanical work appear to be responsible for metabolic changes during split-belt adaptation, few studies assess any kind of mechanical work during split-belt walking (Roemmich et al., 2014; Selgrade et al., 2017). Given the large contributions of the hip and ankle in walking (Farris and Sawicki, 2012; Neptune et al., 2001), analysis of work at these joints would also be valuable, particularly in relation to increased understanding of joint control for legged robotics and in rehabilitation for clinical populations. For example, split-belt walking has the potential to correct step length asymmetries in stroke survivors (Reisman et al., 2013), but understanding the changes in joint work underlying this improved symmetry could show what compensations stroke survivors use to achieve symmetry after split-belt adaptation and where therapeutic interventions might focus to increase efficacy.

Conclusions

This study provides a biomechanical framework describing the initial locomotor response to an asymmetric walking perturbation followed by the neural adaptation to this perturbation driven by minimization of mechanical work. Compared with tied-belt walking, mechanical work done by the legs over the entire stride and particularly in the pendular phase increase with abrupt exposure to split-belt treadmill walking. As subjects adapt to asymmetric walking, they reduce mechanical work of the legs throughout the stride primarily through a reduction of work done during the pendular phase. Preferred gait is characterized by step lengths, widths and frequencies that minimize energy expenditure (Donelan et al., 2001, 2002b); based on this preference for lower energetic cost, the purpose of adaptation may be to lower metabolic cost (Selinger et al., 2015; Finley et al., 2013). Given that whole-body metabolic power and pendular phase work change in the same way during split-belt adaptation, and the previously established relationship between metabolic cost and mechanical work (Ellis et al., 2013; Donelan et al., 2001, 2002b), local changes in mechanical work performed by the legs may be proximate drivers of locomotor adaptation. Switching from pendular phase work to more economical step-to-step transition work reflects a testable framework for how locomotor adaptation may involve an interplay between balance control and energy minimization.

Acknowledgements

The authors thank Dr Teresa Snow for assistance with statistical design and analysis as well as the members of the Comparative Neuromechanics Lab for all their helpful feedback throughout the completion of this work. They also thank Andy Ruina, Art Kuo, Greg Sawicki and Steve Collins for providing helpful insights on this work, and J. Maxwell Donelan for providing thoughtful comments for improving the manuscript.

Footnotes

Competing interests

The authors declare no competing or financial interests.

Author contributions

Conceptualization: M.T., G.E.L., M.E.T., Y.-H.C.; Methodology: M.T., G.E.L., M.E.T., Y.-H.C.; Software: B.P.S., M.T., M.E.T.; Validation: B.P.S., M.E.T.; Formal analysis: B.P.S., M.T., G.E.L., M.E.T.; Investigation: M.T., M.E.T., Y.-H.C.; Data curation: G.E.L.; Writing - original draft: B.P.S., M.T.; Writing - review & editing: B.P.S., M.E.T., Y.-H.C.; Visualization: Y.-H.C.; Supervision: Y.-H.C.; Project administration: Y.-H.C.; Funding acquisition: Y.-H.C.

Funding

This work was supported by National Institute of Neurological Disorders and Stroke (NINDS) 5R01NS069655 and National Institute of Child Health and Human Development (NICHD) 5T32HD055180. Deposited in PMC for release after 12 months.

References

  1. Adamczyk P. G. and Kuo A. D. (2009). Redirection of center-of-mass velocity during the step-to-step transition of human walking. J. Exp. Biol. 212, 2668-2678. 10.1242/jeb.027581 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Chambers A. J. and Cham R. (2007). Slip-related muscle activation patterns in the stance leg during walking. Gait Post. 25, 565-572. 10.1016/j.gaitpost.2006.06.007 [DOI] [PubMed] [Google Scholar]
  3. Collins S. H., Adamczyk P. G., Ferris D. P. and Kuo A. D. (2009). A simple method for calibrating force plates and force treadmills using an instrumented pole. Gait Post. 29, 59-64. 10.1016/j.gaitpost.2008.06.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Donelan J. M. (2016). Motor control: no constant but change. Curr. Biol. 26, R915-R918. 10.1016/j.cub.2016.09.001 [DOI] [PubMed] [Google Scholar]
  5. Donelan J. M., Kram R. and Kuo A. D. (2001). Mechanical and metabolic determinants of the preferred step width in human walking. Proc. R. Soc. Biol. Sci. 268, 1985-1992. 10.1098/rspb.2001.1761 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Donelan J. M., Kram R. and Kuo A. D. (2002a). Simultaneous positive and negative external mechanical work in human walking. J. Biomech. 35, 117-124. 10.1016/S0021-9290(01)00169-5 [DOI] [PubMed] [Google Scholar]
  7. Donelan J. M., Kram R. and Kuo A. D. (2002b). Mechanical work for step-to-step transitions is a major determinant of the metabolic cost of human walking . J. Exp. Biol. 205, 3717-3127. [DOI] [PubMed] [Google Scholar]
  8. Ellis R. G., Howard K. C. and Kram R. (2013). The metabolic and mechanical costs of step time asymmetry in walking. Proc. R. Soc. B Biol. Sci. 280, 20122784 10.1098/rspb.2012.2784 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Emken J. L., Benitez R., Sideris A., Bobrow J. E. and Reinkensmeyer D. J. (2007). Motor adaptation as a greedy optimization of error and effort. J. Neurophysiol. 97, 3997-4006. 10.1152/jn.01095.2006 [DOI] [PubMed] [Google Scholar]
  10. Farris D. J. and Sawicki G. S. (2012). The mechanics and energetics of human walking and running: a joint level perspective. J. R. Soc. Interface 9, 110-118. 10.1098/rsif.2011.0182 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Finley J. M., Bastian A. J. and Gottschall J. S. (2013). Learning to be economical: the energy cost of walking tracks motor adaptation. J. Physiol. 591, 1081-1095. 10.1113/jphysiol.2012.245506 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Giest T. N. and Chang Y.-H. (2016). Biomechanics of the human walk-to-run gait transition in persons with unilateral trans-tibial amputation. J. Biomech. 49, 1757-1764. 10.1016/j.jbiomech.2016.04.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Huang H. J., Kram R. and Ahmed A. A. (2012). Reduction of metabolic cost during motor learning of arm reaching dynamics. J. Neurosci. 32, 2182-2190. 10.1523/JNEUROSCI.4003-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kram R., Griffin T. M., Donelan J. M. and Chang Y. H. (1998). Force treadmill for measuring vertical and horizontal ground reaction forces. J. Appl. Physiol. 85, 764-769. [DOI] [PubMed] [Google Scholar]
  15. Kuo A. D. (2002). Energetics of actively powered locomotion using the simplest walking model. J. Biomech. Engr. 124, 113-120. 10.1115/1.1427703 [DOI] [PubMed] [Google Scholar]
  16. Kuo A. D. (2007). The six determinants of gait and the inverted pendulum analogy: a dynamic walking perspective. Hum. Mov. Sci. 26, 617-656. 10.1016/j.humov.2007.04.003 [DOI] [PubMed] [Google Scholar]
  17. Kuo A. D., Donelan J. M. and Ruina A. (2005). Energetic consequences of walking like an inverted pendulum: step-to-step transitions. Exer. Sport Sci. Rev. 33, 88-97. 10.1097/00003677-200504000-00006 [DOI] [PubMed] [Google Scholar]
  18. Malone L. A. and Bastian A. J. (2010). Thinking about walking: effects of conscious correction versus distraction on locomotor adaptation. J. Neurophysiol. 103, 1954-1962. 10.1152/jn.00832.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Neptune R. R., Kautz S. A. and Zajac F. E. (2001). Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. J. Biomech. 34, 1387-1398. 10.1016/S0021-9290(01)00105-1 [DOI] [PubMed] [Google Scholar]
  20. Ogawa T., Kawashima N., Ogata T. and Nakazawa K. (2014). Predictive control of ankle stiffness at heel contact is a key element of locomotor adaptation during split-belt treadmill walking in humans. J. Neurophysiol. 111, 722-732. 10.1152/jn.00497.2012 [DOI] [PubMed] [Google Scholar]
  21. Oh K., Baek J. and Park S. (2012). Gait strategy changes with acceleration to accommodate the biomechanical constraint on push-off propulsion. J. Biomech. 45, 2920-2926. 10.1016/j.jbiomech.2012.06.032 [DOI] [PubMed] [Google Scholar]
  22. Reisman D. S., Block H. J. and Bastian A. J. (2005). Interlimb coordination during locomotion: what can be adapted and stored? J. Neurophysiol. 94, 2403-2415. 10.1152/jn.00089.2005 [DOI] [PubMed] [Google Scholar]
  23. Reisman D. S., Wityk R., Silver K. and Bastian A. J. (2007). Locomotor adaptation on a split-belt treadmill can improve walking symmetry post-stroke. Brain 130, 1861-1872. 10.1093/brain/awm035 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Reisman D. S., McLean H., Keller J., Danks K. A. and Bastian A. J. (2013). Repeated split-belt treadmill training improves poststroke step length asymmetry. Neurorehab. Neur. Rep. 27, 460-468. 10.1177/1545968312474118 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Roemmich R. T., Hack N., Akbar U. and Hass C. J. (2014). Effects of dopaminergic therapy on locomotor adaptation and adaptive learning in persons with Parkinson's disease. Behav. Brain Res. 268, 31-39. 10.1016/j.bbr.2014.03.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ruina A., Bertram J. E. A. and Srinivasan M. (2005). A collisional model of the energetic cost of support work qualitatively explains leg sequencing in walking and galloping, pseudo-elastic leg behavior in running and the walk-to-run transition. J. Theor. Biol. 237, 170-192. 10.1016/j.jtbi.2005.04.004 [DOI] [PubMed] [Google Scholar]
  27. Schneiders A. G., Sullivan S. J., O'Malley K. J., Clarke S. V., Knappstein S. A. and Taylor L. J. (2010). A valid and reliable clinical determination of footedness. PM&R 2, 835-841. 10.1016/j.pmrj.2010.06.004 [DOI] [PubMed] [Google Scholar]
  28. Selgrade B. P. and Chang Y.-H. (2015). Locomotor control of limb force switches from minimal intervention principle in early adaptation to noise reduction in late adaptation. J. Neurophysiol. 113, 1451-1461. 10.1152/jn.00246.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Selgrade B. P., Toney M. E. and Chang Y. H. (2017). Changes in mechanical work during locomotor adaptation split-belt treadmill walking in trans-tibial amputees. J. Biomech. 53, 136-143. 10.1016/j.jbiomech.2017.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Selinger J. C., O'Connor S. M., Wong J. D. and Donelan J. M. (2015). Humans can continuously optimize energetic cost during walking. Curr. Biol. 25, 2452-2456. 10.1016/j.cub.2015.08.016 [DOI] [PubMed] [Google Scholar]
  31. Soo C. H. and Donelan J. M. (2012). Coordination of push-off and collision determine the mechanical work of step-to-step transitions when isolated from human walking. Gait Post. 35, 292-297. 10.1016/j.gaitpost.2011.09.102 [DOI] [PubMed] [Google Scholar]
  32. Toney M. E. and Chang Y.-H. (2013). Humans robustly adhere to dynamic walking principles by harnessing motor abundance to control forces. Exp. Brain Res. 231, 433-443. 10.1007/s00221-013-3708-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Toney M. E. and Chang Y.-H. (2016). The motor and the brake of the trailing leg in human walking: leg force control through ankle modulation and knee covariance. Exp. Brain Res. 234, 3011-3023. 10.1007/s00221-016-4703-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zeni J. A. and Higginson J. S. (2010). Gait parameters and stride-to-stride variability during familiarization to walking on a split-belt treadmill. Clin. Biomech. 25, 383-386. 10.1016/j.clinbiomech.2009.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Experimental Biology are provided here courtesy of Company of Biologists

RESOURCES