The Statistical Basis for Serial Monitoring in Audiology

Abstract

Objectives

Audiologists regularly use serial monitoring to evaluate changes in a patient’s auditory function over time. Observed changes are compared with reference standards to determine whether further clinical action is necessary. Reference standards are established in a control sample of otherwise healthy subjects to identify the range of auditory shifts that one might reasonably expect to occur in the absence of any pathological insult. Statistical approaches to this seemingly mundane problem typically invoke 1 of 3 approaches: percentiles of the cumulative distribution, the variance of observed shifts, and the “standard error of measurement.” In this article, the authors describe the statistical foundation for these approaches, along with a mixed model–based alternative, and identify several necessary, although typically unacknowledged assumptions. Regression to the mean, the phenomenon of an unusual measurement typically followed by a more common one, can seriously bias observed changes in auditory function and clinical expectations. An approach that adjusts for this important effect is also described.

Design

Distortion product otoacoustic emissions (DPOAEs) elicited at a single primary frequency, f₂ of 3175 Hz, were collected from 32 healthy subjects at baseline and 19 to 29 days later. Ninety percent test–retest reference limits were computed from these data using each statistical approach. DPOAE shifts were also collected from a sample of 18 cisplatin patients tested after 120 to 200 mg of cisplatin. Reference limits established according to each of the statistical approaches in the healthy sample were used to identify clinically alarming DPOAE shifts in the cisplatin patient sample.

Results

Reference limits established with any of the parametric methods were similar. The percentile-based approach gave the widest and least precisely estimated intervals. The highest sensitivity for detecting clinically alarming DPOAE shifts was based on a mixed model approach that adjusts for regression to the mean.

Conclusions

Parametric methods give similar serial monitoring criteria as long as certain critical assumptions are met by the data. The most flexible method for estimating test–retest limits is based on the linear mixed model. Clinical sensitivity may be further enhanced by adjusting for regression to the mean.

INTRODUCTION

In this article, we consider a standard clinical problem: is the change in auditory function that is observed in a particular patient sufficiently alarming to warrant further clinical action? The usual approach is to compare the patient’s change in auditory function with a “normal” population that is homeostatic with respect to the auditory function in question. If the patient’s observed change is within standard test–retest changes, no further action is recommended. If that patient’s change is unusual compared with a homeostatic population, then additional examination may be recommended. Situations in which serial auditory monitoring arise include occupational noise exposure, ototoxic drug exposure, and autoimmune disorders, among others.

As an illustration, consider the problem of ototoxicity monitoring in adult patients treated with cisplatin. Cisplatin is a known ototoxic chemotherapeutic agent that may be dose-limited by cochlear damage. A reasonable monitoring protocol involves distortion product otoacoustic emission (DPOAE) measurements taken at discrete primary frequencies before treatment begins and at follow-up sessions during the course of chemotherapy. For example, 1 patient’s pretreatment DPOAE level was −5.4 dB SPL in response to an f₂ stimulus tone of 3175 Hz presented at a moderate level. After 170 mg cumulative dose of cisplatin, the patient showed a drop in DPOAE level of 3.6 dB down to −9.0 dB SPL. Does a decrease of 3.6 dB warrant audiological follow-up or consultation with the oncologist? In the absence of a gold standard measure of cochlear damage, the observed shift must be compared with an accepted threshold of change established in a suitable control sample.

A standard clinical threshold for DPOAE shifts was established by Beattie and Bleech (2000), suggesting that any shift outside of ± 6 dB should be considered a statistically significant shift. This reference range was computed as $1.96\sqrt{2}$ times the “standard error of measurement,” (SEM; Demorest & Walden 1984), estimated from a reference sample of 55 normal-hearing women. However, like hearing research, statistics is a dynamic field, and much has changed in statistical theory and computational methods since Demorest and Walden’s influential work. We believe that clinical screening practice would benefit from an updated perspective on statistical approaches to establishing test–retest standards. This perspective will familiarize hearing researchers with the statistical foundation of the SEM and other methods, and offer alternatives to traditional approaches.

As it turns out, the suitability of different approaches such as the SEM requires several frequently unexamined, and perhaps unjustifiable, assumptions. Furthermore, regression to the mean, the phenomenon that an unusual measurement is commonly followed by a more typical measurement, virtually ensures that observed shifts in auditory function depend on baseline measurements. These statistical components can have a marked impact on the reference thresholds for test–retest changes, and thus impact clinical practice. While we use serial monitoring of DPOAEs in cisplatin patients for illustration, the methodological issues discussed in the article are appropriate, and the discussion is relevant to any kind of serial auditory measurement.

MATERIALS AND METHODS

Control Sample

The control sample was used to generate 90% reference ranges of DPOAE test–retest shifts according to the statistical methods described later in this article. Control sample data were obtained from 42 ears of 42 healthy, nonhospitalized adults (20 men and 22 women) recruited as part of a larger ototoxicity monitoring study at the Portland VA Medical Center. Subjects underwent 2 tests, baseline and follow-up approximately 3 to 4 weeks apart (mean = 22 days; range 19 to 29 days). This test range was chosen because it most closely coincided with the chemotherapy regime (every 21 days) of our cancer patients receiving cisplatin. Test sessions included otoscopy, tympanometry, air conduction pure-tone thresholds, and DPOAEs in the better hearing ear. Complete details of DPOAE collection are provided elsewhere (Reavis et al. 2008). Briefly, DPOAE responses were obtained for f₂ ranging from 1,000 to 10,000 Hz. The primary frequency ratio was held constant at 1.22 and primary levels were L₁ = L₂ = 65 dB SPL. In-the-ear calibration was done at baseline and at each monitoring appointment to adjust the voltage applied to the ear phones to set the SPL of f₁ and f₂ to desired values. This procedure involved making SPL measurements at the plane of the microphone located at the entrance to the sealed ear canal. Although this technique is commonly used for calibrating DPOAE stimuli (and for measuring DPOAE responses), it can result in errors in the estimation of the SPL reaching the tympanic membrane due to the presence of “standing waves” in the enclosed ear canal. These are pressure nodes caused by interactions between incident and reflected waves (Siegel & Hirohata 1994; Siegel 2007). Calibration strategies that measure sound intensity level or the forward pressure level of the stimulus rather than SPL reduce the effects of standing waves, which theoretically would improve the overall variability in DPOAE measurements (Neely & Gorga 1998; Scheperle et al. 2008). Another strategy to mitigate effects of potential calibration errors is to verify that probe placement is similar across serial measurements, so that calibration is similar (if incorrect) at each test. For the present study, audiologists compared the ear-canal transfer function obtained at baseline with the ear-canal transfer function obtained at follow-up using cross-correlation of the 2 waveforms. The probe was refit and the calibration repeated up to 3 times to bring cross-correlation values to 80% or better. In this way, the baseline in-the-ear calibration provided a target ear-canal transfer function for each successive test to help ensure consistent probe placement and improve test–retest reliability. We purposely chose1 primary frequency, f₂ = 3175 Hz, to illustrate different statistical methods and emphasize that these example results are not intended for clinical application. We also do not recommend such limited frequency testing in clinical practice. The issues involved with multiple frequency testing are briefly addressed in the Discussion section.

Ten subjects were excluded from analysis. Nine subjects were missing emissions at either baseline or follow-up, and 1 subject had an unusually large emission at baseline, which skewed the data distribution. A total of 32 ears from 32 control subjects were included in the analysis. These were 20 normal-hearing subjects (audiometric thresholds ≤20 dB HL for all test frequencies from 250 to 8000 Hz) and 12 hearing-impaired subjects (at least 1 audiometric frequency had a threshold >20 dB HL). Subjects were on average 40 years of age (range 18 to 86) with a mean high-frequency pure-tone average (i.e., 2000, 4000, and 6000 Hz) threshold of 27 dB SPL (range 12 to 68 dB SPL) at baseline. Audiometric thresholds were within 5 dB test–retest limits for all subjects. DPOAE levels at baseline and follow-up are shown in Table 1.

TABLE 1.

Baseline and follow-up distortion product otoacoustic emissions levels at f2 = 3175 Hz taken among 32 reference subjects

ID	Hearing Category	Baseline dB SPL	Follow-Up dB SPL	OAE Shift	Baseline h(dB SPL)	Follow-Up h(dB SPL)	Shift in Transformed OAEs
1	NML	1.7	1.1	−0.6	1.7	1.1	−0.6
2	NML	−2.4	−4.3	−1.9	−2.3	−4.0	−1.7
3	IMP	−7.1	−7.7	−0.6	−6.4	−6.9	−0.5
4	IMP	−6.8	−8.3	−1.5	−6.2	−7.3	−1.2
5	IMP	2.8	0.3	−2.5	2.9	0.3	−2.6
6	IMP	−6.6	−6.1	0.5	−6.0	−5.6	0.4
7	NML	−9.2	−2.0	7.2	−8.0	−1.9	6.1
8	IMP	−9.8	−7.3	2.5	−8.5	−6.6	1.9
9	NML	2.7	3.3	0.6	2.8	3.5	0.7
10	NML	−7.6	−5.6	2.0	−6.8	−5.2	1.6
11	IMP	−2.7	−3.0	−0.3	−2.6	−2.9	−0.3
12	IMP	2.6	3.0	0.4	2.7	3.1	0.4
13	NML	1.3	0.6	−0.7	1.3	0.6	−0.7
14	NML	3.2	4.0	0.8	3.4	4.2	0.9
15	IMP	2.3	−0.3	−2.6	2.4	−0.3	−2.7
16	IMP	−5.5	−6.9	−1.4	−5.1	−6.2	−1.2
17	NML	−1.9	0.1	2.0	−1.8	0.1	1.9
18	NML	2.5	4.1	1.6	2.6	4.4	1.8
19	NML	−3.2	−5.4	−2.2	−3.1	−5.0	−1.9
20	NML	1.1	0.9	−0.2	1.1	0.9	−0.2
21	NML	−5.6	−5.4	0.2	−5.2	−5.0	0.2
22	IMP	−1.5	−2.5	−1.0	−1.5	−2.4	−0.9
23	NML	−1.8	−3.0	−1.2	−1.8	−2.9	−1.1
24	NML	4.2	2.8	−1.4	4.5	2.9	−1.6
25	NML	1.2	2.5	1.3	1.2	2.6	1.4
26	NML	3.3	6.2	2.9	3.5	6.8	3.3
27	IMP	−1.6	−2.5	−0.9	−1.6	−2.4	−0.8
28	IMP	−5.6	−2.8	2.8	−5.2	−2.7	2.5
29	NML	−1.2	1.9	3.1	−1.2	2.0	3.1
30	NML	5.6	6.2	0.6	6.1	6.8	0.7
31	NML	1.3	6.1	4.8	1.3	6.7	5.4
32	NML	0.8	0.1	−0.7	0.8	0.1	−0.7

Follow-ups were taken 19 to 29 days after baseline. Transformed levels are based on Manly’s exponential transformation with φ = 0.03.

IMP, impaired hearing subjects; NML, normal hearing subjects; OAE, otoacoustic emissions.

Patient Sample

DPOAE level shifts in cisplatin patients were used to demonstrate how clinical decisions are affected by the reference range estimation method. The patient sample included 18 ears from 18 male patients undergoing cancer treatment with cisplatin recruited as part of a larger ototoxicity monitoring study at the Portland VA Medical Center. With similar methodology to that used in the control sample, these patients had baseline and follow-up measurements that included otoscopy, tympanometry, air conduction pure-tone thresholds, and DPOAEs in the better hearing ear. DPOAE follow-up measurements at 3175 Hz, which coincided with a drug administration of 120 to 200 mg of cumulative cisplatin dose, were analyzed for level shifts compared with baseline measurements. Subjects were on average 58 years of age (range 22 to 70) with a mean high-frequency pure-tone average (i.e., 2000, 4000, and 6000 Hz) threshold of 41 dB SPL (range 20 to 63 dB SPL) at baseline. These data are shown in Table 2.

TABLE 2.

Distortion product otoacoustic emissions levels and level shifts at 3175 Hz for 18 cisplatin patients tested after 120 to 200 mg cumulative dose of cisplatin

ID	Dose	Baseline dB SPL	Follow-Up dB SPL	OAE Shift	Baseline h(dB SPL)	Follow-Up h(dB SPL)	Shift in Transformed OAEs
A	150	−3.1	−2.4	0.8	−3.0	−2.3	0.7
B	190	−5.1	−13.3	−8.2	−4.7	−11.0	−6.2
C	160	−13.7	−7.9	5.8	−11.2	−7.0	4.2
D	150	−5.1	−3.2	1.9	−4.7	−3.1	1.7
E	120	−12.5	−9.4	3.1	−10.4	−8.2	2.2
F	120	−18.5	−8.5	9.9	−14.2	−7.5	6.7
G	190	−13.6	−18.9	−5.2	−11.2	−14.4	−3.2
H	200	−11.4	−10.1	1.3	−9.7	−8.7	0.9
I	200	−11.8	−12.4	−0.6	−10.0	−10.4	−0.4
J	200	−0.7	−7.5	−6.8	−0.7	−6.7	−6.0
K	190	−14.8	−9.2	5.6	−12.0	−8.1	3.9
L	132	−0.1	4.1	4.2	−0.0	4.4	4.5
M	120	−5.6	−4.9	0.7	−5.2	−4.6	0.6
N	170	−5.4	−9.0	−3.5	−5.0	−7.8	−2.9
O	180	−4.0	−5.0	−1.0	−3.8	−4.6	−0.9
P	160	−7.9	−11.5	−3.6	−7.1	−9.7	−2.7
Q	160	0.3	2.5	2.2	0.3	2.6	2.3
R	200	−6.5	−8.2	−1.8	−5.9	−7.3	−1.4

OAE, otoacoustic emissions.

Statistical Approaches

From a statistical point of view, serial monitoring boils down to a relatively simple algorithm: a patient is measured at baseline and then again at a follow-up appointment. Change from baseline is computed and is compared with a reference standard quantity. If the patient’s change from baseline is greater than the reference standard, then a clinically important change in auditory status is suspected, leading perhaps to further evaluation or intervention. Hidden within this relatively straightforward, generic protocol are statistical issues pertaining to (1) the quantitative definition of change over time, and (2) the definition of the reference standard.

One can think of the quantitative definition of change over time as the difference between a follow-up measurement and what the clinician expects the measurement to be if the patient’s auditory function is stable. Under auditory homeostasis, one expects the measurement at the follow-up appointment to be about the same as the baseline measurement. This expectation suggests the raw shift metric, which is simply the follow-up measure subtracted from the baseline value. If the patient’s auditory function is truly stable, then the clinician expects the raw shift to be close to 0.

The raw shift is the most obvious choice of change metric, but it is not necessarily ideal. In general, under homeostasis it is reasonable to assume that baseline and follow-up measurements should be close to the population average. Under serial monitoring, the follow-up measurement is not observed “in a vacuum” but rather is observed after the baseline measurement has already been taken. Together, these properties suggest that, in a homeostatic population, baseline measures that are greater than the population average will tend to decrease at follow-up, whereas baseline measures that are smaller than the population average will tend to increase at follow-up. This result, formally known as “regression to the mean,” is intuitive, and does not require any special theoretical apparatus to appreciate its effect. Regression to the mean generally guarantees that the raw shift in auditory function depends on the baseline auditory function. Regression to the mean is a property of all measurements, regardless of the type, context, or distributional characteristics. Regression to the mean is extensively discussed in the statistics literature, and an accessible introduction is found in the work by Senn (2011).

The clinical implication of regression to the mean can be serious, because it tells us that, in general, the raw shift is a biased description of the longitudinal auditory function of a patient. If a patient has a larger than average measurement at baseline, then a smaller follow-up is to be expected even when there is no real change in the auditory function of the patient. It is thus desirable to have a quantitative definition of change over time that adjusts for regression to the mean. This metric, to be precisely defined later in this article, is called the adjusted shift.

Given a preference for the raw shift or the adjusted shift, the clinician will compare the observed shift with a suitable reference range. This range is the set of auditory changes that one can reasonably expect to observe in a homeostatic population. Upper and lower reference limits are boundaries containing a desired percentage of the reference population. For example, a 90% reference range is the interval of shifts covering 90% of the reference sample, whereas a 95% reference range is the interval of shifts covering 95% of the reference sample. A larger (e.g., 95%) reference range, which admits a wider range of possible normal values, will identify fewer abnormal patients in a clinical application than a narrower (e.g., 90%) reference range. The percentage of the reference population covered by the reference range depends on the clinical judgment of the audiologist and the acceptability of incorrect follow-up referrals and nonreferrals.

In some applications, only the upper or lower limit is of interest. For example, one is not usually concerned with a patient who scores in the highest percentile on a Speech Recognition test. In other contexts, both reference limits are necessary. In our example DPOAEs arise from vector summation of 2 (or more) generation components, which interfere with each other constructively or destructively within the ear canal (Shera & Guinan 1999). Changes in component amplitudes and phases could cause the DPOAE level at a particular measurement frequency to decrease or increase with damage (e.g., Rao & Long 2011). Helleman et al. (2012) found that enhancements in DPOAE level were often present at f₂ frequencies just below the range of f₂s that showed a decrease in DPOAE level among workers exposed to noise, consistent with the view that enhancements obtained after exposure to an ototoxic drug may indicate damage. Thus, in the DPOAE shift example, both enhancements and decay are clinically concerning and must be compared with suitable upper and lower reference limits.

The reference limits can be identified using parametric or nonparametric methods. Suppose one considers 2 auditory measurements, Y₁ and Y₂, taken at baseline and follow-up time points, respectively. Parametric methods for establishing the reference range almost universally depend on a bivariate normal model of the auditory measurements Y₁ and Y₂ with mean vector (μ₁, μ₂). Homeostasis in the reference population implies that the mean at baseline and follow-up are equivalent so that μ₁ = μ₂ = μ. Similarly, the unconditional variance of baseline and follow-up measurements is assumed to be constant and equal to σ². Covariance between baseline and follow-up measurements is ρ·σ², so that the population correlation between baseline and follow-up measurement is ρ.

According to the bivariate normal model, the raw shift is simply Y₂ − Y₁. The regression to the mean adjusted shift is defined as Y₂ − (Y₁ρ + μ[1 − ρ]) (Jones & Spiegelhalter 2009). Note that when ρ is equal to 1, the adjusted shift is equal to the raw shift. When ρ is close to 0, the adjusted shift is the difference between the observed follow-up measurement Y₂ and the population mean μ, which can be very different from the raw shift.

Under the bivariate normal model, 90% reference limits for the raw shift are given by the following:

$$\pm 1.645·\surd \text{Variance}(Y_2-Y_1)$$ (1)

(similarly, 95% reference limits are defined by substituting 1.96 for 1.645). The statistical problem is that of estimating Variance(Y₂ − Y₁), which standard statistical theory states is

$$\text{Variance}(Y_2-Y_1)=2{\sigma }^2(1-\rho ).$$ (2)

The statistical question is how to estimate the theoretical quantity in Eq. (2) that is subsequently substituted into Eq. (1). The bivariate normal model implies that the difference between the baseline and follow-up measurements is univariate normal with variance defined in Eq. (2). A simple estimator is the sample variance of the observed difference (y₂ − y₁) in the reference sample, and is denoted V_D or

$$V_D=\frac{\sum {((y_2-y_1)-(\overline{y_2-y_1}\left)\right)}^2}{N-1}$$ (3)

where the summation is taken over N subjects in the reference sample. However, by far the most common estimator of Variance(Y₂ − Y₁) used in hearing research is twice the squared SEM (Demorest & Walden 1984), which must not be confused with the standard error of the mean that is also commonly denoted “Sem.” The SEM is computed by substituting the sample variance of all the observed measurements (baseline and follow-ups combined, denoted s²) for σ² and substituting Pearson’s correlation coefficient r between baseline and follow-up measurements for ρ. Thus, Variance(Y₂ − Y₁) based on the SEM is given by the following:

$$V_{\text{SEM}}=2·{\text{SEM}}^2=2·s^2·(1-r)$$ (4)

V_SEM is widely used in hearing research. Some examples include otoacoustic emissions (Keppler et al. 2010), the Words In Noise test (Wilson & McArdle 2007), auditory evoked potentials (Beattie et al. 1992; D’haenens et al. 2008), and Questionnaire scales (Holcomb & Punch 2006; Smith et al. 2009). By substituting either V_D or V_SEM for Variance(Y₂ − Y₁) in Eq. (1), 90% reference limits can be computed. For example, 90% reference limits can be given by $\pm 1.645\sqrt{V_{\mathrm{D}}}$ or by $\pm 1.645\sqrt{V_{\text{SEM}}}$.

The bivariate normal model also suggests a repeated-measures analysis of variance (ANOVA) model for baseline and follow-up measurements. In this model, the unconditional variance σ² is decomposed into the within-subject and among-subject variance denoted ${\sigma }_w^2$ and ${\sigma }_{\alpha }^2$, respectively, so that ${\sigma }^2={\sigma }_w^2+{\sigma }_{\alpha }^2$. As per this model, $\rho ={\sigma }_{\alpha }^2/({\sigma }_w^2+{\sigma }_a^2)\ge 0$ and Eq. (2) is rewritten as follows:

$$\text{Variance}(Y_2-Y_1)=2{\sigma }_w^2.$$ (5)

Equation (5) is estimated by twice the mean squared error after applying the repeated-measures ANOVA model to the baseline and follow-up measurements with subject as a random factor. This estimator is denoted V_M, and can be extracted from repeated-measures ANOVA output or computed directly as:

$$V_{\mathrm{M}}=\frac{\sum ({(y_1-\frac{(y_1+y_2)}{2})}^2+{(y_2-\frac{(y_1+y_2)}{2})}^2)}{N}$$ (6)

(Appendix 1 gives the Statistical Packages for the Social Sciences code for fitting the repeated-measures ANOVA model to the data in Table 1 and for extracting the relevant parameters). As with the other methods, V_M can be substituted in Eq. (1) to give 90% reference limits for the raw shift, or ± 1.645√V_M. Note that Eqs. (2) and (5) are theoretically equivalent so that V_M, V_SEM, and V_D all estimate the same quantity, although in practice results may vary. This is especially true with relatively small sample sizes. However, these 3 estimators will be nearly equal with reasonably large amounts of data.

For the adjusted shift, reference limits of 90% are given by the following:

$$\pm 1.645\sqrt{\text{Variance}({\mathrm{Y}}_2-({\mathrm{Y}}_1\rho +\mu (1-\rho )))}$$ (7)

so that the statistical problem is that of estimating Variance (Y₂ − (Y₁ρ + μ(1 − ρ))). Jones and Spiegelhalter (2009) show that this is

$$\text{Variance}({\mathrm{Y}}_2-({\mathrm{Y}}_1\rho +\mu (1-\rho )))=(1+\rho ){{\sigma }_{\mathrm{w}}}^2.$$ (8)

An estimate of the necessary parameters for the variance of the adjusted shifts, denoted V_adjusted, is also provided by the repeated-measures ANOVA model output. σ_w² is estimated by the mean squared error, whereas ρ is estimated by the intra-class correlation coefficient. The key point is that one can derive the reference range for the adjusted shift using the exact same output one uses for estimating V_M. Further discussion of these derivations and relationship to test–retest literature is found in the work by Jones and Spiegelhalter.

Up to this point, the reference limit estimates have relied on the bivariate normal model. An appealing, nonparametric alternative defines the reference limits from the cumulative distribution function of the observed raw shifts. A nonparametric, 90% reference interval is given by the 5th and 95th percentiles of the cumulative distribution of the raw shifts. The percentile method is simple to apply and does not require any restrictive assumptions about the data distribution. However, one must be aware that percentile estimates are biased in small samples (Wright & Royston 1999; Li et al. 2010). Letting q∈[0,1] be the percentile to be estimated in a sample of N subjects, (N − q·N) < 2 implies that the percentile in question depends on the sample maximum, which underestimates the percentile. For example, q > 0.8 is biased if N = 10, q > 0.9 is biased if N = 20, and q > 0.99 is biased if N = 100. Furthermore, the nonparametric approach appears suitable only for the raw shift because computation of the adjusted shift requires parametric estimates of the population mean μ and correlation ρ.

To review the statistical approach so far: we have defined 2 change metrics for serial monitoring called the raw shift and the adjusted shift. Reference ranges for the raw shift can be estimated using the variance of the observed shifts (V_D), the SEM approach (V_SEM), or the model-based approach (V_M) plugged into Eq. (1). These methods require the bivariate normal data assumption. This assumption can be ignored by using instead the percentile method to estimate reference limits. A reference range for the adjusted shift is derived from the model-based approach. We emphasize that all of these methods are implemented using statistical and computational techniques commonly used by hearing researchers.

To contrast the various reference interval estimates, we evaluated the screening results of 18 cisplatin patients (Table 2) using DPOAE test–retest levels observed in the reference sample (Table 1). We also investigated the precision of each reference interval method, using bootstrap resampling of the reference sample. This was accomplished by sampling, with replacement, 32 rows from Table 1 and repeating the process 10,000 times. Reference intervals were computed for each of these 10,000 bootstrap samples. The mean width and the standard error of the widths of each reference interval method were then computed. Narrower 90% reference intervals indicated higher “true-positive rates” for that method, and smaller standard errors indicated more precisely estimated intervals. Thus, methods giving narrower intervals with smaller standard errors are statistically preferable to other approaches.

RESULTS

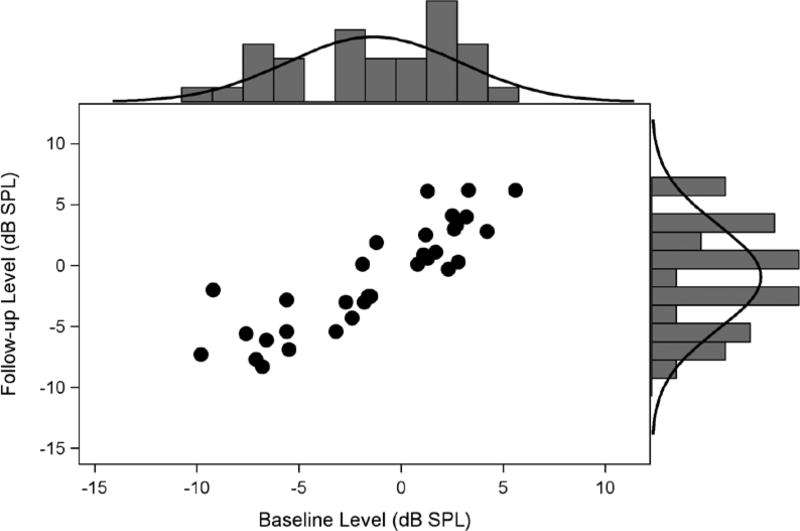
Figure 1 shows follow-up DPOAE levels (y axis) plotted against baseline DPOAE levels (x axis) for the data in Table 1. A histogram of the DPOAE levels at baseline and follow-up, with normal densities overlaid, are shown on the appropriate axes. There is some indication that the data in Figure 1 do not conform to the bivariate normal model. Distributions at each time point are skewed toward lower DPOAE levels, so that univariate Shapiro-Wilk tests indicate marginally significant departure from univariate normality for the baseline (p = 0.06) measures. Mardia’s test of multivariate skewness is also significant (p = 0.04). This indicates that the assumption of multivariate normality that is required for the reference range estimation methods might not be defensible.

Figure 1.

Untransformed DPOAE levels at baseline and after 21 days follow-up in 32 reference subjects (Table 1). DPOAE levels elicited at f₂ = 3175Hz and L₁, L₂ = 65, 65 dB SPL. DPOAE indicates distortion product otoacoustic emissions.

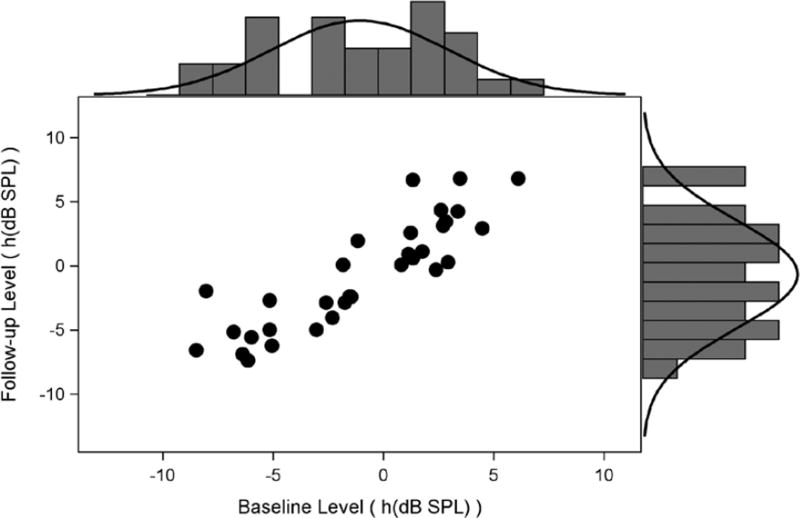
We have two alternatives to the apparent violation of bivariate normality: restrict estimation of reference limits to the nonparametric approach or induce normality with a suitable transformation. We compare both approaches. We applied Manly’s exponential transformation, which is useful for left-skewed, negative-valued data (Wright & Royston 1999), to the data according to $h(\mathit{\text{dBSPL}})=\frac{(e^{\phi (\mathit{\text{dBSPL}})}-1)}{\phi }$, with φ = 0.03. The coefficient φ was determined empirically by minimizing Mardia’s test statistic over a fine grid of candidate φ. It must be emphasized that this transformation was determined for the sample at this f₂ frequency only; other frequencies might suggest other transformations, or none at all, and must be considered on a case-by-case basis. The transformed scatter plot is shown in Figure 2. While the plots are roughly similar, the improvement of fit to the bivariate normal model is indicated by Mardia’s skewness test that is no longer statistically signficiant (p = 0.16). The reference interval estimation methods based on bivariate normality can be safely adopted. It is important to note that it is impossible to back-transform from the Transformed scale to dB SPL, which is more familiar for interpretation. However, we conceive of the screening methods as “Pass/Fail” screening tests, so the actual scale of the shift (or adjusted shift) may not be particularly relevant. This issue is discussed in detail subsequently.

Figure 2.

Transformed results from Figure 1 using the Manly’s exponential transformation and φ = 0.03.

Ninety percent reference limits using each method applied to the Original and Transformed scales are shown in Table 3. Also shown in Table 3 are the bootstrap estimates of the mean and standard error of the interval widths. Several important features are manifest in Table 3. First, all 3 parametric methods applied to the raw shift (V_M, V_SEM, V_D) give roughly similar intervals, as expected, because they are estimating the same quantity. Second, the reference interval widths and standard errors are somewhat smaller using the transformed data. This is not surprising, given the left-skewed nature of the Original dB SPL scale, and indicates that transformation will result in more precisely estimated reference intervals. Third, the widest intervals with the largest standard errors are given by the percentile method. Again, this is not surprising as nonparametric approaches are generally less efficient. Finally, the adjusted shift has the narrowest, most precisely estimated reference intervals. In general, the adjusted shift reference intervals will be narrower than those based on the raw shift, as can be seen by contrasting Eq. (8) with Eq. (5). Unless ρ = 1, the variance of the adjusted shift is always smaller than that of the raw shift.

TABLE 3.

Summary of reference limits and bootstrap mean interval widths and standard errors for transformed and untransformed distortion product otoacoustic emissions levels

Scale	Method	Lower	Upper	Mean Reference Interval Width	Standard Error of Mean Reference Interval Width
Original	Percentile	−2.50	4.80	4.7	1.7
	VD	−3.59	3.59	3.5	0.6
	VSEM	−3.57	3.57	3.4	0.6
	VM	−3.61	3.61	3.0	0.5
	VAdjusted	−3.49	3.49	3.0	0.5
Transformed	Percentile	−2.62	5.37	4.6	1.3
	VD	−3.44	3.44	3.3	0.5
	VSEM	−3.40	3.40	3.3	0.5
	VM	−3.45	3.45	2.9	0.5
	VAdjusted	−3.34	3.34	2.8	0.4

V_D, variance of observed shifts; V_M, variance using the model-based approach; V_SEM, variance based on the standard error of measurement.

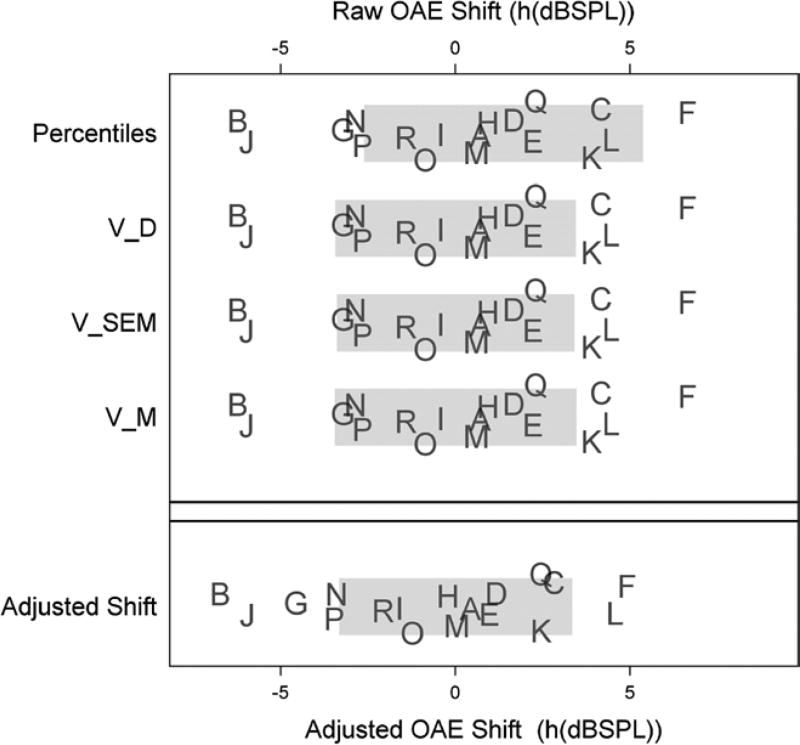
Clinical recommendations for the cisplatin patient data are shown using the transformed reference data in Figure 3. Each plot shows the raw shifts (top panel) and adjusted shifts (bottom panel) for each cisplatin patient in Table 2, identified by their ID letter (patient data are jittered vertically to show variability). Reference ranges based on each method in Table 3 (indicated on the vertical axis) are shown as gray bars. Patient shifts that are inside the gray bars are within reference limits. Patients outside the gray bars are unusual compared with the reference population and would be recommended for further testing and, possibly, intervention.

Figure 3.

Reference limits of 90% (Table 3) for the raw shift metric (top panel) and the adjusted-shift metric (bottom panel). All shifts are computed from the transformed distortion product otoacoustic emissions levels in Table 2. Letters correspond to IDs of cisplatin patient in Table 2. OAE shift indicates otoacoustic emissions; V_SEM, variance of standard error of measurement; V_D, variance of observed shifts; V_M, variance of the model-based approach.

As noted in Table 3, and as theoretically expected, V_M, V_SEM, and V_D give virtually identical reference limits and thus identical clinical recommendations: patients B and J show alarming decay in DPOAE levels, whereas patients K, C, L, and F show unusual enhancements. The percentile method does not flag the enhancements in patients K, C, and L, but identifies clinically significant decays in patients B and J and additionally in patients G, N, and P.

The adjusted shift method, which controls for regression to the mean, gives somewhat different clinical recommendations: as before, B, J, L, and F are flagged for further testing or clinical intervention. In addition, patients G, N, and P show alarming loss of DPOAE levels, whereas patients K and C do not. Patients K and C have some of the smallest baseline DPOAE levels (−14.8 and −13.7 dB SPL, respectively), and are thus expected to increase in level at follow-up due to regression to the mean. Conversely, patient G started with a low-level emission (−13.6 dB SPL) that unexpectedly decreased to −18.9 dB SPL. Clearly, regression to the mean can impact expected shifts over time.

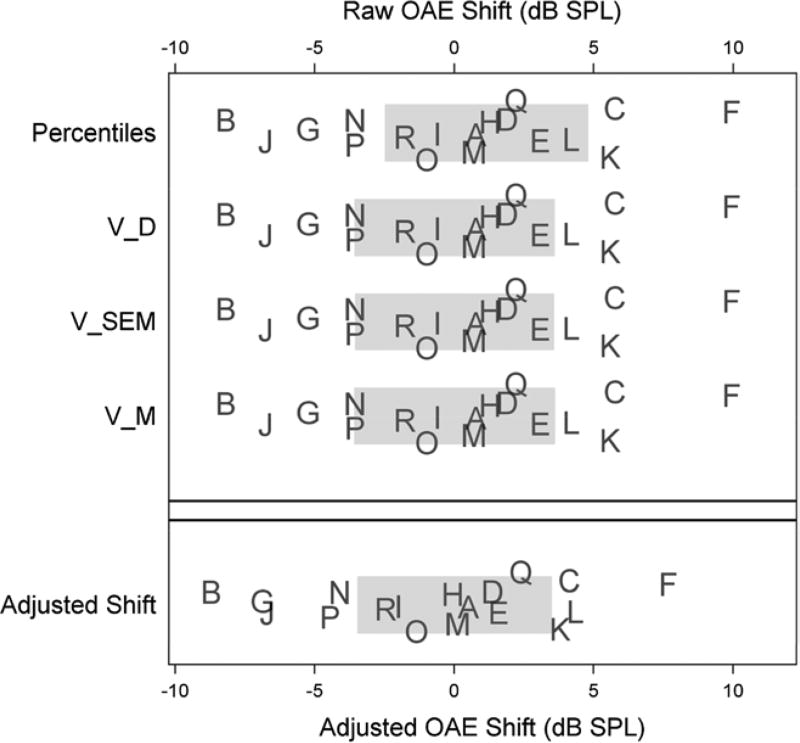
Figure 4 illustrates the effect that deviation from the bivariate normal model can have on clinical recommendations. Figure 4 is organized in the same way as Figure 3, except that the reference intervals are based on the untransformed DPOAE levels of Table 1 and Figure 1 (see Table 3). The reference intervals are somewhat wider due to the inflated variance estimates of the left-skewed levels. Clinical recommendations are different, particularly for patients close to the reference limits. Figure 4 need serve no other purpose than to raise awareness of the important effects that the bivariate normal assumptions have on reference range estimates and clinical recommendations.

Figure 4.

Ninety percent reference limits and clinical recommendations based on the untransformed data. Format is the same as in Figure 3. OAE indicates otoacoustic emissions; V_SEM, variance of standard error of measurement; V_D, variance of observed shifts; V_M, variance of the model-based approach.

DISCUSSION

Serial monitoring reference standards in audiology depend on the reference population, measurement techniques, and measurement characteristics. Here, we have also illustrated the role that statistical procedures and assumptions have on reference standards. We have described 4 reference limit estimators for the raw shift, based on the variance of the shifts (V_D), the SEM approach (V_SEM), the model-based approach (V_M), and the percentile approach. We have also described the effects of regression to the mean on longitudinal changes in auditory measurements, and a reference limit estimation method that corrects this effect (V_Adjusted). In the sample data provided, all of the proposed parametric methods V_D, V_SEM, and V_M give approximately equivalent results with similar bootstrap precision. The percentile method was shown to be less precise, with bootstrap standard errors of the reference intervals being roughly 3 times greater than the parametric approaches. The adjusted shift method corrected for the known effects of regression to the mean, and provided the narrowest, most precisely estimated reference ranges. Whether these observations hold in general will require more experience under a variety of clinical circumstances using different measurements of auditory function with different reference samples.

In practice, we prefer (and recommend) the model-based approach to estimating the relevant parameters for serial monitoring. The reasons for this are 3-fold. First, raw shift and adjusted shift reference intervals are easily identified from the same software output. No additional computation is required for either method. Second, the repeated-measures ANOVA model is a special case of the linear mixed model, which, when fit by maximum likelihood retains all of the data in the analysis. The V_SEM, V_D, and percentile methods all exclude reference subjects who are missing a baseline or a follow-up measure. This is an inefficient use of the available data. A third reason for preferring the model-based approach is its flexibility. Almost any serial measurement data structure can be modeled with a linear mixed model, as long as the mean and covariance structures are suitably identified. For example, the reference data in Table 1 include some normal-hearing and some impaired-hearing subjects. One might suspect that the variance of the shifts (and thus the reference limits) might differ between the 2 groups, as might the mean DPOAE level. In addition to the data in Table 1, we also collected data 1 day after the baseline measurement. The full data are thus composed of 3 measurements (at baseline, 1 day later, and 19 to 29 days later) partitioned between normal-hearing and hearing-impaired listeners. As with most longitudinal data, one expects the correlation to decrease with increasing temporal separation from the baseline measurement. This can cause the reference limits for serial monitoring after 1 day to be considerably narrower than the reference limits for monitoring after 21 days. The mixed model approach is easily expanded to model the correlation among repeated measurements. The simple model correlation ρ is now modeled as ρ^d, where d is the number of days between baseline and follow-up. We fit a linear mixed model to this data to test the following: (1) the effect of hearing impairment on the correlation, (2) the effect of hearing impairment on mean DPOAE levels, and (3) the effect of time on the serial correlation. The results showed a statistically significant effect of hearing impairment on mean level (impaired listeners have on average about 4.6 dB SPL lower emission than normal-hearing listeners) and that the correlation among measurements decays over time so that measures 1 day apart have a correlation of about 0.88, whereas measures 20 days apart have a correlation of about 0.56. This approach showed no significant effect of hearing impairment on the correlation among repeated measures, meaning that the reference limits in this example are the same for normal-hearing and impaired listeners. The linear mixed model thus allows us to conclude that (1) hearing impairment does not impact reference limits of the raw shift (because the covariance is similar between groups); (2) hearing impairment does have an impact on the adjusted shift by impacting the mean DPOAE level; and (3) that the reference limits for either the raw shift or the adjusted shift depend on the time separation between the time points at which the patient is being monitored. We emphasize, however, that these conclusions are based on a limited sample and limited measurements, and serve only to illustrate the utility of the mixed model approach to the problem of reference limit estimation.

The bivariate normal model must be correct for any parametric approach, and it is important to assess the bivariate normality assumption when using any of the described methods of reference interval estimation. Reference ranges can be markedly biased if these assumptions are not met because reference limits, by definition, are estimates of extreme quantiles of the data distribution. These estimates can be grossly inaccurate if the bivariate model is assumed but not met by the data. In fact, a great deal of statistical work in reference interval estimation is dedicated to assessing suitable transformations or robust alternatives to the bivariate normal model (Wright & Royston 1999). These methods are somewhat controversial, but are worthy of further exploration. In this light, the percentile approach is especially appealing because it does not require transformation and thus retains the measurements on their Original scales. We emphasize, however, that percentile approaches require samples that are considerably larger than those required for parametric approaches (Linnet 1987). Careful consideration of the advantages and disadvantages of the parametric and nonparametric approaches is necessary before designing reference interval studies.

Each serially monitored patient must be compared with standards established in a suitably matched reference population. Strictly speaking, the patient must have the exact same variances, means, and covariances as the reference population. This, of course, is impossible to determine for any 1 patient undergoing serial monitoring. The clinician usually selects a sensible subpopulation of reference subjects, such as age- or hearing-matched references and applies that reference standard to the patient being monitored. Of course, in any clinical situation the audiologist has only 1 patient’s DPOAEs, not a sample, so a judgment call must be made. The good news is that reference samples, being otherwise homeostatic and usually healthy, are comparatively easy to recruit and measure compared with sick patients.

It is common clinical practice to measure DPOAE levels at several primary frequencies. An important aspect of the mixed model approach described here is that it is easily extended to reference data measured at several frequencies by fitting the mixed model to the collection of DPOAE measurements and using a flexible model of the covariance structure across frequencies and between time points. This is not a particularly challenging statistical analysis, especially with modern statistical software for fitting general linear models. There remains the open question of how the clinician should interpret the collection of screening results on a particular patient when many primary frequencies are tested. A clinician might consider unusual shifts at several adjacent frequencies as more significant evidence for a physiological change than shifts at widely disparate frequencies. However, DPOAE levels and level shifts at adjacent frequencies are likely to be correlated (McMillan et al. 2012), so that the adjacency criterion might be overly sensitive. The concept of “multivariate reference regions” (as opposed to univariate reference limits) has been proposed in the literature, although they do not appear to be widely accepted. The issue of clinical screening with multiple tests and multiple primary frequencies is an unresolved issue worthy of further development.

The importance of reference range estimation cannot be overstated in any area of medicine. In this article, we have described the statistical basis for reference interval estimation, offered some alternative approaches, and described issues of concern when establishing reference standards. We recommend adjustment for regression to the mean, which is a necessary consequence of serial monitoring. We recognize that clinicians may be cautious about adopting the adjusted shift method, particularly because results can differ from the raw shift. While theoretically sound, a move toward widespread use of an adjusted shift approach will require considerable practice. We expect that the mixed model approach to reference limit estimation will be the most productive because it is the most flexible, is least susceptible to missing data, and attends to both change metrics considered here.