Products of Compartmental Models in Epidemiology

Abstract

We show that many structured epidemic models may be described using a straightforward product structure in this paper. Such products, derived from products of directed graphs, may represent useful refinements including geographic and demographic structure, age structure, gender, risk groups, or immunity status. Extension to multistrain dynamics, that is, pathogen heterogeneity, is also shown to be feasible in this framework. Systematic use of such products may aid in model development and exploration, can yield insight, and could form the basis of a systematic approach to numerical structural sensitivity analysis.

1. Introduction

Simple epidemic models aim at insight through simplicity; complex models aim at realism through detail [1]. Both simple and complex models are still being developed (e.g., [2–7]). Addition of epidemiological refinements, such as age structure, gender, geographic separation, or pathogen strains, in general changes the behavior of simple models, and thus we must systematically compare models with different features.

In this paper, we show that many structured epidemic models may be described using a straightforward product structure. Such products therefore provide a compact representation for a family of related models and could facilitate model comparison and structural sensitivity analysis. Examples include modeling host susceptibility groups, gender, age structure, multiple subtypes, and geographic separation. Our attention will be restricted to compartmental models [8–10], focusing on mathematical epidemiology [10–17].

The product we describe is related to standard graph products. The relation between compartmental models and graph theoretic or network concepts has been long appreciated [18, 19], and, moreover, Markov processes arising on product spaces have been analyzed by probabilists [20]. The graph structure arises when dynamical variables will be represented as vertices of a graph, representing the number of individuals in a given compartment. Individuals may change state, such changes being represented by an arc from one vertex to another, labeled with the instantaneous rate at which such a transition would occur.

2. Motivating Example: Community-Structured Epidemic Model

Consider a simple SI (susceptible to infective) model describing an epidemic with no recovery. Individuals transition from susceptible to infective and never return to the uninfected state. The number of infected individuals is denoted I of susceptible individuals S.

This compartmental model is diagrammed in Figure 1. The corresponding ODE system may be written

$$\begin{array}{c}\frac{dS}{dt}=-\beta SI,\\ \\ \frac{dI}{dt}=\beta SI-\gamma I.\\ \end{array}$$ (1)

Here, β is a transmission coefficient, and γ is the per capita mortality or removal rate due to disease. In this model, we ignore population birth and death due to other causes.

Figure 1.

Directed graph diagram of simple SI model.

A simple extension to include heterogeneous epidemic dynamics in multiple communities was introduced by Watson et al. [21, 22]. In this model, no migration between communities is assumed. However, individuals in one community cause infection in other communities, with the structure seen in Figure 2. The equations are

$$\begin{array}{c}\frac{d{S}_i}{dt}=-{\displaystyle \sum }_j{\beta }_{ij}{S}_i{I}_j,i=\mathrm{1},\dots ,n,\\ \\ \frac{d{I}_i}{dt}={\displaystyle \sum }_j{\beta }_{ij}{S}_i{I}_j-{\gamma }_i{I}_i,i=\mathrm{1},\dots ,n,\\ \end{array}$$ (2)

where n is the number of communities modeled. In the Watson model, in general the transmission coefficients may differ when considering transmission to susceptibles in one community from infectives in any community (whether the same or not). Each community is additionally assumed to have a different rate γ_i of removal of infectives due to mortality (or other causes), though these can be assumed to be identical if desired.

Figure 2.

Directed graph diagram of Watson model [22] defined by adding community structure to the SI model.

This model extends the one-community SI model, by structuring the population into multiple communities. In the following section, we will show that the structured model developed by Watson can be straightforwardly defined as the product of the single-community SI model and a model describing community structure. We will then illustrate other uses of this product, including age structure, gender, heterogeneity of risk, and cotransmission of multiple diseases.

3. Graph Products

A directed graph is defined as a set of vertices, each identified by a unique label, together with a set of arrows, or arcs, each connecting a source vertex to a target vertex. In this paper, we are concerned only with directed graphs, not undirected ones. A number of different products of directed graphs are defined, two of which are relevant.

3.1. Cartesian Product

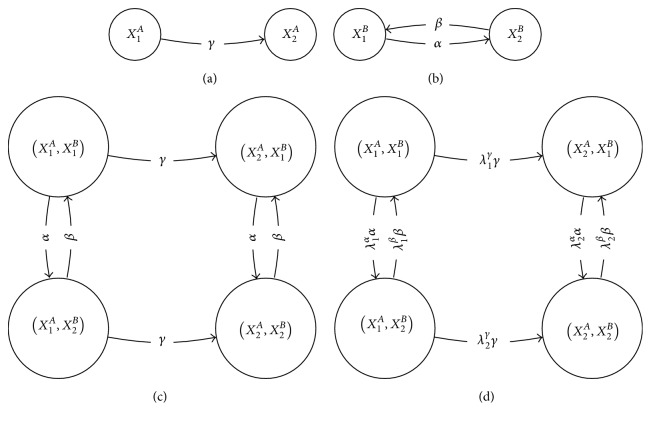
Consider finite directed graphs A and B, with n_A and n_B vertices, respectively. The Cartesian product of these graphs [23] is a graph A □ B whose vertex set is the set of ordered pairs (v, w) for all vertices v of A and w of B (that is, the Cartesian product of the vertex sets of the factor graphs A and B). The arcs of A □ B consist of an arc from (v, w_s) to (v, w_t) for every v, wherever there is an arc from w_s to w_t in the factor graph B and an arc from (v_s, w) to (v_t, w) for every w wherever there is an arc from v_s to v_t in A.

We can speak of “levels” in the sense that each vertex of a factor model corresponds to a subset, or level, of vertices of the product model. The product replicates all the arcs of B at every level of A and all the arcs of A at every level of B. Suppose we have two vertices (a_i, b_j) and (a_k, b_j), whose second coordinate is the same, that is, which map to the same level of B; it will be helpful to call these “siblings” and to say they “descend” from a common “factor vertex” B, similarly for vertices with the same first coordinate.

Figures 3(a), 3(b), and 3(c) illustrate two directed graphs and their Cartesian product, respectively.

Figure 3.

(a, b) Example directed graphs A and B, respectively; (c) Cartesian product A □ B; (d) strong product A⊠B.

More generally, graphs with multiple arcs joining a pair of vertices can be defined, and the Cartesian product definition above can be applied in this case as well.

3.2. Strong Product

The strong product of two directed graphs A and B includes more arcs than the Cartesian product [23]. This product A⊠B has the same vertex set, the Cartesian product of the factors' vertex sets, but in addition to the arcs of the Cartesian product graphs, it also includes all arcs from (v_s, w_s) to (v_t, w_t) where there is an arc from v_s to v_t and an arc from w_s to w_t.

Figure 3(d) illustrates the strong product of the graphs of Figures 3(a) and 3(b).

The symbols □ and ⊠ for these operations are chosen to evoke the structure of the product graphs, as illustrated in Figures 3(c) and 3(d). These graph products are discussed in more detail in the Appendix.

4. Products of Models

4.1. Linear Compartmental Models

A compartmental model (whether in population biology, epidemiology, or pharmacology) is often represented by a diagram such as in Figure 1, which has the form of a directed graph (formally, a directed multigraph) with labels on arcs. Multiple arcs may connect a single pair of compartments, representing multiple processes influencing that transition with potentially different rates. As before, the vertices of the graph are compartments and its arcs are transitions, with labels specifying the transition rates. (We consider a compartmental model to be an abstract object isomorphic to its directed multigraph diagram.) As is well known, a compartmental model diagram can be represented by a system of ordinary differential equations or a continuous Markov jump process (among others). (For instance, a compartmental model with a single compartment N, with a single inflow with rate Λ and outflow with rate μN, can be represented by the simple stochastic immigration-death process [24] or by the elementary ordinary differential equation model dN/dt = Λ − μN.)

The class of linear compartmental models we consider in this section includes the ordinary differential equation models of the form

$$\begin{array}{c}\frac{dX}{dt}=a+MX,\end{array}$$ (3)

where X is a vector of n state variables, a is a vector of constant inflows, and M is an n × n transition rate matrix. The general compartmental model, with sources and sink terms, can be represented in the same graphical way by considering special source and sink vertices in the graph.

A Cartesian product of linear compartmental models will be defined in a way that is similar to the Cartesian product of graphs. Suppose that A₁, A₂,…, A_K are the states in model A; let B₁,…, B_L be the states of model B. The Cartesian product of A with B will have states (A_i, B_j) with i = 1,…, K and j = 1,…, L. Two states (A_i, B_j) and (A_i, B_j′) are siblings in the same level A_i of the product. If we began, for example, with an epidemic model with states susceptible, infective, removed (SIR), and wished to construct a product with a geographic model of multiple regions, we would expect to have susceptibles, infectives, and removed individuals in each region.

The Cartesian product of graphs, as we saw, replicates each arc of each factor graph for each vertex of the other factor graphs. In a compartmental model of a population system, this would correspond to the very common assumption of competing independent exponential risks. For example, consider once again a simple SIR epidemic model, with infection and recovery, and a model of two communities with migration between them. In a Cartesian product of the two, we may wish to allow infection and recovery within each community as well as migration of susceptibles from one community to another, migration of infectives, and migration of recovered individuals. In the product model, infectives in one community, for example, should be able to move to the other community or recover within their own community—a feature exactly reflected in the structure of a Cartesian graph product.

However, note that, in general, we may well wish to assume differences in these parameters. We may wish to assume, for example, that recovery rates are higher in one community or that migration rates of infectives are lower than for susceptibles. Unlike a Cartesian graph product, a Cartesian product of compartmental models must take into account the arc labels, which are the transition rates; in general, new parameters are necessarily introduced.

We propose the following definition for a Cartesian product of linear compartmental models. If a transition in model B from B_j to B_j′ occurs with rate γ, then for every state i in model A, a transition in the product model occurs from (A_i, B_j) to (A_i, B_j′) at rate γ_i. Similarly, if a transition in model A from A_i to A_i′ occurs with rate θ, then for every state j in model B, a transition in the product model occurs from (A_i, B_j) to (A_i′, B_j) at rate θ_j.

The presence of sources and sinks does not add any fundamental complications. If a transition in model B from B_j to a sink occurs with rate μ, then for every state i in model A, a transition from (A_i, B_j) to the sink occurs with rate μ_i (similarly, mutatis mutandis, for transitions in A to a sink). Finally, if a transition from a source to state B_j in model B occurs at rate Λ, then in the product model, for every state i in model A, a transition from a source to (A_i, B_j) occurs at rate Λ_i (and similarly for transitions from the source which appear in model A). These, and only these, transitions constitute the product model.

See the Appendix for more detail on the Cartesian product of linear models.

5. Epidemic Models

How can products like the Cartesian and strong products of graphs be used in formulating epidemic models? As we shall see, the product reviewed above can be extended to this case as well. We must extend the Cartesian product of compartmental models to allow interaction between different populations. (We note that similar considerations apply in the more general ecological modeling setting, including Lotka-Volterra predator-prey and competition equations, but we will not pursue these applications.)

5.1. Structured SI Model

In this section, we return to the classical Watson epidemic model, representing the SI epidemic in multiple regions. We will extend the Cartesian product of linear compartmental models, showing that the Watson model is a product of the simple SI model and a geographic model. In this special case, the geographic model will have no transitions at all.

The SI model of the transmission process is the one discussed above, with two states S and I, and transitions as pictured in Figure 1.

We now define a factor model which distinguishes individuals by community, to be combined with the SI model. If there are n communities, let N₁, N₂,…, N_n be the number of individuals in each community. If no migration takes place, and we ignore demographic turnover, this model corresponds to the differential equation system dN_k/dt = 0 for all k. For simplicity, we will illustrate only the n = 2 case (Figure 4(a)).

Figure 4.

(a) Factor model representing community structure with no migration; (b) simple Cartesian product formula applied to the SI and community structure models, giving an incorrect result.

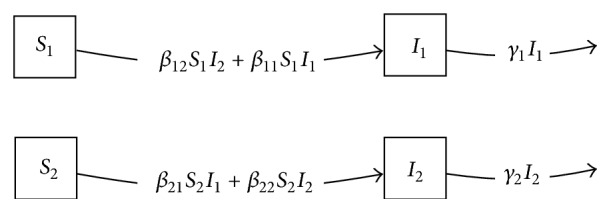
The state space of the product model will consist of the numbers of susceptibles and infectives in community 1 and community 2, ordered pairs such as (S, N₁), which can be given names S₁, I₁, S₂, and I₂. Naive application of the Cartesian product for compartmental models would begin with the observation that the SI factor model includes a transition from S to I at rate βI. We would then iterate over the levels j = 1,2 of the community model. We need a transition from (S, N₁) ≡ S₁ to (I, N₁) ≡ I₁, but at what rate? Generalizing the Cartesian product formula given above in the most direct way produces a model with transition rates β₁S₁I₁ and β₂S₂I₂, corresponding to the graph seen in Figure 4(b). This is a technically valid compartmental model, but it does not account for potential transmission between infectives in one community (e.g., I₂) and susceptibles in the other (e.g., S₁).

We must therefore extend the Cartesian product of compartmental models. In this example, we must take into account that the rate of transmission between a susceptible and an infective individual depends on the community membership of the infective as well as that of the susceptible. The extended definition is as follows.

As above, let A and B be models. The state space for the extended Cartesian product C is, as before, the Cartesian product of the state spaces of A and of B. For A, the transition rates include functional forms f(A_i, A_j), that is, functional dependencies on one or more states of A.

In the example of the Watson epidemic model, we have the following. The transition rate denoting transmission events in the SI model has rate f(S, I) = βSI. We will construct the product model using the rule that, from every compartment S_i ∈ {S₁, S₂}, that is, for every compartment descended from the S compartment, there is a transition to its corresponding sibling descended from the I compartment, at rate f_ij(S_i, I_j) = β_ijS_iI_j, for every I_j ∈ {I₁, I₂}. Note that the infective compartment I_j in this definition is distinct from the target vertex of the transition—the transition arc points from S_i to I_i, on the level i of the source vertex, but the infective compartment I_j ranges over levels j of the product model independently of the source—and this distinction is crucial to defining the correct set of transitions.

Where our earlier definition constructs one arc from each S compartment to its corresponding I compartment, this definition constructs one arc from each S compartment to its I compartment for each infective compartment that can transmit to those susceptibles. This yields the model shown in Figure 5. This extended Cartesian product yields two arcs for transitions from S₁ to I₁, the first reflecting our intent that individuals in community 1 can cause infections in their own community and the second reflecting transmission to community 1 from community 2. This can be canonically represented as a single arc whose rate is the sum of the rates in the individual arcs, which, in this example, is (β₁₁I₁ + β₁₂I₂)S₁, as in the original presentation of this model by Watson [22]. Similarly, two arcs appear for transitions from S₂ to I₂. Thus, the extended Cartesian product correctly represents the Watson model as a product of a within-community epidemic process and a geographic model.

Figure 5.

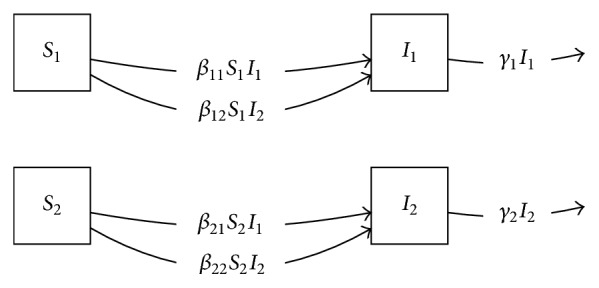
Directed multigraph diagram of Watson model [22] defined by applying the extended Cartesian product operation to the SI and two-community models.

Here we provide a formal definition of this product.

Definition 1 . —

A simple Cartesian product of two compartmental models A and B is a compartmental model A □ B whose set of compartments is the set of ordered pairs (X_i, Y_j) for every compartment X_i of A and Y_j of B.

For every arc α of model A, with per capita transition rate f^α(X_s, Z₁,…, Z_k), source compartment X_s, and target compartment X_t, the arcs of the product model include all arcs of the form

$$\begin{array}{c}{x}_s\stackrel{f_{i,\dots }^{\alpha }\left(x_s,z_{\mathrm{1}},\dots ,z_k\right)}{\to }{x}_t,\end{array}$$ (4)

where x_s, z₁,…, and z_k range over all compartments of the product model descending from X_s, Z₁,…, and Z_k, respectively, and x_t is the compartment descending from X_t that is otherwise on the same level as x_s, together with the corresponding arcs derived from the arcs of factor model B. The subscripts of f_i,…^α distinguish the different arcs by providing the names of the levels to which all of the product compartments x_s, z₁,…, z_k belong. The set of arcs of the product model consists of only the above arcs.

The product transition rates f_i,…^α(x_s, z₁,…, z_k) can be defined as needed, to generate an appropriately concise form for the transition rate functions, set unneeded transition rates to zero, or to do other works of specifying the details of the combined epidemic dynamics. Examples below demonstrate several ways of using these functions to construct specific models.

Before introducing a series of examples of product models with epidemiological application, we note that the product compartments, defined as ordered n-tuples such as (S, N₁), can be assigned variable names such as S₁ in a number of ways. We will use several different naming conventions in our examples. Likewise the parameters such as β and γ need to be mapped in product transitions to differentiated variables such as β₁₂ and γ₁, as appropriate to the application. We consider this to be part of the definition of the function f_ij^α(S_i, I_j) and other rate functions.

5.2. Community Model Featuring Demographics

We note that the disease process factor model may be generalized to include demographic turnover (“vital dynamics”). For example, this may feature a constant inflow of new susceptibles and an exponential mortality or removal; the SI model could be expressed in the form

$$\begin{array}{c}\frac{dS}{dt}=\mathrm{\Lambda }-\beta SI-\mu S,\\ \\ \frac{dI}{dt}=\beta SI-\mu I.\\ \end{array}$$ (5)

Here, Λ is a constant recruitment rate, and μ is a per capita death rate (see, e.g., [10]). If sources and sinks are considered to be special compartments, the above definition encompasses such inflow and outflow transitions. If we construct the extended Cartesian product model of this SI process with the same community model, we obtain the correct product model, with differential equations

$$\begin{array}{c}\frac{d{S}_i}{dt}={\mathrm{\Lambda }}_i-{\displaystyle \sum }_j{\beta }_{ij}{S}_i{I}_j-{\mu }_i{S}_i,\\ \\ \frac{d{I}_i}{dt}={\displaystyle \sum }_j{\beta }_{ij}{S}_i{I}_j-{\mu }_i{I}_i.\\ \end{array}$$ (6)

This model is illustrated in Figure 6.

Figure 6.

Product model of SI process in two communities.

Other elaborations of the epidemic model can be combined with regional models in the same way, including the SIS process (used, for instance, to model gonorrhea (e.g., [25]) and more recently to model infectious trachoma [26]), the SIR model, more complex variants (e.g., [27–29] out of a vast literature), or even models featuring vector-borne transmission (e.g., [30–33]). Useful factor models can include regional models with transportation, host genetics [10, 34, 35], gender, vaccination status, multiple risk groups (e.g., high and low risk of infection), or the presence of a second infectious agent.

5.3. Compartmental Aging

Age-structured models are frequently used in analysis of disease transmission to reflect changes in susceptibility, frequency of complications, or mixing patterns which depend on age. Compartmental model product structure can easily reflect these features, as we illustrate in the following example. Consider the standard SIR model to be the first factor model:

$$\begin{array}{c}\frac{dS}{dt}=-\beta SI,\\ \\ \frac{dI}{dt}=\beta SI-\gamma I,\\ \\ \frac{dR}{dt}=\gamma I,\\ \end{array}$$ (7)

where β and γ are transmission and recovery rates as above.

We then use the following compartmental aging process as the second factor model:

$$\begin{array}{c}\frac{d{A}_{\mathrm{0}}}{dt}=\mathrm{\Lambda }-\alpha A_{\mathrm{0}}-{\mu }_{\mathrm{0}}{A}_{\mathrm{0}},\\ \\ \frac{d{A}_{\mathrm{1}}}{dt}=\alpha A_{\mathrm{0}}-\alpha A_{\mathrm{1}}-{\mu }_{\mathrm{1}}{A}_{\mathrm{1}},\\ \\ \frac{d{A}_{\mathrm{2}}}{dt}=\alpha A_{\mathrm{1}}-\alpha A_{\mathrm{2}}-{\mu }_{\mathrm{2}}{A}_{\mathrm{2}}.\\ \end{array}$$ (8)

Here, α is simply the rate of aging (one year per year), Λ is a constant recruitment rate, and constants μ_i are age-class-specific per capita mortality rates.

The number of age compartments could be chosen to be any positive integer, in principle. Numerically, the use of compartmental aging can yield large stiff systems of equations, but compartmental aging approximates the use of McKendrick-von Foerster equations for aging.

These two models and their Cartesian product model are shown in Figures 7(a), 7(b), and 7(c). In the product model, inflow term Λ_I represents vertical transmission, while Λ_R would represent individuals immune at birth. Either of these rates can be set to zero for specific applications.

Figure 7.

(a) SIR model, (b) age structure model, and (c) product of SIR model with age structure model.

We note that, in this example, we have built recruitment and mortality into the aging model, while in the previous section we included them in the transmission model. There is flexibility in where to include these demographic processes, depending on what subscripts one wishes to have attached to their rates in the product model. If needed they can even be included in multiple factor models and assigned to constant values including zero as appropriate in the product.

5.4. Risk-Stratified STI Model

Sexual behavior is highly heterogeneous, with some individuals having far more partners per unit time than others. Moreover, such individuals may preferentially mix with similar individuals. The epidemiological role of a relatively small group of highly active people in transmission of a sexually transmitted infection (STI) was explored in a mathematical model of gonorrhea [36], and similar approaches were used in HIV modeling [37].

Consider the following simple example. Suppose that we begin with the factor model

$$\begin{array}{c}\frac{dS}{dt}=\mathrm{\Lambda }-\beta cpS\frac{I}{N}-\mu S,\\ \\ \frac{dI}{dt}=\beta cpS\frac{I}{N}-\gamma I-\mu I\\ \end{array}$$ (9)

representing disease transmission in a population of MSM (men who have sex with men) [10]. Here β represents the transmission probability per partnership, c equals a susceptible individual's rate of acquiring new sexual partners, and p is the probability that a susceptible individual's partner is chosen from a specific population of infectives (in the basic factor model, there is only one population I of infectives, and in that model this probability p is taken to have a constant value of 1, but these probabilities will be nontrivial in the product model, in which there are multiple infective populations). Here γ is disease-specific per capita mortality, Λ is a constant inflow rate of susceptibles, and μ is the disease-independent mortality rate. We will multiply this model by a second factor model in which the population is divided into a high risk group A and a low risk group B, with transition rates ρ and σ between them:

$$\begin{array}{c}\frac{dA}{dt}=-\rho A+\sigma B,\\ \\ \frac{dB}{dt}=\rho A-\sigma B.\\ \end{array}$$ (10)

The product model is shown in Figure 8. This model can then represent the presence of a high risk core group with a higher rate c_A of acquiring partners than the other, as well as nonrandom mixing between the groups, expressed by the probabilities p_AA, p_AB, and so forth. Because the mixing probabilities p_AA and p_AB for a susceptible individual in group A must sum to one, and likewise p_BA and p_BB, we could replace p_AB and p_BB by 1 − p_AA and 1 − p_BA, but it is not necessary to do so. As formulated, this system keeps the biologically distinct roles of c and p separate, although in some circumstances it may be desirable to combine them, while respecting the constraint that (S_A + I_A)c_Ap_AB = (S_B + I_B)c_Bp_BA [38]. However, one may desire to have the quantities p as functions of the state variables, reflecting that partner choice probabilities may depend on the dynamically varying group sizes [37, 39], in which case it is advantageous to retain them as separate parameters so that they can be replaced by more complex expressions straightforwardly.

Figure 8.

Product of SI model with risk-structure model.

5.5. Gender in STI Models

Modeling heterosexual transmission of an STI may proceed by dividing the population into males and females. Such a model can be developed along lines very similar to the risk model in the previous section. We may begin with a similar transmission factor model, here shown as an SIS process:

$$\begin{array}{c}\frac{dS}{dt}=\mathrm{\Lambda }-\beta cpS\frac{I}{N}-\mu S+\gamma I,\\ \\ \frac{dI}{dt}=\beta cpS\frac{I}{N}-\gamma I-\mu I.\\ \end{array}$$ (11)

The second factor model will be simply

$$\begin{array}{c}\frac{dF}{dt}=\frac{dM}{dt}=\mathrm{0},\end{array}$$ (12)

where we assume no transitions from male to female or vice versa. In constructing the product model, we incorporate the assumption of heterosexual-only transmission by defining the partner choice probabilities p_ij to be one for opposite-gender combinations (p_FM, p_MF) and zero for the same-gender combinations. The product model is then

$$\begin{array}{c}\frac{d{S}_F}{dt}={\mathrm{\Lambda }}_F-{\beta }_F{c}_F\frac{I_M}{N_M}{S}_F-{\mu }_F{S}_F+{\gamma }_F{I}_F,\\ \\ \frac{d{S}_M}{dt}={\mathrm{\Lambda }}_M-{\beta }_M{c}_M\frac{I_F}{N_F}{S}_M-{\mu }_M{S}_M+{\gamma }_M{I}_M,\\ \\ \frac{d{I}_F}{dt}={\beta }_F{c}_F\frac{I_M}{N_M}{S}_F-{\mu }_F{I}_F-{\gamma }_F{I}_F,\\ \\ \frac{d{I}_M}{dt}={\beta }_M{c}_M\frac{I_F}{N_F}{S}_M-{\mu }_M{I}_M-{\gamma }_M{I}_M,\\ \end{array}$$ (13)

as seen in Figure 9.

Figure 9.

Product of SI model with static two-gender model.

5.6. Interacting Transmission of Leprosy and Tuberculosis

The extended Cartesian product of compartmental models can be applied to problems involving two separate infectious disease processes. In the joint leprosy-tuberculosis model appearing in [40], the epidemiological effects of cross-immunity between two mycobacterial species were analyzed using a compartmental model. This model may be represented as a product of two-factor models, the first being a simple tuberculosis model based on susceptible (X), latent TB (L), and active tuberculosis (T):

$$\begin{array}{c}\frac{dX}{dt}=\mathrm{\Lambda }-\mu X-\beta XT,\\ \\ \frac{dL}{dt}=\left(\mathrm{1}-p\right)\beta XT-\mu L-\nu L,\\ \\ \frac{dT}{dt}=p\beta XT+\nu L-\mu T,\\ \end{array}$$ (14)

where Λ is a recruitment rate, μ is an overall mortality rate, ν is a rate of progression of latent tuberculosis to active disease, β is a transmission coefficient (hazard rate per infective) (β_T in the paper), and p is the probability a newly infected individual will develop active tuberculosis rapidly instead of becoming latently infected with tuberculosis (Figure 10).

Figure 10.

Compartmental model of tuberculosis transmission.

The second factor model represents the progression of leprosy from susceptible U, to latent infection with leprosy (W), and to multibacillary disease (M) or paucibacillary disease (P). The leprosy factor model is then (Figure 11)

$$\begin{array}{c}\frac{dU}{dt}=-\left(bP+cM\right)U,\\ \\ \frac{dW}{dt}=\left(bP+cM\right)U-\left(\theta +\varphi \right)W,\\ \\ \frac{dP}{dt}=\theta W,\\ \\ \frac{dM}{dt}=\varphi W,\\ \end{array}$$ (15)

where here b is the transmission coefficient for paucibacillary leprosy (β_P in the paper), c is the transmission coefficient for lepromatous leprosy (β_M in the paper), θ is the rate at which latently infected individuals develop paucibacillary disease (ν_P in the paper), and ϕ is the rate at which latently infected individuals develop multibacillary disease (ν_M in the paper).

Figure 11.

Compartmental model of leprosy transmission.

The product model (Figure 12) represents the epidemiological interference of the two closely related mycobacterial infections. Individuals latently infected with one may have partial immunity against the other. This product structure could be applied to other settings such as HIV-TB interactions (e.g., [41]).

Figure 12.

Cartesian product of leprosy (Figure 11) and tuberculosis (Figure 10) models, describing interaction of the two transmission processes. Multiple arrows and labels are suppressed for legibility.

6. Strong Products

The extended Cartesian product is too restrictive when constructing models of multiple diseases. For instance, one may be infected by two pathogens during a single encounter with a dually infected person. Thus, it may be necessary to allow individuals to proceed to dual infection directly from the susceptible class without passing through the singly infected states. The extended Cartesian product defined earlier does not permit this possibility.

Just as the Cartesian product of graphs can be extended to a strong product of graphs, an analogous strong product is possible for products of compartmental models. As we will show below, a strong product of compartmental models will permit derivation of multistrain or multidisease models featuring simultaneous transmission.

As an example, consider the following simple SIS epidemic model, which we might apply to transmission of Chlamydia trachomatis, the etiologic agent of trachoma (a blinding disease) [42, 43]. In principle, multiple strains of the trachoma agent can circulate [44]. Consider a model of a single strain, in which S is the number of susceptibles and I is the number of infectives:

$$\begin{array}{c}\frac{dS}{dt}=-\beta S\frac{I}{N}+\gamma I,\\ \\ \frac{dI}{dt}=\beta S\frac{I}{N}-\gamma I,\\ \end{array}$$ (16)

where β is a transmission coefficient, γ is a recovery rate, and N = S + I is the total population.

We can construct a multistrain model with partial cross-immunity [45, 46] using a suitably defined strong product, defined as follows. Let A and B be models, with states labeled A_i and B_j, respectively. The vertices of the strong product model A⊠B are, as in the previously defined products, the Cartesian product of the vertex sets of the factor models. Every arc of each factor model gives rise to one or more arcs within each level of the product model, as in the other products, one for each interaction with product compartments. There are also additional, diagonal arcs in the product model that cross levels, representing more than one of the factor model's transitions taking place simultaneously.

In Figure 13, we present the strong product of the above SIS model with itself.

Figure 13.

Strong product of two strains' SIS dynamics.

The arcs of the Cartesian product of models are present, representing infection of an individual by either strain 1 or 2, but there are additional arcs as well, including the diagonal transition from S to I₁₂ representing simultaneous transmission of both strains 1 and 2 to a fully susceptible individual in a single encounter with an individual carrying both strains.

Unlike the Cartesian product, here a single interaction between compartments can manifest in multiple transitions. The interaction between examples S and I₁₂ can result in transmission of either or both strains, and these cases are represented by three arcs in the diagram, with transmission rates β distinguished by brackets.

A formal definition of the strong product of compartmental models, which generates the above example product, is as follows.

Definition 2 . —

A strong product of two compartmental models A and B is a compartmental model A⊠B whose set of compartments is the set of ordered pairs (X_i, Y_j) for every compartment X_i of A and Y_j of B. Models A and B are considered to be distinct models for the purpose of this definition, and each model's transitions are considered distinct from the other, even when a product is taken of a model with itself.

For every set α = {α₁,…, α_p} of factor models' transitions, belonging to distinct factor models, each with source compartment X_s^α_i, target compartment X_t^α_i, and per capita transition rate f^α_i(X_s^α_i, Z₁^α_i,…, Z_ki^α_i), the product model includes all arcs of the form

$$\begin{array}{c}{x}_s\stackrel{f_{i,\dots }^{{\alpha }_{\mathrm{1}},\dots ,{\alpha }_p}\left(x_s,z_{\mathrm{1}},\dots ,z_k\right)}{\to }{x}_t,\end{array}$$ (17)

where x_s ranges over the compartments of the product model that descend from all the factor vertices {X_s^α₁,…, X_s^α_p}, each z_j ranges over the product compartments that descend from all vertices in the set {Z_j^α_i}, and x_t descends from all of {X_t^α_i} and is otherwise on all the same levels as x_s. The arcs of the product model are only those generated by the above definition. As previously, the subscripts i,… to the rate function f distinguish the different product arcs by indicating the levels to which all the function's arguments belong.

In our SI example, we have defined the rate functions f to produce appropriate products of transmission (β) and recovery (γ) transitions, with distinct but compact subscripts, and to omit transitions in which transmission of one strain occurs simultaneously with recovery from the other one.

7. Exploration of a Family of Models

In this section, we illustrate the use of the extended Cartesian product in model development and exploration, using a model of targeted screening for gonorrhea as a simple example. Such a model can be expressed using four components: a natural history model, a partitioning of the population by gender, a division into low and high risk groups, and a process of screening of individuals (Figure 14). For the natural history model, we will use the simple SIS process as in [25] for illustration, while recognizing that for some STIs a more complex transmission model may be needed, for example, to reflect partial immunity [47]. Because within- and between-gender transmission can vary greatly, we include a division of the model population by gender, with the assumption that rates of gender transition and proportions of nonbinary individuals are small in comparison to the model dynamics. We include a high and low risk group as in [36], with transitions between the risk groups, and finally we include an exposure model tracking the individuals exposed to a control measure such as frequent screening [48].

Figure 14.

Component models for gonorrhea process: (a) transmission model, a classic SIS process; (b) gender model, a male-female binary system, with the assumptions that nonbinary proportions and transition rates are low; (c) risk model, consisting of high and low risk groups; (d) exposure model, consisting of groups unexposed and exposed to screening.

The product of these four models (constructed by extending the above definition of the extended Cartesian product of two models or by taking a product of products) has sixteen compartments and describes a process of transmission with rates affected by the genders, risk group membership, and exposure status of both susceptibles and infectives (Figure 15). The product structure naturally generates a process that includes both homosexual and heterosexual transmission. As drawn here, the effect of the screening program is expressed by changes in the removal rate γ such that screened individuals are removed from the infective state more quickly than those who are not screened.

Figure 15.

Four-level product model of gonorrhea transmission with stratification into gender, risk, and exposure categories. Transmission rate is abbreviated here for readability: λ_abc = S_abcc_bc∑_defβ_bep_bcefI_def, where a, b, c and likewise d, e, f range over exposure, gender, and risk groups, respectively.

Using the extended Cartesian product definition of this model, it is straightforward to generate partial products using subsets of the set of four factor models shown in Figure 14, yielding a spectrum of models of intermediate complexity (Figure 16), which can be evaluated on their ability to fit observed data. Methods to evaluate the goodness of fit of such a model to data might include least squares (e.g., [49]) or likelihood methods (e.g., [50]).

Figure 16.

Some candidate models for explanation of recorded transmission dynamics: (a) transmission with exposure only; (b) with gender only; (c) with risk groups only; (d) with exposure and gender; (e) with exposure and risk groups; and (f) with gender and risk groups.

More importantly, it is also straightforward using this formulation to generate models with greater detail, for example, by using more than two risk groups (Figure 17). In this way, models with arbitrarily large numbers of risk groups can be straightforwardly and systematically evaluated for goodness of fit to find the best description of the true process available in this framework, a process which cannot be undertaken without an automated model generation framework of this sort.

Figure 17.

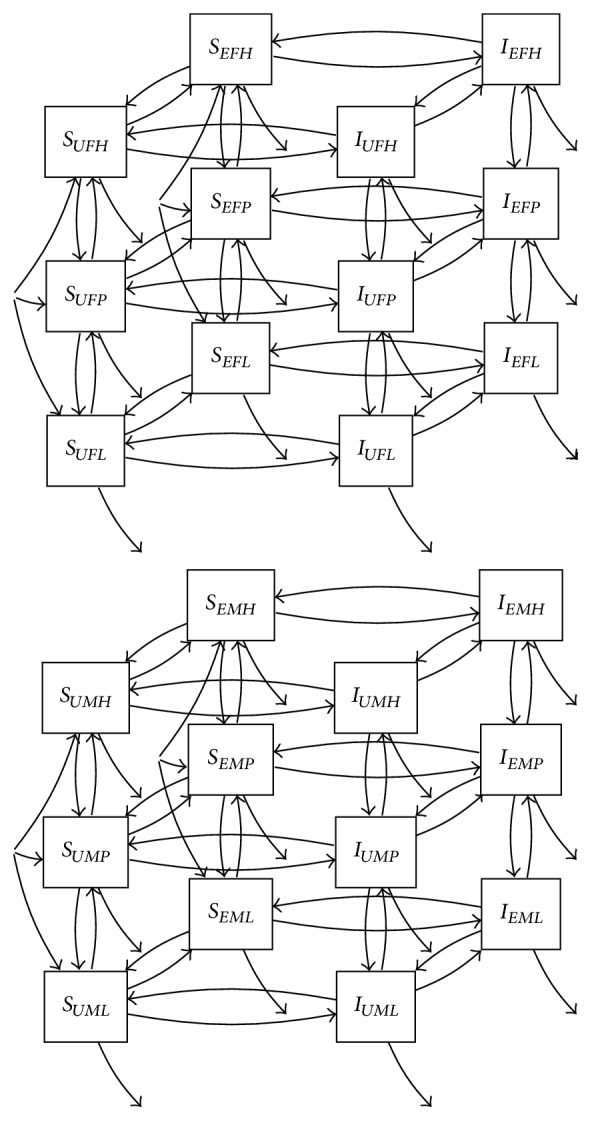
Transmission dynamics with three risk groups (low, partial, and high), together with gender and exposure categories.

8. Discussion

Products of compartmental models, defined as straightforward generalizations of graph products, represent useful operations in developing epidemiological models. Similar mathematical structures arise from addition of age structure, gender, geographic differences, or other forms of heterogeneity to an epidemic model. Such similarities reveal the presence of a “design pattern” [51] that is captured by the extended Cartesian products we define here.

The products presented in this paper by no means represent the full range of possible products of models. For the products we presented, the state space of the product model is the Cartesian product of the state spaces of the factor models. Some cases may require only a subset of this: consider an HIV model in which the infective classes are structured by CD4 count and viral load classes, which are not relevant to the susceptible classes. Such examples can be easily handled by straightforward generalizations of the products given in this paper. More complex products are required when the state space of the product model must include history (for example, the order in which individuals were infected by pathogen strains).

The extended Cartesian product is well suited to the operation of adding host heterogeneity to an epidemic model, and so it may facilitate automated generation of a family of epidemic models. Similarly, the extended strong product is suited to the process of adding pathogen heterogeneity to an epidemic model. We have developed software to implement these products. All models and figures in this paper were generated by this software, which is freely available as a module for the Sage mathematics computing system [52]. This software enables systematic numerical exploration of a large family of related models, to automate evaluation of specific refinements of an epidemic process for relevance to observed dynamics, and could form the basis of a systematic approach to numerical structural sensitivity analysis.

Appendix

A. Graph Products

Formally a directed graph is a set of vertices together with arcs, defined as a set of ordered pairs of vertices. We consider graph products for which the vertices of the graph product are formed from the Cartesian product of the vertices of each of the factor graphs. Notationally, if S₁, S₂,…, S_n are sets of vertices, then their Cartesian product is the set S₁ × S₂ × ⋯×S_n = {(s₁, s₂,…, s_n)∣s₁ ∈ S₁, s₂ ∈ S₂,…, s_n ∈ S_n}, with the elements of S₁ × S₂ × ⋯×S_n being tuples of elements of the component sets S₁, S₂,…, S_n.

For application to mathematical models, the arrows (arcs) will represent transition rates between states represented by vertices. Each arc will therefore require an associated label. We allow multiple arcs between the same vertices and thus we must use multigraphs, represented as a set {(v, w, e)}⊆V × V × E. Here, V is the vertex set of the graph and E is its set of arc labels. Each of these tuples is visualized as an arrow from v to w with label e (which we may denote as $\left\{v\stackrel{e}{\to }w\right\}$).

The Cartesian product G₁ □ G₂ □⋯□ G_n of directed graphs G₁, G₂,…, G_n is a graph whose vertex set is the Cartesian product V₁ × V₂ × ⋯×V_n of the vertex sets V_i of each graph G_i and whose arcs are of the form $(v_{\mathrm{1}},v_{\mathrm{2}},\dots ,v_i,\dots ,v_n)\stackrel{e}{\to }(v_{\mathrm{1}},v_{\mathrm{2}},\dots ,w_i,\dots ,v_n)$, where the two tuples are identical in all but the i′th position and where there is an arc connecting v_i to w_i in G_i. In this paper, the products defined will yield the arc labels (transition rates) in the product graph.

For each vertex in one of the factor models, each vertex in the other model is replicated. If the first factor is a graph with vertices A and B, with an arc from A to B, and the second is a graph with vertices 1 and 2 and an arc from 1 to 2, then the product graph contains vertices which could be denoted as A1, A2, B1, and B2. Each arc of one graph is replicated for every vertex of the other. Thus, for example, the arc from 1 to 2 in the second factor graph corresponds to an arc from A1 to A2 for the first vertex of the first model and also to an arc from B1 to B2 for the second vertex. Similarly, the arc from A to B in the first model corresponds to an arc from A1 to B1 (for arc 1 of the second model) and from A2 to B2 (for the other).

The strong product (or strong Cartesian product) of graphs G₁,…, G_n, written G₁⊠G₂⊠⋯⊠G_n, is the graph whose vertex set is the Cartesian product of the graphs' vertex sets, which has an arc from (v₁,…, v_n) to (w₁,…, w_n) if and only if, for every i, either there is an arc from v_i to w_i, or v_i = w_i. The Cartesian product G₁ □ G₂ □⋯□ G_n of directed graphs G₁, G₂,…, G_n is a graph whose vertex set is the Cartesian product V₁ × V₂ × ⋯×V_n of the vertex sets V_i of each graph G_i and whose arcs are of the form $(v_{\mathrm{1}},v_{\mathrm{2}},\dots ,v_i,\dots ,v_n)\stackrel{e}{\to }(v_{\mathrm{1}},v_{\mathrm{2}},\dots ,w_i,\dots ,v_n)$, where the two tuples are identical in all but the i′th position and where there is an arc connecting v_i to w_i in G_i.

A.1. Adjacency Matrices

The Cartesian product graph can also be defined by its adjacency matrix. Let the adjacency matrices of finite graphs A and B, respectively, be M_A and M_B. Let I_A and I_B be identity matrices of the same size as M_A and M_B, respectively. The Cartesian product graph A □ B has adjacency matrix M_C = M_A ⊕ M_B = M_A ⊗ I_B + I_A ⊗ M_B, where ⊗ is the Kronecker product. Writing M_C′ = M_B ⊕ M_A yields an adjacency matrix for the product graph which is the same, except for the ordering of the vertices in the product (and the order in which the Cartesian product of sets of vertices is taken). More generally, graphs with multiple arcs between two vertices can be defined, in which case the elements a_ji of the adjacency matrix record the number of directed arcs to j from i. The Cartesian product definition above can be applied in this case as well.

The strong product of two directed graphs A and B includes more arcs than the Cartesian product [23]. This product A⊠B has the same vertex set, the Cartesian product of the factors' vertex sets, but in addition to the arcs of the Cartesian product graphs, it also includes all arcs from (v_s, w_s) to (v_t, w_t), where there is an arc from v_s to v_t and an arc from w_s to w_t. Using the same notation as above, the adjacency matrix of the strong product graph is M_D = I_A ⊗ M_B + M_A ⊗ I_B + M_A ⊗ M_B.

Products of more than two graphs can be represented by analogous, though more tedious, matrix operations.

A.2. Linear Compartmental Models

Suppose we consider a compartmental model with states X₀, X₁,…, X_k represented by the first-order linear system

$$\begin{array}{c}\dot{X}=a+MX,\end{array}$$ (A.1)

where a is a vector of exogenous inflow terms and M is a transition rate matrix. In general, M could contain sink terms; for example, let X₁ represent the number of individuals in a population with constant recruitment Λ and constant per capita mortality, so that ${\dot{X}}_{\mathrm{1}}=\Lambda -\mu X_{\mathrm{1}}$. In this case, M is a 1 × 1 matrix [−μ].

Consider two continuous time chains, with state spaces X_i^A, i = 1,…, n_A and X_j^B, j = 1,…, n_B, respectively. Suppose that the transition rate matrix for each is given by M_A and M_B, respectively (assumed time-independent, for simplicity). A transition rate matrix may contain both positive (inflow) terms and negative (outflow) terms. A transition to X_k^A from state X_i^A at rate λ will be represented in M_A by a term in the i, ith element of M_A of −λ and a term in the k, ith element of M_A of λ

$$\begin{array}{c}{M}_A=\left[\begin{array}{ccc}-\lambda & \mu & \sigma \\ \lambda & -\mu -\theta & \mathrm{0}\\ \mathrm{0}& \theta & -\sigma \end{array}\right].\end{array}$$ (A.2)

Any transition rate matrix can be represented as a sum over arcs:

$$\begin{array}{c}{M}_A=\left[\begin{array}{ccc}-\lambda & \mathrm{0}& \mathrm{0}\\ \lambda & \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right]+\left[\begin{array}{ccc}\mathrm{0}& \mu & \mathrm{0}\\ \mathrm{0}& -\mu & \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right]+\left[\begin{array}{ccc}\mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& -\theta & \mathrm{0}\\ \mathrm{0}& \theta & \mathrm{0}\end{array}\right]\\ +\left[\begin{array}{ccc}\mathrm{0}& \mathrm{0}& \sigma \\ \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& -\sigma \end{array}\right].\end{array}$$ (A.3)

A Cartesian product of two Markov chains A and B can then be defined as follows. We will denote the arcs of model A by α_A; for each arc there is a matrix M_A^α_A whose elements are 0, except for the inflow and outflow represented by that arc, as illustrated above. The decomposition of the transition rate matrix M_A by arcs is then M_A = ∑_αAM_A^α_A. Similarly, the transition rate matrix M_B of model B, decomposed by arcs, is M_B = ∑_αBM_B^α_B. If I_A and I_B are identity matrices of the same dimension as M_A and M_B, respectively, a special case of the Cartesian product can be written

$$\begin{array}{c}{M}_C={\displaystyle \sum }_{{\alpha }_A}{I}_B\otimes M_A^{{\alpha }_A}+{\displaystyle \sum }_{{\alpha }_B}{M}_B^{{\alpha }_B}\otimes I_A.\end{array}$$ (A.4)

Figure 18 depicts two such models (Figures 18(a) and 18(b)) and their product as defined here (Figure 18(c)). This special case only represents a model in which the two chains behave completely independently.

Figure 18.

(a) Diagram of states and transition rates, for example, Markov model; (b) diagram for the second example, Markov model; (c) diagram of states and transition rates for simple Cartesian product of models; (d) diagram of states and transition rates for general Cartesian product of models, as defined in the text.

To obtain a more general product, we replace the identity matrices with general diagonal matrices. The elements of the diagonal matrix are not assumed identical. We let Λ_A^α_B be such a diagonal matrix of the same dimension as M_A, representing a scaling matrix for each arc of model B for every state of model A. Similarly, Λ_B^α_A, a matrix of the same dimension as M_B, is a scaling matrix for each arc of model A for every state of model B. A more general product is then expressed by

$$\begin{array}{c}{M}_C={\displaystyle \sum }_{{\alpha }_A}{\mathrm{\Lambda }}_B^{{\alpha }_A}\otimes M_A^{{\alpha }_A}+{\displaystyle \sum }_{{\alpha }_B}{M}_B^{{\alpha }_B}\otimes {\mathrm{\Lambda }}_A^{{\alpha }_B},\end{array}$$ (A.5)

producing a product process like the one pictured in Figure 18(d).

Note that a given arc connecting two vertices may, in applications, represent two separate processes. For instance, we may have a compartment representing live individuals and another dead and wish to model the rate of death due to two causes, say μ₁ and μ₂. Canonically, we may represent the total transition from live to dead as a single arc with rate μ₁ + μ₂ (assuming independent competing risks), but in the decomposition above, if we represent the transition by two separate arcs, the Cartesian product formula may be applied in the same way.

Let us use the notation z ∝ Z to indicate that compartment z descends from factor compartment Z. The transition matrix for the extended Cartesian product model is

$$\begin{array}{c}{M}_C={\displaystyle \sum }_{\alpha }\left[{\displaystyle \sum }_{z_{\mathrm{1}}\propto Z_{\mathrm{1}}^{\alpha }}\cdots {\displaystyle \sum }_{z_k\propto Z_k^{\alpha }}{\mathrm{\Lambda }}_B^{\alpha ,z_{\mathrm{1}},\dots ,z_k}\otimes M_A^{\alpha }\left(z_{\mathrm{1}},\dots ,z_k\right)\right]\\ +{\displaystyle \sum }_{\alpha }\left[{\displaystyle \sum }_{z_{\mathrm{1}}\propto Z_{\mathrm{1}}^{\alpha }}\cdots {\displaystyle \sum }_{z_k\propto Z_k^{\alpha }}{M}_B^{\alpha }\left(z_{\mathrm{1}},\dots ,z_k\right)\otimes {\mathrm{\Lambda }}_A^{\alpha ,z_{\mathrm{1}},\dots ,z_k}\right],\end{array}$$ (A.6)

where k is considered to depend on α.

Conflicts of Interest

The authors declare they each have no conflicts of interest.