An On/Off Berry Phase Switch in Circular Graphene Resonators

Abstract

The phase of a quantum state may not return to its original value after the system's parameters cycle around a closed path; instead, the wavefunction may acquire a measurable phase difference called the Berry phase. Berry phases typically have been accessed through interference experiments. Here, we demonstrate an unusual Berry-phase-induced spectroscopic feature: a sudden and large increase in the energy of angular-momentum states in circular graphene p-n junction resonators when a small critical magnetic field is reached. This behavior results from turning on a π-Berry phase associated with the topological properties of Dirac fermions in graphene. The Berry phase can be switched on and off with small magnetic field changes on the order of 10 mT, potentially enabling a variety of optoelectronic graphene device applications.

Geometric phases are a consequence of a phenomenon that can be described as “global change without local change”. A well-known classical example is the parallel transport of a vector around a path on a curved surface, which results in the vector pointing in a different direction after returning to its origin (Fig. 1A). Extending the classical phenomenon to the quantum realm by replacing the classical transport of a vector by the transport of a quantum state gave birth to the Berry phase, which is the geometric phase accumulated as a state evolves adiabatically around a cycle according to Schrödinger's equation (1–5). Since its discovery (1), non-trivial Berry phases have been observed in many quantum systems with internal degrees of freedom, such as neutrons (6), nuclear spins (7), and photons (8, 9), through a Berry-phase-induced change in quantum interference patterns. Quantum systems in which a Berry phase alters the energy spectrum are comparatively rare; one example is graphene, where massless Dirac electrons carry a pseudospin ½, which is locked to the momentum Π. Because of the spin-momentum locking, the Berry phase associated with the state |Π⟩ can take only two values, 0 or π, which gives rise to the unconventional ‘half-integer’ Landau level structure in the quantum Hall regime (10–12). Yet, in most cases studied to date, the Berry phase in graphene has played a “static” role because controlling the trajectories (and hence |Π ⟩) of graphene electrons is experimentally challenging. Recently introduced graphene electron resonators (13–15) enable exquisite control of the electron orbits by means of local gate potentials, and offer a unique opportunity to alter and directly measure the Berry phase of electron orbital states.

Fig. 1. Dynamics of whispering gallery modes in circular graphene resonators.

(A) The parallel transport of a vector around a closed path C on a curved surface. For parallel transport the vector t remains perpendicular to r, and the orthogonal frame containing t and r does not twist about r (3). The transport results in the angular difference α between initial and final t vectors. (B) (lower) Schematic momentum-space contours for magnetic fields below (blue) and above (red) the critical magnetic field B_c, corresponding to the vectors shown in (D); (upper) the same contours projected on the Dirac cone by evaluating the kinetic energy T(Π). Above B_c (red), the contour encloses the Dirac point leading to a π Berry phase. (C) Schematics of the potential profile in the circular graphene resonator formed by a p-doped graphene center region and n-doped background, and classical orbits for positive m states below (left, blue) and above (right, red) B_c. (D) Schematic phase-space tori corresponding to the orbits shown in (C). The kinematic momenta Π (arrows), uniquely defined on the torus, are shown along the topologically distinct loops C_θ and C_R. Lower panel: For C_R below B_c (blue), the winding number of Π is zero and has a zero Berry phase; above B_c (red), the winding number is one, leading to a π Berry phase.

Here we report the control of the Berry phase of Dirac particles confined in a graphene electron resonator using a weak magnetic field, as recently suggested by theory (16). In this approach, a magnetic field enables fine control of the evolution of |Π ⟩ around the Dirac point for individual resonator states (Fig.1B). A variation in the Berry phase, which is accumulated during the orbital motion of the confined states, can be detected from changes in the energy dispersion of electron resonances. For this reason, we use scanning tunneling spectroscopy (STS) to directly measure the resonator-confined electronic states, giving direct access to the shifts in the quantum phase of the electronic states.

Graphene resonators confine Dirac quasiparticles by Klein scattering from p-n junction boundaries (13–25). Circular graphene resonators comprised of p-n junction rings host the whispering gallery modes analogous to those of acoustic and optical classical fields (13–15). These circular resonators can be produced by a scanning tunneling microscope (STM) probe in two different ways: (i) by using the electric field between the STM probe tip and graphene, with the tip acting as a moveable top gate (13), or (ii) by creating a fixed charge distribution in the substrate, generated by strong electric field pulses applied between the tip and graphene/boron nitride heterostructure (14). Both methods are used in our study of Berry-phase switching of resonator states.

Measurements were performed in a custom built cryogenic STM system (26) on two fabricated graphene/hBN/SiO₂ heterostructure devices, designed specifically for STM measurements (27). The field-induced switching of the graphene resonator states was initially observed in the movable tip-induced p-n junction resonators defined by the STM tip gating potential (13)(Section II of (27)). Subsequently, we created fixed p-n junction resonators, allowing us to study the spectroscopic properties and field dependence in a more controlled manner without a varying p-n junction potential; this report focuses mainly on the data obtained in this latter way. The fixed resonators display a pattern of Berry phase switching of the resonator modes that agrees with the one seen in the movable p-n junctions, demonstrating that different methods for creating the circular graphene resonators in separate devices lead to similar results.

Fixed circular-shaped p-n junctions were created by applying an electric field pulse between the STM probe and graphene device to ionize impurities in the hBN insulator, following Ref (28). This method creates a stationary screening charge distribution in the hBN insulating under-layer, resulting in a fixed circular doping profile in the graphene sheet (Figs. 2, A and B) [see fig. S10 for schematic of the method]. We probe the quantum states in the graphene resonator by measuring the tunneling differential conductance, g(V_b,V_g,r,B) = dI/dV_b, as a function of tunneling bias, V_b, back gate potential, V_g, spatial position, r, and magnetic field, B. The quasi-bound resonances, originating from Klein scattering at the p-n ring, are seen in measurements made at B = 0 as a function of radial distance r (Fig. 2D). The eigenstates in Fig. 2D form a series of resonant levels vertically distributed in energy, and are seen to exist within an envelope region of the confining p-n junction potential outlined by a high intensity state following the p-n junction profile. Because of rotational symmetry, the corresponding quantum states are described by radial quantum numbers, n, and angular momentum quantum numbers, m [Section I of (27)]. Only degenerate states with m = ±1/2 have non-zero wavefunction amplitude in the center of the resonator, as shown by the calculated wavefunctions in Fig. 2C, and dominate the measurements at r = 0 in Fig. 2D (13–15). Higher angular momentum states are observed off-center in the spatial distribution of the resonator eigenstates in Fig. 2D, but can be difficult to distinguish because of overlapping degenerate levels (14, 15). Several calculated wavefunctions and corresponding eigenstates are indicated by color-coded circles in Figs. 2, C and D, respectively, to illustrate some patterns of the states in the spectroscopic map. States with a specific radial quantum number n follow arcs trailing the parabolic outline of the confining potential in Fig. 2D [see fig. S1 for the enumeration of the various (n, m) quantum states].

Fig. 2. Quantum whispering gallery modes of a graphene circular resonator.

(A) Schematic of the potential profile formed by (B) a p-doped graphene center region and n-doped background, created by ionizing impurities in the underlying hBN insulator. (C) Calculated wavefunction components of a circular graphene resonator for a parabolic potential for various indicated (n,m) states. (All scale bars 100 nm). (D) Differential conductance map vs. radial spatial position obtained from an angular average of an xy grid of spectra obtained over the graphene resonator. m = ± 1/2 states appear in the center at r = 0, whereas states with higher angular momentum occupy positions away from center in arcs of increasing m values and common n value, as seen by the associated wavefunctions in (C) [see also fig. S1]. The solid blue line shows a parabolic potential with κ=10 eV/μm² and a Dirac point of 137 mV, which is used as a confining potential in the simulations shown in Figs. 3B and Figs. 4,B-D. The dashed yellow line at r=0, and dashed green line at r=70 nm, indicate the measurement positions for Figs. 3A and 4A.

We probe the magnetic field dependence of the m = ± 1/2 resonator states (Fig. 3A) for the states n = 1 to n =5 corresponding to the energy range indicated by the yellow dashed line in Fig. 2D. We see the degenerate m = ± 1/2 states in the center of the map at B = 0, corresponding to the states seen in the center of Fig. 2D at r = 0. However, as the magnetic field is increased, new resonances suddenly appear between the nth quantum levels, where none previously existed. The spacing between the new magnetic field induced states, δε_m, is about one half the spacing, Δε, at B = 0. A magnified view of the map around the n = 4 level (Fig. 3C) shows the appearance of new resonances switching on at a critical magnetic field, B_C ≈ ±0.11 T. As explained below, the switching transition corresponds to the sudden separation of the m = ±1/2 sublevels, which is very sharp [see Fig. 3D, and fig. S11 for more detail]. This energy separation, on the order of 10 meV at B = 0.1 T, is much larger than other magnetic field splittings, i.e. Zeeman splitting (ε_Z = μ_BB_C ≈ 0.01 meV, with μ_B the Bohr magneton) or orbital effects [ε_orb ≈ 1 meV, see Ref (16)]. As we discuss below, these results correspond to the energy shift of particular quantum states, which suddenly occurs owing to the switching on of a π Berry phase when a weak critical magnetic field is reached.

Fig. 3. The On/Off Berry phase switching in graphene circular resonators.

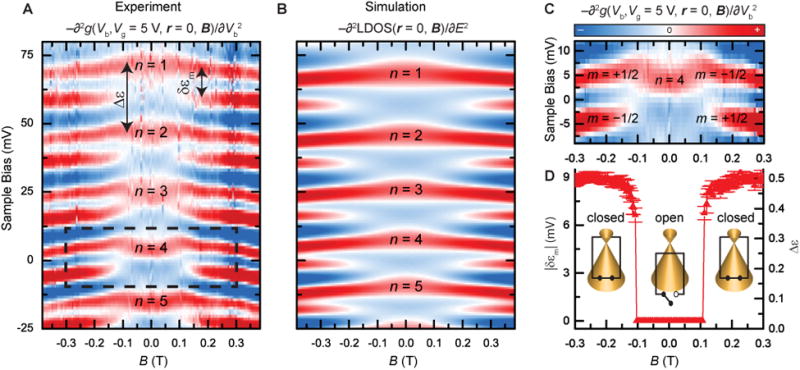
(A). Differential tunneling conductance map vs. magnetic field measured in the center of the graphene resonator for the n=1 to n=5 modes, indicated by the yellow dashed line in Fig. 2D. New resonances suddenly appear at a critical magnetic field of B_c ≈ ±0.11 T in between those present at B = 0 T. (B) Calculated local density of states (LDOS) of the graphene resonator states in a magnetic field to compare with experiment in (A) using a parabolic confining potential with κ = 10 eV/μm² and Dirac point E_D = 137 meV (Fig. 2D). (C) Magnified view of the n = 4 resonance from (A) showing the Berry-phase induced jumping of the m = ±1/2 modes with magnetic field: m = +1/2 only jumps at positive fields, and m = −1/2 only at negative fields. The 2D maps in A-C are shown in the 2^nd derivative to remove the graphene dispersive background. (D) The difference in energy between the m = ±1/2 states, δε_m, for the n = 4 resonance vs. magnetic field. The right axis is in units of the energy difference between the n=4 and n=3 resonances, Δε, at B = 0 T. The uncertainty reported represents one standard deviation and is determined by propagating the uncertainty resulting from a least square fit of Lorentzian functions used to determine the peak position of the resonator modes. The Dirac cones schematically illustrate the switching action: At low fields, the switch is open with zero Berry phase. When the critical field is reached, a π Berry phase is turned on closing the switch.

A simple understanding of the sudden jump in energy observed in the experiment (Fig. 3A) can be drawn from the Bohr-Sommerfeld quantization rule, which determines the energy levels E_n:

$$\frac{1}{ħ}{\oint }_{C_R\left(E_n\right)}\mathit{p}\cdot d\mathit{q}=2\pi (n+\gamma -\frac{\phi B}{2\pi }).$$ (1)

Here q and p are the canonical coordinates and momenta, respectively, ħ is Planck's constant divided by 2π, φ_B is the Berry phase accumulated in each orbital cycle, C_R is a phase-space contour described below, and γ is a constant, the so-called Maslov index (5). The orbits are obtained from the semiclassical Hamiltonian H = E_n = υ_F|Π| + U(r), with U(r) the confining potential and Π = p – eA the kinetic momentum (e is the electron charge and A the vector potential). At zero magnetic field, states with opposite angular momenta ±m are degenerate, and their orbits are time-reversed images of one another (Fig. 1C, left). When a small magnetic field is turned on, the Lorentz force bends the paths of the +m and –m charge carriers in opposite directions, breaking the time-reversal symmetry and slightly lifting the orbital degeneracy. Crucially, at a critical magnetic field B_c, the orbit with angular momentum anti-parallel to the field is twisted by the Lorentz force into a qualitatively different “skipping” orbit (Fig. 1C, right). At this transition, the momentum-space trajectory, defined below, encloses the Dirac point, and φ_B discontinuously jumps from 0 to π; states with ±m, which are degenerate at B = 0, are abruptly pulled apart by half a period.

The intuitive picture described above can be made rigorous by using the Einstein-Brillouin-Keller (EBK) quantization (29, 30). Besides being more rigorous, EBK quantization facilitates visualization of the trajectory of Π along a semiclassical orbit, particularly because the orbits are quasiperiodic. In central force motion, the particle's orbit takes place in an annulus between the two classical turning points, and because the momentum in this annulus is two-valued, one can define a torus on which the momentum is uniquely determined [Section I of (27)]. The EBK quantization rules are formed by evaluating ∮ p · dq along the two topologically distinct loops on this torus, C_R and C_θ (Fig. 1D). The EBK rule along C_θ gives the half-integer quantization of angular momentum; that along C_R (Eq. 1) determines the energy levels for a given angular momentum. The Berry phase term in Eq. 1 is determined by the winding number of Π about the origin, evaluated on C_R. Below B_c, the azimuthal component of Π has the same sign along C_R (Fig. 1E, left): the corresponding II-space loop (Fig. 1B, blue curve) does not enclose the origin and the Berry phase is zero. Above B_c, however, II has a sign change along C_R (Fig. 1E, right): the loop encircles the Dirac point and the Berry phase is π (Fig. 1B, red curve). Fig. 1B provides an intuitive visualization of the switching mechanism: the changing magnetic field shifts the Π-space contour, and at B_c it slips it over the Dirac cone apex, instantly changing the right side of Eq. 1 by π and shifting the energy levels accordingly [see Movie S1].

The semiclassical picture additionally allows us to estimate the strength of the critical field B_c necessary to switch the Berry phase (16). The value of B_c, which is sensitive to the confining potential profile, is obtained by finding the field strength B necessary to bend the electron orbit into a skipping orbit at the outer return point r_o, thus resulting in zero azimuthal momentum: Π_θ = mħ/r_o − eB_cr_o/2 = 0. For a parabolic potential U(r) =κr², which accurately describes the low energy resonances (16), one obtains a simple expression:

$$B_c=\frac{2ħ}{e}\frac{m\kappa }{\varepsilon },$$ (2)

where ε is the energy of the orbit. Using κ = 10 eV/μm² obtained from a parabolic fitting of the potential profile (see Fig.2D) and ε = 65 meV (relative to the position of the Dirac point), which corresponds to the (m = 1/2, n = 1) state in Fig.3A, we find B_c = 0.1 T, in excellent agreement with the magnetic field values measured in the experiment.

A detailed comparison between experiment and theory can be made by solving the 2D Dirac Equation describing graphene electrons in the presence of a confining potential U(r) and a magnetic field B, [υ_F(σ · Π) + U(r)]Ψ(r) = εΨ(r) Following the semiclassical discussion above, we use a simple parabolic potential model U(r) = κr², with κ = 10 eV/μm² to fit the experimental data. The calculated local density of states (LDOS) at the center of the resonator [see Section I of (27) for details (27)] is in good agreement with the experiment (Figs. 3, A and B) and exhibits the half-period jumps between time-reversed states at similar magnetic field values.

Equation 2 also predicts a higher critical field for larger m states, as a larger Lorentz force is needed to induce skipping orbits. These larger angular momentum states have zero wavefunction weight at r = 0 (see Fig.2C), but can be probed at positions away from the center of the resonator (14, 15). Figure 4A shows the spectral conductance map measured at a position of 70 nm away from the center of the p-n junction resonator [see fig. S12 for additional measurements off center], and Fig. 4B shows the calculated LDOS at the same position. Much more complex spectral features are seen in comparison with the on-center measurement (Fig. 3A), which is sensitive only to the m = ±1/2 states. First, at B = 0, twice as many resonances are observed within the same energy range when compared to Fig. 3A. This confirms that additional m states are contributing to the STM maps. Second, both the theory and experimental maps exhibit a “stair case” pattern. Such an arrangement results from an overlap between the field-jumped m state and the next higher non-jumped m state, which are nearly degenerate in energy. For example, at positive fields, the field jumped m = 1/2 state overlaps in energy with the non-jumped m = 3/2 state, giving rise to a strong intensity at this energy. Figures 4, C and D illustrate this effect by showing separately the m= 1/2 and m = 3/2 contributions to the total density of states, respectively; B_c is indicated with a dashed line. In a similar fashion, this behavior continues for all adjacent m levels resulting in the series of staircase steps in the measured and calculated conductance maps in Fig. 4, A and B. Since the states jump by the half of the energy spacing, the staircase patterns can visually form upward and downward looking lines depending on subtle intensity variations at the transitions. For instance, while Fig. 4A shows mostly downward staircase patterns, other measurements (fig. S12) show both down and upward connections at the transitions; the parabolic potential model, Fig. 4B, shows an upward staircase. These behaviors depend on subtle effects, such as the potential shape in the off-center measurement, which are not relevant for our main discussion. More importantly, we plot, as a guide to the eye, B_c in Eq. 2 (dashed lines) for different values of m, showing excellent agreement with the semiclassical estimation above (note that upon summation in Fig. 4B, the positions of the steps, i.e. the white fringes, seem shifted to higher B values; this is expected and analogous to the peak shift observed when summing two Lorentzian functions). Overall, our one-parameter Dirac equation gives a very good description of the resonance dispersion, the critical field B_c, and its dependence on energy and momentum.

Fig. 4. Berry phase switching of higher angular momentum states.

(A) Differential tunneling conductance map vs. magnetic field measured 70 nm off-center of the graphene resonator. Kinks observed in the conductance correspond to the higher m modes which are seen to switch with higher critical magnetic fields. The staircase switching pattern results from m states that jump and overlap in energy the next higher non-switched m state, leading to an increased intensity at that energy (see text). Calculated LDOS vs magnetic field for a position 70 nm off center in a graphene circular resonator for (B) all m states, (C) m = +1/2, and (D) m = + 3/2 . The fan of dashed lines are calculations for the critical magnetic field using Eq. 2 with κ = 10 eV/μm² and E_D = 137 meV and m values as: (A),(B) m = ± $\frac{1}{2}$ to m = ±7/2, and single m values indicated on top of (C,D). The maps are shown in the 2ⁿ derivative (arbitrary values). See fig. S12 for additional off-center measurements.

Implications of these results include possible use in helicity-sensitive electro-optical measurements at THz frequencies with the ability to switch circular-polarized optical signals with small modulations of magnetic fields on the order of 10 mT (Section III.C of (27)). These applications, in conjunction with the fidelity of fabricating a variety of p-n junction and other electrostatic boundaries with impurity doping of boron nitride in graphene heterostructures, will expand the quantum tool box of graphene-based electron optics for future studies and applications.