Identifying Associations Between Brain Imaging Phenotypes and Genetic Factors via A Novel Structured SCCA Approach

Abstract

Brain imaging genetics attracts more and more attention since it can reveal associations between genetic factors and the structures or functions of human brain. Sparse canonical correlation analysis (SCCA) is a powerful bi-multivariate association identification technique in imaging genetics. There have been many SCCA methods which could capture different types of structured imaging genetic relationships. These methods either use the group lasso to recover the group structure, or employ the graph/network guided fused lasso to find out the network structure. However, the group lasso methods have limitation in generalization because of the incomplete or unavailable prior knowledge in real world. The graph/network guided methods are sensitive to the sign of the sample correlation which may be incorrectly estimated. We introduce a new SCCA model using a novel graph guided pairwise group lasso penalty, and propose an efficient optimization algorithm. The proposed method has a strong upper bound for the grouping effect for both positively and negatively correlated variables. We show that our method performs better than or equally to two state-of-the-art SCCA methods on both synthetic and real neuroimaging genetics data. In particular, our method identifies stronger canonical correlations and captures better canonical loading profiles, showing its promise for revealing biologically meaningful imaging genetic associations.

1 Introduction

In recent years, brain imaging genetics becomes a popular research topic in biomedical and bioinformatics studies. Brain imaging genetics refers to the study of modeling and understanding how genetic factors influence the structure or function of human brain using the imaging measurements as the quantitative endophenotype [12, 11, 13]. Both the genetic factors, such as the single nucleotide polymorphisms (SNPs), and the imaging measurements such as the imaging quantitative traits (QTs) are multivariate. Therefore, discovering meaningful bi-multivariate associations is an important task in brain imaging genetics.

Equipped with feature selection, sparse canonical correlation analysis (SC-CA) gains tremendous attention for its powerful ability in bi-multivariate association identification. There are many SCCA methods using different types of shrinkage techniques. The ℓ₁-norm penalty and its variants are widely used, but they only pursuit individual level sparsity [16, 8]. In biomedical studies, the genetic biomarkers usually function simultaneously other than individually [14]. This is also the case for the imaging measurements. Therefore, the structure level sparsity, such as the group structure or the graph/network structure, is of great interest and importance in brain imaging genetics [14, 15].

To capture the high-level structure information, several different structure-aware penalties have been proposed. There are roughly two kinds of structured SCCA methods according to their different penalties [4]. The first kind of SC-CA methods consider the group information using the group lasso regularizer, which is an intra-group ℓ₂-norm and inter-group ℓ₁-norm [1, 6]. The group lasso tends to assign equal weights for those variables in a same group, and each group will be selected or not as a whole [18]. To our knowledge, this type of SCCA methods require the priori knowledge to define the group structure. This limits their applications as it is hard to obtain precise priori knowledge in real biological studies [4]. The second kind of SCCA methods rebuild the structure information via the graph guided or network guided penalty [3, 6, 2, 5, 4]. These SCCA methods can capture the structure information using any available priori knowledge. Moreover, they can also recover the structure information based on the input data [4]. Three types of graph guided penalties have been used: (1) the graph guided fused lasso penalty and its variants [3, 1, 7], (2) the correlation sign based graph guided fused ℓ₂-norm penalty [2], and (3) the improved GraphNet based penalty [4]. Du et al. [4] has shown that the first two types of graph guided penalties could introduce estimation bias because of the sign of the correlations can be wrongly calculated. The reason could be that the sign of the correlations can be easily changed when removing a fraction of the data or perturbing the data as in bootstrap or sub-sampling. The improved GraphNet utilizes ℓ₂-norm with respect to the structure penalty terms, which may not produce desirable sparse results at structure level.

Inspired by the success of group lasso in group selection, we consider a case where each group is made up of only two variables. Both variables will be extracted together with similar or equal weights. Interestingly, this novel group lasso can be used in data-driven mode where no priori knowledge is provided. We call it graph guided pairwise group lasso (GGL) which bridges the gap between the group lasso and graph guided penalties. We then propose a new graph guided pairwise group lasso based sparse canonical correlation analysis model (GGL-SCCA) with intention to recover the structure information automatically. The proposed SCCA method is sample correlation sign independent and it is robust to those existing SCCA methods using graph guided penalty. We also propose an efficient optimization algorithm to solve the problem. Besides, we also provide a quantitative upper bound for the grouping effect of our method to demonstrate its structure identifying ability. Compared with the state-of-art SCCA methods such as NS-SCCA [2] and AGN-SCCA [4], GGL-SCCA can not only obtain higher or equal and more stable correlation coefficients than the competing methods, but also find out cleaner canonical loading patterns on both synthetic data and real imaging genetic data.

2 The Graph Guided Pairwise Group Lasso

Throughout this paper, we denote a vector as the boldface lowercase letter, and a matrix is denoted by a boldface uppercase one. The Euclidean norm of vector u is ‖u‖. Let X = [x¹;…; xⁿ]^T ⊆ ℝ^p and Y = [y¹; …;yⁿ]^T ⊆ ℝ^q be the SNP data and the QT data from the same participants.

We have known that the group lasso tends to extract a subset of the features. However, it depends on the priori knowledge and there is no overlap between groups. The graph guided fused lasso overcomes this limitation, but it requires the sign of the sample correlations to be defined in advance. This will introduce undesirable estimation bias [17]. In this paper, we introduce the graph guided pairwise group lasso penalty by taking advantage of both group lasso and graph guided fused lasso. The GGL penalty is defined as,

$${\Omega }_{\text{GGL}}(\mathbf{u})=\sum _{(i,j)\in E}\sqrt{u_i^2+u_j^2}$$ (1)

where E is the edge set of the graph where those highly correlated features are connected.

The GGL penalty has the following two merits. First, if there is no priori knowledge, every pairwise term will be included to encourage |u_i| ≈ |u_j| which is guaranteed by the pairwise ℓ₂-norm. This holds for both positively and negatively correlated features, which will be demonstrated later in Theorem 1. Second, if some priori knowledge such as the pathway information about genetic markers is provided, the whole penalty will be guided by the pathway information. This will encourage |u_d| = |u_j| no matter whether they are positively or negatively correlated. Therefore, the two genetic markers have very high probability to be selected simultaneously. The same results hold for the imaging measurements if we have the brain connectivity pattern such as the human connectome.

3 Method

3.1 GGL-SCCA Model and Optimization

We then propose the GGL-SCCA model,

$$\underset{\mathbf{u},\mathbf{v}}{min}-{\mathbf{u}}^T{\mathbf{X}}^T\mathbf{Y}\mathbf{v}$$ (2)

$$\mathit{\text{s.t.}}{\Vert \mathbf{X}\mathbf{u}\Vert }^2\le 1,{\Vert \mathbf{Y}\mathbf{v}\Vert }^2\le 1,{\Omega }_{\text{GGL}}(\mathbf{u})\le c_1,{\Omega }_{\text{GGL}}(\mathbf{v})\le c_2$$

where Ω_GGL(u) and Ω_GGL(v) are the GGL penalty to assure structure information. Of note, we use ‖Xu‖² ≤ 1 instead of ‖u‖² ≤ 1 to accommodate the in-set covariance X^TX which can improve the model performance [6].

In order to solve this problem, we write the objective function of GGL-SCCA into matrix form using the Lagrange method,

$$\mathcal{L}(\mathbf{u},\mathbf{v})=-{\mathbf{u}}^T{\mathbf{X}}^T\mathbf{Y}\mathbf{v}+\frac{{\gamma }_1}{2}{\Vert \mathbf{X}\mathbf{u}\Vert }^2+\frac{{\gamma }_2}{2}{\Vert \mathbf{Y}\mathbf{v}\Vert }^2+{\lambda }_1{\Omega }_{\text{GGL}}(\mathbf{u})+{\lambda }_2{\Omega }_{\text{GGL}}(\mathbf{v})$$ (3)

We approximate the objective function by a quadratic function. Obviously, the first term u^TX^TYv is bilinear and biconvex in u and v. We then show the quadratic expression of the GGL term. Let u^t and u^t+1 be the estimation at steps t and t + 1 respectively, the first-order Taylor expansion of term $\sqrt{u_i^2+u_j^2}$ regarding $u_i^2+u_j^2$ is,

$$\begin{array}{c}\sqrt{{(u_i^{t+1})}^2+{(u_j^{t+1})}^2}\approx \sqrt{{(u_i^t)}^2+{(u_j^t)}^2}\\ +\frac{1}{2\sqrt{{(u_i^t)}^2+{(u_j^t)}^2}}(({(u_i^{t+1})}^2+{(u_j^{t+1})}^2)-({(u_i^t)}^2+{(u_j^t)}^2))\\ =\frac{{(u_i^{t+1})}^2}{2\sqrt{{(u_i^t)}^2+{(u_j^t)}^2}}+C\end{array}$$ (4)

where $C=\sqrt{{(u_i^t)}^2+{(u_j^t)}^2}+\frac{{(u_j^{t+1})}^2-({(u_i^t)}^2+{(u_j^t)}^2)}{2\sqrt{{(u_i^t)}^2+{(u_j^t)}^2}}$. From the point of view of optimization, the term C makes no contribution towards optimizing u_i.³

Then the GGL penalty can be simplified,

$${\Omega }_{\text{GGL}}(\mathbf{u})\approx \sum _i\sum _j\frac{{(u_i^{t+1})}^2}{2\sqrt{{(u_i^t)}^2+{(u_j^t)}^2}}+C\ast$$ (5)

with C* being the sum of C across all pairwise penalty terms. Therefore, the GGL penalty is quadratically expressed.

Now the objective function conveys to a quadratic function, and there exists a closed-form solution. Since GGL-SCCA is biconvex in u and v, we take the derivative with respect to them respectively. The solution to the Eq. (3) satisfies,

$$\mathbf{0}\in -{\mathbf{X}}^T\mathbf{Y}\mathbf{v}+({\lambda }_1{\mathbf{D}}_1+{\gamma }_1{\mathbf{X}}^T\mathbf{X})\mathbf{u},$$ (6)

$$\mathbf{0}\in -{\mathbf{Y}}^T\mathbf{X}\mathbf{u}+({\lambda }_2{\mathbf{D}}_2+{\gamma }_2{\mathbf{Y}}^T\mathbf{Y})\mathbf{v},$$ (7)

Algorithm 1 The GGL-SCCA Algorithm
Require:
	X = [x1, …, xn]T, Y = [y1, …, yn]T
Ensure:
	Canonical loadings u and v.
1:	Initialize u ∈ ℝp×1, v ∈ ℝq×1;
2:	while not convergence do
3:	Update the diagonal matrix D1 by taking derivative of Eq. (5);
4:	Solve u according to Eq. (8);
5:	Update the diagonal matrix D2 by taking derivative of Eq. (5);
6:	Solve v according to Eq. (9);
7:	end while
8:	Scale u so that ${\Vert \mathbf{X}\mathbf{u}\Vert }_2^2=1$, and v so that ${\Vert \mathbf{Y}\mathbf{v}\Vert }_2^2=1$

where D₁ can be deduced from the previous step's value of u according to Eq. (5). D₂ can be computed similarly. Therefore, D₁ is a diagonal matrix with the k₁-th element being ${\sum }_{i,i\ne k_1}\frac{1}{\sqrt{u_{k_1}^2+u_i^2}}(k_1\in [1,p])$, and D₂ is a diagonal matrix with the k₂-th element being ${\sum }_{j,j\ne k_2}\frac{1}{\sqrt{{\upsilon }_{k_2}^2+{\upsilon }_j^2}}(k_2\in [1,q])$.⁴

Therefore, u and v have the closed-form updating expressions,

$${\mathbf{u}}^{t+1}={({\lambda }_1{\mathbf{D}}_1^t+{\gamma }_1{\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{X}}^T\mathbf{Y}{\mathbf{v}}^t,$$ (8)

$${\mathbf{v}}^{t+1}={({\lambda }_2{\mathbf{D}}_2^t+{\gamma }_2{\mathbf{Y}}^T\mathbf{Y})}^{-1}{\mathbf{Y}}^T\mathbf{X}{\mathbf{u}}^{t+1}.$$ (9)

We have known that GGL-SCCA model is biconvex with respect to u and v respectively. Then the Alternate Convex Search (ACS) method which is designed to solve the biconvex problem can be employed [10]. According to the ACS method, we address our SCCA model via alternative optimization by updating u and v alternatively. The procedure of the GGL-SCCA is shown in Algorithm 1. In every iteration, u and v are updated in turn till the algorithm converges or reaches a predefined stopping condition.

3.2 The Grouping Effect

In structured learning, a method that can estimate equal or similar values for a group of variables is more desirable [19, 4]. This is called grouping effect and of great importance. We have the following theorem with respect to the grouping effects of the GGL-SCCA method.

Theorem 1. Given two views of data X and Y, and the tuned parameters (λ, 7). Let u* be the solution to our SCCA problem. For the sake of simplicity, we assume there are only two features, e.g. u_i and u_j, are connected on the graph. Let ρ_ij be their sample correlation. Then the optimal u* satisfies,

$$\begin{array}{c}|u_i^{\ast }-u_j^{\ast }|\le \frac{(1+{\gamma }_1)\sqrt{u_i^{\ast 2}+u_j^{\ast 2}}}{{\lambda }_1}\sqrt{2\sqrt{(1-{\rho }_{ij})}},\\ \mathit{\text{if}}{\rho }_{ij}\ge 0,|u_i^{\ast }-u_j^{\ast }|\le \frac{(1+{\gamma }_1)\sqrt{u_i^{\ast 2}+u_j^{\ast 2}}}{{\lambda }_1}\sqrt{2\sqrt{(1-{\rho }_{ij})}},\mathit{\text{if}}{\rho }_{ij}<0.\end{array}$$ (10)

Proof. (1) We first prove the inequations when ρ_ij ≥ 0 indicating features being positively correlated. We have the following two equations,

$$\frac{\partial \mathcal{L}}{\partial u_i}={\lambda }_1{D}_{1,i}{u}_i^{\ast }+{\gamma }_1{\mathbf{x}}_i^T\mathbf{X}\mathbf{u}={\mathbf{x}}_i^T\mathbf{Y}\mathbf{v},\frac{\partial \mathcal{L}}{\partial u_j}={\lambda }_1{D}_{1,i}{u}_i^{\ast }+{\gamma }_1{\mathbf{x}}_i^T\mathbf{X}\mathbf{u}={\mathbf{x}}_i^T\mathbf{Y}\mathbf{v}.$$ (11)

Given u_i and u_j are the only connected features, we have $D_{1,i}=D_{1,j}=\frac{1}{\sqrt{u_i^2+u_j^2}}$. Then we arrive at

$$\frac{{\lambda }_1}{\sqrt{u_i^{\ast 2}+u_j^{\ast 2}}}{u}_i^{\ast }={\mathbf{x}}_i^T\mathbf{Y}\mathbf{v}-{\gamma }_1{\mathbf{x}}_i^T\mathbf{X}\mathbf{u},\frac{{\lambda }_1}{\sqrt{u_i^{\ast 2}+u_j^{\ast 2}}}{u}_j^{\ast }={\mathbf{x}}_j^T\mathbf{Y}\mathbf{v}-{\gamma }_1{\mathbf{x}}_j^T\mathbf{X}\mathbf{u}.$$ (12)

Subtracting these two equations, we have

$$\frac{{\lambda }_1}{\sqrt{u_i^{\ast 2}+u_j^{\ast 2}}}(u_i^{\ast }-u_j^{\ast })={({\mathbf{x}}_i-{\mathbf{x}}_j)}^T(\mathbf{Y}\mathbf{v}-{\gamma }_1\mathbf{X}\mathbf{u})$$ (13)

Taking ℓ₂-norm on both sides, we arrive at

$$\frac{{\lambda }_1}{\sqrt{u_i^{\ast 2}+u_j^{\ast 2}}}|u_i^{\ast }-u_j^{\ast }|=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert \Vert \mathbf{Y}\mathbf{v}-{\gamma }_1\mathbf{X}\mathbf{u}\Vert =\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert \sqrt{\Vert \mathbf{Y}\mathbf{v}\Vert -2{\gamma }_1{\mathbf{u}}^{\top }{\mathbf{X}}^{\top }\mathbf{Y}\mathbf{v}+{\gamma }^2\Vert \mathbf{X}\mathbf{u}\Vert }$$ (14)

Using $\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert -\sqrt{2(1-{\rho }_{ij})}$, ‖Xu‖ ≤ 1, ‖Yv‖ ≤ 1 and −u^TX^TYv ≤ 1, we obtain the upper bound

$$|u_i^{\ast }-u_j^{\ast }|\le \frac{(1+{\gamma }_1)\sqrt{u_i^{\ast 2}+u_j^{\ast 2}}}{{\lambda }_1}\sqrt{2(1-{\rho }_{ij})}.$$ (15)

(2) If ρ_ij < 0, it is clear that sign(u_i) = −sign(u_j). By adding both equations in Eq. (12) instead of subtracting them, we finally arrive at,

$$|u_i^{\ast }+u_j^{\ast }|\le \frac{(1+{\gamma }_1)\sqrt{u_i^{\ast 2}+u_j^{\ast 2}}}{{\lambda }_1}\sqrt{2(1+{\rho }_{ij})}.$$ (16)

Note that GGL-SCCA model is symmetric about u and v, we can obtain the same upper bound of grouping effect for canonical weights v.

The Theorem 1 provides a qualitative theoretical description of the bound for both differences and sums of the coefficients. The bound between two coefficients directly depends on their correlation. If ρ_ij ≥ 0, a higher correlation between two variables makes sure a smaller difference between their estimated coefficients. If ρ_ij < 0, a smaller value assures a smaller sum between their coefficients. This implies that the two coefficients will be approximate in amplitude. Therefore, the GGL-SCCA is capable of capture structure information no matter whether those features are positively or negatively correlated.

3.3 The Complexity Analysis

In Algorithm 1, Steps 2-7 are repeated until convergence. In each iteration, Step 3 is easy to calculate as D₁ can be computed via matrix manipulation to avoid time consuming loop. This is the same case for Step 5. Step 4 and Step 6 are the key steps, and we compute them via solving a system of linear equations with quadratic complexity instead of computing the matrix inverse with cubic complexity. This can reduce the computation burden greatly. Step 8 is a rescale steps and very simple to calculate. Therefore, the algorithm runs fast and efficiently.

In this study, we terminate Algorithm 1 when either of the two conditions satisfies, max{|δ| |δ ∈ (u_t+1 – u_t)} ≤ ∊ and max{|δ| |δ ∈ (v_t+1 – v_t)} ≤ ∊, where ∊ is a desirable estimation error. We chose ∊ = 10⁻⁵ empirically from experiments in this paper.

4 Experimental Study

4.1 Experimental Setup

We compare GGL-SCCA with two structure-aware SCCA methods. The first one is the network guided fused lasso based SCCA (NS-SCCA) which takes the sample correlation signs into consideration [2]. The second method is the AGN-SCCA which uses the absolute value based GraphNet to penalize those correlated variables [4]. These two methods are different in both modeling and optimizing techniques, and is deemed to be among the best structured SCCA methods by now.

We tune the parameters based on the following considerations to reduce time consumption. (1) According to Theorem 1, λ_i=1,2 and γ_i=1,2 contribute to the grouping effect oppositely. (2) The grouping effect is more sensitive to λ_i=1,2 than to γ_i=1,2. Therefore, we fix γ_i=1,2 to a moderate constant, and let γ_i=1,2 = 10 in this paper. Finally, we have only two parameters λ_i=1,2 to be tuned and optimally tune them via a grid search from a moderate range 10⁻² to 10² through nested five-fold cross-validation to make sure efficiency. The parameters that generate the highest correlation coefficients are used.

4.2 Results on Simulation Data

Four different data sets with different properties are generated in this study. We also set the number of observations be smaller than the number of features to simulate a large p small n problem. The details of the data sets are as follows. Firstly, u and v are generated according to the predefined structure. Secondly, a latent variable z ∼ N(0, I_n×n) is generated. And thirdly, X is created by x_i ∼ N(Z_iu, Σ_x), where (Σ_x)_jk = exp^{−|u_j–u_k|}. Similarly, Y with the entry: y_i ∼ N(Z_iv, Σ_y), where (Σ_y)_jk = exp^{−|vj–v_k|} is created. During this procedure, the true signals and the correlation strengths of the data are all distinct to assure diversity. This setup can make a thorough comparison.

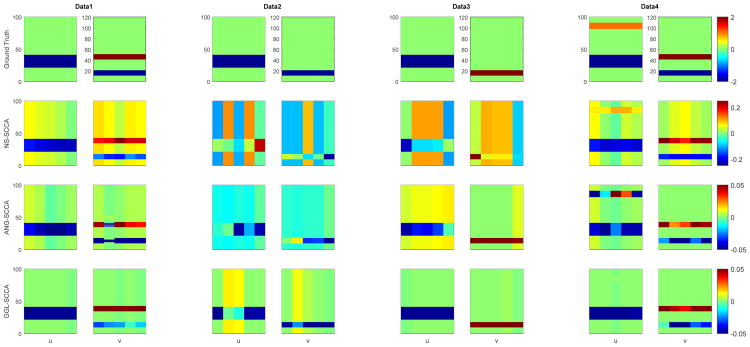
We apply GGL-SCCA, NS-SCCA and AGN-SCCA to all four data sets. The true and estimated canonical loadings u and v are shown in Fig. 1. We observe that both GGL-SCCA and AGN-SCCA identify similar canonical loading profiles that are consistent to the ground truth across all data sets. NS-SCCA produces too many signals which are not so perfect to the ground truth. In addition, we also show the estimated correlation coefficients on both the training and testing sets calculated using the trained SCCA models in Table 1 (Left). The results show that GGL-SCCA obtains highest scores on both training and testing sets. Its testing result is only inferior to the NS-SCCA on the second data. The results implies that GGL-SCCA has better training performance and generalization ability than those benchmarks. The area under ROC (AUC) shown in Table 1 (Right) indicates the sensitivity and specificity. It reveals that GGL-SCCA outperforms the competing methods as it holds the highest values for the most times. In summary, the simulation results demonstrate that GGL-SCCA could identify not only stronger testing associations but also more better signals on these diversified data sets.

Fig. 1.

Canonical loadings estimated on synthetic data. The first row is the ground truth, and each remaining row corresponds to a SCCA method: (1) NS-SCCA, (2) AGN-SCCA, and (3) GGL-SCCA. For each method, the estimated weights of u are shown on the left panel, and those of v are shown on the right.

Table 1.

Performance comparison on synthetic data. Training and testing correlation coefficients (mean±std) of 5-fold cross-validation are shown for NS-SCCA, AGN-SCCA and GGL-SCCA. The best value are shown in boldface. The AUC (area under the curve) values (mean±std) of canonical loadings are also shown.

Data set	Training Correlation Coefficients			Area under ROC (AUC): u
	NS-SCCA	AGN-SCCA	GGL-SCCA	NS-SCCA	AGN-SCCA	GGL-SCCA
data1	0.39±0.07	0.53±0.10	0.60±0.07	1.00±0.00	1.00±0.00	1.00±0.00
data2	0.31±0.08	0.35±0.08	0.48±0.08	0.20±0.45	0.60±0.55	0.60±0.55
data3	0.20±0.07	0.29±0.07	0.40±0.07	0.20±0.45	0.80±0.45	1.00±0.00
data4	0.44±0.08	0.44±0.07	0.50±0.05	1.00±0.00	1.00±0.00	0.93±0.15
	Testing Correlation Coefficients			Area under ROC (AUC): v
data1	0.42±0.10	0.60±0.10	0.62±0.23	1.00±0.00	0.96±0.09	1.00±0.00
data2	0.25±0.18	0.21±0.14	0.22±0.08	0.20±0.45	0.80±0.45	1.00±0.00
data3	0.28±0.19	0.33±0.24	0.43±0.21	0.20±0.45	1.00±0.00	1.00±0.00
data4	0.25±0.10	0.32±0.24	0.44±0.24	1.00±0.00	1.00±0.00	1.00±0.00

4.3 Results on Real Neuroimaging Genetics Data

The real imaging genetics data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public private partnership, led by Principal Investigator Michael W. Weiner, MD. One primary goal of ADNI is to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimers disease (AD). For up-to-date information, please refer to www.adni-info.org.

We use the genotyping and baseline amyloid imaging data (preprocessed [11C] Florbetapir PET scans) contributed by 567 non-Hispanic Caucasian participants. The amyloid imaging data used in this study are downloaded from LONI (adni.loni.usc.edu). Preprocessing is conducted to format this imaging data, and we finally generate 191 ROI level mean amyloid measurements in which the ROIs are defined by the MarsBaR AAL atlas [4]. The genotyping data includes 58 candidate SNP markers from the AD-related genes, such as the APOE gene. The aim is to evaluate the associations between the SNP data and the amyloid data, as well as which SNPs and amyloid measurements are correlated in this AD cohort.

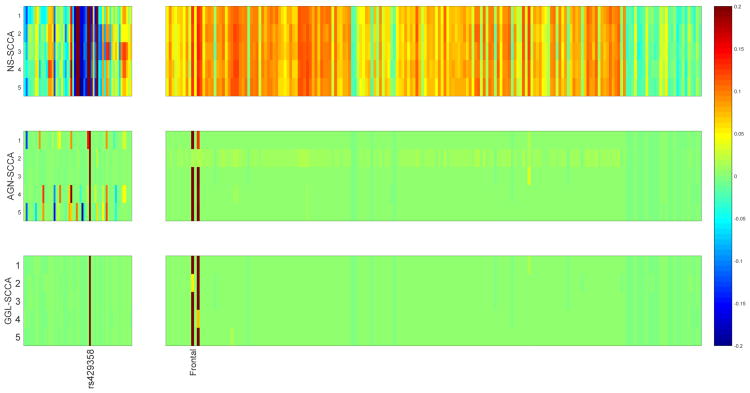
All three SCCA methods are performed on the real neuroimaging genetics data. Shown in Fig. 2 are the canonical loadings obtained from the training data, where the relevant imaging measurements and genetic markers are exhibited. It is clear that GGL-SCCA identifies two relevant ROIs and one SNPs for easy interpretation due to the novel GGL penalty. The two strongest imaging measurements come from the right frontal region, which are positively correlated with SNP rs429358, a confirmed AD related allele in APOE e4. The AGN-SCCA identifies similar results to our method, which however has many interfering signals for the genetic markers. The NS-SCCA finds out too many imaging signals that are very hard to interpret. To give a clear view, we map the canonical loadings regarding the imaging measurements of GGL-SCCA onto the brain. Fig. 3 clearly shows that our method only highlights a small region of the whole brain. Moreover, we present the training and testing correlations in Table 3. GGL-SCCA obtains the highest values on both training set and testing set. Although AGN-SCCA has the same mean on training data, its standard deviation is larger than GGL-SCCA. Moreover, GGL-SCCA obtains better testing results than both competing methods. This implies that GGL-SCCA is more stable and has better generalization ability than AGN-SCCA and NS-SCCA. The results on this real data demonstrate that GGL-SCCA has better bi-multivariate identification ability than the benchmark methods. The strong association between the frontal morphometry and the APOE in AD cohort, indicating GGL-SCCA's promising and potential power in identifying biologically meaningful imaging genetic associations.

Fig. 2.

Canonical loadings estimated on real imaging genetics data set. Each row corresponds to a SCCA method: (1) NS-SCCA, (2) AGN-SCCA, and (3) GGL-SCCA. For each method, the estimated weights of u are shown on the left panel, and those of v are shown on the right.

Fig. 3.

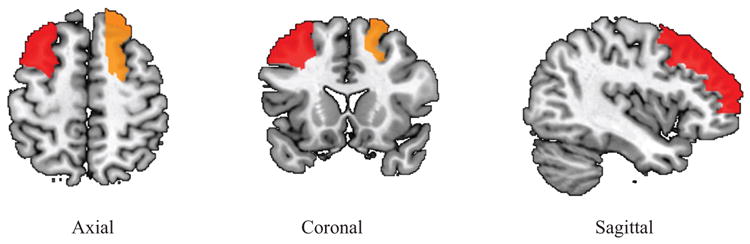
Mapping averaged canonical loading v of GGL-SCCA onto the brain.

Table 3.

Performance comparison on real data. Training and testing correlation coefficients (each fold and mean±std) of 5-fold cross-validation are shown for NS-SCCA, AGN-SCCA and GGL-SCCA. The best mean±std is shown in boldface.

Method	Training Results					mean±std	Testing Results					mean±std
NS-SCCA	0.41	0.40	0.43	0.39	0.41	0.41±0.01	0.37	0.41	0.23	0.43	0.37	0.36±0.08
AGN-SCCA	0.49	0.43	0.52	0.49	0.51	0.49±0.03	0.48	0.46	0.33	0.55	0.43	0.45±0.08
GGL-SCCA	0.48	0.48	0.52	0.46	0.49	0.49±0.02	0.51	0.45	0.34	0.55	0.47	0.46±0.08

5 Conclusions

We have proposed a novel graph guided pairwise group lasso (GGL) based SC-CA method (GGL-SCCA) to identify associations between brain imaging measurements and genetic factors. The existing group lasso based methods [1, 6] were dependent on the priori knowledge which was not always available. The graph/netwrok guided fused lasso based approaches [3, 6, 2, 5, 4] only focus on the positively correlated variables, or depended on the signs of the sample correlation which were sensitive to the partition of the data. Our SCCA method combines the merits of group lasso and the graph/network guided fused lasso, which is independent to not only the signs of the sample correlation, but also the priori knowledge. Moreover, our method can also incorporate the priori knowledge to recover specific structures.

We have compared GGL-SCCA with two state-of-the-art structured SCCA methods on both synthetic data and real imaging genetic data. The results on the synthetic data show that GGL-SCCA performs better than both NS-SCCA and AGN-SCCA across all data sets. The results on real data show that, GGL-SCCA not only reports better canonical correlation values than the competing methods, but also obtains more accurate and cleaner canonical loading patterns. GGL-SCCA finds out a strong associations between the superior frontal morphometry and the APOE e4 SNP, revealing its power in brain imaging genetics. In this paper, we merely use the graph guided pairwise group lasso penalty to induce structured sparsity. In the future work, we will incorporate lasso into the model to assure additional sparsity, and incorporate the priori knowledge to evaluate the performance of GGL-SCCA.

Table 2.

Participant characteristics.

	HC	MCI	AD
Num	196	343	28
Gender(M/F)	102/94	203/140	18/10
Handedness(R/L)	178/18	309/34	23/5
Age (mean±std)	74.77±5.39	71.92±7.47	75.23±10.66
Education (mean±std)	15.61±2.74	15.99±2.75	15.61±2.74