Abstract
In this review, we discuss the experimental static deuteron NMR techniques and computational approaches most useful for the investigation of side-chain dynamics in protein systems. Focus is placed on the interpretation of line shape and relaxation data within the framework of motional modeling. We consider both jump and diffusion models and apply them to uncover glassy behaviors, conformational exchange and dynamical transitions in proteins. Applications are chosen from globular and membrane proteins, amyloid fibrils, peptide adsorbed on surfaces and proteins specific to connective tissues.
Keywords: protein dynamics, static deuteron NMR, solid-state NMR, dynamical transitions
Graphical abstract
Introduction
Static deuterium NMR has been recognized since the early 1970s as an important tool for studies of protein dynamics. It was first applied to amino acids and polymers in either powder or liquid crystalline states(1–7) and then further expanded into a tool to probe protein and nucleic acid systems.(8–15) The purpose of this review is to highlight the static deuteron NMR techniques and computational approaches most useful for probing protein systems as well as review several recent advances in the field.
Deuteron NMR observables are usually dominated by one, single-spin mechanism: the interaction of the nuclear electric quadrupole moment with the electric field gradient at the site of the nucleus. The deuteron has a relatively small electric quadrupole moment, which makes it easy to work with experimentally. Available deuteron NMR techniques cover a very broad range of timescales, from pico- to milliseconds. Experiments are relatively easy to conduct over a broad temperature range. Another subtle advantage of the static technique compared with the more advanced magic-angle spinning approaches is the relative ease of simulations of the motional mechanisms giving rise to the dynamics. This will be discussed in more detail in the last section of the review devoted to modeling approaches. In general, the solid phase permits investigations of the effect of hydration, examples of which will be shown throughout the review.
1. Note on the preparation of samples suitable for static 2H NMR
As static approaches inherently lack site-specific resolution, in order to obtain site-selective information, one must be able to produce samples with selectively introduced deuterium labels. On the other hand, as long as these labels can be introduced into the system, there are no inherent limitations on the sizes of the molecules. The most common techniques are solid-state peptide synthesis,(16) currently permitting the synthesis of peptides of up to about 120 residues in length, and protein expression with media enhancement strategies to label selective residue types.(17) For hydration dependence studies, water is often reintroduced by either vapor diffusion or pipetting the desired amount of water directly into lyophilized powder. The latter approach permits the use of deuterium-depleted water to avoid the NMR signal arising from HOD.
For lyophilized and rehydrated powder samples it is often necessary to confirm that the protein retains its native fold for globular proteins, or that it retains the expected supramolecular structure for the case of the fibril samples. This requires the use of site-resolved approaches such as magic-angle spinning techniques. For villin headpiece subdomain protein, reviewed in this work, this has been accomplished by measuring 15N chemical shifts of backbone nitrogen nuclei belonging to several core residues in selectively 15N-labeled samples. In this case both magic-angle cross-polarization measurements and static measurements of the CSA tensors have been employed.(18, 19) The data confirmed that the structures are similar in solution and in hydrated powder states.
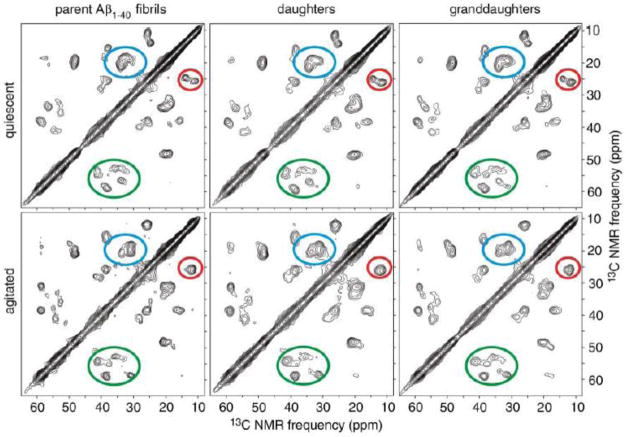
For the preparation of amyloid fibrils samples, we have followed protocols developed by Tycko’s laboratory.(20–22) There is a wide body of 13C magic-angle-spinning characterization/assignments existing for these types of samples in various polymorphs, as well as 15N-13C REDOR distance constraints. One of such examples is presented in Fig. 1, in which finite-pulse radio-frequency driven recoupling (fpRFDR) scheme has been employed.(23) 13C chemical shift assignments were also confirmed by 2D spectra recorded with 50–500 ms dipolar-assisted rotational resonance(24) mixing periods. The “agitated” protocol, the spectra for which are shown in the lower panel of Fig. 1, leads to the 2-fold symmetric morphology of the fibril, while the “quiescent” protocol ( upper panel of the figure) to the 3-fold symmetric morphology. The 2D spectra of quiescent and agitated parent fibrils show pronounced differences in cross-peak patterns that are transmitted to the daughter and granddaughter fibrils. It was concluded that the morphological differences observed by transmission electron microscopy correlate with underlying differences in structure at the molecular level. It is also interesting that the analysis of the Aβ10–40 fragment indicated that the structure is not affected by dehydration.(25) Further in the text we present investigations of dynamics in both the 2-fold and 3-fold symmetric polymorphs with the use of 2H static solids-state NMR techniques. Some of our measurements also assess the role of hydration on the dynamics.
Figure 1.
Two-dimensional solid-state 13C NMR spectra of Aβ1–40 fibrils, prepared with 13C labeling of all carbon sites in amino acid residues F20, D23, V24, K28, G29, A30, and I31 using solid-state peptide synthesis. Spectra were recorded under magic angle spinning. Regions enclosed by ellipses contain Cγ1/Cδ cross peaks of I31 (red), Cβ/Cγ cross peaks of V24 (blue), and Cα/Cβ cross peaks of F20, D23, V24, K28, and I31 (green). fpRFDR-CT data were obtained at 9.4 T, using 110 kHz proton decoupling fields and 15.0 μs 13C π pulses in the dipolar recoupling period, and using pulsed spin locking for sensitivity-enhancement in the detection period. Reprinted from (21), with the permission from American Association for the Advancement of Science, Copyright 2005.
2. Experimental approaches
2.1 Line shape Analysis
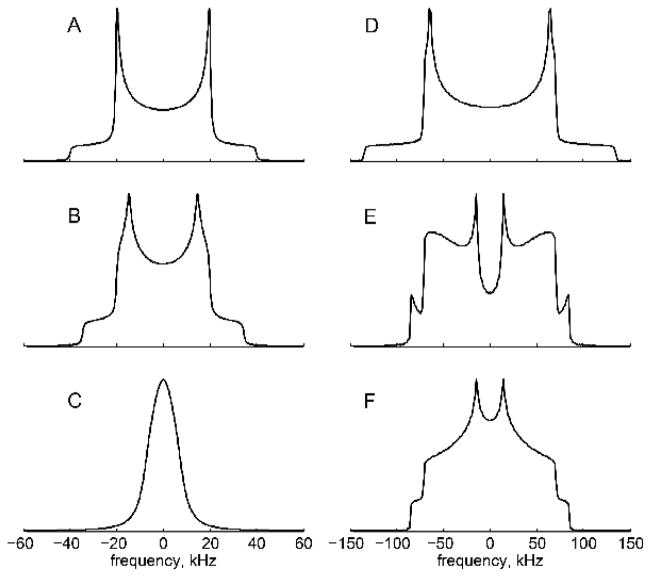
The most straightforward experiment is the measurement of a line shape, which is usually accomplished with the quadrupolar echo (QE) pulse sequence: [90ox-τ −90oy-τ]. Several phase cycling schemes have been suggested.(26–28) The technique is sensitive to motions on the order of the effective quadrupolar coupling constant (Cq).(2) For example, for methyl groups that undergo fast three-fold rotations, the effective constant is of the order of 53–55 kHz,(4, 29, 30), while for an aromatic ring deuteron the constant is of the order of 170–180 kHz.(3, 7, 31) In the absence of motions, a classic Pake pattern for the spin 1 system is expected (Fig. 2A, D), while motions can lead to various degrees of narrowing and distortions of this pattern (Fig. 2B, C, E, F). Small-angle fluctuations lead to relatively subtle but still quantifiable changes in the Pake pattern (Fig. 2B), while large-angle fluctuations such as rotameric jumps can have a dramatic effect on the line shape (Fig. 2C, D, F).
Figure 2.
Line shape simulations, performed using EXPRESS software.(32) A–C methyl groups. A) Pake pattern narrowed by the three-site jump motions with the effective quadrupolar constant of Cq = 53.3 kHz. No methyl axis motions. B) Methyl axis motion along a restricted arc corresponding to the diffusion of the methyl axis occurring in the fast limit with respect to Cq. The arc length is 60o. C) Methyl axis undergoes rotameric motions, simulated by four magnetically distinct conformers with the weight of the major conformer twice that of each of the minor conformers; the jump rate is 2.5×105 s−1. D–F Ortho- and meta-deuterons of phenylalanine rings. D) Static Pake pattern with Cq = 180 kHz and an asymmetry parameter of 0.05. E) π-flip motion in the intermediate regime with a flip rate of 2.5×106 s−1. F) Fast π-flips with a flip rate of 1×108 s−1.
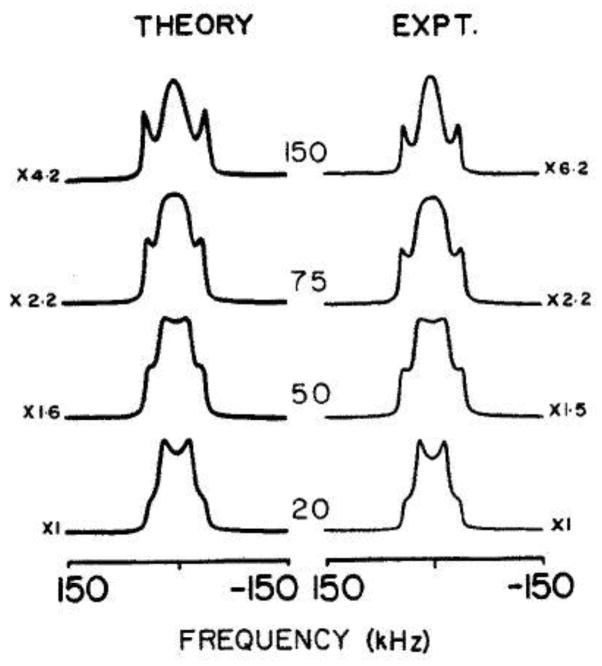
Additionally, the line shapes can be greatly affected when motions fall in the intermediate regime with respect to Cq (i.e., the rate constant becomes comparable to Cq). In this situation, for certain crystallite orientations, the transverse relaxation time becomes comparable to the interpulse delay in the QE pulse sequence, leading to a drastic intensity loss.(5, 33, 34) This effect has been extensively studied for simple systems and an example is shown below for a methyl group in L-alanine (Fig. 3).
Figure 3.
τ dependence in the QE pulse sequence for the line shapes corresponding to the three-site methyl jump motions in L-alanine. τ intervals are in μs. The theoretical line shapes were calculated with a 3 ·106 s−1 jump rate and the experimental spectra were taken at −70 °C. Reprinted from (33), with the permission of AIP Publishing.
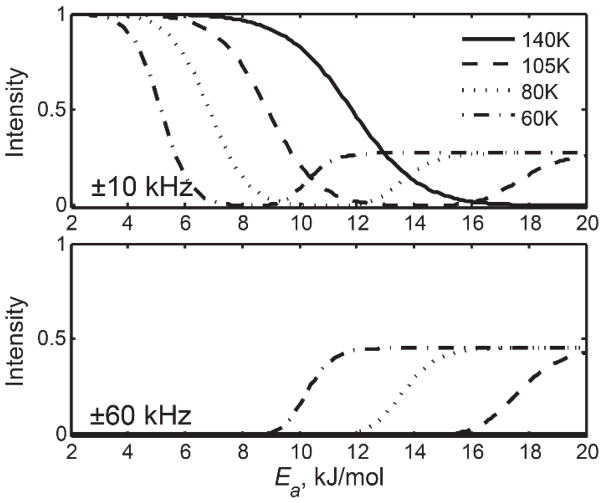
In proteins, due to the presence of a conformational ensemble in the landscape of the folded-state,(35, 36) a distribution of conformers with different motional parameters can be observed. In this situation, the intensity loss function due to transverse relaxation (T2) anisotropy can become very complex. An example is shown below for the methyl rotations of a leucine methyl group in the hydrophobic core of villin headpiece subdomain protein (Fig. 4).(34) The conformers were distinguished by their activation energy values Ea for methyl rotations and, thus, the intensity loss is shown as a function of Ea.
Figure 4.
Simulated intensities for spikelets at ±10 kHz and ±60 kHz frequencies as a function of activation energy Ea for methyl rotations at four temperatures. The QCPMG detection scheme was employed to match the experimental conditions. Reprinted with permission from (34). Copyright (2013) American Chemical Society.
Note that at temperatures at which the rate constants fall in the intermediate regime with respect to Cq, the intensity loss coupled with the relatively low sensitivity of the protein samples precluded the observation of the QE line shape signal even with the signal averaging over 24 hours. Thus, it was necessary to employ the signal-enhancement schemes described in the next section.
Line shape measurements are a useful tool for studying the dynamics of the peptides adsorbed on surfaces,(37) membrane proteins,(14, 15, 38, 39) proteins in dried and lyophilized powder states,(8, 13, 29, 40) and amyloid fibrils.(41, 42) Studies as a function of temperature and hydration levels can be particularly useful for the elucidation of factors governing the dynamics.(9) In principle, there is no limit in how low one can go in temperature, and studies can be performed even at liquid helium temperatures, where tunneling effects predominate.(43, 44) Hydration level dependence can be important for assessing the effect of the solvent on the onset of motions.(45–48) Hydration levels up to about 60–80% by weight can be investigated without introducing the effects of overall tumbling (i.e., dissolving protein) for globular proteins. For samples such as such as amyloid fibrils comprising the amyloid-β protein, water levels can be higher due to negligible effect of tumbling for the large fibril aggregates.
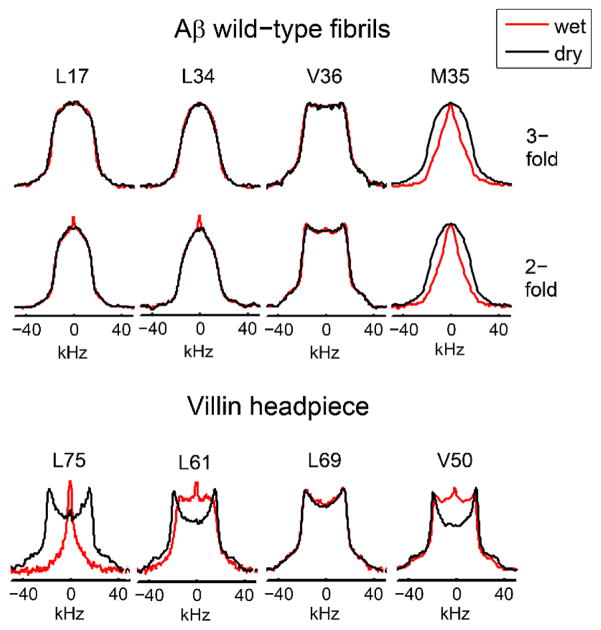
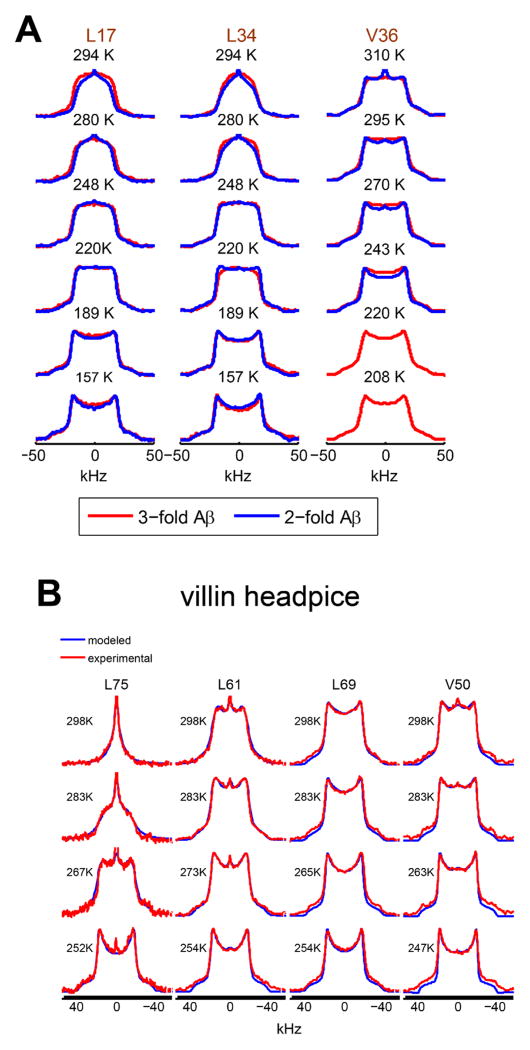
Fig. 5 demonstrates the comparison of the hydration dependence in the hydrophobic core methyl groups of a globular protein, chicken villin subdomain, and amyloid fibrils.(40, 42, 49) The line shapes clearly demonstrate that the dynamics of the core methyl groups of the fibrils are not hydration-dependent, in contrast to what is seen in the globular protein. Further, a methionine side-chain pointing into a hydrophobic cavity is found to exhibit a very strong hydration dependence(42) – an experimental observation that confirms the prediction by molecular dynamic simulations.(50) Studies of temperature dependence can further reveal the details of the mechanisms governing the motions and quantifying the motional parameters. An example is shown in Fig. 6, again comparing the hydrophobic core methyl-bearing side-chains in the globular protein and in amyloid fibrils. The spectra reveal that while for the globular protein the pattern becomes rigid-like below about 250 K, for amyloid fibrils motional narrowing is evident down to at least 200–190 K, signifying that motions persist down to low temperatures. Further, the spectral changes are indicative of large-angle jumps such as rotameric interconversions as the main motional mechanism. The polymorphic state of the fibrils was confirmed by transmission electron microscopy, with the 2-fold and 3-fold symmetric polymorphs giving rise to distinct images.(21)
Figure 5.
Deuteron line shapes in amyloid-β (1–40) wildtype fibrils at 294 K for L17, L34 and V36 and at 310 K for M35 (upper panel) and globular villin headpiece protein hydrophobic core residues at 298 K (lower panel). The spectra were collected at 17.6 T. Adapted with permission from (40). Copyright (2011) American Chemical Society. Also reprinted with permission from (42). Copyright (2016) American Society for Biochemistry and Molecular Biology.
Figure 6.
2H line shapes of the key hydrophobic core methyl-bearing side-chains in A) amyloid fibrils comprising amyloid-β (1–40) protein in the 2-fold symmetric (blue) and 3-fold symmetric (red) polymorphs in the hydrated state. B) Villin headpiece subdomain in the hydrated state (red) overlaid with simulated line shapes (blue). All line shapes were collected at 17.6 T. Modeling was performed using EXPRESS software.(32) Adapted with permission from (40). Copyright (2011) American Chemical Society. Also reprinted with permission from (42). Copyright (2016) American Society for Biochemistry and Molecular Biology.
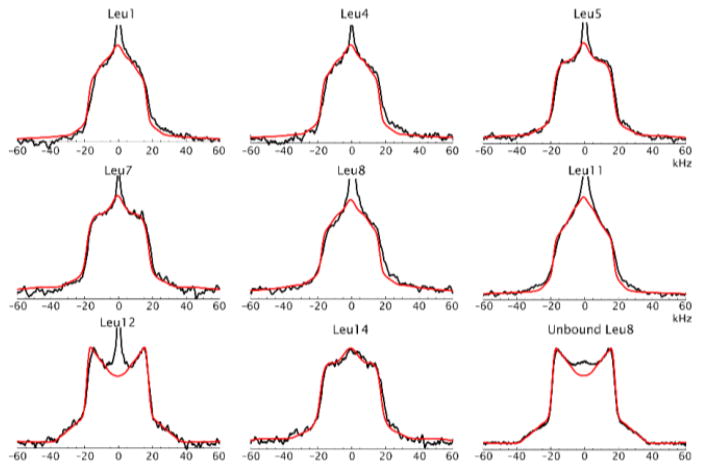
An example of the spectra of a 14 residue leucine-lysine peptide adsorbed on a polystyrene surface is shown in Fig. 7. Combined NMR and sum frequency generation vibrational spectroscopy provided a particularly powerful analysis of the dynamics with the rotameric inter-conversions as the main motional mechanism.(37)
Figure 7.
Deuterium static line shapes in a polystyrene-adsorbed synthetic peptide. Experimental line shapes are in black and simulated in red. (37) Copyright (2011) National Academy of Sciences.
In membrane systems, deuterium NMR is useful for the assessment of the rotational reorientation of one particular fragment within a larger complex, as for example determined for a transmembrane domain of phospholamban.(14) The line shapes of the three consecutive leucine residues (Fig. 8) are consistent with Leu42 oriented toward the lipids, where it exhibits fewer steric contacts, and Leu43 and Leu44 oriented toward helix interfaces that restrict their motion.
Figure 8.
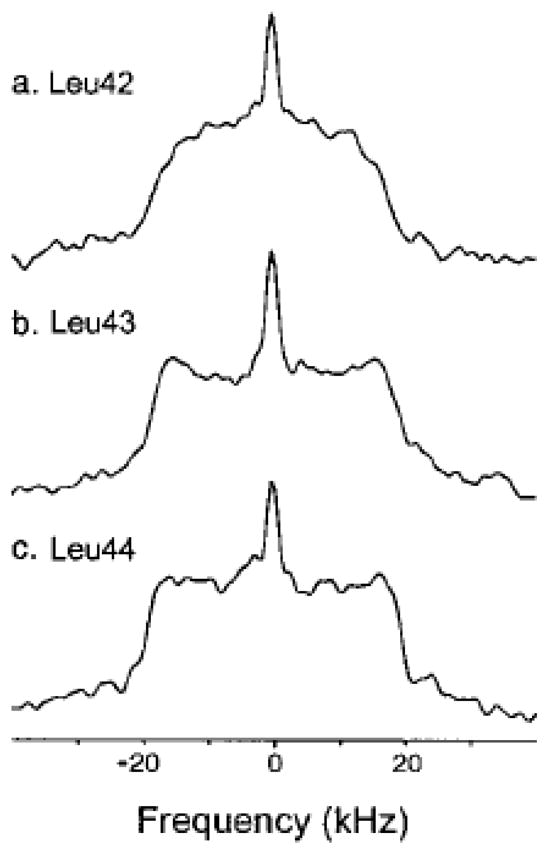
Deuterium NMR spectra of δ-D3-labeled Leu42, Leu43 and Leu44 phospholamban at 5°C and at 55.2 MHz Larmor frequency. Reprinted with permission from (14). Copyright (2000) American Chemical Society.
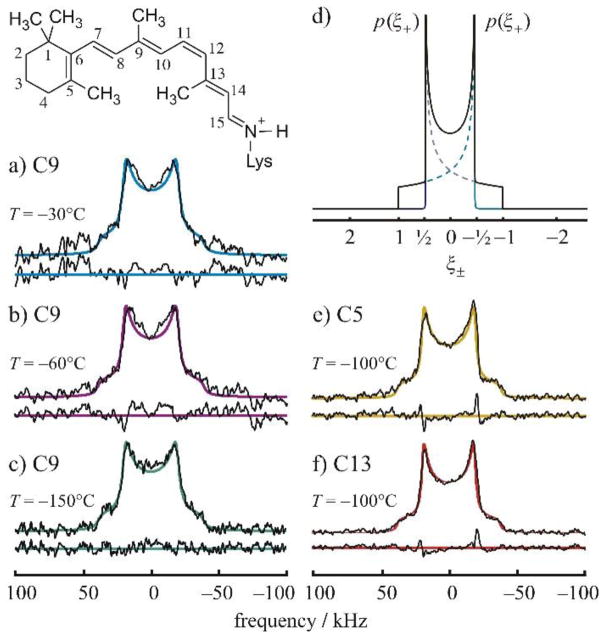
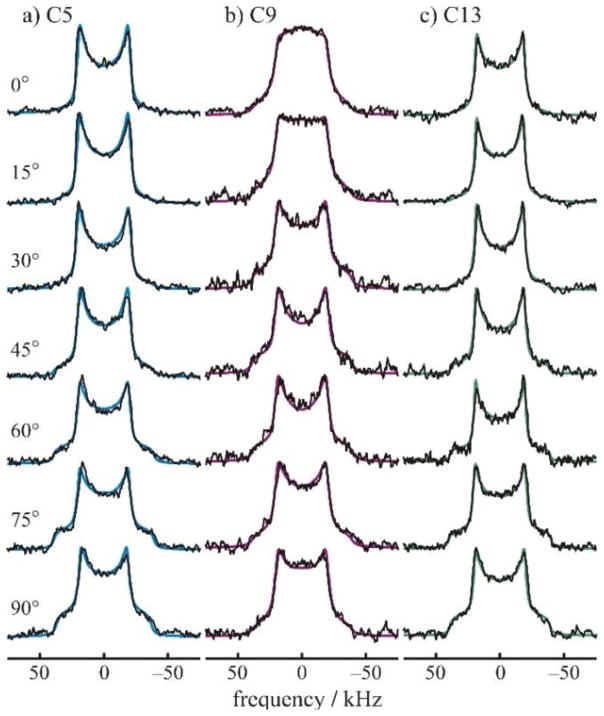
There are a number of important works that apply 2H NMR to the structural dynamics of retinal in rhodopsin.(15) An example is given below (Fig. 9) for 2H-labeled retinal in the dark state.(51) The line shapes in Fig. 8 are indicative of a distribution of effective quadrupolar coupling constants due to differences with respect to the membrane orientation. No large-angle rotameric jumps are observed. Fig. 10 displays the spectra of the tilt series for 11-cis-retinal in the dark state, which reveal methyl bond orientations and the mosaic spread of aligned membranes. Essential features of sample preparation for this system are the following: for the dark and meta I states rhodopsin was recombined with 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) in 1:50 molar ratio. Preparation of meta II required the inclusion of 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE). Quantitative trapping of the meta II state utilized a DOPE/POPC (1:3) mixture with a protein/lipid ratio of 1:75. Membranes were aligned on planar glass substrates using isopotential ultracentrifugation1 or they were investigated as randomly oriented suspensions.
Figure 9.
2H NMR spectra for retinal in the dark state are indicative of rotating methyl groups with large order parameters; collected at 11.7 T. (a)–(c) Experimental 2H NMR spectra for 11-Z-[9-C2H3]-retinylidene rhodopsin, i.e. having 11-cis-retinal deuterated at the C9 methyl group, in gel-phase POPC membranes (1:50 molar ratio) at pH 7 and T=−30 °C (blue), −60 °C, (magenta) and −150 °C (green), respectively. (d) Theoretical 2H NMR spectrum for randomly oriented C–C2H3 groups undergoing fast three-fold rotation on the 2H NMR timescale (<(3χQ/8)-1> ≈10 μs). Probability density p(ξ±) is plotted against reduced frequency ξ± for the two I=1 spectral branches, which is expressed in units of (3/4) χQeff=41.75 kHz for the rotating methyl groups. (e) and (f) Representative 2H NMR spectra for dark-state 11-Z-[5-C2H3]-retinylidene rhodopsin and 11-Z-[13-C2H3]-retinylidene rhodopsin, i.e. with 11-cis-retinal deuterated at the C5 methyl (yellow) or C13 methyl group (red), respectively, in POPC membranes (1:50) at pH 7 and T= 100 °C. Theoretical powder-type 2H NMR spectra for C C2H3 groups undergoing axial rotation (continuous colored lines) are superimposed on the experimental spectra, with residuals below. Reprinted with permission from (52), Copyright (2007) Elsevier, license number 3971590104454.
Figure 10.
Tilt series of 2H NMR spectra for 11-cis-retinal in the dark state. (51) (a)–(c) 2H NMR spectra for 11-Z-[5-C2H3]-retinylidene rhodopsin (blue), 11-Z-[9-C2H3]-retinylidene rhodopsin (magenta), and 11-Z-[13-C2H3]-retinylidene rhodopsin (green), respectively. Experimental 2H NMR spectra, collected at 11.7 T, are shown as a function of the tilt angle of the average normal of the membrane stack to the magnetic field B0 for rhodopsin/POPC bilayers (1:50) at pH 7 and T = −150 °C. Theoretical line shapes (continuous colored lines) assume a static uniaxial distribution of rhodopsin molecules, with rotating C–C2H3 groups of retinylidene cofactor. Reprinted with permission from (52), Copyright (2007) Elsevier, license number 3971590104454.
Similar to polymer systems,(53) any inherent inhomogeneity in the protein/peptide systems, such as due to packing variations, can in principle lead to multiple conformers with somewhat different motional processes in each conformational state. Thus, the resulting line shape can report on the presence of multiple conformers, such as shown in Fig. 11 for a hydrophobic core phenylalanine residue.(31) These line shapes were modeled with a distribution of ring flip rate constants. The signature feature of the presence of the distribution is the widening of the singularities.
Figure 11.
2H line shapes for ring deuterons of F51 in the hydrophobic core of the villin headpiece subdomain protein. Data collected at 295 K and 17.6 T (black). Spectrum in red corresponds to a model that includes the distribution of flip rates and motions inside rotameric wells. Reprinted with permission from (31). Copyright (2015) American Chemical Society.
2.2 Signal enhancement with the use of the multiple echo scheme
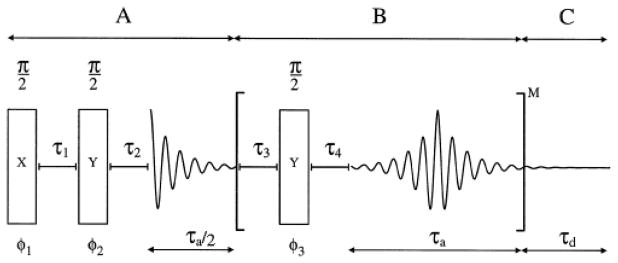
For low sensitivity samples with long relaxation times, the acquisition of line shape data in a reasonable time becomes a challenge and it is desirable to employ techniques that provide signal enhancement. While magic-angle spinning is one of the possibilities, techniques have been also developed for enhancement under static conditions. A multiple echo acquisition scheme, also referred to as Quadrupolar Carr-Purcell Meiboom Gill (QCPMG)(54–56), consists of several loops of quadrupole echo cycles [τ3 −90o-τ4] (Fig. 12). It breaks the powder pattern into a series of spikelets and serves as a static analog of the magic-angle spinning enhancement. The distance between the spikelets is inversely related to the interpulse delay τ3 in the QE sequence.
Figure 12.
Timing scheme for the static QCPMG experiment for deuterium nuclei. Part A corresponds to a quadrupolar echo experiment with τ2 adjusted such that the acquisition starts at an echo maximum. Part B is the repeating unit with the π/2 refocusing pulses bracketed by delays τ3, τ4 followed by an acquisition period τa. Part C is an additional acquisition period ensuring the full decay of the FID. The phases ϕ1–ϕ3 are cycled to select the coherence transfer pathway p= 0→±1→∓1 etc. Reprinted with permission from (57). Copyright (1997) American Chemical Society.
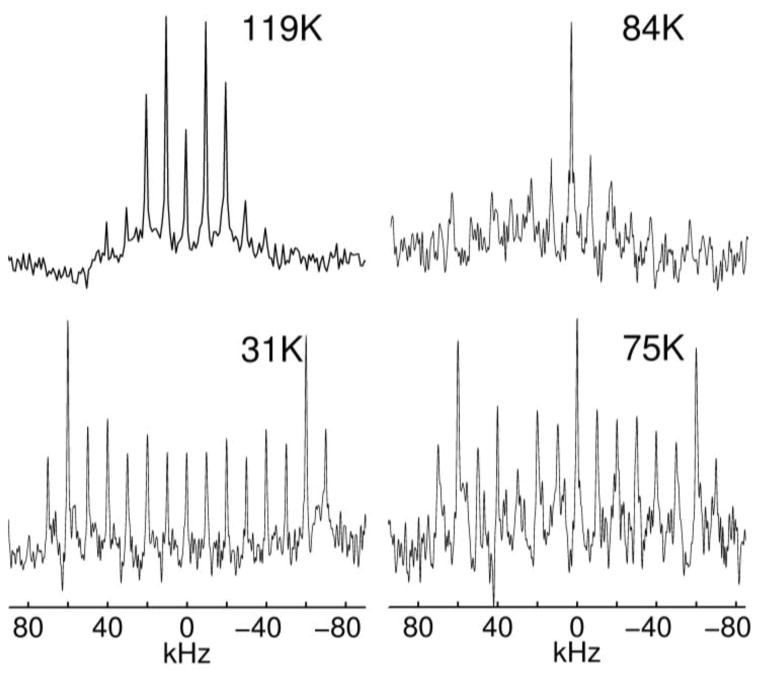
For biological hydrated samples, an important factor in signal enhancement is the interplay between the enhancement provided by multiple echoes, transverse relaxation losses, and potential heating of the sample. Fast transverse relaxation usually prohibits interpulse delays over 50 μs. The maximum number of cycles that does not lead to sample heating has to be determined experimentally and is often limited by 10 to 20 loops. Examples of QCPMG-enhanced spectra are shown in Fig. 13 for a methyl group in a hydrated protein sample.(19)
Figure 13.
Deuteron QCPMG line shapes at three motional regimes with respect to the quadrupolar coupling constant: 119 K fast, 84 and 75 K intermediate and 31 K slow motional regimes; collected at 11.7 T. All intensities are normalized. Numbers of scans were 1024, 3040, 512 and 128, respectively. Interpulse delay in the QCPMG cycle was 50 μs and the number of QCPMG cycles was between 10 and 15. Reprinted with permission from (19). Copyright (2010) American Chemical Society.
2.3 Relaxation rate constant measurement
Relaxation rate constant measurements usually probe faster ps-ns timescales and thus can reveal more local smaller amplitude motions.(28) Traditional examples include fast methyl jumps around the threefold axis or phenylalanine ring flips.(58) Additionally, a more subtle application of relaxation measurements is their sensitivity to the presence of multiple conformers that can appear either as “static”, i.e. no exchange between them on the timescale of the experiment, or exchanging on the timescale of the relaxation measurements.(59) Thus, in addition to fast motions, relaxation measurements can indirectly probe much slower timescales. For example, for methyl groups these can be on the order of tenths of milliseconds.(59)
2.3.1 Longitudinal relaxation
Experimentally, relaxation rate constant measurements such as inversion or saturation recovery can be coupled to either the QE or multiple echo acquisition schemes. Importantly, unlike the MAS analog, QCPMG does not refocus relaxation anisotropy,(56) which can thus be studied under static conditions. Relaxation anisotropy is known to provide important constraints for the determination of the motional mechanisms.(2)
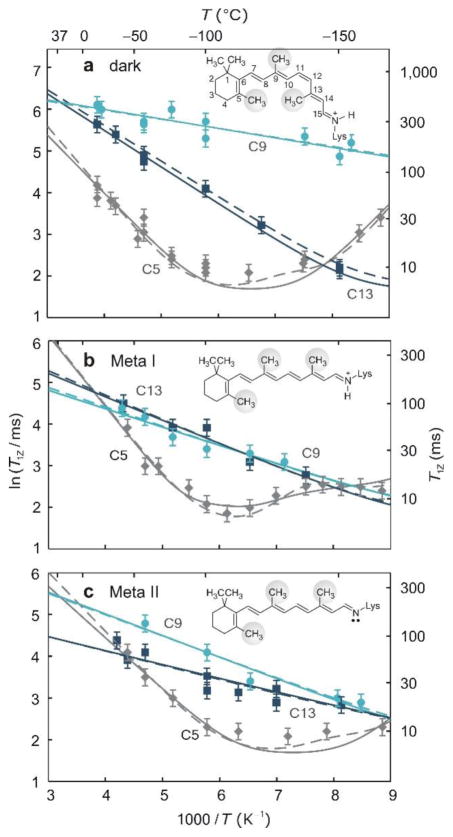
An interesting application of 2H longitudinal relaxation includes studies of retinal bound to rhodopsin.(60) In the dark state, the deformation of retinal via the induced fit produces pronounced differences in methyl dynamics as detected by the 2H T1Z relaxation times shown in Fig. 14.
Figure 14.
Solid-state 2H NMR captures site-specific changes in retinal mobility during the light activation of rhodopsin. (a–c) Spin-lattice (T1Z) relaxation times (±s.d.) of retinylidene methyl groups are shown versus reciprocal temperature in the dark (a), meta I (b) and meta II (c) states (−30 to −160 °C); collected at 11.7 T. Methyl dynamics are described by an axial three-fold jump model or a continuous diffusion model with coefficients D|| and D⊥. In a–c, rotation about the methyl threefold (C3) axis corresponds to solid lines with D⊥ = 0; the dashed lines include restricted off-axial diffusion (D⊥ = D||). Fits for the C5-Me in meta I in b assume D||≠ D⊥ (dashed line) or the presence of two conformers with different bond orientations and axial diffusion coefficients (solid line). Reprinted with permission from (60). Copyright (2011) Nature Publishing Group, license number 3971581205942.
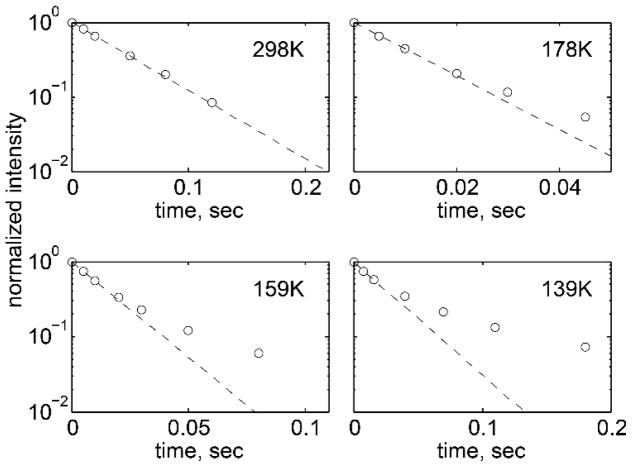
Figs. 15 and 16 display an example of longitudinal relaxation times measurements with the use of the QCPMG scheme for a hydrophobic core leucine group in the chicken villin headpiece subdomain.(59) It is clear that the relaxation decay curves (Fig. 15) are strongly non-exponential at low temperatures, which has led to the development of a model of a distribution of conformers in the core of a protein. This distribution reflects local variations in the packing of the core.
Figure 15.
Normalized magnetization decay curves obtained by the inversion recovery pulse sequence with the QCPMG detection scheme for the L69 residue in the villin headpiece protein; collected at 17.6 T. Circles represent intensities at the ±10 kHz spikelet position of QCPMG spectra. Dotted lines represent fits to the mono-exponential function. Deviation from mono-exponentiality becomes more pronounced as temperature is lowered below 180 K. Reprinted with permission from (59). Copyright (2013) American Chemical Society.
Figure 16.
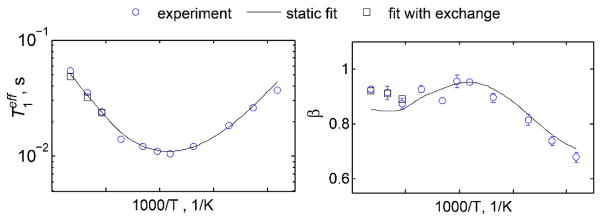
Plots of and β as a function of 1000/T at 17.6 T magnetic field strength for L69 in the villin headpiece protein. The data were fit to the model in which conformers were distinguished by the different values of activation energies for methyl rotations. Conformational exchange is not taken into account for the static fits (solid lines) but is taken into account using modified McConnell equations in the full model (squares). Reprinted with permission from (59). Copyright (2013) American Chemical Society.
Non-exponential relaxation curves are often described phenomenologically by a stretched exponential function of the form:(61, 62)
| (1) |
where M(t) is the signal intensity, is the effective relaxation time and β is the parameter that reflects the degree of non-exponentiality, 0 < β ≤1. β less than 1 corresponds to non-exponential behavior. Note that for the saturation recovery measurements M (0)= 0.
Further, at higher temperatures, the presence of conformational exchange on the timescale of T1 leads to a decrease in non-exponentiality (increase in the value of β). Changes in the values of β can be modeled to extract the rate constant for the exchange process. This is elaborated in the modeling section.
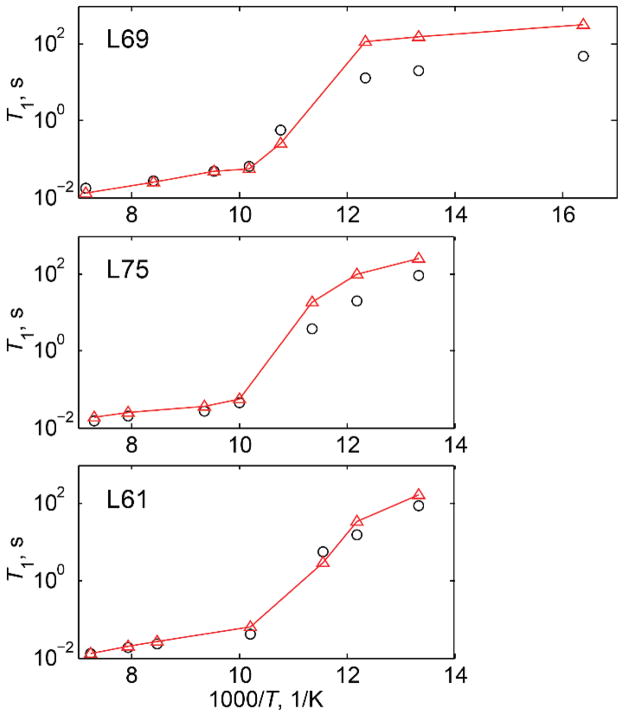
The presence of the distribution of conformers coupled to the intensity loss when motions are in the intermediate regime with respect to Cq can lead to an apparent transition in T1. This has been observed for protein methyl groups (Fig. 17), in which the apparent relaxation times exhibited an abrupt change at around 90 K.(19, 34)
Figure 17.
T1 vs. 1000/T for leucine residues in the hydrophobic core of the villin headpiece subdomain protein in the 140–60 K temperature range at 11.7 T. Experimental data are shown by black circles and simulated by red triangles; the lines are shown to guide the eye. Reprinted with permission from (34). Copyright (2013) American Chemical Society.
It is also interesting to note that at temperatures below 50 K, incoherent tunneling has been observed for protein methyl groups, with relaxation times indicative of the high tunneling efficiency compared with amino acid systems.(19, 63)
2.3.2 Other relaxation rates
The dependence of relaxation rates on spectral densities for a spin-1 system is given by the following expressions:(2)
| (2a) |
| (2b) |
| (2c) |
| (2d) |
where ω0 is the Larmor frequency, J1 and J2 are spectral density functions and Cq refers to the quadrupole coupling constant in the absence of motion. J1 and J2 are dependent on the timescales and type of the underlying motional processes as well as on crystallite orientations. Spectral density functions can be obtained analytically for several simple models of motion.(58) However, motional models with multiple modes usually require computer simulations.
Quadrupolar order relaxation time measurements (T1Q) can be particularly useful in addition to longitudinal relaxation time measurements.(2, 64) Due to their dependence on different spectral density terms, they can be more sensitive to somewhat different transition frequencies, as can be seen from Eqs. (2a–b). In general, T1Q measurements are more demanding experiments than T1Z due to intensity losses in the excitation period. One of the useful pulse sequences for the measurement of the quadrupolar order is the broad-band Jeener-Broekaert variant: [90ox−2τ e−67.5o−y−2τe−45o y−τ−45oy−acq].(64, 65) To avoid substantial signal losses, the excitation delay τe often needs to be limited to 5 μs in hydrated protein systems. The acquisition scheme can be either the QE or, if signal enhancement is desired, QCPMG.(56)
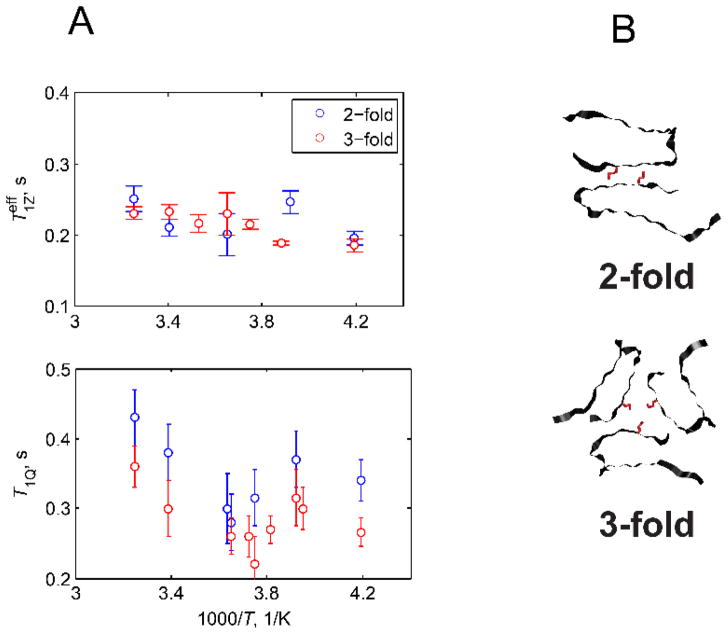
An interesting example (Figs. 18 and 19) is a comparison between two polymorphs in the amyloid fibril samples at the methionine side-chain pointing into a water-exposed hydrophobic cavity: the difference between two different polymorphs is much more clearly seen with the T1Q measurements compared with the T1Z ones.(66)
Figure 18.
Examples of spectra resulting from T1Q relaxation measurements using the QCPMG detection scheme. Spectra are shown for the M35 methyl groups in the amyloid fibrils comprised of amyloid-β(1–40) protein in the 3-fold symmetric polymorph; collected at 17.6 T. Adapted with permission from (66), Copyright (2016) Elsevier, License 3995621063676.
Figure 19.
Plots of and T1Q vs. 1000/T at 17.6 T magnetic field strength for the M35 site in the amyloid fibrils comprised of amyloid-β (1–40) protein in the two-fold and three-fold symmetric polymorphs. The measurements employed the QCPMG signal-enhancement scheme. B) Structural representation of the 2-fold and 3-fold symmetric polymorphs of amyloid-β fibrils, view down the fibril axis.(20, 67) The M35 side-chain pointing into the water-accessible cavity is shown in red. Reprinted with permission from (66), Copyright (2016) Elsevier, License 3995621063676.
Measurements of transverse relaxation rates R2(SQ) and R2(DQ) (Eq. (2c,d)) can in principle provide additional information on the motions occurring at very low frequencies and effects of spin diffusion in deuterated systems.(2, 68) However, in practice, the low sensitivity of protein samples coupled with fast transverse relaxation rates, especially in hydrated samples, makes these measurements technically challenging.
Of note are also two-dimensional correlation T1–T2 and T2-T2 techniques that have been used to study localized water and protein dynamics in mechanically strained elastin.(69) The pulse sequence and typical data from these measurements are shown in Fig. 20. By using this technique, it has been determined that as the applied strain is increased, the correlation time of the random tumbling motion of 2H nuclei in water is observed to decrease, indicating an increase in the orientational entropy of localized water. Combined with other NMR measurements and MD simulations, these results reported on changes in the backbone dynamics that give rise to the development of an entropic elastomeric force in elastin.
Figure 20.
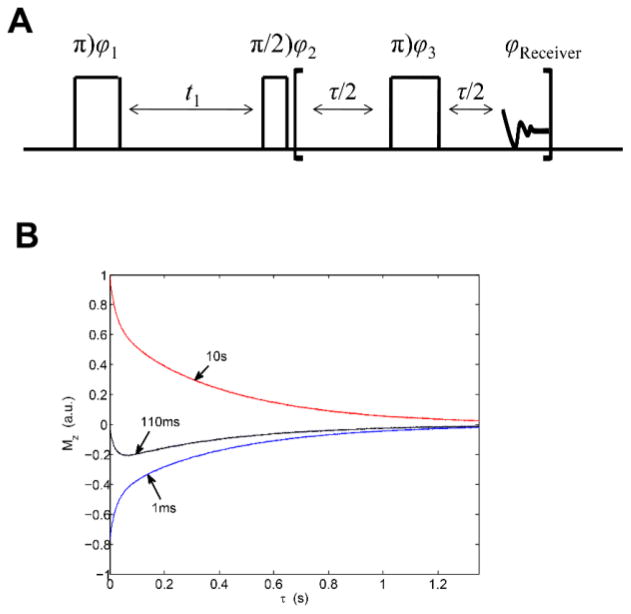
A). NMR pulse sequence used for 2H 2D T1–T2 correlation experiments. φ1 = x, −x; φ2 = x, x, −x, −x; φ3 = y and receiver = x, x, −x, −x. B). Sample raw data resulting from the T1–T2 correlation experiment using the pulse sequence shown in part A; collected at 200 MHz Larmor frequency. The figure shows selected slices from the 2D map for t1 = 1 ms, 110 ms and 1s. The correlation map is obtained by performing inverse Laplace transform. Reprinted with permission from (69). Copyright (2011) American Chemical Society.
3. Motional Modeling
2H static NMR observables are very rich in dynamical information. Our goal in this section is to provide brief practical guidance regarding tools and approaches that can be used for this purpose.
Approaches in the analysis of data vary from “model-free” approaches,(70) in which the extent of motional narrowing from the Pake pattern is used to extract the order parameters characterizing the amplitude of motions,(8) to slowly relaxing local structure models,(71) to the development of motional models specific to the systems under study. We concentrate on the later approach, as we believe it provides the most detailed information. We follow the strategy of devising the simplest possible model consistent with biochemical constraints and the experimental data. Thus, we are able to reach the level of detail in modeling matching the information provided by the experimental data without overfitting.
3.1 Approaches for line shape data modeling
In principle, the best approach is to use minimization procedures between simulated and experimental spectra in order to select the best models and fitting parameters. However, automated minimization is rarely a viable option because RMSD values tend to have large contributions from factors extraneous to model and parameter selection. Thus, in practice, some combination of automatic fitting and visualization is usually undertaken. In many cases the temperature dependence of motions leads to sharp spectral changes which are confined to specific frequency ranges and effects to a much smaller extent other ranges. For example, dramatic changes near singularities at high temperatures can switch to more subtle changes outside singularities for lower temperatures. Yet, naively calculated RMSD will miss the latter changes, which inform us on the changes in motional parameters, in favor of finding the best fit for the regions containing singularities, which, in this temperature range, will be mostly driven by the details of data collection rather than any substantive changes in the dynamics. Thus, to choose a model based on the temperature-dependent spectra one has to focus on specific spectral regions that are affected the most. While it may be possible to parametrize these very specific changes and design an automated procedure of model selection and fitting, at present, it will end up to be mostly dependent on judgement calls made by the investigator, which would not be different from selections made based on simple visual comparisons. If in the future the number of analyzed and fitted systems dramatically increases, standardization and automation of this procedure will become more feasible. Once the model is chosen, minimization using RMSD values becomes more practically attainable, and an example of this approach was used to fit the line shapes in Fig. 14. In this case, a model involving a static uniaxial distribution was employed.(51)
3.1.1 Single mode models
Examples of small-angle fluctuations rendering relatively subtle changes in the spectrum would be small-angle diffusive motions of rotational axes, such as diffusion-in-a-cone or an asymmetric diffusion along a restricted arc. In the latter mode, instead of spanning the full circle of the cone, the motions are restricted to a subset of angles on an arc with a specified length (Fig. 24, mode 2). An example of the resulting spectra is shown for FMOC (Fluorenylmethyloxycarbonyl)-leucine methyl groups(29, 63) for which the length of the arc was determined as 70o with the diffusion occurring in the intermediate-to-fast regime (Fig. 21). This model introduces an effective asymmetry in the quadrupolar coupling tensor. We note that the experimental data often allow us to distinguish the form of the potential necessary to describe the restricted diffusion. In this example and its extension for the protein system,(29) the square potential form was used and was clearly a better fit compared with the Gaussian potential. An interesting example of the sensitivity of biomolecular systems to the form of the potential function is presented in Meints et al.(72).
Figure 24.
Schematic representation of the motional model used to fit the line shapes of the hydrophobic core leucine side-chains in the villin headpiece subdomain protein.(29, 40) The first mode corresponds to the fast 3-site jumps of the methyl group; the second mode corresponds to a restricted diffusion on an arc approximated by small nearest neighbor jumps of the Cγ–Cδ axis; the third mode represents the mode of the rotameric jumps corresponding to hops between four non-equivalent positions of the leucine side-chain out of the nine possible configurations. Adapted with permission from (29). Copyright (2011) American Chemical Society.
Figure 21.
Experimental (red) and simulated (blue) QE line shapes of 5,5,5-d3 FMOC-Leucine at 298 K. Simulations were performed using the model of restricted diffusion on an arc with the length of 70o and the diffusion constant of 1.1 ·105 rad/s. Adapted with permission from (63). Copyright (2010) American Chemical Society.
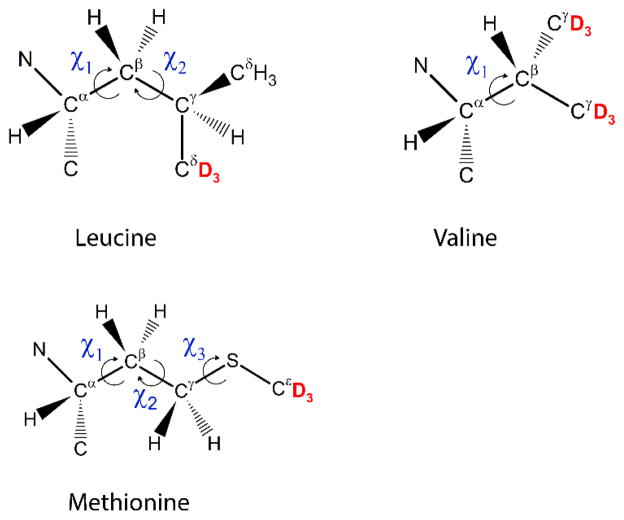
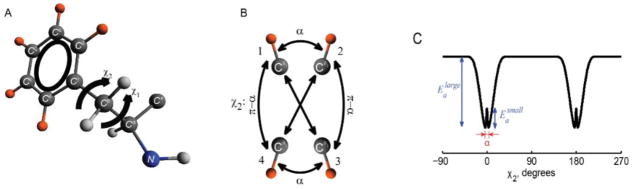
When large-angle jumps such as rotameric inter-conversions are considered to be the main source of the dynamics, one has to make a choice about which conformers should be included into the simulations. For short side-chains such as that of valine, this does not constitute a problem, as there are only three possible rotamers. For many other side-chains, variations in more than one dihedral angle lead to a large number of theoretically possible conformers. For example, for leucine side-chains, 3×3 total rotamers are possible, while for methionine, this number becomes 3×3×3 (Fig. 22).
Figure 22.
Dihedral angles involved in the rotameric interconversion of valine, leucine and methionine side-chains. Labeling patterns of methyl groups for data presented in this review are shown in red.
For efficient modeling without over-parametrizing, some approximation needs to be adopted. One of the approaches is to employ only rotamers that are found to be the most populated in peptides and proteins. For example, for leucine side-chains, a common model is to use the two most populated conformers tg+ and g t.(13, 37) This approach was used to fit the line shapes in Fig. 7. The populations of the two conformers were assumed to be equal. Alternatively, a somewhat more involved approach was used to fit the data in Fig. 6,(42) in which four magnetically inequivalent conformers were employed. Further, one of the four conformers was assumed to be dominant and the three minor ones had the same weights. This approach led to a better fit of the shapes in the ±(30–40) kHz region, as shown in Fig. 23.
Figure 23.

Line shapes simulated with two-site rotameric jumps (magenta), four-site rotameric jumps (blue) and experimental spectrum (red) for L69 in HP36 at 298 K and 17.6 T. Adapted with permission from (29). Copyright (2009) American Chemical Society.
Another example of large-angle fluctuations is aromatic ring flips. The spectra of systems with ring flipping rates faster than about 1×104 s−1 have distinct features with additional singularities appearing at about ±13 kHz (Fig. 2). Broadening the singularities often points to the existence of distributions of parameters governing the spectra. There are cases in which there is an ambiguity about which parameter has an associated distribution with it. For example, in the case of the phenylalanine spectrum in Fig. 11, a similar quality of the fit in principle could be obtained if one has a distribution of ring flip constants or quadrupolar coupling constants. However, the distribution of quadrupolar coupling constants would have to be unphysically wide for a protein system (with a width of ±23 kHz), thus pointing to a more realistic model based on the distribution of rate constants. In this case, additional constraints have also been imposed by the relaxation data, which will be described below.
3.1.2 Multimodal models
In many situations, postulating one mode of motion is not sufficient for the description of the dynamics, in which case several modes can be employed in the model. Note that, in general, the separation of timescales does not have to be applicable. When motions in different modes occur on similar timescales, the resulting fitted values of the motional parameters are different compared with the situation when the data are attempted to be fitted only with the mode that has the largest effect on the line shape. For example, the difference in the rate constants can reach 10–50% between the multimodal and single mode procedures. We note that this situation is no different from any other cases in spectroscopic data fitting that require parametrizations based on specific approaches.
An example of a multi-modal approach is illustrated in Fig. 24.(29, 40) Three modes of motions corresponding to the fast methyl jumps, diffusion on the restricted arc and rotameric jumps all affect the spectrum. In order to obtain relatively unambiguous motional parameters despite the interaction of the motional modes on the same timescales, it is essential to have temperature-dependent data. In this case, the parameters can be constrained to follow a reasonable temperature dependence, such as, for example, Arrhenius law for the rate constant and Boltzmann law for the rotameric populations.
The temperature dependence of the spectra not only provides important constraints on the choice of the motional model, but also allows for the determination of the activation energies of corresponding motions. Further, the temperature-dependent values of the populations or parameters of diffusive motions such as cone apex angle or the length of the arc can yield contributions of dynamics into configurational entropies.(40)
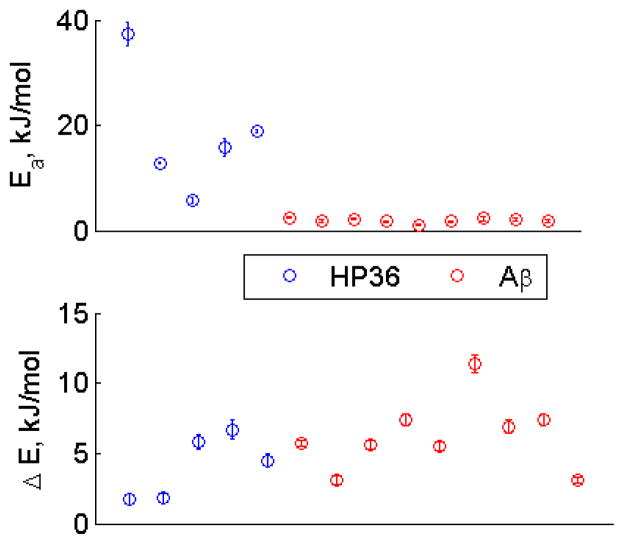
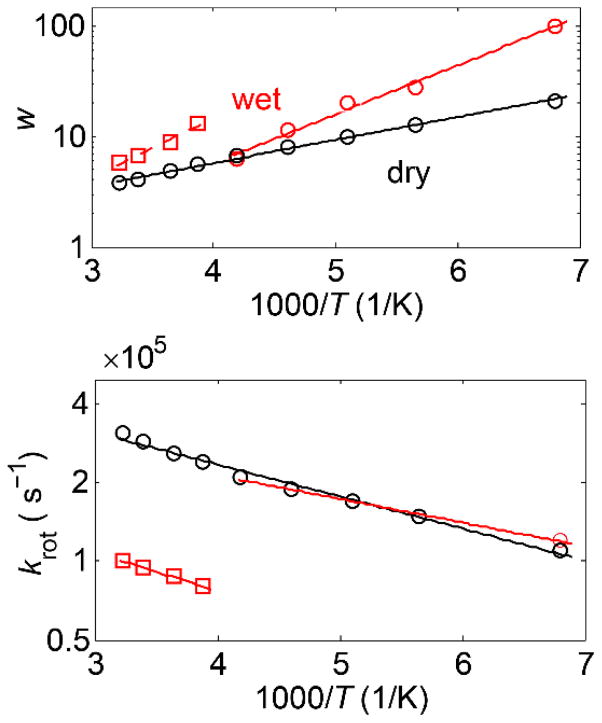
This approach has led to the elucidation of important factors distinguishing the dynamics of hydrophobic core side-chains in globular protein versus in amyloid fibrils (Fig. 25). Namely, the persistence of the dynamics at low temperatures was determined to be due to the low values of activation energies, rather than the statistical (populations) factor.(42) Interestingly, for the amyloid fibrils, the mode of motions inside the rotameric wells was not necessary for leucine and valine side-chains, but had to be included for the long side-chain of methionine.(42) Further, for the methionine side-chain in the hydrated state, it was necessary to include an onset of additional rotameric states: three rotamers corresponding to χ3 dihedral angle rotations could fit the data below 250 K, but above this temperature the data required the involvement of additional rotamers, which was approximated using four symmetrical conformers. Fig. 26 demonstrates the resulting fitted values of the populations and rate constants.
Figure 25.
Activation energies for the rotameric jumps of the methyl axis (top) and energy difference between major and minor rotameric states (bottom) for the hydrophobic core methyl-bearing side-chains of the villin headpiece (HP36, blue circles) protein and amyloid-β(1–40) (red circles).
Figure 26.
Fitted parameters for the rotameric mode for the methyl group of the M35 residue in the amyloid fibrils of amyloid-β (1–40) protein in the wet (red) and dry (black) states.(42) Plots of the fitted values of the weights of the major rotameric conformer w (top panel) and rotameric rate constants krot (bottom panel) versus 1000/T. Linear fits are shown by solid lines. The arc length of 35o with the rate constant in the fast limit was used for all temperatures. Note that for the case of methionine, the methyl axis angle with respect to the Cγ-S axis was taken as 99o.
Usually, in order to devise an unambiguous motional model, data have to be collected at several temperatures and it is preferable to have a combination of both line shape and relaxation data. Information on relaxation anisotropy provides further constraints on the choice of motional mechanism.(2) This is in essence a trial-and-error process that leads to a model consistent with all of the data at hand.
3.2 Approaches to relaxation modeling
In general, the most effective relaxation mechanism is the one with a timescale of the order of the Larmor frequency. For some systems, especially when experiments are done over a wide temperature range, the dominating relaxation mechanism can change, leading to the dynamical transition. Such situations are inherently more difficult to model and we will begin first with the examples where there is a single dominant mechanism of relaxation.
Because the relaxation rate constants depend primarily on the frequency of fluctuations, the model-free approach(70) provides a solid and very successful method in many situations without getting into the specific details of motions. It parametrizes the spectral densities of Eq. (2) through the correlation times and order parameters, the latter of which are responsible for the spatial extent of the fluctuations. However, for functional groups in proteins, we typically have a reasonable understanding of the types of motions in which they are involved, which permits the next level of precision in the description of the dynamics. Several simple modes of motions are amenable to analytical treatment,(58) but even relatively simple modifications require computational modeling.
3.2.1 Modeling the distribution of conformers with and without conformational exchange
The first computational challenge arises from the distribution of relaxation rates, which was observed for several functional groups in proteins.(31, 59) Usually, the overall relaxation decay/build-up can be treated phenomenologically as following the stretched exponential functional form, as defined in Eq. (1). From a modelling perspective, for every temperature one has to generate a distribution of rate constants, model partially relaxed spectra for each of these rates with delays corresponding to experimental ones, construct a weighted average of these spectra and fit the intensities at selected frequency points to the stretched exponential function.
By using the free energy landscape perspective,(35, 73) the existence of the distribution of rate constants at each temperature can be expanded into the activation energy space. In this case, we can describe the origin of this distribution in terms of the existence of multiple conformers characterized by different values of the activation energies for the dominant mechanism.
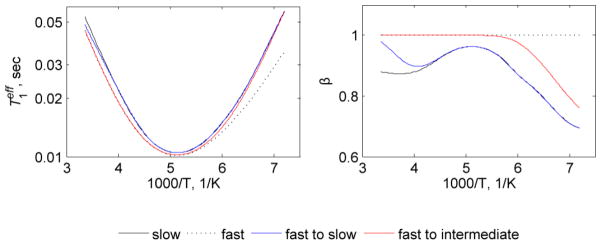
The relaxation data in Figs. 15 and 16 have led to a model in which multiple conformers of the protein core are distinguished by the different values of activation energies for methyl jumps.(59) It was assumed that the distribution of activation energies has a Gaussian shape and can be modeled with discrete states. This model explains the increase in the non-exponentiality of the magnetization decay curves at low temperatures because the distribution in the rate constant is related to the distribution in the activation energy by Ea/T. This model requires us to perform a global fitting procedure, in which the relaxation data for all temperatures are fitted simultaneously. So far, we have assumed that there is no exchange between the conformers on the timescale of and we refer to this case as “static”. The presence of the conformational exchange between conformers can be introduced either in the strong collision limit, in which the rate of transition between the states does not depend on either the initial or the final values of the activation energies, or in the nearest-neighbor limit with short-range stochastic jumps in the activation energy space. The former limit has been considered in the description of the relaxation of guest molecules in glass formers by Roggatz et al.(74) However, for proteins, the nearest-neighbor (or diffusion) limit is more probable. This scenario can be modeled by McConnel-type equations(75). The inclusion of chemical exchange leads to three motional regimes with different effects on the values of and β, as shown in Fig. 27. In the fast regime, the exchange rate constant , in the slow regime such that the distribution becomes static and in the intermediate regime . The effect of the dynamical averaging is to lower the value of and raise the value of β. For the fast regime, β≈1 and , where 〈...〉 denotes the ensemble average.
Figure 27.
Simulated temperature dependence of (semilog scale) and β according to the model of nearest-neighbor exchange. Slow regime (solid black line) corresponds to kex = 0 for all temperatures. Fast regime (dotted black line) with kex,0 = 103 s−1 and Eex = 0. Fast to slow regime (blue line) with kex,0 = 3·105 s−1 and Eex = 20 kJ/mol. Fast to intermediate regime (red line) with kex,0 = 3·108 s−1 and Eex = 20 kJ/mol. The parameters of the three-site methyl jumps are <Ea> = 12 kJ/mol, σ = 1.5 kJ/mol and k0 = 7–1011 s−1. The Larmor frequency is 115 MHz. Reprinted with permission from (59). Copyright (2013) American Chemical Society.
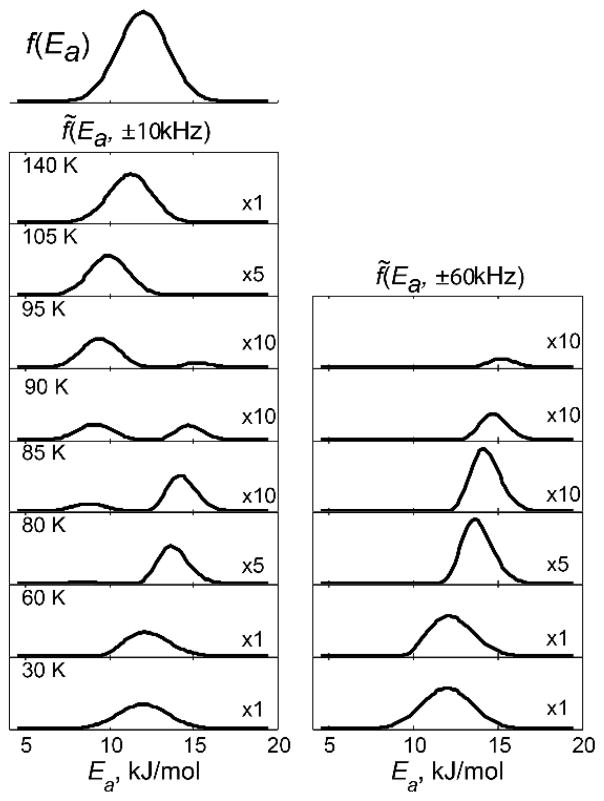
In cases in which the conformers of the distribution can span the motional regime affected by the intensity ~ loss, the effective form of distribution in the activation energy space f̃ (Ea,ω) can be drastically distorted from the functional form assumed in the absence of the intensity loss factor, f(Ea ). The expression for the effective distribution is given by f̃ (Ea,ω)= f(Ea)I (Ea,ω), in which I(Ea,ω) is the intensity loss factor that depends on the chosen frequency of the powder pattern ω.(34) By using the functional form of the intensity loss in Fig. 4, the effective distribution of activation energies for the methyl rotations of the core methyl groups in the villin headpiece has been shown to take the form presented in Fig. 28. Thus, it can be seen that the apparent transition in relaxation times shown in Fig. 17 arises as an interplay of the distribution of methyl rotation rates and intensity losses when the rates are in the intermediate regime with respect to the quadrupolar coupling constant.
Figure 28.
Effective probability distribution of conformers f̃(Ea,ω) for ω=±10 kHz (left column) and ±60 kHz (right column) for several temperatures for the core leucine groups in the villin headpiece subdomain protein. Relative scaling factors are shown in the right bottom corner. The QCPMG detection scheme was employed in the simulations to match the experimental conditions. Reprinted with permission from (34). Copyright (2013) American Chemical Society.
3.2.2 Diffusion in a potential
The most general approach for the description of relaxation encompasses diffusion in a potential. The unified description of motions, which takes into account the possibilities of large-angle transitions between potential wells as well as local motion within each potential well, can be achieved if one considers diffusion models such as the Smoluchowski equation(76) for the motions around a chosen dihedral angle φ.
| (3) |
in which P(φ,t) is the probability density for the distribution over the angle φ at time t, D is the diffusion coefficient, kB is the Boltzmann constant and V (φ) is the potential. The large-angle transitions are then the result of diffusion acting to carry the system over the potential barrier, the process first described by Kramer in relation to the decay of a metastable state.(77, 78)
We will review in more detail here an example of methyl groups in proteins. The simple three-site jump motion is an approximation to the motion in a three-fold symmetric potential for which infinitely thin potential wells are separated by large barriers.(58, 79) The natural extension of such a model is to consider more realistic potentials with wells of a finite width. The simplest choice for the three-fold 1 potential is given by , where V0 is the height of the barrier between the wells. The NMR relaxation of methyl groups under the mechanism of diffusion in the three-fold potential was originally considered by Edholm and Blomberg(79) and compared in detail with the three-site hops mechanism and free diffusion by Torchia and Szabo(58) in the extreme narrowing limit. A discrete version of Eq. (3), written as the Markovian process of the nearest-neighbor jumps between angular positions confined to a sufficiently fine grid, provides a practical computational tool. Diffusion in a potential can also be considered phenomonologically, under the assumption that the main contributions can be separated into inter-well jumps and intra-well motions.(30) Further, under the assumption of the timescale separation between these two contributions, the effect of the intra-well motions on the correlation functions describing much slower inter-well motions can be simplified. Namely, the correlation function is scaled by the order parameters representing the amplitude of intra-well fluctuations , in which is the correlation function for the inter-well jumps, p and q are indices corresponding to the spherical harmonics (ranging from −2 to 2) and Sp and Sq are the order parameters for these harmonics.
A common view is that the intra-well dynamics do not contribute to NMR relaxation in the limit of large barrier heights; however, it was recently shown that this is not the case for protein methyl groups.(30) Relaxation data over a wide temperature range of 300–140 K, such as in Fig. 16, combined with low temperature line shape measurements for the precise determination of quadrupolar coupling constants and geometry, were necessary to detect this distinction.
As another example, the relaxation data for retinal in rhodopsin (Fig. 14) were analyzed using two different models: either the three-site jump model or continuous diffusion.(60) Large site-specific differences were observed for the activation energy barriers between the two models; however, the qualitative picture remained the same. In combination with X-ray and FTIR measurements, these data have led to a proposed mechanism for the activation of rhodopsin in membranes.(60)
3.2.3. Dynamical transitions
One of the unique advantages of 2H static NMR measurements is their ability to detect mechanistic details of dynamical transitions.(31, 80) Dynamical transitions are usually defined as the onset of large-scale solvent-driven anharmonic motions upon heating protein from cryogenic temperatures.(47, 81, 82) Because static 2H NMR is sensitive to mechanistic details, temperature-dependent studies of line shapes and relaxation curves permit us to discern exactly what types of motions are driving the transition at each particular side-chain. One such example is shown below, in which a hydrophobic core phenylalanine residue is shown to undergo a dynamical transition from the dominance of small-amplitude phenyl axis fluctuations at low temperatures to traditional ring flips at high temperatures (Figs. 29 and 30).(31)
Figure 29.
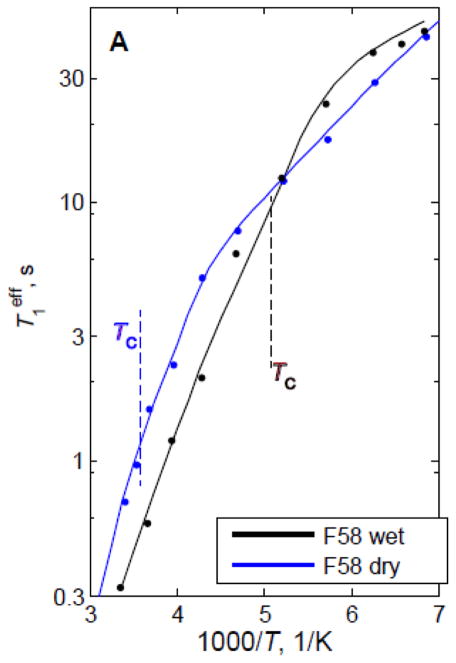
Plots of for the hydrophobic core F58-ring-d5 site in the villin headpiece subdomain protein in the hydrated (black lines) and dry (blue lines) powder states. The dashed lines indicate the dynamical transition temperature Tc. Reprinted with permission from (31). Copyright (2015) American Chemical Society.
Figure 30.
A) The phenylalanine side-chain with the deuteron labeling pattern marked in orange. B) Motional model for the fluctuations around the χ2 dihedral angle in the F58 side-chain of the villin headpiece protein. The diagram displays sites’ connectivities according to the four-site strong collision model, illustrated for one of the Cδ–D bonds. The large-angle flips occur between sites 1–3 and 1–4 with an equal probability; this also holds for the 2–3 and 2–4 pairs. The small-angle jumps with the amplitude α occur between sites 1–2 and 3–4. C) Potential of the model, in which and are the activation energies for the large-angle ring flips and small-angle fluctuations, respectively. Adapted with permission from (31). Copyright (2015) American Chemical Society.
The temperature of the dynamical transition shifts from 195 K in the hydrated protein to 278 K in the dry one. Modeling has allowed us to assess that the low temperature fluctuations occur as jumps over small barriers rather than continuous diffusion inside the potential wells (Fig. 30). Further, in this case, besides numerical modeling, analytical equations for the correlation functions governing the relaxation processes can be derived.
Another interesting example is the methionine side-chain of M35 pointing into a water-exposed cavity in the amyloid fibrils comprised of amyloid-β protein (Figs. 31 and 19).(66) The dynamical transition is manifested at this site as an onset of dominance of the slower diffusive motions of the methyl axis at around 250–240 K in addition to methyl rotations, which dominate at lower temperatures. The diffusive motions are clearly hydration-dependent and are suppressed in the dry samples, in which methyl rotations remain dominant across the entire range.
Figure 31.
Plots of for the methyl groups of M35 in amyloid fibrils comprised of amyloid-β protein in the hydrated (black) and dry (blue) states. The dotted lines indicate the dynamical transition temperature Tc. Adapted with permission from (66), Copyright (2016) Elsevier, License 3995621063676.
Conclusion
Static deuterium NMR can be a powerful tool when the goal is to elucidate the mechanistic details of motions in protein systems. It can be used with relative ease over a very wide temperature range and using a variety of protein hydration patterns. The most powerful combination is line shape and relaxation studies performed over the desired temperature range. Combined with motional modeling techniques, these studies can provide knowledge of motional mechanisms and their changes with temperature and hydration, thus reporting on an important feature of the protein free energy landscape.
Highlights.
Our focus is side-chains dynamics in proteins and peptides
We discuss experimental static deuteron NMR techniques and computational approaches
The focus is placed on modeling based on line shape and relaxation data
We include cases typical of glassy behavior and dynamical transitions
Examples are chosen from globular protein, membrane proteins, amyloid fibrils, and others
Acknowledgments
Support for this work was received from National Institutes of Health Grant 1R15 GM111681-02 to L.V. as well as National Science Foundation Grant MCB-1122154 to L.V.
Glossary
- FID
Free Induction Decay
- FMOC
Fluorenylmethyloxycarbonyl
- MD
Molecular Dynamics
- NMR
Nuclear Magnetic Resonance
- QCPMG
Quadrupolar Carr-Purcell Meiboom Gill
- QE
Quadrupolar Echo
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Vold RR. Deuterium NMR studies of dynamics in solids and liquid crystals. In: Tycko R, editor. Nuclear magnetic resonance probes of molecular dynamics. Kluwer academic Publishers; Dordrecht: 1994. pp. 27–112. [Google Scholar]
- 2.Vold RL, Vold RR. Deuterium relaxation in molecular solids. In: Warren W, editor. Advances in magnetic and optical resonance. Acadenic Press; San Diego: 1991. pp. 85–171. [Google Scholar]
- 3.Hiyama Y, Silverton JV, Torchia DA, Gerig JT, Hammond SJ. Molecular-structure and dynamics of crystalline para-fluoro-d,l-phenylalanine - a combined x-ray NMR investigation. J Am Chem Soc. 1986;108:2715–2723. [Google Scholar]
- 4.Batchelder LS, Niu CH, Torchia DA. Methyl reorientation in polycrystalline aminoacids and peptides - a H-2 NMR spin-lattice relaxation study. J Am Chem Soc. 1983;105:2228–2231. [Google Scholar]
- 5.Wittebort RJ, Olejniczak ET, Griffin RG. Analysis of deuterium nuclear-magnetic-resonance line-shapes in anisotropic media. J Chem Phys. 1987;86:5411–5420. [Google Scholar]
- 6.Rice DM, Wittebort RJ, Griffin RG, Meirovitch E, Stimson ER, Meinwald YC, Freed JH, Scheraga HA. Rotational jumps of the tyrosine side-chain in crystalline enkephalin - H-2 NMR line-shapes for aromatic ring motion in solids. J Am Chem Soc. 1981;103:7707–7710. [Google Scholar]
- 7.Gall CM, Diverdi JA, Opella SJ. Phenylalanine ring dynamics by solid-state H-2 NMR. J Am Chem Soc. 1981;103:5039–5043. [Google Scholar]
- 8.Mack JW, Usha MG, Long J, Griffin RG, Wittebort RJ. Backbone motions in a crystalline protein from field-dependent H-2-NMR relaxation and line-shape analysis. Biopolymers. 2000;53:9–18. doi: 10.1002/(SICI)1097-0282(200001)53:1<9::AID-BIP2>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 9.Krushelnitsky A, Reichert D. Solid-state NMR and protein dynamics. Prog Nucl Magn Reson Spectrosc. 2005;47:1–25. [Google Scholar]
- 10.Wang AC, Kennedy MA, Reid BR, Drobny GP. A solid-state H-2-NMR investigation of purine motion in a 12-base-pair rna duplex. J Magn Reson Ser B. 1994;105:1–10. doi: 10.1006/jmrb.1994.1092. [DOI] [PubMed] [Google Scholar]
- 11.Olsen GL, Echodu DC, Shajani Z, Bardaro MF, Varani G, Drobny GP. Solid-state deuterium NMR studies reveal mu s-ns motions in the hiv-1 transactivation response rna recognition site. J Am Chem Soc. 2008;130:2896–2897. doi: 10.1021/ja0778803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Olsen GL, Bardaro MF, Echodu DC, Drobny GP, Varani G. Hydration dependent dynamics in rna. J Biomol NMR. 2009;45:133–142. doi: 10.1007/s10858-009-9355-6. [DOI] [PubMed] [Google Scholar]
- 13.Batchelder LS, Sullivan CE, Jelinski LW, Torchia DA. Characterization of leucine side-chain reorientation in collagen fibrils by solid-state H-2 NMR. Proc Natl Acad Sci U S A. 1982;79:386–389. doi: 10.1073/pnas.79.2.386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ying WW, Irvine SE, Beekman RA, Siminovitch DJ, Smith SO. Deuterium NMR reveals helix packing interactions in phospholamban. J Am Chem Soc. 2000;122:11125–11128. [Google Scholar]
- 15.Struts AV, BMF . In Advances in biological solid-state NMR. The Royal Society of Chemistry; 2014. Structural dynamics of retinal in rhodopsin activation viewed by solid-state 2h NMR spectroscopy; pp. 320–352. [Google Scholar]
- 16.Albericio F. Solid-phase synthesis: A practical guide. CRC Press; 2000. [Google Scholar]
- 17.Atreya HS, editor. Isotope labeling in biomolecular NMR. 2012. Isotope labeling in biomolecular NMR; pp. 1–219. [Google Scholar]
- 18.Vugmeyster L, Osrovsky D, Fu R. 15N CSA tensors and 15N-1H dipolar couplings of protein hydrophobic core residues investigated by static solid-state NMR. J Magn Reson. 2015;259:225–231. doi: 10.1016/j.jmr.2015.08.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vugmeyster L, Ostrovsky D, Ford JJ, Lipton AS. Freezing of dynamics of a methyl group in a protein hydrophobic core at cryogenic temperatures by deuteron NMR spectroscopy. J Am Chem Soc. 2010;132:4038–4039. doi: 10.1021/ja909599k. [DOI] [PubMed] [Google Scholar]
- 20.Petkova AT, Yau WM, Tycko R. Experimental constraints on quaternary structure in alzheimer’s beta-amyloid fibrils. Biochemistry. 2006;45:498–512. doi: 10.1021/bi051952q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Petkova AT, Leapman RD, Guo ZH, Yau WM, Mattson MP, Tycko R. Self-propagating, molecular-level polymorphism in alzheimer’s beta-amyloid fibrils. Science. 2005;307:262–265. doi: 10.1126/science.1105850. [DOI] [PubMed] [Google Scholar]
- 22.Qiang W, Yau WM, Luo YQ, Mattson MP, Tycko R. Antiparallel beta-sheet architecture in iowa-mutant beta-amyloid fibrils. Proc Natl Acad Sci USA. 2012;109:4443–4448. doi: 10.1073/pnas.1111305109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ishii Y. C-13-C-13 dipolar recoupling under very fast magic angle spinning in solid-state nuclear magnetic resonance: Applications to distance measurements, spectral assignments, and high-throughput secondary-structure determination. J Chem Phys. 2001;114:8473–8483. [Google Scholar]
- 24.Takegoshi K, Nakamura S, Terao T. 13C–1H dipolar-assisted rotational resonance in magic-angle spinning NMR. Chem Phys Lett. 2001;344:631–637. [Google Scholar]
- 25.Paravastu AK, Petkova AT, Tycko R. Polymorphic fibril formation by residues 10–40 of the alzheimer’s β-amyloid peptide. Biophys J. 2006;90:4618–4629. doi: 10.1529/biophysj.105.076927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mananga ES, Roopchand R, Rumala YS, Boutis GS. On the application of magic echo cycles for quadrupolar echo spectroscopy of spin-1 nuclei. J Magn Reson. 2007;185:28–37. doi: 10.1016/j.jmr.2006.10.016. [DOI] [PubMed] [Google Scholar]
- 27.Antonijevic S, Wimperis S. Refocussing of chemical and paramagnetic shift anisotropies in H-2 NMR using the quadrupolar-echo experiment. J Magn Reson. 2003;164:343–350. doi: 10.1016/s1090-7807(03)00272-6. [DOI] [PubMed] [Google Scholar]
- 28.Duer MJ. Solid-state NMR spectroscopy. Blackwell Publishing Ltd; Oxford: 2004. [Google Scholar]
- 29.Vugmeyster L, Ostrovsky D, Ford JJ, BSD, Lipton AS, Hoatson GL, Vold RL. Probing the dynamics of a protein hydrophobic core by deuteron solid-state nuclear magnetic resonance spectroscopy. J Am Chem Soc. 2009;131:13651–13658. doi: 10.1021/ja902977u. [DOI] [PubMed] [Google Scholar]
- 30.Vugmeyster L, Ostrovsky D. Restricted diffusion of methyl groups in proteins revealed by deuteron NMR: Manifestation of intra-well dynamics. J Chem Phys. 2014;140:075101. doi: 10.1063/1.4865412. [DOI] [PubMed] [Google Scholar]
- 31.Vugmeyster L, Osrovsky D, Villafranca TR, Sharp J, Xu W, Lipton AS, Hoatson GL, Vold RL. Dynamics of hydrophobic core phenylalanine residues probed by solid-state deuteron NMR. J Phys Chem B. 2015;119:14892–14904. doi: 10.1021/acs.jpcb.5b09299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vold RL, Hoatson GL. Effects of jump dynamics on solid state nuclear magnetic resonance line shapes and spin relaxation times. J Magn Reson. 2009;198:57–72. doi: 10.1016/j.jmr.2009.01.008. [DOI] [PubMed] [Google Scholar]
- 33.Beshah K, Olejniczak ET, Griffin RG. Deuterium NMR-study of methyl-group dynamics in l-alanine. J Chem Phys. 1987;86:4730–4736. [Google Scholar]
- 34.Vugmeyster L, Ostrovsky D, Lipton AS. Origin of abrupt rise in deuteron NMR longitudinal relaxation times of protein methyl groups below 90 k. J Phys Chem B. 2013;117:6129–6137. doi: 10.1021/jp4021596. [DOI] [PubMed] [Google Scholar]
- 35.Frauenfelder H, Sligar SG, Wolynes PG. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 36.Dyson HJ, Wright PE. Elucidation of the protein folding landscape by NMR. In: James T, editor. Nuclear magnetic resonance of biological macromolecules, part c. 2005. p. 299. [DOI] [PubMed] [Google Scholar]
- 37.Weidner T, Breen NF, Li K, Drobny G, Castner DG. Sum frequency generation and solid-state NMR study of the structure, orientation, and dynamics of polystyrene-adsorbed peptides. Proc Natl Acad Sci U S A. 2010;107:13288–13293. doi: 10.1073/pnas.1003832107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hong M, Zhang Y, Hu FH. Membrane protein structure and dynamics from NMR spectroscopy. In: Johnson MA, Martinez TJ, editors. Annual review of physical chemistry. Vol. 63. 2012. pp. 1–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Strandberg E, Horn D, Reiβer S, Zerweck J, Wadhwani P, Ulrich Anne S. 2h-NMR and md simulations reveal membrane-bound conformation of magainin 2 and its synergy with pgla. Biophys J. 111:2149–2161. doi: 10.1016/j.bpj.2016.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vugmeyster L, Ostrovsky D, Khadjinova A, Ellden J, Hoatson GL, Vold RL. Slow motions in the hydrophobic core of chicken villin headpiece subdomain and their contributions to configurational entropy and heat capacity from solid-state deuteron NMR measurements. Biochemistry. 2011;50:10637–10646. doi: 10.1021/bi201515b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Linser R, Sarkar R, Krushelnitzky A, Mainz A, Reif B. Dynamics in the solid-state: Perspectives for the investigation of amyloid aggregates, membrane proteins and soluble protein complexes. J Biomol NMR. 2014;59:1–14. doi: 10.1007/s10858-014-9822-6. [DOI] [PubMed] [Google Scholar]
- 42.Vugmeyster L, Clark MA, Falconer BI, Ostrovsky D, Gantz D, Qiang W, Hoatson GL. Flexibility and solvation of amyloid -beta hydrophobic core. J Biol Chem. 2016;291:18484–18495. doi: 10.1074/jbc.M116.740530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Diezemann G, Sillescu H, van der Putten D. Spin-lattice relaxation rates of tunneling CD3 groups. Z Phys B Con Mat. 1991;83:245–257. [Google Scholar]
- 44.Haupt J. Influence of quantum effects of methyl group rotation on nuclear relaxation in solids. Z Naturforsch Pt A. 1971;26:1578. [Google Scholar]
- 45.Wood K, Gallat FX, Otten R, van Heel AJ, Lethier M, van Eijck L, Moulin M, Haertlein M, Weik M, Mulder FAA. Protein surface and core dynamics show concerted hydration-dependent activation. Angew Chem Int Ed. 2013;52:665–668. doi: 10.1002/anie.201205898. [DOI] [PubMed] [Google Scholar]
- 46.Hong L, Cheng XL, Glass DC, Smith JC. Surface hydration amplifies single-well protein atom diffusion propagating into the macromolecular core. Phys Rev Lett. 2012;108 doi: 10.1103/PhysRevLett.108.238102. [DOI] [PubMed] [Google Scholar]
- 47.Doster W. The dynamical transition of proteins, concepts and misconceptions. Eur Biophys J. 2008;37:591–602. doi: 10.1007/s00249-008-0274-3. [DOI] [PubMed] [Google Scholar]
- 48.Khodadadi S, Pawlus S, Sokolov AP. Influence of hydration on protein dynamics: Combining dielectric and neutron scattering spectroscopy data. J Phys Chem B. 2008;112:14273–14280. doi: 10.1021/jp8059807. [DOI] [PubMed] [Google Scholar]
- 49.Vugmeyster L, Tien D, Ostrovsky D, Fu R. Effect of subdomain interactions on methyl group dynamics in the hydrophobic core of villin headpiece protein. Prot Sci. 2014;23:145–156. doi: 10.1002/pro.2398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Miller Y, Ma B, Nussinov R. The unique alzheimer’s beta-amyloid triangular fibril has a cavity along the fibril axis under physiological conditions. J Am Chem Soc. 2011;133:2742–2748. doi: 10.1021/ja1100273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Struts AV, Salgado GFJ, Tanaka K, Krane S, Nakanishi K, Brown MF. Structural analysis and dynamics of retinal chromophore in dark and metal states of rhodopsin from H-2 NMR of aligned membranes. J Mol Biol. 2007;372:50–66. doi: 10.1016/j.jmb.2007.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Brown MF, Heyn MP, Job C, Kim S, Moltke S, Nakanishi K, Nevzorov AA, Struts AV, Salgado GFJ, Wallat I. Solid-state H-2 NMR spectroscopy of retinal proteins in aligned membranes. Biochim Biophys Acta, Biomembr. 2007;1768:2979–3000. doi: 10.1016/j.bbamem.2007.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Schadt RJ, Cain EJ, English AD. Simulation of one-dimensional H-2 NMR line-shapes. J Phys Chem. 1993;97:8387–8392. [Google Scholar]
- 54.Larsen FH. Simulation of molecular motion of quadrupolar nuclei in solid-state NMR spectra. In Annual reports on NMR spectroscopy. 2010;71:103–137. [Google Scholar]
- 55.Larsen FH, Jakobsen HJ, Ellis PD, Nielsen NC. High-field qcpmg-mas NMR of half-integer quadrupolar nuclei with large quadrupole couplings. Mol Phys. 1998;95:1185–1195. doi: 10.1006/jmre.1997.1341. [DOI] [PubMed] [Google Scholar]
- 56.Vold RL, Hoatson GL, Vugmeyster L, Ostrovsky D, De Castro PJ. Solid state deuteron relaxation time anisotropy measured with multiple echo acquisition. Phys Chem Chem Phys. 2009;11:7008–7012. doi: 10.1039/b907343d. [DOI] [PubMed] [Google Scholar]
- 57.Larsen FH, Jakobsen HJ, Ellis PD, Nielsen NC. Sensitivity-enhanced quadrupolar-echo NMR of half-integer quadrupolar nuclei. Magnitudes and relative orientation of chemical shielding and quadrupolar coupling tensors. J Phys Chem A. 1997;101:8597–8606. [Google Scholar]
- 58.Torchia DA, Szabo A. Spin-lattice relaxation in solids. J Magn Reson. 1982;49:107–121. [Google Scholar]
- 59.Vugmeyster L, Ostrovsky D, Penland K, Hoatson GL, Vold RL. Glassy dynamics of protein methyl groups revealed by deuteron NMR. J Phys Chem B. 2013;117:1051–1061. doi: 10.1021/jp311112j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Struts AV, Salgado GFJ, Martnez-Mayorga K, Brown MF. Retinal dynamics underlie its switch from inverse agonist to agonist during rhodopsin activation. Natur Struct Mol Biol. 2011;18:392–394. doi: 10.1038/nsmb.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sillescu H. Heterogeneity at the glass transition: A review. J NonCryst Sol. 1999;243:81–108. [Google Scholar]
- 62.Beckmann PA, Schneider E. Methyl group rotation, H-1 spin-lattice relaxation in an organic solid, and the analysis of nonexponential relaxation. J Chem Phys. 2012;136:054508. doi: 10.1063/1.3677183. [DOI] [PubMed] [Google Scholar]
- 63.Vugmeyster L, Ostrovsky D, Moses M, Ford JJ, Lipton AS, Hoatson GL, Vold RL. Comparative dynamics of leucine methyl groups in fmoc-leucine and in a protein hydrophobic core probed by solid-state deuteron NMR over 7–324K temperature range. J Phys Chem. 2010;114:15799–15807. doi: 10.1021/jp1082467. [DOI] [PubMed] [Google Scholar]
- 64.Hoatson GL. Broad-band composite excitation sequences for creating quadrupolar order in H-2 NMR. J Magn Reson. 1991;94:152–159. [Google Scholar]
- 65.Wimperis S. Broad-band and narrow-band composite excitation sequences. J Magn Reson. 1990;86:46–59. [Google Scholar]
- 66.Vugmeyster L, Ostrovsky D, Clark MA, Falconer BI, Hoatson GL, Qiang W. Fast motions of key methyl groups in amyloid-beta fibrils. Biophys J. 2016;111:2135–2148. doi: 10.1016/j.bpj.2016.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Paravastu AK, Leapman RD, Yau WM, Tycko R. Molecular structural basis for polymorphism in alzheimer’s beta-amyloid fibrils. Proc Natl Aca Sci USA. 2008;105:18349–18354. doi: 10.1073/pnas.0806270105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Kircher O, Diezemann G, Bohmer R, Hinze G, Schug KU, Sillescu H, Zimmermann H. Decay of single and double quantum coherences in deuterated glassy ortho-terphenyl. J Chem Phys. 1998;108:8550–8556. [Google Scholar]
- 69.Sun C, Mitchell O, Huang JX, Boutis GS. NMR studies of localized water and protein backbone dynamics in mechanically strained elastin. J Phys Chem B. 2011;115:13935–13942. doi: 10.1021/jp207607r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1.Theory and range of validity. J Am Chem Soc. 1982;104:4546–4559. [Google Scholar]
- 71.Meirovitch E, Liang ZC, Freed JH. Protein dynamics in the solid state from H-2 NMR line shape analysis: A consistent perspective. J Phys Chem B. 2015;119:2857–2868. doi: 10.1021/jp511386b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Meints GA, Miller PA, Pederson K, Shajani Z, Drobny G. Solid-state nuclear magnetic resonance spectroscopy studies of furanose ring dynamics in the DNA Hhal binding site. J Am Chem Soc. 2008;130:7305–7314. doi: 10.1021/ja075775n. [DOI] [PubMed] [Google Scholar]
- 73.Onuchic JN, LutheySchulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 74.Roggatz I, Rossler E, Taupitz M, Richert R. Nonexponential H-2 spin-lattice relaxation and slow translational exchange in disordered systems. J Phys Chem. 1996;100:12193–12198. [Google Scholar]
- 75.McConnell HM. Reaction rates by nuclear magnetic resonance. J Chem Phys. 1958;28:430–431. [Google Scholar]
- 76.Chandrasekhar S. Stochastic problems in physics and astronomy. Rev Mod Phys. 1943;15:0001–0089. [Google Scholar]
- 77.Kramers HA. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 78.Edholm O, Leimar O. The accuracy of kramer’s theory of chemical kinetics. Physica. 1979;98A:313–324. [Google Scholar]
- 79.Edholm O, Blomberg C. Decay of angular-correlation functions by multiple rotational potential diffusion in polymer-chains, with applications to NMR relaxation in paraffin chains of lipid bilayers. Chem Phys. 1979;42:449–464. [Google Scholar]
- 80.Kaempf K, Kremmling B, Vogel M. Vanishing amplitude of backbone dynamics causes a true protein dynamical transition: H-2 NMR studies on perdeuterated c-phycocyanin. Phys Rev E. 2014;89 doi: 10.1103/PhysRevE.89.032710. [DOI] [PubMed] [Google Scholar]
- 81.Khodadadi S, Pawlus S, Roh JH, Sakai VG, Mamontov E, Sokolov AP. The origin of the dynamic transition in proteins. J Chem Phys. 2008;128:5. doi: 10.1063/1.2927871. [DOI] [PubMed] [Google Scholar]
- 82.Miao YL, Yi Z, Glass DC, Hong L, Tyagi M, Baudry J, Jain NT, Smith JC. Temperature-dependent dynamical transitions of different classes of amino acid residue in a globular protein. J Am Chem Soc. 2012;134:19576–19579. doi: 10.1021/ja3097898. [DOI] [PubMed] [Google Scholar]