Identifying mechanisms driving formation of granuloma-associated fibrosis during Mycobacterium tuberculosis infection

Abstract

Mycobacterium tuberculosis (Mtb), the causative agent of tuberculosis (TB), is a pulmonary pathogen of major global concern. A key feature of Mtb infection in primates is the formation of granulomas, dense cellular structures surrounding infected lung tissue. These structures serve as the main site of host-pathogen interaction in TB, and thus to effectively treat TB we must clarify mechanisms of granuloma formation and their function in disease. Fibrotic granulomas are associated with both good and bad disease outcomes. Fibrosis can serve to isolate infected tissue from healthy tissue, but it can also cause difficulty breathing as it leaves scars. Little is known about fibrosis in TB, and data from non-human primates is just beginning to clarify the picture. This work focuses on constructing a hybrid multi-scale model of fibrotic granuloma formation, in order to identify mechanisms driving development of fibrosis in Mtb infected lungs. We combine dynamics of molecular, cellular, and tissue scale models from previously published studies to characterize the formation of two common sub-types of fibrotic granulomas: peripherally fibrotic, with a cuff of collagen surrounding granulomas, and centrally fibrotic, with collagen throughout granulomas. Uncertainty and sensitivity analysis, along with large simulation sets, enable us to identify mechanisms differentiating centrally vs. peripherally fibrotic granulomas. These findings suggest that heterogeneous cytokine environments exist within granulomas and may be responsible for driving tissue scale morphologies. Using this model we are primed to better understand the complex structure of granulomas, a necessity for developing successful treatments for TB.

Introduction

Tuberculosis (TB) is among the most prevalent and most lethal infectious diseases globally (1). Approximately one third of the world’s population is infected with the causative agent of TB, Mycobacterium tuberculosis (Mtb) (1). In lungs of primates (human and non-human), Mtb stimulates the formation of complex immune structures called granulomas, which serve to contain the infection and protect surrounding tissue (2, 3). These can also provide a niche for Mtb to thrive. Granulomas are extremely heterogeneous, with variable abilities to kill Mtb, even in the same host. These structures are composed of macrophages of different types (4), T and B cells (2, 5, 6), and other immune cells. Granulomas can be categorized by size, shape, cellular organization, number of bacteria (colony forming units, CFU), or morphology (3, 4, 7–12) (Figure 1). Common morphological classifications include: caseous, having a necrotic core of dead tissue surrounded by a cuff of live cells, dense cellular, having no distinguishable core but rather cells throughout, suppurative, having a large amount of neutrophil infiltration, and fibrotic, having collagen surrounding the exterior of or distributed throughout the granuloma (5, 13) which eventually calcifies, leading to the final stage known as tubercles.

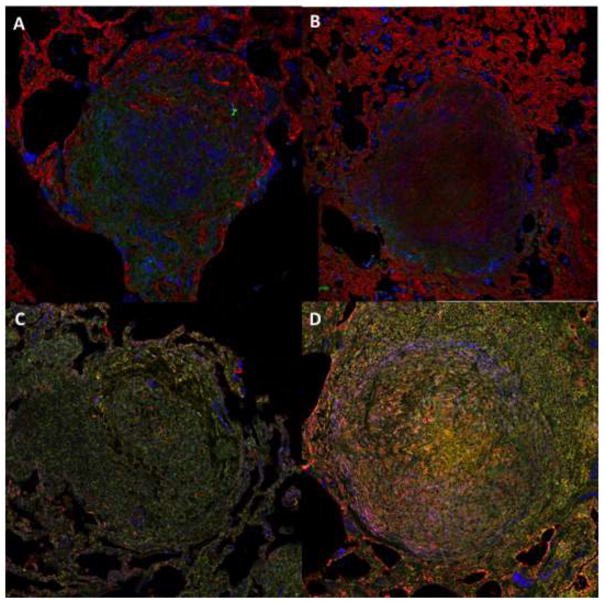
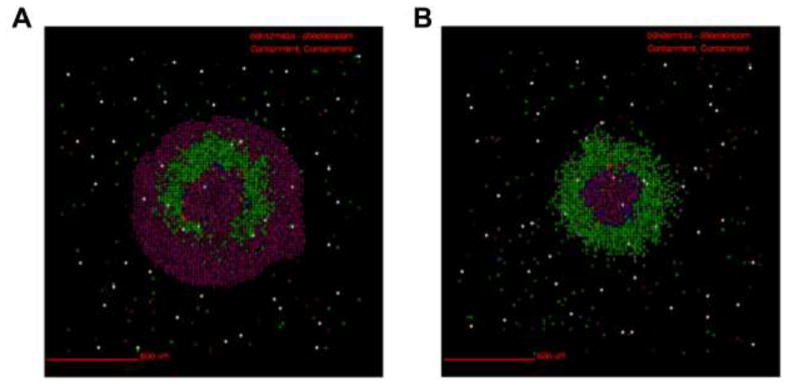
Figure 1. NHP M. tuberculosis granulomas show TGF-β1 driven fibrosis.

Top panels feature granulomas stained for collagen I (red), TGF-β1 signaling (green), and macrophages (primary granuloma cell type) (blue). Bottom panels feature granulomas stained for activated TGF-β1 (red), latent TGF-β1 (green), and myofibroblasts (αSMA) (blue). Magnification ×200. A) Granuloma from an animal following two months of antibiotic treatment. B, C, D) Granulomas are from animals with active TB.

Multiple granulomas are found in infected individuals who show symptoms of TB, as well as those that do not, and each has a unique infection trajectory (13, 14). Fibrotic granulomas can been seen in NHPs and patients weeks, months and even years following infection. Fibrosis surrounding a granuloma can be beneficial to the host, isolating infected tissue from healthy tissue. Excessive fibrosis, however, can be detrimental. Collagen can restrict lung flexibility, inhibit inspiration, and cause difficulty breathing. How and when granuloma-associated fibrosis occurs is not well understood (15). Identifying mechanisms that drive formation of fibrotic granulomas, their complex architecture, and regulation is key to identifying therapeutic treatments for TB that preserve the benefits of fibrosis and reduce the occurrence of negative pathology.

In this work we develop a hybrid multi-scale agent-based model of granuloma formation in the lungs in order to identify key mechanisms driving the formation of fibrotic granulomas. We combine pro-fibrotic cellular agents, cells known as fibroblasts, that we calibrated in a previously published model of fibrotic regulation (16), with our existing multi-scale model of granuloma formation, GranSim (17–21), that includes molecular scale mechanisms of a pro-fibrotic mediator, TGF-β1 (Warsinske et al. JI in review). This next-generation GranSim incorporates fibrotic mechanisms at the molecular, cellular, and tissue scales. Fibroblast agents exist at the cellular scale; however, each individual agent includes molecular scale cytokine (TGF-β1) receptor ligand signaling behavior, and all factors participate in tissue scale dynamics. We calibrate and validate this model against non-human primate (NHP) studies of fibrotic granulomas (15). With this model we focus on contained granulomas, those having relatively stable number of Mtb bacilli (colony forming units, CFUs). Contained granulomas are more prevalent than disseminating (having increasing CFUs) and are more commonly associated with fibrosis (22). We apply uncertainty and sensitivity analyses specifically adapted for use with multi-scale hybrid agent-based models to identify mechanisms that drive formation of fibrotic granulomas under different simulated conditions (23). With this model we seek to recapitulate the morphology of fibrotic primate granulomas and to elucidate mechanisms leading to their formation that would be impossible to explore in vivo.

Fibrosis is a dysregulation of the wound healing process (24, 25). Fibrotic granulomas are often associated with granuloma healing (8, 15, 26–30). They are typically found during latent TB and following TB-specific antibiotic treatment (15). Our understanding of fibrotic granuloma morphology is due in large part to work performed in NHPs, as it is difficult to study human lungs except at death (15). NHPs exhibit two primary fibrotic granuloma morphologies (31). The first is peripheral fibrosis, found in the form of a collagen cuff surrounding the perimeter of granulomas (15, 31). This fibrotic cuff is thought to contribute to granuloma containment and restrict disease dissemination (15, 31) (Figure 1A). The second fibrotic granuloma morphology has a collagenous structure throughout, and can be referred to as centrally fibrotic (15, 31) (Figure 1B). These granulomas look more like scars than contained granulomas and are often associated with sterilization of a granuloma (clearing all the bacteria inside) (32). Central localized fibrosis occurs more frequently following antibiotic treatment than prior to treatment (31).

In all injuries, fibroblasts are the primary cell type responsible for driving wound healing and the development of fibrosis (24, 33–37). Fibroblasts proliferate in wounds where they differentiate into myofibroblasts and secrete extracellular matrix proteins such as collagen (24, 33–37). The collagen secreted by myofibroblasts provides a substrate for re-epithelialization healing of wounds. Myofibroblasts also have a contractile phenotype, which enables them to close the wound gap and further restore tissue integrity (38–43). Both experimental and computational studies of fibrosis have explored these mechanisms in detail (38–42, 44–58). Granulomas, however, are different than traditional wounds because they involve a highly dense organized structure that serves to wall off the infection rather than to restore damaged lung tissue architecture. Fibroblasts have been identified by histology studies to be present in granulomas (15); however, how they arrive there and what purpose they serve is not well understood. Certainly the presence of fibrosis is an indication of fibroblast activity, but what stimulates them in the context of a granuloma is unknown.

High levels of a specific pro-fibrotic cell signaling protein (cytokine), TGF-β1, have been associated with fibrosis (24, 28, 59, 60) and fibrotic granulomas (15). TGF-β1 is known to play an important role in driving fibroblast proliferation, differentiation, and the development of fibrotic tissue in other contexts; however, its role in granuloma formation and function has not been fully characterized (15, 59–63). Another cytokine, IL10, has been associated with reduced fibrosis and the inhibition of TGF-β1 synthesis during pulmonary fibrosis (64–67). Our goal is to better elaborate dynamics that lead to fibrosis and identify factors that distinguish central and peripheral fibrosis, as well as to elaborate relationship cytokines and cells play in the development of fibrotic granulomas.

Materials and Methods

Non-human primate data

The Institutional Animal Care and Use Committee of University of Pittsburgh approved all experiments. The animals were housed and maintained in accordance with standards established in the Animal Welfare Act and the Guide for the Care and Use of Laboratory Animals. The University of Pittsburgh is an AAALAS certified program.

Formalin-fixed paraffin-embedded tissue sections were cut from samples obtained from macaques with active TB or drug treated for active TB as previously described (32, 68). Antigen retrieval and staining were performed as previously described (Mattila 2013 JI). Tissue sections were stained for collagen I, pSMAD-2/3, CD163, L-TGF-β1, TGF-β1, and αSMA as previously described (DiFazio 2016 Fibrogenesis). Staining was then visualized using a FluoView 1000 confocal microscope (Olympus).

Hybrid multi-scale model (GranSim)

In this work we build upon the existing 2D hybrid multi-scale model of primate granuloma formation GranSim (Figure 2) (17, 19, 21, 69–73). GranSim has been updated and validated against experimental data since 2003 and captures molecular, cellular, and tissue scale dynamics of granuloma formation and function. At the molecular scale, GranSim includes secretion, diffusion, and degradation of chemokines (cell recruitment molecules) and cytokines (cell signaling proteins) (74). Diffusion mechanisms are described by partial differential equations (PDEs) while receptor ligand signaling mechanisms are described by ordinary differential equations (ODEs). Diffusion dynamics have been described previously, as well as strategies that we use for efficient numerical implementation of hybrid multi-scale agent-based models (16, 74, 75). At the cellular scale, GranSim accounts for discrete cellular agents whose actions are governed by model rules. A full list of GranSim’s rules can be found at http://malthus.micro.med.umich.edu/GranSim (Figure 2). Granuloma formation occurs as an outcome at the tissue scale and is an emergent behavior of the model. This means that granuloma formation is the product of the actions of individual agents and not a higher-level architecture. Outputs of the model include: chemokine and cytokine concentration gradients over the entire simulation space for every time point, depictions of the simulation space. This information is both quantitative and qualitative and can be directly compared to data from in vitro and in vivo studies. Snapshots of the simulation environment can be linked to produce time-lapse movies (http://malthus.micro.med.umich.edu/lab/movies/TGFB_GranSim/).

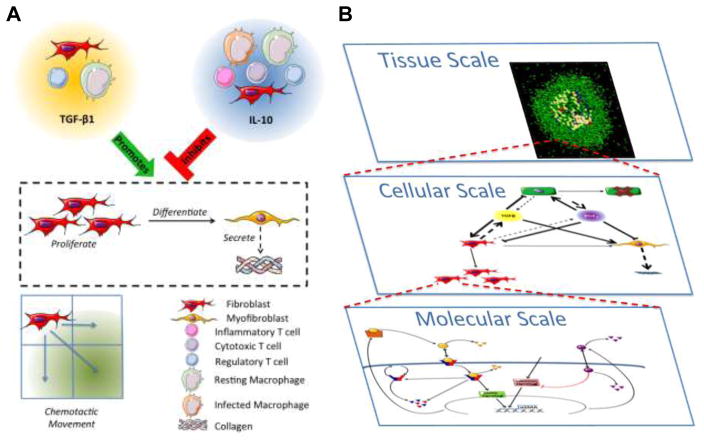
Figure 2. Fibroblast dynamics within hybrid multi-scale model architecture.

A) Cellular and molecular scale interactions of fibroblasts in the hybrid multi-scale computational model. Fibroblasts, regulatory T cells, and resting macrophages secrete TGF-β1. Fibroblasts, resting and infected macrophages, and all T cell types secrete IL10. Fibroblast to myofibroblast differentiation, as well as myofibroblast secretion of collagen, are promoted by TGF-β1 and inhibited by IL-10. Fibroblasts migrate in response to granuloma associated chemokine milieu. Agent based model rules are available at: http://malthus.micro.med.umich.edu/GranSim/. B) Individual scale models are combined to create a single hybrid multi-scale model of lung granuloma formation and function. The molecular scale includes TGF-β1 receptor ligand signaling dynamics within a single fibroblast, cytokine secretion and diffusion within the environment. At the cellular scale, individual agents, including macrophages, T cells, and fibroblasts, respond based on probabilistic rules to stimuli and cytokines within their local environment. The dynamics from Panel A are included within this scale. At the tissue scale we observe emergent behavior that can be characterized and compared to experimental data.

Each model scale is linked to the other scales through cytokine concentrations and/or agent behaviors (Figure 2B) as we have done previously (16–19, 70, 74, 76–78). Molecules that are secreted and diffuse at the molecular scale dictate behavior of cells at the cellular scale (eg. TGF-β1, IL-10, TNF, etc). The actions of cells at the cellular scale dictate the emergent behavior at the tissue scale (macrophages, T cells, fibroblasts, etc). The emergent behavior of the tissue scale defines local environments, which in turn influence cytokine concentrations at the molecular scale.

Next-generation GranSim including fibrotic cell types and cytokines

For this study we develop a next-generation GranSim to include fibroblasts, a new class of cellular scale agents, molecular scale TGF-β1 receptor-ligand signaling dynamics, and rules guiding their behavior (Figure 2A). Fibroblast agents include fine-grained molecular scale TGF-β1 receptor/ligand signaling dynamics (16, 75). Within this updated version of GranSim there are four macrophage states (resting, activated, infected, and chronically infected) and three distinct T-cell types (cytotoxic, regulatory, and IFNγ producing T-cells). This version model also includes two states of fibroblasts (activated fibroblast and myofibroblast), which were imported from a previously published model (16). New rules for fibroblast behavior are described in detail below. The cellular scale captures interaction between these agent groups, and chemokine-directed cellular movement. We integrate these new mechanisms at each biological scale of the model. We link new cellular and molecular scale attributes into the existing model primarily through TGF-β1 and IL10. Cellular and molecular scales operating within the model are linked when cytokines regulated at the molecular scale influence the states and behaviors of agents at the cellular scale. Thus, the cellular and molecular scale aspects of the model are connected by extracellular cytokine and agent behaviors (Figure 2).

Fibroblast and myofibroblast agents

We incorporated fibroblasts into GranSim as a unique agent class originally developed in our study of an in vitro co-culture system (16), and we added additional rules relevant to granuloma biology This agent class contains fibroblasts and their differentiated form, myofibroblasts. Fibroblasts can proliferate in GranSim if they have bound a sufficient amount of TGF-β1 in their lifetime (ζ₉) (79, 80), have not bound more than a maximum amount of IL10 (ζ₇) (81, 82), and are present in a sufficient concentration of TNFα to indicate close proximity to the granuloma (ζ₁₁). Once a fibroblast has proliferated, it cannot attempt proliferation again for 24 hours (83). Fibroblasts have a probability of moving randomly into an available grid compartment if one is available in their Moore neighborhood (the eight compartments that share an edge with the compartment they occupy) (ζ₃). Fibroblasts bind and secrete TGF-β1 according to the equations described previously (75), and are inhibited by IL10, which works to block downstream adhesion signaling (81, 82). Fibroblasts can differentiate into myofibroblasts if the following are true: they have not proliferated in the current time step, have bound a sufficient amount of TGF-β1 in their lifetime (ζ₈) (43, 55, 80), have not bound more than a maximum amount of IL10 (ζ₇) (81, 82), and are present in a sufficient concentration of TNFα to indicate close proximity to the granuloma (ζ₁₁). Because GranSim models granuloma formation and not the surrounding lung tissue, a signal is necessary to inform fibroblasts they have arrived at the site of injury/infection. We use TNFα as a proxy for all the cytokines that signal tissue damage to a fibroblast since as it diffuses, it correlates with the boundary of the granuloma area.

TGF-β1 stimulates myofibroblast synthesis of α-smooth muscle actin (αSMA) and collagen secretion. αSMA is an indicator of fibroblast to myofibroblast differentiation (38–40, 43, 55, 58, 75). Myofibroblasts maintain TGF-β1 binding and receptor ligand signaling but no longer secrete TGF-β1. Molecular scale TGF-β1 signaling dynamics relevant to these cells are described below. Myofibroblasts undergo chemotaxis within the simulation space (they are sensitive to the pro-inflammatory chemokine milieu). They secrete collagen according to the parameter collagen secretion (ω₁), and synthesize αSMA (ω₄). Myofibroblasts have a probability of undergoing apoptosis (ω₂) at each time step.

Fibroblast TGF-β1/IL10 signaling dynamics

We have previously described, TGF-β1 signaling dynamics in a fibroblast in a detailed ODE model system (75). IL10 is used as an inhibitor of TGF-β1 signaling in fibroblasts (66, 81, 82, 84). IL10 acts in the same way as other TGF-β1 inhibiting mediators (PGE₂) by inhibiting the adhesion signaling cascade, a requirement for efficient transmission of the TGF-β1 signal (85, 86). IL10 is present throughout the granuloma (4).

Model parameters, outputs, and simulations

In this work we simulated 500 granulomas 3 times each with large parameter value ranges (Table A1). We refer to this as our wide parameter sweep. These simulations allowed us to explore a large portion of parameter space and corresponding model outcomes. From these simulations we are focused on contained granulomas, those that have relatively stable bacterial numbers. We identified a baseline parameter set for a fibrotic granuloma with CFU that stabilizes over time (see parameter list in Table A1).

Simulation outputs occur at the molecular, cellular and biological scales. They can be reported continuously over time. Outputs at the molecular scale include total cytokine and chemokine concentrations (TGF-β1, TNFα, IL10, CCL2, CCL5, CXCL9), visual cytokine and chemokine distributions, cytokine and chemokine concentrations at any given position in the simulation, total number of TGF-β1 receptors in the simulation, total number of TGF-β1 receptors on any given cell, cell specific bound cytokine concentrations (TGF-β1, TNFα, IL10), cell specific αSMA levels. At the cellular scale model outputs include total cell type and sub-type numbers (fibroblasts, myofibroblasts, resting macrophages, activated macrophages, infected macrophages, chronically infected macrophages, regulatory T cells, cytotoxic T cells, IFNγ producing T cells) for both living and dead cells, and visual distribution of cells. Model outputs at the tissue scale include overall granuloma morphology, total collagen, visual distribution of collagen, total CFU, total caseum, visual localization of caseum.

Secondly, we narrow our parameter sweep to focus on parameters pertaining to fibrosis, fibrotic parameter sweep (Table 1). We simulated 500 granulomas 3 times each from parameter ranges listed in Table 1 in order to generate a fibrotic granuloma set (Figure 9). This fibrotic granuloma set is used for uncertainty and sensitivity analysis studies (Tables 2–4). We selected a representative granuloma from our fibrotic granuloma set for comparative histology studies, and show simulation snapshots at 50, 100, 125, 150, 175, and 200 days post-infection (PI) to capture the onset and progression of fibrosis. We chose a representative granuloma to demonstrate the progression of cells and cytokines over time (Figures 3–8). Additional granuloma outcomes at day 200 can be found in the Appendix that show a range of granuloma and fibrotic outcomes (Figure A1).

Table 1.

Parameter ranges used for fibrotic parameter sweep

Symbol	Parameter name	Value or range	Units
Core model parameters
γ6	Time to heal caseation	[1642, 2462]	days
γ7	Threshold for TNFα-induced apoptosis	[1393, 2089]	molecules
γ8	Rate of TNFα-induced apoptosis	[1.17e–6, 1.76e–6]	1/seconds
γ10	Saturating number of chemokine molecules	[374, 562]	molecules
γ15	Degradation rate of inactive TGF-β1	[9.28e-6, 1.39e–5]	molecules/molecular time step
γ16	Degradation rate of active TGF-β1	[8.0e-4, 0.0012]	molecules/molecular time step
Macrophage parameters
μ1	Fraction of grid compartments with a macrophage	[0.024, 0.036]	n/a
μ2	Number of time steps before an infected macrophage can move	[112, 168]	n/a
μ11	Synthesis rate of inactive TGF-β1 by macrophages	[0.0001, 0.01]	molecules/diffusion time step
μ17	Fraction of inactive TGF-β1 activated by a mac	[1e–6, 1]	n/a
μ18	Amount of TGF-β1 that inhibits macrophages	[1e–6, 1]	molecules
μ19	Fraction of active TGF-β1 in a compartment bound by a mac	[1e–6, 1]	n/a
T cell parameters
τ7	Synthesis rate of TNFα by cytotoxic Tcell	0.015	molecules/diffusion time step
τ8	Probability of a cytotoxic T-cell killing a macrophage	[0.012, 0.18]	n/a
τ9	Probability of a cytotoxic T-cell killing a macrophage and all associated Mtb	[0.61, 0.91]	n/a
τ12	Synthesis rate of TGF-β1 by regulatory T cell	[0.0001, 0.01]	molecules/diffusion time step
τ14	Bound TGF-β1 that inhibits T cells	[0.04, 0.2]	molecules
τ15	Fraction of active TGF-β1 in a compartment bound by a T cell	[1e–4, 0.2]	n/a
Fibroblast Parameters
ζ3	Probability a fibroblast will move	[0.001, 0.5]	n/a
ζ4	Synthesis rate of latent TGF-β1 by a fibroblast	[0.001, 0.1]	molecules/diffusion time step
ζ6	Time until a fibroblast can attempt to proliferate	[24, 48]	hours
ζ7	Bound molecules of IL10 that inhibits fibroblast proliferation/differentiation	[1e4, 2e4]	molecules
ζ8	TGF-β1 myofibroblast differentiation threshold	[2.0e–7, 8.0e-7]	molecules
ζ9	TGF-β1 fibroblast proliferation threshold	[2.0e–7, 8.0e-7]	molecules
ζ10	Minimum ratio of TGF-β1 to IL10 required for myofibroblast differentiation	[1e–11, 1e–9]	n/a
ζ11	TNFα fibroblast proliferation/differentiation threshold	[0.025, 0.5]	molecules
ζ12	Synthesis rate of Il10 by fibroblast	[3.48e–22, 3.48e–16]	molecules/molecular time step
ζ13	Binding rate constant of Il10 by fibroblast	[1e–12, 1e–8]	molecules/molecular time step
ζ14	Fibroblast sensitivity to Il10	[0.001, 10]	n/a
ζ15	Fibroblast sensitivity to TGF-β1	[0.000001, 0.1]	n/a
ζ16	Probability of a fibroblast differentiating into a myofibroblast	[0.1, 5.0]	n/a
Myofibroblast Parameters
ω1	Collagen synthesis rate	[1e–7, 1e–5]	molecules/agent time step
ω2	Probability of apoptosis	[0.002, 0.2]	n/a
ω3	αSMA degradation rate	[0.001, 10]	molecules/molecular time step

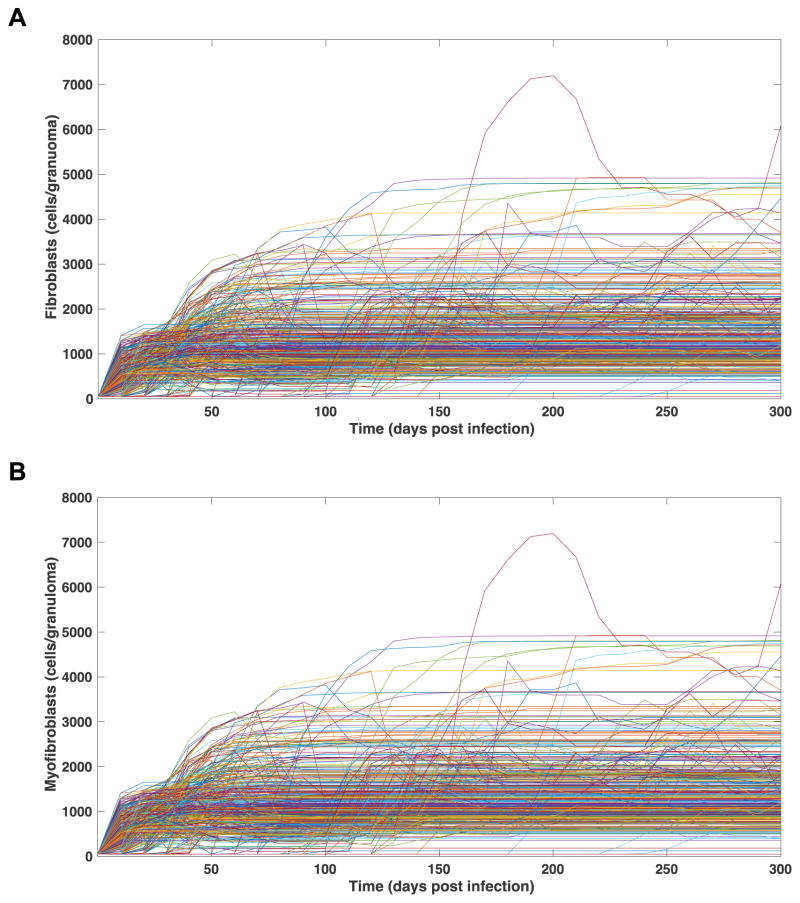
Figure 9. Fibroblast and myofibroblast numbers in 500 simulated granulomas over time.

Each line represents and individual granuloma from the fibrosis parameter set (Table 1). A) Fibroblasts per granuloma over 300 days PI. B) Myofibroblasts per granuloma over 300 days PI.

Table 2.

Significant PRCC values for parameters driving cell number at day 300 PI. p < 0.01

Parameter	Description	PRCC	p value
Fibroblast number
γ18	Degradation rate of active TGF-β1	0.15	1.82*10−5
μ18	Amount of TGF-β1 that inhibits macrophages	−0.11	1.55*10−3
τ14	Bound TGF-β1 that inhibits T cells	0.10	4.04*10−3
τ12	Synthesis rate of TGF-β1 by regulatory T cell	0.09	9.49*10−3
ζ3	Probability a fibroblast will move	0.77	1.68*10−170
ζ7	Fibroblast IL10 proliferation threshold	0.13	1.67*10−4
ζ11	TNFα fibroblast proliferation threshold	−0.09	5.66*10−3
ζ12	Synthesis rate of IL10 by fibroblast	−0.10	3.96*10−3
ζ15	Fibroblast sensitivity to TGF-β1	0.09	8.64*10−3
Myofibroblast number
ζ3	Probability a fibroblast will move	0.17	1.08*10−6
ζ9	TGF-β1 fibroblast proliferation threshold	−0.16	3.23*10−6
ζ8	TGF-β1 fibroblast differentiation threshold	−0.21	4.41*10−10
ζ13	Fibroblast IL10 binding rate	−0.13	1.00*10−4
ζ14	Fibroblast sensitivity to IL10	−0.36	1.52*10−28
ω3	Degradation rate of αSMA	−0.42	5.16*10−39
Collagen concentration
ζ3	Probability a fibroblast will move	0.20	3.08*10−9
ζ9	TGF-β1 fibroblast proliferation threshold	−0.16	1.12*10−6
ζ8	TGF-β1 fibroblast differentiation threshold	−0.22	2.33*10−11
ζ13	Fibroblast IL10 binding rate	−0.14	4.20*10−5
ζ14	Fibroblast sensitivity to IL10	−0.39	2.11*10−32
ω3	Degradation rate of αSMA	−0.42	1.67*10−38

Table 4.

Significant PRCC values for parameters driving fibroblast number within and on the periphery of the granuloma with no fibroblast movement at day 300 PI. p < 0.01

Parameter	Description	PRCC	p value
Fibroblasts within the granuloma
μ4	Number of time steps before an infected macrophage can move	−0.10	1.14*10−4
μ19	Fraction of active TGF-β1 in a compartment bound by a mac	0.07	6,11*10−3
τ8	Probability a cytotoxic T cell will kill a macrophage	−0.07	5.25*10−3
ζ6	Time until a fibroblast can attempt to proliferate	−0.10	1.14*10−4
ζ9	TGF-β1 fibroblast proliferation threshold	0.33	1.77*10−37
ζ8	TGF-β1 fibroblast differentiation threshold	0.08	3.29*10−3
ζ11	TNFα fibroblast proliferation threshold	0.27	3.45*10−25
ω3	Degradation rate of αSMA	0.11	5.62*10−5
Fibroblasts on the periphery of the granuloma
μ4	Number of time steps before an infected macrophage can move	−0.08	3.19*10−3
μ11	TGF-β1 synthesis by macrophage	0.11	1.28*10−5
ζ9	TGF-β1 fibroblast proliferation threshold	−0.35	2.80*10−42
ζ11	TNFα fibroblast proliferation threshold	−0.12	1.84*10−6
ζ16	Probability of a fibroblast differentiating into a myofibroblast	0.07	6.05*10−3

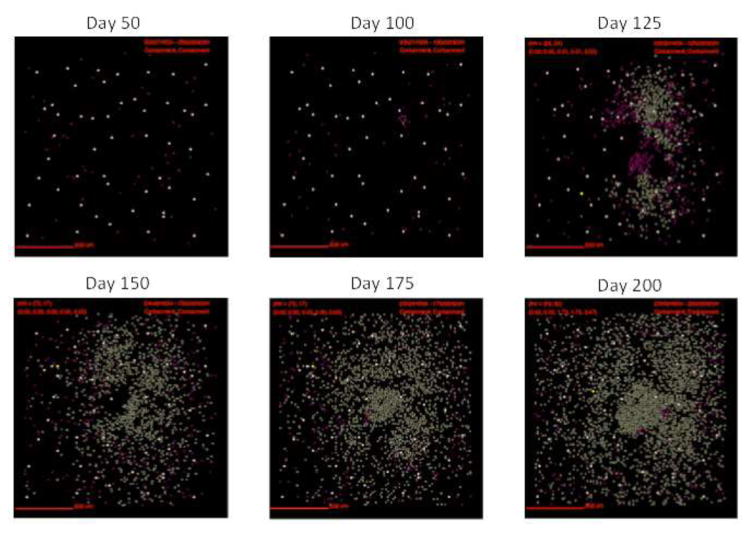
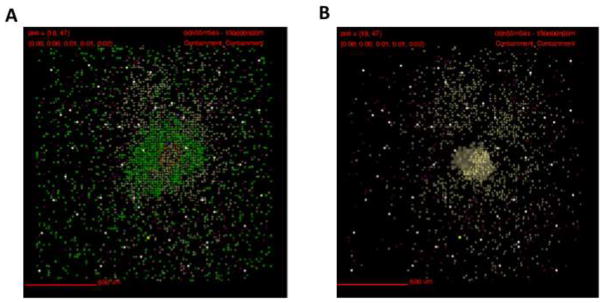
Figure 3. Simulations of cellular localization and granuloma morphology over time.

Representative images of a single granuloma over time generated with baseline parameter set (Table. 1). Shown is simulation of 2mm × 2mm lung tissue. Cells are represented by different colors: resting macrophages are green, activated macrophages are blue, infected macrophages are orange, chronically infected macrophages are red, IFNγ producing T-cells are pink, cytotoxic T cells are violet, regulatory T cells are cyan, fibroblasts are maroon, and myofibroblasts are gold. Caseum is represented in these images as brown compartments. Cytokine distributions are not shown.

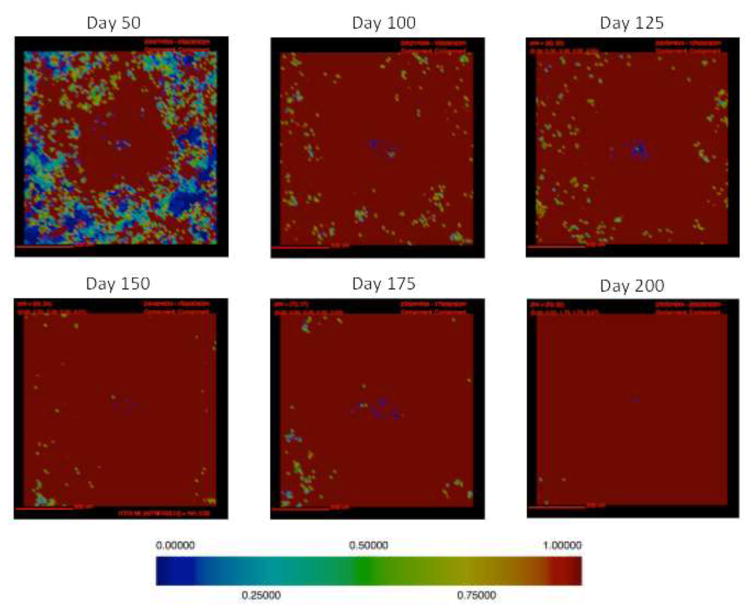
Figure 8. Latent TGF-β1 localization in a simulated fibrotic granuloma over time.

Latent TGF-β1 concentration is represented in the above images for a single representative granuloma. Latent TGF-β1 is visible early in infection and continues be present throughout infection (same simulation as in Figures 3,4,5,6,7). Red represents the highest concentration of latent TGF-β1 and blue represents no latent TGF-β1 (relative color bar shown).

Determining central vs. peripheral fibrosis

In order to characterize fibroblasts and myofibroblasts as inside or outside of the granuloma we need to define the edge of the granuloma. Because granulomas are an emergent feature of GranSim, the edge of the granuloma is determined at every time step by cell density. Because fibroblasts contribute to cell density, and we want to characterize them in reference to granuloma structure, we defined the perimeter of a granuloma before fibroblast proliferation begins. Once the first fibroblast proliferates, the perimeter size of a granuloma is noted and set as a reference value for the remainder of the simulation. The perimeter is used only for reference and in no way affects cell behavior. Fibroblasts that exist within the perimeter are considered centrally located. Fibroblasts on the outside of the perimeter are peripherally located. Some granulomas exhibit both features.

Uncertainty and sensitivity analysis

Uncertainty and sensitivity analysis can quantify how variation in parameter values contributes to variation in model output (23). This analysis can highlight mechanisms and model components responsible for different outcomes. There is a strong precedent for its use with hybrid multi-scale models including GranSim (23). Because GranSim is multi-scale, parameters that contribute to molecular, cellular, or tissue scale mechanisms may also affect outputs at other scales (described as intra-model influence). We perform sensitivity analyses to identify parameters that have a significant influence on individual model outcomes and the extent of their influence on each outcome (23, 87). We use partial rank correlation coefficients (PRCCs) to determine how sensitive a given output is to each parameter. PRCC values range from −1 to +1, indicating the non-linear correlation between a parameter and model output. PRCC values are considered significant with a p-value less than 0.01. PRCC values are not dependent on other PRCC values. Fishers Z test must be applied to determine if PRCC values are significantly different from each other P-value < 0.001, so comparing values within tables is not directly possible without the Z test.

Results

Simulated granulomas capture the morphology of fibrotic NHP granulomas

In this section we track simulated morphological changes of developing fibrotic granulomas over 200 days. We take snapshots at 6 time points: days 50, 100, 125, 150, 175 and day 200 PI, to capture the progression of fibrosis in a single granuloma (see Figure A1 for additional snapshots of different granuloma). We examine model outputs including: overall simulation morphology (Figure 3), fibroblast and myofibroblast localization (Figure 4), and collagen localization (Figure 5) as granulomas progress over time, as well as spatial distributions of all molecules and cells. We compare spatial morphology of simulated granulomas to histology sections of fibrotic granulomas from Mtb infected NHPs (Figure 1). Collagen levels from simulated granulomas recapitulates NHP histology (Figure 5). We find that GranSim can simulate the formation of fibrotic granulomas that qualitatively match sections from NHP samples (15); time points cannot be compared directly because initial time of granuloma formation cannot be identified in NHPs (as granulomas each develop independently and can spawn at later times post-infection).

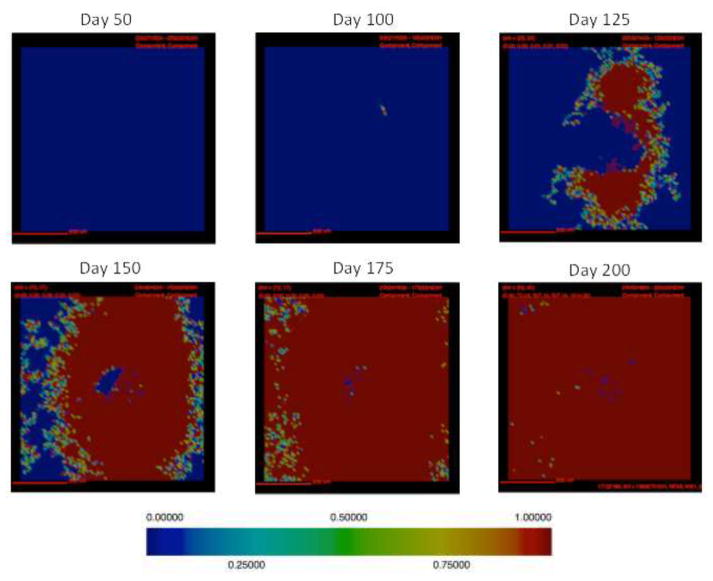
Figure 4. Localization of fibroblasts and myofibroblasts from a simulated fibrotic granuloma over time.

In this representative simulation (same simulation as Figure 3) fibroblasts are represented as maroon, and myofibroblasts are represented as gold. As time progresses the number of both fibroblasts and myofibroblasts increases. They surround and penetrate the granuloma beginning at about 125 day PI.

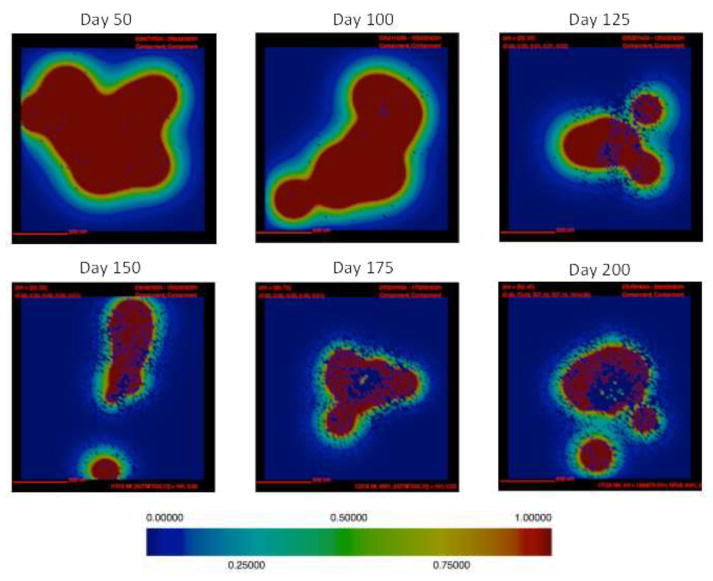
Figure 5. Collagen localization in a simulated fibrotic granuloma over time.

Collagen concentration is represented in the above images with red representing the highest concentration and blue representing no collagen, relative color bar shown (same simulation as Figures 3,4). Collagen formation is first visible at day 100 PI and it continues to accumulate throughout the simulation, until day 200 PI when it covers the entire simulation space.

Following infection we observe the formation of a caseous necrotic granuloma (Figure 3). In this example, the granuloma becomes fibrotic as is evidenced by the presence of fibroblasts and myofibroblasts surrounding the lesion (Figure 4). The localization of fibroblasts and myofibroblasts is comparable to NHP granulomas (Figure 1A, D). In this simulation we observe primarily peripheral localization of fibroblasts and myofibroblasts with some penetration into the center of the lesion by day 200 PI (Figures 3,4). Collagen in simulated granulomas can be found both on the periphery of the granuloma and in the center (Figure 5). Both peripheral (Figure 1A) and central (Figure 1B) collagen localization is also reflected in the NHP granulomas.

Simulated granulomas demonstrate cytokine distributions comparable to fibrotic NHP granulomas

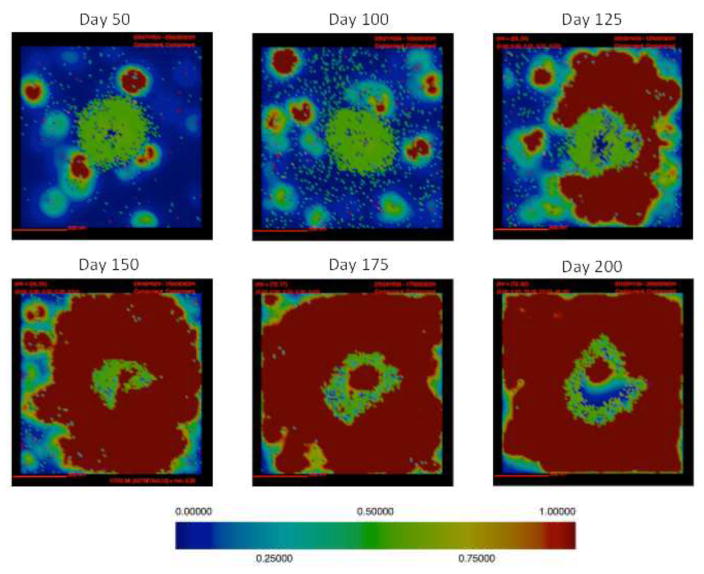
We next compared localization of cytokines between simulated granulomas and NHP histology sections. IL10 is present in simulations somewhat concentric to the granuloma (figure 6), consistent with previously published simulations of GranSim. The amount of IL10 in simulations decreases as the number of fibroblasts and myofibroblasts increases. IL10 concentration appears to be inversely correlated with fibrosis.

Figure 6. IL10 localization in a simulated fibrotic granuloma over time.

IL10 concentration is represented in the above images for a single representative granuloma over time (same simulation as in Figures 3,4,5. IL10 is visible early in infection and continues be present throughout the infection. Red represents the highest concentration of IL-10 and blue represents no IL-10 (relative color bar shown).

Localization of active and latent TGF-β1 in simulated granulomas qualitatively matches NHP granulomas (Figure 1) (15). Active TGF-β1 is visible early in infection and continues to be present throughout infection (Figure 7). Active TGF-β1 is somewhat concentric to the granuloma prior to day 125 PI. As the granuloma becomes more fibrotic, active TGF-β1 increases. The highest concentrations of active TGF-β1 are found on the periphery of the granuloma, consistent with NHP data (Figure 1C, D). Late in infection, the concentration in the center of the granuloma is depleted. Latent TGF-β1 is visible early in infection and continues to be present throughout the course of infection. As is the case for NHP granulomas, latent TGF- β1 is prevalent throughout the granuloma starting at a relatively early time post infection (Figures 1C–D, 7). Latent TGF-β1 is somewhat concentric to the granuloma very early in infection but is rapidly distributed throughout the simulation space. Latent TGF-β1 is present throughout the simulation space for the majority of the simulation.

Figure 7. Active TGF-β1 localization in a simulated fibrotic granuloma over time.

Active TGF-β1 concentration is represented in the above images for a single representative granuloma (same simulation as in Figures 3,4,5,6). Red represents the highest concentration of active TGF-β1 and blue represents no active TGF-β1 (relative color bar shown).

A wide range of fibrosis severity is observed in simulated granulomas

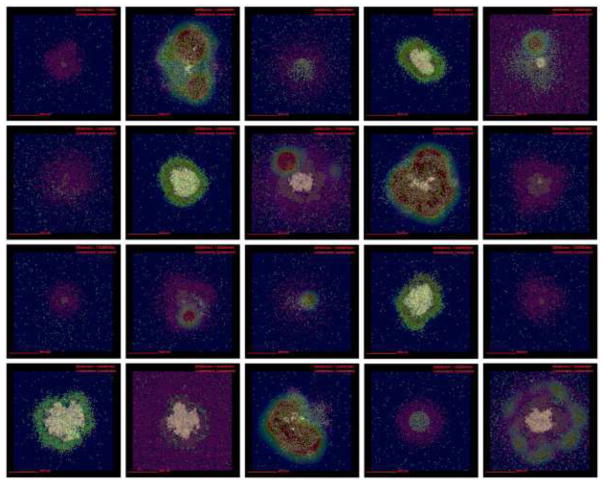
We performed uncertainty analysis to identify all possible fibrotic outcomes in our simulated granulomas. We simulated 500 granulomas 3 times each of our baseline granuloma set to examine the full spectrum of possible outcomes. With this model we are able to generate a wide range of fibrotic granuloma severity (Figure 9) observed via a range in number of fibroblasts and myofibroblasts present (see appendix figure A1 for a full sample of these granulomas). Interestingly, not only do the levels of fibrotic cells present change, but also the timing of onset of fibrosis. Some simulations have very early onset of fibrosis (as early as ~10 days PI), and some simulation have very late onset of fibrosis (beyond day 200 PI). We next explore what drives these differences through statistical analysis of the model using uncertainty and sensitivity analyses.

Mechanisms driving fibrotic cell number in simulated granulomas

We performed a PRCC sensitivity analysis to our set of 1500 baseline granulomas to identify key mechanisms driving different fibrotic outcomes (Table 1). Fibrotic granulomas are characterized by the presence of fibroblasts and myofibroblasts as well as collagen. We found that nine model parameters significantly influence the number of fibroblasts at day 300 PI (Table 2). Among these parameters, the probability that a fibroblast will move (ζ₃) had the greatest correlation to fibroblast number (p < 0.0001). This strong correlation suggests that fibroblasts are highly sensitive to local environments and that the more they migrate the more likely they are to encounter pro-fibrotic environments. We found six parameters that significantly influenced both the number of myofibroblasts and amount of collagen (produced by myofibroblasts) in simulations by day 300 PI (Table 2). Of these parameters, the degradation rate of αSMA (ω₃) and fibroblast sensitivity to IL-10 (ζ₁₄) had the strongest influence on myofibroblast numbers at day 300 PI (p<0.001 for Fisher’s z test). This result suggests that inhibition by IL10 plays a stronger role in preventing differentiation than in preventing proliferation.

Mechanisms driving fibrotic cell number within and on the periphery of the granuloma

In addition to exploring mechanisms driving overall fibroblast number, myofibroblast number, and collagen levels in the simulated granulomas, we sought to further elucidate mechanisms driving numbers of fibroblasts in different locations around the granuloma. As previously described there are two common categorizations of fibrotic granuloma: peripherally fibrotic and centrally fibrotic. We use PRCC to identify key mechanisms driving the occurrence of these different phenotypes in order to better understand the developmental differences between them. We identify the dimensions of the granuloma before fibroblast proliferation begins and define fibroblasts within those dimensions as being within the granuloma for the rest of the simulation (see Methods). Fibroblasts that are located outside of the defined granuloma perimeter are considered fibroblasts on the periphery of the granuloma.

PRCC analysis demonstrates that the number of centrally located fibroblasts correlates with different biological mechanisms than the number of peripheral fibroblasts. The number of centrally located fibroblasts is highly negatively correlated to the TGF-β1 fibroblast proliferation threshold (ζ₉) (Table 3). This result suggests that later initiation of fibroblast proliferation corresponds to greater capacity for fibroblast proliferation and/or increased number of pro-fibrotic compartments in the granuloma. The number of centrally located fibroblasts is negatively correlated with the probability that fibroblasts move (ζ₃) (Table 3). This result indicates that fibroblast movement may promote cells to exit a granuloma and thus not participate in central fibrosis. The number of peripherally located fibroblasts is most highly correlated with the probability that a fibroblast will move. This result suggests that highly heterogeneous cytokine environments exist outside a granuloma in lung tissue. Movement facilitates fibroblast encounters with pro-fibrotic environment. Movement may play a less significant role in the number of fibroblasts within the granuloma because of the high cell density and limited space.

Table 3.

Significant PRCC values for parameters driving fibroblast number within a granuloma and on the periphery of a granuloma at day 300 PI. p < 0.01

Parameter	Description	PRCC	p value
Fibroblasts within the granuloma
μ1	Fraction of grid compartments with a macrophage	0.11	3.13*10−5
μ19	Fraction of active TGF-β1 in a compartment bound by a mac	0.09	5.00*10−4
ζ3	Probability a fibroblast will move	−0.12	4.91*10−6
ζ9	TGF-β1 fibroblast proliferation threshold	0.49	2.62*10−90
ζ11	TNFα fibroblast proliferation threshold	0.19	6.58*10−13
ω3	Degradation rate of αSMA	0.11	1.55*10−5
Fibroblasts on the periphery of the granuloma
γ10	Maximum number of molecules allowing chemotaxis	−0.13	6.04*10−7
γ18	Degradation rate of active TGF-β1	0.12	5.43*10−6
μ1	Fraction of grid compartments with a macrophage	0.11	1.24*10−5
τ12	Synthesis rate of TGF-β1 by regulatory T cell	0.07	5.15*10−3
ζ3	Probability a fibroblast will move	0.69	2.46*10−205
ζ7	Fibroblast Il10 proliferation threshold	0.08	2.80*10−3
ζ11	TNFα fibroblast proliferation threshold	−0.08	2.96*10−3

To further explore which mechanisms differentiate central and peripheral granuloma fibrosis, we repeated simulations performed above but prevented fibroblasts from moving. We found that in the absence of fibroblast movement (ζ₃ = 0) the TGF-β1 fibroblast proliferation threshold (ζ₁₁) continues to significantly correlate with the number of fibroblasts within the granuloma (Table 4). For fibroblasts on the periphery of the granuloma, we observe a strong negative correlation with the TGF-β1 fibroblast proliferation threshold (ζ₉) (Table 4). This result suggests that when fibroblasts cannot move, access to TGF-β1 may be limited. The higher the threshold the fewer cells are able to proliferate. Interestingly, fibroblasts within a granuloma are positively correlated (and fibroblasts on the periphery of the granuloma are negatively correlated) with the TGF-β1 fibroblast proliferation threshold (ζ₉). This result may suggest that TGF-β1 is more accessible within a granuloma than on the periphery. The positive correlation between the number of fibroblasts within a granuloma and the TGF-β1 fibroblast proliferation threshold (ζ₉) at day 300 PI could possibly be explained by fibroblast to myofibroblast differentiation. We do not observe fundamentally different granuloma morphology when inhibiting fibroblast movement in the granuloma (Figure 10).

Figure 10. Snapshots of a simulated granulomas comparing fibroblast localization when fibroblast movement is enabled and inhibited.

Simulation of 2mm ×2mm lung tissue. A) Snapshot of simulated granuloma showing the fibroblasts localization when fibroblast movement is permitted. Cells are represented by different colors as follows: resting macrophages are green, activated macrophages are blue, infected macrophages are orange, chronically infected macrophages are red, IFNγ producing T-cells are pink, cytotoxic T cells are violet, regulatory T cells are cyan, fibroblasts are maroon, and myofibroblasts are gold. B) Snapshot of the same simulated granuloma as shown in A, when fibroblast movement is completely inhibited. Distributions of cytokines not shown.

We repeated the simulations performed above with both restricted fibroblast movement (ζ₃ = 0), and a fixed TGF-β1 fibroblast proliferation threshold (ζ₁₁= 1e–10) (Table 5). The goal of this experiment was to identify additional mechanisms driving either central or peripheral fibrosis while reducing the potential for artifacts resulting from how we define the boundaries of a granuloma. Fibroblast number within the granuloma showed a strong positive correlation with the number of bound molecules of IL10 that inhibits fibroblast proliferation (ζ₇) (p < 0.0001). This result is intuitive; a higher threshold reduces the likelihood that it will be met. Less intuitive, fibroblast numbers within the granuloma showed a strong negative correlation to TGF-β1 synthesis by macrophages (μ₁₁) (p < 0.0001). This result suggests that high levels of TGF-β1 within a granuloma promote fibroblast to myofibroblast differentiation and reduce the overall numbers of fibroblasts present. Fibroblasts on the periphery of a granuloma also showed a strong negative correlation to TGF-β1 synthesis by macrophages (μ₁₁) (p < 0.0001). Fibroblasts on the periphery of the granuloma had a negative correlation with TNFα fibroblast proliferation threshold (ζ₁₁), and a positive correlation with the fraction of active TGF-β1 in a compartment bound by a macrophage (μ₁₉). This suggests, consistent with our snapshots and histology (data not shown), that TNFα is less prevalent outside the granuloma. The correlation between active TGF-β1 in a compartment bound by a macrophage (μ₁₉) and fibroblast number indicates that there may be excess TGF-β1 available outside the granuloma promoting differentiation, and that a median amount of available active TGF-β1 is optimal for fibroblast proliferation.

Table 5.

Significant PRCC values for parameters driving fibroblast number within and on the periphery of the granuloma with no fibroblast movement and fixed TGF-β1 fibroblast proliferation threshold at day 300 PI. p < 0.01

Parameter	Description	PRCC	p value
Fibroblasts within the granuloma
γ7	Threshold for TNFα induced apoptosis	0.09	7.07*10−4
μ1	Fraction of grid compartments with a macrophage	0.07	9.85*10−3
μ11	TGF-β1 synthesis by macrophage	−0.55	1.57*10−116
μ17	Fraction of inactive TGF-β1 activated by a mac	−0.12	6.82*10−6
μ18	Amount of TGF-β1 that inhibits macrophages	−0.07	7.44*10−3
ζ7	Bound molecules of IL10 that inhibits fibroblast proliferation	0.42	5.33*10−11
ζ8	TGF-β1 myofibroblast differentiation threshold	0.17	5.74*10−6
ζ11	TNFα fibroblast proliferation threshold	0.12	8.50*10−12
ζ15	Fibroblast sensitivity to TGF-β1	0.11	7.90*10−3
ω3	Degradation rate of αSMA	0.07	3.73*10−5
Fibroblasts on the periphery of the granuloma
γ7	Threshold for TNFα induced apoptosis	0.10	6.93*10−5
μ11	TGF-β1 synthesis by macrophage	−0.38	6.15*10−52
μ17	Fraction of inactive TGF-β1 activated by a mac	−0.13	1.04*10−6
μ19	Fraction of active TGF-β1 in a compartment bound by a mac	0.28	4.57*10−27
ζ7	Bound molecules of IL10 that inhibits fibroblast proliferation	0.19	1.33*10−13
ζ11	TNFα fibroblast proliferation threshold	−0.28	1.70*10−27
ζ16	Probability of a fibroblast differentiating into a myofibroblast	−0.08	3.47*10−3
ζ15	Fibroblast sensitivity to TGF-β1	0.07	7.24*10−3

Simulated fibrotic granulomas have a high bacterial burden

Fibrotic granulomas that were simulated using GranSim exhibited both peripheral and central fibrosis. Simulated granulomas typically have high bacterial numbers (data not shown). Centrally fibrotic NHP granulomas are more commonly seen following antibiotic treatment and are associated with sterilization (31). Centrally fibrotic granulomas simulated using GranSim differ from those seen in NHPs, as the simulations tend to have much higher bacterial numbers, whereas in NHP they are often associated with bacterial clearance (Figure 11) (31). As shown in Figure 10B, even granulomas with centrally located fibrotic cells tend to have substantial caseous necrosis and bacterial load. Differences between GranSim and the NHP model (such as antibiotic use) may account for the high CFUs.

Figure 11. Snapshot of a simulated granuloma exhibiting central fibrosis at 150 days post infection.

Simulation of 2mm ×2mm lung tissue. A) Snapshot of simulated granuloma showing localization of all cell types. Myofibroblasts can be seen in the center of the lesion. Cells are represented by different colors as follows: resting macrophages are green, activated macrophages are blue, infected macrophages are orange, chronically infected macrophages are red, IFNγ producing T-cells are pink, cytotoxic T cells are violet, regulatory T cells are cyan, fibroblasts are maroon, and myofibroblasts are gold. B) Snapshot of simulated granuloma displaying only fibroblasts, myofibroblasts, and caseum. Caseum is represented in these images as brown compartments. Cytokine distributions not shown.

Discussion

In this work we sought to construct a hybrid multi-scale computation model of fibrotic granuloma formation in order to identify mechanisms driving the formation of Mtb-associated fibrosis. By incorporating cellular agent and molecular signals into GranSim, an existing model of TB lung granuloma formation, we were able to recapitulate the morphology of NHP fibrotic granulomas (Figure 1). We combined simulations and statistical analysis to identify mechanisms driving the formation of peripheral versus central granuloma-associated fibrosis. We first study mechanisms associated with total cell populations from the granuloma and found that both fibroblast and myofibroblast cell numbers at day 400 PI positively correlated with the amount TGF-β1 activated by a macrophage in a given compartment. This result indicates that the prevalence of fibroblasts and myofibroblasts in a granuloma is sensitive to the amount of active TGF-β1 available to them. These results also indicate that total amount of active TGF-β1 in simulated granulomas does not explain the development of either central or peripheral fibrosis. These data are consistent with NHP data showing high concentrations of TGF-β1 throughout both fibrotic and non-fibrotic granulomas (15). Concentrations of active TGF-β1 in specific areas of a granuloma may be key to whether a given cell will proliferate and/or differentiate. The overall availability of active TGF-β1 in a granuloma does not necessarily influence the number of fibrotic cells, nor does it enable us to predict whether a granuloma will become fibrotic; however, the concentration of active TGF-β1 in the vicinity of fibroblasts may be a driving factor for why some granulomas become fibrotic. Together these observations indicated that total TGF-β1 levels in a granuloma are a necessary, but not sufficient, condition for inducing fibrotic outcomes, and that additional mechanisms are responsible for the differences in granuloma morphology.

We also observed from our total cell population studies that the probability that a fibroblast migration is important for the development of fibrotic granulomas. One possible explanation for this is that fibroblasts are very sensitive to local cytokine milieu. Movement enables them to sample many different cytokine environments. The more a fibroblast is able to move the better chance it has of encountering a cytokine environment that is permissive to proliferation. Fibroblast migration in GranSim is probabilistic, chemotactic, and spatially constrained. More detailed studies of fibroblast behavior in the context of the granuloma will further elucidate specific mechanisms driving their migration. TGF-β1 and IL10 concentrations affect the ability of fibroblasts to proliferate and this result further emphasizes that local cytokine concentrations, and not the overall environment of the granuloma, have a major influence on fibroblast behavior. Inhibiting fibroblast movement further supported the hypothesis that specific local concentrations of TGF-β1, and not overall granuloma levels, were highly influential in dictating fibroblast proliferation and differentiation.

These results collectively provide insights into what drives fibrotic granuloma formation as they indicate that reduced granuloma scale outputs (such as overall TGF-β1 levels) alone are not sufficient for understanding the behavior of fibroblasts and myofibroblasts in the context of the granuloma. Our computational model provides us with the ability to further elucidate what drives formation of fibrotic granulomas, and more specifically what drives peripheral versus central granuloma associated fibrosis, by allowing us to track subpopulations of cells. We independently characterized mechanisms driving fibroblast numbers within a granuloma versus those on the periphery of a granuloma. We found that central and peripheral fibroblasts numbers are correlated to different mechanisms, further indicating that local conditions within granulomas have a strong influence on fibroblast behavior. It may be the case that the heterogeneous granuloma environment is key to both whether and where fibrosis occurs.

We found that fibrotic granulomas simulated using GranSim are associated with high bacterial burden. This may be due in part to a lack of antibiotic treatment in our simulations. Fibrotic NHP granulomas, where antibiotics were used, showed lower bacterial burden than those where antibiotics were not used(22). Centrally fibrotic granulomas have been found more commonly following antibiotic treatment, suggesting that antibiotic treatment contributes to the formation of central fibrosis. Centrally fibrotic granulomas simulated herein did not include any antibiotic dynamics, which may explain this difference between simulated and NHP granulomas. Future studies combining antibiotic dynamics incorporated into GranSim (88) with fibrotic dynamics described here, will be poised to address this possibility. It is also plausible that GranSim, in its current version, lacks an important biological feature such as epithelial cells, additional tissue mediators, or mechanical stimuli, making it difficult to simultaneously recapitulate all forms of fibrosis while simultaneously regulating bacterial levels. Our model cannot capture every aspect of this process but this is a good first order start. Future studies will address these questions.

Further characterization of the role of local cytokine concentrations within fibrotic granulomas will require quantifiable spatial outputs. Computational histology combining simulation output with graphical information systems could provide valuable insight into the spatial distribution of cells and cytokines in granulomas that become peripherally or centrally fibrotic (89). Due to the variability of localized cytokine concentrations, these outputs will need to be tracked over time and will require the use of a computational model like GranSim, and in conjunction with computational geometry. The addition of mechanical mechanisms such as the structural properties of collagen and enzymes that remodel collagen architecture would improve our ability to characterize fibrotic granulomas. Understanding the complex structure and regulation of granulomas is essential for developing treatments that promote better drug access and immune cells to kill persistent bacteria, while maintaining the integrity of surrounding tissue. Fibrotic granulomas can be both beneficial and detrimental to the host. Understanding the mechanisms driving the development of fibrotic granulomas, and specifically of the different fibrotic phenotypes seen in the NHP model of TB is essential to better understanding pathology associated with TB. Promoting mechanisms that protect the host while simultaneously inhibiting mechanisms that can be detrimental will allow us to improve therapeutic treatment and patient outcomes.

Highlights.

• We construct a hybrid multi-scale model of fibrotic granuloma formation in the lung

• We predict local cytokine concentration gradients drive fibrotic granuloma outcomes

• We identify differences between centrally vs. peripherally fibrotic granulomas

• We elucidate a role for fibroblast movement in driving fibrotic granuloma formation

• We propose computational histology to improve understanding of granuloma formation

Appendix

Figure A1. Snapshots of numerous simulated granulomas at day 150 PI.

Shown is simulation of 2mm × 2mm lung tissue. Cells are represented by different colors: resting macrophages are green, activated macrophages are blue, infected macrophages are orange, chronically infected macrophages are red, IFNγ producing T-cells are pink, cytotoxic T cells are violet, regulatory T cells are cyan, fibroblasts are maroon, and myofibroblasts are gold. Caseum is represented in these images as brown compartments. Cytokine distributions for active TGF-β1 shown.

Table A1.

Parameters used for wide parameter sweep

Symbol	Parameter name	Value or range	Units
Mtb parameters
α1	Growth rate intracellular Mtb	1.003	cells
α2	Growth rate extracellular Mtb	1.001	cells
α3	Death rate of extracellular Mtb in caseum	1.5	cells
Core model parameters
γ1	Diffusion time step	60	seconds
γ2	Molecular time step	6	seconds
γ3	Diffusion smoother time step	1.2	seconds
γ4	Number of smoother steps	0	n/a
γ5	Number of host cells causing caseation	10	n/a
γ6	Time to heal caseation	[1642, 2462]	days
γ7	Threshold for TNFα induced apoptosis	[1393, 2089]	molecules
γ8	Rate of TNFα induced apoptosis	[1.17e–6, 1.76e–6]	1/seconds
γ9	Minimum number chemokine molecules	[0.514, 0.77]	molecules
γ10	Saturating number of chemokine molecules	[374, 562]	molecules
γ11	Diffusivity of TNFα	5.2e–8	cm2/s
γ12	Diffusivity of IL10	5.2e–8	cm2/s
γ13	Diffusivity of active TGF-β1	5.2e–8	cm2/s
γ14	Diffusivity of chemokines	5.2e–8	cm2/s
γ15	Degradation rate of TNFα	0.00158	molecules/molecular time step
γ16	Degradation rate of IL10	0.00048	molecules/molecular time step
γ17	Degradation rate of inactive TGF-β1	[9.28e-6, 1.39e–5]	molecules/molecular time step
γ18	Degradation rate of active TGF-β1	[8.0e-4, 0.0012]	molecules/molecular time step
Macrophage parameters
μ1	Fraction of grid compartments with a macrophage	[0.024, 0.036]	n/a
μ2	Number of time steps before a resting macrophage can move	2	n/a
μ3	Number of time steps before an activated macrophage can move	16	n/a
μ4	Number of time steps before an infected macrophage can move	[112, 168]	n/a
μ5	Synthesis rate of TNFα	1.5	molecules/diffusion time step
μ6	Synthesis rate of CCL2	6	molecules/diffusion time step
μ7	Synthesis rate of CCL5	6	molecules/diffusion time step
μ8	Synthesis rate of CCL9	12	molecules/diffusion time step
μ9	Synthesis rate of IL10 by an activated macrophage	0.3	molecules/diffusion time step
μ10	Synthesis rate of IL10 by and infected macrophage	0.02	molecules/diffusion time step
μ11	Synthesis rate of Inactive TGF-β1 by macrophages	[0.0001, 0.01]	molecules/diffusion time step
μ12	Number of bacteria a resting macrophage can phagocytose	1	n/a
μ13	Probability of resting macrophage killing bacteria	[0.23, 0.35]	n/a
μ14	Threshold for intracellular bacteria causing chronically infected macrophages	[8,12]	bacteria
μ15	Threshold for intracellular bacteria causing macrophage to burst	[13, 20]	bacteria
μ16	Number of bacteria an activated macrophage can phagocytose	[4, 6]	n/a
μ17	Fraction of inactive TGF-β1 activated by a mac	[1e–6, 1]	n/a
μ18	Amount of TGF-β1 that inhibits macrophages	[1e–6, 1]	molecules
μ19	Fraction of active TGF-β1 in a compartment bound by a mac	[1e–6, 1]	n/a
μ20	Probability of an activated macrophage healing a caseated compartment in its Moore neighborhood	[0.0128, 0.0129]	n/a
T cell parameters
τ1	Probability of a T cell moving to the same compartment as a macrophage	[0.05, 0.08]	n/a
τ2	Probability of a T cell moving to the same compartment as a T cell	0.08	n/a
τ3	Synthesis rate of TNFα by IFNγ-producing T-cell	0.15	molecules/diffusion time step
τ4	IFNγ-producing T-cell probability of inducing Fas/FasL mediated apoptosis	[0.0152, 0.0228]	n/a
τ5	Probability of IFNγ-producing T-cell to secrete TNFα	[0.048, 0.072]	n/a
τ6	Probability of IFNγ-producing T-cell to secrete TNFα	[0.288, 0.432]	n/a
τ7	Synthesis rate of TNFα by cytotoxic T-cell	0.015	molecules/diffusion time step
τ8	Probability of a cytotoxic T-cell killing a macrophage	[0.012, 0.18]	n/a
τ9	Probability of a cytotoxic T-cell killing a macrophage and all associated Mtb	[0.61, 0.91]	n/a
τ10	Probability of cytotoxic T-cell to secrete TNFα	[0.056, 0.084]	n/a
τ11	Synthesis rate of IL10 by regulatory Tcell	0.739	molecules/diffusion time step
τ12	Synthesis rate of TGF-β1 by regulatory T cell	[0.0001, 0.01]	molecules/diffusion time step
τ13	Probability a regulatory T cell will deactivate an activated macrophage	[0.011, 0.016]	n/a
τ14	Bound TGF-β1 that inhibits T cells	[0.04, 0.2]	molecules
τ15	Fraction of active TGF-β1 in a compartment bound by a T cell	[1e–4, 0.2]	n/a
Fibroblast Parameters
ζ1	Maximum fibroblast age 28800 agent timesteps ζ2 Initial number of fibroblasts in a simulation	50	n/a
ζ3	Probability a fibroblast will move	[0.001, 0.5]	n/a
ζ4	Synthesis rate of TGF-β1 by a fibroblast	[0.001, 0.1]	molecules/diffusion time step
ζ5	Units of αSMA synthesized per TGF-β1 binding event	1e–10	n/a
ζ6	Time until a fibroblast can attempt to proliferate	[24, 48]	hours
ζ7	Bound molecules of IL10 that inhibits fibroblast proliferation/differentiation	[1e4, 2e4]	molecules
ζ8	TGF-β1 myofibroblast differentiation threshold	[2.0e–7, 8.0e-7]	molecules
ζ9	TGF-β1 fibroblast proliferation threshold	[2.0e–7, 8.0e-7]	molecules
ζ10	Minimum ratio of TGF-β1 to IL10 required for myofibroblast differentiation	[1e–11, 1e–9]	n/a
ζ11	TNFα fibroblast proliferation/differentiation threshold	[0.025, 0.5]	molecules
ζ12	Synthesis rate of Il10 by fibroblast	[3.48e–22, 3.48e–16]	molecules/molecular time step
ζ13	Binding rate of Il10 by fibroblast	[1e–12, 1e–8]	molecules/molecular time step
ζ14	Fibroblast sensitivity to Il10	[0.001, 10]	n/a
ζ15	Fibroblast sensitivity to TGF-β1	[0.000001, 0.1]	n/a
ζ16	Probability of a fibroblast differentiating into a myofibroblast	[0.1, 5.0]	n/a
Myofibroblast Parameters
ω1	Collagen synthesis rate	[1e–7, 1e–5]	molecules/agent time step
ω2	Probability of apoptosis	[0.002, 0.2]	n/a
ω3	αSMA degradation rate	[0.001, 10]	molecules/molecular time step
ω4	αSMA synthesis rate	[1e–10]	molecules/molecular time step
Recruitment Parameters
ρ1	Maximum macrophage recruitment probability	[0.112, 0.168]	n/a
ρ2	Maximum IFNγ-producing T cell recruitment probability	[0.112, 0.168]	n/a
ρ3	Maximum cytotoxic T cell recruitment probability	[0.079, 0.12]	n/a
ρ4	Maximum regulatory T cell recruitment probability	[0.0232, 0.0348]	n/a