Modeling Spatial Invasion of Ebola in West Africa

Abstract

The 2014–2015 Ebola Virus Disease (EVD) epidemic in West Africa was the largest ever recorded, representing a fundamental shift in Ebola epidemiology with unprecedented spatiotemporal complexity. To understand the spatiotemporal dynamics of EVD in West Africa, we developed spatial transmission models using a gravity-model framework at both the national and district-level scales, which we used to compare effectiveness of local interventions (e.g. local quarantine) and long-range interventions (e.g. border-closures). The country-level gravity model captures the epidemic data, including multiple waves of initial epidemic growth observed in Guinea. We found that local-transmission reductions were most effective in Liberia, while long-range transmission was dominant in Sierra Leone. Both models illustrated that interventions in one region result in an amplified protective effect on other regions by preventing spatial transmission. In the district-level model, interventions in the strongest of these amplifying regions reduced total cases in all three countries by over 20%, in spite of the region itself generating only ~ 0.1% of total cases. This model structure and associated intervention analysis provide information that can be used by public health policymakers to assist planning and response efforts for future epidemics.

1 Introduction

The outbreak of Ebola virus disease (EVD) in West Africa caused 28,646 cases and 11,323 deaths as of March 30, 2016 [1]. The 2014–2016 outbreak was of the EBOV (Zaire Ebola Virus) strain, the most fatal strain [2, 3]. The largest previous outbreaks of the EBOV strain occurred in the Democratic Republic of the Congo in 1976 and 1995, causing 318 and 315 cases respectively [4].

Clinical progression of EVD includes two broad stages of infection, often characterized as early and late [5]. In the first stage, approximately five to seven days, symptoms include fever, weakness, headache, muscle/joint pain, diarrhea, and nausea [5, 6]. In some patients, the disease progresses to a second stage, with symptoms including hemorrhaging, neurological symptoms, tachypnea, hiccups, and anuria [5, 7]. Mortality rates are higher among those exhibiting second-stage symptoms [5, 7]. EVD is transmitted through direct contact with an infected individual [8]. Transmission risk factors include contact with bodily fluids, close contact with a patient, needle reuse, and contact with cadavers, often prepared for burial by the family of the deceased [8–10].

This outbreak was primarily in the contiguous countries of Guinea, Sierra Leone, and Liberia, which experienced widespread and intense transmission [1, 11, 12]. Interventions included quarantine, case isolation, additional treatment centers, border closures, and lockdowns, restricting travel within a region (as in a military-enforced curfew) [13]. Public health authorities must allocate resources effectively, focusing personnel and funds to respond best to outbreaks. However, not all response measures are equally beneficial or cost-effective, and testing the relative benefits of each is often impossible or unethical. Modeling thus provides a valuable tool for comparing interventions and identifying areas where interventions are most effective. Modeling analyses can inform public health policy regarding ongoing and future outbreaks.

Dynamic spatial modeling has been proposed as a useful approach to understand the spread of EVD and evaluate response strategies’ benefits [14]. The recent outbreak has sparked an increase in EVD modeling [15–18]. The spread between contiguous countries in the outbreak highlights the spatial element to its proliferation [1]; however, as previous EVD outbreaks were more localized than the 2014–2015 epidemic [19], there is little historical data on the geospatial spread of Ebola. Mobility data, which may help inform spatial EVD modeling, is limited, although some studies have highlighted its usefulness and extrapolated based on mobility data from other regions [14, 20].

Several spatial EVD models have been developed to examine local spatial spread within Liberia [14, 21–23] and evaluate the potential risk of international spread using data such as airline traffic patterns [21, 24, 25]. For instance, Merler et al. [21] developed a model of Ebola within Liberia using an agent-based spatial model in which the country is represented by a grid with varying population densities. In addition, Santermans and coauthors demonstrated that the outbreak is heterogeneous, with transmission rates differing between locales [26]. This lends credence to the approach of modelling the outbreak as a set of connected local-level outbreaks, as opposed to one homogeneous outbreak.

In this study, we present spatial models of EVD transmission in West Africa, using a gravity model framework, which captures dynamics of local (within-region) and long-range (inter-region) transmission. Gravity models are used in many population-mobility applications, especially to relate spatial spread of a disease to regional population sizes and distances between population centers [27]. Gravity models have been applied to other diseases, including influenza in the US and cholera in Haiti [27, 28], and have been used to examine general mobility patterns in West Africa [14]. Other gravity models for the Ebola outbreak include models by Yang et al. and Backer et al. [23, 29]. Yang et al developed a model for the epidemic in Sierra Leone, using a Kalman filtering approach to fit an SEIR model with a gravity transmission term and varying local mobility rates [29]. Backer and Wallinga developed a district-level gravity-based analysis over all three countries by estimating an instantaneous reproduction number (R_i) for each district, at each time point, and using a gravity term to estimate spatial dispersion of infected individuals [23]. Instead of using a compartmental model, they took a phenomenological approach: the model directly calculates the number of cases observed, based on the previous data values and the estimated R_i.

Our models add to existing spatial models by examining spatially-targeted interventions in the affected countries. Our spatial model is built on a stage-structured compartmental model with funeral transmission (since funeral transmission played a significant role in the outbreak). In addition, we developed gravity models for all three countries at both the country and district levels. Between-country mobility is important in this epidemic because the borders between countries are porous; borders are drawn across community or tribal lines, resulting in frequent border-crossing to visit family, conduct trade, or settle disputes [30].

We demonstrate that the gravity modeling approach fits and forecasts case and death trends in each country, and describes transmission between countries. A district-level model based on the country level model parameters also captures the patterns of local geospatial spread of EVD, indicating that the gravity model framework alone is enough to replicate much of the local spatial heterogeneity. Using these model structures, we examined interventions at country and district scales, evaluating the relative success of intervention types as well as the most responsive regions.

2 Methods

2.1 Country-level Model Structure

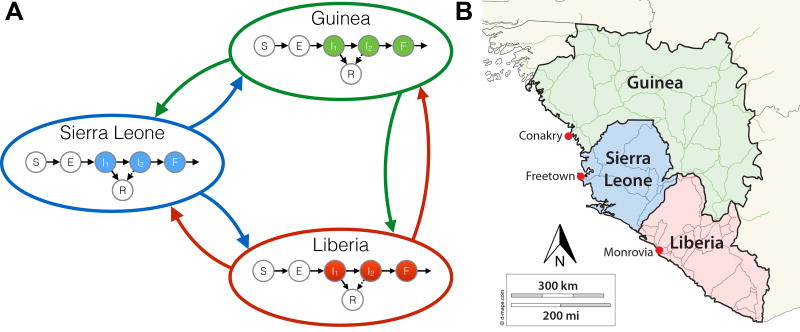
We developed a compartmental gravity model using ordinary differential equations to model spatiotemporal progression of EVD (Figure 1 and Eq (1)). Each country’s compartmental structure includes susceptible (S), latent (E), two-stage infection (I₁, I₂), funeral (F), recovered (R), and deceased (D) classes, based on previous compartmental models [31, 32]. Individuals in stage I₁ can recover or transition to I₂, where they may recover with lower probability or transition to F, based on clinical observations of symptom progression and mortality [7]. The latent period and two-stage infection are based on the clinical progression of EVD, wherein patients become contagious in I₁, with increasing contagiousness in I₂ [5, 8, 15, 32, 33]. Funerals play a role in transmission because of the high viral load of the deceased and frequent contact with susceptible persons due to cultural burial practices [34]. The precise relative magnitude of this contribution is unknown; previous models have shown that the relative contributions of each stage are unidentifiable from early data [32, 35]. Thus, patients in F were assumed to be as contagious as those in I₂.

Figure 1.

A diagram of the model structure (left panel) and a map of West Africa showing the locations of each capital used as a population center for each patch (right panel). In each country, the population is compartmentalized into the following categories: susceptible (S), exposed (E), infected in stage one (I₁), infected in stage two (I₂), died but not yet buried (F), and recovered (R). Transmission is possible from persons in compartments I₁, I₂, or F of any country, to persons in compartment S, either within the country or to the other countries.

The spatial component of the model is a three-patch gravity model. Each country is one patch, with a compartmental model within it and the capital as the population center, similar to previous gravity models, which used political capitals/large cities as centers [27, 28]. After EVD appeared in western Guinea, subsequent cases were in the capital, Conakry, suggesting that the capital acts as the central population hub. Similar progression occurred in each country: after EVD cases appeared in border regions, cases soon appeared in the capital [36].

The model equations are given by:

$${\dot{S}}_n=-({\lambda }_n+{\lambda }_m+{\lambda }_l)S_n$$

$${\dot{E}}_n=({\lambda }_n+{\lambda }_m+{\lambda }_l)S_n-\alpha E_n$$

$${\dot{I}}_{1n}=\alpha E_n-{\gamma }_n{I}_{1n}-r_{1,n}{I}_{1n}$$

$${\dot{I}}_{2n}={\gamma }_n{I}_{1n}-\delta I_{2n}-r_{2,n}{I}_{2n}$$

$${\dot{F}}_n=\delta I_{2n}-{\delta }_2{F}_n$$

$${\dot{R}}_n=r_{1,n}{I}_{1n}+r_{2,n}{I}_{2n}$$ (1)

$${\dot{IC}}_n=k_{\mathit{\text{norm}}}\alpha E_n$$

$${\dot{DC}}_n=k_{\mathit{\text{norm}}}\delta I_{2n}$$

$${\lambda }_n={\beta }_{1,n}{I}_{1n}+{\beta }_{2,n}{I}_{2n}+{\beta }_{F,n}{F}_n$$

$${\lambda }_m={\theta }_{n,m}({\beta }_{1,n}{I}_{1m}+{\beta }_{2,n}{I}_{2m}+{\beta }_{F,n}{F}_m)$$

$${\lambda }_l={\theta }_{n,l}({\beta }_{1,n}{I}_{1l}+{\beta }_{2,n}{I}_{2l}+{\beta }_{F,n}{F}_l)$$

where ${\theta }_{n,m}={\kappa }_n\frac{{\rho }_n{\rho }_m}{{(d_{n,m})}^{\iota }},{\theta }_{n,l}={\kappa }_n\frac{{\rho }_n{\rho }_l}{{(d_{n,l})}^{\iota }}$, and n indicates each patch (Guinea, Sierra Leone, Liberia), and m and l the other two patches (with m ≠ l ≠ n). The risk of new infections from within each patch was represented by the λ_n term for the “home” patch. The risk terms for EVD transmission from outside the patch, λ_m and λ_l, are weighted by θ, the gravity term. The gravity terms include the populations of each patch (ρ_n,ρ_m,ρ_l) and the distances between them (d_n,m,d_n,l). The force-of-infection for a patch is equal to the sum of local and long-range force-of-infection (λ_n + λ_m + λ_l). The overall mortality rate for each country is given by ${\mathrm{\Delta }}_n=\frac{{\gamma }_n}{{\gamma }_n+r_{1,n}}\frac{\delta }{\delta +r_{2,n}}$.

The distance exponent of the gravity term, ι, is fixed at two. A range of values for ι were tested, however we found that changes in ι were compensated by changes in the fitted value of κ. Thus, ι was fixed for clarity, based on values in previous gravity models [28].

There are separate κ for each country, so the rate of transmission into each country is different. This reflects the differing border porosities and rates of travel between countries.

Cumulative cases (IC_n) and deaths (DC_n) are given as the integral of the incidence of each (αE_n and δI_2n respectively), multiplied by k_norm, a correction factor for underreporting and the fraction of the population at risk, among other factors [32]. Cumulative local cases were measured by the number of infections in a patch due to local transmission. Cumulative long-range cases were measured by number of cases due to long-range transmission.

2.2 Data, Initial Conditions, and Simulation Setup

Case and death incidence in each country was collected from World Health Organization (WHO) situation reports on EVD from May 24 to October 31, 2014 [1]. The country-model simulations used data from May 24 through September 30 for fitting model parameters. Data from October was used for validation, to compare model projections to data unused in fitting. Road distance between centers was used for the gravity component [37]. We evaluated direct distance between capitals in the country-level model, yielding similar results. Initial conditions were determined from the initial data for cases and deaths, as well as the total populations of each region, as described in the Supplementary Information.

2.3 Parameter Values and Estimation Methods

Model parameters were determined from clinical literature and fitting to available data on cumulative cases and deaths, similarly to previous models [18, 32, 38]. In the country-level model, nine parameters were fitted to the data: transmission (β) and overall death (Δ) rates as well as three gravity-term constants, κ, were separately fitted for each country. The parameter (κ) adjusts the “gravity” terms to reflect the balance of local and long-range transmission in each country. Parameters, definitions, units, ranges, and sources are given in Supplementary Table S1.

In the country-level model, 500 sets of initial values for all parameters were selected with Latin Hypercube (LH) sampling from realistic ranges for parameters, determined from WHO, CDC, and literature data, given in Supp. Table S1 [5, 7, 16, 31, 32]. For each of the 500 parameter sets, only transmission rates, death rates, and κ were fitted by least-squares, using Nelder-Mead optimization in MATLAB [39]. All other parameters were held constant to the values from the LH sample. Plots display the best 95% of fits from the LH sample, which we denote as the LH-based confidence intervals.

2.4 Country-level Model Intervention Simulations

Interventions were compared by the number of cumulative cases the model forecasted on October 31, 2014, for different levels of local and long-range intervention. Reduction of local transmission represents interventions that limit contact of an EVD patient with others in his or her home country, including quarantine, isolation, hospitalization, and local lockdowns. Reduction of long-range transmission represents border closures, large-scale lockdowns, or other intervention measures that reduce the transmission between countries.

In the country-level model, interventions were simulated by reducing transmission parameters for either local or long-range transmission. Local transmission reductions in country n were simulated by reducing λ_n, the rate of local infections in that country, in increments of one percent of the original value. This reduction was held constant for the entire duration of the simulation: we tested a constant n% reduction in transmission rate for the duration of the simulation, for n = 1, 2, …, 100. Long-range transmission reductions were simulated by reducing λ_m and λ_l, the rates of infections from outside country n, in one-percent increments. Similarly, the level of reduction was held constant for the entire duration of the simulation.

2.5 District-level spatial model

To explore how the country-level parameters might translate to and perhaps explain patterns at the local level, we also developed a more detailed gravity model of West Africa incorporating the 14 districts/areas of Sierra Leone, 15 counties of Liberia, and 34 prefectures of Guinea. This model is structured in a similar way to the country-level model: a compartmental model in each administrative unit, linked to all other patches by gravity terms. The force-of-infection term for patch n consists of local force-of-infection (denoted λ_n in the country-level model) and long-range force-of-infection, defined as follows:

$${\lambda }_m=\sum _m{\theta }_{n,m}({\beta }_{1,n}{I}_{1m}+{\beta }_{2,n}{I}_{2m}+{\beta }_{F,n}{F}_m)$$ (2)

i.e., the sum of long-range force-of-infection from all other patches m ≠ n. The district model was simulated from March 31, 2014 to January 31, 2015. The model was compared to data on the outbreak’s local geospatial progression from each district, using incidence of cases and deaths from WHO updates and the UN OCHA database [36, 40]. The complete district-level model equations and details are given in the Supplementary Information.

In this preliminary exploration of a district-level model, best-fit parameters from the country-level model were used for all parameters except k_norm. A different k_norm was fitted for each district to reflect differing at-risk populations and reporting rates. Since fitting 63 parameters is highly complex, slow, and possibly unidentifiable, k_norm parameters were calculated according to final size, then adjusted to generate curves matching the progression of the outbreak, both overall and in each district. While all other initial conditions were determined from the data as described above, in Conakry, Guinea, the initial conditions were also adjusted independently from k_norm, reflecting possible reporting rate differences between initial situation reports and subsequent data. This highly simplified fitting procedure allows us to generate a parsimonious but more granular spatial model, and test how well the country-level parameters and the gravity framework alone do in explaining local spatial patterns.

2.6 District-level Model Interventions

In the district-level model, in order to test the strength of one patch’s impact on the surrounding patches’ outbreaks, the outbreak in that patch is eliminated in the model by reducing the transmission rates in and out of that patch to 0, for the duration of the outbreak. This allows us to measure the overall impact of that patch’s outbreak on the rest of the dynamics in the model. We felt that, while full elimination is an unrealistic best-case scenario, it sharpens the signal to illustrate the maximum possible impact of that region’s outbreak on the model as a whole.

The effectiveness of this intervention in one district was measured by calculating the cumulative number of cases reduced in all other districts. The percent reduction from intervention in a district and percent reduction relative to size of the original outbreak in that district were calculated.

To quantify the relative impact of intervention as a function of local outbreak size, the Intervention-Amplifying Region (IAR) score was defined as a measure of the impact of intervention in one district on the outbreaks in other districts (the intervention-amplification of the region in which intervention occurred). The IAR score was determined as follows:

$$\text{IAR Score}=\text{ln}\frac{\%\text{ Cases reduced in other districts}}{\%\text{ of total outbreak occurring in intervention district}}$$ (3)

Note that for districts with less than 0.05% of the outbreak’s cases, the IAR score was defined to be 0.

2.7 Stochastic District-level Model

Many of the epidemics at the district level were relatively small in scale, and much of the district scale data involves new introductions and early transmission. These both suggest that stochastic effects may be important. To evaluate this possibility, we also simulated the district-level model using Tau leaping [41].

Implementing the stochastic model necessitated some additional consideration of the size of the population at risk in the model. There was significant uncertainty in the West Africa epidemic both about the fraction of cases which were reported in the data (reporting rate), as well as about the true population size at risk for transmission [32]. As discussed above, in the deterministic model, k_norm represents both of these factors (i.e. k_norm is the product of the reporting rate times the fraction of the population at risk). This is because in the deterministic model the overall population size can be scaled arbitrarily, as long as k_norm and the transmission parameters are also rescaled to compensate (e.g., if we increase the total population size by rescaling the model variables, we can then decrease k_norm and the β parameters, to yield identical reported incidence trajectories). However, for the stochastic model, different choices for the reporting rate and underlying at-risk population size will affect whether we are in the stochastic versus deterministic regime for the model (since a small number of reported cases could represent a large or small number of actual cases in the model, depending on the reporting rate).

We tested a range of possible values that were consistent with the fitted values of k_norm in the deterministic model. For stochastic simulation of a given patch n, let r be the reporting rate, and f the fraction of the population at risk, so that rf = k_norm and the population at risk is fρ_n. We tested reporting rate values r = 1, $\frac{1}{2},\frac{1}{5},\frac{1}{10}$, 3k_norm, 2k_norm, 1.5k_norm, k_norm (corresponding to population-at-risk sizes of fρ_n = k_normρ_n, 2k_normρ_n, 5k_normρ_n, 10k_normρ_n, $\frac{1}{3}{\rho }_n,\frac{1}{2}{\rho }_n,\frac{2}{3}{\rho }_n$, and ρ_n). These values go from perfect reporting (r = 1) with a very small population at risk, to very poor reporting (r = k_norm) with the entire population at risk, as well as a range of more realistic scenarios in between these two extremes.

3 Results

3.1 Country-level Model Fits and Predictions

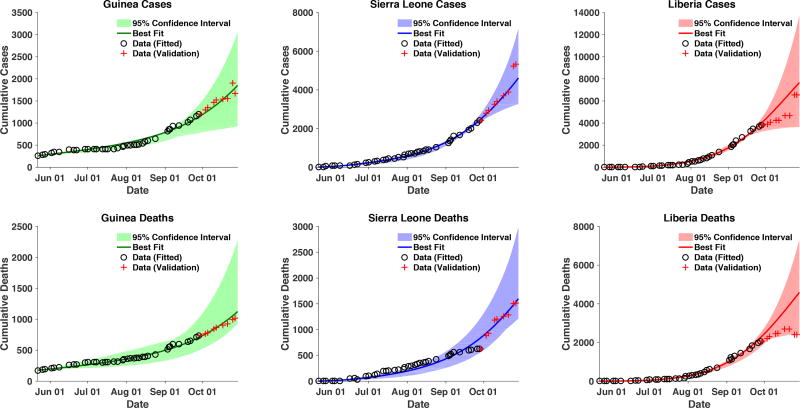
The best-fit accurately fit and forecasted the outbreak data and overall trends for each country (Figure 2). The best-fit model forecast of cases on October 29, 2014, was 14,070; the WHO case data on that date was 13,540 [42]. It is important to note that the data for Liberia and Sierra Leone show some sudden jumps in cumulative cases (both up and downward) which are likely due to reporting changes/errors and reclassification of cases.

Figure 2.

Cumulative cases and deaths for each country. Data depicted with black circles (from May 24, 2014 to September 30, 2014) was used for model fitting to the data. Data depicted with red crosses (from October 1 to October 29) is displayed for validation of the model fits. The model projections are from May 24 to October 31, 2014. The black circles represent the data used for fitting; the red crosses represent the data used for validation. The line represents the model’s overall best fit; the shaded regions represent the 95% likelihood LH-based confidence intervals.

3.2 Local versus Long-Range Transmission

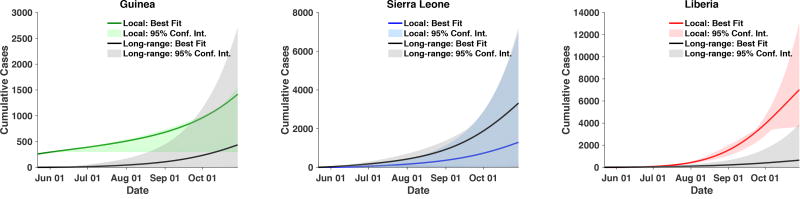
Cumulative cases in each country due to local and long-range transmission are shown in Figure 3. Liberia had more local than long-range transmission. Early on, Guinea had more local transmission, due to initial local cases. As the epidemic progressed, the transmission ranges overlapped, although the best-fit trajectory for long-range transmission remained smaller than the local-transmission contribution. In Sierra Leone, the best-fit trajectory of long-range transmission was more significant than local transmission, but forecasted ranges were similar.

Figure 3.

Cases from local transmission and long-range transmission. Local transmission, from transmission within the country, is depicted in the color of the country in Figure 1. Long-range transmission, or cases from outside the country, is depicted in gray. Model projections are from May 24 to October 31. Shaded ranges represent the 95% LH-based confidence bounds.

3.3 Intervention Simulations: Country-Level

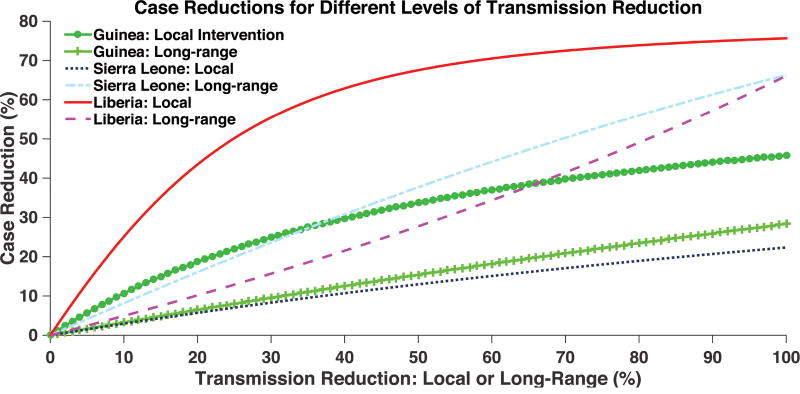
According to our intervention simulations (Figure 4), reduction in local transmission, from interventions such as isolation or improved case-finding and Ebola treatment unit (ETU) capacity, is most effective in Liberia. In the model, eliminating local transmission in Liberia reduced the outbreak by up to 11,000 cases in all countries by October 31, 2014, a 76% reduction. Reduction of long-range transmission was most effective in Sierra Leone. Eliminating long-range transmission into Sierra Leone reduced the outbreak by up to 9,600 cases in all countries by October 31, a 66% reduction. The LH-based confidence bounds for the intervention simulations are given in Supplementary Figure S1.

Figure 4.

Cases reduced by various interventions at the country-level. Transmission reduction represents reduction of local or long-range transmission in increments of one percent. Case reduction is measured by comparing total cases in all 3 countries in the presence of intervention to total cases in the absence of intervention, on October 31, 2014.

3.4 Deterministic District-level Model

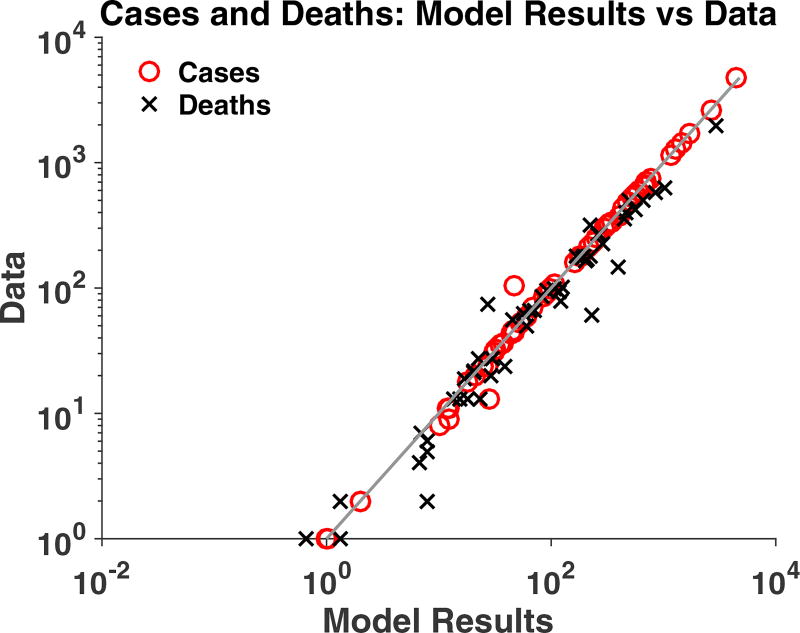
Translation of the country level model to a deterministic district-level model was able to replicate the general patterns of outbreak data for cases and deaths in each district. The model captured the final size of the outbreaks in each district including final total deaths, which were not fitted in any patches, with an R² value of 0.96 (Figure 5) as well as matching the progression of the outbreak (Figure 6). The time-course plots of all 63 district-level fits are included in the Supplementary Information, as is a scatter plot of all data vs model values (R² = 0.83).

Figure 5.

The final size of the outbreak in each of the 63 patches: comparison of deterministic model values (x axis) and data (y axis). R-squared value of 0.9635.

Figure 6.

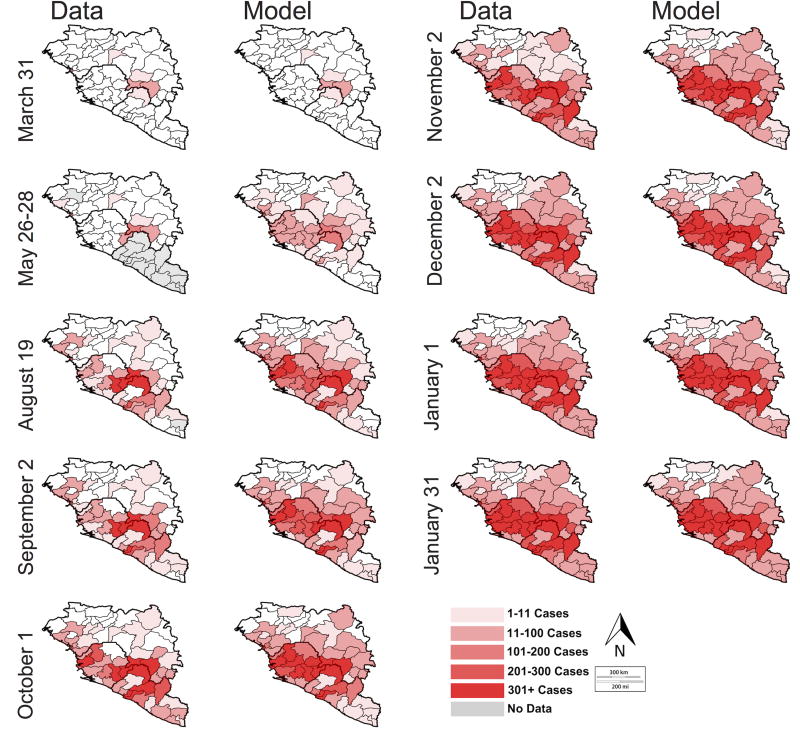
Map of geospatial spread of Ebola as determined by the deterministic district model (right) and WHO data (left). The shaded regions are the regions with cases of EVD; the intensity represents intensity of transmission (number of cases). Gray regions represent districts for which no data is reported on the given date. On the May 26/28 figure, May 26 is used for Sierra Leone and May 28 is used for Guinea.

The district-level model captured the trend of spread of EVD through second-level administrative units (Figure 6). While overall patterns at the district level are captured and show the correct ordering, the actual speed of disease spread in the model was faster than in the data in many districts (Figure A3), likely due to a combination of the stochasticity of introductions, local variations in transmission parameters, and reporting delays. The district-level model was able to forecast, to some extent, local spread of EVD, matching data on spatial progression of EVD to different locales as the outbreak intensified (Figure 6). An animation of the district-level simulation is given in the Web Supplement (Video S1).

3.5 Intervention Simulations: District-Level

Intervention analysis identified regions that seemed to provide significant reductions in cases (Figure 7). Overall, the most successful regions for intervention were Conakry, Coyah, and Dubreka, Guinea, and Lofa, and Monrovia/Montserrado, Liberia.

Figure 7.

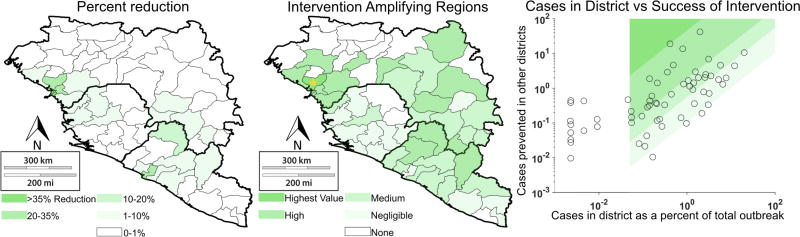
Cases reduced by various interventions at the district-level. Transmission reduction consists of elimination of outbreak in one district. Case reduction is measured by (a) percent reduction of outbreak in other 62 patches and (b) percent reduction in other 62 patches relative to size of the outbreak in the intervention site (Intervention-Amplifying Region score). Panel (c) displays the IAR scores on a scatter plot, with the associated quartiles depicted by the shaded regions. The blank region represents the patches with insufficient cases to be considered for intervention.

To evaluate whether intervention effects were disproportionately significant compared to cases within the target region, we defined the Intervention-Amplifying Region (IAR) level by the ratio of cases prevented in other patches to cases within the patch, for regions with more than 0.05% of the epidemic’s cases. Dubreka, Coyah, and Conakry were the most effective IARs according to the model (Figure 7).

3.6 Stochastic District-level Model

The stochastic district-level model simulations are shown in Figure A3 and in the Supplementary file containing Figures S1–S8. When the population size was large (small reporting rate), the stochastic version of the model largely recaptured the same trajectories as the deterministic version. In this case, each reported case actually represents a large number of unobserved cases, so that the underlying model was largely in the deterministic regime, even for fairly small apparent outbreaks. However, when we assumed a higher reporting rate (i.e. so that the number of observed cases was closer to the number of actual cases), a wide range of trajectories were observed, with the cloud of model realizations more fully capturing the temporal patterns in the data.

4 Discussion

Our results demonstrate that outbreak dynamics in all three countries can be accurately captured using a gravity-model approach. Moreover, country-level model forecasts successfully predicted cumulative cases and deaths one month ahead (Figure 3). The models were able to simultaneously capture the dynamic interactions within and between each region at both country and district levels.

4.1 Local and long-range intervention simulations

In the country-level model, we compared the effects of local and long-range interventions in each country. Local interventions include more strict quarantine and isolation procedures, increased case-finding and ETU capacity, safer burial practices, and other interventions that reduce contact of susceptible persons with infected persons in the local community, as well as behavioral changes that reduce local transmission. Neither local or long-range dominated as the more effective approach in all countries—rather both approaches were effective to varying degrees in each location, largely consistent with the relative contribution of local vs. long-range transmission in each country. The model indicated that the most effective approach was local intervention in Liberia, both in reducing the outbreak in Liberia and mitigating the whole epidemic. Indeed, Liberia’s outbreak had the fastest initial growth rate, it was the first to turn over and end after intervention efforts intensified [1], perhaps illustrating the effectiveness of intervention efforts. Our results suggest that Liberian interventions may have had significant indirect protective effects on the epidemic dynamics in Guinea and Sierra Leone as well.

The most effective long-range transmission reduction was in Sierra Leone, with 66% case reduction across all countries when long-range transmission was completely eliminated. This likely reflects the porous borders of Sierra Leone. Based on the district-level intervention analysis, no single district in Sierra Leone acts as a source of long-range transmission to other locales; rather, all districts play some combined role. Thus, the country-level impact of long-range transmission is possibly a summative combination of two factors across all districts: long-range transmission into Sierra Leone and early introduction of cases from Sierra Leone into Liberia.

These results suggest a sort of “spatial herd protection,” wherein interventions in one region benefit other regions as well, by reducing the spatial transmission. Thus, by intervening sufficiently in regions with strong indirect spatial protection effects, the overall epidemic can be curtailed.

4.2 Intervention-amplifying regions: outsized impact on the outbreak dynamics

To quantify these indirect spatial protection effects, in the district level model we used a score based on the ratio of cases prevented in other regions to the size of the outbreak in the intervention region. In districts high in this score, intervention produced outsized reductions in the overall outbreak beyond the intervention region itself. These are denoted Intervention-Amplifying Regions (IARs), the most significant of which include Boffa, Conakry, Coyah, and Dubreka in Guinea (Figure 7). For instance, Dubreka made up only 0.13% of the outbreak but intervention in Dubreka alone reduced the size of the outbreak in all regions by 21%, drastically higher than its case contribution would suggest. Coyah and Dubreka were the most dramatic IARs because they had relatively small numbers of cases. Their proximity to Conakry (the capital of Guinea), which had a large number of cases and also functioned as an IAR, suggests that Coyah and Dubreka could have influenced outbreak dynamics in Conakry.

Indeed, the importance of the capitals can also be seen in examining the overall effectiveness of intervention by district (i.e. not weighted by the outbreak size in the intervention site itself), where the capitals of Montserrado, Liberia and Conakry, Guinea were highly effective intervention sites. Their large population sizes likely make them important in dictating the dynamics of the outbreak in surrounding regions. Similarly, Dubreka and Coyah, near Conakry, were also effective intervention sites overall, in addition to being IARs.

The outsize importance of IAR districts in the dynamics of the outbreak makes them a possible target for increased intervention during future outbreaks in West Africa. As discussed in the Limitations (Section 4.5), even where the model results are not well-defined enough to draw clear conclusions, the IAR analysis provides an interesting viewpoint on the importance of spatial transmission patterns in exacerbating the outbreak.

4.3 Unique case curve in Guinea

Several papers have noted that Guinea’s peculiar outbreak curve is difficult to fit using simple models, due to the plateau in cumulative incidence between growth periods [18, 25, 43]. However, including spatial interaction between countries allowed the model to capture Guinea’s outbreak dynamics (Figure 2). In particular, Guinea’s time series shows an early inflection point: the curve for cases is concave-down at the beginning of the time-course, but becomes concave-up around July 1. The model successfully captures that inflection point, both the slower initial growth and the later, more rapid growth.

This suggests that spatial interactions, such as local die-outs of EVD followed by long-range reintroductions, may be responsible for the unusual incidence patterns in Guinea. The country-level model’s ability to capture the singular epidemic progression in Guinea, due to its spatial transmission component, demonstrates that long-range dynamics do not just affect introduction, but also later stages of the outbreak.

4.4 Deterministic and stochastic district-level models

The district-level model, which separates the affected countries into 63 patches based on secondary administrative units, was successful in capturing the overall dynamics of spatial transmission. The deterministic model captured the broad patterns of spread of EVD from the initial sites of the outbreak to other locales in the region in an order and overall magnitude similar to the actual progression of the epidemic. This suggests that the district-level model captures the underlying transmission patterns that led to spread of EVD between different locales in the affected districts (Figure 6). These results are perhaps surprising given that the district-level model uses the same transmission parameters for all patches within the same country: this suggests that even though there are likely to be significant local heterogeneities from patch to patch [44], much of the spatial variation can be captured using the relatively simple framework afforded by the gravity model even if the local parameters are unknown.

However, while the deterministic district level model was able to reproduce overall patterns and the final magnitude of cases and deaths in the districts, it was unable to capture the shape of the time series for a number of districts, often increasing earlier than the data. Since introduction and early transmission of disease is often highly stochastic, we tested a stochastic version of the district model, assuming several different possible values for the population-at-risk and reporting rates (Figure A3 and Supplementary files). The stochastic model improved the district-level model fits significantly, better reflecting more stochastic timing of early introduction, and better capturing early transmission and districts with fewer cases.

These results show that stochasticity can explain much of the discrepancy between the deterministic district-level model and the data, though some of the remaining differences may also be due to issues with surveillance. In many districts, one can see patterns where the number of cumulative cases suddenly jumps up or down, which are likely due to reporting catchup or reclassification of cases. Related to this, as surveillance systems ramped up in different districts, this would result in rapid increases in numbers of reported cases, so that improvement in surveillance may be difficult to distinguish from the onset of an outbreak. The combined result of these issues is that it the local epidemics may appear to begin or ramp up later than actually occurred, which may also play a role in why the deterministic model often shows earlier epidemics and smoother increases in cases than are observed in the actual data.

Overall, a model that incorporates local heterogeneities often requires a large amount of case data at the local scale [45]. The deterministic and stochastic district-level gravity models used here provided a reasonable approximation of the dynamics of the outbreak, based on population sizes, road travelling distances, and relatively early surveillance data. While they cannot always precisely fit each district, they were able to capture local differences in transmission with relatively little computational complexity. Thus, such models can be useful for early-outbreak forecasting by providing an indication of the areas at greatest risk for Ebola cases, in order to guide resources and aid to those locations.

4.5 Simplifying Assumptions and Limitations

There were several limitations to this work. Our models focus on the early-to-middle time course of proliferation throughout West Africa: interactions between regions, which led to the spatial spread of Ebola. This portion of the dynamics inclused features of particular interest, such as the early turnover and re-ignition of the epidemic in Guinea, which non-spatial compartmental models were previously unable to explain. However, further work to consider the late dynamics after intervention would be of interest—such work would also need to consider the significant changes in parameters over time due to the massive scale up of intervention efforts and ongoing behavior change [32, 46–48].

In this model, we used a gravity model framework, with cross-transmission terms between regions. Alternative modeling frameworks could also be used, such as the radiation mobility model [49], or linear migration rates between patches (even if still based on the gravity framework). Linear migration terms would capture the physical movement of individuals from place to place, and allow us to examine the potential for cases being reported in another district if they become ill while traveling. For example, West Area Rural, Sierra Leone has a much smaller population than West Area Urban, but both had significant numbers of cases (~ 1500 and ~ 3000), respectively. Since the two regions are contiguous, it is reasonable to believe that there could be cross-reporting from Urban into Rural. Unfortunately, the extent of this cross-reporting is difficult to quantify. Additionally, contact patterns with visitors likely differ from those with household and regular local contacts, so that accounting for physical migration in the model might require additional parameters to account for differences in transmission for visitors versus locals. Finally, as discussed in the Methods, there is significant uncertainty regarding the fraction of the population at risk and reporting rates in each district—in the deterministic model, these two parameters are combined into a single parameter, k_norm. Linear migration rates would necessitate making more detailed assumptions about the size of the population at risk, so that the different regional populations can be coupled. Given that short trips across borders are very common in the region [30], cross-transmission terms provide a simple way to capture the idea of shorter trips where individuals are primarily associated with a ‘home’ patch, but either make trips or interact with visitors from other patches (although as noted, this framework also assumes that all reported cases for a patch are associated with that patch). However, future modeling using more mechanistic movement terms could potentially be highly useful—particularly if more detailed movement data were to be made available, e.g. cell phone data.

In addition, the data also contains some significant discrepancies. The data for Sierra Leone at the end of October contains an unexplained spike, corresponding to a drop in early November: Sierra Leone’s cumulative case count spikes by 1,339 cases between October 25 and 29, 2014. Likewise, Liberia’s cumulative cases spike by 1870 between the two dates. Then, between October 31 and November 5, the cumulative case count drops by 579 cases. Other similar examples can be found in both the country and district level data sets. These examples illustrate the significant practical and logistical challenges in collecting epidemic surveillance data for the West Africa outbreak, and the discrepancies likely reflect issues such as reporting changes and reclassification.

4.6 Future research directions

While the gravity model captures epidemic dynamics without incorporating explicit movement patterns, further mobility data (e.g. from cell phone carriers) combined with explicit movement terms in the model could elucidate dominant movement patterns in West Africa. This data could provide a validation of the gravity model’s success, if the gravity model accounts for these patterns.

The model does not account for a detailed population structure beyond a spatial one, such as organization of individuals into households, villages, or other more detailed networks. The gravity model could be applied with a structured-population (network) model, such as Kiskowski’s model [50]. This model has been applied to study community-based interventions [51]; it could provide a granular simulation of Ebola dynamics, with possible insights into community and differing levels of local intervention.

During the course of the outbreak, parameters such as reporting rates, ETU availability, and intervention rates changed significantly [22, 32, 47]. Models that use a broader time-scale than our model see more benefits to incorporating time-varying parameters [22, 47], and expanding our model to include similar time-varying parameters would be a useful next step. In addition, transmission changes as behavior of infected and susceptible individuals changes [22]. This is an important facet of the outbreak dynamics and would be useful to include in future work.

In the district-level model, subsequent analysis fitting more parameters would be valuable to capture more of the district-to-district heterogeneities: for instance, fitting β transmission parameters separately for each district, to account for potentially differing transmission rates in different regions. Different methods for parameter fitting could be explored in tandem with fitting more parameters. This could ideally be combined with stochastic model simulation, e.g. using iterated filtering or similar methods [52, 53].

Finally, the IAR metric (or similar scores measuring indirect spatial protection) is an promising approach for elucidating the impact of one region on the outbreaks in surrounding regions. Ultimately, this approach can help to identify regions in which interventions might be most impactful, those regions that play the most significant role in spatial transmission. The IAR metric can be applied to other spatial transmission phenomena, including applications where gravity models are a tenable approach (e.g. influenza in the US, cholera in Haiti, etc)[27, 28].

4.7 Conclusions

We developed dynamic transmission models that account for spatial spread of EVD in West Africa using a gravity model framework. The country-level model accurately captures epidemic dynamics and successfully forecasts cases and deaths for all three countries simultaneously. The district-level model captures the progression of EVD between and within districts in West Africa. Our models suggest that reduction of local transmission in Liberia and reduction of long-range transmission in Sierra Leone were the most effective interventions for the outbreak. The models also reveal differences in transmission levels between the three countries, as well as different at-risk population sizes. Our gravity spatial models for EVD provides insight into the geographic spread of EVD in West Africa and the relative effectiveness of interventions on a large, heterogeneous spatial scale. Ultimately, gravity spatial models can be applied by public health officials to understand spatial spread of infectious diseases and guide interventions during disease epidemics.

Highlights.

• We developed gravity spatial models of transmission for the 14–16 Ebola epidemic

• Country and district scale models successfully couple Guinea, Sierra Leone, Liberia

• Local intervention in Liberia was most effective, reducing epidemic in all countries

• Intervention in some regions with few cases substantially reduced overall epidemic

• These spatial indirect protective effects can be used to target intervention efforts

Appendix

Model code is available at https://github.com/epimath/gravity-model-ebola.

Country Model Initial Condition Details

Initial conditions for both models were determined based on the initial values of the data as follows. The total population of each patch was determined using data from the World Bank and national censuses [54–57]. The number of infected persons in I₁ was determined based on the number of new cases in the previous nine days, based on the incubation period for EVD, and the number of infected persons in I₂ was determined by subtracting the number of deaths within the next four days from the number of currently infected persons at the starting date [1]. However, because the data reflects only the reported cases, the total initial cases in each class was then calculated by dividing each of these by k_norm to yield total cases. The number of exposed persons was determined as twice the initial number of infected (I₁ and I₂) persons, based on the ℛ₀ for EVD, which has been estimated to be approximately 2 [16, 58]. From these, the number of susceptible persons was considered to be the population, subtracting number of infected and exposed persons. The number of recovered persons was estimated based on the number of infected persons who did not die within the nine-day period that preceded the starting date. The number of persons in the F class was based on a fraction of the number of persons who died within the period before the starting date, estimated using the burial rate in Table A1. In both cases, we also scaled by k_norm to convert from reported to total individuals. The initial number of infected persons from local versus long-range transmission was estimated based on the origin of the outbreak and the location of cases up until the starting point for the data: since the outbreak began in Guinea, the initial cases in Guinea were considered from local transmission, while the initial cases in Sierra Leone and Liberia were considered to be from long-range transmission from Guinea.

District-level Model Details

Similarly to the country-level model, shown in the methods, the district-level model equations for patch n are given by:

$${\dot{S}}_n=-({\lambda }_1+{\lambda }_2)S_n$$

$${\dot{E}}_n=({\lambda }_1+{\lambda }_2)S_n-\alpha E_n$$

$${\dot{I}}_{1n}=\alpha E_n-{\gamma }_c{I}_{1n}-r_{1,c}{I}_{1n}$$

$${\dot{I}}_{2n}={\gamma }_c{I}_{1n}-\delta I_{2n}-r_{2,c}{I}_{2n}$$

$${\dot{F}}_n=\delta I_{2n}-{\delta }_2{F}_n$$

$${\dot{R}}_n=r_{1,c}{I}_{1n}+r_{2,c}{I}_{2n}$$ (4)

$${\dot{IC}}_{1n}=k_{\mathit{\text{norm}}}\alpha E_n$$

$${\dot{DC}}_n=k_{\mathit{\text{norm}}}\delta I_{2n}$$

$${\lambda }_1={\beta }_{1,n}{I}_{1n}+{\beta }_{2,n}{I}_{2n}+{\beta }_{F,n}{F}_n$$

$${\lambda }_2=\sum _{m=1}^{63}{\theta }_{n,m}({\beta }_{1,n}{I}_{1m}+{\beta }_{2,n}{I}_{2m}+{\beta }_{F,n}{F}_m)$$

$${\theta }_{n,m}={\kappa }_n\frac{{\rho }_n{\rho }_m}{{(d_{n,m})}^{\iota }}$$

where θ_n,n ≔ 0 and c denotes the country to which patch n belongs.

This model structure is similar to that of the country-level model. The main difference is that the long-range transmission is grouped into one λ₂ term, which sums the long-range transmission of every other patch into patch n.

Model Parameter Details

For the district-level model, parameters were determined using sampling from within plausible ranges and from the best-fits of the three-patch models. The β₁ transmission rates were determined at the country level, reflecting the differing risks of transmission in the patches in each country. Each k_norm was calculated to match final outbreak size, then adjusted by hand if needed (e.g. if the final data point was incongruous with the rest of the data). The initial conditions were determined similarly to the country-level model, based on data from the WHO reports and from data compiled by the UN.

The district capitals were considered to be the population centers for all districts except Montserrado, Liberia, and Bonthe, Sierra Leone. Montserrado County is the location of the national capital and largest city, Monrovia, which was considered the population center. The capital of Bonthe is on a coastal island, so Yagoi, the closest city to Bonthe on the coast, was considered the population center.