Inferring patterns of folktale diffusion using genomic data

Significance

This paper presents unprecedented evidence on the transmission mechanism underlying the spread of a broad cross-cultural assemblage of folktales in Eurasia and Africa. State-of-the-art genomic evidence is used to directly assess the relevance of demic diffusion processes, in particular on the distribution of Old World folktales at intermediate geographic scales, and identify individual stories that are more likely to be transmitted through population movement and replacement. The results provide an empirical solution to operate with linguistic barriers and highlight the impossibility of disentangling genetic from geographic relationships at a cross-continental scale, warning against the direct use of extant genetic variability to infer processes of long-range cultural transmission.

Abstract

Observable patterns of cultural variation are consistently intertwined with demic movements, cultural diffusion, and adaptation to different ecological contexts [Cavalli-Sforza and Feldman (1981) Cultural Transmission and Evolution: A Quantitative Approach; Boyd and Richerson (1985) Culture and the Evolutionary Process]. The quantitative study of gene–culture coevolution has focused in particular on the mechanisms responsible for change in frequency and attributes of cultural traits, the spread of cultural information through demic and cultural diffusion, and detecting relationships between genetic and cultural lineages. Here, we make use of worldwide whole-genome sequences [Pagani et al. (2016) Nature 538:238–242] to assess the impact of processes involving population movement and replacement on cultural diversity, focusing on the variability observed in folktale traditions (n = 596) [Uther (2004) The Types of International Folktales: A Classification and Bibliography. Based on the System of Antti Aarne and Stith Thompson] in Eurasia. We find that a model of cultural diffusion predicted by isolation-by-distance alone is not sufficient to explain the observed patterns, especially at small spatial scales (up to $\sim$4,000 km). We also provide an empirical approach to infer presence and impact of ethnolinguistic barriers preventing the unbiased transmission of both genetic and cultural information. After correcting for the effect of ethnolinguistic boundaries, we show that, of the alternative models that we propose, the one entailing cultural diffusion biased by linguistic differences is the most plausible. Additionally, we identify 15 tales that are more likely to be predominantly transmitted through population movement and replacement and locate putative focal areas for a set of tales that are spread worldwide.

Advances in DNA sequencing have opened new ways for exploring the demographic histories of human populations and the relationship between patterns of genetic and cultural diversity around the world. Newly available genome-wide evidence enables us to go beyond the use of linguistic relationship as a measure of common ancestry (1–3) and offers unprecedented support for studying the mechanisms underlying the transmission of cultural information over space and time (4–11) as well as the coevolution of genetic and cultural traits (12–18) across populations.

A key question for research in this area concerns the extent to which patterns of cultural diversity documented in the archaeological and ethnographic records have been generated by demic processes (i.e., the movement of people carrying their own cultural traditions with them) or cultural diffusion (i.e., the transfer of information without or with limited population movement/replacement) (6, 19, 20). Before tackling this question, however, it is critical to note that demic processes and cultural diffusion are not mutually exclusive conditions but rather, are opposite extremes of a continuous gradient, with intermediate and composite positions that more accurately represent empirical reality.

A broadly adopted null model of cultural diffusion draws on the expectation that selectively neutral variants would form geographic clines produced over time by isolation-by-distance (IBD) processes (21). Under an IBD model, individuals or groups that are spatially closer to each other are expected to be more similar than individuals or groups that are located farther apart. A positive correlation between cultural dissimilarity and geographic distance between samples is, therefore, used to infer processes of cultural transmission of nonadaptive information without population replacement (8, 17). However, observed genetic distance is the composite result of serial founder events, long-term IBD, and subsequent migratory events, which imply recent movement and resettling of people (22). A higher correlation between genetic distance and cultural dissimilarity than between culture and geography has, therefore, been proposed as a way to single out the relative effect of demic processes on the distribution of cultural variants (8).

In a recent study, Creanza et al. (17) investigated the process responsible for the observed global distribution of (phonetic) linguistic variability by comparing it with genetic and geographic distances. The authors found high correlation between genetic and geographic distances at a worldwide scale, whereas linguistic distances were spatially autocorrelated only within a range of $\sim$10,000 km. The lack of residual correlation between genetic and linguistic distances up to this spatial scale did not allow the authors to reject their null model and was interpreted as a signal of cultural diffusion being the main driver of the distribution of phonetic variants in human populations.

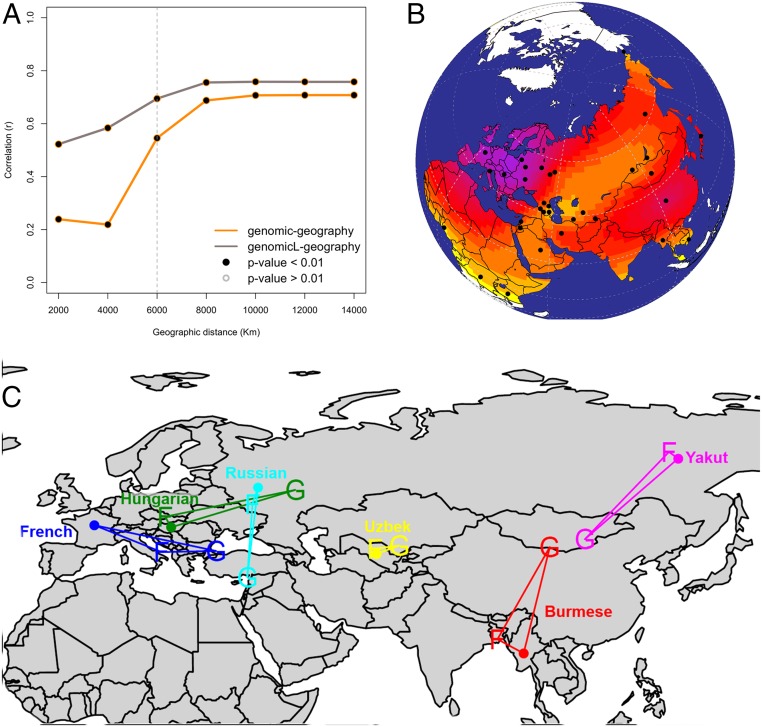
The use of genetic variability as a plausible proxy to reject cultural diffusion as the sole responsible for the distribution of cultural traits depends on being able to disentangle genetic signals from geography. The high correlation between genetic and geographic distances at a global scale (22) lowers the inferential power of this model. However, this relationship is not constant across different geographic scales. We noted that the correlation obtained between pairwise genetic distances is stronger when measured across all possible population pairs at larger geographic scales, whereas it is considerably lower at smaller geographic distances (below $\sim$6,000 km for this dataset), possibly because of more recent and short-range population movements (Fig. 1A, yellow line). It is worth remembering that global trends have been forming over the past $\sim$40,000 y, whereas most cultural traditions are likely to have evolved more recently. This claim is supported by previous studies (17) and suggests that the effect of population movements independent from IBD can be identified only within limited geographic scales. At this spatial resolution, events shaping the distributions of genetic and cultural divergence are more likely to occur at the same temporal scale and hence, be more probably causally related.

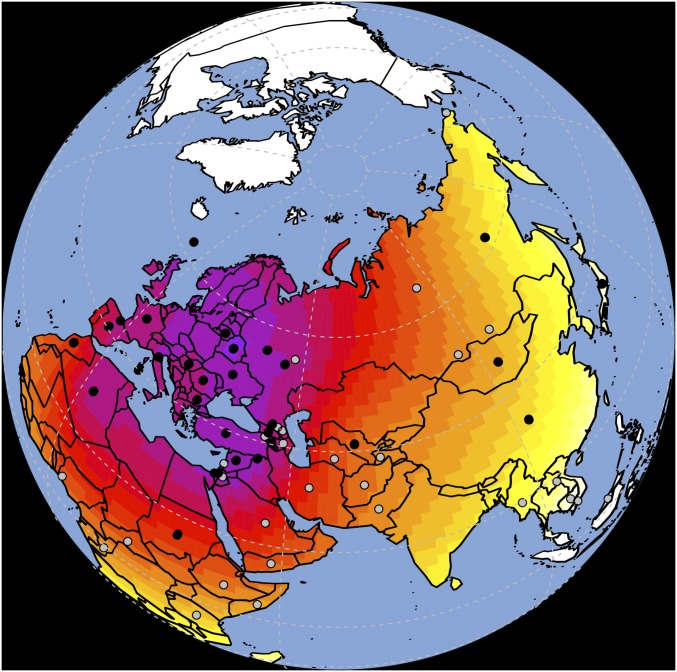
Fig. 1.

(A) Plot of product–moment correlation values between pairwise genetic distance (both whole genome and biased for linguistic barriers) and pairwise geographic distance over cumulative geographic distance. (B) Map showing the spatial distribution of 33 populations in dataset MAIN. Surface colors represent interpolated richness values (i.e., the number of folktales exhibited by each population). Purple indicates higher values, whereas yellow indicates lower numbers. (C) Example of a map with SpaceMix results for genetic and folktale distance both projected on standard geographic coordinates. It is evident how, overall, folktale distribution (F) tends to cluster closer to geographic coordinates (dots), whereas the inferred source and direction of possible genetic admixture (G) are mismatched. For example, Burmese and Yakut exhibit quite segregated folktale assemblages, whereas their putative source of genetic admixture is closer in space. The case of Hungarian is emblematic for its folkloric assemblage rooted in Europe, whereas its putative genetic (and linguistic) source of admixture is located in the Ural region.

An additional confounder is the potential effect of linguistic barriers, which might cause departures from a pure IBD model by constraining the exchange of genetic and/or cultural information between demes belonging to different ethnolinguistic groups. Given the relevance that spoken language has on the transmission of folktales and the light but measurable impact that they have for variants of individual tales in Europe (23), ethnolinguistic barriers should also be considered as key components of plausible alternative models to IBD.

Diffusion of Folktales: Investigating Mechanisms of Cultural Transmission in the Genomic Era

Here, we capitalize on the short-range decoupling of genetic and geographic distance to further infer mechanisms of genetic and cultural coevolution by using newly available genomic evidence (24) as an unbiased proxy of population relatedness. To do so, we analyzed the observed distribution of a set of individual folktales in Eurasia, looking for deviations from the null model of cultural diffusion predicted by geographic distance alone. Folktales are a ubiquitous and rigorously typed form of human cultural expression and hence, particularly well-suited for investigating cultural processes at wider cross-continental scale. Researchers since the Brothers Grimm (25) have long theorized about possible links between the spread of traditional narratives and population dispersals and structure but found mixed levels of support for this hypothesis when using indirect evidence for demic processes, such as linguistic relationships among cultures. One recent study suggested that, within the same linguistic family (Indo-European), the distributions of a substantial number of fairy tales were more consistent with linguistic relationships than with their geographical proximity, suggesting that they were inherited from common ancestral populations (3). This finding is confirmed by the relevance that ethnolinguistic boundaries may have for the transmission of variants of individual folktales in Europe. Ross et al. (23) have shown that, at population level, geographic distribution explains more variability than ethnolinguistic grouping. At this scale, when controlling for the effect of geography, linguistic boundaries do not show any residual significant relationship with folktale variant distribution, suggesting a possible temporal mismatch between folktale and linguistic traditions. However, when individual folktales are considered, ethnolinguistic identity is a significant predictor. This fact suggests that demes belonging to different ethnolinguistic affiliations may undergo higher costs for the transmission of individual folktales, even when they are closer in space. The simultaneous effect of shared linguistic ancestry and spatial proximity was also documented on the distributions of folktales recorded among Arctic hunter-gatherers (26).

Overview of This Study

In this study, we focus on 596 folktales comprising “animal tales” and “tales of magic” (27) typed as present (one) or absent (zero) in 33 populations (dataset MAIN), for which whole-genome sequences are available and exhibiting presence of at least five folktales (Fig. 1B, SI Appendix, and Dataset S1 Tables S1-2.1, S1-2.2, S1-2.3, and S1-2.4). Following previous examples (8), we test for deviations from a null model of pure cultural diffusion without population replacement (IBD), in which geographic distance alone is the best predictor of the decreasing number of shared folktales between pairs of populations. We measure and compare the fit of a number of alternative models comprising (i) a clinal model, in which populations belonging to different ethnolinguistic groups are less likely to share folktales as predicted by IBD (cultural diffusion with linguistic barriers); (ii) population movement and admixture between demes (demic process) as a substantial additional driver of folktale transmission; and (iii) a demic process constrained by linguistic barriers.

We test our hypothesis first by visualizing possible mismatches between actual geographic location of each population and the location inferred by applying explicit models accounting for genetic and cultural admixture (population movement with replacement) (28). We quantify the impact of linguistic barriers on both genetic and folktale variability using analysis of molecular variance (AMOVA) (29). We further investigate this by looking for the set of linguistic barrier parameters (intensity and geographic buffer) that maximizes the fit between genetic distance and geographic distance on the one hand and folktale distance and geographic distance on the other hand. We use this parameter combination to generate alternative models, with fitness that is formally assessed at both a global scale and over cumulative geographic distance. Following the assumptions of previous works (8), we develop a method to identify those folktales that—in the whole corpus—may be more likely to have been transmitted through population movement and replacement, supporting the idea that individual tales may have undergone different processes. To provide a starting point for this additional analysis on the diffusion of individual or smaller packages of tales, we infer potential focal areas—intended as a putative proxy for center of origin—of the most popular tales in the dataset.

Results

Effects of Ethnolinguistic Boundaries.

We use AMOVA (29) to formally assess the impact of ethnolinguistic boundaries on both genetic and folktale variability, focusing only on Eurasian populations (dataset Eurasia; $n=30$) to control for the effect of the Out of Africa expansion on genetic distance (SI Appendix and Dataset S1, Tables S1-3.1, S1-3.2, S1-3.3, and S1-3.4). We assign each population to an ethnolinguistic group (Materials and Methods, SI Appendix, and Dataset S1, Tables S1-4.1 and S1-4.2). Our analysis yielded ${\mathrm{\Phi }}_{ST}=0.036(P<0.001)$ for genetic distance matrix, whereas ${\mathrm{\Phi }}_{ST}=0.1(P<0.001)$ for distances based on folktale distributions. These results confirm the expected differential impact of intergroup boundaries between genetic and cultural variability and are consistent with previous results obtained for population structure on the transmission of cultural traits (23, 30).

We use this evidence to further investigate the separate effects of linguistic barriers on the flow of genetic and cultural information by focusing on two parameters (i.e., intensity and geographic buffer of the cultural barrier) (details are in Materials and Methods). We find that the parameter combinations that resulted in the highest correlation between genetic–geographic distances (intensity = 0.1; radius = 1,500 km) and between folktale–geographic distances (intensity = 0.3; radius = 3,000 km) imply that linguistic barriers have a differential impact of these two kinds of information, and we use this parameter setting to generate two corrected distance matrices for genetics (geneticL) (Dataset S1, Table S1-5.1) and folktales (folktaleL) (Dataset S1, Table S1-5.2), respectively. By using raw and corrected distance matrices, we define alternative models as (i) biased cultural diffusion (folktaleL $\sim$ geographic), (ii) demic diffusion (folktale $\sim$ genetic), and (iii) biased demic diffusion (folktaleL $\sim$ geneticL).

Assessing Models of Folktale Transmission.

We set out to test for deviations from the null model of cultural diffusion caused by IBD. We explore the relationship between our genetic, folktale, and geographic distance matrices using SpaceMix (28) (SI Appendix). We note that, when transformed into pseudospatial coordinates, folktale distances tend to match actual geographic coordinates better than genetic distances (Fig. 1C and SI Appendix, Fig. S1-3.1). The role of geography and ethnolinguistic barriers is also confirmed by a NeighborNet (31) based on folktale distances, showing a broad spatial clustering and proximity/reticulation between demes belonging to the same ethnolinguistic group (SI Appendix).

We then assess the goodness of fit of all of the alternative models at a global scale by comparing Pearson’s product–moment correlation (32), bias-corrected distance correlation (33), and partial distance correlation (34, 35) (Tables 1 and 2; details are in Materials and Methods and SI Appendix). It is evident how, after Bonferroni correction, all alternative models accounting for ethnolinguistic boundaries perform better than the models that do not consider them. With both product–moment correlation coefficient and bias-corrected distance correlation, the best model is the one representing cultural diffusion with linguistic barriers followed by demic processes constrained by linguistic barriers. With distance correlation, however, the difference between the two models is smaller than with standard correlation coefficient. When the dependence between variables is assessed controlling for a third variable through partial distance correlation, linguistic-biased cultural diffusion remains as good a predictor of folktale variability as IBD. This phenomenon could be due to the fact that, at a global scale, correlation between language-corrected genetic distance and geographic distance is higher (Fig. 1) and lowers the residual signal.

Table 1.

Variable association at a global level

Model	cor	P	bcdCor	P
Folktale $\sim$ genetic	0.20	<0.001	0.20	<0.001
Folktale $\sim$ geographic	0.19	<0.001	0.31	<0.001
Genetic $\sim$ geographic	0.71	<0.001	0.84	<0.001
FolktaleL $\sim$ geneticL	0.55	<0.001	0.55	<0.001
FolktaleL $\sim$ geographic	0.64	<0.001	0.57	<0.001
GeneticL $\sim$ geographic	0.76	<0.001	0.83	<0.001

Comparison between null model of cultural diffusion predicted by IBD (folktale ∼ geographic) and alternative models [i.e., demic diffusion (folktale ∼ genetic), cultural diffusion biased by linguistic barriers (folktaleL ∼ geographic), and demic diffusion biased by linguistic barriers (folktaleL ∼ geneticL)]. Values refer to Pearson’s product–moment correlation (cor) and bias-corrected distance correlation (bcdCor) after Bonferroni correction.

Table 2.

Partial distance correlation at a global scale

Model	pdCor	P
Folktale $\sim$ genetic, geographic	-0.11	1.00
Folktale $\sim$ geographic, genetic	0.26	<0.001
FolktaleL $\sim$ geneticL, geographic	0.17	<0.001
FolktaleL $\sim$ geographic, geneticL	0.25	<0.001

Results of partial distance correlation for null (folktale ∼ geographic, genetic) and alternative models [i.e., demic diffusion (folktale ∼ genetic, geographic), cultural diffusion biased by linguistic barriers (folktaleL ∼ geographic, geneticL), and demic diffusion biased by linguistic barriers (folktaleL ∼ geneticL, geographic)] after Bonferroni correction.

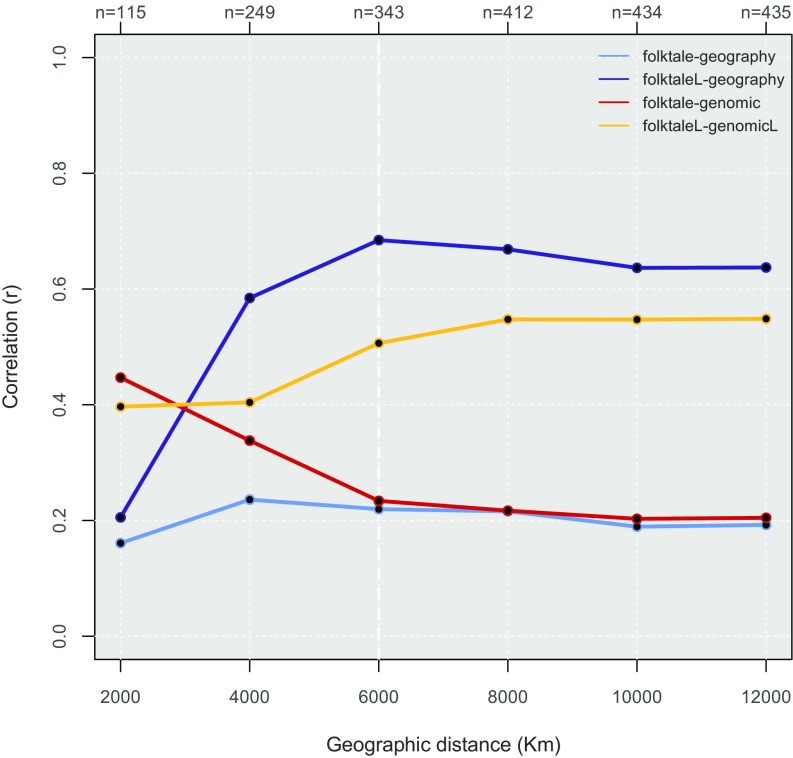
Significant deviations from the null model of cultural diffusion predicted by IBD are further investigated over cumulative geographic distance by comparing Pearson’s correlation coefficients (Fig. 2 and SI Appendix, Table S1-7.1). Above 4,000 km, language-biased cultural diffusion presents with the highest fit at all bins followed by language-biased demic diffusion. Under 4,000 km, folktale distance exhibits stronger dependence from genetic distance than from geographic distance. This relationship is particularly visible under 2,000 km, where the effect of linguistic barriers is the same for genetic and cultural variability.

Fig. 2.

Comparison of the null model of cultural diffusion dictated by IBD (folktale $\sim$ geographic; light blue) against all alternative models: demic diffusion (folktale $\sim$ genetic; red), language-biased cultural diffusion (folktaleL $\sim$ geographic; purple), and language-biased demic diffusion (folktaleL $\sim$ geneticL; yellow) over cumulative geographic distance. Product–moment correlation coefficients are calculated at each geographic bin (size = 2,000 km), with original distance matrices up to 12,000 km.

All results allow us to reject the null model of plain cultural diffusion predicted by IBD and suggest instead that, of all alternative models, the one involving cultural diffusion mitigated by linguistic barriers could be the most plausible one. In addition, as previously pointed out (Fig. 1), results consistently confirm that small geographic scale offers a more efficient disentanglement between possible uncoupled effects of genetic and geographic distances over cultural variables—even after correcting for potential ethnolinguistic barriers.

Uniform Body of Knowledge or Individual Units?

Our results show that, when considering the folktales contained in our dataset as a uniform corpus, the null model dictated by IBD could be rejected. Previous results (23), however, have shown that individual tales or smaller groups of tales may be transmitted across populations as partially independent evolutionary units. If a given cultural trait is not transmitted through population movement and replacement, populations that share it should not exhibit significantly lower genetic distance than populations that do not exhibit it (8). To single out folktales that markedly contradict such null hypothesis, we compare the distribution of pairwise genetic distances corrected for ethnolinguistic boundaries among populations sharing a given tale against distances of the remaining pairs of populations using the Mann–Whitney–Wilcoxon test. We focus on 308 folktales that are present in at least five populations and run two separate tests, the first considering all pairs of populations (Dataset S1, Table S1-6.1) and a second considering only those within a conservative geographic range of 6,000 km (Fig. 1A and Dataset S1, Table S1-6.2). After Bonferroni correction, 15 of 308 analyzed folktales (4.9%) (Dataset S1, Tables S1-7.1 and S1-7.2) present with significantly lower than expected pairwise genetic distance, hence allowing us to reject our null hypothesis and suggesting that these tales may indeed have spread during events of demic diffusion biased by ethnolinguistic barriers.

Folktale Dispersal and Focal Areas.

For a subset of the analyzed folktales, we identify focal areas, representing potential areas of origin and defined as locations that maximize the decay of a given folktale abundance over geographic distance measured with Pearson’s correlation coefficient (Dataset S1, Table S1-8.1). Focal areas were generated for the 19 most widespread folktales, which follow four main trends (SI Appendix). Some of these tales possibly started to be diffused mostly via cultural transmission from Eastern Europe, with subsequent radial diffusion across Eurasia and Africa [such as Aarne Thompson Uther catalog 155 (ATU155): “The Ungrateful Snake Returned to Captivity” in SI Appendix, Fig. S1-8-I 1 or ATU313: “The Magic Flight” in Fig. 3], whereas others probably started their journey from Caucasus (SI Appendix, Fig. S1-8-I 6–8). Examples of the latter are ATU400: “The Man on a Quest for His Lost Wife,” ATU480: “The Kind and Unkind Girls,” ATU531: “The Clever Horse,” and ATU560: “The Magic Ring.” Some narrative plots might have originated in northern Asia—such as the famous “Thumbling” (Tom Thumb) (SI Appendix, Fig. S1-8-I 18)—whereas a last group could have spread from Africa (SI Appendix, Fig. S1-8-I 17), such as in the case of ATU670: “The Man Who Understands Animal Language.”

Fig. 3.

Possible focal area and dispersion pattern for tale ATU313 “The Magic Flight,” one the most popular folktales in this dataset, which may have been additionally spread through population movement and replacement. It is interesting to note how this tale reached locations that are far from its putative origin (such as Japan and southeastern Africa), whereas it was not retained by many populations located in between (gray dots).

Discussion

Using Genetic Evidence to Infer Processes of Cultural Transmission.

Our results resonate with broader questions in cultural evolutionary studies, particularly those concerning the mechanisms of cultural transmission over time and space. They show that the use of newly generated, whole-genome sequences offers a unique opportunity for an unbiased assessment of patterns of cultural variation in the ethnographic and archaeological records. Genetic variability has been already interpreted in the past as a direct proxy of the movement of human groups over time and space, and as such, it has been used as a potential marker of demic mechanisms (8, 17).

We show the effect of ethnolinguistic barriers on both genetic and cultural population structure. By introducing an empirical approach, we find that ethnolinguistic identity has a potentially independent and differential impact on genetic and cultural information. More specifically, our results suggest that linguistic barriers may be twice as effective on the diffusion of cultural traits than on population movement and that the decay over geographic distance of such effect is almost two times slower for culture than for genetic information. Nevertheless, this work very explicitly generates a cautionary tale concerning the use of genomic evidence for investigating such events at a cross-continental or global scale, where geographic clines in genetic variability are the result of different processes that can hardly be disentangled and that may present with considerable temporal mismatch with more recent cultural processes.

Cultural Evolutionary Mechanisms of Folktale Transmission.

Folktales are a prime example of a universal form of cultural expression linked to various vectors of propagation over generations and across geographic and ethnolinguistic barriers that allows us to address questions of cultural evolutionary processes at a cross-cultural and -continental scale. Our results provide insights on the processes driving the spread of folkloric narratives that go beyond previous studies that were limited to a single language family (3).

By correcting for the presence of ethnolinguistic barriers, we find that the null model of cultural diffusion predicted by IBD alone cannot explain the observed distribution of folktales across Eurasia. Instead, beyond $\sim 4,000$ km, cultural diffusion biased by linguistic barriers exhibits the highest correlation at all geographic bins. At small geographic bins ($<4,000$ km), population movements and linguistic barriers may be more relevant than geographic proximity, pointing once again at the possible importance of small-scale processes of cultural transmission for testing more specific hypotheses when using genetic evidence. In addition, processes other than simple cultural diffusion may be more relevant for a smaller group of tales shared by pairs of populations that are genetically closer than populations not exhibiting those tales. Looking for smaller packages of tales or individual tales and their variants can be useful to shed light on the formation process of this vast body of popular knowledge. The long-range patterns detected by our analyses may complement this picture by suggesting a more ancient origin of some of these folktales (SI Appendix) (36–39). On a broader level, these results can be used in the future to infer directional trends of cultural dispersal as well as to test for the emergence of systematic social biases [such as prestige bias, conformism/anticonformism, heterophily, and content-dependent biases (5, 23, 30)] or cultural barriers different from linguistic ones, which have a chronology that may be independently ascertained.

Materials and Methods

Dataset Description.

Folktale data were sourced from the ATU (27). This dataset comprises animal tales (ATU1–299) and tales of magic (ATU300–749). Of 198 societies in which the tales were recorded, 73 matched available genetic data (Dataset S1, Table S1-1). Of these groups, 33 populations exhibiting at least five folktales were selected (Fig. 1B and Dataset S1, Table S1-2.2). Each population is described by a string listing the presence (one) or absence (zero) of any of the included 596 folktales.

Genetic, Folktale, and Geographic Distances.

Genetic distances were estimated by the average pairwise distances between two genomes, one from each population, including both coding and noncoding regions to avoid ascertainment biases. Genetic distance for (i, j) pairs of populations represented by more than one genome was calculated as the average of all possible (i, j) pairs of genomes. As a consequence, the diagonal of the genetic distance matrix was not constrained to be zero (Dataset S1, Table S1-3.2). Folktale distance between population pairs was calculated as asymmetric Jaccard distance (40) (Dataset S1, Table S1-3.3). Geographic distance was calculated as pairwise great circle distance with a waypoint located in the Sinai Peninsula to constrain movement of African demes [through the package gdistance in R (41)]. Coordinates (longitude and latitude in decimal degrees) (Dataset S1, Tables S1-9.1 and S1-9.2) identify the assumed center of the area occupied by a given folkloric tradition as defined by the ATU index.

Transformation of Dissimilarities into Euclidean Distances.

To perform bias-corrected and partial distance correlation, folktale, genetic, and geographic distances were transformed into their exact Euclidean representations (33, 42). The original folktale and genetic distance matrices were scaled through classic multidimensional scaling using the function cmdscale in R and following the procedure for exact representation (34). Euclidean distances were computed from the obtained number of descriptors (n – 2) using the function dist in R (Dataset S1, Tables S1-10.1 and S1-10.2). Euclidean representation of geographic distance (Dataset S1, Table S1-10.3) was instead obtained by reprojecting the original set of coordinates on a plane using two-point equidistant projection through the functions tpeqd in the package mapmisc (43) and spTransform in the package sp in R (44, 45). Euclidean distance between the new set of coordinates was computed using the function rdist in the package fields in R (46).

AMOVA.

To implement AMOVA (29) in our analysis, each population was assigned to an ethnolinguistic group derived from Ethnologue (https://www.ethnologue.com; Dataset S1, Table S1-4.1), and we used the function amova in the package pegas (47) in R. Significance values are obtained through permutation (1,000 iterations).

Variable and Model Comparison.

The relationship between original and biased folktale, genetic, and geographic pairwise distance matrices was quantitatively assessed at global scale and cumulative geographic scales. Measures were obtained through (i) Pearson’s product–moment correlation coefficient using the function cor.test in R, (ii) bias-corrected distance correlation (33) using the function dcor.ttest in the package energy in R (48), and (iii) partial distance correlation using the function pdcor.test in the package energy in R. In parallel, SpaceMix (28) was used to compute folktale and genetic pseudocoordinates, which were compared with actual geographic coordinates to explore inferred processes of admixture.

Estimating the Effect of Ethnolinguistic Barriers on Genetic and Folktale Distance.

We assumed that, if existent, a linguistic barrier would act on pairs of populations that belong to different linguistic families and live within a $d$ geographic distance and artificially increase the actual genetic ($Dgen$) or folktale ($Dfolk$) distance by an intensity factor $f$. We also assumed that parameters $d$ and $f$ may be different when looking at genetic $(d_G\mathit{\text{,}}{f}_G)$ and folktale $(d_F\mathit{\text{,}}{f}_F)$ distances. We assessed the correlation between geographic and genetic or folktale distances at increasing spatial bins before and after correcting for putative linguistic barriers. Particularly, we chose as best pairs of $(d_G\mathit{\text{,}}{f}_G)$ and $(d_F\mathit{\text{,}}{f}_F)$ those that maximized the above-mentioned correlations. Notably, $f_G=0$ or $f_F=0$ (i.e., absence of linguistic barriers) had an equal chance of being picked up as the best values for our parameters. We instead reported (1,500, 0.1) and (3,000, 0.3) as best pairs of genetic and folktale parameters, respectively. To obtain unbiased genetic ($Dgen\prime$) and folktale ($Dfolk\prime$) distances, we, therefore, corrected for the effect of linguistic barriers, so that, for populations $(i,j)$, ${Dgen\prime }_{ij}=Dge{n}_{ij}\times (1-f_G)$ if $d_{ij}⩽d_G$ and $Dfol{k}_{ij}^{\prime }={Dfolk}_{ij}*(1-f_F)$ if $d_{ij}⩽d_F$.

Data Availability and Codes.

R scripts and related commands used to generate all of the results described in the paper are available at doi.org/10.5281/zenodo.821360. Folktale and geographic data as well as genetic distances are also available in Dataset S1. Genetic data used to run SpaceMix are taken from ref. 24 (www.ebc.ee/free_data).