A study of problems encountered in Granger causality analysis from a neuroscience perspective

Significance

Granger causality analysis is a statistical method for investigating the flow of information between time series. Granger causality has become more widely applied in neuroscience, due to its ability to characterize oscillatory and multivariate data. However, there are ongoing concerns regarding its applicability in neuroscience. When are these methods appropriate? How reliably do they recover the functional structure of the system? Also, what do they tell us about oscillations in neural systems? In this paper, we analyze fundamental properties of Granger causality and illustrate statistical and conceptual problems that make Granger causality difficult to apply and interpret in neuroscience studies. This work provides important conceptual clarification of Granger causality methods and suggests ways to improve analyses of neuroscience data in the future.

Abstract

Granger causality methods were developed to analyze the flow of information between time series. These methods have become more widely applied in neuroscience. Frequency-domain causality measures, such as those of Geweke, as well as multivariate methods, have particular appeal in neuroscience due to the prevalence of oscillatory phenomena and highly multivariate experimental recordings. Despite its widespread application in many fields, there are ongoing concerns regarding the applicability of Granger causality methods in neuroscience. When are these methods appropriate? How reliably do they recover the system structure underlying the observed data? What do frequency-domain causality measures tell us about the functional properties of oscillatory neural systems? In this paper, we analyze fundamental properties of Granger–Geweke (GG) causality, both computational and conceptual. Specifically, we show that (i) GG causality estimates can be either severely biased or of high variance, both leading to spurious results; (ii) even if estimated correctly, GG causality estimates alone are not interpretable without examining the component behaviors of the system model; and (iii) GG causality ignores critical components of a system’s dynamics. Based on this analysis, we find that the notion of causality quantified is incompatible with the objectives of many neuroscience investigations, leading to highly counterintuitive and potentially misleading results. Through the analysis of these problems, we provide important conceptual clarification of GG causality, with implications for other related causality approaches and for the role of causality analyses in neuroscience as a whole.

Granger causality is a statistical tool developed to analyze the flow of information between time series. Neuroscientists have applied Granger causality methods to diverse sources of data, including electroencephalography (EEG), magnetoencephalography (MEG), functional magnetic resonance imaging (fMRI), and local field potentials (LFP). These studies have investigated functional neural systems at scales of organization from the cellular level (1–3) to whole-brain network activity (4), under a range of conditions, including sensory stimuli (5–7), varying levels of consciousness (8–10), cognitive tasks (11), and pathological states (12, 13). In such analyses, the time series data are interpreted to reflect neural activity from a particular source, and Granger causality is used to characterize the directionality, directness, and dynamics of influence between sources.

Oscillations are a ubiquitous feature of neurophysiological systems and neuroscience data. They are thought to constrain and organize neural activity within and between functional networks across a wide range of temporal and spatial scales (14–17). Oscillations at specific frequencies have been associated with different states of arousal (18), as well as different sensory (5) and cognitive processes (19, 20). The prevalence of these neural oscillations, as well as their frequency-specific functional associations, spurred initial neuroscientific interest in frequency-domain formulations of Granger causality, such as those developed by Geweke (21, 22). In addition, neuroscience data are often highly multivariate, making it difficult to distinguish direct from indirect influences between system components. Geweke’s conditional causality measure (22) suggested a means to assess direct influences within a larger network. Hence, the Granger–Geweke approach seemed to offer neuroscientists precisely what they wanted—an assessment of direct, frequency-dependent, functional influence between time series—in a straightforward extension of standard time series techniques. Current, widely applied tools for analyzing neuroscience data are based on this Granger–Geweke (GG) paradigm (23–25).

Many limitations of the GG approach are well known, including the requirements that the generative system be approximately linear, stationary, and time invariant. Analyses of the GG approach applied to more general processes, such as neural spiking data (2, 3), continuous-time processes (26), and systems with exogenous inputs and latent variables (4, 27), have been shown to produce results inconsistent with the known functional structure of the underlying system. These examples illustrate the perils of applying GG causality in situations where the generative system is poorly approximated by the vector autoregressive (VAR) model class. Other problems, such as negative causality estimates (28), have been observed even when the generative system belongs to the finite-order VAR model class. Together, these problems raise several important questions for neuroscientists interested in using GG methods: Under what circumstances are these methods appropriate? How reliably do these methods recover the functional structure underlying the observed data? And what do frequency-domain causality measures tell us about the functional properties of oscillatory neural systems?

In this paper, we perform an analysis of GG causality methods to help address these questions. We show how, due to the practical modeling choices required to compute GG causality, the structure of the VAR model can lead to bias in conditional causality estimates. We also show how, for similar reasons, the GG causality measures can be highly sensitive to variations in the estimated model parameters, particularly in the frequency domain, leading to spurious peaks and valleys and even negative values. Finally, we show how the functional properties of the underlying system are not clearly represented in Granger causality measures. As a result, the GG causality measures are prone to misinterpretation. We conclude by discussing how these findings apply to other related measures of causality and how many neuroscience investigations might be more meaningfully analyzed by characterizing system dynamics rather than causality.

Background

Granger Causality.

Granger causality developed in the field of econometric time series analysis. Granger (29) formulated a statistical definition of causality based on the premises that (i) a cause occurs before its effect and (ii) knowledge of a cause improves prediction of its effect. Under this framework, a time series $\{x_{i,t}\}$ is Granger causal of another time series $\{x_{j,t}\}$ if inclusion of the history of $x_i$ improves prediction of $x_j$ over knowledge of the history of $x_j$ alone. Specifically, this is quantified by comparing the prediction error variances of the one-step linear predictor, ${\widehat{x}}_{j,t}$, under two different conditions: one where the full histories of all time series are used for prediction and another where the putatively causal time series is omitted from the set of predictive time series. Thus, $\{x_{i,t}\}$ Granger causes $\{x_{j,t}\}$ if

$$\text{var}(x_{j,t}-{\widehat{x}}_{j,t}\mid x_{j,0:t-1})>\text{var}(x_{j,t}-{\widehat{x}}_{j,t}\mid x_{j,0:t-1},x_{i,0:t-1}).$$

Granger causality can be generalized to multistep predictions, higher-order moments of the prediction distributions, and alternative predictors (30, 31).

In practice, the above linear predictors are limited to finite-order VAR models, and Granger causality is assessed by comparing the prediction error variances from separate VAR models, with one model including all components of the vector time series data, which we term the full model, and a second one including only a subset of the components, which we term the reduced model. To investigate the causality from $\{x_{i,t}\}$ to $\{x_{j,t}\}$, let

$$\left[\begin{array}{c}\hfill x_{j,t}\hfill \\ \hfill x_{i,t}\hfill \end{array}\right]=\sum _{p=1}^P\left[\begin{array}{cc}\hfill A_{j,j}^f\left(p\right)\hfill & \hfill A_{j,i}^f\left(p\right)\hfill \\ \hfill A_{i,j}^f\left(p\right)\hfill & \hfill A_{i,i}^f\left(p\right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_{j,t-p}\hfill \\ \hfill x_{i,t-p}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill w_{j,t}^f\hfill \\ \hfill w_{i,t}^f\hfill \end{array}\right]$$ [1]

be the full VAR(P) model of all time series components, where the superscript $f$ is used to denote the full model. This model may be written more compactly as $x_t={\sum }_{p=1}^P{A}^f\left(p\right)x_{t-p}+w_t^f$. The noise processes $\{w_{j,t}^f\}$ and $\{w_{i,t}^f\}$ are zero mean and temporally uncorrelated with covariance $E\left[w_{t_1}^f{\left(w_{t_2}^f\right)}^T\right]={\mathrm{\Sigma }}^f{\delta }_{t_1-t_2}$. Thus, the full one-step predictor of $x_{j,t}$ in the above causality definition is ${\widehat{x}}_{j,t}^f={\sum }_{p=1}^P{\sum }_{m\in \{i,j\}}{A}_{j,m}^f\left(p\right)x_{m,t-p}$. Similarly, let

$$x_{j,t}=\sum _{p=1}^P{A}^{r\left(i\right)}\left(p\right)x_{j,t-p}+w_{j,t}^{r\left(i\right)}$$

be the reduced VAR(P) model of the $x_j$ (putative effect) components of the time series, omitting the $x_i$ (putative cause) components. We use the superscript $r\left(i\right)$ to denote this reduced model formed by omitting $x_i$. The noise process $\{w_{j,t}^{r\left(i\right)}\}$ is zero mean and temporally uncorrelated with covariance ${\mathrm{\Sigma }}^{r\left(i\right)}$. The reduced one-step predictor of $x_{j,t}$ is thus ${\widehat{x}}_{j,t}^{r\left(i\right)}={\sum }_{p=1}^P{A}^{r\left(i\right)}\left(p\right)x_{j,t-p}$.

Geweke Time-Domain Causality Measures.

Building on Granger’s definition, Geweke (21) defined a measure of directed causality (what he referred to as linear feedback) from $\{x_{i,t}\}$ to $\{x_{j,t}\}$ to be

$${\mathcal{F}}_{x_i⟶x_j}=\ln \frac{\left|\text{var}\left(x_{j,t}-{\widehat{x}}_{j,t}^{r\left(i\right)}\right)\right|}{\left|\text{var}\left(x_{j,t}-{\widehat{x}}_{j,t}^f\right)\right|}=\ln \frac{\left|{\mathrm{\Sigma }}_{j,j}^{r\left(i\right)}\right|}{\left|{\mathrm{\Sigma }}_{j,j}^f\right|},$$

where $|\mathrm{\Sigma }|=\sqrt{det\mathrm{\Sigma }\prime \mathrm{\Sigma }}$. Geweke (22) expanded the previous definition of unconditional (bivariate) causality to include conditional time series components $\{x_{k,t}\}$, purportedly making it possible to distinguish between direct and indirect influences. For example, consider three time series $\{x_{i,t}\}$, $\{x_{j,t}\}$, and $\{x_{k,t}\}$. By conditioning on $x_k$, it is to some extent possible to distinguish between direct influences between $x_i$ and $x_j$, as opposed to indirect influences that are mediated by $x_k$. The conditional measure, ${\mathcal{F}}_{x_i⟶x_j\mid x_k}$, has a form analogous to the unconditional case, except that the predictors, ${\widehat{x}}_{j,t}^f$ and ${\widehat{x}}_{j,t}^{r\left(i\right)}$, and associated prediction-error variances, ${\mathrm{\Sigma }}_{j,j}^f$ and ${\mathrm{\Sigma }}_{j,j}^{r\left(i\right)}$, all incorporate the conditional time series $\{x_{k,t}\}$.

These time-domain causality measures have a number of important properties. First, they are theoretically nonnegative, equaling zero in the case of noncausality. Second, the total linear dependence between two time series can be represented as the sum of the directed causalities and an instantaneous causality (details in S2. Instantaneous Causality and Total Linear Dependence). Finally, these time-domain causality measures can further be decomposed by frequency, providing a frequency-domain measure of causality.

Geweke Frequency-Domain Causality Measures.

The above time-domain measure of causality affords a spectral decomposition, which allowed Geweke (21) to also define an unconditional frequency-domain measure of causality. Let $X\left(\lambda \right)=H^f\left(\lambda \right)W^f\left(\lambda \right)$ be the frequency-domain representation of the moving-average (MA) form of the full model in Eq. 1. $X\left(\lambda \right)$ and $W^f\left(\lambda \right)$ are the Fourier representations of the vector time series $\{x_t\}$ and noise process $\{w_t^{\left(f\right)}\}$, respectively, and $H^f\left(\lambda \right)$ is the transfer function given by

$$H^f\left(\lambda \right)={\left(I-\sum _{p=1}^P{A}^f\left(p\right)e^{-ip\lambda }\right)}^{-1}.$$

As alluded to above, the model can contain instantaneously causal components. The frequency-domain definition requires removal of the instantaneous causality components by transforming the system with a rotation matrix, as described in S3. Removal of Instantaneous Causality for Frequency-Domain Computation and ref. 21. For clarity, we omit this rotation from the present overview of frequency-domain causality, but fully implement the transformation in our computational studies that follow. The spectrum of $\{x_{j,t}\}$ is then

$$S_{x_j,x_j}\left(\lambda \right)=H_{j,j}^f\left(\lambda \right){\mathrm{\Sigma }}_{j,j}^f{H}_{j,j}^{f\ast }\left(\lambda \right)+H_{j,i}^f\left(\lambda \right){\mathrm{\Sigma }}_{i,i}^f{H}_{j,i}^{f\ast }\left(\lambda \right),$$

where $\ast$ denotes conjugate transpose. The first term is the component of the spectrum of $x_j$ due to its own input noise process, whereas the second term represents the components introduced by the $x_i$ time series. The unconditional frequency-domain causality from $\{x_{i,t}\}$ to $\{x_{j,t}\}$ at frequency $\lambda$ is defined as

$$f_{x_i⟶x_j}\left(\lambda \right)=\ln \frac{|S_{x_j,x_j}(\lambda )|}{\left|H_{j,j}^f(\lambda ){\mathrm{\Sigma }}_{j,j}^f{H}_{j,j}^{f\ast }(\lambda )\right|}=\ln \frac{\left|H_{j,j}^f(\lambda ){\mathrm{\Sigma }}_{j,j}^f{H}_{j,j}^{f\ast }(\lambda )+H_{j,i}^f(\lambda ){\mathrm{\Sigma }}_{i,i}^f{H}_{j,i}^{f\ast }(\lambda )\right|}{\left|H_{j,j}^f(\lambda ){\mathrm{\Sigma }}_{j,j}^f{H}_{j,j}^{f\ast }(\lambda )\right|}.$$ [2]

If $\{x_{i,t}\}$ does not contribute to the spectrum of $\{x_{j,t}\}$ at a given frequency, the second term in the numerator of Eq. 2 is zero at that frequency, resulting in zero causality. Thus, the unconditional frequency-domain causality reflects the components of the spectrum originating from the input noise of the putatively causal time series.

As with the time-domain measure, Geweke (22) expanded the frequency-domain measure to include conditional time series. And like the conditional time-domain measure, the conditional frequency-domain definition requires separate full and reduced models. Let $H^f\left(\lambda \right)$ and ${\mathrm{\Sigma }}^f$ be the system function and noise covariance of the full model, and let $H^{r\left(i\right)}\left(\lambda \right)$ and ${\mathrm{\Sigma }}^{r\left(i\right)}$ be the system function and noise covariance of the reduced model. As in the unconditional case, instantaneous causality components must be removed, this time from each model, as described in S3. Removal of Instantaneous Causality for Frequency-Domain Computation and ref. 22. Again, for clarity, we omit this rotation in the equations below, but fully implement this transformation in our computational studies that follow.

The derivation for the conditional form of frequency-domain causality relies on the time-domain equivalence demonstrated by Geweke (22), ${\mathcal{F}}_{x_i⟶x_j\mid x_k}={\mathcal{F}}_{x_i{w}_k^{r\left(i\right)}⟶w_j^{r\left(i\right)}}$. The conditional frequency-domain causality is then defined by $f_{x_i⟶x_j\mid x_k}\left(\lambda \right)=f_{x_i{w}_k^{r\left(i\right)}⟶w_j^{r\left(i\right)}}\left(\lambda \right)$. Thus, we must rewrite our original VAR model in terms of the time series $\{w_{j,t}^{r\left(i\right)}\}$, $\{x_{i,t}\}$, and $\{w_{k,t}^{r\left(i\right)}\}$. Geweke (22) did this by cascading the full model with the inverse of an augmented form of the reduced model,

$$\left[\begin{array}{c}\hfill W_j^{r\left(i\right)}\left(\lambda \right)\hfill \\ \hfill X_i\left(\lambda \right)\hfill \\ \hfill W_k^{r\left(i\right)}\left(\lambda \right)\hfill \end{array}\right]={\left[\begin{array}{ccc}\hfill H_{j,j}^{r\left(i\right)}\left(\lambda \right)\hfill & \hfill 0\hfill & \hfill H_{j,k}^{r\left(i\right)}\left(\lambda \right)\hfill \\ \hfill 0\hfill & \hfill I\hfill & \hfill 0\hfill \\ \hfill H_{k,j}^{r\left(i\right)}\left(\lambda \right)\hfill & \hfill 0\hfill & \hfill H_{k,k}^{r\left(i\right)}\left(\lambda \right)\hfill \end{array}\right]}^{-1}\times \left[\begin{array}{ccc}\hfill H_{j,j}^f\left(\lambda \right)\hfill & \hfill H_{j,i}^f\left(\lambda \right)\hfill & \hfill H_{j,k}^f\left(\lambda \right)\hfill \\ \hfill H_{i,j}^f\left(\lambda \right)\hfill & \hfill H_{i,i}^f\left(\lambda \right)\hfill & \hfill H_{i,k}^f\left(\lambda \right)\hfill \\ \hfill H_{k,j}^f\left(\lambda \right)\hfill & \hfill H_{k,i}^f\left(\lambda \right)\hfill & \hfill H_{k,k}^f\left(\lambda \right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill W_j^f\left(\lambda \right)\hfill \\ \hfill W_i^f\left(\lambda \right)\hfill \\ \hfill W_k^f\left(\lambda \right)\hfill \end{array}\right]$$ [3]

$$=\left[\begin{array}{ccc}\hfill G_{j,j}\left(\lambda \right)\hfill & \hfill G_{j,i}\left(\lambda \right)\hfill & \hfill G_{j,k}\left(\lambda \right)\hfill \\ \hfill G_{i,j}\left(\lambda \right)\hfill & \hfill G_{i,i}\left(\lambda \right)\hfill & \hfill G_{i,k}\left(\lambda \right)\hfill \\ \hfill G_{k,j}\left(\lambda \right)\hfill & \hfill G_{k,i}\left(\lambda \right)\hfill & \hfill G_{k,k}\left(\lambda \right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill W_j^f\left(\lambda \right)\hfill \\ \hfill W_i^f\left(\lambda \right)\hfill \\ \hfill W_k^f\left(\lambda \right)\hfill \end{array}\right].$$ [4]

This combined system relates the reduced-model noise processes and the putatively causal time series to the full-model noise process. It can be viewed as the frequency-domain representation of a VARMA model of the time series $\{w_{j,t}^{r\left(i\right)}\}$, $\{x_{i,t}\}$, and $\{w_{k,t}^{r\left(i\right)}\}$. The spectrum of $\{w_{j,t}^{r\left(i\right)}\}$ is then

$$S_{w_j^{r\left(i\right)},w_j^{r\left(i\right)}}\left(\lambda \right)=G_{j,j}\left(\lambda \right){\mathrm{\Sigma }}_{j,j}^f{G}_{j,j}^{\ast }\left(\lambda \right)+G_{j,i}\left(\lambda \right){\mathrm{\Sigma }}_{i,i}^f{G}_{j,i}^{\ast }\left(\lambda \right)+G_{j,k}\left(\lambda \right){\mathrm{\Sigma }}_{k,k}^f{G}_{j,k}^{\ast }\left(\lambda \right).$$ [5]

Hence, the conditional frequency-domain causality is

$$f_{x_i⟶x_j\mid x_k}\left(\lambda \right)=\ln \frac{|S_{w_j^{r\left(i\right)},w_j^{r\left(i\right)}}\left(\lambda \right)|}{\left|G_{j,j}\left(\lambda \right){\mathrm{\Sigma }}_{j,j}^f{G}_{j,j}^{\ast }\left(\lambda \right)\right|}=\ln \frac{\left|{\mathrm{\Sigma }}_{j,j}^{r\left(i\right)}\right|}{\left|G_{j,j}\left(\lambda \right){\mathrm{\Sigma }}_{j,j}^f{G}_{j,j}^{\ast }\left(\lambda \right)\right|}.$$

The last equality follows from the assumed whiteness of $\{w_{j,t}^{r\left(i\right)}\}$ with covariance ${\mathrm{\Sigma }}_{j,j}^{r\left(i\right)}$.

This equation is similar in form to the expression for unconditional frequency-domain causality in Eq. 2, suggesting, at least superficially, an analogous interpretation. However, the transformations detailed in Eq. 3 suggest a more nuanced interpretation.

Overview of Analysis.

In the next section, we explore several issues that arise in the application of the conditional and unconditional GG causality measures. We demonstrate them with simulated examples and discuss the practical implications of using such methods for analyzing real data, especially neuroscience data. The simulations use finite-order VAR systems to ensure that the problems demonstrated are not due to inaccurate modeling of the generative process, but rather are inherent to GG causality. We place some emphasis on the Geweke conditional approach (22) for several reasons. Although the unconditional approach (21) is more commonly used, the conditional approach enables some degree of distinction between direct and indirect influence and is therefore more relevant to the highly multivariate datasets common in neuroscience. Furthermore, the issues being presented are partly what have limited the use of the conditional approach and have motivated the proposal of related alternative causality measures. We also emphasize the Geweke frequency-domain measures, because they have motivated the adoption of Granger causality analysis and related methods in the neurosciences.

Results

Impact of VAR Model Properties on Conditional Causality Estimates.

In this section, we illustrate how the properties of the VAR model impact estimation of GG causality. We show that the structure of the VAR model class, in combination with the choice to use separate full and reduced models to estimate causality, introduces a peculiar bias–variance trade-off to the estimation of conditional frequency-domain GG causality. In particular, use of the true system model order results in bias, whereas increasing the model order to reduce bias results in increased variance that introduces spurious frequency-domain peaks and valleys. The separate model fits also introduce an additional sensitivity to parameter estimates, exacerbating the problem of spurious peaks and valleys and even producing negative values.

Example 1: VAR(3) three-node series system.

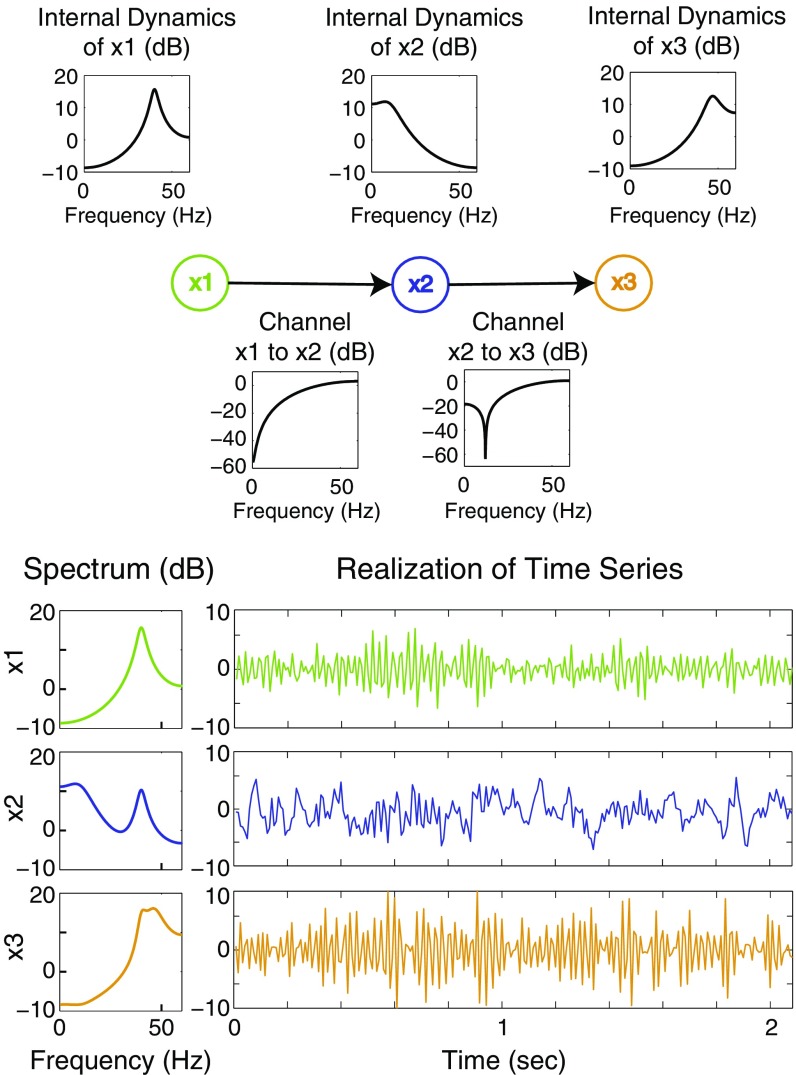
In this simulation study, we analyze time series generated by the VAR(3) system shown in Fig. 1. In this system, node 1, $\{x_{1,t}\}$, resonates at frequency $f_1=40$ Hz and is transmitted to node 2 with an approximate high-pass filter. Node 2, $\{x_{2,t}\}$, is driven by node 1, resonates at frequency $f_2=10$ Hz, and is transmitted to node 3 with an approximate high-pass filter. Node 3, $\{x_{3,t}\}$, is driven by node 2 and resonates at frequency $f_3=50$ Hz. All nodes also receive input from independent, white Gaussian noises, $\{w_{i,t}\}$, with zero mean and unit variance. The VAR equation of the system is thus

$$\left[\begin{array}{c}\hfill x_{1,t}\hfill \\ \hfill x_{2,t}\hfill \\ \hfill x_{3,t}\hfill \end{array}\right]=\underset{{𝐀}_1}{\underbrace{\left[\begin{array}{ccc}\hfill 2r_1\cos \left({\theta }_1\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -0.356\hfill & \hfill 2r_2\cos \left({\theta }_2\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -0.3098\hfill & \hfill 2r_3\cos \left({\theta }_3\right)\hfill \end{array}\right]}}\left[\begin{array}{c}\hfill x_{1,t-1}\hfill \\ \hfill x_{2,t-1}\hfill \\ \hfill x_{3,t-1}\hfill \end{array}\right]+\underset{{𝐀}_2}{\underbrace{\left[\begin{array}{ccc}\hfill -r_1^2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.7136\hfill & \hfill -r_2^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0.5\hfill & \hfill -r_3^2\hfill \end{array}\right]}}\left[\begin{array}{c}\hfill x_{1,t-2}\hfill \\ \hfill x_{2,t-2}\hfill \\ \hfill x_{3,t-2}\hfill \end{array}\right]+\underset{{𝐀}_3}{\underbrace{\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -0.356\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -0.3098\hfill & \hfill 0\hfill \end{array}\right]}}\left[\begin{array}{c}\hfill x_{1,t-3}\hfill \\ \hfill x_{2,t-3}\hfill \\ \hfill x_{3,t-3}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill w_{1,t}\hfill \\ \hfill w_{2,t}\hfill \\ \hfill w_{3,t}\hfill \end{array}\right],$$

where $r_1=0.9$, $r_2=0.7$, and $r_3=0.8$; ${\theta }_i=f_i\mathrm{\Delta }t2\pi$ for $i=1,\mathrm{2,3}$; and the assumed sampling rate is $\frac{1}{\mathrm{\Delta }t}=120$ Hz. See S5. Construction of Simulated Examples for the selection of parameter values for this example.

Fig. 1.

VAR(3) three-node series system of example 1. Top shows the network diagram of the system, with plots showing the frequency response of the internal dynamics (univariate AR behavior) of each node and the frequency responses of the channels connecting the nodes. Bottom shows the spectrum of each node and a corresponding time series of a single realization from the system. The high signal-to-noise ratio of this system and these data is evident in the highly visible oscillations in the time series and in the spectral peaks.

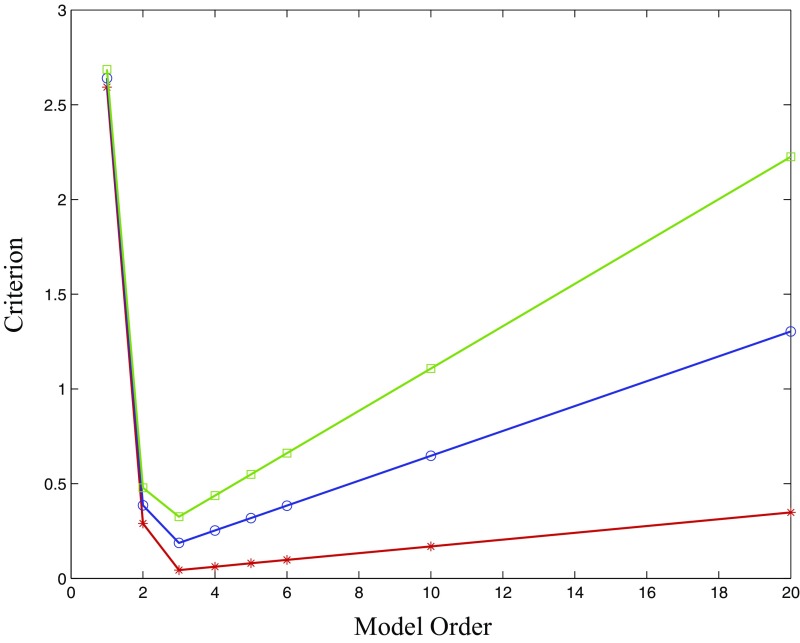
We generated 1,000 realizations of this system, each of length $N=500$ time points (4.17 s). These simulated data have oscillations at the intended frequencies that are readily visible in the time domain, as shown in Fig. 1. The conditional frequency-domain causality was computed for each realization, using separate full- and reduced-model estimates using the true model order $P=3$, as well as model orders $6$ and $20$. The VAR parameters for each model order were well estimated from single realizations of the process (Table S1). We also performed model order selection using a variety of methods—including the Akaike information, Hannan–Quinn, and Schwarz criteria—all of which correctly identified, on average, the true model order to be $P=3$ (Fig. S1).

Table S1.

Nonzero parameters for VAR(3) three-node series system of example 1

System component	Nonzero parameter	True value	Order 3 mean (SD)	Order 6 mean (SD)	Order 20 mean (SD)
	$A_{1\mathit{\text{,}}1}\left(1\right)$	−0.900	−0.900	−0.900	−0.899
Node 1 dynamics			(0.044)	(0.045)	(0.047)
	$A_{1\mathit{\text{,}}1}\left(2\right)$	−0.810	−0.809	−0.813	−0.812
			(0.053)	(0.063)	(0.066)
	$A_{2\mathit{\text{,}}2}\left(1\right)$	1.212	1.211	1.211	1.211
Node 2 dynamics			(0.044)	(0.047)	(0.050)
	$A_{2\mathit{\text{,}}2}\left(2\right)$	−0.490	−0.490	−0.490	−0.492
			(0.062)	(0.075)	(0.079)
	$A_{3\mathit{\text{,}}3}\left(1\right)$	−1.212	−1.212	−1.212	−1.212
Node 3 dynamics			(0.042)	(0.046)	(0.049)
	$A_{3\mathit{\text{,}}3}\left(2\right)$	−0.640	−0.640	−0.643	−0.644
			(0.059)	(0.072)	(0.078)
	$A_{2\mathit{\text{,}}1}\left(1\right)$	−0.356	−0.355	−0.355	−0.354
			(0.045)	(0.046)	(0.048)
Channel 1 to 2	$A_{2\mathit{\text{,}}1}\left(2\right)$	0.714	0.714	0.714	0.715
			(0.052)	(0.062)	(0.065)
	$A_{2\mathit{\text{,}}1}\left(3\right)$	−0.356	−0.355	−0.356	−0.354
			(0.070)	(0.084)	(0.090)
	$A_{3\mathit{\text{,}}2}\left(1\right)$	−0.310	−0.311	−0.310	−0.311
			(0.044)	(0.046)	(0.049)
Channel 2 to 3	$A_{3\mathit{\text{,}}2}\left(2\right)$	0.500	0.501	0.501	0.502
			(0.062)	(0.074)	(0.078)
	$A_{3\mathit{\text{,}}2}\left(3\right)$	−0.310	−0.313	−0.313	−0.313
			(0.039)	(0.079)	(0.085)
Noise 1	${\mathrm{\Sigma }}_{1\mathit{\text{,}}1}$	1	1.000	1.000	1.000
			(0.067)	(0.069)	(0.073)
Noise 2	${\mathrm{\Sigma }}_{2\mathit{\text{,}}2}$	1	1.000	1.000	1.000
			(0.064)	(0.065)	(0.069)
Noise 3	${\mathrm{\Sigma }}_{3\mathit{\text{,}}3}$	1	1.002	1.002	1.002
			(0.063)	(0.064)	(0.068)

Fig. S1.

Several model order selection criteria for various model orders of VAR estimates of the VAR(3) three-node series system of example 1. Mean values (over 1,000 realizations) of the Akaike information criterion (red), the Hannan–Quinn criterion (blue), and the Schwarz criterion (green) are shown. All criteria are minimized (on average) at the true order 3.

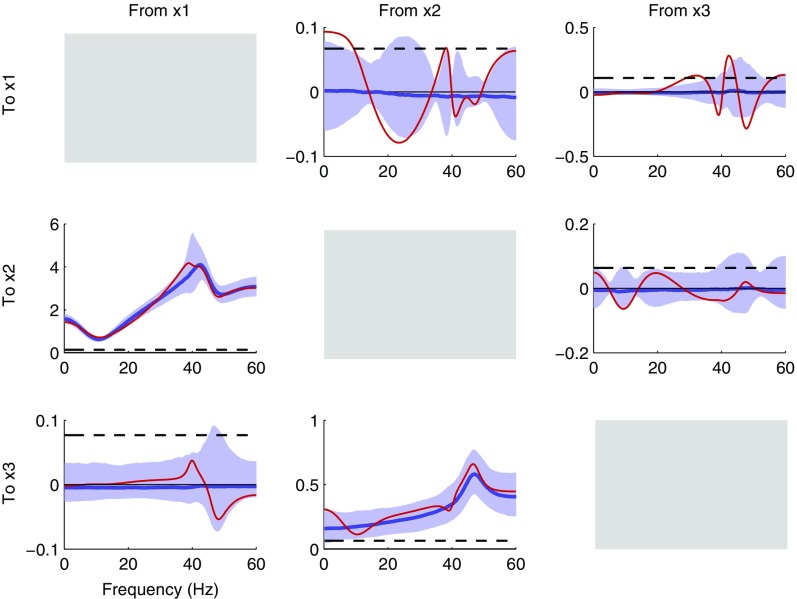
Fig. 2 shows the distributions of causality estimates for different model orders for the truly causal connections from node 1 to node 2 and from node 2 to node 3, as well as the truly noncausal connection from node 3 to node 1. Results for the true model order 3 are shown in Fig. 2, Column 1, whereas those for the order 6 and 20 models are shown in Fig. 2, Columns 2 and 3, respectively. Each plot shows the median (blue line) and 90% central interval (purple shading) of the distribution of causality estimates. In addition, we show estimates for a single realization (red line) and the 95% significance level (black dashes) estimated by permutation (32). The details for the significance level computation are described in S9. Permutation Significance for Noncausality. Fig. 2, Column 4 shows the mean causality values for each order. The causality estimates for all cause–effect pairs for model orders 3, 6, and 20 are shown in Figs. S2, S3, and S4, respectively.

Fig. 2.

Comparison of conditional frequency-domain causality estimates for the VAR(3) three-node series system of example 1 using model orders 3, 6, and 20. Rows 1, 2, and 3 show the results for the truly causal connections from node 1 to node 2 and from node 2 to node 3 and a truly noncausal connection from node 3 to node 1, respectively. Columns 1, 2, and 3 show the results from using the true model order 3 and the increased model orders 6 and 20, respectively. Each subplot shows the median (blue line) and 90% central interval (purple shading) of the distribution of causality estimates, the estimate for a single realization (red line), and the 95% significance level (black dashes) estimated by permutation. For further comparison, Column 4 overlays the mean causality estimates for three model orders: 3 (red), 6 (blue), and 20 (black). The bias from using the true model order is indicated by the qualitative differences between the mean estimates of Column 4 and between the distributions of Column 1 compared with those of Columns 2 and 3, where larger orders were used. Whereas increasing the model order diminishes the bias, the variance is increased, indicated by the increase in the width of the distributions, the increased number of peaks and valleys of the individual realizations, and the increase in the null significance level. The additional sensitivity to variability in the model parameter estimates from the separate full and reduced model fits is most evident from the occurrence of negative causality estimates. This occurs predominantly for the noncausal connection (Row 3), but when the model order is increased to 20, instances of negative causality also occur for the truly causal connection from node 2 to node 3 (Row 2, Column 3).

Fig. S2.

Conditional frequency-domain causality estimates for the three-node series system from example 1 using the true model order 3. Each subplot, corresponding to a cause–effect pair, shows the median (blue line) and 90% central interval (purple shading) of the distribution of the estimates, as well as the 95% significance level (black dashed line) estimated by permutation and the estimate for a single realization (red line).

Fig. S3.

Conditional frequency-domain causality estimates for the three-node series system from example 1, using the increased model order 6. Each subplot, corresponding to a cause–effect pair, shows the median (blue line) and 90% central interval (purple shading) of the distribution of the estimates, as well as the 95% significance level (black dashed line) estimated by permutation and the estimate for a single realization (red line).

Fig. S4.

Conditional frequency-domain causality estimates for the three-node series system from example 1, using the increased model order 20. Each subplot, corresponding to a cause–effect pair, shows the median (blue line) and 90% central interval (purple shading) of the distribution of the estimates, as well as the 95% significance level (black dashed line) estimated by permutation and the estimate for a single realization (red line).

The differences in these causality distributions reflect the trade-off in bias and variance that would be expected with increasing model order. Because the GG causality measure is defined for infinite-order VAR models, high-order VAR models are approximately unbiased. The similarity in the shape of the mean causality curve for high model orders (6 and 20) is consistent with this idea (Fig. 2, Column 4). A pronounced bias is evident when using the true model order 3, reflected in the large qualitative differences in the shape of the distribution compared with the model order 20 case (Fig. 2). This is somewhat disconcerting as one might expect the causality analysis to perform best when the true model order is used.

Whereas the bias decreases as the model order is increased, the number of parameters increases, each with its own variance. This leads to increased total uncertainty in the full and reduced models and in the GG causality estimate. This impacts both the detection of causal connections and the estimation of frequency-domain GG causality. For causality detection, the analysis correctly identifies the significant connections under model orders 3 and 6 for all realizations. At model order 20, the variance in the causality estimates has increased, reflected in the width of the causality distribution and its null distribution, raising the 95% significance threshold obtained by permutation. As a result, 7% of the realizations fail to reject the null hypothesis that no causal connection is present from node 2 to node 3.

We also observe that this increased variance takes a particular form, where the estimates for the individual realizations show numerous causality peaks and valleys as a function of frequency. This occurs because, as the model order increases, so too does the number of modes in the dynamical system. In the frequency domain, this is reflected in the number of poles in the system, each of which represents a peak in the spectral representation (33). Thus, with increasing model order, we see not only an increase in the variance of the causality distribution, but also an increase in the number of oscillatory components, resulting in an increase in the number of peaks and valleys in the causality estimates.

The bias in the conditional GG causality distribution under the true model order occurs because, whereas GG causality is theoretically defined using infinite histories, practical computation requires using a finite order. Unfortunately, the reduced models are being used to represent a subset of a VAR process, and subsets of VAR processes are not generally VAR, but instead belong to the broader class of vector autoregressive MA (VARMA) processes. VAR representations of VARMA processes are generally infinite order. Thus, when a finite-order VAR model is used for the reduced process, as required in conditional Geweke causality computation, some terms will be omitted.

This can be seen more clearly by rewriting the full VAR model,

$$\left[\begin{array}{c}\hfill x_{j,t}\hfill \\ \hfill x_{i,t}\hfill \\ \hfill x_{k,t}\hfill \end{array}\right]=\sum _{p=1}^P\left[\begin{array}{ccc}\hfill A_{j,j}\left(p\right)\hfill & \hfill A_{j,i}\left(p\right)\hfill & \hfill A_{j,k}\left(p\right)\hfill \\ \hfill A_{i,j}\left(p\right)\hfill & \hfill A_{i,i}\left(p\right)\hfill & \hfill A_{i,k}\left(p\right)\hfill \\ \hfill A_{k,j}\left(p\right)\hfill & \hfill A_{k,i}\left(p\right)\hfill & \hfill A_{k,k}\left(p\right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_{j,t-p}\hfill \\ \hfill x_{i,t-p}\hfill \\ \hfill x_{k,t-p}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill w_{j,t}\hfill \\ \hfill w_{i,t}\hfill \\ \hfill w_{k,t}\hfill \end{array}\right].$$

Focusing on the reduced components, we see the VARMA form,

$$\left[\begin{array}{c}\hfill x_{j,t}\hfill \\ \hfill x_{k,t}\hfill \end{array}\right]=\underset{\text{Autoregressive Term}}{\underbrace{\sum _{p=1}^P\left[\begin{array}{cc}\hfill A_{j,j}\left(p\right)\hfill & \hfill A_{j,k}\left(p\right)\hfill \\ \hfill A_{k,j}\left(p\right)\hfill & \hfill A_{k,k}\left(p\right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_{j,t-p}\hfill \\ \hfill x_{k,t-p}\hfill \end{array}\right]}}+\underset{\text{Moving-Average Term}}{\underbrace{\left[\begin{array}{c}\hfill w_{j,t}\hfill \\ \hfill w_{k,t}\hfill \end{array}\right]+\sum _{p=1}^P\left[\begin{array}{c}\hfill A_{j,i}\left(p\right)\hfill \\ \hfill A_{k,i}\left(p\right)\hfill \end{array}\right]x_{i,t-p}}}.$$

For the reduced model, the MA terms, specifically those containing $x_i$, need to be appropriately projected onto the typically infinite histories of the remaining $x_j$ and $x_k$ components. Truncation of the reduced VAR to finite order eliminates nonzero, although diminishing, terms. Thus, when using a finite order, especially the true model order for the full system, the reduced model components can be poorly represented, leading to biased causality estimates.

The stochastic nature of the separate fits can further contribute to artifactual peaks and valleys and even negative causality (28). This is because when the full and reduced models are estimated separately, their frequency structure can be misaligned, producing spurious fluctuations in the resulting causality estimate. As seen in Fig. 2, negative values are extensive for the truly noncausal connection from node 3 to node 1 and even appear at model order 20 for the truly causal connection from node 2 to node 3. This sensitivity to variability in the model parameter estimates can be quite dramatic, depending on the specific system, and compounds the increased variability due to high model order discussed above.

Causality Interpretation: How Are the Functional Properties of the System Reflected in GG Causality?

Given a frequency-domain causality spectrum over a range of frequencies, a face value interpretation would be that peaks represent frequency bands that are more causal or effective, whereas valleys represent frequency bands of lesser effect. At the same time, we know that causality measures are functions of the VAR system parameters and reflect a combination of dynamics from the different components of the system. How then do causality values relate to the underlying structure or dynamics of the generative system?

In this subsection, we examine the relationship between system behavior and causality values by systematically varying the parameters of different parts of the system and assessing the dependence of the causality on the component behaviors. We use the terms “transmitter” to denote putatively causal nodes, “receiver” to denote putative effect nodes, and “channel” to denote the linear relationship linking the two in a particular direction of connection. We will show that GG causality reflects only the dynamics of the transmitter node and channel, with no dependence on the dynamics of the receiver node. This suggests that, even in simple bivariate AR systems, GG causality may be prone to misinterpretation and may not reflect the intuitive notions of causality most often associated with these methods.

Example 2: Transmitter–receiver pair with varying resonance alignments.

In this simulation study, we investigate how GG causality values change as the system’s frequency structure varies, to determine whether the changes in the causality values agree with the face value interpretation of causality described above. We structure the analysis to avoid the model order and model subset issues described in the previous section. Specifically, we examine a bivariate case, such that the unconditional causality can be computed correctly from a single model using the true VAR parameters. By using the true VAR parameters, we also eliminate the uncertainties associated with VAR parameter estimation. Thus, in this example, we focus solely on the functional relationship between system structure and the causality measure.

We compare the causality of a set of similar unidirectional two-node systems, all with the structure shown in Fig. 3, Left. To isolate the influence of transmitter and receiver behaviors, we fix the channel as all pass (i.e., all frequencies pass through the channel without influencing the signal amplitude). In these systems, node 1, $\{x_{1,t}\}$, is driven by a white noise input, $\{w_{1,t}\}$; resonates at frequency $f_1$; and is transmitted to node 2. Node 2, $\{x_{2,t}\}$, is driven by both node 1 and a white noise input, $\{w_{2,t}\}$, and resonates at frequency $f_2$. The channel is fixed as all-pass unit delay, but the transmitter and receiver resonance frequencies are varied. The set of transmitter resonance frequencies is $f_1\in \{\mathrm{10,20,30,40,50}\}$ Hz. The set of receiver resonance frequencies is $f_2\in \{\mathrm{10,30,50}\}$ Hz. The VAR equation of these systems is thus

$$\left[\begin{array}{c}\hfill x_{1,t}\hfill \\ \hfill x_{2,t}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 2r_1\cos \left({\theta }_1\right)\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 2r_2\cos \left({\theta }_2\right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_{1,t-1}\hfill \\ \hfill x_{2,t-1}\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill -r_1^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -r_2^2\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_{1,t-2}\hfill \\ \hfill x_{2,t-2}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill w_{1,t}\hfill \\ \hfill w_{2,t}\hfill \end{array}\right],$$

where $r_i=0.65$ and ${\theta }_i=f_i\mathrm{\Delta }t2\pi$ for $i=1,2$, and the assumed sampling rate is $\frac{1}{\mathrm{\Delta }t}=120$ Hz. The driving inputs are independent white Gaussian noises with zero mean and unit variance. The frequency-domain causality is computed for each system using the single-model unconditional approach with the true parameter values. Fig. 3, Right shows the true frequency-domain causality values for the different systems. Each plot in Fig. 3, Right represents a single receiver resonance frequency, with the different transmitter frequencies. For instance, Fig. 3, Top Right shows the values for all five transmitter settings with the receiver resonance set at 10 Hz. Similarly, Fig. 3, Middle Right and Bottom Right shows the values with the receiver resonance held fixed at 30 Hz and 50 Hz, respectively.

Fig. 3.

System and unconditional frequency-domain causality values for different resonance alignments of the VAR(2) unidirectional transmitter–receiver pair of example 2. The channel is all-pass unit delay. Three receiver resonances are tested: 10 Hz, 30 Hz, and 50 Hz, shown in the Top, Middle, and Bottom rows, respectively. For each setting of the receiver resonance, five transmitter resonances are tested: 10 Hz, 20 Hz, 30 Hz, 40 Hz, and 50 Hz. Left column shows the spectra. Right column shows the causality. As discussed in the text, the causality reflects the spectrum of the transmitter and channel, independent of the receiver dynamics. Hence, all three plots of the Right column are identical and similar to the node 1 spectrum plots of the Left column.

Receiver Independence: GG Causality Does Not Depend on Receiver Dynamics.

Perhaps the most notable aspect of Fig. 3 is that the causality plots in Fig. 3, Right are identical, indicating that the frequency-domain causality values are independent of the resonance frequency of the receiver. This suggests that the unconditional causality is actually independent of the receiver dynamics. We can see this by explicitly writing the causality function in terms of the VAR system components. The transfer function of the system is the inverse of the Fourier transform of the VAR equation,

$$H\left(\lambda \right)={\mathcal{A}}^{-1}\left(\lambda \right)={\left(I-\sum _{p=1}^{P}A\left(p\right){\exp }^{-ip\lambda }\right)}^{-1}.$$

As shown in S6. Receiver Independence of Unconditional Frequency-Domain GG Causality, the unconditional causality (Eq. 2) from node 1 to node 2 can be expressed in terms of the AR matrices associated with each (possibly vector-valued) component

$$f_{x_1⟶x_2}(\lambda )=\ln \frac{\left|H_{\mathrm{2,2}}\left(\lambda \right){\mathrm{\Sigma }}_{\mathrm{2,2}}{H}_{\mathrm{2,2}}^{\ast }\left(\lambda \right)+H_{\mathrm{2,1}}\left(\lambda \right){\mathrm{\Sigma }}_{\mathrm{1,1}}{H}_{\mathrm{2,1}}^{\ast }\left(\lambda \right)\right|}{\left|H_{\mathrm{2,2}}\left(\lambda \right){\mathrm{\Sigma }}_{\mathrm{2,2}}{H}_{\mathrm{2,2}}^{\ast }(\lambda )\right|}=\ln \frac{\left|{\mathrm{\Sigma }}_{\mathrm{2,2}}+{\mathcal{A}}_{\mathrm{2,1}}\left(\lambda \right){\mathcal{A}}_{\mathrm{1,1}}^{-1}\left(\lambda \right)\mathrm{\Sigma }{}_{\mathrm{1,1}}\mathcal{A}_{\mathrm{1,1}}^{-1\ast }\left(\lambda \right){\mathcal{A}}_{\mathrm{2,1}}^{\ast }\left(\lambda \right)\right|}{\left|{\mathrm{\Sigma }}_{\mathrm{2,2}}\right|}.$$ [6]

Note how the ${\mathcal{A}}_{\mathrm{2,2}}\left(\lambda \right)$ system component and hence the $\{A_{\mathrm{2,2}}\left(p\right)\}$ system parameters, which characterize the receiver dynamics, are absent. Thus, the unconditional frequency-domain causality does not reflect receiver dynamics.

Instead, the causality is a function of the transmitter and channel dynamics and the input variances. In Fig. 3, we see that the causality parallels the transmitter spectrum, with the causality peak located at the transmitter resonance frequency. This makes sense, as the channel remains fixed as an all-pass unit delay, so the causality is determined by the transmitter spectrum, ${\mathcal{A}}_{\mathrm{1,1}}^{-1}(\lambda )\mathrm{\Sigma }{}_{\mathrm{1,1}}\mathcal{A}_{\mathrm{1,1}}^{-1\ast }(\lambda )$, in the second term of the numerator in Eq. 6.

Even in this simple bivariate example, we see that the causality analysis is potentially misleading. For example, consider the cases where the 50-Hz transmitter drives either a 10-Hz receiver (Fig. 3, Top row, purple lines) or a 50-Hz receiver (Fig. 3, Bottom row, purple lines). The spectra we observe at the effect nodes in these scenarios are different (“Spectrum 2” in Fig. 3, Middle column); in one case, the spectrum at the effect node has a peak at 10 Hz (Fig. 3, Top Center), whereas in the other one, it has a peak at 50 Hz (Fig. 3, Bottom Center). However, the causality functions are identical. Thus, GG causality will fail to make a distinction between these scenarios. If the analyst’s notion of what should be causal is in any way related to the properties of the observed effect—e.g., 10-Hz alpha waves vs. 50-Hz gamma waves—the face value interpretation of GG causality would be grossly misleading.

Said another way, the receiver independence property of GG causality implies that two systems can have identical causality functions, but completely different receiver dynamics. The frequency response and causality function in these examples reflect merely simple parametric differences in the transmitter dynamics. In a more general scenario, the form of the transmitter and channel VAR parameters can be more complicated, making it even more difficult to interpret causality values without first considering the dynamics of the underlying system components.

Receiver Independence: Unconditional and Conditional Time Domain and Conditional Frequency Domain.

We now show how the remaining forms of GG causality—unconditional time domain, conditional time domain, and conditional frequency domain—also appear to be independent of the receiver dynamics. For time-domain GG causality, we have derived closed-form expressions that illustrate receiver independence for both the unconditional and conditional cases. The details for these derivations are described in S7. Receiver Independence of Time-Domain GG Causality. Briefly, the time-domain GG causality compares the prediction error variances from full and reduced models. The prediction error variance for the full model is simply the input noise variance, so the dependence of the GG causality on the VAR parameters arises through the prediction error variance of the reduced model. In general, the reduced model can be obtained only numerically (25), which obscures the form of its dependence on the full-model VAR parameters. Instead, we use a state-space representation of the VAR to derive an implicit expression for the reduced-model prediction error variance in terms of the VAR parameters (S7. Receiver Independence of Time-Domain GG Causality). We then show that the reduced-model prediction error variance is independent of the receiver node VAR parameters. Hence, the time-domain GG causality is independent of receiver dynamics. This is true for both the unconditional and conditional cases.

At present, we do not have a closed-form expression for the conditional frequency-domain reduced model in terms of the full model parameters. As a consequence, we cannot determine analytically whether the conditional frequency-domain causality depends on the receiver node parameters. However, we can use the relationship between the conditional time- and frequency-domain causality measures to help analyze receiver dependence. We note that the frequency-domain causality is a decomposition of the time-domain causality. In the unconditional case (21),

$$\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{f}_{x_i⟶x_j}\left(\lambda \right)d\lambda \le {\mathcal{F}}_{x_i⟶x_j},$$

with equality if the transmitter node is stable—i.e., iff the roots of $det\left(I-{\sum }_{p=1}^P{A}_{i,i}\left(p\right)z^p\right)$ are outside the unit circle—which is the case for the systems in example 2. Similarly, in the conditional case (22),

$$\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{f}_{x_i⟶x_j\mid x_k}(\lambda )d\lambda \le {\mathcal{F}}_{x_i⟶x_j\mid x_k},$$ [7]

with equality iff the roots of $det\left({\sum }_{p=1}^{\mathrm{\infty }}G\left(p\right)z^p\right)$ are inside the unit circle, where $G$ is the system function of Eq. 4. Hence, the frequency-domain causality is a decomposition of the time-domain causality.

Because the time-domain conditional causality is independent of the receiver node, the relationship expressed in Eq. 7 would, at a minimum, impose strict constraints on the form of any receiver dependence in the frequency-domain conditional causality. Example 1 from the previous subsection qualitatively agrees with this (Fig. 2, Column 3). We see that receiver dynamics do not appear to be reflected in the conditional frequency-domain causality. In the causality estimates from node 1 to node 2 (Fig. 2, Top), the 10-Hz receiver resonance of node 2 appears to be absent. Similarly, in the causality estimates from node 2 to node 3 (Fig. 2, Middle), the 50-Hz receiver resonance of node 3 appears to be absent. Thus, the conditional frequency-domain causality appears to be independent of the receiver dynamics, similar to the other cases considered above.

Example 1 also helps to illustrate the challenge in interpreting GG causality when both the transmitter and the channel have dynamic properties, i.e., a frequency response. From node 1 to node 2, we see that the causality (Fig. 2, Column 3, Top) primarily reflects the spectrum of the transmitter, showing a prominent peak at 40 Hz (node 1, Fig. 1). In contrast, the causality from node 2 to node 3 shows a nadir at ∼15 Hz (Fig. 2, Column 3, Middle), which resembles the channel dynamics more than the node 2 transmitter dynamics (Fig. 1). This example reinforces the earlier observation that causality values cannot be appropriately interpreted without examining the estimated system components.

Discussion

Summary of Results.

In this paper we analyzed several problems encountered during Granger causality analysis. We focused primarily on the Geweke frequency-domain measure and the case where the generative processes were finite VARs of known order. We found the following:

• i)There is a troublesome bias–variance trade-off as a function of the VAR model order that can produce erroneous conditional GG causality estimates, including spurious peaks and valleys in the frequency domain, at both low and high model orders. At low model orders, the GG causality can be biased, due to the fact that subsets of VAR processes—e.g., the putative effect and conditional nodes represented by the reduced model—are VARMA processes, which in general can be represented only by infinite-order VAR models. Crucially, significant biases occur even when the data-generating process is VAR and the true underlying model order is used. As the model order increases, the bias decreases, but each model order introduces new oscillatory modes, whose variance can then introduce spurious peaks in the frequency-domain GG causality.
• ii)GG causality estimates are independent of the receiver dynamics, which can run counter to intuitive notions of causality intended to explain observed effects. Instead, GG causality estimates reflect a combination of the transmitter and channel dynamics, whose relative contributions can be understood only by examining the component dynamics of the estimated model. As a result, causality analyses, even for the simplest of examples, can be difficult to interpret.

Our results illustrate fundamental problems associated with GG causality, in terms of both its statistical properties and its conceptual interpretation. These problems have important practical consequences for neuroscience investigations using GG causality and related methods. Moreover, as we discuss below, these problems can be avoided in large part by paying more careful attention to the modeling and system identification steps that are fundamental to data analysis (Fig. 4).

Fig. 4.

System identification framework. The processes of modeling and data analysis, sometimes referred to as system identification, involve a number of steps shown here (54, 55). Models of one form or another underlie all data analyses, and model selection involves several crucial choices: the class of models from which a model structure is selected, the method(s) by which candidate models are estimated, and the criteria by which model fits are optimized and a structure selected. Subsequent analysis steps also involve important choices, including the properties and statistics to be investigated and the methods by which they are computed. These choices are shaped by the scientific question of interest. Unfortunately, the use of causality analysis methods often hides this process and the associated choices from the investigator (1). Consequently, the many possible points of failure for causality methods are also hidden, such as inappropriate model structure (2) and poor model estimation (3), poor representation of the features of interest (4), and poor statistical properties (5). More fundamentally, application of causality methods can obscure the scientific question of interest, resulting in misinterpretation (6). In addition, different causality measures with different properties or interpretations are often conflated (7).

Alternative Approaches for Estimating GG Causality.

The potential for negative causality estimates and spurious peaks in frequency-domain GG causality has been recognized previously (28). The problem has been framed primarily as one in which conditional causality estimates are sensitive to mismatches between the separate full and reduced models; i.e., spurious values occur when the spectral features of the full and reduced models do not “line up” properly. Our work identifies the bias–variance trade-off in the VAR model order as a more fundamental difficulty. Model order selection is problematic even in the context of single-model parametric spectral estimation. AR models have the property that as model order is increased, the number of potential oscillatory modes increases, which can alter estimated peak locations. This problem is compounded when the full model must be compared with an approximate reduced model.

Alternative approaches have been proposed for estimating conditional frequency-domain GG causality to eliminate the need for separate model fits. Chen et al. (28) suggested using a reduced model featuring a colored noise term formed from the components of the estimated full model. Whereas this method successfully eliminates negative causality values, it does not correctly partition the variance of the putative causal nodes within the reduced model (34). Thus, it is unclear whether the method described in Chen et al. (28) can accurately estimate conditional GG causality. Barnett and Seth (25) have proposed fitting the reduced model and using it to directly compute the spectral components of Eq. 5. However, for the same reasons described above, these reduced-model estimates will generally require high model order representations that would be susceptible to spurious peaks. Moreover, this method would remain sensitive to mismatches between the spectral estimates of the components in Eqs. 3–5.

Potential Problems in Interpreting GG Causality Analyses in Neuroscience Studies.

The statistical problems illustrated in this paper raise obvious concerns for the reliability of Granger causality estimates. However, the problems of interpreting causality values, even if they are estimated accurately, are more fundamental. Receiver independence for a scalar unconditional frequency-domain example was previously noted in ref. 35. In this work, we have shown that this holds more generally, for the vector unconditional frequency-domain, the unconditional time-domain, and the conditional time-domain cases. We have also shown evidence for receiver independence in the conditional frequency-domain case as well. Here we also discuss the conceptual difficulty this poses in neuroscience.

That GG causality is unaffected by and not reflective of the receiver dynamics is entirely understandable from the original principle underlying the definition of Granger causality, that of improved prediction. The use of improvement of prediction makes sense in the context of econometrics, from which GG causality originated, where the objective is often to construct parsimonious models to make predictions. The functional interpretation of the models is considered less important in this context than the accuracy of the predictions. However, in neuroscience investigations, the opposite is generally true: Fundamentally, a mechanistic understanding of the neurophysiological system is sought, and as a result the structure and functional interpretation of the models are most important. In particular, neuroscience investigations seek to determine the mechanisms that produce “effects” observed at a particular site within a neural system or circuit as a function of inputs or “causes” observed at other locations. The effect node dynamics are central to this question, as they determine how the effect node responds to different inputs. In contrast, the predictive notion of causality that underlies Granger causality methods explicitly ignores the effect node dynamics and effect size.

There are numerous examples in neuroscience that illustrate the importance of the effect or receiver node dynamics and effect size. For example, the dynamics of high-threshold thalamocortical neurons are governed by the degree of membrane hyperpolarization, producing tonic firing at the lowest levels of hyperpolarization, burst firing at alpha ($\sim$10 Hz) frequencies at intermediate levels of hyperpolarization, and burst firing at low frequencies (<1 Hz) at even greater levels of hyperpolarization (36). If we viewed the firing behavior or postsynaptic fields generated by these neurons as the effect to be explained, the Granger methods would be blind to their frequency response, which is fundamental to their neurophysiology. As another example, studies of cognition and memory using fMRI have demonstrated that the amplitude of blood–oxygen-level–dependent responses can be modulated by stimulus novelty and cognitive complexity (37). Characterizations of these effects with Granger causality methods would be similarly indeterminate in explaining these amplitude-dependent effects that are central to the cognitive processes being studied. As a final example, we note a recent study by Epstein et al. (38) in which Granger causality was used to analyze electrocorticogram recordings of seizure activity in epilepsy patients, with the goal of informing epilepsy surgery planning. Epileptic seizures are observed electrophysiologically by the localized onset and propagation of characteristic oscillations, often of large amplitude. The seizure effect is therefore defined by both the system dynamics and the amplitude of the electrophysiological response. Unfortunately, because GG causality is indifferent to the receiver dynamics and the amplitude of the measured effects, it cannot specify which influences, for instance at specific foci and frequencies, contribute to the seizure effect. In particular, an epileptogenic focus would not necessarily have large GC values, because the seizure onset and propagation may be due to the effect node’s internal dynamics. At the same time, large GC values do not necessarily suggest a focus, because large GC values relate to prediction error variance and not to the effect at the recording site.

These examples illustrate how Granger causality methods, due to the receiver-independence property, can fail to characterize essential neurophysiological effects of interest and lead to misinterpretation of the causes for those effects. These examples are representative of typical neuroscience problems seeking the “cause” for an “effect,” implying that the misapplication of Granger methods is likely widespread within neuroscience.

Implications for Other Causality Methods.

The conceptual disagreement between GG causality and the mechanistic interpretation of data from neuroscience studies such as Epstein et al. (38) stems fundamentally from a disconnect between the system properties of interest, given the scientific question, and those represented by GG causality. Beyond GG causality, numerous alternative causality measures have also been proposed, including the directed transfer function (DTF) (39, 40), the partial directed coherence (PDC) (41), and the direct directed transfer function (dDTF) (42, 43). Like GG causality, these causality measures are based on a VAR model, but each of these methods represents a different functional combination of the individual system components and thus a conceptually distinct notion of causality. The DTF represents the transfer function, not from the transmitter to the receiver, but instead from an exogenous white noise input at the transmitter to the receiver. Depending on the normalization used, it may actually include the dynamics of all systems components. The DTF essentially captures all information passing from the transmitter directed to the receiver, but this information flow is not direct (42, 43) (Fig. S5). The dDTF claims to characterize direct influences by normalizing the DTF by the partial coherence. The PDC, on the other hand, represents the actual channel between two nodes (44) but, depending on how it is normalized, may contain the frequency content of other components (Fig. S5). These measures all differ from GG causality, which represents a combination of the transmitter and direct channel dynamics, as well as the conditional node variances and their indirect channel dynamics.

Fig. S5.

Diagrammatic comparison of components of several causality measures. The directed graph represents a VAR system of nodes $x_j$, $x_i$, and $x_k$ with white noise inputs $w_j$, $w_i$, and $w_k$. The system components reflected in several causality measures from $x_i$ to $x_j$ are compared. The ARMA relation from $x_i$ to $x_j$ is shown at the top. The transfer function (TF) from $x_i$ to $x_j$ is highlighted in blue and comprises the channel and receiver dynamics. The unnormalized PDC is highlighted in red and contains just the channel. The one-step detection test, noted in Lütkepohl (30), is highlighted in orange and assesses whether the AR coefficients of the channel are all zero. The unnormalized DTF is highlighted in purple. It is the cross-component of the right-sided MA form of the system or equivalently the inverse of the left-sided VAR form and, due to the inverse, possibly contains information from all components. GG causality is highlighted in green and, as we have shown, primarily reflects the channel and transmitter dynamics, but also includes indirectly connected channels and the input noise variances.

Each of the above measures, with the exception of the dDTF, is based on a single-model estimate and thus does not suffer from the model subset or sensitivity issues we have described for GG causality. However, similar to GG causality, all of these methods can be problematic to interpret, because each measure represents a combination of different system components whose contributions cannot be disentangled by examining the causality values alone. Thus, studies using these methods may be subject to a mismatch between the system properties represented by the measures and the properties of interest to the investigator. Despite the clear fundamental differences in how these and other causality measures are defined, these methods are often discussed as interchangeable alternatives or referred to generically as “Granger causality” (35, 44, 45), making it even more difficult to interpret studies using these methods.

In many cases, investigators may wish to detect connections between nodes in a system and may not be concerned with interpreting the form or dynamics of such connections. In such cases, under a VAR model, the direct connection between nodes is represented by the corresponding cross-components of the VAR parameter matrices, which indicate the absence of a connection if all of these parameters are equal to zero. Hypothesis tests for such connections have been described in the time series analysis literature (30, 46). This approach is analogous to that proposed by Kim et al. (1) for point process models of neural spiking data. To our knowledge, the VAR versions (30, 46) of this approach have not been used in neuroscience applications, but may offer potential advantages in computational and statistical efficiency compared with more widely applied permutation-based tests on causality measures, such as those outlined in ref. 25.

A number of causality approaches have been developed that purportedly handle a wider range of generative dynamic systems, beyond those that might be well approximated by VAR models. Transfer entropy methods (31, 47, 48) can be viewed as a generalization of the Granger approach and are applicable to nonlinear systems. However, such methods require significant amounts of data, are computationally intensive, and present their own model identification issues, such as selection of the embedding order. These approaches are strictly time-domain measures, and their similarity to GG causality (31) suggests that they would face similar problems with interpretation such as independence of receiver dynamics. Dynamic causal modeling (DCM) uses neurophysiologically plausible dynamic models to characterize causal relationships (49). The models, estimation methods, and notions of causality involved in DCM are different from the time series-based causality approaches discussed here. The interpretation and statistical properties of DCM are the subject of ongoing analysis (50–53).

Causality Analysis in the Framework of System Identification.

The problems in causality methods that we have discussed arise when these methods are applied without clear reference to the underlying models, their estimation methods and statistical measures, or the scientific question of interest—that is, without clear reference to the process of system identification (54, 55). System identification comprises the set of steps undertaken to study a scientific question (Fig. 4), including the processes of model formulation and model selection. Although these steps can be challenging and complex, they are essentially a quantitative formalization of the scientific method. Unfortunately, causality methods have been used, in effect, to circumvent many of these painstaking steps (Fig. 4, annotation 1). As we have seen in our analysis, this can mask many potential points of failure, including poor representation of the system by the model, and computational and interpretational problems with statistics computed from the model. Perhaps more importantly, the use of causality methods supplants a clear statement of the scientific question of interest with an ambiguous statistic and a loaded concept that carries philosophical connotations, detracting from the question at hand.

In many cases, the scientific question of interest is simply to determine the presence or absence of a direct connection from one region to another. This question can often be answered directly from the estimated model. In the case of VAR models, as discussed earlier, a hypothesis test could be performed on the off-diagonal VAR components (30). In the transfer function case, this is given by the unnormalized PDC. In DCM, this is explicitly represented in the selected model’s connections (49).

In other cases, the scientific question centers on characterizing the mechanistic interactions between components of a system. As we have argued, this can be ascertained by examining the component dynamics from the estimated model. For instance, in the analysis of electrocorticographic oscillations in nonhuman primate somatosensory cortex described in ref. 5, one could examine the component node and channel dynamics to characterize more specific interactions between system components.

Yet in other cases, the scientific question may relate to predicting the effects that structural changes might have on system dynamics. For instance, Epstein et al. (38) wanted to evaluate whether surgical resections could alleviate seizures. This question could also be investigated from the estimated model, by removing connections or nodes, simulating data using the model, and then evaluating the influence of these interventions on the generation of seizure oscillations. The validity of such statements would be incumbent on the applicability of the model and would require experimental validation. However, by structuring the problem in terms of the dynamic systems model, this validation is straightforward, more so than with causality measures.

In the end, causality measures, however elaborate in construction, are simply statistics estimated from the model (Fig. 4, model statistics). If the model does not adequately represent the system properties of interest, subsequent analyses based on the model will fail to address the question of interest. The VAR model class underlying GG causality and other causality measures represents linear relationships within stationary time series data. Although VAR models can, in many cases, adequately approximate properties of nonlinear systems, in general this structure limits the system behaviors that can be modeled. For example, VAR models cannot explicitly represent cross-frequency coupling. Thus, although a model structure may fit some features of the data, its representation of other features and applicability to the system as a whole may not be adequate and must be considered carefully (Fig. 4, postulate models). The inability of the model to represent key features of interest can in turn lead to erroneous assessments of causality (2, 3), independent of the computational and interpretational problems that we describe in this paper. We note that such failures of causality analysis are frequently discussed in the literature, often without identifying modeling misspecification as the key point of failure.

Overall, the problems of GG causality analyzed in this paper, the related problems of other causality methods, and the ongoing confusion surrounding these methods can, in most cases, be resolved by a careful consideration of system identification principles (Fig. 4). Moreover, careful modeling and analysis likely obviate the need for causality measures and their many potential pitfalls.

S1. Relationships Between Different Causality Measures and the System Components of the Underlying VAR Model

As discussed in the main text, many of the causality measures used in neuroscience data analysis are derived from an underlying VAR model. The construction of these causality measures incorporates different components of the VAR system. This is illustrated in Fig. S5. To correctly interpret analyses using these methods, it is important to understand the relationships between the causality measures and the components of the underlying VAR model.

To make the interrelationships between the different causality measures shown in Fig. S5 more clear, we derive here an expression for the transfer function between the putative causal node $x_i$ and the putative effect node $x_j$. From the full VAR model, we can write the model for the single component $x_j$ in an autoregressive moving-average (ARMA) form,

$${\mathcal{A}}_{j,j}\left(\lambda \right)X_j\left(\lambda \right)=-{\mathcal{A}}_{j,i}\left(\lambda \right)X_i\left(\lambda \right)+\sum _{k\ne \{j,i\}}-{\mathcal{A}}_{j,k}\left(\lambda \right)X_k\left(\lambda \right)+W_j\left(\lambda \right).$$

Inverting the left-hand AR transfer function,

$$X_j\left(\lambda \right)=\frac{-{\mathcal{A}}_{j,i}\left(\lambda \right)}{{\mathcal{A}}_{j,j}\left(\lambda \right)}{X}_i\left(\lambda \right)+\sum _{k\ne \{j,i\}}\frac{-{\mathcal{A}}_{j,k}\left(\lambda \right)}{{\mathcal{A}}_{j,j}\left(\lambda \right)}{X}_k\left(\lambda \right)+\frac{1}{{\mathcal{A}}_{j,j}\left(\lambda \right)}{W}_j\left(\lambda \right),$$

we obtain the transfer function from $x_i$ (and those from all other nodes $x_k$) to $x_j$, i.e., $-{\mathcal{A}}_{j,i}\left(\lambda \right)/{\mathcal{A}}_{j,j}\left(\lambda \right)$ (and analogously for other nodes $x_k$).

It is clear from this expression that the transfer function between $x_i$ and $x_j$, the (unnormalized) PDC, and the one-step detection test (30) share in common the channel dynamics represented in $\{A_{j,i}\left(p\right)\}$. In contrast, the (unnormalized) DTF, whose expression is shown in the diagram in Fig. S5 and derived in S3. Removal of Instantaneous Causality for Frequency-Domain Computation, represents the relationship between the white noise input $w_i$ and the putative effect node $x_j$.

S2. Instantaneous Causality and Total Linear Dependence

In addition to the unconditional and conditional directed causality measures, ${\mathcal{F}}_{i⟶j}$ and ${\mathcal{F}}_{i⟶j\mid k}$, Geweke (21, 22) also defined associated (undirected) instantaneous causality measures. The unconditional instantaneous causality is

$${\mathcal{F}}_{i\cdot j}=\ln \frac{\left|\text{var}\left(x_{j,t}-{\widehat{x}}_{j,t}^f\right)\right|\cdot \left|\text{var}\left(x_{i,t}-{\widehat{x}}_{i,t}^f\right)\right|}{\left|\text{var}\left(x_{\cdot ,t}-{\widehat{x}}_{\cdot ,t}^f\right)\right|}=\ln \frac{|{\mathrm{\Sigma }}_{j,j}^f||{\mathrm{\Sigma }}_{i,i}^f|}{\left|{\mathrm{\Sigma }}_{\cdot ,\cdot }^f\right|},$$ [S1]

where the subscript “$\cdot$” denotes all components of the system, i.e., $\{j,i\}$ in the unconditional case. The expression for the instantaneous causality in the conditional case, ${\mathcal{F}}_{i\cdot j\mid k}$, is identical, with the conditional components $k$ included in the models.

An alternative measure quantifying the dependence between two time series, e.g., between $\{x_{i,t}\}$ and $\{x_{j,t}\}$, is the total linear dependence,

$${\mathcal{F}}_{i,j}=\ln \frac{\left|\text{var}\left(x_{j,t}-{\widehat{x}}_{j,t}^{r\left(i\right)}\right)\right|\cdot \left|\text{var}\left(x_{i,t}-{\widehat{x}}_{i,t}^{r\left(j\right)}\right)\right|}{\left|\text{var}\left(x_{\cdot ,t}-{\widehat{x}}_{\cdot ,t}^f\right)\right|}=\ln \frac{\left|{\mathrm{\Sigma }}_{j,j}^{r\left(i\right)}\right|\left|{\mathrm{\Sigma }}_{i,i}^{r\left(i\right)}\right|}{\left|{\mathrm{\Sigma }}_{\cdot ,\cdot }^f\right|}.$$

Hence, one additional motivation of the definition of directed and instantaneous causality of Geweke (21) is that they compose a time-domain decomposition of the total linear dependence, such that

$${\mathcal{F}}_{i,j}={\mathcal{F}}_{i⟶j}+{\mathcal{F}}_{j⟶i}+{\mathcal{F}}_{i\cdot j}.$$

The expression for the total linear dependence in the conditional case, ${\mathcal{F}}_{i,j\mid k}$, is identical, such that the conditional definitions of directed and instantaneous causality of Geweke (22) similarly compose a time-domain decomposition,

$${\mathcal{F}}_{i,j\mid k}={\mathcal{F}}_{i⟶j\mid k}+{\mathcal{F}}_{j⟶i\mid k}+{\mathcal{F}}_{i\cdot j\mid k}.$$

S3. Removal of Instantaneous Causality for Frequency-Domain Computation

The definition of the unconditional frequency-domain causality as a directed decomposition of the spectrum requires any instantaneous correlation between the noise processes, i.e., the instantaneous causality $F_{i\cdot j}$ in Eq. S1, to be removed. This can be achieved by applying a transformation to the system that block diagonalizes the noise covariance ${\mathrm{\Sigma }}^f$ while preserving the model spectrum $S\left(\lambda \right)=H^f\left(\lambda \right){\mathrm{\Sigma }}^f{\left(H^f\left(\lambda \right)\right)}^{\ast }$. Postmultiplying the system function by $D^{-1}$ and premultiplying the noise process by $D$, such that

$$S\left(\lambda \right)=\left(H^f\left(\lambda \right)D^{-1}\right)\left(D{\mathrm{\Sigma }}^f{D}^T\right)\left(D^{-T}{\left(H^f\left(\lambda \right)\right)}^{\ast }\right),$$

where

$$D=\left[\begin{array}{cc}\hfill \text{I}\hfill & \hfill 0\hfill \\ \hfill -{\mathrm{\Sigma }}_{ij}^f{\left({\mathrm{\Sigma }}_{jj}^f\right)}^{-1}\hfill & \hfill \text{I}\hfill \end{array}\right],$$

leaves the output spectrum invariant, but rotates the system to a model with block-diagonal input noise covariance ${\stackrel{\sim }{\mathrm{\Sigma }}}^f=D{\mathrm{\Sigma }}^f{D}^T$ and transformed system function ${\stackrel{\sim }{H}}^f\left(\lambda \right)=H^f\left(\lambda \right)D^{-1}$. Here we are following our ordering convention from the main text, where if we are investigating the causality from $x_i$ to $x_j$, the effect components are ordered before the causal components; i.e., $x_t={\left[\begin{array}{cc}\hfill x_{j,t}^T\hfill & \hfill x_{i,t}^T\hfill \end{array}\right]}^T$.

In the conditional case, the frequency-domain causality computation requires removal of the instantaneous causality from both the full model and the reduced model. For the reduced model, the system function $H^{r\left(i\right)}\left(\lambda \right)$ and noise covariance ${\mathrm{\Sigma }}^{r\left(i\right)}$ are transformed, as above, to ${\stackrel{\sim }{H}}^{r\left(i\right)}\left(\lambda \right)$ and ${\stackrel{\sim }{\mathrm{\Sigma }}}^{r\left(i\right)}$, using

$$D^{r\left(i\right)}=\left[\begin{array}{cc}\hfill \text{I}\hfill & \hfill 0\hfill \\ \hfill -{\mathrm{\Sigma }}_{kj}^{r\left(i\right)}{\left({\mathrm{\Sigma }}_{jj}^{r\left(i\right)}\right)}^{-1}\hfill & \hfill \text{I}\hfill \end{array}\right].$$

Similarly, the system function $H^f\left(\lambda \right)$ and noise covariance matrix ${\mathrm{\Sigma }}^f$ of the full model are transformed to ${\stackrel{\sim }{H}}^f\left(\lambda \right)$ and ${\stackrel{\sim }{\mathrm{\Sigma }}}^f$, but in this case, the transformation matrix for the full model [appendix in Chen et al. (28)] is given by

$$D^f=\left[\begin{array}{ccc}\hfill \text{I}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \text{I}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\left({\mathrm{\Sigma }}_{ki}^f-{\mathrm{\Sigma }}_{kj}^f{\left({\mathrm{\Sigma }}_{jj}^f\right)}^{-1}{\mathrm{\Sigma }}_{jk}^f\right){\left({\mathrm{\Sigma }}_{ii}^f-{\mathrm{\Sigma }}_{ij}^f{\left({\mathrm{\Sigma }}_{jj}^f\right)}^{-1}{\mathrm{\Sigma }}_{ji}^f\right)}^{-1}\hfill & \hfill \text{I}\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill \text{I}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\mathrm{\Sigma }}_{ij}^f{\left({\mathrm{\Sigma }}_{jj}^f\right)}^{-1}\hfill & \hfill \text{I}\hfill & \hfill 0\hfill \\ \hfill -{\mathrm{\Sigma }}_{kj}^f{\left({\mathrm{\Sigma }}_{jj}^f\right)}^{-1}\hfill & \hfill 0\hfill & \hfill \text{I}\hfill \end{array}\right].$$

Note that the nature of the transformations now makes the causality computation dependent on the order of the components in the vector time series. Again, we are following our ordering convention from the main text. When investigating the causality from $x_i$ to $x_j$ conditional on $x_k$, the effect components are ordered before the causal components in both the full and reduced models and the conditional components are appended to the end of the full model, i.e., $\{j,i\}$ and $\{j,i,k\}$.

S4. MA Matrix Recursions for Invertible VAR Systems

In the computation of GG causality, the full and reduced models are assumed to be stable and invertible so that the transfer functions can be computed. The VAR(P) system

$$x_t-\sum _{p=1}^{P}A\left(p\right)x_{t-p}=w_t$$

is invertible if

$$det\left(I-\sum _{p=1}^{P}A\left(p\right)z^p\right)\ne 0\hspace{0.17em}\text{for}|z|\le 1.$$

The transfer function is then

$$H\left(\lambda \right)={\left(I-\sum _{p=1}^{P}A\left(p\right)e^{-ip\lambda }\right)}^{-1}.$$

The transfer function can also be expressed as the Fourier transform of the MA matrices. In MA form, the system is

$$x_t=\sum _{p=0}^{\mathrm{\infty }}\mathrm{\Phi }\left(p\right)w_{t-p},$$

giving the following alternative expression for the transfer function,

$$H\left(\lambda \right)=\sum _{p=0}^{\mathrm{\infty }}\mathrm{\Phi }\left(p\right)e^{-ip\lambda }.$$

Although we do not make use of the MA matrices in the main text, for convenience we note here that the MA matrices can be computed recursively from the AR matrices [Lütkepohl (30)]:

$$\mathrm{\Phi }\left(0\right)=I_M$$

$$\mathrm{\Phi }\left(p\right)=\sum _{j=1}^p\mathrm{\Phi }\left(p-j\right)A\left(j\right)\text{for}\hspace{0.17em}p=1,2,\mathrm{\dots }.$$

S5. Construction of Simulated Examples

In the examples presented in the main text, we used simulated VAR systems with spectral peaks at distinct frequencies. Within the VAR model class, these peaks can be generated by the univariate AR behavior, what we refer to as the internal dynamics, of the individual nodes. For a univariate AR system, a spectral peak requires a model order of two, i.e., $x_t=A\left(1\right)x_{t-1}+A\left(2\right)x_{t-2}+w_t$, and every increase of the order by two adds a peak.

The modes of the system are given by the roots of the characteristic polynomial or equivalently the eigenvalues of the VAR(1)-form system matrix. In the AR(2) case, this is

$$det\left(\lambda I-\left[\begin{array}{cc}\hfill A\left(1\right)\hfill & \hfill A\left(2\right)\hfill \\ \hfill I\hfill & \hfill 0\hfill \end{array}\right]\right)={\lambda }^2-A\left(1\right)\lambda -A\left(2\right)=0.$$ [S2]

To have an oscillatory peak, the roots must be a complex conjugate pair, such that the characteristic equation can be factored as

$$\left(\lambda -r{e}^{i\theta }\right)\left(\lambda -r{e}^{-i\theta }\right)=0.$$ [S3]

Expanding the left-hand side of Eq. S3 and using Euler identities reduce the expression to

$${\lambda }^2-r\left(e^{i\theta }+e^{-i\theta }\right)\lambda +r^2={\lambda }^2-2r\cos \left(\theta \right)\lambda +r^2.$$

Matching terms with Eq. S2 gives expressions for the AR(2) parameters in terms of the desired pole amplitudes and frequencies,

$$\begin{array}{c}A\left(2\right)=-r^2\\ A\left(1\right)=2r\cos \left(\theta \right).\end{array}$$

Here, $\theta$ is the pole angle in radians. It is related to the frequency $f$ in hertz by $\theta =f\mathrm{\Delta }t2\pi$, where the assumed sampling rate is $\frac{1}{\mathrm{\Delta }t}$ Hz. These expressions were used to set the resonance frequencies of the individual nodes in the simulated examples in the main text. For single nodes, i.e., univariate AR, $r<1$ ensures stability. In the multivariate case, the overall stability of the system is guaranteed only if all eigenvalues of the VAR(1)-form system matrix are within the unit circle.

Note that whereas the pole location is given by $\theta$, this frequency is not the exact maximum of the spectrum, only approximate. It is possible to derive an analytical expression for the spectral peak frequency in terms of $r$ and $\theta$ [for example, Priestley (56)], but the expression is quite cumbersome. For ease of discussion, in the main text, we have referred to the pole location $\theta$ as the spectral peak location. Although this is not strictly true, the approximation in our case is reasonable.

S6. Receiver Independence of Unconditional Frequency-Domain GG Causality

In this section, we show that the unconditional frequency-domain GG causality is independent of the receiver dynamics. Without loss of generality, we demonstrate that the causality from transmitter $x_1$ to receiver $x_2$ is independent of the parameters governing the internal receiver dynamics $\{A_{22}\left(p\right)\}$. We begin by writing the full-model transfer function $H\left(\lambda \right)$ in terms of block components. The transfer function is the inverse of the Fourier transform of the VAR, $\mathcal{A}\left(\lambda \right)=I-{\sum }_{p=1}^{P}A\left(p\right)e^{-ip\lambda }$, so from the matrix inversion lemma

$$\left[\begin{array}{cc}\hfill H_{11}\left(\lambda \right)\hfill & \hfill H_{12}\left(\lambda \right)\hfill \\ \hfill H_{21}\left(\lambda \right)\hfill & \hfill H_{22}\left(\lambda \right)\hfill \end{array}\right]={\left[\begin{array}{cc}\hfill {\mathcal{A}}_{11}\left(\lambda \right)\hfill & \hfill {\mathcal{A}}_{12}\left(\lambda \right)\hfill \\ \hfill {\mathcal{A}}_{21}\left(\lambda \right)\hfill & \hfill {\mathcal{A}}_{22}\left(\lambda \right)\hfill \end{array}\right]}^{-1}=\left[\begin{array}{cc}\hfill {\mathcal{A}}_{11}^{-1}+{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}{\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}\hfill & \hfill -{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}{\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}\hfill \\ \hfill -{\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}\hfill & \hfill {\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}\hfill \end{array}\right].$$

Writing the causality in terms of the transfer function and noise covariance components,

$$f_{x_1⟶x_2}\left(\lambda \right)=\ln \frac{\left|H_{22}\left(\lambda \right){\mathrm{\Sigma }}_{22}{H}_{22}^{\ast }\left(\lambda \right)+H_{21}\left(\lambda \right){\mathrm{\Sigma }}_{11}{H}_{21}^{\ast }\left(\lambda \right)\right|}{\left|H_{22}\left(\lambda \right){\mathrm{\Sigma }}_{22}{H}_{22}^{\ast }\left(\lambda \right)\right|}.$$

Substituting in terms of $\mathcal{A}$ components from above,

$$f_{x_1⟶x_2}\left(\lambda \right)=\ln \frac{\left|{\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}\{{\mathrm{\Sigma }}_{\mathrm{2,2}}+{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathrm{\Sigma }}_{11}{\left({\mathcal{A}}_{11}^{-1}\right)}^{*}{\mathcal{A}}_{21}^{*}\}{\left({\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}\right)}^{*}\right|}{\left|{\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}{\mathrm{\Sigma }}_{22}{\left({\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}\right)}^{*}\right|}.$$

Recall that for a matrix $|\mathrm{\Sigma }|=\sqrt{det\mathrm{\Sigma }\prime \mathrm{\Sigma }}$. Because for square matrices the determinant of the product is equal to the product of the determinants, the determinants of all factors in both the numerator and the denominator separate. Consequently, the determinants of the first factors, ${\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}$, the last factors, ${\left({\left({\mathcal{A}}_{22}-{\mathcal{A}}_{21}{\mathcal{A}}_{11}^{-1}{\mathcal{A}}_{12}\right)}^{-1}\right)}^{\ast }$, and their corresponding transposes cancel from the numerator and denominator. This results in the final equality,

$$f_{x_1⟶x_2}\left(\lambda \right)=\ln \frac{\left|{\mathrm{\Sigma }}_{22}+{\mathcal{A}}_{21}\left(\lambda \right){\mathcal{A}}_{11}^{-1}\left(\lambda \right)\mathrm{\Sigma }{}_{11}\mathcal{A}_{11}^{-1\ast }\left(\lambda \right){\mathcal{A}}_{21}^{\ast }\left(\lambda \right)\right|}{|{\mathrm{\Sigma }}_{22}|}.$$

We thus see that the receiver dynamics ${\mathcal{A}}_{22}\left(\lambda \right)$ do not appear. Because the time-domain causality is the integral of the frequency-domain causality, the time-domain unconditional GG causality is independent of the receiver dynamics as well.

S7. Receiver Independence of Time-Domain GG Causality

The GG causality from node i to node j compares the one-step prediction-error variance of the full model, ${\mathrm{\Sigma }}_{jj}^f$, with the one-step prediction-error variance of the reduced model, ${\mathrm{\Sigma }}_{jj}^{r\left(i\right)}$,

$${\mathcal{F}}_{x_i⟶x_j}=\ln \frac{\left|\text{var}\left(x_{j,t}-{\widehat{x}}_{j,t}^{r\left(i\right)}\right)\right|}{\left|\text{var}\left(x_{j,t}-{\widehat{x}}_{j,t}^f\right)\right|}=\ln \frac{\left|{\mathrm{\Sigma }}_{jj}^{r\left(i\right)}\right|}{\left|{\mathrm{\Sigma }}_{jj}^f\right|}.$$

The prediction-error covariance of the full model is just the input noise covariance ${\mathrm{\Sigma }}^f={\mathrm{\Sigma }}_w$, so the dependence of the GG causality on the VAR parameters arises through the prediction-error covariance of the reduced model. We do not have a closed-form expression for the reduced model with respect to the full-model parameters. In general, the reduced model can only be obtained numerically (25), which obscures the form of its dependence on the full-model VAR parameters. Instead, we use a state-space representation of the VAR to derive an expression for the reduced-model prediction-error variance in terms of the VAR parameters. From this, we will see that the receiver node VAR parameters do not enter into the equation for the reduced-model prediction-error variance, and thus, the time-domain GG causality is independent of receiver dynamics. This is true for both the unconditional and conditional cases.

To put the model in state-space form, we write the VAR(P) full model as the augmented VAR(1) state equation,

$${\overline{x}}_t=F{\overline{x}}_{t-1}+G{w}_t=\left[\begin{array}{cccc}\hfill A^f\left(1\right)\hfill & \hfill \mathrm{\cdots }\hfill & \hfill A^f\left(P-1\right)\hfill & \hfill A^f\left(P\right)\hfill \\ & \hfill \text{I}\hfill & & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_{t-1}\hfill \\ \hfill ⋮\hfill \\ \hfill x_{t-p}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill \text{I}\hfill \\ \hfill 0\hfill \end{array}\right]w_t^f,$$ [S4]

where ${\overline{x}}_t={\left[\begin{array}{cccc}\hfill x_t^T\hfill & \hfill x_{t-1}^T\hfill & \hfill \mathrm{\dots }\hfill & \hfill x_{t-\left(P-1\right)}^T\hfill \end{array}\right]}^T$ is the augmented state. The observation equation is

$$y_t=H{\overline{x}}_t+v_t=\left[\begin{array}{cccc}\hfill \left(\begin{array}{cc}\hfill \text{I}\hfill & \hfill 0\hfill \end{array}\right)\hfill & \hfill 0\hfill & \hfill \mathrm{\dots }\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_t\hfill \\ \hfill x_{t-1}\hfill \\ \hfill ⋮\hfill \\ \hfill x_{t-\left(P-1\right)}\hfill \end{array}\right]=x_{j,t},$$ [S5]

where $H$ is a selection matrix that selects the observed components from the top block of the state, the observation noise is zero, $v_t=0$, and our convention is that the observed/effect components are ordered first in each block, $x_t={\left[\begin{array}{cc}\hfill x_{j,t}^T\hfill & \hfill x_{i,t}^T\hfill \end{array}\right]}^T$.

The reduced-model prediction-error covariance is simply the observed components of the state prediction-error covariance,

$${\mathrm{\Sigma }}^{r\left(i\right)}=H{\mathrm{\Sigma }}_{t+1\mid t}{H}^T.$$ [S6]

The state prediction-error covariance and state (filtered)-error covariance are given recursively by the standard Kalman filter equations,

$${\mathrm{\Sigma }}_{t+1\mid t}=F{\mathrm{\Sigma }}_{t\mid t}{F}^T+G{\mathrm{\Sigma }}_w{G}^T$$ [S7]

and

$${\mathrm{\Sigma }}_{t\mid t}={\mathrm{\Sigma }}_{t\mid t-1}-{\mathrm{\Sigma }}_{t\mid t-1}{H}^T{\left(H{\mathrm{\Sigma }}_{t\mid t-1}{H}^T+R\right)}^{-1}H{\mathrm{\Sigma }}_{t\mid t-1},$$ [S8]

where in this case the observation noise covariance is zero, $R=0$. We designate the blocks of the prediction-error and state covariances by

$$\begin{array}{cccc}\hfill {\mathrm{\Sigma }}_{t+1\mid t}=\left[\begin{array}{cc}\hfill K_{t+1}\hfill & \hfill L_{t+1}\hfill \\ \hfill L_{t+1}^T\hfill & \hfill N_{t+1}\hfill \end{array}\right]\hfill & \hfill \text{and}\hfill & \hfill {\mathrm{\Sigma }}_{t\mid t}=\left[\begin{array}{cc}\hfill B_t\hfill & \hfill C_t\hfill \\ \hfill C_t^T\hfill & \hfill D_t\hfill \end{array}\right],\hfill & \hfill \text{respectively.}\hfill \end{array}$$

To see the VAR parameter dependence, we write out the state prediction-error equation, Eq. S7, by components. To demonstrate without loss of generality, we use VAR(2),

$${\mathrm{\Sigma }}_{t+1\mid t}=\left[\begin{array}{cc}\hfill A^{\left(1\right)}\hfill & \hfill A^{\left(2\right)}\hfill \\ \hfill \text{I}\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{cc}\hfill B_t\hfill & \hfill C_t\hfill \\ \hfill C_t^T\hfill & \hfill D_t\hfill \end{array}\right]\left[\begin{array}{cc}\hfill A^{\left(1\right)T}\hfill & \hfill \text{I}\hfill \\ \hfill A^{\left(2\right)T}\hfill & \hfill 0\hfill \end{array}\right]+\left[\begin{array}{c}\hfill \text{I}\hfill \\ \hfill 0\hfill \end{array}\right]{\mathrm{\Sigma }}_w\left[\begin{array}{cc}\hfill \text{I}\hfill & \hfill 0\hfill \end{array}\right].$$ [S9]

In this case, the blocks $K$, $L$, $N$, $B$, $C$, and $D$ all have dimensions $M\times M$, the same dimensions as the VAR matrices $A^{\left(p\right)}$, where $M$ is the number of system components. For notational simplicity, we have removed the superscript $f$ from the VAR matrices and moved the AR lag index to superscript. Because the reduced components are directly observed, $y_t=x_{j,t}$, the associated state-error variances are zero, so the only nonzero components of the blocks are the covariances of the unobserved/omitted components,

$$B_t=\begin{array}{cccc}\hfill \left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{\left(i\right)t,t\mid t}^2\hfill \end{array}\right),\hfill & \hfill C_t=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{\left(i\right)t,t-1\mid t}^2\hfill \end{array}\right),\hfill & \hfill \text{and}\hfill & \hfill D_t=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_{\left(i\right)t-1,t-1\mid t}^2\hfill \end{array}\right).\hfill \end{array}$$

Carrying out the matrix multiplication of Eq. S9 for the prediction-error covariance, we have

$${\mathrm{\Sigma }}_{t+1\mid t}=\left[\begin{array}{cc}\hfill K_{t+1}\hfill & \hfill L_{t+1}\hfill \\ \hfill L_{t+1}^T\hfill & \hfill N_{t+1}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill {\mathrm{\Sigma }}_w+A^{\left(1\right)}{B}_t{A}^{\left(1\right)T}+A^{\left(2\right)}{C}_t^T{A}^{\left(1\right)T}+A^{\left(1\right)}{C}_t{A}^{\left(2\right)T}+A^{\left(2\right)}{D}_t{A}^{\left(2\right)T}\hfill & \hfill A^{\left(1\right)}{B}_t+A^{\left(2\right)}{C}_t^T\hfill & \\ \hfill B_t{A}^{\left(1\right)T}+C_t{A}^{\left(2\right)T}\hfill & \hfill B_t\hfill & \end{array}\right].$$

The top left block of ${\mathrm{\Sigma }}_{t+1\mid t}$ is

$$K_{t+1}={\mathrm{\Sigma }}_w+A^{\left(1\right)}{B}_t{A}^{\left(1\right)T}+A^{\left(2\right)}{C}_t^T{A}^{\left(1\right)T}+A^{\left(1\right)}{C}_t{A}^{\left(2\right)T}+A^{\left(2\right)}{D}_t{A}^{\left(2\right)T}=\left(\begin{array}{cc}\hfill {\mathrm{\Sigma }}_{w_j}+A_{ji}^{\left(1\right)}{\sigma }_{t,t\mid t}^2{A}_{ji}^{\left(1\right)T}+A_{ji}^{\left(2\right)}{\sigma }_{t-1,t\mid t}^2{A}_{ji}^{\left(1\right)T}+A_{ji}^{\left(1\right)}{\sigma }_{t,t-1\mid t}^2{A}_{ji}^{\left(2\right)T}+A_{ji}^{\left(2\right)}{\sigma }_{t-1,t-1\mid t}^2{A}_{ji}^{\left(2\right)T}\hfill & \hfill A_{ji}^{\left(1\right)}{\sigma }_{t,t\mid t}^2{A}_{ii}^{\left(1\right)T}+A_{ji}^{\left(2\right)}{\sigma }_{t-1,t\mid t}^2{A}_{ii}^{\left(1\right)T}+A_{ji}^{\left(1\right)}{\sigma }_{t,t-1\mid t}^2{A}_{ii}^{\left(2\right)T}+A_{ji}^{\left(2\right)}{\sigma }_{t-1,t-1\mid t}^2{A}_{ii}^{\left(2\right)T}\hfill \\ \hfill A_{ii}^{\left(1\right)}{\sigma }_{t,t\mid t}^2{A}_{ji}^{\left(1\right)T}+A_{ii}^{\left(2\right)}{\sigma }_{t-1,t\mid t}^2{A}_{ji}^{\left(1\right)T}+A_{ii}^{\left(1\right)}{\sigma }_{t,t-1\mid t}^2{A}_{ji}^{\left(2\right)T}+A_{ii}^{\left(2\right)}{\sigma }_{t-1,t-1\mid t}^2{A}_{ji}^{\left(2\right)T}\hfill & \hfill {\mathrm{\Sigma }}_{w_i}+A_{ii}^{\left(1\right)}{\sigma }_{t,t\mid t}^2{A}_{ii}^{\left(1\right)T}+A_{ii}^{\left(2\right)}{\sigma }_{t-1,t\mid t}^2{A}_{ii}^{\left(1\right)T}+A_{ii}^{\left(1\right)}{\sigma }_{t,t-1\mid t}^2{A}_{ii}^{\left(2\right)T}+A_{ii}^{\left(2\right)}{\sigma }_{t-1,t-1\mid t}^2{A}_{ii}^{\left(2\right)T}\hfill \end{array}\right).$$ [S10]

The upper right (and transpose of the lower left) block of ${\mathrm{\Sigma }}_{t+1\mid t}$ is

$$L_{t+1}=A^{\left(1\right)}{B}_t+A^{\left(2\right)}{C}_t^T=\left(\begin{array}{cc}\hfill 0\hfill & \hfill A_{ji}^{\left(1\right)}{\sigma }_{t,t\mid t}^2+A_{ji}^{\left(2\right)}{\sigma }_{t-1,t\mid t}^2\hfill \\ \hfill 0\hfill & \hfill A_{ii}^{\left(1\right)}{\sigma }_{t,t\mid t}^2+A_{ii}^{\left(2\right)}{\sigma }_{t-1,t\mid t}^2\hfill \end{array}\right).$$ [S11]

The lower right block of ${\mathrm{\Sigma }}_{t+1\mid t}$ is

$$N_{t+1}=B_t=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \\ \hfill 0\hfill & \hfill {\sigma }_{t,t\mid t}^2\hfill & \end{array}\right).$$ [S12]

Stepping forward the Kalman filter with Eq. S8, the next state-error covariance is

$${\mathrm{\Sigma }}_{t+1|t+1}={\mathrm{\Sigma }}_{t+1|t}-{\mathrm{\Sigma }}_{t+1|t}{H}^T{\left(H{\mathrm{\Sigma }}_{t+1|t}{H}^T\right)}^{-1}H{\mathrm{\Sigma }}_{t+1|t}.$$ [S13]

Expanding,

$$\left[\begin{array}{cc}\hfill B_{t+1}\hfill & \hfill C_{t+1}\hfill \\ \hfill C_{t+1}^T\hfill & \hfill D_{t+1}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill K_{t+1}\hfill & \hfill L_{t+1}\hfill \\ \hfill L_{t+1}^T\hfill & \hfill N_{t+1}\hfill \end{array}\right]-\left[\begin{array}{cc}\hfill K_{t+1}\hfill & \hfill L_{t+1}\hfill \\ \hfill L_{t+1}^T\hfill & \hfill N_{t+1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \text{I}\hfill \\ \hfill 0\hfill \\ –\\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]{\left(K_{t+1,jj}\right)}^{-1}\left[\begin{array}{ccc}\hfill \text{I}\hfill & \hfill 0\mid \mathrm{\hspace{0.17em}0}\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{cc}\hfill K_{t+1}\hfill & \hfill L_{t+1}\hfill \\ \hfill L_{t+1}^T\hfill & \hfill N_{t+1}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill K_{t+1,ii}-K_{t+1,ij}{K}_{t+1,jj}^{-1}{K}_{t+1,ji}\hfill \end{array}\right)\hfill & \hfill \left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill L_{t+1,ii}-K_{t+1,ij}{K}_{t+1,jj}^{-1}{L}_{t+1,ji}\hfill \end{array}\right)\hfill \\ \hfill \left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill L_{t+1,ii}^T-L_{t+1,ji}^T{K}_{t+1,jj}^{-1}{K}_{t+1,ji}\hfill \end{array}\right)\hfill & \hfill \left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill N_{t+1,ii}-L_{t+1,ji}^T{K}_{t+1,jj}^{-1}{L}_{t+1,ji}\hfill \end{array}\right)\hfill \end{array}\right].$$

We see that the state-covariance structure is preserved, as expected, and that the covariances of the unobserved components are given iteratively by

$${\sigma }_{\left(i\right)t+1,t+1\mid t+1}^2=K_{t+1,ii}-K_{t+1,ij}{K}_{t+1,jj}^{-1}{K}_{t+1,ji}{\sigma }_{\left(i\right)t+1,t\mid t+1}^2=L_{t+1,ii}-K_{t+1,ij}{K}_{t+1,jj}^{-1}{L}_{t+1,ji}{\sigma }_{\left(i\right)t,t\mid t+1}^2=N_{t+1,ii}-L_{t+1,ji}^T{K}_{t+1,jj}^{-1}{L}_{t+1,ji}.$$ [S14]

The state prediction- and filtered-error covariances of Eqs. S7 and S8 have been consolidated to Eqs. S10–S12 and S14. From this set of equations, we see that the parameters determining the receiver dynamics, $\{A_{jj}^{\left(p\right)}\}$, do not appear. These equations can be computed recursively, and in steady state, they form a set of nonlinear equations, the solution of which determines the reduced-model prediction-error variance. Hence, because the $\{A_{jj}^{\left(p\right)}\}$ parameters do not appear, the reduced-model prediction-error variance and the time-domain causality are, as seen before in the unconditional frequency domain, independent of the receiver dynamics.

In fact, we see that receiver independence holds for the conditional case, as well, and that the causality is further independent of the dynamics of the conditional nodes. This is because any conditional time series $x_k$ would be included with $x_j$ as directly observed components of the reduced model. We thus find that the causality is only a function, albeit complicated, of the channel parameters $\{A_{ji}^{\left(p\right)}\}$, the transmitter parameters $\{A_{ii}^{\left(p\right)}\}$, and the input noise covariance ${\mathrm{\Sigma }}_w$.

S8. Additional Figures and Table for Example 1

Table S1 and Figs. S1–S4 provide additional information about the VAR parameter and conditional frequency-domain causality estimates of the VAR(3) three-node series system in example 1.

Table S1 shows the mean and SD for the VAR parameter estimates of the full model for orders 3, 6, and 20. The data show that the parameters are estimated appropriately, suggesting that the bias–variance trade-off and separate model mismatch problems described in the main text are not artifacts of poor estimation of the VAR parameters.

Fig. S1 shows the mean values of several order selection criteria—the Akaike information criterion (red), the Hannan–Quinn criterion (blue), and the Schwarz criterion (green)—for various model orders. On average, all three criteria were minimized when using the true model order 3. This shows that for the system in example 1, the true system model order would have been identified by any of the mentioned selection criteria. Despite this, as we demonstrate in the main text, the resulting causality estimates are biased.

Fig. S2 shows the causality estimates for all cause–effect pairs from example 1, using the true model order 3. Figs. S3 and S4 show the estimates from using the increased orders 6 and 20, respectively. Figs. S3 and S4 complement Fig. 2 in the main text by showing the results for all possible connections between nodes. Comparing Figs. S3 and S4 again shows the change in the distributions as the order is increased, reflecting the bias associated with using the true model order. At the same time, increasing the order increases “noisiness” of the estimates of individual realizations due to the additional spectral peaks in the models.

S9. Permutation Significance for Noncausality

Significance levels for the conditional causality estimates are estimated by permutation (32). In example 1, we generate 1,000 realizations of the system. For each cause–effect pair (from i to j conditional on k), 1,000 permuted realizations are formed by randomly selecting realization indexes $I_i$ and $I_{jk}$ from a uniform distribution and recombining the $I_i$th realization of {$x_{i,t}$} with the $I_{jk}$th realization of {$x_{\{j,k\},t}$} to generate a permuted realization. The conditional frequency domain causality is estimated for each permuted realization and the maximal value over all frequencies is identified. The 95% significance level over all frequencies is taken as 95% of the 1,000 maximal values. This significance level is against the null hypothesis of no difference between the causality spectrum and that of a noncausal system. It is the level below which the maximum of 95% of null causality permutations reside. This tests the whole causality waveform against the null hypothesis of no causal connection, and no assessment of significance for particular frequencies, despite the presence of peaks or valleys, can be made. The procedure can be applied to particular frequency bands of interest by identifying the 95% level within the band, but if multiple bands are tested, the appropriate corrections must be applied.