Probing the Binding Modes of a Multidomain Protein to Lipid-based Nanoparticles by Relaxation-based NMR

Abstract

The interactions of two model multidomain proteins—covalently linked diubiquitins, Ub₂—with lipid-based nanoparticles have been quantitatively probed by the measurements of NMR lifetime line broadening, ΔR₂. By combined analysis of ΔR₂ profiles arising from interactions with liposomes of varying sizes, an approach recently developed for the characterization of interactions of monoubiquitin with liposomes, we determine how the parameters of exchange (liposome binding) and dynamics of each individual domain of Ub₂ on the surface of liposomes change when the domains are covalently attached to one another by a flexible linker. Two different covalent linkages were used: K63-linked and K48-linked Ub₂. The possibility of three distinct modes of binding of Ub₂ to liposomes requires the introduction of simple but important modifications to the strategy of analysis originally developed for monoubiquitin.

Graphical Abstract

Reversible binding of peripheral membrane proteins to membrane surfaces is critical to many biological processes including signaling cascades, recognition, membrane trafficking, and anchoring.^1,2 Binding of these proteins is generally accomplished through lipid-interacting protein domains with or without penetration into the hydrophobic core of the membrane. While single-domain proteins or individual domains within multidomain proteins can adopt identical structures upon binding to cellular membranes, the characterization of the conformational states of multidomain proteins is more challenging as a description of the interplay between membrane-binding domains is required. Characterization of membrane binding and its influence on the dynamics of multidomain proteins therefore benefits from the application of atomic resolution techniques. With this in mind, we have undertaken a quantitative study of global dynamics and exchange kinetics of two multidomain model protein systems in the presence of lipid-based nanoparticles (liposomes).

Recently, we characterized the interaction of a model protein, ubiquitin, with the surface of negatively charged liposomes using relaxation-based NMR.³ Because the relative contributions of lifetime and rotational tumbling to the total effective correlation time of the bound protein are modulated by nanoparticle size, parameters describing both exchange and dynamics can be determined simultaneously by quantitative analysis of lifetime line broadening (ΔR₂) profiles obtained with different sized nanoparticles. We showed that during the lifetime of the bound state (~20 μs) ubiquitin undergoes internal rotation on a time scale of ~2 μs about an axis approximately perpendicular to the lipid bilayer surface while simultaneously wobbling in a cone of semiangle 30–55° on a time scale <500 ns.³

Here we extend our previous work³ to a more complex scenario in which the liposome-binding partner is a multidomain protein, as exemplified by covalently linked diubiquitin, Ub₂. Using ΔR₂ measurements, we explore how membrane binding and global dynamics of the individual domains on the surface of liposomes are impacted by two different, naturally occurring covalent linkages, Lys63- and Lys48-linked Ub₂. The rationale for our choice of linkages is based on their different conformational properties in solution: while K63-linked Ub₂ always adopts an extended conformation,^4,5 K48-linked Ub₂ has been shown to exist in both “closed” and “open” forms,^6–10 which interconvert on the tens of nanoseconds time scale.^8,11 Because Ub₂ can potentially bind to liposomes in three distinct modes, simple but important modifications are required to the approach previously developed for monoubiquitin. Comparison of global parameters of exchange and dynamics obtained for the individual domains of K48- and K63-linked Ub₂ provides semiquantitative insights into the character of these binding modes and the interplay between the domains of Ub₂.

Covalently linked diubiquitin (Ub₂) is enzymatically generated through the formation of an isopeptide linkage between the ε-amine of an endogenous lysine side chain from one ubiquitin molecule (Ub₁), denoted as “proximal”, and the C-terminal carboxyl group of a second ubiquitin molecule, denoted as “distal”.^5,7 Because the ¹H_N/¹⁵N chemical shifts of the proximal and distal domains are very similar, only a single domain of the K63- and K48-linked Ub₂ constructs was U- [¹⁵N/²H]-labeled at a time; the other remained at natural isotopic abundance (¹⁴N), thereby ensuring that only a single domain at a time is observed in ¹H–¹⁵N NMR correlation experiments. The details of Ub₂ ligation and isotope labeling are described in the Supporting Information (SI). Negatively charged large (LUV) and small (SUV) unilamellar vesicles (see the SI) had mean diameters of 112 and 28 nm, respectively, as measured by dynamic light scattering. The rotational correlation time (τ_R) for molecular reorientation of LUV and SUV liposomes, estimated from their hydrodynamic radii using the Stokes–Einstein equation, was 128.5 and 2.0 μs, respectively.

The experimental approach employed involves the measurement of lifetime line broadening (ΔR₂), given by the difference in transverse relaxation rates (R₂) of the protein measured in the presence and absence of nanoparticles. Lifetime line broadening arises from rapid decay of magnetization during the lifetime of the bound state that is transferred by exchange to the observable free state.^12,13 The ¹⁵N-ΔR₂ profiles as a function of residue for the different Ub₂ constructs shown in Figure S1 reveal large variations in values ranging from a factor of ~3 for SUVs and ~10 for LUVs, similar to those observed for Ub₁ (Figure S2A). If Ub₁ and Ub₂ were immobilized on the lipid surface during their bound lifetime, then the measured ΔR₂ values would be uniform. The ¹⁵N-ΔR₂ values are dependent both on nanoparticle size (Figure S3A) and magnetic field strength (Figure S3B). The average ratio of ¹⁵N-ΔR₂ at 700 and 500 MHz is 1.19 (Figure S3B), in good agreement with the expected ratio of 1.20 for a relaxation mechanism based on a −170 ppm ¹⁵N chemical shift anisotropy (CSA), allowing one to conclude that the field dependence of ΔR₂ does not arise from chemical exchange (which scales with the square of magnetic field) and that the exchange rate (k_ex) is fast on the transverse relaxation time scale (i.e., $k_{\text{ex}}>R_2^{\mathrm{B}}$, where $R_2^{\mathrm{B}}$ is the ¹⁵N transverse relaxation rate in the bound state).

In the absence of chemical shift differences between the free and bound states of the protein (none were observed in this work), the association of Ub₂ domains with liposomes is quantitatively described by a set of simplified Bloch–McConnell differential equations (SI eq S1). It is straightforward to show (see the SI for details) that, to a good approximation, for the interactions considered here, ΔR₂ can be represented by

$$\mathrm{\Delta }{R}_2\approx k_{\text{on}}^{\text{app}}\frac{R_2^{\mathrm{B}}}{k_{\text{off}}+R_2^{\mathrm{B}}}$$ (1)

where k_off and $k_{\text{on}}^{\text{app}}$ are the dissociation and pseudo-first-order apparent association rate constants, respectively. The relaxation rates $R_2^{\mathrm{B}}$ are related to molecular motions of Ub₂ on the surface of liposomes through their dependence on linear combinations of the spectral density function J(ω) evaluated at a finite number of frequencies ω¹⁴ (see SI eq S3 for the full expression for ¹⁵N-R₂). All information about molecular dynamics is contained in the form and parameters of J(ω). As described in our previous work,³ the variability in ¹⁵N-ΔR₂ values of Ub₂ in the presence of liposomes can be explained by two concurrent motions of each domain on the surface of liposome particles: (1) internal rotation of a domain around an axis fixed in a molecular frame of reference and (2) the reorientation (wobbling) of the axis itself occurring on a time scale faster than internal rotation. The global motions of the protein on the nanoparticle surface can therefore be described by a form of the spectral density function that represents a variation of the extended model-free formalism¹⁵ and is given by

$$J(\omega )=S_{\mathrm{w}}^2{[P_2(cos\alpha )]}^2\frac{{\tau }_C}{1+{(\omega {\tau }_{\mathrm{C}})}^2}+S_{\mathrm{w}}^2(1-{[P_2(cos\alpha )]}^2)\frac{{\tau }_{\mathrm{r}}^{\prime }}{1+{(\omega {\tau }_{\mathrm{r}}^{\prime })}^2}+(1-S_{\mathrm{w}}^2)\frac{{\tau }_{\mathrm{w}}^{\prime }}{1+{(\omega {\tau }_{\mathrm{w}}^{\prime })}^2}$$ (2)

where τ_C = (1/τ_R + 1/τ_ex)⁻¹ is the total effective correlation time; τ_R is the rotational correlation time of molecular reorientation of the complex; ${\tau }_{\text{ex}}={(k_{\text{on}}^{\text{app}}+k_{\text{off}})}^{-1}$ is the lifetime of the bound state; τ_r′ = (1/τ_C + 1/τ_r)⁻¹ and τ_w′ = (1/τ_C + 1/τ_w)⁻¹ are the effective correlation times for internal rotation and wobbling on the nanoparticle surface, respectively, and τ_r and τ_w are the corresponding correlation times; S_w is the order parameter for wobbling within a cone centered about the internal rotation axis; and P₂(cos α) = (3 cos² α − 1)/2 is the second-order Legendre polynomial that represents the order parameter S_r for axially symmetric internal rotation around an axis forming an angle α with the direction of an N–H bond vector.

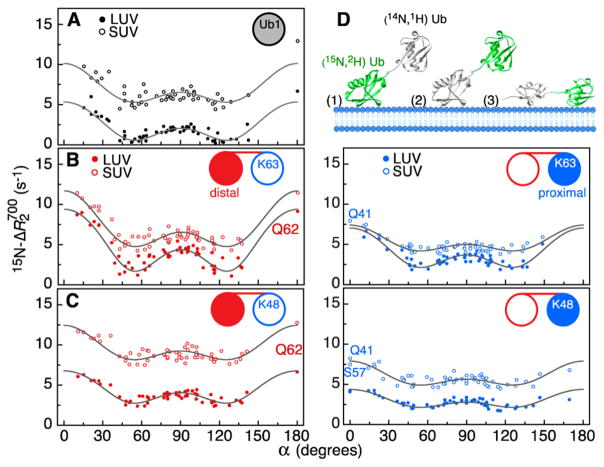
Internal rotation of ubiquitin about an axis fixed in the molecular frame results in a characteristic $S_{\mathrm{r}}^2={[P_2(cos\alpha )]}^2$ dependence of $R_2^{\mathrm{B}}$ (and, consequently, ΔR₂) with two minima: at the magic angle, 54.7° (α = 54.7°) and 180° – 54.7° (α = 125.3°). The “double-dip” profiles of ¹⁵N-ΔR₂ for Ub₁ in the presence of LUV and SUV liposomes at the same protein concentration and protein/lipid ratios as used here for the study of the Ub₂ domains are shown in Figure 1A and serve as a template for the analysis of similar dependencies observed for K63- and K48-linked diubiquitins (Figure 1B,C).

Figure 1.

¹⁵N-ΔR₂ values plotted versus the angles α formed between the H–N bond vectors and the axis of internal rotation for (A) monoubiquitin (Ub₁) and the distal and proximal domains of (B) K63- and (C) K48-linked diubiquitin (Ub₂). Experimental data points are shown as solid and open circles for negatively charged LUVs and SUVs, respectively. The best-fit curves from the combined analysis of the LUV and SUV data (with $S_{\mathrm{w}}^2$ and τ_w set to 0.5 and 300 ns, respectively) are shown with black lines. The [¹⁵N/²H]-labeled domains of Ub₂ are shown as filled-in circles with the distal and proximal domains of Ub₂ in red and blue, respectively, in the cartoons within each panel. (D) Schematic representation of the three potential binding modes of Ub₂ to lipid-based nanoparticles with the [¹⁵N/²H]-labeled (“NMR-active”) domain shown in green. All experimental data were collected at 700 MHz on samples containing 0.22 mM protein and a 1:2 protein/lipid molar ratio at pH 6.8 and 25 °C.

There are potentially three distinct binding modes of Ub₂ to the surface of liposomes (Figure 1D): (1) the U-[¹⁵N/²H]-labeled (“NMR-active”) domain is directly bound to the lipid bilayer; (2) the unlabeled (“NMR-silent”) Ub₂ domain binds, while the domain detected in the NMR experiments is tethered; and (3) both “NMR-active” and “NMR-silent” domains bind simultaneously to the liposome surface. In the most general case, the overall experimentally measured lifetime line broadening, $\mathrm{\Delta }{R}_2^{\text{overall}}$, is therefore composed of a super-position of all of the possible binding modes and can be represented by

$$\mathrm{\Delta }{R}_2^{\text{overall}}=\mathrm{\Delta }{R}_2+F^{\text{iso}}$$ (3)

where ΔR₂ is calculated using eq 1 (see also SI, eqs S1 and S2), the relaxation rates $R_2^{\mathrm{B}}$ are calculated using standard expressions (SI, eq S3) and the form of spectral density in eq 2, and F^iso is a uniform contribution to ${}^{15}\mathrm{N}-\mathrm{\Delta }{R}_2^{\text{overall}}$ that accounts for binding modes 2 and 3 (Figure 1D). One can assume that the tethered “NMR-observable” domain of Ub₂ (binding mode 2) behaves as an isotropic body and reorients fast relative to the bound domain on account of the relatively long and flexible linker connecting the two units of Ub₂, thus contributing a uniform, angle-independent value to ΔR₂. Furthermore, if binding mode 3 (both domains directly bound simultaneously) occurs in practice, then the rotation of each individual domain would be severely hindered by the covalent linkage between the two domains, also resulting in a uniform contribution to ΔR₂ because, in the absence of internal rotation, the large angular dependence of ΔR₂ would be eliminated. Indeed, even a cursory visual comparison of the “double-dip” ΔR₂ profiles for Ub₂ (Figure 1B,C) and Ub₁ (Figure 1A) shows that at least for some of the Ub₂ domains the profiles are simply “offset” by a positive uniform factor relative to those of Ub₁. In principle, there is no reason to assume that the value of F^iso should be the same for interactions of Ub₂ with $\text{LUV}(F_{\text{LUV}}^{\text{iso}})$ and $\text{SUV}(F_{\text{SUV}}^{\text{iso}})$ particles. Likewise, $F_{\text{LUV}}^{\text{iso}}$ and $F_{\text{SUV}}^{\text{iso}}$ can be different for distal and proximal domains of Ub₂ as well as for different types of linkages and should therefore be optimized separately for each Ub₂ domain (see below and the SI for details).

The key to interpretation of ¹⁵N-ΔR₂ values for Ub₂ in terms of exchange ( $k_{\text{on}}^{\text{app}}$ and k_off in eq 1) and microdynamic parameters ( $S_{\mathrm{r}}^2,S_{\mathrm{w}}^2$, and corresponding correlation times in eq 2) lies in the combined use of the ¹⁵N-ΔR₂ data obtained in the presence of vesicles of varying sizes (LUVs and SUVs). The working assumption employed here is that the global motional parameters and the dissociation rate constant are independent of particle size. Specifically, we require that the time scale of internal rotation τ_r, the polar angles (θ and φ) that describe the orientation of the internal rotation axis in a molecular frame of reference, the parameters of the wobbling motion ( $S_{\mathrm{w}}^2$ and τ_w), and the dissociation rate constant k_off are the same for binding to LUV and SUV particles. This approach allows one to quantitatively describe fast binding to liposomes while simultaneously establishing the parameters of global dynamics of the protein on the liposome surface. However, even combined analysis of LUV and SUV ΔR₂ data precludes the determination of the wobbling parameters, $S_{\mathrm{w}}^2$ and τ_w, as the product of the order parameters for internal rotation and wobbling enter into the first and second terms of the spectral density function in eq 2. Therefore, all exchange and dynamics parameters reported here were obtained with $S_{\mathrm{w}}^2$ and τ_w set to values of 0.5 and 300 ns, respectively. We note that these parameters are quite insensitive to the exact values of $S_{\mathrm{w}}^2$ and τ_w, whose lower and upper bounds were established previously for Ub₁–liposome complexes via extensive grid-searches in the parameter space covered by interactions with LUV and SUV liposomes separately.³

The variability of ΔR₂ experimental values for each domain of Ub₂ (see Figure S1, which shows the ΔR₂ profiles versus residue number) can be defined by the ratio R

$$R=(\mathrm{\Delta }{R}_2^{max}-F^{\text{iso}})/(\mathrm{\Delta }{R}_2^{min}-F^{\text{iso}})$$ (4)

For the same wobbling motion parameters ( $S_{\mathrm{w}}^2$ and τ_w) R is predicated upon the degree of separation between the time scale of internal rotation (τ_r) and the total effective correlation times for $\text{LUV}({\tau }_{\mathrm{C}}^{\text{LUV}})$ and $\text{SUV}({\tau }_{\mathrm{C}}^{\text{SUV}})$ particles. The larger the separation between τ_C and τ_r, the larger the variability in the ratio R. In contrast to Ub₁, where F^iso = 0, the calculated value of R in the case of Ub₂ depends on the value of F^iso and therefore provides a good measure of the separation between the τ_C and τ_r time scales (see below).

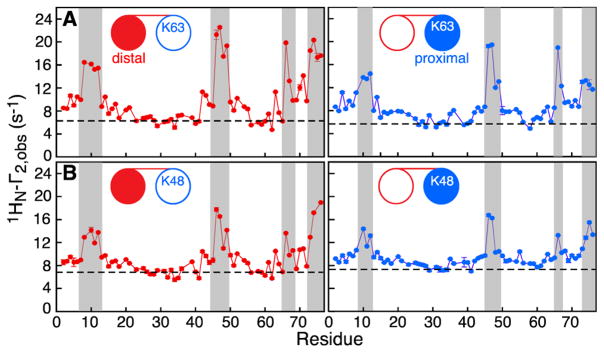
Not all fitted parameters are well-defined from combined analysis of the SUV and LUV ΔR₂ data for the Ub₂ domains owing to (a) the reduced variability of ΔR₂ values (i.e., $\mathrm{\Delta }{R}_2^{max}/\mathrm{\Delta }{R}_2^{min}$ before the “isotropic” contributions F^iso are taken into account) for at least some of the Ub₂ domains and (b) the interdependence of various variable parameters (see below). Therefore, to preserve the robustness of analysis for all domains and linkage types of Ub₂ and to enable direct comparison of the dynamics parameters obtained for different Ub₂ domains, we chose to determine the values of $k_{\text{on}}^{\text{app},\text{LUV}}$ for the different Ub₂–LUV interactions independently from paramagnetic relaxation enhancement (PRE) experiments (Figure 2).¹⁶ Outside the fast exchange regime (k_ex < Γ₂, where Γ₂ is the PRE rate in the bound species), the maximal observed PRE, ${{}^1\mathrm{H}}_{\mathrm{N}}-{\mathrm{\Gamma }}_{2,max}^{\text{app}}$, after background subtraction,³ approaches a limiting value that is a factor of ~1.3 lower than $k_{\text{on}}^{\text{app},\text{LUV}}$ for the exchange parameters previously established for Ub₁.¹⁶ The values of $k_{\text{on}}^{\text{app},\text{LUV}}$ thus estimated from ${{}^1\mathrm{H}}_{\mathrm{N}}-{\mathrm{\Gamma }}_{2,max}^{\text{app}}$ for each Ub₂ domain are reported in the first row of Table 1, which summarizes the parameters of exchange and dynamics obtained by combined analysis of LUV and SUV ΔR₂ data for the distal/proximal domains of K63- and K48-linked Ub₂.

Figure 2.

Amide proton intermolecular PRE profiles obtained at 700 MHz. (A) K63- and (B) K48-linked Ub₂ in the presence of negatively charged Gd³⁺-tagged negatively charged LUVs. The [¹⁵N/²H]-labeled domains of Ub₂ are shown with filled-in circles in the cartoons, and the distal and proximal domains are depicted in red and blue, respectively. The PRE background, due to diffusion of Ub₂ in the magnetic field generated by Gd³⁺-tagged LUVs,³ is shown as a dashed line. The most significant PREs above background are shaded in gray. Sample conditions are as in Figure 1.

Table 1.

Parameters of Exchange and Dynamics Describing the Interactions of K63- and K48-Linked Ub₂ with LUV and SUV Liposomes at pH 6.8, 25°C and 1:2 Ubiquitin/Lipid Molar Ratio^a,b

	K63-linked Ub2		K48-linked Ub2
parameters	distal	proximal	distal	proximal
$k_{\text{on}}^{\text{app},\text{LUV}}({\mathrm{s}}^{-1})$	21	18	14	13
$k_{\text{on}}^{\text{app},\text{SUV}}({\mathrm{s}}^{-1})$	197–211	116–144	195–239	162–210
koff × 103 (s−1)	32 ±1	40 ±1	36 ±1	55 ± 3
$p_{\mathrm{B}}^{\text{LUV}}(\%)$ c	0.07	0.04	0.04	0.02
$p_{\mathrm{B}}^{\text{SUV}}(\%)$ c	0.65 ± 0.03	0.32 ± 0.04	0.58 ± 0.07	0.35 ± 0.05
${\tau }_{\mathrm{C}}^{\text{LUV}}(\mu \mathrm{s})$ c	25.2 ± 0.8	21.0 ± 0.4	22.5 ± 0.9	16.0 ± 0.8
${\tau }_{\mathrm{C}}^{\text{SUV}}(\mu \mathrm{s})$ c	1.9 ± 0.2	1.9 ± 0.2	1.9 ± 0.2	1.8 ± 0.2
τr (μs)	0.4–0.6	0.4–1.0	1.2–2.0	0.6–1.4
θ (deg)d	102.7 ± 0.7	98.4 ± 0.9	103.9 ± 0.8	93.5 ± 1.2
φ (deg)d	−5.3 ± 0.7	−13.7 ± 0.7	−5.1 ± 0.9	−13.7 ± 1.0
$F_{\text{LUV}}^{\text{iso}}({\mathrm{s}}^{-1})$	1.3 ± 0.1	1.7 ± 0.1	2.1 ± 0.1	1.9 ± 0.1
$F_{\text{SUV}}^{\text{iso}}({\mathrm{s}}^{-1})$	1.3–2.0	1.7–3.0	2.1–4.3	1.9–3.4
RSUVe	4.2	4.1	2.6	3.7

^aAll reported the values are obtained with $S_{\mathrm{w}}^2$ and τ_w fixed at 0.5 and 300 ns, respectively; throughout, the upper bounds reported for $F_{\text{SUV}}^{\text{iso}}$ correspond to the lower bounds for $k_{\text{on}}^{\text{app},\text{SUV}}$ and τ_r values in Ub₂ domains (see the text for details).

^bFor comparison, the values of $k_{\text{on}}^{\text{app},\text{LUV}},k_{\text{on}}^{\text{app},\text{SUV}}$, k_off, τ_r, θ, and φ for Ub₁ are 27 s⁻¹, 347 ± 14 s⁻¹, 52(±1.9) × 10³ s⁻¹, 1.5 ± 0.2 μs, 108.4 ± 1.1°, and −2.5 ± 1.1°, respectively.

^cUncertainties in these parameter values are propagated considering only the uncertainties in k_off. Uncertainties in the values of $p_{\mathrm{B}}^{\text{LUV}}$ are equal to ~0.002.

^dPolar angles θ and φ are specified in the coordinate system of the inertia tensor of ubiquitin (PDB accession code 1ubq).

^eCalculated for Ub₂–SUV complexes using the experimental values of ΔR_2,SUV and the upper bounds of the fitted $F_{\text{SUV}}^{\text{iso}}$ values.

The intermolecular amide proton $\text{PRE}({{}^1\mathrm{H}}_{\mathrm{N}}-{\mathrm{\Gamma }}_2^{\text{app}})$ profiles shown in Figure 2 for the distal and proximal domains of K63- and K48-linked Ub₂ in the presence of Gd³⁺-tagged LUVs indicate that the regions with the most significant PREs largely coincide with those measured for Ub₁–LUV complexes (Figure S2B). Thus the location of the binding surface remains largely unchanged in individual domains of Ub₂ relative to Ub₁.

The details of the construction of the target error function and its minimization are described in the SI. In brief, because per eqs 1 and 3 $F_{\text{LUV}}^{\text{iso}}$ and $F_{\text{SUV}}^{\text{iso}}$ are linearly correlated with the corresponding association rate constants for LUV and SUV particles, $k_{\text{on}}^{\text{app},\text{LUV}}$ and $k_{\text{on}}^{\text{app},\text{SUV}}$ (see the SI for full expressions), it is not possible to determine $k_{\text{on}}^{\text{app}}$ and F^iso simultaneously. Therefore, we first performed the analysis with $k_{\text{on}}^{\text{app},\text{LUV}}$ fixed to the values determined as described above and assumed that $F_{\text{LUV}}^{\text{iso}}=F_{\text{SUV}}^{\text{iso}}$. This allowed us to obtain optimal estimates for $k_{\text{on}}^{\text{app},\text{SUV}}$ for each of the Ub₂ domains (listed as upper bounds in Table 1). Subsequently, the values of $k_{\text{on}}^{\text{app},\text{SUV}}$ obtained in this manner were reduced by four times the uncertainty in the fit (listed as lower bounds in Table 1), and $F_{\text{SUV}}^{\text{iso}}$ was used as an optimized parameter in the fit, providing the upper bounds for $F_{\text{SUV}}^{\text{iso}}$ listed in Table 1. Note that the upper bounds determined for $F_{\text{SUV}}^{\text{iso}}$ thus correspond to the lower bounds for $k_{\text{on}}^{\text{app},\text{LUV}}$ and τ_r values, whereas the lower bounds for $F_{\text{SUV}}^{\text{iso}}$ are equal to $F_{\text{LUV}}^{\text{iso}}$ (Table 1).

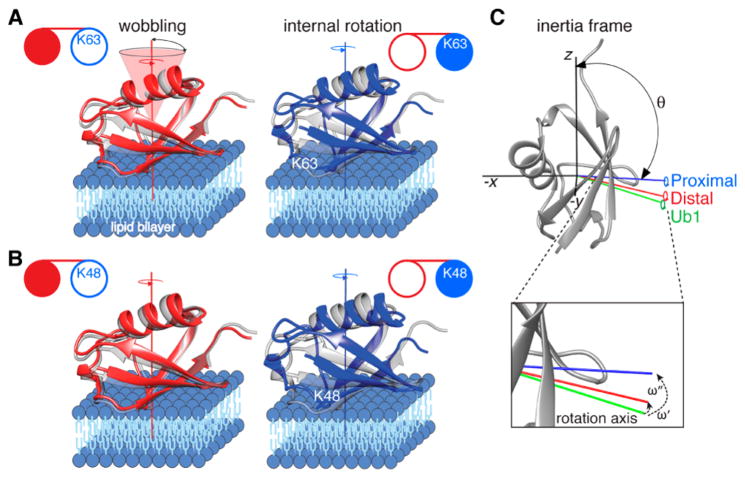
Figure 3 compares the orientations of Ub₁ and the domains of Ub₂ on the surface of liposomes, with the axes of internal rotation aligned in the direction perpendicular to the lipid bilayer. The positions of the internal rotation axes of Ub₁ and the distal and proximal domains of the K48-linked Ub₂ in the coordinate system of the inertia tensor of ubiquitin are illustrated in Figure 3C. The orientations of the Ub₂ domains on the lipid bilayer surface are very similar to that of Ub₁ (Figure 3A,B; Table 1), with the angles ω′ and ω″ formed between the internal rotation axes of Ub₁ and the distal and proximal domains of Ub₂ (Figure 3C) calculated to be 6.1 and 14.5°, respectively, for K63-linked Ub₂ and 4.9 and 18.2° for K48-linked Ub₂. Some differences, however, in the binding affinities and the parameters of dynamics on the surface of liposomes are noteworthy. First, the positions of the axes of internal rotation (defined by the pair of polar angles θ and ϕ) of the distal domains are closer to Ub₁ than those of the proximal domains. Second, the affinity of the distal domains for liposomes is very similar to that of Ub₁ and larger than for their proximal counterparts, as evidenced by their higher bound occupancies (cf. populations of the bound states, p_B, for LUVs and SUVs in Table 1). These two observations imply that perturbations of the liposome-binding surface arising from the linkages in Ub₂ are more pronounced for the proximal than distal domains. This is a direct consequence of the fact that the distal domains are connected to the proximal ones through a flexible and unstructured C-terminus. As a result, the binding interface on the distal domains remains almost intact in the presence of the isopeptide linkage; the latter, however, can lead to a partial occlusion of the binding interface in the case of proximal domains.

Figure 3.

Internal rotation and wobbling of the proximal and distal domains of Ub₂ on the surface of lipid-based nanoparticles. (A) K63- and (B) K48-linked Ub₂. The distal and proximal domains of Ub₂ are shown as red and blue ribbons, respectively, with Ub₁ in gray for comparison. Each domain rotates about an internal axis of rotation, approximately perpendicular to the lipid bilayer, and simultaneously wobbles in a cone centered around this axis. (C) Relationship between the axes (−x, −y, and z) of the inertia tensor (black) in the molecular frame with the internal rotation axes of Ub₁ (green) and the distal (red) and proximal (blue) domains of K48-linked Ub₂. θ is the angle subtended by each internal rotation axis and the z axis of the intertia tensor; φ (not shown) is the angle subtended by the x axis of the inertia tensor and the projection of the internal rotation axis on the x–y plane. The angle formed between the internal rotation axis of Ub₁ (green) and those of the distal (red) and proximal (blue) domains of Ub₂ are denoted by ω′ and ω″, respectively. These angles are calculated from the polar angles (θ_i, φ_i) defining the position of axis i (i = 1,2) in the inertia frame using the relationship cos(ω) = cos(θ₁) cos(θ₂) + sin(θ₁) sin(θ₂)cos(φ₁ − φ₂). The U-[¹⁵N/²H]-labeled domains of Ub₂ are shown as filled-in circles in the cartoons in panels A and B.

A comparison of the binding and kinetic parameters for the K63- and K48-linked Ub₂ is equally instructive, as the former exists exclusively in an extended conformation in solution,^4,5 whereas the latter is a mixture of rapidly interconverting open and closed states.^6–11,17 Mapping of the amide proton intermolecular PREs on the surface of K48- and K63-linked Ub₂ shows that the lipid binding surface on both domains is fully accessible in the open state but completely occluded in the closed one (Figure S4). The ability of the K48-linked Ub₂ to adopt, for at least a small fraction of the time, a liposome-binding incompetent (closed) state may be reflected in slightly larger values of F^iso for the K48- versus K63-linked Ub₂ (Table 1), indicating that binding modes (2) and (3) (cf. Figure 1D) play a slightly more important role when Ub₂ is capable of transiently adopting a closed conformation. The degree of association between the Ub₂ domains may also be related to the observation of somewhat lower values of the internal rotational time scale (τ_r) for K63-linked Ub₂ compared with those of K48-linked Ub₂ (Table 1). Note that lower values of τ_r correspond to higher values of the ratio R (eq 4), as the latter depend on the separation between τ_r and the effective correlation times of LUV and SUV particles (Figure S5).

In conclusion, we have provided a theoretical framework for the quantitative description of the dynamics of two (K48- and K63-linked) diubiquitins on the surface of liposome nanoparticles. The formalism extends our previous work on monoubiquitin³ involving various modes of binding including direct contact and tethered binding of a single domain and simultaneous binding of both domains. It has not escaped out attention that more rigorous (i.e., non-model-free) formulations of the spectral density function (eq 2) are possible if the nature of the motion of the protein on the liposome surface is specified. Indeed, much earlier, Brainard and Szabo¹⁸ derived an expression for a correlation function describing rotation of a bond vector around a symmetry axis defined in the molecular frame with the axis undergoing diffusive motions (i.e., wobbling) about its equilibrium position (see the SI). The use of the corresponding spectral density function (eq S9, SI) yields parameters of exchange and dynamics that are very similar to those reported in Table 1 (using eq 2) and does not affect any of the conclusions of the present work.