Classification of common human diseases derived from shared genetic and environmental determinants

Abstract

In this study, we used insurance claims for over a third of the entire United States population to create a subset of 128,989 families (481,657 unique individuals). We then used these data to: 1) estimate the heritability and familial environmental patterns of 149 diseases, and; 2) infer the genetic and environmental correlations between disease pairs from a set of 29 complex diseases. The majority (52 out of 65) of our study’s heritability estimates matched earlier reports, and 84 of our estimates appear to be obtained for the first time. We used correlation matrices to compute environmental and genetic disease classifications and corresponding reliability measures. Among unexpected observations, we found that migraine, typically classified as a disease of the central nervous system, appeared to be most genetically similar to irritable bowel syndrome and most environmentally similar to cystitis and urethritis, all of which are inflammatory diseases.

Introduction

Disease classifications (nosologies) are used ubiquitously in academic medicine, human genetics, the health industry, and economics. Much like any library’s content catalogue, disease taxonomies strive to group together similar entities for ease of access and analysis. Initially, many of these groupings were largely arbitrary—often guided by topographical, anatomical, or even cultural similarities.^1,2

Historically, changes in these groupings have reflected a progression towards etiologic, common-cause disease classifications.

The evolution of nosologies has closely paralleled the evolution of methods designed for the reconstruction of the universal tree of life. Approaches to species classifications were initially subjective or heuristic,^3–7 and made without any hint of the common-origin interpretation, utilizing only a small subset of all the visible morphological features of any given organism. These early phylogenetic methods were followed by the use of maximum parsimony methods, explicitly minimizing the number of differences between proximal taxonomy leaves. Most recent arrivals to phylogenetics are statistical tree-making methods,⁸ which infer taxonomies from very large datasets using explicit stochastic models of diverging organism traits during speciation.

In this study, we synthesized a synergy of the analytical methods developed for phylogenetic analysis with those established in dissecting the heritable and environmental components of human disease. The main premise of our analysis was that etiological disease taxonomy can and should be constructed using the explicit and objective genetic and environmental correlations between diseases.⁹ Such a classification would maximize genetic and/or environmental disease similarities that have clustered together and would generate the closest yet approximation to the common-cause nosology.

Our study used a dataset summarizing health information for more than one-third of the US population, including more than 40 million families. The most informative subset of these, 481,657 unique individuals grouped into 128,989 families, was chosen for in-depth genetic analysis. In this study, we focused on estimating heritability, and environmental and genetic correlations between common diseases that were unambiguously encoded in the insurance claims. Doing so, we were unable to analyze quantitative traits, which are not represented in insurance claims.

A trait’s narrow-sense heritability is defined as the ratio of its additive genetic variance^10,11 to its total phenotypic variance see ¹², p. 170. The environment-related counterpart to narrow-sense heritability is, consequently, the ratio of the environment-related variance (unique for an individual, shared by siblings, parents, or the entire family) to the total disease-specific phenotypic variance. The environment-related variance portion of this ratio can be called preventability because it indicates the putative efficacy of interventions via changing environmental conditions.

Results

Data

Our dataset was generated by subsampling from a very large collection of families represented in a compilation of insurance claims from Truven MarketScan. By definition, the dataset included only information about insured families, and therefore it is slightly biased towards more affluent urban populations (see Figure 1A). The largest families, as well as the majority of all families, were urban, see Figures 1A and B, with the overall urban population share slightly higher than the 80.7% reported by US Census (see URLs). It is therefore unlikely that our heritability and genetic correlation estimates were affected by the sampling of families from rural areas, where average relatedness of individuals in the same county is potentially higher than the country average.

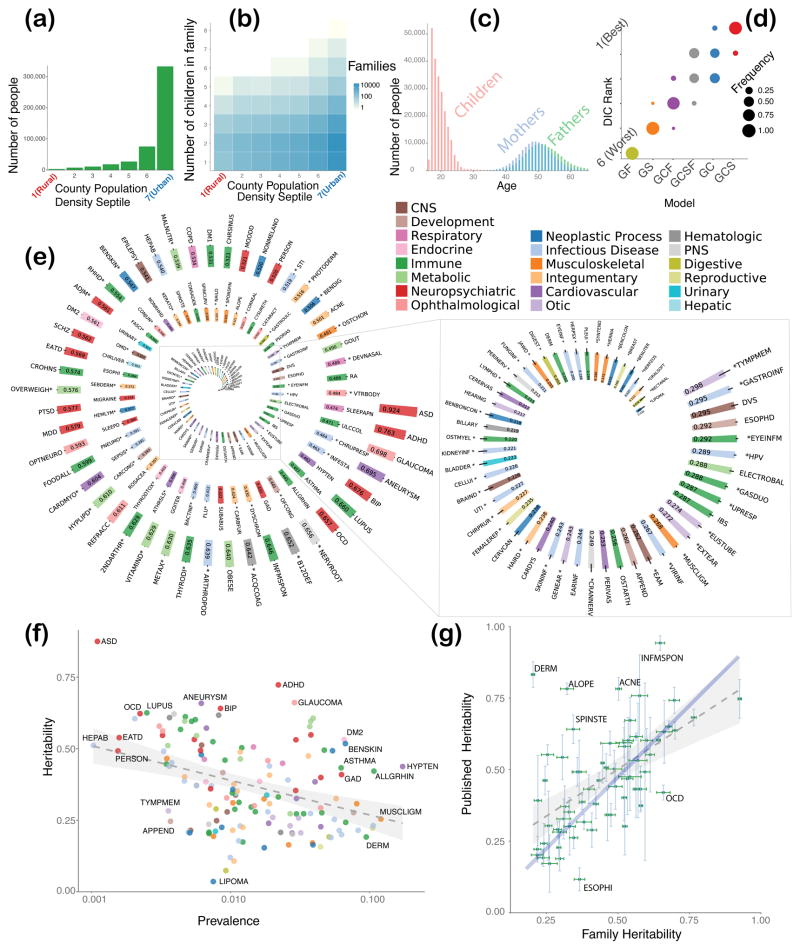
Figure 1.

Information on study population, results of model selection, and analysis of heritability of 149 diseases. (A) Distribution of study population across population density septile; septile 1 corresponds to the most-rural counties and septile 7 most-urban. (B) Number of children in a family as a function of population density septile; septile notations are the same as in the (A). (C) Parent/child age distribution in studied families. (D) Model selection results, using univariate models GF, GS, GCF, GCSF, GC, and GCS, where G stands for additive genetics, F for common family environment, S for common sibling environment, and C for environment common for parental couple; plot shows frequency of corresponding model becoming the “best” (rank 1) as compared by DIC, second best (rank 2), and so on; clearly, the GCS model wins in the majority of cases. (E) Disease heritability estimates with one standard deviation; diseases, heritability for which appears to be measured for the first time are marked with asterisk; heritability values are sorted in decreasing order; color of the bar indicates biological system associated with the disease, see key in the upper right corner; keys to disease acronyms are given in the Supplementary Table 1 and 2. (F) Estimates of disease heritability values against estimates of disease prevalence; the linear correlation is significantly negative, Pearson’s r = −0.212 (95% CI [−0.36 −0.05]), and p = 0.00915. (G) Comparison of our estimates of heritability with the previously published estimates; see Supplement Table 3 for detailed numbers.

The need to focus on a subset of families out of the total 40 million families was two-pronged. First, computational tractability demanded that we significantly restrict the sample: The bivariate analysis of common diseases can become impractical if the sample is too large. Second, in insurance claims, the data of parents and their children are linked for a limited time (see Figure 1C). Typically, US children can only be covered by their parent’s health insurance until the age of 25. As consequence, the apparent disease prevalence in offspring is much lower than in their parents. Therefore, we focused on a set of 128,989 families in which both parents and children were “visible” for the longest time interval, but no less than six years. No individual in the data was “visible” for more than ten years. The methods we used in this study are robust to age-dependent prevalence assuming the same liability with age-dependent threshold (see Methods). We concede that assuming that early-onset and late-onset diseases have the same underlying liability is a limitation of this method; obviously, in principle these disease versions could represent fundamentally different conditions.

Model selection

We started our analysis with a systematic comparison of those mathematical models most likely to describe the structure of our dataset families’ phenotypic variance (see Methods and Figure 1D; DIC stands for Deviance Information Criterion commonly used in Bayesian model selection ¹³). The best model included shared couple (parents) environment, shared sibling environment, and additive genetics (see the GCS model in Figure 1D). The second-best model dropped the shared-sibling environment component, S, (see Figure 1D). We then used the GCS and GC models (whichever fit data best) to estimate liability-scale heritability and its environmental counterpart (“preventability”) for 149 common diseases (see Figure 1E and Supplementary Figure 1; disease abbreviations are spelled out in Supplementary Table 1.)

Estimates of liability-scale heritability

We estimated the narrow-sense heritability for 149 of the most common diseases present in the insurance claim dataset (Figure 1E). To the best of our knowledge, these estimates were obtained for the majority of diseases for the first time in our study: 84 out of 149 estimates (56 percent) are new. These putative first-time estimates are marked with asterisks in Figure 1E (see details in Methods and Supplementary Table 2).

Our liability-scale heritability estimates spanned a wide range of values, from 0.924 (autism) to 0.038 (lipoma). The apparent correlation between our estimates for heritability and disease prevalence turned out to be significantly negative (Figure 1F): The estimated linear regression slope was − 1.20 (se = 0.455, p = 0.00915), with Pearson’s r = −0.212 (95% CI [−0.36 −0.05]), and p = 0.00915.

Out of the 65 diseases in our disease set with previously published heritability estimates, 52 of our estimates agreed with the published estimates within 95 percent CI (see Figure 1G and Supplementary Table 3; specifically, the 95% CIs of the two heritability estimates for the same condition overlapped. Phenotypes that were discordant with our estimates are indicated by bold typeface in Supplementary Table 3). The published and new estimates were highly correlated (r = 0.571, CI (0.379, 0.715), p = 6.902 × 10⁻⁷, linear slope 0.4975, se = 0.0902, p = 6.90 × 10⁻⁷). Furthermore, the error bars for the new heritability estimates (Figure 1G) are predominantly much narrower than those published. The mean values of our heritability estimates are, on average, slightly lower than previously published values, as can be seen by comparing the dotted regression line (slope = 0.5) with the blue line (slope = 1) in Figure 1G. Various possible sources of this trend have been enumerated in the Discussion.

According to common genetics wisdom, diseases with early onset tend to have higher heritability. This assumption was tested by the using heritability and onset estimates of our 149 chosen diseases (see Methods and Supplementary Figures 2a and b). The correlation between the age of onset and disease heritability appears negative for a subset of diseases, including those currently categorized as neuropsychiatric, neoplastic, metabolic, ophthalmologic, and central nervous system diseases. For diseases with strong immune system components, such as autoimmune and infectious diseases, the estimated correlation between heritability and disease onset was positive (see Supplementary Figure 2b). When combined, the heritability estimates for all diseases, contrary to the common wisdom, showed no linear correlation with age of disease onset.

Our analysis also provided estimates of the environmental counterparts of heritability: unique-environment, common-couple, and common-sibling preventability (see Supplementary Figures 1a, b, and c). The common-couple preventability estimates range from 0 (autism) to 0.46 (photo dermatitis); the corresponding common-sibling estimates tend to be smaller, but can be as large as 0.29 (sepsis). The estimates for unique-environment preventability tended to be the largest: In our dataset, estimates ranged from 0.03 (eye infection) to 0.842 (diseases associated with damages to rectum and anus). For example, the largest preventability estimate for migraine is for unique environment (0.534), followed by common-couple (0.11), and negligible common-sibling preventability. Similarly, for sleep disorders, preventability estimates were 0.269, 0.22, and 0.15 for unique, couple, and sibling preventability, respectively.

Genetic and environmental correlations

Our analysis of pairwise disease correlations focused on 29 diseases, all pairs of which were well represented in both the children and parents of our dataset (see Supplementary Table 1). We estimated genetic and environmental correlations across all pairs of these 29 diseases (see Figure 2A–D, Supplementary Table 4).¹⁴ The majority of correlation values in our analysis differed significantly from zero (the null hypothesis r = 0) at a 1% false discovery rate (see Methods). ¹⁵ On average, genetic correlations between diseases tended to be stronger than their corresponding environmental correlations (see Figures 2B and 2C). However, for the majority of neuropsychiatric disease pairs, the environmental correlations are nearly as strong as the genetic correlations. In some cases, such as for the substance abuse and schizophrenia disease pair, the environmental correlation is stronger than the genetic correlation, and nearly equal for other disease pairs, such as schizophrenia and bipolar disorder. This observation is consistent with an earlier finding of nearly equal amounts of shared genetic and environmental effects between schizophrenia and bipolar disorder.¹⁶

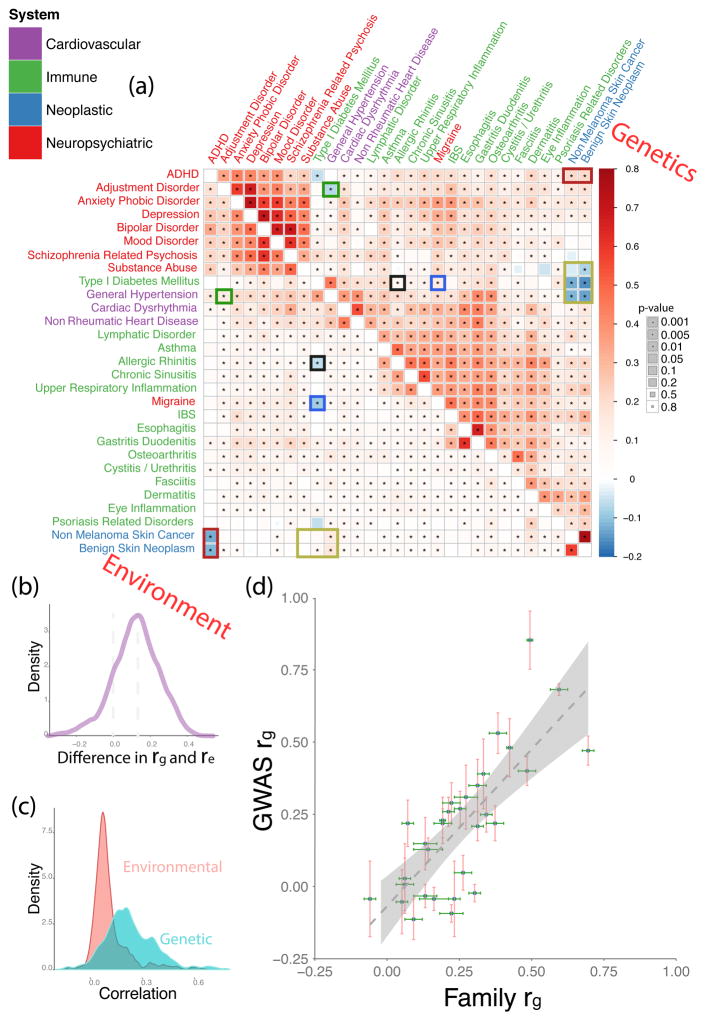
Figure 2.

Genetic and environmental correlations between diseases. (A) Matrix of pairwise genetic correlations (upper half) and corresponding environmental interactions (lower half) colored by sign and magnitude (see legend) The disease color labels indicate biological systems associated; the size of the squares indicates statistical significance, see key on the right. Cells with asterisks indicate pairwise interactions that remained significant at a false discovery rate of 1%.¹⁵ The color boxes within the matrix indicate opposite-sign correlation values for the same pair of diseases. Posterior probabilities of two correlation values (genetic and environmental) for the same pair of diseases having the same sign were 1.869 × 10⁻¹⁴ (ADHD and benign skin neoplasm), 3.376 × 10⁻¹⁴ (ADHD and non-melanoma skin cancer), 4.523 × 10⁻⁹ (adjustment disorder and general hypertension), 8.715 × 10⁻⁴ (migraine and type 1 diabetes mellitus), 9.251 × 10⁻⁵ (benign skin neoplasm and type 1 diabetes mellitus), 6.401 × 10⁻³³ (benign skin neoplasm and general hypertension), 3.712 × 10⁻¹⁷ (non-melanoma skin cancer and general hypertension), 3.933 × 10⁻⁴ (allergic rhinitis and type 1 diabetes mellitus). (B) Distribution of (Genetic correlation − Environmental correlation) values for the same pair of diseases. (C) Individual distributions of genetic and environmental correlations superimposed on the same plot. (D) Comparison of our family-based estimates of genetic correlations between diseases compared to previously published GWAS-based values, the complete data on values and references is provided in the Supplement Table 5. Linear fit with a slope of 1.08 (SE=0.167) is indicated by the dotted line.

Figure 2C indicates that the environmental correlation distribution has a longer positive tail than the more symmetric genetic correlation distribution. Genetic and environmental correlations for the same disease pair were themselves positively correlated, and genetic correlations were also positively correlated with phenotypic correlations (see Supplementary Figures 3a and b).

In a few cases, the direction of a correlation was reversed between genetic and environmental components; this is indicated with color rectangles in Figure 2A. The corresponding Bayesian posterior probabilities for the significance of this sign difference are shown in the figure legend. These cases were particularly unexpected, as they indicate hypothetical scenarios in which genetic and environmental factors act antagonistically in determining a phenotypic path bifurcated between two apparently unrelated diseases.

On average, family-based estimates of genetic correlations obtained in our study have much narrower error bars (with a few exceptions) than earlier genome-wide association study (GWAS) estimates (see Figure 2D and Supplementary Table 5) mostly due to the very large sample size of our dataset. It is quite remarkable that genetic correlations obtained by two different methods agree so well. GWAS genetic correlations and family study genetic correlations estimate different quantities: Family studies estimate the correlation of the total genetic variation (both rare and common), while genetic correlations, estimated using single-nucleotide variants (SNPs), are based on genotyped and imputed common SNPs, which are only a subset of the total genetic variation. Essentially, our data suggest that family-based estimates of genetic correlations reflect predominantly common variants.

The absolute values of genetic correlations are high for several common conditions across all the diseases that we analyzed (for example, asthma, allergic rhinitis, osteoarthritis, and dermatitis). This result is surprising as it suggests that the most prevalent complex diseases share a considerable amount of predisposing variation, even across apparently dissimilar diseases. Human genetic variation associated with common diseases appears highly pleotropic or even omnigenic.¹⁷

In order to get a baseline of the expectedness (or unexpectedness) of observed patterns in genetic and environmental correlations, we used the International Classification of Diseases version 9 (ICD-9, see URLs and see Supplementary Figure 4, left). Based on the ICD9 taxonomy, genetic and environmental correlations for migraine are surprising. As migraine is clearly associated with the central nervous system, one would expect that its etiology is most similar to those of other neuropsychiatric conditions. For example, “mental disorders” (codes 290-319 in ICD9 taxonomy) have a sister group of “diseases of central nervous system and sensory organs” (codes 320-389), containing both migraine and eye inflammation. However, in our analysis of its genetic and environmental correlations, migraine is not similar to other nervous system diseases. Rather, it is much closer to immune system diseases, such as irritable bowel syndrome (IBS) in the genetic correlation space, and to cystitis/urethritis in the environmental correlation space, see Supplementary Figure 5. These findings suggest that migraine is associated with general, not nervous-system-specific, inflammatory processes and can possibly be mitigated with some of the treatments that have been developed for inflammatory diseases.

Inferring nosologies from correlations

Relationships among diseases are unlikely to be appropriately described with a tree-like structure commonly used in disease classifications. As we show with our data, genetic and environmental factors suggest partially incompatible disease classifications. In addition, the tree-like structures are implicitly associated with evolving entities with common origin. Tree-clustering of diseases should be therefore interpreted with caution because evolutionary relationships do not apply to human diseases.

We use automatically generated classifications (Supplementary Figure 5) as a logically consistent way to visualize and examine all the similarities between all disease pairs simultaneously. To do so, we transform the genetic and environmental correlations shown in Figure 2A into distances and then infer objective genetic and environmental disease classifications from those distances. We chose to use the simplest (1 – correlation) distance transformation. The distance-matrix method we used¹⁸ for this purpose is designed to identify the classification topology that approximates the distance-matrix the closest, so that the length of the shortest path connecting two classification leaves closely approximates distance in the input matrix. By repeatedly sampling distances from their posterior distribution, one can compute a tree from the resampled distances each time, counting the percentage of times each disease grouping occurs in the resampled trees ^19–21 (see Supplementary Figures 5a and b). The distances between diseases in a classification is meaningful. For example, two diseases connected with shorter branches are more tightly correlated and more similar genetically or/and environmentally than two diseases connected with very long branches. When a disease group is associated with a reliability number of 100, it means that this particular disease partition was replicated in all trees. In other words, the bootstrap-like numbers ^19–21 indicate the statistical reliability of the classification (see Methods).

In this analysis, the bootstrap-like measures identified a number of remarkably stable disease clusters present in both genetic and environmental trees (Supplementary Figure 5, clusters 1–6). We used the ICD9 disease taxonomy (Supplementary Figure 4, left) as a baseline to identify disease groupings that are expected (based on ICD9 classification), and those that are unexpected (defiant of ICD9 classification, but statistically significant--see Supplementary Figures 5a and b, green and yellow highlights, respectively). Many of the stable disease groups (with high bootstrap-like numbers) lie within the traditional view of disease similarity. However, many stable clusters defy the currently established nosology. For example, type 1 diabetes groups with general hypertension (support 96 and 100 in the environmental and genetic classifications, respectively)—these two diseases are not typically thought to be closely related (see URLs and Supplementary Figure 4). Previously, and collinearly with our results, Farh et al. ²² reported high genetic correlations between type 1 diabetes and other autoimmune diseases.

Migraine in both inferred environmental and genetic classifications appears to be genetically similar to inflammatory diseases, such as irritable bowel syndrome (IBS).²³ However, in the ICD9 taxonomy (see URLs), migraine is placed together with eye inflammation, in the cluster of diseases of the central nervous system and sensory organs. In our study’s genetic tree, eye inflammation is far away from migraine, but is grouped with dermatitis. In the environmental classification, migraine is the closest to inflammations associated with the infections cystitis and urethritis; eye inflammation is weakly grouped with the cluster of migraine-cystitis/urethritis. This suggests that migraine etiology is closely associated with immune system function and that the established disease taxonomy needs revision. In a recent study, Gormley et al.²³ also challenged proximity of migraine to mental disorders; their results were consistent with a vascular etiology of migraine, but while discussing migraine Gormley et al.²³ did not mention irritable bowel syndrome or other inflammatory diseases. Here, we analyzed migraine phenotypes combining both migraine with and without aura. Our data allow distinguishing between these two versions of the disease; therefore, this analysis can be performed with finer disease subdivisions, albeit at the cost of reduced sample size.

Neuropsychiatric diseases stayed in the same stable cluster in both taxonomies (see Supplementary Figure 4).²⁴ However, within the cluster, disease groupings varied considerably. In our genetic classification, depression was significantly grouped with anxiety. This is in contrast to ICD9 taxonomy, which places depression together with mood and bipolar disorders. In our environmental classification, schizophrenia is significantly closer to bipolar and mood disorders than to depression, again contrary to ICD9.

As expected, a classification computed from complete phenotypic correlations represents a compromise between genetic-only and environmental-only classifications (see Supplementary Figure 4, right).

Discussion

We conducted a very large-scale, family-based, phenotypic-variance analysis of numerous complex diseases. Methodologically, our work is indebted to the work of Lichtenstein et al. ¹⁶ and Xia et al. ²⁵ in considering genetic data for nosology inference¹⁶ and careful model selection.²⁵ It has been long suspected that complex diseases have numerous predisposing factors, both in the genetic and environmental realms. For the first time, we were able to compare the contribution of both environmental and genetic determinants to the phenotypic variances and covariances of a broad range of diseases, and transform these covariances into estimates of disease classifications.

Our study contributes to a series of influential, interlinked probes into complex disease heritability and cross-disease genetic correlations.^24,26–29 For example, Munoz et al. 2016 ³⁰ studied 12 complex human diseases using 502,682 participants and the family histories of disease in 1.5 million individuals. As our dataset provides rich phenotypic information for a very large population, we were able to analyze both the heritability and preventability of a collection of diseases (149) an order of magnitude larger than has been previously done, using data for a comparable number of individuals. Furthermore, the statistical power associated with this broad and complex sample provided a new opportunity to contrast genetic correlation estimates from family data with estimates that have been made using DNA variants. Confirming previous findings,^29,31 we observed a near-linear relationship between total phenotypic and family-based genetic correlations with a proportionality constant of 1.150 (se = 0.035, p < 2 × 10⁻¹⁶, see Supplementary Figure 3). With a much smaller standard error, our ratio estimate is within the confidence intervals of published results.^29,31 These results suggest that the largest part of genetic correlation between complex diseases is associated with common variants captured by SNP genotyping.

As is true for most observational studies, there are several possible sources of bias. Family studies based on closely-related individuals may inflate narrow-sense heritability estimates due to unaccounted for effects of shared environment, maternal influences, or epistatic interactions of genetic variants. ^32,33 In agreement with previous findings regarding the significance of shared environmental effects, ^25,30,34 our study provided first-time or updated heritability estimates for 149 diseases. On average, our heritability estimates were lower than those reported by twin/family studies by a factor of 0.90. Thus, we conclude that SNP-based heritability estimates explain, on average, 49% of our family-based heritability estimates, a 13% increase from previous estimates (see Supplementary Table 6). Due to the differences in model selection procedures, agreement between our estimates and previously reported results on environmental effects is harder to ascertain.³² As articulated by Zuk et al., ³³ one of the major sources of bias in estimates of heritability is associated with the choice of mathematical model, as the narrow-sense heritability, by definition, does not account for potential deviations from genetic additive model. The insurance data describes, at best, 54.7 to 69.7% of the US population, depending on age group (see URLs), so a considerable lower-income stratum of US society is not represented in this dataset. Data from insurance claims does not include ethnicity and race; therefore, we were unable to explicitly adjust for these confounders. Another contribution to the estimate bias can be attributed to assortative mating, as the US population is stratified by ethnicity, income, and geography, with all of these factors contributing to assortative marriages.

As would be expected due to the age distribution differences in our sample, parental disease prevalence tends to exceed same-disease prevalence in their children. This trend would be especially pronounced for late-onset conditions, such as Parkinson’s disease and prostate cancer (see Supplementary Table 1). We accounted for this by modeling age-related increase in disease liability with an age-specific, fixed-effect coefficient in our mixed-effect linear model. (See Methods and Supplementary Figure 6 for estimates of dependence of disease liability on age of patient for several late-onset conditions). Note that this type of modeling only accounts for mean differences in liability between age groups, but not differences in heritability between age groups. If the late-onset and early-onset varieties of the same disease were, indeed, shown to have distinct etiologies, their heritability values would have to be estimated separately. ³⁵

While ethnicity is not recorded in the US insurance claims, it can be imputed. For example, according to the US Centers for Disease Control and Prevention,³⁶ sickle cell disease (SCD) affects, on average, one out of every 365 African Americans; the incidence rate of SCD in African Americans is about 88 times higher than the rest of the US population. The incidence rate of SCD in our database is 2.85523 × 10⁻⁴ vs 3.23891 × 10⁻⁴ in the nation on average. Given that the US African American population is 12.2 percent of the total (see URLs)³⁷ African American patients appear to be represented in our data at 10.6% (about 13% lower than the average across the US). Given the very large sample size, the ethnic diversity of our dataset should be a reasonable representation of the multiethnic composition of the US insured population.

When computed solely from genetic information, “genetic correlation is immune to environmental confounding but is subject to genetic confounding.” ²⁴ In the case of family-based analyses, environmental confounding is an issue researchers might address with an appropriate mathematical model of genetic and environmental factors working in consort. Unfortunately, the appropriate model is unknown and, therefore, interpretation of results is conditional on the assumptions of a rather simple, additive-genetic and additive-environment model—a model that is used, in most studies, for lack of a better (experimentally-grounded) alternative. Another conceivable caveat is related to possible biases in the sampling of affected individuals. ²⁴ Finally, our results reflect the medical coding of disease in the healthcare system rather than research-quality disease diagnoses. Extensive study of the correspondence in results of genetic association studies conducted with research diagnoses and those conducted using diagnoses from electronic health records have demonstrated good concordance for large association studies.³⁸

Lichtenstein et al.’s¹⁶ study discussed the difficulties and ambiguities associated with changing uncertain diagnoses (“patients with one diagnosis sometimes evolve into the other diagnosis”), and, to a large extent, their discussion and hedging apply here. Type 1 and type 2 diabetes are excellent examples of this challenge. While type 1 diabetes leads to high blood glucose levels due to autoimmune destruction of the insulin-secreting beta-cells in the pancreas, type 2 diabetes arises from complex metabolic dysregulation of insulin secretion and the insensitivity of peripheral tissues to the action of insulin, the two are commonly conflated in electronic health records, even for the same patient. This is in part because their corresponding ICD9 codes are very close to one another (250.01 and 250.02 for type 1 and 2, respectively), and in part because physicians often lack the data used in research studies to aid in making this distinction: Some type 2 diabetic patients are inevitably classified as type 1 diabetics and, possibly, vice versa. This disclaimer regarding diagnostic uncertainty also applies to phenotypes with overlapping clinical signs, such as schizophrenia, schizoaffective and bipolar disorders, and depression, or benign and malignant skin cancers, but does not apply to diseases from radically different biological systems, such as schizophrenia and skin cancer.

Online Methods

Data

Our study used data from the 2003–2011 Truven Health MarketScan Commercial Claims and Encounters Database, which comprised 115,805,687 individuals and 56,003,690 policies. We defined a family as a group of individuals on a single insurance policy. In each family, we assumed primary and secondary beneficiaries were parents and other dependents were children.

To maximize the probability of correct genetic relatedness, we selected families with parents and dependents having at least 15 years’ age difference. In addition, we set the minimum enrollment time to six years, ran our analysis using 128,989 nuclear families with the fullest medical history in our database and which included children aged 16 and above. The resulting 481,657 individuals had been enrolled in the database for an average of 6.5 years.

We grouped ICD9 diagnostic codes into 568 categories based on their clinical manifestations. We then selected 149 diseases of 20 biological systems for univariate analysis where disease prevalence was larger than 0.3% in parents and children studied, with the standard error calculated as:

$$\text{SE}=\sqrt{\frac{p(1-p)(1-f)}{n}}$$

where n represents the total number of individuals, p is the prevalence, and f is the fraction of the total US population sampled ³⁹. We calculated the age of onset for each disease as the five percent age percentile of all patients with a given disease in the database.

Because all individuals included in this study were between the age of 17 and 65, several late onset diseases have lower prevalence. For example, Parkinson’s disease prevalence among the parents and their children were 0.28% and 0.024%, respectively (see Supplementary Table 1) We excluded these low-young-adult-prevalence diseases from our study due to insufficient sample size.

We then calculated the phenotypes for each relational pair (parent-offspring, siblings, couples) and selected 29 diseases with at least 30 data points per pairwise disease state and relational category, also belonging to the four biological systems of interest (neuropsychiatric, immune, oncological, and cardiovascular) for bivariate analysis. Due to our focus on the four biological systems listed above and the high computational cost of estimation, several diseases included in the univariate analysis were not included in the bivariate analysis.

Statistical analysis

We used a multivariate, generalized, linear mixed model with a probit link⁴⁰, i.e., the probability for an individual to have a disease is measured by an underlying Gaussian latent variable (liability ℓ) ^41,42. This model ⁴³ allows us to infer five kinds of factors influencing disease liability variation: genetic effects associated with pedigree, environmental effects shared by couples, environmental effects shared by siblings, environmental effects shared within families, and unique environmental effects. In addition, disease prevalence differed between males and females, and between parents and their children. We accounted for these differences in disease liability by including age- and gender-specific fixed effects in our model. We assumed that the same disease manifesting itself both in parents and in their children has the same underlying liability, after accounting for the age and gender effects.

The outcome vector y shows a case (y = 1) or control (y = 0) status for each disease on the observed scale. Let liability ℓ = ϕ(y)⁻¹, where ϕ is the Cumulative Distribution Function (CDF) of the standard normal distribution, and

$$\mathit{\ell }=\mathbf{X}\mathrm{\beta }+\mathbf{a}+\mathbf{c}+\mathbf{s}+\mathbf{f}+\mathbf{e}$$

where β is the vector for fixed effects of age and gender. a is the vector of random, additive, genetic effects based on pedigree, c is the vector of environment effects shared by a couple, s is the vector of environment effects shared by siblings, f is the vector of environment effects shared by a family, and e is the vector of unique effects. ⁴³ We followed the naming convention used in Xia et al. ²⁵

The underlying binary traits’ liability (co)variance structure⁴³ is:

$$\text{var}(\mathit{\ell })=\mathbf{G}\otimes \mathbf{A}+{\mathbf{R}}_{\mathbf{c}}\otimes {\mathbf{I}}_{\mathbf{c}}+{\mathbf{R}}_{\mathbf{s}}\otimes {\mathbf{I}}_{\mathbf{s}}+{\mathbf{R}}_{\mathbf{f}}\otimes {\mathbf{I}}_{\mathbf{f}}+{\mathbf{R}}_{\mathbf{e}}\otimes {\mathbf{I}}_{\mathbf{n}}$$

A is the additive genetic relationship matrix (genetic effects are assumed to be additive on the liability scale), I_c is the couple environment matrix, I_s is the sibling environment matrix, I_f is the family environment matrix, I_n is an identity matrix, G is the additive genetic (co)variance, R_c is the couple environment (co)variance, R_s is the sibling environment (co)variance, R_f is the family environment (co)variance, and R_e is the unique environment (co)variance. Furthermore, individual covariance matrices are parameterized as:

$$\begin{array}{c}\mathbf{G}=\left[\begin{array}{cc}{\sigma }_{a,i}^2& {\sigma }_{a,i,j}\\ {\sigma }_{a,i,j}& {\sigma }_{a,j}^2\end{array}\right],{\mathbf{R}}_{\mathbf{c}}=\left[\begin{array}{cc}{\sigma }_{c,i}^2& {\sigma }_{c,i,j}\\ {\sigma }_{c,i,j}& {\sigma }_{c,j}^2\end{array}\right],{\mathbf{R}}_{\mathbf{s}}=\left[\begin{array}{cc}{\sigma }_{s,i}^2& {\sigma }_{s,i,j}\\ {\sigma }_{s,i,j}& {\sigma }_{s,j}^2\end{array}\right],\\ {\mathbf{R}}_{\mathbf{f}}=\left[\begin{array}{cc}{\sigma }_{f,i}^2& {\sigma }_{f,i,j}\\ {\sigma }_{f,i,j}& {\sigma }_{f,j}^2\end{array}\right],{\mathbf{R}}_{\mathbf{e}}=\left[\begin{array}{cc}{\sigma }_{e,i}^2& {\sigma }_{e,i,j}\\ {\sigma }_{e,i,j}& {\sigma }_{e,j}^2\end{array}\right].\end{array}$$

The narrow-sense heritability, couple environmental effects, sibling environmental effects, family environmental effects, and unique environmental effects for disease x are defined on the liability scale in the following way:

$$h_x^2=\frac{V_{a,x}}{V_{p,x}},e_{c,x}^2=\frac{V_{c,x}}{V_{p,x}},e_{s,x}^2=\frac{V_{s,x}}{V_{p,x}},e_{f,xx}^2=\frac{V_{f,x}}{V_{p,x}},e_{u,x}^2=\frac{V_{u,x}}{V_{p,x}}.$$

We calculated the genetic correlation coefficient (r_g) and the environmental correlation coefficient (r_e) as:

$$r_g=\frac{{\sigma }_{a,i,j}}{{\sigma }_{a,i}{\sigma }_{a,j}},r_e=\frac{{\sigma }_{c,i,j}+{\sigma }_{s,i,j}+{\sigma }_{f,i,j}+{\sigma }_{e,i,j}}{\sqrt{{\sigma }_{c,i}^2+{\sigma }_{s,i}^2+{\sigma }_{f,i}^2+{\sigma }_{e,i}^2}\sqrt{{\sigma }_{c,j}^2+{\sigma }_{s,j}^2+{\sigma }_{f,j}^2+{\sigma }_{e,j}^2}}.$$

Due to the binary nature of our phenotypic data ⁴⁴, we estimated variance components using Bayesian methods with the MCMCglmm package.¹⁴ We used a chi-squared prior with one degree of freedom for the univariate analysis⁴⁵ and Half-Cauchy prior for the bivariate analyses.⁴⁶ For the univariate analyses, we ran a burn-in period of 150,000 to 330,000 iterations depending on convergence, and sampled 600,000 iterations with 500 thinning intervals. For bivariate analyses, we ran a burn-in period of 30,000 to 44,000 iterations, and sampled 120,000 iterations.

We checked model convergence using both standard MCMC diagnostic tests^47–49 and visual comparison after the burn-in period. We reported parameter estimations with posterior means, posterior standard deviations, and 95 percent confidence intervals (CI). The posterior distributions represent the distributions of true parameters, given the data and the priors. Posterior probabilities for sign differences between the same disease genetic and environmental correlations were calculated assuming a bivariate normal posterior distribution. We corrected for multiple testing using the Benjamini-Hochberg method ^15,50 and deemed a correlation significant if it passed the false discovery rate of one percent. We also constructed neighbor-joining trees based on a distance definition of 1-correlation for the correlation matrices.¹⁸ We performed 10,000 simulations for each tree by sampling from the correlation posterior distributions. We calculated a bootstrap-like measure indicating the percentage of simulations that replicated the disease partition.

Model selection

We conducted two rounds of model selection to find the most appropriate genetic and environmental models for both univariate and bivariate analysis using deviance information criteria (DIC). ⁵¹ The full model ‘GCSF’, as well as five simpler models, were selected based on 29 diseases involved in both univariate and bivariate analyses. We then conducted a second run of model selection between the top two models on all 149 diseases. Due to the high computational cost of bivariate analysis, we based our bivariate model on univariate model selections and chose ‘GCS’ model for the bivariate analysis.

Pedigree error

Quantitative genetic estimations, such as those for heritability and genetic correlations, rely on the accuracy of the pedigree information. Intuitively, we expect a downward bias in both heritability and genetic covariances due to pedigree errors. Indeed, simulation and population studies have shown that heritability estimates were underestimated, albeit slightly; pedigrees with 20 percent errors led to five percent underestimation of heritability estimates^52,53. Genetic correlation estimates were influenced even less by mis-assigned relations: Both Morrissey et al. ⁵⁴ and Bérénos et al. ⁵² found no biases caused by pedigree errors in genetic correlation estimations using both simulated and real data.

Stepchildren and adopted children

We collected US Census data on children by household types^55,56. The 2010 US Census surveyed a large population and reported data for children of differing age groups, shown in Supplementary Table 7. Supplementary Table 8 is based on US Current Population Survey data from 2007 to 20011 for children under age 18. This data showed that the percentages of children living with both biological parents were consistent with percentages from US Census data.

Pedigree simulation

Following Charmantier and Réale’s⁵³ simulation model, we performed 100 simulations on 5000 nuclear families, of which 2.4% have adoptive children and 6.2% have stepchildren⁵⁵ and estimated parameters with the true pedigrees versus mis-assigned pedigrees. We used a stochastic simulation model to generate pedigrees of two generations, with varying heritability estimates (0.03–0.97) and genetic correlations (0.13–0.85). The parents are assumed to be unrelated and unselected individuals. We simulated two binary traits, following the model y = I(ℓ > 0), ℓ = μ+ Za + e where y is the matrix containing individual phenotypes at both traits, ℓ is the underlying liability, μ contains the population means for liability, a is a matrix of additive genetic effects, and e is a matrix of residual errors. Z represents an incidence matrix of the individual effects a has upon liabilities in ℓ. All models were solved using the MCMCglmm. Indeed, we also found a mean underestimation of 5.6% (SE=0.56) for heritability and no evidence of biases for estimations of either genetic (t-test p=0.8784) or environmental correlations (t-test p=0.9948). We then calculated and reported heritability estimates adjusted for the underestimation.

Heritability comparison

In comparing our heritability estimates with results from other independent studies, we first collected reference family heritability estimates for 65 out of the 149 traits we studied. We also collected 31 GWAS heritability estimates from literature. We reasoned that the two estimates for the same disease agreed with each other when their 95% confidence intervals overlapped. The comparisons are listed in Supplementary Tables 3 and 6.

GWAS and family-based genetic correlations

We compared our genetic correlation estimates with estimates using GWAS data on common pairs of traits. First, we collected genetic correlations from literature^24,28,29,57. Next, we compared those genetic correlation estimates we found in common. To maximize this comparison, we broadened the collection of traits to include non-rheumatic heart disease as a proxy for cardiovascular diseases²⁹, and type I diabetes as a proxy for fasting glucose, see Pippitt et al. ⁵⁸ for justification of this choice. The resulting 30 genetic correlation pairs (shown in Supplementary Table 5) showed a correlation of 0.769, 95% CI (0.571–0.883) between our estimates and GWAS results, along with a linear fit with a proportionality constant of 1.08 (SE=0.167), indicating consistency between the two methods.

Data Availability Statement

All data that support the findings of this study are included in this published article (and its supplementary information files). The raw data are available from Truven MarketScan®; restrictions apply to the availability of these data, which were used under license for the current study. A user license could be obtained by following this link https://marketscan.truvenhealth.com/marketscanportal/

Table 1.

Disease prevalence and heritability estimates for 30 most prevalent diseases in our study.

Disease	Prevalence	h2	h2 SD
Cardiac Dysrhythmia	0.045	0.240	0.011
General Hypertension	0.173	0.462	0.009
Esophageal Disease	0.077	0.292	0.008
Functional Digestive Disorder	0.051	0.203	0.009
Type II Diabetes Mellitus	0.066	0.561	0.010
Allergic Rhinitis	0.108	0.445	0.006
Asthma	0.063	0.457	0.008
Atopic Contact Dermatitis	0.095	0.202	0.006
Chronic Sinusitis	0.047	0.523	0.008
Eye Inflammation	0.045	0.292	0.009
Osteoarthritis	0.068	0.256	0.012
Cellulitis	0.061	0.226	0.007
Ear Infection	0.106	0.244	0.007
Eye Infection	0.053	0.200	0.009
Fungal Infection	0.063	0.211	0.007
UTI	0.083	0.227	0.007
Viral Warts HPV	0.038	0.289	0.009
Acne	0.036	0.501	0.010
Keratosis	0.058	0.344	0.015
General Spondylosis Spine Disorder	0.081	0.325	0.008
Muscle Ligament Disorder	0.121	0.268	0.006
Synovium Tendon Bursa Disorder	0.039	0.180	0.009
Benign Colon Neoplasm	0.039	0.173	0.019
Benign Skin Neoplasm	0.067	0.547	0.007
Non-Melanoma Skin Cancer	0.054	0.520	0.008
Anxiety Phobic Disorder	0.063	0.432	0.007
Depression	0.038	0.579	0.006
Substance Abuse	0.045	0.422	0.010
Breast Disorder	0.044	0.166	0.010
Disease of the Female Reproductive Organs	0.105	0.235	0.009