Decoding with limited neural data: a mixture of time-warped trajectory models for directional reaches

Abstract

Neuroprosthetic devices promise to allow paralyzed patients to perform the necessary functions of everyday life. However, to allow patients to use such tools it is necessary to decode their intent from neural signals such as electromyograms (EMGs). Because these signals are noisy, state of the art decoders integrate information over time. One systematic way of doing this is by taking into account the natural evolution of the state of the body—by using a so-called trajectory model. Here we use two insights about movements to enhance our trajectory model: (1) at any given time, there is a small set of likely movement targets, potentially identified by gaze; (2) reaches are produced at varying speeds. We decoded natural reaching movements using EMGs of muscles that might be available from an individual with spinal cord injury. Target estimates found from tracking eye movements were incorporated into the trajectory model, while a mixture model accounted for the inherent uncertainty in these estimates. Warping the trajectory model in time using a continuous estimate of the reach speed enabled accurate decoding of faster reaches. We found that the choice of richer trajectory models, such as those incorporating target or speed, improves decoding particularly when there is a small number of EMGs available.

1. Introduction

If a person has lost the use of his or her arms due to paralysis, it may be desirable to enable communication through interactions with a computer (Kim et al 2008) or to restore some degree of movement using functional electrical stimulation (FES) (Kilgore et al 2008, Bryden et al 2005) or a robotic device (Wiegner et al 1996). To this end, one of the most challenging problems is the determination of user intent (Wolpaw and McFarland 2004, Kilgore and Kirsch 2004). A neural machine interface (NMI) is often used to estimate user intent from the physiological signals that remain under voluntary control. For example, brain machine interfaces employing ensemble recordings of the activities of single neurons in motor and pre-motor cortical areas have been used to control the movement of robotic arms with multiple degrees of freedom (Velliste et al 2008, Pohlmeyer et al 2009). Less invasive signal sources are more commonly used in clinical practice, and similar decoding methods can be applied to various types of signals.

Amongst individuals with high tetraplegia, one of the most impaired target populations, there is large variation in the available control signals. In most previously implemented systems, pre-programmed arm movements are initiated using switching mechanisms through, for example, contralateral shoulder movements (Smith et al 1996), respiration (Hoshimiya et al 1989) or voice (Nathan and Ohry 1990). For a system that gives the user more flexibility of control, discrete information about potential reach targets may be available from knowledge of object locations or tracking eye movements. Alternatively, residual movements and neural signals can provide continuous information about a desired trajectory. Implanted devices in the brain promise ‘effortless’ user control but are not yet practical for use in most patients (but see Braingate trial (Hochberg et al 2006)), making voluntary movements or electromyograms (EMGs) from voluntarily controlled muscles the most viable continuous signal sources. Unfortunately, in the most severe cases this results in a very limited signal set. Under these conditions, the control of whole arm reaching devices is a challenging problem and requires enormous effort from the user (Kilgore and Kirsch 2004). Because each patient is unique, in this work we have aimed to build a general decoder that can incorporate any type of signal source.

Neural signals are invariably noisy, and the noise statistics often differ depending on the specific signal source. To deal with this problem, many state of the art approaches use recursive Bayesian estimation methods to predict the intended state of the device (e.g. hand dynamics) from the user’s control signals. This involves defining a trajectory model describing the state’s probabilistic evolution over time, and an observation model, which is the probabilistic mapping between the state and the user’s neural control signals, or observations. This is a popular approach for NMIs; it offers a principled way of formalizing our uncertainty about signals and has resulted in improvements over other signal processing techniques (Hochberg et al 2006, Wu et al 2006).

The trajectory model defines our prior assumptions about the nature of the movement to be decoded by modelling the desired evolution of the relevant state. The Kalman filter (KF) (Kalman 1960) belongs to the class of linear-Gaussian priors, where both trajectory and observation model are linear with additive Gaussian noise. One such trajectory model that is often used in movement decoding is the random-walk model, where the hand moves a small amount from one time-step to the next without a directional bias (Wu et al 2006). However, the trajectory model may also represent constraints on the system due to the limb mechanics and the environmental context of the reach (Yu et al 2007). If the available neural information is limited we may especially require a trajectory model with more predictive power. A number of researchers have proposed using available information about probable targets to take advantage of the directional nature of reaching (Yu et al 2007, Mulliken et al 2008, Srinivasan et al 2006, Corbett et al 2010). This would allow us to strengthen our assumptions about the reaching movement, improving performance while reducing the burden on the user.

Prior knowledge of the probable reach targets can tell us a lot about the desired trajectory, but such information is generally noisy. One possible source is neural activity in the dorsal pre-motor cortex that provides information about the intended target prior to movement (Mulliken et al 2008, Hatsopoulos et al 2004). Estimates of the reach target may be found noninvasively by tracking eye movements—people almost always look at a target before reaching for it (Johansson et al 2001). However, since an individual may saccade to multiple locations prior to a reach, we obtain a probabilistic distribution of potential targets. In this work we seek an approach that can handle such target uncertainty while allowing reaches throughout a large, continuous workspace.

Another important characteristic of human reaching, which has not been addressed by standard trajectory models, is that people may want to move at different speeds. Models with linear dynamics only allow for deviation from the average through the noise term, which makes them poor at describing the natural variation of movement speeds during real-world tasks. Explicitly incorporating movement speed into the trajectory model should lead to better movement estimates.

Here we present an algorithm that uses a mixture of extended Kalman filters (EKFs) to combine our insights related to the variation of movement speed and the availability of probabilistic target knowledge to strengthen our trajectory model. Each of the mixture components allows the speed of the movement to vary continuously over time. We tested how well we could use EMGs and eye movements to decode hand position of humans performing a three-dimensional large-workspace reaching task. We find that using a trajectory model that allows for probabilistic target information and variation of speed leads to dramatic improvements in decoding quality, particularly where there is a small amount of neural information available as would be the case for a high-level spinal cord injury (SCI).

2. Methods

2.1. Decoding algorithms

2.1.1. Models for incorporating target information

Most state estimation algorithms for neural decoding have assumed a linear trajectory model with Gaussian noise (Wu et al 2006). The KF (figure 1(a)) provides the optimal solution in this case. The state of the arm x, evolves linearly over time while integrating Gaussian noise:

$${\mathbf{x}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}-1}={[z_t{\dot{z}}_t{\ddot{z}}_t]}^T=A{\mathbf{x}}_{\mathbf{t}-1}+{\mathit{w}}_{\mathit{t}},$$ (1)

where A is the state transition matrix, z_t ∈ ℝ^p represents the arm position, w is the process noise with p(w) ~ N(0, Q), and Q is the state covariance matrix. When used to describe reaches to a number of targets spanning the workspace this model effectively describes a random drift of the hand. Specifically, the model captures the fact that small, smooth movements are more probable than large movements, but no particular movement direction is more probable than another at any individual time-step. This model is therefore incapable of capturing the acceleration profile that is characteristic of natural arm reaches. Invariably, fast velocities will be underestimated and there will be unwanted drift close to the target.

Figure 1.

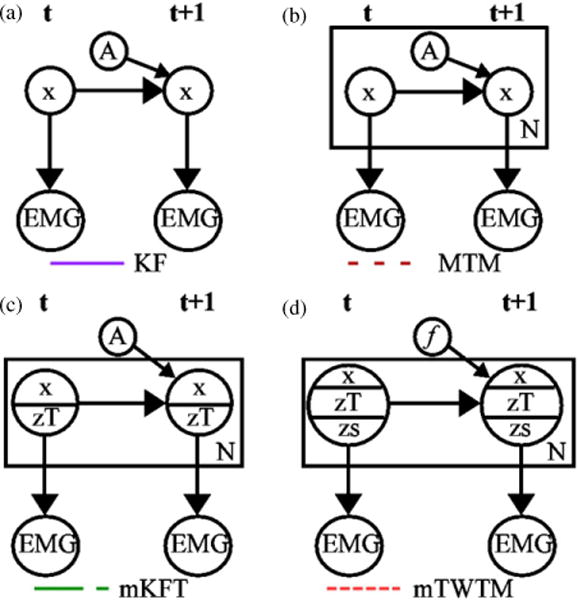
Graphical representation of the algorithm approaches: (a) the generic Kalman filter (KF); (b) mixture of trajectory models (MTM) (Yu et al 2007); (c) mixture of Kalman filters with targets (mKFT); (d) mixture of time-warped trajectory models (mTWTM).

In many decoding applications we may have knowledge of the target that the subject wants to move towards. When modelling a stereotypical reach to a single target, the KF is extremely effective at capturing the dynamics. Yu et al took advantage of this fact in their mixture of trajectory models (MTM) algorithm, where they defined a different trajectory model for each of a small set of fixed, pre-defined targets. They then used a probabilistic mixture over potential targets, resulting in dramatic improvements in decoding accuracy (Yu et al 2007). However, the strength of this model is in capturing stereotypical reach profiles, potentially limiting its generalizability to new regions of the workspace.

A single trajectory model that can incorporate targets from anywhere within a continuous workspace may be expected to perform better when asked to generalize to novel targets. To achieve this we can assume that the effect of the target on the dynamics is linear, and thereby retain the simple form of the KF. Following the literature (Mulliken et al 2008, Kemere et al 2004), we realized this by adding the target to the state space (KFT):

$${\mathbf{x}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}-1}={[z_t{\dot{z}}_t{\ddot{z}}_{t}z{T}_t]}^T=A{\mathbf{x}}_{\mathbf{t}-1}+{\mathit{w}}_{\mathit{t}},$$ (2)

where zT_t ∈ ℝ^g is the vector of target positions, with dimensionality less than or equal to that of z_t. The target estimate is initialized at the beginning of the reach. The effect of the target on the dynamics may now be described, such that the trajectory model will describe a reach to a specific target. The state transition matrix, A, is of the form

$$A=\left(\begin{array}{cccc}{I}_p& \mathrm{\Delta }t\times I_p& 0_{p\times p}& 0_{p\times p}\\ 0_{p\times p}& I_p& \mathrm{\Delta }t\times I_p& 0_{p\times p}\\ {\alpha }_P& {\alpha }_V& {\alpha }_A& {\alpha }_T\\ 0_{g\times p}& 0_{g\times p}& 0_{g\times p}& I_g\end{array}\right)$$ (3)

with I_p as the p-dimensional identity matrix, 0_{p × p} as a p × p matrix of zeros, and Δt as the sample time. Thus, the position states depend only on the previous positions and velocities, the velocities depend on the previous velocities and accelerations, while the target states, zT, remain constant in the trajectory model. The α_P, α_V, α_A and α_T terms, which are matrices representing the effects of the previous position, velocity, acceleration and target states on the current acceleration, may be learned directly from the data (see section 2.3.2). The inclusion of the α_T terms gives the trajectory model a point of attraction, allowing acceleration when the target is distant and deceleration when it is close.

In a real-world decoding situation, there will undoubtedly be uncertainty associated with the target estimates. For example, with gaze-based target estimates, people may saccade to other locations in addition to the target in the period preceding a reach. Here we address the situation where we have a small number of potential target locations indexed by n, $z{T}_t^n$ for which we have obtained a prior distribution, P (zT_t). As is the case in the MTM, we used a mixture model to consider each of the possible targets. We condition the posterior probability for the state on the N possible targets:

$$\mathit{P}({\mathbf{x}}_{\mathit{t}}|{\mathit{y}}_{1\dots \mathit{t}})={\displaystyle \sum _{n=1}^N\mathit{P}({\mathbf{x}}_{\mathit{t}}|{\mathit{y}}_{1\dots \mathit{t}},\mathit{z}{\mathit{T}}_{\mathit{t}}^{\mathit{n}})\mathit{P}(\mathit{z}{\mathit{T}}_{\mathit{t}}^{\mathit{n}}|{\mathit{y}}_{1\dots \mathit{t}})}.$$ (4)

Using Bayes’ rule, this equation becomes

$$\mathit{P}({\mathbf{x}}_{\mathit{t}}|{\mathit{y}}_{1\dots \mathit{t}})={\displaystyle \sum _{n=1}^N\mathit{P}({\mathbf{x}}_{\mathit{t}}|{\mathbf{y}}_{1\dots \mathit{t}},\mathbf{z}{\mathit{T}}_{\mathit{t}}^{\mathit{n}})\frac{\mathit{P}({\mathit{y}}_{1\dots \mathit{t}}|\mathit{z}{\mathit{T}}_{\mathit{t}}^{\mathit{n}})\mathit{P}(\mathbf{z}{\mathit{T}}_{\mathit{t}}^{\mathit{n}})}{\mathit{P}({\mathbf{y}}_{1\dots \mathit{t}})}}.$$ (5)

Essentially, we perform the KF recursion for each possible target, and our solution is a weighted sum of the resultant trajectories, $\mathit{P}({\mathbf{x}}_{\mathbf{t}}|{\mathbf{y}}_{1\dots \mathit{t}},\mathit{z}{\mathit{T}}_{\mathit{t}}^{\mathit{n}})$. The weights are proportional to both the prior probability for the target, $\mathit{P}(\mathit{z}{\mathit{T}}_{\mathit{t}}^{\mathit{n}})$, and the likelihood of the neural data given that target $\mathit{P}({\mathbf{y}}_{1\dots \mathit{t}}|\mathit{z}{\mathit{T}}_{\mathit{t}}^{\mathit{n}})$. P(y_1…t) is independent of the target and therefore does not need to be calculated; instead it is used as a scaling factor to ensure that the weights sum to 1. In this mixture of KFTs (mKFT, figure 1(c)), the weight for the trajectory corresponding to each potential target will be initialized to the prior estimate for the target and converge to the most probable of these trajectories as the neural information is obtained over the course of the reach.

The MTM (figure 1(b)) mixture model is implemented in a similar manner (Yu et al 2007). However, in this case there are multiple trajectory models, A_m, each describing reaches to a specific target, m, and the form of each trajectory model is the same as the KF in equation (1) where the target is not included in the state vector:

$${\mathbf{x}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}-1},m={[z_t{\dot{z}}_t{\ddot{z}}_t]}^T=A_m{\mathbf{x}}_{\mathit{t}-1}+{\mathit{w}}_{\mathit{t}}.$$ (6)

As noted above, this trajectory model effectively captures the dynamics of a reach to a single target and thus the mixture uses the most probable trajectory models to generate an accurate reach. To implement the MTM for M potential targets equation (5) becomes

$$\mathit{P}({\mathbf{x}}_{\mathbf{t}}|{\mathbf{y}}_{1\dots \mathit{t}})={\displaystyle \sum _{\mathit{m}=1}^{\mathbf{M}}\mathit{P}({\mathbf{x}}_{\mathbf{t}}|{\mathbf{y}}_{1\dots \mathit{t}},\mathit{m})\frac{\mathit{P}({\mathbf{y}}_{1\dots \mathit{t}}|\mathit{m})\mathit{P}(\mathit{m})}{\mathit{P}({\mathbf{y}}_{1\dots \mathit{t}})}},$$ (7)

where P(x_t|y_1…t, m) represents the resultant trajectory using the model A_m, P(y_1…t|m) is the likelihood of the neural data for that model and P(m) is the prior probability for the associated target. In summary, while both approaches use a mixture model to account for multiple potential targets, the mKFT uses one trajectory model to incorporate targets from anywhere in the continuous workspace, whereas the MTM has a different trajectory model for each of a discrete set of targets.

2.1.2. Time-warping

If a person wants to move more slowly or quickly than normal, the trajectory dynamics will be warped—stretched or compressed in time. This natural speed variability cannot be accounted for by a linear trajectory model. Here we aim to develop our trajectory model to incorporate the average speed, allowing for this variability. We model the intended average movement speed (S); we append its logarithm to the state vector, ensuring that it remains positive at all times:

$${\mathbf{x}}_{\mathbf{t}}={[z_t{\dot{z}}_t{\ddot{z}}_{t}z{T}_{t}z{s}_t]}^T={[z_t{\dot{z}}_t{\ddot{z}}_{t}z{T}_t{\text{log}}_e(S_t)]}^T$$ (8)

We generated a time-warped trajectory model (TWTM) by noting that if the average rate of a trajectory is to be scaled by a factor S, the position at time t will equal that of the original trajectory at time S × t. Differentiating, the velocity will be multiplied by S, and the acceleration by S². For simplicity, the trajectory noise is assumed to be additive and Gaussian, and the model is assumed to be stationary:

$${\mathbf{x}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}-1}=(\begin{array}{l}{\mathit{z}}_{\mathit{t}}\hfill \\ {\dot{\mathit{z}}}_{\mathit{t}}\hfill \\ {\ddot{\mathit{z}}}_{\mathit{t}}\hfill \\ \mathit{z}{\mathit{T}}_{\mathit{t}}\hfill \\ z{s}_t\hfill \end{array})=f({\mathbf{x}}_{\mathbf{t}-1})+{\mathit{w}}_{\mathit{t}},$$ (9)

where

$$f({\mathbf{x}}_{t-1})=\left(\begin{array}{ccccc}{I}_p& \mathrm{\Delta }t\times I_p& 0_{p\times p}& 0_{p\times p}& 0_{p\times 1}\\ 0_{p\times p}& I_p& \mathrm{\Delta }t\times I_p& 0_{p\times p}& 0_{p\times 1}\\ S_{t-1}^2{\alpha }_P& S_{t-1}{\alpha }_V& {\alpha }_A& S_{t-1}^2{\alpha }_T& 0_{p\times 1}\\ 0_{g\times p}& 0_{g\times p}& 0_{g\times p}& I_g& 0_{g\times 1}\\ 0_{1\times p}& 0_{1\times p}& 0_{1\times p}& 0_{1\times p}& 1\end{array}\right)\times \left(\begin{array}{l}{\mathit{z}}_{\mathit{t}-1}\hfill \\ {\dot{\mathit{z}}}_{\mathit{t}-1}\hfill \\ {\ddot{\mathit{z}}}_{\mathit{t}-1}\hfill \\ \mathit{z}{T}_{\mathit{t}-1}\hfill \\ z{s}_{t-1}\hfill \end{array}\right).$$ (10)

Since the position and velocity states are completely specified from the previous positions, velocities and accelerations, only the α terms used to predict the acceleration states need to be estimated to build the state transition function, f. These terms, estimated from the data (section 2.3.2), remain constant and are scaled as a nonlinear function of zs that acts to multiply the acceleration by S². To achieve this, α_p and α_T are scaled by S², α_V is scaled by S (as ${\dot{\mathit{z}}}_{\mathit{t}-1}$ will have effectively already been scaled by S through the recursive nature of the filter), and α_A is left unchanged as ${\ddot{\mathit{z}}}_{\mathit{t}-1}$ will have also been scaled appropriately. The a priori estimate of the speed state, zs, will be unchanged from the estimate at the previous time-step; any deviations from average in the speed state therefore will be entirely due to the neural observation data, which allows the estimate to change over the course of the reach. No information about the speed of the reach is required in advance.

We realize this nonlinear trajectory model using an EKF, which linearizes the dynamics around the best estimate of the state at each time-step (Simon 2006). The state a priori estimate is found as the function f of the previous state posterior estimate:

$${\widehat{\mathbf{x}}}_{\mathit{t}}^{-}=f({\widehat{\mathbf{x}}}_{\mathit{t}-1}).$$ (11)

In the EKF, the Jacobian matrix of partial derivatives of f, F_t−1, must be calculated with respect to the previous state posterior estimate at each time-step, remembering that S = e^zs:

$$F_{t-1}={\frac{\partial f}{\partial \mathbf{x}}}_{|{\widehat{\mathbf{x}}}_{t-1}}=\left(\begin{array}{ccccc}{I}_p& \mathrm{\Delta }t\times I_p& 0_{p\times p}& 0_{p\times p}& 0_{p\times 1}\\ 0_{p\times p}& I_p& \mathrm{\Delta }t\times I_p& 0_{p\times p}& 0_{p\times 1}\\ S_{t-1}^2{\alpha }_P& S_{t-1}{\alpha }_V& {\alpha }_A& S_{t-1}^2{\alpha }_T& 2S_{t-1}^2{\alpha }_P{\widehat{\mathit{z}}}_{\mathbf{t}-1}+S_{t-1}{\alpha }_V{\widehat{\dot{\mathit{z}}}}_{\mathit{t}-1}+2S_{t-1}^2{\alpha }_T\mathit{z}{\widehat{T}}_{\mathit{t}-1}\\ 0_{g\times p}& 0_{g\times p}& 0_{g\times p}& I_g& 0_{g\times 1}\\ 0_{1\times p}& 0_{1\times p}& 0_{1\times p}& 0_{1\times p}& 1\end{array}\right).$$ (12)

This allows the a priori error covariance estimate, $V_t^{-}$ to be projected from the previous time-step:

$$V_t^{-}=F_{t-1}{V}_{t-1}{F}_{t-1}^T+Q.$$ (13)

The observation update is then performed as in the standard KF. With this approach we implement our nonlinear trajectory model while adding only small computational overhead to the KF recursions. To account for uncertainty in the target estimates, we performed a mixture of TWTMs (mTWTM, figure 1(d)), in exactly the same way as the mKFT above.

2.2. Experimental methods

To evaluate the effectiveness of the algorithms as general-purpose decoding approaches, we measured unconstrained reaching movements from able-bodied subjects while recording neural signals that would be available at different levels of SCI. Five subjects performed reaches within a large workspace at varying speeds, representing a wide range of trajectory dynamics. We recorded arm kinematics, EMGs, head position and gaze direction as they reached to 16 light emitting diode (LED) targets situated in two planes located at the edge of the reachable workspace (figure 2(a)). Subjects provided informed, written consent; and the protocol was approved by Northwestern University’s Institutional Review Board.

Figure 2.

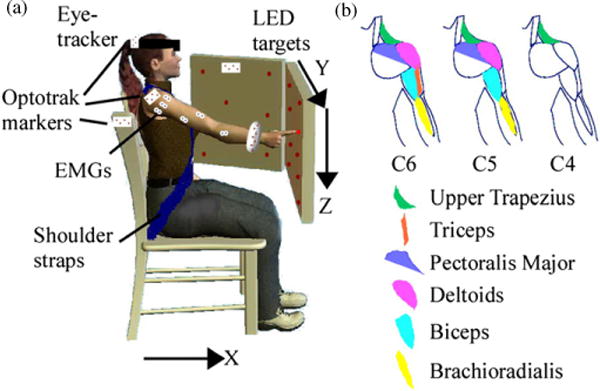
(a) Experimental setup and (b) recorded EMGs used to simulate the neural data available at injury levels C6, C5 and C4.

2.2.1. Data collection

EMG signals were recorded at 2400 Hz from the brachioradialis; biceps; triceps (long head and lateral head); anterior, posterior and middle deltoids; pectoralis major (clavicular head); and upper trapezius muscles. The EMG signals were amplified and band-pass filtered between 10 and 1000 Hz using a Bortec AMT-8 (Bortec Biomedical Ltd, Canada), and subsequently anti-aliased filtered using fifth-order Bessel filters with a cut-off frequency of 500 Hz. Hand, wrist, shoulder and head positions were tracked at 60 Hz using an Optotrak motion analysis system (Northern Digital, Inc, Canada). Joint angles were calculated from the shoulder and wrist marker data using digitized bony landmarks which defined a coordinate system for the upper limb as detailed by Wu et al (2005). We simultaneously recorded eye movements with an EYETRAC-6 head mounted eye tracker (Applied Science Laboratories, Bedford, MA). Signals were synchronized using a common trigger.

2.2.2. Protocols

Subjects were comfortably seated and restrained with lap and shoulder straps as they made the reaching movements. Reaches were performed in 2.5 min blocks at one of three self-selected speeds: slow, normal or fast. The subject was informed of the appropriate speed before beginning each block of reaches, and the order of speeds was randomized. For each reach the target LED was lit for 1 s prior to an auditory cue for initiation, at which time the subject would reach to the target at the appropriate speed. When the LED was switched off, the subject would return to a resting position. Slow, normal and fast reaches were allotted 3, 1.5 and 1 s respectively, but subjects were free to determine the exact speed. Therefore the slow, normal and fast blocks contained 16, 23 and 27 reaches respectively. Each subject performed at least 8 slow, 7 normal and 6 fast blocks, resulting in between 450 and 500 reaches in total.

2.3. Analysis

We used individual reaches towards the LED targets to train and test the KF, mKFT, MTM and mTWTM. Reaches that were visibly jerky, contained incomplete motion capture data or motion artefacts in the EMG were excluded from the analyses. For each subject, 100 reaches were randomly selected for testing the algorithms and those remaining (between 300 and 390 reaches) were used to train the models. Each decoding algorithm used the finger and joint angle positions, velocities and accelerations in the state vector.

2.3.1. Observation models

As the motion data were sampled at 60 Hz, the observation of the state at each time-step was extracted from the corresponding 16.7 ms window of the EMG. We extracted two features from each EMG channel; we used the RMS value and also the number of zero crossings, which is a measure of the frequency content of the signal that has been shown to be a useful feature in prosthetic control (Hudgins et al 1993, Tkach et al 2010). The square root of both of these features was taken for the observations; we found that this resulted in more Gaussian-like distributions. In all cases the observation model was considered to be linear, with Gaussian noise

$${\mathbf{y}}_{\mathbf{t}}=\mathit{C}{\mathbf{x}}_{\mathbf{t}}+{\upsilon }_t,$$ (14)

where y_t is the EMG at time t, C is the observation model, and υ_t is the Gaussian noise with p(υ) ∼ N(0, R), and R is the observation covariance matrix.

To explore the influence of the availability of EMG on decoder performance, we evaluated the algorithms with three different observation models. The models included different subsets of the EMG channels corresponding to muscle groups that simulated residual muscle activity typically available after C6, C5 and C4 level SCIs (figure 2(b)). At the C4 level we used just the upper trapezius, which is the most realistic representation of the signals available to the high tetraplegia population. To simulate a C5 level injury we added the three deltoids, biceps, pectoralis major and the brachioradialis. For the C6 case we also added the triceps long and lateral heads.

2.3.2. Training the models

For the KF and the KFT the parameters A, C, Q and R were estimated from training data of reaches to all targets using the maximum likelihood solution (Wu et al 2006, Ghahramani and Hinton 1996). In the case of the KFT, the final recorded position of the finger was appended to the state vector for training, taking the place of the target estimate. For the MTM, different A and Q were estimated for each target, while the observation model was the same for all mixture components and was constructed from all of the training reaches. To test their ability to generalize to novel targets the KF, mKFT and MTM were also tested using leave-one-out cross-validation, where the algorithms were trained on reaches to all targets except for the one being tested.

The filter parameters for the time-warped model were trained using the expectation maximization (EM) framework, using training reaches to all targets (Ghahramani and Hinton 1996). As the initialization for the variables may be important in EKF learning, S was initialized with the ground truth average reach speeds for each movement relative to the average speed across all movements. The state transition parameters α were estimated using nonlinear least-squares regression, while C, Q and R were estimated linearly for the new system, using the maximum likelihood solution (M-step). For the E-step we used a standard extended Kalman smoother. We thus found the expected values for the states given the current filter parameters. For this computation, and when testing the algorithm, zs was initialized to its average value across all reaches while the remaining states were initialized to their true values. The smoothed estimate for zs was then used, along with the true values for the other states, to re-estimate the filter parameters in the M-step as before. We alternated between E and M steps until the log likelihood converged (which it did in all cases). Following the training procedure, the diagonal of the state covariance matrix Q corresponding to zs was set to the variance of the smoothed zs over all reaches, according to how much this state should be allowed to change during prediction. This allowed the estimate of zs to develop over the course of the reach due to the evidence provided by the observations, better capturing the dynamics of reaches at different speeds.

2.3.3 Incorporating gaze information

We used the gaze data to provide target estimates for the relevant algorithms. We examined the gaze data in the 1 s period preceding each reaching movement—a time interval over which three saccades are typically made. As the targets were located on two planes, we obtained gaze locations for each reach by projecting the subject’s gaze in the relevant time interval onto those planes. To identify potential targets for the mKFT and mTWTM we did not require any knowledge of the target LED positions. While the target locations (finger positions at the end of each reach) were known and used in the training data when the models were being estimated, this information was not required during testing as target positions could be estimated anywhere on the two planes, independent of finger position. This is in contrast to the MTM, where the target locations were required in testing to select the potential trajectory models to include.

For the mKFT and mTWTM we selected three primary gaze locations from specific time-points in the corresponding 1 s interval; the first, middle and final samples were chosen. All other gaze locations were assigned to a group according to which of the primary locations was closest. The mean and variance of each of these three groups were then used to initialize the target estimate in a corresponding mixture component. The priors for the three targets were assigned proportional to the number of samples in their corresponding group. We thus added three-dimensional target estimates to the state space of each mKFT and mTWTM component. This approach ensured, with a high probability, that the correct target would be accounted for in the mixture.

To implement the MTM of Yu et al, the mixture was performed over the trajectory models designed for each of the possible LED targets. Priors for the MTM were found by assigning each gaze location to its closest two LEDs. The priors for each trajectory model was then set proportional to the number of gaze locations assigned to the corresponding LED, divided by its distance from the mean of those gaze locations. A number of different procedures for assigning priors to the MTM were tested and the one presented here gave the best results.

2.3.4. Algorithm evaluation

We evaluated the decoding approaches by comparing their predictions of the finger position in the test reaches, using the EMG and the gaze data. Algorithm accuracy was quantified using the multiple R² (Ljung and Ljung 1987), which is a measure of accuracy that incorporates the entire reaching movement. Intuitively, the multiple R² combines the errors across all three dimensions, weighing the performance in each dimension in proportion to its variance. However, because all targets were in front of the subject, a substantial component of this R² was related to the outward component of the reach common to all targets. We thus also calculated the target variance accounted for (VAF), which quantified the error at the final time of the reach, by scaling the squared error at that time by the variance in the LED target positions:

$$\text{Target}\text{VAF}=1-({\displaystyle {\sum }_{i=X,Y,Z}\left(\frac{{(z_{t\text{final}}^i-{\widehat{z}}_{t\text{final}}^i)}^2}{\text{var}({\text{pLED}}^i)}\right)}/3),$$ (15)

where pLED are the LED locations in space, and i indexes the dimensions X, Y and Z. Accuracies of the mKFT, MTM and KF were compared using an analysis of variance (ANOVA) with algorithm and simulated injury level as fixed effects and each reach as a random effect. When evaluating the effect of time-warping, reach speed was also included as a fixed effect, and the mTWTM, mKFT and KF were the algorithms compared. Tukey tests were performed for post-hoc comparisons, and all statistical comparisons used a significance level of α = 0.05. To visualize how the accuracy varies over time under each condition, we also quantified the percentage error as a function of the time-course of the reach. This was calculated by normalizing the root-mean-squared error at the relevant time point by the distance moved in the reach, and averaging across reaches.

3. Results

We tested how well movements can be decoded from EMGs using data recorded from healthy subjects reaching for an array of targets (figure 2, see methods). To understand which aspects of the different algorithms (figure 1) allow effective, functionally relevant decoding we contrasted their performance under various conditions, emulating realistic neuroprosthetic applications as much as possible. We began by evaluating the MTM and mKFT—two methods for incorporating the gaze-based target information into the trajectory model—and comparing them to the non-directional KF which uses EMG alone. By varying the quantity of EMG, as we simulated different levels of SCI, we could examine the reliance of the different approaches on the strength of the observation model; similarly, by testing how well the algorithms generalize to novel targets we could identify the extent of their reliance on the training data. Finally, we looked at the effect of time-warping at the different reach speeds, again considering the influence of the quantity of neural data.

3.1. Target models

We found that incorporating the gaze-based target information led to dramatic improvements in decoding, at all of the simulated injury levels. Both the MTM and the mKFT produced more accurate predictions than the generic KF. This is illustrated in the example reach (figure 3), where the KF at C4 does well in the vertical (Z) direction, but its predictions in the lateral (Y) and outward (X) directions are inaccurate. This is perhaps unsurprising as the upper trapezius is mostly active in producing upward movements of the arm. In this example, the mKFT and MTM performed well at all simulated injury levels. While the mKFT diverges from the trajectory somewhat in the Y direction, the trajectories converge again as they approach the target. By quantifying the average error over the time-course of the reach trajectories we could clearly see where the errors accumulated for each of the decoders (figure 4(a)). For both of the models incorporating target information the error levelled off about half way through the reach as the predicted trajectory was pulled towards the target, limiting the accumulation of error.

Figure 3.

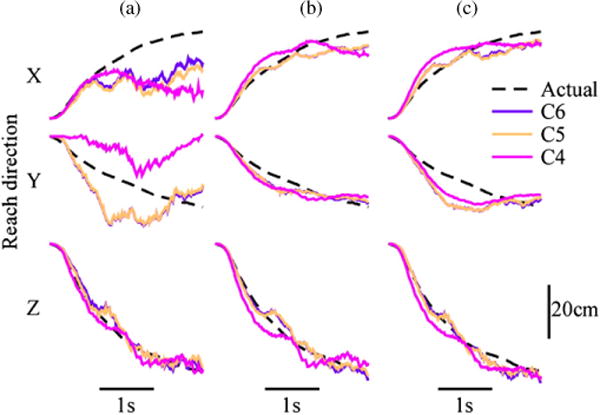
Actual and predicted finger position by (a) KF, (b) MTM and (c) mKFT for a sample reach at the three simulated injury levels. In this example, R² for C6, C5 and C4 respectively were: (a) all 0.98; (b) 0.99, 0.99, 0.98 and (c) 0.91, 0.89, 0.83. The target VAFs were: (a) 0.96, 0.97, 0.96; (b) 0.96, 0.97, 0.90; (c) 0.81, 0.72, 0.14.

Figure 4.

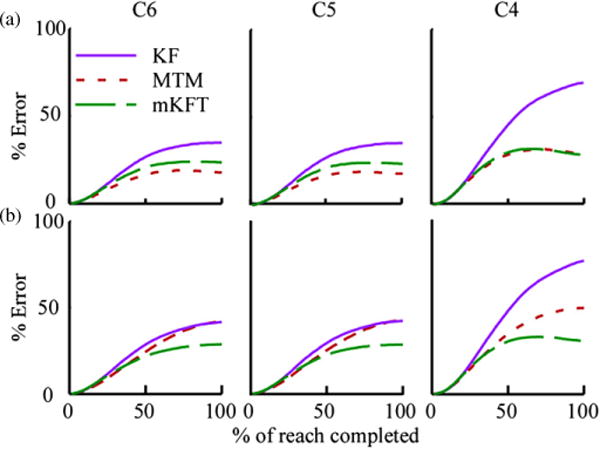
Average prediction errors over the time-course of the reach. (a) Training on all targets; (b) leave-one-out target cross-validation.

The neural information available to the decoders will generally affect their performance, and this influence will be stronger for decoders whose trajectory models are less informative about the reach structure. For all three algorithms, the performance at C5 was almost identical to that at C6, where the triceps EMGs were included in the observation vector for the latter but not the former (figures 3–5). There was no significant difference between them in R² or target VAF (both p > 0.98, figure 5). However, to simulate the C4 level only the upper trapezius EMG was used, resulting in significantly lower accuracy than the other two levels for both the R² and target VAF (all p < 0.0001, figure 5). It has to be emphasized that this was decoding of three-dimensional trajectories from a single muscle—a truly difficult task. This effect of simulated injury level was particularly evident in the KF, the algorithm with the strongest reliance on its observation model, where at C4 the error continued to accumulate over the course of the entire reach trajectory (figure 4). In comparison, the MTM and mKFT were relatively consistent across injury levels.

Figure 5.

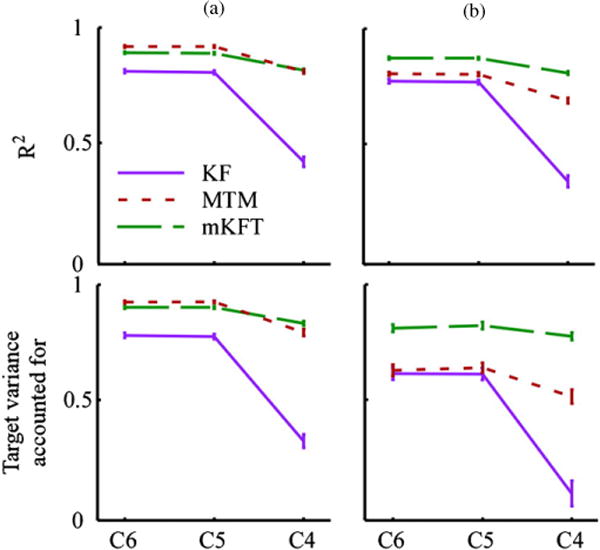
Quantification of the influence of algorithm choice on the precision of predictions: group means and standard errors. (a) Training on all targets; (b) leave-one-out target cross-validation.

We evaluated the approaches both with a fully specified training set and one requiring generalization to novel targets. Overall, the algorithms incorporating target information were significantly better than the KF for all performance measures (all p < 0.0001). When training was performed on reaches to all targets (figure 5(a)), we found no statistically significant difference between the MTM and mKFT (p = 0.09, 0.98 for R² and target VAF, respectively). However, when leave-one-out cross-validation was used to test how well the algorithms generalized to novel targets, the performance of the MTM dropped well below that of the mKFT (both p < 0.0001), which remained relatively consistent (figure 5(b)). In fact, the MTM performance was similar to that of the KF at the C5 and C6 injury levels (figures 4(b) and 5(b)); however, while less than the mKFT, the MTM still provided a large improvement over the KF at C4. Due to accurate target information from eye-tracking, the mKFT performed well, while the MTM was unable to effectively use this information without a fully specified training set.

3.2. Time-warping

The effects of time-warping were examined by comparing the algorithm that does model speed (mTWTM) with an algorithm that does not (mKFT). The MTM was not included in this analysis as its performance was shown above to be similar to that of the mKFT when all targets were included in the training set, and less effective when predicting reaches to targets not included in training. As the mKFT and mTWTM use the same approach to incorporating target information, all differences between them can be attributed to time-warping. The behaviour of these two algorithms is illustrated by example reaches at the three speeds (figure 6). At the normal speed, where the trajectory is close to the ‘average’ we would expect little time-warping to occur and therefore we saw little difference in performance between the two algorithms (figure 6(b)). The effectiveness of the time-warping is clearly illustrated in the fast example, where the mTWTM closely follows the reach trajectory and the mKFT lags behind, underestimating the speed and failing to reach the target (figure 6(c)). In the slow example, the speed of the reach is slightly overestimated by the mKFT (figure 6(a)). Overall, we found that the time-warped model out-performed the mKFT in both R² and target VAF (both p < 0.01, figure 8).

Figure 6.

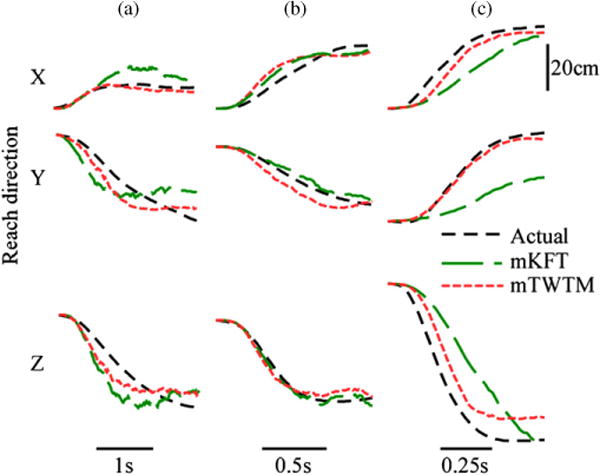
Predicted finger position by the mKFT and mTWTM for sample reaches at (a) slow; (b) normal and (c) fast speeds at the simulated C4 injury level. In this example, R² for the mKFT and mTWTM respectively were: (a) 0.89, 0.96; (b) 0.99, 0.97 and (c) 0.86, 0.98. The target VAFs were: (a) 0.92, 0.97; (b) 0.98, 0.99 and (c) 0.85, 0.9.

Figure 8.

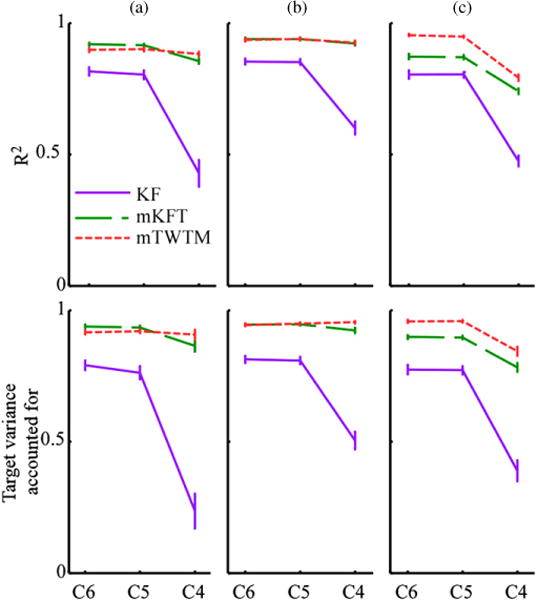
Prediction accuracy quantification of group means and standard errors for the algorithms for different injury levels at (a) slow; (b) normal; and (c) fast speeds.

All algorithms performed best for reaches of average speed. The KF was additionally included in the group comparisons to demonstrate the effect of speed on the naive algorithm. The error profiles at the normal speed (figure 7(b)) demonstrated similar patterns in the mKFT and KF to those seen above, where reaches of all speeds were included in the analysis (figure 4(a)). However, the errors seen here were lower as the reaches at normal speed were reconstructed more accurately than those at the other speeds, by all algorithms and at all simulated injury levels (all p < 0.0001, figure 8). The error profiles of the mTWTM and the mKFT appear almost identical at normal speed, indicating that little time-warping occurred. Indeed, there was no significant difference in R² or target VAF between the mTWTM and mKFT (both p > 0.99, figure 8(b)).

Figure 7.

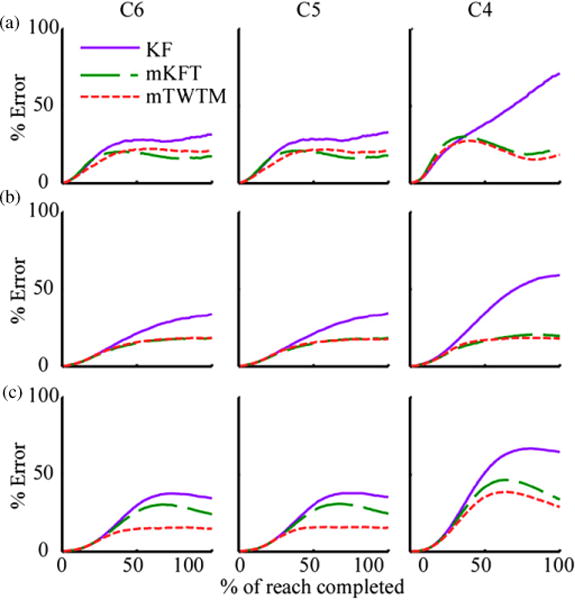
Average prediction errors over the time-course of the reach for the three algorithms, at (a) slow; (b) normal and (c) fast speeds.

Some interesting interactions between the reach speed and the quantity of EMG were observed in the error profiles for the decoders when the speed deviated from normal (figure 7). It was at the fast speed that the time-warping proved to be most useful. At the C5 and C6 levels, the error profiles of the mTWTM appeared very similar to those for the normal-speed reaches. In contrast, the mKFT and the KF continued to accumulate error when the mTWTM had levelled off (figure 7(c)). The error did decrease towards the end of the reach, however, particularly in the case of the mKFT as the reach approached the target. At the C4 level errors were much higher in all cases, with those of the mKFT and mTWTM decreasing towards the end of the reach. The time-warped model outperformed the others at all simulated injury levels in both R² and target VAF (both p < 0.001, figure 8(c)).

The mKFT performed better than expected for the slow reaches. While the trajectory dynamics still deviated from average, there was more neural information integrated over the course of the slow reaches, allowing better performance. The accuracy of the mKFT for the slow reaches was significantly higher than at the fast in both R² and target VAF (both p < 0.01). While time-warping did not provide much advantage at this speed, there was insight to be gained by comparing the error profiles of the models. For all injury levels, the error of the mTWTM was lowest at the beginning of the reach, as the mKFT initially overestimated the speed (figure 7(a)). However, at C5 and C6, while the error of the mTWTM levelled off about half way through the reach the mKFT error profile dipped below that of the mTWTM as it approached the target. At C4, when both algorithms were more reliant on the trajectory model, this decrease in error was seen in both cases and the error profile of the mTWTM remained lower. Over all injury levels, the mTWTM was slightly more accurate than the mKFT for the slow reaches (figure 8(a)). This was statistically significant in the target VAF (p < 0.0001), but not in the R² (p = 0.053). Modelling speed primarily helped for fast movements where neither integrating neural information nor biasing towards averages were successful strategies.

4. Discussion

We designed a trajectory model for NMIs by incorporating two features that prominently influence the trajectory dynamics of the natural reach: the movement speed and the target location. The model deals well with uncertainty about the target location and can generalize to new parts of the workspace. Intuitively, we found that capturing the characteristics of movement in our trajectory model is most useful in the absence of a rich set of neural signals. Additionally, faster reaches in particular were improved by allowing for speed variation through time-warping.

For the severely impaired, it is highly unlikely that a single signal source will suffice to provide adequate control of a neuroprosthesis, particularly if invasiveness is to be minimized. This has led to the development of a number of hybrid brain–computer interfaces (BCIs) (Pfurtscheller et al 2010, Millán et al 2010). For example, Leeb et al (2011) recently improved the performance of a BCI by combining electroencephalographic (EEG) activity with EMG. In this work the two signal sources were both used to classify hand movements and their results were then fused. In contrast, our approach provides a framework to fuse signal sources with distinct roles: combining target and trajectory information. Batista et al (2008) also improved performance of a cortical decoder by monitoring eye position. Because gaze direction influences the neural data, they found that their decoding of targets on a screen was improved by using different neural mappings depending on the eye position. However, they did not explicitly use the gaze data to estimate the target, and they did not attempt to decode reach trajectories.

Eye gaze is an extremely useful signal source for obtaining target estimates; people naturally look at objects before reaching for them giving us a huge amount of information about their intentions. However, it is a problematic input signal when used in isolation (Jacob and Karn 2003). It can be challenging to determine which eye movements are intended as control signals, and it is critical that saccades do not generate unintended movements of an assistive device. It is therefore evident that gaze information is most useful when combined with other voluntary control signals to account for its inherent uncertainty. While we have not explicitly addressed the issue here, the mixture model will converge to the most probable trajectory even when multiple targets have been foveated. Yu et al (2007) demonstrated this with the MTM, which was highly effective with eight trajectories in the mixture. It appears that gaze information can allow precise decoding even in the context of very few available EMG signals.

Clearly, trajectory decoding can be dramatically improved when information about the target is available. The literature provides a few different approaches for incorporating the target into the trajectory model. As demonstrated, the MTM is highly effective when there is a set of known targets (Yu et al 2007). Srinivasan et al augmented the state equation to optimally account for a target state at some known time in the future (Srinivasan et al 2006), and they also extended this work to consider dynamic goals (Srinivasan and Brown 2007). The requirement that the target time be known is somewhat problematic, although Kulkarni and Paninski suggested using a mixture model to account for uncertainty in this parameter (Kulkarni and Paninski 2007). Incorporating the target into the state space, as demonstrated in this work, is a natural way to augment the trajectory model without any knowledge of final time, while retaining the simple form of the KF (Kemere et al 2004). Mulliken et al (2008) have demonstrated the effectiveness of this method in closed loop control by simultaneously decoding both the trajectory and target states from posterior parietal cortical neurons of monkeys. The mixture model framework as presented here could enhance this approach to account for the rich target information available when there are multiple potential target locations.

The advantages of nonlinear time-warping demonstrated in this work could be equally obtained using mixtures over many targets and speeds. While mixtures could incorporate different models for slow and fast movements and any number of potential targets, this strategy will generally require many mixture components. Such an approach would require a lot more training data, as we have shown that it does not generalize well. In contrast, we warp the trajectory through a hidden state that we continuously estimate based on the evidence of the neural data. Wu et al similarly allowed the trajectory model to be influenced by an added hidden state that was estimated from cortical data, which could represent any unobserved influences relevant to the system. They assumed the effect of this state to be linear, thereby retaining the simplicity of the KF, and their model could thus be estimated from the straightforward EM framework (Wu et al 2009). Similar switching approaches have also been employed to account for the nonlinear or non-stationary mappings between the kinematics and EMGs (Artemiadis and Kyriakopoulos 2011), or neural firing rates (Wu et al 2004). However, we found that, with our neural data set, the advantages of time-warping are small in comparison to the advantages of using target information.

We believe that the issues that we have addressed here may be applied to a wide range of NMI applications. In most cases, a probabilistic distribution for a small number of action candidates may be expected—after all there are usually only a small number of actions that make sense in a given environment. Virtually all movements are executed with varying speeds; time-warping may in fact prove to be more useful for applications with higher speed-dependence such as lower-limb prosthetics. Furthermore, the Bayesian framework enables simple extensions to different signal sources such as electrode grid recordings and EEG. Particularly for patients with severe impairments and limited control sources available, the choice of a strong trajectory model should improve the functionality of a neuroprosthetic while reducing their cognitive burden.