The Differences and Similarities Between Two-Sample T-Test and Paired T-Test

Summary

In clinical research, comparisons of the results from experimental and control groups are often encountered. The two-sample t-test (also called independent samples t-test) and the paired t-test are probably the most widely used tests in statistics for the comparison of mean values between two samples. However, confusion exists with regard to the use of the two test methods, resulting in their inappropriate use. In this paper, we discuss the differences and similarities between these two t-tests. Three examples are used to illustrate the calculation procedures of the two-sample t-test and paired t-test.

1. Introduction

In clinical research, we usually compare the results of two treatment groups (experimental and control). The statistical methods used in the data analysis depend on the type of outcome.^[1] If the outcome data are continuous variables (such as blood pressure), the researchers may want to know whether there is a significant difference in the mean values between the two groups. If the data is normally distributed, the two-sample t-test (for two independent groups) and the paired t-test (for matched samples) are probably the most widely used methods in statistics for the comparison of differences between two samples. Although this fact is well documented in statistical literature, confusion exists with regard to the use of these two test methods, resulting in their inappropriate use.

The reason for this confusion revolves around whether we should regard two samples as independent (marginally) or not. If not, what’s the reason for correlation? According to Kirkwood: ‘When comparing two populations, it is important to pay attention to whether the data sample from the populations are two independent samples or are, in fact, one sample of related pairs (paired samples)’.^[2] In some cases, the independence can be easily identified from the data generating procedure. Two samples could be considered independent if the selection of the individuals or objects that make up one sample does not influence the selection of the individuals or subjects in the other sample in any way.^[3] In this case, two-sample t-test should be applied to compare the mean values of two samples. On the other hand, if the observations in the first sample are coupled with some particular observations in the other sample, the samples are considered to be paired.^[3] When the objects in one sample are all measured twice (as is common in “before and after” comparisons), when the objects are related somehow (for example, if twins, siblings, or spouses are being compared), or when the objects are deliberately matched by the experimenters and have similar characteristics, dependence occurs.^[2]

This paper aims to clarify some confusion surrounding use of t-tests in data analysis. We take a close look at the differences and similarities between independent t-test and paired t-test. Section 2 illustrates the data structure for two-independent samples and the matched pair samples. We discuss the differences and similarities of these two t-tests in Sections 3.

In section 4, we present three examples to explain the calculation process of the independent t-test in independent samples, and paired t-test in the time related samples and the matched samples, respectively. The conclusion and discussion are reported in Section 5.

2. Independent samples and matched-paired samples

The t-tests are used for data with continuous outcomes. We first discuss the data structure.

2.1 Two independent samples

Let X_ij, i = 0; 1; j = 1, …., n_i be the observations from two independent samples (i = 0 or 1 denotes control or experimental group). The mean and variances of X_ij are µi and σ_i² (i = 0, 1). There are two levels of independence in the data from two independent samples. The data from two different subjects within the same sample are independent, i.e. X_ij and X_ik are statistically independent if j ≠ k. The data of two subjects from different samples are also independent, i.e. X_0j and X_1k are independent for j = 1,…, n₀ and k = 1, …, n₁.

The sample means and sample variances of these two samples are

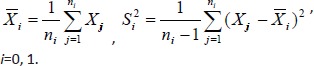Let 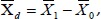, the difference of the sample mean values. It’s very easy to prove that the mean and variance of 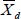are

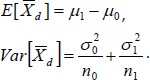(1)

The variance of 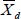can be estimated by simple moment estimator

(2)

If the variance of those two samples are the same, i.e. σ₀² = σ₁², a more efficient estimator of the variance of 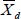is

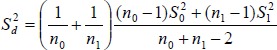2.2 Matched pair data

Suppose two samples are matched pair with outcomes X_j = (X_0j, X1j), i = 1,…, n. Data from different pairs are independent, i.e. X_j and X_k are independent if j ≠ k. However, within each pair i, X_0i and X_1i are correlated. Hence the data in the control group (X₀₁, …, X_0n) and in the treatment group (X₁₁, …, X_1n) are correlated. Assume the correlations are the same within all pairs and denote the common correlation coefficient by ρ.

Let X_dj =X_1j – X_0j and 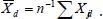. It’s obvious that 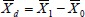and 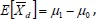, which is the same as in the case of two independent samples (with n₀ =n₁=n). However, the variance of 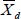is

(3)

The variance of 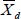can be estmated by

(4)

2.3 The difference between independent samples and matched-pair samples

We discuss the difference between independent samples and matched-pair samples based on the sample mean difference. To simplify our discussion, we assume n₀ = n₁ = n. From the above we know that the formulas to calculate the sample mean difference are always the same, which equals the sample mean of the treatment group minus the sample mean of the control group. One of the differences is their variances, which can be easily seen from (1) and (3). For the matched-pair data, if two observations within the same pair are positively (negatively) correlated, i.e. ρ> 0(< 0), the variance of the mean difference is smaller (larger) than that in the case of independent samples. They are equal if two samples are uncorrelated (ρ= 0).

Another difference is in the estimation of the variance of the sample mean values. In the independent samples, we need the sample variances of both samples in order to estimate the variance of 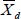(see [2]). In the matched-pair data, we only need the difference within each pair to estimate the variance of 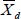, as indicated in (4).

3. T-tests

Suppose we want to test the hypothesis that two samples have the same mean values, i.e. H₀ : µ₀ = µ₁. In the following discussion we assume the data follows bivariate normal distribution. The t-test is of the form sample mean difference/sample standard deviation of the sample mean difference

3.1 Two-sample t-test

The two-sample t-test is of the form

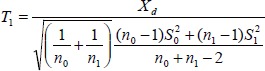Under the null hypothesis H₀, if σ₀ = σ₁, T₁ follows student’s t-distribution with degrees of freedom (df) n₀ + n₁ - 2. If σ₀ ≠ σ₁, the exact distribution of T₁ is very complicated. This is the well-known Behrens-Fisher problem in statistics^{[4, 5]}, which we will not discuss here. When n₀ and n₁ are both large enough, the distribution of T₁ can be safely approximated by standard normal distribution.

3.2 Paired t-test

The paired t-test is of the form

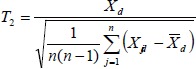It’s obvious that the paired t-test is exactly the one-sample t-test based on the difference within each pair. Under the null hypothesis, T₂ always follows t-distribution with df = n-1.

3.3 Differences between the two-sample t-test and paired t-test

As discussed above, these two tests should be used for different data structures. Two-sample t-test is used when the data of two samples are statistically independent, while the paired t-test is used when data is in the form of matched pairs. There are also some technical differences between them. To use the two-sample t-test, we need to assume that the data from both samples are normally distributed and they have the same variances. For paired t-test, we only require that the difference of each pair is normally distributed. An important parameter in the t-distribution is the degrees of freedom. For two independent samples with equal sample size n, df = 2(n-1) for the two-sample t-test. However, if we have n matched pairs, the actual sample size is n (pairs) although we may have data from 2n different subjects. As discussed above, the paired t-test is in fact one-sample t-test, which makes its df = n-1.

4. Examples

In this section we present some numerical examples to show the differences between the two tests.

4.1 Example 1: two independent samples

To illustrate how the test is performed, we present the data shown in table 1 which compares positive symptom scores on the Positive and Negative Syndrome Scale (PANSS) between the experimental group and the control group, each of which had 10 patients each. We want to test if the mean scores of the two groups are the same.

Table 1.

Positive symptom scores in Positive and Negative Syndrome Scale (PANSS)

	Experimental group	Control group	Difference
Observations	14	11	3
	15	10	5
	16	12	4
	13	9	4
	12	10	2
	13	13	0
	15	14	1
	16	12	4
	14	10	4
	15	11	4
Sum	143	112	31
Mean	14.3	11.2	3.1

* The values of differences are used for the calculation of paired t-test in example 2

The sample mean values of these two groups are 11.2 and 14.3, respectively. The sample variances are 2.40 and 1.70, respectively. The two-sample t-test statistic equals 4.54. From the t-distribution with df = 18, we obtain the p-value of 0.0001, which shows strong evidence to reject the null hypothesis.

4.2 Example 2: Pre- and post-treatment

To illustrate how the test is performed, we still use the data shown in table 1, except for changing the two variables to one group having positive symptom scores of PANSS at baseline and one group having positive symptom scores of PANSS after treatment. Hence there are only 10 subjects in this example. The sample mean difference is the same as that in Example 1. However, the example variance of the sample mean difference is 2.45. The paired t-test statistic equals 6.33. From the t-distribution with df = 9, we obtain the p-value of 0.00007, which shows strong evidence to reject the null hypothesis.

4.3 Example 3: Matched pair data

In addition to the time related samples, paired t-test is also introduced in the data analysis of matched sampling. Such sampling is a method of data collection and organization which helps to reduce bias and increase precision in observational studies.^[6] For example, consider a clinical investigation to assess the repetitive behaviors of children affected with autism. A total of 10 children with autism enroll in the study. Then, 10 controls are selected from healthy children with matched age and gender which may be the confounding factors in the study. Each child is observed by the study psychologist for a period of 3 hours. Repetitive behavior is scored on a scale of 0 to 100 and scores represent the percent of the observation time in which the child is engaged in repetitive behavior (see table 2). Thus, we present the calculation process of paired t-test and independent t-test in the data analysis, respectively, under the assumption that both samples come from normally distributed populations with unknown but equal variances.

Table 2.

Repetitive behavior scores in the groups of children with autism and the healthy controls

	Children with autism	Healthy controls
Observations	85	75
	70	50
	40	50
	65	40
	80	20
	75	65
	55	40
	20	25
	65	45
	30	15
Sum	585	425
Mean	58.5	42.5

In this example, there are 20 subjects. However, each subject in the experimental group is matched with a subject in the control group. We also need to use the matched pair t-test to compare the mean values of the two groups. The paired t-test statistic equals 2.667. From the t-distribution with df = 9, we obtain the p-value of 0.01, which shows strong evidence to reject the null hypothesis.

5. Discussion

Although two-sample t-test and paired t-test have been widely used in data analysis, misuse of them is not uncommon in practice. In this paper, we show the differences and similarities of those tests. Two-sample t-test is used only when two groups are marginally independent. To say more about matching, let us suppose that age is a possible confounding factor of the outcome. During randomization, we first match subjects by age. For two subjects with the same age, they are assigned to two treatment groups by block (of size 2) randomization. Why should we use paired t-test in this case? This is related to the technical notation of conditional independence in statistics. For each pair, their outcomes are independent given the (same) age. However, they are not independent marginally. That’s why the two-sample t-test cannot be used. However, perfect matching is very difficult to implement in practice especially when the factor of matching is a continuous variable (the probability that two subjects have the exact same age is always 0!).

Biography

Manfei Xu obtained a bachelor’s degree in Biomedical engineering from the medical college, Shanghai Jiao Tong University in 2002, and a Master’s degree in Public Health from the University of South Florida, USA in 2010. The same year she started working as a researcher at the Shanghai Mental Health Center in China. Since 2013, she has been the full-time technical editor for the Shanghai Archives of Psychiatry. Her work involves preliminary assessment of manuscripts, consulting on biostatistical analysis, and research into the application of statistical methods in mental health studies.