Abstract
We have prepared a series of MII4L6 tetrahedral cages containing one or the other of two distinct BODIPY moieties, as well as mixed cages that contain both BODIPY chromophores. The photophysical properties of these cages and their fullerene-encapsulated adducts were studied in depth. Upon cage formation, the charge-transfer character exhibited by the bis(aminophenyl)-BODIPY subcomponents disappeared. Strong excitonic interactions were instead observed between at least two BODIPY chromophores along the edges of the cages, arising from the electronic delocalization through the metal centers. This excited-state delocalization contrasts with previously reported cages. All cages exhibited the same progression from an initial bright singlet state (species I) to a delocalized dark state (species II), driven by interactions between the transition dipoles of the ligands, and subsequently into geometrically relaxed species III. In the case of cages loaded with C60 or C70 fullerenes, ultrafast host-to-guest electron transfer was observed to compete with the excitonic interactions, short-circuiting the I → II → III sequence.
Introduction
Supramolecular chemistry has enabled the synthesis of intricate and functional structures. In an approach inspired by nature, increasingly complex two- and three-dimensional structures can be built from simple molecular components using noncovalent interactions.1 The functional properties of these materials can arise as much from the interactions between components as from the properties of constituents considered in isolation. A recent example is the family of metal–organic polyhedra2−13 formed by subcomponent self-assembly,14−18 which have porous surfaces and central cavities reminiscent of biological recognition sites. These cages form inclusion complexes with a wide variety of guest species.19−27 The modular design of these materials enables incorporation of dyes and fluorophores into the architecture, resulting in a high local density of chromophores held in a fixed geometry through noncovalent interactions.28−31 The interaction of these structures with light is a topic of growing interest.32−42 An understanding of their photophysical behavior, and how it arises from the properties of the subcomponents, could unlock the potential of these functional materials in applications from tailored photochemical reactors and sensitive chemical detection to hybrid photovoltaic and light-emitting devices.
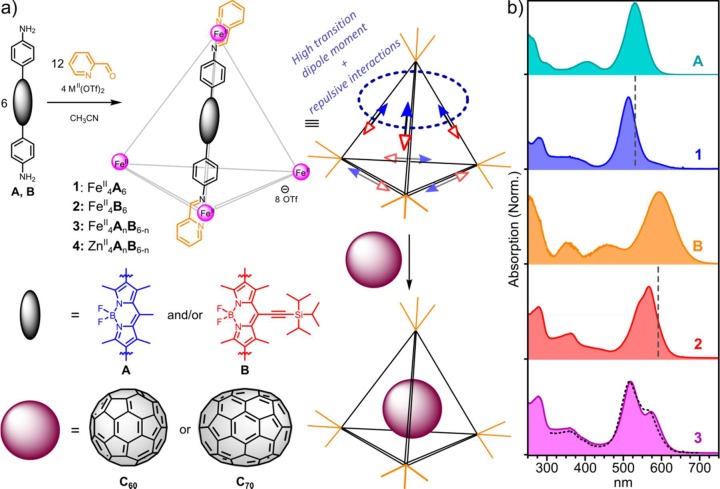
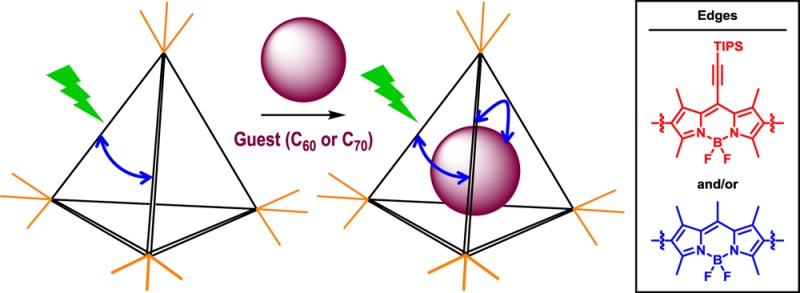
Here, we report the synthesis and photophysical characterization of a family of metal–organic cage frameworks based on emissive BODIPY chromophores (Figure 1a). We have studied the properties of two homoleptic cages (1 and 2) assembled from BODIPY diamines (A and B), as well as the collection of heteroleptic cages (3) composed of a statistical mixture of A and B. Our results show that the edges exhibit strong electronic coupling between at least two chromophores, which we infer to result from strong dipole–dipole coupling between nearby ligands, with an additional contribution from electronic delocalization across the metal vertices. The cage photophysics were found to be dominated by relaxation within the manifold of delocalized states from the high-energy bright state to lower-energy dark or “dim” states and subsequent geometric relaxation. Upon photoexcitation, we observe the same basic three-state progression in homo- and heteroleptic samples: the initial delocalized bright state (species I) rapidly relaxes into a nonemissive delocalized state (giving species II), prompting slight geometric relaxation (generating species III) in response to the redistribution of the electronic wave function. These effects appear to depend only weakly on the metal (ZnII or FeII) at the vertices or electronic nature of the chromophore edges and are thus posited to arise from the architecture of the cage framework itself. When cages 1–3 were loaded with fullerene C60 or C70, the intracage relaxation processes were observed to compete with ultrafast host-to-guest electron transfer from the initial excitonic state.
Figure 1.
(a) Subcomponent self-assembly of BODIPY-based MII4L6 cages 1–4 and encapsulation of fullerenes. Schematic structure (upper middle) indicates possible alignment of BODIPY transition dipoles (arrows). Cooperative alignment (circled) maximizes the transition dipole moment but also generates a high-energy state. Such a state will relax into a configuration with as many “head-to-tail” dipole alignments as possible, resulting in cancellation of transition dipole moments. (b) UV–vis absorption spectra of cages 1–3 and their diamine precursors A and B. Dashed lines over 1 and 2 mark the absorption maxima of the corresponding diamines. The black dashed line over 3 is the best fit from a linear combination of spectra 1 and 2.
Results and Discussion
Syntheses of Ligands and Cages
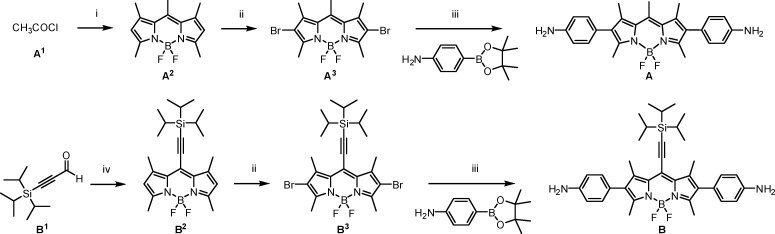
Subcomponents A and B were prepared as shown in Scheme 1. BODIPY derivative A was obtained in three steps starting from acetyl chloride and 2,4-dimethylpyrrole. BODIPY derivative B was similarly synthesized in three steps from 3-(triisopropylsilyl)-1-propynal and 2,4-dimethylpyrrole.43 A full description of synthetic procedures is provided in the Supporting Information section S2.
Scheme 1. Synthesis of BODIPY Ligands A and B.
Reagents and conditions: (i) (a) 2,4-dimethylpyrrole (2.0 equiv), CH2Cl2, reflux, 1 h, (b) NEt3 (3 equiv), BF3·OEt2 (4.5 equiv), CH2Cl2, rt, 10 min; (ii) NBS (3.5 equiv), CH2Cl2, rt, 1 h; (iii) Pd(dppf)Cl2·CH2Cl2 (20 mol %), K2CO3 (6.0 equiv), 1,4-dioxane/H2O (3:1), reflux (110 °C), 90 min; (iv) (a) 2,4-dimethylpyrrole (2.0 equiv), trifluoroacetic acid (5 mol %), CH2Cl2, 0 °C, 1 h, (b) DDQ (1.0 equiv), 5 min, (c) NEt3 (6.0 equiv), BF3·OEt2 (8.0 equiv), 5 min. DDQ = 2,3-dichloro-5,6-dicyano-p-benzoquinone, NBS = N-bromosuccinimide, dppf = 1,1′-bis(diphenylphosphino)ferrocene.
The subcomponent self-assembly of A and B with 2-formylpyridine and iron(II) trifluoromethanesulfonate (FeII(OTf)2) to produce cages 1 and 2, respectively, is shown in Figure 1a. Heteroleptic cage 3 was observed to form upon the reaction of both A and B (3 equiv each) and 2-formylpyridine (12 equiv) with FeII(OTf)2 (4 equiv). When zinc(II)trifluoromethanesulfonate (ZnII(OTf)2) was used in place of the iron salt, the heteroleptic collection of cages 4 was prepared in place of 3. The identities of these MII4L6 cages were established by one- and two-dimensional NMR spectroscopy and mass spectrometry (Figures S1–S8, Supporting Information). 1H NMR spectra of 1–4 were consistent with a mixture of diastereomeric products having frameworks with approximate T, C3, and S4 point symmetries, in which the metal stereocenters adopt mixtures of Λ and Δ configurations, as has been previously observed.44,45 In the cases of the heteroleptic cages 3 and 4, ESI-MS results were consistent with the presence of a statistical mixture of seven constitutionally distinct cages46 (Figures S7 and S8).
The cages were found to be stable in concentrated (∼2.5 mg/mL) solution, but upon dilution to 1–10 μg/mL for spectroscopic measurements, in some cases, they were observed to lose their characteristic UV–vis absorptions and exhibit strong photoluminescence, which we infer to result from the presence of unhydrolyzed A or B imines arising from partially dissociated cages. Thus, for all measurements presented herein, fresh 1 mg/mL cage stock solutions were mixed with 100 mg/mL poly(methyl methacrylate) (PMMA) in acetonitrile and spin-coated onto quartz substrates. These samples were stable, with no detectable change in absorption over the course of at least 6 months. Comparison of the UV–vis absorption of these films with freshly diluted solutions of 1–3 in acetonitrile revealed nearly identical line shapes (Figure S9), aside from a small uniform red-shift in the solid state. As the cages in solution are >1000× more dilute than in the PMMA films, we infer that the films contain isolated cage structures, and that the measurements discussed below reflect intracage photophysics.
Absorption Spectra of Ligands and Cages
The UV–vis absorption spectra of diamines A and B and cages 1–3 are shown in Figure 1b. The spectra of diamines A and B are significantly broadened relative to BODIPY dyes that do not contain polar substituents. This broadening is attributed the polar amine termini, which lend charge-transfer character to the highest-intensity visible absorptions of A and B, even in the ground state.47 Time-resolved measurements in solution reveal ultrafast (<1 ps for A, <200 fs for B) conversion of the bright singlet state I into a distinct charge-transfer state II emitting in the NIR (Figure S10). Interestingly, this behavior was suppressed when A and B were embedded in a rigid PMMA matrix. We infer that the formation of the charge-transfer state required conformational change, for instance, torsion about the BODIPY–phenyl bond, which could extend conjugation to the polar amine units. Upon cage formation, the amines are converted to imines, and this charge-transfer character was accordingly suppressed. We thus observe a narrowing and blue-shifting of the principal absorption bands of both 1 and 2 relative to the corresponding diamines (shown as dashed vertical lines in Figure 1b).
These spectra reflected ensembles of delocalized states formed through dipole–dipole coupling between BODIPY edges within the tetrahedral architecture. These interactions resulted in states delocalized over multiple edges. We illustrate them using the simplifying assumption that the transition dipole moment of each BODIPY moiety, oriented along the long molecular axis,48,49 is parallel to the corresponding cage edge in Figures 1a and S11. In practice, the molecular axis in such cages typically deviates from the tetrahedral edge by a small angle,45 and we choose to neglect this here for simplicity. Regardless of the number of participating edges, these configurations exhibit comparable behavior. Arrangements with the largest number of head-to-head alignments have the strongest transition dipole moments, leading to stronger emission (“bright” states). These bright states will also have higher energy due to electron repulsion at the cage vertices. Arrangements having more head-to-tail interactions are lower in energy but also exhibit substantial cancellation of transition dipole moments.
We thus infer a driving force to exist for the relaxation of high-energy bright states into lower-energy dark or “dim” configurations, potentially changing the degree of delocalization to overcome the dipole frustration intrinsic to the head-to-head states. Accordingly, we assign the long-wavelength tail of the absorption of 1 to dim coupled states, whereas the higher-energy peak corresponds to the dominant bright state. States having varying degrees of transition dipole alignment are less distinct in the ground-state absorption of 2, where we propose that the presence of bulky TIPS groups perturbs the transition dipole moments from their alignments along the edges of the cage, complicating the dipole interactions. This effect is attributed to delocalization onto the triple bond, imparting a significant component to the electronic wave function in the direction orthogonal to the long molecular axis. Nevertheless, the time-resolved data presented below reveal the same fundamental interplay of bright and dark states.
We were not able directly to determine the strength of interchromophore interactions or confirm the nature of the coupling from these UV–vis absorption spectra. The constituent BODIPY–diimine ligands are susceptible to hydrolysis and could not be isolated in pure form; they are stabilized by binding to the metals at the vertices of the cages. However, the spectrum of heteroleptic 3 demonstrates a clear sign of interactions between the ligands within the cage. Heteroleptic 3 is formed from a mixture of diamines A and B, and the resulting cages were observed by ESI-MS (Figure S7) to incorporate a statistical (binomial) distribution of A and B residues. The peak positions and line shape of 3 cannot be reconstructed from a linear combination of 1 and 2 (dashed line), indicating the presence of interaction between the Me- and TIPS-substituted chromophores in the mixed cages. We therefore infer that the ligands are also electronically coupled within pure cages 1 and 2. This result complements and contrasts with the behavior of recently reported perylene-based cages,31,50 in which the chromophores embedded within the ligands appeared not to be coupled. We attribute this different behavior to two critical factors. Our BODIPY cages are smaller (∼3 nm edge vs 4.4 nm31,47), affording an approximately 10-fold enhancement for dipole–dipole interactions between edges. Moreover, in the systems described herein, the lower steric bulk around the phenyl rings allows for a degree of coplanarity between phenyl(imine) and BODIPY units, enabling metal-mediated (i.e., through-bond) delocalization of the electronic wave function over at least two BODIPY “edges”.
Photoluminescence Quenching
We have investigated the photoluminescence (PL) properties of cages 1–4, and all were found to exhibit low quantum efficiencies (<10–4; see Figure S12). A low efficiency for emission in the visible region was anticipated for diamines A and B due to the rapid quenching of the initial singlet state through intramolecular charge transfer (Figure S10), but this mechanism should be deactivated in the diimine-based cages. The behavior of the cages is striking, as BODIPY dyes are typically efficient emitters. We used transient grating photoluminescence spectroscopy51 with a time resolution of <200 fs to track the fate of the bright state on early time scales (Figure 2).
Figure 2.
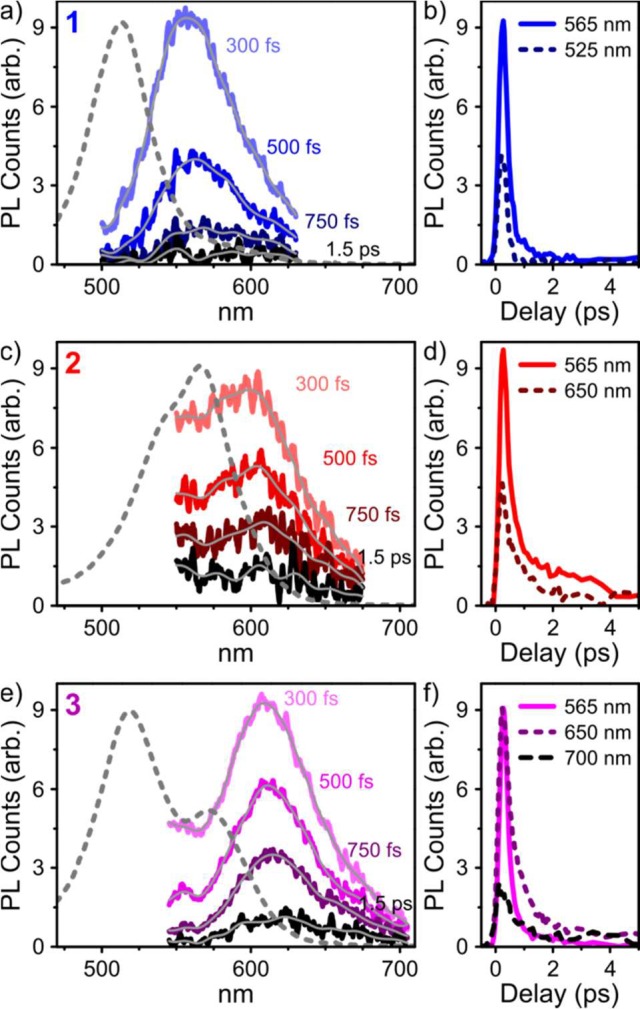
Ultrafast photoluminescence spectra and corresponding kinetics for films of (a,b) 1, (c,d) 2, and (e,f) 3 with <200 fs temporal resolution, at the delay times indicated in the panels. Gray lines are smoothed as a guide for the eye. Dashed lines are UV–vis absorption spectra from Figure 1. Excitation was carried out at 400 nm.
For all cages, we observed prompt emission from the photoexcited state, with a small Stokes shift consistent with the luminescence arising from the singlet state that corresponded to the principal UV–vis absorption. In the case of heteroleptic 3, the emission appeared to be dominated by a species similar, but not identical, to the one observed for 2. However, the strong overlap between 1-type emission and the 550–600 nm absorption band in 3 would strongly attenuate any PL in that spectral region. It is thus unclear whether the very weak 1-type emission detected in 3 is a signature of efficient electronic coupling/energy transfer between Me- and TIPS-substituted units. We observe no dynamics indicative of energy transfer, meaning any such process would have to occur within the instrumental resolution (<200 fs). In all cages, the emissive state exhibited fast decay with a primary time constant of 400–600 fs, and no emission could be detected beyond the few-picosecond time scale. In the absence of polar moieties, such rapid quenching of the emissive state is unexpected for a BODIPY system and not likely to be intrinsic to the chromophore itself. Instead, we infer the quenching to be a consequence of chromophore incorporation into cages, leading to significant interchromophore coupling. Indeed, the observed dynamics are consistent with our hypothesis of relaxation within an aggregate manifold from bright to dark states.52 To understand the pathways that led to these dark states, we turned to transient absorption (TA) spectroscopy.
Homoleptic Cage Photophysics
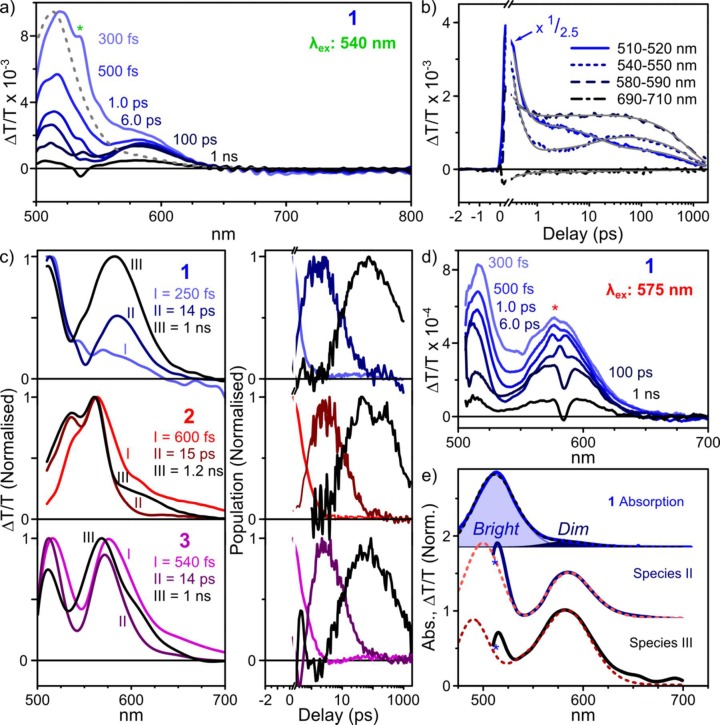
We measured the TA spectra of cages 1–3 following photoexcitation at 515, 540, and 575 nm. Figure 3a,b presents transient absorption spectra and kinetics for 1 following excitation at 540 nm. Results for cages 2 and 3 are qualitatively similar and can be found in Figures S13 and S14 and Figure 4. Full wavelength-dependent data for 1 are presented in Figure S15.
Figure 3.
Transient absorption of empty cages. (a) TA spectra of 1 excited at 540 nm, at selected pump–probe delays. The dashed line is the UV–vis spectrum. (b) Corresponding decay kinetics averaged over the indicated spectral regions. Global triexponential fit is shown in gray. (c) Decomposition into time-independent species-associated spectra (left) and population kinetics (right) reveals smooth, sequential conversion. A comparable progression of states, characterized by qualitatively similar features, was observed for 2 (middle) and 3 (bottom), also excited at 540 nm. Spectra and kinetics were normalized for clarity. (d) TA spectra of 1 following excitation at 575 nm, revealing the absence of species I. (e) Absorption of 1 (top, solid) and decomposition (dashed) into bright and dim aggregate contributions. Species II (middle) and III (bottom) from TA experiments (solid) can be described as combinations of bright- and dim-state bleaching with derivatives of the bright absorption (dashed), consistent with transient modulation of the interchromophore coupling. In spectral plots, “∗” denotes pump laser scatter.
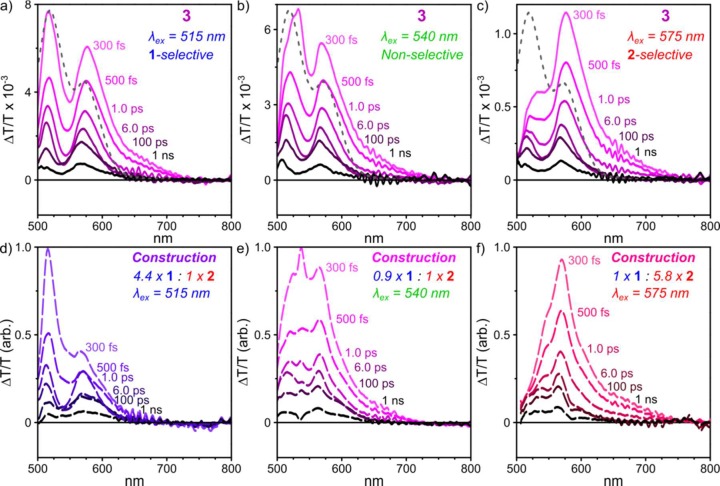
Figure 4.
Strong coupling in heteroleptic cages. TA spectra of 3 at selected pump–probe delays, following excitation at (a) 515 nm, (b) 540 nm, and (c) 575 nm. Dashed spectrum corresponds to UV–vis absorption. (d–f) Synthetic TA spectra constructed from homoleptic cage data, based on differing relative contributions to overall UV–vis absorption (ratio indicated). These constructed spectra fail to reproduce peak positions or relative intensities.
The initial TA spectrum of 1 (Figure 3a) consists almost entirely of positive ΔT/T features, which could correspond either to ground-state bleaching (GSB) or to stimulated emission from a photoexcited state (SE). Comparison of the spectrum at 300 fs to the ground-state absorption (dashed) reveals additional TA signal beyond the absorption line shape, particularly in the range 550–625 nm. This extra ΔT/T intensity agrees with the PL measured above, and we conclude that the initial signal contains a mixture of GSB and SE contributions and can be accordingly assigned to the initial bright singlet. Within the first picosecond, we detect substantial changes to the spectral shape, with loss of the prominent peak at 515 nm and growth of a dip between the two main positive features. Because of the rapid PL quenching described above, the positive bands observed on time scales >1 ps are unlikely to exhibit SE, and we assign both peaks (515 nm, 580 nm) to GSB. Beyond 6 ps, the spectrum evolves further, with a rise of signal intensity in the range 530–550 nm as the peak at 580 nm broadens. This behavior is well captured in the kinetics at 540–550 nm (Figure 1b, short dashed line), where the growth in signal can be clearly distinguished. No further spectral evolution is observed beyond this point, and fast decay leaves little signal at the end of the measurement duration (1.5 ns). This spectral evolution suggests the presence of three distinct species; indeed, the kinetics could not be fitted satisfactorily with fewer than three exponential time constants. We refer to these excited states as species I (shortest-lived), species II, and species III (longest lifetime) in the following discussion.
Singular value decomposition (SVD) analysis indicated the presence of three primary spectral components in the TA data set of 1. We extracted the time-invariant, species-associated spectra and their corresponding population kinetics using linear combinations of the SVD components, subject to such basic physical constraints as non-negative population. The resulting solutions are assigned as species I–III (Figure 3c) and exhibit a clear sequential progression of states for all cages, with similar kinetics. The initial state (I) consists primarily of a GSB peak at 515 nm with additional SE contributions extending to longer wavelengths; on intermediate time scales (II), the weight of the 515 nm peak relative to that at 580 nm sharply reduces, in part due to the loss of SE; and on longer time scales (III), the peak at 580 nm broadens. Intriguingly, this progression could be modified by varying the excitation wavelength. Following excitation at 515 nm, the relative weight of species I is enhanced, whereas excitation at 575 nm directly generates species II with no evidence of I (Figure 3d).
We assign species I, the initial state with 250 fs lifetime, as the bright singlet observed to photoluminesce. To describe the other species, we refer to the UV–vis spectrum (Figure 3e). From the presence of two GSB peaks with distinct kinetics in the TA spectra, we infer that the principal peak and longer-wavelength tail in the absorption of 1 correspond to distinct electronic states. Each was fitted to a Gaussian function (shaded). Based upon our analysis of the possible dipole–dipole coupled states, we assign the weak long-wavelength peak to dim states with a higher proportion of energetically favorable dipole alignments and the short-wavelength peak to higher-energy bright configurations.
Species II can be modeled as a combination of GSB from both of these peaks, with an additional contribution from the first derivative of the excitonic peak. The excited-state electronic wave function thus reflects contributions from the multiple coupled BODIPY chromophores, resulting in a perturbation to the underlying bright state. The fast conversion from I to II is likely to result from the rotational and conformation flexibility of the cage framework. The free rotation of the chromophores, contrasting with more rigid perylene-based structures,31,50 introduces a variable component to the transition dipole moment, perpendicular to the cage edge and offering additional pathways for dipole cancellation (i.e., interconversion between dipole-coupled states). Species III results from a change in the balance of GSB and first-derivative features, as well as further shifts matching the second derivative of the excitonic peak. The slower time scale for species III formation is in accord with typical vibrational relaxation dynamics, and we infer species II → III conversion to be related to structural changes in the cage geometry that occur in response to electronic excitation. Any such structural reorganization would affect the interchromophore geometry within the cages and directly impact the electronic coupling between BODIPYs. This coupling in turn must modify the absorption spectrum of the coupled system, as manifested here in the derivative contributions to species III, which describe slight shifts and broadening.
The photophysics of 1 thus appear to be dominated by the dipole frustration of the initial bright state, leading to ultrafast relaxation into a lower-energy nonemissive configuration. The fact that we can directly photoexcite the dim aggregate state at 575 nm (Figure 3d), resulting in simple conversion from species II to III, indicates that this state has nonzero oscillator strength; we anticipate that it dominates the low-energy absorption tail. By contrast, we do not detect distinct dim-state emission in the transient grating PL experiment, suggesting a low radiative rate.
The same behavior, with an increased prominence of first- and subsequent second-derivative features, can be qualitatively identified in the dynamics of 2 and 3. Based on this observation and the similar time scales observed across species (Figure 3c), we infer that the same model applies across cages.
We note that the presence of FeII at the vertices of cages 1–3 raises the possibility that the rapid PL quenching and I → II conversion we observe involves the Fe d-electron orbitals and would not thus be intrinsic to the chromophore arrangement. To investigate this possibility, we also prepared 4, in which ZnII ions with a full d-shell occupy the tetrahedron vertices in place of FeII. The photophysics of these cages (Figures S9, S12, and S16) are nearly indistinguishable from their FeII analogues, apart from a slight reduction in the interchromophore interaction in wavelength-dependent measurements (as discussed below). This situation provides an intriguing contrast to recently reported phosphorescent PtII-edged cages, in which the presence of Fe or Zn ions at the vertices results in dramatically different steady-state spectra.42 The extension of ligand conjugation onto the covalently linked platinum bridging units in such structures appears to result in a greater role for the metal vertices in the cage photophysics.
Heteroleptic Cage Photophysics
In order to better understand the nature of the initial photoexcited state, we investigated in greater detail the pump wavelength dependence on the TA spectra of heteroleptic cages 3 (Figure 4). The spectra of these cages are dominated by two broad, strong GSB peaks at 515 and 575 nm. These roughly match the primary GSB peaks of 1 and 2; we have thus used the relative intensities of these peaks to gauge whether the excitation is located more on the Me-substituted or TIPS-substituted BODIPY residues of A and B, respectively. By varying the excitation wavelength, we sought to excite selectively either the Me-substituted or TIPS-substituted chromophores. An enhancement in the lower-energy (TIPS-type) GSB was indeed found following excitation at 575 nm (Figure 4c).
We attempted to reconstruct the TA spectrum of 3 from linear combinations of the TA spectra of 1 and 2, based on the relative absorption strengths of 1 and 2 (dashed spectrum overlaid upon the spectrum of 3 in Figure 1b). Comparison of the top and bottom panels of Figure 4 reveals that in no instance could we accurately reproduce the spectra observed for direct excitation of 3. The peak positions did not match, and their ratios demonstrate a higher than expected proportion of TIPS-substituted BODIPY GSB following excitation at 515 nm and a higher proportion of Me-substituted BODIPY GSB following excitation at 575 nm. These effects are observed even in the earliest TA spectra, reflecting the nature of the initial excited state. Recalling the analysis of the UV–vis absorption spectrum of 3 above, we infer that these results can be explained by interchromophore coupling between Me- and TIPS-substituted BODIPYs within the same cage. These chromophores are thus strongly coupled in the ground state, sharing a single electronic wave function, whereby excitation of one component results in simultaneous excitation of the other. The initial excited-state wave function must then be delocalized, at a minimum over two BODIPY edges. We have found this effect of delocalization to be marginally weaker in ZnII-based 4; that is, Me-selective excitation produces less TIPS-type GSB and vice versa (Figure S16). As 3 and 4 are isostructural apart from their metal-ion vertices, we propose that the delocalization must be at least partially mediated by through-bond interactions. We infer that the pump wavelength dependence observed in the initial spectral shape thus arises from preferential excitation of mixed cages with a greater concentration of either Me-substituted or TIPS-substituted BODIPY residues, reflecting the statistical distribution of these different ligands in 3.
Host–Guest Interactions
The central cavities in metal–organic cages analogous to 1–3 have been demonstrated to provide guest binding sites that enable the selective loading of cargoes. To explore the electronic interaction between host and guest molecules, we treated 1–3 with fullerene C60 or C70. Solutions of preassembled cages were mixed with fullerene powder and sonicated for 10 min followed by heating to 50 °C overnight. Uptake of the two fullerenes was observed in NMR and MS measurements (Figures S17–S25, Supporting Information). We were likewise able to distinguish weak PL associated with C70 in cages loaded with that fullerene (Figure S12), although the low absorption cross section of fullerenes as compared to the six strongly absorbing BODIPY edges of each cage prevented the observation of this cargo in the UV–vis absorption spectrum (Figure 5).
Figure 5.
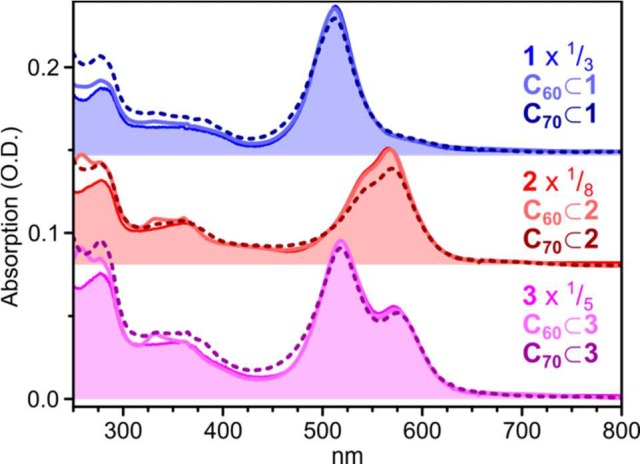
Absorption of fullerene-loaded cages, embedded in PMMA matrix. Empty cage absorption spectra (filled regions) are essentially indistinguishable from C60-loaded spectra (solid lines). Additional intensity in the spectra corresponding to C70-loaded cages (dashed lines) below 500 nm may reflect fullerene absorption or scattering.
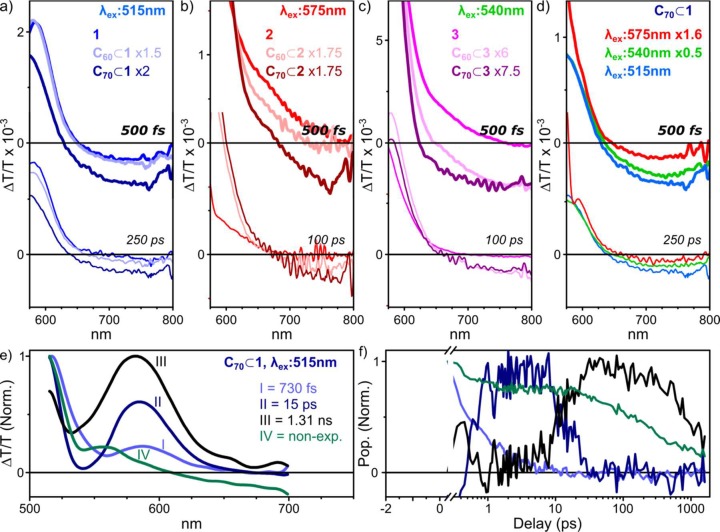
Significant changes were observed upon fullerene encapsulation, however, in the TA dynamics. Principal results are presented in Figure 6, with full data given in Figures S26–S28. In all cases, even on the earliest time scales (Figure 6a–c, top) we observe increased photoinduced absorption (PIA) beyond ∼650 nm. This absorption is weakly apparent in the C60 adducts of 1–3 and especially pronounced in C70-loaded cages. The enhanced PIA persists for hundreds of picoseconds (Figure 6a–c, bottom) and results in a longer time scale for ground-state recovery than observed for empty cages, demonstrating clearly the presence of a new excited state. We infer this state to result from charge transfer between host (cage) and guest (fullerene). For 1–3, we observe the strength of this charge-transfer signal to exhibit pump wavelength dependence, as shown in Figure 6d for 1. The signal strength is weakest following excitation at 575 nm and becomes progressively stronger as the excitation is shifted to 540 nm and then 515 nm. The initial bright-state signal exhibits similar wavelength dependence in empty cages 1–3. These observations allow us to infer that this state is the only precursor for fullerene charge transfer, whereas the species II and III discussed above make little contribution.
Figure 6.
Spectroscopic signatures of host–guest interactions in fullerene-loaded BODIPY cages. TA spectra of (a) 1, C60⊂1, and C70⊂1 following excitation at 515 nm; (b) 2, C60⊂2, and C70⊂2 following excitation at 575 nm; and (c) 3, C60⊂3, and C70⊂3 following excitation at 540 nm, revealing additional PIA (ΔT/T < 0) from charge-separated states which persist for hundreds of picoseconds. (d) Pump wavelength dependence of the fullerene charge-transfer signal for C70⊂1. A similar dependence was observed for C60⊂1, as well as for fullerene-loaded 2 and 3 (see Figures S26–S28). All data sets were scaled as indicated to account for excitation density. Full spectra are provided in the Supporting Information. (e) Spectral decomposition of TA data for C70⊂1 and (f) corresponding population kinetics. Species I–III display decay kinetics similar to those observed in the decomposition of empty 1, with no direct relationship to charge-transfer species IV.
We applied the same spectral decomposition procedure described above for the empty cages to the TA dynamics of C70⊂1. As shown in Figure 6e, the spectral evolution in C70⊂1 can be described using four spectrally distinct species. Species I–III are indistinguishable from those obtained for empty 1 (Figure 3c), exhibiting remarkably similar dynamics. Species IV carries the spectral features associated with a host–guest charge-transfer state, namely, a bleaching of the absorption of 1 and a relatively strong PIA above 600 nm. It is formed within the instrument response (<300 fs), and there is no evidence of growth on later time scales during the decays of I–III. It decays with complicated nonexponential kinetics, with a moderate population persisting beyond the 1.5 ns measurement range. From these results and the excitation wavelength dependence, we may build the following description of host–guest interactions. Charge transfer from cage to fullerene occurs only from the initial bright excitonic state (i.e., I) and proceeds in well under 200 fs due to close spatial proximity between host and guest. Cages which do not have cargo molecules undergo the standard progression of species I → II → III described in Figure 3. When a lower pump photon energy is used (i.e., 540–575 nm), the dim aggregate state II can be directly generated even in cages with an encapsulated fullerene, resulting in markedly lower yields of species IV and thus suggesting that II is too low in energy to undergo host–guest charge transfer.
The photophysics of BODIPY-containing FeII4L6 tetrahedra 1–3 are thus governed by strong electronic coupling between the constituent chromophores. In the ground state, these interactions between BODIPY edges are sufficiently strong to enable delocalization of the wave function over multiple chromophores, ensuring that in heteroleptic cages the “Me-type” and “TIPS-type” excitations are always coupled. The slight weakening of this effect in ZnII-based cages demonstrates the coupling to be mediated in part by through-bond interactions, though we infer through-space dipole–dipole coupling to be the dominant factor. The presence of these strong interactions in the ground state has pronounced effects in the excited-state dynamics, as well, leading to rapid relaxation into low-energy dark states, in which the BODIPY transition dipole moments largely cancel. These relaxation dynamics are not significantly affected by the type of metal ion at the vertices (FeII vs ZnII), revealing no role for metal-to-ligand charge transfer involving the metal d-orbitals. Relaxation is suppressed only in the presence of centrally bound cargo molecules. When loaded with electron-accepting fullerene C60 or C70, all three types of cage exhibit rapid host–guest charge transfer from the initial high-energy bright state.
Basic geometrical considerations can explain the observed charge-transfer behavior. Each constituent BODIPY is closer to the encapsulated fullerene than to the other BODIPY edges of the cage. Moreover, the location of the fullerene in the core of the cage should enable direct overlap with the BODIPY π-orbitals. Host–guest interactions thus dominate the photophysics of fullerene-loaded cages.
It is revealing to compare the photophysical description of BODIPY cages 1–3 to the perylene-based cages recently reported by Würthner.31,50 These latter cages, also generated using subcomponent self-assembly, had similar tetrahedral structures but exhibited little coupling between their constituent ligands. The absorption and emission spectra of the perylene cages can be described in terms of six nearly independent perylene moieties. Their high reported photoluminescence quantum efficiency indicated that interligand interactions only slightly perturbed the molecular photophysics.
The most significant structural differences between this cage system and the one described by Würthner31,50 are size, the design of the metal chelating units, and their connections to the chromophores in the ligand cores. In the larger perylene system, we would anticipate a much smaller role for dipole–dipole coupling. Moreover, in those cages, significant steric bulk holds the phenyl rings rigidly orthogonal to the aromatic ligands of the metal ions. In our BODIPY cages, the absence of substituents on the phenyl spacers and use of amine rather than pyridine aldehyde end groups (Figure 1) enable sufficient torsional freedom to extend electronic conjugation up to the metal chelating units. We infer that these subtle differences enable both through-space and through-bond channels of inter-BODIPY coupling in our structures.
The present work thus provides design principles that may be used to tune interchromophore electronic communication within coordination cages and other complex self-assembled structures. These principles may prove useful in the construction of light-driven molecular machines,53−58 the dynamics of which must be tuned in respect of their excited-state properties. Our results also provide guidelines for the design of systems exhibiting efficient host–guest charge transfer, a phenomenon of critical importance in the context of artificial photosynthesis and solar energy conversion.
Experimental Section
General Experimental Techniques
All reagents and solvents were purchased from commercial sources and used as supplied. All experiments were carried out at room temperature unless otherwise stated. NMR spectra were recorded using either a Bruker DRX-400, a Bruker AVC-500-BB, or a Bruker AVC-500-TCI spectrometer. Chemical shifts of cages are reported in parts per million (δ) calibrated to the residual solvent signals of acetonitrile-d3: δH at 1.94 ppm and δC at 118.26 ppm. High-resolution mass spectrometry was performed on a Waters LCT Premier mass spectrometer featuring a Z-spray source with electrospray ionization and modular LockSpray interface.
Procedure for the Preparation of Cages 1–3
In a Schlenk flask, ligand (1 equiv), 2-formylpyridine (2 equiv), and the divalent metal salt (0.67 equiv) were dissolved in acetonitrile (3 mL). The solution was degassed by three evacuation/nitrogen-fill cycles and heated to 70 °C overnight. After being cooled to room temperature, the solvent was evaporated and any unreacted starting materials were removed by trituration with diethyl ether to yield the cages in >95% yield. Characterization data of cages 1–4 are given in the Supporting Information.
Photophysical Measurements
The photophysical properties of BODIPY diamines and cages were studied with transient grating photoluminescence and transient absorption spectroscopies. In the transient grating technique, a Ti:sapphire amplifier system (Spectra-Physics Solstice Ace) operating at 1 kHz generating 80 fs 800 nm pulses was split into the pump and probe beam arms. The pump beam was generated by second harmonic generation in a BBO crystal and focused onto the sample. Photoluminescence was collimated using a silver off-axis parabolic mirror and focused onto the gate medium. About 80 μJ/pulse of the 800 nm laser output is used for the gate beams, which is first raised 25 mm above the plane of the PL to produce a boxcar geometry and split into a pair of gate beams using a 50/50 beam splitter. The gate beams are focused onto the gate medium (fused silica), crossing at an angle of ∼5° and overlapping with the focused PL. The two gate beams interfere and create a transient grating in the gate medium due to a modulation of the refractive index via the optical Kerr effect.51 Temporal overlap between the two gate beams is achieved via a manual delay stage. The PL is then deflected on the transient grating, causing a spatial separation of the gated signal from the PL background. Two lenses collimate and focus the gated signal onto the spectrometer entrance (Princeton Instruments SP 2150) after long- and short-pass filters remove scattered pump and gate light, respectively. Gated PL spectra are measured using an intensified CCD camera (Princeton Instruments, PIMAX4). The (∼10 ns) electronic shutter of the intensified CCD camera was used to further suppress long-lived PL background. PL spectra at each gate time delay are acquired from ∼10000 laser shots. The time delay between pump and gate beams is controlled via a motorized optical delay line on the excitation beam path and a LabVIEW data acquisition program. Transient absorption measurements were taken on a previously reported system.59 Briefly, broad-band probe pulses were generated using noncollinear optical parametric amplifiers built in-house to cover two separate spectral ranges: 500–800 and 800–1150 nm. The same InGaAs array detector (Hamamatsu G11608-512) was used for all wavelengths. Cages (under vacuum) and diamines (in sealed quartz cuvettes) were excited with the 515, 540, 575, or 625 nm output from an automated OPA (TOPAS, Light Conversion), with a pulse duration of ∼200 fs. The sub-picosecond setup was limited by the length of the mechanical delay stage to delays of ∼2 ns. In all measurements, pump and probe polarizations were set to the magic angle (54.7°).
Acknowledgments
This work was supported by the European Research Council (259352) and the Engineering and Physical Sciences Research Council, U.K. (EP/M005143/1 and EP/G060738/1). The authors thank the Department of Chemistry NMR facility, University of Cambridge, and the EPSRC UK National Mass Spectrometry Facility at Swansea University.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.7b06709.
Synthetic details, NMR and mass spectra, and detailed time-resolved spectroscopic data (PDF)
Author Present Address
∥ (P.P.N.) Institute of Nano Science and Technology, Habitat Centre, Phase 10, Sector 64, Mohali 160062, Punjab, India.
Author Present Address
# (H.M.) Asahi Kasei Corporation.
Author Contributions
⊥ A.J.M. and P.P.N. contributed equally.
The authors declare no competing financial interest.
Supplementary Material
References
- Steed J. W.; Atwood J. L.. Supramolecular Chemistry; John Wiley & Sons, Ltd.: New York, 2009; pp 1–48. [Google Scholar]
- Cook T. R.; Stang P. J. Chem. Rev. 2015, 115, 7001–7045. 10.1021/cr5005666. [DOI] [PubMed] [Google Scholar]
- Fujita D.; Ueda Y.; Sato S.; Mizuno N.; Kumasaka T.; Fujita M. Nature 2016, 540, 563–566. 10.1038/nature20771. [DOI] [PubMed] [Google Scholar]
- Ward M. D.; Raithby P. R. Chem. Soc. Rev. 2013, 42, 1619–1636. 10.1039/C2CS35123D. [DOI] [PubMed] [Google Scholar]
- Holloway L. R.; McGarraugh H. H.; Young M. C.; Sontising W.; Beran G. J. O.; Hooley R. J. Chem. Sci. 2016, 7, 4423–4427. 10.1039/C6SC01038E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansze S. M.; Wise M. D.; Vologzhanina A. V.; Scopelliti R.; Severin K. Chem. Sci. 2017, 8, 1901–1908. 10.1039/C6SC04732G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaudoin D.; Rominger F.; Mastalerz M. Angew. Chem., Int. Ed. 2016, 55, 15599–15603. 10.1002/anie.201609073. [DOI] [PubMed] [Google Scholar]
- Howlader P.; Das P.; Zangrando E.; Mukherjee P. S. J. Am. Chem. Soc. 2016, 138, 1668–1676. 10.1021/jacs.5b12237. [DOI] [PubMed] [Google Scholar]
- Kubota R.; Tashiro S.; Shionoya M. Chem. Sci. 2016, 7, 2217–2221. 10.1039/C5SC04570C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W.; Wang Y.-X.; Yang H.-B. Chem. Soc. Rev. 2016, 45, 2656–2693. 10.1039/C5CS00301F. [DOI] [PubMed] [Google Scholar]
- Frank M.; Johnstone M. D.; Clever G. H. Chem. - Eur. J. 2016, 22, 14104–14125. 10.1002/chem.201601752. [DOI] [PubMed] [Google Scholar]
- Wang M.; Wang K.; Wang C.; Huang M.; Hao X.-Q.; Shen M.-Z.; Shi G.-Q.; Zhang Z.; Song B.; Cisneros A.; Song M.-P.; Xu B.; Li X. J. Am. Chem. Soc. 2016, 138, 9258–9268. 10.1021/jacs.6b04959. [DOI] [PubMed] [Google Scholar]
- Xie T.-Z.; Endres K. J.; Guo Z.; Ludlow J. M.; Moorefield C. N.; Saunders M. J.; Wesdemiotis C.; Newkome G. R. J. Am. Chem. Soc. 2016, 138, 12344–12347. 10.1021/jacs.6b07969. [DOI] [PubMed] [Google Scholar]
- Ronson T. K.; Zarra S.; Black S. P.; Nitschke J. R. Chem. Commun. 2013, 49, 2476–2490. 10.1039/c2cc36363a. [DOI] [PubMed] [Google Scholar]
- Bunzen H.; Nonappa; Kalenius E.; Hietala S.; Kolehmainen E. Chem. - Eur. J. 2013, 19, 12978–12981. 10.1002/chem.201302055. [DOI] [PubMed] [Google Scholar]
- Li X.; Wu J.; Chen L.; Zhong X.; He C.; Zhang R.; Duan C. Chem. Commun. 2016, 52, 9628–9631. 10.1039/C6CC04647A. [DOI] [PubMed] [Google Scholar]
- Saha M. L.; Schmittel M. Inorg. Chem. 2016, 55, 12366–12375. 10.1021/acs.inorgchem.6b02256. [DOI] [PubMed] [Google Scholar]
- Howlader P.; Mukherjee P. S. Chem. Sci. 2016, 7, 5893–5899. 10.1039/C6SC02012G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodríguez J.; Mosquera J.; Couceiro J. R.; Nitschke J. R.; Vázquez M. E.; Mascareñas J. L. J. Am. Chem. Soc. 2017, 139, 55–58. 10.1021/jacs.6b11103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galan A.; Ballester P. Chem. Soc. Rev. 2016, 45, 1720–1737. 10.1039/C5CS00861A. [DOI] [PubMed] [Google Scholar]
- Deraedt C.; Astruc D. Coord. Chem. Rev. 2016, 324, 106–122. 10.1016/j.ccr.2016.07.007. [DOI] [Google Scholar]
- Yang L.; Jing X.; He C.; Chang Z.; Duan C. Chem. - Eur. J. 2016, 22, 18107–18114. 10.1002/chem.201601447. [DOI] [PubMed] [Google Scholar]
- Schmidt A.; Molano V.; Hollering M.; Pöthig A.; Casini A.; Kühn F. E. Chem. - Eur. J. 2016, 22, 2253–2256. 10.1002/chem.201504930. [DOI] [PubMed] [Google Scholar]
- Custelcean R. Chem. Soc. Rev. 2014, 43, 1813–1824. 10.1039/C3CS60371G. [DOI] [PubMed] [Google Scholar]
- Hart-Cooper W. M.; Sgarlata C.; Perrin C. L.; Toste F. D.; Bergman R. G.; Raymond K. N. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 15303–15307. 10.1073/pnas.1515639112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser F.; Schmidt A.; Heydenreuter W.; Altmann P. J.; Casini A.; Sieber S. A.; Kühn F. E. Eur. J. Inorg. Chem. 2016, 2016, 5189–5196. 10.1002/ejic.201600811. [DOI] [Google Scholar]
- Mahata K.; Frischmann P. D.; Würthner F. J. Am. Chem. Soc. 2013, 135, 15656–15661. 10.1021/ja4083039. [DOI] [PubMed] [Google Scholar]
- Yoshizawa M.; Yamashina M. Chem. Lett. 2017, 46, 163–171. 10.1246/cl.160852. [DOI] [Google Scholar]
- Kishimoto M.; Kondo K.; Akita M.; Yoshizawa M. Chem. Commun. 2017, 53, 1425–1428. 10.1039/C6CC09094J. [DOI] [PubMed] [Google Scholar]
- Yazaki K.; Noda S.; Tanaka Y.; Sei Y.; Akita M.; Yoshizawa M. Angew. Chem., Int. Ed. 2016, 55, 15031–15034. 10.1002/anie.201608350. [DOI] [PubMed] [Google Scholar]
- Frischmann P. D.; Kunz V.; Würthner F. Angew. Chem., Int. Ed. 2015, 54, 7285–7289. 10.1002/anie.201501670. [DOI] [PubMed] [Google Scholar]
- Dolgopolova E. A.; Williams D. E.; Greytak A. B.; Rice A. M.; Smith M. D.; Krause J. A.; Shustova N. B. Angew. Chem., Int. Ed. 2015, 54, 13639–13643. 10.1002/anie.201507400. [DOI] [PubMed] [Google Scholar]
- Yang Y.; Chen J.-S.; Liu J.-Y.; Zhao G.-J.; Liu L.; Han K.-L.; Cook T. R.; Stang P. J. J. Phys. Chem. Lett. 2015, 6, 1942–1947. 10.1021/acs.jpclett.5b00783. [DOI] [PubMed] [Google Scholar]
- Splan K. E.; Massari A. M.; Morris G. A.; Sun S.-S.; Reina E.; Nguyen S. T.; Hupp J. T. Eur. J. Inorg. Chem. 2003, 2003, 2348–2351. 10.1002/ejic.200200665. [DOI] [Google Scholar]
- Gong X.; Young R. M.; Hartlieb K. J.; Miller C.; Wu Y.; Xiao H.; Li P.; Hafezi N.; Zhou J.; Ma L.; Cheng T.; Goddard W. A.; Farha O. K.; Hupp J. T.; Wasielewski M. R.; Stoddart J. F. J. Am. Chem. Soc. 2017, 139, 4107–4116. 10.1021/jacs.6b13223. [DOI] [PubMed] [Google Scholar]
- Šolomek T.; Powers-Riggs N. E.; Wu Y.-L.; Young R. M.; Krzyaniak M. D.; Horwitz N. E.; Wasielewski M. R. J. Am. Chem. Soc. 2017, 139, 3348–3351. 10.1021/jacs.7b00233. [DOI] [PubMed] [Google Scholar]
- Saha M. L.; Yan X.; Stang P. J. Acc. Chem. Res. 2016, 49, 2527–2539. 10.1021/acs.accounts.6b00416. [DOI] [PubMed] [Google Scholar]
- Lindsey J. S.; Delaney J. K.; Mauzerall D. C.; Linschitz H. J. Am. Chem. Soc. 1988, 110, 3610–3621. 10.1021/ja00219a041. [DOI] [Google Scholar]
- Flamigni L.; Ventura B.; Oliva A. I.; Ballester P. Chem. - Eur. J. 2008, 14, 4214–4224. 10.1002/chem.200800026. [DOI] [PubMed] [Google Scholar]
- Ortiz M.; Cho S.; Niklas J.; Kim S.; Poluektov O. G.; Zhang W.; Rumbles G.; Park J. J. Am. Chem. Soc. 2017, 139, 4286–4289. 10.1021/jacs.7b00220. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Fulong C. R. P.; Hauke C. E.; Crawley M. R.; Friedman A. E.; Cook T. R. Chem. - Eur. J. 2017, 23, 4532–4536. 10.1002/chem.201700614. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Crawley M. R.; Hauke C. E.; Friedman A. E.; Cook T. R. Inorg. Chem. 2017, 56, 4258–4262. 10.1021/acs.inorgchem.7b00501. [DOI] [PubMed] [Google Scholar]
- Sunahara H.; Urano Y.; Kojima H.; Nagano T. J. Am. Chem. Soc. 2007, 129, 5597–5604. 10.1021/ja068551y. [DOI] [PubMed] [Google Scholar]
- Beissel T.; Powers R. E.; Parac T. N.; Raymond K. N. J. Am. Chem. Soc. 1999, 121, 4200–4206. 10.1021/ja984046s. [DOI] [Google Scholar]
- Meng W.; Clegg J. K.; Thoburn J. D.; Nitschke J. R. J. Am. Chem. Soc. 2011, 133, 13652–13660. 10.1021/ja205254s. [DOI] [PubMed] [Google Scholar]
- Bilbeisi R. A.; Clegg J. K.; Elgrishi N.; Hatten X. d.; Devillard M.; Breiner B.; Mal P.; Nitschke J. R. J. Am. Chem. Soc. 2012, 134, 5110–5119. 10.1021/ja2092272. [DOI] [PubMed] [Google Scholar]
- Hayashi Y.; Yamaguchi S.; Cha W. Y.; Kim D.; Shinokubo H. Org. Lett. 2011, 13, 2992–2995. 10.1021/ol200799u. [DOI] [PubMed] [Google Scholar]
- Bergström F.; Mikhalyov I.; Hägglöf P.; Wortmann R.; Ny T.; Johansson L. B. Å. J. Am. Chem. Soc. 2002, 124, 196–204. 10.1021/ja010983f. [DOI] [PubMed] [Google Scholar]
- Karolin J.; Johansson L. B. A.; Strandberg L.; Ny T. J. Am. Chem. Soc. 1994, 116, 7801–7806. 10.1021/ja00096a042. [DOI] [Google Scholar]
- Frischmann P. D.; Kunz V.; Stepanenko V.; Würthner F. Chem. - Eur. J. 2015, 21, 2766–2769. 10.1002/chem.201405866. [DOI] [PubMed] [Google Scholar]
- Chen K.; Gallaher J. K.; Barker A. J.; Hodgkiss J. M. J. Phys. Chem. Lett. 2014, 5, 1732–1737. 10.1021/jz5006362. [DOI] [PubMed] [Google Scholar]
- Sung J.; Kim P.; Fimmel B.; Würthner F.; Kim D. Nat. Commun. 2015, 6, 8646. 10.1038/ncomms9646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng C.; Stoddart J. F. ChemPhysChem 2016, 17, 1780–1793. 10.1002/cphc.201501155. [DOI] [PubMed] [Google Scholar]
- Collins B. S. L.; Kistemaker J. C. M.; Otten E.; Feringa B. L. Nat. Chem. 2016, 8, 860–866. 10.1038/nchem.2543. [DOI] [Google Scholar]
- Le Bailly B. Nat. Nanotechnol. 2016, 11, 923–923. 10.1038/nnano.2016.246. [DOI] [PubMed] [Google Scholar]
- Niess F.; Duplan V.; Sauvage J.-P. Chem. Lett. 2014, 43, 964–974. 10.1246/cl.140315. [DOI] [Google Scholar]
- Credi A., Silvi S., Venturi M., Eds. Molecular Machines and Motors: Recent Advances and Perspectives; Springer International Publishing: Cham, Switzerland, 2014; pp 1–34. [Google Scholar]
- Cnossen A.; Browne W. R.; Feringa B. L. In Molecular Machines and Motors: Recent Advances and Perspectives; Credi A., Silvi S., Venturi M., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp 139–162. [Google Scholar]
- Musser A. J.; Al-Hashimi M.; Maiuri M.; Brida D.; Heeney M.; Cerullo G.; Friend R. H.; Clark J. J. Am. Chem. Soc. 2013, 135, 12747–12754. 10.1021/ja405427j. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.