Abstract
Expression of a large fraction of genes in bacteria is controlled by riboswitches, which are found in the untranslated region of mRNA. Structurally riboswitches have a conserved aptamer domain to which a metabolite binds, resulting in a conformational change in the downstream expression platform. Prediction of the functions of riboswitches requires a quantitative description of the folding landscape so that the barriers and time scales for the conformational change in the switching region in the aptamer can be estimated. Using a combination of all atom molecular dynamics (MD) and coarse-grained model simulations we studied the response of adenine (A) binding add and pbuE A-riboswitches to mechanical force. The two riboswitches contain a structurally similar three-way junction formed by three paired helices, P1, P2, and P3, but carry out different functions. Using pulling simulations, with structures generated in MD simulations, we show that after P1 rips the dominant unfolding pathway in the add A-riboswitch is the rupture of P2 followed by unraveling of P3. In the pbuE A-riboswitch, after P1 unfolds P3 ruptures ahead of P2. The order of unfolding of the helices, which is in accord with single molecule pulling experiments, is determined by the relative stabilities of the individual helices. Our results show that the stability of isolated helices determines the order of assembly and response to force in these non-coding regions. We use the simulated free energy profile for the pbuE A-riboswitch to estimate the time scale for allosteric switching, which shows that this riboswitch is under kinetic control lending additional support to the conclusion based on single molecule pulling experiments. A consequence of the stability hypothesis is that a single point mutation (U28C) in the P2 helix of the add A-riboswitch, which increases the stability of P2, would make the folding landscapes of the two riboswitches similar. This prediction can be tested in single molecule pulling experiments.
Riboswitches, RNA elements located in the untranslated region of mRNAs, regulate gene expression by sensing and binding target cellular metabolites.1 The function of riboswitches involves allosteric communication between a conserved aptamer domain and the downstream expression platform. In bacteria, specific metabolites bind to the aptamer domain with exquisite selectivity, resulting in a change in the folding patterns of the expression platform, whose conformation controls transcription termination or translation initiation.2,3 Purine riboswitches,4 which are among the simplest, display remarkable discrimination in binding metabolites and carry out entirely different functions despite the structural similarity of the metabolite-binding aptamer domains (Fig. 1). Surprisingly, even the riboswitches that bind the same metabolite function differently in different species.5,6 For instance, the pbuE adenine (A) riboswitch activates gene expression upon metabolite binding by disrupting the formation of a terminator stem in the downstream expression platform. The absence of the terminator hairpin upon ligand binding prevents the polymerase from engaging with the poly-U track, resulting in completion of transcription.5 In contrast, the add adenine riboswitch is a translational activator, which upon ligand binding facilitates the ribosome to recognize the Shine–Dalgarno sequence, thus initiating translation.2 Thus, we classify the pbuE A-riboswitch as an on-switch riboswitch, which implies that gene expression is promoted when the metabolite adenine binds. From this perspective, the add A-riboswitch is an on-switch for translation.
Fig. 1.
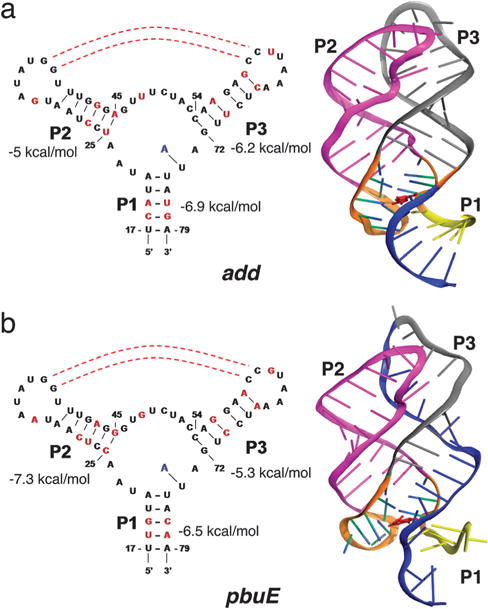
Secondary and tertiray structures of adenine riboswitches. (a) For the add adenine riboswitch aptamer the secondary structure is on the left, and the tertiary structure is on the right. The tertiary structure for the add A-riboswitch aptamer is taken from the crystal structure (PDB Id: 1Y26). (b) Same as (a) except the structures corresponds to the pbuE adenine riboswitch aptamer. The tertiary structure, corresponding to a snapshot at t = 95 ns in the molecular dynamics simulation, is merely a model.
Purine riboswitch aptamers contain a three-way junction, which is formed by helix P1 and hairpins P2 and P3 and are stabilized by tertiary interactions in the folded state (Fig. 1). The ability of riboswitches, and more generally RNA, to adopt alternate folds, a consequence of the modest stability gap7,8 compared to proteins,9 is crucial to regulate transcription and translation. In both pbuE and add A-riboswitches, a part of the aptamer region (a structural element in blue located at the 3′-end of P1 in Fig. 1) is involved in the formation of alternative hairpin structure with nucleotides in the downstream expression platform. The time scales and the barriers associated with the switching strands to form a hairpin with the downstream expression platform determine the dynamic range and efficiency of riboswitch function. Hence, it is important to quantitatively obtain the folding landscapes of the aptamers, which in turn would provide insights into the differences in the functions of the two structurally similar riboswitches.
Single molecule pulling experiments10,11 and carefully designed computer simulations12,13 are ideally suited to obtain the sequence-dependent folding landscapes of riboswitches. In the Laser Optical Tweezers (LOT) experiments a constant mechanical force (f) is applied to the ends of the riboswitches through handles, and the response is monitored by measuring the molecular extension, R, which is conjugate to f. Such experiments have been performed on several riboswitches14 including pbuE10 and add adenine riboswitches.15 The structural changes that occur upon application of force are typically characterized using the free energy profiles, F(R), which provide estimates of the barriers for rupture of various helices. The length gain upon unfolding can be used to decipher the order in which the paired helices unravel.
In our previous report,12 we reported the order of force-induced rupture of add A-riboswitch using simulations of coarse-grained models. The predicted structural transitions for the add A-riboswitch are different from the experimentally inferred pathway for the pbuE A-ribsoswitch10 even though they have nearly identical three-dimensional structures (Fig. 1). The first event in the predominant unfolding pathway of the aptamers is the disruption of helix P1 and the binding pocket formed by the helix junction (Fig. 1). It is the subsequent order of unfolding (P2 unfolds before P3 predicted in our study on the add A-riboswitch aptamer) that differs from the experimental results for the pbuE A-riboswitch aptamer. These results were explained12 by noting that the differences in the folding landscapes are due to variations in the stabilities of individual helices (Fig. 1). Here, we combine molecular dynamics and coarse-grained simulations to further explore the differences in the folding landscapes of these two structurally related aptamers. In order to establish the stability hypothesis, as the principle governing assembly of RNA, we first used all atom molecular dynamics (MD) simulations to obtain putative structures for pbuE A-riboswitches for use in coarse-grained simulations. The combined approaches show that the dominant unfolding pathway is similar to that inferred from experiments.10 The present work also demonstrates that simulations, at different levels of description, can not only predict the outcomes of experiments but also yield (qualitative) insights into sequence-dependent differences in the response of even structurally related RNA aptamers to force.
Results
Stability hypothesis holds even in the presence of tertiary interactions
We used the mfold package16 to estimate the free energy of the isolated secondary paired helices in the aptamers (Fig. 1). The stability of P1 is comparable in both pbuE and add A-aptamers. The P3 helix is more stable by 1.2 kcal mol−1 in the add A-aptamer (Fig. 1a), whereas the predicted free energy of the secondary structure of P3 is larger than P2 by 2 kcal mol−1 in the pbuE A-riboswitch aptamer (Fig. 1b). From stability considerations alone,12 we predicted that the order of unfolding under force from the folded (N) to the globally unfolded state U should be N → ΔP1 → ΔP1ΔP2 → U where ΔP1 denotes rupture of P1 and ΔP1ΔP2 implies that both P1 and P2 are unfolded. This prediction has subsequently been quantitatively validated in experiments.15 Similarly, the predominant unfolding pathway for the pbuE A-riboswitch is expected to be N → ΔP1 → ΔP1ΔP3 → U (see Fig. 1b). The theory based on relative stabilities of isolated P2 and P3 readily explains the experimental findings. However, it is important to examine whether the stability hypothesis is valid in the presence of tertiary contacts as well. Accordingly, we used a combination of all atom MD and Brownian dynamics simulations to determine the F(R) = − kBT lnP(R) (P(R) is the distribution of the extension, R, at a given f) profile of the pbuE A-riboswitch, so that a direct comparison with F(R) obtained in simulations and experiments can be made.
Since the structure of the pbuE A-riboswitch aptamer is not available, we used the crystal structure of the add adenine riboswitch in the metabolite-bound state2 as a template in all atom MD simulations to generate putative structures for use in the coarse-grained self-organized polymer (SOP) model simulations (see Methods). We replaced the nucleobases in the add A-riboswitch with those in the pbuE A-riboswitch. We then used this structure with the pbuE sequence as the initial conformation and performed all-atom MD simulations for 95 ns to generate putative ensemble of folded structures for the pbuE A-riboswitch aptamer at T = 310 K (see Methods). The MD-generated structures are then taken as the native structures in the coarse-grained simulations in which the RNA is represented using the SOP model.17
After the first 10 ns of molecular dynamics run, the root-mean-square deviation (RMSD) of the positions of the backbone nucleotides of the pbuE A-riboswitch aptamer does not change significantly (Fig. 2a). However, there are instances of larger fluctuations, which suggest that the native state ensemble generated in atomically detailed MD simulations is somewhat heterogeneous. Both P2 and P3 remain folded during the simulations as indicated by the stabilizing potential energies of the helices, calculated using the SOP energy function with MD snapshots as the native structures. For all the snapshots recorded at every 10 ps, the average difference in non-bonded energy between P2 and P3 is about ΔUnb = Unb,P2 − Unb,P3 = −3.25 kcal mol−1 with a fluctuation in energy, . The combined use of MD simulations and SOP representation of the aptamer shows that P2 is more stable than P3 in the pbuE A-riboswitch. For the add A-riboswitch the drift in RMSD (Fig. 2b) is less and the ΔUnbUnb = Unb,P3 − Unb,P2 is negative at all times indicating that P3 is more stable than P2. Thus, we surmise that for both the riboswitches the presence of tertiary interactions does not affect the stability of the paired helices.
Fig. 2.
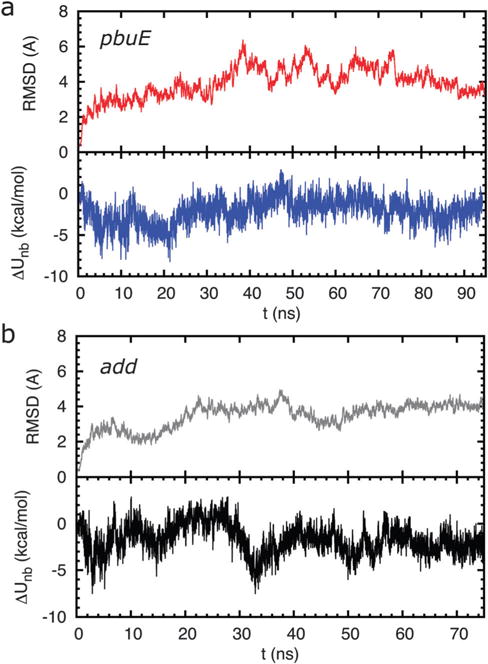
(a) Stability of the folded pbuE A-riboswitch aptamers inferred from all atom MD simulation. (Upper panel) time evolution of the root mean square deviation (RMSD) of backbone nucleotide positions. (Lower panel) fluctuations in the difference between non-bonded energies of helices P2 and P3, ΔUnb = Unb,P2 − Unb,P3, in the aptamer with the metabolite bound during the all atom molecular dynamic simulations. The curve suggests that the putative MD structures for pbuE A-riboswitches are stable. (b) Same as (a) except for the add A-riboswitch aptamer. Here, ΔUnb = Unb,P3 − Unb,P2.
Response of the pbuE A-aptamer to force
We take snapshots from the MD simulations saved at every 500 ps for t >10 ns, which results in a total of 168 structures, as the putative ensemble of native structures in coarse-grained pulling simulations. The average ΔU and its deviation for these chosen structures are similar to the values for all snapshots recorded. Hence, it is reasonable to study the stability of the helices using the ensemble of MD generated structures, assuming that the aptamer fluctuates around the average native structure in equilibrium.
The interplay of stability of helices P2 and P3 in modulating the folding landscape of the aptamers is illustrated by investigating the response of helices to a mechanical force. Among the 168 trajectories generated using the MD snapshots subsequently used in SOP simulations, the folding probability of P2 and P3 varies depending upon the precise starting conformation of the native state ensemble. For example, in the trajectory shown in Fig. 3a, at f = 13 pN, both helices P2 and P3 hop back and forth between the folded and unfolded states, while helix P2 spends more time in the folded state than P3. This shows that P2 is more stable than P3. The time traces of the molecular extension, R, and the free energy landscape (Fig. 3b and c) show three distinguishable folding intermediate states for the pbuE A-riboswitch aptamer at f = 13 pN. The aptamer switches between unfolded, P2 or P3 folded, and both P2 and P3 folded (P2/P3) states, with the corresponding extensions R around 21.5 nm, 16 nm, and 10 nm, respectively. The intermediate state at R ~ 16 nm indicates that only one helix is folded. The probability averaged over time that P2 is folded is ≈ 0.90 whereas the probability that P3 is intact is ≈ 0.10. The folding probability of P2 and P3 remaining intact varies when choosing different MD snapshots as the native structure.
Fig. 3.
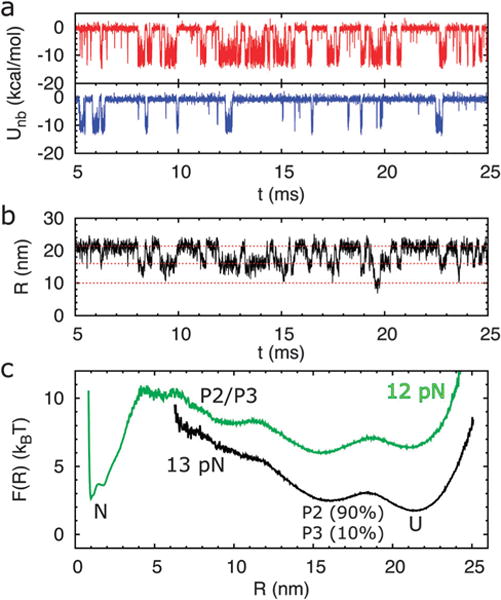
Coarse-grained pulling simulations for the pbuE A-riboswitch using MD generated structures. (a) The time traces of non-bonded energies of helices P2 (red line) and P3 (blue line) in a trajectory showing that P2 spends more time in the folded state than P3 for the pbuE A-riboswitch aptamer at f = 13 pN. (b) The time traces of the end-to-end distance, R, of the riboswitch for the trajectory in (a). (c) The free energy profile obtained based on the time traces for f =12 (green line) and 13 pN (black line). Interestingly, when f is increased by 1 pN from f = 12 to f = 13 pN the folded state is completely destabilized.
When f = 12 pN, the riboswitch switches to the folded state, which is the most stable state with a large unfolding free energy barrier (≈8 kBT). On an average, with the use of 168 different MD snapshots as native structures, we find that in the intermediate state containing only one folded helix, 60% of the time is spent in the P2 folded state, suggesting that P2 is more stable than P3 in the pbuE A-riboswitch. These results are in qualitative agreement with experiments.
We can define the free energy difference between the only-P2-folded and only-P3-folded state by the ratio, i.e., ΔΔG = −kBTln(FP2/FP3), and obtain the histograms of ΔΔG for all the trajectories (Fig. 4a and b). On an average the only-P2-folded state is more stable than the only-P3-folded state by about 0.5 kBT (an underestimate arising from potential inaccuracies in the all atom MD force fields) for the pbuE A-riboswitch aptamer. At f = 13 pN, the relative stability depends modestly on the pulling direction; about 45% of the trajectories show P2 folded more than P3 when pulling from the 5′-end, while the percentage becomes 73% when pulling from the 3′-end. Overall, the stability of P2 is larger than P3 for the pbuE riboswitch aptamer, which is in qualitative accord with the experimental results.10
Fig. 4.
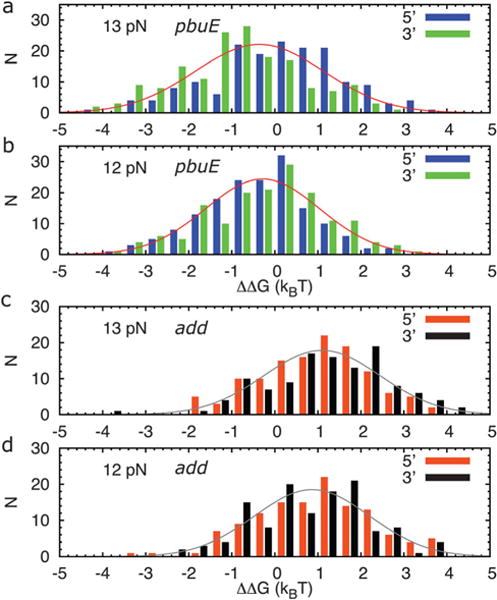
The histograms of the difference in the free energy difference between only-P2-folded and only-P3-folded states, i.e., ΔΔG = −kBT ln(FP2/FP3), for (a) a total of 168 structures for the pbuE A-riboswitch aptamer with forces, f = 13 pN and (b) f =12 pN, applied on either end of the aptamer in the coarse-grained simulations. (c) Same as (a) except for a total of 131 trajectories for the add A-riboswitch aptamer with forces, f = 13 pN and (d) f = 12 pN.
add A-riboswitch aptamer
For comparison and to complement our earlier studies based on the coarse-grained model,12 we also perform MD simulations for the add A-riboswitch aptamer for 75 ns starting with the crystal structure. As shown in Fig. 2b, the dynamics of the system becomes stationary after 10 ns. We take snapshots at every 500 ps for t > 10 ns as the native structures for subsequent use in coarse-grained simulations. The histograms of the difference in the folding probability between P2 and P3 for the 131 trajectories each 27 ms long also indicate a larger relative stability towards P3 (Fig. 4c and d). About three out of four trajectories have P3 spending more time folded than P2 with the pulling direction having little effect on the relative stability of the two helices. We find that the only-P3-folded state is more stable than the only-P2-folded state by about 1 kBT for the add A-riboswitch aptamer. This is opposite to the pbuE A-riboswitch aptamer, where the only-P2-folded state is more stable than the only-P3-folded state. Hence, despite the similar tertiary structures of pbuE and add A-riboswitch aptamers, the relative stabilities of P2 and P3 found in our simulations are different because of variations in the sequence.
Conclusions
The differences in the folding landscapes under tension between add and pbuE A-riboswitches (both bind purine) were explained based on the stability hypothesis12 according to which the order of unfolding is determined by the stability of the individual helices. Here, we have further established the validity of this proposal using a combination of all atom molecular dynamics and coarse-grained (CG) simulations. In particular, the multi scale simulations confirm that helix P2 is more stable than P3 in the pbuE adenine riboswitch aptamer, which is the opposite to that found in the add A-riboswitch aptamer. Despite the similarity of the aptamer structures, the sequence difference results in variations in the relative stability of helices P2 and P3. Surprisingly, the differences in the local contacts within helices are enough for our simple model to capture the relative stability of helices in add and pbuE A-riboswitch aptamers. However, further investigations of the conformations of the aptamer coupled with the downstream expression platform should be carried out to have a complete understanding of the mechanism underlying the functions of the purine riboswitches. We conclude with the following remarks.
A consequence of the stability hypothesis is that the relative probability of unfolding P3 in (using the free energies in Fig. 1a) the add A-riboswitch should be ~e2/(1 + e2) ≈ 0.9. From the histogram of ΔΔG, calculated using MD generated structures in CG simulation, this probability is ≈ 0.8, which is comparable to the estimate based on the stability hypothesis. A similar calculation based on the free energy given in Fig. 1b for the pbuE A-riboswitch predicts that the probability that P3 folds before P2 is only ≈ 0.04. Although the multi scale simulations are in qualitative agreement with experiments qualitatively, the combination of MD and CG simulations suggests that this probability is nearly ten times larger. We attribute the discrepancy to plausible deficiencies in the current nucleic acid force fields. Only recently tetraloop (four nucleobases) structures have been accurately predicted by significantly altering the current RNA force fields.18 Thus, we are only able to obtain qualitative agreement between experiments and simulations for the pbuE A-riboswitch, whereas our earlier predictions for the add A-riboswitch based on CG simulations12 agree quantitatively with single molecule pulling experiments.15 It also follows that currently CG model simulations are more accurate than atomically detailed simulations for nucleic acids.
The stability hypothesis for RNA assembly is similar to the ideas used to predict forced-unfolding of proteins19 where it was shown that the order of unfolding of proteins is determined by the stability of tertiary interactions associated with a given secondary structural element. In both proteins and RNA the f-dependent landscape is determined by the native topology. Because interactions favoring secondary structure formation are much greater than tertiary interactions in RNA, the f-dependent landscape is essentially determined by the relative free energies of isolated helices. This justifies the stability hypothesis.
The free energy profile in Fig. 3c could be used to obtain an approximate bound on the time scales in which switching of the region in P1 responsible for transcription control exerted by the pbuE A-riboswitch. An effective free energy barrier for this switch at f = 0 is ΔF‡(0) ≈ ΔF‡(f) + fΔX‡. In Fig. 3c, f = 12 pN, ΔF‡(f) ≈ 8 kBT, and ΔX‡ ≈ 2 nm, which gives ΔF‡(0) ≈ 14 kBT. The time scale for switching is . Using the estimate for the prefactor τ0 ≈ 1 μs (ref.20) we obtain τS ≈ 1.2 s. Upon binding adenine this time scale is about an order of magnitude greater. Synthesis of downstream nucleotides occurs at a rate of 20 nt s−1. Thus, the decision to terminate transcription must occur in a small window of time on the order of (2–4) seconds (depending on the length of transcript in the expression platform) before the metabolite binds. Thus, it is likely that the folded aptamer regulating transcription in the pbuE A-riboswitch cannot reach thermodynamic equilibrium as the number of folding transitions in the time window cannot exceed unity. We surmise that the function of the pbuE A-riboswitch is under kinetic control lending further support to the conclusion reached in single molecule pulling experiments.
Based on the stability hypothesis, we make a prediction for pulling experiments in a mutant of the add A-riboswitch. The main reason for the different energies of P2 between the two purine riboswitches is that there is one G–U and two G–C base pairs in P2 in the add A-riboswitch, whereas there are three G–C base pairs in P2 in the pbuE A-riboswitch. A U28C point mutation in the add A-riboswitch, resulting in three G–C base pairs in P2, would result in the secondary free energy of P2 to be −7.3 kcal mol−1. Thus, in the U28C mutant of the add A-riboswitch P2 would be more stable than P3 by about 1.1 kcal mol−1. As a consequence, we predict that the very order of unfolding of the add A-riboswitch would be reversed. The folding landscape of the U28C add A-riboswitch would be qualitatively similar to the WT pbuE riboswitch.
Methods
Our goal is to predict the structural basis of the free energy landscape differences between the add A-riboswitch aptamer and the pbuE A-riboswitch aptamer. Because the structure of the pbuE A-riboswitch aptamer is unavailable, we used the following multi scale computational strategy. To create Self-Organized Polymer (SOP) representation of the pbuE A-riboswitch aptamer, we generated an ensemble of equilibrated structures using all atom molecular dynamics simulations using the RNA segment for the pbuE A-riboswitch aptamer with the initial structure corresponding to the add A-riboswitch aptamer. Consistency between MD and coarse-grained simulations allows us to infer the robustness of our conclusions.
Self-organized polymer (SOP) model
To model the riboswitch aptamer, we use a modified form of the self-organized polymer (SOP) model17 that has been used with considerable success in describing complex processes ranging from folding21 to allostery in proteins22 and forced-unfolding of RNA.17 In addition, other studies have also established that coarse-grained models are successful in providing the dynamics and folding of riboswitches.23,24 In the simplest version of the SOP model, each nucleotide as well as the metabolite adenine is represented as a single interaction site. The potential energy of the aptamer in the presence of bound adenine is
| (1) |
where the energy functions of the aptamers are given by
| (2) |
with
| (3) |
and
| (4) |
The term VFENE in eqn (3) describes the chain connectivity with k = 2000 kcal mol−1 nm−2, R0 = 0.2 nm, ri,i+1 is the distance between two adjacent nucleotides i and i + 1, and is the distance in the native structure. The non-bonded interaction term, VNB, in eqn (4) accounts for the stabilizing forces between the nucleotides that are in contact in the native state. The interactions between the nucleotides that form non-native contacts are taken to be repulsive. Two nucleotides i and j are in native contact with Δij =1 (eqn (4)) if the distance rij between them in the native structure is within a cutoff distance, Rc = 1.3 nm, for |i − j| > 2. If rij exceeds Rc, then Δij = 0. The interaction between adenine and the aptamer, VAPT-AD, is taken to be,
| (5) |
We set εA as the interaction between adenine and the nucleotides that are in contact with adenine. In the native structure of the add adenine riboswitch, there are 7 nucleotides that are in contact with adenine. To prevent adenine from drifting away from the aptamer during the simulations, a restraining potential is added between the metabolite and U74.
We use two values for the parameter εh (see eqn (3)) depending upon whether the two nucleotides in native contact are engaged in a secondary or a tertiary interaction. If the two nucleotides are within a hairpin or helix, εh = εs, otherwise, εh = εt. From the largely hierarchical nature of the RNA folding process,25 it follows that the strength of the secondary interaction is greater than the tertiary interaction. In our simulations, we set εs = 0.7 kcal mol−1, and εt/εs = 1/2. The strength of the repulsive interaction is taken to be εl = 1.4 kcal mol−1 for non-native contacts. We chose σ = 0.7 nm, and σ⋆ = 0.35 nm for i, i + 2 pairs to prevent the flattening of the helical structure when the overall repulsion is large. Our previous work12 has shown that riboswitches and other RNA constructs17,26 subject to tension are accurately described using the chosen range of parameters.
Brownian dynamics
The dynamics of the system is described using the Langevin equation in the overdamped limit. The equation of motion for the ith nucleotide is
| (6) |
where γ is the friction coefficient, mi is the mass of nucleotide i, and Fi(t) is the random force, which satisfies
| (7) |
and
| (8) |
where the averages are over an ensemble of realizations or trajectories.
The integration step in the Brownian dynamics simulations is , where the typical value for τL for nucleotides is 4 ps,17 and the integration step size h = 0.03 τL. For the overdamped limit, we use γ = 100 τL−1, which approximately corresponds to the friction coefficient for a nucleotide in water.26 For a typical value of εh = 0.7 kcal mol−1, this results in an integration time step of about 14 ps. To unfold the aptamer, an external force is applied to the 5′-end of the aptamer, while the 3′-end is fixed.
All-atom molecular dynamics (MD) simulation
We used MD simulations to obtain approximate native structures for the pbuE adenine riboswitch aptamer for use in coarse-grained pulling simulations. The NAMD 2.6 molecular dynamics simulation package27 and CHARMM force field28 were used in all energy minimizations.
A total of 71 nucleotides of RNA with the metabolite, adenine, bound and 5 bound magnesium ions were taken from the crystal structure of the aptamer domain of the Vibrio vulnificus add A-riboswitch (PDB code: 1Y26).2 By exploiting the structural similarity between the two riboswitches, we threaded the sequence of pbuE A-riboswitch through the structure of the Vibrio vulnificus add A-riboswitch. We then added 60 sodium ions, with each placed around the phosphate group of the RNA backbone, to make the whole system charge neutral. The system was then solvated using the SOLVATE program in the VMD package29 in an explicit TIP3P30 periodically replicated water solvent box. A buffer of water around the solute of at least 15 Å in all directions was added, resulting in a total of 63 632 atoms in the system. While keeping the positions of RNA, metabolite adenine, and magnesium ions fixed, the water and sodium ions were allowed to move and the energy is minimized for 2000 cycles. Subsequently, the ions and the solvent were relaxed by performing molecular dynamics at constant volume, for 600 ps. In the first 200 ps, the temperature was increased from T = 0 K to T = 310 K gradually, and during the second 200 ps, the temperature remained at T = 310 K. In the final 200 ps, the temperature was reduced from T = 310 K to 0 K gradually.
Non-bonded interactions were smoothly switched to zero between 10 and 12 Å, yielding a cutoff radius of 12 Å. We used the particle-mesh Ewald algorithm for long-range electrostatic interactions with a grid spacing smaller than 1 Å.31 The integration time step in MD simulations was 2 fs. We used the SHAKE method32 for enforcing constraints. The energy of the system was then minimized by gradually releasing the positional restraint of RNA, the metabolite adenine, and magnesium ions in the following way: 1000 energy minimization cycles for each n in the harmonic positional restraints of 10n/4 kcal mol−1 Å−2, n = 4, 3, 2,1, 0, −1, −15, on RNA, adenine, and magnesium ions. We then heated the system from T = 0 K to T = 310 K for 2 ns without any restraint at constant volume, and then kept the system at fixed T = 310 K for 1 ns. The system was then equilibrated by performing molecular dynamics at a constant pressure of p = 1 atmosphere and a constant temperature of T = 310 K for 2 ns with the time step being 1 fs. Finally, we performed a 95 ns production run under constant N, p, and T conditions. The structures for use in the coarse-grained simulations were obtained from the production run. For reasons explained in the final section this procedure is only qualitatively reliable.
Acknowledgments
Part of this work was done while DT was a KIAS scholar. This work was supported in part by a grant from the National Institutes of Health (GML089685) to DT.
References
- 1.Winkler WC, Breaker RR. Annu Rev Microbiol. 2005;59:487. doi: 10.1146/annurev.micro.59.030804.121336. [DOI] [PubMed] [Google Scholar]
- 2.Serganov A, Yuan YT, Pikovskaya O, Polonskaia A, Malinina L, Phan AT, Hobartner C, Micura R, Breaker RR, Patel D. Chem Biol. 2004;11:1729. doi: 10.1016/j.chembiol.2004.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Serganov A, Nudler E. Cell. 2013;152:17. doi: 10.1016/j.cell.2012.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Edwards TE, Klein DJ, Ferre-D’Amare AR. Curr Opin Struct Biol. 2007;17:273. doi: 10.1016/j.sbi.2007.05.004. [DOI] [PubMed] [Google Scholar]
- 5.Mandal M, Breaker RR. Nat Struct Mol Biol. 2003;11:29. doi: 10.1038/nsmb710. [DOI] [PubMed] [Google Scholar]
- 6.Mandal M, Boes B, Barrick JE, Winkler WC, Breaker RR. Cell. 2003;113:577. doi: 10.1016/s0092-8674(03)00391-x. [DOI] [PubMed] [Google Scholar]
- 7.Guo Z, Thirumalai D, Honeycutt JD. J Chem Phys. 1992;97:525. [Google Scholar]
- 8.Goldstein RA, Luthey-Schulten ZA, Wolynes PG. Proc Natl Acad Sci U S A. 1992;89:9029. doi: 10.1073/pnas.89.19.9029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thirumalai D, Hyeon C. Biochemistry. 2005;44:4957. doi: 10.1021/bi047314+. [DOI] [PubMed] [Google Scholar]
- 10.Greenleaf WJ, Frieda KL, Foster DAN, Woodside MT, Block SM. Science. 2008;319:630. doi: 10.1126/science.1151298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Frieda KL, Block SM. Science. 2012;338:397. doi: 10.1126/science.1225722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lin JC, Thirumalai D. J Am Chem Soc. 2008;130:14080. doi: 10.1021/ja8063638. [DOI] [PubMed] [Google Scholar]
- 13.Lin JC, Hyeon C, Thirumalai D. J Phys Chem Lett. 2012;3:3616. doi: 10.1021/jz301537t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Anthony PC, Perez CF, Garcia-Garcia C, Block SM. Proc Natl Acad Sci U S A. 2012;109:1485. doi: 10.1073/pnas.1115045109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Neupane K, Yu H, Foster DAN, Wang F, Woodside MT. Nucleic Acids Res. 2011;39:7677. doi: 10.1093/nar/gkr305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zuker M. Nucleic Acids Res. 2003;31:3406. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hyeon C, Dima RI, Thirumalai D. Structure. 2006;14:1633. doi: 10.1016/j.str.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 18.Chen AA, Garcia AE. Proc Natl Acad Sci U S A. 2013;110:16820. doi: 10.1073/pnas.1309392110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Klimov DK, Thirumalai D. Proc Natl Acad Sci U S A. 2000;97:7254. doi: 10.1073/pnas.97.13.7254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hyeon C, Thirumalai D. Biophys J. 2012;102:L11. doi: 10.1016/j.bpj.2012.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Reddy G, Liu ZX, Thirumalai D. Proc Natl Acad Sci U S A. 2012;109:17832. doi: 10.1073/pnas.1201808109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hyeon C, Lorimer GH, Thirumalai D. Proc Natl Acad Sci U S A. 2006;103:18939. doi: 10.1073/pnas.0608759103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Whitford PC, Schug A, Saunders J, Hennelly SP, Onuchic JN, Sanbonmatsu KY. Biophys J. 2009;96:L7. doi: 10.1016/j.bpj.2008.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Feng J, Walter NG, Brooks CL., III J Am Chem Soc. 2011;133:4196. doi: 10.1021/ja110411m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Brion P, Westhof E. Annu Rev Biophys Biomol Struct. 1997;26:113. doi: 10.1146/annurev.biophys.26.1.113. [DOI] [PubMed] [Google Scholar]
- 26.Hyeon C, Thirumalai D. Biophys J. 2007;92:731. doi: 10.1529/biophysj.106.093062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. J Comput Chem. 2005;26:1781. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.MacKerell AD, Jr, Banavali N, Foloppe N. Biopolymers. 2001;56:257. doi: 10.1002/1097-0282(2000)56:4<257::AID-BIP10029>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 29.Humphrey W, Dalke A, Schulten K. J Mol Graphics. 1996;14:33. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 30.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J Chem Phys. 1983;79:926. [Google Scholar]
- 31.Darden T, York D, Pedersen L. J Chem Phys. 1993;98:10089. [Google Scholar]
- 32.Rickaert JP, Ciccotti G, Berendsen H. J Comput Phys. 1977;23:327. [Google Scholar]


