Spectral purity and tunability of terahertz quantum cascade laser sources based on intracavity difference-frequency generation

Difference frequency generation quantum cascade lasers are well-suited for applications requiring narrow-linewidth emitters.

Abstract

Terahertz sources based on intracavity difference-frequency generation in mid-infrared quantum cascade lasers (THz DFG-QCLs) have recently emerged as the first monolithic electrically pumped semiconductor sources capable of operating at room temperature across the 1- to 6-THz range. Despite tremendous progress in power output, which now exceeds 1 mW in pulsed and 10 μW in continuous-wave regimes at room temperature, knowledge of the major figure of merits of these devices for high-precision spectroscopy, such as spectral purity and absolute frequency tunability, is still lacking. By exploiting a metrological grade system comprising a terahertz frequency comb synthesizer, we measure, for the first time, the free-running emission linewidth (LW), the tuning characteristics, and the absolute center frequency of individual emission lines of these sources with an uncertainty of 4 × 10⁻¹⁰. The unveiled emission LW (400 kHz at 1-ms integration time) indicates that DFG-QCLs are well suited to operate as local oscillators and to be used for a variety of metrological, spectroscopic, communication, and imaging applications that require narrow-LW THz sources.

INTRODUCTION

Two decades after their invention (1), quantum cascade lasers (QCLs) have reached impressive performance levels in the mid-infrared (mid-IR; λ ≈ 2.5 to 30 μm) and terahertz (THz; 0.3 to 10 THz) spectral regions. Mid-IR QCLs can now operate in continuous-wave (CW) mode at room temperature (RT) with multiwatt output power and high wall-plug efficiencies exceeding 20% (2, 3). THz QCL heterostructures embedded in single-plasmon or double-metal waveguides have demonstrated lasing in the 1.2- to 5.4-THz frequency range (4), with peak output powers that can reach watt levels (5, 6). In the CW regime, THz QCLs have established themselves as versatile narrow-linewidth (narrow-LW) sources with applications in high-resolution spectroscopy, gas sensing, and heterodyne detection. To date, cryogenically cooled THz QCLs have shown high spectral purity with intrinsic LWs as low as ~100 Hz (7). Their typical free-running LWs are dominated by excess frequency noise, leading to broadening up to several hundred kilohertz (8–10). When frequency-stabilized, these sources demonstrate narrow LWs of 6.3, 20, and 30 to 60 kHz (8–13), depending on the quality of the reference and of the locking setup. Narrow-LW THz QCL sources are highly desired for a number of applications (14), including heterodyne detection for far-infrared astronomy, molecular frequency metrology (15), high-resolution coherent imaging, and telecommunications, where they can provide the carrier wave for broadband wireless links (16).

Despite the tremendous progress, the onset of temperature-activated longitudinal optical phonon scattering of electrons in the upper laser state, combined with the difficulty of achieving selective electron injection into the closely spaced laser states (17), still limits the operation of the best THz QCLs to temperatures of ~200 K in pulsed mode (18) and slightly below 130 K in CW operation (19). However, RT operation is highly desired for applications and largely simplifies any experimental setup.

To address the need for RT THz sources, an alternative approach has been implemented on the basis of intracavity difference-frequency generation (DFG) in mid-IR QCLs (20, 21). With the introduction of a Cherenkov phase-matching scheme for efficient THz extraction (22, 23), THz DFG-QCLs have made marked progress in the past 5 years (24, 25). This foundational approach has several appealing aspects: Because the intersubband transitions within the QCL material itself provide the χ² nonlinearity, the sources are monolithic and can be operated at RT, similar to other mid-IR QCLs; in addition, wide THz tunability can be obtained with only modest tuning of the mid-IR modes (26–29). Depending on the mid-IR pump spacing, THz emission can be varied in the entire 1- to 6-THz range and beyond (27, 28), with limitations set only by the material losses and reduction of THz DFG efficiency (30).

Despite the mentioned major advances, the THz emission of DFG-QCLs has so far only been characterized using low-resolution (~4 GHz) Fourier transform infrared (FTIR) spectrometers, and their emission LW is still unknown. Here, we report the LW measurement of a free-running THz DFG-QCL. By beating the output of the free-running DFG-QCL at approximately 2.58 THz with that of a free-space THz frequency comb synthesizer (FCS), we retrieve an upper limit for the DFG-QCL emission LW of 125 kHz at 20 μs and 400 KHz at 1 ms. Our work establishes THz DFG-QCLs as a viable alternative to THz QCLs for numerous applications that require narrow-LW emitters.

RESULTS AND DISCUSSION

THz DFG-QCL design and characterization

Details of the DFG-QCL structure are given in Methods. The active region of the devices used in this work was made up of two stacks of 20 In_0.53Ga_0.47As/In_0.52Al_0.48As quantum cascade stages. The stages, based on the bound-to-continuum active region design (30, 31), provide peak gain at λ₁ = 8.5 μm and λ₂ = 9.5 μm. The laser band structure was designed to have giant second-order optical nonlinearity, associated with intersubband transitions. The estimated nonlinearities for a THz DFG at 2.5 THz are |χ²| = 9.3 nm/V and |χ²| = 5.4 nm/V for the short-wavelength and long-wavelength active regions, respectively. Devices were processed into 2-mm-long, 12-μm-wide buried-heterostructure lasers with dual-frequency mid-IR distributed feedback (DFB) gratings along the laser waveguide. The DFB gratings were designed to select mid-IR pump wavelengths at approximately 8.47 and 9.11 μm to produce THz DFG emission at approximately 2.5 THz, within the optical bandwidth of the hot electron bolometer (HEB) used in the experiments. The front facet of the laser bar substrate was polished at 30° for the out-coupling of the THz Cherenkov DFG emission (22), whereas the back device facet was covered with a high-reflective coating with Al₂O₃/Ti/Au = 120 nm/10 nm/60 nm. The laser bars were then mounted in an epi-up configuration on a copper block and cooled in open-loop LN₂ cryostats for the initial characterization.

Figure 1 shows the measured emission data for a 2-mm-long, 12-μm-wide buried-heterostructure waveguide Cherenkov THz DFG-QCLs operated in CW mode at heat-sink temperatures T_H = 65 and 85 K, which we selected for this study. We note that, although our devices did not operate in CW mode at RT, THz DFG-QCL sources with lower threshold current density and better thermal packaging have recently demonstrated up to 14 μW of CW THz power output at RT (24).

Fig. 1. Emission spectra and power output of the DFG-QCL used in our study.

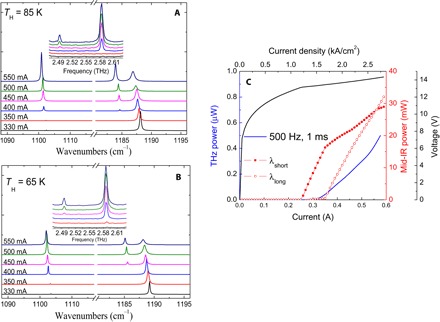
(A and B) FTIR emission spectra of the two mid-IR pumps and the resulting THz DFG, collected at heat-sink temperatures (T_H) of 65 K (A) and 85 K (B) in rapid-scan mode with a 0.125 cm⁻¹ (3.75 GHz) spectral resolution, plotted as a function of the driving current. Identical colors in the mid-IR and THz spectra correspond to identical driving current conditions. (C) Current-voltage and light-current characteristics of the mid-IR pumps and THz DFG for the device operated in CW mode at 85 K.

Figure 1A shows the FTIR spectra, obtained in rapid-scan mode with a spectral resolution of 0.125 cm⁻¹ (3.75 GHz), with the two mid-IR pumps and the THz DFG emission from the device. This device emitted a single THz frequency centered at approximately 2.58 THz at low pump currents; at pump currents above 450 mA, a second THz DFG emission line at 2.49 THz appeared in the spectra. A red shift in the frequency of the mid-IR pumps and in the THz difference frequency is observed as the bias current is increased. This dependence is attributed to an increase in the active region temperature as the pump current increases. Light-current and current-voltage characteristics of mid-IR and THz outputs are shown in Fig. 1 (B and C, respectively).

The temperature tuning and the thermal resistance of our device are determined by measuring the emission spectra in pulsed mode (400-ns pulses at 25-kHz repetition frequency) at T_H varying from 45 to 200 K. Under this pulsed operational regime, we can safely assume that the active region lattice temperature is nearly coincident with the T_H. The spectral positions of the mid-IR pumps and the THz difference frequency as a function of T_H are given in Fig. 2 (A and B, respectively). By comparing the spectral positions of the mid-IR pumps in Figs. 1 and 2A, we can retrieve the thermal resistance of our device, which is approximately 6.6 K/W at 45 K and 7.9 K/W at 85 K.

Fig. 2. Frequency tuning.

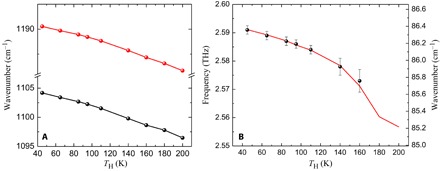
Dependence of mid-IR pump frequencies (A) and THz difference frequency (B) of the THz DFG-QCL on the T_H. The device was operated in pulsed mode, as described in the main text. The solid line in (B) represents the frequency difference of the two mid-IR peaks as extracted from (A), and the round symbols with error bars indicate the experimentally measured THz peak positions.

Detection of the beating signal with a THz FCS and LW characterization

To probe the LW of the THz emission from the device, we investigated the beat note signal arising from the beating between the THz emission from the DFG-QCL and the free-space THz FCS. The experimental setup is shown in Fig. 3A.

Fig. 3. Experimental setup.

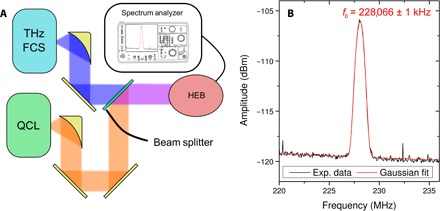
(A) Schematic of the experimental setup: The THz frequency comb is generated in a MgO-doped lithium niobate waveguide by optical rectification with Cherenkov phase matching of a femtosecond mode-locked fiber laser, working at 1.5-μm wavelength. The optical rectification process produces a zero-offset free-space THz comb with a repetition rate of approximately 250 MHz of the pump femtosecond laser. The THz frequency comb and the emission from the DFG-QCL were overlapped on the sensor element of the HEB with a 250-MHz electrical bandwidth. The beat note signals of the THz DFG-QCL emission with the nearby frequency comb lines were analyzed by an FFT spectrum analyzer, having a 40-MHz real-time bandwidth. (B) Typical beat note spectrum observed on a spectrum analyzer for 2-ms integration time. The value of f_b obtained by fitting is used in Eq. 2 for the determination of the QCL emission frequency f_QCL.

The THz frequency comb is generated in a MgO-doped lithium niobate waveguide by optical rectification in the Cherenkov configuration using a femtosecond mode-locked fiber laser emitting around 1.5 μm at a repetition rate (f_rep) adjustable around 250 MHz. The optical rectification process produces a zero-offset free-space THz comb with a spectral content broader than the THz QCL tunability range (11). The frequency (f_n) of each tooth of the THz FCS can be parameterized as

$${\mathit{f}}_{\mathit{n}}=\mathit{n}\times {\mathit{f}}_{\text{rep}}$$ (1)

where n is the comb tooth order.

Both the THz DFG-QCL and reference THz comb beams were collected and collimated by a set of 90° off-axis parabolic mirrors with an equivalent focal length of 25.4 mm. The two beams were then combined on a Mylar film, which acted as a THz beam splitter, and were then sent to the HEB (Scontel model RS 0.3–3T-1), with a 250-MHz electrical bandwidth. The electrical signal from the HEB was sent to a fast Fourier transform (FFT) real-time spectrum analyzer (Tektronix RSA5106A). Within the HEB bandwidth, it is possible to detect both the signal at 250 MHz, generated by the intermodal beating of the THz comb, and the pair of beat notes generated by heterodyning the THz DFG-QCL with the closest right and left comb teeth.

Figure 3B shows one of these beat note signals. In this case, the beating is with the right (higher-frequency) comb tooth, and the beat note frequency (f_b) is given by

$${\mathit{f}}_{\mathrm{b}}=\mathit{N}{\mathit{f}}_{\text{rep}}-{\mathit{f}}_{\text{QCL}}$$ (2)

where f_QCL is the THz DFG-QCL frequency, and N is the order of the closest THz FCS tooth involved. The beat note spectrum in Fig. 3B can be described by a Gaussian function, whose profile has been used to fit each line shape. Because the LW of the THz comb tooth involved in the beating process (~130 Hz at 1 s, as experimentally demonstrated) (11, 15) is negligible with respect to the DFG-QCL THz emission LW, the full width at half maximum (FWHM) of the Gaussian profiles provides an accurate quantitative estimation of the THz emission LW of our device. Moreover, the central value of the beat note frequency, as given by the fit, is determined with an uncertainty of about 1 kHz and is used to retrieve the absolute center frequency of the QCL emission, as explained in the next section.

The LW of the 2.58-THz emission line of the CW-operated device was measured as a function of the observation time t at two different T_H (45 and 78 K), as shown in Fig. 4A. The laser was operated with a pump current of 450 mA for both measurements by using an ultralow noise current driver (ppqSense model QubeCL05). The range of analysis is limited at short time scales at 20 μs, corresponding to the acquisition time of the single FFT spectrum in which the beat note width starts to be limited by the resolution bandwidth of the instrument (in this case, 100 kHz). At this time scale, we measure an upper limit of the QCL LW of 125 kHz.

Fig. 4. LW measurements.

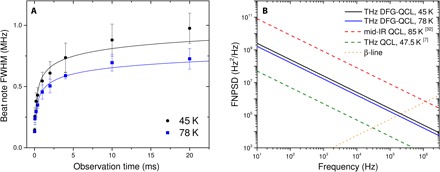
(A) Width of the beat note at different time scales measured at two different operating temperatures of the device. The use of an FFT spectrum analyzer allows retrieval of the beat note spectra over different integration times and therefore evaluation of the THz DFG-QCL emission LW at different time scales (ranging from 20 μs to approximately 20 ms). Solid lines are fits with a logarithmic function. The logarithmic dependence of the LW on time confirms the 1/f nature of the QCL frequency noise (see Methods for details). (B) Reconstruction of the FNPSD of the THz DFG-QCL emission. The plots have been obtained by inverting the approach developed by Di Domenico et al. 36, as discussed in Methods. This procedure allows retrieving the FNPSD for frequencies where it is larger than the β-line [8/π²ln(2)f, dotted in the lower part of the graph. Given the smallest time scale of 20 μs of our setup, our measurements do not include frequencies higher than 50 kHz. The dashed red and green lines refer to the measurements performed by Bartalini et al. (34) and Vitiello et al. (7) for the mid-IR and THz QCLs, respectively, whereas the solid lines refer to the measurements presented in this work.

The data in Fig. 4 show that the LW of THz emission from our device is reduced as the operating temperature increases. This trend is consistent with the previously observed narrowing of the emission LW of mid-IR QCLs at higher temperatures due to the reduction of the coupling efficiency of the spontaneous emission to the pump modes as the mid-IR gain spectrum broadens with temperature (32, 33).

The logarithmic dependence of the LW on t indicates the presence of a 1/f noise component in the frequency noise spectrum between 1 Hz and 1 kHz that likely comes from the typical “pink” frequency noise of the mid-IR pumps of our DFG-QCLs (32, 34). This is also confirmed by the noise decrease at increasing temperatures (see Fig. 4A), in agreement with previous experiments on the 1/f noise of mid-IR QCLs (32, 33, 35) that showed a similar trend.

A quantitative comparison with previous LW measurement reports of mid-IR QCLs can help in understanding the possible correlations between the emission LW of the mid-IR pumps and the THz emission LW. To this purpose, we applied the inverse method proposed by Di Domenico et al. (36) to the data in Fig. 4A to retrieve the frequency noise power spectral density (FNPSD) of our devices (see Methods for details). The FNPSD of THz DFG-QCLs can be directly compared with the FNPSDs of a THz QCL operating at 47.5 K (7) and of a mid-IR QCL operating at 85 K (34), as shown in Fig. 4B. The plot shows that the FNPSD of the DFG-QCL, even in the upper edge of the investigated temperature range (T_H = 45 to 85 K), is almost one order of magnitude lower than that of the mid-IR QCL. The reduction in the emission LW of THz DFG can be explained by the correlation between the phase/frequency noises of the two mid-IR pumps of our device that are, in part, compensated by the DFG process. On the other hand, the FNPSD of a single-mode bound-to-continuum THz QCL exploiting a single plasmon waveguide shows a significantly narrower LW (by approximately a factor of 7). Nevertheless, the reported measurements indicate that the LW of THz DFG-QCLs is already suitable for heterodyne THz detection, and we expect that it can be further reduced with frequency/phase stabilization. Note that no significant dependence of the LW on the driving current is evident.

Absolute emission frequency and tuning coefficients

Equation 2 allows us to determine the absolute frequency of each of the two THz emission peaks in the spectra shown in Fig. 1 and to perform high-resolution studies of the dependence of the emission frequency on the DFG-QCL operating conditions. The measurement is performed by driving the QCL at a current of 540 mA and a T_H of 75 K, for both modes independently. First, by changing f_rep and by measuring f_b, at a fixed value of f_QCL, the value of N can be retrieved, by fitting the data with Eq. 2, as shown in Fig. 5A (see Methods for details). For the first mode, the fit returns the parameter N₁ = 10,328.27 (±0.47), allowing the determination of the order of the comb tooth involved in the beating: N₁ = 10,328 (for the second mode, N₂ = 9974 is obtained). Once N is determined, the same Eq. 2 allows for the calculation of the absolute frequency of the free-running QCL from the measurement of f_b. The value of Nf_rep is known with an accuracy of the order of 100 Hz, whereas f_b is given by the center frequency of the Gaussian fit (see Fig. 3B) with a 1-kHz uncertainty. The resulting relative accuracy on the QCL frequency is therefore on the order of 4 × 10⁻¹⁰. As an example, the absolute center frequency of the first mode shown in Fig. 3B is ν₁ = 2,581,470,537 (±1) kHz.

Fig. 5. Beat note frequency measurements.

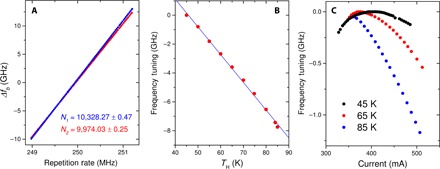
(A) Frequency of the beat note f_b, plotted as a function of the THz frequency comb repetition rate, while keeping the QCL driving current at 540 mA and the T_H fixed at 75 K. This measurement is used for the determination of N. (B) Frequency tuning of the 2.58-THz emission line of the DFG-QCL as a function of the QCL T_H, measured while keeping the QCL driving current fixed at 540 mA. The 2.49-THz emission line shows a similar dependence. (C) QCL frequency tuning of the 2.58-THz emission line as a function of the driving current at different T_H. The 2.49-THz emission line shows a similar dependence.

Figure 5B shows the tuning of the THz emission frequency of the first mode as a function of T_H for the CW operation with a 500-mA pump current. Measurements were performed while varying T_H from 45 to 85 K, which corresponds to QCL waveguide core lattice temperatures varying from ~90 to 140 K, using the device thermal resistances calculated previously. The observed temperature dependence of the THz spectral position is nearly linear with a slope coefficient of about −193 MHz/K. This value agrees with the THz frequency dependence deduced from the data in Fig. 2B for the same range of laser core temperatures.

Figure 5C shows the dependence of the frequency of the first THz mode on device pump current. Surprisingly, for the device operating at T_H = 45 K, the THz emission frequency initially blue-shifts with a tuning rate of about 3.3 ± 0.2 MHz/mA, when the injection current is slightly above the laser threshold. A turning point is visible at ~450 mA, and then, the DFG-QCL frequency red-shifts with a tuning coefficient of approximately −2.16 ± 0.07 MHz/mA. At 65 K, the inversion point is shifted toward the lower current. By further increasing the T_H to 85 K, the data show a monotonic decrease in THz frequency with pump current, with a slope of approximately −6 MHz/mA.

The observed dependence of the THz frequency on pump current cannot be explained by considering only the ohmic heating of the device core, which would predict a monotonic decrease in the THz frequency with a slope of approximately −17 to −20 MHz/mA. The value is obtained using the measured temperature tuning coefficient of −193 MHz/K, the thermal resistance of 6.6 to 7.9 K/W deduced previously, and the current-voltage relation characteristic of the device shown in Fig. 1. The observed trend is likely related to the gain dynamics behind the active region architecture. In semiconductor lasers, the refractive index variations (and corresponding emission frequency variations) due to the gain change with pump current can be estimated via the LW enhancement factor (α_e) (37). Unlike diode lasers, the LW enhancement factor of QCLs can be either positive or negative, depending on the position of the emission frequency relative to the gain peak and the dynamics of the gain spectrum (38–41). Although no precise correlation can be found with the measured FTIR spectra because of the inherent resolution limits, we can tentatively ascribe the different tuning trends to the different values of the α_e for the two mid-IR pumps. Further investigation of this effect will be performed in the future by combining high-resolution mid-IR and THz spectral measurements.

CONCLUSIONS

In conclusion, by assessing the free-running LW, the tuning characteristics, and the absolute frequency of a THz DFG-QCL via a high-resolution heterodyne technique, we have demonstrated, for the first time, that CW THz DFG-QCLs are suitable as metrological tools for high-resolution spectroscopy at THz frequencies and as local oscillators for heterodyne detection. Furthermore, the accuracy of the used technique allowed the unveiling of the current- and temperature-induced tuning, providing relevant information on building low-chirp and low–frequency noise THz emitters by a novel design of the gain media for these devices.

MATERIALS AND METHODS

Device design

The laser structure was grown on a 350-μm-thick semi-insulating InP substrate by a metal organic vapor phase epitaxy system. The growth started with the 400-nm-thick current injection layer doped to 1 × 10¹⁸ cm⁻³, followed by the 5-μm-thick InP lower cladding layer doped to 1.5 × 10¹⁶ cm⁻³, the 200-nm-thick In_0.53Ga_0.47As waveguide layer, the 2.6-μm-thick active region made of two 20-period stacks of quantum cascade stages, and the 300-nm-thick In_0.53Ga_0.47As DFB grating layer. Both In_0.53Ga_0.47As layers were doped to 1.5 × 10¹⁶ cm⁻³. The layer sequence of the short-wavelength stage (bottom stack), starting from the injection barrier, is 4.1/1.8/0.7/5.5/0.9/5.3/1.1/4.8/ 1.5/3.7/1.6/ 3.5/1.6/3.3/1.8/3.1/2.0/2.9/2.4/2.7/2.6/2.7/3.0/2.7, where the layer thickness is given in nanometers. The layer sequence of the long-wavelength stage (top stack) is 3.8/2.0/0.9/6.0/0.9/5.9/1.0/5.0/1.1/4.0/1.5/3.4/1.5/3.3/1.6/3.0/1.9/3.0/2.3/3.1/2.5/3.2/2.9/3.0. The bold and underlined fonts denote the barrier and doped (Si = 1.2 × 10¹⁷ cm⁻³) layers, respectively. A 350-nm-deep first-order mixed DFB grating structure (31) was then implemented in the DFB grating layer and (in part) the device active region using electron-beam lithography and dry etching. The estimated DFB coupling coefficient was 22 cm⁻¹ for both mid-IR pumps. The 12-μm-wide ridges were defined via wet etching and processed into buried heterostructures by lateral overgrowth of an Fe-doped semi-insulating InP layer for surface planarization. The growth was finalized with the 5-μm-thick InP cladding layer doped to 1.5 × 10¹⁶ cm⁻³ and the 15-nm-thick In_0.53Ga_0.47As contact layer doped to 1 × 10¹⁹ cm⁻³. We used the side-injection scheme for lateral current injection and electroplated 5-μm-thick gold on top of our devices for efficient heat extraction.

Determination of the order N of the comb tooth beating with the DFG-QCL

Equation 2 allows one to determine the absolute center frequency of the QCL emission, following the procedure described below. First, the T_H and the driving current of a THz DFG-QCL were stabilized to fix the spectral positions of the THz emission lines from the device. The laser emission was then combined with the FCS emission and sent to the HEB.

Following Eq. 2, we considered a beating involving the QCL and a comb tooth at higher frequency. The same procedure could be adopted in the case of a tooth at lower frequency, by changing the sign of f_b. Because we restricted the beat note observation window to the 125- to 250-MHz range and because the frequency spacing in the THz comb is approximately 250 MHz, the observed beat note was produced by the beating of the DFG-QCL emission line with the second closest THz FCS line, labeled with the index N. To determine N, we acquired the linear frequency shift of the beat note f_b while tuning the repetition rate f_rep of the THz FCS pump laser in a range of approximately ±0.4% around a center frequency of 250 MHz (specifically, f_rep varies approximately from 249 to 251 MHz). The spectral positions of the comb lines shifted accordingly by as much as ±0.4%, and the beat note of the Nth comb mode with the laser line might change by as much as 20 GHz, largely exceeding the 250-MHz HEB detector electrical bandwidth. Nevertheless, it is always possible to indirectly retrieve the frequency of this beat note by observing the transition from the beat note of the laser line with the Nth comb mode to the beat note involving the N − 1, N − 2,… or N + 1, N + 2,… modes of the comb (see Fig. 6).

Fig. 6. Order N determination.

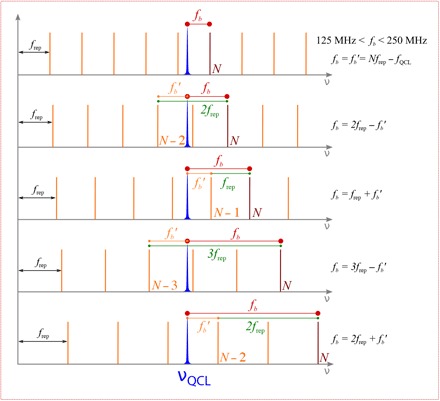
Schematic representation of the process used to retrieve the dependence of f_b on f_rep by measuring the beat notes in the 125- to 250-MHz range.

In this way, we could determine the variation of the beat note frequency f_b between the THz DFG-QCL line and the Nth mode of the THz FCS as a function of f_rep. The results are shown in Fig. 5A. The unknown index N was then determined by fitting the results in Fig. 5A with Eq. 2 and rounding to the nearest integer. We note that the uncertainties in the fit parameters are reduced as the variation of f_rep increases; hence, we varied the value of f_rep over the entire range possible in our FCS system.

Calculation of the 1/f noise level from the LW measurements

Di Domenico et al. (36) provided a simplified method for retrieving the LW of any laser source over a given observation time τ₀ from its FNPSD [S(f)]. According to this procedure and assuming a monotonic trend for the FNPSD, the laser LW δν(τ₀) (FWHM) is recovered by a simple integration of S(f)

$$\mathrm{\delta }\mathrm{\nu }({\mathrm{\tau }}_0)=\sqrt{8\text{ln}(2){\displaystyle {\int }_{{\mathit{f}}_0}^{{\mathit{f}}_{\mathrm{l}}}}\mathit{S}(\mathit{f})\mathit{d}\mathit{f}}$$ (3)

where the lower bound of the integral, f₀, is 1/τ₀, and the upper bound of the integral, f_l, is defined as the frequency at which the FNPSD crosses the so-called β-separation line

$$\mathit{S}({\mathit{f}}_{\mathrm{l}})=\frac{8\text{ln}(2)}{{\mathrm{\pi }}^2}\cdot {\mathit{f}}_{\mathrm{l}}$$ (4)

The procedure well approximates the true value only if the following condition is fulfilled

$$\mathit{S}({\mathit{f}}_0)>\frac{8\text{ln}(2)}{{\mathrm{\pi }}^2}\cdot {\mathit{f}}_0$$ (5)

Assuming that in the explored frequency range (10 Hz to 10 kHz), the FNPSD of the laser has a flicker-type origin [that is, S(f) = A/f], Eq. 3 gives a logarithmic-type function that can be used to fit the experimental values δν(τ₀) of the laser LW at different time scales (Fig. 4A), thus allowing us to determine the parameter A. Figure 4B shows the two flicker-type functions that reproduce, via Eq. 3, the experimental LWs of our device operated at 45 and 78 K, together with the two flicker-type functions that directly fit the experimental FNPSDs measured from a mid-IR QCL operating at 85 K (34) and a THz QCL operating at 47.5 K (7). Figure 4B allows the a posteriori check of the validity of the condition in Eq. 5. The crossing point with the β-separation line falls above 10 kHz, which validates the model assumptions for the explored frequency range of 10 Hz to 10 kHz.