Reservoir Pressure Analysis of Aortic Blood Pressure – an in vivo study at five locations in humans

Abstract

Introduction

The development and propagation of the aortic blood pressure wave remains poorly understood despite its clear relevance to major organ blood flow and potential association with cardiovascular outcomes. The reservoir waveform model provides a unified description of the dual conduit and reservoir functions of the aorta. Reservoir waveform analysis resolves the aortic pressure waveform into an excess (wave related) and reservoir (capacitance related) pressure. The applicability of this model to the pressure waveform as it propagates along the aorta has not been investigated in humans.

Methods

We analysed invasively acquired high-fidelity aortic pressure waveforms from 40 patients undergoing clinically indicated coronary catheterisation. Aortic waveforms were measured using a solid-state pressure catheter at 5 anatomical sites: the ascending aorta, the transverse aortic arch, the diaphragm, the level of the renal arteries and at the aortic bifurcation. Ensemble average pressure waveforms were obtained for these sites for each patient and analysed to obtain the reservoir, Pr(t), and the wave related excess, Px(t), pressures at each aortic position.

Results

SBP increased at a rate of 2.1 mmHg per site along the aorta while DBP was effectively constant. Maximum Pr decreased slightly along the aorta (changing by only -0.7 mmHg per site) while the magnitude of Px increased from the proximal to distal aorta (+4.1 mmHg per site, P<0.001). The time, relative to the start of systolic upstroke, of the occurrence of the maximum excess pressure did not vary along the aorta. Of the parameters used to derive the reservoir pressure waveform the systolic and diastolic rate constants showed divergent changes with the systolic rate constant (ks) decreasing and the diastolic rate constant (kd) increasing along the aorta.

Conclusions

This analysis confirms the proposition that the magnitude of the calculated reservoir pressure waveform, despite known changes in aortic structure, is effectively constant throughout the aorta. A progressive increase of excess pressure accounts for the increase in pulse pressure from the proximal to distal aorta. The reservoir pressure rate constants seem to behave as arterial functional parameters. The accompanying decrease in ks and increase in kd are consistent with a progressive decrease in aortic compliance and increase in impedance. The reservoir pressure waveform therefore provides a heuristic description that might have utility in understanding the generation of central BP and in specific cases might have clinical utility.

Introduction

The physiology of aortic pressure propagation and its dysfunction in disease states is of considerable potential clinical significance. Indeed central blood pressure (cBP) has been suggested to better predict cardiovascular and cerebral events than traditionally measured brachial BP^1–4. Derangements in cBP may also be associated with excessive pressure propagation to more distal arteries with associated pathology including renal dysfunction amongst other common pathologies^5–7. Aortic root BP is a determinant of the response of coronary blood flow to adenosine both pre- and post-angioplasty and therefore is a likely determinant of impaired cardiac function and coronary flow reserve in addition to its well-known association with left ventricular hypertrophy⁸. An enhanced understanding of the mechanisms underlying central aortic pressure generation and the propagation of the pressure wave distally is a necessary prerequisite for the improved management of chronic medical conditions including stroke, chronic coronary syndromes and renal disease.

Traditional paradigms of aortic pressure generation are based on the assumption that aortic pressure is the sum of a single forward-travelling and a single backward-travelling reflected pressure waveform⁹. More recent theories have modified this concept and stressed the relevance of increased proximal aortic stiffness and aortic diameter, accompanied by decreased proximal impedance mismatch as being more relevant in determining the magnitude of aortic BP than reflected wave phenomena⁵.

An alternative approach to describing central aortic function is provided by the reservoir-wave hypothesis. This heuristic hypothesis states that it may be useful to treat the aortic pressure waveform, P(t), as the summation of a reservoir pressure waveform, Pr(t), that accounts for the net compliance of the arteries, and an excess pressure waveform, Px(t), that is determined by local waves.¹⁰ Implicit in this hypothesis is the assumption that Pr(t) is made up from myriad minuscule forward and backward waves. These derive from the forward travelling waves generated in the aortic root by the left ventricle, but are modified as they travel through the arterial circulation by reflection and re-reflection¹¹. The reservoir-wave hypothesis was developed to explain experimental observations in the canine circulation¹² where it has been shown to resolve a number of anomalies that arise in traditional impedance based analysis. The first anomaly is the observation that the forward and backward pressure waveforms are large and equal in magnitude during late diastole^{12, 13}; this assumption is invoked to explain the exponentially decreasing fall in pressure at a time when the flow rate is negligible. These large ‘standing’ waves, if present, should however be evident in transient conditions such as in the presence of ectopic or missing beats when ‘standing’ waves have not had time to die away; in fact it is regularly observed that the exponential fall in pressure continues smoothly from late diastole into the prolonged period before the next, delayed, systole. One of the advantages of the reservoir pressure concept is that virtually all of the measured pressure during diastole is attributed to Pr so that the excess pressure during diastole is very close to zero, matching the diastolic flow^{10, 13, 14}. This obviates the need for the invocation of a large, self-cancelling backward pressure waveform during diastole to account for the fall in pressure while the flow is zero.

Another inconsistency is the observation that the foot of the backward-travelling wave calculated from measurements at different sites along the aorta occurs earlier at the proximal sites than at the more distal sites ¹⁵. This implies that the backward-travelling wave appears to be travelling anomalously in the forward direction.

We and others have suggested that central pressure waveform morphology may be due to cardiac or left ventricular outflow tract influences to a greater extent than to effects related to distal wave reflection. Our earlier results relating to the systolic inflection point, traditionally taken as the temporal indication of the arrival back in the central aorta of a reflected pressure wave during systole, were not consistent with the wave reflection model, occurring later at more distal sites rather than earlier as would be expected if it was due to a backward-travelling wave¹⁵. Similarly, in a meta-analysis performed by Baksi et al, the timing of the systolic pressure wave inflection point was not found to shift markedly from diastole to systole with ageing¹⁶. Other modelling studies have also challenged the contention that pressure wave reflection is the predominant mechanism driving pressure wave augmentation, instead suggesting left ventricular outflow and local vessel mechanical properties may play an important role ^{17, 18}.

Potential conceptual advantages of the reservoir pressure model include that reservoir pressure is affected by global cardiovascular properties, for example total compliance and net resistance, whereas excess pressure varies with location and could be a sensitive indicator of local conditions or focal pathology. Utilisation of these differences may provide useful clinical insight.¹⁹

It is possible to derive the reservoir pressure using only the local measured pressure without need of the clinically more difficult measurement of local flow.²⁰ This pressure-only reservoir pressure algorithm depends on the assumptions that the reservoir pressure waveform is uniform as it propagates throughout the arteries and that the flow waveform at the aortic root is proportional to the excess pressure waveform ²¹. Excess pressure Px(t), defined as the difference between P(t) and Pr(t), may be potentially a better indicator of local wave behaviour because the complexities due to the global storage and release of blood associated with compliant arteries is accounted for by the reservoir pressure. Neither of these assumptions have been tested in the human aorta.

We therefore hypothesised that application of reservoir pressure analysis to the recorded waveforms from well-defined aortic levels may provide further insight into the underlying mechanism of pressure wave propagation in the aorta.

Methods

Forty subjects, 26 male, were studied at the time of coronary angiography (32 subjects) or percutaneous coronary intervention (8 subjects) at MonashHeart in Melbourne, Australia. The study was approved by the Institutional Human Research and Ethics Committee and performed in accordance with institutional guidelines. Participants gave written informed consent. All subjects were in sinus rhythm at the time of the study. Pulse wave analysis of these results has been reported¹⁵.

Data acquisition

Data were acquired following completion of the clinically indicated procedure. Aortic waveforms were acquired using a 2 French Millar Mikro-tip® catheter transducer introduced via a 6 French multipurpose or right coronary guiding catheter positioned at the aortic root under fluoroscopic control. The Millar transducer was positioned just distal to the tip of the guiding catheter. Waveforms were recorded at a sampling rate of 2000 Hz to Chart for PowerLab^® (ADInstruments, Australia), decimated to 200 Hz for analysis. Following the acquisition of 30 seconds of data from the aortic root, the guiding catheter and Millar transducer were pulled back together and similar data were recorded at the level of the transverse aortic arch, the diaphragm, the renal arteries and at the aortic bifurcation sequentially. All positions were confirmed by fluoroscopy, and the levels of the renal arteries and aortic bifurcation were determined by angiography. The physical distance between recording sites was measured by the use of a marker catheter. The electrocardiogram was recorded simultaneously with all pressure measurements. Mean arterial pressure (MAP) was calculated as the integral mean over the ensemble average pressure cycle.

Ensemble averaging and calculation of the reservoir pressure

An automatically generated ensemble average of individual cardiac cycles was used in analysis. The cycle averaged SD of the ensemble averages was 4.4 mmHg which did not vary by site. The time of end of systole, Tn, was determined as the time of the minimum dP/dt after the systolic (peak) pressure. The average duration of the cardiac period (T) is derived from the fundamental peak of the power spectrum of the time series from which the ensemble averages were calculated.

The reservoir pressure, Pr(t), was calculated from the ensemble average measured pressure, P(t). The algorithm assumes that Pr satisfies overall conservation of mass

$$\frac{d{P}_r}{dt}+k_d(P_r-P_{\infty })=\frac{Q_{in}}{C}$$ (1)

kd is the diastolic rate constant (the reciprocal of the diastolic time constant τ = RC, where R is the net resistance to flow through the microcirculation and C is the net compliance of the arteries). Qin is the volume flow rate into the aortic root and P_∞ is the asymptote of the diastolic pressure fall-off. If we further assume that Qin = ζPx, where ζ is a constant related to the characteristic impedance then Equation. 1 can be written

$$\frac{d{P}_r}{dt}+k_d(P_r-P_{\infty })=k_s(P-P_r)$$ (2)

where ks is the systolic rate constant (the reciprocal of ζC). This first-order linear differential equation can be solved as:

$$P_r=e^{-(k_s+k_d)t}{\displaystyle \underset{0}{\overset{t}{\int }}P(t^{\prime })}{e}^{(k_s+k_d)t^{\prime }}d{t}^{\prime }+\frac{k_d}{k_s+k_d}(1-e^{-(k_s+k_d)t})P_{\infty }$$ (3)

The diastolic parameters kd and P_∞ are obtained first by fitting an exponential curve to P during diastole and ks is obtained by minimising the square error between P and Pr obtained over diastole.

Statistical analysis

All continuous variables are presented as their mean±SD, or graphically as the mean ± standard error of the mean. Significance was taken as p < 0.05. The agreement between parameters describing the P, Pr and Px waveforms was summarised using the Intraclass Correlation Coefficient (ICC) function (Stata 13.1, StataCorp, Texas) derived from a linear mixed model analysis with participant as a random effect and location included as ordinal fixed effect rather than a continuous variable. This is appropriate to our data because the aortic sites were defined relative to anatomical locations, not measured distances. Because the beta coefficient (slope) is dimensional (with the same dimensions per unit ordinal scale increase in location as the intercept) it is useful to define the % slope as percentage of the intercept to give a measure of the relative size of the variation in the parameter from site to site. Further statistical analysis was performed using SPSS 11.0 for Windows (SPSS Inc) and Stata (StataCorp, Texas).

Results

Subject characteristics are described in Table 1 and are representative of individuals presenting for coronary investigation at MonashHeart. Participants were predominantly male (65%), with a mean age of 65 years and a high prevalence of hypertension (55%). An automatically generated ensemble average of individual cardiac cycles was used in the analysis.

Table 1. Subject Characteristics.

Number	40
Male Gender, n (%)	26 (65%)
Age (years)	65±12
Height (m)	1.70±0.08
Weight (kg)	79±14
Body Mass Index (kg/m2)	28±5
Percutaneous Coronary Intervention, n (%)	8 (20%)
Smoking (Current) , n (%)	4 (10%)
Hypertension, n (%)	22 (55%)
Diabetes Mellitus, n (%)	9 (23%)
Hypercholesterolaemia, n (%)	34(85%)
Family History CVD, n (%)	9(23%)

Continuous variables are mean ± SD

Parameters describing the measured pressure

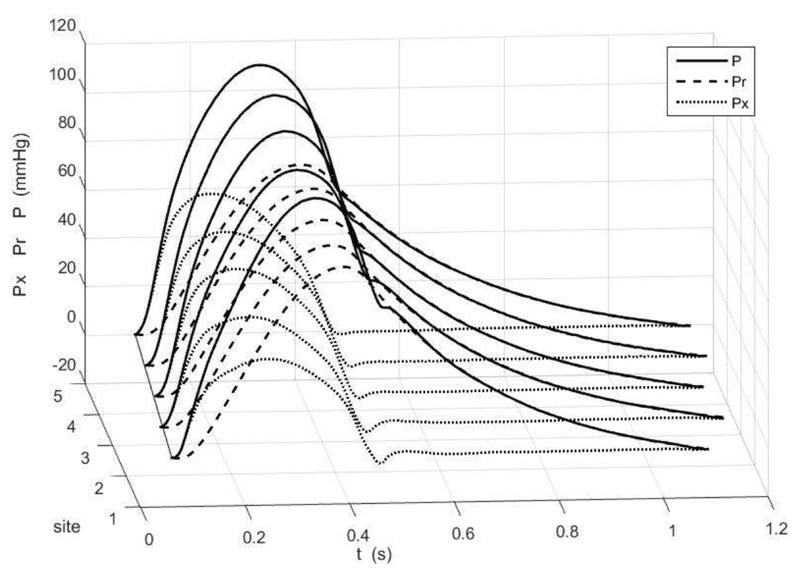
Figure 1 shows the ensemble average of the measured pressure (solid line) at the 5 aortic sites for one patient, together with the reservoir (dashed) and excess (dotted) pressures calculated from the measured pressure. Time zero corresponds to the time of the peak of the R-wave of the simultaneously measured ECG. The thin solid line represents the time at the diastolic point (the start of systole) at each site. The slope of this line is the pulse wave velocity which, as can be seen, is fast compared to the rate of changes of the pressure waveforms.

Figure 1.

The ensemble average of the measured pressure waveform at the 5 aortic sites for one patient (black) together with the reservoir (dashed) and excess (dotted) pressure waveforms. Time is relative to the R-wave of the simultaneously measured ECG. The dotted black line indicates the time of the diastolic point at the different sites, the slope of this line is the pulse wave speed. For ease of comparison of the waveforms, P-Pd and Pr-Pd are plotted.

The measured pulse pressure increases distally. The Pr waveform fits the diastolic pressure very closely and so Px, defined as the difference between P and Pr, is effectively zero throughout diastole.

The blood pressure and pulse wave analysis parameters at the 5 aortic sites have been previously reported.¹⁵ In brief, augmentation index and augmentation pressure decreased with propagation distally from the aortic root whilst the pressure at the systolic inflection point progressively increased. SBP and DBP increased and remained constant respectively moving away from the ascending aorta towards the aortic bifurcation.

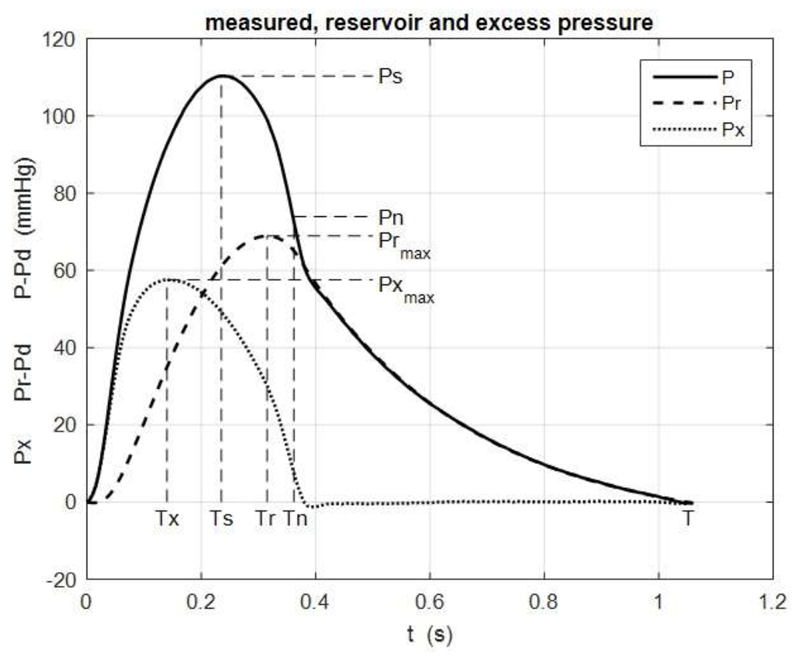
Parameters describing the pressure waveforms are defined in Figure 2 which shows the ensemble average pressure waveform at the aortic bifurcation site in one of the patients. It also shows the calculated reservoir pressure, Pr, and excess pressure, Px. To make comparisons easier the measured and reservoir pressures are plotted relative to the diastolic pressure.

Figure 2.

A typical example of the ensemble average pressure P (solid line) together with the reservoir pressure Pr (dashed line) and excess pressure Px (dotted line). This example is from the aortic bifurcation (site 5). Also shown are the maxima Ps, Pr_max and Px_max and times of the maxima, Ts, Tr and Tx respectively. Tn is the time of minimum dP/dt after Ts which is taken as the end of systole and Pn is the pressure at that time.

Table 2 shows the parameters derived from the waveform analysis at the 5 measurement sites. The parameters include the systolic pressure, Ps, the diastolic pressure, Pd, and the pressure at the end of systole, Pn.

Table 2. Summary of Mean Reservoir Pressure Parameters by Aortic Location.

		Ps (mmHg)	Pd (mmHg)	Prmax (mmHg)	Tr (ms)	Pxmax (mmHg)	Tx (ms)	Tn (ms)	P∞ (mmHg)	Pn (mmHg)	ks (s-1)	kd (s-1)
Aortic Position	Ascending	131.8	65.2	49.4	59	25.3	28	64.0	54.5	115.8	15.39	2.68
	Arch	129.7	64.6	47.5	57	26.5	25	62.7	54.4	113.8	14.00	2.52
	Diaphragm	140.5	69.6	49.07	56	31.8	25	60.6	59.4	122.9	12.20	2.73
	Renal	139.2	67.1	47.24	54	36.1	24	59.4	58.3	119.4	10.46	2.87
	Bifurcation	141.6	66.8	47.16	54	39.4	25	59.1	58.8	120.4	9.78	3.06

Ps – systolic pressure, Pd – diastolic pressure, Pr_max – maximum reservoir pressure, Px_max – maximum excess pressure, Tr – time to Pr_max, Tx – time to Px_max, Pn – pressure at the end of systole, P_∞ - asymptotic fall-off pressure, Tn –time to end of systole, IPr – integral of Pr, kd – diastolic rate constant, ks – systolic rate constant

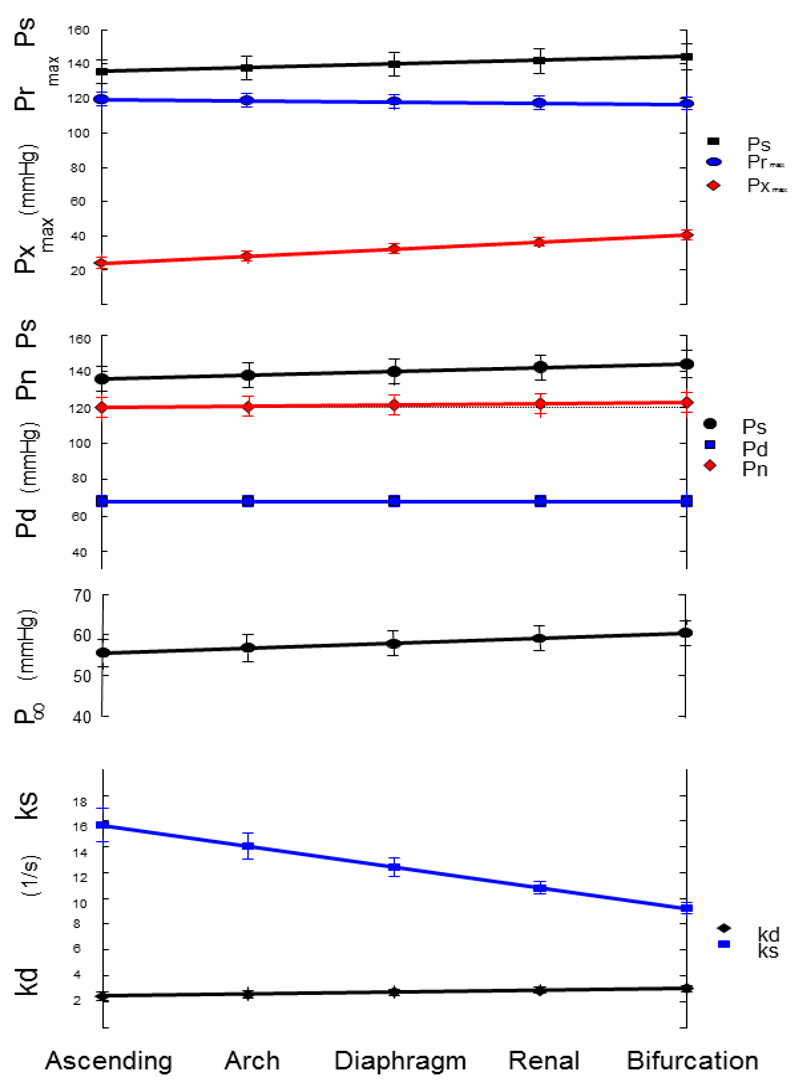
The parameters derived from linear mixed model analysis of the ensemble average pressure waveforms at the 5 aortic sites are given in Table 3 and showed excellent agreement (ICC>0.9) between locations. The cardiac period, T, was unchanged consistent with haemodynamic stability over the period of measurements. Despite the close agreement between aortic sites, there was a significant variation of the reservoir pressure parameters by location (Tables 3-5). A main finding of this analysis relates to the systolic and diastolic rate constants describing aortic behaviour (Table 4). The diastolic rate constant, kd, increased from the aortic root to the bifurcation. Conversely k_s, the systolic rate constant, decreased at all levels of the aorta from the aortic root to the bifurcation. The fractional slope of kd from site to site was 6.7% which corresponds to slightly more than a 25% increase from the root to the aortic bifurcation. Similarly the asymptote of the diastolic pressure fall-off increased by nearly 10% and k_s decreased by more than a third between the aortic root and the aortic bifurcation. (Figure 3). Inspection of the 95% confidence estimates for the slope suggests this is unlikely to be accounted for by chance.

Table 3. Linear mixed model analysis of the Reservoir Pressure Parameters measured at the 5 aortic sites.

	Ps mmHg	Pd mmHg	Pn mmHg	Tn ms	T ms
Intercept	133.6 (126.7,140.5)	68.2 (65.2,71.2)	119.3 (113.9,124.7)	333.0 (321,345)	976.0 (926,1025)
Slope	2.13 (1.66,2.59)	0.06 (-0.24,0.36)	0.71 (0.24,1.17)	-6.0 (-7.0,5.0)	-2.0 (-8.0,3.0)
% slope	1.6%	0.1%	0.6%	-1.8%	-0.2%
ICC	0.964	0.911	0.934	0.977	0.955

Intercept – the intercept of the linear mixed model for the 5 aortic sites for all patients, Slope – the beta coefficient of the linear mixed model, % slope – 100 x slope/intercept, ICC – the intraclass correlation coefficient. Ps – systolic BP, Pd – diastolic BP, Pn – the pressure at the end of systole, Tn – the time of the end of systole relative to the previous end diastole, T – cardiac cycle length.

Table 5. Linear mixed model analysis of the parameters describing Pr and Px.

	Prmax - Pd mmHg	Tr ms	Pxmax mmHg	Tx ms	IPx mmHg s
Intercept	52.1 (47.8,56.3)	308 (297,318)	20.1 (16.6,23.5)	144 (125,163)	4.91 (3.91,5.90)
Slope	-0.68 (-1.01,0.34)	-6 (-7,-5)	4.09 (3.64,4.54)	-3 (-7,1)	0.70 (0.61,0.80)
Fractional slope	-1.3%	1.9%	20.4%	-2.1%	14.3%
ICC	0.978	0.962	0.964	0.914	0.972

Intercept – the intercept of the linear mixed model for the 5 aortic sites for all patients, Slope – the beta coefficient of the linear mixed model, % slope – 100 x slope/intercept, ICC – the intraclass correlation coefficient. Pr_max – maximum of Pr, Tr – time to Pr_max, IPr – the integral of (Pr – Pd) over the cardiac period, Px_max – maximum of Px, Tx – time to Px_max, IPx – integral of Px over the cardiac period. The intercept and slope are given as mean (95% confidence interval).

Table 4. Linear mixed model analysis of the parameters used in the calculation of Pr.

	kd s-1	P∞ mmHg	ks s-1
Intercept	2.26 (1.86,2.66)	54.3 (50.7,57.9)	17.3 (15.6,18.9)
Slope	0.152 (0.067,0.237)	1.22 (0.78,1.66)	-1.61 (-1.96,-1.26)
Fractional Slope	6.7%	2.2%	-9.3%
ICC	0.989	0.903	0.944

Intercept – the intercept of the linear mixed model for the 5 aortic sites for all patients, Slope – the beta coefficient of the linear mixed model, % slope – 100 x slope/intercept, ICC – the intraclass correlation coefficient. kd – diastolic rate constant, P_∞ - asymptote of the exponential diastolic pressure fall-off, ks – systolic rate constant. The intercept and slope are given as mean (95% confidence interval).

Figure 3.

Inter Class Correlation by Aortic Site. The symbols represent the mean values over all patients+/-95% CI. From the top: Ps – systolic pressure (mmHg), Pr_max – maximum reservoir pressure (mmHg), Px_max – maximum excess pressure (mmHg); Ps – systolic pressure (mmHg), Pn – pressure at the end of systole (mmHg), Pd – diastolic pressure (mmHg); P_∞ - asymptotic fall-off pressure (mmHg); ks – systolic rate constant (1/s), kd – diastolic rate constant (1/s).

Reservoir and excess pressure parameters

The change in the reservoir pressure from site to site in the aorta can be described by a number of parameters. In Table 2 we report the peak value of the reservoir pressure relative to the diastolic pressure Pr_rmax, and the time of the peak value Tr. The percentage slopes of the parameters related to Pr are relatively small (Table 5), Pr_max-Pd reduces by 1.3% and Tr increases by 1.9% between measurement sites. Relative to the change in Pr there was a large variation of Px over the 5 aortic sites with 20.4% change in the maximum excess pressure (Px_max) per site distally. This is accompanied by a change in the time to the peak (Tx) by -2.1% per site. These results for the site to site variation of the peaks of P, Pr and Px are shown graphically in Figure 3.

Although P(t) = Pr(t) + Px(t), the peaks in the different waveforms occur at different times and so Ps is not equal to the sum of Pr_max and Px_max. Comparing the results for both reservoir and excess pressure, we note that Px_max occurs significantly earlier than Pr_max and that this difference increases at the more distal sites since the change in Tr is positive and the slope of Tx is negative.

Discussion

This is the first description of reservoir analysis applied at precise anatomical points in the human aorta using pressure waveforms acquired with invasive, high-fidelity, solid state transducers. The application of this model to the in vivo human data of this study provides insights into haemodynamic influences contributing to aortic blood pressure at different sites.

The separation of the measured pressure into a reservoir and an excess pressure is, to date, a heuristic model whose justification depends on its usefulness. The application of this model to the human data collected in this study provides unique insights into what may be the predominant haemodynamic influences contributing to aortic blood pressure at different sites.

Reservoir pressure

The parameters used to calculate the reservoir and hence the excess pressures, ks, kd and P_∞ vary from site to site in the aorta, however, the Pr waveform (Table 5 and Figure 3) exhibits only a small and insignificant variation as it propagates along the aorta. For example, Pr_rmax decreased by 0.68 mmHg per site with a 95% confidence interval which included zero. The agreement between sites was also very close (ICC>0.97). The near uniformity of the reservoir pressure waveform calculated at different sites along the human aorta is consistent with similar measurements made in the canine aorta¹⁰. It also provides a self-consistency check for the algorithm that is used to calculate the reservoir pressure from the measured pressure.

The site by site variation in ks, kd and P_∞, although small, were larger than expected at the outset of the study. Each of these parameters has a physical meaning. kd is the reciprocal of the exponential time constant and P_∞ is the asymptote that the pressure would reach if diastole was extended indefinitely. Both of these parameters are obtained by fitting the ensemble average pressure decay during diastole. ks is the product of the constant of proportionality between the excess pressure and the volume flow rate at the aortic root and the global compliance of the arterial system.

Given the physical meaning of these parameters, changes in the cardiovascular system due to ageing or disease might result in their derangement. This study was not designed to explore this possibility directly but provides indications that this might be a productive avenue for future research.

We conclude that the Pr waveform calculated from the measured pressure is effectively constant as it transverses the aorta (fractional slope = -1.3%). This is in contrast to the peak excess pressure which increased by 4.1 mmHg per site (fractional slope 20.4% per site). The constancy of Pr and the large variation of Px along the aorta supports the basic assumption that Pr depends on global properties of the arterial system while Px depends on local properties. Being able to separate local from global effects will inevitably increase our understanding of the mechanism responsible for the aortic pressure waveform and could be advantageous in clinical measurements of the effects of pathological or pharmacological changes.

As well as decreasing in compliance, the aorta tapers with distance from the aortic root – the effect of branching vessels is to channel off proximal aortic blood volume (e.g. via brachial, subclavian, intercostal, renal, mesenteric, etc. arteries) - with the more distal aortic pulse pressure determined by the incrementally advancing volume of blood, a decreasing cross-sectional area and increasing local stiffness. Anything less than an ideal match of these local properties, for example associated with ageing, will result in admittance mismatches associated with an increased local blood pressure. Reservoir pressure analysis suggests that mismatch between blood volume and aortic compliance causes an increase in local excess pressure and hence local pulse pressure. This is consistent with ageing and disease related processes that have been well identified, but importantly it also suggests that such changes can be better understood in terms of local effects without any discernible influence from distal arterial segments¹¹ or of a predominant single reflected wave as postulated in models based on a uniform tube assumption²².

Limitations

The patients in the study are representative of patients undergoing clinical diagnosis in our catheter lab, but are not necessarily representative of the population as a whole. Nonetheless, we believe that the results can be extrapolated to the general population with some confidence.

Reservoir waveform analysis involves a number of assumptions relating to the aortic pressure waveform, including that waveform decay measured at different aortic locations is similar in diastole. Secondly, it assumes that, at the aortic root, the excess pressure waveform is proportional to the flow waveform. Given these two assumptions, reservoir pressure can be calculated solely from the pressure waveform, without requirement for assessment of flow. Our results need to be interpreted within these inherent assumptions and further work is need to address these assumptions, however this study has demonstrated a substantial degree of self-consistency.

Conclusions

Elevations in central and aortic pulse pressure are associated with incident cardiovascular events. Wave reflection is widely considered to contribute significantly to aortic pulse pressure through pulse pressure augmentation. Based on reservoir-pressure analysis, local wave transmission seems to play a relatively larger role in the distal aortic pressure waveform (as indicated by increasing excess pressure) whilst the reservoir pressure waveform (determined by global aortic compliance) plays a greater role at the ascending aorta.

The major insights from this analysis are that the calculated reservoir pressure waveform, despite known changes in aortic structure and biomechanical properties, is effectively uniform throughout the aorta; the increase in pulse pressure in more distal locations of the aorta is attributable to increasing excess pressure; and that the systolic and diastolic rate constants increase and decrease respectively along the aorta. This variation in the rate constants suggests that they are related to intrinsic functional properties and, as such, may have prognostic implications. The reservoir pressure waveform can provide an heuristic description that might have utility in understanding generation of BP and might have clinical utility in specific cases.

Abbreviations and symbols

BP

blood pressure (mmHg)

cBP

Central blood pressure

SBP

Systolic Blood Pressure

DBP

Diastolic Blood Pressure

LV

left ventricle

Qin

volume flow rate into the aortic root (m³/s)

ICC

inter-class correlation coefficient

SD

standard deviation

SE

standard error

Waveform parameters

kd

diastolic rate constant (s^-1)

ks

systolic rate constant (s^-1)

P(t)

measured pressure (mmHg)

Pd

diastolic (minimum) pressure (mmHg)

Pn

pressure at the end of systole (mmHg)

Pr(t)

reservoir pressure (mmHg)

Pr_max

maximum Pr above DBP (mmHg)

Ps

systolic (peak) pressure (mmHg)

Px(t)

excess pressure (mmHg)

Px_max

maximum Px (mmHg)

P_∞

asymptotic pressure for diastolic pressure fall-off (mmHg)

T

cardiac period (s)

Td

diastolic period (s)

Tn

systolic period (s)

Tr

time of Pr_max (s)

Ts

time of Ps (s)

Tx

time of Px_max (s)