Abstract
Background
Dorsal root ganglia (DRG) are spinal root components that contain the cell bodies of converging primary sensory neurons. DRG are becoming a therapeutic target for electrical neural interfaces. Our purpose was to establish methods for quantifying the non-random nature and distribution of neuronal cell bodies within DRG.
New Method
We identified neuronal cell body locations in 26 feline lumbosacral DRG cross-section histological images and used computational tools to quantify spatial trends. We first analyzed spatial randomness using the nearest-neighbor distance method. Next we overlaid a 6×6 grid, modeling neuronal cellular density in each grid square and comparing regions statistically. Finally we transformed DRG onto a polar map and calculated neuronal cellular density in annular sectors. We used a recursive partition model to determine regions of high and low density, and validated the model statistically.
Results
We found that the arrangement of neuronal cell bodies at the widest point of DRG is distinctly non-random with concentration in particular regions. The grid model suggested a radial trend in density, with increasing density toward the outside of the DRG. The polar transformation model showed that the highest neuronal cellular density is in the outer 23.9% radially and the dorsal ±61.4° angularly.
Comparison with Existing Methods
To our knowledge, DRG neuronal cell distribution has not been previously quantified.
Conclusions
These results confirm and expand quantitatively on the existing understanding of DRG anatomy. Our methods can be useful for analyzing the distribution of cellular components of other neural structures or expanding to three-dimensional models.
Keywords: spinal ganglia, cell density, cats, spatial trend
Graphical Abstract
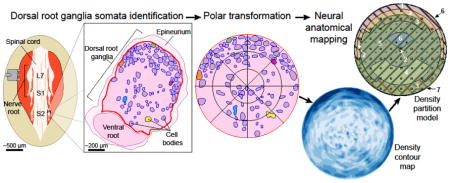
1. Introduction
The dorsal root ganglion (DRG) is a part of the spinal root which contains the cell bodies of converging peripheral sensory neurons. DRG offer a potential neural interfacing location for prosthetics and physiology studies that aim to interact solely with sensory neurons. Although DRG have been well-studied overall, few studies have quantitatively investigated the cell-body distribution of DRG. Anatomical analyses of DRG are dominated by morphological studies of human and animal roots.
Human studies focus on the overall size and alignment of DRG in cadaver dissections [1]–[3] fixed specimens [4], and imaging studies [5]–[7], generally towards clinical pain applications.
The majority of animal studies have focused on characteristics of individual DRG neurons, such as conduction velocity and action potential generation [8]. In addition to studying DRG anatomy and characteristics of individual neurons [9]–[12], animal studies have included population-based analysis of DRG neurons which have provided insight into total cell counts [13]–[15], relative ratios of larger and smaller neurons [14], and somatotopic and/or topographic arrangement of cell bodies [16]–[20]. However, reported DRG parameters can have large variations. For example, the cell body volume ranges from 1 to over 150 cubic micrometers, greater than a 100 fold variation [15]. Cell count studies which only choose to include cells portraying the nucleolus have increased bias as well [15]. To decrease bias, a smaller counting unit must be used, such as smaller comparison regions.
The relative location of neuronal cell bodies within the DRG has not been quantified. There are anecdotal references to superficial cell bodies [21], [22] and occasional figures showing cross-sectional areas [21], [23], [24] from various sources. Of note, several studies have examined cross-sectional areas of cell bodies but have not related them to DRG cell distribution. Instead, these studies focus on the relationship between cell size and conduction velocity [10], central and peripheral branch differences [11], and myelin sheath thickness [23]. Studies have not been completed which incorporate cross-sectional areas of neuronal cell bodies and neuronal cell body location to provide specific insight into DRG cell body distribution.
A limitation to DRG morphology and cytology studies is the few models developed to guide DRG research. McLain developed a qualitative model to provide a comparison to injured ganglia, however a quantitative model of the DRG has not been developed [25]. There is a need for a greater understanding of DRG cellular morphology and cytology, increased quantitative measurements for DRG cell body counts and volume, and a model that provides a better understanding of cell body distribution. In this work we establish methods for determining and modeling the distribution of neuronal cell bodies within DRG, using mid-DRG cross-section images from feline lumbosacral levels. This two-dimensional analysis provides key insights and demonstration of the approach, and can be expanded into three-dimensional analyses if desired.
2. Materials and Methods
We present three methods for assessing neural structure randomization and distribution, applied to DRG neuronal cell bodies in this study: an assessment of spatial randomization (section 2.3.1), a Cartesian grid model of neuronal cell body distribution without tissue transformation (section 2.3.2), and a polar transformation model of neuronal cell body distribution (section 2.3.3). Statistical tests within each section are used to determine the significance of the respective distributions. All MATLAB scripts are available in the Open Science Framework repository (DOI: 10.17605/OSF.IO/Q9UJ7, https://osf.io/q9uj7) [26].
2.1 Sample Acquisition
After experimental use for other objectives, fifteen male adult felines (average weight of 4.9 ± 0.6 kg, average age: 1.0 ± 0.2 years) were euthanized via an intravenous 85–100 mg/kg overdose of sodium pentobarbital. Two animals were perfused transcardially with one liter of phosphate buffered saline followed by one liter of 4% paraformaldehyde (PFA) prior to tissue removal. In the remaining animals, tissue was removed promptly after euthanasia. During prior surgical procedures, a lumbosacral laminectomy to expose spinal roots was performed, thus post-mortem access was prompt. Care was taken to ensure the dorsal root ganglion were not harmed due to surgical intervention through standard surgical techniques. Only vertebrae was removed during the laminectomy procedure, with no surgical tools inserted into or damaging DRG One or more lumbosacral DRG (seventh lumbar – L7; first, second, or third sacral – S1, S2, S3) from one or both sides were isolated and removed from the animal by transections at the junction with the spinal cord and distally on the whole spinal root. During tissue explant, care was taken to not apply any pressure on DRG and to limit handling to proximal and distal nerve roots. Each sample was fixed in PFA at room temperature for at least one week. Not all DRG were removed or used in this analysis from each animal due to surgical limitations or other experimental needs. The University of Michigan Institutional Animal Care and Use Committee approved all animal work, which was carried out in accordance with the National Institute of Health Guide for the Care and Use of Laboratory Animals.
After fixation, roots were cut orthogonally to the mid-axis plane at the largest width (Figure 1(A)), and embedded in paraffin with the cross-section plane facing up. A microtome (Finesse ME+, ThermoScientific, Waltham, Massachusetts, United States) was used to create a four micrometer thick tissue slice from each sample, which was fixed on a slide and stained with hematoxylin and eosin using standard techniques (Figure 1(A)).
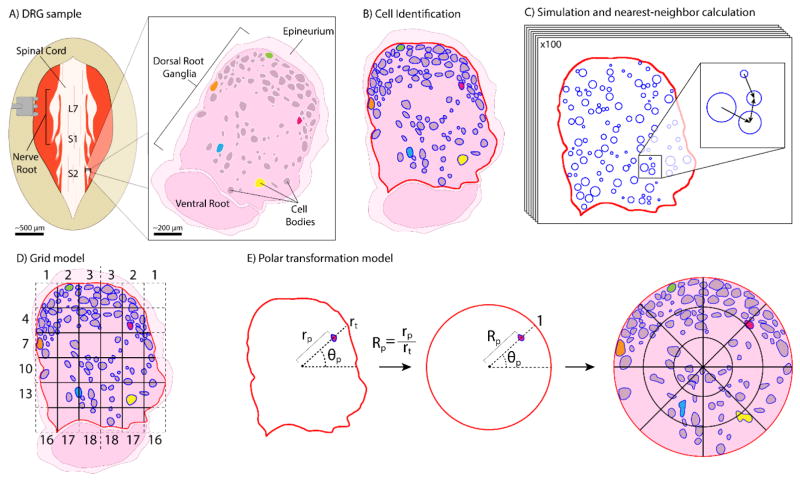
Figure 1.
Representation of tissue collection and analysis methods. (A) Medial tissue slice taken from feline DRG at spinal levels L7-S3. Tissue stained with hematoxylin and eosin, allowing cell bodies to be distinguished from the background. Cell-body containing region is DRG. Several cell bodies highlighted in non-histological colors for clarity through processing steps. (B) Tissue slice oriented with the DRG on top and ventral root underneath. Cell and DRG borders demarcated in blue and red, respectively. (C) MATLAB algorithm used neuronal cell size data and DRG border location to generate 100 random simulations of non-overlapping cell arrangements for comparison to actual arrangement. [inset] Demonstration of nearest-neighbor distance calculation, with arrows pointing toward nearest neighbor of each cell. (D) Division of demarcated DRG into 6×6 grid for calculation of neuronal cell density in each grid square. DRG border takes priority over grid for determining square boundaries. Squares numbered from left to right then top to bottom, with numbers reflected across the vertical axis. (E) For transforming each pixel: angle θp from centroid-horizontal; distance rp from centroid to pixel; distance rt from centroid to DRG border along θp. Transformed polar coordinate is (Rp,θp). [right] Transformed DRG, with a 3×8 radial grid (24 annular sectors) overlaid here for ease of visualization, though a 44×44 radial grid (1,936 annular sectors) was used. Neuronal cell density is calculated in each annular sector, as previously in grid squares.
2.2 Data Collection
The DRG slides were imaged with an inverted microscope (IX83, Olympus, Shinjuku, Tokyo City, Tokyo, Japan), with the brightfield setting at 10 times magnification and Nikon (Minato, Tokyo City, Tokyo, Japan) Element BR 3.2 Software. Any dorsal root ganglion which appeared damaged were not included in samples for analysis. The image was uploaded to the ImageJ (https://imagej.nih.gov/ij/, RRID: SCR_003070) plug-in for ObjectJ (https://sils.fnwi.uva.nl/bcb/objectj/index.html, Vischer, N. & Nastase, S. University of Amsterdam), on a desktop PC.
The image was rotated such that the dorsal root was at the top of the image and the ventral root was at the bottom of the image, ensuring the DRG was oriented in a dorsal-upright position for all analysis (Figure 1(B)). Pixel dimensions were kept constant to ensure accurate scaling. For clarity, the 2D images will be referred to simply as DRG, though the goal of this work was to represent only mid-root cellular distributions with no implied stereotaxic claims.
DRG stained with hematoxylin and eosin have neuronal cell bodies which are visually distinct from the background, but the contrast is too poor to rely on automatic image segmentation. Automated cell identification with other staining methods could be used with our methods. Therefore image processing began in ObjectJ with manual demarcation of the borders of each neuronal cell body (in blue) and the DRG itself (in red). Neuronal cell bodies were identified due to morphological size differences as neuronal cell bodies are larger than other cells within the DRG [27]. Within ObjectJ, two objects were created: Cell Trace and Edge ROI (region of interest). The Cell Trace object was defined as an area tool to trace the borders of each neuronal cell body in blue and calculate area. The Edge ROI tool was defined as an area tool to trace the border of the DRG in red. The DRG border was taken to be within the epineurium (Figure 1(B)).
2.3 Data Analysis
2.3.1 Assessing Spatial Randomness
Our first step in analyzing spatial distribution was to determine whether the DRG sections contained a statistically non-random distribution of neuronal cell bodies. The presence of non-randomness is considered prerequisite to making claims about any specific distribution. To quantify randomness, we utilized a nearest-neighbor distance method. For each DRG, the distance from each neuronal cell body centroid to its nearest neighbor was calculated with a script in MATLAB (Mathworks, Nantick, Massachusetts, United States, RRID: SCR_001622). The mean of these values (d̄A) contains information about the randomness of the section, because a random 2D point process will differ from a biased process in characteristics of its distribution, including inter-point distances [28]. However, the DRG must be compared to representative random cell arrangements to have significance.
To produce random distributions for comparison, in MATLAB we simulated 100 random arrangements of neuronal cell bodies for each DRG. These simulations placed circular “neuronal cell bodies” inside the DRG border, equivalent to the number of neuronal cell bodies found in the original sample. The area of each simulated neuronal cell body was pulled randomly from the areas of neuronal cell bodies in the original sample. Simulated neuronal cell bodies were placed at random locations but, importantly, not allowed to overlap with one another. Mean nearest-neighbor distance was calculated for each simulated arrangement (d̄E) for comparison to the real sample (Figure 1(C)). The ratio D=d̄A/d̄E has a value of 1 in the case of total randomness. If D<1, the sample is non-random towards aggregation, that is, neuronal cells are clustered in particular areas. If D>1, the sample is non-random towards equidistant patterning. D has a theoretical range of 0 to ~2.15 [28]. We calculated D for 100 simulations of each DRG to obtain distributions for statistical comparison with a two-tailed Student’s t-test. DRG with mean D significantly different from 1 (α = 0.01) were considered to have non-random neuronal cell body distributions.
2.3.2 Grid Model
Following the test for randomness, we proceeded to a search for trends in neuronal cell body distribution. In ObjectJ, a Grid Line object was defined as a line tool to create an overlay grid on each DRG slice. A range of grid sizes were considered from 3×3 to 7×7, but a 6×6 grid was chosen as having a balance between resolution and having cell bodies in most grid squares. Smaller or larger grids may be appropriate for neural structures that vary from the typical sizes of feline DRG (1–2 mm cross-section). Data from ObjectJ was output to spreadsheets (Excel, Microsoft, Redmond, Washington, United States) to determine the number and average area of neuronal cell bodies in each of the 36 grid squares. For squares along the perimeter, the DRG tissue area in each was determined for normalization purposes (Figure 1(D)). From these values we calculated for each grid square a normalized neuronal cell area density (percentage of the grid square occupied by neuronal cell bodies). Because each DRG was divided into the same number of grid squares, the neuronal cell densities allowed direct comparison across samples. The values were visualized and analyzed statistically using platforms in the statistical software program JMP (SAS Institute Inc., Cary, North Carolina, United States, RRID: SCR_014242). A contour map was produced to visualize trends. Regional divisions, such as ventral/dorsal or outer/middle/inner layer, were used for initial categorization of the grid squares, with cell densities compared using either a Student’s t-test or ANOVA with Tukey Honestly Standard Difference (Tukey HSD) test for multiple comparisons (α = 0.01).
2.3.3 Polar Transformation Model
While the grid square analysis is useful for determining general trends (see Results), we sought a more detailed and objective analysis, by transforming distributions into a polar model (see Discussion for advantages and limitations of each approach). The demarcated images were loaded into MATLAB for analysis with the Image Processing Toolbox. The images were split into red, blue, and green color channels. Thresholding on the red and blue channels produced binary images highlighting the locations of border pixels. A MATLAB function for detecting connected components in binary images was used to detect and analyze each object, determining the location of the object centroid and all associated pixels. A diagnostic image showing identified regions allowed for necessary corrections to be made to the manual demarcation as necessary to ensure accuracy in image segmentation. The result of this processing is that each histological image could be considered as a large bordered region (the DRG) containing regions of interest (cell bodies) with known properties for analysis.
To prepare for cross-sample comparison, we first mapped the neuronal cell bodies from each DRG to a normalized polar map using a custom MATLAB script with the following steps. The centroid of the overall DRG region was determined to establish an origin. Then, a polar angle θp from 0°–360° was calculated relative to the positive horizontal axis for each pixel in the region, identified as either a “neuronal cell body” or a “non- neuronal cell body” pixel. The distance from the origin to each pixel (rp) was found along this angle, as well as the distance from the origin to the DRG border (rt). The normalized ratio Rp=rp/rt, which varies from 0–1, was taken as the polar radius for the pixel. At this point, each pixel could be identified with a polar coordinate of (Rp, θp), and lay within a unit circle. The perimeter of the circle represents the DRG border (Figure 1(E)). This normalized mapping step allowed direct comparison across irregularly shaped samples.
To screen for trends in neuronal cell density, we divided each normalized DRG into 1,936 annular sectors, that is, each DRG was divided into 44 regular wedge-shaped sectors which were further divided into 44 regular nested rings. In each annular sector, we calculated neuronal cell area density as the number of neuronal cell body pixels divided by total pixels (neuronal cell body + non-neuronal cell body pixels). The 44×44 division was chosen as the smallest number of divisions which yielded at least one annular sector with 100% neuronal cell density in each DRG, that is, which produced sectors approximately on the scale of the largest neuronal cell bodies. Other divisions may be appropriate for analyzing different neural structures. This process yielded a table of data containing information about the original DRG tissue sample (feline source, spinal level) as well as the polar location and density of each annular sector. We again produced a contour map for visualization of trends across all DRG samples. Because our particular histological samples do not preserve sagittal (left-right) orientation, we folded the contour map onto itself along the vertical midline to avoid bias in the analysis presented here. Applications maintaining orientation would not need to do this. Averaged annular sectors in this half-circle were assigned a vertical angle θv, defined as the angle from the positive vertical axis of the DRG with a range of 0°–180°.
To improve objectivity about the division of the DRG into regions of differential density, we utilized the JMP Partition platform for recursive partition modelling. This classification tool splits a distribution of dependent variable values into sub-populations based on several independent variables. This model produces a “decision tree” which, at each node, selects a split value of one independent variable to maximally separate the population by dependent variable. In our data set, the dependent variable was neuronal cell density and the independent variable was annular sector coordinate (Rp, θv). Given the possible inputs, the program first produces a variety of possible models with minimized sum of squared errors. Then it chooses from among the generated models by maximizing the LogWorth statistic, defined as −log10(p-value).
To avoid overfitting, 10-fold cross-validation was used in generation of the partition model. This involved randomly splitting the data set into 10 segments, then iteratively training the model with 90% of the data while testing the fit on the remaining 10%. This cross-validation step not only ensured appropriate partitioning but also provided a stop condition for further splits. We continued splitting the decision tree recursively until the next ten best splits did not improve the mean R2 value of the validation data set. Importantly, however, the resulting model does not necessarily imply statistical significance. To test this, we recategorized the annular sectors into regions following the split values suggested by the partition model. Overall neuronal cell densities in the resulting regions were compared with Tukey HSD tests, allowing us to determine whether the trends suggested by the partition model were statistically significant (α = 0.01).
3. Results
Raw DRG slice images, demarcated DRG slice images, summary spreadsheets, and MATLAB analysis scripts are available in the Open Science Framework repository (DOI: 10.17605/OSF.IO/Q9UJ7, https://osf.io/q9uj7) [26].
3.1 DRG Samples
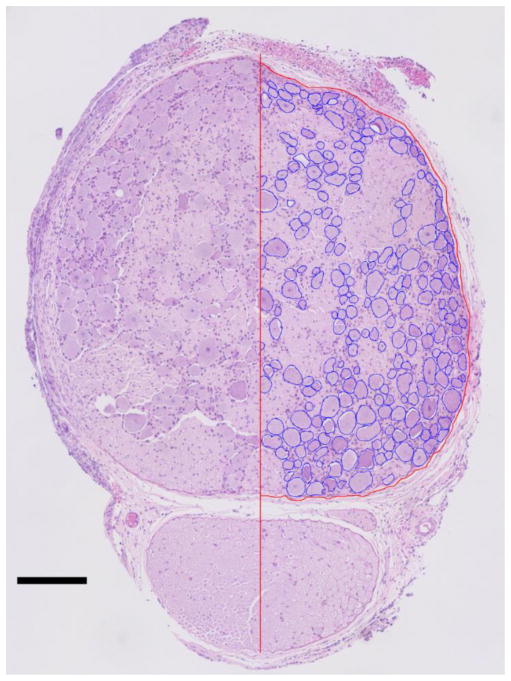
For our evaluation of these methods, twenty-six DRG were analyzed from fifteen adult male cats, with multiple DRG sampled from seven cats. Six DRG were from the L7 level, nine from S1, ten from S2, and one from S3. DRG level was determined by anatomical position. Eight DRG came from the left side of the animal, eighteen from the right side. This imbalance resulted from the accompanying experimental procedures, predominantly on the left side, that sometimes left the DRG unusable for histology. None of the DRG analyzed were directly involved in tests performed on the cat before tissue resection. Figure 2 shows an example of a labeled medial DRG section.
Figure 2.
Sample hematoxylin and eosin stained medial DRG section used for analysis (Experiment 10, right S1). Left half: raw image. Right half: neuronal cell bodies demarcated in blue, DRG border demarcated in red. Scale bar is 200 μm.
3.2 Assessing Spatial Randomness
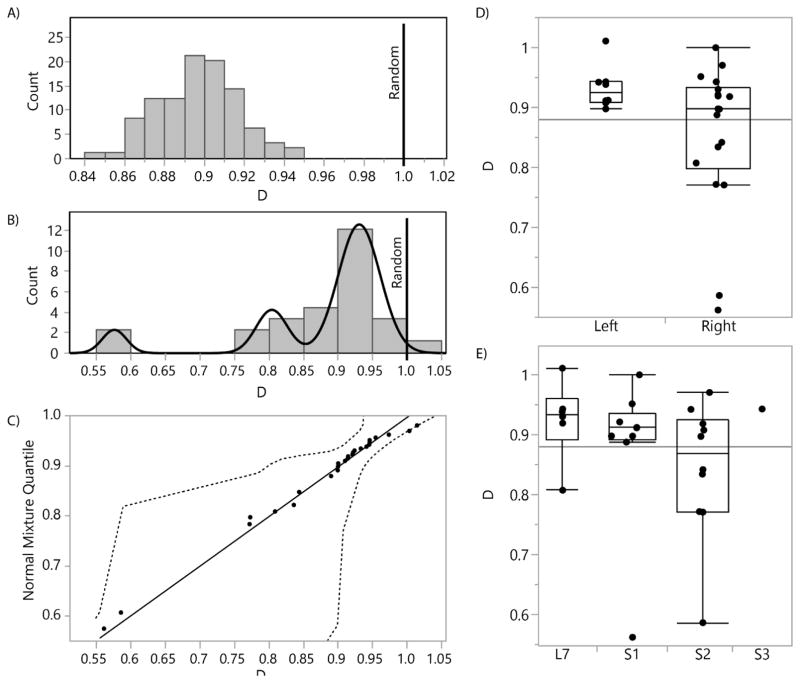
In the assessment of randomness for our samples, we tested the distribution of D for each DRG with a two-tailed Student’s t-test, based on the null hypothesis of equality with 1 (representing a totally random neuronal cell body arrangement) and a threshold p-value of 0.01. We found that 24 of 26 DRG had a mean D significantly less than 1, indicating that most of the DRG have a non-random arrangement of neuronal cell bodies (see Figure 3(A) for an example DRG). Figure 3(B) shows a histogram of D across all sampled DRG. Of the remaining DRG, one had a mean D not significantly different than 1, and the other was significantly greater than 1. The Shapiro-Wilk test for normality showed that the distribution was significantly different than normal (p<0.0001). The best fit was instead a mixture of 3 normal distributions, which had an estimated-actual quantile fit with R2=0.99 (Figure 3(b, c)). The mean D for the distribution subgroups were 0.58, 0.80, and 0.93. These values were less than one, and a Wilcoxan rank test for non-normal distributions showed that the population mean was significantly less than 1 (p<0.0001). This indicated that not only are the neuronal cell body arrangements random in our sample set, but they are aggregated. That is, neuronal cell bodies in the DRG are found clustered together in a group or groups in a fashion which is statistically unlikely to occur in a case of pure randomness. There was not a significantly different degree of randomness across left/right division (Figure 3(D)) or spinal level (p>0.01 for each) (Figure 3(E)). Therefore, our next goal was to determine if there was a trend in where neuronal cell bodies tend to aggregate.
Figure 3.
(A) Histogram of 100 simulated D values for one DRG, with vertical line at D=1.0 (random). Distribution mean (0.90; standard deviation 0.02) is significantly different than 1. D is the ratio of the actual mean nearest neighbor distance to the simulated nearest neighbor distance. (B) Histogram of mean D values for each DRG, with fitted mixture of 3 normal distributions (means at 0.58, 0.80, and 0.93). (C) Diagnostic plot showing predicted versus actual quantile for each of the D values in (B), based on the normal 3 mixture shown in (B). Dashed lines show 95% confidence interval. (D) Box plots comparing mean D values for each DRG by left or right source, showing no significant difference between groups. Horizontal line represents overall mean (0.88). (E) Box plots comparing mean D values for each DRG by spinal level source, showing no significant difference between groups.
3.3 Grid Model
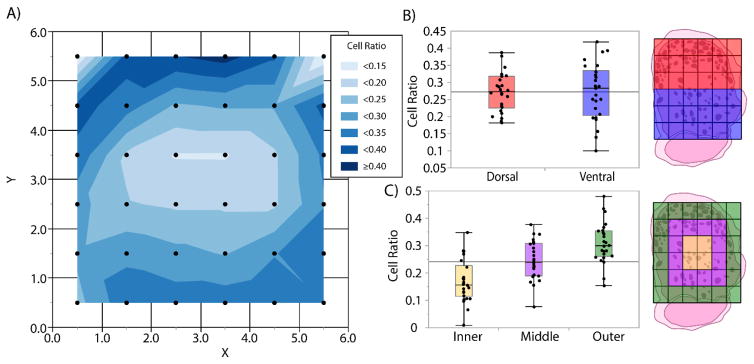
We began by analyzing spatial trends in neuronal cell density gleaned from the 6×6 grid model. To visualize this, we used JMP to produce a contour map of mean neuronal cell density relative to grid position (Figure 4(A)). The contour map suggested a primarily radial gradient of density, with lower density in the innermost DRG region and higher density in the outer coronal region. There also appeared to be a slight trend toward higher density in the dorsal (top) regions than the ventral (bottom), however no significant difference was observed between dorsal and ventral regions (Figure 4(B)).
Figure 4.
(A) Contour map of mean neuronal cell density based on 6×6 grid model. Data represented at center of grid square. (B) Box plots comparing mean neuronal cell density in dorsal and ventral sector for each DRG. No significant difference found between groups. Plot key at right. (C) Box plots comparing mean neuronal cell density in inner, middle, and outer rings for each DRG. All groups significantly different from one another (p < 0.01 for each group comparison). Plot key at right.
We tested the radial gradient hypothesis by dividing the grid into 3 “rings,” an outer, middle, and inner (Figure 4(C)). For each DRG, we calculated mean neuronal cell density in each ring, then compared the rings with a Tukey HSD test for multiple comparisons preceded by an ANOVA test for significance. The tests indicated that there was a significant difference (p < 0.001) between neuronal cell density in each ring, with density rising with increasing radial distance from the center. The outer ring contained a mean neuronal cell density of 0.30, nearly twice the density of the inner ring (0.17).
3.4 Polar Transformation Model
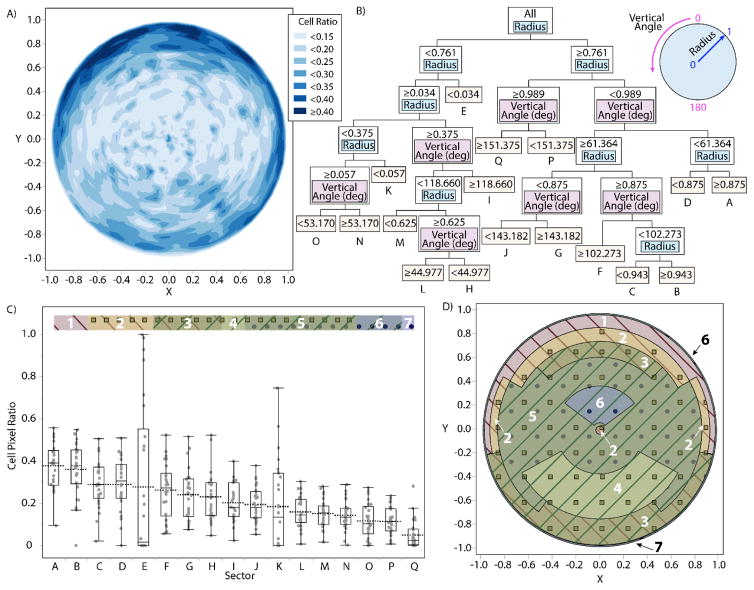
To explore the radial density gradient in depth, we analyzed the polar transformation model. Figure 5(A) shows a contour map of the mean neuronal cellular density for the full 360° annular sector set, as determined by the polar transformation and division into 1,936 (44×44) annular sectors. The partition model of neuronal cellular density by radial and angular location, after folding over the full 360° annular sector set along the vertical midline to a 180° combined set, contained 16 splits (Figure 5(B)), with a testing data set R2 of 0.0583 and a validation data set R2 of 0.0577. This shows that, while the model only explains about 6% of the variation in cellular density for our DRG samples, it is consistently predictive. A comparison of the regions produced with ANOVA and Tukey HSD showed significant differences within the set (p < 0.0001) which are best described by the box plots of Figure 5(C). Figure 5(D) shows a spatial map representing the differential neuronal cellular densities in the regions determined by the partition model and the Tukey test, mirroring the 180° folded data set to create a full circular visualization. The model suggested that the variable of primary importance is radial distance from the center (82% of model variation explained), and that the primary appropriate division is between the inner low-density 76.1% and outer high-density 23.9%, though the outermost 1.1% is a lower density region. The secondary division is likely due to packing of the neuronal cells, which naturally leads to low density at the extreme edges. The highest density area within the larger outer ring is above the vertical angle of 61.4°, or alternately the upper 122.8° of the DRG.
Figure 5.
(A) Contour map of mean neuronal cell density based on polar transformation model with 44 divisions radially and angularly for full 360° annular sector set. (B) Branching tree diagram representing a partition model of neuronal cell density into annular sectors based on vertical angle and radius, after folding over the 360° data set onto the 0–180° midline to minimize lateral bias. Nine divisions were based on radius, seven on vertical angle. Sectors are labeled from A to Q in order of descending mean (C) Box plot comparing cell density in each sector A to Q per partitions in (B). Comparison bar along top indicates statistical significance between groups: groups not connected by the same pattern (diagonal stripes in one of two directions, squares, or circles) are significantly different from one another. Distinct overlapping regions numbered from 1 to 7 (D) Spatial representation of (B) and (C) with the dataset mirrored across midline to provide circular visualization. Note that outer regions 6 and 7 are very thin outer borders which are difficult to visualize.
To give a sense of predictive value of this model, 13/26 of the DRG had the highest cell density in one of the two highest predicted regions (referred to as A or B, respectively, in Figure 5(c, d)). The only major deviation from this trend was in DRG with the highest density predicted in region E, the very center of the DRG. This region had the highest observed density in 7/26 of the DRG. This region exhibited high variability in neuronal cell density, as it was in the bottom two regions for density in 13/26 DRG. This variability is likely explained by the fact that sectors in this area are relatively small and the presence or absence of a single neuronal cell body in this region could be enough to drastically change the observed neuronal cell density.
4. Discussion
In this study we established methods for assessing and modeling the distribution of neuronal cell bodies in dorsal root ganglia sections. As such, this is the first study to quantitatively assess DRG neuronal cell body distribution. Using our methods, we established quantitatively that arrangements of neuronal cell bodies in our DRG samples are non-random, and that these arrangements tend toward having clusters of neuronal cell bodies in certain regions. This claim is based on analysis of nearest-neighbor distances in histology compared to reasonable simulations of random neuronal cell body arrangements (Figure 3). The results suggest several levels of randomness, reflecting the heterogeneity of the neuronal cell body arrangements analyzed. However, the source of our DRG samples (left/right or spinal level) did not significantly affect the level of randomness.
Having established non-randomness, we developed two methods for modeling DRG neuronal cell density, first a grid model then followed by a polar transformation model. The grid model displays neuronal cell density concentrations of neuronal cell bodies in the outer regions with a higher concentration on the perimeter of DRG then in the central ROIs (Figure 4). Outer regions of the DRG for dorsal and ventral regions exhibited higher neuronal cell densities then inner or middle regions. A contour plot analysis exhibited circular ring pattern for neuronal cell density, with an absence of corners. The grid model was relatively straight-forward to generate, however the outer border does not accurately depict the curved perimeter of DRG and neuronal cell placement in a grid region when the average normalized neuronal cell area and the average normalized DRG area are close was difficult. These limitations and a contour analysis of neuronal cell density supported the creation of the polar transformation model.
The polar transformation model displays the proportion of each annular sector area occupied by neuronal cell bodies (Figure 5). There are higher densities on the perimeter, primarily on the dorsal side with lower densities in the central region. This model provides a more accurate representation of DRG, with the round contour and the intuitive application of applying regions in the shape of circular rings, which were supported through statistical analysis of the grid model. However, the polar transformation model includes some distortion due to the circular transformation and irregularly sized sectors. Both computer models demonstrate a characteristic neuronal cell body distribution around the perimeter of the DRG. As a secondary classification, the outer dorsal region exhibited the highest neuronal cell densities for both models.
The results of this study support prior qualitative statements about dorsal, superficial clustering of neuronal cell bodies in DRG [21], [22]. Our mid-section DRG slices also compare favorably to prior examples of cross-sections in the literature, such as in cats [21], [23] and rats [24], which show characteristic neuronal cell body clustering around the periphery. In this study we did not seek to quantify the distribution of neuronal cell body sizes, as our cross-section tissue slices only sample a portion of each neuronal cell body [15]. Although we only focused on feline lumbosacral DRG, we expect our methods will yield similar observations at other spinal levels and in other species [23].
In addition to broadening our understanding of DRG anatomy, the results obtained from our methods provide quantitative information to aid in the design of electrodes for interfacing with DRG for recording or stimulation applications. There are no electrodes specifically designed to accommodate the unique geometry and neuronal cell-body distribution of DRG. Some DRG interfacing applications require cell-selective capabilities and desire the ability to record large signals from cell bodies rather than smaller potentials at axon nodes [29]–[32]. These applications may seek to develop microelectrodes that are very superficial in their access to DRG. A recent study with non-penetrating microelectrodes showed promise for recording DRG cellular potentials [33], and we are continuing this work with the development of thin-film arrays that conform to the DRG surface [34]. Alternatively, DRG interfaces primarily for stimulation [35]–[37] may target axons. These approaches may seek to develop custom microelectrodes that target central regions of DRG, based on our model. Additionally, this work will also be useful in informing the nascent field of DRG stimulation as a clinical pain therapy [38], [39].
Several aspects of our study design may have impacted our observations. During tissue removal and histological processing, compression of the roots could have occurred. Visual comparison of perfused and non-perfused samples suggests no difference in overall morphology and no obvious tissue shrinkage. If tissue shrinkage occurred during processing, our normalization approaches provide mitigation against broad effects. In some cases, multiple samples were collected from individual animals at different spinal levels. This unbalanced sampling may skew data analysis, though no evidence of this was found. User error may have occurred during manual tracing of neuronal cells and roots. Only medial slices were included in this analysis, which does not account for axial cell density variation across DRG. This is a future area for analysis.
We anticipate several approaches for extending the methods used here. The analysis here focused only on DRG slices sampled at the widest point. A full-DRG model that incorporates slices from the spinal cord to the spinal root will provide a three-dimensional neuronal cell-body distribution. We also plan to identify medial and lateral aspects of roots. Analyses of spinal roots at other levels (cervical, thoracic, lumbar) and in other species, including humans, will elucidate the consistency of cellular distribution across these other sources. The incorporation of cell tracing technology [20] would give an ultimate quantification of cellular sources and distribution.
Highlights.
We present a method for quantifying neuronal cell density in dorsal root ganglia.
Normalization of irregular DRG shapes allows direct comparison across samples.
Neuronal somata are concentrated on the outer border of DRG.
Quantifying the neural component arrangements will influence future technologies.
This technique has potential applications in other anatomy and pathology research.
Acknowledgments
Thank you to other members of the Peripheral Neural Engineering and Urodynamics Laboratory (pNEURO Lab), the University of Michigan Microscope Image and Analysis Laboratory (MIL), & Michelle Frazier. Histology was performed by the University of Michigan In Vivo Animal Cores (IVAC). Research reported in this publication was supported by the Craig H. Neilsen Foundation (Grant # 314980) and by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health (Grant Number U18EB021760). The content is solely the responsibility of the authors and does not necessarily represent the official views of the Craig H. Neilsen Foundation or the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Alleyne CH, Cawley CM, Barrow DL, Bonner GD. Microsurgical anatomy of the dorsal cervical nerve roots and the cervical dorsal root ganglion/ventral root complexes. Surg Neurol. 1998 Sep;50(3):213–8. doi: 10.1016/s0090-3019(97)00315-7. [DOI] [PubMed] [Google Scholar]
- 2.Cohen MS, Wall EJ, Brown RA, Rydevik B, Garfin SR. Cauda equina anatomy II: Extrathecal nerve roots and dorsal root ganglia. Spine (Phila Pa 1976) 1990;15(12):1248–51. [PubMed] [Google Scholar]
- 3.Kikuchi S, Sato K, Konno S, Hasue M. Anatomic and radiographic study of dorsal root ganglia. Spine (Phila Pa 1976) 1994;19(1):6–11. doi: 10.1097/00007632-199401000-00002. [DOI] [PubMed] [Google Scholar]
- 4.Ebraheim N, Lu J. Morphometric evaluation of the sacral dorsal root ganglia: a cadaveric study. Surg Radiol Anat. 1998;20(2):105–108. [PubMed] [Google Scholar]
- 5.Hasegawa T, Mikawa Y, Watanabe R, An HS. Morphometric analysis of the lumbosacral nerve roots and dorsal root ganglia by magnetic resonance imaging. Spine (Phila Pa 1976) 1996;21(9):1005–1009. doi: 10.1097/00007632-199605010-00001. [DOI] [PubMed] [Google Scholar]
- 6.Hamanishi C, Tanaka S. Dorsal root ganglia in the lumbosacral region observed from the axial views of MRI. Spine (Phila Pa 1976) 1993;18:1753–1756. doi: 10.1097/00007632-199310000-00006. [DOI] [PubMed] [Google Scholar]
- 7.Shen J, Wang H-Y, Chen J-Y, Liang B-L. Morphologic analysis of normal human lumbar dorsal root ganglion by 3D MR imaging. Am J Neuroradiol. 2006;27:2098–103. [PMC free article] [PubMed] [Google Scholar]
- 8.Devor M. Unexplained peculiarities of the dorsal root ganglion. Pain. 1999 Aug;6:S27–35. doi: 10.1016/S0304-3959(99)00135-9. [DOI] [PubMed] [Google Scholar]
- 9.Miletic V, Lu G-W. Characteristics of action potentials recorded from cat spinal ganglion neurons in vivo. Brain Res Bull. 1993;31:531–538. doi: 10.1016/0361-9230(93)90120-z. [DOI] [PubMed] [Google Scholar]
- 10.Harper A, Lawson S. Conduction velocity is related to morphological cell type in rat dorsal root ganglion neurones. J Physiol. 1985;359:31–46. doi: 10.1113/jphysiol.1985.sp015573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hoheisel U, Mense S. Observations on the morphology of axons and somata of slowly conducting dorsal root ganglion cells in the cat. Brain Res. 1987;423:269–278. doi: 10.1016/0006-8993(87)90849-3. [DOI] [PubMed] [Google Scholar]
- 12.Lee KH, Chung K, Chung JM, Coggeshall RE. Correlation of cell body size, axon size, and signal conduction velocity for individually labelled dorsal root ganglion cells in the cat. J Comp Neurol. 1986;243:335–346. doi: 10.1002/cne.902430305. [DOI] [PubMed] [Google Scholar]
- 13.Aldskogius H, Risling M. Number of dorsal root ganglion neurons and axons in cats of different ages. Exp Neurol. 1989;106(1):70–73. doi: 10.1016/0014-4886(89)90145-3. [DOI] [PubMed] [Google Scholar]
- 14.Chung K, Coggeshall RE. The ratio of dorsal root ganglion cells to dorsal root axons in sacral segments of the cat. J Comp Neurol. 1984;225(1):24–30. doi: 10.1002/cne.902250104. [DOI] [PubMed] [Google Scholar]
- 15.Tandrup T. Unbiased estimates of number and size of rat dorsal root ganglion cells in studies of structure and cell survival. J Neurocytol. 2004 Mar;33(2):173–92. doi: 10.1023/b:neur.0000030693.91881.53. [DOI] [PubMed] [Google Scholar]
- 16.Burton H, McFarlane JJ. The organization of the seventh lumbar spinal ganglion of the cat. J Comp Neurol. 1973;149(2):215–232. doi: 10.1002/cne.901490207. [DOI] [PubMed] [Google Scholar]
- 17.Puigdellívol-Sánchez A, Prats-Galino A, Ruano-Gil D, Molander C. Sciatic and femoral nerve sensory neurones occupy different regions of the L4 dorsal root ganglion in the adult rat. Neurosci Lett. 1998;251(3):169–172. doi: 10.1016/s0304-3940(98)00518-7. [DOI] [PubMed] [Google Scholar]
- 18.Wessels WJT, Feirabend HK, Marani E. Evidence for a rostrocaudal organization in dorsal root ganglia during development as demonstrated by intra-uterine WGA-HRP injections into the hindlimb of rat fetuses. Dev Brain Res. 1990 Jul;54(2):273–81. doi: 10.1016/0165-3806(90)90150-w. [DOI] [PubMed] [Google Scholar]
- 19.Kausz M, Rethelyi M. Lamellar arrangement of neuronal somata in the dorsal root ganglion of the cat. Somatosens Res. 1985;2(3):193–204. doi: 10.3109/07367228509144563. [DOI] [PubMed] [Google Scholar]
- 20.Yan J, Tian R, Horiguchi M. Distribution of sensory neurons of ventral and dorsal cervical cutaneous nerves in dorsal root ganglia of adult rat - a double-label study using DiO and DiI. Okajimas Folia Anat Jpn. 2002;79(5):129–133. doi: 10.2535/ofaj.79.129. [DOI] [PubMed] [Google Scholar]
- 21.Sato M, Austin G. Intracellular potentials of mammalian dorsal root ganglion cells. J Neurophysiol. 1961;24:569–582. doi: 10.1152/jn.1961.24.6.569. [DOI] [PubMed] [Google Scholar]
- 22.Lu H, Chestek Ca, Shaw KM, Chiel HJ. Selective extracellular stimulation of individual neurons in ganglia. J Neural Eng. 2008;5(3):287–309. doi: 10.1088/1741-2560/5/3/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Spencer PS, Raine CS, Wiśniewski H. Axon diameter and myelin thickness - unusual relationships in dorsal root ganglia. Anat Rec. 1973 Jun;176(2):225–43. doi: 10.1002/ar.1091760209. [DOI] [PubMed] [Google Scholar]
- 24.Dobretsov M, Hastings SL, Sims TJ, Stimers JR, Romanovsky D. Stretch receptor-associated expression of alpha-3 isoform of the Na+, K+-ATPase in rat peripheral nervous system. Neuroscience. 2003;116(4):1069–1080. doi: 10.1016/s0306-4522(02)00922-3. [DOI] [PubMed] [Google Scholar]
- 25.McLain RF, Weinstein JN. Morphometric model of normal rabbit dorsal root ganglia. Spine (Phila Pa 1976) 1993;18(13):1746–1752. doi: 10.1097/00007632-199310000-00005. [DOI] [PubMed] [Google Scholar]
- 26.Kulik G, Sperry ZJ, Ostrowski AK, Bruns TM. DRG Cross Section Analysis. Open Science Framework. 2017 doi: 10.17605/OSF.IO/Q9UJ7. [DOI] [Google Scholar]
- 27.Hanani M. Satellite glial cells in sensory ganglia: from form to function. Brain Res Rev. 2005 Jun;48(3):457–76. doi: 10.1016/j.brainresrev.2004.09.001. [DOI] [PubMed] [Google Scholar]
- 28.Clark PJ, Evans FC. Distance to Nearest Neighbor as a Measure of Spatial Relationships in Populations. Ecology. 1954;35(4):445–453. [Google Scholar]
- 29.Bruns TM, Wagenaar JB, Bauman MJ, Gaunt RA, Weber DJ. Real-time control of hind limb functional electrical stimulation using feedback from dorsal root ganglia recordings. J Neural Eng. 2013;10(2):26020. doi: 10.1088/1741-2560/10/2/026020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Umeda T, Seki K, Sato M, Nishimura Y, Kawato M, Isa T. Population coding of forelimb joint kinematics by peripheral afferents in monkeys. PLoS One. 2012 Oct;7(10):e47749. doi: 10.1371/journal.pone.0047749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Aoyagi Y, Pearson KG, Stein RB, Branner A, Normann RA. Capabilities of a penetrating microelectrode array for recording single units in dorsal root ganglia of the cat. J Neurosci Methods. 2003;128:9–20. doi: 10.1016/s0165-0270(03)00143-2. [DOI] [PubMed] [Google Scholar]
- 32.Khurram A, Ross SE, Sperry ZJ, Ouyang A, Stephan CJ, Jiman AA, Bruns TM. Chronic monitoring of lower urinary tract activity via a sacral dorsal root ganglia interface. J Neural Eng. 2017;14:36027. doi: 10.1088/1741-2552/aa6801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gaunt RA, Bruns TM, Crammond D, Tomycz N, Moossy JJ, Weber DJ. Single- and multi-unit activity recorded from the surface of the dorsal root ganglia with non-penetrating electrode arrays. 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society; 2011; pp. 6713–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sperry ZJ, Seymour JP, Wu F, Ross SE, Kim K, Bentley JT, Yoon E, Bruns TM. Dorsal root ganglia neural recordings with a novel non-penetrating thin-film microelectrode array. Society for Neuroscience Annual Meeting; 2015; p. 540.04. [Google Scholar]
- 35.Gaunt RA, Hokanson JA, Weber DJ. Microstimulation of primary afferent neurons in the L7 dorsal root ganglia using multielectrode arrays in anesthetized cats: thresholds and recruitment properties. J Neural Eng. 2009;6:55009. doi: 10.1088/1741-2560/6/5/055009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fisher LE, Ayers CA, Ciollaro M, Ventura V, Weber DJ, Gaunt RA. Chronic recruitment of primary afferent neurons by microstimulation in the feline dorsal root ganglia. J Neural Eng. 2014 Jun;11(3):36007. doi: 10.1088/1741-2560/11/3/036007. [DOI] [PubMed] [Google Scholar]
- 37.Bruns TM, Weber DJ, Gaunt RA. Microstimulation of afferents in the sacral dorsal root ganglia can evoke reflex bladder activity. Neurourol Urodyn. 2015;34(1):65–71. doi: 10.1002/nau.22514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Deer TR, Grigsby E, Weiner RL, Wilcosky B, Kramer JM. A prospective study of dorsal root ganglion stimulation for the relief of chronic pain. Neuromodulation. 2013;16(1):67–72. doi: 10.1111/ner.12013. [DOI] [PubMed] [Google Scholar]
- 39.Krames ES. The dorsal root ganglion in chronic pain and as a target for neuromodulation: A review. Neuromodulation. 2015;18(1):24–32. doi: 10.1111/ner.12247. [DOI] [PubMed] [Google Scholar]