Measured Pulmonary Arterial Tissue Stiffness is Highly Sensitive to AFM Indenter Dimensions

Abstract

The mechanical properties of pulmonary tissues are important in normal function and the development of diseases such as pulmonary arterial hypertension. Hence it is critical to measure lung tissue micromechanical properties as accurately as possible in order to gain insight into the normal and pathological range of tissue stiffness associated with development, aging and disease processes. In this study, we used atomic force microscopy (AFM) micro-indentation to characterize the Young’s modulus of small human pulmonary arteries (vessel diameter less than 100 μm), and examined the influence of AFM tip geometry and diameter, lung tissue section thickness and the range of working force applied to the sample on the measured modulus. We observed a significant increase of the measured Young’s modulus of pulmonary vessels (one order of magnitude) associated with the use of a pyramidal sharp AFM tips (20 nm radius), compared to two larger spherical tips (1 and 2.5 μm radius) which generated statistically indistinguishable results. The effect of tissue section thickness (ranging from 10 to 50 microns) on the measured elastic modulus was relatively smaller (<1-fold), but resulted in a significant increase in measured elastic modulus for the thinnest sections (10 micron) relative to the thicker (20 and 50 micron) sections. We also found that the measured elastic modulus depends modestly (again <1-fold), but significantly, on the magnitude of force applied, but only on thick (50 micron) and not thin (10 micron) tissue sections. Taken together these results demonstrate a dominant effect of indenter shape/radius on the measured elastic modulus of pulmonary arterial tissues, with lesser effects of tissue thickness and applied force. The results of this study highlight the importance of AFM parameter selection for accurate characterization of pulmonary arterial tissue mechanical properties, and allow for comparison of literature values for lung vessel tissue mechanical properties measured by AFM across a range of indenter and indentation parameters.

Graphical abstract

1. Introduction

The mechanical properties of biological tissues and cells play important roles in normal tissue function and pathological processes (Engler et al., 2006; Handorf et al., 2015; Janmey et al., 2013; Miller, 2016; Nagelkerke et al., 2015). For lung tissue, changes in tissue biomechanics are associated with the initialization and progression of pulmonary diseases including pulmonary arterial hypertension, emphysema and pulmonary fibrosis (Liu et al., 2010; Liu et al, 2016; Suki and Bates, 2008; Suki et al., 2011; Thannickal et al, 2014). For lung tissue engineering and regenerative approaches, generation of scaffolds or tissue constructs with mechanical properties matched to normal lung mechanics at the macro and micro scale is highly desirable (Peterson et al., 2010; Suki, 2014; Tan et al., 2017). Thus understanding of pathological lung remodeling and future efforts at lung regeneration critically depend on accurate assessments of tissue mechanical properties.

At the macro-scale, the mechanical properties of the lungs or lung tissue have traditionally been determined by static volume-pressure measurements or punch indentation of intact lungs (Finucane and Colebatch, 1969; Frank et al., 1957; Lai-Fook and Hyatt, 2000; Mead, 1961), or tensile testing of isolated lung tissue (Andrikakou et al., 2016; Banks et al., 1978; Tanaka et al., 2001; Yuan et al., 2000). More recent efforts to characterize lung tissue mechanical non-invasively by magnetic resonance elastography appear promising, but remain challenging to implement (Goss et al., 2006; Marinelli et al., 2017). The lung itself is a complex structural and mechanical tissue at both macroscopic and microscopic scales, including branching networks of airways and vessels, as well as millions of capillary rich alveoli. Moreover, pathological remodeling of the lung can be limited to distinct anatomical and structural compartments, such as the airways in asthma, or the pulmonary arterial vasculature in pulmonary hypertension. It is thus essential to accurately characterize the local changes in tissue mechanics associated with cellular and extracellular matrix (ECM) remodeling in pathological processes (Fredberg and Kamm, 2006).

At the micro scale, atomic force microscopy (AFM) has become the most used technique to measure the elastic modulus (Young’s modulus) of lung tissue by micro-indentation (Liu and Tschumperlin, 2011; Valero et al., 2016). The micro- or nano-dimension of the AFM tip and the high sensitivity of cantilever deflection make AFM a powerful tool to characterize soft materials, and this can be accomplished under relatively physiological hydration and temperature conditions (Engler et al., 2007), with the important limitation that the technique is itself invasive and requires tissue isolation and cutting to expose the surface which is to be characterized. Considering the relative scarcity of biological samples, especially human pathological tissue samples, this technique has the advantage that it require a small amount of tissue (Valero et al., 2016), and the spatial resolution is capable of mapping micro-scale tissue mechanical properties relevant to tissue remodeling processes.

Recent expansion of AFM application to lung tissue has included several new studies on the mechanical properties of normal and decellularized lung tissue by AFM micro-indentation (Booth et al., 2012; Brown et al., 2013; Liu et al., 2010; Liu and Tschumperlin, 2011; Liu et al., 2016; Melo et al., 2014a; Meng et al., 2015; Shkumatov et al., 2015; Uriarte et al., 2016). Importantly, these new studies have begun to investigate anatomical variations in tissue mechanical properties, including comparisons of airways, vessels, pleura and parenchyma, but have also introduced substantial variation in tissue preparation (such as tissue decellularization), section thickness (10 to 1000 μm), and use of AFM tips with widely varying geometry and size. Wide ranges in reported elastic moduli from these studies (Table 1) raise concerns regarding physiologic validity of the underlying measurements.

Table 1.

Comparison of AFM studies on mechanical properties of lung vascular tissue.

Lung Tissue Sample	Tissue Thickness	Tip Radius and Geometry	Young’s Modulus E (kPa)	References
Normal Lung Tissue
Mice
Pulmonary vessel	250 μm	40 nm - pyramidal	3.293 ± 1.177 #	Meng et al., 2015
Rat
Pulmonary artery	50 μm	2.5 μm - spherical	1.66 ± 0.49 # &	Liu et al., 2016
Human
Pulmonary artery	10 μm	2.5 μm - spherical	5.44 ± 2.96 # &	Liu et al., 2016
Decellularized Lung Tissue
Mice
Tunica intima	10 μm	20 nm - pyramidal	79.3 ± 7.2 *	Melo et al., 2014a
Tunica adventitia			41.1 ± 8.0 *

^#Mean ± standard deviation (SD)

^*Mean ± standard error (SE)

^&Young’s modulus E was calculated from shear modulus G values using the relationship E = 2 × (1 + ν) × G (from Liu et al., 2010)

To consider a specific example, we report in Table 1 the estimated Young’s modulus of lung vascular tissues from several AFM characterization studies. Pulmonary vessel walls from human tissue sections cut at 10 μm thickness and measured with a spherical tip of 2.5 μm radius were estimated at 5.44 kPa elastic modulus (Liu et al., 2016). In rat tissue, AFM experiments on thicker 50 μm sections with the same AFM tip reported a lower elastic modulus value of 1.66 kPa. Meng et al. (2015) assessed mouse pulmonary vessels using even thicker sections (250 μm), but also used a sharp pyramidal tip (40 nm radius). They reported elastic modulus of 3.293 kPa. In striking contrast, Melo et al. (2014a) measured the elastic modulus of pulmonary vessel tunica intima and tunica adventitia in 10 μm sections of decellularized mouse lung tissue using sharp (20 nm radius) AFM tips, and reported an order of magnitude higher elastic modulus values (79.3 and 41.1 kPa, respectively). An important omission from most of these studies is any detail regarding the amount of force applied, and the resulting deformations; given the non-linear mechanical properties of lung tissue (Suki and Bates, 1991; Yuan et al., 2000), variations in applied force and deformations may also importantly impact the reported elastic modulus. Considering the wide variation in reported elastic modulus values above, it is clear that a parametric analysis comparing the effect of the AFM tip and the section thickness on measured elastic properties of pulmonary tissue is called for. A similar comparison by Stolz et al. (2004) contrasting variations in the elastic modulus values of cartilage measured due to differences in experimental AFM parameters lends further support to the need for such a study.

In this context, the goal of this study was to characterize the micromechanical properties of human pulmonary vessels by AFM indentation and investigate whether AFM tip shape and dimension, lung tissue section thickness and the range of applied working force affected the observed elastic modulus. Our results highlight the dominant influence of tip geometry (radius) on measured elastic modulus values, with more modest but important effects of working force and section thickness on measured elastic modulus values. Together these observations help reconcile the widely varying literature reports for elastic properties of pulmonary vessels, and highlight important parameters to consider for accurate measurement and reporting of mechanical properties of the lung, and other soft tissues, by AFM micro-indentation.

2. Materials and methods

2.1. Sample preparation

Human lung tissues obtained from the Pulmonary Hypertension Breakthrough Initiative (PHBI) Research Network were from organ donors whose lungs were not suitable for transplantation (Table 2). Samples were obtained from the PHBI under a protocol approved by the Partners Human Research Committee. The ages of the lung donors ranged between 11 and 60 years. Human tissue samples, were embedded in Tissue-Plus O.C.T. Compound (Optimal Cutting Temperature) (Fisher HealthCare), frozen in dry ice-cooled 2-methylbutane and stored at −80°C. Lung tissue slices were cut by cryosection (CM1860 UV, Leica) at 10, 20 and 50 μm thickness at −23 °C and mounted on poly-L-lysine coated glass slides. To avoid drying of samples, PBS was added to each slice and adequate hydration was maintained throughout AFM characterization. The preparation and the AFM analysis of the samples were done in the same day.

Table 2.

List of lung tissue samples from human donors.

Subject Number	Age (Years)	Sex
1	52	Male
2	56	Female
3	49	Female
4	24	Male
5	60	Female
6	11	Male
7	20	Male
8	41	Male
9	30	Male
10	58	Male
11	26	Male
12	25	Male
13	50	Female

2.2. AFM experiments

Human pulmonary arteries with vessel diameter less than 100 μm were identified using bright field imaging with an optical microscope (X200) (Olympus) (Figure 1). Force curves were acquired on a Catalyst Bioscope atomic force microscope (Bruker) using MIRO 2.0 software (NanoScope 9.1, Bruker). Tip calibration and estimation of the spring constant were conducted by the thermal fluctuation method (Thundat et al., 1994) on glass slides and in PBS just prior to force spectroscopy experiments. Lung tissue samples were maintained in PBS solution at room temperature. The AFM experiments were performed using a ramp size of 10 μm and a rate of 20.6 μm/s (according to experimental instructions of Liu and Tschumperlin (2011)). Following the tip calibration, the AFM system defines automatically a range of working force with a maximum limit (threshold value) which can be applied on the sample during the indentation. These working force range and limit values are dependent of the characteristics of the AFM tip (spring constant k) and the sensitivity S of the photodiode. We defined application of a force equal to the threshold value defined by the AFM system as 100% of the working force. For AFM experiments, unless otherwise noted, force curves were measured using a working force of 97% of the maximum force allowed by the system, with an average magnitude of applied force of approximately 26 nN.

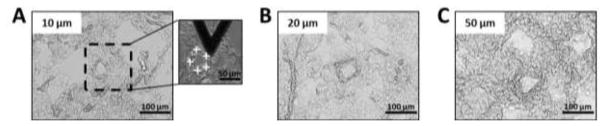
Figure 1.

Bright field images (X200) of human lung tissue cut at (A) 10, (B) 20 and (C) 50 μm section thicknesses and mounted on glass slides. Scale bar = 100 μm. Presence of one pulmonary artery in the lung section. In the inset of (A) is shown an optical image of an AFM tip indenting lung tissue. White crosses indicate the location of the 5 points of measurement onto the vessel wall. Scale bar = 50 μm.

To evaluate the effect of AFM tip size and geometry on Young’s modulus values of pulmonary arteries, lung tissues from 4 donors spanning the age range of our population, included in Table 2 (samples 4, 8, 9 and 10), were analyzed. Lung tissue sections were cut at 10 μm thickness. After the identification of a vessel under optical microscopy, we collected ~30 force curves at different locations around the vessel perimeter, using three different AFM tips:

• Pyramidal DNP-AFM tip (Bruker), cantilever D with a contact radius of 20 nm, a half-angle of 18° and tip height between 2.5 and 8 μm;

• Spherical AFM tip (Novascan) with a 1 μm radius borosilicate sphere;

• Spherical AFM tip (Novascan) with a 2.5 μm radius borosilicate sphere.

The spring constants k of the AFM tips were estimated by the thermal fluctuation method at ~ 138, 90 and 99 pN/nm, respectively (average values). In total, we analyzed one vessel per donor. Each time, the same vessel was assessed by the three AFM tips, with the order of analysis randomized to avoid any bias associated with repeated sampling.

In order to examine the effect of section thickness, mechanical properties of pulmonary arteries were characterized on lung tissue sections cut at 10, 20 and 50 μm thicknesses from all donors (all samples included in Table 2). In total, 44, 40 and 45 vessels were identified and analyzed for lung sections cut respectively at 10, 20 and 50 μm. Between 2 and 6 vessels were analyzed per patient from each tissue section. A total of 5 force curves were performed for each vessel at different locations around the perimeter of the vessel wall (inset of Figure 1A). Spherical AFM tips with a 2.5 μm radius borosilicate sphere were used (Novascan). On average, the spring constant k of the AFM tips was estimated at 110 pN/nm.

During these AFM experiments, we also tested the reproducibility of Young’s modulus values measured at the same location on a vessel wall. For these experiments, 10 force curves were performed consecutively on the same area using the spherical AFM tip (2.5 μm radius) for lung tissue slices cut at 10, 20 and 50 μm thickness.

Finally, we compared the effect of variations in applied force on the measured mechanical properties of vessels. Lung tissues from 3 different donors included in Table 2 (samples 4, 8 and 9) were cut at 10 and 50 μm thickness. Two pulmonary arteries per patient were identified and analyzed by AFM force spectroscopy with a 2.5 μm radius AFM tip (spring constant k ~ 96 pN/nm). Five locations were tested in each vessel (as shown in the inset of Figure 1A). Each time, on the same area of measurement, force curves were performed with working forces of 50, 60, 70, 80, 90 and 97% of the maximum working force allowed by the AFM system. The force was progressively increased from 50 to 97%, corresponding numerically to a range of working force from 11–13 nN to 23–25 nN.

2.3. Data analysis

To quantify the mechanical properties of biological samples by AFM microindentation, the most common approach is to use the Hertz theory to extract the elastic modulus based on the deformation of two bodies in contact under load (Hertz, 1881). For the indentation of an AFM tip into a lung tissue section, this approach is based on several assumptions:

• The material properties of the tip and the tissue are isotropic and homogeneous;

• The tissue section is assumed to be an infinite half-space;

• No adhesion and no friction are present between the tip and the sample;

• The contact geometry is axisymmetric and continuous;

• Small deformations or strains are applied to the tissue.

Several extended models have been developed for alternative tip geometries (Lin et al., 2007; McKee et al., 2011).

For experiments using spherical AFM tips, force curves were analyzed by NanoScope Analysis (Bruker) using the Hertz spherical indentation model (Dimitriadis et al., 2002; Hertz, 1881; Lin et al., 2007; Long et al, 2011; Mahaffy et al., 2000) to determine the elastic modulus E (Young’s modulus) following the relationship:

$$E=\frac{3}{4}\frac{(1-v^2)}{R^{1/2}{\delta }^{3/2}}F$$ Eq. (1)

With R the tip radius, ν the Poisson’s ratio (estimated at 0.4 for lung tissue (Butler et al., 1986)) and where F, the force deflecting the cantilever applied on the sample, is defined by the expression:

$$F=k\mathit{\Delta }d$$ Eq. (2)

With k the spring constant of the cantilever and Δd the cantilever deflection depending on the piezo translation Δz and the sample indentation δ given by the relation:

$$\mathit{\Delta }d=\mathit{\Delta }z-\delta$$ Eq. (3)

The contact radius a for a spherical tip is defined by:

$$a={(R\delta )}^{1/2}$$ Eq. (4)

During the indentation, the projected contact area S_c of the tip in contact with the sample can be calculated with this expression:

$$S_c=2\pi R\delta$$ Eq. (5)

For pyramidal AFM tips, Hertz theory has been extended to four-sided pyramids to extract the elastic modulus by fitting force curves (Table 3) with α the face angle of the pyramidal tip (Alcaraz et al., 2003; Bilodeau, 1992; Rico et al., 2005). However, these models are not available on the Bruker system employed here (or other standard commercial analysis software). Instead, conical Hertz indentation models developed based on Sneddon’s work (Sneddon, 1965) are routinely applied to analyze force curves with pyramidal tips. The elastic modulus using Sneddon approximation is defined as:

$$E=\frac{\pi }{2}\frac{(1-v^2)}{\mathit{tan}\alpha {\delta }^2}F$$ Eq. (6)

Table 3.

Expression of pyramidal Hertz models.

Model	Expression of Elastic Modulus E	Multiplier Factor	References
Sharp pyramidal tip	$\frac{2}{1.4906}\frac{(1-v^2)}{tan\alpha {\delta }^2}\mathrm{F}$	$\frac{2}{1.4906}=1.341$	Bilodeau, 1992
Sharp pyramidal (developed from Bilodeau, 1992)	$\frac{4}{3}\frac{(1-v^2)}{tan\alpha {\delta }^2}\mathrm{F}$	$\frac{4}{3}=1.333$	Alcaraz et al., 2003
Blunted pyramidal tip	$\sqrt{2}\frac{(1-v^2)}{tan\alpha {\delta }^2}\mathrm{F}$	$\sqrt{2}=1.414$	Rico et al., 2005

With α the half-angle of the tip (estimated at 18° for DNP tip).

The expression for elastic modulus in this function of the applied force is close to the pyramidal Elasticity-Force relationship (Table 3) with a similar multiplier factor (for conical model, multiplier factor is of 1.571 (= π/2)). Radmacher et al. (1995) have previously employed this method to fit force curves performed on gelatin with pyramidal indenters.

The contact radius a and the projected contact area S_c for a pyramidal AFM tip during the indentation are given by the relationships:

$$a=\frac{\delta tan\alpha }{\sqrt{2}}$$ Eq. (7)

With α the half-angle of the tip (estimated at 18° for DNP tip), and:

$$S_c=n\frac{(a\ast h)}{2}$$ Eq. (8)

With n the number of sides of the pyramidal base, n = 4 for four-sided pyramidal tip (DNP AFM tip), a the contact radius considered as the side of the pyramid base and h the pyramid apothem given by the expression:

$$h=\sqrt{{\delta }^2+{\left(\frac{a}{2}\right)}^2}$$ Eq. (9)

2.4. Statistical analysis

Data are presented as mean ± standard deviation (SD). Statistical analysis was performed using Prism software (GraphPad Software, Version 7). Data groups were compared using one-way analysis of variance (ANOVA), Tukey’s post-hoc test and Mann-Whitney test with an accepted statistical significance at p < 0.05.

3. Results

3.1. Identification of pulmonary arteries

To characterize the mechanical properties of human pulmonary arterial vessels, it is important to identify them unambiguously under the optical microscope. We focused our study on micro-vessels with a diameter of less than 100 μm. Representative optical images (X200) of lung tissue sections cut at 10, 20 and 50 μm thicknesses and mounted on poly-L-lysine coated glass slides are shown in Figure 1. Small vessels were identified by their characteristic round shape and wall thickness, and were observed embedded within surrounding parenchymal tissue. In the two thinner section sizes (10 and 20 μm thickness), it was relatively easy to identify vessels based on their characteristic features within the relatively thin sections. For the 50 μm thick sections it was somewhat more challenging based on the three-dimensional complexity of lung tissue, but positive identification of vessels remained straightforward. Nevertheless, certainty regarding AFM tip location within the vessel wall necessarily suffers with thicker sections due to greater ambiguity of wall feature identification in thick sections; such ambiguity could be improved in future studies by coupling AFM to confocal fluorescence imaging to focus on vessel features at the AFM contact surface. Previously, we have described immunofluorescence-based methods to visualize vessels (e.g. anti-CD31) in parallel with AFM experiments (Liu et al., 2016), which may also assist in orienting the AFM contact surface to the vessel wall in thick sections.

3.2. Influence of AFM tip geometry and size

To evaluate the effect of the geometry and size of the AFM tip on the Young’s modulus of human pulmonary arteries, we performed AFM indentation on 4 vessels with three different AFM tips: one pyramidal tip with a radius at 20 nm (half-open angle of 18°) and two spherical tips at 1 and 2.5 μm radius. Each vessel was analyzed by the three probes. Lung sections came from 4 donors (in Table 2) (one vessel per donor). The pyramidal tip force curves were analyzed with Sneddon’s model, while the spherical tip force curves were analyzed with Hertz’s model, as detailed above.

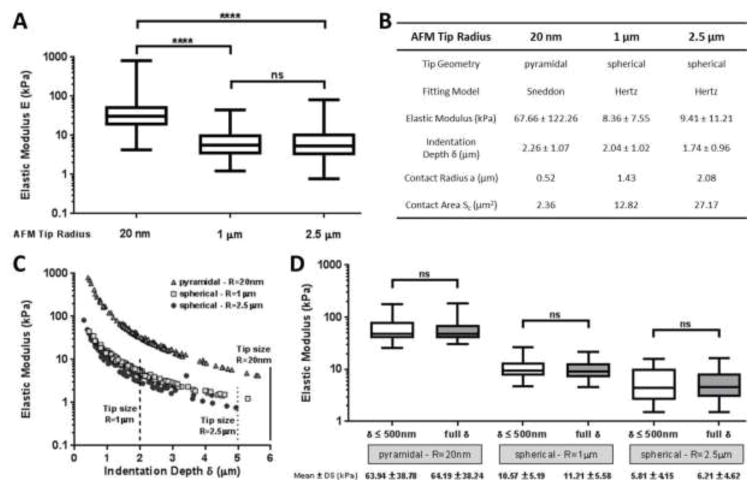
The Young’s modulus of micro-vessels measured using the pyramidal tip geometry (E = 67.66 ± 122.26 kPa with a range of 4.24–804.00 kPa) was significantly higher (p < 0.0001) than values observed using either 1 μm (E = 8.36 ± 7.55 kPa with a range of 1.24–45.20 kPa) or 2.5 μm (E = 9.41 ± 11.21 kPa with a range of 0.76–82.30 kPa) radius spherical tips (Figure 2A). Statistically, there was no difference between the elastic values observed using the two spherical tip sizes, indicating the relative insensitivity of elastic modulus values to tip size within this range. We noticed a wide stiffness distribution, particularly with the pyramidal tip, likely reflecting the structural heterogeneity of the vascular wall (Jeffery and Morrel, 2002; Stolz et al., 2004; Townsley, 2013) and the size-dependent contact of the smaller pyramidal tip with smaller and more varied micromechanical elements (e.g. extracellular matrix fibers) within the tissue.

Figure 2.

(A) Elastic modulus of human pulmonary vessels estimated by AFM indentation performed with three different AFM tips: sharp pyramidal tip at 20 nm radius (half-open angle of 18°), spherical tip at 1 μm radius and spherical tip with a radius of 2.5 μm. Force curves were performed on 4 vessels from 4 different lung donors (one vessel per donor). (B) Mean ± SD of elastic modulus determined by fitting force curves with Sneddon’s (for pyramidal AFM tip) and Hertz’s (for spherical AFM tip) models. Contact radii a and areas S_c were calculated from the equations (4) and (5) for spherical tips and (7) and (8) for pyramidal tip with the mean value of the indentation depth δ. (C) Elastic modulus extracted from force curves performed with three different AFM tips on human pulmonary arteries, plotted as a function of the indentation depth. The size of the AFM tips is indicated to compare with the indentation depth values range. For the pyramidal tip, the tip height is estimated as 6 μm. (D) Elastic modulus estimated by fitting force curves considering large (entire curve) or limited (δ ≤ 500 nm) indentation depths. Analysis shown for all curves from one sample (from Table 2). Comparison of mean values for each tip was conducted using a Mann-Whitney test for each of the three AFM tips.

The contact radius a and the projected contact area S_c were calculated by using the relationships (7) and (8) for the pyramidal AFM tip and (4) and (5) for the spherical tips with the mean of the indentation depths extracted from all the force curves with the equations (1) (Hertz’s model) and (6) (Sneddon’s model) (Figure 2B). During the indentation, the contact area between the tip and the sample was ~5 and ~11 times smaller for the pyramidal tip compared to the spherical tips (1 μm and 2.5 μm radius, respectively), while the elastic modulus was ~7-times higher for the pyramidal tip, consistent with sharp pyramidal tips substantially overestimating the Young’s modulus by nearly an order of magnitude.

One potential concern with these measurements is that indentation depth δ was quite large, and even approached the dimensions of the AFM tip, clearly violating an assumption of the Hertz model. As shown in Figure 2B, δ is lowest for the 2.5 μm radius spherical AFM tip (1.74 ± 0.96 μm), while both the pyramidal (2.26 ± 0.96 μm) and the 1 μm radius spherical tip (2.04 ± 1.02 μm) resulted in slightly larger δ values. According to Bruker, DNP tips have a height estimated between 2.5 and 8 μm, quite close at the low end to the average δ, while δ for the 1 μm radius spherical tip slightly exceeds the tip diameter (2 μm) on average. In Figure 2C, the Young’s modulus values are shown as a function of the indentation depth for the three AFM tips. Clearly, for the 1 μm radius spherical tip, the majority of the stiffness results were computed for large indentations relative to tip size (2 μm diameter). Large indentations with smaller AFM tips risk contact of the AFM cantilever during indentation, which would contribute to experimental errors (Harris and Charras, 2011). The use of larger AFM tips (e.g. 2.5 μm radius) avoids this problem, and as discussed below, limiting the applied force and resulting indentation would also mitigate against the risk of cantilever contact. Even without the concern regarding indentation depth relative to tip size, the above moduli were computed using indentations larger than 1.70 μm on average (Figure 2B) for the three AFM tips, violating the small deformation assumption in the Hertz model. To assess the effect of large vs smaller indentations, we compared moduli computed using the original large indentations (entire force curve) to those computed by fitting with Hertz model using only the first 500 nm of the indentation data for each curve (δ ≤ 500 nm) from one donor (from Table 2). In Figure 2D, we compared these moduli computed by fitting the full and limited indentation data by Mann-Whitney test for the three AFM tips, and found that the Young’s moduli exhibited no statistically significant difference for any of the three tips across these two analyses. Therefore, we conclude that while large indentations are not ideal, and violate an assumption of the Hertz contact model, their use does not fundamentally compromise the ability to extract meaningful Young’s moduli results or compare the results across the three tips.

3.3. Influence of tissue thickness

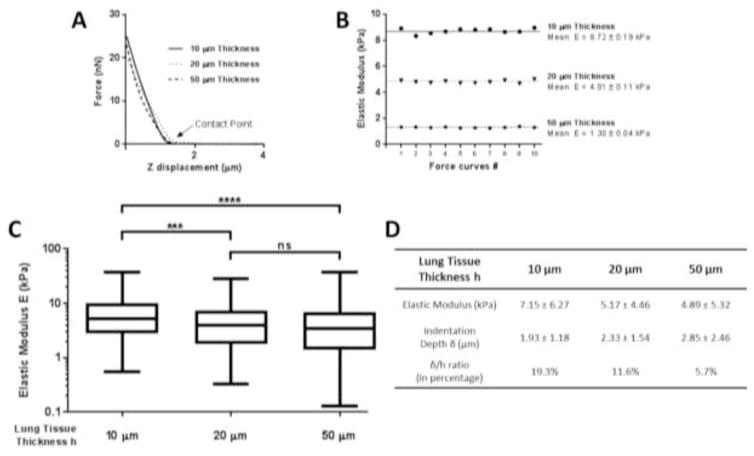
Using a large spherical AFM tip (2.5 μm radius), we analyzed the impact of the lung tissue section thickness on the Young’s modulus values of pulmonary arteries. AFM indentation was performed on lung tissue sections cut at 10, 20 and 50 μm thickness from all lung donors indicated in Table 2. Force curves were collected around the perimeter of the vessel wall (5 force curves per vessel as shown in Figure 1A). Figure 3A illustrates examples of typical force curves collected from vessels cut at each of the three section thickness values (extend curve).

Figure 3.

(A) Representative force curves (force - z displacement) obtained on pulmonary arteries at different lung tissue thicknesses. (B) Dispersion of elastic values for 10 force curves taken at the same location. (C) Elastic modulus of human pulmonary arteries from force curves performed on lung tissue sections cut at 10, 20 and 50 μm thicknesses. (D) Mean ± SD of Young’s modulus of micro vessels. Mean ± SD of indentation depth calculated from equation (1) for all the force curves.

To test the variability of repeated measurements, we also collected 10 consecutive force curves at one location on the vessel wall for lung tissues cut at each thickness (Figure 3B). No significant difference of elastic values was observed between these consecutive measurements. The coefficient of variation (CoV) was lower than 0.1. The small variations of the modulus (standard deviation less than 10%) upon repeated sampling are likely due to the curve analysis and do not reflect tissue damage or permanent deformation (Rico et al., 2005). These results establish that a single force curve is sufficient to measure the elastic modulus at each tissue location, and demonstrate the high repeatability of elastic modulus measurements and the absence of permanent deformation or altered mechanical properties caused by indentation.

Figure 3C–D reports the elastic modulus of human pulmonary arteries measured from 10, 20 and 50 μm thick sections from all donor samples. For 50 μm thick sections, the observed elastic modulus of vessels was lowest (4.89 ± 5.32 kPa with a range of 0.13–37.8 kPa, 200 measurements for 40 vessels), and was statistically indistinguishable from the values observed from 20 μm thick sections (5.17 ± 4.46 kPa with a range of 0.32–28.6 kPa, 225 measurements for 45 vessels). In contrast, the observed elastic modulus values on 10 μm thick sections were the highest (7.15 ± 6.27 kPa with a range of 0.54–37 kPa, 219 measurements for 44 vessels), and were significantly elevated relative to values observed from both 20 and 50 μm thick sections (P < 0.001). These results demonstrate a modest but significant increase in observed elastic modulus as section thickness decreases. We noted also a large variability of elastic modulus values (three decade range), with the largest occurring on the thickest sections. Rico et al. (2005) previously reported that a large standard deviation in AFM measurements can reflect the heterogeneity of the sample, and as discussed above, thickness-dependent variations may also reflect the relative lack of precision in positioning the AFM tip relative to the vessel wall on the thickest tissue sections.

From Eq. (1) (spherical Hertz’s model), we computed the indentation depth δ of the AFM tip into lung tissue for all the force curves we performed. We indicated in Figure 3D the mean value and standard deviation of δ. The indentation is deeper for 50 μm thickness lung tissue with a value of 2.85 μm. The smallest value is for tissues cut at 10 μm thickness (1.93 μm). To estimate the proportion of tissue slice indented during the elasticity measurement, δ/h ratio was calculated. The indentation by the spherical AFM tip represents a proportion of 19.3%, 11.6% and 5.7% of the lung tissue slice cut at 10, 20 and 50 μm thicknesses respectively. Gavara and Chadwick (2012) reported the elastic modulus is higher for thin samples because of the influence of the underlying hard substrate. For a δ/h ratio greater than 10%, the indentation can be considered too deep, thereby violating one of the assumptions of the Hertz model (Dimitriadis et al., 2002; Mahaffy et al., 2000). The large displacements relative to tissue thickness on 10 μm slices, and to a lesser extent on 20 μm slices, exceed this limit, and may explain why the Young’s modulus is higher on 10 μm slices and significantly different from the results at 20 and 50 μm thickness. While Radmacher et al. (1995) described a changing slope of the force curve, reflecting the presence of a rigid underlying substrate apparent during deep indentation, such a change was not clearly observed on our experimental curves (Figure 3A). Nevertheless, the modest increase in measured elastic modulus on tissue of decreasing thickness is consistent with contributions of the underlying rigid substrate, in agreement with the increasing violation of this assumption of the Hertz model with decreasing section thickness.

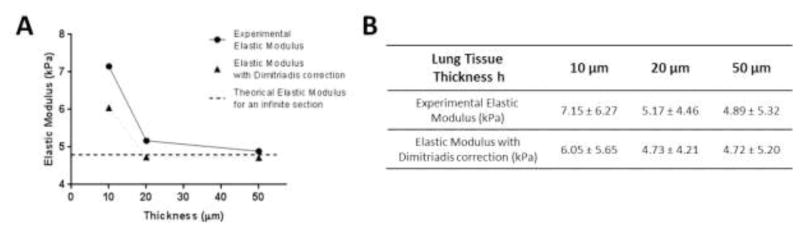
Dimitriadis et al. (2002) developed a correction factor for the Hertz’s model for finite thickness section samples. In Figure 4, we applied this correction model to our experimental results, considering lung tissue section bonded to the glass slide and no friction between the tip and sample (correction model assumption). The numerical values are reported in Figure 4B. The application of this correction reduces the elastic values in particular for 10 μm thickness (thinner section), but the corrected value is still higher (around 25% higher) than an idealized Young’s modulus for an infinite section extrapolated from our experimental and corrected results at 50 μm thickness. This lack of full correction may indicate that the finite section effect is not the only reason why elasticity is significantly higher for thin tissue sections. Hertz and Dimitriadis models assume homogeneity and isotropy of samples, however pulmonary vessels are composed of different cell layers and are described as anisotropic (Dobrin, 1978; Kohn et al., 2015); variations in the influence of tissue anisotropy may also contribute to the effect of tissue thickness of the measured elastic modulus. It is important to note that while our results indicate that thin tissue sections modestly affect measured elastic modulus, the effect size is small relative to that detailed above as a function of AFM tip size.

Figure 4.

(A) Elasticity of pulmonary vessels measured by AFM indentation. Correction factor developed by Dimitriadis et al. (2002) applied on the experimental results. Mean ± SD are presented in (B). Lung tissue was considered bonded to the glass slide with no adhesion between the tip and the sample.

3.4. Influence of working force

For AFM indentation experiments, the working force is another potentially critical parameter. For low loading force, the experimental noise may be high and lead to misidentification of the contact point, a potentially major source of error (Harry and Charras, 2011; Rico et al., 2005; Soucy et al., 2011). Applying too high of a loading force on the sample may induce a large indentation which can damage the tissue and cause experimental errors (large strains, underlying hard substrate) (Gavara and Chadwick, 2012; Mahaffy et al., 2000).

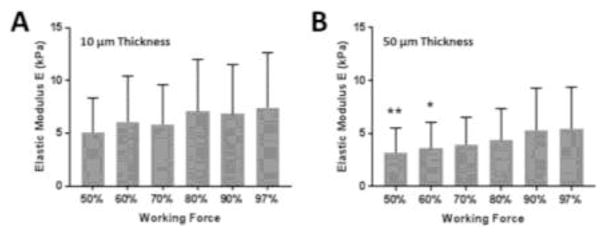
To understand the influence of the working force on the measured Young’s modulus of pulmonary arteries, we performed force curves on pulmonary arteries with different values of working force (Figure 5). We assessed 6 vessels (2 per donor, from 3 donors in Table 2) from lung tissue sections cut at 10 (Figure 5A) and 50 μm (Figure 5B) thicknesses. Five different locations around the perimeter of each vessel were tested as shown on Figure 1A. For each area, force curves were performed with working force progressively increasing from 50 to 97% of the maximum working force (threshold, determined automatically by the AFM system and depending on the calibration of the AFM tip). In total, 30 elastic modulus values were collected for each working force value, with statistical comparisons made to E values at 97% as a reference by ANOVA.

Figure 5.

Elastic modulus of pulmonary arteries from force curves performed at different working forces. Lung tissue sections cut at 10 μm (A) and 50 μm (B) thicknesses. E values at 97% were used as a reference for statistical comparisons by ANOVA (p < 0.05).

For both section thickness values, the measured elastic modulus increased progressively with the elevation of the working force: from 5.10 kPa at 50% to 7.43 kPa at 97% for the thinnest section and from 3.21 kPa at 50% to 5.44 kPa at 97% for 50 μm thickness (mean values). Statistically, on 10 μm thick sections, there was no significant difference of elasticity across the chosen working force values used to perform force curves. However, for thicker 50 μm sections, E values were significantly lower at 50 and 60% of maximum loading force compared to results at 97% of maximum loading. These results demonstrate a modest but significant dependence of measured elastic modulus on the applied working force. The relatively larger effect of applied force on thicker sections suggests that this effect is not a reflection of the underlying rigid substrate, which would be more pronounced on thin sections, but rather reflects the non-linear properties of lung tissue (Suki and Bates, 1991; Yuan et al., 2000), as well as the underlying inhomogeneity in the mechanical properties of micro-vessels (Sokolov et al., 2013).

4. Discussion

In this work, we characterized the micro-mechanical properties of small human pulmonary arteries by AFM micro-indentation, and identified a dominant influence of AFM tip geometry (radius) on measured elastic modulus, with additional modest but significant effects of section thickness and AFM working force.

Our results highlight the observation that sharp AFM tips (pyramidal geometry) overestimate the Young’s modulus of pulmonary vessels, in agreement with prior studies reporting similar observations on cells and polyacrylamide hydrogels (Dimitriadis et al., 2002; Harris and Charras, 2011; Rico et al., 2005). Dimitriadias et al. (2002) explored several explanations for why a sharp tip is inappropriate for thin and soft samples. Given a small tip radius size, they argued that an error in the estimated radius of curvature of the tip may induce a large error in E, particularly for thin samples. Moreover, at these nanometric dimensions, the tip can penetrate and probe inside the sample which may cause unpredictable results, in particular if the sample is inhomogeneous, as is common for biological samples. Stolz et al. (2004) described stiffness variations for sharp tips due to different arrangements of collagen fibers within the complex cartilage structure. Similarly, the wall of pulmonary vessels has a heterogeneous structure and composition (Jeffery and Morrel, 2002; Townsley, 2013), hence the elastic value for sharp pyramidal tips may reflect the interaction of the AFM tip with biological elements of the vascular wall such as extracellular matrix compounds and not the global micromechanical properties of the vessel. Rico et al. (2005) also highlighted the potential role of the tilt of the AFM tip as an explanation for the increased elastic modulus for measured with a sharp pyramidal tip. Generally, to avoid having the cantilever touch the sample, the AFM tip (cantilever and probe) is placed in the AFM tip holder so that the tip is tilted with an angle of 10–20°. But during indentation, because of this inclination, each face of the pyramid doesn’t contribute equally to the total force applied to the sample, leading to a potential overestimation of E. Thus while the advantages of sharp tips are theoretically attractive, including better resolution for probing smaller cellular and extracellular matrix features (Engler et al., 2007; Jorba et al., 2016; Luque et al., 2013; Melo et al., 2014a; Melo et al., 2014b; Stolz et al., 2004;), in practice the Young’s modulus determined with larger spherical probes is much less sensitive to these errors, and as has been noted in several studies, spherical probes provide E values much closer to macroscopic results for soft biological tissues (Dimitriadis et al., 2002; Stolz et al., 2004; Thomas et al., 2013). Spherical tips also have the advantage of minimizing strain, better fulfilling the assumption of small strains in Hertz’s model (Mahaffy et al., 2000). Importantly, our results demonstrated no significant difference in measured micro-vessel elasticity for spherical tips at 1 and 2.5 μm radius, in agreement with prior observations of Dimitriadis et al. (2002) using 2 and 5 μm radius probes to characterize soft hydrogels, demonstrating insensitivity of AFM elastic modulus values to spherical probe size in this range. One remaining caveat with spherical probes is that the indentation depth and the size of the sphere must be considered in order to avoid contact between the sample and cantilever (Harris and Charras, 2011), but this is a simple precaution to take in practice to avoid such errors.

A second, though less dramatic, effect on the elastic modulus was found relating to the section thickness of analyzed tissue. As section thickness decreased, measured elastic modulus values increased. These results are consistent with the observations of Liu et al. (2016) on pulmonary vessels. Such observations are predictable, as with decreasing section thickness the assumptions of the Hertz model of a semi-infinite sample thickness is increasingly violated, and the influence of the underlying rigid substrate is increasingly observed (Gavara and Chadwick, 2012; Mahaffy et al., 2000). However, it should be noted that to characterize micro-anatomical variations in the elasticity of lung tissue, it is important to accurately identify the structural components of lung to be studied in tissue sections. Under the optical microscope, micro-vessels (diameter less than 100 μm) are easily recognizable by their shape and architecture when using thin sections (10 or 20 μm) (Jorba et al., 2016). At larger thickness (such as 50 μm), it becomes more difficult to recognize vessels, and to accurately contact the vessel wall with the AFM tip. The larger range of elastic modulus values observed for 50 μm sections (standard deviation 5.32 kPa) may reflect the loss of precision in accurately identifying areas of interest on the vessel wall. Thus it is clear that section thickness selection reflects a tradeoff between optical quality for identification of anatomical targets, and accurate mechanical assessments with minimal influence of the underlying rigid substrate. In our studies, 20 μm sections represented a good compromise, with no statistical difference observed from thicker sections, but sufficient optical quality to easily identify anatomical features of interest.

An additional important point to consider is that the effects of section thickness are inextricably linked to the depth of AFM indentation, as it is recommended to indent soft tissue at indentation depths that maintain a δ/h ratio lower than 10%, in compliance with the small strain assumption in the Hertz model (Mahaffy et al., 2000). When we modulated the applied working force we observed a small but systematic effect on measured elastic modulus. These results likely reflect, at least in part, the influence of the underlying rigid substrate, as δ/h is reduced with decreasing applied forces. However, we also noted that the influence of applied force was still apparent, and indeed reached statistical significance for the most extreme differences in applied force on 50 μm thick sections, where the δ/h values were within the acceptable range (<10%) throughout. This intriguing result suggests that the non-linear strain-stiffening properties of lung tissue (Suki and Bates, 1991; Yuan et al., 2000) influence the reported elastic modulus values. Thus careful consideration and reporting of applied working force and resulting indentation depths should be included in future studies for comparison of results across investigations. Given the apparent influence of large indentations and the desire to minimize δ/h, it would appear desirable to minimize applied working force for AFM experiments. However, it is also important to recognize that determination of the contact point during force curve analysis is essential to accuracy, and is increasingly challenging as lower working forces are applied and noise becomes more predominant. Thus errors associated with contact point mis-identification can introduce large errors in reported Young’s modulus values (Engler et al., 2007; Rico et al., 2005). Once again, a tradeoff is needed to select an appropriate working force. In our studies, working force values of 21 nN (80 % max working force) represented a good compromise allowing unambiguous contact point identification, potentially serving as a useful benchmark for future studies.

In comparing our findings to those in the literature, we note that Melo et al. (2014a) used a sharp tip and a thin tissue slice to determine the Young’s modulus of decellularized lung vessels. While the modulus values reported by Melo et al. (79.3 ± 7.2 kPa for tunica intima and 41.1 ± 8.0 kPa for tunica adventitia (Table 1), differ substantially from our measurements with larger spherical tips, they are in good agreement with our results using a sharp pyramidal indenter (67 ± 122.26 kPa, Figure 2), helping to resolve the apparent differences in lung vessel stiffness values reported in prior work (Table 1). One additional difference between our study and that of Melo et al. is that their tissues were decellularized prior to analysis. Prior work by this group Melo et al. (2014b) demonstrated that the specific decellularization process affects the elastic modulus tissues, thus it is important to recognize that the additional variable of tissue preparation (frozen intact tissue versus decellularized) is not identical between the two studies and may also account for some of the observed differences. In support of this concept, it is notable that the mechanical properties of acellular ECM tissues are stiffer than normal lung tissue (Gimenez et al., 2017; Ott et al., 2010), though the explanation for this effect remains to be determined. In contrast to these comparable results with sharp tips, Meng et al. (2015) reported similar elastic modulus values to those of Liu et al. (2016) and our current results using larger spherical tips, but did so with the use of a sharp pyramidal tip (40 nm radius) and relatively thick tissue section. Their elastic modulus values are not comparable with our current observations with sharp tips, and may reflect additional parametric variations from our study, including the use of QNM (Quantitative NanoMechanical property) mode (Bruker) to estimate the elasticity of lung tissue using much higher loading rates and retraction force curves. Additional comparisons of this approach with the quasi-static approach employed in our study seem warranted to resolve these differences in future work.

As a final point for consideration, we note that the pulmonary vascular wall is structured in multiple cell layers (Jeffery and Morrel, 2002; Townsley, 2013). For larger vessels, the elasticity of these layers has been determined by tactile mapping system (Oie et al., 2009) and AFM indentation (Melo et al., 2014a). However, for diameters less than 100 μm, the identification of cell layers is more challenging, and potentially complicates both the identification of regions of interest, and interpretation of micro-indentation measurements using AFM. Future efforts using fluorescent markers may improve our ability to recognize and separately analyze the different structural layers of pulmonary arteries (Liu et al., 2016). With the current approach, the inhomogeneity and anisotropy of the vascular wall is a clear limitation, as it violates assumptions inherent in the Hertz model and may introduce errors into the estimates of Young’s modulus. One approach to this complication identified in the literature (Valero et al. 2016) is the use of finite element simulation to study the response of different materials (soft materials with elastic, isotropic hyperelastic and anisotropic hyperelastic properties) using AFM nano-indentation. Future efforts in this direction could lead to more accurate micro-mechanical characterization incorporating correction factors for thin samples, tissue anisotropy and complex layered structure of lung vessels (hyperelasticity of arterial layers modeling by Gasser et al. (2006)).

5. Conclusion

In this study, we compared the effects of indenter dimensions, tissue thickness and applied working force on the Young’s modulus of human pulmonary small arteries measured by AFM micro-indentation. Our results highlight that micron scale-spherical AFM tips are preferred to sharp pyramidal AFM tips in order to avoid overestimation of Young’s modulus. Furthermore, compromises must be made between the capacity to accurately identify lung structures, supported by thinner sections, and using thicker sections which better comply with the assumptions of the Hertz model. Similarly, the applied working force has to be adjusted to compromise between the desire to minimize strains, while also avoiding errors associated with contact point mis-identification. Taken together, our study helps resolve differences in previously reported lung tissue stiffness measurements, and serves as a reference for rational selection of relevant AFM parameters for accurate characterization of the mechanical properties of the lung and other soft biological tissues.

Highlights.

• Stiffness of human pulmonary arteries was characterized by AFM micro-indentation.

• Comparison of effects of AFM tip geometry on measured elastic modulus.

• Sharp AFM tips significantly overestimate the elastic modulus of pulmonary vessels.

• Comparison of effects of tissue thickness and working force on measured E modulus.

• Tissue thickness and working force: smaller but significant effects on E modulus.